правила, примеры, решения, как умножать десятичные дроби

В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Умножение десятичных дробей: общие принципы

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Пример 1

Вычислите произведение 1,5 и 0,75.

Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.

Ответ: 1,125.

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Пример 2

Умножьте одну периодическую дробь 0,(3) на другую 2,(36).

Решение

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611

Следовательно, 0,(3)·2,(36)=13·2611=2633.

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0,(3)·2,(36)=0,(78).

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Пример 3

Вычислите произведение 5,382… и 0,2.

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.

Ответ: 5,382…·0,2≈1,076. 

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

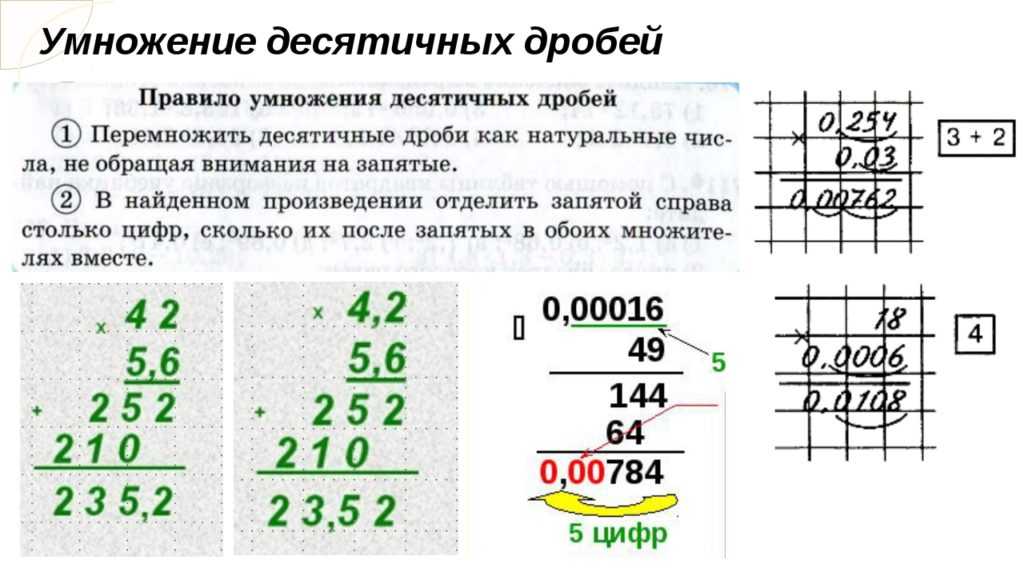
1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63,37 и 0,12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3,37·0,12=7,6044.

Пример 5

Подсчитайте, сколько будет 3,2601 умножить на 0,0254.

Решение 

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3,2601·0,0254=0,08280654.

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Определение 2

Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.

Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.

Пример 6

Умножьте 9,4 на 0,0001.

Решение

Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.

Ответ: 0,00094.

Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.

Как перемножить десятичную дробь с натуральным числом

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Пример 7

Подсчитайте, сколько будет 15·2,27.

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Ответ: 15·2,27=34,05.

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Пример 8

Вычислите произведение 0,(42) и 22.

Решение

Приведем периодическую дробь к виду обыкновенной.

0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433

Далее умножаем:

0,42·22=1433·22=14·223=283=913

Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).

Ответ: 0,(42)·22=9,(3).

Бесконечные дроби перед подсчетами надо предварительно округлить.

Пример 9

Вычислите, сколько будет 4·2,145….

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

4·2,145…≈4·2,15=8,60. 

Ответ: 4·2,145…≈8,60.

Как умножить десятичную дробь на 1000, 100, 10 и др

Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:

Определение 3

Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули.

Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.

Покажем на примере, как именно это делать.

Пример 10

Выполните умножение 100 и 0,0783.

Решение

Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83​​​​​Нули, стоящие слева, можно отбросить и записать результат как 7,38.

Ответ: 0,0783·100=7,83.

Пример 11

Умножьте 0,02 на 10 тысяч.

Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.

Ответ: 0,02·10 000=200.

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Пример 12

Вычислите произведение 5,32(672) на 1 000.

Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).

Ответ: 5,32(672)·1 000=5 326,(726).

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Как перемножить десятичную дробь с обыкновенной или со смешанным числом

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Пример 13

Умножьте 0,4 на 356

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.

Далее считаем: 0,4·356=25·236=2315=1815.

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).

Ответ: 1,5(3).

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Пример 14

Вычислите произведение 3,5678…·23

Решение 

Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.

Ответ: 3,5678…·23≈2,380

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

правила, примеры, решения, как умножать десятичные дроби

В этой статье мы рассмотрим такое действие, как умножение десятичных дробей. Начнем с формулировки общих принципов, далее покажем, как умножить одну десятичную дробь на другую и рассмотрим метод умножения столбиком. Все определения будут проиллюстрированы примерами. Потом мы разберем, как правильно умножить десятичные дроби на обыкновенные, а также на смешанные и натуральные числа (в том числе 100, 10 и др.)

В рамках этого материала мы коснемся только правил умножения положительных дробей. Случаи с отрицательными разобраны отдельно в статьях об умножении рациональных и действительных чисел.

Умножение десятичных дробей: общие принципы

Сформулируем общие принципы, которых надо придерживаться при решении задач на умножение десятичных дробей.

Вспомним для начала, что десятичные дроби есть не что иное, как особая форма записи обыкновенных дробей, следовательно, процесс их умножения можно свести к аналогичному для дробей обыкновенных. Это правило работает и для конечных, и для бесконечных дробей: после их перевода в обыкновенные с ними легко выполнять умножение по уже изученным нами правилам.

Посмотрим, как решаются такие задачи.

Пример 1

Вычислите произведение 1,5 и 0,75.

Решение: для начала заменим десятичные дроби на обыкновенные. Мы знаем, что 0,75 – это 75/100, а 1,5 – это 1510. Мы можем сократить дробь и произвести выделение целой части. Полученный результат 1251000 мы запишем как 1,125.

Ответ: 1,125.

Мы можем использовать метод подсчета столбиком, как и для натуральных чисел.

Пример 2

Умножьте одну периодическую дробь 0,(3) на другую 2,(36).

Решение

Для начала приведем исходные дроби к обыкновенным. У нас получится:

0,(3)=0,3+0,03+0,003+0,003+…=0,31-0,1=0,39=39=132,(36)=2+0,36+0,0036+…=2+0,361-0,01=2+3699=2+411=2411=2611

Следовательно, 0,(3)·2,(36)=13·2611=2633.

Полученную в итоге обыкновенную дробь можно привести к десятичному виду, разделив числитель на знаменатель в столбик:

Ответ: 0,(3)·2,(36)=0,(78).

Если у нас в условии задачи стоят бесконечные непериодические дроби, то нужно выполнить их предварительное округление (см. статью об округлении чисел, если вы забыли, как это делается). После этого можно производить действие умножения с уже округленными десятичными дробями. Приведем пример.

Пример 3

Вычислите произведение 5,382… и 0,2.

Решение

У нас в задаче есть бесконечная дробь, которую нужно предварительно округлить до сотых. Получится, что 5,382…≈5,38. Второй множитель округлять до сотых смысла не имеет. Теперь можно подсчитать нужное произведение и записать ответ: 5,38·0,2=538100·210=1 0761000=1,076.

Ответ: 5,382…·0,2≈1,076. 

Как умножать десятичные дроби столбиком

Метод подсчета столбиком можно применять не только для натуральных чисел. Если у нас есть десятичные дроби, мы можем умножить их точно таким же образом. Выведем правило:

Определение 1

Умножение десятичных дробей столбиком выполняется в 2 шага:

1. Выполняем умножение столбиком, не обращая внимание на запятые.

2. Ставим в итоговом числе десятичную запятую, отделяя ей столько цифр с правой стороны, сколько оба множителя содержат десятичных знаков вместе. Если в результате не хватает для этого цифр, дописываем слева нули.

Разберем примеры таких расчетов на практике.

Пример 4

Умножьте десятичные дроби 63,37 и 0,12 столбиком.

Решение

Первым делом выполним умножение чисел, игнорируя десятичные запятые.

Теперь нам надо поставить запятую на нужное место. Она будет отделять четыре цифры с правой стороны, поскольку сумма десятичных знаков в обоих множителях равна 4. Дописывать нули не придется, т.к. знаков достаточно:

Ответ: 3,37·0,12=7,6044.

Пример 5

Подсчитайте, сколько будет 3,2601 умножить на 0,0254.

Решение 

Считаем без учета запятых. Получаем следующее число:

Мы будем ставить запятую, отделяющую 8 цифр с правой стороны, ведь исходные дроби вместе имеют 8 знаков после запятой. Но в нашем результате всего семь цифр, и нам не обойтись без дополнительных нулей:

Ответ: 3,2601·0,0254=0,08280654.

Как умножить десятичную дробь на 0,001, 0,01, 01, и т.д

Умножать десятичные дроби на такие числа приходится часто, поэтому важно уметь делать это быстро и точно. Запишем особое правило, которым мы будем пользоваться при таком умножении:

Определение 2

Если мы умножим десятичную дробь на 0,1, 0,01 и т.д., в итоге получится число, похожее на исходную дробь, запятая которого перенесена влево на нужное количество знаков. При нехватке цифр для переноса нужно дописывать нули слева.

Так, для умножения 45,34 на 0,1 надо перенести в исходной десятичной дроби запятую на один знак. У нас получится в итоге 4,534.

Пример 6

Умножьте 9,4 на 0,0001.

Решение

Нам придется переносить запятую на четыре знака по количеству нулей во втором множителе, но цифр в первом для этого не хватит. Приписываем необходимые нули и получаем, что 9,4·0,0001=0,00094.

Ответ: 0,00094.

Для бесконечных десятичных дробей мы пользуемся тем же правилом. Так, к примеру, 0,(18)·0,01=0,00(18) или 94,938…·0,1=9,4938…. и др.

Как перемножить десятичную дробь с натуральным числом

Процесс такого умножения ничем не отличается то действия умножения двух десятичных дробей. Удобно пользоваться методом умножения в столбик, если в условии задачи стоит конечная десятичная дробь. При этом надо учитывать все те правила, о которых мы рассказывали в предыдущем пункте.

Пример 7

Подсчитайте, сколько будет 15·2,27.

Решение

Умножим столбиком исходные числа и отделим два знака запятой.

Ответ: 15·2,27=34,05.

Если мы выполняем умножение периодической десятичной дроби на натуральное число, надо сначала поменять десятичную дробь на обыкновенную.

Пример 8

Вычислите произведение 0,(42) и 22.

Решение

Приведем периодическую дробь к виду обыкновенной.

0,(42)=0,42+0,0042+0,000042+…=0,421-0,01=0,420,99=4299=1433

Далее умножаем:

0,42·22=1433·22=14·223=283=913

Итоговый результат можем записать в виде периодической десятичной дроби как 9,(3).

Ответ: 0,(42)·22=9,(3).

Бесконечные дроби перед подсчетами надо предварительно округлить.

Пример 9

Вычислите, сколько будет 4·2,145….

Решение

Округлим до сотых исходную бесконечную десятичную дробь. После этого мы придем к умножению натурального числа и конечной десятичной дроби:

4·2,145…≈4·2,15=8,60. 

Ответ: 4·2,145…≈8,60.

Как умножить десятичную дробь на 1000, 100, 10 и др

Умножение десятичной дроби на 10, 100 и др. часто встречается в задачах, поэтому мы разберем этот случай отдельно. Основное правило умножения звучит так:

Определение 3

Чтобы умножить десятичную дробь на 1000, 100, 10 и др., нужно перенести ее запятую на 3, 2,1 цифры в зависимости от множителя и отбросить слева лишние нули. Если цифр для переноса запятой недостаточно, дописываем справа столько нулей, сколько нам нужно.

Покажем на примере, как именно это делать.

Пример 10

Выполните умножение 100 и 0,0783.

Решение

Для этого нам надо перенести в десятичной дроби запятую на 2 цифры в правую сторону. Мы получим в итоге 007,83​​​​​Нули, стоящие слева, можно отбросить и записать результат как 7,38.

Ответ: 0,0783·100=7,83.

Пример 11

Умножьте 0,02 на 10 тысяч.

Решение: мы будем переносить запятую на четыре цифры вправо. В исходной десятичной дроби нам не хватит для этого знаков, поэтому придется дописывать нули. В этом случае будет достаточно трех 0. В итоге получилось 0,02000,перенесем запятую и получим 00200,0. Игнорируя нули слева, можем записать ответ как 200.

Ответ: 0,02·10 000=200.

Приведенное нами правило будет работать так же и в случае с бесконечными десятичными дробями, но здесь следует быть очень внимательным к периоду итоговой дроби, так как в нем легко допустить ошибку.

Пример 12

Вычислите произведение 5,32(672) на 1 000.

Решение: первым делом мы запишем периодическую дробь как 5,32672672672…, так вероятность ошибиться будет меньше. После этого можем переносить запятую на нужное количество знаков (на три). В итоге получится 5326,726726… Заключим период в скобки и запишем ответ как 5 326,(726).

Ответ: 5,32(672)·1 000=5 326,(726).

Если в условиях задачи стоят бесконечные непериодические дроби, которые надо умножать на десять, сто, тысячу и др., не забываем округлить их перед умножением.

Как перемножить десятичную дробь с обыкновенной или со смешанным числом

Чтобы выполнить умножение такого типа, нужно представить десятичную дробь в виде обыкновенной и далее действовать по уже знакомым правилам.

Пример 13

Умножьте 0,4 на 356

Решение

​Cначала переведем десятичную дробь в обыкновенную. Имеем: 0,4=410=25.

Далее считаем: 0,4·356=25·236=2315=1815.

Мы получили ответ в виде смешанного числа. Можно записать его как периодическую дробь 1,5(3).

Ответ: 1,5(3).

Если в расчете участвует бесконечная непериодическая дробь, нужно округлить ее до некоторой цифры и уже потом умножать.

Пример 14

Вычислите произведение 3,5678…·23

Решение 

Второй множитель мы можем представить как 23=0,6666…. Далее округлим до тысячного разряда оба множителя. После этого нам будет нужно вычислить произведение двух конечных десятичных дробей 3,568 и 0,667. Посчитаем столбиком и получим ответ:

Итоговый результат нужно округлить до тысячных долей, так как именно до этого разряда мы округляли исходные числа. У нас получается, что 2,379856≈2,380.

Ответ: 3,5678…·23≈2,380

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р. Реферат от 1 дня / от 700 р.

Умножение десятичных дробей – объяснение и примеры

Как умножать десятичные дроби?

В этой статье мы научимся выполнять умножение двух десятичных дробей, а также умножение десятичного числа и целого числа. Умножение десятичных чисел очень похоже на умножение целых или целых чисел. Существуют разные правила умножения десятичных и целых чисел. Рассмотрим правила умножения десятичных дробей.

 Умножение десятичных чисел на десятичные числа

• Считайте десятичные числа целыми, удаляя десятичную точку и умножая их.
• Поместите десятичную точку после цифр, равных общему количеству знаков после запятой в обоих числах.
• Не забудьте поставить десятичную точку, начиная с правой стороны продукта.

Пример 1

Умножение: 43,5 × 4,1

• Сначала выполните умножение, игнорируя десятичную точку.
• Считайте десятичные дроби целыми числами: 435 × 41 = 17835
• Теперь вставьте десятичную точку в произведение (17835), чтобы получить в произведении столько знаков после запятой, сколько в множимых.
• В этом случае каждое множимое содержит один десятичный разряд, поэтому общее количество знаков после запятой равно двум. Поэтому в произведении поставьте два десятичных знака.
• Следовательно, 43,5 × 4,1 = 178,35

Пример 2

Найти 81,32 × 8,3

• Рассматривайте десятичные числа как целые числа и умножайте их.
• 8132 × 83 = 674956
• В этом примере общее количество знаков после запятой в множимом равно 3. Десятичное число 81,32 содержит 2 знака после запятой, а 8,3 содержит 1 знак после запятой. Следовательно, сумма знаков после запятой в обоих числах равна 3.
• Поместите в произведение такое же количество знаков после запятой, как и в сумме множимых. Начинайте отсчет справа от произведения.
• Следовательно, 81,32 × 8,3 = 674,956

Умножение десятичных дробей на целые числа

Правила умножения десятичных чисел и целых чисел аналогичны правилам умножения только десятичных дробей. Единственная разница в этом случае состоит в том, что одно из множимых является целым числом. Вот некоторые из правил:

• Примите десятичное число как целое число, удалив десятичную точку и умножив его.
• Разместите в произведении столько десятичных знаков, сколько десятичных знаков в десятичном числе.
• Отсчет десятичной точки начинается с правой стороны произведения.

Пример 3

Вычислить 4,5 × 3

• Выполните умножение, игнорируя десятичную точку.
• 45 × 3 = 135
• Поместите в произведение столько десятичных знаков, сколько в десятичном числе. Здесь количество знаков после запятой равно 1,
• Следовательно, 4,5 × 3 = 13,5

Пример 4

Найдите произведение 91,3012 и 83.

• Выполните операцию умножения, игнорируя десятичную точку.
• 913012 x 83 =
• Разместите такое же количество знаков после запятой, как и в десятичном числе. Здесь десятичное число содержит 4 знака после запятой, следовательно, произведение также будет содержать 4 знака после запятой.
• Ответ: 7577,9996

Свойства умножения десятичных чисел

• Произведение двух десятичных чисел остается неизменным даже при изменении порядка умножения. Например: 4 × 0,8 = 0,8 × 1,4 = 1,12 и
• Произведение десятичного числа на 1 и есть само десятичное число. Например:

2,519 × 1 = 2,519

• Произведение десятичного числа с нулем равно нулю. Например: 008 × 0 = 0
• При умножении десятичных чисел порядок групп может быть изменен без изменения произведения. Например: 02 × (11,2 × 2,3) = (1,02 × 2,3) × 11,2.
• Произведение целого числа на десятичное число остается неизменным при умножении чисел в любом порядке. Например: 1,8 × 11 = 11 × 1,8 = 19,8.

 

Практические вопросы

1. Что из нижеследующего показывает, что 4 долл. США умножить на 12,2 $?

48,08 $

48,8 $

48,88 $

48,088 $

2. Что из следующего показывает значение $2 \times 3,4 \times 1,5$?

5,1$

9$.6$

$10,2$

$12,8$

3. Цена книги $\$49,75$. Сколько будет стоить покупка 16 таких книг?

$\$298,50$

$\$396$

$\$398,50$

$\$796$

4. Скорость поезда $45,8$ км в час. Какое расстояние проедет поезд за $5,5$ часов?

$229$ км

$247,50$ км

$251,90$ км

$297,70$ км

5. Если на одну партию печенья требуется 5,67$ кг муки для выпечки, то сколько килограммов муки потребуется на десять таких же партий печенья?

45$ килограммов

46,75$ килограммов

56,07$ килограммов

56,7$ килограммов

 

Предыдущий урок | Главная страница | Следующий урок

десятичных знаков | SkillsYouNeed

Дроби и десятичные дроби — это два разных способа представления частей целого числа. Десятичные дроби — это способ выражения десятых, сотых, тысячных (и более) долей единицы.

Работа с десятичными знаками может показаться немного сложной для начала, но не волнуйтесь, это всего лишь числа, и они подчиняются правилам, как и другие числа.

Работа с десятичными дробями

Сложение и вычитание десятичных дробей

Десятичные дроби расширяют систему счисления за пределы простых «сотни, десятки, единицы» до «десятых долей единиц», «сотых долей единиц» и так далее.

Таким образом, работа с десятичными дробями практически ничем не отличается от работы с любым другим числом.

После просмотра наших страниц Числа , Сложение и Вычитание , у вас не возникнет проблем с добавлением тысяч к смеси, так зачем беспокоиться о десятых и сотых долях?

Если бы вы складывали числа без десятичных знаков, вы бы начали с единиц и переходили к десяткам, затем к тысячам и так далее. То же правило применяется, если есть десятичные дроби. Сначала сложите их, затем единицы, затем десятки и так далее.

Самое важное правило, которое следует помнить, это выровнять десятичные точки в вашем вычислении , следя за тем, чтобы десятичная точка в ответе также совпадала с десятичными точками над ней.

Если вас не устраивает «перенос» при добавлении или вычитании, см. наши страницы Сложение и Вычитание для справки.

---

Умножение десятичных дробей

При умножении и делении десятичных дробей вычисления выполняются так же, как и для целых чисел. Мы умножаем числа так, как если бы десятичной точки вообще не было. В конце расчета убеждаемся, что в нашем ответе стоит десятичная запятая на правильном месте:

Начиная с ответа, который вы получили путем умножения чисел, переместите запятую на такое же количество знаков в слева, так как есть числа после запятой в двух множителях.

---

Деление десятичных дробей

Умножение и деление на 10

---

Умножение на 10 сдвигает десятичную точку на один разряд вправо ( увеличивает исходное число в 10 раз). Деление на 10 перемещает его на одну позицию влево ( уменьшает исходное число на в 10 раз).

Вы можете использовать этот факт, чтобы сделать деление десятичных дробей намного проще. Умножьте на 10 число, на которое вы делите (знаменатель), пока оно не станет целым числом. Умножьте на 10 число, которое вы делите (числитель) столько же раз . Затем сделайте расчет.

Главный совет

Если вы выполнили умножение или деление с использованием десятичных дробей, проверьте, выглядит ли ответ правильным. Другими словами, если вы уберете числа после запятой и округлите их в большую или меньшую сторону до целого числа, будет ли это примерно правильно?

Если ваш ответ кажется слишком большим или слишком маленьким, проверьте положение десятичной точки. Это вполне может быть позиция в любом направлении.

---

Преобразование дробей в десятичные числа

Преобразование десятичных чисел в дроби довольно просто. Любое число можно представить в виде дроби, просто положив его на единицу.

То же правило применяется к десятичным дробям.

Поместите десятичную запятую на единицу, а затем умножьте верхнее и нижнее число на 10, пока не останется десятичная точка. Затем, если возможно, преобразуйте вашу дробь в смешанное число и/или уменьшите ее до наименьшей формы.

См. нашу страницу Фракции для получения дополнительной информации.

Преобразование дробей в десятичные

Преобразование дробей в десятичные немного сложнее, но становится легче, когда вы понимаете, что дробь на самом деле является вычислением деления.

Например, одна половина, ¹ / ₂ , на самом деле 1 делится на 2, что также равно ⁵ / ₁₀ , или пять десятых, что выражается как 0,5 в десятичных дробях. Это потому, что десятичные дроби основаны на числах, кратных десяти. (См. наши страницы на An Знакомство с числами и Системы измерения для получения дополнительной информации.)

Таким образом, чтобы преобразовать дробь в десятичную, рассматривайте дробь как вычисление деления, добавляя нули после запятой, если это необходимо для его завершения.

Всегда есть несколько путей!

---

По мере того, как мы все больше и больше практикуемся в подобных вычислениях, мы начинаем находить способы облегчить получение ответа.