Фрагмент урока на тему «Умножение на 5 и соответствующие случаи деления» | План-конспект урока по математике на тему:
Фрагмент урока (тема, основная дидактическая цель, планируемые результаты, Образовательные ресурсы; этапы: актуализация базовых знаний учащихся, открытие новых знаний, первичное закрепление (с проговариванием во внешней речи) на тему «Умножение на 5 и соответствующие случаи деления»
Тема урока ««Умножение на 5 и соответствующие случаи деления»
Основная дидактическая цель: сконструировать таблицу умножения и деления на 5; формировать у учеников умения воспроизводить результаты табличных случаев умножения и деления при решении задач.
Планируемые результаты:
‒ личностные:
— формировать мотивационные основы учебной деятельности,
— способствовать развитию интереса к математике;
‒ регулятивные:
— уметь определять и формулировать цель урока;
— учиться планировать учебную деятельность на уроке;
— оценивать правильность выполнения действий на уроке;
‒ познавательные:
— ориентироваться в материале учебника находить нужную информацию;
-оценивать правильность решения задач;
‒ коммуникативные:
— уметь с достаточной полнотой и точностью выражать свои мысли;
— слушать и понимать речь других;
— уметь работать в паре, группе;
— формулировать собственное мнение и позицию.
предметные:
-актуализировать ранее изученные знания табличных случаев умножения и деления при решении задач на увеличение и уменьшение «в» и «на»;
— познакомить с таблицей умножения и деления на 5 на основе ранее сформированных представлений знания таблиц умножения и деления на 2, 3, 4;
— учить приемам умножения и деления на 5 в ходе практической работы при выполнении вычислительных действий, при решении задач и уравнений.
уметь выбирать рациональный способ решения.
Образовательные ресурсы:
1. Белошистая А. В. Методика обучения математики в начальной школе: курс лекций: учеб. пособ. для студентов вузов, обучающихся по специальности»Педагогика и методика начального образования»/А.В. Белошистая. – М. : Гуманитар. Изд. центр ВЛАДОС, 2007. – 455с.
2. Математика. 3 класс. Учеб. для общеобраз. учреждений. В 2ч. Ч1 [М. И. Моро, М. А.Бантова, Г. В. Бельтюкова и др.]. – 2-е изд. — : Просвещение, 2012. – 112с.
3. Математика. Рабочая тетрадь. Пособие для уч. Общеобраз. учр.. В 2-х ч..Ч1 [М. И. Моро, С. И. Волкова]. – 2-е изд. — : Просвещение, 2012. – 79с.
Пособие для уч. Общеобраз. учр.. В 2-х ч..Ч1 [М. И. Моро, С. И. Волкова]. – 2-е изд. — : Просвещение, 2012. – 79с.
4. Рудницкая В. Н. Тесты по математике: 1-4 класс: к учебнику М.И.Моро и др. «Математика. 3 класс. В 2-х частях» / В. Н. Рудницкая. — М.: «Экзамен», 2012.
Оборудование и ресурсы:
компьютер, мультимедиа проектор, интерактивная доска, презентация.
Актуализация базовых знаний учащихся
Устный счет.
1. «Математические горелки» (задания демонстрируются на интерактивной доске)
Дети показывают ответы на математических веерах.
— Найдите произведение чисел 4 и 6.
— Чему равно частное чисел 36 и 9?
— Если по 3 взять 3 раза, то сколько получится?
— Первый множитель 2, а второй 5. Найди произведение.
— Делимое 24, делитель 6. Чему равно частное?
— Я задумала число, разделила его на 4 и получила 5. Какое число я задумала?
— Если произведение равно 21, первый множитель 3, чему равен второй множитель?
— Во сколько раз 2 меньше 12?
— На сколько число 2 меньше 12?
— Сделайте вывод о том, как узнать, во сколько раз одно число больше или меньше другого? (Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее число).
2. Что означает выражение 75=35? (по 7 взяли 5 раз с помощью действия сложения).
— Когда можно заменить сумму умножением? (при сложении одинаковых слагаемых).
Даны числа 3, 6, 18 – составьте выражения на умножение и деление.
36=18
63=18
— Как называют компоненты действия умножения?
— Какое свойства произведения применили ? (От перестановки множителей , произведение не меняется).
— Какое действие является обратным для умножения?
— Как найти неизвестный множитель для произведения?
18:3= 6
18:6=3
2.
Открытие новых знаний.
Сделаем «заготовку» для таблицы умножения на 5.
51=
52=
53=
54=
55=
56=
57=
58=
59=
При составлении предыдущих таблиц умножения одним из основных вычислительным приемом является введение операции умножения через нахождение суммы одинаковых слагаемых. Проверим справедливость полученных равенств, используя рисунок (для умножения 6 на 1, 2, 3).
.Деятельность учителя | Деятельность ученика (ученики словесно проговаривают свои ответы) |
Сделаем «заготовку» для таблицы умножения на 5. | 51= 52= 53= 54= 55= 56= 57= 58= 59= |
Какие из произведений мы можем вычислить, применяя переместительное свойство? | 51=15=5 52=25=10 53=35=15 54=45=20 |
Какие произведения мы должны еще вычислить? | 55= 56= 57= 58= 59= |
Можем ли мы здесь воспользоваться переместительным свойством умножения? | Нет, так как не знаем таблицы умножения на 5, 6, 7, 8, 9. |
Чему равно произведение 55? | 55=5+5+5+5+5=25 |
Как более рационально вычислить это произведение? | Произведение 55 содержит 5 слагаемых, каждое из которых равно 5. В предыдущем случае найдено произведение 54=20. Следовательно , 55=54+5=25 |
Продолжите вычисления | 56=55+5=30 57=56+5=35 58=57+5=40 59=58+5=45 |
Какое действие является обратным по отношению к умножению? | Деление |
Как найти неизвестный множитель? | Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель |
Рассмотрим равенство 56=30. Используя данное произведение , найдите частные 30:5= 30:6= Ответ обоснуйте. | 30:5=6 30:6=5 |
Аналогичным образом найдите частные для остальных произведений | |
В итоге мы получили таблицу умножения и деления на 5 | |
Первичное закрепление с проговариванием во внешней речи.
1.
После заполнения таблицы ученики классом проговаривают данную таблицу. Учитель предлагает ученикам объяснить некоторые из результатов табличного деления.
2.
3. Из чисел от 1 до 20 выпиши по порядку те, которые делятся без остатка на 5.
4. Вычислите.
5. Реши уравнения, используя знание таблиц умножения и деления
Педагогическое сообщество «Урок.
 рф» — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
рф» — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7Содержание
Умножение 5, на 5 и соответствующие случаи деления
Урок математики в 3 классе
Учитель: Веденякина Ксения Вячеславовна.
Тема: Умножение 5, на 5 и соответствующие случаи деления.
Задачи: составлять таблицы умножения 5, на 5 и соответствующие случаи деления; закреплять умение решать задачи.
Планируемые результаты:
Предметные: составлять таблицы умножения 5, на 5 и соответствующие случаи деления; решать простые и составные задачи; закреплять знания таблицы умножения и деления.
Метапредметные: выполнять мыслительные операции анализа и синтеза,
делать умозаключения по результатам исследования; искать разные способы решения
задачи; излагать и аргументировать свою точку зрения; слушать собеседника и
вести диалог; объяснять найденные способы действий при решении новых учебных
задач и находить способы их решения.
Личностные:
Ресурсы урока: Рабочая программа; учебник «Математика», ч.1, с.36; презентация; проектор; экран; карточки.
Ход урока:
1. Организационный момент
Игра «Ладошки».
— Возьмите друг друга за руки. Закройте глаза. Почувствуйте тепло других ладошек в своих руках. Мысленно пожелайте всем добра. А теперь откройте глаза и садитесь, не производя ни малейшего шума.
Вот и начинается новый урок. Сегодня мы в очередной раз отправимся в путь по дороге знаний.
Вспомним правила посадки.
Руки на месте (на месте),
Ноги на месте (на месте),
Локти на месте (на месте, у края),
Спинка прямая (прямая).
Не забывайте о том, что правильная осанка, залог здоровья.
Откройте тетрадки и запишите сегодняшнее число 13 октября.
— Запишите цифры: 1, 3 чередуя
2. Проверка домашнего задания
С. 39 №4,5.
Актуализация знаний. Устный счет.
А теперь друзья за дело
Математика нас ждет,
Начинаем устный счет!
Посчитайте десятками до 100 и обратно. (Молодцы!)
— Ежик предлагает нам решить веселые задачки.
Взял Антон лукошко, В лес пошёл Антон.
Набрал грибов немножко…И их считает он:
3 лисички, 3 волнушки, 3 груздя и 3 чернушки.
Сколько же грибов в лукошко Положить успел Антошка?
6 пар танцуют польку,
А всех танцоров сколько? (12)
В поле бабочки летали
Лепестки цветов считали. На одном цветке их 5.
На одном цветке их 5.
Сможете вы сосчитать? Сколько будет лепестков,
Если 3 всего цветков? (15)
Мышка зёрна собирала,
По 2 зёрнышка таскала. Принесла уж 9 раз.
Каков мышкин стал запас? (18)
4 друга не знали грибов,
Экая умора! И в корзинки положили
5 мухоморов. Сколько мухоморов нашли друзья? (20)
3. Объяснение нового учебного материала.
Самоопределение к деятельности. (слайд 4)
— Вычислите.
— Что помогло вам выполнить быстро вычисления? (Знания таблицы умножения с числами 2,3,4)
— Каким правилом вы воспользовались при вычислении ответов в примерах второго столбика? (От перестановки множителей произведение не меняется).
— Какой пример будет следующим? (5х5)
— Что нужно знать, чтобы быстро вычислить ответ в этом примере? (Таблицу умножения с числом 5).
-Сформулируйте
тему и задачи урока.
Да, я согласна с вами. Мы сегодня с вами составим таблицу умножения и деления на 5 и будем работать над её запоминанием
Каждый математик любит цифру «5»,
Сегодня мы продолжим таблицы составлять.
Таблицы не простые, а важные такие,
Две на умножение и на деление две.
Откройте с. 40
С помощью рисунка попробуем составить таблицу умножения. слайд
посмотрите на первый столбик таблицы. Как вычислили значение произведения 5 • 5? (5 + 5 + 5 + + 5 + 5или20 + 5.)
На сколько больше будет каждое следующее произведение? (На 5.)
Запишите таблицу умножения на 5 в тетрадь. Самостоятельно составьте таблицу умножения числа 5. (Проверка.)
— Каким правилом вы воспользовались? (От перестановки множителей произведение не меняется.) слайд
— Посмотрите на значения произведений. Что интересное вы заметили?
(Все ответы
заканчиваются на 0 или на 5. )
)
— Какие примеры на деление можно составить из произведения 5 • 5? (25:5 = 5.)
— Каким правилом вы воспользовались? (Если разделить произведение на один из множителей, то получится другой множитель)
— Самостоятельно составьте таблицу деления с числом 5. (Проверка.)слайд
№ 1 (с. 40)слайд.(Самостоятельное выполнение. Проверка. Учащиеся хором называют числа: 5, 10, 15, 20; 4, 8, 12, 16, 20.) слайд
ФИЗМИНУТКА
Если я называю число, которое делится на пять, то вы приседаете.
Если я называю число, которое не делится на пять, то вы подпрыгиваете.
4. Закрепление учебного материала
Первичное закрепление.
Самостоятельная работа.
-А теперь поработаем самостоятельно. У каждого из вас есть карточки, выполните на них следующее задание:
Закрась числа, которые делятся на 5.
26 | 30 | 45 | 15 | 23 |
38 | 10 | 42 | 40 | 36 |
44 | 25 | 14 | 50 | 21 |
27 | 20 | 24 | 35 | 39 |
А теперь
поменяйтесь карточками с соседом, и проверьте. Оцените работу товарища.
Оцените работу товарища.
На доске карточки
— Игра «Найди пару»
5х4= 35: 5=
8х5= 45:9=
5х7= 20: 5=
9х5= 40: 8=
-Какая связь между делением и умножением?
Работа над пройденным материалом.
Работа по учебнику
Решение задачи №3.
Прочитайте задачу.
— О чем говорится в задаче?
— Какой длины был кусок ткани?
— Как его использовали?
-Что сшили из оставшейся ткани?
— Что можно сказать про детские пальто?
— Можем ли мы сразу ответить на вопрос задачи? Почему?
-Рассмотрите схематический чертеж к задаче.
-Какой вопрос главный?
-Сколько действий в задаче?
-Что мы будем находить сначала?
-Каким действием узнать?
-Сколько надо ткани на пальто?
-Теперь можем узнать сколько ткани пойдет на одно пальто?
-Каким действием?
-Можно ли эту задачу решить выражением?
— Запишите
выражение в тетрадь. Проверьте себя.
Проверьте себя.
№ 2 (4 столбик) (слайд 21)
-Вспомним порядок действий.
Решаем самостоятельно.
Работа в парах
Множитель |
| 6 | 3 | 5 | 8 | 2 | |
Множитель | 5 | 4 |
|
| 5 |
| 9 |
Произведение |
| 16 | 30 | 27 |
| 32 |
|
Подведение итога урока
-Чему мы сегодня учились на уроке?
-Кто уже запомнил таблицу на пять?
8. Рефлексия.
Рефлексия.
— Встаньте те, кто считает, что он хорошо сегодня поработал? Почему ты так считаешь? Какие были трудности на уроке?
-Поднимите руку те, кому надо еще поработать над этой темой.
-А кому трудно было сегодня на уроке? Как вы считаете, почему?
9. Д/з выучить таблицу умножения на 5. № 2
10. Заключение. (слайд 24)
— Благодарю всех за урок. Вы отлично потрудились сегодня на уроке математики, и я желаю вам счастливого пути по дороге знаний!
Оцените себя!
10 – 9 баллов «5»
8-6 баллов «4»
5 -3 балла «3»
Лист самооценки ФИ______________________
| БАЛЛЫ ВСЕ ВЕРНО – 2 БАЛЛА 1-2 ОШИБКИ- 1 БАЛЛ 3 И БОЛЕЕ ОШИБОК – 0 БАЛЛОВ |
1. |
|
2. № 1 (с. 40) |
|
3. Закрась числа, которые делятся на 5. |
|
4. Задача №3. (с. 40) |
|
5. Работа в парах |
|
Всего: |
|
Лист самооценки ФИ______________________
| БАЛЛЫ ВСЕ ВЕРНО – 2 БАЛЛА 1-2 ОШИБКИ- 1 БАЛЛ 3 И БОЛЕЕ ОШИБОК – 0 БАЛЛОВ |
1.Составить таблицу умножения |
|
2. |
|
3. Закрась числа, которые делятся на 5. |
|
4. Задача №3. (с. 40) |
|
5. Работа в парах |
|
Всего: |
|
Лист самооценки ФИ______________________
| БАЛЛЫ ВСЕ ВЕРНО – 2 БАЛЛА 1-2 ОШИБКИ- 1 БАЛЛ 3 И БОЛЕЕ ОШИБОК – 0 БАЛЛОВ |
1.Составить таблицу умножения |
|
2. № 1 (с. 40) |
|
3. |
|
4. Задача №3. (с. 40) |
|
5. Работа в парах |
|
Всего: |
|
Фрагмент урока на тему «Умножение на 5 и соответствующие случаи деления» | План-конспект урока по математике на тему:
Фрагмент урока (тема, основная дидактическая цель, планируемые результаты, Образовательные ресурсы; этапы: актуализация базовых знаний учащихся, открытие новых знаний, первичное закрепление (с проговариванием во внешней речи) на тему «Умножение на 5 и соответствующие случаи деления»
Тема урока ««Умножение на 5 и соответствующие случаи деления»
Основная дидактическая цель: сконструировать таблицу умножения и деления на 5; формировать у учеников умения воспроизводить результаты табличных случаев умножения и деления при решении задач.
Планируемые результаты:
‒ личностные:
— формировать мотивационные основы учебной деятельности,
— способствовать развитию интереса к математике;
‒ регулятивные:
— уметь определять и формулировать цель урока;
— учиться планировать учебную деятельность на уроке;
— оценивать правильность выполнения действий на уроке;
‒ познавательные:
— ориентироваться в материале учебника находить нужную информацию;
-оценивать правильность решения задач;
‒ коммуникативные:
— уметь с достаточной полнотой и точностью выражать свои мысли;
— слушать и понимать речь других;
— уметь работать в паре, группе;
— формулировать собственное мнение и позицию.
предметные:
-актуализировать ранее изученные знания табличных случаев умножения и деления при решении задач на увеличение и уменьшение «в» и «на»;
— познакомить с таблицей умножения и деления на 5 на основе ранее сформированных представлений знания таблиц умножения и деления на 2, 3, 4;
— учить приемам умножения и деления на 5 в ходе практической работы при выполнении вычислительных действий, при решении задач и уравнений.
уметь выбирать рациональный способ решения.
Образовательные ресурсы:
1. Белошистая А. В. Методика обучения математики в начальной школе: курс лекций: учеб. пособ. для студентов вузов, обучающихся по специальности»Педагогика и методика начального образования»/А.В. Белошистая. – М. : Гуманитар. Изд. центр ВЛАДОС, 2007. – 455с.
2. Математика. 3 класс. Учеб. для общеобраз. учреждений. В 2ч. Ч1 [М. И. Моро, М. А.Бантова, Г. В. Бельтюкова и др.]. – 2-е изд. — : Просвещение, 2012. – 112с.
3. Математика. Рабочая тетрадь. Пособие для уч. Общеобраз. учр.. В 2-х ч..Ч1 [М. И. Моро, С. И. Волкова]. – 2-е изд. — : Просвещение, 2012. – 79с.
4. Рудницкая В. Н. Тесты по математике: 1-4 класс: к учебнику М.И.Моро и др. «Математика. 3 класс. В 2-х частях» / В. Н. Рудницкая. — М.: «Экзамен», 2012.
Оборудование и ресурсы:
компьютер, мультимедиа проектор, интерактивная доска, презентация.
Актуализация базовых знаний учащихся
Устный счет.
1. «Математические горелки» (задания демонстрируются на интерактивной доске)
«Математические горелки» (задания демонстрируются на интерактивной доске)
Дети показывают ответы на математических веерах.
— Найдите произведение чисел 4 и 6.
— Чему равно частное чисел 36 и 9?
— Если по 3 взять 3 раза, то сколько получится?
— Первый множитель 2, а второй 5. Найди произведение.
— Делимое 24, делитель 6. Чему равно частное?
— Я задумала число, разделила его на 4 и получила 5. Какое число я задумала?
— Если произведение равно 21, первый множитель 3, чему равен второй множитель?
— Во сколько раз 2 меньше 12?
— На сколько число 2 меньше 12?
— Сделайте вывод о том, как узнать, во сколько раз одно число больше или меньше другого? (Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее число).
2. Что означает выражение 75=35? (по 7 взяли 5 раз с помощью действия сложения).
— Когда можно заменить сумму умножением? (при сложении одинаковых слагаемых).
Даны числа 3, 6, 18 – составьте выражения на умножение и деление.
36=18
63=18
— Как называют компоненты действия умножения?
— Какое свойства произведения применили ? (От перестановки множителей , произведение не меняется).
— Какое действие является обратным для умножения?
— Как найти неизвестный множитель для произведения?
18:3= 6
18:6=3
2.
Открытие новых знаний.
Сделаем «заготовку» для таблицы умножения на 5.
51=
52=
53=
54=
55=
56=
57=
58=
59=
При составлении предыдущих таблиц умножения одним из основных вычислительным приемом является введение операции умножения через нахождение суммы одинаковых слагаемых. Проверим справедливость полученных равенств, используя рисунок (для умножения 6 на 1, 2, 3).
.Деятельность учителя | Деятельность ученика (ученики словесно проговаривают свои ответы) |
Сделаем «заготовку» для таблицы умножения на 5. | 51= 52= 53= 54= 55= 56= 57= 58= 59= |
Какие из произведений мы можем вычислить, применяя переместительное свойство? | 51=15=5 52=25=10 53=35=15 54=45=20 |
Какие произведения мы должны еще вычислить? | 55= 56= 57= 58= 59= |
Можем ли мы здесь воспользоваться переместительным свойством умножения? | Нет, так как не знаем таблицы умножения на 5, 6, 7, 8, 9. |
Чему равно произведение 55? | 55=5+5+5+5+5=25 |
Как более рационально вычислить это произведение? | Произведение 55 содержит 5 слагаемых, каждое из которых равно 5. В предыдущем случае найдено произведение 54=20. Следовательно , 55=54+5=25 |
Продолжите вычисления | 56=55+5=30 57=56+5=35 58=57+5=40 59=58+5=45 |
Какое действие является обратным по отношению к умножению? | Деление |
Как найти неизвестный множитель? | Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель |
Рассмотрим равенство 56=30. Используя данное произведение , найдите частные 30:5= 30:6= Ответ обоснуйте. | 30:5=6 30:6=5 |
Аналогичным образом найдите частные для остальных произведений | |
В итоге мы получили таблицу умножения и деления на 5 | |
Первичное закрепление с проговариванием во внешней речи.
1.
После заполнения таблицы ученики классом проговаривают данную таблицу. Учитель предлагает ученикам объяснить некоторые из результатов табличного деления.
2.
3. Из чисел от 1 до 20 выпиши по порядку те, которые делятся без остатка на 5.
4. Вычислите.
5. Реши уравнения, используя знание таблиц умножения и деления
Математика Умножение числа 5 и на число 5, и соответствующие случаи деления
Этап усвоения новых знаний
Мы с вами вышли на полянку, где нас встречают лесные звери. Они тоже хотят учиться вместе с нами. Звери хотят, чтобы мы им помогли составить таблицу умножения и деления с числом 5, и они нам покажут дорогу к Лесовичку.
Давайте вспомним, какие числовые выражения умножения на 5 мы уже хорошо знаем.
5·2=10
5·3=15
5·4=20
Теперь продолжим составлять таблицу.
Первый множитель 5, второй множитель 5, произведение равно 25.
Первый множитель 5, второй множитель 6, произведение равно 30.
Первый множитель 5, второй множитель 7, произведение равно 35.
Первый множитель 5, второй множитель 8, произведение равно 40.
Первый множитель 5, второй множитель 9, произведение равно 45.
Теперь, ребята, зная таблицу умножения на 5, давайте составим таблицу деления на 5.
Для этого давайте еще раз вспомним правило, как найти множитель, зная произведение.
Правильно, чтобы найти множитель, нужно произведение разделить на второй множитель.
Рассуждайте так:
Произведение 10 делим на множитель 5, в ответе получаем 2.
Зная правило, мы теперь можем составить таблицу деления на 5.
Произведение 15 делим на множитель 5, в ответе получаем 3.
Произведение 20 делим на множитель 5, в ответе получаем 4.
Произведение 25 делим на множитель 5, в ответе получаем 5.
Произведение 30 делим на множитель 5, в ответе получаем 6.
Произведение 35 делим на множитель 5, в ответе получаем 7.
Произведение 40 делим на множитель 5, в ответе получаем 8.
Произведение 45 делим на множитель 5, в ответе получаем 9.
Чтобы быстро и правильно решать, таблицу умножения нужно отлично знать
Урок математики в 3-м классе по теме «Умножение пяти, на 5 и соответствующие случаи деления»
Цели:
- Составить таблицу умножения пяти и на 5, рассмотреть соответствующие случаи деления; закрепить умножение, решать составные задачи, знания о порядке выполнения действий.
- Развивать вычислительные навыки, математическую речь мышление,
- Формировать интерес к математике, дружеские отношения.
Оборудование:
- таблица «Город умножения»,
- таблица умножения пяти и соответствующие случаи деления,
- цветик-семицветик и 9 цветков с пятью лепестками,
- таблица для устного счета,
- краткая запись задачи № 401,
- примеры для № 402,
- жетоны для оценивания, аббаки.

ХОД УРОКА
1. Проверка домашнего задания.
– У меня в руках цветик-семицветик, который будет исполнять сегодня все наши желания. Но только желания тех учеников, которые будут стараться, будут прилежными и внимательными.
а) Первое желание.
– “Лети, лети лепесток, через запад на восток, через север,через юг, возвращайся, сделав круг. Лишь коснешься ты земли быть по-моему вели…
– Вели, чтобы домашнее задание учеников были выполнены верно…”
стр. 35 № 3
Взаимопроверка учащимися, они меняются тетрадями карандашами, исправляют ошибки. Примеры проверяются по листочкам с правильными ответами. Если есть неправильные примеры, то вместе решают эти примеры. Если нет ошибок, то задаются вопросы:
– Какие правила вы знаете о порядке выполнения действий в выражениях без скобок?
2. Устный счёт.
б) Второе желание.
– “Лети, лети лепесток, через запад на восток, через север,через юг, возвращайся, сделав круг. Лишь коснешься ты земли быть по-моему вели …
– Вели, чтобы мы оказались в городе “Умножения…”.
(Открывается карта города “Умножения»).
– Как зовут жителей города “Умножения”? (1 множитель, 2 множитель и произведение).
– Жители города “Умножения”
1 множить 5 4 7 9 2множить 3 3 2 5 произвел. 24 18 27 10
(Ответы показывают на аббаках. Объясняют
правила нахождения. 1 множит., 2 множит.)
Объясняют
правила нахождения. 1 множит., 2 множит.)
3. Новая тема.
– У нашего цветика – семицветика есть младший брат, цветок с пятью лепесточками.
(В вазу ставится 1 цветок с пятью лепестками).
– Он всегда грустный и наверно скоро завянет, если мы ему не поможем найти друзей.
в) Третье желание.
– “Лети, лети лепесток, через запад на восток, через север, через юг, возвращайся, сделав круг. Лишь коснешься ты земли быть по-моему вели …
– Вели, чтобы у цветочка с пятью лепестками появились друзья …”.
(В вазу ставят еще 1 цветок с пятью лепестками).
– Сколько стало лепестков? (по 5 взяли 2 раза = 10)
(Каждый раз в вазу добавляется 1 цветок с пятью лепестками).
– Сколько стало теперь лепестков? (по 5 взяли 3 раза = 15)
– Сколько стало теперь лепестков? (по 5 взяли 4 раза = 20)
– Сколько стало теперь лепестков? (по 5 взяли 5 раз = 25)
– Сколько стало теперь лепестков? (по 5 взяли 6 раз = 30)
– Сколько стало теперь лепестков? (по 5 взяли 7 раз = 35)
– Сколько стало теперь лепестков? (по 5 взяли 8 раз = 40)
– Сколько стало теперь лепестков? (по5 взяли 9 раз = 45)
– У цветочка с 5 лепестками появилось много
друзей. Мы помогли не только цветочку,но и себе.
Чем помогли мы себе? Кто догадался? (составили
таблицу умножения).
Мы помогли не только цветочку,но и себе.
Чем помогли мы себе? Кто догадался? (составили
таблицу умножения).
(В карте города “Умножения“ открывается домик № 5).
– Но посмотрите на доску. Почему эта таблица умножения пяти начинается с примера
5 * 5 = 25
5 * 6 =30
5 * 7 = 35
5 * 8 = 40
5 * 9 = 45
– На сколько ответы становятся больше? (на 5)
– Прочитайте эти примеры разными способами.
г) Четвёртое желание.
– “Лети, лети лепесток, через запад на восток, через север, через юг, возвращайся, сделав круг. Лишь коснешься ты земли быть по-моему вели …
– Вели, чтобы все записи в тетрадях были аккуратными…”
(Запись 1 столбика в тетрадь).
– Что произойдет, если поменять множители местами?
– Прочитайте эти примеры с переставленными множителями.
– А теперь мы с вами попадем на улицу деления.
Как зовут жителей этой улицы? (делимое, делитель,
частное).
– Объясните, как появился второй столбик?
25: 5 =
30: 5=
35: 5 =
45: 5 =(у доски записывают ответы, прочитывая примеры разными способами)
– Как появился 3 столбик?
(Примеры решаются по цепочке у доски).
– Почему отсутствует 1 пример? (Потому что он повторяется).
4. Физ. минутка.
Раз – подняться, подтянуться.
Два – согнуться, разогнуться.
Три – в ладоши три хлопка,
Головою три кивка.
На четыре руки шире,
Пять – руками помахать.
Шесть – за парты тихо сесть.
5. Закрепление (стр.36).
– Посетим несколько домов города “Умножения».
Дом № 2. 1-й подъезд (№2 – 1 столбик)
(С комментарием в тетрадках).
Дом. Задание №2 (3,4,5 столбик)
6. Решение задач.
– В городе “Умножения” есть и своя школа, и свой спортивный зал.
Адрес школы: г. Умножения д. № 4
– Прочитайте задачу:
– Что известно?
– Что требуется найти?
(На обратной стороне доски краткая запись задачи – открыть).
Взяли – 4 м.
Осталось – 12 м.
На сколько мячей больше осталось, чем взяли?
– Можем ли мы ответить на главный вопрос задачи? (да)
– Какое правило применим? (Чтобы узнать, на сколько больше или на сколько меньше, надо от большего числа отнять меньшее).
(Все решают в тетрадях, а 1 ученик за доской).
12 – 4 = 8 (м.)
7. Занимательный материал.
– В городе «Умножения»произошло несчастье. В доме №5 убежали числа и равенства не могут понять: верные они или неверные.
д) Пятое желание.
– “Лети, лети лепесток, через запад на восток,
через север,через юг, возвращайся, сделав круг. Лишь коснешься ты земли быть по-моему вели …
Лишь коснешься ты земли быть по-моему вели …
– Вели, чтобы всё встало на свои места…”.
– Исправим ошибку и вернём числа на место.
b + 18
b= 0 0 + 18 = 18 b= 2 2 + 18 = 20 b= 5 5 + 18 = 23 b= 10 10+ 18= 28
(Все решают в тетрадях, тот кто 1 решит идёт к доске. По 2 ученика работают на листочках – за правильный ответ, получают жетоны.)
8. Итог.
– В г. “Умножение” все должны хорошо знать таблицу умножения и деления. Ведь надо уважать правило того города, в котором мы гостим.
– Проверим, как вы уважаете правила этого города.
Игра “Мяч” по таблице умножения и деления на
пять.
(Учитель называет пример и кидает мяч, а ученики возвращают его учителю с ответом.)
9. Оценивание.
– Город “Умножения” большой и мы продолжим путешествие по нему на следующих уроках. А теперь посмотрим, что мы заработали на уроке:
5 жетонов – 5
4 жетона – 4
3 жетона – 3
Конспект урока по Математике «Умножение шести,на 6 и соответствующие случаи деления» 3 класс
Урок математики в 3-м классе
Учитель:Федотова Галина Дмитриевна
МКОУ»Фролово-Горетовская ООШ»
Сухиничский район
Тема: «Умножение шести,на 6 и соответствующие случаи деления
Вид урока: урок изучения нового материала
Целевые установки:
Планируемые цели для учителя:
сконструировать таблицу умножения 6, опираясь на различные свойства умножения;
исследовать связь между изменяющимся множителем и цифрами в произведении;
найти закономерности и особенности данной таблицы с целью быстрого её запоминания;
решать задачи на нахождение произведения и суммы.

Планируемые метапредметные результаты:
Личностные:
формировать положительное отношение к учению,
уважительное отношение к собеседнику,
развивать интерес к различным видам решения поставленной учебной задачи и к расширению математических знаний.
Регулятивные:
уметь определять и формулировать цель на уроке;
учиться совместно с учителем обнаруживать и формулировать учебную проблему;
планировать свои действия в связи с поставленной задачей.
понимать, принимать и сохранять учебную задачу; осуществлять самооценку учебных действий;
Познавательные:
уметь ориентироваться в своей системе знаний;
ориентироваться в предложенном материале, находить нужную информацию
отличать новое от уже известного; добывать новые знания.
Коммуникативные:
уметь с достаточной полнотой и точностью выражать свои мысли;
слушать и понимать речь других;
уметь работать в паре, группе;
формулировать собственное мнение и позицию.

Планируемые предметные результаты.
Обучающиеся:
закрепят знания изученных таблиц, устных приёмов вычисления примеров разного вида;
усовершенствуют умения решать задачи;
повторят понятия уравнения, подбор корня уравнения;
усовершенствуют умения ориентироваться в геометрическом материале, в нахождении периметра.
смогут проанализировать, найти закономерности при составлении таблицы;
смогут составить, усвоить и частично запомнить таблицу умножения на 6;
сумеют применить полученные знания на практике;
смогут сотрудничать при групповой работе и работе в парах, задавать вопросы, учитывать мнение одноклассников, отстаивать свою точку зрения.
будут адекватно себя оценивать на уроке;
Здоровьесберегающие:
— развивать мелкую моторику кисти;
— Формировать правильную посадку при письме;
— контролировать эмоциональную и физическую перегрузку детей с помощью физкультурных пауз .
Методы: практический, проблемный, частично-поисковый, словесный.
Время реализации занятия: 45 минут.
Оборудование:
Для учителя:
-Учебник для третьего класса. Авторы: М.И. Моро, С.И. Волкова, С.В. Степанов
— интерактивная доска, карточки, смайлики, таблица умножения, рабочие тетради.
-карточки для индивидуальной работы, работы в группах и парах
Этапы урока и их продолжительность:
I.Организационный момент 1мин
II.Актуализация знаний. 7мин
III .Самоопределение к деятельности. 10мин
V. Дыхательная медитация. Физмининутка. 3мин
VI. Проверка усвоения нового материала 10мин
VII.Закрепление изученного материала 10мин
VIII этап.Рефлексия. 2мин
VIII.Подведение итогов урока 1мин
IX. Домашнее задание 1мин
Домашнее задание 1мин
Ход урока
I.Организационный момент
Здравствуйте ребята! Садитесь!
«Все расселись по местам,
Никому не тесно!
По секрету скажу Вам,
Будет интересно!
Будем мы считать, писать,
И решать задачи!
Чтоб сегодня как всегда,
В руки шла удача!
Узнаем новый материал,
Закрепим умения,
Чтобы каждый мог сказать,
Это всё умею я!»(слайд 2)
– Ребята, на доске девиз нашего урока: «С хорошим настроением принимайся за работу!»(слайд 3)
-Улыбнитесь друг другу. Подарите и мне свои улыбки. Ваши улыбки располагают к приятному общению, создают хорошее настроение. Всем удачи.
Возьмите смайлики и нарисуйте свое настроение.
Работа в тетрадях: (слайд 4)
И ещё убедительная просьба: ответить хочешь, не шуми, а только руку подними.
II.Актуализация знаний.
1. Проведение минутки чистописания
Открыли тетради. И перед тем как вы начнёте писать, я хочу задать вам несколько вопросов.
И перед тем как вы начнёте писать, я хочу задать вам несколько вопросов.
Посмотрите на доску и ответьте мне на несколько вопросов:
Какое сегодня число? (20 октября.) (слайд 6)
(20-двузначное ( состоит из 2 д. и 0 единиц). Соседи числа 19 и 21,
чётное.)
Скажите ребята, а число 20 встречается в изученном нами табличном умножении?(Да)
Что вы можете мне сказать о словах – октябрь, работа, классная?
(Словарные слова.)
А какими частями речи они выражены?
(Существительное .Прилагательное)
Оформление тетрадей.
Открыли тетради и выполнили грамотную и аккуратную запись.
(Далее самостоятельно выполняют запись в тетради.)
А теперь проведём минутку чистописания. Для чего нам нужны минутки чистописания?(ответы детей)
Задание №1
Даня и Стёпа — от 10 до 20
Настенька, Даша и Алина – записывают по порядку числа от 25 до 35.
Молодцы, ребята!Я вижу на уроке внимательныx ,аккуратныx ребят.
Оцените свою работу с помощью смайлика
2.Решение задач.
Чтобы быстро считать,
Задачи без труда решать,
Нам надо себя тренировать.
В математике любая работа
Не обходится без устного
счёта. (слайд8)
а).Работа над задачами
Дарит бабушка-лисица
Трём внучатам рукавицы:
Это вам на зиму, внуки,
Рукавичек по две штуки.
Берегите, не теряйте!
Сколько всех, пересчитайте! (слайд 9)
б)Если знаешь ты таблицу,
На вопрос ответишь смело:
Сколько птичек-невеличек
На кормушку прилетело?
Воробьёв драчливых пара,
И синичек тоже пара,
Пара сизых голубей
И две пары снегирей . (слайд 10)
Молодцы!
3.Математический диктант
(Учитель читает высказывания. Если учащиеся согласны, они ставят знак +, если нет — знак —. )
)
Произведение чисел 4 и 6 равно 24. (+)
6 больше 2 в 12 раз. (—)
Если к 35 прибавить 18; получится 43. (—)
20 — четное число. (+)
В таблице умножения на 4 есть число, которое оканчивается цифрой 0. (+)
Частное чисел 36 и 5 равно 7. (—)
Число 25 не делится на 2. (+)
Из произведения чисел 8 и 0 число 6 не вычитается. (+) (Проверка индивидуальной работы у доски.)
( взаимопроверка, оценки) слайд 12
III .Самоопределение к деятельности.
Найди закономерность.
(Запись на слайде № 15)
12 25 16 30 24 35 28 40 32 48
Учитель:
Посмотрите на доску и прочитайте числа. Что вы можете сказать про эти числа?
(Дети:
Это произведения из таблицы умножения на 4 и 5)
Учитель: Назовите произведения из таблицы умножения на 5?
(Дети: 25 30 40)
Учитель: Назовите произведения из таблицы умножения на 4?
(Дети:12 16 24 28 40 32)
(-Составляем таблицы умножения и деления на 3,4,5)
(- Нет, мы проводим исследования, ищем закономерности, подбираем , на -xодим пути для лучшего запоминания таблицы. )
)
Постановка проблемы.
А теперь я предлагаю Вам решить примеры.
3х9=27
4х8=32
5х7=35
7х5=35
8х4=32
9х3=27 (слайд 16)
Исследование проблемы и нахождение пути её преодоления.
Давайте проведём исследование данного столбика примеров.
-Что интересного вы увидели сами?
-По какому принципу составлены примеры?
(Взаимообратные)
-Как мы называем такие примеры?
-Какое правило здесь используется?
Ответьте мне математическим языком, как учёные математики.
(От перестановки множителей произведение не меняется.)
-А почему мы смогли решить эти примеры?
(Мы знаем таблицу умножения на 3, на 4 и на 5.)
-Хорошо, идем дальше. Продолжаем проводить наше исследование.
-Посмотрите внимательно ещё раз на данный столбик примеров и скажите, а какого примера не хватает в столбике?
(6х6) (слайд 17)
-Как вы думаете, почему я его пропустила? Чего побоялась?
(Мы не знаем таблицу умножения на 6. )
)
-Так какова же тема нашего урока?
(Составление таблицы умножения и деления на 6.) ( слайд 18)
А какие цели мы ставим сегодня на уроке?
(Составить, записать таблицу умножения на 6 и научиться её использовать.)
IV.Работа по теме урока.
1.Составление таблицы умножения и деления с числом 6
Составление таблицы умножения на 6 (работа в группе)
Ребята работают группой.
Группа :
Настенька, Даша,
Даня, Стёпа и Алина
Составляют таблицу умножения и деления( проверка у доски)
Давайте проверим, как Вы справились? (слайд 19)
(Таблица появляется на слайде. )
Ответственные проверяют и дают оценку, как они справились с работой.
Исследование таблицы умножения
А теперь ребята давайте поищем закономерности, пути к лучшему запоминанию таблицы.
Посмотрите внимательно и скажите, что интересного вы увидели?
6х2=12
6х3=18
6х4=24
6х5=30
6х6=36
6х7=42
6х8=48
6х9=54
Закономерности:
второй множитель увеличивается на1
первый множитель неизменный
произведение увеличивается
на 6 (сверху вниз, а снизу вверх уменьшается на 6)
все произведения двузначные числа
сумма цифр в произведении чередуется так 3,9.
 6,3,9,6,9 (кроме 48)
6,3,9,6,9 (кроме 48)
Слышится рифма, волшебные слова.
Проговорить:
6х2=12
6х4=24
6х6=36
6х8=48
Итак, ребята, достигли мы поставленной цели ?(Да!)
А теперь наша задача состоит в том, чтобы научиться практически использовать таблицу и запомнить её, насколько это возможно!
Давайте запишем таблицу в тетради, но я вам предлагаю записать только 4 примера, почему?
(остальные примеры нам знакомы из других таблиц, а почему не берём умножение на 1, умножение на10?)
-Где пригодится знание таблицы умножения?
(При решении задач ,уравнений, примеров)
А в жизни?(Ответы детей)
Составляем таблицу на деление вместе (слайд 20)
Оцените работу с помощью смайлика
V. Дыхательная медитация. Физминутка
Сядьте ровно, расслабьтесь, закройте глаза. Вы идёте по лесу. Вдох. Выдох. Какой чистый воздух. Вдох. Выдох. Вот елочка в осеннем наряде. Вдох. Выдох. Как красиво кругом. Вдох. Выдох. Открываем глаза.
Вдох. Выдох. Как красиво кругом. Вдох. Выдох. Открываем глаза.
Раз, два — дружно встали, (Шаги на месте.)
Руки прямо мы поставим. (Руки на поясе.)
Три, четыре — разведем,(Руки в стороны.)
Заниматься мы начнем.(Наклоны вперед с касанием носка правой ноги
левой рукой, а носка левой ноги — правой рукой.)
Вправо, влево посмотрели,(Повороты головы вправо и влево.)
На носочках мы присели (Присесть.)
И, как птички, полетели. (Учащиеся разбегаются по классу.) (слайд 21)
VI. этап Проверка усвоения нового материала
Работа по учебнику № 1 (с. 44).(слайд 22)
VII.Закрепление изученного материала
1.Работа по учебнику №4 (с. 44).
(Устное выполнение.)
(Аналогично разбираются остальные уравнения.)
Оцените работу соседа.
№6 (с. 44).(слайд 23)
(Самостоятельное выполнение. Один ученик работает на откидной доске. Тем, кто испытывает затруднения, учитель дает карточку-помощницу с краткой записью.)
Один ученик работает на откидной доске. Тем, кто испытывает затруднения, учитель дает карточку-помощницу с краткой записью.)
Было — 50 кг.
Израсходовали — ?, 2 • 6 (кг).
Осталось — ?
Проверка по шаблону.
VIII этап.Рефлексия.
(«Проверь себя» (учебник, с. 44). Самостоятельное выполнение. Проверка по образцу.)
Решение: 4 • 3 = 12 4 • 5 = 20 4 • 6 = 24 4 • 10 = 40
А теперь я хочу, чтобы вы оценили свою работу на уроке.
– Понравился ли вам урок?
– Какие задания вы выполнили с удовольствием.
Поднимите:
зелёный кружок, кому было на уроке легко и всё понятно.
жёлтый – если что-то не понял на уроке, и надо поработать дополнительно.
красный- красный, кому было трудно на уроке, и надо подойти к учителю за помощью.
— Кто доволен своей работой?
(Дети дают самооценку своей работе.) (слайд 24)
VIII.Подведение итогов урока
— Назовите тему урока.
(слайд 24)
IX.Домашнее задание
Учить таблицу умножения и деления на 6.
На «5»- придумать задачи на деление и умножение на 6 и записать решение в тетрадь.
На «4»- учебник с. 44 №2,№5
На «3»-записать таблицу умножения 6 и соответствующие случаи деления в тетрадь
Закончен урок и выполнен план.
Спасибо, ребята, огромное вам!
За то что упорно и дружно трудились
Что на уроке вы не ленились!
Спасибо за урок!
:
Урок математики 3 класс » Умножение 5, на 5 и соответствующие случаи деления.» УМК Перспектива
Урок математики в 3 классе
МБОУ СОШ №2 г.ПытьЯх Рачковская Л.П. учитель начальных классов
УМК «Перспектива» 3класс. Математика.
Тема: Умножение 5, на 5 и соответствующие случаи деления.
Задачи: составлять таблицы умножения 5, на 5 и соответствующие случаи
деления; закреплять умение решать задачи.
Тип урока : Урок изучения и первичного закрепления новых знаний
Формы работы обучающихся : фронтальные, индивидуальные, групповые
Планируемые результаты:
Предметные: составлять таблицы умножения 5, на 5 и соответствующие
случаи деления; решать простые и составные задачи; закреплять знания
таблицы умножения и деления. Метапредметные: выполнять мыслительные операции анализа и синтеза,
делать умозаключения по результатам исследования; искать разные способы
решения задачи; излагать и аргументировать свою точку зрения; слушать
собеседника и вести диалог; объяснять найденные способы действий при
решении новых учебных задач и находить способы их решения.
Личностные: осваивать позитивный стиль общения со сверстниками и
взрослыми в школе и дома; проявлять учебно познавательный интерес к новому
учебному материалу и способам решения учебных и практических задач.
Межпредметные связи: окружающий мир, моделирование различных ситуаций
в виде схем.
Ресурсы урока: Рабочая программа; учебник «Математика», ч.1, с.98;
презентация; проектор; экран; карточки «Математическое лото»; карточки для
самостоятельной работы для групп, в парах, индивидуально.
Ход урока:
1.Включение в учебную деятельность.
Добрый день.
Прозвенел и смолк звонок,
Начинается урок.
Он немного необычный
В основном вполне, привычный.
Уравнения, задачи,
Игры, шутки все для вас.
Метапредметные: выполнять мыслительные операции анализа и синтеза,
делать умозаключения по результатам исследования; искать разные способы
решения задачи; излагать и аргументировать свою точку зрения; слушать
собеседника и вести диалог; объяснять найденные способы действий при
решении новых учебных задач и находить способы их решения.
Личностные: осваивать позитивный стиль общения со сверстниками и
взрослыми в школе и дома; проявлять учебно познавательный интерес к новому
учебному материалу и способам решения учебных и практических задач.
Межпредметные связи: окружающий мир, моделирование различных ситуаций
в виде схем.
Ресурсы урока: Рабочая программа; учебник «Математика», ч.1, с.98;
презентация; проектор; экран; карточки «Математическое лото»; карточки для
самостоятельной работы для групп, в парах, индивидуально.
Ход урока:
1.Включение в учебную деятельность.
Добрый день.
Прозвенел и смолк звонок,
Начинается урок.
Он немного необычный
В основном вполне, привычный.
Уравнения, задачи,
Игры, шутки все для вас. Я желаю вам удачи!
За работу, в добрый час!
2. Мотивация познавательной деятельности.
В альбоме я нашла старые фотографии, и вот эти предметы.( галстук и
звезда). Кто вспомнил, в каком произведении, которое мы читали с вами на уроках
внеклассного чтения встречаются эти предметы?( « Тимур и его команда»
Кто написал это произведение?
Кто главные герои? Кто такой герой? Что делала его команда? Для чего они
это делали? Да , это моё детство, наше движение так и называлось
« Тимуровское движение».
А в наше современное время кто выполняет эту миссию, помогать другим?
А мы можем с вами организовать такое движение в классе ?
Я разбила вас на команды, не для соревнования , а чтобы вы показали, что
вместе трудиться легко.
Потрите ваши руки, а теперь возьмитесь за руки, и почувстуйте тепло,
своего товарища.
Выберите командира вашей команды, его задача за правильные ответы
выдавать вам звездочки ,они у вас на столе.
Соберем портрет современного добровольца, активиста. Есть даже
всемирный праздник 17 февраля это «День спонтанного проявления
доброты.
Я желаю вам удачи!
За работу, в добрый час!
2. Мотивация познавательной деятельности.
В альбоме я нашла старые фотографии, и вот эти предметы.( галстук и
звезда). Кто вспомнил, в каком произведении, которое мы читали с вами на уроках
внеклассного чтения встречаются эти предметы?( « Тимур и его команда»
Кто написал это произведение?
Кто главные герои? Кто такой герой? Что делала его команда? Для чего они
это делали? Да , это моё детство, наше движение так и называлось
« Тимуровское движение».
А в наше современное время кто выполняет эту миссию, помогать другим?
А мы можем с вами организовать такое движение в классе ?
Я разбила вас на команды, не для соревнования , а чтобы вы показали, что
вместе трудиться легко.
Потрите ваши руки, а теперь возьмитесь за руки, и почувстуйте тепло,
своего товарища.
Выберите командира вашей команды, его задача за правильные ответы
выдавать вам звездочки ,они у вас на столе.
Соберем портрет современного добровольца, активиста. Есть даже
всемирный праздник 17 февраля это «День спонтанного проявления
доброты. » У каждого волонтера должно быть огромное и доброе сердце.
(прикрепить плакат).
Мы отправляемся в путь знаний, где будем проявлять все лучшие качества
волонтера.
3.Актуализация знаний.
Устный счет.
а)Приготовились, на парте у вас есть математическое лото, отвечайте на мои
вопросы и закрашивайте цифру с правильным ответом, сегодня желтый день,
возьмите желтый карандаш.
Разделите число 12 на 2
Найдите произведение 4 и 7
Первый множитель 5, второй множитель 3. Найдите произведение?
Делимое 27, делитель 3. Найдите частное.
Найдите сумму чисел 24 и 16
Найдите разность 50 и 18
Увеличьте число 9 в 4 раза Уменьшите 56 на 9
Увеличьте 36 на 7
— Уменьшите 24 в 6 раз.
б) Веселые задачки
Я предлагаю вам решить веселые задачки.
8 пар танцуют польку,
А всех танцоров сколько? (16)
Испекла нам бабушка
Вкусные оладушки.
» У каждого волонтера должно быть огромное и доброе сердце.
(прикрепить плакат).
Мы отправляемся в путь знаний, где будем проявлять все лучшие качества
волонтера.
3.Актуализация знаний.
Устный счет.
а)Приготовились, на парте у вас есть математическое лото, отвечайте на мои
вопросы и закрашивайте цифру с правильным ответом, сегодня желтый день,
возьмите желтый карандаш.
Разделите число 12 на 2
Найдите произведение 4 и 7
Первый множитель 5, второй множитель 3. Найдите произведение?
Делимое 27, делитель 3. Найдите частное.
Найдите сумму чисел 24 и 16
Найдите разность 50 и 18
Увеличьте число 9 в 4 раза Уменьшите 56 на 9
Увеличьте 36 на 7
— Уменьшите 24 в 6 раз.
б) Веселые задачки
Я предлагаю вам решить веселые задачки.
8 пар танцуют польку,
А всех танцоров сколько? (16)
Испекла нам бабушка
Вкусные оладушки. Всего оладий 27
По три нам хватило всем.
Кто ответит из ребят,
Сколько будет же внучат? (9)
Полюбуйтеська сами:
Мчатся тройки с бубенцами.
Сосчитать коней мы просим,
Если было троек 8. (24)
Подарил утятам ёжик
8 кожаных сапожек.
Сколько ж маленьких утят
Ёжика благодарят? ( 4)
На заборе расфуфырились коты,
Распушили свои длинные хвосты.
А хвостов то было 8.
Сколько лап ?
У кого спросим? (32)
Кто был внимателен, сколько задачек мы решили? (5)
Молодцы! Что помогло, нам справится с этими заданиями, какое качество?
(Ум)
Вывешиваем на доску.
4. Самоопределение к деятельности.
Давайте запишем в тетрадях число, классная работа.
Продолжите закономерность. На доске:
3,6,9,12 ….. ( в первой прибавляем по 3)
4,8,12,16,20 ( во второй прибавляем по 4)
5.10,15,20.25 ( в третьей прибавляем по 5)
Кто сформулирует тему нашего урока ?
«Закрепение табличного случая деления и умножения числа 5»
Решим ребусы и узнаем какую, цифру будем прописывать на минутке
чистописания
У звезды есть пять детей
Пять сверкающих лучей
Всем светить они хотят.
Всего оладий 27
По три нам хватило всем.
Кто ответит из ребят,
Сколько будет же внучат? (9)
Полюбуйтеська сами:
Мчатся тройки с бубенцами.
Сосчитать коней мы просим,
Если было троек 8. (24)
Подарил утятам ёжик
8 кожаных сапожек.
Сколько ж маленьких утят
Ёжика благодарят? ( 4)
На заборе расфуфырились коты,
Распушили свои длинные хвосты.
А хвостов то было 8.
Сколько лап ?
У кого спросим? (32)
Кто был внимателен, сколько задачек мы решили? (5)
Молодцы! Что помогло, нам справится с этими заданиями, какое качество?
(Ум)
Вывешиваем на доску.
4. Самоопределение к деятельности.
Давайте запишем в тетрадях число, классная работа.
Продолжите закономерность. На доске:
3,6,9,12 ….. ( в первой прибавляем по 3)
4,8,12,16,20 ( во второй прибавляем по 4)
5.10,15,20.25 ( в третьей прибавляем по 5)
Кто сформулирует тему нашего урока ?
«Закрепение табличного случая деления и умножения числа 5»
Решим ребусы и узнаем какую, цифру будем прописывать на минутке
чистописания
У звезды есть пять детей
Пять сверкающих лучей
Всем светить они хотят. Нарисуем без отрыва звезду.
Давайте выберем девиз нашего урока .
По очереди решаем цепочку примеров.
«Спешите делать добро».
Какое качество вам помогло? ( Выносливость, дружба)
Повторим как вы выучили таблицу на 5.
( слайды в стихах на запоминание таблицы на 5)
Что помогло вам выполнить быстро вычисления? (Знания таблицы умножения
на 5)
5. Организация познавательной деятельности
Объяснение нового материала.
С какого числа мы начнем умножение? (Запись в тетрадях)
5х5=25
5х6=30
5х7=35
5х8=40
5х9=45 5х10=50
Что интересного мы наблюдаем?
А сейчас я посмотрю, как вы внимательно работали с таблицей умножения на 5.
Посмотрите на значение произведений. Что интересное вы заметили? (Все
ответы заканчиваются на 0 и на 5)
Какую закономерность мы с вами наблюдаем?
Если умножаем на четное число, получается …(Круглое)
Каким правилом вы воспользовались при вычислении ответов в примерах
второго столбика? (От перестановки множителей произведение не меняется).
Какой пример будет следующим? (5х5)
Что нужно знать, чтобы быстро вычислить ответ в этом примере? (Таблицу
умножения с числом 5).
Нарисуем без отрыва звезду.
Давайте выберем девиз нашего урока .
По очереди решаем цепочку примеров.
«Спешите делать добро».
Какое качество вам помогло? ( Выносливость, дружба)
Повторим как вы выучили таблицу на 5.
( слайды в стихах на запоминание таблицы на 5)
Что помогло вам выполнить быстро вычисления? (Знания таблицы умножения
на 5)
5. Организация познавательной деятельности
Объяснение нового материала.
С какого числа мы начнем умножение? (Запись в тетрадях)
5х5=25
5х6=30
5х7=35
5х8=40
5х9=45 5х10=50
Что интересного мы наблюдаем?
А сейчас я посмотрю, как вы внимательно работали с таблицей умножения на 5.
Посмотрите на значение произведений. Что интересное вы заметили? (Все
ответы заканчиваются на 0 и на 5)
Какую закономерность мы с вами наблюдаем?
Если умножаем на четное число, получается …(Круглое)
Каким правилом вы воспользовались при вычислении ответов в примерах
второго столбика? (От перестановки множителей произведение не меняется).
Какой пример будет следующим? (5х5)
Что нужно знать, чтобы быстро вычислить ответ в этом примере? (Таблицу
умножения с числом 5). ФИЗМИНУТКА
Если я называю число, которое делится на пять, то вы приседаете.
Если я называю число, которое не делится на пять, то вы
подпрыгиваете.
(15,32.10,25,64,45,12,40.5)
6.Первичное закрепление.
Самостоятельная работа.
А теперь поработаем самостоятельно. У каждого из вас есть карточки,
выполните на них следующее задание:
Закрась числа, которые делятся на 5.
А теперь поменяйтесь карточками с соседом, и проверьте. Оцените работу
товарища.
Соотнесите значение с выражением.
5х5= 45
7х5= 25
9х5= 35
6х5= 40
8х5= 30
Игра «Найди пару»
5х4= 35: 5=
8х5= 45:9=
5х7= 20: 5=
9х5= 40: 8=
Какая связь между делением и умножением?
ФИЗМИНУТКА для глаз (презентация)
7. Работа над пройденным материалом.
Решение задачи №3.
Запишите уравнения. Проверьте себя ( 2 ученика у доски)
Решаем самостоятельно. 8. Подведение итога урока
Чему мы сегодня учились на уроке?
Кто уже запомнил таблицу на пять?
9. Рефлексия.
Встаньте те, кто считает, что он хорошо сегодня поработал? Почему ты так
считаешь? Какие были трудности на уроке?
Поднимите руку те, кому надо еще поработать над этой темой.
ФИЗМИНУТКА
Если я называю число, которое делится на пять, то вы приседаете.
Если я называю число, которое не делится на пять, то вы
подпрыгиваете.
(15,32.10,25,64,45,12,40.5)
6.Первичное закрепление.
Самостоятельная работа.
А теперь поработаем самостоятельно. У каждого из вас есть карточки,
выполните на них следующее задание:
Закрась числа, которые делятся на 5.
А теперь поменяйтесь карточками с соседом, и проверьте. Оцените работу
товарища.
Соотнесите значение с выражением.
5х5= 45
7х5= 25
9х5= 35
6х5= 40
8х5= 30
Игра «Найди пару»
5х4= 35: 5=
8х5= 45:9=
5х7= 20: 5=
9х5= 40: 8=
Какая связь между делением и умножением?
ФИЗМИНУТКА для глаз (презентация)
7. Работа над пройденным материалом.
Решение задачи №3.
Запишите уравнения. Проверьте себя ( 2 ученика у доски)
Решаем самостоятельно. 8. Подведение итога урока
Чему мы сегодня учились на уроке?
Кто уже запомнил таблицу на пять?
9. Рефлексия.
Встаньте те, кто считает, что он хорошо сегодня поработал? Почему ты так
считаешь? Какие были трудности на уроке?
Поднимите руку те, кому надо еще поработать над этой темой. А кому трудно было сегодня на уроке? Как вы считаете, почему?
На доске сердце, дети приклеивают звездочки, которые им выдавал капитан, весь
урок.
10. Д/з
11. Заключение.
Благодарю всех за урок. Вы отлично потрудились сегодня на уроке математики,
и я желаю вам счастливого пути по дороге знаний!
А кому трудно было сегодня на уроке? Как вы считаете, почему?
На доске сердце, дети приклеивают звездочки, которые им выдавал капитан, весь
урок.
10. Д/з
11. Заключение.
Благодарю всех за урок. Вы отлично потрудились сегодня на уроке математики,
и я желаю вам счастливого пути по дороге знаний!
Умножение четырех, на 4 и соответствующие случаи деления — Студопедия
7.8.1.1. Умножение и деление с числом 4 [MATHEMAT 281]
ВЫЧИСЛИ
4*4=?? 32:4=? 5*4=?? 7*4=?? 28:4=?
9*4=?? 16:4=? 4*6=?? 36:4=? 8:4=?
7.8.1.2. Умножение и деление с числами 2,3 и 4 [MATHEMAT 282]
ВЫЧИСЛИ
2*4=? 27:3=? 3*6=?? 4*9=?? 8*3=??
6:3=? 12:4=? 2*5=?? 24:4=? 10:2=?
Умножение пяти, на 5 и соответствующие случаи деления.
7.8.2.1. Умножение и деление с числом 5 [MATHEMAT 285]
ВЫЧИСЛИ
45:5=? 5*6=?? 40:5=? 5*8=?? 30:5=?
6*5=?? 9*5=?? 25:5=? 5*5=?? 35:5=?
7. 8.2.2. Умножение и деление с числами 2,3,4 и 5 [MATHEMAT 286]
8.2.2. Умножение и деление с числами 2,3,4 и 5 [MATHEMAT 286]
ВЫЧИСЛИ
6*5=?? 12:4=? 27:3=? 4*6=?? 9:3=?
20:5=? 2*4=? 5*9=?? 8*4=?? 15:3=?
Закрепление изученного материала.
Сравнение числовых выражений.
7.8.3.1.1. Сравнение числовых выражений, содержащих действие умножения [MATHEMAT 287]
РАССТАВЬ ЗНАКИ
9*5?5*8 6*3?3*6 8*2?2*9 4*5?4*6
3*4?4*4 9*4?4*8 4*4?4*3 8*3?3*8
7.8.3.1.2. Сравнение числовых выражений, содержащих действия умножения, деления и вычитания [MATHEMAT 37]
РАССТАВЬ ЗНАКИ
5*7?5*8 45:5?36:4 5*5?5*4-5 32:8?35:7
4*8-4?4*7 24:8?24:6 4*6?6*5 21:7?24:8
7.8.3.1.3. Кратное сравнение чисел [MATHEMAT 67]
ВО СКОЛЬКО РАЗ?
| 27 больше, чем 3:? | 25 больше, чем 5:? | 24 больше, чем 6:? | 36 больше, чем 9:? |
| 4 меньше, чем 16:? | 8 меньше, чем 24:? | 9 меньше, чем 45:? | 7 меньше, чем 28:? |
Заполнение таблицы на умножение.
7.8.3.2.1. Заполнение таблицы на нахождение произведения [TABLE 45]
НАЙДИ ПРОИЗВЕДЕНИЕ
| Множитель | ||||||||
| Множитель | ||||||||
| Произведение |
7.8.3.2.2. Заполнение таблицы на нахождение неизвестного множителя [TABLE 46]
НАЙДИ МНОЖИТЕЛЬ
| Множитель | ||||||||
| Множитель | ||||||||
| Произведение |
7. 8.3.2.3. Заполнение таблицы на нахождение неизвестного множителя и произведения [TABLE 47]
8.3.2.3. Заполнение таблицы на нахождение неизвестного множителя и произведения [TABLE 47]
ЗАПОЛНИ ТАБЛИЦУ
| Множитель | ||||||
| Множитель | ||||||
| Произведение |
Заполнение таблицы на деление.
7.8.3.3.1. Заполнение таблицы на нахождение частного [TABLE 48]
НАЙДИ ЧАСТНОЕ
| Делимое | ||||||||
| Делитель | ||||||||
| Частное |
7. 8.3.3.2. Заполнение таблицы на нахождение неизвестного делимого [TABLE 49]
8.3.3.2. Заполнение таблицы на нахождение неизвестного делимого [TABLE 49]
НАЙДИ ДЕЛИМОЕ
| Делимое | ||||||||
| Делитель | ||||||||
| Частное |
7.8.3.3.3. Заполнение таблицы на нахождение неизвестного делителя [TABLE 50]
НАЙДИ ДЕЛИТЕЛЬ
| Делимое | ||||||||
| Делитель | ||||||||
| Частное |
7. 8.3.3.4. Заполнение таблицы на нахождение неизвестных компонентов и результата деления [TABLE 51]
8.3.3.4. Заполнение таблицы на нахождение неизвестных компонентов и результата деления [TABLE 51]
ЗАПОЛНИ ТАБЛИЦУ
| Делимое | ||||||
| Делитель | ||||||
| Частное |
Умножение шести, на 6 и соответствующие случаи деления.
7.8.4.1. Умножение и деление с числом 6 [MATHEMAT 288]
ВЫЧИСЛИ
5*6=?? 30:6=? 3*6=?? 6*5=?? 42:6=?
9*6=?? 24:6=? 36:6=? 4*6=?? 48:6=?
7.8.4.2. Умножение и деление с числами 2,3,4,5 и 6 [MATHEMAT 289]
ВЫЧИСЛИ
6*5=?? 18:3=? 4*5=?? 24:8=? 3*9=??
8*5=?? 27:3=? 2*6=?? 12:4=? 24:3=?
Умножение семи, на 7 и соответствующие случаи деления.
7.8.5.1. Умножение и деление с числом 7 [MATHEMAT 290]
ВЫЧИСЛИ
49:7=? 3*7=?? 6*7=?? 42:7=? 8*7=??
21:7=? 35:7=? 9*7=?? 14:7=? 4*7=??
7.8.5.2. Умножение и деление с числами 2,3,4,5,6 и 7 [MATHEMAT 291]
ВЫЧИСЛИ
4*7=?? 27:3=? 5*4=?? 9*4=?? 14:7=?
12:4=? 3*5=?? 24:8=? 7*5=?? 14:2=?
Умножение восьми, на 8 и соответствующие случаи деления.
7.8.6.1. Умножение и деление с числом 8 [MATHEMAT 284]
ВЫЧИСЛИ
4*8=? 40:8=? 6*8=?? 5*8=?? 32:8=?
8*8=?? 24:8=? 3*8=?? 48:8=? 7*8=??
7.8.6.2. Умножение и деление с числами 2,3,4,5,6,7 и 8 [MATHEMAT 280]
ВЫЧИСЛИ
24:6=? 5*8=?? 8*3=?? 27:9=? 5*8=??
3*3=? 24:3=? 42:7=? 9*3=?? 27:3=?
Умножение девяти, на 9 и соответствующие случаи деления.
7.8.7.1. Умножение и деление с числом 9 [MATHEMAT 279]
ВЫЧИСЛИ
6*9=?? 63:9=? 2*9=?? 27:9=? 7*9=??
8*9=?? 36:9=? 45:9=? 4*9=?? 9*9=??
7. 8.7.2. Умножение и деление с числами 2,3,4,5,6,7,8 и 9 [MATHEMAT 278]
8.7.2. Умножение и деление с числами 2,3,4,5,6,7,8 и 9 [MATHEMAT 278]
ВЫЧИСЛИ
56:8=? 6*7=?? 49:7=? 8*2=?? 5*4=??
8*9=?? 48:6=? 5*5=?? 35:7=? 6*3=??
Таблица умножения.
7.8.8.1. Упражнение 1 [TABLE 52]
ЗАПОЛНИ ТАБЛИЦУ
| Множители | *[2] | *[3] | *[4] | *[5] | *[6] | *[7] | *[8] | *[9] |
| [2] | ||||||||
| [3] | ||||||||
| [4] | ||||||||
| [5] | ||||||||
| [6] | ||||||||
| [7] | ||||||||
| [8] | ||||||||
| [9] |
7. 8.8.2. Упражнение 2 [TABLE 53]
8.8.2. Упражнение 2 [TABLE 53]
ДОПОЛНИ ТАБЛИЦУ УМНОЖЕНИЯ
| *[2] | *[3] | *[4] | *[5] | *[6] | *[7] | *[8] | *[9] | |
| [2] | ||||||||
| [3] | ||||||||
| [4] | ||||||||
| [5] | ||||||||
| [6] | ||||||||
| [7] | ||||||||
| [8] | ||||||||
| [9] |
Закрепление изученного материала.
Выполнение табличного умножения со случайно заданными компонентами.
7.8.9.1.1. Упражнение 1 (10 заданий) [CALCULAT 33]
Модульное деление через мультипликативное обратное знаменатель
Модульное деление с помощью обратного мультипликативного
знаменатель
Next: Инвертирование модульно-арифметических функций Вверх: Содержание Предыдущий: Модульное умножение
Модульное деление сложнее. Мы исходим из того, что деление должно быть противоположно умножению. Мы видели это в моде 7 арифметика, 5 умножить на 6 дает 2. Отсюда следует, что 2 разделить на 6 должно получиться 5.Это действительно так.
Однако это не всегда будет работать. По модулю 15, на что 10 разделить
5? Ну, можно было бы подумать, что ответ будет 2. С другой стороны,
поскольку в приведенном выше примере 5 умножить на 5 равно 10, возможно, ответ будет 5.
Опять же, в другом примере выше, 8 умножить на 5 равно 10, можно сказать
ответ 8.
Вместо того, чтобы допускать несколько ответов, мы бы сказали в этом случае, что нет ответа. Это аналогично делению на ноль в обычном арифметика.
Концепция мультипликативного обратного поможет нам получить ответ когда он есть, и поможет нам предсказать, когда его нет отвечать.Мультипликативным обратным числом b является число c . так что b умножить на c равно 1. В обычной арифметике мультипликативное обратное число b является обратным числом b , а именно 1/ b . Например, предположим, что мы работаем с модулем 7. мультипликативное число, обратное 3, равно 5, потому что 3 умножить на 5 равно 1. (Для по той же причине мультипликативное значение, обратное 5, равно 3.) Мы можем найти мультипликативные инверсии путем построения таблицы умножения.Вот таблица умножения по модулю 7.
Глядя на таблицу, мы видим, что мультипликативная величина, обратная 1, равна
1, мультипликативное обратное 2 равно 4 (и наоборот),
мультипликативное значение, обратное 3, равно 5 (и наоборот), и
мультипликативное значение, обратное 6, равно 6. Обратите внимание, что 0 не имеет
мультипликативное обратное. Это соответствует факту в обычном
арифметика, что 1 разделить на 0, не имеет ответа.
Обратите внимание, что 0 не имеет
мультипликативное обратное. Это соответствует факту в обычном
арифметика, что 1 разделить на 0, не имеет ответа.
Теперь мы знаем, как делить 1 на разные числа по модулю 7: а именно, 1, деленная на b , является мультипликативной инверсией b .Как мы разделить другие числа? Для целей этого класса ответ таков: чтобы разделить a на b , просто разделите 1 на b , а затем умножьте результат от до . Например, разделим 5 на 4 (по модулю 7). Сейчас 1 разделить на 4 равно 2, потому что 2 умножить на 4 равно 1. Следовательно, мы умножаем 5 на 2, получая 3. В Mathese,
следовательно
следовательно
Это сработало? Должны ли мы принять это? Ну, умножь с обеих сторон по 4.С левой стороны получаем 5. С правой стороны получаем получить, что действительно соответствует 5.
Ниже приведены дополнительные примеры мода 7. Проверьте результат, умножив обе части по знаменателю.
Для некоторых модулей некоторые числа не имеют мультипликативных
инверсии. Например, по модулю 15 число 12 не имеет
мультипликативное обратное. Нет числа, которое при умножении на
12 дает результат, конгруэнтный по модулю 15:1.Если вы построите
mod 15 таблица умножения, вы найдете множество других стандартных
имена (в частности, 0, 3, 5, 6, 9 и 10) не имеют
мультипликативные инверсии. Это явление исследуется в следующем
раздел.
Например, по модулю 15 число 12 не имеет
мультипликативное обратное. Нет числа, которое при умножении на
12 дает результат, конгруэнтный по модулю 15:1.Если вы построите
mod 15 таблица умножения, вы найдете множество других стандартных
имена (в частности, 0, 3, 5, 6, 9 и 10) не имеют
мультипликативные инверсии. Это явление исследуется в следующем
раздел.
Обратите внимание, однако, что все еще бывают случаи, когда по модулю 15 деление на 12 имеет смысл. Например, поскольку , это имеет смысл определить как 9. Теория чисел рассчитать такие дроби немного сложнее, чем Теория чисел рассматривается в этом классе, поэтому мы не будем просить вас вычислять такие подразделения.
Next: Обращение модульно-арифметических функций Вверх: Содержание Предыдущий: Модульное умножение
Лиза ЭкштейнПн, 21 октября, 22:56:24 по восточному поясному времени 1996
Что такое произведение в математике? — Определение и обзор — Видео и стенограмма урока
Как найти произведение
Умножение часто называют повторным сложением , потому что задача на умножение говорит вам о том, что у вас есть определенное количество групп чего-либо, каждая из которых содержит определенное число. Еще не запутались? Вот пример.
Еще не запутались? Вот пример.
У вас есть 3 пакета конфет, в каждом пакете 5 конфет. Сколько у тебя конфет?
Есть два способа решить эту проблему. Первый — сложить конфеты:
5 + 5 + 5 = 15
Другой способ решить — использовать умножение, потому что у вас есть 3 группы конфет по 5 штук в каждом мешочке.
3 * 5 = 15
Ответом на эту задачу на умножение является произведение, которое в данном случае равно 15.
Вот еще пример. В классе 8 рядов стульев, в каждом ряду по 7 стульев. Сколько здесь стульев?
Опять же, вы можете добавить:
7 + 7 + 7 + 7 + 7 + 7 + 7 + 7 = 56
Или вы можете найти произведение, умножив:
7 * 8 = 56
Свойства Умножение
Есть четыре основных свойства умножения, которые верны независимо от того, что перемножается.
1. Коммутативное свойство : При умножении двух чисел произведение будет одинаковым независимо от порядка их записи.
Например:
5 * 7 = 7 * 5
2. Ассоциативное свойство : При умножении трех или более чисел результат будет одинаковым независимо от того, какие два числа умножаются первыми.
Ассоциативное свойство : При умножении трех или более чисел результат будет одинаковым независимо от того, какие два числа умножаются первыми.
Например:
(2 * 4) * 6 = 2 * (4 * 6)
8 * 6 = 2 * 24
48 = 48
3. Свойство мультипликативной идентичности : произведение любого число и 1 это число.
Например:
3 * 1 = 3
4. Распределительное свойство : Сумма двух чисел, умноженная на третье число, равна сумме каждого слагаемого, умноженного на третье число.
Например:
2 * (3 + 4) = 2 * 3 + 2 * 4
2 * 7 = 6 + 8
14 = 14
Специальные продукты
Следует упомянуть два специальных продукта.
1. Произведение любого числа, умноженного на 1, есть это число. Вы узнали об этом в примере с мультипликативным свойством идентичности выше.
Например:
7 * 1 = 7
2,376 * 1 = 2,376
2. Произведение любого числа, умноженного на 0, равно 0. = 0
Краткий обзор урока
Произведение — это ответ на задачу на умножение. Вы можете найти продукт с помощью процесса, называемого повторным сложением , то есть путем сложения количества групп в задаче. Есть четыре свойства, которые определяют правила решения задач на умножение: коммутативное , ассоциативное , мультипликативное тождество и дистрибутивное .Есть также два специальных правила произведения: произведение любого числа, умноженного на единицу, будет этим числом, а произведение любого числа, умноженного на ноль, будет равно нулю.
Вы можете найти продукт с помощью процесса, называемого повторным сложением , то есть путем сложения количества групп в задаче. Есть четыре свойства, которые определяют правила решения задач на умножение: коммутативное , ассоциативное , мультипликативное тождество и дистрибутивное .Есть также два специальных правила произведения: произведение любого числа, умноженного на единицу, будет этим числом, а произведение любого числа, умноженного на ноль, будет равно нулю.
Поиск продукта
- Произведение является ответом на задачу на умножение.
- Чтобы найти продукт, вы можете использовать многократное сложение или умножение.
- Задачи на умножение обладают четырьмя свойствами: коммутативным, ассоциативным, мультипликативным, тождественным и дистрибутивным.
- Любое число, умноженное на 1, равно самому себе, а любое число, умноженное на 0, равно 0.
Результаты обучения
Изучите этот урок, чтобы точно выполнить следующие действия:
- Распознать произведение задачи на умножение
- Продемонстрировать два метода поиска продукта
- Перечислите четыре свойства умножения
- Расчет специальных продуктов
Иллюстративная математика — Учителя | Кендалл Хант
Объем и последовательность
Рассказ
Основные идеи 5 класса включают в себя: развитие беглости при сложении и вычитании дробей, развитие понимания умножения и деления дробей в ограниченных случаях (единицы дробей, разделенные на целые числа, и целые числа, разделенные на единичные дроби), расширение деления до двух- делители цифр, развитие понимания операций с десятичными дробями до сотых, развитие беглости с целыми числами и десятичными операциями, а также развитие понимания объема.
Математическая работа для 5 класса разбита на 8 частей:
- В поисках тома
- Дроби как частные и умножение дробей
- Умножение и деление дробей
- Завершение умножения и деления многозначных чисел
- Образцы разрядных значений и десятичные операции
- Дополнительные операции с десятичными дробями
- Формы на координатной плоскости
- Собираем все вместе
Часть 1: В поисках тома
Модуль Цели обучения
- Учащиеся находят объем прямоугольных призм и объемных фигур, составленных из двух прямоугольных призм.
Этот модуль знакомит учащихся с понятием объема, опираясь на их понимание площади и умножения.
В 3 классе учащиеся узнали, что площадь двумерной фигуры – это количество квадратных единиц, покрывающих ее без пробелов и наложений. Сначала они нашли площади, считая квадраты, и интуитивно поняли, что площадь аддитивна. Позже они определили площадь прямоугольника как произведение длин его сторон и нашли площадь более сложных фигур, состоящих из прямоугольников.
Здесь учащиеся узнают, что объем объемной фигуры – это количество единичных кубов , которые заполняют ее без промежутков и перекрытий. Во-первых, они измеряют объем, считая единичные кубы, и наблюдают его аддитивный характер. Они также узнают, что разные объемные фигуры могут иметь одинаковый объем.
Затем они переключают свое внимание на правильные прямоугольные призмы: строят их с помощью единичных кубов, анализируют их структуру и находят их объем. Они пишут числовые выражения для представления своих стратегий рассуждений и работают со все более абстрактными представлениями призм.
Позже учащиеся обобщают, что объем прямоугольной призмы можно найти, умножив размеры ее сторон (\(\text{длина} \times \text{ширина} \times \text{высота}\)) или путем умножения площадь основания и его высота (\(\text{площадь основания} \times \text{высота}\)). Анализируя, записывая и оценивая различные выражения, представляющие объем одной и той же призмы, учащиеся возвращаются к знакомым свойствам операций из более ранних классов.
Позже в этом модуле учащиеся применяют эти знания, чтобы найти объем объемных фигур, состоящих из двух непересекающихся прямоугольных призм, и решить реальные задачи, связанные с такими фигурами.При этом они также переходят от использования кубов к использованию стандартных единиц измерения объема.
Секция A: кубы единиц измерения и объем
Согласование стандартов
| Адресация | 5.MD.C.3, 5.MD.C.3.b, 5.MD.C.4, 5.MD.C.5.a, 5.OA.A.2 |
Раздел Цели обучения
- Описать объем как пространство, занимаемое твердым объектом.
- Измерьте объем прямоугольной призмы, найдя количество единичных кубов, необходимых для ее заполнения.
- Используйте многослойную структуру в прямоугольной призме, чтобы найти объем.
В этом разделе учащиеся понимают объем как измерение трехмерных фигур, строя объекты с помощью единичных кубов и считая кубы. Они экспериментируют с разными фигурами, сделанными из одного и того же количества кубиков, и видят, что они имеют одинаковый объем.
Они экспериментируют с разными фигурами, сделанными из одного и того же количества кубиков, и видят, что они имеют одинаковый объем.
Затем учащиеся строят правильные прямоугольные призмы и анализируют изображения призм, составленных из единичных кубов. Чтобы найти объем этих тел, учащиеся смотрят на их структуру и соотносят количество горизонтальных и вертикальных слоев с общим количеством кубов (MP7).Они обращаются к коммутативным и ассоциативным свойствам умножения, поскольку рассуждают об объеме прямоугольных призм, ориентированных по-разному.
ПЛК: Урок 4, Занятие 1, Слои в прямоугольных призмах
Раздел B: Выражения для нахождения объема
Согласование стандартов
| Адресация | 5.MD.C.4, 5.MD.C.5.a, 5.MD.C.5.b, 5.OA.A.1, 5.OA.A.2 |
Раздел Цели обучения
- Опишите вычисления из предыдущего раздела как $\text{длина} \times \text{ширина} \times \text{высота}$ или $\text{площадь основания} \ раз \text{высота}$.

- Найдите объем, используя $\text{длина} \times \text{ширина} \times \text{высота}$ или $\text{площадь основания} \times \text{высота}$.
В этом разделе учащиеся продолжают работать с правильными прямоугольными призмами и связывать измерения сторон с объемом. Они заметили, что умножение количества слоев кубов в призме на количество кубов в одном слое дает ее объем. Они также видят, что количество кубов в одном слое по сути равно площади прямоугольника.
Затем учащиеся обобщают объем прямоугольной призмы как произведение длин ее сторон, \(\text{длина} \times \text{ширина} \times \text{высота}\) и как произведение площади его основание и его высота, \(\text {базовая площадь} \times \text {высота}\).
Чтобы способствовать гибкому использованию измерений и осмыслению при нахождении объема, учащиеся связывают эти математические термины с числовыми выражениями, представляющими объем, а не полагаются на алгебраические формулы. Эта работа усиливает ассоциативное свойство умножения и подчеркивает, что объем прямоугольной призмы может быть представлен эквивалентными выражениями умножения.
ПЛК: Урок 5, Занятие 2, Растущая призма
Секция C: Объем твердых фигур
Согласование стандартов
| Адресация | 5.MD.C, 5.MD.C.5, 5.MD.C.5.c, 5.OA.A.1, 5.OA.A.2 |
Раздел Цели обучения
- Найти объем фигуры, составленной из прямоугольных призм.
В этом разделе учащиеся применяют свое понимание объема для решения реальных и математических задач. Они сталкиваются с твердыми фигурами, состоящими из двух или более правильных прямоугольных призм, что укрепляет их понимание аддитивной природы объема.
Описание: 6-гранная прямоугольная призма.Прямые стороны. Все длины сторон сходятся под прямым углом. Длины сторон. Нижний, 6 футов. Правая сторона поднимается на 2 фута, затем уходит на 4 фута влево, поднимается на 3 фута, затем идет на 2 фута влево, затем опускается на 5 футов. Ширина указана как 3 фута.
Ширина указана как 3 фута.
Учащиеся также работают с более длинными сторонами, чем в предыдущих разделах, что побуждает их активировать стратегии умножения из более ранних классов. Работа напоминает учащимся, что они могут разлагать многозначные множители по разрядному значению, чтобы найти свой продукт, прокладывая путь к стандартному алгоритму умножения в более поздних единицах.
ПЛК: Урок 10, Упражнение 2, Найдите объем разными способами
Расчетное количество дней: 11–12
Модуль 2: дроби как частные и умножение дробей
Модуль Цели обучения
- Учащиеся развивают понимание дробей как деления числителя на знаменатель, то есть $a \div b = \frac{a}{b}$, и решают задачи на умножение целое число и дробь, включая дроби больше 1.
В этом разделе учащиеся учатся интерпретировать дробь как частное и расширяют свое понимание умножения целых чисел и дробей.
В 3 классе учащиеся научились умножать и делить целые числа на равные по размеру группы. В 4 классе они использовали умножение для представления групп одинакового размера с дробным количеством в каждой группе и для выражения сравнения.
В 4 классе они использовали умножение для представления групп одинакового размера с дробным количеством в каждой группе и для выражения сравнения.
Например, \(4 \times \frac{1}{3}\) может представлять «4 группы \(\frac{1}{3}\)» или «в 4 раза больше, чем \(\frac{ 1}{3}\)».
Сумма в обоих случаях может быть представлена заштрихованными частями диаграммы следующим образом:
Здесь учащиеся узнают, что дробь типа \(\frac{4}{3}\) также может представлять:
- ситуация разделения, когда 4 объекта совместно используются 3 человеками, или \(4 \div 3\)
- часть группы, в данном случае \(\frac{1}{3}\) группы из 4 объектов или \(\frac{1}{3} \times 4\)
Учащиеся также интерпретируют произведение целого числа на дробь через длины сторон прямоугольника.Выражение \(6 \times 1\) представляет собой площадь прямоугольника, которая составляет 6 единиц на 1 единицу. Точно так же \(6 \times \frac{2}{3}\) представляет единицу, равную 6 единицам на \(\frac{2}{3}\) единицу.
Коммутативные и ассоциативные свойства становятся очевидными, когда учащиеся связывают разные выражения с одной и той же диаграммой. Распределительное свойство вступает в игру, когда учащиеся умножают целое число и дробь, записанные в виде смешанного числа, например: \(2 \times 3\frac{2}{5} = (2 \times 3) + (2 \times \frac{2}{5})\).
В этом модуле предполагается, что совместное использование всегда является равноправным, независимо от того, указано это явно или нет. Например, в приведенной выше ситуации 4 объекта используются поровну тремя людьми.
Раздел A: Дроби как частные
Согласование стандартов Цели обучения по разделам
- Представление и объяснение отношений между делением и дробями.
- Решите задачи на деление целых чисел, чтобы ответы были дробями.
В этом разделе учащиеся учатся видеть дробь как частное, результат деления числителя на знаменатель. Они решают последовательность задач о ситуациях, связанных с равным использованием целого ряда объектов. Путем повторных рассуждений они замечают закономерность в результате деления (MP8) и обобщают, что \(\frac{a}{b} = a \div b\).
Путем повторных рассуждений они замечают закономерность в результате деления (MP8) и обобщают, что \(\frac{a}{b} = a \div b\).
Например, 3 объекта, которые поровну делят 2 человека, можно представить выражением \(3 \div 2\) и диаграммой.Доля каждого человека может быть показана заштрихованными частями на диаграмме, например:
или
Каждый человек получит половину из 3 объектов или 3 группы \(\frac{1}{2}\) объекта. Значение этого выражения равно \(\frac{3}{2}\) или \(1\frac{1}{2}\).
ПЛК: Урок 3, Упражнение 2, Интерпретация выражений
Раздел B: Доли целых чисел
Согласование стандартов
| Адресация | 5.NF.B, 5.NF.B.3, 5.NF.B.4, 5.NF.B.4.a, 5.OA.A.2 |
Раздел Цели обучения
- Соединить деление с умножением целого числа на нецелую дробь.
- Соединить деление с умножением целого числа на дробную часть.

- Исследуйте взаимосвязь между умножением и делением.
В 4 классе учащиеся увидели, что неединичная дробь может быть выражена как произведение целого числа и единичной дроби или целого числа и неединичной дроби с одним и тем же знаменателем.Например, \(\frac{8}{3}\) может быть выражено как \(8 \times \frac{1}{3}\), как \(4 \times \frac{2}{3}\ ), или как \(2 \times \frac{4}{3}\). В предыдущем разделе учащиеся интерпретировали дробь вида \(\frac{8}{3}\) как частное: \(8 \div 3\).
Этот раздел позволяет учащимся соединить эти две интерпретации \(\frac{8}{3}\) и связать \(8 \times \frac{1}{3}\) и \(8 \div 3\).
Учащиеся используют схемы и контексты, чтобы разобраться в ситуациях деления, в результате которых получается дробное частное.Когда они интерпретируют и пишут выражения, представляющие величины, учащиеся наблюдают коммутативное свойство умножения. Например, они интерпретируют \(8 \times \frac{1}{3}\) и \(\frac{1}{3} \times 8\) как 8 групп из трети и трети из 8 соответственно.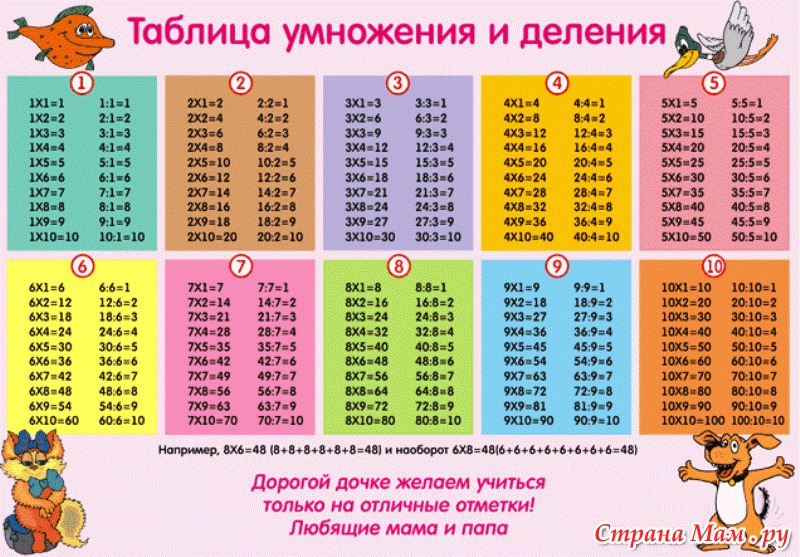 и признать, что оба равны \(\frac{8}{3}\).
и признать, что оба равны \(\frac{8}{3}\).
Эти знания затем помогут учащимся понять другие выражения умножения и деления, которые могут быть представлены той же диаграммой и иметь такое же значение:
\(4 \times \frac{2}{3}\)
\(\frac{2}{3} \times 4\)
\(4 \раз (2 \дел 3)\)
\(2 \раз (4 \дел 3)\)
PLC: Урок 7, Задание 1, Как далеко они пробежали?
Секция C: площадь и части длины сторон
Согласование стандартов
| Адресация | 5.NF.B, 5.NF.B.3, 5.NF.B.4, 5.NF.B.4.a, 5.NF.B.4.b, 5.OA.A, 5.OA. А.1 |
Раздел Цели обучения
- Найти площадь прямоугольника, если длина одной стороны представляет собой целое число, а длина другой стороны — дробное или смешанное число.
- Представлять и решать задачи на умножение целого числа на дробь или смешанное число.
- Напишите, интерпретируйте и оцените числовые выражения, представляющие умножение целого числа на дробь или смешанное число.

В этом разделе учащиеся узнают, что они могут рассуждать о площади прямоугольника с дробной длиной стороны так же, как и с прямоугольниками с целочисленными длинами сторон: используя диаграммы и умножение.
Чтобы найти площадь таких прямоугольников, учащиеся работают с последовательностью дробных длин сторон: единичная дробь (\(\frac{1}{3}\)), неединичная дробь (\(\frac{2} {3}\)), дробь больше 1 (\(\frac{5}{3}\)) и смешанное число (\(1\frac{2}{3}\)).Они пишут и интерпретируют выражения умножения, такие как \(6 \times \frac{1}{3}\) и \(6 \times \frac{5}{3}\), которые представляют площадь таких прямоугольников. Учащиеся используют заштрихованные диаграммы и свое понимание дробей, чтобы рассуждать о значении выражений.
Попутно становится очевидным ассоциативное свойство умножения. Например, учащиеся видят, что выражения \(6 \times \frac{2}{5}\), \(6 \times 2 \times \frac{1}{5}\) и \(12 \times \ frac{1}{5}\) могут описать площадь заштрихованной области на этой диаграмме.
Распределительное свойство иллюстрируется тем, что учащиеся рассуждают о площади прямоугольника, длины сторон которого представляют собой целое и смешанное числа. Например, чтобы найти \(2 \times 3 \frac{2}{5} \), учащиеся могут разложить прямоугольник, сгруппировав целые и дробные единицы и умножив их по отдельности перед их объединением, в результате чего получится выражение например, \((2 \times 3) + \left (2 \times \frac{2}{5}\right)\).
ПЛК: Урок 11, Упражнение 1, Больше одного
Расчетное количество дней: 15–17
Модуль 3: Умножение и деление дробей
Модуль Цели обучения
- Учащиеся изучают умножение и деление целых чисел, чтобы умножать дроби на дроби и делить целое число и единичную дробь.
В этом модуле учащиеся находят произведение двух дробей, делят целое число на единичную дробь и делят единичную дробь на целое число.
Раньше учащиеся понимали произведение целого числа и дроби на длины сторон и площади прямоугольника. Здесь они одинаково понимают умножение двух дробей. Учащиеся интерпретируют диаграммы площадей с двумя долями единиц длины сторон, затем с долей единицы и долей неединиц, а затем с двумя дробями неединиц.
Здесь они одинаково понимают умножение двух дробей. Учащиеся интерпретируют диаграммы площадей с двумя долями единиц длины сторон, затем с долей единицы и долей неединиц, а затем с двумя дробями неединиц.
Посредством повторяющихся рассуждений учащиеся замечают закономерность в стоимости продукта (MP8). Они обобщают, что его можно найти путем умножения числителей и умножения знаменателей множителей:
\(\displaystyle{\frac{a}{b} \times \frac{c}{d} = \frac{a\times c}{b\times d}}\)
Например, \(\frac{2}{4} \times \frac{3}{5}\) равно \(\frac{2 \\times \ 3}{4 \\times \ 5}\) потому что во всем квадрате \(4 \times 5\) равных частей и \(2 \times 3\) части заштрихованы.
Затем учащиеся разбираются в ситуациях деления и выражениях, включающих целое число и дробную часть. Они напоминают, что деление можно понимать с точки зрения нахождения количества групп одинакового размера или нахождения размера каждой группы.
Например, учащиеся интерпретируют \(\frac{1}{3} \div 4\) как нахождение размера одной части, если \(\frac{1}{3}\) разделить на 4 равные части, и \(4 \div \frac{1}{3}\) означает нахождение количества \(\frac{1}{3}\) в числе 4.
Учащиеся рассматривают, как изменение делимого или делителя меняет значение частных, и ищут закономерности (MP8). Они используют ленточные диаграммы, чтобы представлять и рассуждать о ситуациях деления и выражениях.
Позже в модуле учащиеся применяют полученные знания для решения задач. Связь между умножением и делением усиливается, когда они замечают, что обе операции могут использоваться для решения одной и той же задачи.
Раздел A: Умножение дробей
Согласование стандартов
| Адресация | 5.NF.B.4, 5.NF.B.4.a, 5.NF.B.4.b, 5.NF.B.6 |
Раздел Цели обучения
- Осознать, что $\frac{a}{b} \times \frac{c}{d}=\frac{a \\times \ c}{b \\times \ d} $ и использовать это обобщение для численного умножения дробей.
- Представлять и описывать умножение дроби на дробь с использованием понятий площади.

В этом разделе учащиеся рассуждают об умножении двух дробей. Они начинают с рассмотрения ситуаций, связанных с нахождением доли дроби.Они представляют ситуации, рисуя диаграммы, которые имеют для них смысл.
Например, «Кастрюля с макаронами и сыром \(\frac {1}{3}\) полна. Киран ест \(\frac {1}{4}\) макарон с сыром. Сколько из всей сковороды съела Киран?»
Разделив первую треть сковороды на четверти и проделав то же самое с двумя другими третями, учащиеся могут увидеть, что Киран съела \(\frac{1}{12}\) всей сковороды.
Описание: Схема.Квадрат, длина и ширина, 1. Разделен по горизонтали на 3 равных прямоугольника. верхний прямоугольник разделен по вертикали на 4 равных прямоугольника. 1 прямоугольник заштрихован темно-синим, 3 прямоугольника заштрихован светло-голубым.
Учащиеся связывают произведение двух дробей с площадью прямоугольника с дробными сторонами. При умножении единичных дробей учащиеся видят знаменатель как количество равных частей в единичном квадрате, структурированном в виде массива. Таким образом, разделив одну сторону прямоугольника на четверти, а другую на трети, можно создать массив 4 на 3.Каждая часть массива равна \(\frac{1}{12}\) одного целого.
Таким образом, разделив одну сторону прямоугольника на четверти, а другую на трети, можно создать массив 4 на 3.Каждая часть массива равна \(\frac{1}{12}\) одного целого.
Площадь прямоугольника, который равен \(\frac{1}{4}\) на \(\frac{1}{3}\), таким образом, \(\frac{1}{12}\) или \ (\frac{1}{4} \times \frac{1}{3} = \frac{1}{4 \\times \ 3} = \frac{1}{12}\). Студенты обобщают это как:
\ (\ displaystyle {\ frac {1} {b} \ times \ frac {1} {d} = \ frac {1} {b \ \ times \ d}} \)
Они расширяют это понимание, чтобы найти произведение неединичных дробей, включая дроби больше 1.
Например, значение \(\frac{3}{4} \times \frac{7}{5}\) равно \(\frac{3 \ \times \ 7}{4 \ \times \ 5} \) потому что \(3 \times 7\) части заштрихованы и в 1 целом есть \(4 \times 5\) равные части.
\(\displaystyle{\frac{a}{b} \times\frac{c}{d} = \frac{a \\times\c}{b \\times\d}}\)
ПЛК: Урок 3, Упражнение 1, Шаблоны уведомлений в выражениях
Секция B: Фракция
Согласование стандартов
| Адресация | 5. NF.B.7, 5.NF.B.7.a, 5.NF.B.7.b, 5.NF.B.7.c NF.B.7, 5.NF.B.7.a, 5.NF.B.7.b, 5.NF.B.7.c |
Раздел Цели обучения
- Разделить дробную часть на целое число, используя понятия деления целых чисел.
- Разделите целое число на дробную часть, используя принцип деления целых чисел.
В 3-м классе учащиеся узнали, что деление можно понимать с точки зрения групп одинакового размера и интерпретировать двумя способами. Например, \(8 \div 4\) может означать нахождение размера каждой группы, если 8 разложить на 4 равные группы, или нахождение количества групп по 4 в 8.
В этом разделе учащиеся расширяют эту идею, чтобы разделить дробную единицу на целое число и разделить целое число на дробную единицу.Они интерпретируют \(\frac{1}{2} \div 5\) как определение размера одной части, если \(\frac{1}{2}\) разделить на 5 равных частей, а \(5 \ div \frac{1}{2}\) как способ узнать, сколько \(\frac{1}{2}\) содержится в 5.
Чтобы развить это понимание, учащиеся рассуждают о ситуациях, диаграммах и выражениях, представляющих деление. Они ищут закономерности и оценивают обоснованность найденных частных.
Они ищут закономерности и оценивают обоснованность найденных частных.
Учащиеся могут заметить, что для нахождения \(5 \div \frac{1}{2}\) им нужно умножить 5 на 2, потому что в каждом из 5 целых есть 2 половинки.Однако на этом этапе учащиеся не обязательно обобщают деление дробей, поскольку они будут делать это в 6-м классе.
ПЛК: Урок 12, Занятие 2, Работа Прии
Раздел C: Решение задач с дробями
Согласование стандартов
| Адресация | 5.NF.B, 5.NF.B.4, 5.NF.B.6, 5.NF.B.7, 5.NF.B.7.b, 5.NF.B.7.c |
Раздел Цели обучения
- Решение задач на умножение и деление дробей.
В этом разделе учащиеся решают задачи на умножение и деление дробей. Когда они рассуждают о ситуациях и интерпретируют ленточные диаграммы, они видят, что одну и ту же ситуацию или диаграмму можно выразить с помощью умножения или деления.
Например, если \(\frac{1}{2}\) галлона лимонада делится поровну между 5 друзьями, каждый друг получит \(\frac{1}{2} \div 5\) галлонов лимонада. Это также означает, что каждый друг получает \(\frac{1}{5}\) из \(\frac{1}{2}\) галлонов, что можно выразить как \(\frac{1}{5} \times \frac{1}{2}\).
Учащиеся интерпретируют ситуации и диаграммы с точки зрения одной или обеих операций, в зависимости от того, что имеет смысл в данном контексте. На этой диаграмме заштрихованная часть представляет как \(\frac{1}{2} \div 5\), так и \(\frac{1}{5} \times \frac{1}{2}\).
ПЛК: Урок 17, Упражнение 1, Информационный пробел: Плитки
Расчетное количество дней: 17–20
Модуль 4: Завершение умножения и деления многозначных чисел
Модуль Цели обучения
- Учащиеся используют стандартный алгоритм для умножения многозначных целых чисел.Они делят целые числа до четырех цифр на двузначные делители, используя стратегии, основанные на разрядности и свойствах операций.

В этом разделе учащиеся умножают многозначные целые числа, используя стандартный алгоритм, и начинают работать над беглостью речи, ожидаемой в конце класса. Они также находят целые числа с до четырехзначными делимыми и двузначными делителями.
В 4 классе учащиеся использовали стратегии, основанные на разрядном значении и свойствах операций, для умножения однозначного целого числа и целого числа до четырех цифр, а также для умножения пары двузначных чисел.Они разложили факторы по разрядным значениям и использовали диаграммы и алгоритмы, использующие частичные произведения, для записи своих рассуждений.
Здесь учащиеся используют эти стратегии, чтобы понять стандартный алгоритм умножения. Они признают, что это также основано на стоимости места, но регистрирует частичные продукты в сжатом виде.
Хан и Елена использовали разные алгоритмы, чтобы найти значение \(3 \times 318\).
Объясните своему партнеру, что сделали Хан и Елена.Что представляет собой 2 в алгоритме Елены?
В 4-м классе учащиеся также находили частное целых чисел, используя стратегии разрядных значений и взаимосвязь между умножением и делением. Они разлагали дивиденды различными способами и находили частичные частные. Числа, с которыми они столкнулись тогда, были ограничены четырехзначными делителями и однозначными делителями. В этом модуле они расширяют эту работу, чтобы включить двузначные делители.
Они разлагали дивиденды различными способами и находили частичные частные. Числа, с которыми они столкнулись тогда, были ограничены четырехзначными делителями и однозначными делителями. В этом модуле они расширяют эту работу, чтобы включить двузначные делители.
По мере того, как они строят свое устройство с многозначным умножением и делением, учащиеся решают задачи на площадь и объем и укрепляют свое понимание этих понятий.
Раздел A: Многозначное умножение с использованием стандартного алгоритма
Согласование стандартов
| Адресация | 5.MD.C.3, 5.MD.C.5, 5.NBT, 5.NBT.B, 5.NBT.B.5, 5.NF.B.4, 5.OA.A.2 |
Раздел Цели обучения
- Умножать многозначные целые числа по стандартному алгоритму.
В этом разделе представлен стандартный алгоритм умножения, расширяющий предыдущую работу учащихся по умножению. В 4 классе учащиеся использовали диаграммы и алгоритмы частичного произведения, чтобы найти произведение однозначного числа и числа до четырех цифр, а также произведение двух двузначных чисел. Они озаботились ролью места на этом пути.
В 4 классе учащиеся использовали диаграммы и алгоритмы частичного произведения, чтобы найти произведение однозначного числа и числа до четырех цифр, а также произведение двух двузначных чисел. Они озаботились ролью места на этом пути.
Учащиеся возвращаются к этим стратегиям и представлениям здесь, но работают с множителями с большим количеством цифр, чем встречалось в 4 классе. Они устанавливают связи между частичными произведениями на диаграммах и предыдущими алгоритмами с числами в стандартном алгоритме.Они также узнают, как записывать новые разрядные единицы, полученные в результате нахождения частичных произведений.
При использовании стандартного алгоритма для умножения двузначного и трехзначного числа учащиеся, как и раньше, учитывают разрядность умножаемых цифр.
Например, 3 в 23 представляет 3 единицы, поэтому \(3 х 123\) равно 369.
Однако 2 в 23 представляет 2 десятка, поэтому частичное произведение равно \(2 \times 10 \times 123\) или 2460, а не \(2 \times 123\) или 246.
Частичные произведения 369 и 2460 также можно увидеть на диаграмме.
Описание: умножить. сто двадцать три раза 23. 5 ряд. Первый ряд: сто двадцать три. Второй ряд: символ умножения, 23. Горизонтальная черта. Третий ряд: триста шестьдесят девять. Четвертый ряд: плюс две тысячи четыреста шестьдесят. Горизонтальная линия. Пятая строка: две тысячи восемьсот двадцать девять
.
После того, как учащиеся попрактиковались в записи продуктов таким образом, они учатся умножать множители, требующие составления новых единиц, таких как \(264 \times 38\).
Описание: умножить. двести шестьдесят четыре раза 38. 5 рядов. Первый ряд: двести шестьдесят четыре. Второй ряд: символ умножения, 38. Горизонтальная черта. Третий ряд: две тысячи сто двенадцать. Четвертый ряд: плюс семь тысяч девятьсот двадцать. Горизонтальная линия. Пятый ряд: десять тысяч тридцать два
ПЛК: Урок 6, Упражнение 1, Создание нового блока
Раздел B: Многозначное деление с использованием неполных частных
Согласование стандартов
| Адресация | 5. НБТ.Б.5, 5.НБТ.Б.6, 5.НФ.Б.3, 5.ОА.А.2 НБТ.Б.5, 5.НБТ.Б.6, 5.НФ.Б.3, 5.ОА.А.2 |
Раздел Цели обучения
- Деление многозначных целых чисел с использованием стратегий, основанных на разрядности, свойствах операций и связи между умножением и делением.
В 4-м классе учащиеся находили целые числа и остатки с делимыми до четырех цифр и делителями с одной цифрой, используя стратегии, основанные на разрядном значении и частичных частных. В 5 классе они расширяют эту работу, чтобы включить частные с двузначными делителями.
Учащиеся начинают с исследования, которое связывает деление больших чисел с контекстом реального мира. Они используют стратегии, основанные на позиционном значении и взаимосвязи между умножением и делением, чтобы оценить, как можно разделить самую длинную лапшу в мире. Затем они анализируют и используют различные способы разложения дивиденда.
Например, вот два способа разделить 448 на 16:
\(\displaystyle{\begin{align} 160\div 16&= 10\\ 160\div 16 &= 10\\ 80 \div 16 &= \phantom{0}5 \\48 \div 16 &= \phantom {0}3 \\\overline {\hspace{5mm}448 \div 16} &\overline{\hspace{1mm}= 28 \phantom{000}}\end{align}}\)
Описание: Разделить.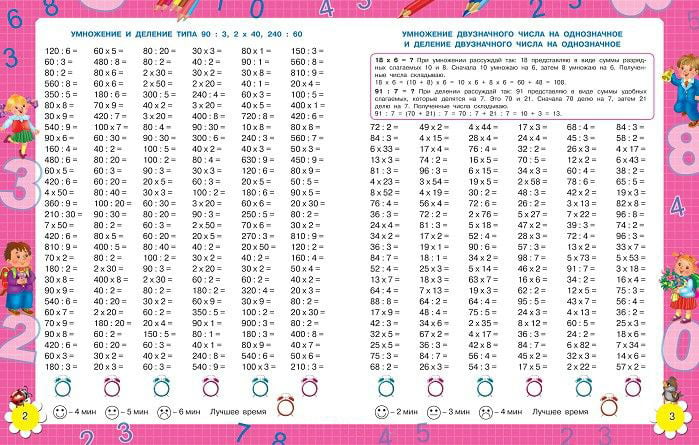 четыреста сорок восемь разделить на 16, 11 рядов. Первый ряд: 28. Второй ряд: 3. Третий ряд: 5. Четвертый ряд: 20. Пятый ряд: 16, длинный символ деления, внутри которого четыреста сорок восемь. Шестой ряд: минус триста двадцать. В скобках 20 раз по 16. Горизонтальная черта. Седьмой ряд: сто двадцать восемь. Восьмой ряд: минус 80. В скобках 5 раз по 16. Горизонтальная черта. Девятый ряд: 48. Десятый ряд: минус 48. В скобках 3 раза по 16. Горизонтальная линия. Одиннадцатый ряд: 0.
четыреста сорок восемь разделить на 16, 11 рядов. Первый ряд: 28. Второй ряд: 3. Третий ряд: 5. Четвертый ряд: 20. Пятый ряд: 16, длинный символ деления, внутри которого четыреста сорок восемь. Шестой ряд: минус триста двадцать. В скобках 20 раз по 16. Горизонтальная черта. Седьмой ряд: сто двадцать восемь. Восьмой ряд: минус 80. В скобках 5 раз по 16. Горизонтальная черта. Девятый ряд: 48. Десятый ряд: минус 48. В скобках 3 раза по 16. Горизонтальная линия. Одиннадцатый ряд: 0.
Учащиеся видят, что некоторые разложения могут быть более полезными, чем другие, для нахождения целочисленных частных.Они используют это понимание, чтобы понять алгоритмы, использующие более сложные частичные частные.
Обратите внимание, что использование стандартного алгоритма деления не является ожидаемым в 5 классе, но учащиеся могут начать развивать концептуальное понимание, необходимое для этого. Представленные здесь алгоритмы с частичными частными основаны на позиционном значении, что позволит учащимся понять логику стандартного алгоритма, который они изучат в 6 классе.
ПЛК: Урок 11, Упражнение 1, Выражения деления
Раздел C: Приступим к работе
Согласование стандартов
| Адресация | 5.МД.С.5, 5.НБТ.Б, 5.НБТ.Б.5, 5.НБТ.Б.6 |
Раздел Цели обучения
- Умножение и деление для решения реальных и математических задач, связанных с площадью и объемом.
В последнем разделе учащимся предлагается использовать умножение и деление целых чисел для оценки больших величин и решения реальных и математических задач.
Учащиеся сталкиваются с проблемами площади и объема в контексте географии — площади штатов — и повседневного потребления — объема потребляемого молока, площади пластиковых отходов в Тихом океане и объема перерабатываемого пластика, отправляемого за границу для переработки.
Нью-Мексико имеет длину около 596 км и ширину 552 км. Что больше, мусорное пятно или Нью-Мексико?
Автор: Phoenix2. CC-BY-SA 3.0. Викимедиа. Источник.
CC-BY-SA 3.0. Викимедиа. Источник.
Раздел завершается дополнительной возможностью математического моделирования. Учащиеся оценивают и рассчитывают вес пищевых отходов, производимых в Соединенных Штатах за год, используя среднее количество на человека. Они также оценивают и анализируют количество собственных пищевых отходов.
ПЛК: Урок 19, Занятие 1, Квадратные километры
Расчетное количество дней: 19–21
Модуль 5: Образцы разрядных значений и десятичные операции
Модуль Цели обучения
- Учащиеся, опираясь на понимание разрядного значения в 4-м классе, понимают, что в многозначном числе цифра в одном разряде представляет в 10 раз больше, чем цифра в разряде справа от нее, и $\frac{ 1}{10}$ того, что он представляет слева от него. Они используют это понимание разрядности для округления, сравнения, упорядочивания, сложения, вычитания, умножения и деления десятичных дробей.
В этом модуле учащиеся расширяют свои знания о десятичных дробях, чтобы читать, писать, сравнивать и округлять десятичные дроби до тысячных. Они также расширяют свое понимание разряда и десятичных чисел, выполняя операции с десятичными дробями до сотых.
Они также расширяют свое понимание разряда и десятичных чисел, выполняя операции с десятичными дробями до сотых.
В 4 классе учащиеся записывали дроби со знаменателем 10 и 100 в виде десятичных дробей. Они поняли, что обозначения 0,1 и \(\frac{1}{10}\) выражают одно и то же количество и оба называются «одной десятой». Они использовали сотые сетки и числовые линии для представления и сравнения десятых и сотых долей.
Здесь учащиеся также полагаются на диаграммы и свое понимание дробей, чтобы понимать десятичные дроби до тысячных. Они видят, что «одна тысячная» относится к размеру одной части, если сотая делится на 10 равных частей, и что ее десятичная форма равна 0,001. Диаграммы помогают учащимся визуализировать величину каждого десятичного знака и сравнивать десятичные дроби.
Найдите 0,001 в каждой числовой строке.
Затем учащиеся применяют свои знания о десятичных дробях и операциях с целыми числами, чтобы складывать, вычитать, умножать и делить десятичные числа до сотых, используя стратегии, основанные на разрядности и свойствах операций.
Они видят, что стратегии рассуждений и алгоритмы, которые они использовали для работы с целыми числами, применимы и к десятичным дробям. Например, сложение и вычитание можно выполнять, обращая внимание на разрядное значение цифр в числах, а умножение и деление можно понимать с точки зрения групп одинакового размера.
В 6 классе учащиеся будут опираться на эту работу, чтобы достичь ожидаемой способности свободно складывать, вычитать, умножать и делить многозначные десятичные числа, используя стандартный алгоритм для каждой операции.
Раздел A: Числа до тысячных
Согласование стандартов
| Адресация | 5.НБТ.А, 5.НБТ.А.1, 5.НБТ.А.3, 5.НБТ.А.3.а, 5.НБТ.А.3.б, 5.НБТ.А.4 , 5.ОА.А |
Раздел Цели обучения
- Сравнить, округлить и упорядочить десятичные дроби до тысячных в соответствии со значением цифр в каждом разряде.

- Читать, писать и представлять десятичные дроби с точностью до тысячных, в том числе в развернутом виде.
В этом разделе учащиеся рассуждают о десятичных дробях с точностью до тысячных. Они начинают с представления десятичных знаков на диаграммах с координатной сеткой, где большой квадрат имеет значение 1, а каждый маленький квадрат внутри представляет \(\frac{1}{100}\). Учащиеся узнают, что если каждый маленький квадрат разделить на десятые доли, каждая из этих частей представляет тысячную часть большого квадрата.
На диаграмме показаны взаимосвязи между разрядными значениями. Например, каждая тысячная — это \(\frac{1}{10}\) сотой, а каждая сотая — 10 тысячных.
Это также помогает проиллюстрировать структуру числа в развернутом виде. В этом случае заштрихованная область включает 3 десятых, 6 сотых и 8 тысячных, что можно записать как \((3 х 0,1) + (6 х 0,01) + (8 х 0,001)\).
Это знание помогает подготовить учащихся к умножению десятичной дроби на целое число позже в модуле.
Затем учащиеся переходят к использованию числовых линий для представления десятичных дробей, их сравнения, упорядочивания и округления.Эта числовая линия показывает, что \(92,415
ПЛК: Урок 7, Занятие 1, Золотые Дублоны
Раздел B: Сложение и вычитание десятичных знаков
Соответствие стандартам Раздел Цели обучения
- Сложение и вычитание десятичных долей до сотых с использованием стратегий, основанных на позиционном значении.
В этом разделе учащиеся складывают и вычитают десятичные дроби до сотых. Они начинают с сложения и вычитания способами, которые имеют для них смысл, что побуждает их соотносить операции с операциями над целыми числами. Это также позволяет учителю принимать к сведению стратегии и алгоритмы, которые он выбирает, включая стандартный алгоритм и те, которые используют расширенную форму.
Сложение и вычитание десятичных знаков с использованием стандартного алгоритма поднимает новый вопрос о том, как должны быть выровнены цифры. Чтобы подчеркнуть это соображение, учащиеся анализируют распространенную ошибку, как показано здесь.
Чтобы подчеркнуть это соображение, учащиеся анализируют распространенную ошибку, как показано здесь.
Прежде чем использовать стандартный алгоритм, учащиеся используют рассуждение о разрядных значениях, чтобы решить, разумны ли суммы и разности, и убедиться, что цифры в числах выровнены правильно. Заботясь о том, чтобы выровнять десятые с десятыми и сотые с сотыми, учащиеся практикуют внимание к точности (MP6).
ПЛК: Урок 11, Упражнение 2, Целевые числа: добавление десятых или сотых долей
Раздел C: Умножение десятичных знаков
Согласование стандартов
| Адресация | 5.НБТ.А.1, 5.НБТ.Б.7, 5.НФ.Б.4, 5.ОА.А, 5.ОА.А.1, 5.ОА.А.2 |
Раздел Цели обучения
- Умножение десятичных дробей на произведения, приводящие к сотым, с использованием рассуждений о разрядности и свойств операций.
В этом разделе учащиеся учатся умножать десятичные дроби. Они продолжают мыслить с точки зрения разрядности, устанавливать связи с целыми числами и использовать диаграммы для поддержки своих рассуждений.
Они продолжают мыслить с точки зрения разрядности, устанавливать связи с целыми числами и использовать диаграммы для поддержки своих рассуждений.
Учащиеся начинают с умножения целого числа на десятичную дробь.Чтобы найти \(2 \умножить на 0,43\), например, они заштриховали 43 сотых в каждом из двух больших квадратов и увидели, что 86 заштрихованных частей или 86 сотых, что составляет 0,86.
Диаграммы также помогают учащимся связать произведения десятичных дробей и произведения целых чисел. На этой диаграмме показаны 2 группы по 43 заштрихованных фрагмента, где каждый фрагмент равен 0,01. Таким образом, объединенная заштрихованная область представляет \((2 \times 43) \times 0,01\).
Аналогично, \(15 \times 0,26\) можно рассматривать как 15 групп по 26 сотых или \(15 \times 26\) сотых.Поскольку \(15 \times 26\) равно 390, значение \(15 \times 0,26\) равно 390 сотым или 3,90.
Затем учащиеся рассуждают о произведении двух десятичных знаков. Здесь также помогут диаграммы.
Например, \(1,5 х 0,4\) можно представить как площадь прямоугольника с длинами сторон 1,5 и 0,4.
Учащиеся видят, что результат равен 60 сотым или 0,60, потому что есть \(15 \х4\) или 60 заштрихованных частей, каждая из которых представляет сотые доли.
Они также признают, что могут разложить заштрихованную область и найти \(1 х 0.4\) (заштрихованная площадь в первом большом квадрате) и \(0,5 х 0,4\) (заштрихованная площадь во втором большом квадрате) и добавьте эти частичные произведения: \((1 х 0,4) + (0,5 \ раз 0,4)\).
ПЛК: Урок 20, Занятие 1, Произведение десятых долей
Раздел D: Деление десятичных дробей
Согласование стандартов
| Адресация | 5.НБТ.А.3, 5.НБТ.Б.7, 5.ОА.А.2 |
Раздел Цели обучения
- Деление десятичных дробей с частными, приводящими к сотым, с использованием рассуждений о разрядности и свойств операций.

В этом разделе учащиеся используют взаимосвязь между умножением и делением и идею равных групп, чтобы разобраться в делении десятичных дробей так же, как они делали это с целыми числами и дробями.
Ранее учащиеся узнали, что выражение \(8 \div 2\) может означать определение количества групп по 2 в одной группе, если 8 разделить на 2 равные группы, или определение количества групп по 2 в группе 8.
Здесь учащиеся интерпретируют \(8 \div 0.1\) как определение количества групп из 1 десятых в числе 8.В 1 10 десятых, поэтому в 8 должно быть 80 десятых, значит \(8 \div 0.1 = 80\). Это понимание дает учащимся основу для деления целого числа на любое количество десятых или сотых долей.
Например, чтобы найти значение \(2 \div 0.2\), мы можем посмотреть, сколько групп из 2 десятых содержится в 2.
В 1 5 групп по 2 десятых, поэтому должно быть \(2 \times 5\) или 10 групп по 2 десятых в 2, как показано на диаграмме.
\(2 \дел 0,2 = 10\)
При делении десятичной дроби на целое другая интерпретация деления может быть более интуитивной.
Например, \(0,2 \дел 5\) может означать разбиение числа 0,2 на 5 равных групп и определение размера каждой группы. На диаграмме показано по 4 сотых в каждой группе, поэтому \(0,2 \дел 5 = 0,04\).
Далее в этом модуле учащиеся используют эквивалентные выражения для нахождения частных. Например, они считают, что \(6 \div 0.4\) эквивалентно \(60 \div 4\), потому что и делимое, и делитель умножаются на 10. Если значение \(60 \div 4\) равно 15 , то значение \(6 \div 0.4\) также равно 15.
ПЛК: Урок 22, Занятие 1, Шаблоны деления на десятичные единицы
Расчетное количество дней: 24–26
Модуль 6. Дополнительные операции с десятичными дробями
Модуль Цели обучения
- Учащиеся решают многошаговые задачи, включающие преобразование измерений, линейные графики и операции с дробями, включая сложение и вычитание дробей с разными знаменателями. Они также объясняют закономерности при умножении и делении на степени 10 и интерпретируют умножение как масштабирование путем сравнения произведений с коэффициентами.

В этом разделе учащиеся углубят свое понимание отношений разряда и значения чисел в десятичной системе счисления, преобразования единиц измерения, операций с дробями с разными знаменателями и мультипликативного сравнения. Работа здесь основана на нескольких важных идеях из 4 класса.
В 4 классе учащиеся узнали, что значение каждой цифры в целом числе в 10 раз превышает значение той же цифры, стоящей справа от него. Здесь они расширяют это понимание, чтобы включить десятичные дроби до тысячных.Учащиеся узнают, что значение каждой цифры в разряде (включая десятичные знаки) равно \(\frac {1}{10}\) значению той же цифры в разряде слева от него.
Эта идея подчеркивается, когда учащиеся выполняют преобразование измерений в метрических единицах.
Раньше учащиеся учились переводить большие единицы измерения в меньшие. Здесь они учатся преобразовывать меньшую единицу в большую. Они наблюдают, как цифры сдвигаются при умножении или делении на степень 10, и учатся использовать экспоненциальную запись для степеней 10 для представления больших чисел. 6\)
6\)
Затем учащиеся обращают внимание на дроби. В младших классах учащиеся понимали эквивалентные дроби, складывали и вычитали дроби с одинаковым знаменателем, прибавляли десятые и сотые доли. В этом блоке складывают и вычитают дроби с разными знаменателями. Они видят, что ключ в том, чтобы найти общий знаменатель и проанализировать различные методы для этого.
Затем учащиеся решают задачи, связанные с данными измерений (в половинках, четвертях и восьмерках), которые отображаются на линейных графиках.
В последнем разделе учащиеся рассуждают о величине произведения дробей и множителей. Эта работа основана на мультипликативной сравнительной работе в 4 классе, в которой учащиеся сравнивали целое число как «_____ раз больше (или столько же)» другого целого числа. Здесь учащиеся рассуждают о продуктах целого числа и дроби, не находя значения каждого продукта. Они используют диаграммы и выражения для поддержки своих рассуждений.
Напишите \(\) или \(=\) в каждом пробеле, чтобы получить верные утверждения.
\(\frac{4}{5} \times 851 \, \underline{\hspace{0.7cm}} \, 851\)
\(\frac{1}{4} \, \underline{\hspace{0.7cm}} \, \frac{5}{5} \times \frac{1}{4}\)
\(\frac{99}{8} \times \frac{23}{22} \, \underline{\hspace{0.7cm}} \, \frac{99}{8}\)
\(\frac{100}{7} \times \frac{9}{13} \, \underline{\hspace{0.7cm}} \, \frac{9}{13}\)
Раздел A. Преобразование величин и степени числа 10
Согласование стандартов
| Адресация | 5.МД.А.1, 5.НБТ.А, 5.НБТ.А.1, 5.НБТ.А.2 |
Раздел Цели обучения
- Объяснить закономерности при умножении и делении на степени 10.
- Решите многошаговые задачи, связанные с преобразованием измерений.
В этом разделе учащиеся расширяют свое понимание разряда и применяют его для выполнения преобразований между различными, в основном метрическими, единицами измерения.
Учащиеся начинают с того, что замечают, что значение цифры в каждом разряде в 10 раз превышает значение той же цифры в разряде справа от нее и \(\frac{1}{10}\) значение той же цифры в место слева от него.Они видят, что это относится не только к целым числам, но и к десятичным разрядам. Затем учащиеся учатся использовать экспоненциальную запись для степеней 10 и использовать эту запись для представления очень больших чисел, таких как 1 миллион или 1 миллиард.
Затем учащиеся рассуждают о преобразовании измерений в метрических и обычных единицах измерения. Преобразование в метрические единицы дополнительно подчеркивает отношение разряда к значению в числах с основанием десять. Например, в этой таблице некоторые расстояния указаны в сантиметрах, метрах и километрах.
| см | метров (м) | километров (км) |
|---|---|---|
| 1 500 | 15 | 0,015 |
| 15 000 | 150 | 0,15 |
| 150 000 | 1 500 | 1,5 |
Учащиеся замечают, что умножение или деление на степень 10 сдвигает положение цифр в десятичном числе вправо или влево.
Выполняя преобразования из больших единиц в меньшие и наоборот, учащиеся применяют полученные знания о выполнении операций с целыми и десятичными числами.
PLC: Урок 2, Занятие 1, Население Делавэра и Индии
Раздел B: Сложение и вычитание дробей с разными знаменателями
Согласование стандартов
| Адресация | 5.MD.B.2, 5.NF.A.1, 5.NF.A.2, 5.NF.B.4 |
Раздел Цели обучения
- Сложение и вычитание дробей с разными знаменателями.
- Создавайте линейные графики для отображения дробных данных измерений и используйте эту информацию для решения задач.
- Решите задачи на сложение и вычитание дробей.
В этом разделе учащиеся учатся складывать и вычитать дроби (включая смешанные числа) с разными знаменателями и применять полученные знания для решения задач.
Учащиеся начинают складывать и вычитать дроби, используя приемы и диаграммы, которые им понятны, опираясь на то, что они знают о сложении и вычитании дробей с одинаковыми знаменателями и с эквивалентными дробями. Затем они рассматривают способы записи эквивалентных дробей, чтобы у дробей в выражении был один и тот же знаменатель. Позже они анализируют, а затем используют численные стратегии для нахождения общих знаменателей, такие как умножение знаменателей и нахождение общего кратного.
Затем они рассматривают способы записи эквивалентных дробей, чтобы у дробей в выражении был один и тот же знаменатель. Позже они анализируют, а затем используют численные стратегии для нахождения общих знаменателей, такие как умножение знаменателей и нахождение общего кратного.
В конце раздела учащиеся создают линейные графики для отображения данных измерений в дробных единицах (половинах, четвертях и восьмых), интерпретируют данные на линейных графиках и используют все четыре операции с дробями для решения задач, связанных с дробными измерениями.
Все ли абрикосы Мэй вместе весят больше или меньше фунта?
Описание: Точечный график под названием Mai’s Apricots от 0 до 3 на 1’s. Решётка по восьмым. Горизонтальная ось, вес абрикосов в унциях. Начиная с 7 восьмых, количество крестиков над каждым восьмым шагом равно 1, 0, 2, 0, 0, 2, 5, 3, 1, 0, 0, 0, 1.
ПЛК
: Урок 8, Упражнение 2, Сложение и вычитание
Раздел C: Размер продуктов
Согласование стандартов
| Адресация | 5. MD.B.2, 5.NF.A.2, 5.NF.B.4, 5.NF.B.5, 5.NF.B.5.a, 5.NF.B.5.b, 5.ОА.А MD.B.2, 5.NF.A.2, 5.NF.B.4, 5.NF.B.5, 5.NF.B.5.a, 5.NF.B.5.b, 5.ОА.А |
Раздел Цели обучения
- Интерпретировать умножение как масштабирование (изменение размера).
- Делайте обобщения относительно умножения целого числа на дробь, большую, меньшую и равную 1.
В этом разделе учащиеся опираются на свое понимание умножения, чтобы включить концепцию масштабирования. Они интерпретируют выражения умножения как количество, размер которого изменяется или масштабируется с помощью коэффициента.Эта идея основана на мультипликативном сравнении, которое учащиеся 4-го класса выполняли с целыми числами.
Чтобы лучше понять эту концепцию, учащиеся сравнивают значения выражений умножения, не выполняя умножение. В начале раздела выражения таковы, что один фактор один и тот же, а другой другой.
Какое выражение представляет наибольший продукт?
Например, они считают, что \(\frac{7}{6} \times 4\) больше, чем \(\frac{5}{8} \times 4\) и \(\frac{1}{2 } \times 4\), потому что в каждом выражении 4 умножается на дробь, а \(\frac{7}{6}\) является наибольшим из трех.
Учащиеся используют визуальные представления для сравнения продуктов. Например, следующие диаграммы могут представлять \(\frac{2}{7} \times 3\) и \(\frac{2}{7} \times 5\).
Учащиеся также рассуждают о продуктах с одним неизвестным фактором, что побуждает их проводить сравнения на основе величины другого фактора.
ПЛК: Урок 19, Упражнение 1, Сравнение произведений дробей в числовой строке
Расчетное количество дней: 19–21
Модуль 7: Формы на координатной плоскости
Модуль Цели обучения
- Учащиеся наносят пары координат на координатную сетку и классифицируют треугольники и четырехугольники в иерархии на основе свойств длины стороны и меры угла.Они генерируют, идентифицируют и отображают взаимосвязи между соответствующими терминами в двух числовых шаблонах с учетом двух правил, а также представляют и интерпретируют реальный мир и математические задачи на координатной сетке.
В этом разделе учащиеся узнают о координатной сетке, углубят свои знания о двухмерных формах и используют координатную сетку для изучения взаимосвязей пар чисел в различных ситуациях.
Здесь учащиеся узнают о сетках, пронумерованных в двух направлениях.Они видят, что структура координатной сетки позволяет нам точно передавать расположение точек и фигур.
Студенты также продолжают изучать двухмерные формы и их атрибуты. В 3 классе классифицировали треугольники и четырехугольники по наличию прямых углов и сторон одинаковой длины. В 4 классе они узнали об углах и параллельных и перпендикулярных прямых, что позволило им еще больше различать формы. В этом модуле учащиеся используют эти идеи, чтобы понять иерархию форм.
Далее в этом модуле учащиеся анализируют и создают числовые шаблоны на основе пар правил и графических пар чисел на координатной сетке. Они также интерпретируют точки на координатной сетке с точки зрения ситуаций, строят точки, чтобы лучше понять взаимосвязь между двумя наборами чисел, и используют координатную сетку для решения проблем.
Секция A: Координатная плоскость
Выравнивание стандартов Раздел Цели обучения
- Найдите точки на координатной сетке.

В этом разделе учащиеся знакомятся с координатной сеткой.
Учащиеся начинают рисовать прямоугольники, основываясь только на словесных описаниях. Сначала они делают это без сетки, затем на неразмеченной сетке и, наконец, на координатной сетке. Попутно они узнают, что пронумерованные линии сетки позволяют им находить точки и точно передавать особенности форм.
Затем учащиеся учатся использовать числа на горизонтальной и вертикальной осях для описания положения точек и нанесения их на координатную сетку.Они узнают, что пары чисел, такие как \((1,4)\), называемые координатами, описывают количество единиц, в которых точка удалена от осей, и точка \((0,0)\), которая называется началом координат. .
Например, \((7,0)\) находится на 7 единиц справа от \((0,0)\) и находится на горизонтальной оси. Точка \( (1,4)\) находится на 1 единицу правее \( (0,0)\) и на 4 единицы выше.
Другими словами, первое число говорит нам о его горизонтальном положении, а второе число говорит нам о его вертикальном положении.
Затем учащиеся практикуются в построении точек по заданным координатам и определении координат точек на сетке.
ПЛК: Урок 2, Упражнение 1, В чем смысл?
Раздел B: Иерархия форм
Согласование стандартов
| Адресация | 5.GB, 5.GB.3, 5.GB.4 |
Раздел Цели обучения
- Классифицировать треугольники и четырехугольники в иерархии на основе размеров углов и длин сторон.
В этом разделе учащиеся классифицируют четырехугольники и треугольники по разным категориям и изучают отношения между категориями.
Они начинают с сортировки большого набора четырехугольников удобным для них способом, используя такие атрибуты, как угловые меры (особенно прямые углы) и пары параллельных сторон. Затем они сосредотачиваются на связывании атрибутов трапеций, прямоугольников, параллелограммов, квадратов и ромбов.
Учащиеся изучают два способа определения трапеций. Один способ — сказать, что параллелограмм — это трапеция, а другой — сказать, что параллелограмм не является трапецией. В этом курсе используется прежнее (включающее) определение.
Затем учащиеся изучают отношения между квадратами и ромбами, а также между прямоугольниками и параллелограммами. Они строят эти фигуры зубочистками и видят, что квадрат — это особый вид ромба, а прямоугольник — особый вид параллелограмма.
Узнавая больше об отношениях между четырехугольными категориями, учащиеся используют диаграмму Венна, чтобы подчеркнуть свое понимание.
ПЛК: Урок 5, Задание 1, Что такое трапеция?
Раздел C: Числовые образцы
Согласование стандартов
| Адресация | 5.Г.А.2, 5.НБТ.Б.7, 5.ОА.А.2, 5.ОА.Б.3 |
Раздел Цели обучения
- Генерация, идентификация и графическое отображение взаимосвязей между соответствующими терминами в двух шаблонах по заданному правилу.

- Представление и интерпретация реальных и математических задач на координатной сетке.
В этом разделе учащиеся применяют концепции этого модуля при анализе числовых отношений между двумя величинами в различных контекстах.
Учащиеся начинают с изучения закономерностей в числах, полученных в результате следования паре правил.Они записывают шаблоны в таблицу и интерпретируют отношения между парами чисел. Учащиеся узнают, что они могут формировать упорядоченные пары, используя соответствующие термины из каждого шаблона, и эти пары могут быть отображены на координатной сетке, что позволяет им лучше понять поведение шаблонов.
Правило 1: Начните с 0. Продолжайте добавлять 10.
Правило 2: Начните с 0. Продолжайте добавлять 40.
Используйте правила, чтобы заполнить таблицу.
| А | Б | С | Д | Е | Ф | |
|---|---|---|---|---|---|---|
| правило 1 | ||||||
| правило 2 |
Нанесите числа из таблицы на координатную сетку. Обозначьте точки.
Обозначьте точки.
Затем учащиеся используют координатную сетку, чтобы исследовать взаимосвязь пар значений в различных ситуациях. Например, они смотрят на количество выпавших орлов и решек в результате подбрасывания монеты определенное количество раз, количество монет и достоинство монет, а также длину и ширину прямоугольников с фиксированным периметром или фиксированной площадью.
ПЛК: Урок 11, Занятие 2, Шаблоны на координатной сетке, Часть 2
Расчетное количество дней: 13
Модуль 8: Собираем все вместе
Модуль Цели обучения
- Учащиеся закрепляют и укрепляют свое понимание различных концепций и навыков, связанных с основной работой класса.Они также продолжают работать над достижением целей по беглости в классе.
В этом разделе учащиеся возвращаются к основным заданиям и целям по беглости речи, применяя полученные за год знания.
В разделе A учащиеся углубят свое понимание стандартного алгоритма умножения и попрактикуются в его использовании для нахождения стоимости произведений. Они также пересматривают алгоритмы, которые используют частичные частные для деления целых чисел. В разделе B учащиеся решают реальные задачи на объем и имеют возможность моделировать с помощью математики.
Они также пересматривают алгоритмы, которые используют частичные частные для деления целых чисел. В разделе B учащиеся решают реальные задачи на объем и имеют возможность моделировать с помощью математики.
Основание Великой пирамиды Египта представляет собой квадрат.
Длина одной стороны основания 230 метров.
Высота пирамиды 140 метров.
Если бы пирамида имела форму прямоугольной призмы,
каков был бы объем призмы?
Атрибуция: Мстислав Чернов. CC-BY-SA 3.0. Викисклад. Источник.
Раздел C посвящен работе с десятичными и дробными числами.В заключительном разделе учащиеся анализируют основную работу своего класса, поскольку они создают задания в формате упражнений для разминки, с которыми они сталкивались в течение года («Замечание и удивление», «Исследование с оценкой», «Разговор о числах», «Правда или ложь» и «Какой из них не работает»). не принадлежит?).
Разделы в этом разделе являются автономными разделами, и их не обязательно заполнять по порядку. Внутри раздела уроки также можно проходить выборочно и без завершения предыдущих уроков. Цель состоит в том, чтобы предоставить учащимся широкие возможности для интеграции полученных знаний и отработки навыков, связанных с ожидаемой беглостью в классе.
Внутри раздела уроки также можно проходить выборочно и без завершения предыдущих уроков. Цель состоит в том, чтобы предоставить учащимся широкие возможности для интеграции полученных знаний и отработки навыков, связанных с ожидаемой беглостью в классе.
Раздел A: Умножение и деление целых чисел
Согласование стандартов
| Адресация | 5.ГБ3, 5.ГБ4, 5.НБТ.Б.5, 5.НБТ.Б.6 |
Раздел Цели обучения
- Деление многозначных целых чисел с использованием разрядных стратегий и свойств операций.
- Свободно перемножайте многозначные целые числа, используя стандартный алгоритм.
В этом разделе учащиеся закрепят свое понимание стандартного алгоритма умножения и попрактикуются в его использовании.Они используют оценку, чтобы определить обоснованность своих ответов, распознают и объясняют закономерности позиционного значения при умножении многозначных чисел и учатся использовать алгоритм, когда один или несколько множителей имеют несколько нулей.
Вот как Киран нашел значение \(650 \х27\).
Разумный ли ответ?
Описание: умножить. 6сот пятьдесят раз 27. 5 рядов. Первый ряд: 6сот пятьдесят. Второй ряд: символ умножения, 27.Горизонтальная линия. Третий ряд: 4 тысячи 5сот пятьдесят. Четвертый ряд: плюс одна тысяча 3 сотни. Горизонтальная линия. Пятый ряд: 5 тысяч 8сот пятьдесят.
Найдите стоимость каждого продукта.
Какая связь между \(260 \times 35\) и \(2,\!600 \times 35\)?
Учащиеся также учатся делить многозначные целые числа, используя алгоритм с частичными частными, который они изучили в модуле 4.
ПЛК: Урок 1, Занятие 1, Обсуждение
Раздел B: Применение концепций объема
Согласование стандартов
| Адресация | 5.MD.C, 5.MD.C.5, 5.NBT.B.5, 5.NBT.B.6 |
Раздел Цели обучения
- Решить многошаговые задачи на объем.

В этом разделе учащиеся возвращаются к значению объема и применяют свое понимание для решения задач. На каждом уроке учащиеся оценивают и вычисляют объем прямоугольных призм в различных контекстах.Числа, используемые в этом разделе, больше, чем числа, которые учащиеся использовали в начальной части, когда они впервые научились вычислять объем прямоугольных призм.
Атрибуция: Бисваруп Гангули. СС BY 3.0. Викисклад. Источник.
Предприятие упаковывает по 126 кубиков сахара в каждую коробку.
Коробка представляет собой прямоугольную призму.
Как можно упаковать кубики?
Длина сторон коробки составляет примерно \(1\frac{7}{8}\) дюймов на \(3\frac{3}{4}\) дюймов на \(4\frac{3}{8) дюймов }\) дюймы.
Что можно сказать о том, как упакованы кубики сахара?
Эта работа побуждает учащихся делать разумные оценки, рассматривать подходящие размеры единиц в данном контексте и учитывать преобразование единиц измерения при решении задач на объем.
Используйте изображение фургона, чтобы оценить длину, ширину и высоту кузова фургона.
Затем улучшите свою оценку объема вагона.
ПЛК: Урок 6, Разминка, Оценка Исследование: кубики сахара
Раздел C: Дробные и десятичные операции
Согласование стандартов
| Адресация | 5.NBT.B.7, 5.NF.A.1, 5.NF.B.4 |
В этом разделе учащиеся укрепляют свое понимание операций с дробями и десятичными знаками, играя в различные игры. Каждое занятие строится как игровой день.
Учащиеся начинают с игр, в которых используются сложение и вычитание дробей, цель которых состоит в том, чтобы найти наибольшую или наименьшую сумму или разность.
Раунд 1
\(\ frac {\ boxed {\ phantom {111 \ frac {1} {1}}}} {\ boxed {\ phantom {111 \ frac {1} {1}}}} \, — \, \ frac {\ в штучной упаковке {\ фантом {111 \ гидроразрыва {1} {1}}}} {\ в штучной упаковке {\ фантом {111 \ гидроразрыва {1} {1}}}} \, = \)
- Вращайте спиннер.

- Напишите номер в пустом поле. Держите выбранный ящик скрытым от глаз.
- После того как число записано, его нельзя изменить.
- Продолжайте вращать и писать числа, пока все 4 клетки не будут заполнены.
- Найди отличия. Человек с наибольшей разницей выигрывает раунд.
Затем учащиеся тренируются в сложении и вычитании десятичных дробей. Игры здесь также побуждают учащихся к достижению определенных целей, таких как нахождение наибольшего десятичного числа или достижение 1, 0,1 или 0,01.
В конце раздела учащиеся играют в игру, в которой нужно умножать дроби. Все игры с дробями предлагают учащимся задуматься о значении числителя и знаменателя и сделать стратегический выбор в отношении чисел, которые они используют в этих позициях.
ПЛК: Урок 13, Задание 2, Сравнение дробей, раунд 2
Раздел D: Создание и проектирование
Согласование стандартов
| Адресация | 5. G, 5.MD, 5.MD.C.3, 5.NBT, 5.NBT.B.5, 5.NBT.B.6, 5.NF, 5.NF.A.1, 5 .NF.B.3, 5.ОА G, 5.MD, 5.MD.C.3, 5.NBT, 5.NBT.B.5, 5.NBT.B.6, 5.NF, 5.NF.A.1, 5 .NF.B.3, 5.ОА |
Раздел Цели обучения
- Проанализируйте основную работу класса, создав и разработав учебные программы.
На протяжении всего курса учащиеся выполняли упражнения для разминки, такие как «Заметить и удивиться», «Исследовательская оценка», «Правда или ложь», «Разговор о числах» и «Какое из них не принадлежит?» Этот раздел позволяет им применить изученную математику для разработки разминки, включающей эти упражнения.
Каждый урок посвящен определенному упражнению. Учащиеся начинают с выполнения как минимум двух частично созданных заданий, в каждом из которых нужно выполнить больше недостающих частей, чем в предыдущем. Они практикуются в предвидении ответов, которые другие могут дать на подсказки, которые они излагают.
Выберите 3 фигуры из набора карточек.
Нарисуйте четвертую фигуру, чтобы завершить задание «Какая фигура не принадлежит?»
Для каждой формы обсудите одну причину, по которой каждая фигура не подходит.
Какой из них не принадлежит?
ПЛК: Урок 16, Разминка, Числовой разговор: Дивизион
Расчетное количество дней: 17–18
Руководство по темпу и диаграмма зависимостей ›
Разделяй и властвуй | Набор 5 (умножение матриц Штрассена)
Даны две квадратные матрицы A и B размера n x n каждая, найдите их матрицу умножения.
Наивный метод
Ниже приведен простой способ умножения двух матриц.
C ++
C ++
С
|
Java
+ + + + |
python3
+
+ 3 |
C #
Javascript
|
Время сложности вышеуказанного метода (N 3 ).
Разделяй и властвуй
Ниже приведен простой метод «Разделяй и властвуй» для умножения двух квадратных матриц.
1) Разделите матрицы A и B на 4 подматрицы размером N/2 x N/2, как показано на диаграмме ниже.
2) Рекурсивно вычислить следующие значения. ae + bg, af + bh, ce + dg и cf + dh.
В приведенном выше методе мы делаем 8 умножений для матриц размера N/2 x N/2 и 4 сложения. Сложение двух матриц занимает время O(N 2 ).Таким образом, временная сложность может быть записана как
T(N) = 8T(N/2) + O(N 2 ) Из теоремы Мастера временная сложность вышеуказанного метода составляет O (N 3 ) который, к сожалению, такой же, как и вышеупомянутый наивный метод.
Простой разделяй и властвуй также приводит к O(N 3 ), может ли быть лучший способ?
В приведенном выше методе «разделяй и властвуй» основным компонентом высокой временной сложности является 8 рекурсивных вызовов. Идея метода Штрассена состоит в том, чтобы уменьшить количество рекурсивных вызовов до 7.Метод Штрассена похож на описанный выше простой метод «разделяй и властвуй» в том смысле, что этот метод также делит матрицы на подматрицы размера N/2 x N/2, как показано на диаграмме выше, но в методе Штрассена четыре подматрицы результата рассчитываются по следующим формулам.
Идея метода Штрассена состоит в том, чтобы уменьшить количество рекурсивных вызовов до 7.Метод Штрассена похож на описанный выше простой метод «разделяй и властвуй» в том смысле, что этот метод также делит матрицы на подматрицы размера N/2 x N/2, как показано на диаграмме выше, но в методе Штрассена четыре подматрицы результата рассчитываются по следующим формулам.
Временная сложность метода Штрассена
Сложение и вычитание двух матриц занимает O(N 2 ) времени. Таким образом, временная сложность может быть записана как
T(N) = 7T(N/2) + O(N 2 ) Из теоремы Мастера временная сложность вышеуказанного метода равна O(N Log7 ), что примерно равно O(N 2.8074 )
Как правило, метод Штрассена не является предпочтительным для практического применения по следующим причинам.
1) Константы, используемые в методе Штрассена, высоки, и для типичного приложения Наивный метод работает лучше.
2) Для разреженных матриц существуют лучшие методы, специально разработанные для них.
3) Подматрицы в рекурсии занимают дополнительное место.
4) из-за ограниченной точности компьютерной арифметики на неотъемлевых значениях, большие ошибки накапливаются в алгоритме страженных, чем в наивный метод (источник: CLRS Book)
Python3
Простой способ запоминания Матричное уравнение Штрассена
Ссылки:
Introduction to Algorithms 3rd Edition by Clifford Stein, Thomas H. Cormenson, Charles E. Leis0. com/watch?v=LOLebQ8nKHA
https://www.youtube.com/watch?v=QXY4RskLQcI
Пожалуйста, пишите комментарии, если вы обнаружите что-то неверное или хотите поделиться дополнительной информацией по теме, обсуждавшейся выше
об арифметических операторах — PowerShell
- Статья
- 11 минут на чтение
Полезна ли эта страница?
Полезна ли эта страница?
да Нет
Любая дополнительная обратная связь?
Отзыв будет отправлен в Microsoft: при нажатии кнопки отправки ваш отзыв будет использован для улучшения продуктов и услуг Microsoft.Политика конфиденциальности.
Представлять на рассмотрение
В этой статье
Краткое описание
Описывает операторы, выполняющие арифметические действия в PowerShell.
Подробное описание
Арифметические операторы вычисляют числовые значения. Вы можете использовать один или несколько арифметические операторы для сложения, вычитания, умножения и деления значений, а также для вычислить остаток (модуль) операции деления.
Кроме того, оператор сложения ( + ) и оператор умножения ( * )
также работают со строками, массивами и хеш-таблицами. Оператор сложения
объединяет ввод. Оператор умножения возвращает несколько копий
ввода. Вы даже можете смешивать типы объектов в арифметическом операторе. То
метод, который используется для оценки оператора, определяется типом
самый левый объект в выражении.
Вы даже можете смешивать типы объектов в арифметическом операторе. То
метод, который используется для оценки оператора, определяется типом
самый левый объект в выражении.
Начиная с PowerShell 2.0, все арифметические операторы работают в 64-разрядных системах. числа.
Начиная с PowerShell 3.0, -shr (сдвиг вправо) и -shl (shift-left) добавлены для поддержки побитовой арифметики в PowerShell.
PowerShell поддерживает следующие арифметические операторы:
| Оператор | Описание | Пример |
|---|---|---|
| + | Складывает целые числа; объединяет | 6 + 2 |
| строк, массивов и хеш-таблиц. | "файл" + "имя" | |
@(1, "один") + @(2.0, "два") | ||
@{"один" = 1} + @{"два" = 2} | ||
| + | Делает число из объекта | + 123 |
| — | Вычитает одно значение из другого | 6 - 2 |
| значение | ||
| — | Вычисляет противоположное число | - -6 |
(получить дату). | ||
| * | Умножение чисел или копирование строк | 6*2 |
| и массивы указанного числа | @("!") * 4 | |
| раз. | "!" * 3 | |
| / | Делит два значения. | 6 / 2 |
| % | Модуль— возвращает остаток от | . 7 % 2 |
| дивизионная операция. | ||
| — полоса | Побитовое И | 5-диапазонный 3 |
| -бнот | Побитовое НЕ | - бнот 5 |
| -бор | Побитовое ИЛИ | 5 -бор 0x03 |
| -бксор | Побитовое исключающее ИЛИ | 5-боксор 3 |
| -шл | Сдвигает биты влево | 102 -шл 2 |
| -шр | Сдвигает биты вправо | 102 -шр 2 |
Побитовые операторы работают только с целочисленными типами.
Приоритет оператора
PowerShell обрабатывает арифметические операторы в следующем порядке:
| Приоритет | Оператор | Описание |
|---|---|---|
| 1 | () | Скобки |
| 2 | - | Для отрицательного числа или унарного оператора |
| 3 | * , / , % | Для умножения и деления |
| 4 | + , - | Для сложения и вычитания |
| 5 | - полоса , - шпилька | Для побитовых операций |
| 5 | -бор , -бксор | Для побитовых операций |
| 5 | -шр , -шл | Для побитовых операций |
PowerShell обрабатывает выражения слева направо в соответствии с
правила приоритета. В следующих примерах показано влияние приоритета
правила:
В следующих примерах показано влияние приоритета
правила:
| Выражение | Результат |
|---|---|
3+6/3*4 | 11 |
3+6/(3*4) | 3,5 |
(3+6)/3*4 | 12 |
Порядок, в котором PowerShell оценивает выражения, может отличаться от других языки программирования и сценариев, которые вы использовали.Следующее В примере показан сложный оператор присваивания.
$а = 0 $б = @(1,2) $с = @(-1,-2) $b[$a] = $c[$a++]
В этом примере выражение $a++ оценивается до $b[$a] .
Вычисление $a++ изменяет значение $a после его использования в
оператор $c[$a++] ; но до того, как он будет использован в $b[$a] . Переменная $a в $b[$a] равно 1 , а не 0 ; Таким образом, оператор присваивает значение $b[1] , а не $b[0] .
Приведенный выше код эквивалентен:
$а = 0 $б = @(1,2) $с = @(-1,-2) $тмп = $с[$а] $а = $а + 1 $b[$a] = $tmp
Деление и округление
Если частное операции деления является целым числом, PowerShell округляет
значение до ближайшего целого числа. Когда значение равно .5 , оно округляется до
ближайшее четное целое.
В следующем примере показан результат округления до ближайшего четного значения. целое число.
| Выражение | Результат |
|---|---|
[целое число]( 5 / 2 ) | 2 |
[целое число]( 7 / 2 ) | 4 |
Обратите внимание, что 5/2 = 2.5 округляется до 2 . Но, 7/2 = 3,5 получается округляется до 4 .
Вы можете использовать класс [Math] , чтобы получить другое поведение округления.
| Выражение | Результат |
|---|---|
[int][Math]::Round(5 / 2,[MidpointRounding]::AwayFromZero) | 3 |
[int][Математика]::Потолок(5 / 2) | 3 |
[int][Math]::Floor(5 / 2) | 2 |
Для получения дополнительной информации см. Мат.Круглый метод.
Сложение и умножение нечисловых типов
Вы можете добавлять числа, строки, массивы и хеш-таблицы. И вы можете умножать числа, строки и массивы. Тем не менее, вы не можете умножить хэш столы.
При добавлении строк, массивов или хеш-таблиц элементы объединены. Когда вы объединяете коллекции, такие как массивы или хэши таблиц создается новый объект, содержащий объекты из обоих коллекции. Если вы попытаетесь объединить хеш-таблицы с одним и тем же ключом, операция не удалась.
Например, следующие команды создают два массива, а затем добавляют их:
$а = 1,2,3 $b = "А", "В", "С" $а + $б
1 2 3 А Б С
Вы также можете выполнять арифметические операции с объектами разных типов. То
операция, которую выполняет PowerShell, определяется типом Microsoft .NET
самый левый объект в операции. PowerShell пытается преобразовать все
объектов в операции к типу .NET первого объекта.Если это удастся
при преобразовании объектов он выполняет операцию, соответствующую .NET
Тип первого объекта. Если не удается преобразовать какой-либо из объектов,
операция не удалась.
То
операция, которую выполняет PowerShell, определяется типом Microsoft .NET
самый левый объект в операции. PowerShell пытается преобразовать все
объектов в операции к типу .NET первого объекта.Если это удастся
при преобразовании объектов он выполняет операцию, соответствующую .NET
Тип первого объекта. Если не удается преобразовать какой-либо из объектов,
операция не удалась.
Следующие примеры демонстрируют использование сложения и
операторы умножения; в операциях, включающих разные объекты
типы.
Предположим, что $массив = 1,2,3 , $red = [ConsoleColor]::Red , $blue = [ConsoleColor]::Blue :
| Выражение | Результат |
|---|---|
"файл" + 16 | файл16 |
Массив $ + 16 | 1 , 2 , 3 , 16 |
$массив + "файл" | 1 , 2 , 3 , файл |
Массив $ * 2 | 1 , 2 , 3 , 1 , 2 , 3 |
"файл" * 3 | файлфайлфайл |
Синий + 3 | Красный |
Красный - 3 | Синий |
$синий - $красный | -3 |
+ «123» | 123 |
Поскольку метод, используемый для оценки утверждений, определяется
крайний левый объект, сложение и умножение в PowerShell не строго
коммутативный. Например,
Например, (a + b) не всегда равно (b + a) , а (ab) не всегда равно (ba).
Следующие примеры демонстрируют этот принцип:
| Выражение | Результат |
|---|---|
"файл" + 16 | файл16 |
16 + "файл" | Не удается преобразовать значение «файл» в тип «System.Int32». |
Ошибка: «Вводимая строка имеет неверный формат». | |
В строке:1 символ:1 | |
| ˙+ 16 + «файл»` |
Хэш-таблицы — это немного другой случай. Вы можете добавить хеш-таблицы в другая хэш-таблица, если в добавленных хеш-таблицах нет дубликатов ключи.
В следующем примере показано, как добавлять друг к другу хеш-таблицы.
$hash3 = @{a=1; б=2; с=3}
$hash4 = @{c1="Server01"; c2="Сервер02"}
$хэш2 + $хэш3
Имя Значение ---- ----- c2 Сервер02 1 Би 2 c1 Сервер01 с 3
В следующем примере возникает ошибка, поскольку один из ключей дублируется. в обеих хеш-таблицах.
в обеих хеш-таблицах.
$hash3 = @{a=1; б=2; с=3}
$hash4 = @{c1="Server01"; c="Сервер02"}
$хэш2 + $хэш3
Элемент уже добавлен. Ключ в словаре: 'c' Добавляемый ключ: 'c'
В строке:3 символ:1
+ $хэш2 + $хэш3
+ ~~~~~~~~~~~~~~~
+ CategoryInfo: OperationStopped: (:) [], ArgumentException
+ FullyQualifiedErrorId : System.ArgumentException
Также к массиву можно добавить хеш-таблицу; и вся хеш-таблица становится элементом массива.
$array1 = @(0, "Hello World", [datetime]::Now)
$хэш2 = @{а=1; б=2}
$массив2 = $массив1 + $хэш2
$массив2
0 Привет мир 12 июня 2017 г., 15:05:46 Ключ: а Значение : 1 Имя: а Ключ : б Значение : 2 Имя : б
Однако в хэш-таблицу нельзя добавить какой-либо другой тип.
$хеш2 + 2
Хэш-таблицу можно добавить только в другую хэш-таблицу. В строке:3 символ:1 + $хеш2 + 2
Хотя операторы сложения очень полезны, используйте присваивание
операторы для добавления элементов в хеш-таблицы и массивы. Чтобы получить больше информации
см. about_assignment_operators. То
В следующих примерах используется оператор присваивания
Чтобы получить больше информации
см. about_assignment_operators. То
В следующих примерах используется оператор присваивания += для добавления элементов в
массив:
$массив = @()
(0..9).foreach{$массив += $_}
$массив
0 1 2
Преобразование типа для соответствия результату
PowerShell автоматически выбирает числовой тип .NET, который лучше всего выражает результат без потери точности. Например:
2 + 3,1 (2).ПолучитьТип().ПолноеИмя (2 + 3.1).ПолучитьТип().ПолноеИмя
5.1 Система.Int32 Система.Двойной
Если результат операции слишком велик для типа, тип результата расширяется для размещения результата, как в следующем примере:
(512 МБ).GetType().Полное имя (512MB * 512MB).GetType().FullName
System.Int32 Система.Двойной
Тип результата не обязательно будет таким же, как один из операндов.
В следующем примере отрицательное значение не может быть приведено к беззнаковому
целое число, а целое число без знака слишком велико для приведения к Int32 :
([int32]::minvalue + [uint32]::maxvalue).gettype().полное имя
System.Int64
В этом примере Int64 может поддерживать оба типа.
Исключением является тип System.Decimal . Если любой из операндов имеет десятичное число тип, результат будет десятичного типа. Если результат слишком велик для
тип Decimal , он не будет преобразован в Double . Вместо этого возникает ошибка.
| Выражение | Результат |
|---|---|
[Десятичный]::maxvalue | 7 |
625142643375
[Десятичный]::maxvalue + 1 Значение слишком велико или слишком мало для Десятичный.Арифметические операторы и переменные
Вы также можете использовать арифметические операторы с переменными. Операторы действуют на
значения переменных. Следующие примеры демонстрируют использование
арифметические операторы с переменными:
Следующие примеры демонстрируют использование
арифметические операторы с переменными:
| Выражение | Результат |
|---|---|
$intA = 6 $intB = 4 $intA + $intB | 10 |
$a = «Питание» $b = «Оболочка» $a + $b | PowerShell |
Арифметические операторы и команды
Обычно вы используете арифметические операторы в выражениях с числами, строки и массивы.Однако вы также можете использовать арифметические операторы с объекты, которые возвращаются командами, и со свойствами этих объектов.
В следующих примерах показано, как использовать арифметические операторы в выражениях. с командами PowerShell:
(дата получения) + (новый временной интервал -день 1)
Оператор скобок принудительно выполняет оценку командлета Get-Date и
оценка выражения командлета New-TimeSpan -Day 1 в указанном порядке. Оба
затем результаты добавляются с помощью оператора
Оба
затем результаты добавляются с помощью оператора + .
Процесс получения | Где-Объект {($_.ws * 2) -gt 50mb}
Обрабатывает NPM(K) PM(K) WS(K) VM(M) CPU(s) Id ProcessName
------- ------ ----- ----- ----- ------ -- -----------
1896 39 50968 30620 264 1572,55 1104 исследователь
12802 78 188468 81032 753 3 676,39 5676 ПРОГНОЗ
660 9 36168 26956 143 12,20 988 PowerShell
561 14 6592 28144 110 1010.09 496 услуги
3476 80 34664 26092 234 ...45,69 876 свхост
967 30 58804 59496 416 930,97 2508 WINWORD
В приведенном выше выражении каждое рабочее пространство процесса ( $_.ws ) умножается на 2 ; и, результат, сравните с 50mb , чтобы увидеть, больше ли он, чем
тот.
Побитовые операторы
PowerShell поддерживает стандартные побитовые операторы, включая побитовое И.
( -bAnd ), включающие и исключающие операторы побитового ИЛИ ( -bOr и -bXor ) и побитовое НЕ ( -bNot ).
Начиная с PowerShell 2.0, все побитовые операторы работают с 64-битными целыми числами.
Начиная с PowerShell 3.0, -shr (сдвиг вправо) и -shl (shift-left) введены для поддержки побитовой арифметики в PowerShell.
PowerShell поддерживает следующие побитовые операторы.
| Оператор | Описание | Выражение | Результат |
|---|---|---|---|
-ленточный | Побитовое И | 10-диапазонный 3 | 2 |
-бор | Побитовое ИЛИ (включительно) | 10 -бор 3 | 11 |
-бксор | Побитовое ИЛИ (исключающее) | 10-бксор 3 | 9 |
-бнот | Побитовое НЕ | -bНе 10 | -11 |
-шл | Сдвиг влево | 102 -шл 2 | 408 |
-шр | Сдвиг вправо | 102 -шр 1 | 51 |
Побитовые операторы действуют на двоичный формат значения. Например, бит
структура числа 10 — 00001010 (на основе 1 байта), а бит
структура числа 3 — 00000011. Когда вы используете побитовый оператор для
сравнить 10 с 3, сравниваются отдельные биты в каждом байте.
Например, бит
структура числа 10 — 00001010 (на основе 1 байта), а бит
структура числа 3 — 00000011. Когда вы используете побитовый оператор для
сравнить 10 с 3, сравниваются отдельные биты в каждом байте.
В побитовой операции И результирующий бит устанавливается в 1 только тогда, когда оба входа биты 1.
1010 (10) 0011 ( 3 ) -------------- группа 0010 ( 2 )
В операции побитового ИЛИ (включительно) результирующий бит устанавливается в 1, когда один или оба входных бита равны 1.Результирующий бит устанавливается в 0 только тогда, когда оба входные биты установлены на 0.
1010 (10) 0011 ( 3 ) -------------- БОР (включительно) 1011 (11)
В операции побитового ИЛИ (исключающее) результирующий бит устанавливается только в 1 когда один входной бит равен 1.
1010 (10) 0011 ( 3 ) -------------- bXOR (эксклюзивный) 1001 ( 9 )
Побитовый оператор НЕ является унарным оператором, который производит двоичное
дополнение стоимости.Биту 1 присваивается значение 0, а биту 0 присваивается значение 1.
Например, двоичное дополнение 0 равно -1, максимальное целое число без знака (0xffffffff), а двоичное дополнение -1 равно 0,
.
-bНе 10
-11
0000 0000 0000 1010 (10) ------------------------- бНЕ 1111 1111 1111 0101 (-11, хфффффффф5)
В операции побитового сдвига влево все биты перемещаются на «n» позиций в слева, где «n» — значение правого операнда.Ноль вставляется в те место.
Если левый операнд представляет собой целое (32-разрядное) значение, младшие 5 битов правый операнд определяет, сколько битов левого операнда сдвигается.
Если левый операнд представляет собой длинное (64-битное) значение, младшие 6 бит правый операнд определяет, сколько битов левого операнда сдвигается.
| Выражение | Результат | Двоичный результат |
|---|---|---|
21 -шл 0 | 21 | 0001 0101 |
21 -шл 1 | 42 | 0010 1010 |
21 -шл 2 | 84 | 0101 0100 |
В операции побитового сдвига вправо все биты перемещаются на «n» позиций в
right, где «n» определяется правым операндом. Сдвиг вправо
оператор (-shr) вставляет ноль в крайнее левое место при сдвиге
положительное или беззнаковое значение справа.
Сдвиг вправо
оператор (-shr) вставляет ноль в крайнее левое место при сдвиге
положительное или беззнаковое значение справа.
Если левый операнд представляет собой целое (32-разрядное) значение, младшие 5 битов правый операнд определяет, сколько битов левого операнда сдвигается.
Если левый операнд представляет собой длинное (64-битное) значение, младшие 6 бит правый операнд определяет, сколько битов левого операнда сдвигается.
| Выражение | Результат | Двоичный | Шестнадцатеричный |
|---|---|---|---|
21 -шр 0 | 21 | 0001 0101 | 0x15 |
21 -шр 1 | 10 | 0000 1010 | 0x0A |
21 -шр 2 | 5 | 0000 0101 | 0x05 |
21 -шр 31 | 0 | 0000 0000 | 0x00 |
21 -шр 32 | 21 | 0001 0101 | 0x15 |
21 -шр 64 | 21 | 0001 0101 | 0x15 |
21 -шр 65 | 10 | 0000 1010 | 0x0A |
21 -шр 66 | 5 | 0000 0101 | 0x05 |
[число]::MaxValue -shr 1 | 1073741823 | 0x3FFFFFFFF | |
[число]::MinValue -shr 1 | -1073741824 | 0xC0000000 | |
-1 -шр 1 | -1 | 0xFFFFFFFF |
См.
 также
такжеСтепени и степени (предварительная алгебра, открытие дробей и множителей) – Mathplanet
Мы знаем, как вычислить выражение 5 х 5.{3}$$
алгебраических выражений — ChiliMath
Как и любой язык, математика позволяет передавать идеи. Алгебраическое выражение – это компактный способ описания математических объектов с использованием 90 268 комбинаций 90 269 чисел, переменных (букв) и арифметических операций, а именно сложения, вычитания, умножения и деления.
Другими словами, тремя основными компонентами алгебраических выражений являются числа , переменные и арифметические операции .
Примеры: 1, 6, 8, 27, 32 и т. д.
Примеры: x, y, a, h, p и т. д.
Примеры: + (сложение), — (вычитание), \times (умножение), ÷ (деление)
Ниже приведены простые примеры, которые помогут вам ознакомиться с операциями сложения, вычитания, умножения и деления.
сумма x и 5 → x+5
разница у и 3 → у-3
произведение n и 2 → 2n
частное k и 7 → \Large{{k \over 7}}
Написание алгебраических выражений Пошаговые примеры
Давайте рассмотрим еще примеры.
Пример 1: Сумма удвоенного числа и 3
Ответ: Пусть переменная x будет неизвестным числом. Таким образом, удвоенное число означает 2x. Сумма (используйте символ плюса) удвоенного числа и 3 может быть записана как 2x+3.
Пример 2: Разница тройного числа и 5
Ответ: Пусть переменная y будет неизвестным числом. Таким образом, тройное число означает 3 года. Разность (используйте символ минус) тройного числа и 5 должна быть записана как 3y — 5.
Пример 3: Сумма частного m и 2 и произведения 4 и n.
Ответ: В этом случае неизвестные числа уже представлены как m и n. Это одним поводом для беспокойства меньше.
Ключ в том, чтобы признать, что мы собираемся добавить частное и произведение .
- частное m и 2 выражается как \Large{{m \over 2}}
- произведение 4 на n выражается как 4n
Таким образом, сумма частного и произведения равна {\ большой {{м\свыше 2}}} + 4н.
Пример 4: Разность произведения 7 и w и частного 2 и v.
Ответ: В этом случае неизвестным номерам были присвоены соответствующие переменные w и v.
Суть в том, чтобы понять, что мы собираемся вычесть произведение на частное некоторых выражений .
— {\ Большой {{2 \ над v}}}.
Общие слова или термины для обозначения сложения, вычитания, умножения и деления
Теперь давайте рассмотрим некоторые общеупотребительные слова или фразы, описывающие четыре арифметические операции. Очень важно, чтобы вы знали эти слова или фразы, чтобы успешно писать или интерпретировать любое заданное алгебраическое выражение.
Преобразование математических фраз в алгебраические выражения
Ключом к обучению является изучение множества примеров!
| Математические фразы | алгебраические выражения | ||
| номер плюс 9 | Y + 9 | ||
| сумма ряд и 10 | м + 10 | ||
| Всего номера и 5 | 9| | | |
| x + 4 | H|||
| H Убирайте 2 | H — 2 | ||
| 2 Убрать номер | 2 — H | ||
| номер минус 11 | K — 11 | ||
| 11 минус номер | 11 — K | ||
| a ряд уменьшился 7 | y − 7 | ||
| разница n и 25 | n − 25 | ||
| 8 n 25 и | разница|||
| 8 — N | |||
| 5 меньше, чем номер | x — 5 | ||
| X меньше, чем номер 5 | 5 — x | Продукт R и 4 | 4R |
| 7 раз a a a 99 | 7P 9P | ||
| 2x | |||
| Тройной номер | 3x | ||
| a Число, разделенное на 4 | w / 4 | ||
| Квартир W и 6 | W / 6 | ||
| Квартир 12 и м | 12 / м | ||
| Разделенные на 3 | F / 3 | T 3T более 7 | T / 7 |
| 5 на номер | A / 5 | ||
| a ряд на 5 9 0208 | 5 / A 9/1 | ||
| Сумма X и 7, разделенных на 2 | (x + 7) / 2 | Разница в м и 3 более 5 | (м — 3 ) / 5 |
| 11 Больше, чем продукт 3 и Y | 3Y + 11 | ||
| 60209 | |||
| 6 Менее чемцем C и 10 | (C / 10) — 6 | ||
| 3 минус товар 5 и номер | 3 — 5x | ||
| сумма 5 и фактор Z и 7 | (Z / 7) + 5 | Разница в разницу двойного числа и 3 | 2m − 3 |
Вас также может заинтересовать:
Работающие примеры алгебраических выражений
Проблемы со словами на алгебраические предложения
.
Математика Умножение числа 5 и на число 5, и соответствующие случаи деления
Материалы к уроку
12. Умножение числа 5 и на число 5, и соответствующие случаи деления.doc
44.5 KBСкачать12. Умножение числа 5 и на число 5, и соответствующие случаи деления.ppt
5.57 MBСкачать
Конспект урока
|
12. Умножение числа 5 и на число 5, и соответствующие случаи деления
Организационный этап
Начинается урок. Сегодня на уроке мы будем составлять таблицу умножения и деления на 5. А также научимся узнавать, во сколько раз одно число больше или меньше другого.
Актуализация знаний
Устный счёт
Задание К нам пришло письмо, которое написал один сказочный герой. А как его зовут, мы узнаем, выполнив задание. 1. Найдите сумму чисел 77 и 23… 100 2. На сколько 90 больше, чем 12… на 78 3. Увеличьте 6 в 2 раза… 12 4. Уменьшите 15 в 3 раза…. 5 5. Найдите произведение чисел 3 и 7… 21 6. 7. Уменьшите 10 в 2 раза… 5 8. Первый множитель — 4, второй множитель — 9. Найдите произведение… 36 9. Сколько будет 18:3… 6
Какой герой написал сказочное письмо?
Правильно, Лесовичок. |
||||||||||||||||||
|
Лесовичок пригласил нас в гости и в своём письме передал карту. Медвежонок нашёл нашу карту и разорвал её на части. Нам предстоит её правильно сложить. А для этого нужно решить числовые выражения с объяснением. На какие группы можно разделить все числовые выражения? Все примеры разделим на нахождение суммы и произведения Давайте заменим сложение умножением. Что у нас получилось? Таблица умножения на 5. Сегодня мы познакомимся с таблицей умножения и деления на 5. Карта перед нами. В путь. Постараемся в пути показать умения. |
||||||||||||||||||
|
Этап усвоения новых знаний
Мы с вами вышли на полянку, где нас встречают лесные звери. Они тоже хотят учиться вместе с нами. Звери хотят, чтобы мы им помогли составить таблицу умножения и деления с числом 5, и они нам покажут дорогу к Лесовичку. Давайте вспомним, какие числовые выражения умножения на 5 мы уже хорошо знаем. 5·2=10 5·3=15 5·4=20 Теперь продолжим составлять таблицу. Первый множитель 5, второй множитель 5, произведение равно 25. Первый множитель 5, второй множитель 6, произведение равно 30. Первый множитель 5, второй множитель 7, произведение равно 35. Первый множитель 5, второй множитель 8, произведение равно 40. Первый множитель 5, второй множитель 9, произведение равно 45. Теперь, ребята, зная таблицу умножения на 5, давайте составим таблицу деления на 5. Для этого давайте еще раз вспомним правило, как найти множитель, зная произведение. Правильно, чтобы найти множитель, нужно произведение разделить на второй множитель. Рассуждайте так: Произведение 10 делим на множитель 5, в ответе получаем 2. Зная правило, мы теперь можем составить таблицу деления на 5. Произведение 15 делим на множитель 5, в ответе получаем 3. Произведение 20 делим на множитель 5, в ответе получаем 4. Произведение 25 делим на множитель 5, в ответе получаем 5. Произведение 30 делим на множитель 5, в ответе получаем 6. Произведение 35 делим на множитель 5, в ответе получаем 7. Произведение 40 делим на множитель 5, в ответе получаем 8. Произведение 45 делим на множитель 5, в ответе получаем 9. Чтобы быстро и правильно решать, таблицу умножения нужно отлично знать |
||||||||||||||||||
|
Закрепление материала
Чтобы узнать, какая дорога ведет к домику Лесовичка, нужно решить числовые выражения.
Выполните действия. 7·5 40:5 6·5+(40-18) 5·9 30:5 Проверьте себя и оцените свои успехи. 7·5=35 40:5=8 5·9=45 30:5=6
6·5+(40-18)=52 |
||||||||||||||||||
|
Мы с вами вышли к домику Лесовика. А к нему в гости пришли звери. Они предлагают решить нам задачу. Решите задачу. В мяч играли 5 зайчиков и 7 белочек. Для игры они разделились на 2 команды. Сколько зверей в каждой команде? Проверьте себя и оцените свои успехи. В первом действии узнаем, сколько зверей играло в мяч: 5+7=12 зверей. Во втором действии узнаем, сколько зверей было в каждой команде: общее количество зверей разделим на 2, т. Ответ: в каждой команде было по 6 зверей.
А вот и Лесовичок. Трудна была ко мне дорога, |
||||||||||||||||||
|
Посмотрите, на веточке сидят 6 воробьев и 3 сороки. Во сколько раз воробьев больше, чем сорок. Во сколько раз сорок, меньше, чем воробьев? Чтобы узнать, во сколько раз одно число меньше или больше другого, надо большее число разделить на меньшее. Чтобы узнать, во сколько раз воробьев больше чем сорок, надо 6:3, получим 2. Значит, воробьев больше чем сорок в 2 раза. Чтобы узнать, во сколько раз сорок, меньше чем воробьев, надо 6:3, получим 2. Значит сорок меньше чем воробьев в 2 раза. Решите задачу. На поляне растет 12 дубов и 4 березы. Во сколько раз дубов больше чем берез? Проверьте себя и оцените свои успехи. Чтобы узнать, во сколько раз одно число меньше или больше другого, надо большее число разделить на меньшее. Значит, 12 делим на 4, будет 3. Ответ: дубов больше чем берез в 3 раза. |
||||||||||||||||||
|
Подведение итогов
Как узнать, во сколько раз одно число больше или меньше другого?…… Чтобы узнать, во сколько раз одно число меньше или больше другого, надо большее число разделить на меньшее.
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Конспект урока по Математике «Умножение шести,на 6 и соответствующие случаи деления» 3 класс
Урок математики в 3-м классе
Учитель:Федотова Галина Дмитриевна
МКОУ»Фролово-Горетовская ООШ»
Сухиничский район
Тема: «Умножение шести,на 6 и соответствующие случаи деления
Вид урока: урок изучения нового материала
Целевые установки:
Планируемые цели для учителя:
сконструировать таблицу умножения 6, опираясь на различные свойства умножения;
исследовать связь между изменяющимся множителем и цифрами в произведении;
найти закономерности и особенности данной таблицы с целью быстрого её запоминания;
решать задачи на нахождение произведения и суммы.

Планируемые метапредметные результаты:
Личностные:
формировать положительное отношение к учению,
уважительное отношение к собеседнику,
развивать интерес к различным видам решения поставленной учебной задачи и к расширению математических знаний.
Регулятивные:
уметь определять и формулировать цель на уроке;
учиться совместно с учителем обнаруживать и формулировать учебную проблему;
планировать свои действия в связи с поставленной задачей.
понимать, принимать и сохранять учебную задачу; осуществлять самооценку учебных действий;
Познавательные:
уметь ориентироваться в своей системе знаний;
ориентироваться в предложенном материале, находить нужную информацию
отличать новое от уже известного; добывать новые знания.
Коммуникативные:
уметь с достаточной полнотой и точностью выражать свои мысли;
слушать и понимать речь других;
уметь работать в паре, группе;
формулировать собственное мнение и позицию.

Планируемые предметные результаты.
Обучающиеся:
закрепят знания изученных таблиц, устных приёмов вычисления примеров разного вида;
усовершенствуют умения решать задачи;
повторят понятия уравнения, подбор корня уравнения;
усовершенствуют умения ориентироваться в геометрическом материале, в нахождении периметра.
смогут проанализировать, найти закономерности при составлении таблицы;
смогут составить, усвоить и частично запомнить таблицу умножения на 6;
сумеют применить полученные знания на практике;
смогут сотрудничать при групповой работе и работе в парах, задавать вопросы, учитывать мнение одноклассников, отстаивать свою точку зрения.
будут адекватно себя оценивать на уроке;
Здоровьесберегающие:
— развивать мелкую моторику кисти;
— Формировать правильную посадку при письме;
— контролировать эмоциональную и физическую перегрузку детей с помощью физкультурных пауз .
Методы: практический, проблемный, частично-поисковый, словесный.
Время реализации занятия: 45 минут.
Оборудование:
Для учителя:
-Учебник для третьего класса. Авторы: М.И. Моро, С.И. Волкова, С.В. Степанов
— интерактивная доска, карточки, смайлики, таблица умножения, рабочие тетради.
-карточки для индивидуальной работы, работы в группах и парах
Этапы урока и их продолжительность:
I.Организационный момент 1мин
II.Актуализация знаний. 7мин
III .Самоопределение к деятельности. 10мин
V. Дыхательная медитация. Физмининутка. 3мин
VI. Проверка усвоения нового материала 10мин
VII.Закрепление изученного материала 10мин
VIII этап.Рефлексия. 2мин
VIII.Подведение итогов урока 1мин
IX. Домашнее задание 1мин
Домашнее задание 1мин
Ход урока
I.Организационный момент
Здравствуйте ребята! Садитесь!
«Все расселись по местам,
Никому не тесно!
По секрету скажу Вам,
Будет интересно!
Будем мы считать, писать,
И решать задачи!
Чтоб сегодня как всегда,
В руки шла удача!
Узнаем новый материал,
Закрепим умения,
Чтобы каждый мог сказать,
Это всё умею я!»(слайд 2)
– Ребята, на доске девиз нашего урока: «С хорошим настроением принимайся за работу!»(слайд 3)
-Улыбнитесь друг другу. Подарите и мне свои улыбки. Ваши улыбки располагают к приятному общению, создают хорошее настроение. Всем удачи.
Возьмите смайлики и нарисуйте свое настроение.
Работа в тетрадях: (слайд 4)
И ещё убедительная просьба: ответить хочешь, не шуми, а только руку подними.
II.Актуализация знаний.
1. Проведение минутки чистописания
Открыли тетради. И перед тем как вы начнёте писать, я хочу задать вам несколько вопросов.
И перед тем как вы начнёте писать, я хочу задать вам несколько вопросов.
Посмотрите на доску и ответьте мне на несколько вопросов:
Какое сегодня число? (20 октября.) (слайд 6)
(20-двузначное ( состоит из 2 д. и 0 единиц). Соседи числа 19 и 21,
чётное.)
Скажите ребята, а число 20 встречается в изученном нами табличном умножении?(Да)
Что вы можете мне сказать о словах – октябрь, работа, классная?
(Словарные слова.)
А какими частями речи они выражены?
(Существительное .Прилагательное)
Оформление тетрадей.
Открыли тетради и выполнили грамотную и аккуратную запись.
(Далее самостоятельно выполняют запись в тетради.)
А теперь проведём минутку чистописания. Для чего нам нужны минутки чистописания?(ответы детей)
Задание №1
Даня и Стёпа — от 10 до 20
Настенька, Даша и Алина – записывают по порядку числа от 25 до 35.
Молодцы, ребята!Я вижу на уроке внимательныx ,аккуратныx ребят.
Оцените свою работу с помощью смайлика
2.Решение задач.
Чтобы быстро считать,
Задачи без труда решать,
Нам надо себя тренировать.
В математике любая работа
Не обходится без устного
счёта. (слайд8)
а).Работа над задачами
Дарит бабушка-лисица
Трём внучатам рукавицы:
Это вам на зиму, внуки,
Рукавичек по две штуки.
Берегите, не теряйте!
Сколько всех, пересчитайте! (слайд 9)
б)Если знаешь ты таблицу,
На вопрос ответишь смело:
Сколько птичек-невеличек
На кормушку прилетело?
Воробьёв драчливых пара,
И синичек тоже пара,
Пара сизых голубей
И две пары снегирей . (слайд 10)
Молодцы!
3.Математический диктант
(Учитель читает высказывания. Если учащиеся согласны, они ставят знак +, если нет — знак —. )
)
Произведение чисел 4 и 6 равно 24. (+)
6 больше 2 в 12 раз. (—)
Если к 35 прибавить 18; получится 43. (—)
20 — четное число. (+)
В таблице умножения на 4 есть число, которое оканчивается цифрой 0. (+)
Частное чисел 36 и 5 равно 7. (—)
Число 25 не делится на 2. (+)
Из произведения чисел 8 и 0 число 6 не вычитается. (+) (Проверка индивидуальной работы у доски.)
( взаимопроверка, оценки) слайд 12
III .Самоопределение к деятельности.
Найди закономерность.
(Запись на слайде № 15)
12 25 16 30 24 35 28 40 32 48
Учитель:
Посмотрите на доску и прочитайте числа. Что вы можете сказать про эти числа?
(Дети:
Это произведения из таблицы умножения на 4 и 5)
Учитель: Назовите произведения из таблицы умножения на 5?
(Дети: 25 30 40)
Учитель: Назовите произведения из таблицы умножения на 4?
(Дети:12 16 24 28 40 32)
(-Составляем таблицы умножения и деления на 3,4,5)
Просто составляем?
(- Нет, мы проводим исследования, ищем закономерности, подбираем , на -xодим пути для лучшего запоминания таблицы. )
)
Постановка проблемы.
А теперь я предлагаю Вам решить примеры.
3х9=27
4х8=32
5х7=35
7х5=35
8х4=32
9х3=27 (слайд 16)
Исследование проблемы и нахождение пути её преодоления.
Давайте проведём исследование данного столбика примеров.
-Что интересного вы увидели сами?
-По какому принципу составлены примеры?
(Взаимообратные)
-Как мы называем такие примеры?
-Какое правило здесь используется?
Ответьте мне математическим языком, как учёные математики.
(От перестановки множителей произведение не меняется.)
-А почему мы смогли решить эти примеры?
(Мы знаем таблицу умножения на 3, на 4 и на 5.)
-Хорошо, идем дальше. Продолжаем проводить наше исследование.
-Посмотрите внимательно ещё раз на данный столбик примеров и скажите, а какого примера не хватает в столбике?
(6х6) (слайд 17)
-Как вы думаете, почему я его пропустила? Чего побоялась?
(Мы не знаем таблицу умножения на 6. )
)
-Так какова же тема нашего урока?
(Составление таблицы умножения и деления на 6.) ( слайд 18)
А какие цели мы ставим сегодня на уроке?
(Составить, записать таблицу умножения на 6 и научиться её использовать.)
IV.Работа по теме урока.
1.Составление таблицы умножения и деления с числом 6
Составление таблицы умножения на 6 (работа в группе)
Ребята работают группой.
Группа :
Настенька, Даша,
Даня, Стёпа и Алина
Составляют таблицу умножения и деления( проверка у доски)
Давайте проверим, как Вы справились? (слайд 19)
(Таблица появляется на слайде. )
Ответственные проверяют и дают оценку, как они справились с работой.
Исследование таблицы умножения
А теперь ребята давайте поищем закономерности, пути к лучшему запоминанию таблицы.
Посмотрите внимательно и скажите, что интересного вы увидели?
6х2=12
6х3=18
6х4=24
6х5=30
6х6=36
6х7=42
6х8=48
6х9=54
Закономерности:
второй множитель увеличивается на1
первый множитель неизменный
произведение увеличивается
на 6 (сверху вниз, а снизу вверх уменьшается на 6)
все произведения двузначные числа
сумма цифр в произведении чередуется так 3,9.
 6,3,9,6,9 (кроме 48)
6,3,9,6,9 (кроме 48)
Слышится рифма, волшебные слова.
Проговорить:
6х2=12
6х4=24
6х6=36
6х8=48
Итак, ребята, достигли мы поставленной цели ?(Да!)
А теперь наша задача состоит в том, чтобы научиться практически использовать таблицу и запомнить её, насколько это возможно!
Давайте запишем таблицу в тетради, но я вам предлагаю записать только 4 примера, почему?
(остальные примеры нам знакомы из других таблиц, а почему не берём умножение на 1, умножение на10?)
-Где пригодится знание таблицы умножения?
(При решении задач ,уравнений, примеров)
А в жизни?(Ответы детей)
Составляем таблицу на деление вместе (слайд 20)
Оцените работу с помощью смайлика
V. Дыхательная медитация. Физминутка
Сядьте ровно, расслабьтесь, закройте глаза. Вы идёте по лесу. Вдох. Выдох. Какой чистый воздух. Вдох. Выдох. Вот елочка в осеннем наряде. Вдох. Выдох. Как красиво кругом. Вдох. Выдох. Открываем глаза.
Вдох. Выдох. Как красиво кругом. Вдох. Выдох. Открываем глаза.
Раз, два — дружно встали, (Шаги на месте.)
Руки прямо мы поставим. (Руки на поясе.)
Три, четыре — разведем,(Руки в стороны.)
Заниматься мы начнем.(Наклоны вперед с касанием носка правой ноги
левой рукой, а носка левой ноги — правой рукой.)
Вправо, влево посмотрели,(Повороты головы вправо и влево.)
На носочках мы присели (Присесть.)
И, как птички, полетели. (Учащиеся разбегаются по классу.) (слайд 21)
VI. этап Проверка усвоения нового материала
Работа по учебнику № 1 (с. 44).(слайд 22)
VII.Закрепление изученного материала
1.Работа по учебнику №4 (с. 44).
(Устное выполнение.)
(Аналогично разбираются остальные уравнения.)
Оцените работу соседа.
№6 (с. 44).(слайд 23)
(Самостоятельное выполнение. Один ученик работает на откидной доске. Тем, кто испытывает затруднения, учитель дает карточку-помощницу с краткой записью.)
Один ученик работает на откидной доске. Тем, кто испытывает затруднения, учитель дает карточку-помощницу с краткой записью.)
Было — 50 кг.
Израсходовали — ?, 2 • 6 (кг).
Осталось — ?
Проверка по шаблону.
VIII этап.Рефлексия.
(«Проверь себя» (учебник, с. 44). Самостоятельное выполнение. Проверка по образцу.)
Решение: 4 • 3 = 12 4 • 5 = 20 4 • 6 = 24 4 • 10 = 40
А теперь я хочу, чтобы вы оценили свою работу на уроке.
– Понравился ли вам урок?
– Какие задания вы выполнили с удовольствием.
Поднимите:
зелёный кружок, кому было на уроке легко и всё понятно.
жёлтый – если что-то не понял на уроке, и надо поработать дополнительно.
красный- красный, кому было трудно на уроке, и надо подойти к учителю за помощью.
— Кто доволен своей работой?
(Дети дают самооценку своей работе.) (слайд 24)
VIII.Подведение итогов урока
— Назовите тему урока.
(слайд 24)
IX.Домашнее задание
Учить таблицу умножения и деления на 6.
На «5»- придумать задачи на деление и умножение на 6 и записать решение в тетрадь.
На «4»- учебник с. 44 №2,№5
На «3»-записать таблицу умножения 6 и соответствующие случаи деления в тетрадь
Закончен урок и выполнен план.
Спасибо, ребята, огромное вам!
За то что упорно и дружно трудились
Что на уроке вы не ленились!
Спасибо за урок!
:
Методика изучения таблицы умножения и соответствующих случаев деления в курсе математики начальных классов.
Тема: «Смысл умножения и деления. Свойства умножения. Связь компонентов и результатов действий умножения и деления. Таблица умножения и соответствующие случаи деления»
Методика изучения таблицы умножения и соответствующих случаев деления в курсе математики начальных классов.
Перед составлением таблицы умножения и деления рассматриваем теоретическую основу этой таблицы.
К теоретической основе табличного умножения и деления относят:
1) смысл умножения;
2) переместительное свойство умножения;
3) связь между компонентами и результатом действий умножения и деления.
Эти вопросы изучают на I этапе темы «Табличное умножение и деление».
По мере рассмотрения теоретических вопросов учащихся знакомят с табличными приемами умножения и деления. При изучение каждого теоретического вопроса, вводится прием.
1 ПРИЁМ умножения однозначных чисел 7 * 3 = 21
7+7+7 = 21
7 умножить на 3, значит по 7 берем 3 раза.
Теоретическая основа – конкретный смысл действия умножения.
ПРИЁМ умножения однозначных чисел.
Знаем, что 7 * 7 = 49
Найти 7 * 8 = (7+7+7+7+7+7+7) +7 = 7*7+7 = 56
Если мы знаем, что 7 * 7 = 49, то мы можем посчитать, сколько будет 7 * 8. По 7 взяли 8 раз – это значит, по 7 взять 7 раз и прибавить еще 7.
По 7 взяли 8 раз – это значит, по 7 взять 7 раз и прибавить еще 7.
В соответствии с этим приёмом новый случай сводят к такому случаю, который детям известен.
7 * 8 = 7 * 4 + 7 * 4 =…
7*8 = 7 * 10 – 7 * 2=…
Таким образом, любой случай умножения можно подвести к тому случаю, который детям уже известен.
Теоретическая основа:
Конкретный смысл действия умножения;
Сочетательное свойство сложения;
Знание некоторых случаев умножения;
Сложение в пределах 100.
3 ПРИЁМ умножения однозначного числа используют для случаев, когда второй множитель больше первого 3 * 7 = 21
3 * 7 = 7 * 3 = 21
7 + 7 + 7 =21 – так быстрее
Это приём перестановки множителей.
Теоретическая основа: переместительный закон умножения и знание некоторых случаев умножения.
ПРИЁМ деления двузначного или однозначного на однозначное число.
Чтобы разделить вспоминаем соответствующий случай умножения.
21 – это 7 умножить насколько? (на 3)
21 : 7 =
21 = 7 * 3
21 : 7 = 3
Если произведение разделить на один множитель получится другой.
Теоретическая основа:
Знание таблицы умножения;
Зависимость между множителями и произведением.
5 ПРИЁМ деления основан на способе подбора частного.
Опираемся на правило: если частное умножить на делитель, то получим делимое.
21 : 7 = 3
7 * 2 = 14 14 < 21
7 * 3 = 21 21 = 21
Способ подбора основан на взаимосвязи между делимым, делителем и частным: если частное умножить на делитель, получим делимое. Подбор начинают с числа 2, т.к. при умножении 1, получают то же число.
Подбор начинают с числа 2, т.к. при умножении 1, получают то же число.
Теоретическая основа: связь между делимым, делителем и частным, знание таблицы умножения.
Прием № 5 позволяет заучить таблицу.
Основываясь на эти приёмы, на II этапе, составляют таблицы умножения и деления.
С каждым числом составляют по 4 таблицы умножения и деления (по 4 столбика).
1 столбик: таблица умножения по постоянному первому множителю. Для его составления используют приёмы №1 и №2. 1-й, столбик начинают со случая одинаковых множителей:
2 *2 = 󠇔󠇔 4 4:2=2
2+2=4
2*3=6 3*2=6 6:2=3 6:3=2
2+2+2=6
2*4=8 4*2=8 8:2=4 8:4=2
2+2+2+2=8
2*5=10 5*2=10 10:2=5 10:5=2
2+2+2+2+2=10
2*6=12 6*2=12 12:2=6 12:6=2
2*6=2*5+2=12
2*7=14 7*2=14 14:2=7 14:7=2
2*7=2*6+2=14
2*8=16 8*2=16 16:2=8 16:8=2
2*8=2*7+2=16
2*9=18 9*2=18 18:2=9 18:9=2
2*9=2*8+2=18
Теоретическая основа 1 таблицы – конкретный смысл действия умножения.
Случаи 2*1 и 2*10 в таблице не разбирают, т.к. это частные случаи, их разбирают потом.
2 столбик: столбик умножения по постоянному второму множителю. Для его составления используют приём №3.
Теоретическая основа 2 таблицы – переместительное свойство умножения. Учитель даёт задание: поменяйте множители в 1 столбике местами, изменится ли произведение? Составьте второй столбик самостоятельно. 2 столбик начинают со второй строки.
3 столбик: деление по постоянному делителю. Составляется на основе использования приема № 4 из 1 столбика. 1 столбик в таблице считается самым главным.
Сравните различные методические подходы к составлению и заучиванию таблиц умножения и деления, используемые в альтернативных учебниках математики для начальных классов.
М2М ч.2 с.82. М2М ч.2 с.83.
На с.83 изучают третий теоретический вопрос – связь между множителями и произведением, составляют столбики на деление, заучивают их.
На страницах 90-94 сначала для чисел 2 и 3 используют 2 подход, т.е. по очереди изучают теоретические вопросы и сразу же составляют столбики с числами 2 и 3. Они оказываются разорванными.
М2М ч.2 с.90. М2М ч.2 с.91.
М2М ч.2 с.92.
| М2М ч.2 с.93. |
М3М ч.1 с.34-35, 40-65.
М3М ч.1 с.34. М3М ч.1 с.35.
М3М ч.1 с.40. М3М ч.1 с.44.
М3М ч.1 с.48. М3М ч.1 с.62.
М3М ч. 1 с.65.
1 с.65.
М3М ч.1 с.68.
На с.68 составляют сводную таблицу умножения.
С.80-81.
Заучивание продолжают до с.81. Предлагают проверочную работу (тесты). Рассматриваются различные способы выполнения заданий, учащимся предлагаются задания на соотнесение изучаемого с ранее изученным материалом.
М3М ч.1 с.82-85.
Далее учащиеся знакомятся с особыми (частными) случаями умножения любого числа на 1 и 0. На с.82 вводится правило умножения любого числа на 1: при умножении любого числа на 1 получается то число, которое умножали.
На с.83 вводится правило умножения любого числа на 0: при умножении любого числа на нуль получается нуль. Замечается, что на 0 делить нельзя!
С.84.
С.85.
На данной странице учащиеся знакомятся с делением нуля на число. Дается формулировка: если произведение 0 разделить на число, не равное 0, получим 0.
Дается формулировка: если произведение 0 разделить на число, не равное 0, получим 0.
В учебнике М.И. Моро мало упражнений развивающих логическое мышление, внимательность. Практически отсутствуют задания с элементами занимательности. Упражнения однотипны. Поэтому просто необходимо дополнять данные в учебнике задания упражнениями, дополнительными заданиями развивающего характера.
М2И ч.2 с.64. УМК «Гармония».
Табличные случаи умножения и соответствующие им случаи деления
учащиеся должны усвоить на уровне навыка. Это сложный и длительный процесс, в котором можно выделить два основных этапа. Первый этап связан с составлением таблиц, второй — с их усвоением, т. е. прочным запоминанием.
По программе Истоминой Н.Б. во втором классе учащиеся при ознакомлении с таблицами умножения и деления используют 2 подход, т.е. опираются на конкретный смысл умножения, начинают составлять первые столбики с разными числами, но в отличие от учебника Моро, начинают с числа 9, т. к. по мнению автора, эти случаи самые сложные. Изучают эти случаи не целым столбиком, а частями. Например, на первом уроке М2И ч.2 с.64 случаи: 9*5, 9*6, 9*7, на другом уроке: 9*2, 9*3, 9*4, на третьем уроке: 9*8, 9*9. Учитель дает установку на
к. по мнению автора, эти случаи самые сложные. Изучают эти случаи не целым столбиком, а частями. Например, на первом уроке М2И ч.2 с.64 случаи: 9*5, 9*6, 9*7, на другом уроке: 9*2, 9*3, 9*4, на третьем уроке: 9*8, 9*9. Учитель дает установку на
запоминание, которая распределяется во времени: сначала дается установка на запоминание трех табличных случаев, затем еще трех и напоследок — двух табличных равенств.
М2И ч.2 с.64.
С.69.
С.71.
В учебнике достаточно много различных упражнений, которые способствуют усвоению случаев табличного умножения с числом 9.
С.60.
С.69.
С.70.
С.71.
С.73.
С.77.
Случаи табличного умножения числа 8 усваиваются учащимися в процессе изучения переместительного свойства умножения и понятия «увеличить в несколько раз». Заданий на закрепление изученных случаев также достаточно.
Заданий на закрепление изученных случаев также достаточно.
С.82.
В 3 классе изучают смысл деления и связь между множителями и произведением, и разбирают табличные случаи с делением.
М3И ч.1 с. 35. УМК «Гармония».
С.37.
С.41.
С.43.
С.49.
М3И ч.1 с. 56. М3И ч.1 с. 57.
М3И ч.1 с. 62.
Таблица деления не составляется, деление рассматривается, как действие обратное умножению.
С.54.
Составление таблицы умножения на 5.
С.64.
В данной теме вводится понятие «действие первой ступени» и «действие второй ступени». Дана формулировка правила порядка действий: если в выражение без скобок есть действия разных ступеней, то сначала выполняют по порядку все действия второй ступени (умножение и деление), а затем все действия первой ступени (сложение и вычитание).
С.63.
Составление таблицы умножения на 6.
С.66.
Составление таблицы умножения на 7.
С.68.
Составление таблицы умножения на 8.
С.70.
Составление таблицы умножения на 9.
С.74.
На данной странице представлена сводная таблица умножения. На основании переместительного закона умножения выполняется сокращение составленных столбиков таблицы. Дается установка на заучивание.
Таким образом, в системе Л.В. Занкова таблицы умножения и деления составляются по второму постоянному множителю до изучения необходимой теории, после чего происходит постепенное сокращение числа равенств, необходимых для заучивания. В данном учебнике представлены различные задания для закрепления табличных случаев умножения.
С.66.
На 27 уроке учащиеся составляют таблицу умножения на 2.
С. 72.
72.
Составляется таблица деления числа на 2.
С.80.
На 33 уроке проводится связь между умножением и делением.
С.88.
На 37 уроке учащиеся составляют таблицу умножения на 3. Таблица умножения и деления на 3 рассматривается аналогично таблице умножения и деления на 2, на нее отводится один урок.
С.98.
На 41 уроке учащиеся составляют таблицу умножения на 4.
С.14.
На 5 уроке учащиеся составляют таблицу умножения на 6.
С.23.
На 8 уроке учащиеся составляют таблицу умножения на 7.
С.31.
На 11 уроке учащиеся составляют таблицы умножения на 8 и 9.
Несмотря на то, что основное внимание уделяется на этих уроках новым таблицам, необходимо систематически включать изученные табличные случаи. На изучение и закрепление табличных случаев умножения по учебнику Л. Г. Петерсон отводится от 5 до 3 уроков.
Г. Петерсон отводится от 5 до 3 уроков.
В данном учебнике присутствуют задания разноуровнего характера, такие же задания присутствуют и в учебнике математике М.И. Моро, но в учебнике Л.Г. Петерсон имеются разнообразные дидактические игры, задания с блок-схемами, блиц – турниры, в этом учебнике в основном задания развивающего характера.
М2Д ч.2 с.58. УМК «Школа 2100».
Учащиеся составляют таблицы умножения на 3. Рассматривается и переместительное свойство умножения.
С.60.
С.63.
Проводится связь между умножением и делением. Вводится формулировка правила: если произведение разделить на один множитель, то получим другой множитель.
С.64.
Учащиеся предлагается найти значения выражений, пользуясь таблицей умножения. Таким образом, составляется таблица деления числа на 2.
С.65.
С.66.
При закреплении таблиц умножения и деления на 2 учащиеся знакомятся с понятиями чётные и нечётные числа. Дается формулировка: числа 4, 6, 8, 10 делятся на 2. Они называются чётными. Числа 3, 5, 7, 9 не делятся на 2. Они называются нечётными. Чётные и нечётные числа в ряду чередуются.
Дается формулировка: числа 4, 6, 8, 10 делятся на 2. Они называются чётными. Числа 3, 5, 7, 9 не делятся на 2. Они называются нечётными. Чётные и нечётные числа в ряду чередуются.
С.31.
Учащиеся составляют таблицы умножения и деления на 3. Дается установка на запоминание изученных случаев.
С.72.
Рассматривается новая тема: «Порядок действий в выражении». Дана формулировка правила порядка действий: в выражении без скобок сначала выполняют умножение и деление, а потом сложение и вычитание по порядку слева направо.
С.74.
Продолжается изучение темы: «Порядок действий в выражении». Дана формулировка правила порядка действий: в выражении со скобками сначала выполняются действия в скобках, а далее по изученному выше правилу.
С.76.
Учащиеся составляют таблицы умножения и деления на 4. Дается установка на запоминание изученных случаев.
М2Д ч.3 с.4. УМК «Школа 2100».
Учащиеся составляют таблицы умножения и деления на 5. Дается установка на запоминание изученных случаев.
С.16.
Учащиеся составляют таблицы умножения и деления на 6. Дается установка на запоминание изученных случаев.
С.28.
Учащиеся составляют таблицы умножения и деления на 7. Дается установка на запоминание изученных случаев.
С.44.
Учащиеся составляют таблицы умножения и деления на 8 и 9. Дается установка на запоминание изученных случаев.
Заданий на закрепление табличных случаев умножения в учебнике достаточно.
С.84.
С.85.
На данной странице учащиеся знакомятся с делением нуля на число. Дается формулировка: если произведение 0 разделить на число, не равное 0, получим 0.
Заданий для закрепления частных случаев умножения и деления недостаточно → дает сам учитель.
С.78.
На данной странице предлагается задание, раскрывающее связь между умножением и делением. Сначала учащиеся находят значения произведений, затем с помощью получившихся равенств находят значения частных, с опорой на записи делают вывод. Формулировки правила «деление на 1» в учебнике нет󠇄 → дает сам учитель. При деление любого числа на 1, получается тоже самое число. Например, 5 : 1 = 5. Если число разделить на самого себя, получим 1. Например, 5 : 5 = 1.
С.82.
Учащимся предлагается сравнить выражения, вычислить их значения, заменив умножение сложением, затем сделать вывод и закончить правило: При умножение числа 0 на натуральное число получится …
В качестве подсказки дается общий вид правила: 0 * а = 0
Далее рассматривается другое равенство: а * 0 = 0, учащиеся пользуясь правилом находят значения выражений: 6 * 0, 27 * 0 и т.д.
С.83.
Учащимся предлагается порассуждать: можно ли по материалу задания №451 сделать вывод: Если хотя бы один множитель равен 0, то и значение произведения равно 0.
С.84.
Дается задание на закрепление пройденного материала, учащиеся заполняют таблицу. Затем предлагается найти значения частных, используя равенства, полученные в пункте 2, формулируется вывод. Учащиеся читают правило записанное в пункте 5: если 0 разделить на любое натуральное число, получится 0. Записывают правило в общем виде: 0 : а = 0.
С.87.
Учащиеся рассуждают по теме вопроса: Можно ли найти значения этих частных?
После чего учитель сообщает, что на 0 делить нельзя! Потому что если делитель 0, то число не делится на части, а значит нет действия. Это правило необходимо запомнить.
Упражнений на закрепление частных случаев умножения и деления в учебнике не много → дает сам учитель.
М2Д ч.2 с.56. УМК «Школа 2100».
В учебнике Демидовой 2 класс на уроке 2.40 вводится новая тема: «Умножение с нулем и единицей». Учащиеся находят значения произведений, заменив умножение их суммами, затем предлагается найти значение выражения 1 * 20, не заменяя его суммой. Делают вывод и сравнивают его с правилом: при умножении единицы на любое число получается то число, на которое умножали, дается общий вид правила: 1 * а = а, например, 5 * 1 = 5. Аналогичное задание выполняют и с умножением на 0. Делают вывод и сравнивают его с правилом: при умножении 0 на любое число, получается 0. Дается общий вид правила: 0 * а = 0. Аналогично формулируются правила умножения любого числа на 1 и 0.
Делают вывод и сравнивают его с правилом: при умножении единицы на любое число получается то число, на которое умножали, дается общий вид правила: 1 * а = а, например, 5 * 1 = 5. Аналогичное задание выполняют и с умножением на 0. Делают вывод и сравнивают его с правилом: при умножении 0 на любое число, получается 0. Дается общий вид правила: 0 * а = 0. Аналогично формулируются правила умножения любого числа на 1 и 0.
Упражнений на закрепление частных случаев умножения практически нет → дает сам учитель.
М2Д ч.3 с.10. УМК «Школа 2100».
На уроке 2.56 вводится новая тема: «Деление с нулем и единицей». Учащиеся находят значения произведений, отвечают на вопрос как деление связано с умножением?
Затем находят значения второго выражения в каждом столбце, опираются на связь умножения с делением. Делают вывод и сравнивают его с правилом: при делении любого числа на единицу получаем это же число, дается общий вид правила: а : 1 = а, например, 5 : 1 = 5. Учащиеся рассуждают по теме вопроса: Существует ли значение выражения: 5 : 0, 7 : 0? Можно ли подобрать такое число, умножив которое на 0, получили бы 5 или 7? С опорой на уже имеющиеся знания, учащиеся приходят к выводу: на 0 делить нельзя. Учитель сообщает, что на 0 делить нельзя! Потому что если делитель 0, то число не делится на части, а значит нет действия. Это правило необходимо запомнить. Учащиеся находят значения второго выражения в каждом столбце, опираются на связь умножения с делением. Делают вывод и сравнивают его с правилом: при делении 0 на любое число, не равное 0, получим 0. Дается общий вид правила: 0 : а = 0. Аналогично формулируется правило деления любого числа на 1: при делении любого числа, не равного 0, самого на себя получаем единицу. Дается общий вид правила: а : а = 1.
Учащиеся рассуждают по теме вопроса: Существует ли значение выражения: 5 : 0, 7 : 0? Можно ли подобрать такое число, умножив которое на 0, получили бы 5 или 7? С опорой на уже имеющиеся знания, учащиеся приходят к выводу: на 0 делить нельзя. Учитель сообщает, что на 0 делить нельзя! Потому что если делитель 0, то число не делится на части, а значит нет действия. Это правило необходимо запомнить. Учащиеся находят значения второго выражения в каждом столбце, опираются на связь умножения с делением. Делают вывод и сравнивают его с правилом: при делении 0 на любое число, не равное 0, получим 0. Дается общий вид правила: 0 : а = 0. Аналогично формулируется правило деления любого числа на 1: при делении любого числа, не равного 0, самого на себя получаем единицу. Дается общий вид правила: а : а = 1.
Упражнений на закрепление частных случаев умножения практически нет → дает сам учитель.
М2Д ч.1 с.59.
В данном учебнике на с.59 вводится новая тема: «Умножение чисел 0 и 1». Перед каждым правилом дано задание, которое подводит к правилу. Учащиеся выполняют задание, формулируют вывод и сравнивают его с правилом из учебника: при умножении числа 1 на любое число получается то же самое число.
Перед каждым правилом дано задание, которое подводит к правилу. Учащиеся выполняют задание, формулируют вывод и сравнивают его с правилом из учебника: при умножении числа 1 на любое число получается то же самое число.
С.60.
Учащиеся выполняют задание, формулируют вывод и сравнивают его с правилом из учебника: при умножении числа 0 на любое число получается 0.
М2Д ч.2 с.85.
На данной странице вводится новая тема: «умножение на 0 и на 1». Учащиеся выполняют задание, используя переместительное свойство умножения, формулируют выводы и сравнивают их с правилами из учебника: при умножении числа на 1 всегда получают то число, которое умножали. При умножении числа на 0 всегда получается 0.
Упражнений на закрепление частных случаев умножения в учебнике недостаточно → дает сам учитель.
М3Д ч.1 с.76.
Изучая таблицы умножения, составляются таблицы деления, в которые включается частный случай деления любого числа на 1.
С.83.
С.98.
Формулировки правил: на 0 делить нельзя; при делении 0 на любое число, не равное 0, получим 0, в данном учебнике нет → дает сам учитель. Упражнений на закрепление частных случаев деления недостаточно → дает сам учитель.
М2И ч.2 с. 57. УМК «Гармония».
В данном учебнике на с.57 учащимся предлагается найти значения выражений, заменив умножение сложением. Выполнив действия, учащиеся формулируют вывод, отвечают на вопрос: почему некоторые выражения находятся в рамках? Сверяют свои ответы с рассуждением Миши и Маши, выясняют кто из ребят прав. Затем читают правила представленные ниже.
М3И ч.1 с.78. УМК «Гармония».
В 3 классе так же дано задание и рассуждение Миши и Маши, но уже правило деление 1 и 0.
В данном учебнике на с.78 учащимся предлагается найти значения выражения, используя равенство. Таким образом проводится связь между умножением и делением. Выполнив действия, учащиеся формулируют вывод. Сверяют свои ответы с рассуждением Миши и Маши. Затем читают правила представленные ниже.
Выполнив действия, учащиеся формулируют вывод. Сверяют свои ответы с рассуждением Миши и Маши. Затем читают правила представленные ниже.
С.79.
Упражнений на закрепление частных случаев умножения и деления недостаточно → дает сам учитель.
С.78.
Аналогично проводится работа и на рассмотрение частных случаев деления.
Упражнений на закрепление частных случаев умножения и деления недостаточно → дает сам учитель.
Тема: «Смысл умножения и деления. Свойства умножения. Связь компонентов и результатов действий умножения и деления. Таблица умножения и соответствующие случаи деления»
Методика изучения таблицы умножения и соответствующих случаев деления в курсе математики начальных классов.
Перед составлением таблицы умножения и деления рассматриваем теоретическую основу этой таблицы.
К теоретической основе табличного умножения и деления относят:
1) смысл умножения;
2) переместительное свойство умножения;
3) связь между компонентами и результатом действий умножения и деления.
Эти вопросы изучают на I этапе темы «Табличное умножение и деление».
По мере рассмотрения теоретических вопросов учащихся знакомят с табличными приемами умножения и деления. При изучение каждого теоретического вопроса, вводится прием.
1 ПРИЁМ умножения однозначных чисел 7 * 3 = 21
7+7+7 = 21
7 умножить на 3, значит по 7 берем 3 раза.
Теоретическая основа – конкретный смысл действия умножения.
Урок по математике для 3 класса Умножение 5, на 5 и соответствующие случаи деления
Урок математики в 3 классе
Тема: Умножение 5, на 5 и соответствующие случаи деления.
Задачи: составлять таблицы умножения 5, на 5 и соответствующие случаи деления; закреплять умение решать задачи.
Планируемые результаты:
Предметные: составлять таблицы умножения 5, на 5 и
соответствующие случаи деления; решать простые и составные задачи;
закреплять знания таблицы умножения и деления.
Метапредметные: выполнять мыслительные операции анализа и синтеза, делать умозаключения по результатам исследования; искать разные способы решения задачи; излагать и аргументировать свою точку зрения; слушать собеседника и вести диалог; объяснять найденные способы действий при решении новых учебных задач и находить способы их решения.
Личностные: осваивать позитивный стиль общения со сверстниками и взрослыми в школе и дома; проявлять учебно- познавательный интерес к новому учебному материалу и способам решения учебных и практических задач.
Межпредметные связи: окружающий мир, моделирование различных ситуаций в виде схем.
Ресурсы урока: Рабочая программа; учебник «Математика», ч.1, с.36; презентация; ноутбук; проектор; экран; карточки «Математическое лото»; карточки для самостоятельной работы.
Ход урока:
1.Включение в учебную деятельность. (слайд 1)
Игра «Ладошки».
— Возьмите друг друга за руки. Закройте глаза. Почувствуйте тепло других ладошек в своих руках. Мысленно пожелайте всем добра. А теперь откройте глаза и садитесь, не производя ни малейшего шума.
Вот и начинается новый урок. Сегодня мы в очередной раз отправимся в путь по дороге знаний. Откройте тетрадки и запишите сегодняшнее число 18 октября.
— Что вы можете рассказать о числе 18?
— Какое время года за окном? А какое следующее? Какие осенние месяцы вы знаете? Зимние?
2. Мотивация познавательной деятельности.
— На партах у вас лежат карточки. Возьмите карточку под №1. Прочитайте предложения на этих карточках и подумайте, как бы вы хотели их закончить.
— Я буду заниматься математикой, потому что …
— Я хочу выполнить больше заданий, потому что…
— От нового урока математики я жду…
Дети. Ответы детей.
— В конце урока мы узнаем, получите ли вы от урока то, что
ожидаете.
А теперь друзья за дело
Математика нас ждет,
Начинаем устный счет!
3.Актуализация знаний. Устный счет.
а)Веселые задачки(слайд 2)
-Я предлагаю вам решить веселые задачки.
8 пар танцуют польку,
А всех танцоров сколько? (16)
Испекла нам бабушка
Вкусные оладушки.
Всего оладий 27
По три нам хватило всем.
Кто ответит из ребят,
Сколько будет же внучат? (9)
Полюбуйтесь-ка сами:
Мчатся тройки с бубенцами.
Сосчитать коней мы просим,
Если было троек 8. (24)
Подарил утятам ёжик
8 кожаных сапожек.
Сколько ж маленьких утят
Ёжика благодарят? ( 4)
На заборе расфуфырились коты,
Распушили свои длинные хвосты.
А хвостов то было 8.
Сколько лап ?
У кого спросим? (32)
-Кто был внимателен, сколько задачек мы решили?
б)Игра «Математическое лото» (слайд 3)
-А сейчас я предложу сыграть вам со мной в математическое лото. Каждый из вас получил свою игровую карточку. Итак, я даю задание, а
вы зачеркиваете число, которое получите. Все готовы? Начинаем.
Каждый из вас получил свою игровую карточку. Итак, я даю задание, а
вы зачеркиваете число, которое получите. Все готовы? Начинаем.
— Разделите число 12 на 2
— Найдите произведение 4 и 7
— Первый множитель 5, второй множитель 3. Найдите произведение?
— Делимое 27, делитель 3. Найдите частное.
— Найдите сумму чисел 24 и 16
— Найдите разность 50 и 18
— Увеличьте число 9 в 4 раза
— Уменьшите 56 на 9
— Увеличьте 36 на 7
— Уменьшите 24 в 6 раз. /6, 28, 15, 9, 40, 32, 36, 47, 43, 4/
— Какие числа вы зачеркнули?
-Сколько чисел вы зачеркнули?
-Разделите это число на 2. Что получите?
4. Самоопределение к деятельности. (слайд 4)
— Вычислите.
2х5
3х5
4х5
5х2
5х3
5х4
— Что помогло вам выполнить быстро вычисления? (Знания таблицы умножения с числами 2,3,4)
— Каким правилом вы воспользовались при вычислении ответов в
примерах второго столбика? (От перестановки множителей произведение
не меняется).
— Какой пример будет следующим? (5х5)
— Что нужно знать, чтобы быстро вычислить ответ в этом примере? (Таблицу умножения с числом 5).
-Сформулируйте тему и задачи урока. (слайд 5)
Да, я согласна с вами. Мы сегодня с вами составим таблицу умножения и деления на 5 и будем работать над её запоминанием
Каждый математик любит цифру «5»,
Сегодня мы продолжим таблицы составлять.
Таблицы не простые, а важные такие,
Две на умножение и на деление две.
5. Организация познавательной деятельности
Объяснение нового материала.
А кто ответит, что такое умножение?
Стихотворение «Что такое умножение?» (слайд 6)
Что такое Умножение?
Это умное сложение.
Ведь умней — умножить раз,
Чем слагать всё целый час.
Умножения таблица
Всем нам в жизни пригодиться.
И недаром названа
УМНОжением она!
— С какого числа мы начнем умножение? (Запись в тетрадях) (слайды 7- 12)
5х5=25
5х6=30
5х7=35
5х8=40
5х9=45
5х10=50
Что интересного мы наблюдаем?
-Какое математическое правило надо применить, чтобы составить таблицу умножения на 5?
-Кто может это сделать на доске?
-А что мы знаем о действии делении?
-Составим таблицу деления на 5. (слайд 13)
(слайд 13)
-Сколько всего вам надо выучить дома выражений?
-А сейчас я посмотрю, как вы внимательно работали с таблицей умножения на 5.
— Посмотрите на значение произведений. Что интересное вы заметили? (Все ответы заканчиваются на 0 и на 5)
— Какую закономерность мы с вами наблюдаем?
— Если умножаем на четное число, получается …(Круглое)
ФИЗМИНУТКА (слайд 14)
Если я называю число, которое делится на пять, то вы приседаете.
Если я называю число, которое не делится на пять, то вы подпрыгиваете.
Первичное закрепление.
Самостоятельная работа. (слайд 15-16)
-А теперь поработаем самостоятельно. У каждого из вас есть карточки, выполните на них следующее задание:
Закрась числа, которые делятся на 5.
А теперь поменяйтесь карточками с соседом, и проверьте. Оцените работу товарища.
-Соотнесите значение с выражением. (слайд 17)
(слайд 17)
5х5= 45
7х5= 25
9х5= 35
6х5= 40
8х5= 30
— Игра «Найди пару» (слайд 18)
5х4= 35: 5=
8х5= 45:9=
5х7= 20: 5=
9х5= 40: 8=
-Какая связь между делением и умножением?
ФИЗМИНУТКА для глаз (презентация) (слайд 19)
6. Работа над пройденным материалом.
Работа по учебнику
Решение задачи №3. (слайд 20)
Прочитайте задачу.
— О чем говорится в задаче?
— Какой длины был кусок ткани?
— Как его использовали?
-Что сшили из оставшейся ткани?
— Что можно сказать про детские пальто?
— Можем ли мы сразу ответить на вопрос задачи? Почему?
-Рассмотрите схематический чертеж к задаче.
-Какой вопрос главный?
-Сколько действий в задаче?
-Что мы будем находить сначала?
-Каким действием узнать?
-Сколько надо ткани на пальто?
-Теперь можем узнать сколько ткани пойдет на одно пальто?
-Каким действием?
-Можно ли эту задачу решить выражением?
— Запишите выражение в тетрадь. Проверьте себя.
Проверьте себя.
№ 2 (4 столбик) (слайд 21)
-Вспомним порядок действий.
Решаем самостоятельно.
Работа в парах
(слайд 22)
7. Подведение итога урока
-Чему мы сегодня учились на уроке?
-Кто уже запомнил таблицу на пять?
8. Рефлексия.
— Встаньте те, кто считает, что он хорошо сегодня поработал? Почему ты так считаешь? Какие были трудности на уроке?
-Поднимите руку те, кому надо еще поработать над этой темой.
-А кому трудно было сегодня на уроке? Как вы считаете, почему?
9. Д/з выучить таблицу умножения на 5. № 2 (1 -3 столбики) С.36. (слайд 23)
10. Заключение. (слайд 24)
— Благодарю всех за урок. Вы отлично потрудились сегодня на уроке математики, и я желаю вам счастливого пути по дороге знаний!
Как разделить на 5
Математические курсы / Математика для 3–5 классов: практика и повторение Курс / Практика навыков подразделения Глава
Инструктор: Дана Спаркман
В этом уроке вы изучите четырехэтапный процесс деления на 5, а также узнаете, как проверить свою работу. Мы также кратко рассмотрим основы деления и умножения, прежде чем приступить к задаче, связанной с делением на 5.
Мы также кратко рассмотрим основы деления и умножения, прежде чем приступить к задаче, связанной с делением на 5.
Краткий обзор: деление и умножение
Предположим, вы отправились на пляж со своей семьей и собрали 43 ракушки. Вернувшись домой, вы решаете подарить ракушки членам своей семьи. В вашей семье 5 человек, поэтому, если вы хотите получить поровну, вам нужно разделить все количество ракушек на 5.
Прежде чем мы начнем делить на 5, чтобы решить нашу задачу, давайте рассмотрим некоторые основы деления. Как известно, деление — это когда вы делите что-то на равные части. Это тесно связано с умножением — мы можем думать об умножении и делении как о 9.0015 обратные операции . Это означает, что они противоположны, и одно может «отменить» другое.
Почему умножение важно для нас прямо сейчас? Делить на 5 будет намного проще, если вы знаете факты умножения на 5.
Есть простой способ определить, делится ли число на 5 без остатка: если оно оканчивается на 0 или 5, то число делится на 5 без остатка. Посмотрите на приведенный выше список фактов. Все ответы заканчиваются на 0 или 5. Если число не делится на 5 без остатка (оно не заканчивается на 0 или 5), то у вас останется остаточное число или 9.0015 остаток .
Посмотрите на приведенный выше список фактов. Все ответы заканчиваются на 0 или 5. Если число не делится на 5 без остатка (оно не заканчивается на 0 или 5), то у вас останется остаточное число или 9.0015 остаток .
Как разделить на 5
Существует простой четырехэтапный процесс деления на 5:
- Разделить
- Умножить
- Вычесть
- Проверка остатков
Вернемся к нашему примеру с ракушкой и решим задачу. У вас есть 43 ракушки, которые нужно разделить на 5:
43 ÷ 5 = ?
Шаг 1 Разделите
Эта задача спрашивает вас: Сколько пятерок в 43? Когда вы делите, думайте о факте умножения, который приближает вас к большому числу, которое вы делите, не перебирая. Другими словами, ответ какого факта умножения 5 ближе всего к 43? Из наших фактов об умножении пятерок вы знаете, что 5 x 8 равно 40, что ближе всего к 43 без перебора.
Запишите свой ответ на данный момент: 8.
Шаг 2: Умножьте
Умножьте свой ответ (называемый частным) на делитель (число, на которое вы разделили):
8 x 5 = 40
Шаг 3: Вычтите
Вычтите 40 из 43. Остается 3.
Остается 3.
Шаг 4: Проверьте остатки
На последнем шаге у вас осталось 3. Это 3 — остаток — это то, что осталось после того, как вы сделали деление. Вы не можете разделить 3 на 5, потому что это недостаточно велико. Тогда ответом на эту задачу является 8 с остатком 3. Мы показываем, что ответ имеет остаток, используя заглавную R, например:
Проверка вашей работы
Как мы обсуждали выше, вы можете «отменить» деление с помощью умножения. Итак, чтобы проверить нашу задачу на деление, мы делаем обратное — умножаем.
Умножьте частное (ответ) на делитель (число, на которое вы разделили). Если у вас есть остаток, добавьте его к ответу. Если сумма равна исходному числу, которое вы делили, ваш ответ правильный.
В нашей задаче о ракушках мы получили ответ 8 R3.
Итак, умножьте: 8 х 5 = 40.
Добавьте к остатку: 40 + 3 = 43.
Поскольку мы начали с 43 ракушек, мы знаем, что ответ 8 R3 правильный!
Итоги урока
В этом уроке вы научились делить на 5, используя следующие четыре шага:
- Разделить
- Умножить
- Вычесть
- Проверка остатков
Знание фактов умножения на 5 упрощает деление на 5, а понимание того, что умножение и деление являются обратными операциями, поможет вам проверить свою работу после решения задачи. Помните, что когда число не делится без остатка на 5, у вас будет остаток.
Помните, что когда число не делится без остатка на 5, у вас будет остаток.
Чтобы разблокировать этот урок, вы должны быть участником Study.com.
Создайте свою учетную запись
Зарегистрируйтесь для просмотра этого урока
Вы студент или преподаватель?
Разблокируйте свое образование
Убедитесь сами, почему 30 миллионов человек используют Study.com
Станьте участником Study.com и начните учиться прямо сейчас.
Стать участником
Уже являетесь участником? Войти
Назад
Ресурсы, созданные учителями для учителей
Более 30 000 видеоуроков и учебные ресурсы‐все в одном месте.
Видеоуроки
Тесты и рабочие листы
Интеграция в классе
Планы уроков
Я определенно рекомендую Study.com своим коллегам. Это как учитель взмахнул волшебной палочкой и сделал работу за меня.
 Я чувствую, что это спасательный круг.
Я чувствую, что это спасательный круг.
Дженнифер Б.
Учитель
Попробуй это сейчас
Спинка
Комплексные числа: умножение
Комплексные числа: умножениеАлгебраическое умножение.
 Комплексное умножение — более сложная операция для понимания как с алгебраической, так и с геометрической точки зрения. Давайте сначала сделаем это алгебраически и возьмем определенные комплексные числа для умножения, скажем, 3 + 2 i и 1 + 4 i. В каждом из них по два слагаемых, поэтому, умножив их, мы получим четыре слагаемых:
Комплексное умножение — более сложная операция для понимания как с алгебраической, так и с геометрической точки зрения. Давайте сначала сделаем это алгебраически и возьмем определенные комплексные числа для умножения, скажем, 3 + 2 i и 1 + 4 i. В каждом из них по два слагаемых, поэтому, умножив их, мы получим четыре слагаемых:Теперь 12 i + 2 i упрощаются до 14 i, , конечно. А как насчет 8 i 2 ? Помните, мы ввели i как сокращение от √1, квадратного корня из 1. Другими словами, i — это число, квадрат которого равен 1. Таким образом, 8 i 2 равняется 8. Следовательно, произведение (3 + 2 i )(1 + 4 i ) равно 5 + 14 i.
Если обобщить этот пример, то получится общее правило умножения
Помните, что ( xu yv ), действительная часть произведения, есть произведение действительных частей минус произведение мнимых частей, но ( xv + yu ), мнимая часть произведения произведение, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте рассмотрим некоторые частные случаи умножения.
Умножение комплексного числа на действительное число
В приведенной выше формуле для умножения, если v равно нулю, вы получаете формулу для умножения комплексного числа x + yi и действительного числа u вместе: Другими словами, вы просто умножаете обе части комплексного числа на действительное число. Например, 2 умножить на 3 + i — это всего лишь 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваивайте расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C в 2 раза от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Умножение и абсолютное значение.
Несмотря на то, что мы рассмотрели только один случай умножения, достаточно предположить, что абсолютное значение zw (т. е. расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение . ж. Это было, когда w было реальным числом u чуть выше. На самом деле, это верно в целом:Проверка этого тождества является упражнением в алгебре. Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не нужно иметь дело с квадратными корнями. Мы покажем | ZW | 2 = | из | 2 | с | 2 . Пусть z будет x + yi, и пусть z будет u + vi. Тогда по формуле умножения zw равно ( xu yv ) + ( xv + yu ) i. Напомним из раздела об абсолютных значениях, что
Точно так же у нас есть
и, поскольку zw = ( xu yv ) + ( xv + yu ) i,
Итак, чтобы показать | ZW | 2 = | из | 2 | с | 2 , все, что вам нужно сделать, это показать, что
 v 2 )
v 2 )и это простое упражнение по алгебре.
Полномочия
i. Для нашего следующего частного случая умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i 2 = 1. Как насчет i 3 ? Это просто i 2 умножить на i , и это 1 умножить на i. Следовательно, i 3 = i. Вот интересно: куб i есть собственное отрицание. Далее рассмотрим i 4 . Это квадрат i 2 , то есть квадрат 1. Таким образом, i 4 = 1. Другими словами, i является корнем четвертой степени из 1. Вы можете показать, что i является еще одним корнем четвертой степени из 1. А поскольку и 1, и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, 1 и i. Это наблюдение связано с основной теоремой алгебры, поскольку уравнение z 4 = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.
Higher powers of i are easy to find now that we know i 4 = 1. For example, i 5 is i times i 4 , and that’s just i . Вы можете уменьшить силу i на 4 и не изменить результат. Другой пример: i 11 = i 7 = i 3 = i.
Как насчет отрицательных сил и ? Чему равно число i, ?
то есть i 1 ? По той же причине, по которой вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i 1 = i 3 = i. Таким образом, обратное число i равно i. Представьте себе число, обратное значение которого является его собственным отрицанием! Конечно, легко проверить, что i раз i равно 1, так что, конечно, i и i обратны.
Корни единства.
Различные корни из 1 называются корнями из единицы. В общем, по основной теореме алгебры число n -й корень из единицы равен n, так как имеется n корней уравнения n -й степени z u 1 = 0. Квадратные корни из единицы равны 1 и 1. Четвертые корни составляют ± 1, ± i, , как отмечалось ранее в разделе об абсолютном значении. Кроме того, в этом разделе упоминалось, что ±√2/2 ± i √2/2 были квадратными корнями из i и i, , а теперь с помощью формулы умножения это легко проверить. Следовательно, восемь восьмикореней из единицы равны ±1, ± i, и ±√2/2 ± i √2/2. Обратите внимание, как эти восемь корней единства равномерно распределены по единичному кругу. Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте немного подождем их.
Умножение комплексного числа на
i. В нашей цели найти геометрическую интерпретацию комплексного умножения, давайте рассмотрим следующее умножение произвольного комплексного числа z = x + yi на i.Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на х единиц правее мнимой оси и на y единиц выше действительной оси. Точка z и расположены на и юнитов левее и х юнитов выше. Произошло то, что умножение на i повернуло к точке z 90° против часовой стрелки вокруг начала координат к точке z i. Говоря короче, умножение на дает поворот на 90° против часовой стрелки примерно на 0.
Таким же образом можно проанализировать, что делает умножение на i . Вы найдете это умножение на i дает поворот на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что предполагается против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Вы найдете это умножение на i дает поворот на 90° по часовой стрелке относительно 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, что предполагается против часовой стрелки. Тогда мы можем сказать, что умножение на i дает поворот на 90° относительно 0 или, если хотите, поворот на 270° относительно 0.
Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока мы увидим результаты без обоснования. Мы видели два особых случая умножения, один на вещественные числа, что приводит к масштабированию, другой на 9.0055 i , что приводит к вращению. Общий случай представляет собой комбинацию масштабирования и поворота. Пусть z и w — точки комплексной плоскости C . Нарисуйте линии от 0 до z и от 0 до w . Длины этих линий являются абсолютными значениями | из | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | ZW | что равно | г | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Длины этих линий являются абсолютными значениями | из | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | ZW | что равно | г | | с |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Что мы не делаем знать направление линии от 0 до zw.
Ответ: «углы складываются». Мы будем определять направление линии от 0 до z по определенному углу, называемому аргументом от z , иногда обозначаемым arg( з ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — линия от 0 до z. Другая точка w имеет угол arg( w ). Тогда произведение zw будет иметь угол, являющийся суммой углов arg( z ) + arg( w ). (На диаграмме arg( z ) составляет около 20°, а arg( w ) составляет около 45°, поэтому arg( zw ) должно быть около 65°. )
)
Таким образом, у нас есть два уравнения, которые определяют, где zw находится в C :
Что такое ассоциативная собственность? Определение, факты и примеры
Что такое ассоциативное свойство в математике?
Ассоциативность определяется тем, что при сложении или умножении более двух чисел результат остается одним и тем же, независимо от того, как они сгруппированы.
Например,
2 × (7 × 6) = (2 × 7) × 6
2 + (7 + 6) = (2 + 7) + 6
Ассоциативное свойство сложения
Ассоциативное свойство сложения подразумевает, что независимо от как числа сгруппированы, окончательная сумма чисел останется прежней. Это может быть выражено как:
( x + Y ) + Z = Z = Z = . 0146 y + z )
0146 y + z )
Ассоциативное свойство умножения
Ассоциативное свойство группы умножения остается тем же самым, независимо от того, как ассоциативное свойство группы умножения остается неизменным. Это может быть выражено как:
P × (Q × R) = (P × 9000 Q) = (P × Q) = (P ×
Q) =.0006 × rРазличие между ассоциативным свойством и переместительным свойством
Переместительное свойство Переместительное свойство подразумевает, что при выполнении умножения или сложения результата остается одно и то же. договоренность.
договоренность.
Теперь, когда вы знаете об обоих свойствах, вы, должно быть, поняли, что единственная разница заключается в количестве чисел, участвующих в операции.
Два числа участвуют в свойстве коммутативности и более двух чисел участвуют в свойстве ассоциативности.
Применимы ли ассоциативные свойства к делению и вычитанию?
Вам должно быть интересно, почему эти свойства неприменимы к делению и вычитанию. Давайте возьмем пример, чтобы ответить на это «Почему?».
В случае вычитания:12 – (6 – 2) = 12 – 4 = 8
(12 – 6) – 2 = 6 – 2 = 4
Отсюда следует, 12 – (6 – 2) ≠ (12 – 6) – 2. Значит, свойство ассоциативности для вычитания неприменимо.
В случае деления:(24 ÷ 4) ÷ 2 = 6 ÷ 2 = 3
24 ÷ (4 ÷ 2) = 24 ÷ 2 = 12
Отсюда следует, (24 ÷ 4) ÷ 2 ≠ 24 ÷ (4 ÷ 2). Итак, свойство ассоциативности для деления неприменимо.
Интересный факт!
Ассоциативное свойство получило свое название от слова «ассоциировать» и относится к группировке чисел.
Решенные примеры
Пример 1: Если (30 × 20) × 15 = 9000, то используйте ассоциативное свойство, чтобы найти (15 × 30) × 20,
Решение: Согласно ассоциативному свойству умножения, (30 × 20) × 15 = (15 × 30) × 20.
Учитывая, что (30 × 20) × 15 = 9000, ) × 20 = 9000.
Пример 2: Проверьте, подразумевается ли ассоциативность сложения в следующих уравнениях.
- 20 + (60 + 5) = (20 + 60) + 5
- 30 + (40 + 20) = (30 + 10) + 50
Решение:
LHS : 20 + (60 + 5)
20 +(65)
85
RHS : (20 + 60) + 5
(80) + 5
85
левый = правый. Таким образом, в этом уравнении подразумевается ассоциативное свойство сложения.
- По ассоциативному свойству сложения 30 + (40 + 20) = (30 + 10) + 50. Проверяем дальше,
LHS: 30 + (40 + 20)
30 + (60)
90
RHS: (30 + 10) + 50
(40) + 50
90
LHS ás. Таким образом, в этом уравнении не подразумевается ассоциативное свойство сложения.
Пример 3: В соответствии с ассоциативным свойством вставьте пропущенное число.
(5 + 10) + 4 = (5 + 4) + __ = 14
Решение: Согласно свойству ассоциативности, при сложении более двух чисел результат остается одним и тем же независимо от того, как они сгруппированы . Следовательно, (5 + 10) + 4 = (5 + 4) + 10 = 14
Практические задачи
2, 4
5, 6
4, 6
7, 8
Правильный ответ: 5, 6 одинаковы, независимо от того, как они сгруппированы.
Следовательно, $2 × (5 × 6) = (2 × 5) × 6$ к ассоциативному свойству, когда добавляется более двух чисел, результат остается одним и тем же независимо от того, как они сгруппированы.
Следовательно, $20 + 9 + 5 = 9 + 5 + 20$
$(2 + 3) + 6 = 2 × (3 + 6)$
$(5 + 6) + 4 = 5 + (6 + 4)$
$(7 — 10) — 15 = 7 — (10 — 15)$
$(9 ÷ 3) ÷ 3 = 9 ÷ (3 ÷ 3)$
Правильный ответ: $(5 + 6) + 4 = 5 + (6 + 4)$
Ассоциативность справедлива только для сложения и умножения. Это свойство неприменимо к вычитанию или делению, поэтому остальные уравнения неверны.
Часто задаваемые вопросы
Ассоциативное свойство сложения и умножения можно использовать для скольких чисел?
Ассоциативность сложения и умножения сохраняется для 3 и более чисел.
Применяется ли свойство ассоциативности к дробным числам?
Да, ассоциативное свойство сложения и умножения верно для дробных чисел.
Применяется ли свойство ассоциативности к уравнению, в котором есть 0?
Да, свойство ассоциативности верно для уравнения, в котором есть 0.
Умножение и деление дробей: примеры и методы
Джон был приглашен на день рождения Эми, и она пригласила в общей сложности 7 друзей, чтобы отпраздновать ее день рождения. Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.
Чтобы получить одинаковые кусочки торта, каждый из участников должен иметь \(\frac{1}{8}\) торта. Случайно Эми уронила свой кусок пирога, поэтому Джон решил отдать ей часть своего. Он разделил свой кусок пирога на 2 и отдал половину Эми.
Можем ли мы посчитать, какая часть пирога досталась Эми в итоге? Ответ состоит в том, чтобы разделить дробь Джона на 2, то есть \(\dfrac{\dfrac{1}{8}}{2}=\dfrac{1}{16}\) торта.
В этой статье мы научимся выполнять операции умножения и деления с дробями.
Умножение и деление дробей шаг за шагом
Нас интересуют операции умножения и деления дробей. Прежде всего, давайте вспомним наши знания о дробях.
Дробь представляет часть целого . Он состоит из двух частей – числителя и знаменателя. Числитель пишется над чертой, а знаменатель — под чертой. Знаменатель не может быть равен нулю.
\(\dfrac{2}{3}, \dfrac{1}{2}, \dfrac{7}{8}, \cdots\) являются примерами дробей.
Мы знакомы с умножением и делением двух чисел. Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.
Теперь вопрос в том, как выполнять эти операции над дробями, а не над целыми числами.
Предположим, вам даны две дроби, скажем, \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), мы хотим знать, что мы подразумеваем под \(\dfrac{ a}{b}\times \dfrac{c}{d}\) и \(\dfrac{\dfrac{a}{b}}{\dfrac{c}{d}}.\)
Умножение и деление правила дробей
Правила умножения дробей
Чтобы умножить две дроби \(\dfrac{a}{b}\) и \(\dfrac{c}{d}\), необходимо умножить числители вместе и знаменатели вместе. Таким образом. имеем
\[\dfrac{a}{b}\times \dfrac{c}{d}=\dfrac{a\times b}{c\times d}.\]
Мы, по сути, следуем следующие шаги, чтобы умножить дроби вместе.
Шаг 1. Перемножьте числители двух дробей вместе и знаменатели вместе.
Шаг 2. Разделите полученные числа, чтобы получить новую дробь.
На этом мы можем остановиться. Однако, если числитель и знаменатель новой дроби имеют общие делители, мы переходим к следующему шагу, чтобы получить простейшую форму дроби.
Шаг 3. Найдите общий делитель числителя и знаменателя новой дроби. Разделите числитель и знаменатель на этот общий множитель. Это дает простейшую форму дроби.
Перемножьте дроби \(\dfrac{3}{7}\) и \(\dfrac{5}{11}\).
Решение
Шаг 1. Перемножая числители дробей вместе, мы получаем \[3\times 5=15.\]
Перемножая знаменатели дробей вместе, мы получаем \[7\times 11=77.\]
Шаг 2. Деление полученных чисел дает новую дробь \(\dfrac{15}{77}.\)
Так как числитель и знаменатель новой дроби не имеют общих факторов, это самая простая форма.
Умножить\(\dfrac{2}{5}\) и \(\dfrac{7}{9}\).
Решение
Перемножая числители и знаменатели, получаем
\[\dfrac{2}{5}\times \dfrac{7}{9}=\dfrac{2\times 7}{5 \times 9}=\dfrac{14}{45}.\]
Умножить \(\dfrac{5}{8}\) и \(\dfrac{2}{3}.\)
Решение
Шаг 1. Перемножая числители двух дробей вместе, мы получаем
Перемножая числители двух дробей вместе, мы получаем
\(5 \times 2=10.\) Точно так же, делая то же самое со знаменателями, получаем \(8\times 3=24.\)
Шаг 2. Разделив полученные числа, мы получим новую дробь \(\dfrac{10}{24}.\)
Заметим, что числитель и знаменатель новой дроби имеют общий делитель 2.
Шаг 3. Мы получаем простейшую форму этой дроби, разделив общий делитель 2 из числителя 10 и знаменателя 24. Это дает нам \(10 \divsymbol 2=5\)и \(24\divsymbol 2=12\).
Таким образом, простейшая дробь равна \(\dfrac{5}{12}.\)
Правила деления дробей
Чтобы разделить две дроби, вы по существу инвертируете дробь, на которую делите, а затем умножаете ее на первую. Таким образом, деление двух дробей вида
\[\frac{a}{b}\divsymbol\frac{c}{d}=\frac{\frac{a}{b}}{\frac{c} {d}}\]
равносильно умножению дробей \[\frac{a}{b}\times \frac{d}{c}.\] Таким образом, мы имеем
\[\frac{a }{b}\divsymbol\frac{c}{d} =\frac{a}{b}\times\frac{d}{c}. \]
\]
Поскольку мы уже видели, как умножать две дроби, просто следуйте этим шагам отсюда.
Таким образом, мы выполняем следующие шаги для выполнения деления на дроби,
Шаг 1. Инвертируем делитель дроби – числитель становится знаменателем, а знаменатель становится числителем.
Шаг 2. После инверсии перемножьте полученные дроби вместе, используя шаги, описанные для умножения дробей.
Разделить \(\dfrac{5}{8}\) на \(\dfrac{2}{3}.\)
Решение
Шаг 1. Обратив делитель, получим \(\dfrac{3}{2}\).
Шаг 2. Теперь выполняем умножение полученных дробей,
\(\dfrac{5}{8}\) и \(\dfrac{3}{2}\), чтобы получить,
\ [\dfrac{5}{8}\times \dfrac{3}{2}=\dfrac{5\times 3}{8\times 2}=\dfrac{15}{16}.\]
Поскольку числитель и знаменатель не имеют общих делителей, это простейшая форма.
Найдите \(\dfrac{2}{5}\divsymbol \dfrac{3}{8}\).
Решение
Здесь \(\dfrac{2}{5}\) — дробь делимого, а \(\dfrac{3}{8}\) — дробь делителя.
Шаг 1. Инвертируем делитель, получаем \(\dfrac{8}{3}.\)
Шаг 2. Теперь умножаем полученные дроби,
\[\frac{2}{ 5}\divsymbol\frac{3}{8}=\frac{2}{5}\times \frac{8}{3}=\frac{2\times 8}{3\times 5} =\frac{ 16}{15}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
При умножении или делении дроби на целое число \(a\), \(a\) может быть записано как его эквивалентная форма \(\dfrac{a}{1}\), поэтому никаких изменений в процедуре не требуется .
Найти \(\dfrac{\dfrac{2}{5}}{3}.\)
Решение
Здесь \(\dfrac{2}{5}\) — дробь делимого, а \( 3=\dfrac{3}{1}\) — делитель дроби.
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{1}{3}\).
Шаг 2. Теперь умножьте дроби, чтобы получить
\[\dfrac{2}{5}\times \dfrac{1}{3}=\dfrac{2\times 1}{5\times 3 }=\dfrac{2}{15}. \]
\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
Упростить \(\dfrac{4}{\dfrac{7}{9}}\).
Решение
Здесь \(4=\dfrac{4}{1}\) — дробь делимого, а \(\dfrac{7}{9}\) — дробь делителя.
Решение
Шаг 1. Переворачиваем делитель, получаем \(\dfrac{9}{7}\).
Шаг 2. Теперь перемножьте дроби, чтобы получить
\[\dfrac{4}{\dfrac{7}{9}}=\dfrac{4}{1}\times \dfrac{9} {7}=\dfrac{4\times 9}{1\times 7}=\dfrac{36}{7}.\]
Так как числитель и знаменатель не имеют общих множителей, это самая простая форма.
Чтобы упростить нашу работу, избегая гигантских умножений, мы можем «отменить» общие множители между числителями и знаменателями в начале, прежде чем мы перемножим члены вместе. Это изменит шаги для умножения дробей на следующие:
Шаг 1. Если какие-либо числитель и знаменатель имеют общий множитель, разделите соответствующий числитель и знаменатель на общий множитель, чтобы «сократить» общий множитель. Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.
Делайте это до тех пор, пока между числителями и знаменателями не останется общих множителей.
Шаг 2. Выполнить умножение полученных дробей.
В следующих примерах мы использовали вышеупомянутый метод.
Примеры умножения и деления дробей
До сих пор мы рассматривали примеры операций умножения и деления двух дробей. Вы можете умножать / делить несколько дробей вместе, используя те же правила, что описаны выше. Если есть цепочка из нескольких умножений и делений, вы должны сначала инвертировать члены делителя.
Упростить \(\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}\)
Решение
Здесь умножаются три дроби. Первый шаг состоит в том, чтобы умножить числители дробей вместе \(5\умножить на 18\умножить на 21\) и знаменатели вместе \(9\умножить на 13\умножить на 20.\)
Здесь мы видим, что мы получаем умножение огромных чисел. Чтобы избежать этого, мы собираемся сначала отменить общие факторы, где это возможно.
Шаг 1 . Числители 5,18,21, а знаменатели 9,13,20. Мы видим, что 9 и 18 имеют 9 в качестве общего делителя, а 5 и 20 имеют 5 в качестве делителя, таким образом, мы имеем
\[\frac{5}{9}\times\dfrac{18}{13}\times\dfrac{ 21}{20}=\dfrac{1}{1}\times\dfrac{2}{13}\times\dfrac{21}{4}.\]
Далее, мы можем упростить 2 и 4, разделив на 2, чтобы получить
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{1}{13} \times\dfrac{ 21}{2}.\]
Шаг 2. И окончательный ответ:
\[\dfrac{5}{9}\times\dfrac{18}{13}\times\dfrac{21}{20}=\dfrac{21}{13\times 2 }=\dfrac{21}{26}.\]
Упростить \[\dfrac{14}{39}\times\dfrac{12}{35}\divsymbol\dfrac{8}{13}\times\dfrac {2}{9}\]
Решение
Шаг 1. Инвертируйте дробь делителя, чтобы получить
\[\dfrac{14}{39}\times\dfrac{12}{35}\ divsymbol\dfrac{8}{13}\times\dfrac{2}{9}=\dfrac{14}{39}\times\dfrac{12}{35}\times\dfrac{13}{8}\times \dfrac{2}{9}\]
Шаг 2. Теперь попробуем привести термы к простейшему виду. Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим
Теперь попробуем привести термы к простейшему виду. Разделив 14 и 35 на 7, 13 и 39 на 13, 12 и 9 на 3, 2 и 8 на 2, получим
\[\dfrac{14}{39}\times\frac{12}{35}\ раз\dfrac{13}{8}\times\dfrac{2}{9}=\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times \dfrac{1}{3}\]
Шаг 3 . Отбросив 4, мы получим \[\dfrac{2}{3}\times\dfrac{4}{5}\times\dfrac{1}{4}\times\dfrac{1}{3}=\dfrac {2}{5}\times\dfrac{1}{5}\times \dfrac{1}{3}=\dfrac{2}{45}.\]
В следующем примере мы выполняем умножение и деление смешанных дробей.
Смешанная дробь представляет собой комбинацию целого числа и дроби. Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
Упростить
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \dfrac{3}{5}.\]
Решение
Преобразование смешанного дроби на неправильные дроби, получаем
\[4\dfrac{2}{7}\times 2\dfrac{1}{3}\div \frac{3}{5} = \dfrac{30}{7}\times \dfrac{7} {3} \div \dfrac{3}{5}. 3}\div \dfrac{y}{x}\) 92}. \]
3}\div \dfrac{y}{x}\) 92}. \]
Умножение и деление дробей – Ключевые выводы
- Чтобы умножить дроби, нужно перемножить числители вместе и знаменатели вместе. Таким образом, умножение формы \( \dfrac{a}{b}\times \dfrac{c}{d}\) эквивалентно \(\dfrac{a\times c}{b\times d}.\)
- Чтобы разделить число (целое число или дробь) на дробь, мы должны сначала инвертировать делитель и применить процесс умножения к оставшейся части выражения.
- Чтобы умножить или разделить смешанные дроби, сначала преобразуйте их в неправильные дроби, а затем продолжите стандартный процесс.
3.2: Свойства определителей — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14511
- Кен Каттлер
- Университет имени Бригама Янга через Lyryx
Свойства определителей I: Примеры
У определителей много важных свойств. Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение.
Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение.
Определение \(\PageIndex{1}\): операции со строками
Операции со строками состоят из следующих
- Переключить два ряда.
- Умножить строку на ненулевое число.
- Заменить строку числом, кратным другой строке, добавленной к самой себе.
Теперь рассмотрим влияние операций со строками на определитель матрицы. В следующих разделах мы увидим, что использование следующих свойств может сильно помочь в поиске определителей. В этом разделе теоремы будут использоваться в качестве мотивации для предоставления различных примеров полезности свойств.
Первая теорема объясняет влияние на определитель матрицы перестановки двух строк.
Теорема \(\PageIndex{1}\): Переключение строк
Пусть \(A\) будет матрицей \(n\times n\), а \(B\) будет матрицей, полученной в результате переключения двух строк из \(A. \) Тогда \(\det \left( B\right) = — \det \left( A\right) .\)
\) Тогда \(\det \left( B\right) = — \det \left( A\right) .\)
Когда мы переставляем две строки матрицы, определитель умножается на \ (-1\). Рассмотрим следующий пример.
Пример \(\PageIndex{1}\): переключение двух строк
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\) и пусть \(B=\left[ \begin{array} {rr} 3 и 4 \\ 1 и 2 \end{массив} \right]\). Зная, что \(\det \left( A \right) = -2\), найдите \(\det \left( B \right)\).
Решение
По определению 3.1.1, \(\det \left(A\right) = 1 \times 4 — 3 \times 2 = -2\). Обратите внимание, что строки \(B\) являются строками \(A\), но перепутаны. По теореме \(\PageIndex{1}\), так как две строки \(A\) были переставлены местами, \(\det \left(B\right) = — \det \left(A\right) = — \left (-2\справа) = 2\). Вы можете убедиться в этом, используя Определение 3.1.1.
Следующая теорема демонстрирует влияние на определитель матрицы, когда мы умножаем строку на скаляр.
Теорема \(\PageIndex{2}\): умножение строки на скаляр
Пусть \(A\) — матрица \(n\x n\), а \(B\) — матрица, которая от умножения некоторой строки \(A\) на скаляр \(k\). Тогда \(\det \left( B\right) = k \det \left( A\right)\).
Тогда \(\det \left( B\right) = k \det \left( A\right)\).
Обратите внимание, что эта теорема верна, когда мы умножаем одну строку матрицы на \(k\). Если бы мы умножили 9п \дет(А)\).
Рассмотрим следующий пример.
Пример \(\PageIndex{2}\): умножение строки на 5
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \ right] ,\ B=\left[ \begin{array}{rr} 5 & 10 \\ 3 & 4 \end{array} \right].\) Зная, что \(\det \left( A \right) = -2\), найти \(\det \left( B \right)\).
Решение
По определению 3.1.1, \(\det \left( A\right) = -2.\) Мы также можем вычислить \(\det \left(B\right)\), используя определение 3.1.1 , и мы видим, что \(\det \left(B\right) = -10\).
Теперь давайте вычислим \(\det \left(B\right)\), используя теорему \(\PageIndex{2}\), и посмотрим, получим ли мы тот же ответ. Обратите внимание, что первая строка \(B\) в \(5\) раз больше первой строки \(A\), а вторая строка \(B\) равна второй строке \(A\) . По теореме \(\PageIndex{2}\), \(\det \left( B \right) = 5 \times \det \left( A \right) = 5 \times -2 = -10. \)
\)
Вы можете видеть, что это соответствует нашему ответу выше.
Наконец, рассмотрим следующую теорему для последней операции со строками — прибавления числа, кратного одной строке, к другой строке.
Теорема \(\PageIndex{4}\): добавление кратного строки к другой строке
Пусть \(A\) — матрица \(n\x n\), матрица, которая получается в результате прибавления числа, кратного одной строке, к другой строке. Тогда \(\det \left( A\right) =\det \left( B \right)\).
Следовательно, когда мы прибавляем кратное одной строки к другой строке, определитель матрицы не меняется. Обратите внимание, что если матрица \(A\) содержит строку, кратную другой строке, \(\det \left(A\right)\) будет равно \(0\). Чтобы убедиться в этом, предположим, что первая строка \(A\) равна \(-1\), умноженной на вторую строку. По теореме \(\PageIndex{4}\) мы можем добавить первую строку ко второй строке, и определитель не изменится. Однако эта операция строки приведет к строке нулей. Используя разложение Лапласа по ряду нулей, мы находим, что определитель равен \(0\).
Рассмотрим следующий пример.
Пример \(\PageIndex{3}\): добавление строки к другой строке
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\) и пусть \(B=\left[ \begin{array}{rr} 1 & 2 \\ 5 & 8 \end{array} \right] .\) Найти \(\det \left(B \Правильно)\).
Решение
По определению 3.1.1, \(\det \left(A\right) = -2\). Обратите внимание, что вторая строка \(B\) в два раза больше первой строки \(A\), добавленной ко второй строке. По теореме \(\PageIndex{1}\), \(\det \left( B\right) = \det \left( A \right) = -2\). Как обычно, вы можете проверить этот ответ, используя Определение 3.1.1.
Пример \(\PageIndex{4}\): Несколько строк
Пусть \(A = \left[ \begin{array}{rr} 1 & 2 \\ 2 & 4 \end{array} \right ]\). Покажите, что \(\det \left( A \right) = 0\).
Решение
Используя определение 3.1.1, определитель задается выражением \[\det \left( A \right) = 1 \times 4 — 2 \times 2 = 0\nonumber \]
Однако обратите внимание, что второй строка равна \(2\), умноженной на первую строку. Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).
Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).
До сих пор основное внимание уделялось операциям со строками. Однако мы можем выполнять те же операции со столбцами, а не со строками. Три операции, описанные в определении \(\PageIndex{1}\), можно выполнять со столбцами, а не со строками. В этом случае в теоремах \(\PageIndex{1}\), \(\PageIndex{2}\) и \(\PageIndex{4}\) слово «строка» можно заменить словом «столбец». «.
Есть несколько других важных свойств определителей, которые не включают операции со строками (или столбцами). Первым является определитель произведения матриц.
Теорема \(\PageIndex{5}\): определитель произведения
Пусть \(A\) и \(B\) — две матрицы \(n\times n\). Тогда \[\det \left( AB\right) =\det \left( A\right) \det \left( B\right)\nonumber \]
Чтобы найти определитель произведения матриц, мы можно просто взять произведение определителей.
Рассмотрим следующий пример.
Пример \(\PageIndex{5}\): определитель произведения
Сравните \(\det \left( AB\right)\) и \(\det \left( A\right) \det \left ( B\right)\) для \[A=\left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{array} \right], B=\left[ \begin{array }{rr} 3 и 2 \\ 4 и 1 \end{массив} \right]\nonumber \]
Решение
Первое вычисление \(AB\), которое задается \[AB=\left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{array} \right] \ left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \end{array} \right] = \left[ \begin{array}{rr} 11 & 4 \\ -1 & -4 \end {array} \right]\nonumber \] и, следовательно, по определению 3.1.1 \[\det \left( AB\right) =\det \left[ \begin{array}{rr} 11 & 4 \\ -1 & -4 \end{массив} \right] = -40\nonumber \]
Теперь \[\det \left( A\right) =\det \left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{массив} \right] = 8\nonumber \] и \[\det \left( B\right) =\det \left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \end{массив} \right] = -5\nonumber \] 9{-1}) = \frac{1}{\det(A)}\nonumber \]
Рассмотрим следующий пример.
Пример \(\PageIndex{7}\): определитель обратимой матрицы
Пусть \(A = \left[ \begin{array}{rr} 3 & 6 \\ 2 & 4 \end{array} \ справа], B = \left[ \begin{array}{rr} 2 & 3 \\ 5 & 1 \end{array} \right]\). Для каждой матрицы определите, является ли она обратимой. Если да, то найти определитель обратного.
Решение
Сначала рассмотрим матрицу \(A\). Используя определение 3.1.1, мы можем найти определитель следующим образом: \[\det \left( A \right) = 3 \times 4 — 2 \times 6 = 12 — 12 = 0\nonumber \] {7}\) \(А\) необратима. 9n a_{1,i} \mathrm{cof}(A)_{1,i}.\] Если \(n=1\), то \(\det A=a_{1,1}\).
Следующий пример является простым и настоятельно рекомендуется в качестве средства для привыкания к определениям.
Пример \(\PageIndex{8}\):
(1) Пусть \(E_{ij}\) — элементарная матрица, полученная перестановкой \(i\)-й и \(j\)-й строк матрицы \ (Я\). Тогда \(\det E_{ij}=-1\).
(2) Пусть \(E_{ik}\) — элементарная матрица, полученная умножением \(i\)-й строки \(I\) на \(k\). Тогда \(\det E_{ik}=k\). 9Т\).
Тогда \(\det E_{ik}=k\). 9Т\).
Многие доказательства в этом разделе используют принцип математической индукции. Эта концепция обсуждается в Приложении A.2 и для удобства рассмотрена здесь. Сначала проверим, что утверждение верно для \(n=2\) (случай \(n=1\) либо совсем тривиален, либо бессмыслен).
Далее предположим, что утверждение верно для \(n-1\) (где \(n\geq 3\)) и докажем его для \(n\). Как только это будет выполнено, по принципу математической индукции мы можем заключить, что утверждение верно для всех матриц \(n\times n\) для каждого \(n\geq 2\).
Если \(A\) является \(n\times n\) матрицей и \(1\leq j \leq n\), то матрица, полученная удалением \(1\)-го столбца и \(j\ )-я строка из \(A\) является матрицей \(n-1\times n-1\) (ниже мы будем обозначать эту матрицу через \(A(j)\)). Поскольку эти матрицы используются при вычислении кофакторов \(\mathrm{cof}(A)_{1,i}\), для \(1\leq i\neq n\), к этим матрицам применимо предположение индукции.
Рассмотрим следующую лемму.
Лемма \(\PageIndex{1}\):
Если \(A\) — матрица \(n\times n\) такая, что одна из ее строк состоит из нулей, то \(\det A=0 \).
- Доказательство
Мы докажем эту лемму с помощью математической индукции.
Если \(n=2\) это просто (проверьте!).
Пусть \(n\geq 3\) таково, что каждая матрица размера \(n-1\times n-1\) со строкой, состоящей из нулей, имеет определитель, равный нулю. Пусть \(i\) таково, что \(i\)-я строка \(A\) состоит из нулей. Тогда мы имеем \(a_{ij}=0\) для \(1\leq j\leq n\).
Исправьте \(j\in \{1,2, \dots ,n\}\) так, чтобы \(j\neq i\). Тогда матрица \(A(j)\), используемая при вычислении \(\mathrm{cof}(A)_{1,j}\), имеет строку, состоящую из нулей, и по нашему индуктивному предположению \(\mathrm{cof }(A)_{1,j}=0\). 9n a_{1,j} \mathrm{cof}(A)_{1,j}=0\nonumber \], так как каждое из слагаемых равно 0,
Лемма \(\PageIndex{2}\):
Предположим, что \(A\), \(B\) и \(C\) являются \(n\×n\) матрицами, которые для некоторого \(1\ leq i\leq n\) удовлетворяют следующему.
- \(j\)-е строки всех трех матриц одинаковы, для \(j\neq i\).
- Каждая запись в \(j\)-й строке \(A\) является суммой соответствующих записей в \(j\)-х строках \(B\) и \(C\).
Тогда \(\det A=\det B+\det C\).
- Доказательство
Проверить на \(n=2\) несложно (проверьте!).
Теперь предположим, что утверждение леммы верно для \(n-1\times n-1\) матриц, и зафиксируем \(A,B\) и \(C\), как в утверждении. Предположения утверждают, что мы имеем \(a_{l,j}=b_{l,j}=c_{l,j}\) для \(j\neq i\) и для \(1\leq l\leq n \) и \(a_{l,i}=b_{l,i}+c_{l,i}\) для всех \(1\leq l\leq n\). Поэтому \(A(i)=B(i)=C(i)\), а \(A(j)\) обладает тем свойством, что его \(i\)-я строка является суммой \(i\) строки \(B(j)\) и \(C(j)\) для \(j\neq i\), а остальные строки всех трех матриц идентичны. Следовательно, согласно нашему индуктивному предположению, мы имеем \(\mathrm{cof}(A)_{1j}=\mathrm{cof}(B)_{1j}+\mathrm{cof}(C)_{1j}\) для \(j\neq i\).
 9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.
9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.
Теорема \(\PageIndex{8}\):
Пусть \(A\) и \(B\) — матрицы \(n\times n\).
- Если \(A\) получается перестановкой \(i\)-й и \(j\)-й строк \(B\) (с \(i\neq j\)), то \(\det А=-\det В\).
- Если \(A\) получается умножением \(i\)-й строки \(B\) на \(k\), то \(\det A=k\det B\).
- Если две строки \(A\) идентичны, то \(\det A=0\).
- Если \(A\) получается умножением \(i\)-й строки \(B\) на \(k\) и прибавлением его к \(j\)-й строке \(B\) (\( i\neq j\)) затем \(\det A=\det B\).
- Доказательство
Докажем все утверждения по индукции. Случай \(n=2\) легко проверить напрямую (и настоятельно рекомендуется проверить его).
 n b_{1l} B_{1l} =\det B.\nonumber \]
n b_{1l} B_{1l} =\det B.\nonumber \]Итак, мы доказали случай (1), когда \(j=i+1\). Для доказательства общего случая понадобится следующий факт. Если \(i
(2) Это как (1)… но гораздо проще. Предположим, что (2) верно для всех \(n-1\times n-1\) матриц. У нас есть это \(a_{ji}=k b_{ji}\) для \(1\leq j\leq n\). В частности \(a_{1i}=kb_{1i}\), а при \(l\neq i\) матрица \(A(l)\) получается из \(B(l)\) умножением одного из его строки на \(k\).
 Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).
Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).(3) Это следствие (1). Если две строки \(A\) идентичны, то \(A\) равна матрице, полученной путем перестановки этих двух строк и, следовательно, согласно (1) \(\det A=-\det A\). Отсюда следует \(\det A=0\).
(4) Предположим, что (4) верно для всех \(n-1\times n-1\) матриц, и зафиксируем \(A\) и \(B\) так, что \(A\) получается умножением \ (i\)-я строка \(B\) на \(k\) и добавление ее к \(j\)-й строке \(B\) (\(i\neq j\)) затем \(\det А=\дет В\). Если \(k=0\), то \(A=B\) и доказывать нечего, поэтому можно считать \(k\neq 0\).
Пусть \(C\) — матрица, полученная заменой \(j\)-й строки \(B\) на \(i\)-ю строку \(B\), умноженной на \(k\). По лемме \(\PageIndex{2}\) мы имеем, что \[\det A=\det B+\det C\nonumber \], и нам «всего лишь» нужно показать, что \(\det C=0\).
 Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
Теорема \(\PageIndex{9}\):
Пусть \(A\) и \(B\) две матрицы \(n\times n\). Тогда \[\det \left( AB\right) =\det \left( A\right) \det \left( B\right)\nonumber \]
- Proof
Если \(A\) является элементарной матрицей любого типа, то умножение на \(A\) слева имеет тот же эффект, что и выполнение соответствующей операции с элементарной строкой. Поэтому равенство \(\det (AB) =\det A\det B\) в этом случае следует из примера \(\PageIndex{8}\) и теоремы \(\PageIndex{8}\).
Если \(C\) является редуцированной ступенчатой формой \(A\), то мы можем написать \(A=E_1\cdot E_2\cdot\dots\cdot E_m\cdot C\) для некоторых элементарных матриц \( E_1,\точки, E_m\).

Теперь рассмотрим два случая.
Предположим сначала, что \(C=I\). Затем \(A=E_1\cdot E_2\cdot \dots\cdot E_m\) и \(AB= E_1\cdot E_2\cdot \dots\cdot E_m B\). Применяя приведенное выше равенство \(m\) раз, а затем \(m-1\) раз, мы получаем, что \[\begin{aligned} \det AB&=\det E_1\det E_2\cdot \det E_m\cdot \det B\\ &=\det (E_1\cdot E_2\cdot\dots\cdot E_m) \det B\\ &=\det A\det B. \end{aligned}\]
Теперь предположим \(C\neq I\). Поскольку он находится в редуцированной строчно-эшелонной форме, его последняя строка состоит из нулей, а по (4) примера \(\PageIndex{8}\) последняя строка \(CB\) состоит из нулей. По лемме \(\PageIndex{1}\) имеем \(\det C=\det (CB)=0\) и, следовательно, \[\det A=\det (E_1\cdot E_2\cdot E_m)\cdot \ det (C) = \det (E_1\cdot E_2\cdot E_m)\cdot 0=0\nonumber \], а также \[\det AB=\det (E_1\cdot E_2\cdot E_m)\cdot \det (C B ) =\det (E_1\cdot E_2\cdot\dots\cdot E_m) 0 =0\nonnumber \] следовательно \(\det AB=0=\det A \det B\). 9Т\).
Приведенные выше рассуждения позволяют нам теперь доказать теорему 3. n a_{j,i} \mathrm{cof}(A)_{j,i}.\nonumber \] Докажем случай когда \(j=2\). 9T\), что равно разложению сомножителя по столбцу \(1\) матрицы \(A\). Таким образом, доказательство завершено.
n a_{j,i} \mathrm{cof}(A)_{j,i}.\nonumber \] Докажем случай когда \(j=2\). 9T\), что равно разложению сомножителя по столбцу \(1\) матрицы \(A\). Таким образом, доказательство завершено.
Эта страница под названием 3.2: Свойства детерминантов распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет
- Теги
- Детерминанты
- строковые операции
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра
Алгебраические выражения — ChiliMath
ПоискМатематика, как и любой другой язык, имеет способ передачи идей. алгебраическое выражение — это краткий способ описания математических объектов с помощью чисел, переменных (букв) и арифметических операций, таких как сложение, вычитание, умножение и деление.
Тремя основными компонентами алгебраических выражений являются числа , переменные и арифметические операции .
- Числа или константы
Примеры: 1, 6, 8, 27, 32 и т. д.
- Переменные или буквы
Примеры: x, y, a, h, p и т. д.
- Арифметические операции
Примеры: + (сложение), — (вычитание), \times (умножение), ÷ (деление)
2 Ниже приведены простые примеры, которые помогут вам ознакомиться с операциями сложения, вычитания, умножения и деления.

- Сложение
сумма x и 5 → x+5
- Вычитание
разность y и 3 → y-3
- Умножение
произведение n и 2 → 2n
- Деление
- частное m и 2 выражается как \Large{{m \over 2}}
- произведение 4 и n выражается как 4n
- произведение 7 и w выражается как 7w
- частное 2 и v выражается как \Large{{2 \over v}}
900 более 7}}
Написание алгебраических выражений Пошаговые примеры
Давайте рассмотрим другие примеры.
Пример 1: Сумма удвоенного числа и 3
Ответ: Пусть переменная x будет неизвестным числом. Таким образом, удвоенное число означает 2x. Сумма (используйте символ плюса) удвоенного числа и 3 может быть записана как 2x+3.
Пример 2: Разница тройного числа и 5
Ответ: Пусть переменная y будет неизвестным числом. Таким образом, тройное число означает 3 года. Разность (используйте символ минус) тройного числа и 5 должна быть записана как 3y — 5. .
.
Ответ: В этом случае неизвестные числа уже представлены как m и n. Это одним поводом для беспокойства меньше.
Ключ в том, чтобы признать, что мы собираемся добавить частное и произведение.
Таким образом, сумма частного и произведения равна { \большой{{м\свыше 2}}} + 4н.
Пример 4: Разность произведения 7 и w и частного 2 и v.
Ответ: В этом случае неизвестным числам были присвоены соответствующие переменные w и v
Суть в том, чтобы понять, что мы собираемся вычесть произведение на частное некоторых выражений.
Следовательно, разность произведения и частного составляет 7w — {\ Большой {{2 \ над v}}}.
Общие слова или термины для обозначения сложения, вычитания, умножения и деления
Давайте рассмотрим некоторые общие слова или фразы, которые описывают четыре арифметических действия. Очень важно, чтобы вы понимали эти слова или фразы, чтобы успешно написать или интерпретировать любое заданное алгебраическое выражение.
Преобразование математических фраз в алгебраические выражения
Ключом к обучению является изучение МНОГО примеров!
| MATH PHRASES | ALGEBRAIC EXPRESSIONS | ||||
|---|---|---|---|---|---|
| a number plus 9 | y + 9 | ||||
| the sum of a number and 10 | m + 10 | ||||
| сумма числа и 5 | б + 5 | ||||
| Число увеличилось до 4 | x + 4 | ||||
| H Уберите 2 | H — 2 | ||||
| 2 ВЫКЛАВАЯ ПОДЕЛАНИЯ | |||||
2 2. Удаляйте на номер Удаляйте на номер | |||||
| 2 2 | |||||
| 2. | Число минус 11 | K — 11 | |||
| 11 минус | 11 — K | ||||
| Число уменьшилось на | |||||
| . п и 25 | n — 25 | ||||
| Разница 25 и N | 25 — N | ||||
| 5 Меньше всего номера | 5 x – 5 | 5 40026 | 5 x – 5 | . | 5 − x |
| the product of r and 4 | 4r | ||||
| 7 times a number | 7p | ||||
| double a number | 2x | ||||
| triple a number | 3x | ||||
| a number divided by 4 | w / 4 | ||||
| the quotient of w and 6 | w / 6 | ||||
| the quotient of 12 and m | 12 / m | ||||
| a number divided by 3 | f / 3 | ||||
| t over 7 | t / 7 | ||||
| 5 into a number | a / 5 | ||||
| a number into 5 | 5 / a | ||||
| the sum of x and 7 divided by 2 | ( x + 7 ) / 2 | ||||
| the difference of m and 3 over 5 | ( m − 3) / 5 | ||||
| 11 more than the product of 3 and y | 3y + 11 | ||||
| 6 less чем частное c и 10 | ( c / 10 ) − 6 | ||||
| 3 minus the product of 5 and a number | 3 − 5x | ||||
| the sum of 5 and the quotient of z and 7 | ( z / 7) + 5 | ||||
| Разница в два раза больше и 3 | 2m — 3 |
Вы также можете быть заинтересованы в
AlgebraiC.


 Составить таблицу умножения
Составить таблицу умножения № 1 (с. 40)
№ 1 (с. 40) Закрась числа, которые делятся на
5.
Закрась числа, которые делятся на
5.




 6,3,9,6,9 (кроме 48)
6,3,9,6,9 (кроме 48)