Школа Гениальности

Николай Александрович Зайцев

Зайцев Николай Александрович (1939) — известный российский автор знаменитого пособия «Кубики Зайцева» и многих других методик раннего развития детей.

Все его пособия, главным и наиболее известным из которых являются «Кубики Зайцева», основаны на естественной потребности любого ребенка в игре.

Суть методики в том ,что, весь материал подается в игровой форме. Методики Н. Зайцева характеризуются специалистами (физиологами, медиками, психологами) как природосообразные, здоровьесберегающие и универсально-адаптивные, учитывающие индивидуальные особенности различных групп детей, в том числе и с особенностями психофизического развития.

Пособия Н. Зайцева представляют собой комплекты учебных материалов по обучению чтению, каллиграфии, математике, грамматике русского языка, английскому языку.

В основе методик Н. Зайцева лежит неукоснительное соблюдение основных дидактических принципов:От общего к частному и от частного к общему.

• От конкретно-образного через наглядно-действенное к словесно-логическому.
• Обеспечение наглядности с использованием различных каналов восприятия.
• Системная подача материала.
• Алгоритмизация учебных действий.
• Учет физиологии восприятия учебной информации.
• Охрана здоровья учащихся.

С помощью таблиц-тренажёров у ребенка формируется точный образ-представление, раскрывающий сущность понятия или предмета. Таблицы выполняют роль многофункционального посредника между ребенком и взрослым: обучают, информируют, ориентируют в учебном материале, тренируют и формируют необходимые навыки.

Система таблиц создает информационное поле предмета, рассчитанное на быстрое в него погружение и использование при решении многочисленных и разнообразных задач и примеров. Каждая из них нужна при введении, осмыслении, закреплении и повторении материала, призвана напоминать о проделывавшейся ранее, с опорой на нее, работе. Появляются возможности для взаимообучения учащихся.

Кубики Николая Александровича Зайцева

Кубики Зайцева — это новая методика обучения детей чтению, основанная на чтении слова по складам (не путать со слогами). По мнению автора методики, таким способом можно научить детей читать с 2-3х летнего возраста. Складовой принцип чтения — основа Зайцевского метода обучения детей чтению. Склад — это пара из согласной с гласной, или из согласной с твердым или мягким знаком, или же одна буква. Пользуясь этими складами (каждый склад находится на отдельной грани кубика), ребенок начинает составлять слова. Кубики различаются по цвету, размеру, издают разные звуки. Они бывают железные и деревянные. Эти особенности помогают детям почувствовать разницу между гласными и согласными, звонкими и мягкими. Детям 3,5-4 лет методика дает возможность научится читать на первых же занятиях, а малышам от 1 года — начать говорить и читать одновременно. Для освоения слогов автор предлагает слушать, манипулировать слогами и петь их уже с детишками 3-4 лет, используя кубики с изображенными на них сочетаниями букв: «БА», «БЕ», «БИ» и так далее.

Эффективность

Как показывает широчайшая практика, через 15-20 часовых занятий дети четырех-пяти лет начинают читать, складывать и вычитать в пределах ста. В дальнейшем идет работа по укреплению навыков чтения, письма и счета.

К шести-семи годам, опять же при двух занятиях в неделю, не менее 80-90% детей способны учиться по нынешним программам для второго, третьего, четвертого классов.

По мнению психолингвистов, занятия с кубиками Зайцева особенно полезны для детей с доминантно развитым правым полушарием, для которых образное мышление является основным способом усвоения знаний. Пособие предполагает эмоциональное обучение, связанное с пением, что позволяет даже младшим дошкольникам, аналитическое мышление которых еще не вполне развилось, моментально ухватывать сущность процесса соединения складов в слово.

Эта методика позволяет также развить музыкальный слух и творческое мышление. Однако родителям, которые научили детей читать при помощи системы Зайцева, стоит в период подготовки к школе, дать будущему первокласснику хотя бы элементарные знания о фонемном составе слова. Это поможет малышу быстрее справиться с программой изучения русского языка и не испытывать сложности с выделением частей слова, которые часто возникают у тех учеников, которые видят в словах только склады.

Охрана здоровья, развитие психологических характеристик учащихся

Характерной чертой, отмечается учеными, педагогами, специалистами, является отсутствие перегрузок, ослаблений зрения и осанки, столь характерных для большинства современных методик. Занятия проводятся в игровой и соревновательной форме, с пропеванием учебных материалов (обеспеченных аудиозаписью), в движении, исключается монотонность, длительное пребывание учащихся в сидячем положении и связанные с этим школьные стрессы. Методическое обеспечение позволяет проводить занятия на воздухе.

 

Зрение и осанка часто даже улучшаются.

Раннее обучение чтению и счету по методикам Н.Зайцева — надежнейшее средство диагностики. Дети ярко проявляются в деятельности, через несколько занятий любому педагогу без специальных тестов ясно, кто есть кто. Определяются как талантливые, чрезвычайно способные к обучению дети — быстрые, так и медленные, требующие особого внимания, а некоторые даже специального обследования. Чем раньше это выявляется, тем больше будет шансов их выправить.

Методика Зайцева, математика. Обучение для детей

Математика, счет чисел и выполнение простейших арифметических действий сопровождают каждого человека на протяжении всей жизни с момента, как он научается просить два конфетки и до глубокой старости, когда нужно подвести итог жизни и сказать, что у него семь внуков, двенадцать правнуков и уже праправнуки на подходе…

Возникает вопрос: почему тогда часто встречаются дети, которые терпеть не могут математику чуть ли не с первых дней обучения в школе. Возможно, это происходит потому, что был упущен момент, когда стоило начать учить математику. И знакомить ребенка с числами, их количественным составом и простыми действиями с ними нужно раньше, еще до школы?

На этот вопрос однозначно дает положительный ответ педагог-новатор Зайцев, который предложил свою методику обучению математике дошкольников.

Содержание

• 1  Методика Зайцева, математика
  • 1.1 База математической методики Зайцева
  • 1.2 Этапы методики Зайцева в изучении математики

     Математика по Зайцеву позволяет вырастить ребенка эрудированного, умеющего логически рассуждать, обобщать и анализировать, и при этом развить у него творческие способности.

Возраст для занятий по методике Зайцева неограничен, как только малыш научился говорить и повторять слова, ему можно предложить запомнить и названия чисел вместе с их схематическим изображением. А для шестилетки такие пособия помогут вспомнить и систематизировать знания по математике, чтобы быть готовыми к восприятию новых сведений из курса начальной школы.

Если предложить ребенку изучать числа с помощью пособий, которые предлагает методика Зайцева, математика станет возможностью развить память и решать математические примеры, как простейшие головоломки.

База математической методики Зайцева

Для изучения основ математики с помощью методики Зайцева, нужно приобрести или сделать самостоятельно карточки, которые носят название «Стосчет».

Это сто карточек с написанными на них числами от 0 до 99 и еще карточки, которые будут наглядно показывать состав чисел. Эти карточки разлинованы в виде таблицы с двумя строками и пятью столбцами. Для обозначения цифры «ноль» такая карточка не будет закрашена совсем. У цифры «один» будет закрашена одна ячейка таблицы, у цифры «два» — две, и так далее.

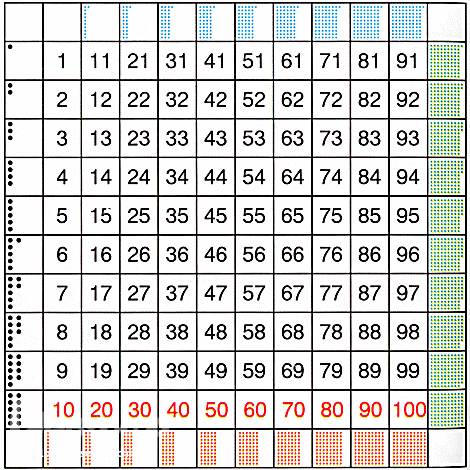
Когда подходит время обозначать десятки, то потребуется несколько карточек: полностью закрашенные по количеству десятков, расположенные одна под другой, и карточка единиц, которую нужно поместить справа от десятков.

Располагать такие карточки рекомендуется по стенам детской комнаты немного выше уровня глаз ребенка. Так, по мере изучения чисел появляется длинная цепочка карточек, которая наглядно демонстрирует порядок чисел и их состав. И у ребенка всегда можно в игре спросить какое-либо число, чтобы закрепить полученные знания.

Уже при освоении чисел первого десятка Зайцев предлагает знакомить ребенка со сложением и вычитанием.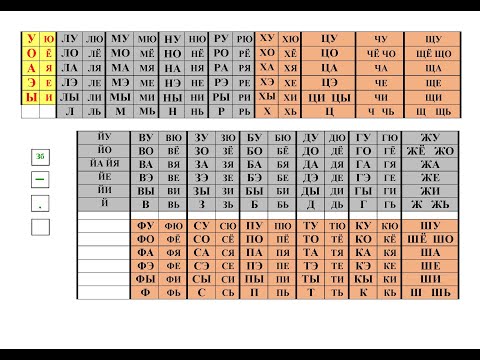 При этом он рекомендует не записывать их примерами, а изучить наглядно. Для этого нужно выбрать число на ленте чисел и спросить, какое число получится если прибавить к нему / вычесть из него другое число и перемещаться вдоль цепочки чисел в сторону увеличения/уменьшения чисел.

Этапы методики Зайцева в изучении математики

В скором времени ребенок легко справляется с такими примерами в пределах первой сотни. И тогда можно будет воспользоваться другими пособиями. Например, «Мне в сотне тесно», в которой ребенку предлагается выйти за рамки первой сотни и познакомиться с числами первой тысячи.

После этого можно приступать к абстрактному изображению чисел и действий с ними и здесь на помощь придет игра «Пять в кубе».

Методика Зайцева предлагает знакомить детей и более сложными арифметическими действиями. Например, для усвоения таблицы умножения разработано пособие «Пифагор». Здесь же дети знакомятся с простыми и десятичными дробями.

Геометрические знания не остаются в стороне.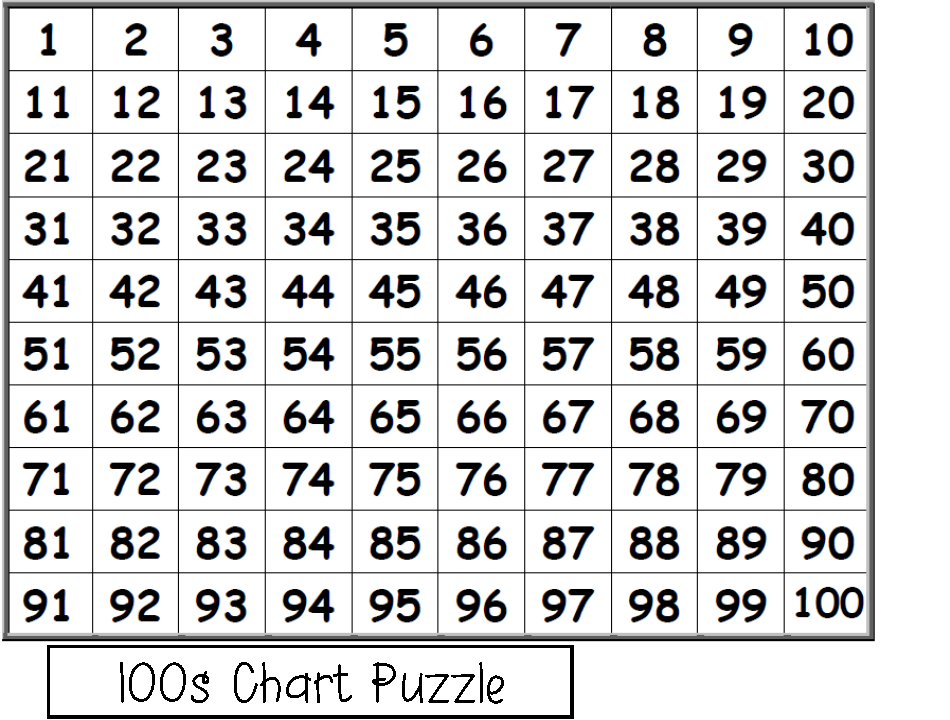 Запомнить названия и особенности геометрических фигур планиметрии и объемных тел стереометрии помогут методики Зайцева «Платоновы тела» и «Орнамент».

Полезные статьи:

ЗАНЯТИЯ ПО КУБИКАМ ЗАЙЦЕВА

ИГРЫ ДЛЯ ОБУЧЕНИЯ СЧЕТУ

БЫСТРЫЙ СПОСОБ ВЫУЧИТЬ ТАБЛИЦУ УМНОЖЕНИЯ

ЦИФРЫ КАРТОЧКИ РАСПЕЧАТАТЬ

[PDF] НАБОР ДЛЯ СИНТЕЗА ФУНКЦИЙ НЕЧЕТКОЙ ЛОГИКИ ПО ТАБЛИЦЕ ВЫБОРА

• ID корпуса: 212613653

  title={НАБОР ИНСТРУМЕНТОВ ДЛЯ СИНТЕЗА ФУНКЦИЙ НЕЧЕТКОЙ ЛОГИКИ НА ТАБЛИЦЕ ВЫБОРА},
  автор={Дмитрий А. Зайцев},
  год = {2017}
} 

• Д. Зайцев
• Опубликовано в 2017 г.
• Информатика

Набор инструментов для синтеза функций нечеткой логики на таблице выбора, доступный для бесплатного скачивания на GitHub, реализован на языке C. Ранее опубликованный метод синтеза функций непрерывной (нечеткой) логики на таблице выбора был адаптирован для быстрого разбиения исходной таблицы выбора набором функций нечеткой логики.

Инструментарий реализует стиль программирования командной строки, используя данные, расположенные в текстовых файлах простых интуитивно понятных форматов. Набор инструментов может быстро обрабатывать большие данные… 

Daze.ho.ua

Computing с модульными роботами

• G. J. Martínez, A. Adamatzky, L. N. Oliva-Moreno

• Computer Science

  Arxiv

• 229

• Arxiv

• 22

• . в небольших модульных роботах Cubelets объединяются в каналы и соединения, структуры, разработанные Cubelets, распространяют сигналы параллельно и асинхронно.
  ПОКАЗАНЫ 1-10 ИЗ 14 ССЫЛОК

  Сортировка Byrelevancemost влияет на документы

  Синтез непрерывных логических функций, определенных в табличной форме

  • D. Zaitsev, V. G. Sarbei, A. I. Sleptsov

  • Computing Science, Mathematics

  • 999999999999999999969

  • Computip Science, Mathematics

  • 999999999999999999999969

  • . заданная таблица выбора определяет некоторую функцию непрерывной логики, и выводится простой алгоритм синтеза функции из таблицы.

    Алгоритмы многоуровневого синтеза нечетких функций

    В статье представлен новый метод многоуровневого синтеза нечетких функций, полученных из описания поведения реализуемой нечеткой системы. Новая методология зависит от представления …

    минимизации дизъюнктивных нормальных форм нечетких логических функций

    • K. BHAT

    • Компьютерная наука

    • 1981

    ГЛАВИЧЕСКАЯ АЛГИТМА ДВУМА предложен новый эвристический алгоритм, основанный на методе нечеткого консенсуса, для двухуровневой минимизации функций нечеткой логики, и его результаты сравниваются с результатами точных методов.

    Программирование на сетевом языке Слепцова для управления системами

    • Д. Зайцев, Ю. Юрьенс

    • Информатика

    • 2016

    Принципы программирования на сетевом языке доработаны с учетом ограничений на языке Слепцова на поток управления и его композицию с данными и сформулированы дополнительные ограничения на копирование параметров модулей и использование глобальных переменных.

    ОЦЕНКА ВРЕМЕНИ ОТКЛИКА КОММУТИРУЕМОЙ ETHERNET С ПОМОЩЬЮ ЦВЕТНОЙ СЕТИ ПЕТРИ, МОДЕЛЬ

    • Зайцев Д., Шмелева Т.

    • Информатика

    • 2006

    Представлена ​​модель коммутируемой ЛВС корпоративного класса в виде цветной сети Петри и влияние таких особенностей, как ограничения буфера коммутатора оценивались размер и динамическое обслуживание таблицы коммутации.

    Нечеткие множества

    • Роберт Лин

    • Информатика

      Энциклопедия ГИС

    • 2017

    Представлены усовершенствования для основной статьи о нечетких множествах для дистрибутивного закона, выпуклых комбинаций и выпуклых нечетких множеств, чтобы помочь исследователю усвоить исходную статью.

    Проверка протоколов сетки квадратной связи через Infinite Petri Nets

    • Shmeleva

    • Компьютерная наука

    • 2009

    Доказано, что принужденная буферизация пакетов Inevibly приводит к возможным блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокируемым блокировке, потому что поездка на основе конъюнкции, покончивших обои. цикл блокировок и изоляции.

    State equations and equivalent transformations for timed petri nets

    • D. Zaitsev, A. I. Sleptsov

    • Mathematics

    • 1997

    Fuzzy Mathematical Techniques With Applications

    • A. Kandel

    • Mathematics

    • 1986

    Правило Зайцева — Органическая химия Видео

    Гл. 9 — Алкены и алкины Рабочий листПосмотреть все главы

    90
    90
    908 3 — Кислоты и основания 91647 90 Гл. 4 — Алканы и циклоалканы55 5 — Хиральность

    80

    80 9 — Алкены и алкины

    11 — Радикальные реакции80
    80164 Гл. 12 — спирты, эфиры, эпоксиды и тиолы955 14 — Синтетические методы
    15
    15 Гл. 15 — Аналитические методы: IR, ЯМР, Mass Spect
    4 18 — Реакции ароматических соединений: EAS и не только 90. 24 — Углеводы44. 26 — Аминокислоты, пептиды и белки

    Гл. 1 — Обзор общей химии		4 часа и 48 минут	Выполнено 0 %	Рабочий лист Скачать рабочий лист видеоурока Начало 18409	2 — Молекулярные представления		1 час и 12 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	2 часа и 45 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	4 часа и 19 минут	0% завершено	Рабочий лист Скачать рабочий лист видеоурока Начало		3 часа и 33 минуты	Выполнено 0%	Рабочий лист Скачать рабочий лист видеоурока Начало
    Гл. 6 — Термодинамика и кинетика		1 час и 19 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало	5	7 — Реакции замещения		1 час и 46 минут	0% завершения	Рабочий лист Скачать рабочий лист видеоурока Начало
    Гл. 8 — Реакции исключения		2 часа и 25 минут	0% завершено	Рабочий лист Загрузить рабочий лист видеоурока Начало		2 часа и 10 минут	Выполнено 0%	Рабочий лист Скачать рабочий лист видеоурока Старт
    Гл. 10 — Реакции сложения		3 часа и 32 минуты	0% завершено	Рабочий лист Загрузить рабочий лист видеоурока Начало 130		1 час и 55 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	2 часа и 42 минуты	0%. Завершите	Рабочий лист . 13 — Спирты и карбонильные соединения		2 часа и 14 минут	Выполнено 0%	Рабочий лист Скачать рабочий лист видеоурока Начало
    	1 час и 28 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	7 часов и 20 мин	0%. 16 — Сопряженные системы		5 часов и 49мин.	Выполнено 0%	Рабочий лист Скачать рабочий лист видеоурока Начало
    Гл. 17 — Ароматичность		2 часа и 24 минуты	0% завершено	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	4 часа и 31 минута	0% завершения	Рабочий лист Скачать рабочий лист видеоурока Старт
    Гл. 19 — Aldehydes and Ketones: Nucleophilic Addition		4hrs & 54mins	0% complete	Worksheet Download the video lesson worksheet Start
    Ch. 20 — Производные карбоновой кислоты: NAS		2 часа и 3 минуты	0% выполнения	Рабочий лист Скачать рабочий лист видеоурока Старт
    Гл. 21 — Химия еноляции: реакции на альфа -углероде		1HR & 56Mins	0%. Завершите	Рабочий лист . 22 — Химия конденсации		2 часа и 13 минут	0% завершено	Рабочий лист Скачать рабочий лист видеоурока Старт
    Гл. 23 — Амины		1 час и 43 минуты	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Начало
    	5 часов и 56 минут	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока Старт
    Гл. 25 — Фенолы		15 минут	Выполнено 0%	Рабочий лист Скачать рабочий лист видеоурока Начало
    	2 часа и 54 минуты	Выполнено 0%	Рабочий лист Загрузить рабочий лист видеоурока 3 8 Начало 64 Гл. 26 — Transition Metals		5hrs & 33mins	0% complete	Worksheet Download the video lesson worksheet Start

    See all sections

    Sections
    Стабильность алкенов	7 мин.	0 завершено0180
    Zaitsev Rule	25 mins	0 completed	Learn Summary
    Dehydrohalogenation	8 mins	0 completed	Learn
    Double Elimination	9 мин	0 завершено	Обучение
    Ацетилид	15 мин	0 завершено	Learn
    Hydrogenation of Alkynes	17 mins	0 completed	Learn Summary
    Dehydration Reaction	27 mins	0 completed	Learn Сводка
    Дегидратация POCl3	6 минут	0 завершено	Обучение
    Alkynide Synthesis	16 mins	0 completed	Learn Summary

    LearnSummary

    Next SectionDehydrohalogenation

    Elimination reactions often can yield multiple products. Однако не все эти продукты будут иметь одинаковую стабильность. Правило Зайцева (также называемое правилом Сайтцева) помогает нам предсказать основной продукт.

    Зайцев против Хофмана Продукт

    Концепция № 1: Определение правила Зайцева

    Правило Зайцева предсказывает, что в большинстве случаев предпочтение будет отдаваться продукту с наибольшей заменой. Это также известно как изделие Зайцева . Нарисуйте продукт Зайцева следующей реакции:

    Пример #1: Пример продукта Зайцева.

    Исключением из этого правила является использование больших оснований . Они способствуют образованию менее замещенного продукта.

    • Наиболее распространенными объемными основаниями являются диизопропиламид лития (LDA) и трет-бутоксид (t-BuO ^–)

    Менее замещенный продукт называется продуктом Хофмана. Нарисуем продукт Хофмана следующей реакции:

    Пример №2: пример продукта Хофмана.

    Термодинамическое и кинетическое произведение

    Концепция № 2: Использование диаграммы свободной энергии для объяснения термодинамического и кинетического произведений.