Состав числа
По совету Утры завожу новый топик: Посоветуйте, пожалуйста, приемы объяснения/автоматизации состава числа для дошкольника. Спасибо заранее!
Выучить таблицы наизуть, как таблицу умножения. Сначала пусть подряд рассказывает как «отче наш», а потом уже вразброс по таблице гоняйте.
На айпаде приложение-игру установить)
мы и таблицу-то умножения по стихам Усачева учили. так намного легче.И тут можно игру какую-то придумать, детям же интереснее.
Объяснения — практически любые пособия для дошкольников. «Ступеньки» Петерсон, математика в «Ломоносовской школе», «Состав числа» у Весны-дизайн, «Состав числа» у Буракова.
В том топике уже писАла про игры —
Pig10, игры от Банды умников — Турбосчет, Фрукто 10.
Если есть возможность заказа за границей, то это Pop for Addition and Subtraction, 7 ate 9, Math War Addition &Subtraction.
Некоторые игровые приемы описаны у Жени Кац в книге «Пирог с математикой». Например, Вы с ребенком договариваетесь, что должны вместе показать 8 пальцев.
1 это 1 и 0 или 0 и 1
2 это 0 и 2, 2 это 1 и 1, 2 это 2 и 0
3 это 0 и 3, 3 это 1 и 2, 3 это 2 и 1, 3 это 3 и 0
4 это… до 10 включительно
проговаривали на подготовишках как мантру, учили практически как таблицу умножения
но вначале купить айпад
это то, что вы говорили? http://www.amazon.com/POP-ADDITION-SUBTRACTION-LEARNING-RESOURCES/dp/B00ANSIWU4/ref=sr_1_fkmr2_2?s=office-products&ie=UTF8&qid=1360755693&sr=1-2-fkmr2&keywords=Pop+for+Addition+and+Subtraction%2C+7+ate+9%2C+Math+War+Addition+%26Subtraction
В чем там смысл игры, а то в описании не нашла
вот так рождается ненависть к математике )))
на обычной винде тоже море всяких тренировалок.
они по-сути все одинаковые.
Да, она.
Участники по очереди крутят вертушку и вытаскивают себе столько кружков с примерами, какое число выпало на вертушке. Игрок должен назвать решение каждого примера, если решено правильно, то он забирает кружок себе. Когда кружки в общей коробке закончились, то считают, у кого сколько. Набравший бОльшее количество — выигрывает.
Можно играть с секундомером на время, типа надо дать ответ за 10 секунд, если ответа нет, то кружок считается проигранным.
Есть несколько кружков с надписью Pop — по стандартным правилам если игрок вытащил такой кружок, то все свои заработанные кружки он должен вернуть в общую коробку (они как бы сгорели). Но там комментаторы предложили свой вариант, чтобы не разочаровывать детей — если выпадает Pop, то можно сделать что-нибудь приятное, например, попрыгать. Т.е. этот кружок становится поощрением, а не наказанием. Мы играем именно таким образом.
У нас в первом классе состав числа автоматизируется,так сказать,с помощью книжечки Узоровой/Нефёдовой «3000 примеров по математике»
http://my-shop.
ru/shop/books/295552.html
До этого рисовали этот состав числа кто в виде домиков,кто в виде веточек.В учебнике математики (у нас Моро) на внутренней стороне обложки есть таблица сложения (тот же самый состав числа).
ред. простите,пропустила,что у Вас дошкольник.
да у Дошкольников такая же фигня.
На подготовишках по Петерсону те же домики.
Ничего нового в этой сфере придумать думаю уже нельзя
Объяснения для дошкольника- это только руками- на орехах, машинках, конфетах и тыды. И домики рисовать и на стенку в видном месте повесить.
Нам в школе игру показали с мячиком: Сперва договариваемся, что «в корзинке 8 яблок». Дальше учитель кидает мяч ребенку и называет, сколько он взял.
А ребенок должен поймать мяч и ответить, сколько осталось, кидая мяч обратно учителю. Быстро. И так, пока все варианты из восьмерки не переберут. Потом ребенок называет, сколько взял, а учитель отвечает.Еще один вариант игры — вытаскивается 1 кружок и вертушка потом определяет, сколько примеров с таким же результатом, как на кружке, игрок должен придумать самостоятельно. Если игрок назвал примеры правильно, то кружок он может забрать себе. Победитель определяется бОльшим числом кружков.
Почему? Я в детстве тоже так учила и таблицу умножения тоже, но для меня в этих таблицах была заключена некая мелодика чисел, их понимание что ли. Вот до сих пор грамматические ошибки для меня не значимы, они меня не раздражают, но вот неточности с числами просто бесят и я улавливаю их автоматически.
Все мы разные, кому надо облекать математику в игровую форму, а для кого то это уже увлекательнейшая из игр.
Это хорошо бы нарисовать, конечно, а то объяснять долго и непонятно) но попробую))
например, делаете ромашку с 10-ю лепестками — рисуете, или вырезаете из бумаги серединку и 10 лепестков.
делаете 10 лепестков одного цвета и 10 лепестков — другого. Потом составляете ромашку, используя лепестки двух цветов так, чтобы всего было всегда 10. Т.е. 9красных и 1 белый, потом 8красных 2 белых и т.д. Можно записывать эти «составы числа», только не в виде примеров 9+1=10, а в виде ответвления ()блин нарисовать бы вам) 10 — это 9 и 1. 10 — это 8 и 2. 10 — это 7 и 3.
Можно нарисовать ромашку где-нибудь в Power Point, чтобы можно было лепестки одним движением мышки перекрашивать — и так играть.
А самое лучшее наглядное пособие для обучения составу числа 10 — это РУКИ РЕБЕНКА))
Графических представлений очень много —
и делать ряд одинаковых предметов и раскрашивать его каждый раз по-разному
и набирать число из двух видов предметов каждый раз по-разному
и на числовом отрезке рисовать отрезки разной длины и разными цветами
и просто «резать» числовой отрезок в разных местах и смотреть, какой длины части получились
Это уж какому ребенку как больше нравится.
сын мой в 1 классе ,а сейчас таким же образом учит умножение(не тупое зазубривание) так:
например,нарисованы 3 яблока,рядом еще 5,ребенку надо посчитать,плюс он может глазами оценить сколько ж это 3 и 5,потом уже автоматически начнет определять.Еще дайте счеты ребенку,сын в 1 классе на счетах считал,им учитель сама рекомендовала
Это два разных процесса: объяснение и автоматизация.
Объяснение Вам уже написали много вариантов: и ромашки, и домики, и др.
А автоматизация — только дриль. Есть время — в игровой форме. Нет — в режиме вопрос-ответ.
Я именно так и делала, по дороге, например, в бассейн «играла» с детьми в цифры.
Поразглядывала это замечательное пособие повнимательнее:на обложке написано- для 1-го класса,в аннотации — для дошкольников тоже
Загляните ко мне в паспорт, папка «Пазлы, лото, мозаики и проч.»
Сейчас полетят помидоры и тапки. Ну на кой этот состав числа? Мой ребенок вообще запутался с ним, без состава прекрасно считал.
Как только ввели этот состав числа у нас просто каша в голове.
ну если совсем грубо, то не зная состав числа считать невозможно
возможно, и именно считать, а не заучить и знать. Мой если например 5+2, то сидит и в уме считает:5,6,7 т.е. равно 7. И никогда мы никакие таблицы не учили. Как-то мне было интересно, а как же он большие числа прибавлять будет (8 или 9 например), все нормально ни разу не запутался. Поначалу какие-то точечки вокруг числа ставил и считал (то ли их так учительница учила, то ли сам придумал).
Ну это называть то как угодно можно) Я под составом числа понимаю автоматическое умение складывать и отнимать в определенных пределах)
его не учат назубок , если вы это имели ввиду, это понимание, что 7 это 5и2 . Если это в голове автоматизировано ( состав число 20 и идеале), дети очень быстро считают 2,3,4 значные числа в уме, перекидывая эти единицы куда надо, не задумываясь и невысчитывая как у Тани «.
Мой если например 5+2, то сидит и в уме считает:5,6,7 т.е. равно 7. «
обалдела от вашей системы хранения, все по полочкам, порядок такой. класс!
с сыном домики рисовали и вписывали числа, все быстро понял.
Ребенку (и мне) очень понравилась игра 10 свинок, как раз для автоматизации элементарного счета и для состава числа.
то, о чем вы говорите — это операции с ЦИФРАМИ, а настоящая математика — это оперирование КОЛИЧЕСТВАМИ. согласна с предыдущим оратором: без понимания состава числа вычисления затруднительны. Это пока нужно к 6 прибавить 3, ваш ребенок может «в уме просчитать»: семь, восемь, девять. А для более крупных чисел и других действий необходимо чувство числа, сформированные аналогии. Если 2+7=9, то 32+7=? Для ребенка, понимающего состав числа, это вообще не вопрос. А кто-то опять начнет «в уме считать»: 33,34, 35…..
Настоящая математика начинается с правильных КОЛИЧЕСТВЕННЫХ представлений, что такое ПЯТЬ — из чего состоит, что «внутри»?. У многих людей, например есть свои представления чисел — кто-то в виде таблицы представляет, кто-то в виде длинной числовой прямой, у кого-то числа маленькие-большие буквально, у кого-то толстые, тяжелые… это и есть «чувство числа», когда ты точно понимаешь, где больше, где меньше, в какой стороне, во сколько раз примерно…)
Нет, конечно, можно жить и с такими представлениями можно считать цифры всю жизнь и плохо понимать математику, повесить на ребенка клеймо «мы не математики, мы гуманитарии» — бухгалтерами им точно не быть))) но и никто не умрёт)) Есть люди, которые всю жизнь так считают и представляют число 68 исключительно в виде двух цифр — шесть и восемь))
но с другой стороны, почему бы не дать ребенку верные представления, настоящие — математические? вдруг это ему в жизни пригодится?
совершенно верно.
если ребенок понимает состав числа, он точно знает, что
7 — это 5 и 2 (и наоборот))
7 — это 4 и 3 (и наоборот)
7 — это 1 и 6 (и наоборот))
В таком случае, если ему нужно решить пример 5+2 — он ничего не считает, он просто знает, что 5 и 2 — это 7
А что значит «большие» числа?
Я оценила важность этого самого «состава числа» тогда, когда у сына пошли примеры вроде «44+7» или «55-8» (на минус — особенно). Просто ставить точечки или считать «44,45,46, 47,…» — слишком долго и неудобно. А сейчас у сына вообще трехзначные числа пошли…
ну «большие» я имею в виду что у каждого человека какие-то собственные представления:
скажешь 52 и 78 — человек, допустим «видит» 52 среднего размера, а 78 — бОльшего) кто-то сверху-вниз представляет, кто-то слева-направо, кто-то вообще сплошным множеством чисел…)
это я просто о «чувстве числа» рассуждала))
вот если математику сказать: «Тридцать семь!», то у него возникает конкретное «видение» числа, его наполненность, как бы «тело» )))
а многие люди (нематематики) видят только цифры: 37))
у меня, например, так было вплоть до тех пор, пока я не начала когда-то заниматься с детьми количественной математикой вот и сама подтянулась)))
http://alicepush.
ucoz.ru/index/0-4
Мне очень нравится, как один математик, весьма остроумный человек (не помню, к сожалению, его фамилии) сравнивает такой «счет цифрами» со «счетом по-японски». «Давайте встанем на место ребенка и попробуем сами учиться арифметике… но только по-японски! Итак, вот вам первые десять чисел: йти, ни, сан, си, го, року, сити, хати, ку, дзю. Интересно, сколько времени вам потребуется, чтобы хотя бы только выучить эту последовательность наизусть? Когда это наконец удастся, попробуйте считать в обратном направлении, от дзю до ити. Если же и это удается, давайте начнем вычислять. Отвечайте, желательно без запинки и по возможности не переводя, даже в уме, на русский язык: сколько будет к року прибавить сан? А от сити отнять го? А хати поделить на си? А теперь давайте решим задачу: мама купила на базаре ку яблок и дала по ни яблок каждому из си детей; сколько яблок у нее осталось? (Все ответы следует давать тоже по-японски» Если после месяца активных тренировок мы с вами освоим всю эту нелегкую науку и научимся беглому счету в пределах дзю, то нас можно будет поздравить с превосходной механической памятью.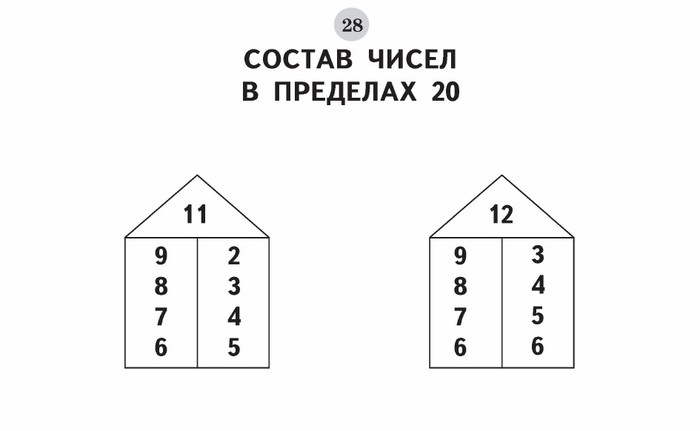
Но мы будем все так же далеки от математики.
это цитата из статьи «Количественная математика» — ссылка выше)
Вот отличная игра.
http://www.elc-russia.ru/razvivajuschaja-igra-vesy-i-cifry.html
Цифр от 1 до 5 по две,дальше по одной.Сначала расстроилась,а на практике это плюс,ребенок заменяет суммой других чисел.я ее сначала учила вешать на одну часть одну цифру-на другую две,думала она легкие примеры будет решать.А она так увлеклась по 4,5,6 цифр вешает.например на одну часть 8 и 9,а на противоположную надо и 8 и 9 разложить и если нужного числа нет ,то и его раскладывает.Вот такой скрытый потенциал у игры
А когда теоремы пойдут, он тоже каждый раз будет вычислять, что сумма квадратов катетов равна квадрату гиппотенузы, или всё-таки согласится это ЗАУЧИТЬ и просто ЗНАТЬ?
Блоки Дьенеша. Это навсегда, и проверено поколениями)
Он прекрасно считал, представляя себе в голове цифры в виде предметов сложения: 3 шара да 5 шаров — будет 8.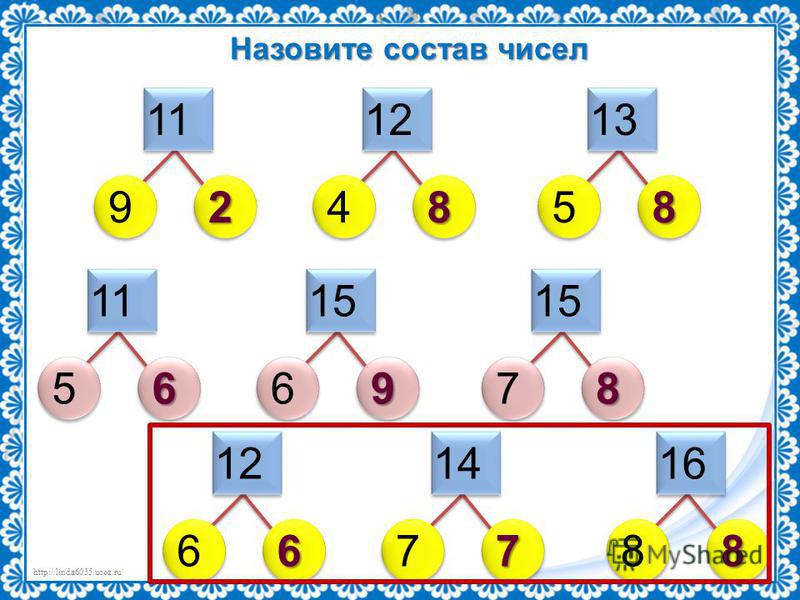
До какого-то момента это прокатывает — счет каждый раз, как в первый раз. Потом всплывает кошмар — ребенок не автоматизировал факт, что 3 да 5 = 8, а каждый раз считает по новой. Вот в этом и затык. Я такое дело со старшим сыном пережила)
Не знаю, в какой программе — как, а у нас в обоих случаях этот дидактический материл прилагался к учебнику, в первом случае прошло, как по маслу, во втором — ноль результата, учились на живых фруктах
Я не понимаю, что стоит за фразой «учить состав числа»? Это понимать, что цифра 3 состоит из 2+1 единиц чего либо и 3 шт по 1, так?
Я свою не заставляла заучивать все это. Мы в магазин играем: деньги есть 1,2,3 и 5 р а товары от 1 до 10.
Сначала она у меня покупала все без сдачи ( денег мало, не все номиналы есть одновременно), потом я у неё покупала ( у меня только 10 р — давайте сдачу!)
Такие игры подходят? потом цены выросли от 10 до 20 и т.д
Я по ребенку вижу разницу между выученным составом числа и невыученным.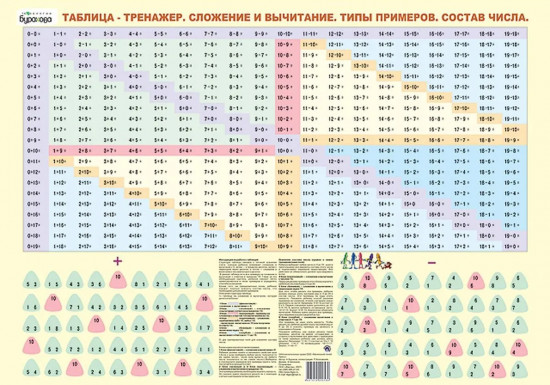
Я в детстве не учила его, просто всегда вычисляла результат. До сих пор в магазине двузначные числа в сложении вызывают проблемы, про более сложные вычисления и речи нет — калькулятор — это мое все. Сын-второклассник, просидевший весь прошлый год на дурацких примерах 5+3, 5-3 (я тихо бесилась) мгновенно выдает мне результаты там, где я только еще задумываюсь, что и к чему надо прибавить.
Учить состав числа — это доводить этот состав до такого состояния, что увидев две цифры, ребенок не задумывась выдает третью, не вычисляя ее, а просто зная, из каких двух меньших цифр состоит большая.
т.е. как таблицу умножения? но тогда 8 — это 1+7, 2+6 и еще масса комбинаций. Все учить наизусть?
Ну да. Детям под это дело несколько лет дается, вполне реально выучить.
жуть. я не выучила до 40+ лет, несмотря на все мои ученые степени и звания
+ 100000 Тоже к.т.н., победитель мат.олимпиад и т.
п.
30 лет назад такого понятия не было, а вот считали дети значительно лучше. Я специально залезла в старый учебник математики — там числа до 10 тоже раскладывали на слагаемые, но как бы между делом, в контексте решения задачи, а специально для тупого зазубривания ничего подобного не было
Все лето перед школой по столбику решали http://www.labirint.ru/books/300762/
и я к вам — мои дети сейчас на подготовке этот состав проходят, я его напрочь не понимаю (в смысле не понимаю, зачем). Что-то раньше так не учили….
ну так хорошо, что начали учить.
пока не поймет ее, зубрежка мало толку даст. ее именно понять надо, а потом отработать.
раньше тоже это было, только над ним так не сидели.
у меня ребёнок 7 лет, полгода назад чтобы сложить 6 цифр на талончике тратил минут 10-15, сейчас даю талончик через 5 секунд ответ
состав числа нужен с ним проще жить и считать быстрее продавца
Я не очень понимаю, как в такой форме можно понять «мелодику чисел».
ладно, уговорили, буду считать и учить детей так Но кстати, я и так считаю быстрее продавца
значит, этот пресловутый состав числа в голове у вас есть
ну навееерно….
Не подскажите -для айпада -как называется? Спасибо
Сын на подготовке занимается по книжке Узоровой/Нефёдовой «3000 примеров по математике». Там столько этих примеров, что хочешь-не хочешь, в автоматизм войдетНу и классические домики с цифрами вначале были.
Дочке нравится складывать числа (до 100), поэтому мы делаем это в любой удобный момент: пока заплетаемся перед садиком, пока одеваемся, идём по улице, иногда перед сном и т.д. Мне кажется, именно частая практика помогает прочувствовать состав чисел.
Когда мы начали с деткой тренировать устный счет, я ей чаще всего давала примеры со сложением и вычитанием двузначного и однозначного числа.
И терпеливо ждала, пока она скалькулирует в уме, сколько это будет. Если до этой практики ребенок периодически нашептывал себе 5+4=5..6..7..8..9!, то с двузначными был вынужден каждый раз применять знание о составе числа, потому что так проще. И то ли девочка просто более логична и сообразительна в математике, то ли этот прием помог, но устный счет встал на крыло заметно проще и быстрее, чем со старшей, с которой мы отрешивали кучу простейших примеров по узоровой-нефедовой.
И мы сочетаем счёт двузначных чисел и однозначных. А еще с десятками/пятерками отрабатываем счёт (10+10+10=30, 95+5=100, 5+5+5=15 и т.д.), тоже замечаю, что постепенно перестаёт считать в уме (5..6..7..8), а всё чаще почти сразу отвечает.
просто в определённый момент ребёнок дорастает до счёта и мозг начинает шустрее работать
Как выучить состав числа до 10 быстро
Главная » Подготовка к школе
Просмотров 1.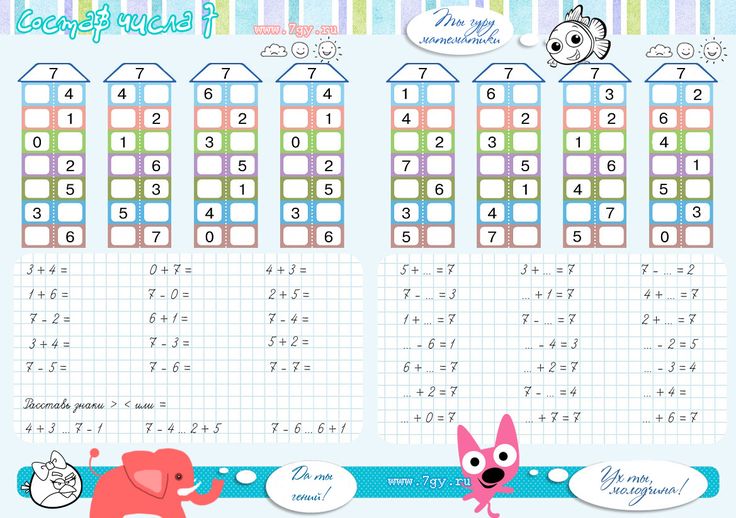
4к. Опубликовано
Обновлено
Содержание
Хорошее знание состава числа в пределах 10 – основа уверенного выполнения любых счетных операций. Поэтому родители дошкольников и особенно будущих первоклассников при подготовке к школе интересуются, как выучить состав числа до 10 быстро.
Наиболее распространенные методы
Если ввести такой запрос в поиске или задать педагогу, чаще всего порекомендуют:
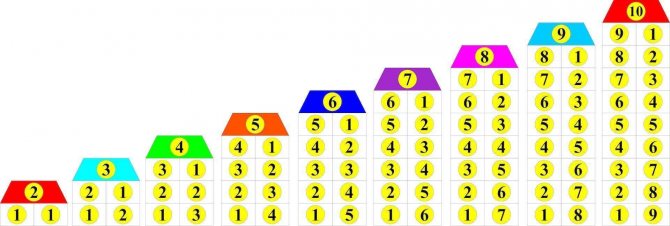
- Таблицу состава числа
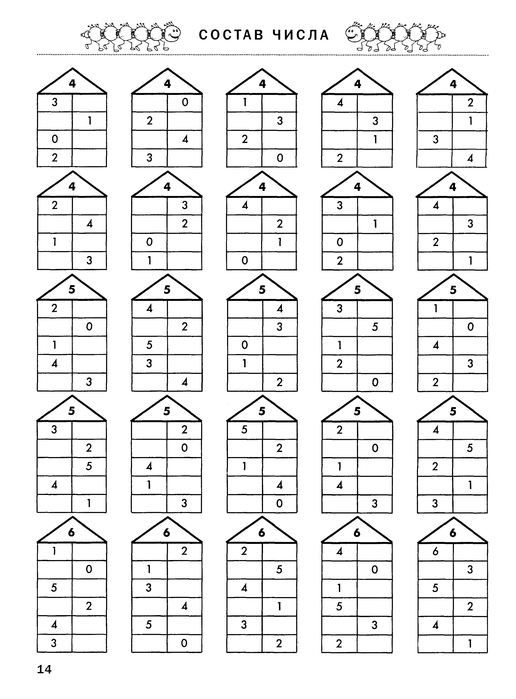
- Числовые домики
Первый способ подразумевает чисто механическое заучивание. То есть ребенок, имея перед глазами квадратную табличку, путем многократного повторения зазубривает, из каких двух компонентов состоит каждое число в пределах первого десятка.
А дальше идет отработка быстрого воспроизведения на многочисленных примерах.
Работает способ? Работает. Быстро? Сильно зависит от особенностей памяти ребенка. У кого-то механическая память развита хорошо – и он запомнит буквально за пару дней.
Но! Требуется постоянная отработка, иначе, как ребенок запомнил – так же быстро и забудет.
Второй способ имеет под собой некий игровой момент. Есть десять (или девять) домиков. Каждый имеет номер. И этажи, на каждом из которых «живут» два числа, в сумме составляющие номер дома.
В основе метода лежит то же самое механическое запоминание, слегка «подслащенное» наглядностью и игровым элементом.
Ребенок изучает домики по одному и потом путем многократного повторения запоминает состав числа, заполняя домики с пропусками или пустые.
Важно! Большинство пособий, которые обещают помочь выучить состав числа до 10 быстро, представляют собой вариации этих методов. И в основе лежит все то же механическое запоминание путем многократного повторения.
Почему эти методы плохо работают у дошкольников?
Чтобы понять, почему для дошкольников данные методы подходят плохо, надо немного углубиться в особенности дошкольного возраста. Так, процесс запоминания у дошкольника непроизвольный, равно как и внимание. При этом способ мышления развивается от наглядно-действенного (в раннем дошкольном возрасте) к наглядно образному (ближе к 7 годам).
То есть, чтобы что-то запомнить, ребенку-дошкольнику требуется сначала многократно оперировать реальными предметами, а потом – их образами. А числа – абстрактны, и потому запомнить их для ребенка очень сложно. И даже запомнив, он будет путаться, потому за числом не будет стоять образ.
Не напрасно дети, чуть что, начинают считать «на пальцах». Именно они и помогают лучше всего запомнить состав числа. И главное – это «учебное пособие» всегда с собой.
Как на самом деле быстро выучить состав числа до 10 с дошкольником?
Считать. Все подряд. Тарелки и ложки, камушки и листики. Повод находится по 20 раз в день, а сам процесс счета занимает буквально минуты.
- Идете в детский сад? Сосчитайте деревья по пути. А на обратном пути вспомните, сколько их – и считайте снова, каждый раз пытаясь отгадать, сколько осталось и проверяя себя.
- Отдыхаете на пляже? Возьмите 10 камешков. Посчитайте, перекладывая из одной кучки в другу. А потом пусть ребенок закроет глаза, а вы спрячьте в кулаке несколько камешков. Ребенок пусть сосчитает оставшиеся. И угадает, сколько спрятано. Эта игра увлекает ребенка надолго. И он готов играть снова и снова. Проверено.
- Накрываете на стол? Считайте столовые приборы, печенье, куски хлеба…
Такие ежедневные упражнения дадут отличный эффект. Конечно, за 1 день таким образом вы состав числа не выучите. А за месяц – вполне. И главное – этот способ соответствует типу мышления ребенка, формирует прочные навыки.
За числом стоит его образ, а значит, ребенок может свободно оперировать в своем воображении любым количеством).
математика
Оцените автора
Составные числа от 1 до 100
Список из составных чисел от 1 до 100 содержит все числа от 1 до 100, имеющие более двух делителей. Составные числа — это натуральные числа, которые имеют более двух делителей (1 и само число). Другими словами, если число имеет делители, отличные от 1 и самого числа, оно считается составным числом. Давайте рассмотрим все составные числа от 1 до 100 в этой статье и изучим их с помощью таблицы для лучшего понимания.
| 1. | Что такое составные числа от 1 до 100? |
| 2. | Список составных чисел от 1 до 100 |
| 3. | Нечетные составные числа от 1 до 100 |
| 4. | Четные составные числа от 1 до 100 |
5. | Составные числа от 1 до 100 Таблица |
| 6. | Часто задаваемые вопросы о составных номерах от 1 до 100 |
Что такое составные числа от 1 до 100?
Составные числа от 1 до 100 — это натуральные числа от 1 до 100, которые имеют более двух делителей (то есть имеют делители, отличные от 1 и самого числа). Всего у нас есть 74 таких составных числа от 1 до 100. Некоторые из составных чисел от 1 до 100 — это 4, 6, 8, 9, 10, 12, 14, 15 и т. д. Эти числа имеют делители, отличные от 1 и сам номер. Давайте посмотрим на множители некоторых составных чисел от 1 до 100.
- Коэффициенты 4: 1, 2, 4
- Коэффициенты 6: 1, 2, 3, 6
- Факторы 9: 1, 3, 9
- Факторы 10: 1, 2, 5, 10
Все вышеперечисленные числа имеют более двух множителей. Итак, все они являются составными числами и лежат в диапазоне от 1 до 100. Давайте пройдемся по списку составных чисел от 1 до 100 в следующем разделе.
Список составных чисел от 1 до 100
Всего 74 составных числа от 1 до 100. Список составных чисел от 1 до 100 включает 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44 , 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76 , 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99 и 100. Все остальные числа от 1 до 100, кроме это простые числа.
Нечетные составные числа от 1 до 100
Под нечетными составными числами понимаются все нечетные числа, не являющиеся простыми. Например, 63, 55, 69, и так далее. Всего существует 25 нечетных составных чисел от 1 до 100. Список нечетных составных чисел от 1 до 100 включает 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95 и 99.
Четные составные числа от 1 до 100
Четные составные числа — это четные числа, имеющие более двух делителей.
Как известно, все четные числа, кроме 2, составные. Итак, все четные числа, кроме 2 от 1 до 100, являются составными числами. Итак, список четных составных чисел от 1 до 100: 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40. , 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98 и 100.
Составные числа от 1 до 100 Таблица
Таблица составных чисел от 1 до 100 поможет вам быстро проверить, является ли число составным или простым. Если число составное, то мы можем перечислить его множители, используя метод простой факторизации. Например, 10 — составное число, а его делители — 1, 2, 5 и 10. Если число не является составным, это означает, что делителями этого числа являются 1 и само число. Например, мы можем видеть, что 29в приведенной ниже таблице отмечено как простое число, поэтому мы можем сказать, что 29 имеет 2 делителя: 1 и 29.
оттенки синего — составные числа.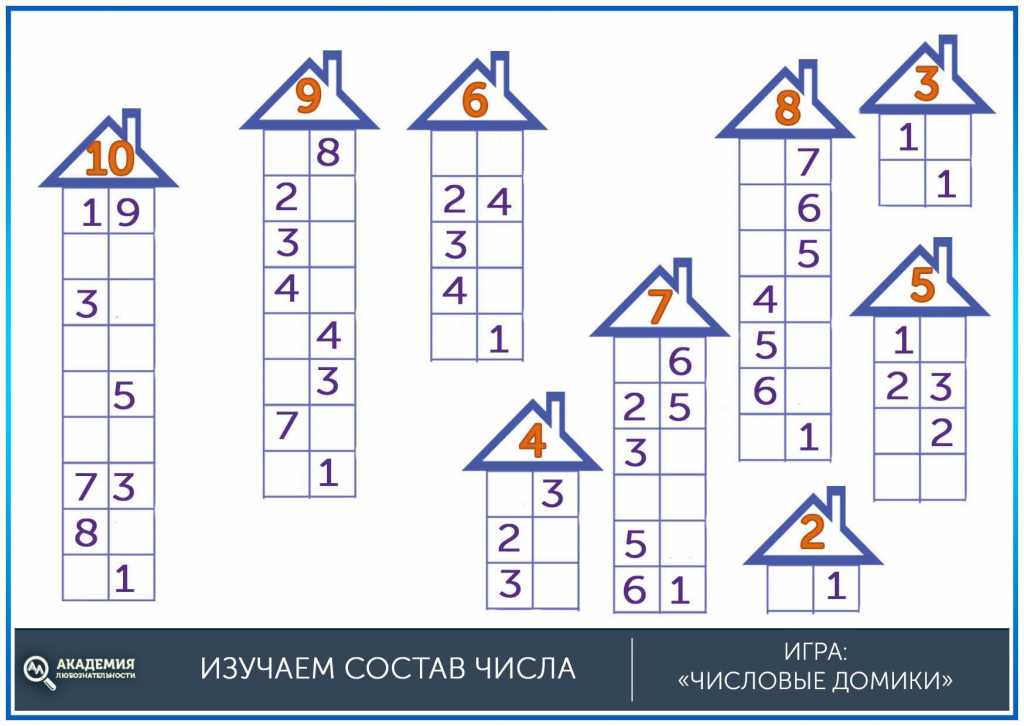
Например, 4, 6, 8, 9, 10 и так далее.
Важные примечания о составных числах от 1 до 100
- Существует 74 составных числа от 1 до 100.
- Все четные числа, кроме 2, являются составными числами от 1 до 100.
- Составные числа от 1 до 100 — это натуральные числа от 1 до 100, которые имеют более двух делителей.
☛ Статьи по теме
- Простые числа от 1 до 1000
- Составные числа от 1 до 1000
- Имена номеров от 1 до 100
- Целые числа от 1 до 100
- Натуральные числа от 1 до 100
- Целые числа
- Реальные числа
- Подсчет чисел
- Рациональные числа
Часто задаваемые вопросы о составных номерах от 1 до 100
Что такое составные числа от 1 до 100?
Составные числа от 1 до 100 — это числа, которые делятся более чем на 2 числа. Другими словами, эти числа имеют делители, отличные от 1 и самого числа.
Что такое простые и составные числа от 1 до 100?
Простые числа — это те, которые имеют только два делителя — 1 и само число. Составные числа — это те числа, которые имеют более двух делителей. Таким образом, все простые числа в диапазоне от 1 до 100 могут быть перечислены как 2, 3, 5, 7, 11, 13, 17, 19., 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. Остальные числа в диапазоне от 1 до 100 являются составными числами от 1 и 100. Например, 7 — простое число, а 77 — составное число, поскольку оно имеет более двух делителей: 1, 7, 11 и 77.
Как найти составные числа от 1 до 100?
Чтобы найти составные числа от 1 до 100, мы можем использовать метод простой факторизации. Мы можем перечислить все факторы заданного числа и посмотреть, больше двух факторов или нет. Если конкретное число имеет делители, отличные от 1 и самого себя, то это составное число.
Сколько составных чисел от 1 до 100?
Существует 74 составных числа от 1 до 100.
Среди них 4 — самое маленькое, а 100 — самое большое составное число в списке составных чисел от 1 до 100.
Какие примеры составных чисел от 1 до 100?
Примерами составных чисел от 1 до 100 являются 4, 10, 18, 22, 50, 100 и так далее.
Что такое нечетные составные числа от 1 до 100?
Список нечетных составных чисел от 1 до 100 включает 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87, 91, 93, 95 и 99.
Что такое четные составные числа от 1 до 100?
Все четные числа, кроме 2 от 1 до 100, являются составными числами. Список четных составных чисел от 1 до 100: 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42. , 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92 , 94, 96, 98 и 100.
Простые числа: что это такое и как их найти
В сегодняшней статье вы узнаете разницу между простыми и составными числами. Кроме того, мы покажем вам несколько примеров, чтобы помочь вам лучше понять их.
Что такое простые числа?
Простые числа — это числа, которые делятся только на себя и на 1, другими словами, если мы попытаемся разделить их на другое число, результатом будет не целое число. Итак, если вы разделите число на что-либо, кроме единицы или самого себя, вы получите остаток, отличный от нуля.
Простые числа до 100
Мы создадим таблицу со всеми простыми числами до 100. составные числа, так как они будут делиться на 2. Вычеркиваем в таблице все числа, кратные 2.
Следующее простое число — 3, поэтому мы можем вычеркнуть все числа, кратные 3, поскольку они будут составными числами.
После 3 следует простое число 5, поэтому мы вычеркиваем все числа, кратные 5.
Затем у нас есть простое число 7, и мы вычеркиваем все числа, кратные 7.
Следующее простое число — 11, поэтому мы вычеркиваем все числа, кратные 11, то есть 22, 33, 44, 55, 66. , 77, 88 и 99. Все эти числа уже были вычеркнуты, поэтому мы закончили вычеркивать все составные числа в нашей таблице.
Это наш список простых чисел от 1 до 100. Вам не нужно запоминать их, но было бы лучше, если бы вы запомнили меньшие числа, такие как 2, 3, 5, 7, 11, 13.
Сколько существует простых чисел?
Греческий математик Эратосфен (3 век до н.э.) разработал быстрый способ нахождения всех простых чисел до любого заданного числа. Это процесс , называемый Решетом Эратосфена.
Обратите внимание, что между 1 и 100 есть 25 простых чисел. Сколько всего простых чисел? Мы с давних времен знаем, что — это бесконечное количество , поэтому невозможно перечислить их все. Поскольку Евклид, который первым показал, что их бесконечное количество в 4 веке до н.э., не знал концепция бесконечности он сказал ”простые числа больше, чем любое их фиксированное множество” это означает, что если вы представите 100, их будет больше, а если вы представите один миллион, то их будет еще больше.
Простые числа от 100 до 1000
Давайте посмотрим на простые числа от 100 до 1000.
К сожалению, мы не можем показать их все, так как вы знаете, что их бесконечное количество. 😉
Примеры простых чисел
Чтобы помочь вам лучше понять простые числа, мы объясним одно упражнение.
У Сары есть 6 конфет, которыми она хочет поделиться, но она не знает, со сколькими людьми она может ими поделиться, чтобы все получили одинаковое количество и ни одного лишнего. Сколькими способами она может это сделать?
Вот Сара и ее 6 конфет:
Как их разделить?
Первый и самый простой способ — дать их одному человеку, другими словами, разделить на 1. Таким образом, у этого человека будет 6 конфет.
Следующая возможность — разделить их между 2 людьми. Так как 6 разделить на 2 равно 3, то каждый получит по 3 конфеты!
Мы собираемся продолжить со следующего числа, 3. Если мы разделим 6 конфет между 3 людьми, это также будет точное деление, и каждый получит по 2 конфеты:
Продолжим с цифрами.
У нас нет точного деления на 4 и 5, но есть на 6.
Поскольку 6 разделить на 6 равно 1, мы можем дать 6 детям по 1 конфете.
Мы собираемся собрать некоторую информацию. У нас есть 6 конфет, которые мы можем разделить (с точным разделением) между 1, 2, 3 и 6 человек . Другими словами, мы можем разделить число 6 и получить 0 в остатке при делении его на 1, 2, 3 и 6. Эти числа известны как делители 6 .
Попробуем с другим номером, например 7.
Теперь у Сары есть 7 конфет, и она хочет ими поделиться, но не знает, со сколькими людьми она может ими поделиться, чтобы все получили одинаковое количество и ни одного лишнего. Сколькими способами она может это сделать?
Генри так повезло! Он получил все конфеты!
Есть ли другие способы сделать это? Мы не можем разделить 7 на 2, 3, 4, 5 или 6, … но 7 можно!
Сара может разделить конфеты между 7 людьми, дав каждому по одной конфете :
Итак, 7 можно разделить только на 1 и 7, его единственные делители — 1 и 7.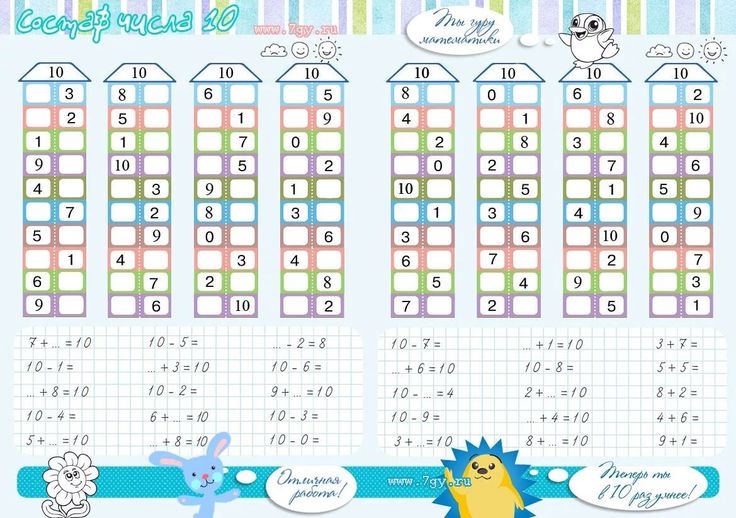
Это типы чисел мы называем простыми числами .
Есть ли еще простые числа? Конечно! Поищем еще:
- 4? Нет! Поскольку его делители равны 1, , 2, и 4, .
- 5? Да! Потому что его делители равны 1 и 5.
- 8? Нет! Потому что его делители равны 1, , 2, 4, и 8. .
Короче говоря, число является простым, если оно имеет только 2 делителя: 1 и само себя.
Теперь вы можете искать множество простых чисел!
Как найти простые числа
Будьте внимательны! Мы собираемся дать вам трюк, чтобы узнать, является ли число простым или нет, без необходимости искать его делители, но более увлекательным способом, который дает нам делители (если они есть).
Давайте выберем случайное число, например 16.
Чтобы проверить, простое это число или нет, мы будем использовать таблицу, которая очень похожа на карты Монтессори для умножения.
И мы получим столько шаров, сколько мы выбрали. В данном случае 16 шаров.
Когда у нас есть стол и шары, мы должны разместить их на столе, начиная с первой клетки, пытаясь сформировать прямоугольник. Числа, составляющие стороны прямоугольника, являются делителями этого числа.
Если нам удастся сформировать прямоугольник только с тем же числом, которое мы используем, и числом 1, это будет простое число .
Например, в этом случае мы размещаем 8 шаров в первом ряду и еще 8 во втором. Как видите, мы образовали прямоугольник и видим, что 8, как и 2, являются делителями числа 16. Следовательно, 16 не является простым числом, потому что, как известно, простых числа — это те, которые делятся только сами по себе и 1.
Можно попробовать с другим числом, например 7.
Как мы видим, мы не могли сделать полный прямоугольник, мы потеряли бы шар. Поскольку мы не можем составить прямоугольник, мы можем сказать, что число 7 не имеет других делителей, кроме самого себя и 1, как мы можем видеть на следующем изображении.
Следовательно, 7 — простое число!
Попробуйте любой другой номер, вы увидите, как это работает! Вы можете использовать графическую бумагу и искать прямоугольники, используя это количество квадратов.
Почему важны простые числа?
Простые числа являются ключом к арифметике, ниже вы увидите пример, демонстрирующий их важность не только в математике, но и в природе.
Что мы имеем в виду, когда говорим, что простые числа являются ключом к арифметике?
Это потому, что любое число состоит из уникального произведения, состоящего из ряда этих чисел.
Считается, что они изучались около 20 000 лет, когда один из наших предков записал ряд простых чисел (11, 13, 17 и 19).) на кости Ишанго. Как будто это было совпадением, было подтверждено, что древние египтяне работали с ними 4000 лет назад.
Кроме того, природа очень хорошо их знает, и некоторые виды смогли обнаружить их в ходе своей эволюции и использовать для выживания.
Я имею в виду несколько видов цикад, таких как Magicicada septendecium , обитающий в Северной Америке . Этот вид цикад установил свой цикл размножения около 13 или 17 лет, а не 12, 14, 15, 16 или 18 — именно 13 или 17. Это позволяет им избегать хищников, которые также имеют периодические репродуктивные циклы; представьте себе хищника с 4-летний репродуктивный цикл .
Если бы жизненный цикл цикады составлял 12 или 14 лет, то он очень часто совпадал бы с хищником, гораздо чаще, чем если бы он составлял 13 или 17 лет. Ровно 2 раза в 100 лет, иначе они совпали бы в 11 циклах, что поставило бы под угрозу развитие вида.
Безопасность электронной связи также основана на простых числах. Каждое зашифрованное сообщение, отправленное через Интернет (сети обмена сообщениями, покупки или электронный банкинг), имеет большое количество связанных с ним номеров, и очень трудно понять, где оно является основным, а где нет.
У получателя есть один из его делителей, поэтому они могут его расшифровать. Таким образом, наличие простых чисел имеет решающее значение для нашей конфиденциальности при электронном общении.
Что такое составные числа?
Составные числа — это числа, которые делятся на 1 и на себя, а также на другие числа.
Мы рассмотрим пример простого числа и составного числа.
11 можно записать как умножение 1 x 11, но нельзя записать как любое другое умножение натуральных чисел. У него есть только делители 1 и 11, поэтому это простое число .
12 можно записать как умножение 1 х 12, 3 х 4 и 2 х 6. Поскольку 12 делится на большее количество чисел, чем 1 и само себя, 12 равно 9.0003 составной номер.
Является ли 1 простым числом?
Есть люди, которые так считают, потому что они говорят, что 1 можно разделить только на 1 и на себя, но в математике число 1 было отброшено как простое число, потому что оно имеет только один делитель.
Фактически, критерий «натуральное число является простым, если оно имеет ровно два положительных делителя» используется для исключения единицы из списка простых чисел. Это не потому, что мы придирчивы к этому, но если бы число один считалось простым, то о многих математических свойствах пришлось бы говорить по-другому.
Итак, 1 — составное число?
Ну, это тоже не составное, так как его нельзя представить как произведение простых чисел. Число 1 не является простым или составным. И прежде чем вы спросите, ноль также не является простым или составным, но это потому, что все соображения, которые мы объясняли для положительных чисел, то есть больше нуля.
Делители числа
Делитель числа — это значение, которое делит число на точные части, другими словами, имеет остаток 0,
В качестве примера мы собираемся вычислить делители 24.
Начнем деление с наименьших чисел, начиная с 1.
- 24 / 1 = 24. И 1, и 24 являются делителями.
- 24/2 = 12. Итак, 2 и 12 — делители.
- 24/3 = 8. Значит, 3 и 8 — делители.
- 24/4 = 6. Итак, 4 и 6 — делители.
- 24 / 5 = 4. Это не точное деление, остаток равен 4, поэтому 5 не является делителем.
Следующее число 6, но поскольку мы уже знаем, что 6 является делителем 24, мы закончили вычисление делителей 24.
Видео: Факторизация и простые числа
Если вы хотите узнать больше о простых и составных числах , посмотрите следующее видео. Вы также изучите концепцию факторинга, используя таблицу Монтессори.
Это видео является одним из наших интерактивных учебных пособий, и хотя оно не является интерактивным, вы все равно можете смотреть его столько раз, сколько вам нужно, и делиться им с друзьями. Если вы хотите получить доступ к нашим интерактивным руководствам, зарегистрируйтесь в Smartick! Онлайн-метод, помогающий детям в возрасте от 4 до 14 лет изучать и практиковать математику.