Числа от 10 до 20
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
«Моя математика» 1 класс
Урок 84
Тема урока: «Числа от 10 до 20»
Советы учителю.
Презентация к уроку составлена на основе заданий, расположенных в учебнике.
Рекомендую открыть учебник на странице с данным уроком, прочитать задания и
просмотреть их в данной презентации в режиме демонстрации.
Внимание!
Некоторые задания можно выполнять интерактивно.
сравнить или вставить пропущенные числа. Для этого презентацию надо
перевести в режим редактирования.
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
Задание из « Методических рекомендаций»
10 пуговиц
10 палочек
один десяток
10 яиц
один десяток
десять единиц один десяток
! Так мы будем теперь
обозначать один десяток.
один десяток
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
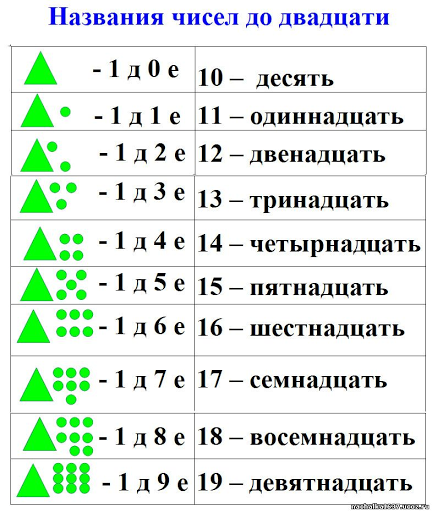
1. Познакомься с новыми числами. Для этого прочитай и
объясни, что написано в каждой строке таблицы.
?
Разряд
десятков
Разряд
единиц
Число
Название
1 0
1 д. 0 ед. = 10
десять
1 1
1 д. 1 ед. = 10 + 1 = 11
одиннадцать
1 2
1 д. 2 ед. = 10 + 2 = 12
двенадцать
1 3
1 д. 3 ед. = 10 + 3 = 13
тринадцать
1 4
1 д. 4 ед. = 10 + 4 = 14
четырнадцать
1 5
1 д. 5 ед. = 10 + 5 = 15
пятнадцать
1 6
1 д. 6 ед. = 10 + 6 = 16
шестнадцать
1 7
1 д.
 7 ед. = 10 + 7 = 17
7 ед. = 10 + 7 = 17семнадцать
1 8
1 д. 8 ед. = 10 + 8 = 18
восемнадцать
1 9
2 0
девятнадцать
1 д. 9 ед. = 10 + 9 = 19
2 д. 0 ед. = 1 д. + 1 д. = 2 д. = 20 двадцать
Урок 84. Числа от 10 до 20
1
11
12
1
13
1
14
1
15
1
МАТЕМАТИКА
16
1
17
1
18
1
19
1
ДВУЗНАЧНЫЕ ЧИСЛА
? Сколько знаков в записи каждого числа?
Как можно
назвать такие числа?
! Цифра слева показывает число десятков.
! Цифра справа показывает число единиц.
2
20
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
3. Вова дал задание птицам установить порядок в числовом
ряду. Помоги им выполнить задание Вовы.
10
14
16
Назови
последующее и предыдущее число, для чисел
Внимание!
Данное задание можно выполнить интерактивно. Для этого презентацию надо
перевести в режим редактирования.
20
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
3.
 Вова дал задание птицам установить порядок в числовом
Вова дал задание птицам установить порядок в числовомряду. Помоги им выполнить задание Вовы.
10
14
16
20
Назови
последующее и предыдущее число, для чисел
обозначенных красной точкой.
ПРОВЕРЬ!
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
4. Какие слагаемые здесь пропущены? Преврати записи
Лены в верные равенства.
12 = 10 + 2
14 = 10 + 4
17 = 10 + 7
Внимание!
Данное задание можно выполнить интерактивно. Для этого презентацию надо
перевести в режим редактирования.
0
1
2
3
4
5
6
7
8
9
10
Урок 84. Числа от 10 до 20
МАТЕМАТИКА
4. Какие слагаемые здесь пропущены? Преврати записи
Лены в верные равенства.
12 = 10 + 2
14 = 10 + 4
! 12, 14 и 17 – двузначные числа.
17 = 10 + 7
Они
записаны в виде
ПРОВЕРЬ!
суммы разрядных слагаемых.
14
12
10
0
1
10
2
2
3
4
5
6
17
10
4
7
8
9
10
7
МАТЕМАТИКА
Спасибо!
English Русский Правила
Урок 4.
 Изучение чисел
Изучение чиселЛюбое обучение счету и числам всегда должно начинаться с усвоения элементарных количественных понятий, таких как «много», «мало», «больше», «меньше», «поровну» и т.п. И дети легко уясняют их еще в ясельном возрасте. Ваша основная родительская задача – просто помочь им в этом. Формировать же навыки количественного сравнения можно в процессе каждодневной жизни. Так, вместе с малышом можно сравнивать количество конфет или бутербродов, квартир на площадках и ступенек на лесенках, косичек и бантиков у девчушек и т.д. Однако приниматься сразу за большие группы предметов не нужно, ведь все должно начинаться с малого.
После освоения количественных понятий наступает пора знакомства малыша с миром чисел. Как вам уже известно, происходить это должно в интересной и увлекательной для ребенка форме, для чего и следует применять методы, рассмотренные нами в первых уроках.
Рассказывать крохе о числах нужно, не спеша и не стремясь «загрузить» в дитя как можно больше информации.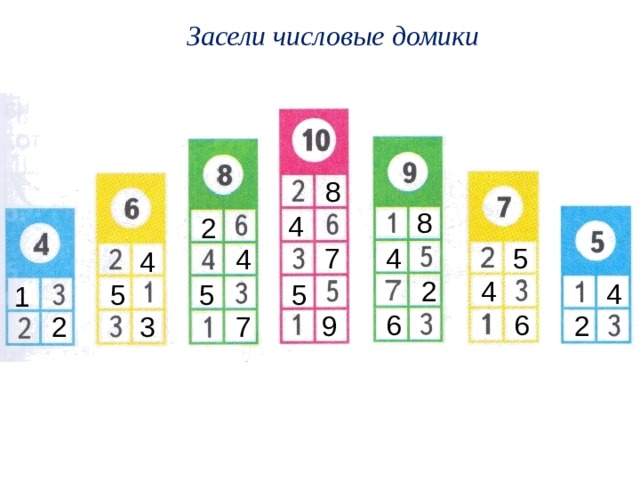 Для начала осваивайте числа первого десятка, чтобы они хорошенько запомнились и усвоились, а также, чтобы была уяснена их очередность. Делать все это нужно ненавязчиво, занимаясь обычными домашними делами. Считайте, сколько людей находится дома, сколько чашек на столе, сколько окон в квартире, сколько пуговиц на куртке и т.д.
Для начала осваивайте числа первого десятка, чтобы они хорошенько запомнились и усвоились, а также, чтобы была уяснена их очередность. Делать все это нужно ненавязчиво, занимаясь обычными домашними делами. Считайте, сколько людей находится дома, сколько чашек на столе, сколько окон в квартире, сколько пуговиц на куртке и т.д.
Когда знакомство с миром чисел будет завершено, можно приступать к разбору состава числа и решению простых задач.
Содержание:
- Как познакомить ребенка с составом числа
- Дополнительные рекомендации и советы
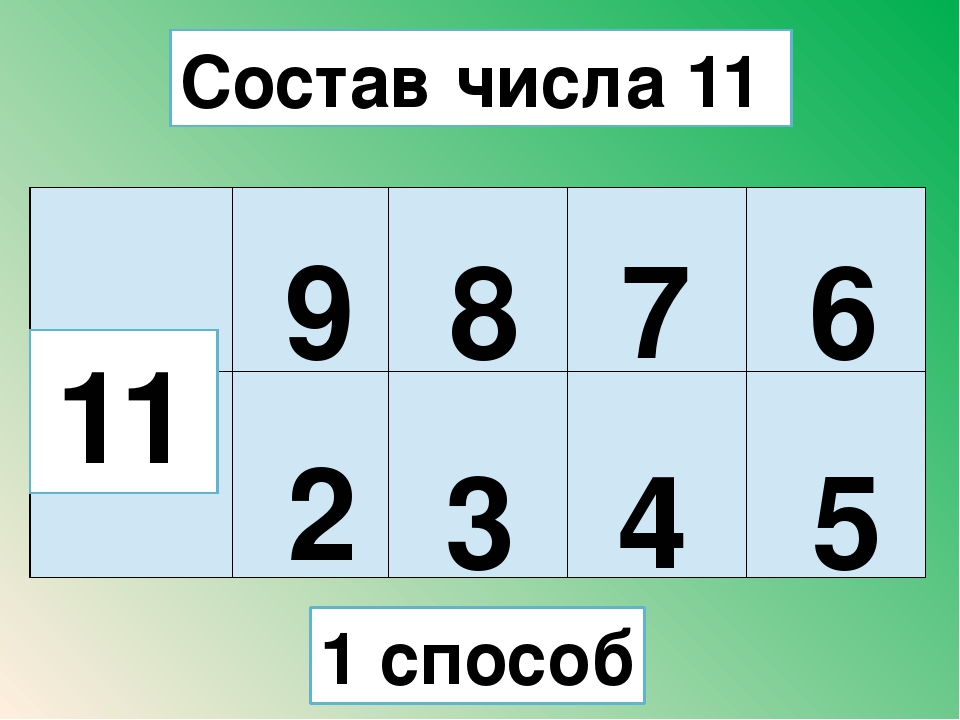
Как познакомить ребенка с составом числа
Как известно, все числа, помимо единицы, можно раскладывать на другие числа. Например, двойку можно разложить на две единицы, тройку – не единицу и двойку и т.д. Под этим и следует понимать состав числа, и объяснять его нужно в тот момент, когда ребенок освоил счет по порядку.
Дело в том, что разбирая числа на составляющие, малыш будет сразу же осваивать навык решения простых примеров. К примеру, уяснив для себя, что число «3» – это не только « 1», 1» и «1», но также «2» и «1», он автоматически поймет, что если сложить двойку и единицу, получится три.
К примеру, уяснив для себя, что число «3» – это не только « 1», 1» и «1», но также «2» и «1», он автоматически поймет, что если сложить двойку и единицу, получится три.
Когда учите складывать своего малютку, следите, чтобы он не складывал разнородные объекты.
Помимо прочего, научить ребенка составу числа можно и при помощи специальных методов. Об одном из них мы расскажем ниже.
Для реализации метода вам нужно подготовить:
- Карточки на состав числа*
- Большое количество кубиков, шариков или других одинаковых объектов
- Шашки разного цвета (могут подойти и одинаковые разноцветные пуговицы)
*Пример карточки на состав числа
Как только дидактический материал будет готов, можно начинать занятия. Алгоритм таков:
- Для первого занятия подготовьте подобранные ранее объекты счета. Размер и внешний вид не имеют никакого значения. Главное, чтобы объекты относились к одной категории. Начинать занятие нужно с числа «2».
 Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.
Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами. - Возьмите другие объекты и повторите задание с ними. Юный счетовод должен уяснить, что число «2» всегда будет состоять из двух единиц, независимо от того, какими он манипулирует объектами.
- Когда станет понятно, что число «2» освоено, незамедлительно начинайте работать с числом «3». Состав этого числа может быть представлен уже тремя вариантами: «1 + 1 +1», «1 + 2» и «2 + 1». Раскладывайте перед крохой объекты в самых разных вариациях, но с одной особенностью: если рассматриваете вариант сложения трех единиц, путь каждый предмет лежит на одинаковом расстоянии друг от друга; если рассматриваете вариант сложения единицы и двойки, то два предмета должны лежать рядом, а один – на расстоянии от них.
 Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам. - Занятия с шашками выполняются параллельно занятиям с игрушками, либо отдельно от них. Задача проста: попросите ребенка положить перед собой (или на доску для шашек) четыре одинаковых шашки. Потом спросите, сколько будет шашек, если сложить две черных и две белых? Смысл в том, чтобы показать, что одно и то же число может быть представлено несколькими вариантами (в данном случае – независимо от цвета).
- Перед работой с карточками на состав числа их нужно приобрести или изготовить самостоятельно. Такие карточки бывают разных модификаций, и будет хорошо, если у вас тоже будет два варианта. Первый комплект состоит из разрезанных на две половинки карточек. На одной половинке изображается один объект, а на другой – 1, 2, 3 – 9 аналогичных объектов (кстати, половинки могут соединяться знаком «+», но полезно иметь и отдельный знак «+», а также отдельный знак «-»).
 Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами. - Продемонстрируйте малышу карточку, например, с пятью объектами. Попросите подобрать остальные изображения так, чтобы они составляли число пять. Здесь еще удобно меняться ролями, т.е. время от времени просите ребенка давать задания и вам, а вы не ленитесь их выполнять, причем иногда стоит специально ошибаться, чтобы малыш контролировал ваши действия и указывал на то, что вы делаете неправильно.
- Точно такое же задание можно выполнять с использованием карточек с цифрами. К примеру, вы можете показать ребенку карточку с цифрой «7», а он пусть сложит остальные карточки так, чтобы в разных вариантах получить это же число. Впоследствии переходите к более сложным числам (более десяти), объясняя малышу, что чем больше число, тем больше есть вариантов его составления.

Проводить занятия нужно систематически, но не стоит сильно усердствовать. Дважды в день по 20-25 минут будет более чем достаточно. Уже через 1,5-2 месяца таких занятий ваше чадо в достаточной мере освоит состав числа и научится выполнять основные математические операции. Но чтобы повысить шансы на успех, в дополнение к предложенному методу вы можете использовать и составленные нами рекомендации.
Дополнительные рекомендации и советы
Знакомя ребенка с составом числа (и обучая счету вообще), старайтесь обращать как можно больше внимания на поведение своего чада. Наиболее частыми явлениями во время занятий являются отвлекаемость и невнимательность. Практически всегда это свидетельствует о том, что малыш потерял интерес к процессу и новая информация им уже не воспринимается.
Чтобы исправить положение дел, совсем необязательно прекращать домашний урок. Иногда бывает полезно просто повторить то, что уже было изучено. Вспомнив знакомый материал, выполнив несколько заданий и убедившись, что у него все получается, ребенок снова заинтересуется и будет готов к усвоению новых знаний.
Не гонитесь за результатом – обучайте свое чадо в умеренном темпе и давайте информацию постепенно. Вопреки ошибочному мнению, это вовсе не тормозит развитие маленького ученика, ведь небольшой объем знаний закрепляется прочнее, а это значит, что и переход к новым темам не за горами.
Арифметические задачи становятся для дошколят гораздо интереснее, если использовать в них игрушки, игры, монетки, разноцветные счетные палочки. Сначала считайте их сами, произнося цифры вслух, а затем просите ребенка повторить за вами.
Будет просто супер, если вы сделаете упражнения как можно более зрелищными. Можно выстраивать дорожки из монеток, делать городки и пирамидки из кубиков, разнообразными способами раскладывать карточки и картинки. Добавляя и убирая объекты, вы будете учить свое дитя прямому и обратному счету, сложению и вычитанию, соотнесению чисел и количества. Приобретя такие навыки еще в дошкольном возрасте, а также разобравшись с составом числа, ребенок будет намного легче справляться со школьными заданиями по математике и быстро выучит таблицу умножения (о том, как сделать это еще до школы, мы с вами тоже поговорим в одном из уроков).
Регулярные занятия прекрасно развивают логическое, пространственное, предметное и абстрактно-образное мышление, благодаря чему уже в 3-4 года маленький ученик сможет показывать хорошие результаты.
Тема освоения состава числа и простейших чисел, как вы заметили, совсем небольшая и несложная. Несколько труднее научить ребенка считать до 20 и до 100. В шестом уроке мы познакомим вас с эффективными принципами обучения детей счету и предложим несколько действенных методик, позволяющих научить детей считать до 10, до 20 и до 100, а также производить вычисления столбиком.
Проверьте свои знания
Если вы хотите проверить свои знания по теме данного урока, можете пройти небольшой тест, состоящий из нескольких вопросов. В каждом вопросе правильным может быть только 1 вариант. После выбора вами одного из вариантов, система автоматически переходит к следующему вопросу. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что вопросы каждый раз разные, а варианты перемешиваются.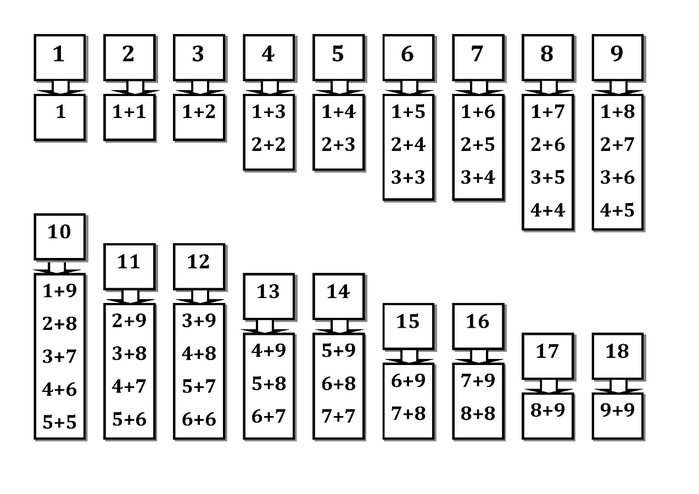
Cтатистика На весь экран
Кирилл
← 3 Подготовка к счету5 Принципы обучения счету →
Как композиторы от Моцарта до Баха создавали свою музыку | Классическая музыка
Какое следующее число в этой последовательности? 5, 10, 20, 30, 36…? А следующий в этом? 640, 231, 100, 91…?
Если вы знаете своего Моцарта, то вы идентифицируете 43 как число, которое идет после 36 в первой последовательности. Это вступительные строки «Женитьбы Фигаро», которые Фигаро поет, измеряя комнату, которую он разделит с Сюзанной, когда они поженятся. Это любопытный набор чисел, которые при сложении дают 144, или 12 в квадрате: возможно, совпадение, а может быть, числовое представление надвигающегося союза Фигаро и его невесты Сюзанны.
Вторая последовательность продолжается цифрой 1003, числом женских завоеваний Дона Жуана в Испании. Другие номера являются частью знаменитой арии Каталога, которую исполняет Лепорелло, слуга Дон Жуана, в которую входят другие его завоевания: 640 в Италии, 231 в Германии, 100 во Франции, 91 в Турции.
Моцарт любил числа. Иоганн Андреас Шахтнер, придворный трубач и друг семьи Моцарта, писал о молодом Вольфганге: «Когда он решал задачи, стол, стул, стены и даже пол были покрыты мелом».
Во взрослом возрасте одержимость чисел Моцарта не уменьшилась. Он разбрасывал числа в своих письмах семье и друзьям. Его семья использовала секретный код, чтобы скрыть политически чувствительные комментарии от глаз цензоров. Но он также использовал числа в более интимных разговорах. Его поцелуи неизменно выдавались единицами из 1000, хотя иногда он выбирал более интересный набор чисел, чтобы осыпать своего корреспондента.
Любопытная цепочка цифр 1095060437082 появляется в письме его жене Констанце. Одно из предложенных расшифровок этой последовательности предполагает, что мы добавляем 10+9+50+60+43+70+82, чтобы получить 324, то есть 18 в квадрате, опять же, как в начале «Фигаро», выражая связь любви между Моцартом и Констанцей. . В другом письме он подписался как «Друг Дома чисел»; в то время как Констанце рассказала биографу после смерти Моцарта о «своей любви к арифметике и алгебре».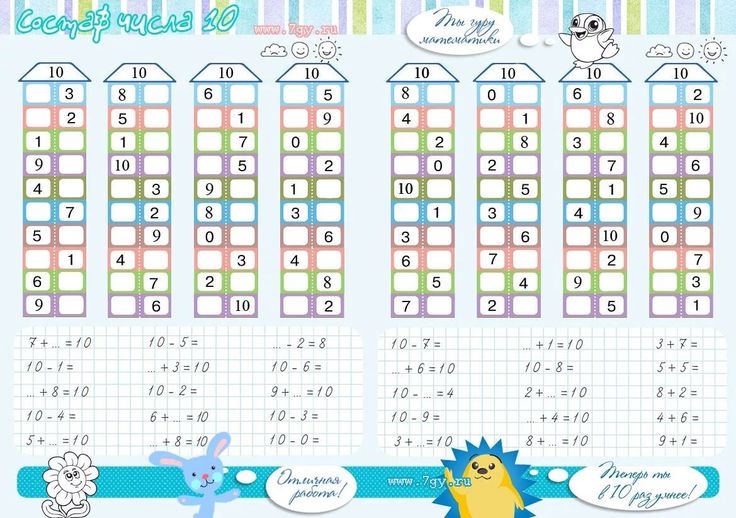
Моцарт — не единственный композитор, очарованный музыкой, числами и кодами. Имя Баха представляет собой серию музыкальных нот, которые Бах часто использует в произведениях, как будто он музыкально подписывает свое произведение. Другие композиторы эпохи барокко использовали каббалистический код, который превращал буквы в цифры, которые затем можно было использовать в музыкальной композиции, чтобы скрыть слова. Например, заменив каждую букву в алфавите соответствующей цифрой, имя Баха переводится как 2+1+3+8=14. Некоторые комментаторы пытались определить одержимость числом 14, пронизывающую творчество и жизнь Баха. Очевидно, когда его попросили присоединиться к Обществу музыкальных наук Мизлера, он отложил это до 1747 года, просто чтобы убедиться, что он может стать 14-м членом, присоединившимся к нему.
Шуман тоже был заядлым пользователем музыкальных криптограмм. Совсем недавно Альбан Берг считал 23 своим фирменным номером, как футболиста, которого идентифицируют по номеру его футболки.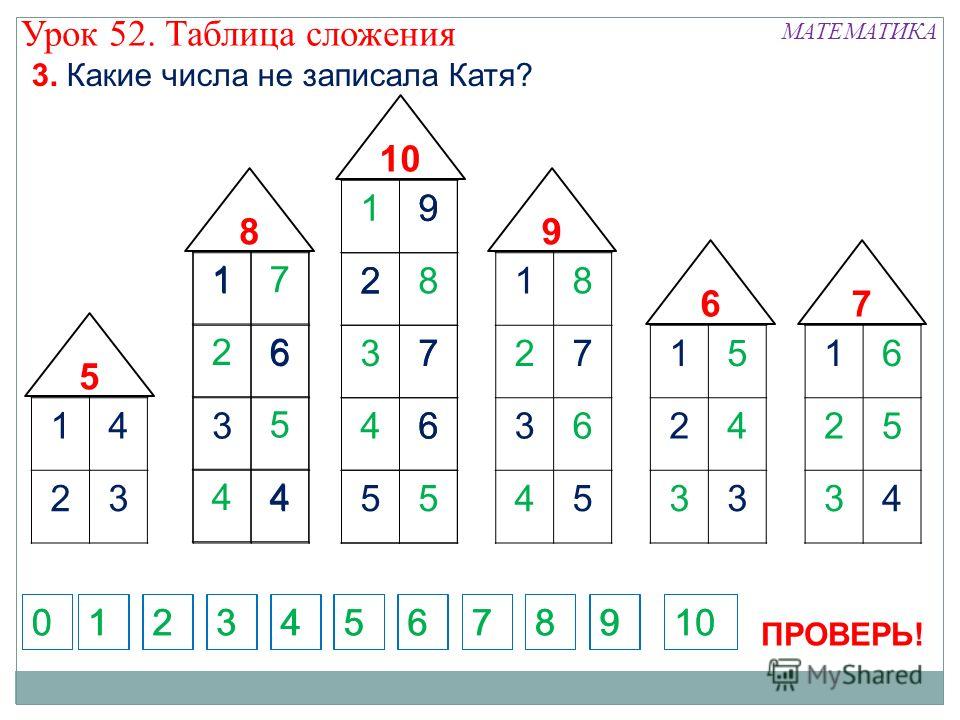 Например, Лирическая сюита состоит из последовательности фраз из 23 тактов. В произведение встроено музыкальное представление о любовной связи Берга в то время. Его возлюбленная была обозначена последовательностью из 10 тактов, которую он переплел со своей собственной подписью, 23, используя комбинацию математики и музыки, чтобы исполнить серенаду своему роману.
Например, Лирическая сюита состоит из последовательности фраз из 23 тактов. В произведение встроено музыкальное представление о любовной связи Берга в то время. Его возлюбленная была обозначена последовательностью из 10 тактов, которую он переплел со своей собственной подписью, 23, используя комбинацию математики и музыки, чтобы исполнить серенаду своему роману.
Но это, вероятно, последняя опера Моцарта, «Волшебная флейта», произведение, наиболее насыщенное символикой и числовыми образами. Опера полна масонских символов, которые, в свою очередь, основаны на математике — Моцарта семь лет назад приняли в Венскую ложу милосердия. Число три, например, очень значимо в масонской практике. Три стука в дверь ложи, которые являются частью церемонии инициации нового масона, снова и снова звучат на протяжении всей оперы. Как заявил коллега-каменщик Гёте: «Толпа должна получать удовольствие от созерцания этого зрелища: в то же время его высокое значение не ускользнет от посвященных».
Помимо ритмической последовательности из трех нот, число три пронизывает оперу множеством способов. Большая часть масонской музыки Моцарта написана ми-бемоль мажор, тональность с тремя бемолями, хотя это может быть больше связано с тем, что тональность лучше всего подходит для духовых инструментов, которые использовал Моцарт. Многие персонажи идут по трое: три дамы, служащие Королеве Ночи, три мальчика. Трехчастная гармония изобилует.
Большая часть масонской музыки Моцарта написана ми-бемоль мажор, тональность с тремя бемолями, хотя это может быть больше связано с тем, что тональность лучше всего подходит для духовых инструментов, которые использовал Моцарт. Многие персонажи идут по трое: три дамы, служащие Королеве Ночи, три мальчика. Трехчастная гармония изобилует.
В опере тоже полно пар. День и ночь, огонь и вода, Осирис и Исида, золото и серебро, солнце и луна. Роль играет число пять, еще одно важное число для масонов, учитывая их выбор символа пентаграммы или пятиконечной звезды. Трио уступают место квинтетам, а не квартетам. И в конечном счете сила Зарастро заключена в мистической печати семи кругов солнца.
Для Моцарта «Волшебная флейта» также является выражением его веры в изменяющийся порядок не только в политическом, но и в музыкальном плане. Премьера произведения состоялась в Вене в 1791 году, через два года после революции, охватившей улицы Парижа. Масонский орден подвергся репрессиям, потому что власти опасались просвещенных идей, продвигаемых этим тайным обществом. Этот переход от античности к просвещению запечатлен в музыке. Богато украшенная музыка Царицы ночи уступает место новому звучанию, которое, как надеялся Моцарт, станет его наследием.
Этот переход от античности к просвещению запечатлен в музыке. Богато украшенная музыка Царицы ночи уступает место новому звучанию, которое, как надеялся Моцарт, станет его наследием.
Эта статья была изменена 5 апреля 2013 года. В оригинале 1001 было указано как количество женских завоеваний Дон Жуана в Испании. Должно было быть 1003, и это было исправлено.
Составление и разложение чисел для сложения и вычитания
Трудно ли вашим ученикам составлять и разлагать числа при сложении и вычитании ? Моим ученикам трудно разбить число на части и использовать его части для вычислений. Этот тип чувства числа требует тонны практики, и это тяжелая работа!
Старые крылатые фразы, такие как заимствование и перенос, больше не используются в Common Core. Они не имеют никакого отношения к математическому мышлению, поэтому я думаю, что хорошо, что мы их не используем. Точно так же интересно запоминать запоминающиеся фразы и стихи, но мне интересно, насколько студенты понимают и могут объяснить, что происходит в процессе.
Моя цель состоит в том, чтобы мои ученики поняли, как работают числа , как числа можно разбивать на части и складывать вместе разными способами . Я хочу, чтобы они гибко думали о числах и применяли эту гибкость к сложению и вычитанию.
В начале года мы начали с разложения и составления меньших чисел, чтобы получить 10. Используя факты +8 и +9, мы рассмотрели, как составление 10 может помочь нам решить проблемы.
Хотя я дал студентам стратегию, им потребовалось много практики, чтобы помочь им понять преимущества ее использования, а не считать на пальцах. Я создал пакет математических станций, посвященных использованию 10 для сложения (+9).& +8). С этого началось наше путешествие по разложению чисел.
Позже в том же году, когда мы перешли к сложению больших чисел, мы снова пересмотрели стратегию составления 10 для сложения чисел, но работали над сложением десятков и сложением 100.
Одна из стратегий, которая хорошо сработала для учащихся, заключалась в том, чтобы они рисовали палочки, обозначающие количество десятков в каждом числе, а затем считали и вычеркивали каждую палочку по мере подсчета. Когда ученик доходил до 100, он останавливался и писал 100, затем начинал заново и считал оставшиеся палочки.
Когда ученик доходил до 100, он останавливался и писал 100, затем начинал заново и считал оставшиеся палочки.
Благодаря этому упражнению учащиеся начали понимать «понятные числа» и научились использовать 100 при сложении.
Другим ресурсом, который мы использовали в этом году, были «Разложение числовых головоломок». Это помогло учащимся понять, что 44 равно 40 + 4, что также равно 30 + 14 и 30 + 10 + 4. Не все мои детишки смогли понять, как все эти числа связаны между собой и как разложить числа. У нас еще осталось совсем немного работы!
Мы использовали числовые головоломки в ноябре, и зимой я снова вытащил их, чтобы обсудить с несколькими моими учениками, которым нужно немного укрепить их.
Последнее, что я недавно сделал, это давал ученикам рамки предложений при вычитании. Пару недель назад я перешел от написания горизонтальной задачи к задаче на вычитание по вертикали. Они не знали, что делать! Это было так тяжело для них!
Мое решение состояло в том, чтобы дать студентам рамки предложений. Я начал с простых, например: «Есть/недостаточно единиц, чтобы вычесть _____ единиц. Вы не должны / должны разлагать десятку. Теперь есть ___ десятков и ___ единиц».
Я начал с простых, например: «Есть/недостаточно единиц, чтобы вычесть _____ единиц. Вы не должны / должны разлагать десятку. Теперь есть ___ десятков и ___ единиц».
Честно говоря, я бы не дал ученику разложить десятку, чтобы вычесть 4, но нам нужно было попрактиковаться в этой концепции с меньшими числами, прежде чем переходить к большим числам.
«Разложи десятку» — это набор рамок предложений и заданий типа беготни, в которых учащиеся смотрят, нужно ли им разложить десятку, прежде чем решать задачи.
Мы также использовали числовые ряды, и я попросил учеников нарисовать блоки с основанием 10. Мои ученики добились наибольшего успеха в использовании числовых рядов и счете от вычитаемого.
У меня есть ряд занятий по математике, на которых учащиеся тренируются в вычитании, используя различные стратегии и инструменты. Эти занятия действительно заставляют учащихся думать о математике и гибко обращаться с числами.
Как вы развиваете концептуальное понимание составления и разложения чисел в классе? Как вы помогаете учащимся гибко мыслить о числах? Я хотел бы услышать больше идей!
Если вы преподаете во втором классе, вам могут понравиться несколько страниц из некоторых моих двузначных продуктов на сложение и вычитание.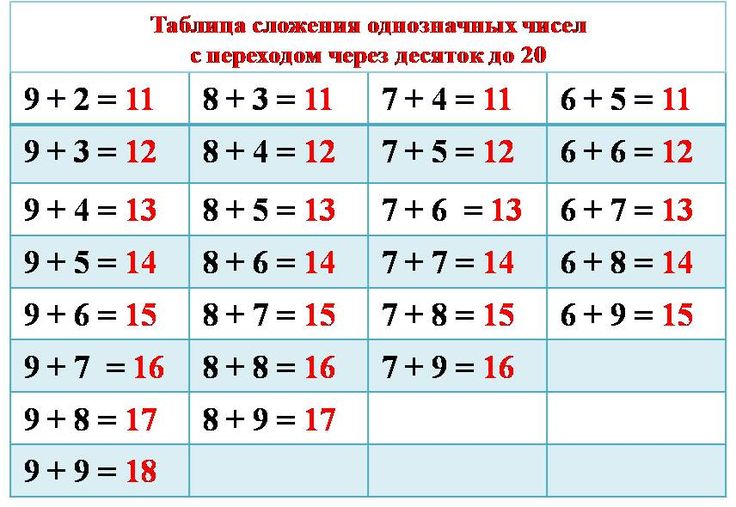
 Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.
Попросите своего малыша положить на стол один предмет, а затем поинтересуйтесь, что нужно, чтобы объектов стало два. Если ребенок затрудняется с ответом, обязательно делайте подсказки. Также спрашивайте, из каких чисел можно собрать число «2». Сопровождайте процесс наводящими вопросами.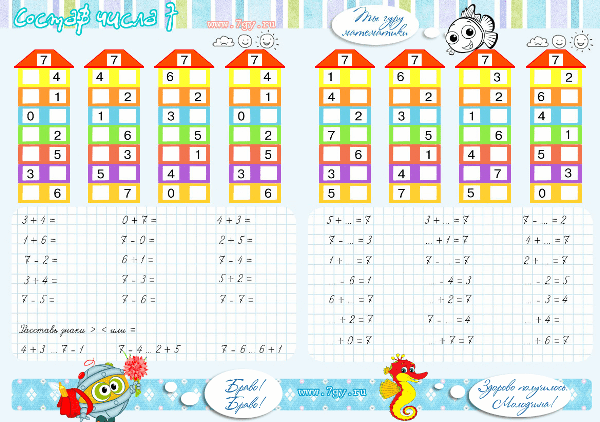 Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам.
Это позволит малышу не запутаться и понять, что от него требуется. После освоения тройки переходите к следующим числам. Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.
Второй комплект карточек является набором картинок, где те же самые объекты изображены в одном множестве, т.е. без какого-либо разделения. Алгоритм применения карточек выражается в демонстрации их ребенку. Он должен сопоставлять числа с количеством объектов, складывать и вычитать объекты. Не забудьте подготовить отдельные карточки с цифрами.