Сперва сложение или умножение: Ошибка 403 — доступ запрещён

Содержание

«Порядок выполнения арифметических действий»

«Коррекция вычислительных навыков» для учащихся 4 класса

Тема «порядок выолнения действий»

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ

• СЛОЖЕНИЕ И ВЫЧИТАНИЕ чисел называют действиями первой ступени.

• УМНОЖЕНИЕ И ДЕЛЕНИЕ чисел называют действиями второй ступени Порядок выполнения действий при нахождении значений выражений определяется правилами.

Порядок выполнения действий при нахождении значений выражений определяется следующими правилами:

Если в выражении нет скобок и оно содержит действия только одной ступени, то их выполняют по порядку слева направо.
Если выражение содержит действия первой и второй ступени и в нем нет скобок, то сначала выполняют действия второй ступени, потом – действия первой ступени.
Если в выражении есть скобки, то сначала выполняют действия в скобках (учитывая при этом правила 1 и 2)

ПОРЯДОК ДЕЙТВИЙ

Выполняю действие в скобках.
Выполняю умножение и деление.
Выполняю сложение и вычитание.

Каждое выражение задает программу своего вычисления

Она состоит из команд

(814 + 36 * 27) : (101 – 2052 : 38) = 38

1. Перемножить числа 36 и 27 (972)

2. Сложить 814 с результатом (1786) команды 1. (54)

3. Разделить 2052 на 38

4. Вычесть из 101 результат (47) команды 3

5. Разделить результат команды (38) 2 на результат команды 4.

Расставьте порядок выполнения действий в схемах

1 3 2

Расставь порядок действий и выполни вычисления

1 3 2 4

13 821

( 8 094 · 4 + 24 592 : 8 ) – 24 869 =

( 63 725 + 41 375 – 103 228 ) : 4 · 6 =

13 257 + 4 326 : 7 · 8 – 7 543 =

( 60 000 – 32 216 + 54 674 ) : 9 · 3 =

847 · 8 + ( 42 000 – 39 918) : 6 =

602 630 – 297 480 : 37 · 69 + 8 653 =

424 410 : 47 – 261 + 608 · 34 =

347 · 608 + 89 324 – 799 533 : 259 =

1 2 3 4

5 808

3 1 2 4

10 658

1 2 3 4

27486

2 4 1 3

42 123

3 1 1 4

56 523

1 3 4 2

29 441

1 3 4 2

297 213

Составь из следующих предложений выражения

со скобками и реши их Из числа 176 вычти сумму чисел 108 и 36. Из числа 394 вычти сумму чисел 259 и 28. Сумму чисел 713 и 125 вычесть из числа 939.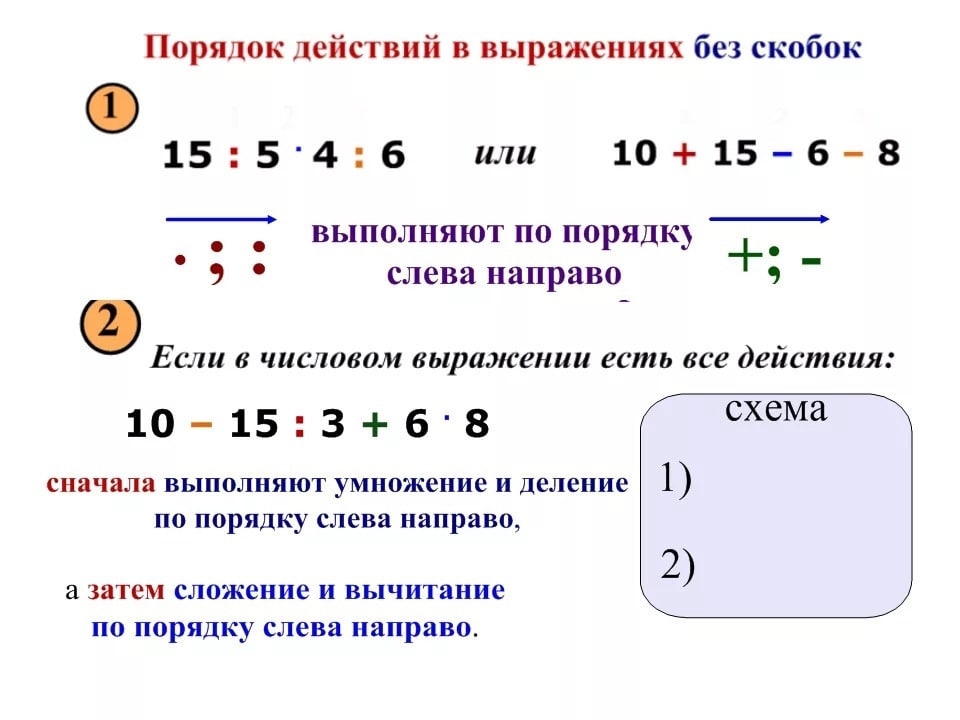 Разность чисел 816 и 93 прибавь к числу 396 Разность чисел 488 и 298 прибавь к числу 816.

Реши уравнения

164 : У = 345 – 304 У : 30 = 4085 + 2365

164:У=41

У:30=6 450

У=164:41

У=6450*30

У=4

У=193 500

164:4= 345- 304

193 500 : 30 = 4085 + 2365

41=41

6 450= 6 450

Реши задачи, сперва составив правильно выражения, а за тем последовательно их решив:

Папа принёс из леса мешок с орехами. Коля взял из мешка 25 орешков и съел. За тем Маша взяла из мешка 18 орешков. Мама то же взяла из мешка 15 орешков, но положила обратно 7 из них. Сколько осталось в итоге орешков в мешке, если в начале их было 78? Мастер ремонтировал детали. В начале рабочего дня их было 38. В первой половине дня он смог отремонтировать 23 из них. После полудня ему принесли еще столько же, сколько было в самом начале дня. Во второй половине он отремонтировал еще 35 деталей. Сколько деталей ему осталось отремонтировать?

25+18+15-7=51 (Орешков) взяли из мешка. 78-51=27 (орешков) Ответ: 27 орешков осталось в итоге.

38 — 23 = 15 (деталей) осталось отремонтировать мастеру к первой половине дня.

15 + 38 = 53 (детали) предстояло отремонтировать мастеру, кода ему принесли еще столько же деталей.

53 — 35 = 18 (деталей)

Ответ: 18 деталей осталось отремонтировать.

Битва | ALIMOK

Онлайн-сервис дистанционного образования для детей от 3 до 10 лет

РЕГИСТРАЦИЯ

Раздел «Битва» на сайте www. alimok.com — это система, которая учит думать, ставить цели, проявлять упорство, заявлять о себе. «Битва» направлена на развитие и закрепление навыков устного счёта.

Развитый устный счёт — это не только успех в математике , но и в любой другом школьном предмете, где требуется умение сосредотачиваться, запоминать, переключаться, воспринимать информацию на слух и зрительно.

В методике математики принято выделять устные и письменные способы вычисления. К устным способам можно отнести все способы вычислений в пределах 100, а также способы вычислений за пределами 100, когда вычисление сводится к способу вычислений в пределах 100.

На сегодня, в «Битве» нашли свое отражение такие темы, как «Сложение и вычитание в пределах 10, 20, 100», «Табличное умножение и деление», «Умножение двузначного числа на однозначное», «Деление двузначного числа на однозначное», «Деление с остатком» и «Смешанные». Каждая из данных тем содержит некоторое количество уровней. Уровни отличаются друг от друга количеством заданий, которые нужно выполнить за определённое время. Перейти на следующий уровень можно только после победы соперника.

Если Вы или Ваш ребёнок хотите научиться считать быстро и без ошибок, то раздел «Битва» поможет Вам развить навык быстрого устного счета.

Битва включает следующие разделы математики:

• Сложение и вычитание в пределах 10.

В данной категории дети столкнутся с примерами на сложение и вычитание чисел в пределах 10, которые могут содержать как одно, так и несколько арифметических действий. Всего в данной категории 7 уровней. С каждым уровнем увеличивается количество примеров, которые нужно решить в течение 1 минуты. Если Ваш малыш дойдёт до последнего уровня, то Вы можете быть уверены, что он полностью усвоил навык сложения и вычитания натуральных чисел в пределах 10.

• Сложение и вычитание в пределах 20

В этой категории даны примеры на сложение и вычитание чисел в пределах 20, как с переходом через десяток, так и без перехода. Всего в данной категории 7 уровней. На последнем уровне, чтобы победить Алимка, ребёнок должен будет решить 30 примеров за 1 минуту.

• Сложение и вычитание в пределах 100

В этой категории закрепляются навыки счёта в пределах 100. Затронуты такие темы, как сложение и вычитание чисел с переходом через разряд и без перехода, вычитание однозначного или двузначного числа из круглого десятка, вычитание однозначного числа из двузначного с переходом через разряд. С каждым уровнем количество примеров увеличивается, а успех в битве зависит от того, насколько быстро и без ошибок Ваш ребёнок может складывать и вычитать.

• Табличное умножение и деление

В данной категории рассматриваются случаи умножения однозначных натуральных чисел на однозначное число и соответствующие случаи деления. На каждый уровень даётся максимум 1 минута, за которую нужно правильно решить указанное количество примеров. С каждым уровнем количество примеров увеличивается, а успех в битве зависит от того, насколько быстро и без ошибок ребёнок умеет умножать и делить.

• Умножение двузначного числа на однозначное

Эта одна из самых сложных категорий. В этой категории нужно будет решить примеры на внетабличное умножение двузначного числа на однозначное, умножение числа на круглый десяток, на 11. Ребёнок сможет перейти на следующий уровень, если хорошо знает таблицу умножения и выработал навык умножение числа на сумму.

• Деление двузначного числа на однозначное

В этой категории участник столкнётся с примерами вида: деление круглых двузначных чисел на однозначное, с примерами, в которых число десятков и число единиц делится на данное, а также с выражениями, где нужно будет использовать метод разложения числа на «удобные» слагаемые.

• Деление с остатком

В этой категории даны примеры на деление с остатком в пределах 100. Все задания категории поделены на два подтипа: на примеры, где нужно найти остаток от деления, и примеры, где требуется найти само целое число. Если Ваш ребёнок хочет победить Алимка, то должен решать примеры быстро и безошибочно.

• Смешанное

В данной категории школьники смогут показать насколько хорошо у них развит навык устного счёта. Здесь собраны примеры на сложение и вычитание в пределах 100 с переходом и без перехода через разряд, примеры на табличное и внетабличное умножение и деление, деление с остатком. Навыки, полученные в этой категории, сослужат детям хорошую службу в повседневной жизни.

Логика

— Почему сложение и умножение включены в сигнатуру арифметики Пеано первого порядка?

В вопросе есть некоторая путаница:

Например, я читал, что мы можем определить сложение в арифметике второго порядка, написав
$x+0 = x$
$x+S(y) = S(x+y).$

Почему это работает во втором порядке арифметики, но не в первом порядке?

Это не работает в арифметике второго порядка. Это неявная характеристика функции сложения, но не явная определение функции сложения в терминах функции-преемника.

Настоящим определением является формула $\phi(n,m,p)$ на языке без символа сложения $+$ такая, что для всех натуральных чисел $n,m,p$ имеем $n + m = p$ тогда и только тогда, когда выполняется $\phi(n,m,p)$. «Псевдоопределение», которое может ссылаться на определяемый объект, называется неявным определением, но неявная определяемость намного слабее фактической определяемости.

Одно реальное определение сложения натуральных чисел в арифметике второго порядка: $$ n + m = p \Leftrightarrow (\forall f)\left[ \left( f(0) = n \land (\forall k)[f(S(k)) = S(f(k)]\right ) \to f(m) = p\right]. $$ Здесь $n,m,p$ — натуральные числа, $(\forall k)$ квантифицирует натуральные числа, а $(\forall f)$ квантифицирует все унарные функции от натуральных чисел до самих себя. Обратите внимание, что в правой части не упоминается $+$. В конкретном определении мы могли бы также переписать его с квантором экзистенциальной функции: $$ n + m = p \Leftrightarrow (\exists f)\left( f(0) = n \land (\forall k)[f(S(k)) = S(f(k))] \land f(m ) = р \ справа.) $$

Почему это определение не работает в логике первого порядка? Потому что в односортной теории арифметики первого порядка невозможно количественно оценить функции так, как это делает определение.

Это не доказывает, что невозможно определить сложение натуральных чисел в терминах последователя. Это только показывает, что определение в арифметике второго порядка не проходит без изменений.

Один из способов увидеть, что сложение не определяется по преемнику, описан в этом ответе Алексом Крукманом. Ключевым моментом является то, что если мы посмотрим на теорию натуральных чисел первого порядка с последователем и константой для 0, то каждая формула в этом языке (с некоторыми свободными переменными) эквивалентна бескванторной формуле в языке (с одни и те же свободные переменные). Доказательство этому приводит здесь Ричард Кэй. Таким образом, если бы в этой структуре можно было определить сложение, то его можно было бы определить с помощью бескванторной формулы. Но анализируя форму такой формулы, мы можем показать, что она не может определять сложение.

На самом деле известно больше. Ни сложение, ни умножение не могут быть определены только по преемнику; умножение не определяется последовательностью и сложением; но сложение определяется над $\mathbb{N}$ от преемника и умножения. Теория натуральных чисел с умножением и сложением неразрешима, но ограничение на простое сложение разрешимо, а ограничение на простое умножение разрешимо. Ссылка Обзор арифметической определимости 9В комментариях упоминался 0018 от Bés с гораздо более подробными результатами.

Порядок операций

Порядок операций — это определенный порядок или набор правил, согласованных математиками, которым необходимо следовать при выполнении арифметических операций для упрощения выражений.

Порядок выполнения операций

Ниже приведен порядок выполнения операций, который необходимо соблюдать в указанном ниже порядке, чтобы избежать разных ответов при упрощении выражений. Если используются символы группировки, такие как скобки, скобки или фигурные скобки, сначала выполните операции внутри символов группировки. Затем переходите к показателям и т. д….

1. Упростите любое выражение в круглых и квадратных скобках или символах группировки: ( ) [ ] { }

2. Упростите степени или выражения, включающие показатели степени: 4 ² , 2 ⁵ или 5 ^{3 9005 0}

3 . Умножьте и разделите слева направо: × и ÷

4. Сложите и вычтите слева направо: + и —

Проблемы с порядком операций

Внимательно изучите пример на рисунке ниже, чтобы понять понять, как использовать порядок операций!

Другие примеры, показывающие, как использовать порядок операций

Пример №1:

4 ² — 6 × 2 ÷ 4 × 3 + 5

Показатель степени:

16 — 6 × 2 ÷ 4 × 3 + 5

Умножить и разделить слева направо

16 — 12 ÷ 4 × 3 + 5

16 — 3 × 3 + 5

16 — 9 + 5

Сложение и вычитание слева направо

16 — 9 + 5

7 + 5

Пример #2:

(2 + 5 ² ) + 4 × 3 — 10

В скобках:

(2 + 25) + 4 × 3 — 10

27 + 4 × 3 — 10

Выполнить умножение

27 + 12 — 10

Добавить

39 — 10

Sub тракт

Пример №3:

10 — 14 ÷ 2 = 10 — 7 = 3 (деление предшествует вычитанию)

Помните, что если вы видите умножение и деление одновременно, выполняйте операцию слева направо.

Пример №4:

4 + 5 ÷ 5 × 6 = 4 + 1 × 6 = 4 + 6 =10

Как запомнить порядок операций легче для вам запомнить порядок действий.

PEMDAS (используется в основном в Соединенных Штатах Америки, а также во Франции)

BODMAS (используется в основном в Великобритании, Австралии и Индии)

BEDMAS (используется в Канаде и Новой Зеландии)

BIDMAS

Следующая мнемоника может помочь вам запомнить правило PEMDAS: Тетя Салли)

Буквы P для круглых скобок

E означает степень

M означает умножение

D означает деление

A означает сложение

S означает вычитание

Несмотря на то, что M стоит перед D в PEMDAS, эти две операции имеют одинаковый приоритет. Тот же приоритет означает, что умножение не более важно, чем деление. Точно так же, хотя A предшествует S, обе операции имеют одинаковый приоритет. Сложение не более важно, чем вычитание.

На мой взгляд, гораздо лучший способ написать PEMDAS — это P-E-MD-AS.

В P-E-MD-AS операции с одинаковым приоритетом не имеют дефисов между собой.

Например, поскольку сложение и вычитание имеют одинаковый приоритет, между ними нет необходимости ставить дефис.

Однако между P и E стоит дефис, поскольку P имеет более высокий приоритет, чем E.

Все четыре буквы в MDAS, DMAS, DMAS и DMAS относятся к умножению, делению, сложению и вычитанию.

В правиле BODMAS буква B означает скобку, а буква O — порядок. Порядок может быть силами или корнями.

В правиле BEDMAS буква B обозначает скобку, а буква E – показатель степени.

В правиле BIDMAS буква B обозначает скобку, а I — индексы. Индексы представляют собой такие степени, как 6 ²

. Имейте в виду также, что PEMDAS, BODMAS, BEDMAS и BIDMAS являются правильными способами выполнения операций с ордерами. Ни один из них не лучше другого. Это просто названия, которые используются в зависимости от страны, чтобы упростить запоминание правил.

Как насчет вложенных скобок в порядке операций?

Пример №5:

Упростить √4 + 1 + {2 — [(6 — 2) × 5] + 13}.

Сначала работайте с самым внутренним набором скобок или (6 — 2).

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {2 — [4 × 5] + 13}

Далее снова поработайте сначала с внутренним набором скобок или [4 × 5].

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {2 — 20 + 13}

Оставайтесь в скобках, пока не закончите. Работая внутри скобок, обратите внимание, что вам нужно складывать и вычитать слева направо.

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + {-18 + 13}

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = √4 + 1 + -5

Согласно правилу BODMAS, сначала нужно выполнить root.

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = 2 + 1 + -5

Снова сложить и вычесть слева направо

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = 3 + -5

√4 + 1 + {2 + [(6 — 2) × 5] + 13} = -2

Окончательный ответ — 2

Реальный пример PEMDAS

Порядок действий — очень важный навык, поскольку вы используете его каждый день, даже если не осознаете этого.
Например, вы идете в супермаркет. Предположим, арахис стоит 3 доллара за фунт, а бутылка воды — 1 доллар. Вы получаете 2 фунта арахиса и 1 бутылку воды.
Сколько денег вы платите?
Поскольку 1 фунт арахиса стоит 3 доллара, а вы купили 2 фунта, арахис стоит 6 долларов. Добавьте это к сумме, которую вы платите за воду (1 доллар), вы заплатили в общей сложности 7 долларов.
Возможно, вы разобрались с этим без особых проблем. Однако, если я представлю вам следующее уравнение, которое является моделью вышеописанной проблемы, у вас может возникнуть тенденция прибавлять 3 к 1 и умножать результат на 2. Это будет неправильный способ сделать это!
2 × 3 + 1
Это даст 8 и не равно 7.
Правильный способ — сначала умножить, а затем прибавить произведение к 1.
Тест на порядок действий. Посмотрите, как вы понимаете этот урок.
Математический тест SAT: как подготовиться к встрече с ним и выжить
09, 23 июня 12:04
Математический раздел SAT известен своей сложностью.

РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7