«Состав числа второго десятка»
Конструкт
урока математики по производственной практике
ПМ.01 «Преподавание по программам начального общего образования в начальных классах компенсирующего и коррекционно-развивающего образования»
студентки группы 36 «Б»
специальности «Коррекционная педагогика в начальном образовании»
Землянухиной Екатерины Андреевны
Дата: 27.01.17
ОО: МАОУ СОШ №34
Класс: 1 «Г»
УМК: «Школа России» Подпись ____________________
ФИО учителя класса: Кулакова Наталья Корнеевна
ФИО методиста: Титова Наталья Федоровна
Тема урока: состав чисел второго десятка
Планируемые результаты:
Личностные: проявляют заинтересованность в приобретении и расширении знаний и способов действий.
Метапредметные: обучающиеся демонстрируют личностные УУД: самоопределение. Обучающиеся демонстрируют регулятивные УУД: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено обучающимся, и того, что еще неизвестно; волевая саморегуляция как способность к мобилизации сил и энергии. Обучающиеся демонстрируют коммуникативные УУД: умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Обучающиеся демонстрируют познавательные УУД: общеучебные: поиск и выделение необходимой информации; применение методов информационного поиска; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Предметный: могут использовать таблицу сложения, составляя равенства и неравенства; знают состав чисел второго десятка и пользуются таблицей сложения чисел в пределах 20.
Задачи:
Воспитательная: воспитывать интерес в приобретении и расширении знаний и способов действий.
Развивающая: способствовать развитию личностных УУД: самоопределение. Способствовать развитию регулятивных УУД: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено обучающимся, и того, что еще неизвестно; волевая саморегуляция как способность к мобилизации сил и энергии. Способствовать развитию коммуникативных УУД: умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка. Способствовать развитию познавательных УУД: общеучебные: поиск и выделение необходимой информации; применение методов информационного поиска; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
Образовательная: учиться использовать таблицу сложения, составляя равенства и неравенства; закрепить состав чисел второго десятка; совершенствовать умения пользоваться таблицей сложения в пределах 20
Принципы воспитания: создание положительного эмоционального подъема, воспитание через взаимодействие.
Принципы обучения:
Принцип непрерывности (результат деятельности на каждом предыдущем этапе обеспечивает начало следующего этапа)
Принцип систематичности и последовательности (педагог выстраивает от простого к сложному, от знакомого к незнакомому)
Принцип диалогизации (учитель с помощью диалога взаимодействует с обучающимися)
Принцип наглядности
Принцип деятельности
Методы обучения и воспитания:
Методы обучения:
По источнику получения знаний:
Словесные: беседа, работа с учебником, объяснение
Наглядные: иллюстрация, демонстрация
Практические: упражнения
По дидактическим целям:
Методы формирования умений и навыков, применения знаний.
Методы проверки и оценки знаний, умений и навыков
По уровню включения в продуктивную деятельность:
На основе методологии целостного подхода к деятельности
Методы самостоятельной работы
Методы стимулирования учебно-познавательной деятельности (развитие познавательного интереса)
Методы контроля и самоконтроля
Методы организации учебно–познавательной деятельности:
Методы выработки учебных умений и накопления социального опыта (упражнение)
Методы закрепления и повторения изученного материала (беседа, повторение)
Методы стимулирования учебно-познавательной деятельности (поощрение, художественное слово)
Методы организации взаимодействия учащихся и накопления социального опыта
Методы воспитания:
1. Методы формирования соц. опыта: педагогическое требование.
Методы формирования соц. опыта: педагогическое требование.
2. Методы стимулирования и коррекции действий и отношений детей в воспитательном процессе: поощрение.
Форма организации учебной деятельности обучающихся: фронтальная, индивидуальная
Оборудование:
Демонстрационное:
Индивидуальное:
Информационные источники:
1. Федеральный государственный образовательный стандарт начального общего образования: текст с изм. и доп. на 2011 год./М-во образования и науки Рос. Федерации. – М.: Просвещение, 2011. – 33 с. – (Стандарты второго поколения). – ISBN 978-5-09-025287-4.
2. Производственная практика «Преподавание по программам начального общего образования в начальных классах и начальных классах компенсирующих и коррекционно-развивающего образовании» [Текст]: рекомендации студентам/ Т.В.Чащина. – Каменск-Уральский, 2015. – 26с.
3. Примерная основная образовательная программа. Образовательная система «Школа России», Москва 2011.
Образовательная система «Школа России», Москва 2011.
4. Моро М.И. Математика. 1 класс. Учебник для общеобразовательных учреждений. В 2 ч. Ч. 1/М.И. Моро, С.И. Волкова, С.В. Степанова. – М.: Просвещение, 2011. – 127с.: ил. – (Школа России).
Тип урока: Урок совершенствования способов действий (урок закрепления)
Структура урока:
1. Мотивация к учебной деятельности (4 мин)
2. Актуализация опорных знаний и способов действий (6 мин)
3. Усвоение новых знаний и способов действий по изученному материалу (25 мин)
Физкультминутка (2 мин)
4. Организация контроля и самоконтроля (взаимоконтроля) (6 мин)
5. Рефлексия учебной деятельности (2 мин)
Макет доски:
Поезд со станциями 28 апреля. Классная работа. Запись примеров и равенств/неравенств | Числовой дом |
Ход урока
Этапы урока, задачи | Методы и приемы обучения и воспитания | Деятельность учителя и обучающихся | Планируемые результаты |
1. Задача: мотивировать детей на предстоящую деятельность | Методы стимулирования (Художественное слово) Методы формирования соц. опыта (педагогическое требование) Методы стимулирования учебно-познавательной деятельности (развитие познавательного интереса) | — Подравняйтесь, чтобы каждый ряд был ровным, каждый стоял друг за другом. — А теперь послушаем, какой ряд сядет тише. – Здравствуйте, садитесь. — Молодцы. — Меня зовут Екатерина Андреевна. Сегодня урок математики проведу у вас я. Мы пришли сюда учиться – Не лениться, а трудиться. Работаем старательно, Слушаем внимательно. Проверим вашу готовность к уроку. На парте у вас должны лежать учебник, тетрадь, пенал и дневник. | Личностные УУД: самоопределение; Регулятивные УУД: волевая саморегуляция. |
2.Актуализация опорных знаний и способов действий Задача: актуализировать знания, по теме «Состав чисел второго десятка» | По дидактическим целям: (Методы формирования умений и навыков, применения знаний, Методы проверки и оценки знаний, умений и навыков) Методы стимулирования учебно-познавательной деятельности (художественное слово) Методы закрепления и повторения изученного материала (беседа, повторение | — Ребята, сегодня мы с вами отправимся в увлекательное путешествие и будем останавливаться на разных станциях. На стациях нас ожидают математические препятствия, а чтобы их успешно выполнить, какими нам нужно быть? (умными, смелыми, находчивыми и др.) Замечательно, я вижу, вы к математическому путешествию! — Наша первая станция называется «Числовой дом». 5 7 3 9 — Чтобы повторить состав чисел второго десятка, мы поиграем в игру числовой домик. — Какое число на крыше домика? (11) — 11 – это 5 и 6 — Какую цифру нужно прибавить к 7, чтобы получилось число 11? (4) — Хорошо. А какую цифру нужно прибавить к 3, чтобы получилось число 11? (8) — Отлично! А какую цифру нужно прибавить к 9, чтобы получилось число 11? (2) — Молодцы ребята! Какой мы можем вывод сделать? (Число 11 это 5 и 6; 7 и 4; 8 и 3; 9 и 2.) — А сейчас на крыше домика число 12. 6 7 8 2 — Какое число мы поставим в это окошечко? (Показываю) (6) — А в это? (5) — В это? (4) — В это? (3) — Значит, какой вывод мы можем сделать? (12 это 6 и 6; 3 и 7; 8 и 4; 9 и 2) — А теперь на крыше дома число 13. 7 8 4 — Какое число поставим в это окошечко? (6) — А в это? (5) — В это? (9) — Значит, какой мы вывод можем сделать? (Число 13 это 7 и 6; 5 и 8; 4 и 9) — Что мы с вами сейчас повторили? (Состав чисел) — Вторая наша станция называется « Знаки». — Чтобы повторить таблицу сложения, выполним такое упражнение. На доске даны примеры. Нужно поставить такую цифру, чтобы получился верный ответ. — Давайте откроем тетрадочки и запишем число и классная работа. Отступите от предыдущей работы 2 строчки. 9+_=14 — Посмотрите на доску, какую цифру нужно ставить, чтобы получилось число 14? (5) — Хорошо! Запишите к себе в тетрадь. — Следующий пример. _+7=15 — Какую цифру нужно подставить, чтобы получилось число 15? (8) — Молодцы! — Кто хочет поработать за доской? — А сейчас вы остальные 3 примера запишите самостоятельно. (Один ребенок работает за доской) 8+_=16 _+9=17 9+_=18 — А сейчас давайте проверим. Ребята, у кого получилось так же, поднимите руку. Молодцы. | Регулятивные УУД: волевая саморегуляция; оценка — выделение и осознание, что усвоено и что еще подлежит усвоению. Коммуникативные УУД: умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. |
Физкультминутка Задача: снять мышечное и эмоциональное напряжение | Методы стимулирования учебно-познавательной деятельности (художественное слово) По уровню включения в продуктивную деятельность (репродуктивные) | — Давайте не много отдохнем! Попрошу всех встать. Раз – подняться, потянуться, Два – согнуться, разогнуться, Три – в ладоши три хлопка, Головою три кивка. На четыре – руки шире, Пять – руками помахать, Шесть – за парту тихо сесть. Присаживайтесь. | Регулятивные УУД: волевая саморегуляция. |
3. Усвоение новых знаний и способов действий по изученному материалу. Задача: применить таблицу сложения в процессе составления равенств и неравенств | Словесные (беседа, работа с учебником, объяснение) Практические (упражнения) На основе методологии целостного подхода к деятельности (Методы самостоятельной работы) | — Следующая станция «Решайкино» — Следующая наша станция называется «Решайкино», на ней мы повторим решение задач. — В ваших учебниках на стр 72 есть задача, под номером 2 — Прочитайте задачу про себя. Весной Даша и Наташа были одинакового роста. За лето Даша выросла на 5 см, а Наташа – на 2 см. На сколько сантиметров одна девочка стала выше другой? Назови ее имя. — О чем говорится в задаче? (О двух девочках) — Что они сделали? (Выросли) — На сколько выросла Даша? (Даша выросла на 5 см) — На сколько выросла Наташа? (Наташа выросла на 2 см) — Что нам нужно узнать? — На сколько см одна девочка стала выше другой и назвать ее имя. — Что мы можем узнать, зная, что Даша выросла на 5 см, а Наташа на 2см? (На сколько см Даша стала больше Наташи.) — А каким действием? (Вычитание) — Как? (5см – 2см ) — Сколько получится? (3см) — Запишите к себе в тетрадь с пояснением. А … работает за доской. Ребенок открывает доску. — Поднимите руку, у кого получилось так же. — Хорошо. Как запишем ответ? (3 см) — Запишите, пожалуйста. — Молодцы ребята, на данной станции мы с вами повторили решение задач. — Следующая наша станция называется «равенства и неравенства» — Чтобы научиться использовать таблицу сложения для составления равенств и неравенств, решим упражнение на стр. 72 под номером 4. — Прочитайте задания про себя. — …., прочитай вслух. — Если равенства, то это какой знак? (=) — А если неравенства? (Знаки больше и меньше) — Давайте составим равенство. Возьмем число 13. Какие числа нужно взять, чтобы получилось 13? (7+6) — Отлично. Отступите от предыдущей работы 1 строчку и запишите данное равенство к себе в тетрадь. — Попробуйте составить еще одно равенство в парах и запишите его к себе в тетрадь. — Какое равенство получилось у вас? (Записываю на доске) — Отлично. — А сейчас попробуем составить неравенство. Возьмем число 15. Какие числа нужно взять, чтобы число 15 оказалось больше чем второе? (5+6) — Сколько это получится? (11) — А 15 больше 11 (Записываю на доске) — Запишите данное неравенство к себе в тетрадь. — А сейчас попробуйте сами в парах составить любое неравенство и запишите его к себе в тетрадь. — Какое неравенство получилось у вас? (Записываю на доске) -Хорошо. Ребята, вы хорошо поработали и вы научились использовать таблицу сложения в составлении неравенств. | Регулятивные УУД: волевая саморегуляция; оценка — выделение и осознание, что усвоено и что еще подлежит усвоению. Коммуникативные УУД: умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. Познавательные УУД общеучебные: поиск и выделение информации. логические: построение логической цепи рассуждения. |
4.Организация контроля и самоконтроля (взаимоконтроля) Задача: закрепить знания и умения детей | Методы организации взаимодействия учащихся и накопления социального опыта (Метод взаимной проверки) Методы стимулирования и коррекции действий и отношений детей в воспитательном процессе (поощрение) Методы контроля и самоконтроля | — Мы с вами прибыли на последнюю станцию «Я сам» — Чтобы проверить как вы усвоили состав чисел второго десятка, предлагаю вам самостоятельно поработать с домиком. — Для каждого ряда, я приготовила по одному домику. Подберите и впишите нужные числа в каждый этаж. А затем мы проверим. — А Миша, Дима и Маша, будут работать на отдельных домиках. Закрывайте учебники и начинайте выполнять задание. — А сейчас давайте проверим. Ребята с большими домиками, выходите к доске. Давайте проверим. — Приготовьте сигналы. Если вы считаете, что домик сделан правильно, то показывайте зеленый сигнал, если нет, то красный. — Домик с первого ряда. Расскажи 11 это …. — Домик со второго ряда. 12 это …. — Домик с третьего ряда. 13 это …. — Ребята, встаньте те, кто не допустил ни одной ошибки при выполнении этого задания. Вы молодцы и хорошо сегодня поработали на уроке. А поднимите руку те, кто допустил 1 ошибку. Я рада, что таких детей в нашем классе нет. (Вам нужно еще немного повторить тему состав чисел второго десятка). — Вы хорошо усвоили тему «Состав чисел второго десятка. Молодцы! | Познавательные УУД: общеучебные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. |
5.Рефлексия учебной деятельности Задача: подвести итог урока, провести рефлексию деятельности | По дидактическим целям (Методы проверки и оценки знаний, умений и навыков) Методы контроля и самоконтроля | — Ребята, наш урок подходит к концу. — Что мы сегодня повторяли? (Состав чисел, решение задач, использовали таблицу сложения) — Хорошо. Я вам раздала кружки. — Если вам понравился урок, и вы много узнали, то нарисуйте веселый смайлик. Если вам не очень понравился урок, и вы почти ничего не узнали, то поставьте нейтральный смайлик. А если вам совсем не понравился урок и вы ничего не узнали, то поставьте грустный смайлик. Большое спасибо вам за урок. — Петя, ты хорошо работал на станции «…..» — Маша, ты хорошо работала с равенствами и неравенствами — Миша, ты хорошо работал над задачей. — Мне очень понравилось, как на уроке работал ……. — Петя, Маша и Никита сдайте мне, пожалуйста, после урока тетради. Мне очень понравилось с вами работать! Урок окончен! До свидания! Сдать тетради (конкретно кто) | Личностные УУД: самоопределение. Познавательные УУД: общеучебные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности. |
Лекция 6. Разряды числа
1. Числа второго десятка (двадцаток).
2. Числа первой сотни.
3. Числа первой тысячи.
4. Многозначные числа.
5. Системы счисления.
Числа второго десятка (И, 12, 13, 14, 15, 16, 17, 18, 19, 20) —двузначные числа.
Для
записи двузначного числа используются
две цифры. Первая цифра справа в записи
двузначного числа называется цифрой
первого разряда или разряда
единиц, вторая
цифра справа — цифрой
второго разряда или разряда
десятков.
Числа второго десятка во всех учебниках математики для начальных классов рассматриваются отдельно от других двузначных чисел. Это объясняется тем, что названия чисел второго десятка противоречат способу их записи. Поэтому многие дети некоторое время путают порядок записи цифр в числах второго десятка, хотя называть их при этом могут правильно.
Например, при записи на слух числа 12 (две-на-дцать) ребенок первым словом слышит «две(а)», поэтому он может записать цифры в таком порядке 21, но прочитать эту запись как «двенадцать».
Формирование представления о двузначных числах строится на основе понятия «разряд».
Понятие разряда является базовым в десятичной системе счисления. Под разрядом понимается определенное место в записи числа в позиционной системе счисления (разряд — это позиция цифры в записи числа).
Каждая
позиция в этой системе имеет свое
название и свое условное значение:
цифра, стоящая на первой позиции справа,
означает количество единиц в числе;
цифра, стоящая на второй позиции справа,
означает количество десятков в числе
и т.
Цифры от 1 до 9 называют значащими, а нуль является незначащей цифрой. При этом его роль в записи двузначных и других многозначных чисел очень важна: нуль в записи двузначного (и т. д.) числа означает, что число содержит обозначенный нулем разряд, но значащих цифр в нем нет, т. е. наличие нуля справа в числе 20, обозначает, что цифра 2 должна восприниматься как символ десятков, и при этом число содержит только два целых десятка; запись 23 будет означать, что кроме 2 целых десятков число содержит еще 3 единицы, дополнительно к целым десяткам.
Понятие «разряд» играет большую роль в системе изучения нумерации, а также является основой для освоения так называемых «нумерационных» случаев сложения и вычитания, в которых действия производятся целыми разрядами:
27-20
365-300
27-7
365-60
20+7
305+ 60
Умение
узнавать и выделять в числах разряды
является основой умения раскладывать
числа на разрядные
слагаемые: 34
= 30 + 4.
Для чисел второго десятка понятие «разрядный состав» совпадает с понятием «десятичный состав». Для двузначных чисел, содержащих более одного десятка — эти понятия не совпадают. Для числа 34 десятичный состав — это 3 десятка и 4 единицы. Для числа 340 разрядный состав — это 300 и 40, а десятичный — это 34 десятка.
Знакомство с числами второго десятка (11—20) удобно начинать со способа их образования и названия чисел, сопровождая его сначала моделью на палочках, а затем чтением числа по модели:
один-на-дцать три-на-дцать сем-на-дцать
Запоминание
названий двузначных чисел в этом случае
не будет затруднено для детей противоречащей
названию записью: 11, 13,17. (Ведь в соответствии
с традицией чтения в европейских
письменностях слева направо в названии
этих чисел сначала должна была бы идти
цифра десятков, а потом цифры единиц!)
В связи с такой особенностью чисел
второго десятка, многие дети в первом
классе долго путаются при записи их на
слух и чтении по записи. Раннее введение
символики играет в данном случае
отрицательную роль как для запоминания
названий чисел второго десятка, так и
для понимания их структуры. Для
формирования правильного представления
о структуре двузначного числа следует
всегда класть десятки слева, а единицы
справа. Таким образом ребенок зафиксирует
во внутреннем плане правильный образ
понятия, без специальных многословных
и не всегда понятных ему объяснений.
Раннее введение
символики играет в данном случае
отрицательную роль как для запоминания
названий чисел второго десятка, так и
для понимания их структуры. Для
формирования правильного представления
о структуре двузначного числа следует
всегда класть десятки слева, а единицы
справа. Таким образом ребенок зафиксирует
во внутреннем плане правильный образ
понятия, без специальных многословных
и не всегда понятных ему объяснений.
На следующем этапе предлагаем ребенку соотнесение вещественной модели и символической записи:
13 15 17
Затем переходим на графические модели и к чтению чисел по графической модели:
Далее вводятся схематические разрядные модели:
а затем символическая запись разрядного состава чисел второго десятка:
17=10 + 7.
В дальнейшем в школе вводят понятие разряда и знакомят детей с понятием «разрядные слагаемые»: 37 = 30 + 7; 624 = 600 + 20 + 4.
Использование десятичной модели вместо разрядной для знакомства со всеми двузначными числами позволяет без введения понятия «разряд» познакомить ребенка как со способом образования этих чисел, так и научить его читать число по модели (и наоборот, строить модель по названию числа), а затем и записывать:
При изучении детьми чисел второго порядка рекомендуем педагогу использовать следующие виды заданий:
1) на способ образования чисел второго десятка:
Покажи
тринадцать палочек. Сколько это десятков
и сколько еще отдельных палочек?
Сколько это десятков
и сколько еще отдельных палочек?
2) на принцип образования натурального ряда чисел:
Сделай рисунок к задаче и реши ее устно. «В городе было 10 кинотеатров. Построили еще 1. Сколько кинотеатров стало в городе?»
Уменьши на 1: 16, 11, 13, 20
Увеличь на 1: 19, 18, 14, 17
Найди значение выражения: 10 + 1; 14 + 1; 18 — 1; 20 — 1.
(Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 — к получению числа предыдущего.)
3) на поместное значение цифры в записи числа:
Что обозначает каждая цифра в записи числа: 15, 13, 18, 11, 10, 20?
(В
4) на место числа в ряду чисел:
Вставь
пропущенные числа: 12. ……..16
17
… 19
20
……..16
17
… 19
20
Вставь пропущенные числа: 20 … 18 17………13 … 11
(При выполнении задания ссылаются на порядок чисел при счете.)
5) на разрядный (десятичный) состав:
10 + 3 = … 13-3 = … 13-10 = …
12= 10 + … 15 = …+ 5
При выполнении задания ссылаются на разрядную (десятичную) модель числа из десятка (пучка палочек) и единиц (отдельных палочек),
6) на сравнение чисел второго десятка:
Какое из чисел больше: 13 или 15? 14 или 17? 18 или 14? 20 или 12?
При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 13 две единицы получим 15, значит 15 больше, чем 13).
Сравнивая числа второго десятка с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные:
Назови
самое большое и самое маленькое из этих
чисел: 12
6
18
10 7 20.
При сравнении чисел второго десятка удобно пользоваться линейкой.
I I I I I I I I I I I I I I I I I I I I I I I I I I
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Сравнивая длины соответствующих отрезков, ребенок наглядно определяет постановку знака сравнения: 17 < 19.
Педагогическая технология изучения чисел второго десятка. Автор к.п.н. Петкевич Н.В.
Согласно требованием программы к концу второго класса должны быть сформированы вычислительные навыки табличных случаев сложения и вычитания однозначных чисел.
Комплексное использование демонстрационных и индивидуальных наглядных пособий обеспечит достижение положительного результата с наименьшими затратами сил и времени как учителя, так и ученика, что является необходимым условием здоровьесберегающих педтехнологий.
Использование пособий в определенной последовательности обеспечивает этапы усвоения информации по формированию понятия о сложении однозначных чисел с переходом через десяток и вычислительных навыков, путем построения предметных (рисунки овощей), графических (кружочки) и знаковых (цифры) моделей.
Благодаря демонстрационным пособиям с подвижными деталями учащиеся имеют возможность увидеть в динамике формируемые понятия и действия сложение и вычитание, а при наличии у детей комплектов индивидуальных наглядных пособий «Математика от 1 до 20. Суперпапка» выполнить эти же действия самим.
Большинство из представленных ранее пособий используется и для изучения чисел второго десятка. Это обеспечивает преемственность в предъявлении содержания учебного материала от простого к сложному и преемственность в последовательности выполнения учебных действий. Ориентиром в этой работе выступит последовательность использования наглядности.
I. Образование чисел от 11 до 20
1. Предъявление образа чисел. Работа с таблицами из демонстрационных наглядных пособий«Сказочный счет».
2. Образование чисел из одного десятка и нескольких единиц. Работа со второй частью демонстрационного и индивидуального наглядного пособия «Линейка «Счет от 1 до 20».
3. Построение предметной модели чисел при помощи «Абака».
4. Построение графической, цветовой и знаковой модели чисел с использованием «Компьютера».
II. Сложение однозначных чисел с переходом через десяток
1. Построение предметной модели задачи при помощи «Абака».
2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации.
3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20». Запись на доске.
III. Состав чисел II десятка
1. Построение графической, цветовой и числовой модели состава чисел. Работа с демонстрационным и индивидуальным пособием «Компьютер».
2. Закрепление знаний. Самостоятельная работа в тетради.
3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка».
4. Взаимопроверка знаний. Работа «в паре» с индивидуальными пособиями «Радужная горка», «Числовая горка», «Столбик таблицы сложения однозначных чисел».
5. Проверка знаний учителем. Работа с «Цветовыми сигнальными карточками» и «Цветовой сигнальной лентой».
ТЕХНОЛОГИЯ ИЗУЧЕНИЯ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА
I. Образование числа 11
1 . Предъявление образа числа 11. Работа с таблицами из «Сказочного счета».
а) б) Рис. 1
Иллюстрации к сказкам «Про Козленка, который умел считать до десяти» и «Красная шапочка». Образование числа 11.
Рис. 1 а подсказывает название числа – одиннадцать (дцать – это сокращенное десять), а рис. 1 б, как его образовать. Дети находят число 11 на корпусе парусника и его модель в «Радужной горке» (нижний ряд 1 десяток и 1 белый с точкой шарик вверху).
Аналогично происходит знакомство с числами 12, 13…19.
2. Образование числа 11.
Работа со второй частью «Линейки «Счет от 1 до 20». Сначала учитель, а затем учащиеся устанавливают окошко на своих линейках, как показано на рис. 2, и видят, что если к 10 прибавить 1, получается 11.
2, и видят, что если к 10 прибавить 1, получается 11.
Рис. 2.
Линейка «Счет от 1 до 20» II ч. Модель числа 11.
3. Построение предметной модели числа 11 при помощи «Абака» (рис. 3).
По картинкам составляется задача: «В вазе лежало 10 яблок. В нее положили 1 грушу. Сколько фруктов стало в вазе?». Дети хором: 10 + 1 = 11(фр.).
Рис. 3. «Абак». Модель задачи.
4. Построение графической, цветовой и знаковой модели числа 11 с использованием «Компьютера».
Учащиеся, проговаривая, строят модель этой задачи при помощи «Компьютера» (рис. 4).
Рис. 4. «Компьютер». Модель задачи.
Таким образом, в процессе работы с наглядными пособиями ученики знакомятся с десятичным составом чисел от 11 до 19.
II. Сложение однозначных чисел с
переходом через десяток
1. Построение предметной модели задачи при помощи «Абака».
Чтобы не допустить «отлета математики от действительности» и обеспечить мотивацию путем распознавания в повседневной жизни проблем, требующих практического применения математических знаний, начнем работу с решения задачи. Например. Задача: «Хозяйка купила 7 помидоров и 5 огурцов. Сколько всего овощей купила хозяйка?» Условие задачи моделируется при помощи «Абака» (рис. 5).
Например. Задача: «Хозяйка купила 7 помидоров и 5 огурцов. Сколько всего овощей купила хозяйка?» Условие задачи моделируется при помощи «Абака» (рис. 5).
Рис. 5. «Абак». Предметная модель задачи.
2. Построение ее графической, цветовой и знаковой модели с использованием «Компьютера» и ее преобразование, создание проблемной ситуации.
Учитель предлагает учащимся построить модель условия задачи при помощи полосок из персонального «Компьютера» (рис. 6, а). «Сколько овощей купила хозяйка?» – спрашивает он. Учащиеся затрудняются дать ответ сразу. Кто-то пересчитывает все овощи, кто-то присчитывает к 7 кружочкам 5 по одному.
а) б) в)
Рис. 6 (а, б, в,) «Компьютер». Построение и преобразование модели задачи.
Учитель создает условие для выполнения вычислений более рациональным способом. Он хочет поставить полоску с 5 кружочками в верхний карман «Компьютера» Она не входит, поэтому она накладывается на него. Учитель спрашивает: «Что можно сделать с числом 5, чтобы разместить в «Компьютере»?
Учитель спрашивает: «Что можно сделать с числом 5, чтобы разместить в «Компьютере»?
И дети предлагают заменить его двумя полосками с 3 и 2 кружочками. Учитель ставит в верхний карман полоску с 3 кружочками, а в нижний – с 2 (рис. 6, в).
– Сколько овощей купила хозяйка? (12)
– Что мы сделали со II слагаемым?
– Заменили числами 3 и 2. Учитель обобщает: «Мы заменили II слагаемое – 5 суммой удобных слагаемых 3 и 2, чтобы 7 дополнить до 10, и прибавили 2.
Учащиеся моделируют эту же задачу на своих «Компьютерах» с проговариванием.
3. Построение знаковой модели при помощи «Линейки «Счет от 1 до 20».
Учитель на демонстрационном пособии «Линейка «Счет от 1 до 20» строит знаковую модель задачи (рис. 7).
Рис. 7. «Линейка «Счет от 1 до 20».
Знаковая модель задачи. Учащиеся строят эту же модель при помощи индивидуальных «Линеек «Счет от 1 до 20», сопровождая свои действия рассуждениями (хором): «Чтобы к 7 прибавить 5, надо к 7 прибавить 3, получится 10, (на линейке дана подсказка – удобное слагаемое 3), и к 10 прибавить 2, получится 12. Действия и рассуждения детей письменно оформляются на доске и в тетрадях в виде развернутой записи:
Действия и рассуждения детей письменно оформляются на доске и в тетрадях в виде развернутой записи:
7 + 5 = 7 + (3 + 2) = (7 + 3) + 2 = 12
Таким образом, при последовательном использовании комплекса наглядных пособий формируется понятие о сложении однозначных чисел с переходом через десяток.
При формировании вычислительного навыка мы должны стремиться к свертыванию информации, т.е. избавиться от промежуточного результата 10, ибо он тормозит процесс вычислений. Поэтому фундаментом вычислительных навыков при сложении и вычитании однозначных чисел с переходом через десяток является знание состава чисел 11,12,…,18.
Алгоритм изучение состава чисел рассмотрим на примере числа 11.
III. Состав числа 11
1. Построение графической, цветовой и числовой модели состава числа 11.
Работа с демонстрационным и индивидуальным пособием «Компьютер». Для ограничения 10 кружков на доске нужно провести вертикальную линию, а на парту положить лист бумаги, ограничивающий десяток. В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8).
В процессе совместной учебной деятельности строится модель числа 11. Учитель прикрепляет полоски при помощи магнитов и рядом записывает равенства, учащиеся размещают полоски на парте (рис. 8).
Рис. 8. Развернутые модели состава числа 11.
Построение данных моделей позволяет за счет цвета и графики ярко и четко предъявить информацию и обеспечить переход от конкретного – к абстрактному.
2. Закрепление знаний. Самостоятельная работа в тетради.
Учащиеся в тетрадях по клеточкам вычерчивают карандашом модели числа 11 (рис. 9).
Рис. 9. Запись в тетради.
Эта работа дает возможность акцентировать внимание на том, что I слагаемые уменьшаются на 1, а II — увеличиваются на 1, а сумма остается без изменения, и многократно повторить систематизированную информацию, что является необходимым условием запоминания таблицы сложения.
Полностью таблица представлена как справочный материал на правом клапане «Суперпапки».
Для закрепления состава числа 11 можно составить целую серию задач с использованием таблиц «Сказочный счет». Например. «В гости к героям сказки «Волк и семеро козлят» пришли герои сказки «Сестрица Аленушка и братец Иванушка». Сколько стало героев сказок?» (9 + 2 = 11) и т. д.
Например. «В гости к героям сказки «Волк и семеро козлят» пришли герои сказки «Сестрица Аленушка и братец Иванушка». Сколько стало героев сказок?» (9 + 2 = 11) и т. д.
3. Применение полученных знаний на новых информационных полях и в новых ситуациях. Работа с демонстрационными пособиями «Радужная горка» и «Числовая горка».
На иллюстрации к сказке «Про Козленка, который умел считать до десяти» из комплекта «Сказочный счет» изображен парусник, на парусе которого шариками представлены числа от 1 до 10, а на корпусе – числа от 11 до 20.
Данную информацию можно использовать для закрепления знания состава числа. Работая в паре у доски, учащиеся устанавливают соответствие между а) парами шариков на парусе и числом 11 на корпусе парусника; б) парами шариков на парусе и парами чисел, составляющими число 11 в вертикальном столбике «Числовой горки».
Обращается внимание на то, что из всех чисел, расположенных между 1 и 10, объединив их в пары, можно получить число 11. Эту зависимость дети видели при изучении состава чисел первого десятка.
Рис. 10.
На данном этапе было бы очень полезно составить задачи по моделям. Во-первых, мы замедлим темп урока, чтобы никто не отстал на самом важном этапе, а во-вторых, подключим воображение, фантазию, усилим ассоциативные связи.
Например.
1) В одной коробке лежало 9 простых карандашей, а в другой – 2 красных. Сколько карандашей в двух коробках?
2) Для приготовления баклажанной икры повар взял 8 баклажанов и 3 помидора. Сколько всего овощей пошло на баклажанную икру?
3) Для приготовления компота мама взяла 7 синих слив и 4 желтых. Сколько всего слив пошло на компот?
4. Взаимопроверка знаний. Работа в парах.
Учащиеся раскрывают «Суперпапку» и кладут ее на парту так, чтобы сверху были обе горки и клапан с таблицей сложения (рис. 11).
Рис.11
1) Один ученик показывает кружочки: 9 серых и 2 красных кружочков, а другой – числа: 9 в сером квадрате и 2 в красном; 8 и 3 и т. д. Модели показываются сначала по порядку, а затем вперемешку. Проверяются по столбику выражений на клапане. Таким образом, они знакомятся с местом расположения данного столбика в системе знаний (рис. 10). Далее закрепление состава числа 11, обеспечивается переходом от абстрактного к конкретному, то есть от знаковой модели к предметной.
д. Модели показываются сначала по порядку, а затем вперемешку. Проверяются по столбику выражений на клапане. Таким образом, они знакомятся с местом расположения данного столбика в системе знаний (рис. 10). Далее закрепление состава числа 11, обеспечивается переходом от абстрактного к конкретному, то есть от знаковой модели к предметной.
2) Один ученик показывает — 9 + 2, а другой – 9 серых шариков и 2 красных и т.д.
3) Один показывает на корпусе лодки число 11, а другой – на парусе 8 фиолетовых кружочков и 3 желтых и т.д.
5. Проверка знаний учителем. Игра «Сигнальщики».
На доске вывешивается «Цветовая сигнальная лента», в которой цвета радуги расположены по порядку, и рядом записываются соответствующие им числа, из которых можно составить число 11 – это 2, 3….9.
Учитель, например, показывает число 8 или фиолетовый цвет на ленте, а учащиеся – оранжевую карточку (3).
Итак, вся предыдущая работа была направлена на понимание и запоминание столбика таблицы сложения однозначных чисел с ответом 11, который является подсистемой в системе знаний.
Работа над составом чисел 12, 13….18 проводится аналогично.
Для проверки всей таблицы вывешивается «Цветовая сигнальная лента», в которой цвета радуги перемешаны, и рядом записываются по порядку числа 11, 12….18.
Учитель, например, называет выражение 5 + 9 (или показывает зеленую и серую карточку из веера).
Учащиеся видят, что число 14 написано рядом, например, с красным цветом и показывают красную карточку. (Цвет значения не имеет, он служит для обратной связи).
Можно придумать много других игр и заданий.
С огромным удовольствием дети работают с «Телефоном – справочником». Он же является самоучителем.
При помощи «Квадрата с уголком», благодаря подвижной детали, можно построить всю таблицу сложения и вычитания. Многочисленные варианты работы с каждым пособием, входящим в комплект, описаны в методических рекомендациях.
Эти учебно-наглядные пособия могут использоваться на всех этапах урока, в разных сочетаниях с другими средствами обучения, в том числе, и с учебником. Причем, детям предоставляется право выбирать наглядное пособие, при помощи которого можно выполнить то или иное задание из него.
Причем, детям предоставляется право выбирать наглядное пособие, при помощи которого можно выполнить то или иное задание из него.
В начало статьи
Наглядные пособия
Главная
Свод федеральных правил | GovInfo
Чтобы распечатать эту страницу: Нажмите Control + P на клавиатуре
Чтобы помочь нам улучшить эту информацию: Нажмите «Отзыв» вверху любой страницы
Поиск Просмотр
Перейти к: Образцы поисковых запросов │ Примеры URL-адресов │ Поля и значения метаданных │ Связанные ресурсы
О Своде федеральных правил
Что такое Свод федеральных правил?
Ежегодное издание Свода федеральных правил (CFR) представляет собой кодификацию общих и постоянных правил, опубликованных в Федеральном реестре департаментами и агентствами федерального правительства.
Онлайн CFR — это совместный проект, санкционированный издателем, Управлением Федерального реестра (OFR) Национального управления архивов и документации (NARA) и Правительственным издательством (GPO) для предоставления общественности расширенного доступа к правительственной информации. .
Примечание. В официальной версии в бумажном переплете и официальных версиях в формате PDF издания 2007 г. раздела 49, том 6, части 400-599, заголовок неправильно читается как «(10-1-06 Edition)», а должен был читаться как «(10- 1-07 издание)».Когда обновится?
CFR на govinfo соответствует опубликованной печатной версии CFR. Когда выпускаются печатные издания, становится доступной и онлайн-версия. Если название или том CFR не указан в списке CFR, этот том еще не опубликован.
50 тем содержат один или несколько отдельных томов, которые обновляются один раз в календарный год на поэтапной основе. Годовой цикл обновления следующий:
Годовой цикл обновления следующий:
- заголовки 1-16 пересмотрены по состоянию на 1 января
- заглавия 17-27 пересмотрены по состоянию на 1 апреля
- заглавия 28-41 пересмотрены по состоянию на 1 июля
- заглавия 42-50 пересмотрены по состоянию на 1 октября
Что доступно?
- говинфо в настоящее время содержит заголовки с 1996 по настоящее время . Тома CFR добавляются одновременно с выпуском бумажных изданий. Когда добавляются пересмотренные тома CFR, предыдущие выпуски остаются на govinfo как исторический набор.
- Массовая загрузка XML-файлов Кодекса федеральных правил доступна для широкой публики через Data.gov и репозиторий массовых данных GPO. Информацию о правовом статусе, подлинности и схеме XML-представлений Свода федеральных правил можно найти в Документ Руководства пользователя — Код Федерального реестра XML-представление .

- Чтобы просмотреть недавно обновленных наименований CFR, посетите электронный свод федеральных правил (e-CFR), регулярно обновляемый неофициальный редакционный сборник материалов CFR и поправок Федерального реестра. eCFR обновляется ежедневно.
- Чтобы увидеть совокупный список разделов CFR, которые были изменены в любое время с момента последнего обновления каждого заголовка CFR, просмотрите Список затрагиваемых разделов CFR (LSA)
- Чтобы найти окончательные и предлагаемые правила, влияющие на CFR и опубликованные в Федеральном реестре в течение последних 24 часов, недели, месяца или в течение определенного диапазона дат, просмотрите CFR Затронутые детали из Федерального реестра
Как это организовано?
CFR разделен на 50 наименований, которые представляют широкие области, регулируемые федеральным законодательством. Каждое название разделено на главы, которые обычно носят название агентства, выдавшего документ. Каждая глава далее подразделяется на части, которые охватывают определенные области регулирования. Большие части могут быть разделены на подчасти. Все части организованы в разделы, и большинство ссылок на CFR относятся к материалам на уровне раздела.
Каждая глава далее подразделяется на части, которые охватывают определенные области регулирования. Большие части могут быть разделены на подчасти. Все части организованы в разделы, и большинство ссылок на CFR относятся к материалам на уровне раздела.
Какова структура ссылки на CFR (например, 21 CFR 310.502, редакция от 1 апреля 1997 г.)?
Ниже описано, как информация содержится в цитировании CFR.
- Заголовок: Числовое значение слева от «CFR»
- Часть: Числовое значение справа от «CFR» и перед точкой («.»»)
- Раздел/Подчасть: Числовое значение справа от точки («».») Подчасть — это буква алфавита (A-Z), которая используется для извлечения всей части CFR, а не множества отдельных разделов. Например: Подчасть E.
- Год пересмотра: Год из четырех цифр в тексте «Пересмотрено с» представляет год, на который делается ссылка.
 Год редакции не всегда доступен при цитировании CFR.
Год редакции не всегда доступен при цитировании CFR.
Пример: 21 CFR 310.502 Пересмотрено 1 апреля 1997 г.
- Название: 21
- Деталь: 310
- Секция: 502
- Год: 1997
Параллельная таблица полномочий и правил для Свода федеральных правил и Кодекса США
В Параллельной таблице полномочий и правил перечислены полномочия по нормотворчеству (кроме 5 U.S.C. 301) для правил, кодифицированных в Своде федеральных правил. Также включены статутные цитаты, которые отмечены как толкуемые или применяемые этими правилами.
Таблица разделена на четыре сегмента, и в каждом сегменте ссылки расположены в порядке номеров:
- Для ссылок на Кодекс США, по названию и разделу;
- Для больших ссылок на Уставы США с указанием тома и номера страницы;
- Для ссылок на публичное право, по номеру;
- Для ссылок на президентские документы (прокламации, указы и планы реорганизации) по номеру документа.

Записи в таблице взяты непосредственно из цитаты нормотворческого органа, предоставленной федеральными агентствами в их правилах. Федеральные агентства несут ответственность за поддержание актуальности и точности этих ссылок. Поскольку федеральные агентства иногда представляют эти цитаты непоследовательно, таблица не может считаться всеобъемлющей. Часть таблицы, в которой перечислены цитаты из Кодекса США, является наиболее полной, поскольку эти цитаты вводятся в таблицу всякий раз, когда они даются в авторитетных цитатах, предоставленных агентствами. Ссылки на Законы США в целом и публичное право приводятся в таблице только в том случае, если соответствующие ссылки на Кодекс США отсутствуют.
Начиная с 2017 года, таблица доступна в томах публикации CFR Index and Finding Aids по адресу govinfo . Вы можете загрузить весь том CFR Index and Finding Aids или только Parallel Table of Authorities and Rules.
- 2016: PDF | Текст
- 2015: PDF | Текст
- 2014: PDF | Текст
- 2013: PDF | Текст
- 2011: PDF | Текст
- 2009: PDF | Текст
Поиск в своде федеральных правил
Вы можете найти и выполнить поиск в Своде федеральных правил по телефону:
- Используя Basic Search для поиска по ключевым словам и метаданным,
- Использование расширенного поиска ; поля, относящиеся к CFR, будут отображаться после того, как вы выберете Свод федеральных правил в столбце «Уточнить по коллекции»,
- Использование Citation Search для получения одного документа Свода федеральных правил в формате PDF, если вы знаете том и страницу документа,
- Уточнение результатов поиска путем нажатия на ссылки на панели «Уточнить поиск» в левой части страницы (разделы «Уточнить поиск» соответствуют метаданным, доступным для документов), и
- Просмотр Свода федеральных правил.

Общие советы по поиску govinfo
Примеры поиска
Поиск по цитированию — например, 7 CFR 1951.7 от 2016 г.
- Используя обычный поиск, введите: collection:cfr and citation:»7 CFR 1951.7″ и publishdate:2016
- Используя расширенный поиск, выберите Свод федеральных правил в разделе «Уточнить по коллекции», затем в разделе «Поиск в» выберите Citation в первом поле и введите « 7 CFR 1951.7″ во втором поле
- Используя поиск по цитированию, выберите Свод федеральных правил в поле «Выбор коллекции» выберите 2016 в поле «Выбрать год», выберите 7 в поле «Выбрать номер названия», а затем введите 1951 в поле «Часть» и 7 в поле «Раздел» .
Поиск по номеру заголовка — например, документы CFR из раздела 7.
- Используя обычный поиск, введите: collection:cfr and cfrtitlenum:7
- С помощью расширенного поиска выберите Свод федеральных правил в разделе «Уточнить по коллекции», затем в разделе «Поиск в» выберите CFR Title Number в первом поле и введите 7 во втором поле
Поиск по названию и номеру детали — документы CFR из раздела 7, часть 1951.
- Используя обычный поиск, введите: collection:cfr и cfrtitlenum:7 и cfrpartnum:1951
- С помощью расширенного поиска выберите Свод федеральных правил в разделе «Уточнить по коллекции», затем в разделе «Поиск в» выберите CFR Title Number в первом поле введите 7 во втором поле нажмите + Дополнительные критерии, выберите CFR Part Number в появившемся поле и введите 1951 в следующем поле
Поиск по ключевому слову — Например, документы Свода нормативных актов со словом «выбросы» в полном тексте публикации.
- С помощью основного поиска введите: выбросы и сбор:cfr
- Используя расширенный поиск, выберите Свод федеральных правил в поле «Уточнить по коллекции», затем в разделе «Поиск в» введите выбросы во втором поле
Образец URL-адресов Свода федеральных правил
Govinfo использует две ключевые части информации для построения предсказуемых URL-адресов документов и страниц сведений:
- Идентификатор гранулы для Свода федеральных правил используется для идентификации конкретного раздела, части , подраздел, глава или подглава в томе публикации.

- Идентификатор пакета используется для идентификации отдельного тома публикации.
| Идентификатор | Поле структуры/метаданных | Примеры |
|---|---|---|
| Номер гранулы | Глава Подраздел Part Subpart Раздел Примечание. Когда глава, подглава, часть, раздел или подчасть разбиты на несколько томов, комбинированные файлы недоступны, и доступ к прямым ссылкам на документы должен осуществляться на более детальном уровне. | CFR-2008-title39-vol1-chapI CFR-2008-title39-vol1-chapI-subchapB CFR-2008-title39-vol1-part20 CFR-2008-title39-vol1-part777-subpartA CFR-2008-title39-vol1-sec20-2 |
| Идентификатор пакета | CFR-{год}-название{номер названия CFR}-vol{номер тома CFR} | CFR-2008-title39-vol1 |
Наконечник: Вы также можете использовать службу ссылок и API для создания предсказуемых ссылок.
Страница сведений для определенного раздела, части, подраздела, главы или подраздела
Структура: https://www.govinfo.gov/app/details/{идентификатор пакета}/{идентификатор гранулы}
Пример: https://www.govinfo.gov/app/details/CFR-2008-title39-vol1 /CFR-2008-title39-vol1-sec20-2
PDF-файл для определенного раздела, части, подраздела, главы или подраздела
Структура: https://www.govinfo.gov/content/pkg/{ID пакета}/pdf/{ID гранулы}. pdf
pdf
Пример: https://www.govinfo.gov/content/pkg/CFR-2008-title39-vol1/pdf/CFR-2008-title39-vol1-sec20-2.pdf
XML-файл для определенного раздела, части, подраздела, главы или подраздела
Структура: https://www.govinfo.gov/content/pkg/{Идентификатор пакета}/xml/{Идентификатор гранулы}.xml
Пример: http://www.govinfo.gov/content/pkg/CFR-2008 -title39-vol1/xml/CFR-2008-title39-vol1-sec20-2.xml
Страница сведений для всего тома
Структура: https://www.govinfo.gov/app/details/{ID пакета}
Пример: http://www.govinfo.gov/app/details/CFR-2008-title39-vol1
PDF-файл для всего тома
Структура: https://www.govinfo.gov/content/pkg/{Идентификатор пакета}/pdf/{Идентификатор пакета}.pdf
Пример: http://www.govinfo.gov/content/pkg/CFR-2008 -title39-vol1/pdf/CFR-2008-title39-vol1.pdf
XML-файл для всего тома
Структура: https://www.govinfo.gov/content/pkg/{Идентификатор пакета}/xml/{Идентификатор пакета}. xml
xml
Пример: http://www.govinfo.gov/content/pkg/CFR-2008 -title39-vol1/xml/CFR-2008-title39-vol1.xml
Поля и значения метаданных
Поля и значения метаданных можно использовать для повышения релевантности ваших поисков. Поля метаданных, доступные для Свода федеральных правил, перечислены в таблице ниже. Поля и значения метаданных используются в govinfo для
- Сужение поиска,
- Просмотр правительственных публикаций,
- Полевые операторы,
- Расширенный поиск и
- Отображение на страницах сведений.
Поля и значения метаданных можно вводить в поле Basic Search с помощью операторов полей. Операторы полей, доступные для Свода федеральных правил, перечислены в таблице ниже вместе с примерами для каждого поля метаданных. Использование полевых операторов
Некоторые из этих полей метаданных доступны для использования в Advanced Search . Значения метаданных можно вводить в том же формате, что и поля, доступные на странице расширенного поиска. Использование расширенного поиска
Использование расширенного поиска
| Отображаемое имя поля метаданных | Определение поля метаданных | Полевой оператор | Пример(ы) полевого оператора |
|---|---|---|---|
| Коллекция | Коллекция, к которой принадлежит документ. Обычно то же, что и публикация или серия. | коллекция: | Коллекция: cfr Примечание: «cfr» используется для Свода федеральных правил | .
| Правительственный автор | Названия правительственных организаций, ответственных за авторство или сборку документа. | правительствоавтор: | правительство автор: «управление федерального регистра» |
| Дата публикации | Дата, когда документ впервые стал общедоступным. | Дата публикации: | publishdate:2016-01-01 Формат даты: ГГГГ, ГГГГ-ММ или ГГГГ-ММ-ДД |
| Язык | Код языка исходного документа из стандарта ISO639-2b. | язык: | язык:eng |
| Бывший идентификатор пакета | Идентификатор документа «пакета». | моды:идентификатор:(@type:»прежний идентификатор пакета»:»______») | mods:identifier:(@type:»прежний идентификатор пакета»:»44CFR») |
| Номер класса SuDoc | Номер класса SuDoc от Управляющего документами США, который классифицирует правительственные публикации по издательским агентствам. | судоккласс: | sudocclass:»AE 2.106/3:» Примечание. Номера классов SuDoc находятся на уровне основы класса, а не на уровне номера книги. |
| Дата приема | Дата поступления документа в репозиторий для сохранения. | дата приема: | ingestdate:2009-12-29 Формат даты: ГГГГ-ММ-ДД |
| Электронный адрес (URL) | URL-адрес, по которому находится документ или документ в контексте (страница сведений о содержимом). | адрес: | URL: pkg/CFR-2016-title1-vol1/pdf/CFR-2016-title1-vol1-sec1-1. pdf pdf |
| Издатель | Государственная организация, которая публикует документ или публикацию. Обычно это не государственное издательство (которое служит типографом и распространителем), за исключением публикаций Конгресса. | издатель: | издатель: «Управление Федерального реестра, Национальное управление архивов и документации» |
| Филиал | Ветвь правительства, ответственная за содержание документа. | филиал: | филиал:исполнительный Примечание: Возможные значения:исполнительный, законодательный, судебный |
| Тип ресурса | Тип носителя для документа, обычно «текст». Определяется как часть стандарта MODS Библиотеки Конгресса. | тип ресурса: | тип ресурса:текст |
| Имя базы данных WAIS | Имя базы данных WAIS, к которой принадлежал документ в прежней системе доступа GPO. | waisdbname: | waisdbname:2016_cfr_1v1 |
| Запись происхождения | Способ первоначального создания записи. Обычно «сгенерировано машиной». Обычно «сгенерировано машиной». | записьпроисхождение: | Recordorigin: «сгенерировано машиной» |
| Титул | Название публикации. | заголовок: | название:»сельское хозяйство» |
| Номер раздела CFR | CFR Title Number, целое число от 1 до 50. | cfrtitlenum: | cfrtitlenum:7 |
| Номер детали CFR | Номер деталиCFR, целое число части в названии. | номер детали: | cfrpartnum:1951 |
| Номер раздела CFR | Номер раздела CFR. | cfrsectionnum: | cfrsectionnum:94.1 |
| Товарная позиция | Поиск заголовка. | Рубрика: | заголовок: «часть 2» заголовок: «подчасть I» заголовок: «глава 9» |
| Тематическая группа CFR | Тематическая группа для разделов, обычно используемая для очень больших частей, таких как часть Налогового управления о подоходном налоге. | cfrsubject: | cfrsubject:»подоходный налог» |
| CFR Цитата | Ссылки на Свод федеральных правил. | ссылка: | ссылка: «40 CFR часть 32» |
| Раздел CFR | cfrpartheading: | cfrpartheading:»часть 2″ | |
| Раздел CFR | cfrparttitle: | cfrparttitle:»фонд капитального строительства» | |
| CFR Подраздел Заголовок | cfrsubpartheading: | cfrsubpartheading:»подчасть b» | |
| CFR Заголовок подраздела | cfrsubparttitle: | cfrsubparttitle:»регистрация пилотов» | |
| Раздел CFR | cfrchapterheader: | cfrchapterheading:»глава 2″ | |
| CFR Название главы | cfrchaptertitle: | cfrchaptertitle:»Жилищная служба в сельской местности» | |
| CFR Приложение Заголовок | cfrappзаголовок: | cfrappheading:»приложение А» | |
| Приложение CFR Название | cfrapptitle: | cfrapptitle:»альтернативные продукты для приема пищи» | |
| Заявление о содержании книги | cfrbookcontents: | cfrbookcontents:»части с 1 по 199 дюймов | |
| Управление CFR | cfrauthority: | cfrauthority:»44 USC Ch. 35″ 35″ | |
| Источник CFR | cfr источник: | cfrsource:»38 FR 25170″ | |
| Перекрестная ссылка CFR | cfrxref: | cfrxref:»42 CFR 110″ | |
| Редакционные примечания CFR | cфр.: | cfreditorial:»70 FR 57994″ | |
| Текст цитирования CFR: | код ссылки: | cfrcitationtext:»60 FR 13895, 15 марта 1995 г., с поправками 69 FR 42100, 14 июля 2004 г.» | |
| Цитата | Стандартный метод GPO для поиска ссылок на цитаты из выбранной публикации. | цитирование: | цитирование: «9 CFR 2.2» |
| Ссылка на законопроекты Конгресса | Ссылки на законопроекты Конгресса. | счетацитирование: | billscitation:»hr 1″ |
| Ссылка на отчет Конгресса | Ссылки на отчеты Конгресса. | Код: | Ссылка: «Отчет С. 99-296» |
| Справочник по государственному и частному праву | Ссылки на публичное или частное право. | цитата: | цитата:»общественное право 71-126″ |
| Код цитирования США | Ссылки на Кодекс США. | код нас: | uscodecitation:»42 U.S.C. 3121″ |
| Законы о крупных цитированиях | Ссылки на Уставы в целом. | уставСсылка: | ссылка на закон: «70 Стат. 1046» |
| Ссылка в Федеральном реестре | Ссылка на Федеральный реестр в стандартном формате цитирования. | трение: | фрикцион: «52 FR 49386» |
| Ссылка | Ссылка на другой документ в тексте документа. | повторное обращение: | рецитация: «42 USC 3121» |
Свод федеральных правил Связанные ресурсы
- Список затрагиваемых разделов CFR — Предложенные, новые и измененные федеральные правила, которые были опубликованы в Федеральном реестре с даты последней редакции раздела CFR.
- Просмотр затронутых частей CFR из Федерального реестра — окончательные и предлагаемые правила, влияющие на CFR и опубликованные в Федеральном реестре в течение последних 24 часов, недели, месяца или в течение определенного диапазона дат.

- Электронный свод федеральных правил (e-CFR) — регулярно обновляемая неофициальная редакционная подборка материалов CFR и поправок к Федеральному реестру, выпускаемая Управлением Национального архива и документации Федерального регистра и Государственным издательством.
- Правила.gov — Находите, просматривайте и отправляйте комментарии к федеральным правилам, которые открыты для комментариев и опубликованы в Федеральном реестре. Управляется Управлением программы электронного нормирования Агентства по охране окружающей среды США.
- Руководство по нормотворческому процессу (PDF) — Подготовлено Управлением Федерального регистра, Национальным управлением архивов и документации.
- Обратитесь в местную Федеральную депозитарную библиотеку — Включая выпуски до 1996 года с использованием Справочника Федеральной депозитарной библиотеки.
- Приобрести отдельные названия CFR в печатном виде — Из книжного интернет-магазина GPO
- Загрузить пакет CFR (годовой) в формате XML —
Из репозитория групповых данных GPO.

- Параллельная таблица полномочий и правил — Для Кодекса федеральных правил и Кодекса Соединенных Штатов
- Федеральный реестр — Издаваемый Управлением Федерального реестра, Национальным управлением архивов и документации (NARA), Федеральный реестр является официальным ежедневным изданием правил, предлагаемых правил и уведомлений федеральных агентств и организаций, а также распоряжений и других президентских документов.
- FederalRegister.gov — Неофициальное издание ежедневного Федерального реестра в формате HTML (на основе XML), предоставленное Управлением Федерального реестра, Национальным управлением архивов и документации.
- Reginfo.gov — Предоставляет достоверную и прозрачную информацию о разрабатываемых правилах
Свод федеральных правил Часто задаваемые вопросы
Когда публикуется Свод федеральных правил?
Свод федеральных правил (CFR) соответствует опубликованной печатной версии CFR. Когда выпускаются печатные издания, становится доступной и онлайн-версия. Если название или том CFR не указан в списке CFR, этот том не был опубликован в то время. Дата публикации конкретного Заголовка CFR варьируется в зависимости от Заголовка и тома и зависит от издателя. Свод федеральных правил публикуется Управлением Федерального регистра, Национальным управлением архивов и документации.
Если название или том CFR не указан в списке CFR, этот том не был опубликован в то время. Дата публикации конкретного Заголовка CFR варьируется в зависимости от Заголовка и тома и зависит от издателя. Свод федеральных правил публикуется Управлением Федерального регистра, Национальным управлением архивов и документации.
Как правило, тома CFR обновляются (не публикуются) один раз в календарный год поэтапно в соответствии с ежегодным циклом обновления. Годовой цикл обновления выглядит следующим образом: заголовки 1-16 обновляются с 1 января; Титулы 17-27 обновлены по состоянию на 1 апреля; Заголовки 28-41 обновлены по состоянию на 1 июля; Титулы 42-50 обновлены по состоянию на 1 октября.
В качестве альтернативного ресурса можно использовать Электронный свод федеральных правил (eCFR) — обновленную в настоящее время версию CFR. Это не официальное юридическое издание CFR. Электронный CFR представляет собой редакционную подборку материалов CFR и поправок к Федеральному реестру, подготовленных Управлением Федерального реестра (OFR) Национального управления архивов и документации (OFR) и Государственным издательством. OFR ежедневно обновляет материалы в e-CFR.
OFR ежедневно обновляет материалы в e-CFR.
Как получить доступ к электронному своду федеральных правил (eCFR)?
Электронный CFR доступен на сайте www.ecfr.gov.
Как сообщить об ошибках в своде федеральных правил (CFR) или e-CFR?
О технических ошибках на этом сайте следует сообщать в askGPO. Это поможет нам быстрее устранить проблему, если вы включите следующее:
- какое устройство вы используете (мобильное устройство, настольный компьютер и т. д.)
- конкретный URL-адрес страницы, к которой вы пытались получить доступ,
- шаги, которые вы предприняли, которые привели к ошибке,
- любые конкретные условия поиска или просмотра, которые вы использовали, и/или
- скриншот страницы, на которой произошла ошибка .
По вопросам или комментариям, касающимся редакционного содержания, функций или дизайна e-CFR, обращайтесь по электронной почте [email protected]
По вопросам, касающимся программирования и доставки e-CFR, обращайтесь по электронной почте [email protected]
Об ошибках, допущенных агентством, выдавшим документ следует сообщить в орган, издавший постановление. Агентство, издавшее постановление, указано в заголовке главы. Агентства исправляют свои ошибки, публикуя документы о поправках к CFR в Федеральном реестре. Документы по исправлению агентства обычно называются «окончательными исправлениями правил» или «техническими поправками».
Агентство, издавшее постановление, указано в заголовке главы. Агентства исправляют свои ошибки, публикуя документы о поправках к CFR в Федеральном реестре. Документы по исправлению агентства обычно называются «окончательными исправлениями правил» или «техническими поправками».
Как получить доступ к историческим изданиям Свода федеральных правил (CFR) или другим сборникам на этом сайте?
Этот сайт предоставляет доступ к большинству коллекций примерно с 1994 года (103-й Конгресс). Годы охвата каждой коллекции указаны рядом с названием коллекции на странице «Обзор от А до Я». Исторические версии или коллекции за годы можно получить в Федеральной депозитарной библиотеке. Федеральные публикации и другие информационные продукты доступны для бесплатного публичного использования в федеральных депозитарных библиотеках на всей территории Соединенных Штатов. В дополнение к публикациям, обученные библиотекари могут помочь в их использовании. Найдите Федеральную депозитарную библиотеку.
У вас есть единый файл PDF для всего издания или полных заголовков Свода федеральных правил?
В настоящее время невозможно загрузить целые издания или полные заголовки Свода федеральных правил (CFR) по адресу govinfo в виде одного файла PDF, за исключением случаев, когда все название состоит из одной книги/тома. Часто под одним названием имеется несколько томов (или печатных книг). Например, Title 49 напечатан в 9 томах. Вы не можете получить все название в одном электронном файле, потому что это не способ обработки документа. Электронные тома соответствуют печатным.
Что это значит, когда я вижу [Reserved] в CFR?
«[Зарезервировано]» — это термин, используемый в качестве заполнителя в Своде федеральных правил. Агентство использует «[Зарезервировано]», чтобы просто указать, что оно может вставить нормативную информацию в это место в будущем. Иногда «[Зарезервировано]» используется для обозначения того, что часть CFR была намеренно оставлена пустой, а не случайно удалена из-за ошибки печати или компьютера.
Содержание кальция в пищевых продуктах | Обучение пациентов
Молочные и соевые продукты | Сумма | Кальций (мг) |
Молоко (обезжиренное, обезжиренное, цельное) | 1 чашка | 300 |
Пахта | 1 чашка | 300 |
Творог | 0,5 стакана | 65 |
Мороженое или ледяное молоко | 0,5 стакана | 100 |
Сметана, кисломолочная | 1 чашка | 250 |
Соевое молоко, обогащенное кальцием | 1 чашка | от 200 до 400 |
Йогурт | 1 чашка | 450 |
Йогуртовый напиток | 12 унций | 300 |
Мгновенный завтрак с гвоздикой | 1 пакет | 250 |
Горячее какао, обогащенное кальцием | 1 пакет | 320 |
Молоко сухое обезжиренное | 5 столовых ложек | 300 |
Сыр Бри | 1 унция | 50 |
Твердый сыр (чеддер, джек) | 1 унция | 200 |
Моцарелла | 1 унция | 200 |
Сыр пармезан | 1 столовая ложка | 70 |
швейцарский или грюйерский | 1 унция | 270 |
Овощи
Тыква из желудей, приготовленная | 1 чашка | 90 |
Руккола, сырая | 1 чашка | 125 |
Бок Чой, сырой | 1 чашка | 40 |
Брокколи, приготовленная | 1 чашка | 180 |
Мангольд или бамия, приготовленные | 1 чашка | 100 |
Цикорий (кудрявый эндивий), сырой | 1 чашка | 40 |
Листовая капуста | 1 чашка | 50 |
Кукуруза в рассоле | 1 чашка | 10 |
Зелень одуванчика, сырая | 1 чашка | 80 |
Капуста, сырая | 1 чашка | 55 |
Бурые водоросли или Комбе | 1 чашка | 60 |
Листья горчицы | 1 чашка | 40 |
Шпинат, приготовленный | 1 чашка | 240 |
Зелень репы, сырая | 1 чашка | 80 |
Продолжить чтение
Фрукты
Инжир, сушеный, сырой | 1 чашка | 300 |
Киви, сырой | 1 чашка | 50 |
Апельсиновый сок, обогащенный кальцием | 8 унций | 300 |
Апельсиновый сок из концентрата | 1 чашка | 20 |
Бобовые
Фасоль гарбанзо, приготовленная | 1 чашка | 80 |
Бобовые, в целом, приготовленные | 0,5 стакана | от 15 до 50 |
Фасоль пинто, приготовленная | 1 чашка | 75 |
Соевые бобы, вареные | 0,5 стакана | 100 |
Темпе | 0,5 стакана | 75 |
Тофу, твердый, кальциевый набор | 4 унции | от 250 до 750 |
Тофу, мягкий обычный | 4 унции | от 120 до 390 |
Белая фасоль, приготовленная | 0,5 стакана | 70 |
Зерновые
Зерновые (обогащенные кальцием) | от 0,5 до 1 чашки | от 250 до 1000 |
Амарант, приготовленный | 0,5 стакана | 135 |
Хлеб, обогащенный кальцием | 1 срез | от 150 до 200 |
Рис коричневый, длиннозерный, сырой | 1 чашка | 50 |
Овсяные хлопья быстрого приготовления | 1 упаковка | от 100 до 150 |
Тортильи кукурузные | 2 | 85 |
Орехи и семена
Миндаль, поджаренный небланшированный | 1 унция. | 80 |
Семена кунжута, жареные целиком | 1 унция. | 280 |
Тахини с кунжутом | 1 унция. (2 столовые ложки) | 130 |
Семена подсолнечника сушеные | 1 унция. | 50 |
Рыба
Скумбрия консервированная | 3 унции. | 250 |
Лосось, консервированный, с костями | 3 унции. | от 170 до 210 |
Сардины | 3 унции. | 370 |
Прочее
Меласса, меласса | 1 столовая ложка | 135 |
* Когда указан диапазон, содержание кальция зависит от продукта.
* Содержание кальция в растительных продуктах различно. Большинство овощей, бобовых, орехов, семян и сухофруктов содержат некоторое количество кальция. Перечислены избранные важные источники хорошо усваиваемого кальция.
Каталожные номера:
- База данных USDA, Справочник 8 по программе Palm
- Боуз и Черч
Сколько вам нужно?
Возраст | Кальций (мг) |
1–3 года | 500 мг |
4–8 лет | 800 мг |
9-18 лет | 1300 мг |
19–50 лет | 1000 мг |
51–70 лет | 1200 мг |
70 лет и старше | 1200 мг |
Медицинские специалисты UCSF Health изучили эту информацию. Он предназначен только для образовательных целей и не предназначен для замены рекомендаций вашего врача или другого поставщика медицинских услуг. Мы рекомендуем вам обсудить любые вопросы или опасения, которые могут у вас возникнуть, с вашим поставщиком медицинских услуг.
Он предназначен только для образовательных целей и не предназначен для замены рекомендаций вашего врача или другого поставщика медицинских услуг. Мы рекомендуем вам обсудить любые вопросы или опасения, которые могут у вас возникнуть, с вашим поставщиком медицинских услуг.
Рекомендуемое чтение
Содержание холестерина в продуктах
Используйте эти таблицы для проверки содержания холестерина и жира в продуктах, которые вы едите. Это поможет вам следить за ежедневным потреблением холестерина.
Фолат
Диетическое эталонное потребление фолиевой кислоты или фолиевой кислоты составляет 400 микрограммов (мкг) в день. Тем не менее, многие люди не достигают этой цели. Узнайте больше здесь.
Получение достаточного количества кальция
Кальций важен для поддержания здоровья костей и зубов. Потребность в кальции наиболее высока во время роста и после менопаузы у женщин. Учить больше.
Рекомендации по диете с низким содержанием холестерина и насыщенных жиров
Ознакомьтесь с этими рекомендациями по диете с низким содержанием холестерина и насыщенных жиров, в том числе о том, как выбирать мясо, молочные продукты, фрукты и овощи и многое другое.
Рекомендации по диете с низким содержанием натрия
Основным источником натрия является поваренная соль. Средний американец съедает пять или более чайных ложек соли каждый день, что примерно в 20 раз больше, чем нужно организму. Учить больше.
Увеличение потребления клетчатки
Диета с высоким содержанием клетчатки снижает риск развития различных заболеваний и важна для здоровья пищеварительной системы и снижения уровня холестерина. Учить больше.
Содержание соевого белка в продуктах питания
Соя содержит изофлавоны генистеин и диадзен, которые не содержатся ни в каких других продуктах и, как доказано, снижают уровень холестерина в крови и замедляют потерю костной массы. Учить больше.
Ваш визит к врачу
Посмотрите наши 10 лучших советов, как сделать визит к врачу UCSF максимально беззаботным и продуктивным.
Связанные клиники
Клиника консультирования по вопросам питания в Центре семейной медицины в Лейкшоре
1569Бульвар Слоат, офис 333
Сан-Франциско, Калифорния 94132
(415) 353-2291
Среда, 8:30 — 16:45
Консультация по питанию на Парнасе
проспект Парнас, 400, второй этаж
Сан-Франциско, Калифорния 94143
(415) 353-2291
Пн-Пт, 8:00-16:45
4.
 Дополнительные инструменты потока управления — документация по Python 3.10.8
Дополнительные инструменты потока управления — документация по Python 3.10.8 Помимо только что введенного оператора while , Python использует обычный
операторы управления потоком, известные из других языков, с некоторыми особенностями.
4.1.
if Операторы Возможно, наиболее известным типом оператора является оператор if . За
пример:
>>> x = int(input("Пожалуйста, введите целое число: "))
Пожалуйста, введите целое число: 42
>>> если х < 0:
... х = 0
... print('Отрицательное значение изменено на ноль')
... Элиф х == 0:
... печать('Ноль')
... элиф х == 1:
... печать('Одиночный')
... еще:
... печать('Еще')
...
Более
Может быть ноль или более elif детали, а еще детали
по желанию. Ключевое слово « elif » является сокращением от «else if» и полезно.
во избежание чрезмерного отступа. если … элиф … elif … последовательность заменяет переключатель или case операторов найдено на других языках.
Если вы сравниваете одно и то же значение с несколькими константами или проверяете определенные типы или
атрибуты, вам также может пригодиться оператор match . Для большего
подробности см. в Заявлениях о матче.
4.2.
для Заявления Оператор for в Python немного отличается от того, что вы можете использовать.
в C или Pascal. Вместо того, чтобы всегда повторять арифметическую прогрессию
чисел (как в Паскале) или предоставление пользователю возможности определять как
шаг итерации и условие остановки (как C), оператор Python for перебирает элементы любой последовательности (списка или строки) в том порядке, в котором
они появляются в последовательности. Например (без каламбура):
>>> # Измерить несколько строк: ...words = ['кот', 'окно', 'дефенестрировать'] >>> для w прописью: ... напечатать (ш, лен (ш)) ... кошка 3 окно 6 открыть 12
Код, который изменяет коллекцию во время повторения этой же коллекции, может
быть сложным, чтобы получить право. Вместо этого обычно проще зациклить
над копией коллекции или для создания новой коллекции:
Вместо этого обычно проще зациклить
над копией коллекции или для создания новой коллекции:
# Создать коллекцию образцов
users = {'Ганс': 'активный', 'Элеонора': 'неактивный', '景太郎': 'активный'}
# Стратегия: перебирать копию
для пользователя, статус в users.copy().items():
если статус == 'неактивный':
удалить пользователей [пользователь]
# Стратегия: создать новую коллекцию
активные_пользователи = {}
для пользователя, статус в users.items():
если статус == 'активный':
active_users[пользователь] = статус
г.4.3. Диапазон
() Функция Если вам нужно перебрать последовательность чисел, встроенная функция range() пригодится. Генерирует арифметические прогрессии:
>>> для i в диапазоне (5): ... печать (я) ... 0 1 2 3 4
Данная конечная точка никогда не является частью сгенерированной последовательности; диапазон(10) генерирует
10 значений, допустимые индексы для элементов последовательности длины 10. Это
можно позволить диапазону начинаться с другого числа или указать другое
приращение (даже отрицательное; иногда это называют «шагом»):
Это
можно позволить диапазону начинаться с другого числа или указать другое
приращение (даже отрицательное; иногда это называют «шагом»):
>>> список (диапазон (5, 10)) [5, 6, 7, 8, 9] >>> список (диапазон (0, 10, 3)) [0, 3, 6, 9] >>> список(диапазон(-10,-100,-30)) [-10, -40, -70]
Для перебора индексов последовательности вы можете комбинировать range() и len() следующим образом:
>>> a = ['Мария', 'была', 'а', 'маленькая', 'ягненок'] >>> для i в диапазоне (len(a)): ... печать (я, а [я]) ... 0 Мария 1 было 2 часа 3 маленьких 4 ягненка
Однако в большинстве таких случаев удобно использовать перечислить () см. Техники зацикливания.
Странная вещь происходит, если вы просто печатаете диапазон:
>>> диапазон(10) диапазон(0, 10)
Во многих отношениях объект, возвращаемый range() , ведет себя так, как если бы это был список,
но на самом деле это не так. Это объект, который возвращает последовательные элементы
желаемую последовательность, когда вы повторяете ее, но на самом деле это не делает
список, тем самым экономя место.
Мы говорим, что такой объект является итерируемым, то есть подходящим в качестве цели для
функции и конструкции, которые ожидают чего-то, от чего они могут
получать последовательные предметы, пока запас не будет исчерпан. Мы видели это
9Оператор 1972 for является такой конструкцией, а пример функции
который принимает итерацию, равен sum() :
>>> сумма(диапазон(4)) # 0 + 1 + 2 + 3 6
Позже мы увидим больше функций, которые возвращают итерации и принимают итерации как
аргументы. В главе «Структуры данных» мы более подробно обсудим список() .
4.4.
break и continue Операторы и else Пункты в циклах Оператор break , как и в C, вырывается из самой внутренней оболочки. вместо или при цикле .
могут иметь предложение else ; он выполняется, когда цикл
завершается из-за исчерпания итерации (с вместо ) или когда
условие становится ложным (с в то время как ), но не тогда, когда цикл
завершается оператором break . Примером этому служит
следующий цикл, который ищет простые числа:
Примером этому служит
следующий цикл, который ищет простые числа:
>>> для n в диапазоне (2, 10): ... для x в диапазоне (2, n): ... если n % x == 0: ... print(n, 'равно', x, '*', n//x) ... ломать ... еще: ... # цикл сорвался, не найдя множителя ... print(n, 'является простым числом') ... 2 это простое число 3 это простое число 4 равно 2 * 2 5 это простое число 6 равно 2 * 3 7 это простое число 8 равно 2 * 4 9 равно 3 * 3
(Да, это правильный код. Посмотрите внимательно: еще пункт принадлежит
цикл for , не оператор if .)
При использовании с циклом предложение else имеет больше общего с предложением else пункт оператора try , чем с предложением if утверждения: выполняется предложение try оператора else когда не возникает никаких исключений, и предложение цикла else выполняется, когда нет break имеет место. Подробнее о 9Оператор 1972 try и исключения, см.
Обработка исключений.
Подробнее о 9Оператор 1972 try и исключения, см.
Обработка исключений.
Оператор continue , также заимствованный из C, продолжается следующим
итерация цикла:
>>> для числа в диапазоне (2, 10):
... если число% 2 == 0:
... print("Найдено четное число", число)
... Продолжать
... print("Найдено нечетное число", число)
...
Нашел четное число 2
Нашел нечетное число 3
Нашел четное число 4
Нашел нечетное число 5
Нашел четное число 6
Нашел нечетное число 7
Нашел четное число 8
Нашел нечетное число 94.5.
проход Заявления Оператор pass ничего не делает. Его можно использовать, когда оператор
требуется синтаксически, но программа не требует никаких действий. Например:
>>> пока верно: ... pass # Занят-ожидание прерывания клавиатуры (Ctrl+C) ...
Обычно используется для создания минимальных классов:
>>> класс MyEmptyClass: ... проходить ...
Другое место пропуск можно использовать в качестве заполнителя для функции или
условное тело, когда вы работаете над новым кодом, позволяя вам продолжать думать
на более абстрактном уровне.
пропуск молча игнорируется:
>>> по умолчанию initlog(*args): ... pass # Не забудьте реализовать это! ...
4.6.
соответствие Операторы Оператор match принимает выражение и сравнивает его значение с последовательным
шаблоны, представленные в виде одного или нескольких блоков case. это на первый взгляд
похож на оператор switch в C, Java или JavaScript (и многие
других языках), но это больше похоже на сопоставление с образцом в
языки, такие как Rust или Haskell. Только первый шаблон, который соответствует
выполняется, а также может извлекать компоненты (элементы последовательности
или атрибуты объекта) из значения в переменные.
Простейшая форма сравнивает предметное значение с одним или несколькими литералами:
по умолчанию http_error(статус):
статус матча:
случай 400:
вернуть "Неверный запрос"
дело 404:
вернуть "Не найдено"
дело 418:
вернуть "я чайник"
кейс _:
вернуть "Что-то не так с интернетом"
Обратите внимание на последний блок: «имя переменной» _ действует как подстановочный знак и
никогда не перестает совпадать. Если ни один случай не совпадает, ни одна из ветвей не выполняется.
Если ни один случай не совпадает, ни одна из ветвей не выполняется.
Вы можете объединить несколько литералов в один шаблон, используя | ("или"):
чехол 401 | 403 | 404:
вернуть "Не разрешено"
Шаблоны могут выглядеть как задания распаковки и использоваться для привязки переменные:
# точка представляет собой кортеж (x, y)
пункт совпадения:
случай (0, 0):
печать("Происхождение")
случай (0, у):
печать (е "Y = {y}")
случай (х, 0):
распечатать (ф"Х={х}")
случай (х, у):
печать (f"X={x}, Y={y}")
кейс _:
поднять ValueError("Нет точки")
г. Внимательно изучите это! Первый шаблон имеет два литерала и может
можно рассматривать как расширение буквального шаблона, показанного выше. Но
следующие два шаблона объединяют литерал и переменную, а
переменная связывает значение из субъекта ( точка ). Четвертый
шаблон захватывает два значения, что делает его концептуально похожим на
назначение распаковки (x, y) = точка .
Если вы используете классы для структурирования данных вы можете использовать имя класса, за которым следует список аргументов, напоминающий конструктор, но с возможностью захвата атрибутов в переменные:
класс Точка:
х: интервал
у: интервал
определение где_есть (точка):
пункт совпадения:
случай Point(x=0, y=0):
печать("Происхождение")
случай Point(x=0, y=y):
печать (е "Y = {y}")
случай Point(x=x, y=0):
распечатать (ф"Х={х}")
случай Точка():
печатать("Где-то еще")
кейс _:
print("Ни за что")
Вы можете использовать позиционные параметры с некоторыми встроенными классами, которые предоставляют
порядок их атрибутов (например, классы данных). Вы также можете определить конкретный
положение атрибутов в паттернах, установив __match_args__ специальный
атрибут в ваших классах. Если он установлен на («x», «y»), все следующие шаблоны
эквивалент (и все привязывают атрибут y к переменной var ):
Точка(1, вар) Точка(1, у=вар) Точка(х=1, у=вар) Точка (у = вар, х = 1)
Рекомендуемый способ чтения паттернов — смотреть на них как на расширенную форму того, что вы
поставил бы слева от присваивания, чтобы понять, какие переменные будут установлены в
какие. Только автономные имена (например,
Только автономные имена (например, var выше) назначаются оператором соответствия.
Имена с точками (например, foo.bar ), имена атрибутов ( x= и y= выше) или имена классов
(обозначаются знаком «(…)» рядом с ними, например, , пункт выше) никогда не назначаются.
Шаблоны могут быть произвольно вложены друг в друга. Например, если у нас есть короткий список точек, мы могли бы сопоставить его так:
очков матча:
кейс []:
print("Нет очков")
случай [Точка (0, 0)]:
print("Происхождение")
case [Точка (x, y)]:
print(f"Одна точка {x}, {y}")
случай [Точка (0, y1), Точка (0, y2)]:
print(f"Два по оси Y в точках {y1}, {y2}")
кейс _:
печатать("Что-то еще")
г. Мы можем добавить к шаблону предложение if , известное как «защита». Если
guard ложно, соответствует , чтобы попробовать следующий блок case. Примечание
этот захват значения происходит до оценки защиты:
точки совпадения:
case Point(x, y), если x == y:
print(f"Y=X в {x}")
случай Точка (х, у):
print(f"Не по диагонали")
Несколько других ключевых особенностей этого утверждения:
Подобно назначениям распаковки, шаблоны кортежей и списков имеют в точности одинаковое значение и фактически соответствуют произвольным последовательностям.
 Важно
исключение состоит в том, что они не соответствуют итераторам или строкам.
Важно
исключение состоит в том, что они не соответствуют итераторам или строкам.Шаблоны последовательности поддерживают расширенную распаковку:
[x, y, *rest]и(x, y, *остальное)работа аналогична распаковке заданий. имя после*также может быть_, поэтому(x, y, *_)соответствует последовательности не менее чем из двух элементов без привязки остальных элементов.Шаблоны сопоставления:
{"полоса пропускания": b, "задержка": l}фиксирует"пропускная способность"и"задержка"значения из словаря. В отличие от последовательности шаблоны, лишние ключи игнорируются. Распаковка вроде** остальныетакже поддерживается. (Но**_было бы лишним, поэтому это недопустимо.)Подмаски могут быть захвачены с использованием ключевого слова
Случайas:(точка (x1, y1), точка (x2, y2) как p2): .
 ..
..
захватит второй элемент ввода как
p2(пока ввод последовательность из двух точек)Большинство литералов сравниваются на равенство, однако синглтоны
True,FalseиNoneсравниваются по идентичности.Шаблоны могут использовать именованные константы. Это должны быть имена с точками чтобы они не интерпретировались как переменная захвата:
из импорта enum Enum Цвет класса (перечисление): КРАСНЫЙ = «красный» ЗЕЛЕНЫЙ = «зеленый» СИНИЙ = «синий» color = Color(input("Введите по вашему выбору "красный", "синий" или "зеленый": ")) соответствует цвету: чехол Цвет.КРАСНЫЙ: print("Я вижу красное!") цвет корпуса.ЗЕЛЕНЫЙ: print("Трава зеленая") чехол Цвет.СИНИЙ: print("Меня тошнит :(")г.
Более подробное объяснение и дополнительные примеры вы можете найти в PEP 636 , который написан в формате учебника.
4.7. Определение функций
Мы можем создать функцию, которая записывает ряд Фибоначчи в произвольное граница:
>>> def fib(n): # записать ряд Фибоначчи до n ... """Выведите ряд Фибоначчи до n.""" ... а, б = 0, 1 ... в то время как a < n: ... печать (а, конец = '') ... а, б = б, а+б ... Распечатать() ... >>> # Теперь вызовите функцию, которую мы только что определили: ... выдумка (2000) 0 1 1 2 3 5 8 13 21 34 55 89144 233 377 610 987 1597
Ключевое слово def вводит определение функции . Это должно быть
за которым следует имя функции и список формальных параметров в скобках.
Операторы, формирующие тело функции, начинаются со следующей строки.
должны быть с отступом.
Первый оператор тела функции необязательно может быть строковым литералом;
этот строковый литерал является строкой документации функции или docstring .
(Подробнее о строках документации можно найти в разделе Строки документации.)
Существуют инструменты, которые используют строки документации для автоматического создания онлайн или печатных материалов. документацию или позволить пользователю интерактивно просматривать код; это хорошо
потренируйтесь включать строки документации в код, который вы пишете, так что сделайте это привычкой.
документацию или позволить пользователю интерактивно просматривать код; это хорошо
потренируйтесь включать строки документации в код, который вы пишете, так что сделайте это привычкой.
выполнение функции вводит новую таблицу символов, используемую для локального
переменные функции. Точнее, все присвоения переменных в
функция сохраняет значение в локальной таблице символов; тогда как ссылки на переменные
сначала посмотрите в локальную таблицу символов, затем в локальные таблицы символов
включающие функции, затем в глобальную таблицу символов и, наконец, в таблицу
встроенных имен. Таким образом, глобальные переменные и переменные объемлющих функций
нельзя напрямую присвоить значение внутри функции (если только для глобального
переменные, названные в глобальный оператор или, для переменных включения
функции, названные в нелокальном операторе ), хотя они могут быть
упоминается.
Фактические параметры (аргументы) вызова функции введены в локальный
таблица символов вызываемой функции при ее вызове; таким образом, аргументы
передается с использованием вызова по значению (где значение всегда является ссылкой объекта ,
не стоимость объекта). 1 Когда функция вызывает другую функцию,
или вызывает себя рекурсивно, новый
для этого вызова создается локальная таблица символов.
1 Когда функция вызывает другую функцию,
или вызывает себя рекурсивно, новый
для этого вызова создается локальная таблица символов.
Определение функции связывает имя функции с объектом функции в Текущая таблица символов. Интерпретатор распознает объект, на который указывает это имя как определяемая пользователем функция. Другие имена также могут указывать на то же самое. функциональный объект, а также может использоваться для доступа к функции:
>>> выдумка <функция выдумки по адресу 10042ed0> >>> f = выдумка >>> f(100) 0 1 1 2 3 5 8 13 21 34 55 89
Приходя из других языков, вы можете возразить, что fib не функция, а
процедура, так как она не возвращает значение. На самом деле, даже работает без
Оператор return действительно возвращает значение, хотя и довольно скучное. Этот
значение называется None (это встроенное имя). Запись значения Нет обычно подавляется интерпретатором, если это единственное записанное значение. Вы можете увидеть это, если действительно хотите использовать
Вы можете увидеть это, если действительно хотите использовать print() :
>>> выдумка(0) >>> печать (выдумка (0)) Никтог.
Несложно написать функцию, которая возвращает список номеров Ряд Фибоначчи вместо печати:
>>> def fib2(n): # вернуть ряд Фибоначчи до n ... """Вернуть список, содержащий последовательность Фибоначчи до n.""" ... результат = [] ... а, б = 0, 1 ... в то время как a < n: ... result.append(a) # см. ниже ... а, б = б, а+б ... вернуть результат ... >>> f100 = fib2(100) # вызываем >>> f100 # пишем результат [0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
Этот пример, как обычно, демонстрирует некоторые новые возможности Python:
Оператор
returnвозвращает значение из функции.возвращаетбез аргумента выражения возвращаетНет. Падает конец функции также возвращаетNone.Оператор
result.append(a)вызывает метод объекта спискарезультат. Метод — это функция, которая «принадлежит» объекту и называется
Метод — это функция, которая «принадлежит» объекту и называется obj.methodname, гдеobj— некоторый объект (это может быть выражение), аимя_метода— имя метода, определяемого типом объекта. Разные типы определяют разные методы. Методы разных типов могут иметь одно и то же имя, не вызывая двусмысленности. (Можно определить самостоятельно типы объектов и методы, используя классы , см. Классы) Методappend(), показанный в примере, определен для объектов списка; Это добавляет новый элемент в конец списка. В этом примере это эквивалентнорезультат = результат + [a], но более эффективный.
4.8. Подробнее об определении функций
Также можно определять функции с переменным числом аргументов. Есть три формы, которые можно комбинировать.
4.8.1. Значения аргумента по умолчанию
Наиболее полезная форма — указать значение по умолчанию для одного или нескольких аргументов. Это создает функцию, которую можно вызвать с меньшим количеством аргументов, чем она есть.
определено, чтобы позволить. Например:
Это создает функцию, которую можно вызвать с меньшим количеством аргументов, чем она есть.
определено, чтобы позволить. Например:
def ask_ok(приглашение, повторных попыток=4, напоминание='Пожалуйста, попробуйте еще раз!'):
пока верно:
ок = ввод (подсказка)
если все в порядке ('y', 'ye', 'yes'):
вернуть Истина
если все в порядке ('n', 'нет', 'нет', 'нет'):
вернуть ложь
повторы = повторы - 1
если повторных попыток < 0:
поднять ValueError('неверный ответ пользователя')
распечатать (напоминание)
Эту функцию можно вызвать несколькими способами:
с указанием только обязательного аргумента:
ask_ok('Вы действительно хотите уйти?')с одним из необязательных аргументов:
ask_ok('Можно перезаписать файл?', 2)или даже со всеми аргументами:
ask_ok('Хорошо перезаписать файл?', 2, 'Давай, только да или нет!')
Этот пример также вводит ключевое слово в . Это проверяет, является ли или
не последовательность содержит определенное значение.
Это проверяет, является ли или
не последовательность содержит определенное значение.
Значения по умолчанию оцениваются в точке определения функции в , определяющий область действия , так что
я = 5
защита f (аргумент = я):
печать (аргумент)
я = 6
е()
напечатает 5 .
Важное предупреждение: Значение по умолчанию оценивается только один раз. Это делает разница, когда по умолчанию используется изменяемый объект, такой как список, словарь или экземпляры большинства классов. Например, следующая функция накапливает аргументы, переданные ему при последующих вызовах:
по определению f(a, L=[]):
L. добавить (а)
вернуть л
печать (ф (1))
печать (ф (2))
печать (ф (3))
г.Это напечатает
[1] [1, 2] [1, 2, 3]
Если вы не хотите, чтобы значение по умолчанию использовалось для последующих вызовов, вы можете вместо этого напишите такую функцию:
по определению f(a, L=Нет):
если L равно None:
Л = []
L. добавить (а)
вернуть л
добавить (а)
вернуть л
4.8.2. Аргументы ключевого слова
Функции также можно вызывать с помощью аргументов ключевого слова.
вида kwarg=значение . Например, следующая функция:
def parrot (напряжение, состояние = 'жесткий', действие = 'voom', тип = 'Норвежский синий'):
print("-- Этот попугай не стал бы", action, end=' ')
print("если вы поместите", напряжение, "вольты через него.")
print("-- Красивое оперение, тип")
print("-- Это", состояние, "!")
г. принимает один обязательный аргумент ( напряжение ) и три необязательных аргумента
( состояние , действие и тип ). Эта функция может быть вызвана в любом
из следующих способов:
parrot(1000) # 1 позиционный аргумент
parrot(voltage=1000) # 1 ключевой аргумент
parrot(voltage=1000000, action='VOOOOOM') # 2 ключевых аргумента
parrot(action='VOOOOOM', voltage=1000000) # 2 ключевых аргумента
parrot('миллион', 'лишенный жизни', 'прыжок') # 3 позиционных аргумента
parrot('тысяча', state='раздвигает ромашки') # 1 позиция, 1 ключевое слово
г.
, но все следующие вызовы будут недействительны:
parrot() # отсутствует обязательный аргумент parrot(voltage=5.0, 'dead') # аргумент без ключевого слова после аргумента ключевого слова parrot(110, voltage=220) # повторяющееся значение для одного и того же аргумента parrot(actor='John Cleese') # неизвестный ключевой аргумент
В вызове функции аргументы ключевого слова должны следовать за позиционными аргументами.
Все переданные аргументы ключевого слова должны соответствовать одному из аргументов
принимается функцией (например, год актер не является веским аргументом в пользу функции попугая ), и их порядок не важен. Это также включает
необязательные аргументы (например, попугай (напряжение = 1000) также допустимы).
Ни один аргумент не может принимать значение более одного раза.
Вот пример, который не работает из-за этого ограничения:
>>> функция определения (а): ... проходить ... >>> функция(0, а=0) Traceback (последний последний вызов): Файл "г.", строка 1, в TypeError: функция() получила несколько значений для аргумента 'a'

При наличии окончательного формального параметра вида **имя он получает
словарь (см. Типы сопоставления — dict), содержащий все аргументы ключевого слова, кроме
те, которые соответствуют формальному параметру. Это может сочетаться с формальным
параметр вида *имя (описано в следующем подразделе), который
получает кортеж, содержащий позиционный
аргументы вне списка формальных параметров. ( *имя должно встречаться
до **имя .) Например, если мы определим такую функцию:
def cheeseshop(вид, *аргументы, **ключевые слова):
print("-- У вас есть", kind, "?")
print("-- Извините, у нас все кончилось", kind)
для arg в аргументах:
печать (аргумент)
печать("-" * 40)
для кВт в ключевых словах:
печать (квт, ":", ключевые слова [квт])
Можно было бы назвать так:
cheeseshop("Лимбургер", "Очень жидко, сэр.",
«Он действительно очень, ОЧЕНЬ жидкий, сэр».
владелец магазина = "Майкл Пэйлин",
клиент = "Джон Клиз",
sketch="Эскиз сырной лавки")
г.
и, конечно же, будет напечатано:
.-- У вас есть Лимбургер ? -- Извините, мы все из Лимбургера Он очень жидкий, сэр. Он действительно очень, ОЧЕНЬ жидкий, сэр. ---------------------------------------- владелец магазина: Майкл Пэйлин клиент: Джон Клиз эскиз : Эскиз сырного магазина
Обратите внимание, что порядок, в котором печатаются аргументы ключевого слова, гарантирован. чтобы соответствовать порядку, в котором они были предоставлены в вызове функции.
4.8.3. Специальные параметры
По умолчанию аргументы могут быть переданы в функцию Python либо по позиции или явно по ключевому слову. Для удобочитаемости и производительности имеет смысл ограничить способ передачи аргументов, чтобы разработчику нужно было только смотреть в определении функции, чтобы определить, передаются ли элементы по положению, по положение или ключевое слово, или по ключевому слову.
Определение функции может выглядеть так:
def f(pos1, pos2, /, pos_or_kwd, *, kwd1, kwd2):
----------- ---------- ----------
| | |
| Позиционное или ключевое слово |
| - Только ключевое слово
-- Только позиционное
г.
, где / и * являются необязательными. Если они используются, эти символы указывают на тип
параметр тем, как аргументы могут быть переданы в функцию:
только позиционные, позиционные или ключевые слова и только ключевые слова. Параметры ключевого слова
также называются именованными параметрами.
4.8.3.1. Позиционные или ключевые аргументы
Если / и * отсутствуют в определении функции, аргументы могут
передаваться в функцию по позиции или по ключевому слову.
4.8.3.2. Только позиционные параметры
Если посмотреть на это немного подробнее, то можно отметить определенные параметры
как позиционно-только . Если позиционно-только , порядок параметров имеет значение, и
параметры не могут быть переданы по ключевому слову. Только позиционные параметры
ставится перед / (косая черта). / используется для логического
отделить позиционные параметры от остальных параметров. Если нет
Если нет / в определении функции нет позиционных-только
параметры.
Параметры, следующие за /, могут быть позиционными или ключевыми словами или только ключевыми словами .
4.8.3.3. Аргументы, содержащие только ключевые слова
Чтобы пометить параметры как только ключевое слово , указав, что параметры должны быть переданы
по аргументу ключевого слова, поместите * в список аргументов непосредственно перед первым Параметр , содержащий только ключевое слово.
4.8.3.4. Примеры функций
Рассмотрим следующие примеры определений функций, обращая особое внимание на
маркеры / и *:
>>> по умолчанию стандартный_аргумент (аргумент): ... печать (аргумент) ... >>> def pos_only_arg(arg, /): ... печать (аргумент) ... >>> def kwd_only_arg(*, arg): ... печать (аргумент) ... >>> def Combined_example(pos_only, /, standard, *, kwd_only): ... print(pos_only, standard, kwd_only)
Первое определение функции, standard_arg , самая знакомая форма,
не накладывает ограничений на соглашение о вызовах, и аргументы могут быть
передано по позиции или ключевому слову:
>>> стандартный_аргумент (2) 2 >>> стандартный_аргумент (аргумент = 2) 2
Вторая функция pos_only_arg ограничена использованием только позиционных
параметры, так как в определении функции есть /:
>>> pos_only_arg(1) 1 >>> pos_only_arg(arg=1) Traceback (последний последний вызов): Файл "г.", строка 1, в TypeError: pos_only_arg() получил некоторые позиционные аргументы, переданные как аргументы ключевого слова: 'arg'
Третья функция kwd_only_args разрешает только аргументы ключевых слов, как указано
по * в определении функции:
>>> kwd_only_arg(3) Traceback (последний последний вызов): Файл "", строка 1, в TypeError: kwd_only_arg() принимает 0 позиционных аргументов, но был задан 1 >>> kwd_only_arg(arg=3) 3
И последний использует все три соглашения о вызовах в одной и той же функции определение:
>>> комбинированный_пример (1, 2, 3) Traceback (последний последний вызов): Файл "г.", строка 1, в TypeError: Combine_example() принимает 2 позиционных аргумента, но было задано 3 >>> комбинированный_пример(1, 2, kwd_only=3) 1 2 3 >>> комбинированный_пример(1, стандартный=2, kwd_only=3) 1 2 3 >>> комбинированный_пример (pos_only=1, стандарт=2, kwd_only=3) Traceback (последний последний вызов): Файл " ", строка 1, в TypeError: в Combined_example() некоторые позиционные аргументы передаются как аргументы ключевого слова: 'pos_only'

Наконец, рассмотрим это определение функции, которое имеет потенциальную коллизию между позиционным аргументом имя и **kwds , который имеет имя в качестве ключа:
определение foo(имя, **kwds):
вернуть «имя» в kwds
Нет возможного вызова, который заставит его вернуть True в качестве ключевого слова 'имя' всегда будет привязан к первому параметру. Например:
>>> foo(1, **{'имя': 2})
Traceback (последний последний вызов):
Файл "", строка 1, в
TypeError: foo() получил несколько значений для аргумента «имя»
>>>
г. Но использование / (только позиционные аргументы) возможно, так как это позволяет имя в качестве позиционного аргумента и «имя» в качестве ключа в аргументах ключевого слова:
def foo(имя, /, **kwds):
вернуть «имя» в kwds
>>> foo(1, **{'имя': 2})
Истинный
Другими словами, имена позиционных параметров могут использоваться в **kwds без двусмысленности.
4.8.3.5. Резюме
Вариант использования определяет, какие параметры использовать в определении функции:
def f(pos1, pos2, /, pos_or_kwd, *, kwd1, kwd2):
В качестве руководства:
Используйте только позиционные, если вы хотите, чтобы имена параметров не доступны пользователю. Это полезно, когда имена параметров не имеют реального значение, если вы хотите обеспечить порядок аргументов, когда функция или если вам нужно взять некоторые позиционные параметры и произвольные ключевые слова.
Использовать только ключевые слова, когда имена имеют смысл и определение функции более понятным, указав имена или вы хотите предотвратить пользователи полагаются на позицию передаваемого аргумента.
Для API используйте только позиционирование, чтобы предотвратить критические изменения API если имя параметра будет изменено в будущем.
4.8.4. Списки произвольных аргументов
Наконец, наименее часто используемый параметр — указать, что функция может быть
вызывается с произвольным количеством аргументов. Эти аргументы будут упакованы
вверх в кортеже (см. Кортежи и последовательности). Перед переменным числом аргументов
может встречаться ноль или более нормальных аргументов.
Эти аргументы будут упакованы
вверх в кортеже (см. Кортежи и последовательности). Перед переменным числом аргументов
может встречаться ноль или более нормальных аргументов.
def write_multiple_items(файл, разделитель, *аргументы):
file.write(разделитель.join(аргументы))
Обычно эти аргумента с переменным числом аргументов будут последними в списке формальных
параметры, потому что они собирают все оставшиеся входные аргументы, которые
передается в функцию. Любые формальные параметры, которые идут после *args являются аргументами «только для ключевого слова», что означает, что они могут использоваться только как
ключевые слова, а не позиционные аргументы.
>>> def concat(*args, sep="/"):
... вернуть sep.join(аргументы)
...
>>> concat("земля", "марс", "венера")
'земля/марс/венера'
>>> concat("Земля", "Марс", "Венера", sep=".")
'земля.марс.венера'
г.4.8.5. Распаковка списков аргументов
Обратная ситуация возникает, когда аргументы уже находятся в списке или кортеже
но должны быть распакованы для вызова функции, требующей отдельного позиционного
аргументы. Например, встроенная функция
Например, встроенная функция range() ожидает отдельного начинают и останавливают аргументов. Если их нет отдельно, напишите
вызов функции с оператором * для распаковки аргументов из списка
или кортеж:
>>> list(range(3, 6)) # обычный вызов с отдельными аргументами [3, 4, 5] >>> аргументы = [3, 6] >>> list(range(*args)) # вызов с аргументами, распакованными из списка [3, 4, 5]
Таким же образом словари могут предоставлять аргументы ключевых слов с ** -оператор:
>>> def parrot(voltage, state='жесткий', action='voom'):
... print("-- Этот попугай не стал бы", action, end=' ')
... print("если положить", напряжение, "вольт через него.", end=' ')
... print("Е", состояние, "!")
...
>>> d = {"voltage": "четыре миллиона", "state": "погиб", "action": "VOOM"}
>>> попугай(**d)
-- Этот попугай не БУДЕТ, если через него пропустить четыре миллиона вольт. E's bleedin 'умер!
г.4.8.6. Лямбда-выражения
Небольшие анонимные функции можно создавать с помощью ключевого слова lambda . Эта функция возвращает сумму двух своих аргументов:
Эта функция возвращает сумму двух своих аргументов: lambda a, b: a+b .
Лямбда-функции можно использовать везде, где требуются функциональные объекты. Они есть
синтаксически ограничивается одним выражением. Семантически они просто
синтаксический сахар для нормального определения функции. Как вложенная функция
определений, лямбда-функции могут ссылаться на переменные из содержащего
объем:
>>> по умолчанию make_incrementor(n): ... вернуть лямбда x: x + n ... >>> f = make_incrementor(42) >>> ф(0) 42 >>> ф(1) 43
В приведенном выше примере используется лямбда-выражение для возврата функции. Другое использование это передать небольшую функцию в качестве аргумента:
>>> пары = [(1, 'один'), (2, 'два'), (3, 'три'), (4, 'четыре')] >>> pairs.sort (ключ = лямбда-пара: пара [1]) >>> пары [(4, 'четыре'), (1, 'один'), (3, 'три'), (2, 'два')]г.
4.8.7. Строки документации
Вот некоторые соглашения о содержании и форматировании документации
струны.
Первая строка всегда должна быть кратким, кратким описанием объекта. цель. Для краткости не следует явно указывать имя или тип объекта. так как они доступны другими способами (за исключением случаев, когда имя является глагол, описывающий работу функции). Эта строка должна начинаться с большой буквы букву и заканчивать точкой.
Если в строке документации больше строк, вторая строка должна быть пустой, визуально отделяющий сводку от остального описания. следующие строки должны быть одним или несколькими абзацами, описывающими вызов объекта условности, его побочные эффекты и т. д.
Синтаксический анализатор Python не удаляет отступы из многострочных строковых литералов в
Python, поэтому инструменты, обрабатывающие документацию, должны удалять отступы, если
желанный. Это делается с использованием следующего соглашения. Первая непустая строка после первая строка строки определяет величину отступа для
вся строка документации. (Мы не можем использовать первую строку, так как она
обычно рядом с открывающими кавычками строки, поэтому ее отступ не
очевидно в строковом литерале. ) Пробелы, «эквивалентные» этому отступу,
затем с самого начала удаляются все строки строки. Линии, которые
отступ меньше не должен встречаться, но если они встречаются, все их начальные пробелы
следует раздеться. Эквивалентность пробелов должна быть проверена после расширения
табов (до 8 пробелов, обычно).
) Пробелы, «эквивалентные» этому отступу,
затем с самого начала удаляются все строки строки. Линии, которые
отступ меньше не должен встречаться, но если они встречаются, все их начальные пробелы
следует раздеться. Эквивалентность пробелов должна быть проверена после расширения
табов (до 8 пробелов, обычно).
Вот пример многострочной строки документации:
>>> определение my_function():
..."""Ничего не делайте, но документируйте это.
...
... Нет, правда, ничего не делает.
... """
... проходить
...
>>> print(my_function.__doc__)
Ничего не делайте, но документируйте это.
Нет, правда, ничего не делает.
4.8.8. Аннотации функций
Аннотации функций являются полностью необязательными метаданными. информация о типах, используемых пользовательскими функциями (см. ПЭП 3107 и PEP 484 для получения дополнительной информации).
Аннотации хранятся в __аннотациях__ атрибут функции как словарь и не влияет ни на какую другую часть
функция. Аннотации параметров определяются двоеточием после имени параметра, за которым следует
выражением, вычисляющим значение аннотации. Возвращаемые аннотации
определяется литералом
Аннотации параметров определяются двоеточием после имени параметра, за которым следует
выражением, вычисляющим значение аннотации. Возвращаемые аннотации
определяется литералом -> , за которым следует выражение между параметром
список и двоеточие, обозначающее конец 9Заявление 1972 года защиты .
следующий пример имеет обязательный аргумент, необязательный аргумент и возвращаемое значение
аннотированное значение:
>>> def f(ветчина: ул, яйца: ул = 'яйца') -> ул:
... print("Аннотации:", f.__annotations__)
... print("Аргументы:", ветчина, яйца)
... вернуть ветчину + ' и ' + яйца
...
>>> f('спам')
Аннотации: {'ветчина': , 'return': <класс 'str'>, 'яйца': }
Аргументы: спам-яйца
спам и яйца
4.9. Интермеццо: стиль кодирования
Теперь, когда вы собираетесь писать более длинные и сложные фрагменты Python,
самое время поговорить о стиле кодирования . На большинстве языков можно писать (или более
лаконичный, отформатированный ) в разных стилях; некоторые более читабельны, чем другие. Всегда полезно сделать так, чтобы другие могли легко читать ваш код.
хороший стиль кодирования очень помогает в этом.
Всегда полезно сделать так, чтобы другие могли легко читать ваш код.
хороший стиль кодирования очень помогает в этом.
Для Python PEP 8 стал руководством по стилю, которого придерживается большинство проектов; он способствует очень читабельному и приятному для глаз стилю кодирования. Каждый питон разработчик должен прочитать его в какой-то момент; вот самые важные моменты извлечено для вас:
Использовать отступы в 4 пробела и без табуляции.
4 пробела — хороший компромисс между небольшими отступами (позволяет увеличить глубина вложенности) и большие отступы (легче читать). Вкладки представляют путаницы, и их лучше не использовать.
Переносите строки так, чтобы их длина не превышала 79 символов.
Это помогает пользователям с небольшими дисплеями и позволяет иметь несколько файлы кода рядом на больших дисплеях.
Используйте пустые строки для разделения функций и классов, а также больших блоков код внутри функций.

По возможности размещайте комментарии на отдельной строке.
Использовать строки документации.
Используйте пробелы вокруг операторов и после запятых, но не непосредственно внутри скобочные конструкции:
a = f(1, 2) + g(3, 4).Назовите свои классы и функции последовательно; соглашение заключается в использовании
UpperCamelCaseдля классов иlowercase_with_underscoresдля функций и методы. Всегда используйтеselfкак имя первого аргумента метода (дополнительную информацию о классах и методах см. в разделе Первый взгляд на классы).Не используйте причудливые кодировки, если ваш код предназначен для использования в международных среды. Python по умолчанию, UTF-8 или даже простой ASCII лучше всего работают в любом кейс.
Аналогично, не используйте не-ASCII-символы в идентификаторах, если есть только малейший шанс, что люди, говорящие на другом языке, будут читать или поддерживать код.

 Мотивация к учебной деятельности
Мотивация к учебной деятельности

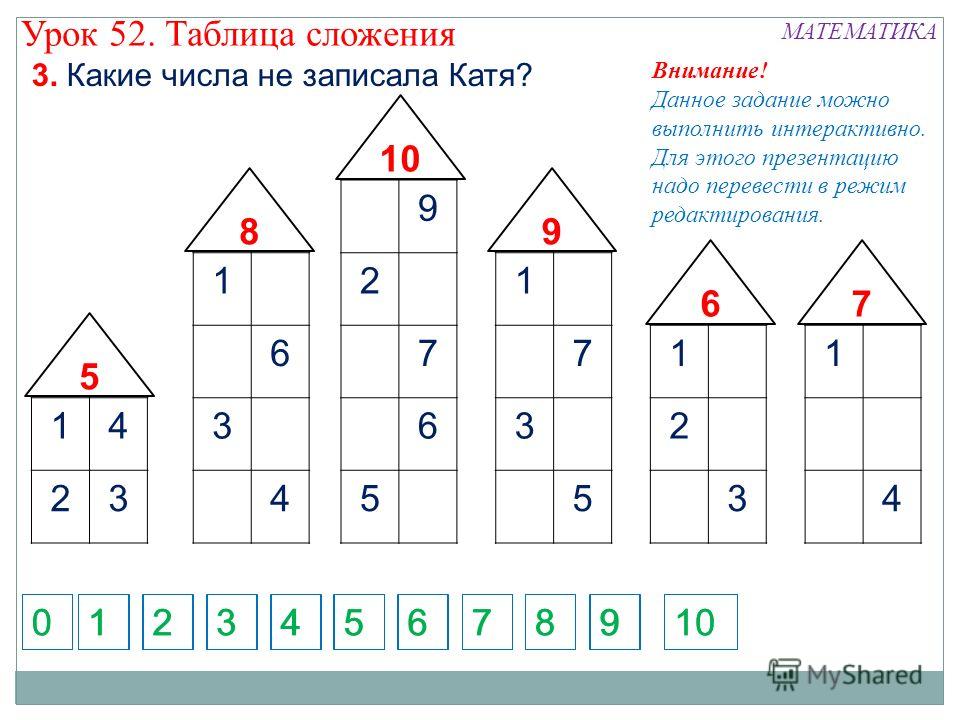



 . вы сегодня получаете отметку 5. Подойдите с дневниками после урока.
. вы сегодня получаете отметку 5. Подойдите с дневниками после урока.