а) Работа с  демонстрационным наглядным пособием «Абак с предметными картинками» (далее «Абак»).

б) Работа с картинкой из индивидуального наглядного пособия «Суперпапка», изображающей образ числа предметом реальной действительности.

в) Работа с таблицей из «Сказочного счета»: счет героев сказки,изображение их количества цифрой, на что она похожа и ее написание.

2. Расположение числа в натуральном ряду чисел и цветовом спектре. 

а) Работа с демонстрационным и индивидуальным пособиями «Линейка «Счет от 1 до 10».

б) Работа с нижней частью таблицы из «Сказочного счета» и правым верхним клапаном «Суперпапки».

3. Определение состава числа по готовой модели. 

Работа с иллюстрацией к сказке из комплекта таблиц «Сказочный счет».

4. Построение фиксированной предметной и числовой модели.  

Работа с демонстрационным наглядным пособием «Абак».

5. Построение динамичной предметной модели состава числа. 

Работа с демонстрационным наглядным пособием «Круги по составу чисел первого десятка».

6. Построение предметной, числовой и цветовой модели состава числа и предъявление информации в развернутом виде. 

Работа с демонстрационным и индивидуальным пособием «Компьютер».

7. Закрепление состава числа. Самостоятельная работа в тетради.

8. Систематизация знаний.

Работа с демонстрационными и индивидуальными наглядными пособиями «Радужная горка» и «Числовая горка». Взаимопроверка и самопроверка.

9. Проверка знаний учителем. 

Работа с индивидуальными «Цветовыми сигнальными карточками».

Реализацию алгоритма изучения чисел первого десятка рассмотрим на примере изучения числа 6.

ТЕХНОЛОГИЯ ИЗУЧЕНИЯ ЧИСЕЛ ПЕРВОГО ДЕСЯТКА 

1. Знакомство с числом и цифрой 6 

а) Работа с демонстрационным наглядным пособием «Абак» ( рис. 1).

 Учитель: «Ребята, на прошлых уроках мы с вами познакомились с числом 5. (Учитель показывает на «Абаке».) Сегодня познакомимся со следующим числом (учитель делает паузу и отодвигает полоску, и дети видят, что появилось шестое яблочко). Учащиеся хором: «Шесть». Учитель: «Правильно. Число «шесть» обозначается цифрой 6». Учитель отодвигает верхнюю полоску, появляется цифра 6 . 

Рис. 1 

б) Работа с картинкой из «Суперпапки». 

Учитель: «Как вы думаете, почему на рисунке изображена божья коровка? (У насекомых 6 лапок). 

Рис. 2

в) Работа с таблицей из «Сказочного счета» «Репка». 

Дети считают героев сказки, находят изображение их количества цифрой 6 в голубых прямоугольниках. Для усиления ассоциативных связей учитель читает стихотворение:  Цифра шесть – дверной эамочек: Сверху крюк, внизу кружочек Написание цифры 6. Образец прописной цифры дается в таблице (рис. 3) и ее написание на верхнем левом клапане «Суперпапки. 

 Рис. 3

2. Расположение числа 6 в натуральном ряду чисел 

а) Работа с демонстрационной (рис. 4) и индивидуальной (рис.5) линейкой «Счет от 1 до 10». 

«Посчитаем хором», – говорит учитель и передвигает окошко вправо на демонстрационной линейке (Один, два, три, четыре, пять). А если к пяти прибавим один, – продолжает он, – получится? (Шесть). Учитель передвигает окошко, и в нем появляется цифра 6. 

Рис. 4 

«Достаньте из «Суперпапки…» линейки с обезъянкой. Передвигая окошко, хором посчитаем до шести. Посмотрите на соседей числа 6 и назовите предыдущее число (5), последующее (7)». 

Рис.5

Работа в парах. Закрепление понятий «предыдущее» число и «последующее», соседи «справа» и «слева». 

б) Работа с нижней частью таблицы из «Сказочного счета». 

Учащиеся видят, что число 6 находится на шестом месте в прямоугольнике голубого цвета и в правом верхнем клапане «Суперпапки» оно тоже обозначено голубым цветом. 

3. Определение состава числа по готовой модели.  

Работа с иллюстрацией к сказке «Репка». 

Учитель спрашивает: «Сколько людей изображено на картинке и сколько животных? (3 и 3). Сколько героев сказки тянут репку, и сколько дожидается своей очереди? (4 и 2). Сколько держится за репку и сколько не держится? (1 и 5) и т. д. 

4. Построение фиксированной предметной 

модели состава числа 6. 

Работа с «Абаком» (рис.6). 

Учитель открывает 5 матрешек, а затем 1 мишку. «Составьте равенства по картинкам и продиктуйте их мне» – говорит учитель и записывает на доске и т. д. 

 5 + 1 = 6 

4 + 2 = 6 

3 + 3 = 6 

Рис. 6

5. Построение динамичной предметной 

модели состава числа 6.

Работа с демонстрационным наглядным пособием «Круги по составу чисел первого десятка» (рис. 7). 

Учитель вращает два круга, соединенные по радиусу щелевым креплением. На светло-голубом круге расположены тюльпаны, а на темно-голубом – розы (рис.5). – Итак, ребята, посмотрите на круги.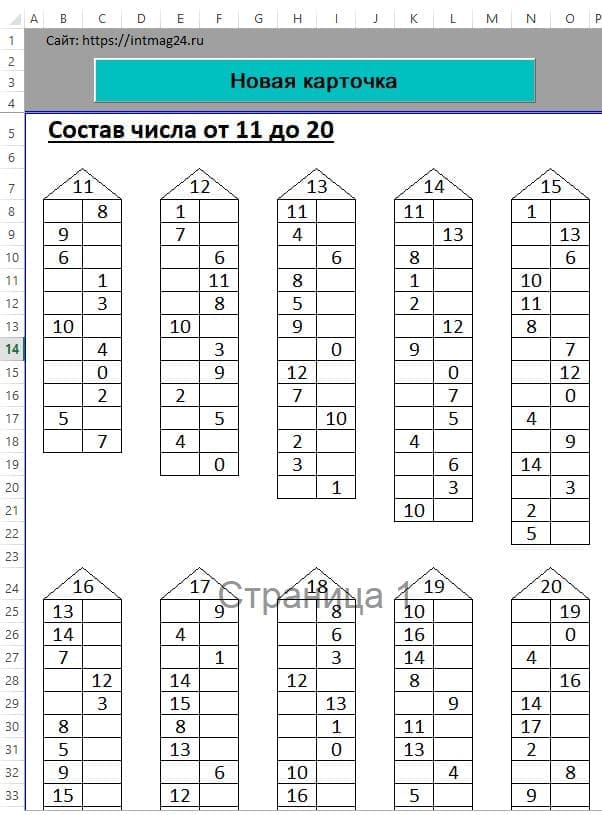 Они нам подсказывает, что 6 – это… – дети хором называют 5 и 1, 4 и 2, 3 и 3, 2 и 4, 1 и 5 (Продолжается формирование понятия о переместительном свойстве сложения). 

Рис. 7 

6. Построение предметной, цветовой и 

цифровой модели состава числа 6 

«Работа с демонстрационным и индивидуальным наглядным пособием «Компьютер». Учитель берет из «Компьютера» полоску с шестью голубыми кружочками и цифрой 6 и ставит ее в наборное полотно (нижний карман) (рис. 8 а). Учащиеся выполняют то же, используя индивидуальное пособие «Математика от 1 до 20. Суперпапка».

           а)                     б)                             в)              Рис. 8

Учитель берет полоску с пятью зелеными кружочками и цифрой 5 и полоску с белым кружочком и цифрой 1, накладывает их на первую. Учащиеся видят, что сумма длин этих полосок равна длине полоски с цифрой 6 и повторяют действия учителя на своих «Компьютерах» (рис. 8 б). Затем учитель берет полоску с четырьмя желтыми кружочками и цифрой 4 и полоску с двумя красными кружочками и цифрой 2 и ставит в наборное полотно, накладывая на предыдущие полоски (рис. 8 в).

  Полоска с 3-мя оранжевыми кружочками одна, поэтому она накладывается справа, и учащиеся видят 3 желтых и 3 оранжевых кружочка. 

Рис. 9

Предъявление информации в развернутом виде

 Учитель вынимает полоски, укрепляет их на доске и делает соответствующую запись, а учащиеся раскладывают на партах так, как показано на рисунке 9. 

7. Построение системы знаний «Состав числа 6» 

Самостоятельная работа. 

После работы со своим «Компьютером», учащиеся строят схемы по клеткам в тетради и записывают равенства (рис.10). Кружочки рисуются простым карандашом, вторые слагаемые заштриховываются. Сверка полученных знаний со справочным материалом – «домиком» голубого цвета на правом клапане «Суперпапки». 

Рис. 10 

8. Систематизация полученных знаний 

Работа с демонстрационными и индивидуальными наглядными пособиями «Радужная горка», «Числовая горка» и «Домик». 

На таблице к числу 10 в «Сказочном счете» дана иллюстрация к сказке Альфа Прейсена «Про Козленка, который умел считать до десяти». На ней изображен парусник, а на его парусе – «Радужная горка» (рис. 11). Каждое число первого десятка выражено определенным количеством цветных шариков. Следовательно, «Радужная горка» является предметной и цветовой моделью таблицы сложения в пределах 10. 

Как видим, эта таблица используется так же при изучении чисел от 1 до 9. Только нужно закрыть полосками бумаги ее верхнюю и нижнюю часть. «Числовая горка» (рис. 12) является цветовой, графической и знаковой моделью таблицы. 

«Домик» в «Суперпапке» – знаковой моделью. Он расположен на «улице», которую дети построили сами, и назвать ее можно «Улицей первого десятка». 

Каждое из этих пособий представляет систему знаний. Состав каждого числа первого десятка является ее составной частью и занимает в ней определенное место. 

Совершая перевод информации из одной системы в другую, ученики кодируют и декодируют ее. Значимость такой работы заключается в том, что, человеческая психика формируется в процессе работы с разными знаковыми системами (Л. С. Выготский). 

Работа с демонстрационными пособиями.

                                                       Рис. 11                                                Рис. 12 

Вызываются 2 ученика. Линейкой ограничиваются 6 голубых шариков. 

1) Работа в паре. Один ученик показывает 5 зеленых шариков, а другой – 1 белый; один – 2 красных, другой – 4 желтых; один – 3 оранжевых, другой – их же. 

2) Взаимопроверка. Найди пару в Радужной горке» и «Числовой горке». Один ученик показывает, например, в «Радужной горке» 5 зеленых шариков и 1 белый, а другой для проверки – 5 и 1 в «Числовой горке» (оба числа в прямоугольниках красного цвета – значит задание выполнено правильно). 

Работа с индивидуальными пособиями. 

«Суперпапка» разворачивается так, чтобы сверху были обе горки и «домики». Длинной линейкой ограничивается 6 голубых шариков и ряд чисел 6, 5, 4, 3, 2, 1 (рис. 13). 

Рис.13 

В паре выполняются те же задания. 

Самопроверка. 

Ученик двумя пальцами левой руки показывает пары шариков, например, 4 и 2, а пальцами правой – пары чисел 4 и 2, если они расположены в одинаковых геометрических фигурах (они в кругах), то задание выполнено верно. Сверяется с «домиком». 

9. Проверка знаний учителем 

Работа с «Цветовыми сигнальными карточками». 

Учитель называет одно из слагаемых числа 6, например, 4, а дети показывают при помощи карточек другое слагаемое – 2. На обороте карточек можно написать соответствующие цвету цифры, например, на красной – 2. 

Таким образом, в течение нескольких секунд учитель имеет возможность при помощи средств оперативной обратной связи проверить знание всеми учащимися состава числа 6. 

По данному алгоритму изучаются все случаи сложения и вычитания я в пределах первого десятка. 

Реализация технологии предполагает точное следование определенному алгоритму. В педагогической технологии соблюсти данное требование сложно, да и нецелесообразно, чтобы не подавить проявление творчества учителя и ученика, так как одной из основных задач школы является формирование творческой личности.

В начало статьи

Наглядные пособия

Главная

2. Вычислительные приемы для чисел первого десятка

Вычислительные приемы первого десятка изучаются в теме «Сложение и вычитание в пределах 10» в 1 классе при обучении по любому учебнику математики для начальных классов. Результатом изучения данной темы должно явиться формирование осознанной самостоятельной вычислительной деятельности ребенка. При этом программой оговорена необходимость знания наизусть результатов действий сложения и вычитания в пределах 10 (так называемое «табличное сложение и вычитание»).

Присчитывание и отсчитывание

Первым вычислительным приемом, который осваивает первоклассник, является прием вида a ± 1. Основой данного приема является принцип образования чисел в натуральном ряду: каждое следующее число на единицу больше предыдущего.

Усвоение ребенком этого принципа являлось

Следствием этого принципа является способ нахождения значений выражений вида 5 + 1; 8 + 1; 6 — 1; 7 — 1 и т. п. путем называния либо следующего, либо предыдущего числа. Иными словами, для нахождения значения данных выражений нет необходимости выполнять какой-то прием арифметических действий, достаточно понимать, что добавление 1 ведет к получению следующего по счету числа, а убавление 1 — к появлению предыдущего по счету числа. Именно для получения результатов в таких выражениях ребенок заучивал наизусть названия чисел в прямом и обратном порядке.

Число предыдущее стоит в ряду чисел левее данного. При счете называется непосредственно перед данным, количественно оно содержит на одну единицу меньше данного.

Число последующее (следующее) стоит в ряду чисел правее данного. При счете называется непосредственно после данного, количественно оно содержит на одну единицу больше данного.

Хорошее понимание принципа построения натурального ряда чисел ведет к легкому освоению приемов присчитывания и от-считывания по 1 и легкому выполнению вычислительной деятельности в случаях:

7+1 17+ 1 177+ 1 10 277 + 1

7- 1 17- 1 177- 1 10 277-1

Во всех случаях ссылка на принцип построения натуральной последовательности чисел является наиболее рациональной вплоть до 4 класса (общий прием вычислений):

— прибавляя к числу 1, получаем следующее по счету;

— вычитая из числа 1, получаем предыдущее по счету.

Этот же прием является действующим и в трудных случаях (вплоть до 4 класса):

9+ 1 19+ 1 199 + 1 999 + 1 99 999 +1

10- 1 20- 1 200 — 1 1 000 — 1 100 000 — 1

При нахождении ответа в данных примерах удобно ссылаться на порядок счета: следующим за числом 99 999 является число 100 000; предшествующим числом для числа 1 000 является 999.

В «Методике преподавания математики в начальных классах» (авт. М.А. Бантова, Г.В. Бельтюкова) отмечается, что «на специально отведенном уроке… под руководством учителя дети составляют таблицы «прибавить 1» и «вычесть 1» и затем заучивают их наизусть». При хорошем усвоении принципа образования чисел в натуральном ряду нет необходимости организовывать специальное заучивание результатов этой таблицы, поскольку умение ребенка называть ее результаты связано с хорошим знанием прямой и обратной последовательности чисел в пределах 10.

Использование линейки в качестве наглядной опоры для запоминания последовательности чисел, а также для усвоения способа нахождения числа последующего и предыдущего создает хорошие условия для

Для детей с ведущим кинестезическим восприятием и ведущим кинестезическим типом памяти (т. е. требующим обязательной поддержки словесной информации мышечным усилием, двигательным действием) следует не только допускать, но и поощрять использование пальцевого счета при изучении всех вычислительных приемов первого десятка. Естественно, этот вариант внешнего подкрепления вычислительной деятельности является более медленным, многим учителям он кажется недопустимым для школьников, а потому старательно искореняется уже при обучении вычислениям в пределах первого десятка. В качестве аргумента защиты использования этого способа подкрепления вычислительной деятельности для детей с ведущим кинестезическим типом можно привести многочисленные исследования психологов последних десятилетий, подтверждающие, что при исключении двигательных действий у этих детей и при ориентации на заучивание результатов без подкрепления предметной деятельностью усвоение происходит на формальном уровне, по принципу зазубривания без понимания, а в дальнейшем это крайне осложняет формирование вычислительной деятельности с числами в пределах сотни, тысячи и т.

Прибавление и вычитание по частям

Следующую группу вычислительных приемов в пределах первого десятка составляют случаи вида: a ± 2, a ± 3, a ±4, результаты которых могут быть найдены с помощью последовательного присчитывания или отсчитывания:

2 + 3 = 2 + 1 + 1 + 1; 7-4 = 7-1-1-1-1 или с помощью прибавления и вычитания по частям:

2 + 3 = 2 + 1 + 2; 7-4 = 7-2-2

Подготовительным приемом к обучению ребенка этим случаям вычислений является прием вида: я+1 + 1ия-1-1,в основе которого лежит последовательное отсчитывание по 1 или присчитывание по 1.

Знакомство с этим приемом является очень важным. Во-первых, осваивая данный вычислительный прием, ребенок впервые встречается с выражением, содержащим более одного знака действий. Во-вторых, при выполнении вычислений впервые в неявном виде (т. е. без сообщения ребенку самого правила) используется правило порядка выполнения действий одной ступени без скобок:

При выполнении действий одной ступени без скобок, действия выполняются по порядку слева направо.

В-третьих, при выполнении данного вида вычислений не нужны специальные вычислительные действия какого-то нового вида, а требуется лишь последовательное применение принципа образования чисел в натуральном ряду.

Например:

Вычислите 6 + 1 + 1.

(Прибавляя к 6 единицу, получаем число следующее — это 7; прибавляя к 7 единицу, получаем следующее число — это 8. Значит, 6+1+1 — 8.)

В качестве наглядной модели удобно использовать линейку — прибавляя единицу дважды, ребенок делает вправо от числа 6 два «шага», получая ответ наглядно (на первых порах эти «шаги» полезно прослеживать пальцем).

При использовании пальцевого счета, ребенок отгибает (или загибает) последовательно два пальца, присчитывая их к 6 пальцам, или, в крайнем случае, сосчитывая заново все количество отогнутых (загнутых) пальцев.

Аналогично ребенок действует в случае вычислений вида

Вычислительный прием а ±2 является случаем, объединяющим последовательное присчитывание (отсчитывание) двух единиц к числу, производимое в предыдущем случае.

При прибавлении к любому числу двух, ребенок заменяет его на сумму двух единиц и последовательно присчитывает (отсчитывает) их от числа.

Например: 3 + 2 = 3+1 + 1

1 1

В качестве наглядной модели удобно использовать линейку — прибавляя два, ребенок делает вправо от числа два «шага», получая ответ наглядно.

В качестве наглядной модели удобно также использовать счеты, поскольку прибавляя или вычитая 2, ребенок чаще всего перебрасывает дважды по одной косточке, фактически моделируя приведенную выше схему приема. Если ребенок сначала сосчитывает на счетах две косточки, а потом перебрасывает их, он, как правило, затем при нахождении результата сосчитывает заново все количество оставшихся (полученных) косточек.

При использовании пальцевого счета, ребенок отгибает (или загибает два пальца, присчитывая (или отсчитывая) два или сосчитывая весь результат.

Методически ставится цель довести умение ребенка прибавлять и отнимать 2 до состояния навыка, т. е. до запоминания результатов прибавления и вычитания двух в пределах 10

1+2=3 2+2=4 3+2=5 4+2=6

5+2=7 6+2=8 7+2=9 8+2=10

3-2=1 4-2=2 5-2=3 6-2=4

7-2=5 8-2=6 9-2=7 10-2=8

Таблица сложения и вычитания двух содержит самое большое количество случаев, а поскольку она изучается первой, многие дети испытывают большие трудности, пытаясь заучить этот объем.

Если ребенок хорошо владеет приемами присчитывания и отсчитывания, он всегда может вычислить забытый случай из таблицы, используя осознанную вычислительную деятельность. Для многих детей с проблемами процессов запоминания (это характерно для многих часто болеющих детей, что обусловлено действием некоторых медицинских препаратов, для детей с синдромом дефицита внимания, с гиперподвижностью, для детей с задержкой развития и т.д.) формирование осознанной вычислительной деятельности — это единственно возможный путь избежать мучительного и бессмысленного зазубривания.

Если при изучении чисел в пределах 10 (в разделе «нумерация в пределах 10»), ребенок выучил наизусть состав однозначных чисел и легко его воспроизводит, то проще всего для запоминания таблицы сложения и вычитания связать соответствующие случаи с составом однозначных чисел:

3 значит 3 = 1 + 2 тогда 1 + 2 = 3,а3-2 =1

1 2

7 значит 7 = 5 + 2 тогда 5 + 2 = 7,а7-2 = 5

5 2

При опоре на состав числа имеет смысл сразу ориентировать ребенка на составление и запоминание тройки взаимосвязанных равенств:

8 6 + 2 = 8, 8-2 = 6, 8-6 = 2

6 2

Умение прибавлять и вычитать 2 является опорным умением для формирования дальнейшей вычислительной деятельности.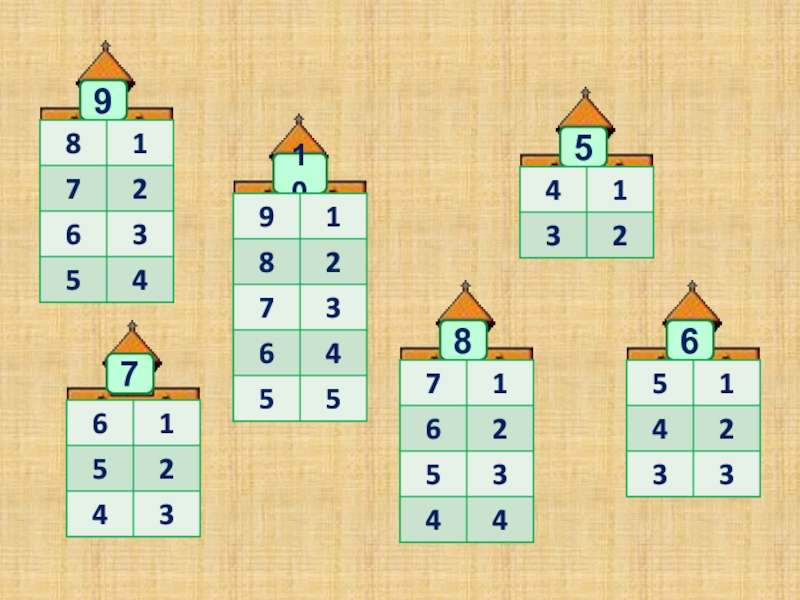

Вычислительные приемы а + 3 и а ± 4 могут выполняться последовательным присчитыванием или отсчитыванием по 1:

8-4 = 8-1-1-1-1; 6 + 3 = 6+1 + 1 + 1

В этом случае используется ссылка на понятие числа предыдущего и последующего. Может быть использована линейка, по которой ребенок делает нужное количество «шагов» вправо или влево от заданного числа, или пальцевый счет. Методически этот способ считается менее совершенным, чем прибавление и вычитание по частям для данных вычислительных приемов.

57

Прибавление (или вычитание) по частям предполагает раскладывание второго слагаемого (или вычитаемого) на удобные для выполнения вычислений составные части, и последовательное их прибавление (или вычитание):

Например:

Приведенные примеры показывают, что с приемами а±Зиа±А легче справиться тем детям, которые помнят наизусть результаты случаев прибавления и вычитания двух, или могут достаточно быстро найти (вычислить) эти результаты.

Именно для освоения вычислений вида а±3иа±4 предыдущую таблицу для случая а ± 2 учитель требовал заучивать наизусть.

После освоения приема вычислений по частям, составляют таблицы для случаев а ± 3:

1+3=4	2+3=5	3+3=6
4+3=7	5+3=8	6+3=9	7+3=10
4-3=1	5-3=2	6-3=3
7-3=4	8-3=5	9-3=6	10-3=7

а также а ± 4:

1+4=5	2+4=6	3+4=7
4+4=8	5+4=9	6 +4=10
5-4=1	6-4=2	7-4=3
8-4 = 4	9-4 = 5	10-4 = 6

Первая таблица содержит 14 случаев, вторая таблица содержит 12 случаев. В сумме с 16 случаями таблицы прибавления двух получается 42 случая. Неудивительно, что очень многие дети на этапе изучения табличного сложения и вычитания в пределах 10 испытывают массу трудностей, в связи с необходимостью в достаточно короткие сроки заучить наизусть большой объем формализованного материала. При этом единственным мотивом изучения этого объема наизусть для ребенка выступает требование учителя. Все задания на решение примеров в этот период (а также на решение задач, на сравнение выражений и т. п.) требуют воспроизведения наизусть табличных случаев сложения и вычитания вразбивку. Поэтому, если ребенок учил таблицу наизусть подряд (например, по возрастанию результатов и т. п.), то даже легко отвечая ее результаты подряд, он может ошибаться при воспроизведении таблицы вразбивку, и тем более при необходимости воспроизводить вразбивку случаи из разных таблиц.

В связи с этим при запоминании таблиц для случаев вида а±3 и а ± 4 многие учебники математики для 1 класса ориентируют ребенка на использование состава числа как основы для запоминания таблиц сложения и вычитания.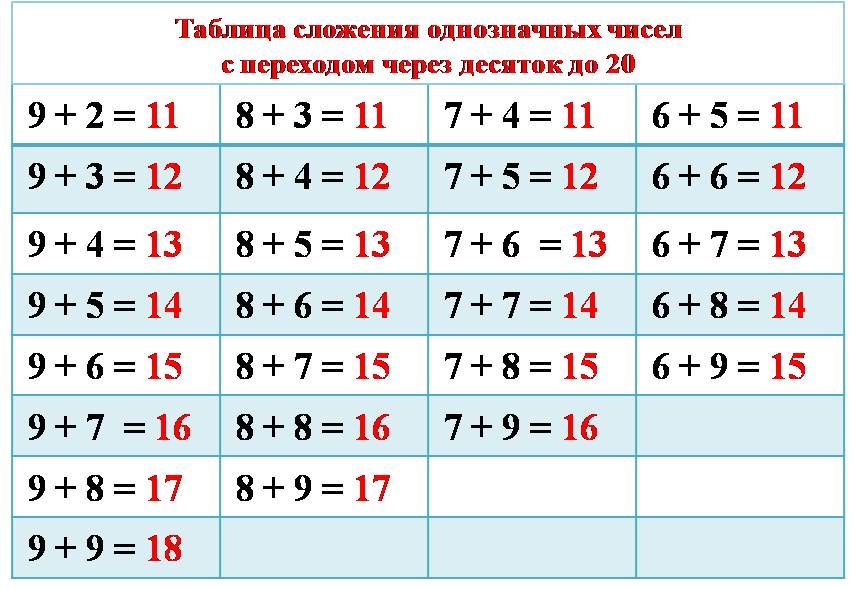 При ориентации на состав числа удобнее делать акцент не на составление и заучивание таблицы каждого случая целиком, а на составление и запоминание взаимосвязанных троек:

9 9 = 5 + 4, значит, 5 + 4 = 9; 9-4 = 5; 9-5 = 4

5 4

В качестве внешней опоры при вычислении случаев вида а±3 и а + 4 может быть использована линейка, счеты, пальцевый счет. Для ускорения вычислений в домашних условиях (при выполнении домашней работы) часто используют треугольную таблицу, помогающую найти результат суммирования любых пар чисел в пределах 10. Такая таблица может быть повешена над столом ребенка. Постоянное обращение к ней при выполнении домашних заданий более полезно, чем использование калькулятора, поскольку зрительный образ соответствующих случаев постепенно запоминается ребенком, пополняя тем самым количество запомненных наизусть случаев табличного сложения и вычитания.

Таблица сложения и вычитания:

Перестановка слагаемых Правило перестановки слагаемых:

От перестановки слагаемых сумма не изменяется.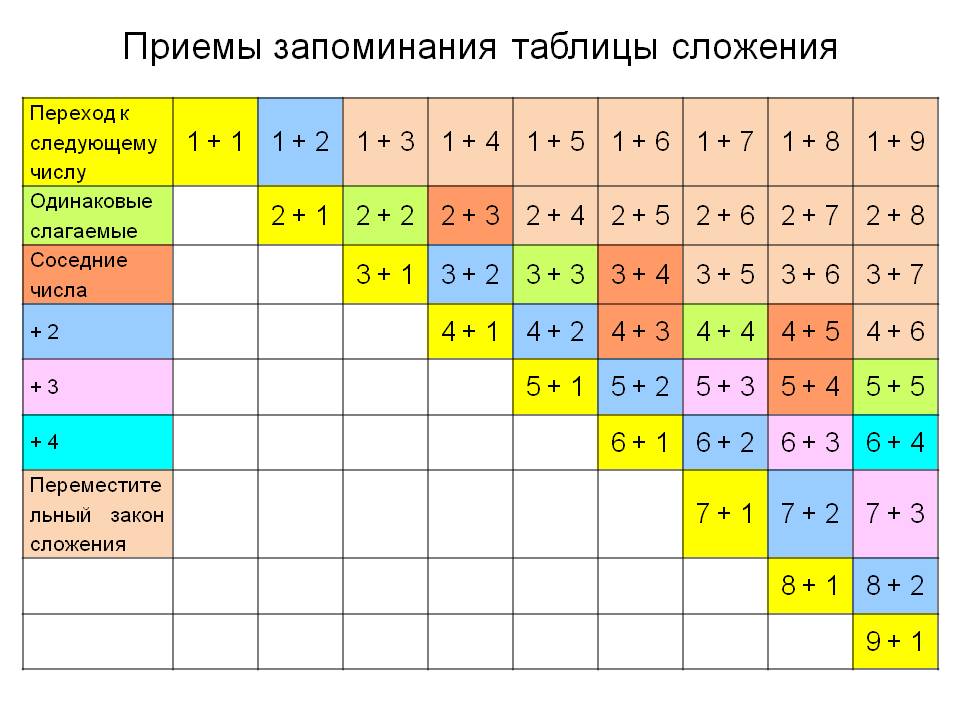

Свойство перестановки слагаемых (переместительное свойство сложения) используется в 1 классе при знакомстве с вычислительными приемами видая + 5, а + 6, а + 7, а + 8 и а + 9.

В этих случаях второе слагаемое больше первого (поскольку рассматриваются случаи сложения в пределах 10). Применение при вычислениях перестановки слагаемых позволяет свести все эти случаи к ранее изученным.

Например: 2 + 8 = 8 + 2 = 10.

Перестановка слагаемых может рассматриваться как прием вычислений.

Этот вычислительный прием облегчает вычислительную деятельность и является общим приемом вычислений при сложении любых чисел.

Например: 12 + 346 = 346 + 12 = 358

Прием перестановки слагаемых позволяет составить краткую таблицу сложения в пределах 10:

С учетом свойства перестановки слагаемых данная таблица включает все случаи сложения в пределах 10. Таблица содержит 15 случаев и, безусловно, ее заучивание для ребенка намного более легкая задача, чем заучивание полной таблицы.

Данная таблица появляется значительно позднее, чем начинается заучивание таблиц (для случаев а + 1, а ± 2, а ± 3, а ± 4) сложения и вычитания в пределах 10, поэтому не выполняет своей облегчающей вычисления задачи. На данный момент дети уже заучивали 42 случая предыдущих таблиц, и поэтому все случаи часто смешиваются. В связи с этим, некоторые альтернативные учебники (например, учебник Н.Б. Истоминой) сначала знакомят детей со сложением, его свойствами и таблицей сложения, а после того, как эти таблицы ребенком усваиваются, знакомят первоклассника с действием вычитания и таблицу вычитания рассматривают отдельно от таблицы сложения.

Случаи вида «вычесть 5, 6,7,8,9», символически обозначаемые в учебниках □ — 5, □ — 6, □ — 7, □ — 8, □ — 9, являются вычислительными приемами, основанными на составе однозначных чисел и взаимосвязи между суммой и слагаемыми.

С правилом взаимосвязи суммы и слагаемых дети знакомились ранее (см. выше). Состав чисел изучался в разделе «Нумерация в пределах 10».

Используя эти знания, дети осваивают прием вычитания чисел больше 5:

8-5 = 3 7-6=1 10-7 = 3

3 5 6 1 7 3

(8 — это Зи5;8 без 5 — это 3.)

Сложение и вычитание с нулем

Основное свойство нуля:

Прибавление и вычитание нуля результата не меняет.

В общем виде это свойство можно записать так: а±0⁼⁼аи0±а = а.

Порядок действий в выражениях без скобок

Порядок действий в выражениях без скобок в первом классе определяется следующим образом:

В выражении, содержащем сложное вычитание, или несколько знаков сложения, или несколько знаков вычитания, действия выполняются по порядку слева направо.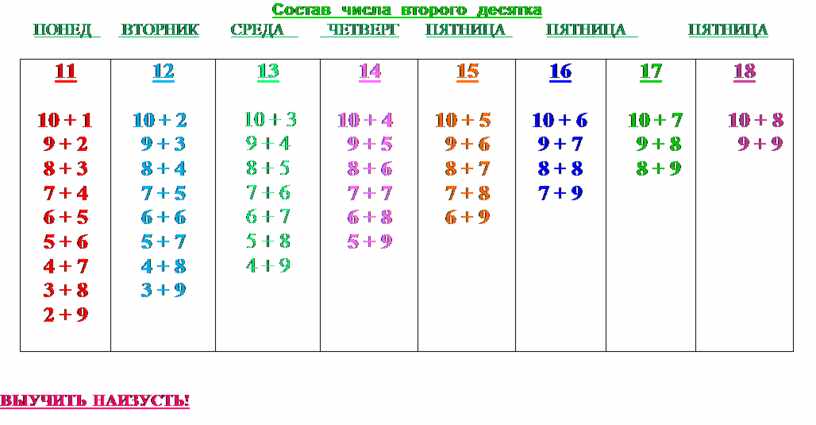

Это правило не содержится в учебнике, учитель знакомит с ним детей в процессе решения соответствующих примеров. Например:

Вычисли:

3 + 6 ~ 7 = 8-2 + 4 = 7-3-2 = 5 + 2 + 3 = …

При решении этих примеров детям в 1 классе не разрешается пользоваться правилом группировки слагаемых, являющимся приемом рациональных вычислений.

Это правило появляется только во втором классе при изучении приемов вычислений в пределах 100, где детям сообщается:

Два соседних слагаемых можно заменить их суммой.

Такой методический подход объясняется тем, что раннее знакомство с этим приемом может быть воспринято ребенком как общее свойство для случаев сложения нескольких чисел, а также вычитания нескольких чисел.

В практике иногда наблюдается, что ребенок, полагающий, что это правило общее для сложения и вычитания, выполняет вычитание нескольких чисел следующим образом:

8 — 3 г- 2 = 7, так как 3 — 2 — 1, а 8 — 1 = 7,

что, естественно, неправильно.

Поскольку в большинстве учебников для начальных классов действия сложения и вычитания рассматриваются одновременно, для избежания подобных ошибок при выполнении действий правило группировки слагаемых в первом классе не используется. В этом случае правило порядка выполнения действий в выражениях без скобок в первом классе является единым.

Группировка слагаемых

В некоторых альтернативных учебниках (например, в учебнике Н.Б. Истоминой) правило группировки слагаемых в неявном виде (без сообщения его учащимся) используется уже при изучении вычислительных приемов первого десятка. Это объясняется тем, что дети знакомятся сначала только со сложением и потому рассматривают все правила только относительно сложения (перестановка слагаемых, группировка слагаемых).

Например:

Можно ли утверждать, что значение выражений в каждом столбике одинаковы?

1 + 2 + 2+ 1 2+1 + 1 + 1

1+4+1 2+2+1

1+2+3 2+1+2

1+5 2+3

Подразумевается, что при объяснении равенства значений выражений в каждом столбике ребенок суммирует слагаемые, начиная со второго, т. е. такой прием считается допустимым.

(Сумма чисел 2,2 и 1 равна 5, сумма 4 и 1 также равна 5, сумма 2 и 3 также равна 5. Во всех случаях первое слагаемое равно 1 и к нему прибавляются одинаковые суммы, значит результаты равны.)

Какие первые 10 натуральных чисел?

В повседневной жизни мы используем числа. Их часто называют цифрами . Мы не можем считать предметы, дату, время, деньги или что-либо еще без чисел. Эти цифры иногда используются для измерения, а иногда для маркировки. Числа обладают свойствами, позволяющими производить над ними арифметические операции. Эти цифры выражаются как цифрами, так и словами. Например, 3 записывается как три, 33 записывается как тридцать три и так далее. Для дальнейшего изучения учащиеся могут попрактиковаться в написании цифр от 1 до 100 словами.

В математике мы изучаем различные типы чисел. Натуральные и целые числа, нечетные и четные числа, рациональные и иррациональные числа и т. д. — все это примеры. В этой статье мы рассмотрим все разновидности. Кроме того, числа используются в различных приложениях, включая числовые ряды, арифметические таблицы и так далее.

• Число — это арифметическое значение, которое используется для представления и расчета количества. Числа представлены цифрами, которые представляют собой письменные символы, такие как «2».
• Система счисления — это метод записи чисел, в котором для их представления используются логические цифры или символы.

Система счисления — это система классификации чисел по множествам. В математике существует несколько различных типов чисел:

1. Натуральные числа: Натуральные числа — это положительные целые числа от 1 до бесконечности, которые содержат положительные целые числа от 1 до бесконечности. Набор натуральных чисел обозначается буквой «N» и состоит из N = 1, 2, 3, 4, 5, …………
2. Целые числа: Неотрицательные целые числа, часто называемые целыми числами, представляют собой неотрицательные целые числа, не содержащие дробных или десятичных частей. Он обозначается буквой «W», а набор целых чисел содержит W = 0, 1, 2, 3, 4, 5,…………
3. Целые числа: Целые числа — это множество всех целых чисел, но они также включают набор отрицательных натуральных чисел. Целые числа представлены буквой «Z», а набор целых чисел Z = -3, -2, -1, 0, 1, 2, 3,
4. Вещественные числа: Вещественные числа — это все положительные и отрицательные целые, дробные и десятичные числа, не содержащие мнимых значений. Для его обозначения используется буква «Р».
5. Рациональные числа: Рациональные числа — это любые числа, которые могут быть выражены как отношение одного числа к другому числу. Подходит любое число, которое может быть записано в виде p/q. Рациональное число представлено символом «Q».
6. Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены как отношение одного к другому и обозначаются буквой P.
7. Комплексные числа: Комплексные числа (C) — это числа, которые могут быть выражены в форме a+bi, где «a» и «b» — действительные числа, а I — мнимое число.

Натуральные числа — это подмножество системы счисления, которое охватывает все положительные целые числа от 1 до бесконечности и используется для счета. Оно не содержит числа ноль. На самом деле цифры 1,2,3,4,…. часто называют счетными числами.

Натуральные числа — это подмножество действительных чисел, которое включает только положительные целые числа, такие как 1, 2, 3, 4, 5, 6 и т. д., и не включает ноль, дроби, десятичные дроби и отрицательные числа.

Отрицательные числа и 0 не включаются в натуральные числа.

В этой статье вы узнаете больше о натуральных числах, включая их определение, сравнение с целыми числами, представление на числовой прямой, атрибуты и многое другое.

Примеры Натуральные числа

Положительные целые числа (также известные как неотрицательные целые числа) включены в натуральные числа, и некоторые примеры включают 1, 2, 3, 4, 5, 6,… Натуральные числа, другими словами, представляют собой совокупность всех целых чисел. числа, исключая 0.

103, 42 33, 9999, 101101 и т. д. — все это примеры натуральных чисел.

Каковы первые 10 натуральных чисел?

Так как Натуральные числа — это подмножество действительных чисел, которое включает только положительные целые числа, такие как 1, 2, 3, 4, 5, 6 и т. д., и не включает ноль, дроби, десятичные дроби и отрицательные числа.

Таким образом, первые 10 натуральных чисел — это 1, 2, 3, 4, 5, 6, 7, 8, 9 и 10. , 2, 3, 4, 5, 6, 7, 8, 9 и 10.

Вопрос 1. Какие примеры натуральных чисел?

Ответ:

Примеры натуральных чисел: 4, 56, 678, 2345, 87654 и т. д.

Вопрос 2. Является ли «0» натуральным числом?

Ответ:

«Нет», — это ответ на этот вопрос. Натуральные числа, как мы уже знаем, находятся в диапазоне от 1 до бесконечности и являются целыми положительными числами. Однако, когда мы объединяем 0 с целым положительным числом, таким как 10, 20 или любым другим числом, мы получаем натуральное число. По правде говоря, 0 — это полное число, не имеющее смысла.

Что такое простое число? Объяснение для учителей, родителей и детей

Простое число — это число, которое можно разделить только само на себя и на 1 без остатка. Здесь мы подробно объясним, что это значит, дадим вам список простых чисел, которые дети должны знать в начальной и средней школе, и предоставим вам несколько практических вопросов и примеров.

Простое число — это целое число больше 1, имеющее только два делителя — само себя и 1.

Простое число нельзя разделить ни на какое другое положительное целое число без остатка, десятичной дроби или дроби.

Примером простого числа является 13. Его делителями являются только 1 и 13. Деление простого числа на другое натуральное число приводит к остатку чисел. Например, 13 ÷ 6 = 2 остаток 1.

15 не является примером простого числа, поскольку оно делится на 5 и 3, а также само на себя и на 1.

15 является примером составного числа, поскольку оно имеет более двух делителей.

Простые числа часто рассматриваются математиками в качестве «кирпичиков» в теории чисел. Основная теорема арифметики гласит, что составное число можно представить в виде произведения простых чисел.

См. также: Правила делимости

Пакет летних математических заданий

Сосредоточьтесь на математике с помощью этих веселых математических игр и заданий, которые учащиеся могут взять домой на каникулах! Пакет включает в себя 4 отдельных рабочих листа, содержащих до 20 задач, основанных на нескольких темах.

Примеры простых чисел

Как определить, является ли заданное число простым или составным, на основе свойств простых чисел.

• 8 простых чисел меньше 20: 2, 3, 5, 7, 11, 13, 17 и 19.
• Первые 10 простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
• Существует 25 простых чисел от 1 до 100.
• Простые числа включают большие числа и могут продолжаться далеко за пределы 100.
• Например, 21 577 — простое число.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Обратите внимание, что этот список простых чисел содержит только нечетные числа, за исключением числа 2.

2 — наименьшее простое число. Кроме того, это единственное четное простое число — все остальные четные числа могут делиться как минимум сами на себя, на 1 и 2, то есть у них будет как минимум 3 делителя.

Греческий математик Евклид (один из самых известных математиков классической эпохи) записал доказательство того, что среди множества простых чисел нет наибольшего простого числа. Тем не менее, многие ученые и математики все еще пытаются найти его в рамках Великого Интернет-поиска простых чисел Мерсенна.

наибольшее известное простое число (по состоянию на ноябрь 2020 г.) равно 2 ^{82 589 933} − 1, число, состоящее из 24 862 048 цифр при записи по основанию 10. До этого самым большим известным простым числом было 2 ^{77 232 917.}  – 1 , имеющий 23 249 425 цифр.

К тому времени, как вы это прочтете, он может стать еще больше, но вы можете следить за его развитием в Википедии.

Часто задаваемые вопросы о простых числах

Простое число — это число, которое можно разделить только на себя и на 1 без остатка.

Простые числа от 1 до 100: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

1 не является простым числом, потому что оно имеет только один делитель, а именно 1. Простые числа должны иметь ровно два делителя.

2 — простое число, потому что его единственными делителями являются 1 и оно само.

51 не является простым числом, потому что оно имеет 3 и 17 в качестве делителей, а также само себя и 1. Другими словами, 51 имеет четыре делителя.

Пакет летних математических занятий

Сосредоточьтесь на математике с помощью этих веселых математических игр и заданий, которые учащиеся могут взять домой на каникулах! Пакет включает в себя 4 отдельных рабочих листа, содержащих до 20 задач, основанных на нескольких темах.

Одним из наиболее важных применений простых чисел является кибербезопасность — обеспечение большей безопасности информации, передаваемой через Интернет.

Чтобы зашифровать (защитить) такие вещи, как данные кредитной карты, медицинские записи и даже некоторые службы обмена сообщениями, такие как WhatsApp, инженеры-программисты создают алгоритмы, используя простые числа.

Перемножая два очень больших простых числа (некоторые компании используют простые числа, состоящие из сотен цифр!), мы получаем еще большее число, исходные делители которого (два очень больших простых числа) известны только нам. Затем мы используем это еще большее число для шифрования нашей информации.

Если кто-то еще хочет узнать, какую информацию мы посылаем, он должен выяснить, каковы были наши первоначальные факторы. С такими длинными простыми числами, как те, которые мы использовали, им могут потребоваться годы или даже десятилетия постоянных проб и ошибок, прежде чем они найдут хотя бы одно. Такая криптография с открытым ключом обеспечивает безопасность нашей информации.

Хотите знать, как объяснить своим детям другие ключевые слова по математике? Ознакомьтесь с нашим Первичным математическим словарем или попробуйте эти основные математические термины:

• Что такое число в кубе: объяснение для основных родителей и детей
• Что такое наименьшее общее кратное: объяснение для основных родителей и детей
• Что такое наивысший общий фактор: объяснение для основных родителей и детей

1) Квадратное число и простое число имеют в сумме 22. Какие это два числа?

A: 9 и 13

2) Эмма думает о двух простых числах. Она складывает два числа вместе. Ее ответ — 36. Напишите все возможные пары простых чисел, которые могла придумать Эмма.

А: 3 и 33; 5 и 31; 7 и 29; 13 и 23; 17 и 19

3) Обведите два простых числа – 29, 59, 39, 69, 29

A: 29 и 59

4) Запишите три простых числа, при умножении которых получается 231.

A: 3 x 7 x 11

ЗАДАЧА: Чен выбирает простое число. Он умножает его на 10, а затем округляет до ближайшей сотни. Его ответ — 400. Напишите все возможные простые числа, которые мог выбрать Чен.

A: 37, 41 или 43.

Онлайн-центр Third Space Learning Maths Hub содержит сотни математических ресурсов для учителей начальной школы и родителей, которые можно использовать в школе и дома. Регистрация на бесплатных математических ресурсах выполняется быстро, легко и доступна для всех сотрудников вашей школы. Чтобы получить доступ к премиум-ресурсам, вашей школе потребуется премиум-подписка Maths Hub. Кроме того, доступ ко всем ресурсам премиум-класса включен бесплатно для школ, подписавшихся на наше онлайн-обучение по математике.

Рабочие листы с простыми числами

• Готовые уроки Умножение и деление 5 класса (осенний блок 4) Слайды и рабочие листы
• Готовые уроки 6 класс 4 Операции (Осенний блок 2) Слайды и рабочие листы
• Рабочий лист 5-го класса: умножение и деление 1
• Рабочий лист 6-го класса: четыре операции

Видео о простых числах

• Как учить простые и составные числа

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте своим учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.