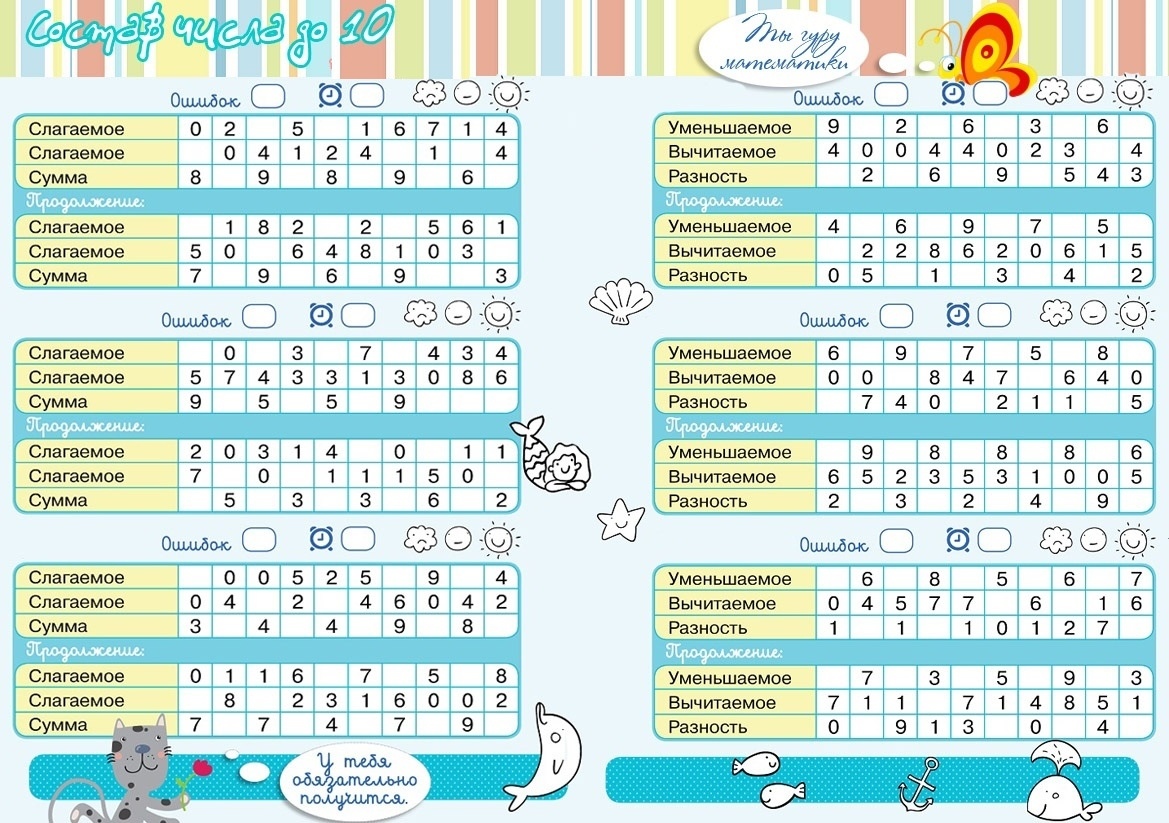
Примеры на время (состав 10) | Тренажёр по математике (1 класс):
3 + 7 = 10 – 2 = 2 + 8 = 10 – 4 = 7 + 3 = 8 + 2 = 5 + 5 =
10 – 2 = 1 + 9 = 10 – 0 = 10 + 0 = 10 – 1 = 3 + 7 = 10 – 2 =
2 + 8 = 10 – 5 = 8 + 2 = 10 – 5 = 5 + 5 = 10 – 1 = 1 + 9 =
10 – 3 = 3 + 7 = 10 – 1 = 1 + 9 = 10 – 5 = 8 + 2 = 10 – 4 =
7 + 3 = 10 – 1 = 5 + 5 = 10 – 3 = 8 + 2 = 10 – 6 = 3 + 7 =
10 – 2 = 2 + 8 = 10 – 2 = 7 + 3 = 10 – 0= 6 + 4 = 10 – 7 =
4 + 6 = 10 – 2 = 2 + 8 = 10 – 8 = 6 + 4 = 10 – 5 = 8 + 2 =
10 – 0 = 5 + 5 = 10 – 3 = 4 + 6 = 10 – 1 = 9 + 1 = 10 – 2 =
8 + 2 = 10 – 0 = 0 + 10 = 10 – 4 = 1 + 9 = 10 – 7 = 9 + 1 =
10 – 1 = 1 + 9 = 10 – 7 = 7 + 3 = 10 – 3 = 7 + 3 = 10 – 4 =
9 + 1 = 10 – 2 = 1 + 9 = 10 – 9 = 3 + 7 = 10 – 2 = 2 + 8 =
10 – 5 = 9 + 1 = 10 – 1 = 4 + 6 = 10 – 5 = 8 + 2 = 10 – 5 =
0 + 10 = 10 – 5 = 8 + 2 = 10 – 2 = 8 + 2 = 10 – 1 = 6 + 4 =
10 – 4 = 2 + 8 = 10 – 9 = 5 + 5 = 10 – 7 = 0 + 10 = 10 – 1 =
7 + 3 = 10 – 1 = 7 + 3 = 10 – 8 = 6 + 4 = 10 – 4 = 5 + 5 =
10 – 6 = 4 + 6 = 10 – 4 = 2 + 8 = 10 – 0 = 7 + 3 = 10 – 6 =
1 + 9 = 10 – 2 = 1 + 9 = 10 – 3 = 1 + 9 = 10 – 5 = 2 + 8 =
10 – 0 = 2 + 8 = 10 – 2 = 8 + 2 = 10 – 2 = 4 + 6 = 10 – 3 =
6 + 4 = 10 – 7 = 6 + 4 = 10 – 5 = 3 + 7 = 10 – 4 = 8 + 2 =
10 – 1 = 3 + 7 = 10 – 2 = 6 + 4 = 10 – 6 = 7 + 3 = 10 – 0 =
6 + 4 = 10 – 3 = 0 + 10 = 10 – 5 = 7 + 3 = 10 – 5 = 5 + 5 =
10 – 9 = 9 + 1 = 10 – 7 = 1 + 9 = 10 – 4 = 4 + 6 = 10 – 1 =
0 + 10 = 10 – 4 = 1 + 9 = 10 – 2 = 4 + 6 = 10 – 5 = 3 + 7 =
10 – 0 = 5 + 5 = 10 – 0 = 10 + 0 = 10 – 1 = 0 + 10 = 10 – 3 =
1 + 9 = 10 – 6 = 0 + 10 = 10 – 3 = 6 + 4 = 10 – 2 = 9 + 1 =
10 – 4 = 7 + 3 = 10 – 8 = 4 + 6 = 10 – 5 = 8 + 2 = 10 – 0 =
5 + 5 = 8 + 2 = 4 + 6 = 10 – 3 = 3 + 7 = 10 – 2 = 6 + 4 =
Состав числа 10.
 Примеры. — Kid-mama — «Семья и Школа»
Примеры. — Kid-mama — «Семья и Школа»Содержание
Тренажер «Состав числа до 10»
50,00 ₽
Задания на состав числа в пределах 10. Для решения на компьютере (в Excel без печати).
Артикул: i-13876 Категория: Для учебы Метки: Дошкольники, Состав числа, 1 класс
- Описание
- Детали
- Отзывы (0)
Описание
Тренажер «Состав числа до 10» – это программа, которая формирует задания на состав числа в пределах 10, чтобы решать их на компьютере (не распечатывая). Задания генерируются случайным образом, количество генераций не ограничено.
Программа написана в Excel с помощью макросов. Для решения задания нужно выбрать число, для которого будут формироваться задания.
При нажатии кнопки «Начать»
 При нажатии кнопки «Начать» счетчик обнуляется.
При нажатии кнопки «Начать» счетчик обнуляется.Для удобства внизу карточки есть кнопки с цифрами, которые нужно нажимать при выборе ответа.
Генератор будет полезен как для подготовки к школе, так и для закрепления состава числа учеников 1 класса. Практика счета поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день.
На сайте также можно скачать программу «Состав числа в пределах 10» для печати в виде домиков.
Другие программы, которые помогут закрепить навыки счета в пределах 10:
- Умная раскраска «Примеры до 10»
- Сложение и вычитание в пределах 10
- Цепочки примеров в пределах 10 (сложение и вычитание)
- Математический лабиринт (состав числа)
- Арифметический маршрут 1 (сложение и вычитание в пределах 10-100)
- Математический диктант для дошкольников
На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Вам также будет интересно…
Главные праздники России
70,00 ₽В корзинуТренажер счета в пределах 10
Оценка 5.00 из 5
Распродажа! 0,00 ₽ В корзинуВыучить 12 месяцев
Оценка 5.00 из 5
70,00 ₽В корзинуАрифметический маршрут 1 (сложение и вычитание в пределах 10-100)
70,00 ₽В корзинуСложение и вычитание в пределах 10
Оценка 5.00 из 5
Распродажа! 0,00 ₽ В корзинуСборник заданий для дошкольников
Распродажа! 320,00 ₽ В корзинуЧасы для изучения времени детям
Оценка 5.
70,00 ₽В корзину 00 из 5
00 из 5Умная раскраска «Примеры до 10»
60,00 ₽В корзинуСостав числа в пределах 10
50,00 ₽В корзину
Состав числа в пределах 10. Тренажер
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравненияПодготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Состав числа
в пределах 10
Математика 1 класс
4
1
3
2
2
3
1
Заселяем
домики
5
1
4
2
3
3
2
4
1
Заселяем
домики
6
1
2
3
4
5
5
4
3
2
1
Заселяем
домики
7
1
2
3
4
5
6
6
5
4
3
2
1
Заселяем
домики
1
2
3
4
5
6
7
8
7
6
5
4
3
2
1
Заселяем
домики
1
2
3
4
5
6
7
8
9
8
7
6
5
4
3
2
1
Заселяем
домики
1
2
3
4
5
6
7
8
10
9
8
7
6
5
4
3
2
Заселяем
домики
Игра «Круговые примеры»
2+1
5–3
4+1
3–2
1+3
Игра «Круговые примеры»
8–3
10 – 2
9–2
Игра «Круговые примеры»
6+4
8–3
10 – 2
9–3
5+4
Дополни до 10
10
1 2 34 56 7 8 9
9 8 7 6 5 4 3 2 1
Запиши недостающее число
9
4 5
8
6
7
4 4 4 2 4 3
Запиши недостающее число
9
3 6
8
6
7
3 5 3 3 3 4
Запиши недостающее число
9
2 7
5
6
7
2 3 2 4 2 5
Запиши недостающее число
9
1 8
5
6
7
3 2 5 1 6 1
Запиши недостающее число
10
2 8
7
9
6
2 5 2 7 2 4
Запиши недостающее число
10
4 6
7
9
6
4 3 4 5 4 2
Запиши недостающее число
10
3 7
7
9
6
3 4 3 6 3 3
Запиши недостающее число
10
1 9
7
9
6
1 6 1 8 1 5
7
3
4
1
6
2
5
4
3
Заселяем
домики
8
4
4
2
6
5
3
7
1
Заселяем
домики
Найди недостающий листочек
7
9
5
3
2
4
6
73
5
1
8
4
2
6
5
4
2
3
4
6
Найди недостающий листочек
5
6
5
3
2
1
3
4
3
2
1
8
2
3
4
5
4
2
3
4
6
Найди недостающий листочек
10
6
5
3
2
1
3
4
3
4
7
7
6
3
10
5
5
1
9
8
2
Разложи конфеты на тарелки
2+3
3+4
1+4
5+2
8-1
6-1
8-3
9-2
5
7
Разложи конфеты на тарелки
6+3
3+4
7+2
5+2
8-1
5+4
8+1
9-2
9
7
Разложи конфеты на тарелки
2+4
3+5
4+2
6+2
4+4
3+3
5+1
7+1
6
8
Разложи ягоды на тарелки
2+3
8-1
3+4
6-1
5
1+4
5+2
8-3
9-2
7
Разложи ягоды на тарелки
3+3
6+2
4+4
2+4
6
1+5
5+3
4+2
7+1
8
Разложи кубики по корзинам
5+1
5+3
4+2
3+3
7+1
6+2
4+4
6
8
Разложи кубики по корзинам
8-1
5+2
5+4
4+3
6+1
7+2
8+1
6+3
4+5
7
9
Раздели курочек на
группы
9+1
7+1
6+2 5+3
8
7+3
5+5
4+4 8+2
6+4
10
Раздели курочек на
группы
8+1
2+5
6+1 5+2
7
6+3
3+6
4+3 7+2
5+4
9
6+2
3+7
4+5
8
8+2
4+4
3+5
6+3
7+2
6+4
10
Разложи бананы по корзинам
9
6
Какой грибочек белочка положит в
корзинку? (щелкни по грибку)
Игра «Продолжи цепочку»
1
6
1
+2
–1
+2
3
5
3
+2
–1
+2
5
4
5
+1
–1
+2
6
3
7
–2
–1
+2
4
2
9
Игра «Продолжи цепочку»
7
6
1
–1
–1
+3
6
5
4
–1
–3
+1
5
2
5
–2
+2
–1
3
4
4
–2
–2
–3
1
2
1
Реши примеры
2 + 1 + 1 =43 + 1 + 1 =5
5 + 1 + 1 =7
6 + 1 + 1 =8
4 + 1 + 1 =6
2–1–1=0
3–1–1=1
5–1–1=3
6–1–1=4
4–1–1=2
Реши примеры
4 + 1 + 1 =6
6 + 1 + 1 =8
7 + 1 + 1 =9
8 + 1 + 1 = 10
3 + 1 + 1 =5
10 – 1 – 1 =8
7–1–1=5
9–1–1=7
8–1–1=6
6–1–1=4
Вставь пропущенный знак
9
7 < 10–1
10
6 > 5 4 < 8 10 = 9+1
2
1 < 4 –2
8
6 < 9–1
7< 8 9 > 6
English Русский Правила
Изучение состава числа
Когда ребенок понимает состав числа, он понимает, что числа состоят из других чисел.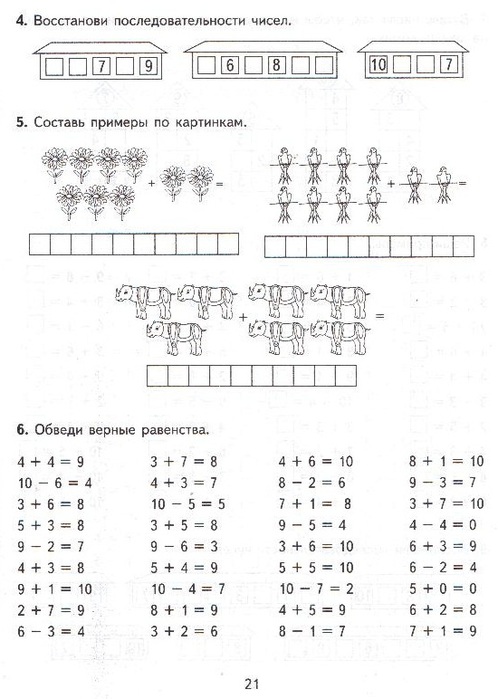 Они «видят числа внутри» других чисел: во-первых, что все числа состоят из единиц, а затем, что их можно составить из пар больших чисел.
Они «видят числа внутри» других чисел: во-первых, что все числа состоят из единиц, а затем, что их можно составить из пар больших чисел.
Так, например, 5 состоит из «пяти единиц», или из «1 и 4», или из «2 и 3».
Символы CBeebies Numberblocks демонстрируют это своей способностью разделяться на другие символы, как показано в этом клипе:
Понимание состава числа имеет основополагающее значение для понимания структуры отношений часть-часть-целое, которые могут быть представлены с помощью модели часть-часть-целое, как показано ниже:
Если 5 разделить на 3 и 2, то 3 будет частью, 2 будет частью, а 5 будет целым.
Концепция композиции позволяет детям развивать беглость с числовыми связями — не только числовыми связями 10, но и все число облигаций внутри числа. Итак, вернемся к примеру с числом 5: числовые связи числа 5: 0 и 5, 1 и 4, 2 и 3.
Понимание состава также поддерживает понимание коммутативности: если вы узнали, что 2+3=5, то вы также знаете, что 3+2=5 без необходимости заучивать это как новый факт.
Композиция также имеет решающее значение для понимания сложения и вычитания и их обратных отношений. Для тех, кто понимает состав числа, помните, что 2 + 3 = 5 и 5-2 = 3, и то, как соотносятся эти два факта, — это не столько повторение и запоминание, сколько применение структурного понимания. Когда мы складываем, мы составляем: когда мы вычитаем, мы разлагаем.
В рамках программы NCETM/Maths Hubs Mastering Number, занятия предназначены для понимания состава числа для детей в приемной, 1-го и 2-го классов. рекомендуется «субитизировать» (см. без подсчета) меньшие числа «внутри» больших чисел.
Что ты видишь? Может 4 в квадрате, а нечетная 1?
Что вы видите, если они окрашены в такой цвет? Вероятно, 2 и 3.
Детей можно попросить сказать: «Я знаю, что это 5, потому что я вижу 3 красные точки и 2 черные точки».
Различное расположение цветных точек в венгерских числовых рамках помогает развивать распознавание различных конфигураций 3 и 2 и, следовательно, 5.
Перемещение птиц между разными проводами позволяет детям увидеть, что разные пары чисел составляют 5.
Для чисел от 5 до 10 детям предлагается, опять же с помощью используемых представлений, увидеть структуру «5 с небольшим». Понимание чисел по отношению к 5 и 10 важно для разработки эффективных стратегий расчета. Так что увидеть 5 (и немного) в 6, 7, 8 и 9 особенно полезно.
Помимо определения того, что 5 является частью чисел 6,7,8 и 9, другие связи этих чисел также исследуются отдельно.
Различные представления 6 используются для демонстрации различных композиций 6: «5 и немного», а также «3 и 3» или «2 и 2 и 2».
Рисунок кубика подчеркивает «3 и 3»:
Сетка из 9 позволяет переместить одиночные фишки из знакомой схемы игры в кости, чтобы увидеть, что у нас все еще есть 6.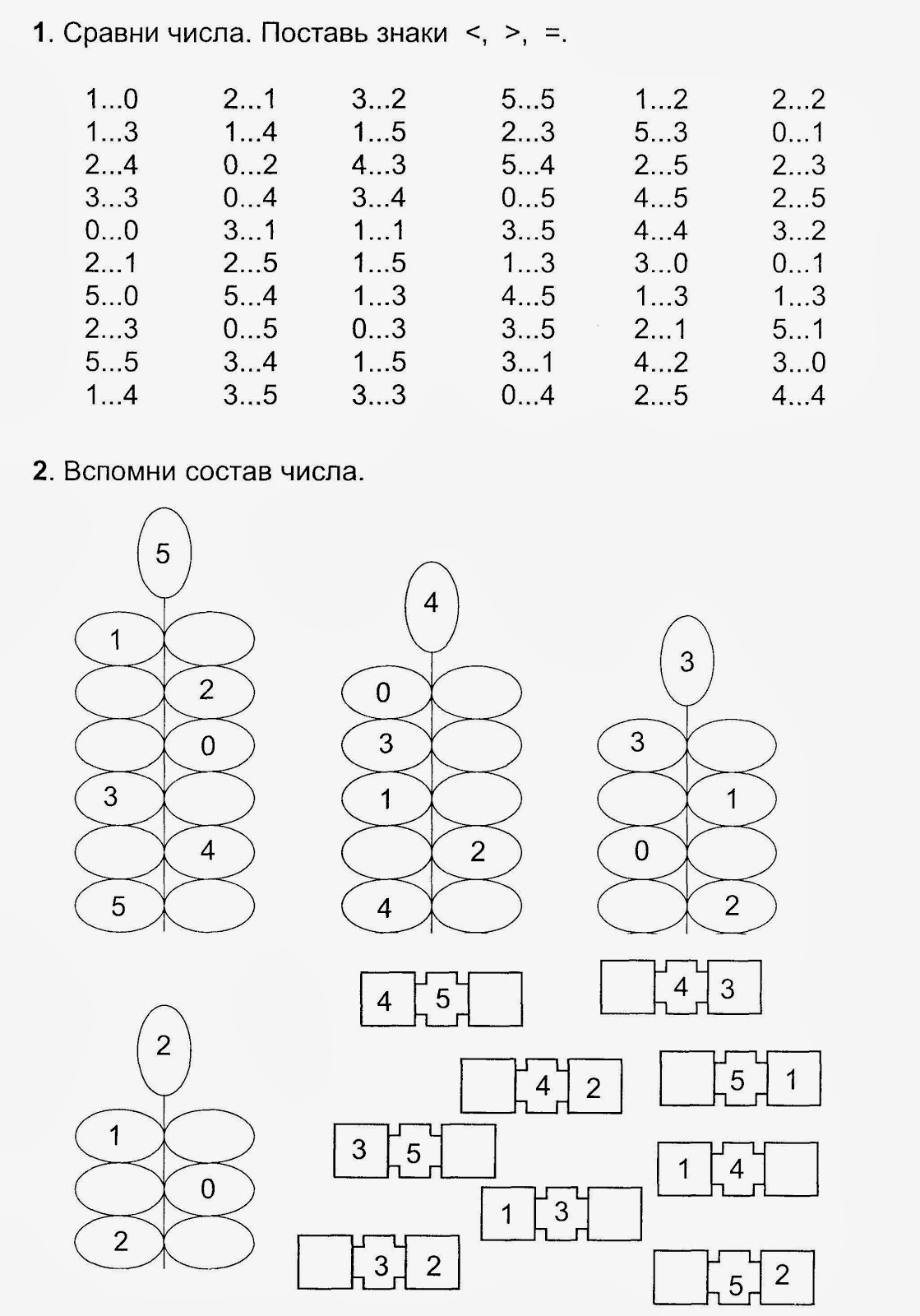 Исследуются различные способы деления чисел в пределах 6 для составления 6.
Исследуются различные способы деления чисел в пределах 6 для составления 6.
Использование ящика для яиц позволяет разделить яйца на коричневые и белые и использовать истории о яйцекладке, чтобы увидеть разные числа в пределах 6.
Более подробная информация о композиции, в том числе идеи для занятий, графики прогресса, типичные ошибки и то, на что следует обращать внимание при работе с маленькими детьми, содержится на странице «Композиция для детей младшего возраста». Вас также могут заинтересовать другие статьи из этого набора: «Количественность и числовой смысл» и «Обучение порядкового порядка — больше, чем просто первая, вторая и третья».
NCETM и Maths Hubs рассматривают программу освоения чисел на 2022/23 год. Если вы заинтересованы в участии, пожалуйста, заполните Форму выражения заинтересованности.
Состав чисел: 6–10 | NCETM
Состав чисел: 6–10 | НЦЭТМ- Мастерство PD Материалы
Состав чисел: 6–10
Корешок 1: Число, сложение и вычитание – Тема 1. 4
4
Введение
Расширьте структуру деления на числа от шести до десяти, изучите структуру чисел пять с а бит и познакомьте детей с понятием четных и нечетных чисел.
Точки обучения
- Точка обучения 1: Числа от шести до девяти состоят из «пяти с небольшим».
Простые числа и составные числа
Простое число — это целое число, большее единицы, единственными делителями которого являются само себя и единица.
Примеры простых чисел (из математической игры Bubbly Primes)
Это может показаться сложнее, чем есть на самом деле. Дело в том, что математики любят быть очень точными в своем языке; им нравится говорить то, что абсолютно правильно. Иногда это приводит к тому, что простые вещи кажутся более запутанными, чем это необходимо.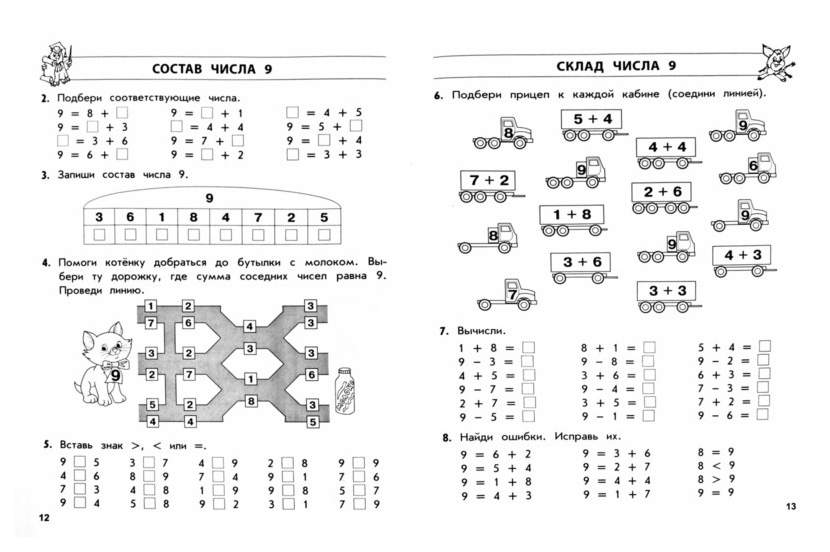
Мы только что почтили математическую традицию точным определением, поэтому теперь дадим простое объяснение. К концу этой страницы у вас будет четкое представление о том, что такое простые числа и почему. Не волнуйтесь — скоро все станет ясно.
Прежде чем мы продолжим, мы хотим убедиться, что всем понятно, что такое множитель: множителя — это числа, которые умножаются друг на друга, чтобы получить произведение .
Возможно, самый простой способ понять, что такое простое число, — это понять, чем оно не является.
Что такое составные числа?
Составное число — это произведение двух целых чисел, больших единицы.
Примеры составных чисел (как показано в математической игре Bubbly Primes)
Это стоит прочитать дважды, потому что это точное определение (снова). В обычной жизни, если вы говорите что-то довольно ясное, а затем умный парень указывает, что вы ошибаетесь из-за формальности, вы просто игнорируете умного парня. Но в математике люди стараются убедиться, что они никогда не ошибаются, даже из-за технических деталей. Если бы нас не беспокоили такие детали, как ноль, единица, дроби и т. д., мы могли бы просто сказать: «Когда вы умножаете два числа, вы получаете составное число». Но, поскольку это математика, мы осторожны с надоедливыми деталями, даже за счет того, что их немного сложнее понять.
Но в математике люди стараются убедиться, что они никогда не ошибаются, даже из-за технических деталей. Если бы нас не беспокоили такие детали, как ноль, единица, дроби и т. д., мы могли бы просто сказать: «Когда вы умножаете два числа, вы получаете составное число». Но, поскольку это математика, мы осторожны с надоедливыми деталями, даже за счет того, что их немного сложнее понять.
(Основная идея будет заключаться в том, что составные числа имеют делители, а простые – нет. Но, чтобы быть по-настоящему правдой, мы должны углубиться в детали и обязательно расставить точки через каждые i. и перекрестите каждые t .)
Кстати, мы создали математическую игру, чтобы помочь учащимся научиться разбивать составные числа на простые множители, потому что это очень важный навык. Если вы хотите использовать игру для обучения и практики, вы можете найти ее в App Store.
Таблицы умножения Показать составные числа.
Вот таблица умножения. Мы сделали это, используя только целые числа больше единицы. Факторами являются числа с белым фоном сверху и слева. В таблице их продукты показаны друг с другом в середине таблицы фиолетовым цветом. Все эти числа являются составными числами, потому что каждое из них является произведением двух целых чисел, больших единицы.
Факторами являются числа с белым фоном сверху и слева. В таблице их продукты показаны друг с другом в середине таблицы фиолетовым цветом. Все эти числа являются составными числами, потому что каждое из них является произведением двух целых чисел, больших единицы.
Таблица умножения множителей больше единицы
В таблице показана целая куча составных чисел до 100, но есть проблема.
Отображает ли таблица
Все Составные числа до 100? Нет — к сожалению, нет. Например, 22 — составное число (это 2 x 11), но его нет в таблице, потому что мы умножали только числа до 10. Однако мы знаем, что у нас есть все составные числа до 10, потому что при умножении числа больше 1, вы всегда получаете числа больше, чем вы начали. На самом деле мы знаем, что у нас есть все составные числа до 20, потому что мы пробовали каждое число до 10, и наименьшее число, на которое их можно было умножить, было 2. Используя эту логику, если бы мы хотели найти все составные числа до 100, мы могли бы составить таблицу умножения 50 на 50. Однако это было бы слишком много работы. Слишком много работы!! Вместо этого мы можем использовать чрезвычайно хитрую технику, называемую решетом Эратосфена.
Однако это было бы слишком много работы. Слишком много работы!! Вместо этого мы можем использовать чрезвычайно хитрую технику, называемую решетом Эратосфена.
Решето Эратосфена
Настоятельно рекомендуем вам изготовить Решето Эратосфена самостоятельно. Это не займет много времени, и вы многому научитесь. Пожалуйста? Выполняя это упражнение, вы получите более глубокое представление о том, что на самом деле представляют собой простые числа и как они работают. Вы, вероятно, даже начнете задавать некоторые из тех же вопросов, которые занимали воображение математиков на протяжении тысячелетий.
…
Когда вы делали решето Эратосфена, вы заметили, что, находя составные числа, вы также находили и простые числа?
Давайте ответим на некоторые распространенные вопросы.
Является ли 0 простым числом? Является ли 1 простым числом?
Нет, ни ноль, ни единица не являются простыми числами. Простая, но, вероятно, бесполезная причина заключается в том, что определение простых чисел тщательно сформулировано, чтобы специально исключить ноль и единицу. Но с чего бы математикам вообще беспокоиться о такой формулировке? Они хотят, чтобы простые числа работали как мультипликативные строительные блоки. Ноль и единица не работают как строительные блоки. Такой образ мышления может стать более осмысленным после рассмотрения следующего вопроса:
Но с чего бы математикам вообще беспокоиться о такой формулировке? Они хотят, чтобы простые числа работали как мультипликативные строительные блоки. Ноль и единица не работают как строительные блоки. Такой образ мышления может стать более осмысленным после рассмотрения следующего вопроса:
Является ли два простым числом?
Да. Хотя оно четно, его единственными факторами являются оно само и одно. Если вы думаете о простых числах как о строительных блоках, то двойка — это стандартный блок, используемый для того, чтобы сделать все остальные четные числа четными. Размышляя об этом таким образом, вы можете понять, почему математики не хотели бы, чтобы «1» считалось простым числом, даже если его единственными делителями являются она сама и единица. «1» не работает как строительный блок, потому что вы можете умножить его на число миллион раз и все равно получить то же число. Строительные блоки должны работать не так. Например, если вы составите составное число с другим количеством двоек, вы получите другое число. Две двойки и тройка дают 2 x 2 x 3 = 12, а три двойки и тройка дают 2 x 2 x 2 x 3 = 24. Ноль на самом деле не работает как строительный блок. Он действует скорее как динамитная шашка, которая сносит все остальные строительные блоки всякий раз, когда вы пытаетесь умножить на них.
Две двойки и тройка дают 2 x 2 x 3 = 12, а три двойки и тройка дают 2 x 2 x 2 x 3 = 24. Ноль на самом деле не работает как строительный блок. Он действует скорее как динамитная шашка, которая сносит все остальные строительные блоки всякий раз, когда вы пытаетесь умножить на них.
Мы почти готовы повторить причудливое определение простых чисел в верхней части страницы. Но, во-первых, есть еще одна вещь, которая постоянно всплывает — такие слова, как «целые числа».
Есть разные числа?
Мы продолжаем настаивать на том, чтобы простые и составные числа были целыми числами. Существуют разные виды чисел, которые полезны для разных целей. Если это звучит странно (странно), тогда почитайте о разных видах чисел.
Представьте, что рациональные числа (те, которые содержат дроби) могут быть простыми. Говорить о них было бы очень скучно. Причина в том, что каждое рациональное число, кроме нуля, является множителем любого другого рационального числа. Это означало бы, что все числа были бы составными, и не было бы такого понятия, как простое число! Чтобы избежать этого, в некоторых определениях простых чисел говорится, что они являются счетными числами (те, которые вы используете для подсчета овец), а в других — что они являются целыми числами (теми, которые могут быть как положительными, так и отрицательными).
На самом деле, не имеет значения, говорится ли в определениях, что они являются счетными числами, натуральными числами, целыми числами или целыми числами. Причина в том, что они также должны указывать «должно быть больше единицы», что исключает отрицательные числа, ноль и единицу. Отрицательные числа и ноль — это разница между счетными числами, натуральными числами и целыми числами. Вот почему до сих пор мы намеренно говорили «целые числа», потому что все более или менее знают, что это значит, и до сих пор мы не хотели теряться в длинном обсуждении различных видов чисел.
ОК! Теперь, когда мы подробно рассмотрели важные побочные темы, давайте снова зададим исходный вопрос.
Что такое простое число?
Ну, мы хотели бы сказать: «Простые числа — это числа, которые не являются составными». Но, Упси Дудлз! Это игнорировало бы эти раздражающие мелкие детали, и наши друзья-умники доставили бы нам массу нытья: «полтора не является составным, так разве это не простое число?». Давайте исправим это, дав хорошее простое определение:
Давайте исправим это, дав хорошее простое определение:
- Простые числа — это целые числа больше единицы, которые не являются составными.
- Составные числа — это произведения целых чисел, больших единицы.
Почему важны простые числа?
На этот вопрос есть много ответов, в зависимости от того, хотите ли вы узнать практические причины, по которым стоит обращать внимание на простые числа, или более глубокие причины.
Простые числа и практическая математика:
Некоторые практические вещи, для которых хороши простые числа, включают:
- Упрощение дробей
- Взаимное сокращение
- поиск LCD (наименьшие общие знаменатели)
- поиск GCF (наибольшие общие множители)
Криптология
Важно просто найти гигантские простые числа. Требуется огромный объем работы, чтобы выяснить, являются ли действительно большие числа простыми. По этой причине простые числа важны в криптологии, изучающей способы создания секретных кодов. Они используются для таких практических целей, как обеспечение безопасности банковских счетов. Простые числа — большие деньги!!!
Они используются для таких практических целей, как обеспечение безопасности банковских счетов. Простые числа — большие деньги!!!
Гипотеза Римана
Простые числа также связаны с некоторыми из самых интересных математических задач, которые еще не решены. Математики называют нерешенные проблемы «открытыми проблемами». Самая известная на сегодняшний день — это, вероятно, гипотеза Римана. Требуется много объяснений, чтобы понять, и на самом деле никто еще не докопался до сути. Это связано с угадыванием вероятности того, что число будет простым, исходя из того, насколько оно велико. Здесь мы не можем рассказать об этом подробнее, хотя можем порекомендовать книгу об этом людям, не являющимся математиками. Кстати, большие призы ждут всех, кто сможет решить важные открытые задачи, включая гипотезу Римана.
Почему простые числа определяются именно так?
Хороший вопрос! Часто люди просто принимают определения такими, какие они есть, не задаваясь вопросом, почему они были определены такими, какие они есть. В конце концов, все определения могут быть сделаны так, как мы хотим, пока мы принимаем последствия нашего выбора. Итак, зачем исключать единицу из числа простых? Почему не отрицательные числа? Причина в том, что, определив простые числа так, как это делаем мы — без отрицательных чисел, нуля или единицы — мы можем простым способом сформулировать удивительное свойство целых чисел: основную теорему арифметики.
В конце концов, все определения могут быть сделаны так, как мы хотим, пока мы принимаем последствия нашего выбора. Итак, зачем исключать единицу из числа простых? Почему не отрицательные числа? Причина в том, что, определив простые числа так, как это делаем мы — без отрицательных чисел, нуля или единицы — мы можем простым способом сформулировать удивительное свойство целых чисел: основную теорему арифметики.
Следующая тема: Основная теорема арифметики
Об этой странице помощи Bubbly Primes Math
Список составных чисел от 1 до 100
Составное число — это целое число, которое можно разделить нацело на другие целые числа, кроме самого себя и 1. Другими словами, составное число — это число, имеющее несколько делителей.
Число 12 является составным числом, поскольку его можно разделить без остатка на 1, 2, 3, 4, 6 и 12. Число 10 не является составным числом, поскольку его можно разделить без остатка только на 1 и 10.
Заполните форму для экспертного академического руководства!
Класс
— Класс 6 Класс 7 Класс 8 Класс 9 Класс 10 Класс 11 Класс 12
Целевой экзамен
JEENEETCBSE
+91
Предпочтительный временной интервал для звонка 1:0012 pm1 pm2 pm3 pm4 pm5 pm6 pm7 pm8 pm9 22:00
Укажите, что вас интересует
Занятия в реальном времениЗаписи занятийСерия тестовСамообучение
Язык
—АнглийскийХиндиМаратхиТамильскийтелугуМалайялам
Подтвердите OTP-код (обязательно)
Я согласен с условиями и политикой конфиденциальности.
Составные числа важны в математике, потому что их можно использовать для нахождения простых чисел. Простое число — это число, которое можно разделить без остатка только само на себя и на 1. Чтобы найти простое число, вы начинаете с составного числа и продолжаете делить его на другие числа, пока не найдете число, которое больше нельзя делить без остатка.
Например, начнем с числа 12. Мы знаем, что 12 — составное число, потому что его можно без остатка разделить на 1, 2, 3, 4, 6 и 12.
Если мы разделим 12 на 2, мы получим 6. 6 — составное число, потому что его можно разделить без остатка на 1, 2, 3 и 6.
Если мы разделим 6 на 3, мы получим 2. 2 — это простое число, потому что оно делится без остатка только само на себя и на 1.
Если мы разделим 12 на 3, мы получим 4. 4 — составное число, потому что его можно разделить без остатка на 1, 2 и 4.
Если мы делим 4 на 4, получаем 1. 1 не простое число, потому что его можно разделить без остатка только на себя.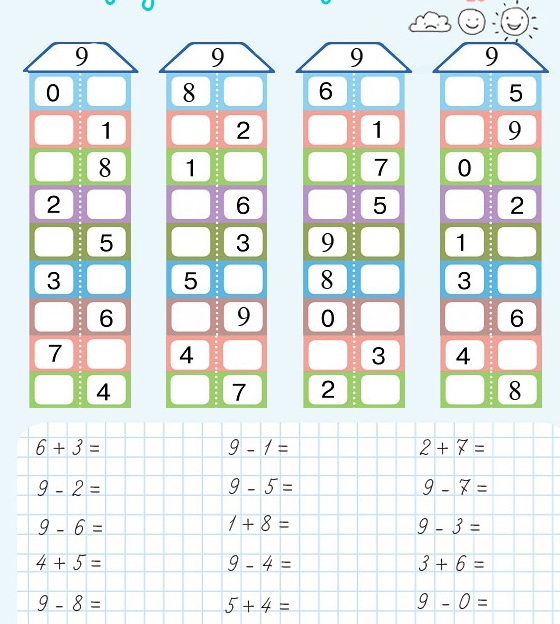
Мы можем продолжать этот процесс, пока не найдем составное число, которое нельзя разделить без остатка ни на какое другое число. Например, если бы мы начали с числа 14, то в конце концов дошли бы до 7, которое является простым числом.
Составные числа также известны как «факторы». Число 1 не является составным числом, поскольку делится только на 1. Число 4 является первым составным числом, поскольку делится на 1, 2 и 4.
Список составных чисел от 1 до 100
Список составных чисел от 1 до 100 следующий:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27 , 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60 , 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100
Нечетные и четные составные числа
Нечетные составные числа — это числа, которые одновременно являются нечетными и составными.
Существует много нечетных составных чисел от 1 до 100.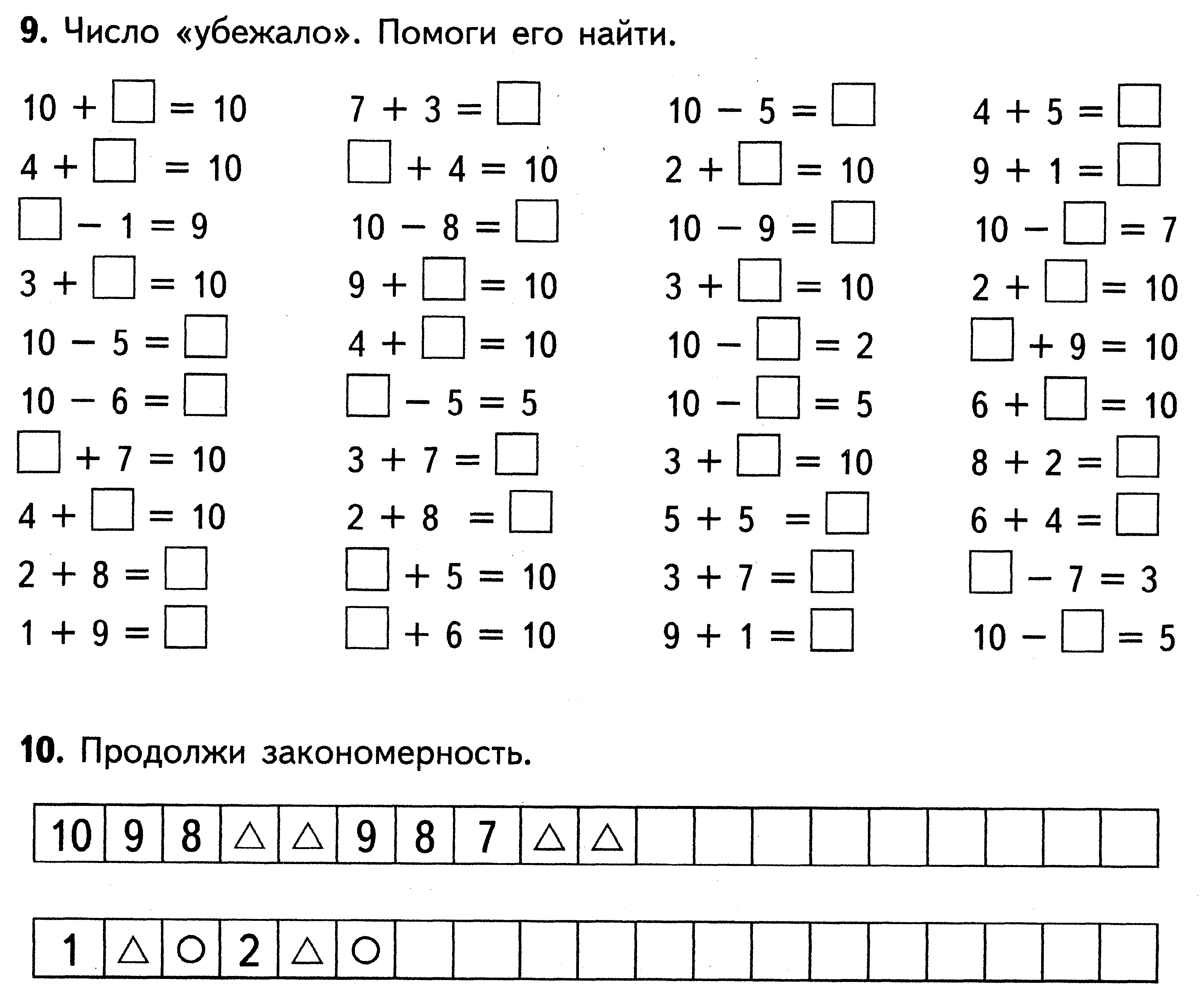 Вот некоторые из них: 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 63, 65, 69, 75, 77. , 81, 85, 87, 93, 99.
Вот некоторые из них: 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 63, 65, 69, 75, 77. , 81, 85, 87, 93, 99.
Четные составные числа — это числа, которые одновременно являются четными и составными.
Существует несколько четных составных чисел от 1 до 100. Некоторые из этих чисел включают: 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34. , 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84 , 86, 88, 90, 92, 94, 96, 98 и 100.
Свойства составных чисел, отличающие их от других чисел:
Составные числа обладают несколькими свойствами, отличающими их от других чисел. Например, составные числа всегда делятся по крайней мере еще на одно число, кроме самих себя и единицы. Это означает, что если вы возьмете любое составное число и разделите его на любое число, кроме единицы или самого себя, вы всегда получите целочисленный ответ.
Еще одним свойством составных чисел является то, что они никогда не бывают простыми числами.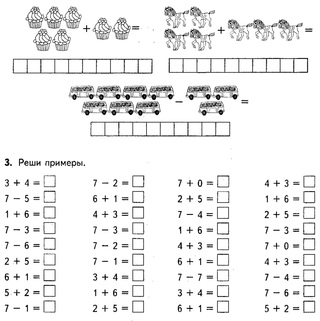 Простое число — это число, которое делится только на единицу и само на себя. Поскольку составные числа делятся на числа, отличные от единицы и самих себя, они никогда не могут быть простыми.
Простое число — это число, которое делится только на единицу и само на себя. Поскольку составные числа делятся на числа, отличные от единицы и самих себя, они никогда не могут быть простыми.
Наконец, составные числа всегда имеют делитель, отличный от единицы. Множитель — это число, которое без остатка делится на другое число. Так, например, делители 12 — это 1, 2, 3, 4, 6 и 12. Как видите, все делители 12 — составные числа, кроме 1. Это потому, что 1 — единственное число, которое может делиться на себя поровну.
Составные числа являются важной частью математики и играют роль во многих различных областях дисциплины. Понимая свойства, которые отличают составные числа от других чисел, учащиеся могут лучше понять роль, которую они играют в математике.
Приложение Infinity Learn
Теперь вы можете найти ответы на все интересующие вас вопросы и подготовиться к экзаменам в нашем приложении для подготовки к экзаменам — Infinity Learn.
Сопутствующее содержимое
| Прямой угол – определение, формула, примеры и часто задаваемые вопросы |
| Геометрические фигуры – объяснение с примерами и списком геометрических фигур | 902 22
| Сложный процент – определение, формула, расчет, Методы и примеры решений |
| 1 миллиард рупий — преобразование, решенные примеры и часто задаваемые вопросы s для математики 12 класса |
| Введение К трехмерной геометрии, системе координат и формулам |
Решения NCERT для математического упражнения по обработке данных 6 класса 9. |
 00 из 5
00 из 5