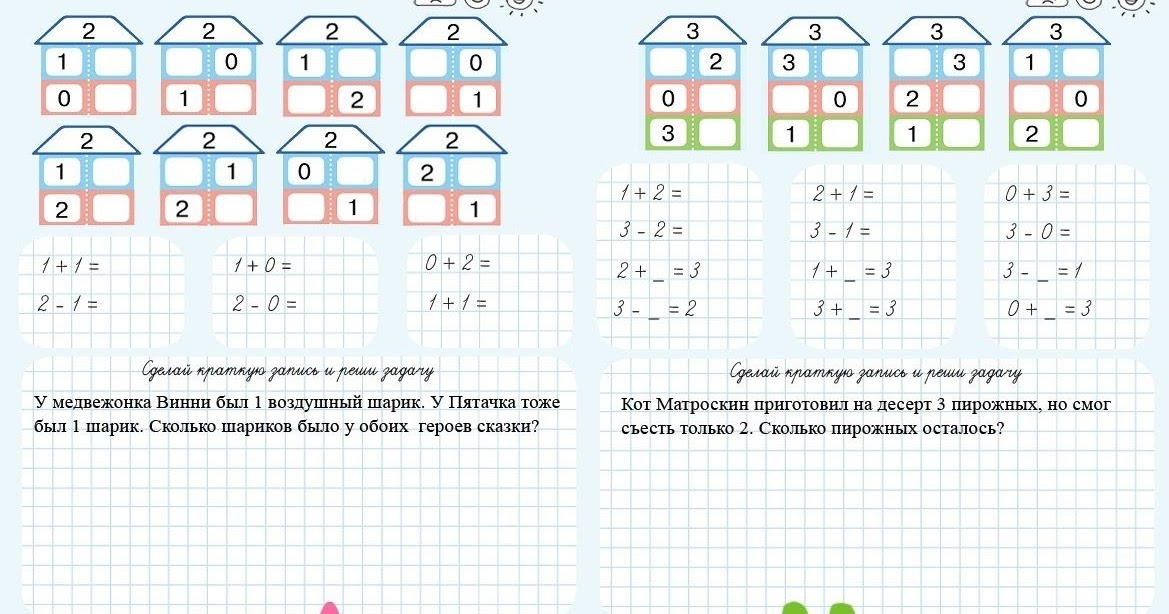
состав числа
состав числаИскать…
————————————————————————————
Все работы детей, объяснялки и тренинги сконвертированы из Power Point в универсальный формат HTML5 с помощью лицензионной программы iSpring Suite
Если вы смотрите объяснялки и тренинги на смартфоне,
лучше разворачивать его в «альбомный» вариант
- 1502
{jcomments off}
Тренинг на состав чисел 6-9 «вперемешку». Если выбрано правильное число, стрелочка «позовет» на следующий пример.
Подробнее…
- 1384
{jcomments off}Это возможность убедиться, что Ваш малыш хорошо усвоил состав числа, а не заучил его по порядку.
Подробнее…
- 1619
{jcomments off}
Можно использовать для выборочного повторения, для закрепления, для контрольного опроса
Подробнее…
- 1189
{jcomments off}
Предлагаем для ознакомления и повторения. Каждое число появляется «неторопливо». И в таком же темпе «сбегаются» с разных сторон составляющие его числа. Одинаковые числа не «пишутся». Просто число «надувается» от гордости, что его используют дважды
Подробнее. ..
..
- 1334
{jcomments off}
Подробнее…
- 1558
{jcomments off}
Подробнее…
- Вы здесь:
- математика org/ListItem»> состав числа
математика-интерактив
состав числа
количество и счет
мир вокруг меня
сравнения
формы
решаем примеры
начертание
графический диктант
время
решаем задачи
цветовосприятие
пазлы
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинетаИзменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 7 из 7 Автор: Н.И. Скобцева Журнал «Начальная школа» . 2004. № 10 https://vk.com/away.php?to=https%3A%2F%2Fn-shkola.ru%2Fstorage%2Farchive%2F1407239526-7717874.pdf&cc_key= ст82 Хотелось бы поговорить о проблеме, с которой сталкиваются многие учителя начальной школы: это изучение состава чисел. Учителя хорошо знают, что ученики легко усваивают состав чисел от 2 до 9, легко дополняют числа до 10 и 20, а вот состав чисел от 11 до 18 усваивают с трудом, что в дальнейшем затрудняет работу по формированию вычислительных навыков. Для того чтобы облегчить запоминание состава чисел от 11 до 18, предлагаю использовать наряду с традиционными методическими приемами другой, на мой взгляд, более легкий способ запоминания состава двузначных чисел в пределах 20. А помогут при этом знание состава чисел от 2 до 9 и умение дополнять числа до 10 и 20. 11 — это целое. Дополним целое до 20. 20 — это 11 и 9. 9 — тоже целое. Ученикам известно, что 9 — это 8 и 1. 8 и 1 — это части. Каждую часть дополним до 10. Это 2 и 9. Это состав числа 11. 9 — это 7 и 2. Дополним эти части числа 9 до 10. 3 и 8 — это состав числа 11. 9 — это 6 и 3. Дополним эти части числа 9 до 10. 4 и 7 — это состав числа 11. 9 — это 5 и 4. Дополним эти части числа 9 до 10. 5 и 6 — это состав числа 11. Детям очень нравится такая работа на уроке. И учитель ничего не теряет, так как параллельно с изучением состава чисел от 11 до 18 идет закрепление состава чисел от 2 до 9 и умения дополнять числа до 10 и 20. Конечно, это не обычный, но один из наиболее легких, удобных, отнимающих минимум времени способов. А самое главное, он помогает быстро усвоить состав двузначных чисел в пределах 20.
Сосчитай! Автор: Т.Н. Кочемова Журнал «Начальная школа» 2004. № 10 https://vk.com/away.php?to=https%3A%2F%2Fn-shkola.ru%2Fstorage%2Farchive%2F1407239526-7717874.pdf&cc_key= ст83 По небу плыли облака: 4 замка, 2 быка, 3 крокодила, 3 кита, Дракон, русалка, 2 кота. Так у кого ответ готов: На небе сколько облаков? • У осьминога — 8 ног, У лошади — 4. 16 ринулись в галоп И столько же — поплыли. И осьминогов поскорей Ты посчитай, и лошадей. • Наряжали елку дети: На колючие на ветви 7 повесили шаров, 10 шишек, 6 грибов, 5 петрушек, 7 слонов, 9 звезд и 5 цветов, 6 снежинок, 3 хлопушки. Сосчитайте все игрушки!
Задачи в стихах Автор: О.Г. Полончук Журнал «Начальная школа» 2004. № 6 https://vk.com/away.php?to=https%3A%2F%2Fn-shkola.ru%2Fstorage%2Farchive%2F1407239323-1717597922. Хочу предложить занимательные задачи в стихах, которые так любят младшие школьники. Рифмованные задачи активизируют работу класса, вносят элемент занимательности, развивают воображение, внимание, мышление. Они помогают учителю проводить сюжетные уроки, уроки-сказки; их можно использовать и во внеурочной работе. ⇐ Предыдущая1234567 Читайте также: Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте |
|
Последнее изменение этой страницы: 2021-04-13; просмотров: 94; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Составные функции — объяснение и примеры
В математике функция — это правило, связывающее данный набор входных данных с набором возможных выходных данных. Важно отметить, что каждый вход связан ровно с одним выходом.
Процесс именования функций известен как нотация функций. Наиболее часто используемые обозначения функций включают в себя: «f(x) = …», «g(x) = …», «h(x) = …» и т. д.
В этой статье мы узнаем , что такое композит функции и способы их решения.
Что такое составная функция?
Если нам даны две функции, мы можем создать другую функцию, вставив одну функцию в другую. Шаги, необходимые для выполнения этой операции, аналогичны тому, когда любая функция решается для любого заданного значения. Такие функции называются составными функциями.
Такие функции называются составными функциями.
Составная функция — это обычно функция, написанная внутри другой функции. Композиция функции осуществляется путем замены одной функции на другую функцию.
Например, , f [g (x)] — составная функция f (x) и g (x). Составная функция f [g (x)] читается как «f of g of x ». Функция g(x) называется внутренней функцией, а функция f(x) — внешней функцией. Следовательно, мы можем также прочитать f [g (x)] как «функция g является внутренней функцией внешней функции f ».
Как решать составные функции?
Решение сложной функции означает нахождение композиции двух функций. Мы используем маленький кружок (∘) для обозначения функции. Вот шаги по решению составной функции:
- Перепишите композицию в другой форме.
Например,
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x) = f [g (x)]
(f ∘ g) (x² ) = f [g (x²)]
- Замените переменную x во внешней функции на внутреннюю.

- Упрощение функции.
Примечание: Порядок в составе функции важен, потому что (f ∘ g) (x) НЕ совпадает с (g ∘ f) (x).
9Пример 1 (Икс).Решение
Подставим x на 2x – 1 в функции f(x) = x 2 + 6.
(f ∘ g) (x) = (2x – 1) 2 + 6 = ( 2x – 1) (2x – 1) + 6
Применение ФОЛЬГИ
= 4x 2 – 4x + 1 + 6
= 4x 2 – 4x + 7
Пример 2
Учитывая функции g (x) = 2x – 1 и f (x) = x 2 + 6, найдите (g ∘ f) (x).
Решение
Подставить x на x 2 + 6 в функции g (x) = 2x – 1
(g ∘ f) (x) = 2(x 2 2 + 6) – 1
= 2x 2 + 12 – 1
= 2x 2 + 11
0002 Учитывая f (x) = 2x + 3, найти (f ∘ f) (x).
Решение
(F ∘ F) (x) = F [F (x)]
= 2 (2x + 3) + 3
= 4x +
Пример 4
Найдите (g ∘ f) (x), учитывая, что f (x) = 2x + 3 и g (x) = –x 2 + 5
⟹ (g ∘ f) (x) = g [f (x )]. 5
5
= –4x 9Пример 5 g (x) = x – 3
Решение
Сначала найдите значение f(g(x)).
⟹ f (g (x)) = 5(x – 3) + 4
= 5x – 15 + 4
= 5x – 11
Теперь подставим x в f(g(x)) на 6
⟹ 5(6) – 11
⟹ 30 – 11
= 19
Следовательно, f [g (6)] = 19
Пример 6
Найдите f [g (5)], учитывая, что f (x) = 4x + 3 и g (x) = x – 2. значение f[g(x)].
⟹ f(x) = 4x + 3
⟹ g(x) = x – 2
f[g(x)] = 4(x – 2) + 3
= 4x – 8 + 3
= 4x – 5
Теперь оцените f [g (5)], заменив x в f[g(x)] на 5.
f [g (x)] = 4(5) – 5
= 15
Следовательно, f [g (5)] = 15,9Пример 7 ) = f [g(x)]
Замените x в f(x) = 8x² на (2x + 8)
⟹ (f ∘g) (x) = f [g(x)] = 8(2x + 8) ²
⟹ 8 [4x² + 8² + 2(2x) (8)]
⟹ 8 [4x² + 64 + 32x]
⟹ 32x² + 512 + 256 x
x 0 03 + 1 256 32x²
Пример 8
Найти (g ∘ f) (x), если f(x) = 6 x² и g(x) = 14x + 4
Решение
⟹ (g ∘ f) (x) = g [f(x)]
Подставить x в g(x) = 14x + 4 с 6 x²
⟹g [f(x)] =14 (6 x²) + 4
= 84 x² + 4
Пример 9
Рассчитайте (f ∘ g) (x), используя f(x) = 2x + 3 и g(x) = — x 2 + 1,
Решение
(f ∘ g) (x) = f(g(x))
= 2 (g(x)) + 3
= 2(-x 2 + 1) + 3
= – 2 x 2 + 5
Пример 10
Учитывая f(x) = √ (x + 2) и g(x) = ln (1 – x 2 ), найдите область значений (g ∘ f) (x).
Решение
⟹ (g ∘ f) (x) = g(f(x))
⟹ ln (1 – f(x) 2 ) = ln (1 – √ (x + 2) 2 )
⟹ ln (1 – (x + 2))
= ln (- x – 1)
Присвоить x + 2 значение ≥ 0
Следовательно, домен: [-2, -1]
Пример 11
Даны две функции: f = {(-2, 1), (0, 3), (4, 5)} и g = {(1, 1), (3, 3), (7 , 9)}, найти (g ∘ f) и определить его область определения и область значений.
Решение
⟹ (g ∘ f) (-2) = g [f (-2)] = g (1) = 1
⟹ (g ∘ f) (0) = g [f (0) ] = g(3) = 3
⟹ (g ∘ f)(4) = g[f(4)] = g(5) = undefined
Следовательно, g ∘ f = {(-2, 1), ( 0, 3)}
Следовательно, Домен: {-2, 0} и Диапазон: {1, 3}
Состав функций | Calc Medic
Блок 1
День 1
День 2
День 3
День 4
День 5
День 6
День 7
День 8
День 9
День 10
День 11
День 12
День 13
День 14
День 15
Все модули
Цели обучения
Поймите, что при составлении двух функций выходные данные одной функции становятся входными данными другой
Интерпретация ввода и вывода составных функций в контексте
Вычислите и напишите уравнения для композиций функций, подставив внутреннюю функцию в качестве независимой переменной внешней функции
Найти область определения композиции функций
Краткий план урока
Первый опыт
На этом уроке учащиеся строят свою собственную составную функцию, выражая регулярность в повторяющихся рассуждениях. Во-первых, учащиеся рассматривают вопрос о том, как длина бассейна определяет количество плиток, необходимых для создания границы бассейна. Алгебраически есть много способов составить это выражение, поэтому предложите учащимся использовать цвет, чтобы продемонстрировать, как они «видят» добавляемые плитки. Это прекрасная возможность поговорить об эквивалентности выражений!
Во-первых, учащиеся рассматривают вопрос о том, как длина бассейна определяет количество плиток, необходимых для создания границы бассейна. Алгебраически есть много способов составить это выражение, поэтому предложите учащимся использовать цвет, чтобы продемонстрировать, как они «видят» добавляемые плитки. Это прекрасная возможность поговорить об эквивалентности выражений!
После определения количества плиток учащиеся переходят к расчету стоимости этих плиток с включенной платой за доставку. Наблюдая за группами, задавайте учащимся такие вопросы, как «от чего зависит стоимость проекта?» или «как/почему увеличение длины пула повлияет на стоимость?» Учащиеся должны объяснить, что количество плиток определяет стоимость, а длина пула определяет количество плиток. Прислушивайтесь к фразам вроде «увеличение длины бассейна увеличивает количество плиток, что увеличивает стоимость проекта». Этот вид последовательного рассуждения имеет решающее значение для развития у учащихся понимания составных функций.
При заполнении таблицы будет полезно, если учащиеся покажут свою работу по расчету количества плиток и стоимости проекта. Когда учащиеся видят 2(18)+16=52, а в следующем столбце 52(5,75)+9,99, становится очевидным, как выход первой функции становится входом второй функции. Наконец, мы хотим, чтобы учащиеся увидели, как это можно выразить в одном уравнении, а именно, вставив выражение 2x+16 в уравнение стоимости, чтобы представить количество плиток (определяемое длиной бассейна).
На протяжении всего опыта студентов просят обращать внимание на виды значений, которые входят в функцию, и те, которые выходят. Ограниченные домены для длины пула создают ограниченный диапазон для количества тайлов; что в конечном итоге определяет диапазон цен для завершения проекта.
Формализация позже
Как всегда, многие формальные обозначения опускаются в эксперименте, а затем добавляются во время формализации. Помогите учащимся увидеть, как C(n(x)) демонстрирует последовательность уравнений, а также входные и выходные данные каждого «этапа».

 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
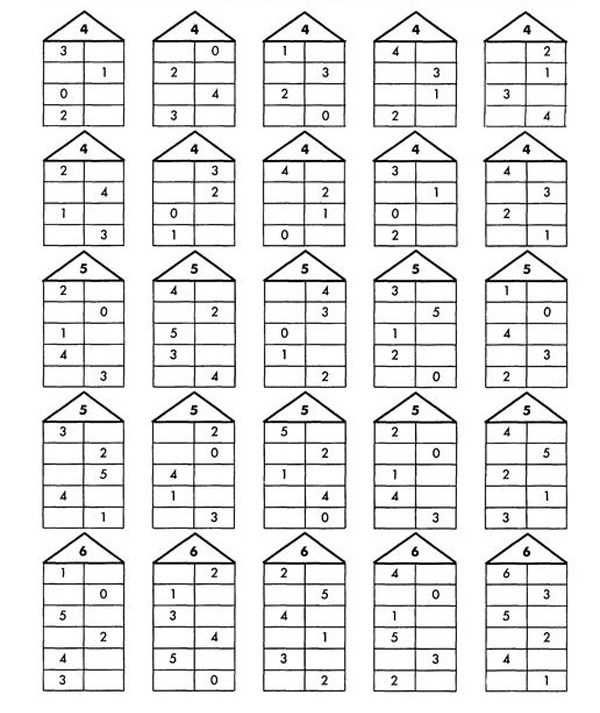 Рассмотрим состав числа 11, используя прием, который зафиксирован на соответствующих табличках, складывающихся по полам.
Рассмотрим состав числа 11, используя прием, который зафиксирован на соответствующих табличках, складывающихся по полам.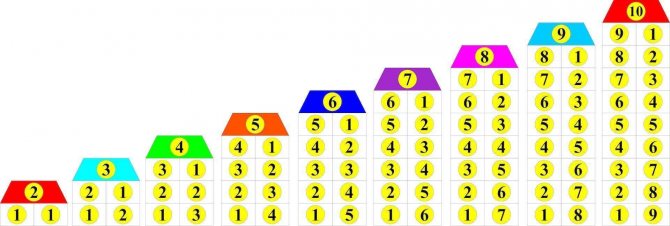
 pdf&cc_key= ст100
pdf&cc_key= ст100