Как обьяснить «состав числа»?

04.11.2011 01:34

Мамы, хелп, у меня мозг сплющился ужо. Обьясните, пожалуйста, как будто мне 6 лет, что такое состав числа? Ну, в смысле, это ваще можно обьяснить, или просто монотонно повторяем, что 6-это 6+0, 5+1, 2+4…, пока наизусть не выучим? (помню, дочка в 1 классе именно наизусть зазубривала таблицу сложения в пределах 20. Но сынище такой фигней не занимается, ему обьяснения внятные хочется)

зира ***

04.11.2011 01:43

Пишите цифру, под ней рисуете вертикальную линию, получая таким образом как бы два столбика под цифрой. Пусть это будет 7. Слева в столбике пишите цифры от 1 до 6 вниз, справа в столбике напротив 1 будет написано 6, напротив 2 — 5 ну и т.д. чтобы получалось 7. Столбики весьма понятные получаются и право говоря до безобразия понятные.

У меня деть в 4,6 уже через пару минут сам прибился числа все раскладывать :).

Фeмида C.S.

04.11.2011 04:36

В книжном магазине купите плакат «Состав числа», вот такой: Ну или сами нарисуйте вместе с ребенком 🙂

Марина Шадрина C.S.

04.11.2011 05:00

О! Точняк! Спасибо. Мозг просветлел.

зира ***

04.11.2011 07:02

Да не за что 🙂 Повесьте на стену — ребенок сам выучит 🙂

Марина Шадрина C.S.

25.11.2017 06:54

Есть приложение — интерактивный тренажер для iPad и iPhone которое облегчает ребенку процесс запоминания превращая его в игру с привлекательными фишками и звуками.

Вы можете скачать приложение «Состав числа до 10 — игра тренажер — математика» в App Store: https://itunes.apple.com/ru/app/id575132700 Для лучшего эффекта стимулируйте ребенка на прохождение игры и обязательно повторите прохождение через пару дней.

AllaStepashina +

25.11.2017 11:59

https://www.labirint.ru/books/429002/ Мой ребенок до школы занимался по этому пособию,в 1 классе проблем не возникало.

Евгешка80 F

28.11.2017 18:25

это две руки десять пальцев если два загнуть, то восемь останутся разогнутыми и так далее и все числа больше 10 состоят из отпечатков двух полных пар и последней неполной зачем повторять, если можно воспользоваться свои встроенным калькулятором, это вполне прилично запомнится со временем, когда часто пользуешься

Dezzi D**

28. 11.2017 18:27

карточные игры и пасьянсы тоже помогают

Dezzi D**

04.11.2011 11:08

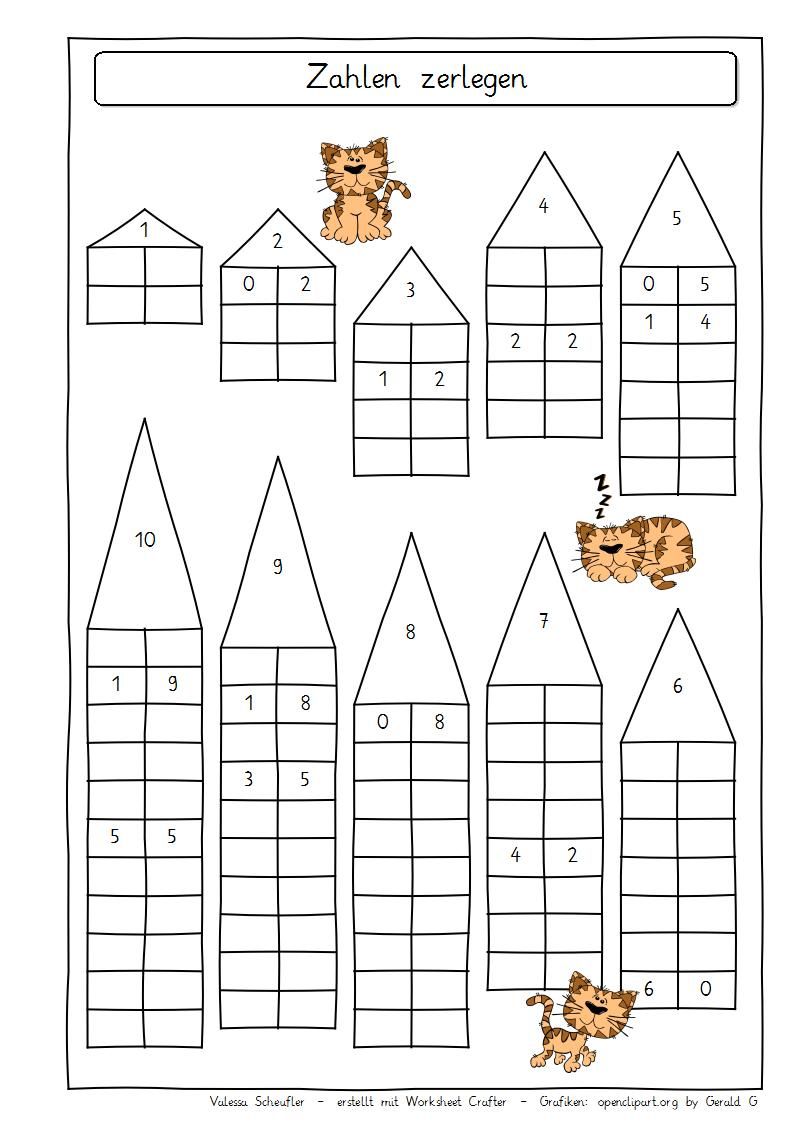
Рисовала на небольших карточках домики: крыша, внутри пишите число, например 5, сам домик — прямоугольник, разделенный пополам, а потом на квадратики (окна), в которых живут цифры (0 напротив 5, 1 напротив 4, и т.д.) Очень наглядно для ребенка, запоминается легко, можно с собой брать и между делом повторять и т.п.

ЗелЁный апельсин *

04.11.2011 11:39

+ 1 к домикам. Очень наглядно и удобно.

Valentinka C.G.

04.11.2011 19:46

Ага, всем спасибо. Рисую домики))

зира ***

25. 11.2017 11:49

Поддержу, сын по домикам быстро понял и выучил, до этого затык был…

Timosha KF**

25.11.2017 21:58

Домики во всех детски пособиях, как вы уже поняли. Еще мы карандаши перекладывали из руки в руку. Например 5 это — берем 5 карандашей и перекладываем — 5 и 0, 4 и 1, 3 и 2 и т.д.

Anonymous

25.11.2017 22:09

палочки, карандаши, спички

Anonymous

25.11.2017 23:54

А школе не учат?

Anonymous

26.11.2017 09:35

в школе сейчас не учат, только рассказывают, как надо родителям учить

Anonymous

26.11.2017 13:01

Так автор же не в России.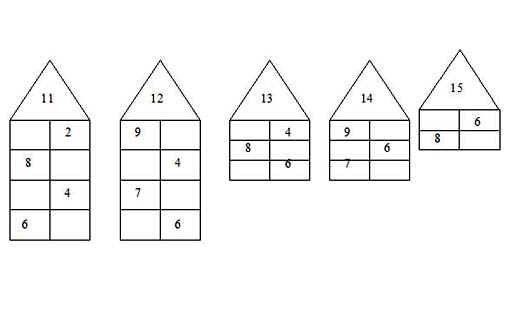

Anonymous

27.11.2017 00:41

Домики. Объяснить, а потом тупо вызубрить. Что б от зубов отскакивало.

Boлшeбницa ♤** Noblesse

29.11.2017 13:57

А в каком возрасте надо уже понимать состав числа?С какого возраста начинать объяснять?

katya091 KF**

29.11.2017 14:21

выше ссылку давали https://www.labirint.ru/books/429002/ я своей такой в 6,5 «подсунула» — он много разовый. очень удобно и доходчиво для ребенка. советую.

Кот рыжий OH*

30.11.2017 10:43

В пять уже отлично понимают. У нас в саду пятилетки эти домики «заселяют» только в путь 🙂

JUNE BUG SD*

29. 11.2017 22:19

Думаю, что про числовые домики уже без меня написали. Просто тупо учим-учим. И да, на сайте uchi.ru много заданий-игр как раз на состав чисел.

LadyWi SD*

Открыть в форуме

Целые числа — определение, символы, свойства и примеры

целых числа являются частью системы счисления, которая включает в себя все положительные целые числа от 0 до бесконечности. Эти числа существуют в числовой строке. Следовательно, все они действительные числа. Мы можем сказать, что все целые числа являются действительными числами, но не все действительные числа являются целыми числами. Таким образом, мы можем определить целые числа как набор натуральных чисел и 0. Целые числа — это набор целых чисел и отрицательных натуральных чисел. Следовательно, целые числа включают как положительные, так и отрицательные числа, включая 0. Действительные числа представляют собой набор всех этих типов чисел, т. е. натуральных чисел, целых чисел, целых чисел и дробей.

Полный набор натуральных чисел вместе с «0» называется целыми числами. Примеры: 0, 11, 25, 36, 999, 1200 и т. д.

Узнайте больше о числах здесь.

Содержание: Определение Символ Свойства Крышка Коммутативный Добавка Мультипликатив Ассоциативный Распределительный Целые числа и натуральные числа Решенные примеры Практические задачи Видео урок Часто задаваемые вопросы

Определение целых чисел

целых числа — это числа без дробей, представляющие собой набор положительных целых чисел и нуля. Он представлен символом «W» и набором чисел {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,……………}. Ноль в целом не представляет ничего или нулевое значение.

Целые числа: W = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10……} Натуральные числа: N = {1, 2, 3, 4, 5, 6, 7, 8, 9,…} Целые числа: Z = {….-9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7 , 8, 9,…} Числа для подсчета: {1, 2, 3, 4, 5, 6, 7,….}

Эти числа являются целыми положительными числами, включая ноль, и не включают дробные или десятичные части (3/4, 2,2 и 5,3 не являются целыми числами). Кроме того, над целыми числами возможны такие арифметические операции, как сложение, вычитание, умножение и деление.

Символ

Символом для представления целых чисел является буква «W» заглавными буквами.

Вт = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,…}

Таким образом, список из целых чисел включает 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ….

Факты:

Все натуральные числа являются целыми числами Все счетные числа являются целыми числами Все положительные целые числа, включая ноль, являются целыми числами Все целые числа действительные числа

Если у вас все еще есть сомнения, что такое целое число в математике? Более полное представление о целых числах можно получить из следующей таблицы:

Свойства целых чисел

Свойства целых чисел основаны на арифметических операциях, таких как сложение, вычитание, деление и умножение. Два целых числа, если их сложить или умножить, сами дадут целое число. Вычитание двух целых чисел может не дать целых чисел, т. е. это тоже может быть целое число. Кроме того, в некоторых случаях при делении двух целых чисел получается дробь. Теперь давайте посмотрим еще некоторые свойства целых чисел и их доказательства с помощью примеров здесь.

Свойство закрытия

Их можно замкнуть относительно сложения и умножения, т. е. если x и y — два целых числа, то x. у или х + у тоже целое число.

Пример:

5 и 8 — целые числа.

5 + 8 = 13; целое число

5 × 8 = 40; целое число

Следовательно, целые числа закрыты при сложении и умножении.

Коммутативное свойство сложения и умножения

Сумма и произведение двух целых чисел будут одними и теми же независимо от порядка их сложения или умножения, т. е. если x и y — два целых числа, то x + y = y + x и x . у = у . х

Пример:

Рассмотрим два целых числа 3 и 7.

3 + 7 = 10

7 + 3 = 10

Таким образом, 3 + 7 = 7 + 3.

Также

3 × 7 = 21

7 × 3 = 21

Таким образом, 3 × 7 = 7 × 3

Следовательно, целые числа коммутативны при сложении и умножении.

Аддитивный идентификатор

Когда к 0 прибавляется целое число, его значение остается неизменным, т. е. если x — целое число, то x + 0 = 0 + x = x

Пример:  

Рассмотрим два целых числа 0 и 11.

0 + 11 = 11

11 + 0 = 11

Здесь 0 + 11 = 11 + 0 = 11

Поэтому 0 называется аддитивной единицей целых чисел.

Мультипликативная идентичность

При умножении целого числа на 1 его значение остается неизменным, т. е. если x — целое число, то x.1 = x = 1.x

Пример:

Рассмотрим два целых числа 1 и 15.

1 × 15 = 15

15 × 1 = 15

Здесь 1 × 15 = 15 = 15 × 1

Таким образом, 1 является мультипликативной единицей целых чисел.

Ассоциативное свойство

Когда целые числа складываются или умножаются как набор, их можно группировать в любом порядке, и результат будет одинаковым, т. е. если x, y и z — целые числа, то x + (y + z) = (x + у) + г и х. (y.z)=(x.y).z

Пример:

Рассмотрим три целых числа 2, 3 и 4.

2 + (3 + 4) = 2 + 7 = 9

(2 + 3) + 4 = 5 + 4 = 9

Таким образом, 2 + (3 + 4) = (2 + 3) + 4

2 × (3 × 4) = 2 × 12 = 24

(2 × 3) × 4 = 6 × 4 = 24

Здесь 2 × (3 × 4) = (2 × 3) × 4

Следовательно, целые числа ассоциативны при сложении и умножении.

Распределительная собственность

Если x, y и z — три целых числа, распределительное свойство умножения над сложением равно x. (y + z) = (x.y) + (x.z), аналогично, распределительное свойство умножения над вычитанием равно x. (y – z) = (x.y) – (x.z)

Пример:

Рассмотрим три целых числа 9, 11 и 6.

9 × (11 + 6) = 9 × 17 = 153

(9 × 11) + (9 × 6) = 99 + 54 = 153

Здесь 9 × (11 + 6) = (9 × 11) + (9 × 6)

Также

9 × (11 – 6) = 9 × 5 = 45

(9 × 11) – (9 × 6) = 99 – 54 = 45

Итак, 9 × (11 – 6) = (9 × 11) – (9 × 6)

Таким образом, доказано распределительное свойство целых чисел.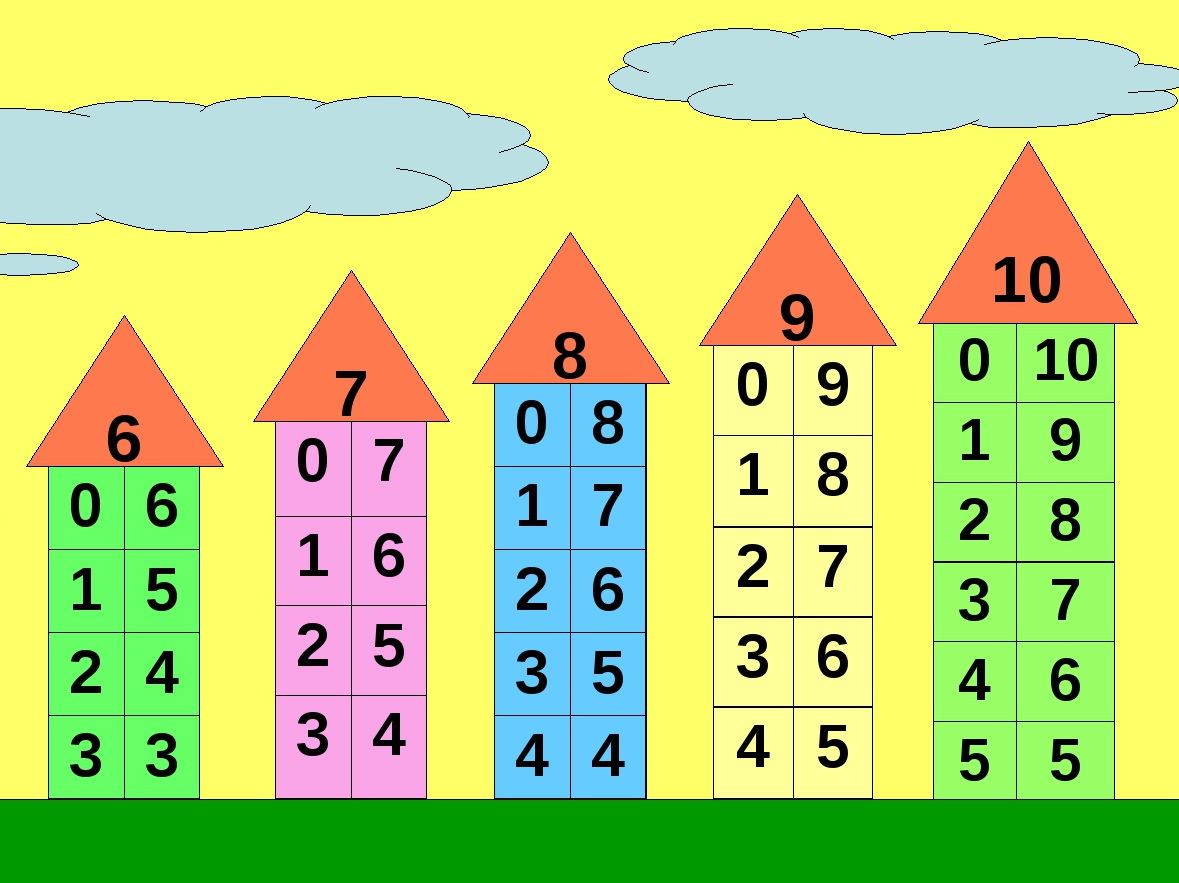

Умножение на ноль

Когда целое число умножается на 0, результат всегда равен 0, т. е. x.0 = 0.x = 0

Пример:

0 × 12 = 0

12 × 0 = 0

Здесь 0 × 12 = 12 × 0 = 0

Таким образом, при умножении любого целого числа на 0 результат всегда равен 0.

Деление на ноль

Деление целого числа на o не определено, т. е. если x — целое число, то x/0 не определено.

Также проверьте: Калькулятор целых чисел

Разница между целыми числами и натуральными числами

Разница между целыми и натуральными числами
Целые числа	Натуральные числа
Целые числа: {0, 1, 2, 3, 4, 5, 6,…..}	Натуральные числа: {1, 2, 3, 4, 5, 6,……}
Счет начинается с 0	Счет начинается с 1
Все целые числа не являются натуральными	Все натуральные числа являются целыми числами

Рисунок ниже поможет нам понять разницу между целым числом и натуральными числами:

Могут ли целые числа быть отрицательными?

Целое число не может быть отрицательным!

Согласно определению: {0, 1, 2, 3, 4, 5, 6, 7,……до положительной бесконечности} — целые числа. Здесь нет места отрицательным числам.

Является ли 0 целым числом?

Целые числа — это множество всех натуральных чисел, включая ноль. Так что да, 0 (ноль) — это не только целое число, но и первое целое число.

Решенные примеры

Пример 1:  Являются ли 100, 227, 198, 4321 целыми числами?

Решение: Да. 100, 227, 198 и 4321 — целые числа.

Пример 2 : Решите 10 × (5 + 10), используя свойство распределения.

Решение:  Распределительное свойство умножения при сложении целых чисел:

х × (у + г) = (х × у) + (х × г)

10 × (5 + 10) = (10 × 5) + (10 × 10)

= 50 + 100

= 150

Следовательно, 10 × (5 + 10) = 150

Однако мы можем показать несколько примеров целых чисел, используя свойства целых чисел.

Практические задачи

1. Запишите целые числа от 12 до 25.
2. Чему равна аддитивная величина, обратная целому числу 98?
3. Сколько целых чисел находится между -1 и 14?

Чтобы узнать больше о таких понятиях, как натуральные и действительные числа, в более увлекательной форме, зарегистрируйтесь на сайте BYJU’S. Кроме того, смотрите интересные видеоролики на различные темы по математике, загрузив BYJU’S — The Learning App из Google Play Store или магазина приложений.

Видео урок

Часто задаваемые вопросы о целых числах

Q1

Что такое целые числа?

Целые числа определяются как положительные целые числа, включая ноль. Целое число не содержит ни десятичной, ни дробной части. Это означает, что он представляет собой целое без частей. Набор целых чисел математически представляется как:
W = (0, 1, 2, 3, 4, 5,……}

Q2

Могут ли целые числа быть отрицательными?

Нет, целые числа не могут быть отрицательными , Целые числа начинаются с 0, 1, 2, 3, … и т. д. Все натуральные числа считаются целыми числами, но все целые числа не являются натуральными числами. Таким образом, отрицательные числа не считаются целыми числами.

Q3

Каковы свойства целых чисел?

Целые числа обладают следующими свойствами:
Целые числа замкнуты относительно сложения и умножения
Сложение и умножение целых чисел коммутативны
Сложение и умножение целых чисел ассоциативны
Оно подчиняется дистрибутивному свойству умножения над сложением
Аддитивная идентичность целых чисел равна 0
Мультипликативная идентичность целых чисел равна 1

Q4

Является ли 10 целым числом?

10 — это целое, а также натуральное число. Это пишется как Десять прописью. Хотя -10 тоже представляет собой целое, а не дробь.

Q5

Какие числа не являются целыми числами?

Числа, не существующие между 0 и бесконечностью, не являются целыми числами. Отрицательные целые числа, дроби или рациональные числа не являются целыми числами. Примеры: -1, -5, ½, 9/4, пи и т. д. не являются целыми числами.

Q6

Все ли целые числа являются действительными числами?

Действительные числа — это те числа, которые включают в себя рациональные числа, целые числа, целые числа и натуральные числа. Все целые числа являются действительными числами, но не все действительные числа являются целыми.

Q7

Являются ли все натуральные числа целыми числами?

Натуральные числа — это те, которые начинаются с 1 и заканчиваются на бесконечность, тогда как целые числа начинаются с 0 и заканчиваются на бесконечность. Все натуральные числа являются целыми числами, но не все целые числа являются натуральными.

Q8

Являются ли натуральные числа и счетные числа одним и тем же?

Натуральные числа — это числа, начинающиеся с 1 и доходящие до бесконечности. Счетные числа используются для подсчета предметов, людей или всего, что можно сосчитать. Следовательно, мы всегда начинаем считать с 1.

.

Меняющееся лицо Конгресса в 8 таблицах: раса, этническая принадлежность, пол, поколение, статус иммигранта, образование и т. д.

член Палаты представителей США был приведен к присяге рано утром 7 января 2023 года. Для The Washington Post через Getty Images)

118-й Конгресс достиг множества демографических результатов, когда его члены вступили в должность в январе. Поколение Z теперь представлено в национальном законодательном органе, а Вермонт впервые отправил женщину-законодателя на Капитолийский холм. Тем не менее Конгресс по ряду демографических показателей отстает от более широких слоев населения США.

Вот восемь диаграмм, которые показывают, как профиль Конгресса изменился с течением времени, с использованием исторических данных из CQ Roll Call, Исследовательской службы Конгресса и других источников.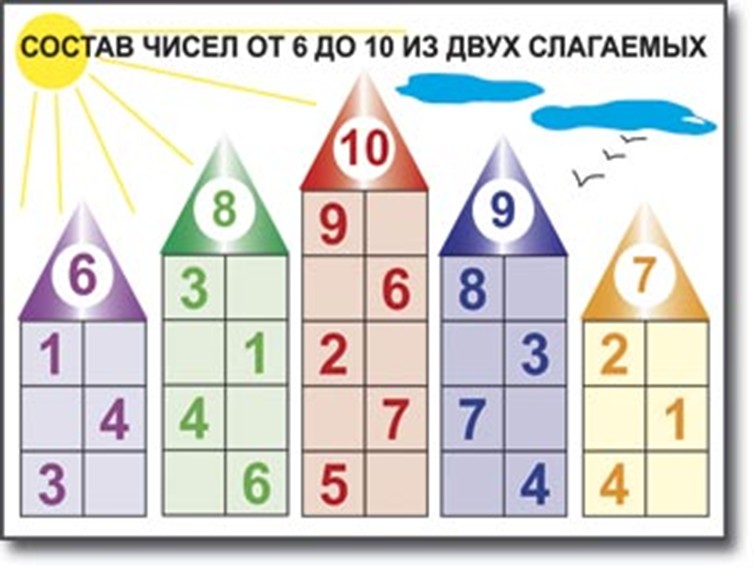

Как мы это сделали

В этом анализе Pew Research Center рассматривается изменение демографического профиля Конгресса с течением времени. Он основан на ранее опубликованных исследованиях Центра. Для получения информации об источниках и методологии этих исследований перейдите по ссылкам в тексте этого анализа.

Почти все результаты этого анализа основаны на членах Конгресса с правом голоса и исключают членов без права голоса. Однако анализ женщин в Конгрессе основан как на членах без права голоса, так и на членах с правом голоса.

118-й Конгресс является самым разнообразным в расовом и этническом отношении в истории.  В целом 133 законодателя считают себя чернокожими, латиноамериканцами, американцами азиатского происхождения, американскими индейцами, коренными жителями Аляски или представителями разных рас. Вместе эти законодатели составляют четверть Конгресса, в том числе 28% Палаты представителей и 12% Сената. Для сравнения, когда в 1945 году к власти пришел Конгресс 79-го созыва, небелые законодатели представляли всего 1% Палаты представителей и Сената вместе взятых.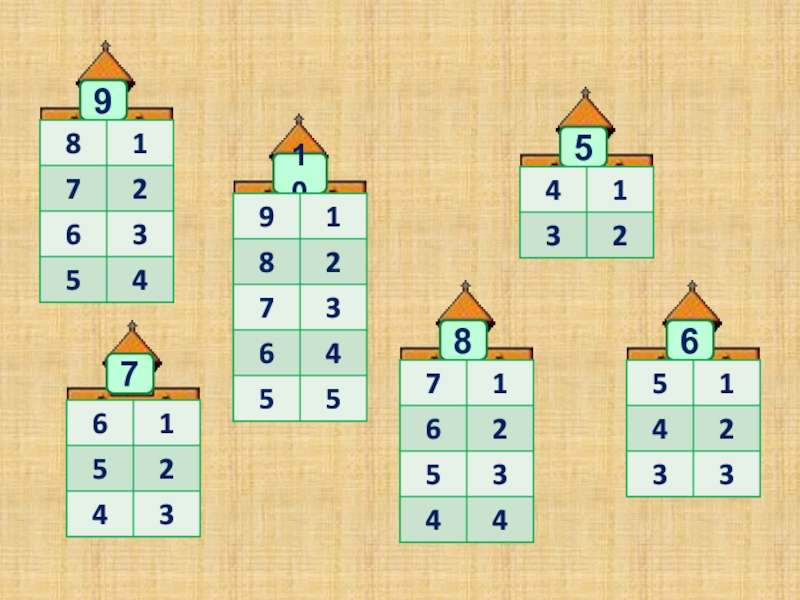

Несмотря на это растущее расовое и этническое разнообразие, Конгресс остается менее разнообразным, чем нация в целом. Белые американцы неиспаноязычного происхождения составляют 75% членов с правом голоса в новом Конгрессе, что значительно больше, чем их 59% доли населения США.

Число женщин в Конгрессе находится на рекордно высоком уровне. Спустя немногим более столетия после того, как республиканка Жаннет Рэнкин из Монтаны стала первой женщиной, избранной в Конгресс, в национальный законодательный орган входят 153 женщины, что составляет 28% всех членов. (Сюда входят шесть членов Палаты представителей без права голоса, которые представляют округ Колумбия и территории США, четыре из которых являются женщинами.)% от состава палаты. В эту цифру входят 22 недавно избранных женщины-конгрессмена, в том числе Бекка Балинт, демократ из Вермонта, которая стала первой женщиной и первым открыто ЛГБТК-лицом, избранным в Конгресс от штата. С избранием Балинта все 50 штатов в какой-то момент получили представительство женщин в Конгрессе США.

В настоящее время в Сенате работают 25 женщин, что является рекордным числом мест, которые они занимали в 116-м Конгрессе. Сенат получил всего одну новую женщину-члена:
республиканец Кэти Бритт, которая стала первой избранной женщиной-сенатором от Алабамы. Как и в предыдущем Конгрессе, в четырех штатах — Миннесоте, Неваде, Нью-Гэмпшире и Вашингтоне — сенатские делегации состоят исключительно из женщин.

В Палате наблюдается медленный, но неуклонный рост числа женщин-членов с 1920-х годов, когда женщины получили право голоса. Рост в Сенате был медленнее. До 102-го Конгресса, который начался в 1991 году, в Сенате не было более трех женщин. Доля женщин в Конгрессе остается намного ниже их доли по стране в целом (28% против 51%). .

Тринадцать членов Конгресса с правом голоса идентифицируют себя как лесбиянки, геи или бисексуалы — самое большое число в истории. Сюда входят два сенатора и 11 членов Палаты представителей. На сегодняшний день не было ни одного открытого трансгендера.

Число законодателей в этой группе увеличилось более чем втрое за последнее десятилетие. На 112-м Конгрессе 2011–2012 годов только четыре члена — все представители — идентифицировали себя как геи или лесбиянки, и ни один из них не был бисексуалом.

13 лесбиянок, геев и бисексуалов-членов Конгресса составляли около 2% из 534 голосующих законодателей по состоянию на 3 января 2023 года. Для сравнения, американцы ЛГБ составляют 6,5% взрослого населения США в целом, согласно 2021 Опрос Гэллапа.

Доля миллениалов и представителей поколения X в Конгрессе за последние годы немного выросла. В нынешнем Конгрессе 12% членов Палаты представителей, или 52 законодателя, являются миллениалами (поколение в возрасте от 27 до 42 лет в 2023 году). Эта доля выросла с 1% в начале 115-го Конгресса в 2017 году. И 166 членов Палаты представителей (38%) являются представителями поколения X — в возрасте от 43 до 58 лет в 2023 году — по сравнению с 27% на 115-м Конгрессе.

Теперь в Сенате трое членов-миллениалов, по сравнению с одним — первым из когда-либо избранных — на последнем Конгрессе. В Конгрессе 115-го созыва 23 сенатора из поколения X по сравнению с 16.

В то время как представители молодого поколения увеличили свое представительство в Конгрессе, старшее поколение по-прежнему составляет наибольшую долю законодателей в обеих палатах. Бэби-бумеры (которым в этом году от 59 до 77 лет) составляют 45% членов Палаты представителей с правом голоса в дополнение к 66 из 100 сенаторов.

В последние годы в Конгрессе сократилось количество представителей молчаливого поколения (в возрасте от 78 до 95 лет в 2023 году). В обеих законодательных палатах 5% депутатов, или 29члены, являются частью молчаливого поколения, по сравнению с 14%, или 61 членом, в 115-м Конгрессе в начале 2017 года.

Доля иммигрантов в Конгрессе выросла, но остается намного ниже исторического максимума. В 118-й Конгресс входят 18 законодателей иностранного происхождения, в том числе 17 в Палате представителей и один в Сенате: Мази Хироно, демократ с Гавайских островов, родившийся в Японии.

Эти законодатели составляют 3% членов с правом голоса, что немного выше, чем доля на других недавних Конгрессах, но ниже доли на гораздо более ранних Конгрессах. На 50-м съезде 1887-89 гг., например, 8% членов родились за границей. Текущая доля законодателей иностранного происхождения в Конгрессе также намного ниже доли иностранного происхождения во всем населении США, которая составляла 13,6 % по состоянию на 2021 год. больше участников имеют хотя бы одного  родителя  , родившегося в другой стране. Вместе иммигранты и дети иммигрантов составляют не менее 15% нового Конгресса, что немного выше, чем в прошлом Конгрессе (14%).

Сейчас гораздо меньше членов Конгресса имеют личный военный опыт, чем в прошлом.  В нынешнем Конгрессе 97 членов служили в армии в какой-то момент своей жизни — это одно из самых низких показателей со времен, по крайней мере, Второй мировой войны, согласно Military Times. В 118-м Конгрессе ветеранов-республиканцев почти в три раза больше, чем ветеранов-демократов (72 против 25). Примерно одинаковые доли нынешних представителей (18,4%) и сенаторов (17%) служили в армии.

Со второй половины 20-го века резко сократилось число членов Конгресса с военным опытом. В период с 1965 по 1975 год не менее 70% законодателей в каждой законодательной палате имели военный опыт. Доля членов с военным опытом достигла пика в 75% в 1967 году в Палате представителей и 81% в 1975 году в Сенате.

В то время как относительно немногие члены Конгресса сегодня имеют военный опыт, еще меньшая доля американцев имеет его. По данным Бюро переписи населения США, в 2021 году около 6% взрослого населения США были ветеранами — по сравнению с 18% в 1980, вскоре после окончания эры призыва в армию.

Почти все законодатели в Конгрессе имеют высшее образование. На 118-м Конгрессе 94% членов Палаты представителей и все, кроме одного сенатора, имеют степень бакалавра или более высокое образование.

В Палате почти две трети представителей (64%) имеют ученую степень. Пять представителей (1%) имеют степень младшего специалиста, но не бакалавра. Еще 22 члена (5%) не имеют ученой степени. В эту группу входит один член, имеющий профессиональный сертификат: демократ Кори Буш из Миссури имеет зарегистрированный диплом медсестры.

Среди нынешних сенаторов 78 имеют хотя бы одну ученую степень. Республиканец Маркуэйн Маллин из Оклахомы — единственный сенатор без степени бакалавра. Он имеет степень младшего специалиста Технологического университета штата Оклахома. Сенатор Рэнд Пол, республиканец из Кентукки, получил степень доктора медицины в Медицинской школе Университета Дьюка, но не имеет степени бакалавра.

Уровень образования членов Конгресса намного превышает уровень взрослого населения США. По данным Бюро переписи населения, в 2021 году около четырех из десяти взрослых американцев в возрасте от 25 лет и старше (38%) имели степень бакалавра или более высокий уровень образования.

Христиане остаются крупнейшей религиозной группой в Конгрессе, но их ряды со временем немного сократились. Подавляющее большинство нынешних законодателей в Конгрессе — 469 членов — идентифицируют себя как христиане, но это самый низкий показатель с 2009 года, когда исследовательский центр Pew начал анализировать эту тенденцию. В каждом из восьми последних Конгрессов было не менее 470 христианских законодателей, а в 1970 году их число превысило 500.

Тем не менее, доля христиан в Конгрессе превышает их долю в более широкой американской общественности. По состоянию на 3 января 2023 года почти девять из десяти членов Конгресса (88%) являются христианами по сравнению с 63% взрослого населения США в целом.

Напротив, доля нерелигиозных взрослых на Капитолийском холме намного ниже их доли в общей численности населения США: в то время как 29% американцев говорят, что они атеисты, агностики или «ничего особенного», всего один законодатель – независимый сенатор Кирстен Sinema of Arizona — идентифицирует себя как религиозно неаффилированный. (Депутат-демократ Джаред Хаффман из Калифорнии называет себя гуманистом, а религиозная принадлежность 20 законодателей классифицируется как неизвестная.