Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями. Поделиться:    Доли и дроби. Арифметические действия с дробями. Сокращение дроби. Умножение и деление дроби на натуральное число. Умножение и деление дробей. Сложение и вычитание дробей с различными знаменателями. Дробь: это одна или несколько долей целого Знаменатель дроби (то, что записывется под чертой): это число долей, на которое делилось целое Числитель дроби (то, что записывется над чертой): это сколько таких долей было взято Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Правила сокращения дробей при умножении. Дробь

В прошлый раз мы научились складывать и вычитать дроби (см. урок «Сложение и вычитание дробей »). Наиболее сложным моментом в тех действиях было приведение дробей к общему знаменателю.

Теперь настала пора разобраться с умножением и делением. Хорошая новость состоит в том, что эти операции выполняются даже проще, чем сложение и вычитание. Для начала рассмотрим простейший случай, когда есть две положительные дроби без выделенной целой части.

Чтобы умножить две дроби, надо отдельно умножить их числители и знаменатели. Первое число будет числителем новой дроби, а второе — знаменателем.

Чтобы разделить две дроби, надо первую дробь умножить на «перевернутую» вторую.

Обозначение:

Из определения следует, что деление дробей сводится к умножению. Чтобы «перевернуть» дробь, достаточно поменять местами числитель и знаменатель. Поэтому весь урок мы будем рассматривать в основном умножение.

В результате умножения может возникнуть (и зачастую действительно возникает) сократимая дробь — ее, разумеется, надо сократить. Если после всех сокращений дробь оказалась неправильной, в ней следует выделить целую часть. Но чего точно не будет при умножении, так это приведения к общему знаменателю: никаких методов «крест-накрест», наибольших множителей и наименьших общих кратных.

По определению имеем:

Умножение дробей с целой частью и отрицательных дробей

Если в дробях присутствует целая часть, их надо перевести в неправильные — и только затем умножать по схемам, изложенным выше.

Если в числителе дроби, в знаменателе или перед ней стоит минус, его можно вынести за пределы умножения или вообще убрать по следующим правилам:

1. Плюс на минус дает минус;
2. Минус на минус дает плюс.

До сих пор эти правила встречались только при сложении и вычитании отрицательных дробей, когда требовалось избавиться от целой части. Для произведения их можно обобщить, чтобы «сжигать» сразу несколько минусов:

1. Вычеркиваем минусы парами до тех пор, пока они полностью не исчезнут. В крайнем случае, один минус может выжить — тот, которому не нашлось пары;
2. Если минусов не осталось, операция выполнена — можно приступать к умножению. Если же последний минус не зачеркнут, поскольку ему не нашлось пары, выносим его за пределы умножения. Получится отрицательная дробь.

Задача. Найдите значение выражения:

Все дроби переводим в неправильные, а затем выносим минусы за пределы умножения. То, что осталось, умножаем по обычным правилам. Получаем:

Еще раз напомню, что минус, который стоит перед дробью с выделенной целой частью, относится именно ко всей дроби, а не только к ее целой части (это касается двух последних примеров).

Также обратите внимание на отрицательные числа: при умножении они заключаются в скобки. Это сделано для того, чтобы отделить минусы от знаков умножения и сделать всю запись более аккуратной.

Сокращение дробей «на лету»

Умножение — весьма трудоемкая операция. Числа здесь получаются довольно большие, и чтобы упростить задачу, можно попробовать сократить дробь еще до умножения . Ведь по существу, числители и знаменатели дробей — это обычные множители, и, следовательно, их можно сокращать, используя основное свойство дроби. Взгляните на примеры:

Задача. Найдите значение выражения:

По определению имеем:

Во всех примерах красным цветом отмечены числа, которые подверглись сокращению, и то, что от них осталось.

Обратите внимание: в первом случае множители сократились полностью.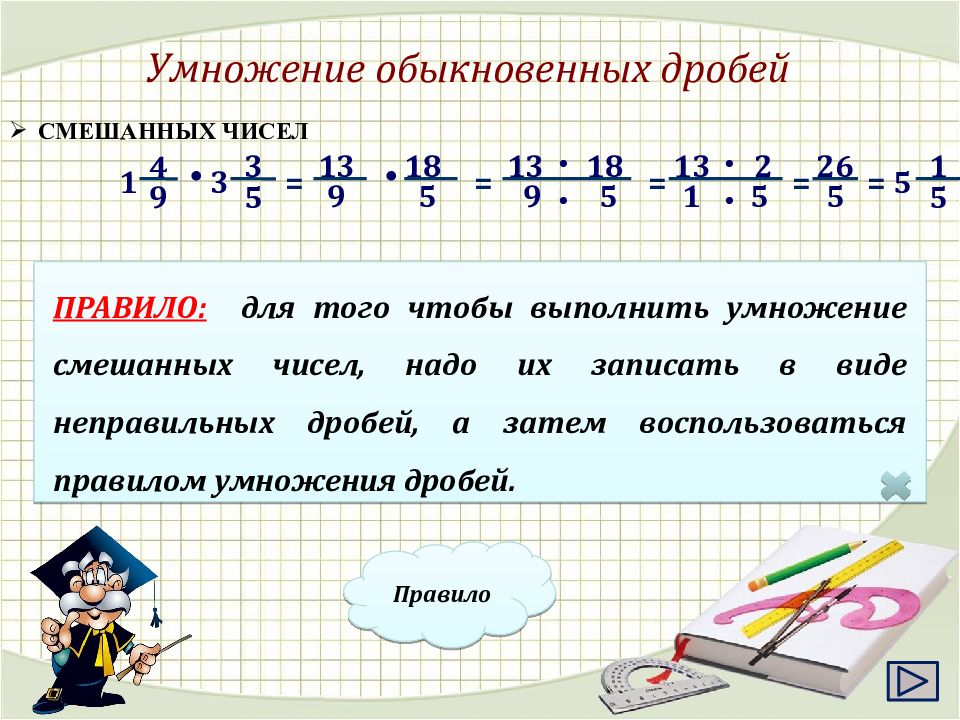 На их месте остались единицы, которые, вообще говоря, можно не писать. Во втором примере полного сокращения добиться не удалось, но суммарный объем вычислений все равно уменьшился.

Однако ни в коем случае не используйте этот прием при сложении и вычитании дробей! Да, иногда там встречаются похожие числа, которые так и хочется сократить. Вот, посмотрите:

Так делать нельзя!

Ошибка возникает из-за того, что при сложении в числителе дроби появляется сумма, а не произведение чисел. Следовательно, применять основное свойство дроби нельзя, поскольку в этом свойстве речь идет именно об умножении чисел.

Других оснований для сокращения дробей просто не существует, поэтому правильное решение предыдущей задачи выглядит так:

Правильное решение:

Как видите, правильный ответ оказался не таким красивым. В общем, будьте внимательны.

Умножение обыкновенных дробей рассмотрим в нескольких возможных вариантах.

Умножение обыкновенной дроби на дробь

Это наиболее простой случай, в котором нужно пользоваться следующими правилами умножения дробей .

Чтобы умножить дробь на дробь , надо:

• числитель первой дроби умножить на числитель второй дроби и их произведение записать в числитель новой дроби;
• знаменатель первой дроби умножить на знаменатель второй дроби и их произведение записать в знаменатель новой дроби;

Прежде чем перемножать числители и знаменатели проверьте нельзя ли сократить дроби. Сокращение дробей при расчётах значительно облегчит ваши вычисления.

Умножение дроби на натуральное число

Чтобы дробь умножить на натуральное число нужно числитель дроби умножить на это число, а знаменатель дроби оставить без изменения.

Если в результате умножения получилась неправильная дробь, не забудьте превратить её в смешанное число, то есть выделить целую часть.

Умножение смешанных чисел

Чтобы перемножить смешанные числа, надо вначале превратить их в неправильные дроби и после этого умножить по правилу умножения обыкновенных дробей.

Другой способ умножения дроби на натуральное число

Иногда при расчётах удобнее воспользоваться другим способом умножения обыкновенной дроби на число.

Чтобы умножить дробь на натуральное число нужно знаменатель дроби разделить на это число, а числитель оставить прежним.

Как видно из примера, этим вариантом правила удобнее пользоваться, если знаменатель дроби делится без остатка на натуральное число.

Действия с дробями

Сложение дробей с одинаковыми знаменателями

Сложение дробей бывает двух видов:

• Сложение дробей с одинаковыми знаменателями
• Сложение дробей с разными знаменателями

Сначала изучим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения. Например, сложим дроби и . Складываем числители, а знаменатель оставляем без изменения:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части.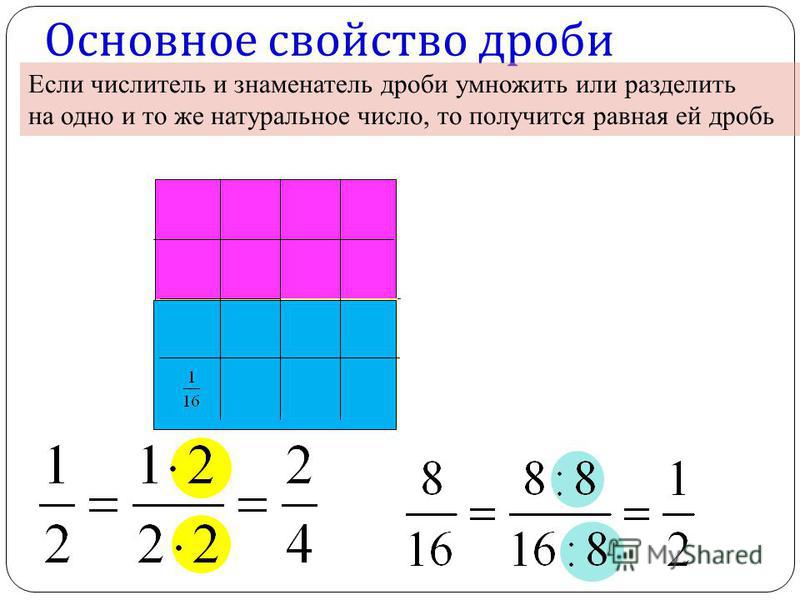

Если к пиццы прибавить пиццы, то получится пиццы:

Пример 2. Сложить дроби и .

Опять же складываем числители, а знаменатель оставляем без изменения:

В ответе получилась неправильная дробь . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два равно единице:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к пиццы прибавить еще пиццы, то получится одна целая пицца:

Пример 3 . Сложить дроби и .

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к пиццы прибавить ещё пиццы, то получится пиццы:

Пример 4. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:

Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы и ещё прибавить пиццы, то получится 1 целая и ещё пиццы.

Как видите в сложении дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:

1. Чтобы сложить дроби с одинаковыми знаменателя, нужно сложить их числители, а знаменатель оставить прежним;
2. Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями

Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.

Например, дроби и сложить можно, поскольку у них одинаковые знаменатели.

А вот дроби и сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.

Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.

Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.

Пример 1 . Сложим дроби и

У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.

В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6

НОК (2 и 3) = 6

Теперь возвращаемся к дробям и . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.

Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.

Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:

Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:

Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели.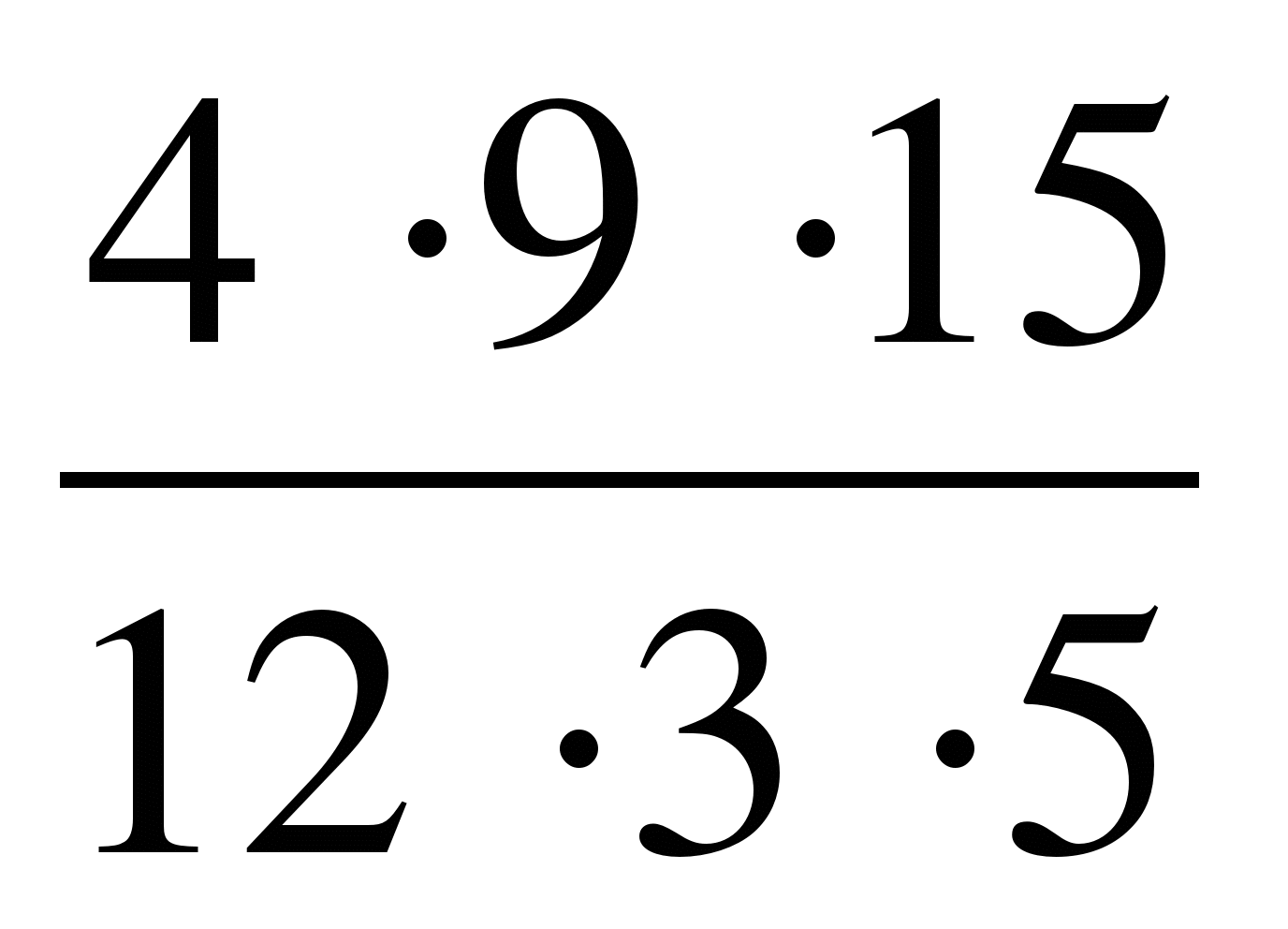 А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Таким образом, пример завершается. К прибавить получается .

Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить пиццы, то получится одна целая пицца и еще одна шестая пиццы:

Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и к общему знаменателю, мы получили дроби и . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).

Первый рисунок изображает дробь (четыре кусочка из шести), а второй рисунок изображает дробь (три кусочка из шести). Сложив эти кусочки мы получаем (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили (одну целую пиццу и еще одну шестую пиццы).

Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:

Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби? «.

Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:

3. Найти НОК знаменателей дробей;
4. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
5. Умножить числители и знаменатели дробей на свои дополнительные множители;
6. Сложить дроби у которых одинаковые знаменатели;
7. Если в ответе получилась неправильная дробь, то выделить её целую часть;

Пример 2. Найти значение выражения .

Воспользуемся схемой, которую мы привели выше.

Шаг 1. Найти НОК для знаменателей дробей

Находим НОК для знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4. Нужно найти НОК для этих чисел:

Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби

Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:

Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:

Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:

Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители

Умножаем числители и знаменатели на свои дополнительные множители:

Шаг 4. Сложить дроби у которых одинаковые знаменатели

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:

Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.

Шаг 5. Если в ответе получилась неправильная дробь, то выделить её целую часть

У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:

Получили ответ

Вычитание дробей с одинаковыми знаменателями

Вычитание дробей бывает двух видов:

8. Вычитание дробей с одинаковыми знаменателями
9. Вычитание дробей с разными знаменателями

Сначала изучим вычитание дробей с одинаковыми знаменателями. Тут всё просто. Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.

Например, найдём значение выражения . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним. Так и сделаем:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от пиццы отрезать пиццы, то получится пиццы:

Пример 2. Найти значение выражения .

Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем прежним:

Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части.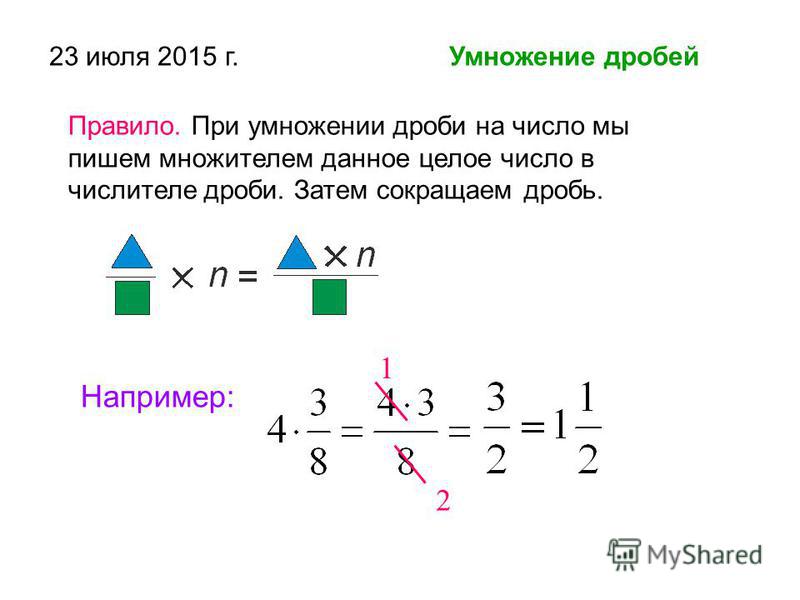 Если от пиццы отрезать пиццы, то получится пиццы:

Пример 3. Найти значение выражения

Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:

В ответе получилась неправильная дробь. Если пример завершен, то от неправильной дроби принято избавляться. Давайте и мы избавимся от неправильной дроби в ответе. Для этого выделим ее целую часть:

Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:

Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним;

Если в ответе получилась неправильная дробь, то нужно выделить её целую часть.

Вычитание дробей с разными знаменателями

Например, от дроби можно вычесть дробь , поскольку у этих дробей одинаковые знаменатели. А вот от дроби нельзя вычесть дробь , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.

Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.

Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.

Пример 1. Найти значение выражения:

Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12

НОК (3 и 4) = 12

Теперь возвращаемся к дробям и

Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:

Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:

Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:

Получили ответ

Попробуем изобразить наше решение с помощью рисунка. Если от пиццы отрезать пиццы, то получится пиццы

Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:

Приведение дробей и к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби и . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):

Первый рисунок изображает дробь (восемь кусочков из двенадцати), а второй рисунок — дробь (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь и описывает эти пять кусочков.

Пример 2. Найти значение выражения

У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.

Найдём НОК знаменателей этих дробей.

Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30

НОК (10, 3, 5) = 30

Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.

Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:

Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:

Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:

Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:

Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.

Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:

В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще и эстетичнее. А что можно сделать? Можно сократить эту дробь. Напомним, что сокращением дроби называется деление числителя и знаменателя на наибольший общий делитель числителя и знаменателя.

Чтобы грамотно сократить дробь нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.

Нельзя путать НОД с НОК. Самая распространённая ошибка многих новичков. НОД — это наибольший общий делитель. Его мы находим для сокращения дроби.

А НОК — это наименьшее общее кратное. Его мы находим для того, чтобы привести дроби к одинаковому (общему) знаменателю.

Сейчас мы будем находить наибольший общий делитель (НОД) чисел 20 и 30.

Итак, находим НОД для чисел 20 и 30:

НОД (20 и 30) = 10

Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби на 10:

Получили красивый ответ

Умножение дроби на число

Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить прежним.

Пример 1 . Умножить дробь на число 1 .

Умножим числитель дроби на число 1

Запись можно понимать, как взять половину 1 раз. К примеру, если пиццы взять 1 раз, то получится пиццы

Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение , записать как , то произведение по прежнему будет равно . Опять же срабатывает правило перемножения целого числа и дроби:

Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется пиццы:

Пример 2 . Найти значение выражения

Умножим числитель дроби на 4

Выражение можно понимать, как взятие двух четвертей 4 раза. К примеру, если пиццы взять 4 раза, то получится две целые пиццы

А если поменять множимое и множитель местами, то получим выражение . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:

Умножение дробей

Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.

Пример 1. Найти значение выражения .

Получили ответ . Желательно сократить данную дробь. Дробь можно сократить на 2. Тогда окончательное решение примет следующий вид:

Выражение можно понимать, как взятие пиццы от половины пиццы. Допустим у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:

У нас получится пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:

Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения равно

Пример 2 . Найти значение выражения

Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:

В ответе получилась неправильная дробь.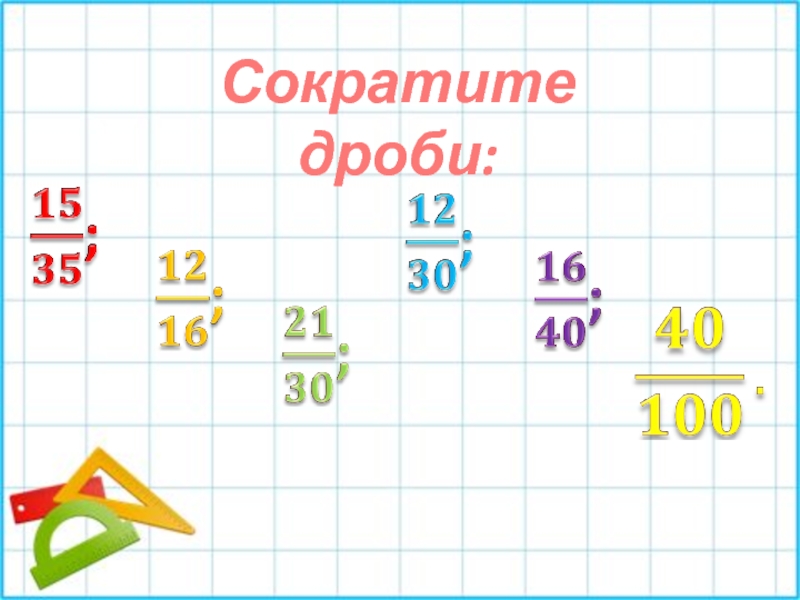 Выделим в ней целую часть:

Пример 3. Найти значение выражения

В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, её нужно разделить на НОД числителя и знаменателя. Итак, найдём НОД чисел 105 и 450:

НОД для (105 и 150) равен 15

Теперь делим числитель и знаменатель нашего ответа на НОД:

Представление целого числа в виде дроби

Любое целое число можно представить в виде дроби. Например, число 5 можно представить как . От этого пятёрка своего значения не поменяет, поскольку выражение означает «число пять разделить на единицу», а это, как известно равно пятёрке:

Обратные числа

Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».

Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.

Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:

Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.

Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:

Затем умножить эту дробь на саму себя, только поменять местами числитель и знаменатель. Другими словами, умножить дробь на саму себя, только перевёрнутую:

Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:

Значит обратным к числу 5, является число , поскольку при умножении 5 на получается единица.

Обратное число можно найти также для любого другого целого числа.

• обратным числа 3 является дробь
• обратным числа 4 является дробь

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.

В курсе средней и старшей школы учащиеся проходили тему «Дроби». Однако это понятие гораздо шире, чем дается в процессе обучения. Сегодня понятие дроби встречается достаточно часто, и не каждый может провести вычисления какого-либо выражения, к примеру, умножение дробей.

Что такое дробь?

Так исторически сложилось, что дробные числа появились из-за необходимости измерять. Как показывает практика, часто встречаются примеры на определение длины отрезка, объема прямоугольного прямоугольника.

Первоначально ученики знакомятся с таким понятием, как доля. К примеру, если разделить арбуз на 8 частей, то каждому достанется по одной восьмой арбуза. Вот эта одна часть из восьми и называется долей.

Доля, равная ½ от какой-либо величины, называется половиной; ⅓ — третью; ¼ — четвертью. Записи вида 5 / 8 , 4 / 5 , 2 / 4 называют обыкновенными дробями. Обыкновенная дробь разделяется на числитель и знаменатель. Между ними находится черта дроби, или дробная черта. Дробную черту можно нарисовать в виде как горизонтальной, так и наклонной линии. В данном случае она обозначает знак деления.

Знаменатель представляет, на сколько одинаковых долей разделяют величину, предмет; а числитель — сколько одинаковых долей взято. Числитель пишется над дробной чертой, знаменатель — под ней.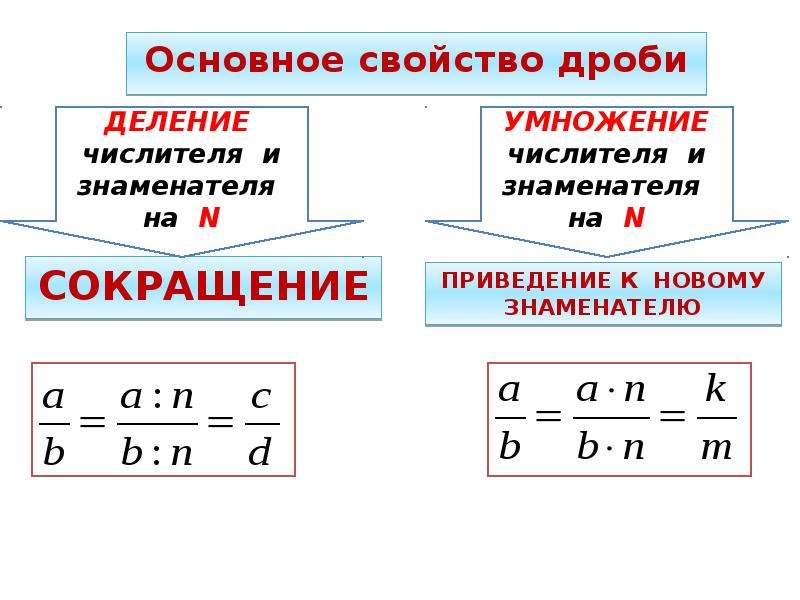

Удобнее всего показать обыкновенные дроби на координатном луче. Если единичный отрезок разделить на 4 равные доли, обозначить каждую долю латинской буквой, то в результате можно получить отличное наглядное пособие. Так, точка А показывает долю, равную 1 / 4 от всего единичного отрезка, а точка В отмечает 2 / 8 от данного отрезка.

Разновидности дробей

Дроби бывают обыкновенные, десятичные, а также смешанные числа. Кроме того, дроби можно разделить на правильные и неправильные. Эта классификация больше подходит для обыкновенных дробей.

Под правильной дробью понимают число, у которого числитель меньше знаменателя. Соответственно, неправильная дробь — число, у которого числитель больше знаменателя. Второй вид обычно записывают в виде смешанного числа. Такое выражение состоит из целой и дробной части. Например, 1½. 1 — целая часть, ½ — дробная. Однако если нужно провести какие-то манипуляции с выражением (деление или умножение дробей, их сокращение или преобразование), смешанное число переводится в неправильную дробь.

Правильное дробное выражение всегда меньше единицы, а неправильное — больше либо равно 1.

Что касается то под этим выражением понимают запись, в которой представлено любое число, знаменатель дробного выражения которого можно выразить через единицу с несколькими нулями. Если дробь правильная, то целая часть в десятичной записи будет равна нулю.

Чтобы записать десятичную дробь, нужно сначала написать целую часть, отделить ее от дробной с помощью запятой и потом уже записать дробное выражение. Необходимо помнить, что после запятой числитель должен содержать столько же цифровых символов, сколько нулей в знаменателе.

Пример . Представить дробь 7 21 / 1000 в десятичной записи.

Алгоритм перевода неправильной дроби в смешанное число и наоборот

Записывать в ответе задачи неправильную дробь некорректно, поэтому ее нужно перевести в смешанное число:

• разделить числитель на имеющийся знаменатель;
• в конкретном примере неполное частное — целое;
• и остаток — числитель дробной части, причем знаменатель остается неизменным.

Пример . Перевести неправильную дробь в смешанное число: 47 / 5 .

Решение . 47: 5. Неполное частное равняется 9, остаток = 2. Значит, 47 / 5 = 9 2 / 5 .

Иногда нужно представить смешанное число в качестве неправильной дроби. Тогда нужно воспользоваться следующим алгоритмом:

• целая часть умножается на знаменатель дробного выражения;
• полученное произведение прибавляется к числителю;
• результат записывается в числителе, знаменатель остается неизменным.

Пример . Представить число в смешанном виде в качестве неправильной дроби: 9 8 / 10 .

Решение . 9 х 10 + 8 = 90 + 8 = 98 — числитель.

Ответ : 98 / 10.

Умножение дробей обыкновенных

Над обыкновенными дробями можно совершать различные алгебраические операции. Чтобы перемножить два числа, нужно числитель перемножить с числителем, а знаменатель со знаменателем. Причем умножение дробей с разными знаменателямине отличается от произведения дробных чисел с одинаковыми знаменателями.

Случается, что после нахождения результата нужно сократить дробь. В обязательном порядке нужно максимально упростить получившееся выражение. Конечно, нельзя сказать, что неправильная дробь в ответе — это ошибка, но и назвать верным ответом ее тоже затруднительно.

Пример . Найти произведение двух обыкновенных дробей: ½ и 20 / 18 .

Как видно из примера, после нахождения произведения получилась сократимая дробная запись. И числитель, и знаменатель в данном случае делится на 4, и результатом выступает ответ 5 / 9 .

Умножение дробей десятичных

Произведение десятичных дробей довольно сильно отличается от произведения обыкновенных по своему принципу. Итак, умножение дробей заключается в следующем:

• две десятичные дроби нужно записать друг под другом так, чтобы крайние правые цифры оказались одна под другой;
• нужно перемножить записанные числа, несмотря на запятые, то есть как натуральные;
• подсчитать количество цифр после знака запятой в каждом из чисел;
• в получившемся после перемножения результате нужно отсчитать справа столько цифровых символов, сколько содержится в сумме в обоих множителях после запятой, и поставить отделяющий знак;
• если цифр в произведении оказалось меньше, тогда перед ними нужно написать столько нулей, чтобы покрыть это количество, поставить запятую и приписать целую часть, равную нулю.

Пример . Вычислить произведение двух десятичных дробей: 2,25 и 3,6.

Решение .

Умножение смешанных дробей

Чтобы вычислить произведение двух смешанных дробей, нужно использовать правило умножения дробей:

• перевести числа в смешанном виде в неправильные дроби;
• найти произведение числителей;
• найти произведение знаменателей;
• записать получившийся результат;
• максимально упростить выражение.

Пример . Найти произведение 4½ и 6 2 / 5.

Умножение числа на дробь (дроби на число)

Помимо нахождения произведения двух дробей, смешанных чисел, встречаются задания, где нужно помножить на дробь.

Итак, чтобы найти произведение десятичной дроби и натурального числа, нужно:

• записать число под дробью так, чтобы крайние правые цифры оказались одна над другой;
• найти произведение, несмотря на запятую;
• в полученном результате отделить целую часть от дробной с помощью запятой, отсчитав справа то количество знаков, которое находится после запятой в дроби.

Чтобы умножить обыкновенную дробь на число, следует найти произведение числителя и натурального множителя. Если в ответе получается сократимая дробь, ее следует преобразовать.

Пример . Вычислить произведение 5 / 8 и 12.

Решение . 5 / 8 * 12 = (5*12) / 8 = 60 / 8 = 30 / 4 = 15 / 2 = 7 1 / 2.

Ответ : 7 1 / 2.

Как видно из предыдущего примера, необходимо было сократить получившийся результат и преобразовать неправильное дробное выражение в смешанное число.

Также умножение дробей касается и нахождения произведения числа в смешанном виде и натурального множителя. Чтобы перемножить эти два числа, следует целую часть смешанного множителя умножить на число, числитель помножить на это же значение, а знаменатель оставить неизменным. Если требуется, нужно максимально упростить получившийся результат.

Пример . Найти произведение 9 5 / 6 и 9.

Решение . 9 5 / 6 х 9 = 9 х 9 + (5 х 9) / 6 = 81 + 45 / 6 = 81 + 7 3 / 6 = 88 1 / 2.

Ответ : 88 1 / 2.

Умножение на множители 10, 100, 1000 или 0,1; 0,01; 0,001

Из предыдущего пункта вытекает следующее правило. Для умножения дроби десятичной на 10, 100, 1000, 10000 и т. д. нужно передвинуть запятую вправо на столько символов цифр, сколько нулей во множителе после единицы.

Пример 1 . Найти произведение 0,065 и 1000.

Решение . 0,065 х 1000 = 0065 = 65.

Ответ : 65.

Пример 2 . Найти произведение 3,9 и 1000.

Решение . 3,9 х 1000 = 3,900 х 1000 = 3900.

Ответ : 3900.

Если нужно перемножить натуральное число и 0,1; 0,01; 0,001; 0,0001 и т. д., следует передвинуть влево запятую в получившемся произведении на столько символов цифр, сколько нулей находится до единицы. Если необходимо, перед натуральным числом записываются нули в достаточном количестве.

Пример 1 . Найти произведение 56 и 0,01.

Решение . 56 х 0,01 = 0056 = 0,56.

Ответ : 0,56.

Пример 2 . Найти произведение 4 и 0,001.

Решение . 4 х 0,001 = 0004 = 0,004.

Ответ : 0,004.

Итак, нахождение произведения различных дробей не должно вызывать затруднений, разве что подсчет результата; в таком случае без калькулятора просто не обойтись.

Обыкновенные дробные числа впервые встречают школьников в 5 классе и сопровождают их на протяжении всей жизни, так как в быту зачастую требуется рассматривать или использовать какой-то объект не целиком, а отдельными кусками. Начало изучения этой темы — доли. Доли — это равные части , на которые разделен тот или иной предмет. Ведь не всегда получается выразить, допустим, длину или цену товара целым числом, следует принять во внимание части или доли какой-либо меры. Образованное от глагола «дробить» — разделять на части, и имея арабские корни, в VIII веке возникло само слово «дробь» в русском языке.

Дробные выражения продолжительное время считали самым сложным разделом математики. В XVII веке, при появлении первоучебников по математике, их называли «ломаные числа», что очень сложно отображалось в понимании людей.

Современному виду простых дробных остатков, части которых разделены именно горизонтальной чертой, впервые поспособствовал Фибоначчи — Леонардо Пизанский. Его труды датированы в 1202 году. Но цель этой статьи — просто и понятно объяснить читателю, как происходит умножение смешанных дробей с разными знаменателями.

Умножение дробей с разными знаменателями

Изначально стоит определить разновидности дробей :

• правильные;
• неправильные;
• смешанные.

Далее нужно вспомнить, как происходит умножение дробных чисел с одинаковыми знаменателями. Само правило этого процесса несложно сформулировать самостоятельно: результатом умножения простых дробей с одинаковыми знаменателями является дробное выражение, числитель которой есть произведение числителей, а знаменатель — произведение знаменателей данных дробей. То есть, по сути, новый знаменатель есть квадрат одного из существующих изначально.

При умножении простых дробей с разными знаменателями для двух и более множителей правило не меняется:

a/ b * c/ d = a*c / b*d.

Единственное отличие в том, что образованное число под дробной чертой будет произведением разных чисел и, естественно, квадратом одного числового выражения его назвать невозможно.

Стоит рассмотреть умножение дробей с разными знаменателями на примерах:

• 8/ 9 * 6/ 7 = 8*6 / 9*7 = 48/ 63 = 16/2 1 ;
• 4/ 6 * 3/ 7 = 2/ 3 * 3/7 2*3 / 3*7 = 6/ 21 .

В примерах применяются способы сокращения дробных выражений. Можно сокращать только числа числителя с числами знаменателя, рядом стоящие множители над дробной чертой или под ней сокращать нельзя.

Наряду с простыми дробными числами, существует понятие смешанных дробей. Смешанное число состоит из целого числа и дробной части, то есть является суммой этих чисел:

1 4/ 11 =1 + 4/ 11.

Как происходит перемножение

Предлагается несколько примеров для рассмотрения.

2 1/ 2 * 7 3/ 5 = 2 + 1/ 2 * 7 + 3/ 5 = 2*7 + 2* 3/ 5 + 1/ 2 * 7 + 1/ 2 * 3/ 5 = 14 + 6/5 + 7/ 2 + 3/ 10 = 14 + 12/ 10 + 35/ 10 + 3/ 10 = 14 + 50/ 10 = 14 + 5=19.

В примере используется умножение числа на обыкновенную дробную часть , записать правило для этого действия можно формулой:

a * b/ c = a*b / c.

По сути, такое произведение есть сумма одинаковых дробных остатков, а количество слагаемых указывает это натуральное число. Частный случай:

4 * 12/ 15 = 12/ 15 + 12/ 15 + 12/ 15 + 12/ 15 = 48/ 15 = 3 1/ 5.

Существует еще один вариант решения умножения числа на дробный остаток. Стоит просто разделить знаменатель на это число:

d * e/ f = e/ f: d.

Этим приемом полезно пользоваться, когда знаменатель делится на натуральное число без остатка или, как говорится, нацело.

Перевести смешанные числа в неправильные дроби и получить произведение ранее описанным способом:

1 2/ 3 * 4 1/ 5 = 5/ 3 * 21/ 5 = 5*21 / 3*5 =7.

В этом примере участвует способ представления смешанной дроби в неправильную, его также можно представить в виде общей формулы:

a b c = a * b + c / c, где знаменатель новой дроби образуется при умножении целой части со знаменателем и при сложении его с числителем исходного дробного остатка, а знаменатель остается прежним.

Этот процесс работает и в обратную сторону. Для выделения целой части и дробного остатка нужно поделить числитель неправильной дроби на ее знаменатель «уголком».

Умножение неправильных дробей производят общепринятым способом. Когда запись идет под единой дробной чертой, по мере необходимости нужно сделать сокращение дробей, чтобы уменьшить таким методом числа и проще посчитать результат.

В интернете существует множество помощников, чтобы решать даже сложные математические задачи в различных вариациях программ. Достаточное количество таких сервисов предлагают свою помощь при счете умножения дробей с разными числами в знаменателях — так называемые онлайн-калькуляторы для расчета дробей. Они способны не только умножить, но и произвести все остальные простейшие арифметические операции с обыкновенными дробями и смешанными числами. Работать с ним несложно, на странице сайта заполняются соответствующие поля, выбирается знак математического действия и нажимается «вычислить». Программа считает автоматически.

Тема арифметических действий с дробными числами актуальна на всем протяжении обучения школьников среднего и старшего звена. В старших классах рассматривают уже не простейшие виды, а целые дробные выражения , но знания правил по преобразованию и расчетам, полученные ранее, применяются в первозданном виде. Хорошо усвоенные базовые знания дают полную уверенность в удачном решении наиболее сложных задач.

В заключение имеет смысл привести слова Льва Николаевича Толстого, который писал: «Человек есть дробь. Увеличить своего числителя — свои достоинства, — не во власти человека, но всякий может уменьшить своего знаменателя — своё мнение о самом себе, и этим уменьшением приблизиться к своему совершенству».

Действия с дробями | LAMPA

Как же теперь привести дроби 27\frac{2}{7}72​ и 34\frac{3}{4}43​ к знаменателю 282828?

Вспоминаем, что если умножить и числитель, и знаменатель дроби на одно и то же число, то значение дроби не изменится. Например, 15\frac{1}{5}51​ и 210\frac{2}{10}102​ — это одно и тоже число.

То есть нужно домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получился общий знаменатель дробей (в случае дробей 27\frac{2}{7}72​ и 34\frac{3}{4}43​ — число 282828).

Числитель и знаменатель дроби 27\frac{2}{7}72​ нужно умножить на 444:

27=2⋅47⋅4=828\frac{2}{7}=\frac{2\cdot 4}{7\cdot 4}=\frac{8}{28}72​=7⋅42⋅4​=288​,

— а числитель и знаменатель 34\frac{3}{4}43​ — на 777:

34=3⋅74⋅7=2128\frac{3}{4}=\frac{3\cdot 7}{4\cdot 7}=\frac{21}{28}43​=4⋅73⋅7​=2821​.

Теперь можно без труда сложить получившиеся дроби: 828+2128=2928=1128\frac{8}{28}+\frac{21}{28}=\frac{29}{28}=1 \frac{1}{28}288​+2821​=2829​=1281​.

Общая формула, которой можно пользоваться для сложения дробей: ab+cd=ad+bcbd\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}ba​+dc​=bdad+bc​

Пользуясь этой формулой, мы получим, что 13+16=1⋅6+3⋅13⋅6=918\frac{1}{3}+\frac{1}{6}=\frac{1\cdot 6+3\cdot 1}{3\cdot 6}=\frac{9}{18}31​+61​=3⋅61⋅6+3⋅1​=189​. Как мы видим, эту дробь можно сократить на 999. Получится 12\frac{1}{2}21​.

Наименьший общий знаменатель

Можно ли сразу получить дробь, которую не надо было бы сокращать, то есть дробь с наименьшим возможным знаменателем?

Да, можно! Для этого вместо перемножения знаменателей необходимо вычислить их . То есть наименьшее число, которое делится на оба знаменателя. Наименьшее общее кратное чисел bbb и ddd обозначается НОК(b,d)\text{НОК}(b,d)НОК(b,d).

Например:

НОК(3,6)=6\text{НОК}(3,6)=6НОК(3,6)=6

НОК(10,15)=30\text{НОК}(10,15)=30НОК(10,15)=30. 2\cdot 5=902⋅32⋅5=90.

Репетитор по математике — подготовка к ЕГЭ, ОГЭ, экзаменам по математике в школе и вузе

Наконец-то школа позади, наступило лето! Три месяца круглосуточного отдыха  без длинных нудных уроков и домашних заданий. Без скучных учебников и надоевших формул, задач и теорем.  Как хорошо – никакой учебы!

Конечно, есть школьники, которые используют время на каникулах не только для отдыха, но и для саморазвития: готовятся  в профильных лагерях к предметным олимпиадам, учат иностранные языки в различных языковых школах, самостоятельно или с репетиторами начинают подготовку к ЕГЭ. Таких ребят сейчас становится всё больше. Но пока они чаще встречают не поддержку, а удивление или откровенное неодобрение: так нельзя,  лето – это святое. Надо отдыхать, набираться сил! Учеба подождет.

Однако через три месяца наши отдохнувшие, загоревшие, выросшие дети вернутся за парты.  И тут обнаружится, что все знания, которые с таким трудом добывались в течение учебного года, легким дуновением летнего ветерка унесло в неведомые дали. Такое бывает каждый год, и каждый год мы  недоумеваем: как так, только сентябрь, а ребенок уже отстал по всем предметам?!

Но не терять же лето?  Отдыхать – когда?

Давайте подумаем!  Отдых – это смена деятельности, а потому непрерывный отдых тоже утомителен. Значит, занятия летом – отдыху не помеха, а, скорее, подспорье. Надо только выбрать нужные занятия и правильный темп подготовки. Ведь по разным данным, школьники, которые не прекращают занятия летом, в следующем классе показывают на 12-25% более высокую успеваемость по предмету, нежели их тотально отдыхавшие товарищи. И эта успеваемость достигается не увеличением затраченного на учебу времени, а именно той «форой», которую обеспечивает обучение на каникулах.

Математика летом

Когда речь заходит пользе летних занятий математикой, большинство вспоминает о подготовке к ЕГЭ. И это вполне понятно: математика, пожалуй, один из самых сложных предметов. Только лишь за последний учебный год освоить объем материала, требующийся для успешной сдачи профильного экзамена, просто невозможно. А уровень, который считается «успехом», год от года растет. Вместе с ростом проходных баллов в вузы, принимающие результаты профильного ЕГЭ.

Поэтому школьникам, планирующим поступать на фундаментальные (и престижные) специальности технических и экономических вузов определять свою «индивидуальную образовательную траекторию» нужно как можно раньше. И, конечно, эффективный план подготовки должен строиться с учетом летних занятий.

Но от занятий на каникулах выигрывают не только старшеклассники, готовящиеся к важным экзаменам, – «летняя математика» принесет пользу  ученикам любых классов. Почему?

Считается, что математика не забывается. Забыть, если долго не пользуешься,  можно лексику и синтаксис иностранного или даже родного  языка, но не алгоритмы сложения и умножения дробей или теорему Пифагора. К сожалению, как показывает практика, это не так. И после каникул многие, уже хорошо освоенные,  математические навыки становятся для ребят «чужими»: четвероклассники теряют алгоритмы умножения в столбик и деления уголочком, семиклассники – логику арифметических действий с отрицательными числами и вынесения за скобки общих множителей, девятиклассники –  решение неравенств и тригонометрические функции. Отведенных на повторение двух недель не хватает, программа идет вперед, а потому каждый учебный год ребенок начинает с довольно сильного стресса.

А ведь чтобы избежать такого неприятного начала учебы, не надо летом заниматься математикой каждый день, как это традиционно происходит с сентября по май. Сейчас наш ученик свободен от школьной  нагрузки, а потому каникулы – именно то время, когда можно малыми средствами и усилиями достичь очень многого.  Одного-двух занятий в неделю вполне хватит, чтобы не только поддержать достигнутый за год уровень, но и существенно его расширить. Более того, летние занятия очень помогают мотивированным школьникам без экстремальных усилий и не в ущерб остальным предметам углубить свои знания математики до олимпиадного уровня.

Сегодня всё больше и больше преподавателей математики работают дистанционно, с использованием различных интерактивных онлайн-досок. А потому общение с репетитором вовсе не предполагает обязательного присутствия в городе: для совмещения летнего отдыха и занятий ученику достаточно иметь ноутбук или планшет, стабильный Интернет  и, конечно, мотивацию.

Все мы знаем, что наши дети быстрее всего растут летом. Свежий воздух, солнце, витамины делают свое дело, и заказанная весной на весь класс школьная форма к осени уже половине класса безнадежно мала. Но мало кто из родителей подозревает, что летом мы может ускорить не только физический, но умственный рост ребенка.  Если к перечисленным выше «природным» факторам добавим еще и умеренную интеллектуальную нагрузку.

Хорошего вам лета! И не забывайте о занятиях математикой!

Умножение дробей, деление дробей

Умножение обыкновенных дробей

Определение 1

Умножение дробей рассматривается как действие нахождения дроби от дроби.

Рассмотрим пример.

Пусть на тарелке лежит $\frac{1}{3}$ часть яблока. Нужно найти $\frac{1}{2}$ часть от нее. Необходимая часть является результатом умножения дробей $\frac{1}{3}$ и $\frac{1}{2}$. Результат умножения двух обыкновенных дробей — это обыкновенная дробь.

Умножение двух обыкновенных дробей

Правило умножения обыкновенных дробей:

Результатом умножения дроби на дробь является дробь, числитель которой равен произведению числителей умножаемых дробей, а знаменатель равен произведению знаменателей:

Пример 1

Выполнить умножение обыкновенных дробей $\frac{3}{7}$ и $\frac{5}{11}$.

Решение.

Воспользуемся правилом умножения обыкновенных дробей:

\[\frac{3}{7}\cdot \frac{5}{11}=\frac{3\cdot 5}{7\cdot 11}=\frac{15}{77}\]

Ответ: $\frac{15}{77}$

Если в результате умножения дробей получается сократимая или неправильная дробь, то нужно ее упростить.

Пример 2

Выполнить умножение дробей $\frac{3}{8}$ и $\frac{1}{9}$.

Решение.

Используем правило умножения обыкновенных дробей:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}\]

В результате получили сократимую дробь (по признаку деления на $3$. Числитель и знаменатель дроби разделим на $3$, получим:

\[\frac{3}{72}=\frac{3:3}{72:3}=\frac{1}{24}\]

Краткое решение:

\[\frac{3}{8}\cdot \frac{1}{9}=\frac{3\cdot 1}{8\cdot 9}=\frac{3}{72}=\frac{1}{24}\]

Ответ: $\frac{1}{24}.$

При умножении дробей сокращать числители и знаменатели можно до нахождения их произведения. При этом числитель и знаменатель дроби раскладывается на простые множители, после чего сокращаются повторяющиеся множители и находится результат.

Пример 3

Вычислить произведение дробей $\frac{6}{75}$ и $\frac{15}{24}$.

Решение.

Воспользуемся формулой умножения обыкновенных дробей:

\[\frac{6}{75}\cdot \frac{15}{24}=\frac{6\cdot 15}{75\cdot 24}\]

Очевидно, что в числителе и знаменателе есть числа, которые попарно можно сократить на числа $2$, $3$ и $5$. Разложим числитель и знаменатель на простые множители и произведем сокращение:

\[\frac{6\cdot 15}{75\cdot 24}=\frac{2\cdot 3\cdot 3\cdot 5}{3\cdot 5\cdot 5\cdot 2\cdot 2\cdot 2\cdot 3}=\frac{1}{5\cdot 2\cdot 2}=\frac{1}{20}\]

Ответ: $\frac{1}{20}.$

При умножении дробей можно применять переместительный закон:

Умножение обыкновенной дроби на натуральное число

Правило умножения обыкновенной дроби на натуральное число:

Результатом умножения дроби на натуральное число является дробь, у которой числитель равен произведению числителя умножаемой дроби на натуральное число, а знаменатель равен знаменателю умножаемой дроби:

где $\frac{a}{b}$ — обыкновенная дробь, $n$ — натуральное число.

Пример 4

Выполнить умножение дроби $\frac{3}{17}$ на $4$.

Решение.

Воспользуемся правилом умножения обыкновенной дроби на натуральное число:

\[\frac{3}{17}\cdot 4=\frac{3\cdot 4}{17}=\frac{12}{17}\]

Ответ: $\frac{12}{17}.$

Не стоит забывать о проверке результата умножения на сократимость дроби или на неправильную дробь.

Пример 5

Умножить дробь $\frac{7}{15}$ на число $3$.

Решение.

Воспользуемся формулой умножения дроби на натуральное число:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}\]

По признаку деления на число $3$} можно определить, что полученную дробь можно сократить:

\[\frac{21}{15}=\frac{21:3}{15:3}=\frac{7}{5}\]

В результате получили неправильную дробь. Выделим целую часть:

\[\frac{7}{5}=1\frac{2}{5}\]

Краткое решение:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{21}{15}=\frac{7}{5}=1\frac{2}{5}\]

Сократить дроби также можно было заменой чисел в числителе и знаменателе на их разложения на простые множители. В таком случае решение можно было записать так:

\[\frac{7}{15}\cdot 3=\frac{7\cdot 3}{15}=\frac{7\cdot 3}{3\cdot 5}=\frac{7}{5}=1\frac{2}{5}\]

Ответ: $1\frac{2}{5}.$

При умножении дроби на натуральное число можно использовать переместительный закон:

Деление обыкновенных дробей

Операция деления является обратной к умножению и результатом ее является дробь, на которую нужно умножить известную дробь чтобы получить известное произведение двух дробей.

Деление двух обыкновенных дробей

Правило деления обыкновенных дробей:

При делении обыкновенной дроби $\frac{a}{b}$ на дробь $\frac{c}{d}$ необходимо делимое умножить на число, которое является обратным делителю:

Пример 6

Выполнить деление дробей $\frac{7}{4}$ и $\frac{3}{5}$.

Решение.

Числом, обратным делителю $\frac{3}{5}$, является дробь $\frac{5}{3}$. Воспользуемся правилом деления обыкновенных дробей:

\[\frac{7}{4}:\frac{3}{5}=\frac{7}{4}\cdot \frac{5}{3}=\frac{7\cdot 5}{4\cdot 3}=\frac{35}{12}\]

Ответ: $\frac{35}{12}. $

Результат деления дробей необходимо проверять на сократимость дроби и на возможность выделения целой части из неправильной дроби.

Пример 7

Выполнить деление дробей $\frac{8}{15}:\frac{12}{35}$.

Решение.

Применим правило деления дробей:

\[\frac{8}{15}:\frac{12}{35}=\frac{8}{15}\cdot \frac{35}{12}=\frac{8\cdot 35}{15\cdot 12}\]

Очевидно, что числитель и знаменатель полученной дроби можно разложить на простые множители и произвести сокращение:

\[\frac{8\cdot 35}{15\cdot 12}=\frac{2\cdot 2\cdot 2\cdot 5\cdot 7}{3\cdot 5\cdot 2\cdot 2\cdot 3}=\frac{2\cdot 7}{3\cdot 3}=\frac{14}{9}\]

В результате получили неправильную дробь, из которой выделим целую часть:

\[\frac{14}{9}=1\frac{5}{9}\]

Ответ: $1\frac{5}{9}.$

Умножение дробей и значение слова «от» . Математика для взрослых. Лайфхаки для повседневных вычислений

Складывать и вычитать дроби бывает неудобно, но, к счастью, с умножением и делением все обстоит гораздо проще.

Умножение дробей часто скрывается за словом «от». Если вы говорите «три четверти от двенадцати», на самом деле вы имеете в виду 3/4 ? 12. При умножении целого числа на дробь нужно выполнить две операции: умножить число на числитель и разделить на знаменатель. Вот как это будет выглядеть для 3/4 ? 12.

Чтобы перемножить две дроби, нужно просто перемножить их верхние и нижние части.

Предположим, вы каждые субботу и воскресенье по 7 часов наблюдаете за птицами. Какая это будет часть от целой недели? Суббота и воскресенье составляют 2/7 недели, а поскольку в сутках 24 часа, вы тратите 7/24 от них, пытаясь выследить пеструю камышовку или хохлатого зяблика. Получается выражение

Наверное, вы заметили, что 14 и 168 делятся на 14, что даст в результате 1/12. А не лучше ли вообще не связываться с такими большими числами? При умножении дробей всегда стоит поискать возможность их по ходу дела сократить. Самое оптимальное – найти одно и то же число в числителе и знаменателе дробей, потому что тогда эти числа взаимно уничтожаются.

Вернемся к выражению

Взгляните на две семерки: вверху дроби и внизу. Подсчитав верхнюю и нижнюю части дроби, мы в итоге придем туда, откуда начали, то есть 14/168. Вместо этого зачеркнем обе семерки и заменим их единицами. Давайте посмотрим, что еще можно сделать.

Итак, теперь вы знаете, что тратите двенадцатую часть недели на наблюдения за птицами. Это соответствует одной минуте из каждых 12 минут вашей жизни или же целому месяцу в год! (Если вы начнете высчитывать дроби для всех своих регулярных занятий, например для хобби или поездок на работу, результаты могут вас шокировать. К примеру, большинство людей проводят в ванной комнате около 10 дней в году.)

Есть одна старая математическая головоломка, которую время от времени перепечатывают в газетах. Сколько будет 9/10 ? 8/9 ? 7/8 ? 6/7 ? 5/6 ? 4/5 ? 3/4 ? 2/3 ? 1/2? Тот, кто решает это опубликовать, наверняка сидит в своем кабинете, поглаживая белую кошку, и демонически хохочет, предвкушая, как читатели засядут за вычисления. Однако не тут-то было: эти числа взаимно уничтожаются, и в итоге остается 1/10.

Пожалуйста, объясните как делятся, умножаются и сокращаются дроби.

Обыкновенные дроби:
Для начала поговорим о «строении» обыкновенных дробей. Возьмем для примера дробь . Сама дробь показывает, что мы делим целое(единицу) на 7 частей и берем две. 2 — числитель, 7 — знаменатель, а черточка обозначает деление.
Сокращение:
Вообще, у обыкновенных дробей есть основное свойство — при делении или умножении числителя и знаменателя на одно и тоже число дробь не изменится(ну визуально изменится). Для примера возьмем . Разделим 1 на 2(вспоминаем, что черточка обозначает деление). Получится 0,5. А теперь умножим числитель и знаменатель, предположим, на 3. Получится . Разделите 3 на 6. Получится тоже 0,5. Понятно? Это пригодится в изучении обыкновенных дробей.
Приступим к сокращению.
Оно применяется, тогда, когда можно сделать дробь с максимально наименьшим числителем и знаменателем. Но в дроби не должно быть десятичных дробей(0,5 или 0,6, например, то есть цифр с запятыми, и да, это только при сокращении, бывают пропорции с десятичными дробями в обыкновенных). То есть возьмем . Можно ли ее сократить? Есть ли общие делители у 2 и 7? Или они взаимно простые? Конечно, они взаимно простые. Значит и сократить нельзя. То есть для сокращении обыкновенных дробей нужны делители знаменателя и числителя.  — сократите. Получилось? Думаем над общими делителями. 6 и 15 делятся на 3. Делим. Получится 2/5. Ну а дальше делителей нет. Значит все. Думаю, насчет сокращения все понятно.
Умножение обыкновенных дробей
Умножьте числитель на числитель и знаменатель на знаменатель. Если же умножаем на целое число или целое число на дробь, то умножаем целое на числитель, а знаменатель оставляем. И не забываем сокращать результат. Также можно делать интересную вещь. Представим умножение . Можно умножать числитель на числитель и знаменатель на знаменатель сразу. НО,почему бы не сократить 6 и 2, 10 и 20. Это делать можно. Можно сокращать числа, как дроби, если одно число в числителе, другое в знаменателе. То есть можно получить 3 и 1,  1 и 2. Получим . А дальше легко. 3*2=6. 1*1=1. Получим результат 6/1. Или 6(да, еще один пункт про сокращение. Просто разделите числитель на знаменатель. Получите  6. И вообще, если знаменатель равен 1, его можно выкидывать). Предположим умножение на целое число. Пусть будет . Тут можно сократить 4 и 2(можно сокращать целые числа и числители). Получим 1/5 *2. Умножаем числитель на целое, знаменатель оставляем. 2/5. Если встретилось число по типу  — это смешанное число. Нужно из него получить дробь. Умножаем знаменатель(9( на целое(2) и прибавляем числитель(2). Получим . 
Деление обыкновенных дробей
Есть понятие обратных дробей. Это перевернутая дробь. То есть на место знаменателя стает значение числителя, а на место числителя значение знаменателя. То есть у дроби обратной будет . У числа 2 обратным будет (ведь 2 — это ).Если смешанное число, то переводим в дробь(выше описывал). Чтобы делить дроби нужно делитель сделать обратной дробью, заменить знак деления на знак умножения и умножать. Приведем пример . Обратное число двух — 1/2. Заменяем деление на умножение. Получим . Умножаем. 1*1=1, 3*2=6. Получим 1/6. Или приведем пример . Да, есть соблазн сократить 45 и 45. Но делать это пока нельзя. На данном этапе вообще сокращать нельзя. Сначала нужно преобразовать деление в умножение. Получим . Теперь сокращаем. Можно сократить 81 и 45(делятся на 9) и 35 и 45(делятся на 5). Сокращаем. Получаем . Сократить нельзя? Можно. 9/9 — 1. Получаем 7/5 умножить на 1. Получаем 7/5. Но эту дробь можно перевести в смешанное число. Сколько раз 5 помещается в 7? один раз. Значит тут есть целое(1). Вычитаем теперь это целое, то есть 5/5 из 7/5. Получаем 2/5. Значит ответ в нашем делении — . А тут даже можно перевести в неправильную дробь) Разделите 2 на 5. Получим 0,4. И в правду, 2/5=0,4. Значит можно и ответить 1,4. Но переводить в десятичную дробь совсем не обязательно.
P.s в моих объяснениях есть числа по типу 2/1 и 3/6 — это те же самые дроби, просто в интернете их пишут так, т.е вышеприведенные дроби равносильны /
Надеюсь, что теперь уж точно все понятно, и что эти 40 минут я потерял не просто так(хотя сейчас на знаниях в это время суток мало вопросов для меня)

Упростите дроби перед их умножением

На этом уроке 5-го класса я объясняю, как упростить дроби перед их умножением. Это чрезвычайно полезный метод. Это значительно упрощает умножение дробей, потому что умножаемые числа после упрощения становятся меньше.

Новое обозначение Мы начнем используя новый способ обозначения упрощающих дробей.Когда числитель или знаменатель упростится, мы зачеркнем его знаком. косой чертой и напишите новый числитель или знаменатель рядом с ним (либо над ним, либо под этим). Число вы делите на (4), не указывается ли , а не способ! Вы только думаете об этом в уме: «Я делю 12 на 4 и получаю 3. I разделите 20 на 4 и получите 5. » Вы можете не видеть никаких преимуществ по «старому» методу пока нет, но этот ярлык скоро пригодится.

1. Упростите дроби. Писать упрощенный числитель и знаменатель над и под старыми.

а. 14 16

б. 33 27

с. 12 26

г. 9 33

Перед тем, как умножить, вы можете написать другой эквивалент, более простая дробь вместо дроби. В первый пример на справа, 3/6 упрощается до 1/2 перед умножением. Мы напишите крошечную «1» над «3» 1 3 6 2 × 5 8 = 5 16 3 7 × 2 4 10 5 = 6 35 и крошечная цифра «2» ниже цифра «6».В другом примере 4/10 — это упрощается до 2/5 перед умножением. Почему это работает? Очевидно, мы можем написать 1/2 вместо 3/6 или 2/5 вместо 4/10, поскольку они эквивалентны .

2. Упростите одно или обе дроби перед умножением. Используйте эквивалентные дроби. Посмотрите на пример.

а. 3 6 10 5 × 1 2 14 7 = 3 × 1 5 × 7 = 3 35	б. 2 4 × 3 15 =
c. 8 12 × 1 2 =	d. 8 32 × 14 21 =
е. 6 15 × 6 9 =	ф. 27 45 × 21 49 =

Вы также можете упростить «крест-накрест». Посмотрите на этот пример: → Мы упрощаем 3 и 6, записывая вместо них 1 и 2. Думайте об этом как о дробь 3/6 упрощена до 1/2, но 3 и 6 расположены напротив друг друга.

Почему разрешены упростить таким образом? Сравните вышеуказанную проблему с этой: 7 9 × 3 6 . (Это почти то же самое, не правда ли?) Наверняка вы можете видеть, что в этой задаче мы могли бы перед умножением упростите 3/6 до 1/2. И эти две задачи умножения по сути та же проблема , потому что они оба приводят к одному и тому же выражению и одному и тому же ответу: первое становится 7 × 3 6 × 9 = 21 54 , а также второй становится 7 × 3 9 × 6 = 21 54 (без упрощения).Следовательно, поскольку вы можете упростите 3/6 в 1/2 в одной задаче, вы можете сделать то же самое и в другом.

3. Упростите «крест-накрест», прежде чем умножать.

а. 8 9 × 6 11	б. 3 10 × 2 5	c. 4 7 × 1 12
d. 7 4 × 3 21	е. 3 16 × 8 5	ф. 3 8 × 12 11

Можно даже упростите крест-накрест несколько раз перед умножением.

Сначала упростим 3 а также 6 в 1 и 2.

Затем упростим 5 и 15 в 1 и 3.

4. Прежде чем умножать, упрощайте.

а. 7 8 × 2 7	б. 3 5 × 5 6	c. 5 12 × 4 10
d. 9 15 × 3 18	е. 8 11 × 3 4	ф. 12 100 × 4 15

Упростить 2 7 45 × 45. Вы можете подумать об этом проблема двумя способами: 1) Думайте о дробной линии как о делении. Таким образом, проблема в том то же, что 27 ÷ 45 × 45. Всякий раз, когда вы умножаете и делите на одно и то же число, вы получаете по сути ничего не сделал. Итак, вы можете вычеркнуть в исходной задаче обе цифры 45, и ответ будет просто 27. 2) Сначала замените целое число 45 на дробь 45/1.Проблема сейчас 27 45 × 45 1 . Теперь вы можете упростить кросс-кросс, и умножаем: = 27.

5. Упрощайте и умножайте.

а. 82 77 × 77 =	г. 13 × 49 13 =	г. 14 × 16 14 =
г. 5 6 × 24 =	e. 54 × 2 9 =	ф. 16 × 5 8 =

6.Игрушечный блок имеет высоту 3/8 дюйма. Какова высота стопки из 8 штук?

Стопка из 20 штук?

7. Сандра покупает 3/4 кг мяса каждую неделю. Сколько мяса она покупает в год?

8. На следующее утро после дня рождения Сэма приготовили 12/20 праздничных торта. оставил. Он съедает 2/3 того, что осталось.
Когда вы умножаете эти две дроби, каков ваш ответ? значит или тебе сказать?

Для умножения трех или более дробей применяются те же принципы.Вы умножаете все числители и все знаменатели, чтобы получить числитель и знаменатель для ответа. Пример. Мы можем многое упростить перед умножением на Эта проблема: 14 25 × 10 9 × 5 6
1.Упростим 10 и 25 в 2 и 5 (разделив на 5).	2. Упростите 14 и 6 в 7 и 3.	= 14 27 3. Наконец, упростите 5 и 5, оставив 1 и 1.

9. Умножьте три дроби. Упростите перед умножением.

а. 4 5 × 3 4 × 2 3 =	г. 11 8 × 6 8 × 2 3 =
г. 9 10 × 5 2 × 2 7 =	г. 3 5 × 6 12 × 5 3 =
e. 4 5 × 9 8 × 10 24 =	ф. 7 12 × 3 5 × 6 7 =

10. а. Нарисуйте стержневую модель для этой ситуации. Мэтью платит 1/5 своего зарплата в налогах.
Из того, что осталось, он использует 1/4 для покупать продукты.

г. Предположим, что зарплата Мэтью составляет 2450 долларов.
Посчитайте, сколько он использует для продукты.

Эпилог: Что произойдет, если не упростить до умножения ? Сравните две задачи справа → Джек сделал все принадлежащий упрощение до умножение. Тина упрощенная после умножения. Оба они получили правильный ответ. Упрощение перед умножением не НЕ измените окончательный ответ — это просто упрощает умножить , потому что цифры меньше !

7 35 × 6 8 = 42 280 = 21 140 = 3 20 Тина умножает первой и получает 42/280. Наконец, она упрощает свой ответ за два шага , сначала до 21/140, а затем до 3/20.

1 7 35 5 × 3 6 8 4 = 3 20 Джек упрощает перед умножением.

---

Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.

---

Перекрестное сокращение и как это сделать — Руководство по Bubbly Primes

Перекрестное сокращение — это ярлык, который можно использовать, чтобы упростить умножение дробей. Иногда вам нужно упростить дроби после выполнения с ними арифметических операций.Кросс-аннулирование — это упрощение, которое можно сделать раньше. Это замечательно, потому что упрощение до означает, что когда вы действительно умножаете, у вас будут меньшие числа, и с меньшими числами легче работать.

Вы это уловили? Перекрестное сокращение упрощает дроби.

Но для какой операции можно использовать кросс-отмену? Умножение дробей .

В математике мы используем слово операция для чего-то простого, что вы делаете с числом.Наиболее распространенными примерами операций являются сложение, вычитание, умножение и деление (есть и другие, но не будем сейчас вдаваться в подробности).

Перекрестное сокращение и деление

Помимо умножения, перекрестное сокращение может использоваться для упрощения вычислений при делении дробей. Это потому, что вы всегда можете преобразовать задачу деления на дробь в задачу умножения дроби. Просто возьмите величину, обратную делителю. Взятие , обратного дроби, означает просто поменять местами числитель и знаменатель (поместите верхнюю часть снизу, а нижнюю часть сверху).Делитель — это число, на которое вы делите.

Как сделать перекрестную отмену?

Систематическую перекрестную отмену можно отменять, но есть и быстрые клавиши. Вот систематический способ перекрестного сокращения:

1. Если задача деления преобразуется в умножение, сначала перепишите ее, преобразовав делитель в обратную величину.
2. Найдите разложение на простые множители числителя и знаменателя обеих дробей.
3. Если какой-либо из факторов не был в простейшей форме, выполните упрощение сейчас.
4. Отмените все множители, найденные как в числителе, так и в противоположном знаменателе. Фактически, именно потому, что эти факторы расположены по диагонали друг от друга, мы называем это взаимной отменой. Если присутствует несколько копий какого-либо фактора, обработайте их, удалив только то количество копий, которое присутствует в противоположном месте (так же, как при упрощении дробей).
5. Повторите предыдущий шаг с другой диагональю.
6. Умножьте все множители в верхней части обеих дробей, чтобы получить числитель ответа, и умножьте все множители в нижней части обеих дробей, чтобы сформировать знаменатель ответа.

   Пошаговый пример перекрестной отмены

Вы всегда должны все это делать? Нет, не всегда. Вы заметили, где мы использовали слово систематический , чтобы описать этот пошаговый способ выполнения перекрестной отмены? Некоторые люди, вероятно, игнорировали это слово, а некоторые другие, возможно, задавались вопросом, что оно означает, и у них возникло чувство, что мы используем красивые слова, и вскоре все может перестать иметь смысл. Пожалуйста, не волнуйтесь. Под систематическим мы подразумевали то, что любой, кто сможет выполнить эти шаги, в конце получит правильный ответ.Когда вы знакомы с процессом, вы обычно можете комбинировать или пропускать шаги, использовать альтернативные методы или делать короткие пути.

Перекрестное аннулирование с помощью ярлыка GCF

Вы можете сэкономить работу, если числа относительно малы и вы можете увидеть некоторые общие факторы. В таком случае вам не нужно искать полное разложение на простые множители. Вместо этого мы обычно зачеркиваем числа по диагонали и пишем числа замены рядом с ними, удаляя наибольшие общие факторы. Вот пример того, как выглядит эта техника.

Пример использования GCF для упрощения дроби

Перекрестное сокращение и упрощение дробей

Перекрестное сокращение — это действительно специальная версия упрощения дробей. Воспользоваться этим можно только при умножении или делении дробей. Сначала стоит попрактиковаться в упрощении дробей, чтобы получить более широкую перспективу и понять, насколько это полезно. Фактически, преимущество перекрестного сокращения перед умножением и последующим упрощением состоит в том, что перед умножением числа становятся меньше и с ними легче работать.Вы получите тот же ответ, если сначала умножите, а затем упростите, но это может потребовать гораздо больше работы. Перекрестная отмена — это всего лишь ярлык, но хороший.

Как у вас получается хорошо справляться с кросс-отменой?

Чтобы добиться успеха в большинстве вещей, нужна практика. Мы создали игру Bubbly Primes с целью дать студентам много практических занятий по факторингу, чтобы они получили возможность видеть общие факторы, как в методе GCF. Это интересный способ развить навыки, которые традиционно возникают в результате много времени на рабочие листы и тесты.Мы рекомендуем вам потратить некоторое время на игру.

В чем разница между перекрестным отменой и перекрестным умножением?

Иногда студенты путают перекрестное сокращение с перекрестным умножением. Это легко сделать, потому что имена похожи, оба имеют отношение к дробям, и, более того, оба имеют отношение к умножению. Однако:

• Используйте перекрестное умножение , чтобы алгебраически манипулировать равенством, включающим дроби по обе стороны от знака равенства, обычно для поиска переменной.
• Используйте Перекрестное сокращение как метод упрощения при умножении двух дробей.

Обычно эти два метода предназначены для решения совершенно разных проблем. Вот пример каждого.

Следующая тема: Виды чисел

Об этой странице справки по математике Bubbly Primes

Обзор «

дробей: уменьшение дробей» | Purplemath

Purplemath

В дальнейшем иногда будет полезно помнить, что дроби могут указывать на деление.Например, ¹ / ₃ может означать «один, разделенный на три», а также «одна часть из трех частей». Фактически, давайте перейдем к делу; запомните это предложение: «Дроби — это деление».

Вы знаете, что любое число, разделенное само на себя, равно 1. Этот факт используется при уменьшении дробей. Если вы можете преобразовать часть заданной дроби в умноженную на 1, то вы можете игнорировать эту часть, потому что умножение на 1 ничего не меняет.

MathHelp.com

Например, вот как можно найти и использовать форму 1 для уменьшения ⁴ / ₈ :

Чтобы быть предельно ясным, цель нахождения общего множителя (в данном случае 4) состоит в том, чтобы позволить вам преобразовать часть дроби в 1.Поскольку ⁴ / ₄ = 1, то то, что я сделал выше, было следующим:

---

Предупреждение: обратите внимание, как я переключился с дроби на произведения (в числителе и знаменателе):

… произведению дробей:

Этот переключатель в порядке, пока вы умножаете:

…но это очень НЕ, если вы добавляете. Например:

Левая часть выше, представляющая собой дробь, содержащую сложение, равна ⁵ / ₆ , а правая часть выше, являясь добавкой, содержащей дроби, равна 1 ¹ / ₂ , поэтому два выражения — это совсем не одно и то же значение. Просто помните: для дробей умножение намного проще, чем сложение.А теперь вернемся к делу …

---

В дополнение к методу отмены, который я использовал выше (с розовыми единицами), вы также могли видеть одно из следующих сокращений для отмены:

Подходит любой из этих форматов. Последние два, вероятно, самые простые для домашнего задания, написанного от руки; первый легче набирать.

---

Если у вас есть обычный (научный, деловой и т. Д.) Калькулятор, который может обрабатывать дроби, вы можете ввести дробь, а затем нажать кнопку «равно», чтобы получить уменьшенную дробь. Если у вас есть графический калькулятор с командой дроби, вы можете ввести дробь как деление (потому что ⁴ / ₈ означает «четыре, разделенные на восемь»), а затем преобразовать в дробную форму. Проверьте свое руководство.

Если ваш калькулятор не может обрабатывать дроби или если знаменатель слишком велик для него, вот как вы сокращаете числа вручную.

• Преобразовать в простейшую форму.

Я возьму свой калькулятор и немного бумаги для вырезок и множу числитель (верхнее число) и знаменатель (нижнее число). Краткое сокращение для получения простого факторизации каждого из этих чисел продемонстрировано ниже в стековом делении (простыми числами) 2940:

.

Чтобы найти факторизацию, я просто считал простые множители с внешней стороны перевернутого деления.Из вышесказанного я вижу, что 2940 факторов как 2 × 2 × 3 × 5 × 7 × 7.

Партнер

Затем я разложу на множители знаменатель, являющийся числом 3150:

.

Итак, 3150 множителей как 2 × 3 × 3 × 5 × 5 × 7.

Теперь я могу уменьшить дробь, отбросив общие множители:

---

В следующем разделе рассматриваются смешанные числа и неправильные (или «вульгарные») дроби….

---

URL: https://www.purplemath.com/modules/fraction.htm

Уменьшайте простые или сложные дроби с помощью пошагового решения математических задач

ПРОДУКТОВ ФРАКЦИЙ

Произведение двух дробей определяется следующим образом.

Произведение двух дробей — это дробь, числитель которой является произведением числителей, а знаменатель — произведением знаменателей данных дробей.

в символах,

Любой общий множитель, встречающийся как в числителе, так и в знаменателе любой дроби, может быть разделен до или после умножения.

Пример 1 Найдите произведение

Решение

Те же процедуры применяются к дробям, содержащим переменные.

Пример 2 Найдите произведение

Решение Сначала мы разделим числитель и знаменатель на общие множители, чтобы получить

.

Теперь, умножая оставшиеся множители числителей и знаменателей, получаем

.

Если к какому-либо из факторов добавлен отрицательный знак, рекомендуется действовать так, как если бы все факторы были положительными, а затем прикрепить соответствующий знак к результату.Положительный знак прилагается, если на факторах нет отрицательных знаков или четного количества отрицательных знаков; отрицательный знак ставится, если у факторов нечетное количество отрицательных знаков.

Пример 3

Когда дроби содержат алгебраические выражения, необходимо по возможности разложить множители и разделить общие множители перед умножением.

Пример 4 Найдите произведение.

Решение Во-первых, мы должны разложить числители и знаменатели на множители, чтобы получить

.

Теперь, разделив общие множители, получим

.

Теперь умножим оставшиеся множители числителей и знаменателей, чтобы получить

Обратите внимание, что при написании дробных ответов мы умножаем числитель и оставляем знаменатель в факторизованном виде.Очень часто в таком виде более полезны дроби.

В алгебре мы часто переписываем выражение, например, как эквивалентное выражение. Используйте ту форму, которая наиболее удобна для конкретной задачи.

Пример 5

Распространенные ошибки: помните, что мы можем разделять только общие факторы, а не общие термины! Например,

, потому что x — это термин, который нельзя разделить. Аналогично

, потому что 3 не является множителем всего числителя 3y + 2.

КОЛИЧЕСТВО ФРАКЦИЙ

При делении одной дроби на другую мы ищем число, умножение которого на делитель дает делимое. Это в точности то же самое понятие, что и деление одного целого числа на другое; a ÷ b — это число q, частное, такое, что bq = a.

Чтобы найти, ищем такое число q, что. Чтобы решить это уравнение относительно q, мы умножаем каждый член уравнения на. Таким образом,

В приведенном выше примере мы называем номер обратной величиной.В общем, дробь является обратной величиной. То есть, мы получаем обратную дробь, «инвертируя» дробь. В целом

Частное двух дробей равно произведению дивиденда на обратную величину делителя.

То есть, чтобы разделить одну дробь на другую, мы инвертируем делитель и умножаем. В символах,

Пример 1

Как и при умножении, когда дроби в частном имеют знаки, рекомендуется продолжить решение проблемы, как если бы все факторы были положительными, а затем прикрепить соответствующий знак к решению.

Пример 2

Некоторые частные встречаются так часто, что полезно распознать эквивалентные формы напрямую. Один футляр

В целом

Пример 3

Когда дроби в частном включают алгебраические выражения, необходимо по возможности разложить на множители и разделить общие множители перед умножением.

Пример 4

СУММЫ И РАЗЛИЧИЯ ФРАКЦИЙ С ПОДОБНЫМИ ДЕНОМИНАТОРАМИ

Сумма двух или более арифметических или алгебраических дробей определяется следующим образом:
Сумма двух или более дробей с общими знаменателями — это дробь с одинаковым знаменателем и числителем, равная сумме числителей исходных дробей.

В целом

Пример 1

Когда используется вычитание, перед сложением полезно перейти к стандартной форме.

Пример 2

Мы должны быть особенно осторожны с биномиальными числителями. Например, мы должны переписать

, где весь числитель заключен в круглые скобки.

СУММ ДОРОЖЕК С НЕПОДХОДЯЩИМИ ЗНАМЕНИТОРАМИ

В разделе 6.3 мы добавили дроби с одинаковыми знаменателями. В этом разделе мы добавим дроби с разными знаменателями.

НАИМЕНЕЕ ОБЩЕЕ ЗНАЧЕНИЕ

Как правило, наименьшее натуральное число, кратное каждому знаменателю набора дробей, называется наименьшим общим знаменателем (ЖКД) набора дробей. Иногда мы можем получить ЖК-дисплей путем осмотра. Если ЖК-дисплей не виден сразу, мы можем использовать специальную процедуру, чтобы найти его.

Чтобы найти ЖК-дисплей:

1. Полностью разложите каждый знаменатель на множители, по возможности выровняв общие множители.
2. Включите в ЖК-дисплей каждый из этих множителей, максимальное количество раз, когда он встречается в любом единственном знаменателе.

Пример 1 Найдите наименьший общий знаменатель дробей

Решение Наименьший общий знаменатель для содержит среди своих факторов множители 12, 10 и 6.

Таким образом, на ЖК-дисплее отображается 60. (Это наименьшее натуральное число, которое делится на 12, 10 и 6.)

ЖК-дисплей набора алгебраических дробей — это простейшее алгебраическое выражение, кратное каждому знаменателю в наборе.Таким образом, ЖКД дробей

, потому что это простейшее выражение, кратное каждому знаменателю.

Пример 2 Найдите ЖКИ дробей

Решение Следуя методике из Примера 1, получаем

Таким образом, ЖК-дисплей равен x ² (x + l) (x — 1).

Мы можем складывать дроби с разными знаменателями, сначала преобразовывая дроби в эквивалентные дроби с одинаковыми знаменателями, а затем складывая.

Чтобы сложить дроби с разными знаменателями:

1. Найдите на ЖК-дисплее набор дробей.
2. Преобразуйте каждую дробь в эквивалентную дробь с ЖК-дисплеем в качестве знаменателя.
3. Сложите дроби, используя свойство
   

Пример 3 Запишите суммы и как отдельные члены.

Решение В каждом случае на ЖК-дисплее отображается 10. Мы строим каждую дробь до дроби со знаменателем 10. Таким образом,

эквивалентно

, откуда получаем

Иногда знаменатели дробей являются двучленами.

Пример 4 Запишите сумму в виде одного члена.

Решение На ЖК-дисплее (x + 2) (x — 1). Строим каждую дробь до дроби со знаменателем (x + 2) (x — 1), вставляя круглые скобки по мере необходимости, и получаем

Теперь, когда у нас есть одинаковые знаменатели, мы можем сложить числители, упростить и получить

Пример 5 Запишите сумму в виде одного члена.

Решение Сначала мы разложим знаменатели на множители, чтобы получить ЖК-дисплей.

Теперь мы преобразовываем каждую дробь в дроби с этим знаменателем и получаем

Теперь мы можем сложить числители, упростить и получить

Распространенные ошибки Обратите внимание, что мы можем складывать только дроби с одинаковыми знаменателями.Таким образом,

Кроме того, мы добавляем только числители дробей с одинаковыми знаменателями. Таким образом,

РАЗЛИЧИЯ ФРАКЦИЙ С НЕДОСТАТОЧНЫМИ ЗНАЧИТЕЛЯМИ

Мы вычитаем дроби с разными знаменателями аналогично сложению дробей. Однако сначала запишем каждую дробь в стандартном виде. Таким образом, любая дробь в виде

сначала записывается как

Теперь мы можем складывать дроби.

Пример 1 Запишите разницу в виде одного члена.

Решение Начнем с записи в стандартной форме как. ЖК-дисплей 12x. Мы строим каждую дробь до эквивалентной дроби с этим знаменателем, чтобы получить

Теперь, сложив числители, получаем

Опять же, следует проявлять особую осторожность с биномиальными числителями.

Пример 2 Запишите разницу в виде одного члена.

Решение сначала следует записать как

, где весь числитель заключен в круглые скобки.Затем мы получаем ЖК-дисплей 6 и строим каждую дробь до дробей со знаминателем 6, складываем числители и упрощаем.

В следующих примерах используются биномиальные знаменатели.

Пример 3 Запишите разницу в виде одного члена.

Решение Начнем с записи в стандартной форме как. ЖК-дисплей равен (x — l) (x + 2), и мы строим каждую дробь до эквивалентной дроби с этим знаменателем, чтобы получить

Теперь добавляем числители и упрощаем результаты

Пример 4 Запишите разницу

как единый термин

Решение. Сначала разложим знаменатели на множители и запишем дроби в стандартной форме, чтобы получить

.

Мы находим ЖК-дисплей (x + 7) (x — 3) (x + 3) и строим каждую дробь до эквивалентной дроби с этим знаменателем, чтобы получить

Теперь добавляем числители и упрощаем yield

КОМПЛЕКСНЫЕ ФРАКЦИИ

Дробь, содержащая одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих, называется комплексной дробью.Например,

— сложные дроби. Как и простые дроби, сложные дроби представляют собой частные. Например,

В случаях, подобных уравнению (1), в котором числитель и знаменатель комплексной дроби не содержат сумм или разностей, мы можем просто инвертировать делитель и умножить. То есть

В случаях, подобных уравнению (2), в котором числитель или знаменатель комплексной дроби содержит суммы или разности, мы не можем просто инвертировать делитель и умножить.Однако мы можем использовать фундаментальный принцип дробей для упрощения сложных дробей. Фактически, мы также можем использовать фундаментальный принцип для упрощения сложных дробей приведенной выше формы (1).

Пример 1 Упростите, используя фундаментальный принцип дробей.

Решение Умножаем числитель и знаменатель на ЖК-дисплей всех дробей в числителе и знаменателе; в этом случае на ЖК-дисплее отображается 4. Результат — простая дробь, эквивалентная данной сложной дроби.

В следующем примере показано упрощение уравнения (2) на стр. 255.

Пример 2 Упростить

Решение Умножаем числитель и знаменатель на ЖК-дисплей всех дробей в числителе и знаменателе; в данном случае LCD 6. Получаем

ДРОБНЫЕ УРАВНЕНИЯ

Чтобы решить уравнение, содержащее дроби, обычно проще всего сначала найти эквивалентное уравнение, не содержащее дробей. Мы делаем это, умножая каждый член уравнения на наименьший общий знаменатель дробей.

Хотя мы можем применять изученные нами алгебраические свойства в любом порядке, следующие шаги показывают порядок, наиболее полезный при решении уравнения, когда решение неочевидно. Конечно, не всегда все шаги необходимы.

Чтобы решить уравнение:

1. Очистите дроби, если они есть, умножив каждый член уравнения на ЖК-дисплей.
2. Запишите любое выражение, содержащее круглые скобки, как выражение без скобок.
3. Объедините любые одинаковые термины в любом члене.
4. Получить все термины, содержащие переменную в одном члене, и все термины, не содержащие переменную в другом члене.
5. Разделите каждый член на коэффициент переменной, если он отличается от 1.
6. Проверьте ответ, был ли каждый член уравнения умножен на выражение, содержащее переменную.

Пример 1 Решить.

Решение Мы умножаем каждый член на ЖК-дисплей 15, чтобы получить эквивалентное уравнение, не содержащее дроби.

Свойство умножения равенства (раздел 3.4) позволяет нам умножить каждый член уравнения на ненулевое значение, чтобы получить эквивалентное уравнение. Таким образом, для решения уравнения

, мы умножим каждый член на ЖКД 4 (x — 5). Отметим, что x не может равняться 5, поскольку 4 (x — 5) равно 0, если x = 5. Полное решение показано в следующем примере.

Пример 2 Решить.

Решение Мы умножаем каждый член на ЖКД 4 (x — 5), чтобы получить

Применяя распределительное свойство, получаем

Решение относительно x дает

-21x = -189; х = 9

Обратите внимание, что 4 (x — 5) не равно нулю для a = 9.Таким образом, a = 9 является допустимым решением уравнения.

Когда уравнения содержат более одной переменной, иногда желательно найти одну переменную в терминах другой переменной (переменных).

Пример 3 Решите относительно a через a, b и c.

Решение Мы умножаем каждый член на LDC 3xc, чтобы получить

Теперь, разделив каждый член на 2x, мы получим

ПРИЛОЖЕНИЯ

Проблемы со словами в следующих упражнениях приводят к уравнениям с дробями.В это время вы можете просмотреть шаги, предлагаемые для решения задач со словами, и шаги, предлагаемые на странице 260, для решения уравнений, содержащих дроби.

Пример 1 Если к числу прибавить определенное число, то получится 11. Найдите число.

Решение

Шаги 1-2 Сначала мы записываем то, что хотим найти (число), в виде словосочетания. Затем мы представляем число в виде переменной.
Номер: x

Шаг 3 Эскиз не применим.

Шаг 4 Теперь мы можем написать уравнение. Помните, что «of» означает умножение.

Шаг 5 Решение уравнения дает

Шаг 6 Число 12.

Уравнения для задач, связанных с движением, иногда включают дроби. Основная идея задач движения состоит в том, что пройденное расстояние d равно произведению скорости перемещения r и времени путешествия t. Таким образом, d = rt. Мы можем решить эту формулу относительно r или t, чтобы получить:

Таблица, подобная показанной в следующем примере, полезна при решении проблем с движением.

Пример 2 Экспресс проходит 180 миль за то же время, что и грузовой поезд — 120 миль. Если экспресс идет на 20 миль в час быстрее, чем груз, найдите скорость каждого из них.

Шаги решения 1-2. Мы представляем две неизвестные величины, которые мы хотим найти, в виде словосочетаний. Затем мы представляем словосочетания в терминах одной переменной.

Скорость грузового поезда: r

Скорость экспресса: r + 20

Шаг 3 Затем мы составляем таблицу, в которой указаны расстояния, скорости и время.

Шаг 4 Поскольку времена обоих поездов одинаковы, мы можем приравнять выражения для времени, чтобы получить

Шаг 5 Теперь мы можем решить для r, сначала умножив каждый член на ЖК-дисплей r (r + 120), и мы получим

Шаг 6 Скорость грузового поезда составляет 40 миль в час, а скорость экспресса — 40 + 20, или 60 миль в час.

СООТНОШЕНИЕ И ПРОПОРЦИЯ

Частное двух чисел a ÷ b или иногда называют отношением и читают как «отношение a к b».»Это удобный способ сравнить два числа.

Пример 1 Выразите в виде отношения.

а. От 3 до 5 дюймов
b. От 8 до 12 метров
c. С 6 по 10

Решения

Утверждение, что два отношения равны, например

называется пропорцией и читается как «2 равно 3, как 4 равно 6» и «a соответствует b, как c соответствует d». Числа a, b, c и d называются первым, вторым, третьим и четвертым членами пропорции соответственно. Первый и четвертый члены называются крайними точками пропорции, а второй и третий члены называются средними значениями пропорции.

Пример 2 Выразите как пропорцию.

Если каждое соотношение в пропорции

умножаем на bd, получаем

Таким образом,

В любой пропорции произведение крайностей равно произведению средних.

Доля — это особый тип дробного уравнения. Приведенное выше правило получения эквивалентного уравнения без знаменателей является частным случаем нашего общего подхода.

Пример 3 Решите пропорцию.

Решение Применяя свойство (1) выше, мы получаем

КОНВЕРСИИ

Мы можем использовать пропорции для преобразования английских единиц измерения в метрические единицы и наоборот. Следующие ниже базовые отношения будут полезны при настройке соответствующих пропорций для конверсий.

1 метр (м) = 39,37 дюйма (дюйм)

1 килограмм (кг) = 2,2 фунта (фунта)

1 километр (км) = 0,62 мили (миль)

1 литр (1) = 1,06 кварты (кварты)

1 фунт (фунт) = 454 грамма (г)

1 дюйм (дюйм.) = 2,54 см (см)

При преобразовании единиц проще всего выполнить шесть описанных шагов.

Пример 4 Измените 8 дюймов на сантиметры.

Решение

Шаги 1-2 Представьте, что нужно найти (в сантиметрах), в словосочетании и в терминах переменной.
Сантиметров: x

Шаг 3 Составьте таблицу, показывающую основные отношения между дюймами и сантиметрами.

Шаг 4 Используя таблицу из шага 3, запишите соотношение дюймов к сантиметрам.

Шаг 5 Решите относительно x, приравняв произведение средних к произведению крайних значений.

8 (2,54) = 1 · x
20,32 = x

Шаг 6 Восемь дюймов равны 20,32 сантиметра.

РЕЗЮМЕ ГЛАВЫ

1. Следующие свойства используются для перезаписи произведений и частных дробей.

2. Наименьшее натуральное число, кратное каждому знаменателю набора дробей, называется наименьшим общим знаменателем (ЖКД) дробей.Следующие свойства используются для перезаписи сумм и разностей дробей.

3. Дробь, содержащая одну или несколько дробей либо в числителе, либо в знаменателе, либо в обоих, называется комплексной дробью . Мы можем упростить сложную дробь, умножив числитель и знаменатель на ЖК-дисплей всех дробей в числителе и знаменателе.

4. Мы можем решить уравнение, содержащее дроби, получив эквивалентное уравнение, в котором решение очевидно при осмотре.Как правило, лучше всего получить эквивалентное уравнение, не содержащее дробей, путем умножения каждого члена уравнения на ЖКД дробей.

5. Частное двух чисел называется отношением ; Утверждение, что два соотношения равны, называется соотношением . В пропорции

   a и d называются крайними значениями , пропорции, а b и c называются средствами . В любой пропорции этой формы

   ad = bc

Поиск эквивалентных дробей и простейшей формы

Демонстрация

Просмотрите словарный запас и то, что учащиеся знают об эквивалентных дробях.Покажите модели эквивалентных дробей и объясните, что, хотя числители и знаменатели в дробях различаются, дроби представляют собой одинаковое количество, что означает, что они эквивалентны.

Используйте модели, чтобы показать дроби 1/2 и 2/4, или нарисуйте их для учащихся. Попросите учащихся указать, что они знают о дробях. Приведите их к выводу, что на чертеже 2/4 фигур вдвое больше, чем на чертеже 1/2, но они представляют такое же количество.

Проверьте, что числа, умноженные на единицу, равны одному и тому же числу.Попросите студентов привести несколько примеров единицы в виде дроби, например: 3/3, 4/4, 2/2. Напишите 1/2 x 2/2 = 2/4 и покажите, что числитель и знаменатель удвоены, чтобы показать новую дробь. Объясните, что это еще один способ найти эквивалентные дроби.

Умножьте числитель и знаменатель на то же число, чтобы найти эквивалентную дробь. Или разделите числитель и знаменатель на одно и то же число. Важно записывать дроби как «сложенные», а не рядом. Это поможет ученикам при умножении и делении.

Покажите несколько примеров:

3/12 x 4/4 = 12/48
3/12 (знак деления) 3/3 = 1/4
Все эти дроби эквивалентны, потому что они называют одно и то же количество: 1 / 4

После нескольких примеров предложите учащимся придумать правило для этого принципа. Они должны быть в состоянии сказать вам, что если вы умножите или разделите числитель и знаменатель на одно и то же число, новая дробь будет эквивалентна исходной дроби. Единственный раз, когда это не сработает, — это если ученики умножат на ноль.

Объясните, что иногда дроби нужно переименовывать, чтобы с ними было легче работать. Подчеркните, что дроби по-прежнему будут равны или эквивалентны, но числитель и знаменатель будут отличаться от исходной дроби.

Чтобы упростить дроби, найдите общий множитель, который равномерно разделит числитель и знаменатель. Например, покажите студентам эту дробь: 12/18

Найдите множители числителя и знаменателя. Множители 12 равны 2, 3, 4 и 6.Множители 18 — это 2, 3, 6 и 9. Общие делители — 2, 3 и 6.

Чтобы упростить дробь, разделите на 6, так как 6 является наибольшим общим делителем. Покажите учащимся, как разделить дробь: 12/18 (знак деления) 6/6 = 2/3

Объясните, что дробь имеет простейшую форму, если 1 является единственным общим делителем числителя и знаменателя. Попросите учащихся определить, является ли эта дробь простейшей формой.
2/3 — простейшая форма 12/18.

Чтобы уменьшить дробь до наименьшего значения, объясните, что учащиеся могут делить на любой общий множитель, и продолжать до тех пор, пока он не станет наименьшим, или они могут разделить на наибольший общий множитель.Например, учащиеся могут разделить дробь 12/18 на 2/2, а затем разделить на 3/3, чтобы показать дробь в простейшей форме. Или студенты могут разделить 12/18 на 6/6 и показать дробь 2/3 за один шаг.

Обсудите значение слова эквивалент и то, что делает дроби эквивалентными. Попросите студентов написать в своих дневниках, как они могут найти эквивалентные дроби. Попросите их ответить на вопрос: как узнать, что у вас есть дробь в простейшей форме?

11.1 — Упрощение алгебраических дробей

11.1 — Упрощение алгебраических дробей

11.1 — Упрощение алгебраических дробей

Некоторые определения

• Обычная дробь — это число, записанное в форма или a / b , где a , числитель и b , знаменатель , оба являются целыми числами. Обычная дробь используется для описания части или части целого объекта.Обозначение означает, что мы разбиваем объект на b равные части, и у нас есть и таких частей. Часть или часть объекта, который у нас есть — это a / b .
• Раздел определяется в терминах умножения. Деление числа a на число b дает число c такое, что c умноженное на b дает a . Мы используем то же обозначение дроби: a / b , чтобы обозначить деление a на b , потому что когда a и b были целыми числами, тогда деление a / b дает обыкновенную дробь a / b .
• Алгебраическая дробь — это дробь, числитель или знаменатель которой являются алгебраическими выражения. Два примера алгебраических дробей:

  и .

• Рациональная алгебраическая дробь — это алгебраическая дробь, числитель и знаменатель являются полиномами. Первый пример выше — рациональная алгебраическая дробь; второй нет.
• Правильная обыкновенная дробь — обыкновенная дробь, числитель которой меньше ее знаменатель, и неправильная обыкновенная дробь — это тот, числитель которого больше или равен его знаменателю.Смешанная дробь — это сумма целого числа и правильной дроби. Длинное деление можно использовать для преобразования неправильная дробь в смешанную дробь.
• Правильная алгебраическая дробь — рациональная алгебраическая дробь числитель которой ниже степени чем его знаменатель, а несобственная алгебраическая дробь равна единице числитель которого больше или равен знаменателю. Смешанное выражение — это сумма полинома и правильной алгебраической дроби. Длинное деление можно использовать для преобразования несобственная алгебраическая дробь к смешанному выражению.

---

Деление на ноль

Эта операция недопустима в математике. Щелкните здесь, чтобы узнать почему. Это означает, что в алгебраической дроби

,

x не может равняться 1 или −3, потому что эти значения x вызовут дробь должна иметь нулевой знаменатель.

---

Приведение алгебраической дроби к младшим членам

Посмотрите на алгебру, которую мы здесь делаем:

• Начнем с дроби a / b .
• Умножаем его на 1. Это не изменит его значения.
• Мы запишем «1» как дробь d / d .
• Умножаем две дроби. Числитель новой дроби — до , знаменатель — bd .
• Конечная дробь составляет , что эквивалентно первой дроби.

Если мы пойдем в обратном направлении, мы скажем, что уменьшаем дробь до ее простейшая эквивалентная дробь или наименьшие термины .Для этого мы находим любой множитель, который содержится как в числителе, так и в знаменателе. и вычеркнуть или вычеркнуть , например:

---

Пример: Сократите обычные дроби 10/6 и 10/5 до наименьших значений.

	Разделите числитель и знаменатель на множители. Сократить общий множитель 2.
	Разделите числитель и знаменатель на множители.Отмените общий множитель 5. Результат деления — целое число. Мы говорим, что знаменатель делит без остатка в числитель.

---

Если числитель и знаменатель алгебраической дроби — одночленов , то выполните все следующие шаги , чтобы уменьшить дробь до наименьшего значения :

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

Знак — ставится либо перед результатом или перед числителем; никогда перед знаменателем. Уменьшите коэффициент 6/9 до самые низкие сроки.

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

Два знака — заменены знаком +, который нам не нужно отображать.Коэффициент уменьшается до ¼. В числителе есть другие множители, поэтому цифру 1 в числителе можно не указывать. Объедините экспоненты с основанием x , используя свойства экспоненты.

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

Спереди ставится знак -. Коэффициент снижается до 1/3.Идентичные множители x 3 в числителе и знаменателе отменяют. В числителе нет других факторов, поэтому на этот раз необходимо отобразить 1.

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

После проведения всех упрощений знаменатель равен 1, поэтому нам не нужно его отображать.Таким образом, результатом является обычное выражение, не алгебраическая дробь.

---

Если числитель и знаменатель алгебраической дроби являются полиномами , то в дополнение к шагам, перечисленным выше, попробуйте следующие шаги , чтобы уменьшить дробь до наименьших значений :

• Разделите на множители числитель или знаменатель, или оба сразу. Иногда это вызывает новые отменяющие факторы, чтобы появиться.
• Фактор a — вынести из числителя или знаменателя. Иногда это приводит к появлению нового отменяющего фактора.

В следующих примерах мы предполагаем, что вы уже знаете как сделать факторинг поэтому мы просто покажем, как использовать множители для уменьшения алгебраических дробей до самые низкие сроки.

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

Разделите числитель и знаменатель на множители. Сократить общий множитель x .

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.
Решение:

Разложите множитель в числителе. Сократить общий множитель x — 2.

---

Пример: Уменьшить алгебраическую дробь на самые низкие сроки.

Решение: Это та же алгебраическая дробь, что и в предыдущем примере, за исключением что знаменатель отличается знаком -.

Разложите числитель на множитель и множитель a — выход знаменателя. Сократить общий множитель x — 2. Поднесите знак — к числителю и распределите его.

---

---

Если вы нашли эту страницу в поиске в Интернете, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.

Сокращение уравнений умножением

176.Неизвестная величина вместо того, чтобы быть связана с известной величиной знаком + или -, может быть разделена на на , как в уравнении x / a = b.

Здесь сокращение не может быть произведено, как в предыдущих случаях, путем транспонирования. Но если оба члена будут умножены на (статья 167), уравнение станет
х = ab.

Ибо дробь вводится в знаменатель в миллиметрах путем удаления знаменателя. Это доказано свойствами дробей.(Статья 156.) Это также очевидно из шестой аксиомы.

Таким образом, x = ax / a = 3x / 3 = [(a + b) x] / (a ​​+ b) = (dx + 5x) / (d + 5). Ведь в каждом из этих случаев x умножается и делится на одно и то же количество; и это не меняет значения. Следовательно,

177. Когда неизвестная величина равна делению на известную величину, уравнение сокращается на , умножая каждой стороны на эту известную величину.

В этом случае необходимо произвести те же транспозиции, что и в предыдущих примерах.Также необходимо отметить, что каждые членов уравнения необходимо умножить. Поскольку несколько членов в каждом члене составляют составное множимое, которое должно быть умножено в соответствии со ст. 96.

Бывший. 1. Приведите уравнение x / c + a = b + d
Умножение обеих сторон на c
Произведение: x + ac = bc + cd.
И x = bc + cd — ac.

2. Приведите уравнение x / (a ​​+ b) + d = h
Умножение на a + b x + ad + bd = ah + bh.
А х = ag + bh — ad — bd.

178. Когда неизвестная величина находится в знаменателе дроби , уменьшение производится аналогичным образом, умножая уравнение на этот знаменатель.

Бывший. 3. Сократите уравнение 6 / (10 — x) + 7 = 8
Умножение на 10 — x 6 + 70 — 7x = 80 — 8x
И х = 4.

179. Хотя обычно не является необходимым , тем не менее часто бывает удобно удалить знаменатель из дроби, состоящей только из известных величин.Это может быть сделано таким же образом, как знаменатель удаляется из дроби, которая содержит неизвестную величину.

Возьмем, например, x / a = d / b + h / c
Умножение на a x = ad / b + ah / c
Умножение на b bx = ad + abh / c
Умножение на c bcx = acd + abh.

Или мы можем умножить на произведение всех знаменателей сразу.

В том же уравнении x / a = d / b + h / c
Умножение на abc abcx / a = abcd / b + abch / c

Затем, удаляя из каждого члена букву, общую для его числителя и знаменателя (ст.142,), как и раньше, имеем bcx = acd + abh. Следовательно, 180. Уравнение можно очистить от дробей , умножив каждую сторону на все знаменатели .

При очистке уравнения дробей необходимо заметить, что знак, стоящий перед любым действием ft, означает, что все значение должно быть вычтено (статья 139), что делается путем изменения знаков всех в числителе.

Уравнение (a — d) / x = c — (3b — 2hm — 6n) / r
совпадает с ar — dr = crx -3bx + 2hmx + 6nx.

.