1 сформулируйте сочетательное свойство умножения. Сочетательное и распределительное свойства умножения

Назад Вперёд

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цель: учить упрощать выражение, содержащее только действия умножения.

Задачи (Слайд 2):

• Познакомить с сочетательным свойством умножения.
• Формировать представление о возможности использования изученного свойства для рационализации вычислений.
• Развивать представления в возможности решения «жизненных» задач средствами предмета «математика».
• Развивать интеллектуальные и коммуникативные общеучебные умения.
• Развивать организационные общеучебные умения, в том числе умения самостоятельно оценивать результат своих действий, контролировать самого себя, находить и исправлять собственные ошибки.

Тип урока: изучение нового материала.

План урока:

1. Организационный момент.
2. Устный счёт. Математическая разминка.
Строка чистописания.
3. Сообщение темы и задач урока.
4. Подготовка к изучению нового маериала.
5. Изучение нового материала.
6. Физкультминутка
7. Работа по закреплению н. м. Решение задачи.
8. Повторение пройденного материала.
9. Итог урока.
10. Рефлексия
11. Домашнее задание.

Оборудование: карточки с заданием, наглядный материал (таблицы), презентация.

ХОД УРОКА

I. Организационный момент

Прозвенел и смолк звонок.
Начинается урок.
Вы зa парты тихо сели
На меня все посмотрели.

II. Устный счёт

– Посчитаем устно:

1) «Весёлые ромашки» (Слайды 3-7 таблица умножения)

2) Математическая разминка. Игра «Найди лишнее» (Слайд 8)

• 485 45 864 947 670 134 (классификация на группы ЛИШНЕЕ 45 – двузначное, 670 – в записи числа нет цифры 4).
• 9 45 72 90 54 81 27 22 18 (9 – однозначное, 22 не делится на 9)

Строка чистописания. Прописать в тетради числа, чередуя: 45 22 670 9
– Подчеркнуть самую аккуратную запись числа

III. Сообщение темы и задач урока. (Слайд 9)

– Запишите число, тему урока.
– Прочитайте задачи нашего урока

IV. Подготовка к изучению нового материала

а) Верно ли выражение

На доске запись:

(23 + 490 + 17) + (13 + 44 + 7) = 23 + 490 + 17 + 13 + 44 + 7

– Назовите используемое свойство сложения. (Сочетательное)
– Какую возможность даёт сочетательное свойство?

Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок.

43 + 17 + (45 + 65 + 91) = 91 + 65 + 45 + 43 + 17

– Какие свойства сложения мы применяются в данном случае?

Сочетательное свойство даёт возможность записывать выражения, содержащие только сложение, без скобок. При этом вычисления можно выполнять в любом порядке.

– В таком случае как называется ещё одно свойство сложения? (Переместительное)

– Вызывает ли это выражение затруднение? Почему?(Мы не умеем умножать двузначное число на однозначное)

V. Изучениенового материала

1) Если мы будем выполнять умножение в том порядке, в каком записаны выражения, то возникнут трудности. Что же поможет нам снять эти трудности?

(2 * 6) * 3 = 2 * 3 * 6

2) Работа по учебнику с. 70, № 305 (Выскажи своё предположение о результатах, которые получат Волк и Заяц. Проверь себя, выполнив вычисления).

3) № 305. Проверь, равны ли значения выражений. Устно.

Запись на доске:

(5 2) 3 и 5 (2 3)
(4 7) 5 и 4 (7 5)

4) Сделай вывод. Правило.

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего.
– Расскажите сочетательное свойство умножения.
– Объясните сочетательное свойство умножения на примерах

5) Коллективная работа

На доске: (8 3) 2, (6 3) 3, 2 (4 7)

VI. Физминутка

1) Игра «Зеркало». (Слайд 10)

Свет мой зеркальце, скажи,
Да всю правду доложи.
Мы ль на свете всех умнее,
Всех забавней и смешнее?
Повторяйте все за мной
Веселые движения физминутки озорной.

2) Физминутка для глаз «Зоркие глазки».

– Закройте глаза на 7 секунд, посмотрите направо, затем налево, вверх, вниз, затем сделайте глазами 6 кругов по часовой стрелке, 6 кругов против часовой стрелки.

VII. Закрепление изученного

1)Работа по учебнику. решение задачи. (Слайд 11)

(с. 71, № 308) Прочитайте текст. Докажите, что это задача. (Есть условие, вопрос)
– Выделите условие, вопрос.
– Назовите числовые данные. (Три, 6, трёхлитровые)
– Что они обозначают? (Три ящика. 6 банок, в каждой банке по 3 литра сока)
– Какая это задача по структуре? (Составная задача, т. к. нельзя сразу ответить на вопрос задачи или для решения требуется составление выражения)
– Тип задачи? (Составная задача на последовательные действия))
– Решите задачу без краткой записи составлением выражения. Для этого используйте следующую карточку:

Карточка-помощница

– В тетради решение задачи можно оформить следующим образом: (3 6) 3

– Можем ли мы решить задачу в таком порядке?

(3 6) 3 = (3 3) 6 = 9 6 = 54 (л).
3 (3 6) = (3 3) 6 = 9 6 = 54 (л)

Ответ: 54 литра сока во всех ящиках.

2) Работа в парах (по карточкам): (Слайд 12)

– Поставь знаки, не вычисляя:

(15 * 2) *4 15 * (2 * 4) (–Какое свойство?)
(8 * 9) * 6 7 * (9 * 6)
(428 * 2) * 0 1 * (2 * 3)
(3 * 4) * 2 3 + 4 + 2
(2 * 3) * 4 (4 * 2) * 3

Проверка: (Слайд 13)

(15 * 2) * 4 = 15 * (2 * 4)
(8 * 9) * 6 > 7 * (9 * 6)
(428 * 2) * 0 (3 * 4) * 2 > 3 + 4 + 2
(2 * 3) * 4 = (4 * 2) * 3

3) Самостоятельная работа (по учебнику)

(с. 71, № 307 – по вариантам)

1 в. (8 2) 2 = (6 2) 3 = (19 1) 0 =
2 в. (7 3) 3 = (9 2) 4 = (12 9) 0 =

Проверка:

1 в. (8 2) 2 = 32 (6 2) 3 = 36 (19 1) 0 = 0.

2 в. (7 3) 3 = 63 (9 2) 4 = 72 (12 9) 0 = 0

Свойства умножения: (Слайд 14).

• Переместительное свойство
• Сочетательное свойство

– Зачем нужно знать свойства умножения? (Слайд 15).

• Чтобы быстро считать
• Выбирать рациональный способ счета
• Решать задачи

VIII. Повторение пройденного материала. «Ветряные мельницы». (Слайд 16, 17)

• Числа 485, 583 и 681 увеличить на 38 и записать три числовых выражения (1 вариант)
• Числа 583, 545 и 507 уменьшить на 38 и записать три числовых выражения (2 вариант)

485 + 38 523		583 + 38 621		681 + 38 719
583 – 38 545		545 – 38 507		507 – 38 469

Учащиеся выполняют задания по вариантам (двое учащихся решают задания на дополнительных досках).

Взаимопроверка.

IХ. Итог урока

– Чему учились сегодня на уроке?
– В чём же заключается смысл сочетательного свойства умножения?

Х. Рефлексия

– Кто считает, что понял смысл сочетательного свойства умножения? Кто доволен своей работой на уроке? Почему?
– Кто знает, над чем ему еще надо поработать?
– Ребята, если вам урок понравился, если вы довольны своей работой, то поставьте руки на локти и покажите мне ладошки. А если вы были чем-то расстроены, то покажите мне обратную сторону ладошки.

XI. Информация о домашнем задании

– Какое домашнее задание вы бы хотели получить?

По выбору:

1. Выучить правило с. 70
2. Придумать и записать выражение на новую тему с решением

Сочетательное свойство умножения

Цели: познакомить учащихся с сочетательным свойством умножения; научить пользоваться сочетательным свойством умножения при анализе числовых выражений; повторить свойства сложения и переместительное свойство умножения; совершенствовать вычислительные навыки; развивать умение анализировать, рассуждать.

Предметные результаты:

познакомиться с сочетательным свойством умножения, формировать представления о возможности использования изученного свойства для рационализации вычислений.

Метапредметные результаты:

Регулятивные: планировать своё действие в соответствии с поставленной задачей, принимать и сохранять учебную задачу.

Познавательные:

использовать знаково-символические средства, модели и схемы для решения задач, ориентироваться на разнообразие способов решения задач; устанавливать аналогии.

Коммуникативные : строить речевые высказывания в устной и письменной форме, формировать собственное мнение, задавать и отвечать на вопросы, доказывая правильность своего мнения.

Личностные : развивать способность к самооценке, способствовать успешности в овладении материалом.

Тип урока : изучение нового материала.

Оборудование : карточки с заданием, наглядный материал (таблицы), презентация.

ХОД УРОКА

I. Организационный момент (эмоциональный настрой)

Долгожданный дан звонок

Начинается урок.

Отдохнуть вы все успели?

А теперь — вперед, за дело!

Ребята давайте пожелаем, друг другу на уроке быть внимательными, собранными, старательными. Поприветствуем друг друга улыбками и начнём урок.

II. Актуализация опорных знаний + Целеполагание

На доске неполная запись темы ______________________свойство умножения

Глядя на неполную запись, подумайте, чем мы будем заниматься на уроке и какова тема сегодняшнего урока. (Рассуждения детей)

Сегодня мы познакомимся с новым свойством умножения, название которого мы узнаем,выполнив задания устного счёта и заданий, внесённых в ваши листы –карты урока, научимся пользоваться новым свойством умножения при анализе числовых выражений; повторим свойства сложения и переместительное свойство умножения;; будем развивать вычислительные навыки, умение анализировать, рассуждать.

Работать мы будем дружно и творчески, в парах и самостоятельно, выполним задания и сделаем выводы.

В ваших картах после каждого задания вы должны будете оценить свою работу. Если вы справились с заданием без ошибок вы поставите себе + , если не справились, то —

А для чего нам это нужно?

Где мы сможем применять полученные знания?

Пословица

Математику учить – ум точить

Как вы понимаете смысл данной пословицы?

«Математику уже затем учить надо, что она ум в порядок приводит»

М.Ломоносов

III. Устный счёт

1.Игра «Истина – ложь». Дети показывают знак + или —

Сумма чисел 6 и 5 равна 12

Разность чисел 16 и 6 равна 9

9 увеличить на 5 равно 14

100 – это самое большое трёхзначное число

Куб – это объёмная фигура

Прямоугольник – это плоская фигура

На доске открывается буква С

2.Задание на смекалку

К любимой оценке ученика прибавить количество цветов радуги.

К количеству месяцев в году прибавить число дней в неделе.

На доске открывается буква 0

3.Задача на логику

В саду росли 2 березы, 4 яблони, 5 вишен. Сколько всего фруктовых деревьев росло в саду? На доске открывается буква Ч

4.На какие группы можно распределить следующие фигуры

На доске открывается буква Е

На доске открывается буква Т

На доске открывается буква А

7. Можно ли утверждать, что площадь данных фигур одинаковая?

На доске открывается буква Т

8. Работа в парах: Разбей числа на две группы.

Запиши каждую группу в порядке возрастания (Знак дружной работы) е

499 75 345 24 521 86

На доске открывается буква Е

9. Самостоятельная работа

Заполни карточку

На доске открывается буква Л

10. Выбери нужный знак (+ или )

Увеличить на 6

Увеличить в 3 раза

На доске открывается буква Ь

11. ,

2 · 6 … 6 + 6 + 6

5 · 6 … 6 · 4

8 · 6 … 6 · 8

На доске открывается буква Н

12. Какое числовое выражение является лишним? Почему?

(2 +7) 0 365 0

(9 2) 1 (94-26) 0

На доске открывается буква О

13.Фронтальная работа

Вставьте пропущенные числа:

– Какие свойства сложения и умножения помогли вам выполнить задание? (Переместительное и сочетательное свойства сложения; переместительное свойство умножения.) На доске открывается буква Е

На доске открывается тема Сочетательное свойство умножения

Физминутка

Для начала мы с тобой

Для начала мы с тобой

Крутим только головой.

(Вращения головой.)

Корпусом вращаем тоже.

Это мы, конечно, сможем.

(Повороты вправо и влево.)

Напоследок потянулись

Вверх и в стороны.

Прогнулись.

(Потягивания вверх и в стороны. )

III. Сообщение нового материала

1. Постановка учебной проблемы

Можно ли утверждать, что значения выражений в данном столбике одинаковы?

(Для 1 и 2 выражения применимо сочетательное свойство сложения- 2 соседних слагаемых можно заменять суммой и значения выражений будут одинаковы;

3и1 выражение- применили переместительное свойство сложения

4и2 выражение- переместительное свойство.)

-Какие же свойства применимы для вычисления данных

выражений ?

(Переместительное и сочетательное свойство)

— А можно ли утверждать, что значения выражений в этом столбике одинаковы?

На этот вопрос нам и предстоит ответить.

Мы сегодня узнаем, можно ли пользоваться сочетательным свойством при умножении?)

2.Первичное усвоение новых знаний

Посчитайте разными способами число всех маленьких квадратов и запишите выражением.

1 способ :(6*4)*2 = 24*2=48

(В одном прямоугольнике 6 квадратов, умножая 6 на 4, мы узнаем сколько квадратов в одном ряду. Умножая результат на 2, узнаем, сколько квадратиков в двух рядах).

2 способ : 6*(4*2)= 6*8=48

(Сначала выполняем действие в скобках- 4*2, то есть узнаем, сколько всего прямоугольников в двух рядах. В одном прямоугольнике 6 квадратов. Умножив 6 на полученный результат, отвечаем на поставленный вопрос.)

Вывод: Таким образом, и то и другое выражение обозначает, сколько всего маленьких квадратиков на рисунке.

Значит: (6*4)*2=6*(4*2)- сочетательное свойство умножения

З н а к о м с т в о с ф о р м у л и р о в к о й сочетательного свойства умножения и сравнение ее с формулировкой сочетательного свойства сложения.

IV . Первичная проверка понимания

Откройте учебник на странице 50 и найдите № 160

Объясните, что обозначают числовые равенства под каждым рисунком?

(4*3)*2= 4*(3*2)

(по 4 снежинки поместили в 3 квадрата и взяли 2 ряда или 4 снежинки поместили в 3 квадрата по 2 ряда.)

(по 6 квадратиков взяли 5 рядов и поместили в 2 больших квадрата или 6 квадратиков взяли по 5 рядов в двух больших квадратах)

Давайте прочитаем правило:

Первичное закрепление Работа у доски

Найдите № 161 (1 столбик)

Читаем задание: (Запиши каждое выражение в виде произведения трех однозначных чисел)

Найдите № 162 (1 столбик)

Читаем задание: Верно ли утверждение, что значения выражений в каждом столбце одинаковы?

Работаем самостоятельно по рядам (проверяем у доски), применяя сочетательное свойство: Чтобы произведение двух чисел умножить на третье, можно первое число умножить на произведение второго и третьего чисел.

Подведение итогов занятия.

Оценивание

Давайте вернемся к числовым выражениям, с которыми мы с вами встретились в начале урока. Скажите, а можно ли утверждать, что значения выражений в этом столбике одинаковы?

Какое открытие вы сегодня сделали на уроке? Где его можно применять?

(Познакомились с новым свойством умножения)Чтобы произведение двух чисел умножить на третье, можно первое число умножить на произведение второго и третьего чисел.

Домашнее задание: правило с.50, № 163 *Найди пословицы или высказывания известных людей о математике

Выставление оценок.

Оценки «5» получают те, ребята, у кого нет минусов в карте.

У кого 1-2 минуса получает «4»

3-5 минусов –«3»

Более 5 минусов –«2»

Рефлексия

Закончи фразу

Сегодня на уроке я…..

Самым сложным для меня было…..

Сегодня я понял…

Сегодня я научился…

Реши для себя

Рассмотрим пример, подтверждающий справедливость переместительного свойства умножения двух натуральных чисел.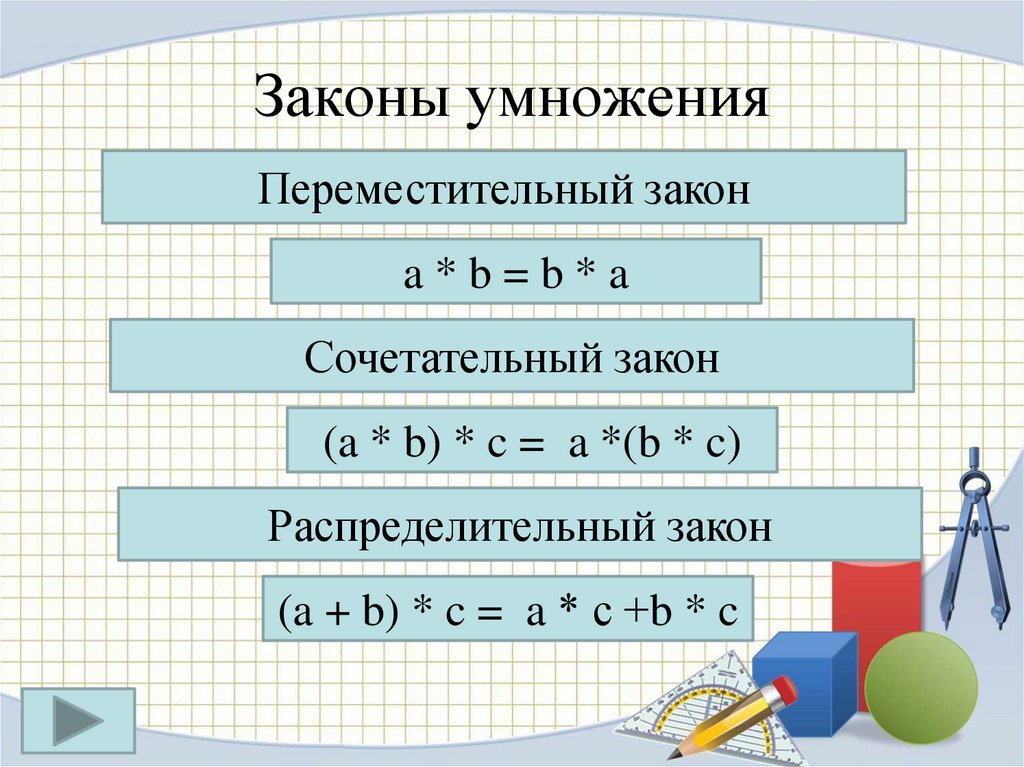 Отталкиваясь от смысла умножения двух натуральных чисел , вычислим произведение чисел 2 и 6 , а также произведение чисел 6 и 2 , и проверим равенство результатов умножения. Произведение чисел 6 и 2 равно сумме 6+6 , из таблицы сложения находим 6+6=12 . А произведение чисел 2 и 6 равно сумме 2+2+2+2+2+2 , которая равна 12 (при необходимости смотрите материал статьи сложение трех и большего количества чисел). Следовательно, 6·2=2·6 .

Приведем рисунок, иллюстрирующий переместительное свойство умножения двух натуральных чисел.

Сочетательное свойство умножения натуральных чисел.

Озвучим сочетательное свойство умножения натуральных чисел: умножить данное число на данное произведение двух чисел – это то же самое, что умножить данное число на первый множитель, и полученный результат умножить на второй множитель . То есть, a·(b·c)=(a·b)·c , где a , b и c могут быть любыми натуральными числами (в круглые скобки заключены выражения, значения которых вычисляются в первую очередь).

Приведем пример для подтверждения сочетательного свойства умножения натуральных чисел. Вычислим произведение 4·(3·2) . По смыслу умножения имеем 3·2=3+3=6 , тогда 4·(3·2)=4·6=4+4+4+4+4+4=24 . А теперь выполним умножение (4·3)·2 . Так как 4·3=4+4+4=12 , то (4·3)·2=12·2=12+12=24 . Таким образом, справедливо равенство 4·(3·2)=(4·3)·2 , подтверждающее справедливость рассматриваемого свойства.

Покажем рисунок, иллюстрирующий сочетательное свойство умножения натуральных чисел.

В заключении этого пункта отметим, что сочетательное свойство умножения позволяет однозначно определить умножение трех и большего количества натуральных чисел .

Распределительное свойство умножения относительно сложения.

Следующее свойство связывает сложение и умножение. Оно формулируется так: умножить данную сумму двух чисел на данное число – это то же самое, что сложить произведение первого слагаемого и данного числа с произведением второго слагаемого и данного числа . Это так называемое распределительное свойство умножения относительно сложения.

С помощью букв распределительное свойство умножения относительно сложения записывается как (a+b)·c=a·c+b·c (в выражении a·c+b·c сначала выполняется умножение, после чего – сложение, подробнее об этом написано в статье ), где a , b и c – произвольные натуральные числа. Отметим, что силу переместительного свойства умножения, распределительное свойство умножения можно записать в следующем виде: a·(b+c)=a·b+a·c .

Приведем пример, подтверждающий распределительное свойство умножения натуральных чисел. Проверим справедливость равенства (3+4)·2=3·2+4·2 . Имеем (3+4)·2=7·2=7+7=14 , а 3·2+4·2=(3+3)+(4+4)=6+8=14 , следовательно, равенство (3+4)·2=3·2+4·2 верно.

Покажем рисунок, соответствующий распределительному свойству умножения относительно сложения.

Распределительное свойство умножения относительно вычитания.

Если придерживаться смысла умножения, то произведение 0·n , где n – произвольное натуральное число, большее единицы, представляет собой сумму n слагаемых, каждое из которых равно нулю. Таким образом, . Свойства сложения позволяют нам утверждать, что последняя сумма равна нулю.

Таким образом, для любого натурального числа n выполняется равенство 0·n=0 .

Чтобы оставалось справедливым переместительное свойство умножения примем также справедливость равенства n·0=0 для любого натурального числа n .

Итак, произведение нуля и натурального числа равно нулю , то есть 0·n=0 и n·0=0 , где n – произвольное натуральное число. Последнее утверждение представляет собой формулировку свойства умножения натурального числа и нуля.

В заключении приведем пару примеров, связанных с разобранным в этом пункте свойством умножения. Произведение чисел 45 и 0 равно нулю. Если умножить 0 на 45 970 , то тоже получим нуль.

Теперь можно смело начинать изучение правил, по которым проводится умножение натуральных чисел .

Список литературы.

• Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
• Математика. Любые учебники для 5 классов общеобразовательных учреждений.

Умножение натуральных чисел и его свойства 5 класс онлайн-подготовка на Ростелеком Лицей

Определение умножения

 

Пример 1. Есть 4 класса, и в каждом классе 30 учеников. Все классы написали контрольную работу. Сколько работ необходимо проверить?

 

Так как в каждом классе по 30 человек, то работ будет:

Эту же запись мы можем записать немного короче:

Умножить число a на число b – значит вычислить сумму, в которой число a повторено b раз.

a и b называются сомножителями, а то, что получится, называется произведением.

В нашем примере 30 и 4 – сомножители, а произведение равно 120.

 

Свойства умножения

 

 

1. Переместительное свойство умножения

 

Пример 2. Предположим, у Маши есть по одной страничке в четырех социальных сетях. На каждой страничке у нее выложены 3 фотографии: первая – фото, где Маша, вторая – фото, где Маша с мамой, третья – фото, где Маша с папой. Сколько всего фото у Маши на страничках?

Мы можем сказать, что на каждой страничке 3 фотографии, а всего страничек 4, значит, всего фото:

Или:

С другой стороны, мы можем посчитать количество фотографий по-другому.

Сколько всего фото, где Маша одна? Их 4 – в каждой социальной сети по одной. Сколько фотографий выложено у Маши с мамой? Тоже 4. С папой? Тоже 4. Итого:

Но общее количество фотографий одинаково. Оно не зависит от того, как мы его считали: по социальным сетям или по типу фото. Поэтому мы получаем, что 3 умножить на 4 – это то же самое, что 4 умножить на 3.

То есть,

Данное свойство называется переместительным свойством умножения: можно менять местами сомножители, и от этого произведение не изменится. Это свойство иногда называют переместительным законом.

2. Сочетательное свойство умножения

Пример 3. Предположим, у Сергея есть 3 флешки, на каждой флешке по 4 папки, а в каждой папке 2 файла. Сколько всего файлов у Сергея?

Сколько файлов будет внутри одной флешки?

Всего флешек 3, а значит, всего файлов:

С другой стороны, у нас есть 3 флешки. На каждой флешке 4 папки:

А в каждой папке 2 файла:

Но мы могли посчитать количество файлов на одной флешке – 8, а потом умножить полученное на 3:

То есть мы выяснили, что переставлять сомножители можно не только тогда, когда их два, но и когда их 3, как в нашем примере, или больше.

То есть,  

Такое свойство умножения называется сочетательным. Иногда его называют свойством раскрытия скобок. То есть порядок, в котором мы будем умножать, неважен.

 

---

Научные названия свойств

Переместительное свойство иначе называется коммутативным (commutativus – меняющийся (лат.)). Мы меняем порядок сомножителей, а произведение от этого не меняется. Есть коммутативность умножения (при перестановке сомножителей произведение не меняется). Также есть коммутативность сложения (от перестановки слагаемых сумма не меняется).

Сочетательный закон иначе называется ассоциативным (association – соединение (лат.)). Существует ассоциативность умножения и сложения.

---

 

 

Частные случаи умножения

 

 

Частные случаи

 

1. Что будет, если умножить некоторое число n на 1? Необходимо сложить данное число один раз. То есть мы берем n один раз, а не складываем его с собой. Иначе мы используем n два раза.

Аналогично:

2. Если мы умножаем 0 на что-то, то получаем 0. Ведь сколько бы раз мы ни складывали 0 с собой, мы все равно получим 0.

Аналогично:

Как читается произведение двух сомножителей

Данная запись читается так: «Произведение ста семидесяти пяти и трехсот двенадцати».

 

---

Пример использования свойств

Пример 4.

Мы можем умножить числа так, как они записаны. А можем немного изменить запись и упростить вычисления.

Мы использовали сочетательное свойство умножения (поменяли порядок сомножителей).

Пример 5.

Произвести такие вычисления достаточно трудно. Давайте заметим, что 5 «хорошо» умножается на 2. Поэтому, если бы у нас был сомножитель, равный двум, наши вычисления стали бы проще. Давайте разложим число 684 на произведение двойки и чего-то еще.

Вернемся к нашему выражению:

---

 

Заключение

Мы познакомились с таким действием, как умножение натуральных чисел; выяснили, какими свойствами обладает это действие; и рассмотрели несколько частных случаев.

 

Список рекомендованной литературы

1. Виленкин Н. Я., Жохов В. И., Чесноков А. С., Шварцбурд С. И. Математика, 5 класс (в 2 частях). ООО «ИОЦ МНЕМОЗИНА».
2. Мерзляк А. Г., Полонский В. Б., Якир М. С. Математика. 5 класс – М.: Вентана-Граф.

 

Рекомендованные ссылки на ресурсы сети Интернет

1. Презентация (Источник)
2. Учебник Н. Я. Виленкина. Математика 5 класс (Источник)
3. Презентация (Источник)

 

Домашнее задание

1. Запишите в виде суммы и произведения:

а) Число а сложили с собой 12 раз;

б) Число 5 сложили с собой k раз.

2. Запишите сумму в виде произведения и найдите значение выражения:

а) 

б) 

в) 

г) .

3. У Жени есть 6 коробок с игрушками. В каждой коробке по 3 машины. Сколько всего машинок в коробках?

4. Найдите значение выражения наиболее удобным способом:

а) 

б) 

в) 

г) 

 

Что такое переместительное свойство умножения

Что такое переместительное свойство умножения в математике?

Коммутативный происходит от слова «коммутировать», которое можно определить как передвижение или путешествие. Согласно свойству перестановочности умножения изменение порядка умножаемых чисел не меняет произведения.

Давайте разберемся на примере.

Пример коммутативного свойства умножения

Поместите 3 кирпича в ряд.

Теперь положите еще один ряд кирпичей над этим рядом.

Повторите этот процесс 4 раза.

 Теперь подсчитайте количество использованных кирпичей.

Всего кирпичей $=$ Количество рядов $\times$ Количество кирпичей в каждом ряду 

                      $=  4 \times 3$

                                    

Поместите еще два ряда над этим рядом.

Всего кирпичей $=$ Количество рядов $\times$ Количество кирпичей в каждом ряду

                    $=  3 \times 4$ 

                     $ = 12$

Мы заметили, что замена количества рядов на количество кирпичей в каждом ряду не меняет общего количества необходимых кирпичей.

Родственные игры

Что такое умножение?

Умножение есть не что иное, как многократное сложение. Он обозначается символами «*», «.» и «✕».

Посмотрим, что такое многократное сложение на данном примере:

Пример: Обезьяна прыгает с одной точки на другую. Он преодолевает одну единицу расстояния с каждым прыжком. Сколько юнитов он покроет за 5 прыжков?

Решение: Из приведенного выше утверждения мы можем сказать, что 1 прыжок $= 1$ единице. Давайте посмотрим на это изображение.

Итак, мы видим, что обезьяна покрывает $1+1+1+1+1 = 5$ единиц

Мы также можем записать это как $1 \times 5 = 5$ единиц.

Теперь обратите внимание, что для каждого шага нам нужно добавить «1» к предыдущему. Вот почему мы можем сказать, что умножение есть не что иное, как многократное сложение.

Давайте рассмотрим еще один пример.

Пример: Робин хочет купить 3 плитки шоколада. Каждый слиток стоит $\$$ 10. Сколько денег нужно Робину, чтобы купить 3 слитка?

Эту задачу можно решить двумя разными способами.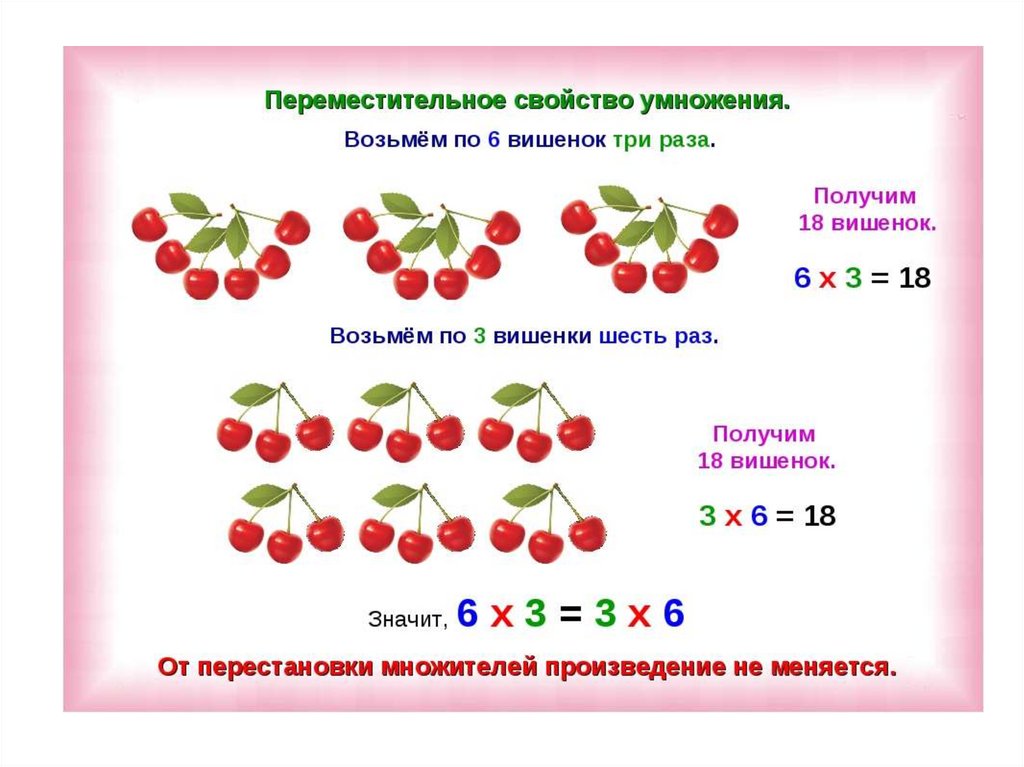 Рассмотрим оба метода.

Метод 1:  

Количество шоколадок  $\times$ Стоимость каждой шоколадки 

$= 3$ $\times $ $\$$ 10

$=$ $\$$ 30

Метод :  

Стоимость каждой шоколадки $\times$ Количество шоколадок

 $=$ $\$$ 10 $\times$ $3$ 

  $=$ $\$$ 30

Мы заметили, что  порядок в которую мы умножили на количество плиток шоколада и стоимость каждой плитки не меняется на требуемое количество.

Связанные рабочие листы

Коммутативное свойство умножения 

Вы должны быть знакомы с таблицами до 5.

Вы наблюдали 

$1 \times 2 = 2 \times 1 = 2$

$2 \times 4 = 4 \times 2 = 8$ 

$3 \times 5 = 5 \times 3 = 15$

Итак, мы можем заключить, что порядок умножения чисел не меняет окончательный ответ.

Вы знаете?  

Если вы помните таблицы до 5, вы можете вычислить умножение больших таблиц, используя свойство коммутативности.

Например:

Если вы знаете 

Пять умножить на восемь, т. е. $5 \times 8 = $ ?

Вы также можете ответить 

Восемь раз по пять, т. е. $8 \times 5  =$ ?

Оба равны 40. 

Факт для запоминания

Свойство коммутативности применимо только к сложению и умножению, но не к вычитанию и делению.

Давайте разберемся на примерах.

Альтернативный тег: свойство перестановочности выполняется в случае умножения

Таким образом, мы можем заключить, что свойство перестановочности применимо к сложению и умножению, а не к вычитанию и делению.

Заключение

В заключение можно сказать, что

• Умножение есть не что иное, как многократное сложение.
• Коммутативное свойство означает, что конечный результат не изменится, если мы изменим порядок.
• Умножение и сложение следуют коммутативному свойству.

Решенные примеры

Пример 1: Заполните пропуски.

1. $4 \times 5 = 5 \times \underline{}$

      Решение:   $4  \times 5  =  5 \times  4$

2. $3 \times = 6 \times \underline{}$

Решение:  $3 \times \underline{} $6$ \underline{} = 6 \times 3$

3. $2  \times  1  = 1  \times \underline{}$

Решение:  $2  \times 1  = 1  \times  2$

4. $3 \times 3 {}underline \times 2 \times 6$

      Решение:  $3 \times 6 \times 2 =  3 \times 2 \times 6$

5. 16 $ \times 2 \times 4 = 2 \times \underline{} \times 4$

Решение: $16 \times 2 \times 4 = 2 \times 16 $

2 4 $

\times \underline{} \times  2  =   8 \times \underline{} \times 2$ 

       Решение : $9 \times \underline{} 8 \times 2  =   8 \times 9 \times 2$

Пример 2: Дополните следующий оператор:

Свойство коммутативности говорит о том, что порядок чисел в _________ и _________ не меняет результат.

Решение: 

Переместительное свойство говорит о том, что порядок чисел в умножении и сложении не меняет результат.

Только умножение и сложение следуют свойству коммутативности.

Практические задачи

1

Какое выражение равно $6 \times 4 \times 5$ согласно свойству коммутативности?

$5 \x 6 \times 4$

$645$

$6+4+5$

Ничего из вышеперечисленного

Правильный ответ: $5 \times 6 \times 4$
Объяснение: Согласно свойству перестановочности умножения, если изменить порядок чисел, произведение останется прежним.

2

A $\times$ B = B $\times$ A есть

Переместительное свойство при сложении

Переместительное свойство при умножении

Ассоциативное свойство при умножении

Ассоциативное свойство при сложении

Правильный ответ: Переместительное свойство при умножении
Объяснение: Согласно переместительному свойству умножения, если изменить порядок чисел, произведение останется прежним.

3

$A + B = B + A$

Переместительное свойство при сложении

Переместительное свойство при умножении

Ассоциативное свойство при умножении

Ассоциативное свойство при сложении

Правильный ответ:
Объяснение: Согласно коммутативному свойству сложения, если изменить порядок чисел, сложение останется прежним.

4

Какое выражение совпадает с $6 + 4 + 5$ согласно свойству коммутативности?

$6 \times 4 \times 5$

$645$

$6 + 5 + 4$

$546$

Правильный ответ: $6 + 5 + 4$
Пояснение: Согласно коммутативному свойству сложения, если порядок чисел изменен, сложение останется прежним.

Часто задаваемые вопросы

Какие операции не следуют коммутативному свойству?

Вычитание и деление не следуют свойству коммутативности.

Можем ли мы применить свойство коммутативности к умножению 4 чисел?

Да, мы можем применить свойство коммутативности для умножения 4 чисел.

Например, $4 \times 5 \times 6 \times 7 = 7 \times 5 \times 6 \times 4$

В чем разница между ассоциативным и коммутативным свойством умножения?

Ассоциативный признак умножения утверждает, что при изменении группировки чисел произведение чисел остается прежним. $(\text{A B})$ $\text{C} = \text{A}$ $(\text{B C})$ так выражается ассоциативное свойство умножения.

Коммутативное свойство умножения утверждает, что даже если изменить порядок чисел, произведение двух или более целых чисел останется прежним. Коммутативность умножения представлена ​​в виде $\text{A B C} = \text{C B A}$.

Переписывание выражений с использованием коммутативных и ассоциативных свойств

Результаты обучения

• Определение ассоциативных и коммутативных свойств сложения и умножения
• Использовать ассоциативные и коммутативные свойства сложения и умножения для перезаписи алгебраических выражений

Подумайте о добавлении двух чисел, таких как [латекс]5[/латекс] и [латекс]3[/латекс].

[латекс]\begin{array}{cccc}\hfill 5+3\hfill & & & \hfill 3+5\hfill \\ \hfill 8\hfill & & & \hfill 8\hfill \end{array} [/латекс]

Результаты те же. [latex]5+3=3+5[/latex]

Обратите внимание, порядок добавления не имеет значения. То же самое верно и при умножении [латекс]5[/латекс] и [латекс]3[/латекс].

[латекс]\begin{array}{cccc}\hfill 5\cdot 3\hfill & & & \hfill 3\cdot 5\hfill \\ \hfill 15\hfill & & & \hfill 15\hfill \end{ array}[/latex]

Опять же, результаты те же! [латекс]5\cdot 3=3\cdot 5[/латекс]. Порядок, в котором мы умножаем, не имеет значения.

Эти примеры иллюстрируют коммутативные свойства сложения и умножения.

Коммутативные свойства

Коммутативное свойство сложения : если [latex]a[/latex] и [latex]b[/latex] — действительные числа, то

[latex]a+b=b+a[/ латекс]

Коммутативное свойство умножения : если [латекс]а[/латекс] и [латекс]b[/латекс] — действительные числа, то

[латекс]а\cdot b=b\cdot a[/ латекс]

Коммутативные свойства связаны с порядком. Если изменить порядок чисел при сложении или умножении, результат будет тот же.

пример

Используйте коммутативные свойства, чтобы переписать следующие выражения:
1. [латекс]-1+3=[/латекс]
2. [латекс]4\cdot 9=[/латекс]

Решение:

1.
	[латекс]-1+3=[/латекс]
Используйте свойство коммутативности сложения, чтобы изменить порядок.	[латекс]-1+3=3+\влево(-1\вправо)[/латекс]

2.
	[латекс]4\cdot 9=[/латекс]
Используйте свойство перестановочности умножения, чтобы изменить порядок.	[латекс]4\cdot 9=9\cdot 4[/латекс]

 

попробуй

Как насчет вычитания? Имеет ли значение порядок, когда мы вычитаем числа? Дает ли [латекс]7 — 3[/латекс] тот же результат, что и [латекс]3 — 7?[/латекс]

[латекс]\begin{array}{ccc}\hfill 7 — 3\hfill & & \ hfill 3 — 7\hfill \\ \hfill 4\hfill & & \hfill -4\hfill \\ & \hfill 4\ne -4\hfill & \end{array}[/latex]
Результаты не совпадают. [latex]7 — 3\ne 3 — 7[/latex]

Поскольку изменение порядка вычитания не дало того же результата, можно сказать, что вычитание некоммутативно.

Давайте посмотрим, что произойдет, если мы разделим два числа. Является ли деление коммутативным?

[латекс]\begin{array}{ccc}\hfill 12\div 4\hfill & & \hfill 4\div 12\hfill \\ \hfill \frac{12}{4}\hfill & & \hfill \ frac{4}{12}\hfill \\ \hfill 3\hfill & & \hfill \frac{1}{3}\hfill \\ & \hfill 3\ne \frac{1}{3}\hfill & \ конец{массив}[/латекс]

Результаты разные. Итак, [latex]12\div 4\ne 4\div 12[/latex]

Поскольку изменение порядка деления не дало того же результата, деление не является коммутативным.

Сложение и умножение коммутативны. Вычитание и деление не коммутативны.

Предположим, вас попросили упростить это выражение.

[латекс]7+8+2[/латекс]

Как бы вы это сделали и каким был бы ваш ответ?

Некоторые люди думают, что [латекс]7+8\текст{ равен }15[/латекс], а затем [латекс]15+2\текст{ равен }17[/латекс]. Другие могут начинаться с [латекс]8+2\текст{ дает }10[/латекс], а затем [латекс]7+10\текст{ дает }17[/латекс].

Оба способа дают одинаковый результат, как показано ниже. (Помните, что круглые скобки — это символы группировки, указывающие, какие операции следует выполнить в первую очередь.)

При добавлении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство сложения.

Тот же принцип справедлив и для умножения. Предположим, мы хотим найти значение следующего выражения:

[латекс]5\cdot \frac{1}{3}\cdot 3[/latex]

Изменение группировки чисел дает тот же результат.

При умножении трех чисел изменение группировки чисел не меняет результат. Это известно как ассоциативное свойство умножения.

Если мы умножим три числа, изменение группировки не повлияет на произведение.

Вы, наверное, знаете это, но терминология может быть для вас новой. Эти примеры иллюстрируют ассоциативные свойства .

Ассоциативные свойства

Ассоциативное свойство сложения : если [латекс]а,б[/латекс] и [латекс]с[/латекс] — действительные числа, то

[латекс]\влево(а+б\вправо)+ c=a+\left(b+c\right)[/latex]

Ассоциативное свойство умножения : если [latex]a,b[/latex] и [latex]c[/latex] — действительные числа, затем

[latex]\left(a\cdot b\right)\cdot c=a\cdot \left(b\cdot c\right)[/latex]

 

пример

Используйте ассоциативные свойства для перезаписи следующее:

1. [латекс]\влево(3+0,6\вправо)+0,4=[/латекс]
2. [латекс]\влево(-4\cdot \frac{2}{5}\вправо)\cdot 15 =[/latex]

Показать решение

 

попробуйте

Помимо использования ассоциативных свойств для упрощения вычислений, мы часто будем использовать их для упрощения выражений с переменными.

пример

Используйте ассоциативное свойство умножения для упрощения: [латекс]6\влево(3х\вправо)[/латекс].