Сложение и вычитание дробей с разными знаменателями | Материал по математике (6 класс):

Опубликовано 08.11.2020 — 13:52 — Самигуллина Ирина Анaтольевна

Карточки по теме Сложение и вычитание дробей с разными знаменателями 

Скачать:

Предварительный просмотр:

Карточки по теме: Сложение и вычитание дробей с разными знаменателями

Карточка №1 Вычислить:	Карточка №2 Вычислить:	Карточка №3 Вычислить:
Карточка №4 Вычислить:	Карточка №5 Вычислить:	Карточка №5 Вычислить:

По теме: методические разработки, презентации и конспекты

Сложение и вычитание дробей с разными знаменателями.

Цели урока: приобщение учащихся к разнообразным формам и методам изучения материала; воспитание любви к предмету; систематизация и обобщение знаний обучающихся по теме «Сложение и вычитан…

Урок-путешествие по теме «Сложение и вычитание дробей с разными знаменателями»

Цели урока: систематизация знаний учащихся по данной теме;закрепление знаний правил сложения и вычитания обыкновенных дробей с разными знаменателями;развитие интереса учащихся к изучению математ…

Урок алгебры в 8 классе на тему:»Сложение и вычитание дробей с разными знаменателями»

Урок обобщения знаний по данной теме . Урок постройн по плану игры «Кто хочет стать миллионером»….

Урок алгебры в 8 классе по теме:»Сложение и вычитание дробей с разными знаменателями»

Урок обобщения знаний. Конспект урока построен в виде игры «Кто хочет стать миллионером». Три не сгораемые оценки……

Сложение и вычитание дробей с разными знаменателями

Урок по изучению нового материала с применением модулей ЦОР. Конспект урока представлен ввиде технологической карте….

Конспект урока в 6 классе «Основное свойство дроби. Сложение и вычитание дробей с разными знаменателями»

Обобщающий урок…

Зачетная работа по алгебре 8 класс по теме «Сложение и вычитание дробей с разными знаменателями. Умножение и деление дробей»

Работа состоит из 6 блоков по 10 заданий и охватывает все дейтвия с дробями….

Поделиться:

 

Сложение и вычитание обыкновенных дробей с разными знаменателями

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике.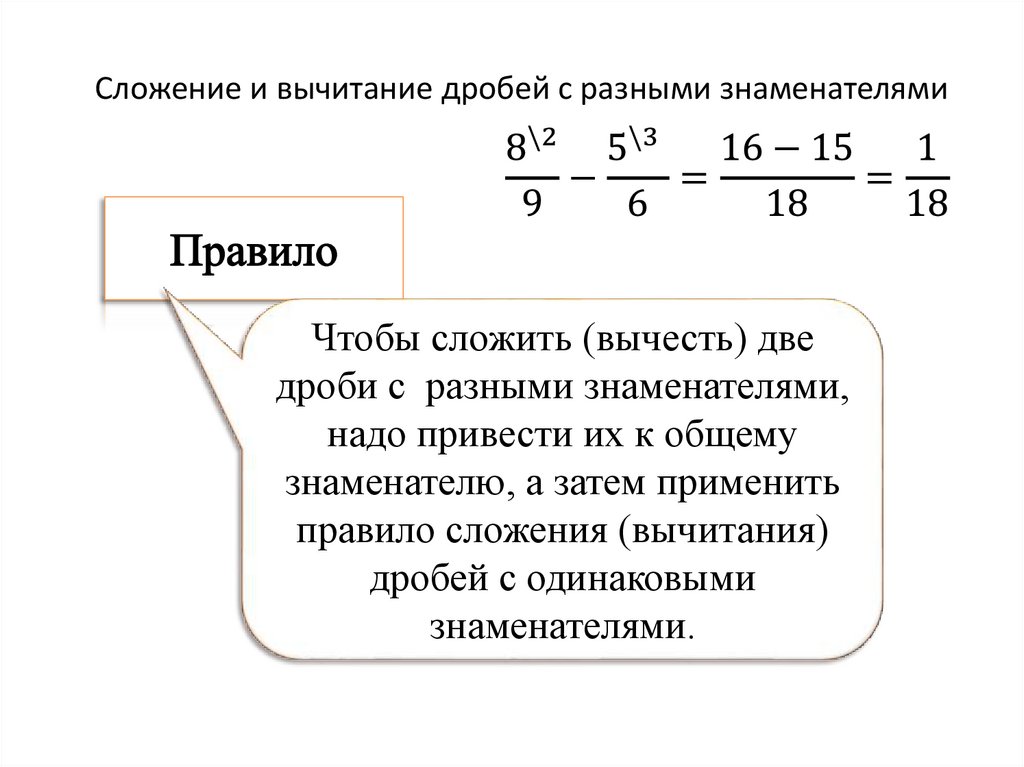

Базовый уровень Сложные задачи

1. Сложение и вычитание обыкновенных дробей с разными знаменателями

15 14
17 15
4 11
9 27
Сложение и вычитание
обыкновенных дробей с
разными знаменателями
4 1
11 2
1 7
4 8
11 7
13 2
с.Городок, 2010 – 2011 гг.

2. Самостоятельная работа

Вариант 1
Найдите сумму дробей 3 è 1
Напишите правило
вычитания дробей с
одинаковыми
знаменателями
7
2.
Вычислите разность
единицы и дроби 2
3.
Найдите разность дробей
4.
13
7 1
è
8 8
7
1.
5
6
è
11 11
Сумму дробей
уменьшите на число
5 3
è
9 9
5.
3
10
Вариант 2
7
Найдите разность 1 è
15
Напишите правило
сложения дробей с
одинаковым
знаменателем
Вычислите сумму
дробей 2 è 3
10 10
Найдите разность дробей
7
2
è
Разность дробей 15 15
увеличьте на число
2
3

3.

Оценки за самостоятельную работуПравильно выполнено 5 заданий оценка 5
Правильно выполнено 4 заданий оценка 4
Правильно выполнено 3 заданий оценка 3

4. Ответы к самостоятельной работе

Вариант 1
1.
4
7
2. Чтобы выполнить вычитание
дробей с одинаковыми
знаменателями, надо из
числителя уменьшаемого
вычесть числитель
вычитаемого, а знаменатель
оставить без изменения.
3.
11
13
6 3
8 4
11 3
3 10 3
7
1
5.
11 10
10 10 10 10
4.
1.
8
15
Вариант 2
2. Чтобы выполнить сложение
дробей с одинаковыми
знаменателями, надо сложить
их числители, а знаменатель
оставить без изменения.
5 1
3.
10 2
3 1
4.
9 3
5. 5 2 1 2 3 1
15 3 3 3 3

5. Повторение

1.
Выполните действия
2
5
5 2
4 7
18 15
;
;
;
10 10 7 7 13 13 31 31
2.
Сравните дроби
7 5
4 4
è ;
è ;
9 9 10 7
3 5
è ;
4 8
7 2
è .
9 3

6. Изучение нового материала

Вычислите, в случае
затруднений
воспользуйтесь
рисунком:
5 2
8 4
8 4
16 8
Найдите значения выражений
9 3
9
6 9 6 15
5
1
1 1
10 5 10 10
10
10
10
2
7 2 5
7 1
8 4
8 8 8

8. Правила сложения и вычитания обыкновенных дробей с разными знаменателями

Для того чтобы выполнить сложение (вычитание) дробей
с разными знаменателями, надо:
привести их к общему знаменателю;
сложить (вычесть) полученные дроби, используя правило
сложения (вычитания) дробей с одинаковым знаменателем;
в полученном результате, если это возможно, выполнить
сокращение дроби или выделить целую часть.
3
5
9 20 9 20 29
5
1
8
6 24 24
24
24
24
3
4
Число, которое надписывают над дробью, называют
дополнительным множителем, на него умножают числитель и
знаменатель дроби.

9. Задания на закрепление

№440, №441, №445
1
2
Закрасьте
синим цветом, 14 красным, 18 — желтым, 161 — зеленым.
Какая часть фигуры осталась
незакрашенной? Какая часть
закрашена? Составьте примеры для
задания.
Резервное задание: №434.

10. Это интересно

1 1 1 3 2 1 6
1
2 3 6 6 6 6 6
Аликвотные дроби – числитель равен 1
1 целая – мама, у которой
1
Красоты 6 1
Мудрости 13
Терпения 2

11. Подведение итогов

Ответьте письменно на вопросы:
Достигли ли вы цели урока «Знакомство с
правилами сложения и вычитания дробей с
разными знаменателями»?
Что вам понравилось на уроке? Что не
понравилось?
С какими трудностями столкнулись? Смогли ли
вы их преодолеть?
Какую бы оценку за работу на уроке вы
поставили?

12. Домашнее задание

Прочитать материал параграфа с. 122
Выучить правила сложения и вычитания
дробей с разными знаменателями
Выполнить задания № 442, № 444
Спасибо, за работу на уроке!
Молодцы!

English     Русский Правила

Сложение дробей с разными знаменателями

Звук:

Вы знаете, что ½ + ½ = 1.

• Что такое ½ + ¼?

• Вы умеете складывать дроби с разными знаменателями?

Дроби показывают часть целого.

Верхнее число числитель . Нижнее число знаменатель .

Чтобы сложить дроби, мы должны сначала посмотреть на знаменатель. Если знаменатель в двух дробях один и тот же, мы можем просто сложить числители и оставить знаменатель одинаковым.

• Что произойдет, если знаменатели двух дробей различны?

Посмотрите на две дроби ниже:

• Вы видите, что синяя и красная секции имеют разные размеры?

Мы не можем сложить две дроби с разными знаменателями. Итак, мы должны найти общий знаменатель, чтобы сделать их одинаковыми.

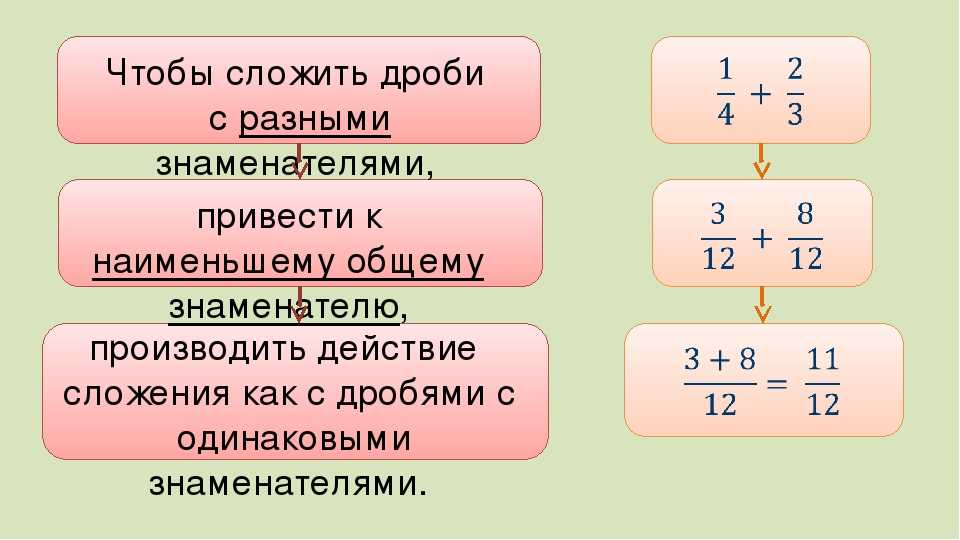
Чтобы сложить дроби с разными знаменателями, выполните следующие действия:

Шаг 1: Найдите общий знаменатель.

В приведенной выше модели первая коробка разделена на две части. Вторая коробка разделена на четыре части.

Мы можем использовать нашу картинку для создания одинаковых единиц для каждой дроби:

Разделите первую коробку на четыре части, как вторую. Разделите вторую коробку на две части, как и первую коробку.

Теперь мы можем подсчитать заштрихованные единицы.

Из восьми частей в первой рамке четыре части заштрихованы. Наша дробь ⁴ ⁄ ₈ .

Из восьми частей второго блока две части заштрихованы. Наша дробь равна ² ⁄ ₈ .

Шаг 2: Добавьте числители.

4 + 2 = 6

Шаг 3: Оставьте знаменатель прежним.

Наш ответ: ⁶ ⁄ ₈ .

Шаг 4: Упрощение.

Шесть и восемь можно разделить на два, поэтому мы можем упростить эту дробь:

	6	→ ÷ 2 →	3
	8	→ ÷ 2 →	4

 

Теперь мы рассмотрим другую стратегию сложения дробей с разными знаменателями.

Эта стратегия будет использовать наименьшее общее кратное (НОК) для поиска общих знаменателей.

Посмотрите на дроби ниже:

	1	+	1
	3		6

 

У них разные знаменатели, поэтому их пока нельзя складывать.

Шаг 1: Найдите общий знаменатель.

Сначала мы перечислим кратные для каждого знаменателя.

Помните, что кратные — это числа, которые вы получите, если умножите данное число на каждое целое число или пропустите счет.

Кратные 3:

3, 6, 9, 12, 15, 18

Кратные 6:

6, 12, 18, 24, 30, 36

Далее обратите внимание на любые общие кратные:

3 и 6 имеют общие кратные 6 и 12.

Однако 6 является наименьшим, поэтому это НОК, и он станет нашим общим знаменателем.

Преобразуем ¹ / ₃ в дробь со знаменателем 6.

Мы знаем, что 3 x 2 даст нам 6. Затем умножим верх и низ дроби на одно и то же число, что в это дело 2:

Далее замените ¹ / ₆ на дробь со знаменателем 6.

Подождите! У этой дроби уже есть знаменатель 6, поэтому все, что нам нужно сделать, это умножить верх и низ на 1:

Шаг 2: Сложите числители.

2 + 1 = 3

Шаг 3: Оставьте знаменатель прежним.

Наш ответ: ³ ⁄6.

Шаг 4: Упрощение.

Три и шесть можно разделить на три, поэтому мы можем упростить эту дробь:

	3	→ ÷ 3 →	1
	6	→ ÷ 3 →	2

---

Знаменатель показывает количество равных частей в целом. Нельзя складывать две дроби, если у них разные знаменатели.

Вот почему важно найти наименьший общий знаменатель, прежде чем складывать дроби.

Чтобы попрактиковаться, перейдите к Понял? раздел!

Как складывать дроби с разными знаменателями для детей? Пошаговое объяснение для детей

При сложении дробей числители складываются, а знаменатель остается постоянным. Сложение с теми же знаменателями — не сложная задача. Проблема возникает, когда дроби имеют разные знаменатели, потому что нам нужны одни и те же знаменатели для сложения.

Перед тем, как приступить к внутренней теме, нам нужно понять, что такое дробь, подобная и непохожая дробь и как преобразовать непохожую дробь в подобную дробь.

Читайте также: Ведические математические хитрости для детей: инновационный способ изучения математики

Фракция для детей пытается объяснить, как работать с фундаментальной математикой с ее помощью. Это также один из важных навыков в высшей математике.

Таким образом, дети должны быть в состоянии полностью осознать эту идею и осуществить то же самое, когда придет время.

Объясняемые дроби — это не что иное, как части суммы, используемые для представления меньших частей большей вещи.

Части могут даже составлять свои номера, но вместе они составляют цельную картину.

Три

Части дроби

Три части дроби:

Числитель: верхняя часть дроби, число над разделительной чертой.

Знаменатель: младшая часть дроби, число под разделительной чертой.

И Разделительная линия: Это маленькая линия, которая разделяет числитель и знаменатель.

Например, вы испекли 8 кусочков вашего любимого шоколадного торта. Поскольку вы не уверены во вкусе своего шоколадного торта, вы решили поделиться 4 кусочками со своим другом, чтобы узнать, как он готовится.

В математической форме это записывается как 4/8, где 4 в числителе над разделительной линией и 8 в знаменателе под разделительной линией.

Подобные

Дроби

Дроби с разными числителями и одинаковыми знаменателями называются подобными дробями. Их можно легко добавить.

Примеры: (1/4, 2/4, 3/4) и (2/5, 1/5, 4/5).

В отличие от

Дроби

Дроби с разными числителями и разными знаменателями называются В отличие от дробей. Перед сложением их нужно преобразовать в одинаковые дроби.

Примеры: (1/2, 3/4, 1/5) и (3/6, 2/7, 5/8).

Как

преобразовать одинаковые дроби в разные дроби?

Чтобы преобразовать непохожую дробь в подобную дробь, мы должны рассмотреть наименьшее общее кратное знаменателей, а затем найти эквивалентные дроби, умножив их, чтобы получить L.C.M в качестве знаменателя.

Например, 2/4 и 1/3 не являются дробями, здесь наименьшее общее кратное 4 и 3 равно 12. Теперь нам нужно найти дроби, эквивалентные 2/4 и 1/3, у которых 12 в знаменателе . Умножьте числитель и знаменатель 2/4 на 3, а числитель и знаменатель 1/3 умножьте на 4.

Таким образом, 6/12 и 4/12 подобны дробям с одинаковыми знаменателями.

Читайте также:  Как сделать математическую игру для детей? Полное руководство, как сделать так, чтобы ваш ребенок сиял в математике

Сложение

непохожих дробей

Вот пошаговая процедура сложения дробей с разными знаменателями.

Для начала нам нужно преобразовать непохожие дроби в подобные дроби.

# Шаг 1: Найдите наименьшее общее кратное всех знаменателей разнородных членов.

# Шаг 2: Умножьте числитель и знаменатель непохожего члена так, чтобы знаменатель был равен наименьшему общему кратному. Повторите то же самое для всех непохожих терминов.

# Шаг 3: Сохраняя знаменатели постоянными, добавьте числители одинаковых членов. Отсюда вычисляется сумма дробей.

Посмотрите приведенные ниже примеры решений и проанализируйте шаги, на которых решается проблема.

Пример

1

1/2+3/5

# Шаг 1. Наименьшее общее кратное знаменателей, равных 2 и 5, равно 10.

# Шаг 2. Найдите эквивалентные дроби 1/2 и 3/5 со знаменателем 10, умножьте числитель и знаменатель 1/2 на 5 и умножьте числитель и знаменатель 3/5 на 2.

# Шаг 3: Сложите эквивалентные дроби: 5/10 + 6/10 = 11/10.

# Шаг 4: Следовательно, сумма данных различных слагаемых 1/2 и 3/5 равна 11/10.

Пример

2

1/6+2/4

# Шаг 1. Наименьшее общее кратное знаменателей, равных 6 и 4, равно 24.

# Шаг 2. Найдите эквивалентные дроби 1/6 и 2/4 со знаменателем 24, умножьте числитель и знаменатель 1/6 на 4 и умножьте числитель и знаменатель 2/4 на 6.

# Шаг 3: Сложите эквивалентные дроби: 4/24 + 12/24 = 16/24.

# Шаг 4: Следовательно, сумма данных различных слагаемых 1/6 и 2/4 равна 16/24.

Как

объяснять дроби для детей?

Терпение и мотивация являются наиболее важными вещами, когда вы пытаетесь непредвзято относиться к трудностям, с которыми сталкиваются дети. Дети нуждаются в должном внимании и уважении. Поощрение ребенка со всей поддержкой — это все, что требуется для улучшения его светлого будущего.

Вот несколько способов, которыми вы можете отвлечь внимание ребенка от предмета и следить за тем, чтобы он не отставал от обсуждаемой темы, что является дробью для детей-

# Надлежащее руководство и поддержка необходимы для того, чтобы направлять ребенка вдоль пути.