C++ | Арифметические операции
Последнее обновление: 09.02.2023
Арифметические операции производятся над числами. Значения, которые участвуют в операции, называются операндами. В языке программирования C++ арифметические операции могут быть бинарными (производятся над двумя операндами) и унарными (выполняются над одним операндом). К бинарным операциям относят следующие:
+
Операция сложения возвращает сумму двух чисел:
int a {10}; int b {7}; int c {a + b}; // 17 int d {4 + b}; // 11В этом примере результат операций применяется для инициализации переменных, но мы также можем использовать операцию присвоения для установки значения переменных:
int a {10}; int b {7}; int c = a + b; // 17 int d = 4 + b; // 11—
Операция вычитания возвращает разность двух чисел:
int a {10}; int b {7}; int c {a - b}; // 3 int d {4 - b}; // -3*
Операция умножения возвращает произведение двух чисел:
int a {10}; int b {7}; int c {a * b}; // 70 int d {4 * b}; // 28/
Операция деления возвращает частное двух чисел:
int a {26}; int b {5}; int c {a / b}; // c = 5 int d {4 / b}; // d = 0При делении стоит быть внимательным, так как если в операции участвуют два целых числа, то дробная часть (при ее наличии) будет отбрасываться, даже если результат присваивается переменной
floatилиdouble:#include <iostream> int main() { int a {26}; int b {5}; float c {a / b}; // c = 5 double d {4 / b}; // d = 0 std::cout << "c = " << c << std::endl; std::cout << "d = " << d << std::endl; }Чтобы результат представлял число с плавающей точкой, один из операндов также должен представлять число с плавающей точкой:
#include <iostream> int main() { float a {26}; int b {5}; float c {a / b}; // c = 5. 2
double d {4.0 / b}; // d = 0.8
std::cout << "c = " << c << std::endl;
std::cout << "d = " << d << std::endl;
}
2
double d {4.0 / b}; // d = 0.8
std::cout << "c = " << c << std::endl;
std::cout << "d = " << d << std::endl;
}
%
Операция получения остатка от целочисленного деления:
int a {26}; int b {5}; int c {a % b}; // c = 26 % 5 = 26 - 5 * 5 = 1 int d {4 % b}; // d = 4 % 5 = 4
Некоторые особенности при работе с числами с плавающей точкой
При сложении или вычитании чисел с плавающей точкой, которые сильно отличаются по значению, следует проявлять осторожность. Например, сложим число 0.000123) и
3.65E+6 (3650000). Мы ожидаем, что сумма будет равна 3650000,000123. Но при преобразовании в число с плавающей запятой
с точностью до семи цифр это становится следующим
3.650000E+06 + 1.230000E-04 = 3.650000E+06
Или соответствующий код на С++:
#include <iostream>
int main()
{
float num1{ 1. 23E-4 }; // 0.000123
float num2{ 3.65E+6 }; // 3650000
float sum {num1 + num2}; // sum =3.65e+06
std::cout << "sum =" << sum << "\n";
}
23E-4 }; // 0.000123
float num2{ 3.65E+6 }; // 3650000
float sum {num1 + num2}; // sum =3.65e+06
std::cout << "sum =" << sum << "\n";
}
То есть первое число никак не изменилось, поскольку для хранения точности отводится только 7 цифр.
Также стоит отметить, что стандарт IEEE, который реализуется компиляторами С++, определяет специальные значения для чисел с плавающей точкой, в которых мантисса на бинарном уровне состоит только из нулей, а экспонента,
которая состоит из одних единиц, в зависимости от знака представляет значения +infinity (плюс бесконечность +∞) и -infinity (минус бесконечность -∞).
И при делении положительного числа на ноль, результатом будет +infinity, а при делении отрицательного числа на ноль — -infinity.
Другое специальное значение с плавающей точкой, определенное этим стандартом, представляет значение NaN (не число). Это значение
представляет результат операции, который не определяется математически, например, когда ноль делится на ноль или бесконечность на бесконечность. Результатом любой операции, в которой один или оба операнда являются
Это значение
представляет результат операции, который не определяется математически, например, когда ноль делится на ноль или бесконечность на бесконечность. Результатом любой операции, в которой один или оба операнда являются NaN.
Для демонстрации рассмотрим следующую программу:
#include <iostream>
int main()
{
double a{ 1.5 }, b{}, c{}, d {-1.5};
double result { a / b };
std::cout << a << "/" << b << " = " << result << std::endl;
result = d / c;
std::cout << d << "/" << c << " = " << result << std::endl;
result = b / c;
std::cout << b << "/" << c << " = " << result << std::endl;
std::cout << result << " + " << a << " = " << result + a << std::endl;
}
В выражении a / b число 1. 5 делится на 0, поэтому результатом будет плюс бесконечность.
5 делится на 0, поэтому результатом будет плюс бесконечность.
Аналогично в выражении d / c число -1.5 делится на 0, поэтому результатом будет минус бесконечность.
В выражении b / c число 0 делится на 0, поэтому результатом будет NaN.
Соответственно последнее выражение result + a будет аналогично NaN + 0, соответственно результатом тоже будет NaN
Консольный вывод программы
1.5/0 = inf -1.5/0 = -inf 0/0 = nan nan + 1.5 = nan
Инкремент и декремент
Также есть две унарные арифметические операции, которые производятся над одним числом: ++ (инкремент) и — (декремент). Каждая из операций имеет две разновидности: префиксная и постфиксная:
Префиксный инкремент.
Увеличивает значение переменной на единицу и полученный результат используется как значение выражения ++x
#include <iostream> int main() { int a {8}; int b {++a}; std::cout << "a = " << a << std::endl; // a = 9 std::cout << "b = " << b << std::endl; // b = 9 }Постфиксный инкремент.

Увеличивает значение переменной на единицу, но значением выражения x++ будет то, которое было до увеличения на единицу
#include <iostream> int main() { int a {8}; int b {a++}; std::cout << "a = " << a << std::endl; // a = 9 std::cout << "b = " << b << std::endl; // b = 8 }Префиксный декремент.
Уменьшает значение переменной на единицу, и полученное значение используется как значение выражения —x
#include <iostream> int main() { int a {8}; int b {--a}; std::cout << "a = " << a << std::endl; // a = 7 std::cout << "b = " << b << std::endl; // b = 7 }Постфиксный декремент.
Уменьшает значение переменной на единицу, но значением выражения x— будет то, которое было до уменьшения на единицу
#include <iostream> int main() { int a {8}; int b {a--}; std::cout << "a = " << a << std::endl; // a = 7 std::cout << "b = " << b << std::endl; // b = 8 }
Приоритет и ассоциативность операторов
Операторы могут быть левоассоциативными — такие операторы выполняются слева направо и правоассоциативными — выполняются справа налево. Подавляющее большинство операторов левоассоциативны (например, бинарные арифметические операции), поэтому большинство выражений
оценивается слева направо. Правоассоциативными операторами являются все унарные операторы,
различные операторы присваивания и условный оператор.
Подавляющее большинство операторов левоассоциативны (например, бинарные арифметические операции), поэтому большинство выражений
оценивается слева направо. Правоассоциативными операторами являются все унарные операторы,
различные операторы присваивания и условный оператор.
Кроме того, одни операции имеют больший приоритет, чем другие и поэтому выполняются вначале. Операции в порядке уменьшения приоритета:
| + (инкремент), — (декремент) |
| * (умножение), / (деление), % (остаток от деления) |
| + (сложение), — (вычитание) |
Приоритет операций следует учитывать при выполнении набора арифметических выражений:
int a = 8; int b = 7; int c = a + 5 * ++b; // 48
Хотя операции выполняются слева направо, но вначале будет выполняться операция инкремента ++b, которая увеличит значение переменной
b и возвратит его в качестве результата, так как эта операция имеет больший приоритет.
5 * ++b,
и только в последнюю очередь выполняется сложение a + 5 * ++bСледует учитывать, что если в одной инструкции для одной переменной сразу несколько раз вызываются операции инкремента и декремента, то результат может быть неопределенным, и много зависит от конкретного компилятора. Например:
int count {1};
int result = ++count * 3 + count++ * 5;
Так, и g++, и clang++ скомпилируют данный код, и результат переменной result будет таким, как в принципе и ожидается — 16, но компилятор clang++ также сгенерирует предупреждение.
Переопределение порядка операций
Скобки позволяют переопределить порядок вычислений. Например:
#include <iostream>
int main()
{
int a {8};
int b {7};
int c {(a + 5) * ++b}; // c = 104
std::cout << "c = " << c << std::endl;
}
Несмотря на то, что операция сложения имеет меньший приоритет, но вначале будет выполняться именно сложение, а не умножение, так как операция сложения заключена в скобки.
НазадСодержаниеВперед
Хорошо, но ПОЧЕМУ умножение/деление предшествует сложению/вычитанию? — Фактические вопросы
РикДжей 1
То есть я знаю, что да. Я знаю, что это
Скобки/круглые скобки (зависит от того, где вы живете)
Экспоненты/порядки (зависит)
Деление
Умножение
Сложение
Вычитание
Я вижу смысл иметь скобки, так как тогда вы можете изменить порядок и экспоненты net, но почему перед сложением и вычитанием поставили div/multiply? Есть ли в этом преимущество? Или просто так случайно выбрали?
Тадлоу_Боинк 2
То, что умножение предшествует сложению, является соглашением, то есть оно было выбрано таким образом. Но не случайно. Это упрощает работу с математическими выражениями и делает их менее неудобными благодаря свойствам сложения и умножения, которые не являются просто условными, например, тот факт, что умножение распределяется по сравнению с сложением.
Но не случайно. Это упрощает работу с математическими выражениями и делает их менее неудобными благодаря свойствам сложения и умножения, которые не являются просто условными, например, тот факт, что умножение распределяется по сравнению с сложением.
Кимсту 3
Досовременное использование порядка операций могло быть обусловлено очень древними особенностями построения числовых слов. Мы говорим, например, «четыреста двадцать девять», т. е. четыре сотни и два десятка и девять единиц. Мы не складываем вместе сто, десять и единицу, а затем умножаем сумму на что-то.
Таким образом, соглашение об «умножении перед сложением» может иметь корни в элементарных аспектах объединения групп различных мер.
Тадлоу_Боинк 4
О, это проницательно! Теперь, когда вы упомянули об этом, я вижу параллель между выражением вроде «Есть три семерки и четыре девятки» (т. е. 3\cdot7 + 4\cdot9) и выражением вроде «Есть три кошки и четыре собаки» или даже «Есть черные кошки и коричневые собаки».
Сенегоид 5
В некоторых задачах из реальной жизни возникает «сумма произведений». То есть у вас есть куча пар чисел, вы умножаете два числа в каждой паре, а затем складываете эти произведения. Оказывается, эта модель операций встречается в огромном количестве контекстов. Напротив, я не думаю, что «произведение сумм» встречается почти так часто.
Как упоминалось выше, этот порядок операций является просто стандартизированным соглашением, принятым потому, что он полезен. Для этого нет внутренней математической причины. Заметьте также, что необходимость указывать порядок операций необходима, прежде всего, из-за нашей традиционной фиксированной нотации для арифметических выражений. Существуют и другие обозначения для арифметики, в частности польское (префиксное) обозначение и обратное польское (постфиксное) обозначение, в которых операции просто выполняются в том порядке, в котором они записываются слева направо. Никакого БЕДЛАМА с этим!
Для этого нет внутренней математической причины. Заметьте также, что необходимость указывать порядок операций необходима, прежде всего, из-за нашей традиционной фиксированной нотации для арифметических выражений. Существуют и другие обозначения для арифметики, в частности польское (префиксное) обозначение и обратное польское (постфиксное) обозначение, в которых операции просто выполняются в том порядке, в котором они записываются слева направо. Никакого БЕДЛАМА с этим!
Сенегоид 6
Вот два примера распространенных задач из реальной жизни, связанных с суммой продуктов:
(1) Суммирование счета за продукты:
Вы покупаете 6 банок бобов по 1,38 каждая; десяток лимонов по 0,30 каждый; и 2 бутылки молока по 3,89 каждая. Сколько это стоит?
Вы умножаете количество каждого предмета на количество каждого предмета (это продукты), затем складываете их (сумма этих продуктов):
( 6 * 1,38 ) + ( 12 * 0,30 ) + ( 2 * 3,89 ) = 19,66
Обратите внимание, что круглые скобки в приведенном выше примере избыточны из-за правил BEDMAS, но их всегда полезно включать, чтобы сделать их явными. Именно для таких расчетов и были созданы правила BEDMAS!
Именно для таких расчетов и были созданы правила BEDMAS!
(2) Этот расчет близок и дорог сердцу всех учащихся средних школ и колледжей: ваш средний балл.
Общая процедураУмножьте вашу оценку в каждом классе (число от 0 до 4 в большинстве распространенных систем) на количество единиц в этом классе. Это произведения, которые представляют собой количество баллов для каждого класса.
Затем сложите их, чтобы получить общее количество баллов (это сумма этих произведений).
Затем также сложите общее количество юнитов всех ваших классов, чтобы получить общую загрузку юнитов. Затем разделите общее количество баллов на это, и вы получите средний балл. Снова обратите внимание на «сумму продуктов» в этом расчете.
Вот еще один пример, с которым вы все знакомы, даже если не знаете его: определение центра тяжести загруженного самолета. Это очень важно: центр тяжести должен находиться в очень узком диапазоне, иначе ваш самолет не оторвется от земли (или, что еще хуже, оторвется от земли, но будет очень неустойчив в воздухе). Есть рабочие листы, где вы указываете положение всех ваших пассажиров и их вес, положение и вес любого багажа, количество и вес топлива на борту и, возможно, даже количество и вес моторного масла. Затем следует определенная последовательность вычислений для вычисления положения центра тяжести. И угадайте, что: это включает в себя сумму продуктов!
Есть рабочие листы, где вы указываете положение всех ваших пассажиров и их вес, положение и вес любого багажа, количество и вес топлива на борту и, возможно, даже количество и вес моторного масла. Затем следует определенная последовательность вычислений для вычисления положения центра тяжести. И угадайте, что: это включает в себя сумму продуктов!
И как получилось, что вы уже знаете эту процедуру, даже если не знаете, что знаете ее? Потому что шаги точно такие же, шаг за шагом, как и при подсчете среднего балла! Оба этих расчета являются лишь примерами средневзвешенного значения , которое используется во многих ситуациях.
боб_2 7
Это сделано для того, чтобы люди могли публиковать посты/приманки на Facebook с глупыми математическими задачами, предназначенными для того, чтобы сбить с толку неосторожных и заставить некоторых людей почувствовать свое превосходство.
наита 8
В большинстве повседневных ситуаций порядок довольно очевиден из контекста. Если у вас есть список количества и цен на товары, вы умножаете количество на цену, а затем суммируете. Если у вас есть список длин сторон вашего забора, и вам нужно по три доски на каждую сторону, вы складываете длины, а затем умножаете на два. Вы, вероятно, не беспокоитесь о скобках, вы просто пишете большой X2, и вы знаете, что вы имели в виду.
Я думаю, условность исходит из уравнений. У нас много выражений типа 2x + 3y и 2(3x + y). При обратном порядке операций они были бы (2x) + (3y) и 2(3x) + y. И без порядка операций (2x) + (3y) и 2((3x) + y). Скобок было бы намного больше.
Игнорирование подразумеваемого умножения, идея о том, что 2x понимается как 2*x. У нас могло быть сложение/вычитание перед умножением, но подразумевалось умножение перед любым из них.
Хари_Селдон 9
Все это иллюстрирует, почему RPN проще и почему я считаю, что калькулятор RPN проще в использовании. Однозначно, 3,4,5+\times=27, а 3,4,5\times+=60. Запятые обозначают клавишу ввода на калькуляторе. Скобки никогда не нужны, не нужны,
Другой момент заключается в том, что любой, кто пишет 3+4\умножить на 5, просит, чтобы его неправильно поняли. Любой математик использовал скобки.
RayMan 10
Хари_Селдон:
Однозначно [. . .] 3, 4, 5 \раз + = 60
Нет.
Получеловек_Полуразум 11
Хм, я всегда думал, что это потому, что обычно умножение (над натуральными числами) определяется рекурсивно в терминах сложения. Таким образом, x\cdot S(y), где S() — функция-преемник, задается как x+x\cdot y, что вместе с x\cdot 0 = 0 позволяет однозначно разрешать любое умножение с точки зрения повторного сложения. . Таким образом, в этом смысле 3+4\cdot 5 можно свести к 3 + 4 + 4 + 4 + 4 + 4,9.y в \underbrace{x\cdot x \cdot \ldots \cdot x}_{\text{y times}}, которые затем можно разложить на суммы.
Хари_Селдон 12
RayMan:
Нет.
23.
Сенегоид 13
Возможная проблема с RPN: я подумал о том, можно ли переписать всю алгебру, используя RPN вместо традиционных обозначений, и решил, что это тоже не сработает.
Одна особая проблема заключается в обозначении деления: Традиционное обозначение использует числитель сверху, горизонтальную черту под ним и знаменатель под ним. Это позволяет довольно легко обнаружить общие множители в числителе и знаменателе, которые затем можно «отменить». Это сложнее увидеть, если все это написано с использованием RPN.
Хронос 14
Вы можете или не можете писать алгебру, используя польскую нотацию, но когда вы делаете вычисления, вы почти всегда делаете это. Может показаться, что вы используете другие методы, но в основном они преобразуются в польский язык. Вот почему использование польского языка в первую очередь более эффективно: никаких преобразований не требуется.
Вот почему использование польского языка в первую очередь более эффективно: никаких преобразований не требуется.
Порядок действий ч.2 — УРОКИ МАТЕМАТИИ КЕЙТ
Порядок действий Страница 2 из 4
Давным-давно математики разработали набор правил для упрощения выражений. Они решили, что все будут следовать одному и тому же порядку, чтобы упростить задачу. Если у вас есть выражение с более чем одной операцией, вам нужно следовать следующему порядку: Простой способ запомнить порядок — запомнить фразу « Пожалуйста, извините, моя дорогая тетя Салли 9».0152 » или запомнить аббревиатуру PEMDAS . Есть несколько разных способов описать порядок операций. Например, некоторые учителя могут сказать «Квадратные скобки» вместо «Скобки» или «Индексы» вместо «Экспоненты». Давайте рассмотрим шаги более подробно. Шаг 1. Круглые скобки — это всего лишь один из способов группировки. Вы также можете увидеть квадратные скобки, такие как [ ] или { }. Операции внутри любого из этих группирующих символов должны выполняться в первую очередь. Если имеется более одного типа круглых скобок или квадратных скобок, сначала упростите то, что находится внутри самых внутренних, а затем переходите к внешним. Шаг 2: Показатель степени (или корни) Некоторые учителя, особенно в Европе, называют этот шаг «Приказами». Порядки такие же, как и экспоненты. |
 2
double d {4.0 / b}; // d = 0.8
std::cout << "c = " << c << std::endl;
std::cout << "d = " << d << std::endl;
}
2
double d {4.0 / b}; // d = 0.8
std::cout << "c = " << c << std::endl;
std::cout << "d = " << d << std::endl;
}
 23E-4 }; // 0.000123
float num2{ 3.65E+6 }; // 3650000
float sum {num1 + num2}; // sum =3.65e+06
std::cout << "sum =" << sum << "\n";
}
23E-4 }; // 0.000123
float num2{ 3.65E+6 }; // 3650000
float sum {num1 + num2}; // sum =3.65e+06
std::cout << "sum =" << sum << "\n";
}

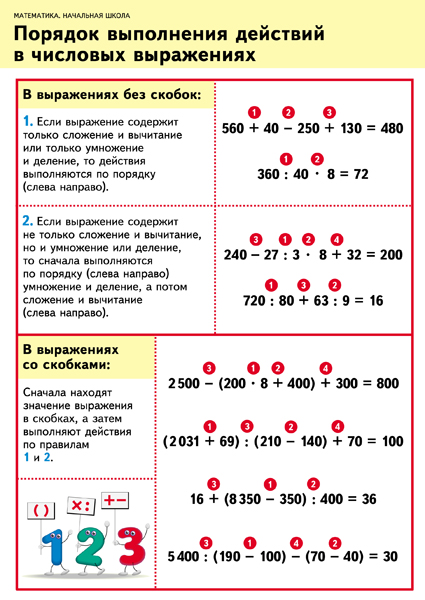 Скобки (или другие символы группировки)
Скобки (или другие символы группировки)