Конспект урока «Сложение и вычитание десятичных дробей и целых чисел» 8 класс
Государственное казенное образовательное учреждение Пензенской области «Сердобская школа – интерната для обучающихся по адаптированным образовательным программам»3.
Должность
учитель
4.
Предмет
математика
5.
Класс
8
6.
Тема урока
Сложение и вычитание десятичных дробей и целых чисел.
7.
Базовый учебник
Математика. 8 класс. Учеб. Для специальных (коррекц.) образоват. Учреждений 8 вида / В.В.Эк. – 9-ое изд. – М.: Просвещение, 2013.
Цель урока: обобщение и систематизация знаний, умений, навыков учащихся при выполнении арифметических действий с десятичными дробями.
Задачи:
Образовательная
Воспитательная: установить связь материала урока с жизнью и практической деятельностью, использовать знания в новых условиях, воспитывать адекватную самооценку и коммуникативные качества личности.
Коррекционная: коррекция логического мышления учащихся на основе решения арифметических задач, развитие речи в ходе ответов на вопросы учителя.
Здоровье сберегающие: способствовать сохранению здоровья учащихся через создание оптимальных условий работы на уроке.
Тип урока: обобщение и систематизация знаний, умений, навыков.
Формы работы обучающихся: фронтальная, работа в парах, индивидуальная, работа на доске и в тетрадях.
Оборудование: компьютер, мультимедийный проектор, экран, карточки для самостоятельной работы.
Методы и приемы работы:
— объяснение
— работа с учебником
— устный контроль
— письменный контроль
Ход урока.
Виды деятельности.
Деятельность учителя.
Деятельность учащихся.
Какие задачи решались в ходе выполнения заданий.
Индивидуальная работа.
Организационный момент
Приветственное слово учителя.
Громко прозвенел звонок –
Начинается урок.
Ваши ушки на макушке,
Глазки широко раскрыты.
Слушайте, запоминайте,
Ни минуты не теряйте!
На уроке наши глаза внимательно смотрят и все … (видят).
Уши внимательно слушают и всё …(слышат).
Голова хорошо … (думает).
Я желаю вам успехов на уроке!
Приветствует учеников, Проверка готовности учащихся к уроку (тетрадь, учебник, дневник, ручка, карандаш, линейка).
Приветствуют учителя, проверяют подготовку рабочих мест. Рапорт дежурного.
Создание психологического настроя.
Проверка домашнего задания.
«Найди ошибку»
Слайд№1
Отвечают на вопросы учителя.
Устный счет.
Слайд №2
Прочитайте дроби.
— Как называются эти дроби? (десятичные дроби)
— Прочитайте по цепочке.
Слайд №3Замените целые числа, полученными при измерении десятичными дробями.
Отвечают на вопросы.
Активизация внимания учащихся.
Развитие навыков устного счёта.
Актуализация опорных знаний учащихся.
Давайте вспомним, как же мы выполняем сложение и вычитание целых чисел?
24р56к – 3р 8к
Давайте вспомним правило сложения и вычитания десятичных дробей.
88,32 + 5,003
Кто мне скажет, какая тема сегодняшнего урока?
Учащиеся проговаривают правило, решают пример у доски.
Учащиеся проговаривают правило, решают пример у доски.
Учащиеся проговаривают правило, решают пример у доски.
Развитие памяти и речи учащихся.
Сложение целых чисел
2 346 + 3459
7845 — 2310
Сообщение темы урока
Решение примеров.
Решение уравнений.
Слайд №4
А теперь открываем тетради, записываем сегодняшнюю дату. Какое сегодня число? Какой день недели? Какой месяц? Какой по счету месяц февраль? Какой сейчас год?
Стр. 140 №369 – 2 ст.
Х + 12 648 = 20 010
8т15кг + Х = 10т
Учащиеся отвечают на вопросы и записывают дату и тему урока.
Поочередно решают уравнения у доски.
Повторение мер времени.
Закрепление навыка решения уравнений.
6 класс стр. 67 №271
Физкультминутка.
Дружно с вами мы считали и про числа рассуждали,
А теперь мы дружно встали, свои косточки размяли.
На счет раз кулак сожмем, на счет два в локтях сожмем.
На счет три — прижмем к плечам, на 4 — к небесам
Хорошо прогнулись, и друг другу улыбнулись
Про пятерку не забудем — добрыми всегда мы будем.
На счет шесть прошу всех сесть.
Выполняют упражнения динамической гимнастики.
Работа над задачей.
Задача.
Начертите прямоугольник ABCD, длина 5,5см, а ширина 4,5см.
Каков периметр данного прямоугольника?
Развитие навыков осмысленного чтения.
3 уровень прямоугольник со сторонами 5см и 4см.
(готовая карточка)
Разбор задачи:
— О чем говорится в задаче? Показать прямоугольник (Слайд №5) и рассказать свойства прямоугольника.
— Что известно в задаче?
— Какой вопрос в задаче?
— Во сколько действий задача?
— Как будем решать задачу?
— Записываем решение задачи в тетрадь.
Фронтальная проверка.
Отвечают на вопросы учителя.
Дети формулируют ответ.
Коррекция мышления.
Развитие речи.
Закрепление.
Самостоятельная работа.
Работа в парах.
Выполните вычисления в десятичных дробях.
I, II уровень.
34ц 40кг – 2ц 56кг
4,309кг + 6кг 2г
15м 5мм + 46м 8мм
III уровень.
7 369 + 4 874
8 961 – 6 450
34,56 + 23,31
Фронтальная проверка.
Учащиеся работают самостоятельно по карточкам.
Развитие навыков самостоятельной работы.
Работают в паре (с помощью учителя)
Рефлексия.
У детей на партах таблички со знаками «+» и «-».
Дети поднимают таблицы («+» — если урок понравился, «-« если урок не понравился.
Домашнее задание.
Стр. 140 № 369 (3столбик)
Слайд №6
Индивидуальные карточки
Итог урока.
Подведение итогов урока.
Оценивание учителем деятельности учащихся.
Слайд №7
Этап урока. Виды деятельности. | Деятельность учителя. | Деятельность учащихся. | Какие задачи решались в ходе выполнения заданий. | Индивидуальная работа. |
| Приветственное слово учителя. | Проверяют свою готовность к уроку. | Создание психологического настроя. | |
| С. 90 № 255 (пункт 2) | Отвечают на вопросы учителя. | ||
| На доске вывешены карточки с числами. а) 2,07; 0,300; 56,9; 2,90; 0,001; 64,7; 86,406; 1,30; 6,4. — Как называются дроби, написанные на 1 строчке? (десятичные дроби) — Прочитайте по цепочке. — Какие дроби из них можно преобразовать? ( с 0 в конце дроби ). б) Прочитайте дроби на второй строчке: 35/4; 9/18; 14/21; 13/13; 10/15; 15/25; 18/8; 8/40. — Какие дроби называются неправильными? Зачеркните неправильные дроби. — Как называются оставшиеся дроби? ( правильные) — Как их можно преобразовать? (сократить) -Что значит сократить дробь? (числитель и знаменатель разделить на одно и тоже число) | Отвечают на вопросы. | Активизация внимания учащихся. Развитие навыков устного счёта. | |
| Давайте вспомним, как же мы выполняем сложение и вычитание целых чисел? Давайте вспомним правило сложения и вычитания десятичных дробей. Давайте вспомним правило сложения и вычитания обыкновенных дробей с одинаковыми знаменателями. Давайте вспомним правило сложения и вычитания обыкновенных дробей с разными знаменателями. Кто мне скажет, какая тема сегодняшнего урока? | Учащиеся проговаривают правило, решают пример у доски. Учащиеся проговаривают правило, решают пример у доски. Учащиеся проговаривают правило, решают пример у доски. Учащиеся проговаривают правило, решают пример у доски. | Развитие памяти и речи учащихся. | |
Решение уравнений. | А теперь открываем тетради, записываем сегодняшнюю дату. Какое сегодня число? Какой день недели? Какой месяц? Какой по счету месяц февраль? Какой сейчас год?
Х + 12 648 = 20 010 Х – 7,089 = 13,72 13 1\7 – х = 10 3\14 | Учащиеся отвечают на вопросы изаписывают дату и тему урока. Поочередно решают уравнения у доски. | Повторение мер времени. Закрепление навыка решения уравнений. | |
Физкультминутка. | Дружно с вами мы считали и про числа рассуждали, А теперь мы дружно встали, свои косточки размяли. На счет раз кулак сожмем, на счет два в локтях сожмем. На счет три — прижмем к плечам, на 4 — к небесам Хорошо прогнулись, и друг другу улыбнулись Про пятерку не забудем — добрыми всегда мы будем. На счет шесть прошу всех сесть. | Выполняют упражнения динамической гимнастики. | ||
Работа над задачей. | Задача. Начертите прямоугольник ABCD, длина 5,7 см, а ширина 4 см. Каков периметр данного прямоугольника? | Читают условие задачи вслух. | Развитие навыков осмысленного чтения. | |
Разбор задачи: — О чем говорится в задаче? — что известно в задаче? — Какой вопрос в задаче? — Во сколько действий задача? — Как будем решать задачу? — Записываем решение задачи в тетрадь. Фронтальная проверка. | Образец ответов: Дети формулируют ответ. | Коррекция мышления. Развитие речи. | Кириленко Даниил – инд. карточка с решением задачи. | |
Самостоятельная работа. | Дифференцированная работа на карточках. I уровень. 2\4 + 4\6 = 12 578 + 96,47 = 14 – 6\20 = II уровень. 37\50 + 12\50 = 74,96 – 14,62 = III уровень. 17 369 + 14 874 78 961 – 20 450 Фронтальная проверка. | Учащиеся работают самостоятельно. | Развитие навыков самостоятельной работы. | Работа по вариантам. |
| У детей на партах таблички со знаками «+» и «-». | Дети поднимают таблицы. | ||
| С. 90 № 255 (пункт 3) | |||
| Подведение итогов урока. Оценивание учителем деятельности учащихся. |
Сложение, вычитание и умножение десятичных дробей
Сложение, вычитание и умножение десятичных дробей
Сложение и вычитание десятичных дробей выполняются так же, как сложение и вычитание целых чисел; нужно только записывать каждый разряд под разрядом того же наименования.
Пример. 2,3 + 0,02 + 14,96= 17,28.
Умножение десятичных дробей.
Перемножаем данные числа как целые, не обращая внимания на запятую. Затем ставим в результате запятую, пользуясь следующим правилом: в произведении число знаков после запятой равно сумме чисел знаков после запятой во всех сомножителях.
Пример 1. 2,064 • 0,05. Перемножаем целые числа 2064 • 5 = 10 320. В первом сомножителе было три знака после запятой, во втором — два. В произведении число знаков после запятой должно быть пять.
Отделяем их справа; получаем 0,10320. Нуль, стоящий в конце дроби, можно отбросить: 2,064 · 0,05 =- 0,1032.
До постановки запятой отбрасывать нули при этом способе нельзя.
Пример 2. 1,125 • 0,08; 1125 • 8 = 9000. Число
знаков после запятой должно быть 3 + 2 = 5. Приписывая к 9000 нули слева (009000), отделяем справа пять знаков. Получаем 0,09000 = 0,09.
Деление десятичной дроби на целое число
Если делимое меньше делителя, записываем в целой части частного нуль и ставим после него запятую.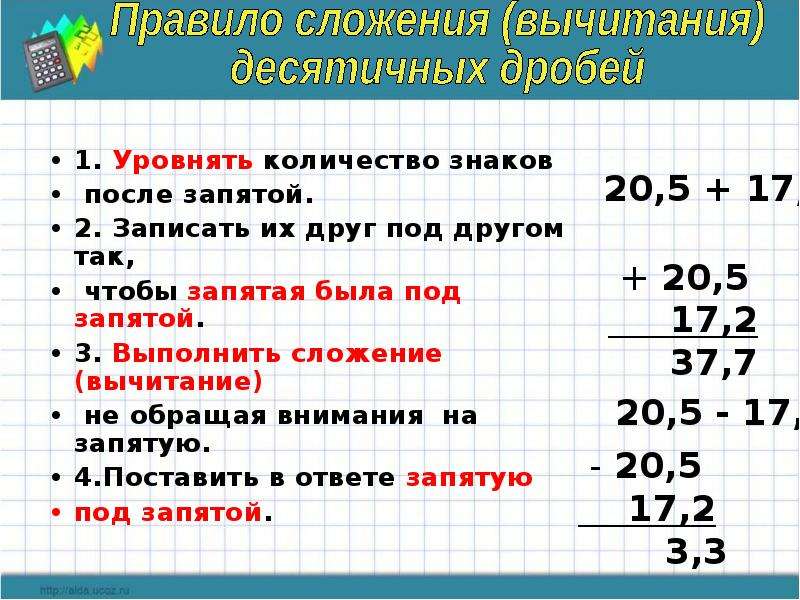
Замечание. Возможно, что описанный процесс деления никогда не закончится. В таком случае
частное нельзя точно выразить десятичной дробью, но, остановившись на некоторой цифре, получим приближенный результат.
Обращение десятичной дроби в простую и обратно
Чтобы обратить десятичную дробь в простую, нужно, отбросив запятую, сделать получившееся
число числителем дроби; знаменателем же нужно взять число, показывающее, какие доли представляет последний десятичный знак.
Полученную дробь желательно сократить, если это возможно.
Если десятичная дробь превосходит единицу, то предпочтительно обращать в простую дробь только ту ее часть, которая стоит после запятой, целую же часть оставить без изменения.
Пример: 0,0125 обратить в простую дробь.
Последний десятичный знак представляет десятитысячные доли. Поэтому знаменатель будет 10 000 имеем
Пример:
Предпочтительно, однако, производить вычисление первым из двух указанных способов, т. е., оставляя без изменения двойку, стоящую слева от запятой, обращать в простую дробь число 0,75.
Пример: дробь обратить в десятичную. Делим 7:8 получаем 0,875.
В большинстве случаев этот процесс деления может продолжаться бесконечно. Тогда простая дробь не может быть обращена в десятичную точно. На практике этого никогда и не требуется. Деление заканчивают в тот момент, когда в частном получены все те десятичные доли, которые имеют практический интерес.
Пример: Требуется разделить 1 кг сахара на три равные части Масса каждой части .
Чтобы взвесить это количество, нужно выразить его в десятичных долях килограмма. Делим 1 на 3, получим 1:3=0.333……. Деление можно продолжать до бесконечности в частном будут появляться все новые тройки. Практический интерес имеют лишь сотые доли килограмма (10 г). Поэтому берем
Для большей точности принято учитывать величину первой отбрасываемой цифры. Если она превышает 5, то удерживаемая цифра увеличивается на 1
Пример: Обратить дробь в десятичную. Точное значение будет 0,21875. В зависимости от требуемой степени точности, деление заканчивается на второй, третьей и т.д. цифре частного и берут
Исторические сведения о дробях
Понятие о дроби могло возникнуть у людей лишь после того, как у них образовались некоторые представления о целых числах. Как и понятие целого числа, понятие дроби появилось не сразу. Представление о «половине» возникло гораздо раньше, чем о «третях» и «четвертях», а об этих последних— раньше, чем о дробях с другими знаменателями Первые представления о пелом число возникли в процессе счета; первые представления о дробях — и г; процесса измерения (длин, площадей, массы и т.
д.). Следы исторической связи исчисления дробей и системы мер можно обнаружить у многих народов. Так, в вавилонской системе мер массы (и денег) 1 талант составлял 60 мин, а одна мина — 60 шекелей. Соответственно с этим в вавилонской математике широко применялись шестидесятеричные дроби. В древнеримской системе измерения массы 1 асе делился на 12 унций; согласно с этим римляне пользовались двенадцатеричными дробями. Дробь, которую мы называем 1/12 , римляне именовали «унцией», даже если бы она употреблялась для измерения длины или иной величины; дробь, которую мы называем 1/8 , римляне называли «полторы унции» и т. п.
Наши «обыкновенные дроби» широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским ученым Брамагуптой (8 в. н. э.), лишь немногим отличаются от наших. Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель, но чаще пользовались другими записями, например писали (конечно, своими знаками) 3 5х (три пятых).
Индийское обозначение дробей и правила действий над ними были усвоены в 9 веке в мусульманских странах благодаря Мухаммеду Хорезмскому (аль-Хваризми,. Они были перенесены в Западную Европу итальянским купцом и ученым Леонардо Фибоначчи иг Пизы (13 в.)
Наряду с «обыкновенными» дробями применялись (преимущественно в астрономии) шестидесятеричные дроби. Они были позднее вытеснены десятичными дробями. Последние впервые ввел выдающийся самаркандский ученый Гиясэддин Джемшид г Каши (14—15 вв.). В Европе десятичные дроби были введены в практику нидерландским купцом и выдающимся
ученым-инженером Симоном Стевином (1548—1620).
Сложение и вычитание целых чисел и десятичных дробей
1. Сложение и вычитание целых чисел и десятичных дробей
1 + 79 = 80;67 *
10 —
0
=0;
10 = 0;
4
98 :
0
: 4 = 1;
1
= 98;
:2 = 0
: 0 = на нуль делить нельзя
3. Сами с усами Вопрос: чему посвящен 2013 год?
5000 + 3000Л
7000 – 4000
И
9000 – 8000
К
6000 + 3000
О
1000+ 4000
Э
9000 – 2000
Я
2000 + 2000
Г
7000 — 5000
О
5000
1000
2000
8000
9000
4000
3000
7000
ЭКОЛОГИЯ
5.
Узнавайка Задача 1.Общая площадь Лесного района составляет 163 299
гектаров. Охраняемая территория на 108 866
гектаров меньше общей площади района. Найдите
охраняемую территорию района?
54 433 га
Задача 2.
В некотором царстве, в Лесном
государстве жил-был Иван — царевич.
Было у него 3 брата. Решил он их
проведать и отправился в путь. Долго
ли ехал, коротко ли… На пути у него
возник огромный валун, который
мешал проехать Ивану – царевичу к
своим братьям. А на том камне –
валуне надпись: «Чтобы меня
отодвинуть , нужно решить 3
уравнения».
7. Порогский каменюка
1.Х + 2 = 6, 2
1. 4,2
2.
19 – Х = 16, 7
2.
2,3
3.
97,6 + Х = 100
3. 2,4
9. Путь в космос
Задача 3Первый спутник Земли
полетел в космос 4 октября
1957 году, а аллея была
заложена в мае 1958
года.
Сколько лет березам?
Когда эта дата исполни
лась в 2013 году?
55 лет
май 2013 г
10.
Задача 4 У школы в с. Михайловское посажана аллея лиственниц. Все деревья имеют разные размеры (по толщине): 1,8 м; 2,08 м; 1,008 м ; 0,98 м. Расположите впорядке возрастания размеры
деревьев.
0,98 м; 1,008 м; 1,8 м; 2,08 м
11. Почтовая
42
1
1
3
3
озер
о
2
2
1
3
бол
ото
5
2
1
4
Озеро ИЛОВЕЦ
Его площадь 512 га
13. курган
14. БОБР РЫСЬ ЛОСЬ
15. Глухарь
Найдите фигуру, которая нарушаетзакономерность.
Как расположены фигуры?
17. Итог урока
Повторили сложение и вычитание целыхчисел, десятичных дробей,
возрастание десятичных дробей.
Памятники природы в Лесном районе.
СПАСИБО ЗА УРОК!
| 1. | Сложение десятичных дробей | 1 вид — рецептивный | лёгкое |
1 Б.
|
Сложение десятичных дробей, до 0,1. |
| 2. | Сложение десятичной дроби и целого числа | 1 вид — рецептивный | лёгкое | 1 Б. | Сложение десятичной дроби и целого числа в столбик. |
| 3. | Сложение десятичных дробей, до 0,01 | 1 вид — рецептивный | лёгкое |
1 Б.
|
Сложение десятичных дробей в столбик, до 0,01. |
| 4. | Сложение десятичных дробей | 2 вид — интерпретация | среднее | 1 Б. | Сложение десятичных дробей, разное количество знаков после запятой. |
5.
|
Прямоугольник | 2 вид — интерпретация | среднее | 2 Б. | Периметр прямоугольника. |
| 6. | Вычитание целого числа и десятичной дроби, до 0,1 | 2 вид — интерпретация | среднее |
1 Б.
|
Вычитание целого числа и десятичной дроби. |
| 7. | Вычитание десятичных дробей, до 0,1 | 2 вид — интерпретация | среднее | 1 Б. | Вычитание десятичных дробей. |
| 8. | Вычитание (тысячные) | 2 вид — интерпретация | среднее |
1 Б.
|
Вычитание, разное количество знаков в целых и дробных частях чисел. |
| 9. | Сложение и вычитание десятичных дробей | 2 вид — интерпретация | среднее | 1 Б. | Сложение и вычитание десятичных дробей в столбик. |
10.
|
Текстовая задача (килограммы и граммы) | 2 вид — интерпретация | среднее | 4 Б. | Решение текстовой задачи. |
| 11. | Число, большее разности чисел | 2 вид — интерпретация | среднее |
2 Б.
|
Число, большее разности чисел. |
| 12. | Текстовая задача (килограммы и тонны) | 2 вид — интерпретация | среднее | 5 Б. | Решение текстовой задачи. |
| 13. | Разложение числа по разрядам | 2 вид — интерпретация | среднее |
2 Б.
|
Разложение числа по разрядам. |
| 14. | Уравнение (сумма) | 2 вид — интерпретация | сложное | 2 Б. | Решение уравнения. |
| 15. | Уравнение (разность) | 2 вид — интерпретация | сложное |
2 Б.
|
Решение уравнения. |
Страница не найдена — Школа «Возможность»
Он-лайн запись на «родительский контроль питания
Уважаемые родители!
Информируем вас о том, что записаться на «Родительский контроль» — проект по оценке качества питания в школах — в Подмосковье теперь можно в режиме онлайн. Сделать это можно на Школьном портале региона. Регистрация проходит быстро — вся процедура займет не более трех минут.
— Нужно выбрать вкладку «Родительская»;
— Перейти в раздел «Школьное питание»;
— Выбрать желаемую дату и время;
— Нажать кнопку «Записаться».
Школа автоматически получит заявку и в назначенное время родителя будет ожидать классный руководитель или ответственный за питание.
Опрос для родителей
Уважаемые родители! Вы можете пройти опрос по ссылке:
https://анкета.
независимаяоценкакачества.рф/
Опрос проводится в целях выявления мнения граждан о качестве условий осуществления образовательной деятельности образовательными организациями.
Пожалуйста, ответьте на вопросы анкеты. Ваше мнение позволит улучшить работу образовательной организации и повысить качество оказания услуг населению.
Опрос проводится анонимно.
Контроль школьного питания
Уважаемые родители! Вы можете пройти опрос по организации и качеству питания школьников на Школьном портале по ссылке https://school.mosreg.ru/feedback/school-meals
Родительский контроль питания
1. Каждый родитель в любой день и время может попробовать школьное питание2. Для записи на дегустацию Вам необходимо записаться по телефону: +7(985) 976-90-14
3. Время и дата дегустации с Вами будет согласована
4. В назначенный день и время в школе Вас встретит ответственный за питание –
Шишлянникова Светлана Семеновна
5.
После дегустации свои замечания Вы можете оставить ответственному за питание и отправить свой отзыв на Добродел (через QR-код)
6. Все обращения по питанию (замечания, положительные отзывы) Вы можете направить: в ЦУР или директору школы «Возможность» — Смирновой В.А. по адресу: [email protected]
«Уважаемые родители!
Информируем Вас о размещении следующих материалов:
1. Методические рекомендации по порядку блокирования информации, причиняющей вред здоровью и развитию детей, распространяемой в сети Интернет.
2. Алгоритм действий по предупреждению суицидов среди несовершеннолетних.
3. Алгоритм действий по профилактике суицидов учащихся образовательных организаций.
Подробнее по ссылке: http://wp.me/P8nqEd-1I
Поздравляем!
Наша школа вошла в рейтинге лучших общеобразовательных организаций Московской области по итогам 2017-2018 учебного года в «Топ-5» специальных коррекционных школ (социальная адаптация учащихся)!!!
Уважаемые родители!
С 29.
10.2018 запись в школу в порядке перевода из другого образовательного учреждения будет производиться только посредством РПГУ. https://uslugi.mosreg.ru/
Уважаемые родители!
Предлагаем вам пройти опрос по электронным учебникам. Ссылки на опросы также опубликованы в личных кабинетах родителей на «Школьном портале».Страница не найдена | МАОУ Слобода-Бешкильская СОШ
Страница, которую Вы ищете, видимо, удалена или не существовала ранее.
Однако вы можете попробовать поискать необходимую информацию в следующих статьях:
- Квест «Мы вместе»
- Дорожная безопасность
- 14 мая команда ЮИД Рассветовской СОШ приняла участие в районном конкурсе «Безопасное колесо».
- Волонтерский отряд МАОУ Слобода-Бешскильской СОШ занял второе место в районном профилактическом квесте «Наш выбор — здоровье»
- Последний звонок
- Порядок и условия приёма абитуриентов в военные вузы Министерства обороны Российской Федерации
- #окнаПобеды #Мы_потомкигероев #маоуслободабешкильскаясош семья Бёрдовых
- #Мы_потомкигероев #маоуслободабешкильскаясош
- Окна Победы
- Квест «Запусти ракету!» #ДеньКосмонавтики #Поехали #ИсетскийРайон
- Четвёртый день «Недели космических путешествий» #ДеньКосмонавтики #Поехали #ИсетскийРайон
- Региональный этап Всероссийского турнира по шахматам на кубок РДШ. Младшая группа
- Сегодня третий день «Недели космических путешествий» #ДеньКосмонавтики #Поехали #ИсетскийРайон
- Новый сезон «Большой перемены» стартует 26 марта 2021 года
- Сегодня второй день предметной недели, посвящённой Дню космонавтики #ДеньКосмонавтики #Поехали #ИсетскийРайон
- Неделя космических путешествий #ДеньКосмонавтики #Поехали #Исетскийрайон
- Что делать если в семье кто-то заболел гриппом или коронавирусной инфекцией?
- Всероссийская историческая интеллектуальная игра «Космос рядом»
- #Областная_зарядка Рассветовская СОШ
- Гимнастические пирамиды
- Участие в Региональном этапе Всероссийского турнира по шахматам на кубок РДШ. Старшая группа
- 31 марта в МАОУ Слобода-Бешкильской СОШ прошел семейный фестиваль «Мама, папа, я – интеллектуальная семья!».
- Как обезопасить детей на дороге
- 25 марта на базе Рассветовской школы состоялся турнир по фригеймсу
- Ребята нашей школы участвуют во Всероссийском дистанционном командном квесте для студентов и школьников «Вокруг информатики. Космические олимпийские игры».
- Знать правила дорожного движения должен каждый ученик
- #Крымскаявойна #РоссияСевастопольКрым #РассветовскаяСОШ Библиотекарь с. Рассвет — О. Д. Маркова провела мероприятие посвященное Крымской войне.
- С 1 апреля на портале https://education.admtyumen.ru/ будет доступна подача заявлений в школу
- «Прощание с азбукой» Архангельская ООШ
- Итоги недели естественно-математического цикла. Архангельская ООШ
- Неделя естественно-математического цикла. Архангельская ООШ
- Команда Рассветовской СОШ ГТО 2021 г. — 1 место
- «Геологу». Вагин Всеволод Архангельская ООШ
- Неделя естественно-математического цикла. Архангельская ООШ
- Лыжные гонки. Архангельская ООШ
- Товарищеская встреча в Архангельской школе по волейболу
- Результаты «Конференции первого доклада». Архангельская ООШ
- Ежегодно (а точнее, уже 15 лет) наша школа, принимает участие в конкурсе «Инфознайка».
- 3 марта в Верхнебешкильской школе состоялась товарищеская встреча по Фригеймсу среди сборных команд Верхнебешкильской школы и Архангельской.
- 3 марта ребята 7 класса Слобода-Бешкильской школы приняли участие в добровольческом проекте «Учителю с любовью»
- Детское телевидение «PROнас» представляет вашему вниманию выпуск 4 «Люди, события, факты»
- В Рассветовской школе продолжает свою работу детское телевидение «PROнас». Смотрите выпуск 3 «Репортаж из школьного музея»
- 25 февраля в Верхнебешкильской ООШ была проведена военно- спортивная игра » Зарница» для учащихся 5-9 классов
- Сегодня, 25.02.2021 г., на базе МАОУ Слобода-Бешкильской СОШ состоялся I (школьный) этап Всероссийского турнира по шахматам на кубок Российского движения школьников
- «Приватность в цифровом мире» Архангельская ООШ
- «Афганистан-память и боль…» Архангельская ООШ
- КМО начальных классов
- 32 года со дня вывода войск из Афганистана. Рассветовская СОШ
- 15 февраля День вывода советских войск из Афганистана
- Уважаемые родители! Доводим до вашего сведения, что в школе работает служба школьной медиации.
Младшая группа
Космические олимпийские игры».
Рассветовская СОШоткрытых учебников | Сиявула
Математика
Наука
- Читать онлайн
Учебники
Английский
класс 7А
Марка 7Б
Класс 7 (вместе A и B)
Африкаанс
Граад 7А
Граад 7Б
Граад 7 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 8A
марка 8Б
Оценка 8 (вместе A и B)
Африкаанс
Граад 8А
Граад 8Б
Граад 8 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 9А
Марка 9Б
Оценка 9 (комбинированные A и B)
Африкаанс
Граад 9А
Граад 9Б
Граад 9 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 4A
класс 4Б
Класс 4 (вместе A и B)
Африкаанс
Граад 4А
Граад 4Б
Граад 4 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
Марка 5А
Марка 5Б
Оценка 5 (комбинированные A и B)
Африкаанс
Граад 5А
Граад 5Б
Граад 5 (A en B saam)
Пособия для учителя
- Читать онлайн
Учебники
Английский
класс 6А
класс 6Б
Класс 6 (вместе A и B)
Африкаанс
Граад 6А
Граад 6Б
Граад 6 (A en B saam)
Пособия для учителя
Наша книга лицензионная
Эти книги не просто бесплатные, они также имеют открытую лицензию! Один и тот же контент, но разные версии (брендированные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете делать ксерокопии, распечатывать и распространять их сколько угодно раз. Вы можете скачать их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственным ограничением является то, что вы не можете адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, спонсорские логотипы и одобрены Департаментом базового образования. Для получения дополнительной информации посетите Creative Commons Attribution-NoDerivs 3.0 Непортированный.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без бренда)
Эти небрендированные версии одного и того же контента доступны для вас, чтобы вы могли делиться ими, адаптировать, трансформировать, модифицировать или дополнять их любым способом, с единственным требованием — дать соответствующую оценку Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
вычислений, дроби, десятичные дроби и проценты
вычисления, дроби, десятичные дроби и проценты Вычисления, дроби, десятичные дроби и проценты
Щелкните здесь, чтобы просмотреть указатель глоссария!
Общие дроби
Состоит из двух чисел, разделенных горизонтальной или диагональной линией:
Знаменатель
Нижний номер:
Указывает количество частей, на которые делится одна (1)
Числитель
Верхний номер:
Указывает количество тех частей, которые нас интересуют
Например, дробь половина, записанная как 1/2, означает, что одна была разделена на две части, поскольку нас интересует одна из этих двух частей.Дробь 3/4 означает, что одна была разделена на четыре части, и нас интересуют три из этих четырех частей
Правильные дроби
Числитель меньше знаменателя
1 = числитель
2 = знаменатель
3 = числитель
4 = знаменатель
Неправильные дроби
Числитель больше знаменателя
Происходит, когда дробь имеет значение больше 1
6 = числитель
5 = знаменатель
Здесь дробь имеет большее значение, чем 1
При работе с дробями полезно принять к сведению некоторые общие принципы, касающиеся того, что происходит, когда вы выполняете определенные математические операции с числителями и знаменателями.
(Обратите внимание, что ниже мы внимательно указываем, что множитель или делитель больше (> 1). В каждом случае, если это число меньше единицы (<1), мы получаем противоположный результат.)
Операции с числителями
Если умножить числитель на число> 1, значение дроби увеличится
Если разделить числитель на число> 1, значение дроби уменьшится.
Операции со знаменателями
Если знаменатель умножить на число> 1, значение дроби уменьшится.
Если делить знаменатель на число> 1, значение дроби увеличивается.
Операции над числителем и знаменателем
Общие принципы с дробями:
Если умножить числитель и знаменатель на одно и то же число, значение дроби останется прежним
Если вы разделите числитель и знаменатель на одно и то же число, значение дроби останется прежним
Эта информация пригодится при работе с дробями, поскольку позволяет выполнять определенные математические операции с дробями, когда вам необходимо изменить форму дроби.
Различные примеры, приведенные ниже, иллюстрируют этот момент.
В аптеке от нас часто требуется выполнять математические операции с дробью. Наиболее распространенные операции проиллюстрированы ниже:
Сложение дробей
Сложите числа, знаменатели останутся прежними
Пример: сложение дробей (02040010)
Чтобы знаменатель оставался неизменным, он должен быть одинаковым для обеих добавляемых дробей.
Что делать, если знаменатели другие?
Пример: добавление разных знаменателей (02040020)
В этом случае можно применить принцип, который гласит, что если вы умножаете числитель и знаменатель на одно и то же число, значение дроби остается неизменным.Дробь 1/4 может быть заменена на дробь с тем же значением, но со знаменателем 8, умножив числитель и знаменатель фракции на число 2.
Сделайте знаменатели одинаковыми, умножив числитель и знаменатель на одно и то же число (см. Общие принципы).
Пример: общий знаменатель — 1 (02040030)
Замените эту новую дробь, затем добавьте:
Пример: общий знаменатель — 2 (02040040)
Иногда необходимо изменить форму обеих фракций.
В этом случае ближайший общий знаменатель равен 12, поэтому числитель и знаменатель дроби 1/4 должны быть умножены на 3, чтобы получить 3/12, а числитель и знаменатель дроби 2/3 должны быть умножены на 4. сделать ставку 8/12
Затем можно произвести сложение
Пример: сложение дробей (02040050)
Вычитание дробей
Вычитание дробей очень похоже на сложение дробей
Вычтите числители, знаменатель останется прежним
Пример: вычитание дробей (02040060)
Как и при сложении, если знаменатели разные, измените одну или обе дроби так, чтобы они были одинаковыми, а затем вычтите.
Пример: вычитание различных знаменателей (02040070)
Как и в приведенном выше примере, дробь 2/3 изменяется на 8/12, а дробь 1/4 изменяется на 3 // 12, и выполняется указанная математическая операция вычитания.
Пример: вычитание дробей (02040080)
Умножение дробей
Умножаем числители вместе = новый числитель
Умножаем знаменатели вместе = новый знаменатель
Пример: умножение дробей (02040090)
Умножение легко, потому что числители умножаются вместе.
В отличие от сложения и вычитания, в знаменателе нет необходимости использовать общее число.
На дробь
Оберните делитель и произведите умножение.
Пример: деление дроби -1 (02040100)
Инвертируем 3/4 и умножаем:
Деление на дроби — 2 (02040200)
Сокращение обыкновенных дробей до наименьших членов
Дроби обычно выражаются в самой простой возможной форме = сокращение дроби до наименьшего числа.
Пример: сокращение обыкновенных дробей (02040300)
Разделите числитель и знаменатель на 3. Эта дробь выражается эквивалентной, но более простой дробью 4/5.
Это более простое выражение получается делением числителя и знаменателя на одно и то же число. Из общих принципов вы помните, что когда вы это сделаете, вы получите другую дробь, но с тем же значением.
Числитель и знаменатель дроби проверяются, чтобы определить, существует ли у каждой из них общий множитель.
В дроби 12/15 число 3 является общим множителем, поскольку и 12, и 15 делятся на 3.
Это число делится как на числитель, так и на знаменатель.
Пример: уменьшение дроби (02040400)
Сокращение неправильных дробей до наименьших значений
Неправильная дробь (в которой числитель больше знаменателя) сокращается до наименьших членов, заменяя дробь смешанным числом.
Разделите числитель на знаменатель, а остаток представьте в виде правильной дроби.
Пример № 1: Неправильная дробь — 1 (02040500)
Пример № 2: Неправильная дробь — 2 (02040600)
Умножение и деление смешанных чисел
Пример: умножение смешанной фракции (02040700)
Умножение и деление невозможно выполнить с использованием смешанных чисел:
Если смешанное число должно быть умножено или разделено, оно должно быть сначала заменено на неправильную дробь.
Чтобы преобразовать смешанное число в дробь, умножьте целое число на знаменатель и прибавьте его к числителю, затем запишите эти результаты как новый числитель над исходным знаменателем.
Пример: смешанные числа (02040800)
Подставьте эту неправильную дробь вместо смешанного числа, затем умножьте дробь.
Пример: замена неправильной дроби (02040900)
Выразите ответ 110/24 в виде смешанного числа, сокращенного до наименьшего числа.
Пример: сокращение смешанных чисел (02041000)
Десятичные дроби
Дробь, знаменатель которой равен 10 или кратен 10, называется десятичной дробью или десятичной дробью. Однако вместо записи дроби в виде двух чисел, разделенных линией, используется десятичная точка.
В десятичных дробях размещение десятичной точки используется для обозначения числа, кратного десяти, в знаменателе.
Фактически записываются только числа числителя.
Пример: дроби как десятичная таблица (02041100)
При выполнении любой математической операции все термины должны быть в одной системе. Следовательно, если некоторые числа даны как обычные дроби, а некоторые как десятичные дроби, вы должны сначала преобразовать все числа в одну общую форму.
Преобразование между обыкновенной и десятичной дробями
Десятичное число = обыкновенные дроби
0,0011 = 11 / 10,000
Используйте десятичное число I (11) в качестве числителя.Знаменатель кратен десяти и определяется положением десятичной запятой. (Один ноль на каждое место.)
Обыкновенная дробь = Десятичная
5/8 = 0,625
Разделите числитель дроби на знаменатель. В приведенном выше примере разделите 5 на 8, чтобы получить 0,625.
Обратите внимание, что для некоторых дробей деление не получается четным и дает повторяющееся число. Например, 1/3 дает 0,333.
Математические операции с десятичными знаками
Чаще всего, когда мы выполняем математические операции с десятичными числами, мы используем калькулятор, и он автоматически дает ответ с десятичной дробью в нужном месте.Если вам пришлось выполнять эти операции вручную, следует запомнить несколько правил.
При сложении или вычитании десятичных знаков вы должны сначала выровнять числа так, чтобы десятичные точки находились непосредственно друг под другом.
Затем сложите или вычтите, как если бы вы делали целые числа.
Чтобы добавить 0,1 + 0,33 + 0,017: Добавление десятичных знаков (02041200)
Чтобы вычесть 0,56 из 0,7: Вычитание десятичных знаков (02041300)
Чтобы умножать десятичные дроби, умножайте числа так же, как и на целые числа
Для определения положения десятичной точки в ответе:
Подсчитайте количество разрядов справа от десятичной точки для каждого из множителей.
Сложите это вместе.
Отсчитайте это количество знаков в ответе, начиная с крайнего правого числа.
Пример: при умножении 0,849 на 0,62 в двух множителях складываются пять знаков справа от десятичной дроби. Следовательно, при определении десятичного разряда в произведении 52638 отсчитайте пять разрядов слева от крайнего правого числа (в данном случае 8)
Умножение десятичных знаков (02041400)
Если в ответе недостаточно цифр, используйте нули в качестве хранителей места.
В приведенном выше примере, если число 0,62 равно 0,062 и нам нужно шесть десятичных знаков, ответ будет 0,052638.
Чтобы разделить десятичные дроби, расположите числа для деления в столбик так же, как для целых чисел.
Если в делителе есть десятичный разряд, переместите десятичную точку до упора вправо от числа, затем переместите десятичную точку делимого (делимого числа) на такое же количество разрядов вправо.
Если делимое целое число, вам нужно будет добавить ноль справа от последнего числа делимого для каждого необходимого десятичного разряда.Например, чтобы разделить 16,8 на 0,12, переместите десятичную запятую 0,12 вправо на два места, чтобы получить 12; аналогичным образом переместите десятичную запятую для делимого, 16.8, на две позиции вправо. Затем выполните деление как обычно.
Пример: разделение десятичных знаков (02041500)
Правила десятичных знаков при написании доз лекарств
Десятичные точки должны быть четко написаны при написании доз лекарственного средства, поскольку пропущенная или неверно прочитанная десятичная точка может привести к десятикратной ошибке в дозе
Никогда не добавляйте «конечный ноль» при записи целых чисел
Используйте 25 мг, а не 25.
0 мг
Никогда не записывайте «голую десятичную дробь» при записи десятичной дроби вместо числа меньше 1
Используйте 0,25 мг, а не 0,25 мг
процентов
Проценты — это просто специальный вид дроби. Термин «процент» (обозначенный%) означает «за сотню».
Пример: 50% означает 50 на 100
Всегда переводите проценты в обыкновенные или десятичные дроби перед выполнением любых математических операций.
Процент = Десятичное
Переместите десятичную запятую на два разряда влево и опустите знак процента.
Пример: 50% = 0,50 или просто 0,5
Пример: 12,5% = 0,0125
Десятичное число = Процент
Переместите десятичную запятую на два разряда вправо и добавьте знак процента.
Пример: 0,5 = 50%
Пример: 0,0125 = 12,5%
Процент = правильная фракция
Используйте число в числителе и 100 в качестве знаменателя.
50% = 50/100 (или 1/2 при сокращении до наименьшего значения)
Пример: 12.
5%
Первая запись выражается обыкновенной дробью —12,5 / 100
Поскольку мы обычно не смешиваем десятичные дроби в обычных дробях, эту дробь можно преобразовать в эквивалентную десятичную дробь без дроби, умножив числитель и знаменатель на 10 — 125/1000
Эта дробь может быть уменьшена до наименьшего числа путем деления числителя и знаменателя на общий множитель 125, что дает 1/8
12,5% = 125./100 = 125/100 = 1/8 (при уменьшении до самых низких значений)
Правильная фракция = процент
Преобразуйте дробь в десятичную дробь, затем преобразуйте десятичную дробь в проценты.
Пример: = 0,025 = 25%
Сами по себе проценты, как и обыкновенная и десятичная дробь, представляют собой просто числа без каких-либо единиц или размеров. Однако существуют определенные правила использования процентов при описании концентраций лекарственных препаратов. Они обсуждаются в разделе, посвященном количеству, концентрации, дозе и режиму дозировки
.Pass Assured, LLC, Системы обучения фармацевтов
Сложение и вычитание десятичных знаков с двумя десятичными цифрами
Это полный урок с инструкциями и упражнениями по сложению и вычитанию десятичных знаков с двумя десятичными знаками (сотые).Сначала он сравнивает десятичное сложение со сложением дроби и использует числовые линии, чтобы помочь учащимся понять, как складывать десятичные дроби мысленно. Урок содержит упражнения, задачи со словами и упражнения по шаблонам.
| 1. Попробуйте , чтобы решить эти проблемы без чтения урок! Каждый раз пишите соответствующие дроби ниже десятичных знаков. |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||
Вы можете складывать или вычитать сотые и целые числа отдельно. Примеры:
|
2.Сложите и вычтите мысленно. Подумайте, сколько сотых в каждом числе.
а. 0,03 + 0,09 = ______ 2,03 + 2,09 = ______ | б. 0,52 + 0,43 = ______ 1,55 + 1,25 = ______ | г. 1,03 — 0,03 = ______ 4,03 — 2,01 = ______ | г. 0,10 — 0,08 = ______ 20,06 — 1,03 = ______ |
Часто нужно использовать тот факт, что 100 сотых составляют одно целое.Обратите внимание:
Ярлык: когда все чисел в
проблема у всех сотых, сложите или вычтите, как если бы было |
3. Сложить и вычесть. Будь осторожен и помните, что 100 сотых составляют одно целое.
а. 0,97 + 0,04 = ______ 2,96 + 0,06 = ______ | б. 0,95 + 0,11 = ______ 8,91 + 0,11 = ______ | г. 1,03 — 0,04 = ______ 7,01 — 0,05 = ______ | г. 1,12 — 0,16 = ______ 4,01 — 0,50 = ______ |
Попробуйте добавить их, не читая дальше.потом читать дальше!
| |||||||||||||||||||||||||||||||||||||
0,2 + 0,05 = _____ Как вы думаете? Если вы на 0,2 и пойдете на пять сотых (0,05) дальше, то где вы завершить? | |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
Давайте проверим две другие проблемы, которые вы пытались решить ранее. Мы будем напишите их так, чтобы в слагаемых было такое же количество десятичных знаков, как .
| |||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||
Не уверен в этом «Пометить ноль»? Смотрите ниже:
|
4. Добавьте мысленно. Перед добавлением отметьте
ноль к числу с одним десятичным знаком, так что слагаемое
будет иметь такое же количество десятичных знаков. Писать
проблемы с использованием дробей также.
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
5.Добавьте мысленно. Перед добавлением вы можете добавить к номеру ноль только с одним десятичным знаком.
| а. 0,11 + 0,5 = _______ | г. 0,24 + 0,2 = _______ | г. 0,3 + 0,39 = _______ |
| г. 0,22 + 0,7 = _______ | e. 0,2 + 0,41 = _______ | ф. 0,27 + 0,8 = _______ |
6. Продолжаем выкройки.
а. 0,91 + 0,02 = _____ + 0,02 = _____ + 0,02 = _____ + 0,02 = _____ + 0,02 = _____ + 0.02 = _____ | г. 0,80 — 0,05 = _____ — 0,05 = _____ — 0,05 = _____ — 0,05 = _____ — 0,05 = _____ — 0,05 = _____ | г. 2,90 + 0,03 = _____ + 0,03 = _____ + 0,03 = _____ + 0.03 = _____ + 0,03 = _____ + 0,03 = _____ | г. 1,77 + 0,11 = _____ + 0,11 = _____ + 0,11 = _____ + 0,11 = _____ + 0,11 = _____ + 0,11 = _____ |
7. Добавьте сотые доли, чтобы получилось следующее целое. десятый .Помните, 0,5 = 0,50.
|
|
|
8. Объясните, почему следующие добавления неверны.
| а. 0,99 + 0,1 = 1 | г. 0,43 + 0,59 = 0,102 |
9. Вычтите из целого числа.
|
|
|
| Помните? 100 см составляет один метр. Следовательно, 1 см — это одна сотая часть 1 метра. Другими словами, 1 см = 0,01 м . | 5 см = 0,05 м 64 см = 0,64 м 2 м 12 см = 2,12 м |
10. Преобразование между метрами и сантиметры, и решим проблемы.
а. 0,73 м = __________ см г. 2,82 м = __________ см | г. _________ м = 9 м 80 см г. _________ м = 306 см |
| e. Мальчик ростом 1,15 м и
куст 156 см высотой . Что выше? Насколько выше? | ф. Стол длиной 2,40 м
и 0,90 м шириной. Найдите его периметр в метрах. |
| г. Дверь 90 см
широкий будет декоративная доска над ним. Декоративный плата теперь 1.25 м длиной. Сколько нужно отрезать от доски так, чтобы она подошла? | ч. Высота помещения 2,25 м.
Сколько места осталось над головой человека у кого рост 186 см? |
11.Сложите и вычтите мысленно. Вы можете пометить от нуля до десятичной дроби только с точностью до десятых.
| а. 0,04 + 0,1 =
_______ 0,14 + 0,1 = _______ | б. 0,28 + 0,1 =
_______ 0,25 + 0,5 = _______ | г. 2,04 + 0.1 =
_______ 3,08 + 0,6 = _______ |
| d. 13,53 + 0,4 =
_______ 5,03 + 2,25 = _______ | е. 0,3 + 0,05 = _______ 0,03 + 0,5 = _______ | ф. 0,8 — 0,09 = _______ 0.9 — 0,08 = _______ |
| г. 1,3 — 0,07 = _______ 1,3 — 0,7 = _______ | ч. 6,2 — 1,2 = _______ 6,2 — 1,25 = _______ | и. 2 — 0,1 =
_______ 3 — 0,08 = _______ |
12. Найдите то, что было добавлено!
| ||||||||||||||||||||||||||||||||||||
Этот урок взят из книги Марии Миллер Math Mammoth Decimals 1 и размещен на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.
Вся элементарная математика — Учебное пособие — Арифметика
Сложение и вычитание десятичных знаков. Умножение десятичных знаков.Деление десятичных знаков. Деление десятичной дроби на целое число.
Деление десятичной дроби на другую.
Сложение и вычитание десятичных знаков. Эти операции выполняются как сложение и вычитание целого числа. Достаточно только написать соответствующие десятичные разряды друг под другом.
E x a m p l e.
Умножение десятичных знаков. На первом этапе давайте умножим дроби на целые числа, не вводя десятичную точку в рассмотрение. После этого мы используем следующее правило: количество десятичных знаков в продукте. равен сумме десятичных знаков во всех множителях. Примечание : перед десятичной точкой в продукте запрещается отбрасывать нули в конце!
E x a m p l e.
Сумма десятичных знаков в множителях равна: 3 + 4 = 7. Сумма цифр в произведении равна 6. Следовательно, необходимо добавить слева один ноль: 0197056 и поставить перед ним десятичную точку: 0,0197056.
Деление десятичных знаков.
Деление десятичной дроби на целое число.
Если делимое меньше делителя , запишите ноль в целой части частного и поставьте после него десятичную точку.Тогда, не считая десятичной дроби точку деления, присоедините к ее целой части следующую цифру дробной части и снова сравните полученную целую часть дивиденд с делителем. Если новое число снова меньше делителя, поместите еще один ноль после десятичной точки в частном и присоедините к целой части делимого — следующая цифра его дробной части. Таким образом, повторяйте этот процесс до тех пор, пока полученный дивиденд не будет больше делителя. После этого можно выполнять деление как на целые числа.Если Дивиденд больше делителя или равен ему , сначала разделите его целую часть, запишите результат деления в частное и поставьте десятичную точку. После этого можно продолжить деление как для целых чисел.
E x a m p l e. Разделите 1,328 на 64.
С о л ю т и н а:
Деление одной десятичной дроби на другую.
Сначала перенесите десятичные знаки в делимое и делитель на количество десятичных знаков делителя, т.е.е. делать делитель целое. Теперь делим так же, как и в предыдущем случае.
E x a m p l e. Разделите 0,04569 на 0,0006.
С о л ю т и н. Перенесите десятичные знаки на 4 разряда вправо и разделите 456,9 на 6:
.Сложение и вычитание десятичных знаков | Помощь с математикой
Сложение десятичных знаков с использованием разрядаМы можем использовать диаграмму разряда и счетчики, чтобы понять роль разряда в добавлении десятичных знаков.Примеры ниже показывают, как это можно сделать. Обратите внимание, что в первых двух примерах нет перегруппировки.
Обратите внимание, как тринадцать десятых перегруппированы в одну целую единицу и три десятых. Приведенные ниже примеры иллюстрируют перегруппировку тысячных, сотых и десятых долей.
Добавление десятичных знаков в числовую строкуИспользование числовых линий дает альтернативное визуальное представление добавления десятичных знаков, как показано в двух приведенных ниже примерах.
3,6 + 1.7 = 5,3
1,55 + 0,26 = 1,81
Числовые строки снабжены аннотациями и градуируются с интервалами от десятых до сотых. Поощряйте своих детей использовать наброски на пустых числовых строках, поскольку их арифметические навыки должны выходить за рамки сложения или вычитания путем счета отдельных единиц.
Вычитание десятичных знаков с использованием разрядаВычитание десятичных знаков часто требует перегруппировки (или разложения) 1 единицы на 10 меньших единиц. Прежде чем двигаться дальше, убедитесь, что вашим детям это удобно.При необходимости попрактикуйтесь с вопросами, подобными приведенным ниже, и / или используйте блоки Base-10 для моделирования перегруппировки.
32 = (3 x 10) + (2 x 1)
32 = (2 x 10) + (12 x 1)
0,23 = (2 x 0,1) + (3 x 0,01)
0,23 = (1 x 0,1) + (13 х 0,01)
Как и в случае с сложением, мы можем показать вычитание на диаграмме разряда со счетчиками, как показано в приведенных ниже примерах.
Убедитесь, что ваши дети знают, что, как и в приведенном выше примере, им не всегда нужно перегруппироваться при выполнении арифметической операции.
Вычитание десятичных знаков в числовой строкеМы можем использовать числовую линию для моделирования десятичного вычитания, как показано ниже, аналогично тому, как мы показали сложение.
5,6 — 1,8 = 3,8
Возможно, ваши дети разработали стратегии для выполнения арифметических операций с целыми числами, и эти же стратегии следует поощрять. Например, вычитание, показанное в числовой строке выше, можно рассматривать как вычитание двух целых единиц с последующим добавлением двух десятых для корректировки вычислений, как показано ниже.
Сложение и вычитание десятичной дроби — алгоритмОбладая безопасным пониманием десятичных знаков, ваши дети могут использовать стандартные алгоритмы сложения и вычитания. Это понимание поможет обеспечить соблюдение основного шага по выравниванию десятичных знаков.
Обязательно укажите десятичную точку в ответе.
Когда ноль ничего не значитВы можете обсудить с ребенком, как при сложении или вычитании целых чисел можно добавлять нули слева от числа, не влияя на его значение.
Та же самая логика может быть применена к десятым, сотым и тысячным долям, используя блоки с основанием 10 в качестве визуального ориентира.
Это поможет при сложении и вычитании чисел с разным количеством цифр.
Распространенные ошибки при сложении и вычитании десятичных знаковВ приведенном ниже примере показана распространенная ошибка, которая совершается при сложении и вычитании с десятичными знаками.
Выравнивание десятичной точки при вертикальном сложении или вычитании значительно упрощает вычисления.Также может потребоваться добавление нулей справа от десятичных чисел. При сложении десятичных и целых чисел учащимся также может потребоваться добавить десятичную точку справа от целого числа. Наконец, оценка ответа и сравнение его с рассчитанным ответом поможет избежать ошибок, которые не имеют смысла.
Задания
Попробуйте генератор листов десятичных разрядов. Он предоставляет неограниченное количество вопросов с добавлением десятичных знаков. Здесь также есть вопросы по вычитанию и умножению.
дробей и десятичных знаков — сложение и вычитание десятичных знаков
сложение и вычитание десятичных знаков
Переход на следующий уровень в нашей любимой видеоигре был крутым, но в то же время некоторым разочарованием. Следующий уровень почти такой же, как и предыдущий, но с добавлением еще нескольких проблем. Сложение и вычитание десятичных знаков такое же. Это в основном похоже на сложение целых чисел, но с еще одной или двумя задачами.
Во-первых, когда мы складываем и вычитаем десятичные дроби , нам нужно складывать числа друг на друга, как целые числа.Новая задача состоит в том, что нам также необходимо, чтобы десятичные точки в каждом номере выстраивались друг над другом. Это заставляет также выстраивать значения мест.
Здесь может пригодиться миллиметровая бумага. При необходимости вы можете бесплатно распечатать миллиметровую бумагу в Интернете.
Самое важное, чтобы сохраняла десятичную точку в нужном месте для каждого числа, которое вы добавляете или вычитаете. Когда десятичные дроби выстроены правильно, все остальное становится на свои места.
Другая проблема возникает, когда в разряде одного числа нет цифры, но есть для другого. Чтобы преодолеть эту проблему, все, что нам нужно сделать, это заполнить пустые места нулями.
Как сложить десятичные дроби
В задаче 0.569 + 45.1 первое число имеет 6 на десятом месте и 9 на тысячных. Но второе число, 45.1, не имеет цифры ни в одном из этих значений. Второе число также имеет разряд десятков, а первое — нет.
Когда мы складываем их и выстраиваем десятичные дроби, они выглядят так:
Что это за зияющая дыра над четверкой? А как насчет тех, что ниже 6 и 9? Это какой-то портал, через который монстр может пройти и забрать наш потрясающий тайник с золотом? Давайте заполним эти дыры нулями.
Теперь мы можем складывать как обычно.
00.569
+ 45.100
45.669
Пример задачи
Что такое 0,3 + 0,04 + 0,001?
Чтобы добавить десятичные дроби, мы помещаем нули в любые пустые значения по мере необходимости, чтобы все числа имели одинаковое количество десятичных знаков.
0,300
0,040
+ 0,001
0,341
Вычитание аналогично. Чтобы вычесть одно десятичное число из другого, сначала дайте двум десятичным знакам одинаковое количество десятичных знаков, добавляя нули по мере необходимости. Выровняйте десятичные точки, а затем произведите вычитание точно так же, как если бы вы делали это с целыми числами.
Целые числа против дробей или десятичных дробей
Скажите: «Целые числа — это числа, такие как 1, 3, 17 или 45. В числах нет частей, таких как дроби или десятичные дроби.”
Термины и определения:
Целое число — Число, не имеющее дробных частей (или десятичных знаков) и не являющееся отрицательным.
Дробь — значение, не являющееся целым числом. Обычно пишется с числителем (вверху) и знаменателем (внизу). Люди часто хотят, чтобы все дроби были «правильными» дробями — меньше 1. К дробям вроде 35/8 не относятся положительно.
Десятичное число — значение, не являющееся целым числом и записанное без использования знаменателей.Это потому, что «знаменатель» в десятичных дробях всегда примерно равен 10, 100, 1000 и т. Д. Вы пишете числитель справа от десятичной точки. Например, число 3,14 — это дробь 314/100 или 3 14/100.
Поддерживаемые концепции:
- Распознавание целых чисел
- Знание разницы между целыми числами и частями (дробями и десятичными знаками)
- Ценные значения, которые могут применяться к различным концепциям, включая расстояния
- Определение целых чисел в числовой строке
Полезное видео:
Обсуждение целых чисел, используемых для определения расстояний (вместе с некоторым их добавлением).
Другие ресурсы:
Рабочие листы для разметки линейки (используйте те, которые читаются как «целые» — верхний ряд в каждом разделе на этой странице)
Более длительная деятельность
Поддерживаемые стандарты:
TEKS 2 (9) (C) — Геометрия и измерения.
Учащийся применяет стандарты математического процесса для выбора и использования единиц измерения длины, площади и времени. Ожидается, что учащийся представит целые числа как расстояния от любого заданного места на числовой прямой.
CCSS.MATH.CONTENT.2.MD.B.6
Представляйте целые числа как длины от 0 на числовой линейной диаграмме с равноотстоящими точками, соответствующими числам 0, 1, 2,…, и представляйте целые числа суммы и разности в пределах 100 на числовой линейной диаграмме.
Способы изменения или расширения разговора:
Посмотрите вместе с ребенком на то, что вас окружает, и укажите целые числа, которые вы видите. Когда вы видите десятичные дроби или дроби, обратите на них внимание и скажите: «Это НЕ целые числа, потому что они содержат дробную или десятичную дробь.В целых числах нет дробей или десятичных знаков «. Поощряйте ребенка также указывать на некоторые из них.
Обсудите, где можно использовать целые числа и где вам действительно нужны части. Некоторые идеи — кексы против торта и небольшая порционная упаковка молока против галлона.