Сложение дробей с целой частью с разными знаменателями: Сложение и вычитание смешанных чисел (разные знаменатели) — урок. Математика, 5 класс.

Содержание

§ Сложение дробей с разными знаменателями. Как найти общий знаменатель

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь

Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Если вам нечего ответить своему оппоненту, не всё потеряно: вы можете сказать, что вы о нём думаете.

Элберт Хаббард

на главную

Введите тему

Поддержать сайт

Дроби. Числитель и знаменатель Сокращение дробей Сравнение дробей Смешанные числа. Выделить целую часть Сложение дробей. Общий знаменатель Вычитание дробей Умножение дробей Деление дробей Нахождение дроби от числа Нахождение целого по известной дроби

При сложении дробей могут встретиться разные случаи.

Сложение дробей с одинаковыми знаменателями

Такой случай наиболее простой. При сложении дробей с равными знаменателями складывают числители, а знаменатель оставляют тот же.

Пример.

C помощью букв это правило сложения можно записать так:

Запомните!

Записывая ответ, проверьте нельзя ли полученную дробь сократить.

Сложение дробей с разными знаменателями

Чтобы сложить дроби с разными знаменателями нужно воспользоваться следующими правилами.

Привести данные дроби к наименьшему общему знаменателю (НОЗ). Для этого найти наименьшее общее кратное знаменателей.

Пример. Сложить дроби.

Как найти общий знаменатель

Находим НОК (15, 18).

НОК (15, 18) = 3 · 2 · 3 · 5 = 90

Найти дополнительные множители для каждой дроби. Для этого наименьший общий знаменатель (НОК из пункта 1) делим по очереди на знаменатель каждой дроби.
Полученные числа и будут дополнительными множителями для каждой из дробей. Множители записываем над числителем дроби справа сверху.
90 : 15 = 6 — дополнительный множитель для дроби
.
90 : 18 = 5 — дополнительный множитель для дроби
.
Числитель и знаменатель каждой дроби умножаем на свой дополнительный множитель, пользуясь основным свойством дроби.
После умножения в знаменателях обеих дробей должен получиться наименьший общий знаменатель. Затем складываем дроби как дроби с одинаковыми знаменателями.
Проверяем полученную дробь.
- Eсли в результате получилась неправильная дробь, результат записываем в виде смешанного числа. Проверим нашу дробь.
  38 < 90
  У нас дробь правильная.
- Если в результате получилась сократимая дробь, необходимо выполнить сокращение.
Ещё раз весь пример целиком.

Сложение смешанных чисел

Сочетательное и переместитительное свойства сложения позволяют привести сложение смешанных чисел к сложению их целых частей и к сложению их дробных частей.

Чтобы сложить смешанные числа нужно.

Отдельно сложить их целые части.
Пример.
Складываем целые части.
Отдельно сложить дробные части.
Если у дробных частей знаменатели разные, то сначала приводим их к общему знаменателю, а затем складываем.
Сложить полученные результаты из пунктов 1 и 2.
Если при сложении дробных частей получилась неправильная дробь, то нужно выделить целую часть из этой дроби и прибавить к полученной в пункте 1 целой части.

Ещё один пример на

сложение смешанных чисел.

Смешанные числа. Сложение и вычитание

Смешанные числа: определения, примеры

Смешанное число — это число, состоящее из натурального числа и обыкновенной дроби. Пишут в виде .

Где n — целая часть, — дробная часть.

Смешанное число равно сумме своей целой и дробной части. То есть .

Примеры смешанных чисел

Каждое такое смешанное число содержит целую и дробную части.

Чтобы точно определять, какая именно перед вами дробь, запомните:

Дробь виданазывается правильной дробью. В ней числитель всегда меньше знаменателя.
Дробь виданазывается неправильной. В таких дробях числитель больше знаменателя или равен ему.
Дробь виданазывается смешанной дробью/смешанным числом. Такая дробь состоит из целой части (натуральное число) и дробной части.

Смешанные числа можно складывать, вычитать, умножать и делить. Давайте узнаем, как именно это делать.

Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Сложение смешанных чисел

Всего мы рассмотрим три типа сложения со смешанными числами. В каждом подпункте приведено необходимое правило и примеры выполнения решений.

Сложение смешанного числа и натурального числа

Запоминаем

Чтобы сложить смешанное число и натуральное число, прибавьте натурально число к целой части смешанного числа, а дробную часть оставьте нетронутой.

Представим первое правило в виде буквенных выражений.

Выполним сложение смешанного числа и натурального числа d.

Известно, что любое смешанное число равное сумме целой и дробной частей.

Это значит, что .

Тогда .

Рассмотрим примеры сложения смешанных чисел с натуральными числами.

Пример 1. Выполните сложение смешанного числа и натурального числа 18.

Как решаем:

Записываем выражение

Согласно правилу, прибавляем к натуральному числу целую часть смешанного числа и вычисляем: .

Ответ: .

Пример 2. Выполните сложение смешанного числа и натурального числа 10.

Как решаем:

Записываем выражение: .

Ответ: .

Пример 3. Выполните сложение смешанного числа и натурального числа 2.

Как решаем:

Записываем выражение:

Ответ: .

Сложение смешанного числа со смешанным числом

Запоминаем

Чтобы сложить смешанное число с другим смешанным числом, сложите сначала целые части этих чисел, а затем — дробные части.

Представим правило в виде буквенных выражений.

Выполним сложение смешанного числа и смешанного числа .

Следуя правилу, запишем выражение в виде: .

Рассмотрим примеры сложения смешанных чисел.

Пример 1. Сложите смешанное число и смешанное число .

Как решаем:

Записываем выражение: .

Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части:

Решаем: складываем целые части 2 + 7 = 9.

Чтобы выполнить сложение дробных частей, воспользуемся правилом сложения дробей с разными знаменателями: приведем дроби к наименьшему общему знаменателю и выполним сложение.

Наименьшее общее кратное 5 и 15 — 15.

Если в результате сложения получилась сократимая дробь, сокращайте, не задумываясь: сокращаем на 3, получим дробь.

Ответ: .

Пример 2. Сложите смешанное число и смешанное число .

Как решаем:

Записываем выражение: .

Согласно правилу, складываем последовательно целые части смешанных чисел, затем складываем дробные части: .

Решаем: складываем целые части 13 + 2 = 15.

Складываем дробные части

Наименьшее общее кратное 12 и 20 равно 60.

Сокращаем дробь на .

Ответ:

Таким же образом можно складывать три, четыре и больше натуральных чисел. Не забывайте сокращать дроби и выделять целые части из неправильных дробей.

Сложение смешанного числа и правильной дроби

Запоминаем

Чтобы выполнить сложение смешанного числа и правильной дроби, прибавьте к дроби дробную часть смешанного числа, а целую часть оставьте без изменений.

Представим правило в виде буквенного выражения.

Если нам нужно сложить смешанное число и правильную дробь , то запишем следующее выражение: .

Рассмотрим примеры сложения смешанных чисел с обыкновенными дробями.

Пример 1. Выполните сложение обыкновенной дроби и смешанного числа

Как решаем:

Записываем выражение:

Согласно правилу, складываем дробь с дробной частью смешанного числа:

Складываем дроби .

Наименьшее общее кратное 5 и 20 равно 20.

, сокращаем на 5, получается .

Ответ: .

Пример 2. Выполните сложение правильной дроби и смешанного числа .

Как решаем:

Записываем выражение: .

Следуя правилу, складываем дробь с дробной частью смешанного числа:

Складываем дроби .

Наименьшее общее кратное 4 и 2 равно 4.

Ответ: .

Чтобы выполнить сложение смешанного числа и неправильной обыкновенной дроби, выделите целую часть из неправильной дроби и выполните сложение смешанных чисел.

Вычитание смешанных чисел

Рассмотрим три типа вычитания со смешанными числами. В каждом подпункте вы найдете правила и решение примеров с разбором.

Вычитание одного смешанного числа из другого

Запоминаем

Любое смешанное число можно представить в виде суммы целой и дробной части.

Это значит, что .

Исходя из значения дробных частей, вычитание можно выполнять тремя способами.

Если дробная часть уменьшаемого больше дробной части вычитаемого , то выполняем вычитание целой части вычитаемого из целой части уменьшаемого, затем выполняем вычитание дробных частей. Вот так:

Пример. Выполните вычитание .

Как решаем:

Чтобы решить пример, нужно выяснить, какая из дробных частей больше:

или .

Чтобы сравнить две дроби, приведем их к общему знаменателю — 8:

По правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, чей числитель больше.

Это значит, что .

Следуя правилу, выполняем вычитание .

Вычитаем дробные части .

НОК = 8

Ответ: .

Запоминаем

Если дробные части смешанных чисел равны, то есть , то разность этих смешанных чисел будет равна разности их целых частей.

при .

Пример. Выполните вычитание:

Как решаем:

Дробные части смешанных чисел равны. Это значит, что .

Следуя правилу, выполним вычитание:

Ответ: .

Запоминаем

Если дробная часть уменьшаемого меньше дробной части вычитаемого , то вычитание выполняется вот так .

Пример. Найдите значение разности смешанных чисел и

Как решаем:

Запишем выражение

Сначала выясним, как из дробных частей больше. Для этого приведем их к НОЗ.

НОК 5 и 15 = 15.

Следуя правилу, решаем:

Представим число 21 в виде смешанной дроби и выполним вычитание дроби из натурального числа:

Ответ: .

Вычитание смешанного числа из натурального числа

Запоминаем

Чтобы из целого числа вычесть смешанное число, сначала отнимите от натурального числа целую часть смешанного числа, а затем отнимите от этой разности дробную часть смешанного числа.

Представим правило в виде буквенного выражения: .

Пример. Отнимите от натурального числа 15 смешанное число

Как решаем:

Запишем выражение: .

Следуя правилу, выполним вычитание целой части смешанного числа из натурального числа:

Ответ:

Умножение смешанных чисел

Давайте разберемся как выполнять умножение в примерах, где есть смешанные числа.

Умножение смешанного числа на смешанное число

Запоминаем

Чтобы умножить одно смешанное число на другое, нужно перевести оба смешанных числа в неправильные дроби, а затем выполнить умножение по правилу умножения дробей.

Пример. Выполните умножение смешанного числа и

Как решаем:

Запишем выражение

Следуя правилу, переведем смешанные числа в неправильные дроби.

Выполним умножение: .

Из полученной неправильной дроби выделяем целую часть .

Ответ: .

Умножение смешанного числа на обыкновенную дробь

Запоминаем

Чтобы выполнить умножение смешанного числа и обыкновенной дроби, представьте смешанное число в виде неправильной дроби и выполните умножение дробей.

Пример. Умножьте смешанное число на обыкновенную дробь

Как решаем:

Запишем выражение

Представим смешанное число в виде неправильной дроби.

Выполним умножение дробей

Выделим из полученной неправильной дроби целую часть

Ответ: .

Умножение целого числа на дробь

Запоминаем

Чтобы умножить целое число на дробь, просто умножьте это число на числитель дроби.

Пример. Выполните умножение числа 7 на обыкновенную дробь

Как решаем:

Запишем выражение:

Выделим из получившейся неправильной дроби целую часть .

Ответ:

Деление смешанных чисел

Вы уже рассмотрели три типа арифметических действий со смешанными числами. Осталось разобраться, как выполнять деление в примерах, где есть смешанные числа. Давай научимся это делать.

Деление смешанного числа на смешанное число

Запоминаем

Чтобы разделить одно смешанное число на другое, переведите оба числа в неправильные дроби и выполните деление, следуя правилу деления дробей.

Пример. Найдите результат деления смешанного числа на смешанное число

Как решаем:

Запишем выражение:

Следуя правилу, переведем оба смешанных числа в неправильные дроби.

Пользуясь правилом деления дробей, находим частное:

Ответ: .

Деление смешанного числа на целое число

Запоминаем

Чтобы разделить смешанное число на целое число, переведите смешанное число в неправильную дробь и выполните деление.

Пример. Разделите смешанное число на натуральное число 15

Как решаем:

Запишем выражение

Следуя правилу, переведем смешанное число в неправильную дробь

Выполним деление

Ответ: .

Деление целого числа на смешанное число

Запоминаем

Чтобы разделить целое число на смешанное число, переведите смешанное число в неправильную дробь и выполните деление.

Пример. Выполните деление натурального числа 30 на смешанное число

Запишем выражение

Представим смешанное число в виде неправильной дроби .

Выполним деление .

Выделим из полученной неправильной дроби целую часть .

Ответ: .

Деление смешанного числа на обыкновенную дробь

Запоминаем

Чтобы разделить смешанное число на обыкновенную дробь, представьте смешанное число в виде неправильной дроби и выполните деление.

Пример. Разделите смешанное число на обыкновенную дробь

Как решаем:

Запишем выражение .

Представим смешанное число в виде неправильной дроби .

Выполним деление, следуя правилу деления дробей: .

Ответ: .

Сложение и вычитание дробей с разными, одинаковыми знаменателями. Вычитание смешанных дробей в 2023 году

Как складывать дроби

Говоря о сложении дробей следует выделить сложение дробей с одинаковыми знаменателями и сложение дробей, имеющих разные знаменатели. Поэтому начнем с первого и более простого варианта.

Сложение дробей с одинаковыми знаменателями

Для того чтобы понять, как добавляются дроби с одинаковыми знаменателями, рассмотрим задачу.

Пример. На столе лежит три седьмых части арбуза, через некоторое время на стол положили еще две седьмые части арбуза. Сколько всего частей арбуза стало на столе?

Действие сложения можем записать так: 3/7 + 2/7

В результате на столе стало 3 + 2 = 5 седьмых частей арбуза, то есть 5/7. Таким образом, 3/7 + 2/7 = 5/7

Следовательно, в результате сложения дробей с одинаковым знаменателем мы получили дробь, числитель которой равен сумме числителей прилагаемых дробей, а знаменатель равен знаменателю исходных дробей.

Запишем действие добавления дробей в общем виде, где b – одинаковый знаменатель, a и c – числители прилагаемых дробей.

Чтобы добавить дроби с одинаковыми знаменателями, нужно добавить их числители и знаменатель оставить без изменений.

Обратите внимание, при сложении дробных чисел можно пользоваться свойствами и законами сложения натуральных чисел. Переставной, связующий законы действуют также и при сложении дробей.

Приклад. Как сложить дроби 3/43 і 9/43

Поскольку дроби имеют одинаковые знаменатели, следует добавить числители и знаменатель оставить без изменений: 3 + 9 = 12 запишем в числителе суммы, знаменатель суммы – 43.

Ответ: 12/43

Еще одно важное правило: если после сложения дробей получили дробь, которую можно сократить, то нужно выполнить действие сокращения. Если в сумме получили неправильную дробь, то нужно превратить ее в смешанное число.

Пример. Найти сумму дробей 3/14 і 5/14

В результате сложения получили дробь, которую можно сократить, ведь числитель и знаменатель можно разделить на 2

Пример. Найти сумму дробей 7/24 і 21/24

В результате получили неправильную сократимую дробь, которую нужно сократить.

После сокращения получили неправильную дробь 7/6, которую можно превратить в правильную, выделив целую часть.

Сложение дробей с разными знаменателями

Поскольку мы умеем сложить дроби с одинаковыми знаменателями, то для того чтобы сложить дроби с разными знаменателями, нужно их сначала свести к общему знаменателю.

Правило сложения в данном случае звучит так:

Для того чтобы сложить дроби с разными знаменателями, нужно их сначала свести к общему знаменателю, после этого следует сложить числители и в знаменатель записать общий знаменатель дробей.

Пример. Сложить дроби 5/6 і 3/12

Поскольку дроби имеют разные знаменатели, сначала сведем их к общему знаменателю.

НОК (6; 12) = 12

Дополнительные множители: 12 : 6 = 2, 12 : 12 = 1

Получим следующие дроби:

Выполним сложение дробей:

После сложения получили неправильную дробь 13/12, которую превратили в смешанное число 1 1/12

Сложение обыкновенной дроби и натурального числа

При сложении натурального числа и правильной дроби получим смешанное число, целая часть которого соответствует натуральному числу, а дробная – прилагаемой дроби.

Например,

При сложении целого числа и неправильной дроби следует выделить из дроби целую часть. После этого натуральное число суммируют с выделенной целой частью и добавляют дробную часть.

Сложение смешанных чисел

При сложении смешанных чисел пользуются переставным и связующими законами сложения. Благодаря этим свойствам удобнее добавить целые и дробные части смешанных чисел. Следовательно, адлгоритм сложения смешанных чисел будет следующим:

Добавляем целые части смешанных чисел
Добавляем дробные части чисел. Если дробные части имеют разные знаменатели, то перед добавлением сводим их к общему знаменателю
Добавляем полученные результаты и при необходимости сокращаем дробь, выделяем целую часть.

Пример. Найти сумму смешанных чисел:

Аналогично добавляются дроби, смешанные числа, содержащие три и более слагаемых.

Пример:

В данном примере мы использовали переставной и связующий законы сложения, что позволило упростить расчеты и быстро найти сумму.

Как отнимать дроби?

Вычитание дробей с одинаковыми знаменателями

Чтобы понять суть вычитания дробей, имеющих одинаковые знаменатели, рассмотрим задачу.

Задача. На столе лежало 5/7 частей арбуза, Олег съел 2/7 частей. Сколько частей арбуза осталось?

Логично, что осталось 5 – 2 = 3 седьмых части (3/7).

Чтобы отнять дроби с одинаковыми знаменателями, надо от числителя уменьшаемого отнять числитель вычитаемого и оставить знаменатель без изменений.

Пример. Отнять 3/17 от дроба 15/17

При необходимости полученную дробь в разности следует сократить или выделить целую часть.

Пример. Из 24/15 вычесть 4/15

После выполнения вычитания получили неправильную дробь, которую можно сократить, поделив числитель и знаменатель на 5. Получим дробь 4/3, перевторив в смешанное число, получили результат одна целая одна третья.

Вычитание дробей с разными знаменателями

Для того чтобы отнять дроби с разными знаменателями, нужно их сначала свести к общему знаменателю, после этого от числителя уменьшаемого надо отнять числитель вычитаемого, в знаменатель дроби записать общий знаменатель.

Пример. Вычесть дроби: 2/9 і 1/15

В первую очередь сводим дроби к общему знаменателю, определив наименьшее общее кратное число 9 и 15:

НОК (9; 15) = 45

Находим дополнительные множители: 45 : 9 = 5 і 45 : 15 = 3

Перемножим числители дробей на соответствующие дополнительные множители, получим числитель первой дроби: 5 ⋅ 2 =10, а числитель второй дроби: 1 ⋅ 3 = 3.

Вычтем числители: 10 – 3 = 7, знаменатель дроби 45

Пример. Из дроби 11/12 вычесть дробь 5/8

Вычитание смешанных дробей (смешаных чисел) с разными знаменателями

Для того чтобы вычесть смешанные числа, нужно сначала свести их к общему знаменателю. После этого поочередно вычитаем целые и дробные части.

Пример. Найти разность смешанных дробей:

Решение:

Если дробная часть уменьшаемого меньше дробной части вычитаемого, то надо взять одну единицу из целой части уменьшаемого, дробить ее в те частицы, в которых выражена дробная часть, и добавить к дробной части уменьшаемого.

На примере это будет выглядеть так:

Пример. Найти разность смешанных чисел:

Вычитание дроби из натурального числа

Для того чтобы отнять от натурального числа дробь, можно натуральное число представить в виде дроби.

Пример. Из числа 8 вычесть 2/3

Рассмотрим еще несколько примеров на вычитание натуральных и смешанных чисел

Пример. Найти разность чисел 4 и три целых три пятых

Пример. Найти разность чисел 1065 и 13/62

Представим уменьшаемое 1065 как сумму чисел 1064 и 1 и выполним вычисление:

Вычитание натурального числа из обычной дроби: как отнять целое число из дроби

Для выполнения данного действия следует отразить натуральное число в виде обычной дроби со знаменателем единицей и свести к общему знаменателю.

Таким образом, для сложения и вычитания дробей можно использовать правила, законы и свойства сложения и вычитания натуральных чисел. Удобно группировать числа с числами, дроби с дробями, как в примерах ниже:

Смешанные числа

В предыдущих уроках было сказано, что дробь, состоящая из целой и дробной части, называется смешанной.

Все дроби, имеющие целую и дробную часть, носят одно общее название — смешанные числа.

Смешанные числа так же как и обыкновенные дроби можно складывать, вычитать, умножать и делить. В данном уроке мы рассмотрим каждое из этих действий по отдельности.

Сложение целого числа и правильной дроби

Встречаются задачи, в которых требуется сложить целое число и правильную дробь. Например, сложить число 2 и дробь . Чтобы решить этот пример, нужно число 2 представить в виде дроби . Затем сложить дроби с разными знаменателями:

А теперь внимательно посмотрим на этот пример. Смотрим на его начало и на его конец. Начало у него выглядит так: , а конец так: . Различие в том, что в первом случае число 2 и дробь соединяются знаком сложения, а во втором случае они записаны вместе. На самом деле это одно и то же. Дело в том, что это свёрнутая форма записи смешанного числа, а — развёрнутая.

Когда перед нами смешанное число вида , мы должны понимать, что знак сложения опущен.

Какой можно сделать вывод? Если потребуется сложить целое число и правильную дробь, можно опустить плюс и записать целое число и дробь вместе.

Значит значение выражения равно

Если к двум целым пиццам прибавить половину пиццы, то получится две целые пиццы и ещё половина пиццы:

Пример 2. Найти значение выражения

Представим число 3 в виде дроби . Затем сложим дроби с разными знаменателями:

Это первый способ. Второй способ намного проще. Можно поставить знак равенства и записать целую и дробную часть вместе. То есть опустить знак сложения:

Пример 3. Найти значение выражения

Можно записать вместе число 2 и дробь , но этот ответ не будет окончательным, поскольку в дроби можно выделить целую часть.

Поэтому в данном примере сначала нужно выделить целую часть в дроби . Пять вторых это две целых и одна вторая:

Теперь в главном выражении вместо дроби запишем смешанное число

Получили новое выражение . В этом выражении смешанное число запишем в развёрнутом виде:

Применим сочетательный закон сложения. Сложим две двойки, получим 4:

Теперь свернём полученное смешанное число:

Это окончательный ответ. Подробное решение этого примера можно записать следующим образом:

Сложение смешанных чисел

Встречаются задачи, в которых требуется сложить смешанные числа. Например, найти значение выражения . Чтобы решить этот пример, нужно целые и дробные части сложить по отдельности.

Для начала запишем смешанные числа в развёрнутом виде:

Применим сочетательный закон сложения. Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 2 + 3 = 5. В главном выражении заменяем выражение в скобках (2 + 3) на полученную пятёрку:

Теперь вычислим дробные части. Это сложение дробей с разными знаменателями. Как складывать такие дроби мы уже знаем:

Получили . Теперь в главном выражении заменяем дробные части на полученную дробь

Теперь свернем полученное смешанное число:

Таким образом, значение выражения равно . Попробуем изобразить это решение в виде рисунка. Если к двум целым и половине пиццы прибавить три целые и одну восьмую пиццы, то получится пять целых пицц и ещё пять восьмых пиццы:

Подобные примеры нужно решать быстро, не останавливаясь на подробностях. Находясь в школе, нам пришлось бы записать решение этого примера следующим образом:

Если в будущем увидите такое короткое решение, не пугайтесь. Вы уже понимаете, что откуда взялось.

Пример 2. Найти значение выражения

Запишем смешанные числа в развёрнутом виде:

Сгруппируем целые и дробные части по отдельности:

Вычислим целые части: 5 + 3 = 8. В главном выражении заменяем выражение в скобках (5 + 3) на полученное число 8

Теперь вычислим дробные части:

Получили смешанное число . Теперь в главном выражении заменяем выражение в скобках на полученное смешанное число

Получили выражение . В данном случае число 8 надо прибавить к целой части смешанного числа . Для этого смешанное число можно временно развернуть, чтобы было понятнее, что с чем складывать:

Сложим целые части. Получаем 9

Сворачиваем готовый ответ:

Таким образом, значение выражения равно .

Полное решение этого примера выглядит следующим образом:

Для решения подобных примеров существует универсальное правило. Выглядит оно следующим образом:

Чтобы сложить смешанные числа, надо:

привести дробные части этих чисел к общему знаменателю;
отдельно выполнить сложение целых и дробных частей.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть в этой дроби и прибавить ее к полученной целой части.

Применение готовых правил допустимо в том случае, если суть темы полностью понятна. Решение по-шаблону, поглядывая в другие подобные примеры, приводит к ошибкам на обнаружение которых уходит дополнительное время. Поэтому, сначала разумнее понять тему, а затем пользоваться готовым правилом.

Пример 3. Найти значение выражения

Воспользуемся готовым правилом. Приведём дробные части к общему знаменателю, затем по отдельности сложим целые и дробные части:

Сложение целого и смешанного числа

Встречаются задачи, в которых нужно сложить целое и смешанное число. Например, сложить 2 и смешанное число . В этом случае целые части складываются отдельно, а дробная часть остаётся без изменения:

Здесь смешанная дробь была развёрнута в ходе решения, затем целые части были сгруппированы и сложены. В конце целая и дробная части были свёрнуты. В результате получили ответ .

Попробуем изобразить это решение в виде рисунка. Если к двум целым пиццам прибавить три целые и треть пиццы, то получятся пять целых и треть пиццы:

Пример 2. Найти значение выражения

В этом примере, как и в предыдущем, нужно сложить целые части:

Осталось свернуть целую и дробную части, но дело в том, что дробная часть представляет собой неправильную дробь. Сначала нужно выделить целую часть в этой неправильной дроби. Затем целую часть этой дроби прибавить к 4, а дробную часть оставить без изменения. Продолжим данный пример на новой строке:

Вычитание дроби из целого числа

Встречаются задачи, в которых требуется вычесть дробь из целого числа. Например, вычесть из числа 1 дробь . Чтобы решить такой пример, нужно целое число 1 представить в виде дроби , и выполнить вычитание дробей с разными знаменателями:

Если имеется одна целая пицца и мы вычтем из неё половину пиццы, то у нас получится половина пиццы:

Пример 2. Найти значение выражения .

Представим число 2 в виде дроби , и выполним вычитание дробей с разными знаменателями:

Если имеются две целые пиццы и мы вычтем из низ половину, то останется одна целая и половина пиццы:

Такие примеры можно решать в уме. Достаточно суметь воспроизвести их в своём воображении. К примеру, найдём значение выражения , не приводя на бумаге никаких вычислений.

Представим, что число 3 это три пиццы:

Нужно вычесть из них . Мы помним, что треть выглядит следующим образом:

Теперь представим, во что превратятся три пиццы, если отрезать от них эту треть

Получилось (две целых и две трети пиццы).

Чтобы убедиться в правильности решения, можно найти значение выражения обычным методом, представив число 3 в виде дроби, и выполнив вычитание дробей с разными знаменателями:

Пример 3. Найти значение выражения

Представим число 3 в виде дроби . Затем выполним вычитание дробей с разными знаменателями:

Вычитание смешанного числа из целого числа

Теперь мы готовы к тому, чтобы вычесть смешанное число из целого числа. Найдём значение выражения .

Чтобы решить этот пример, число 5 нужно представить в виде дроби, а смешанное число перевести в неправильную дробь. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:

Если из пяти целых пицц вычесть одну целую и половину пиццы, то останутся три целые пиццы и половина пиццы:

Пример 2. Найти значение выражения

Представим 6 в виде дроби , а смешанное число , в виде неправильной дроби. После перевода смешанного числа в неправильную дробь, получим дробь . Теперь выполним вычитание дробей с разными знаменателями:

Примеры на вычитание дроби из числа или вычитание смешанной дроби из числа опять же можно выполнять в уме. Этот процесс легко поддаётся воображению.

К примеру, если нужно быстро найти значение выражения , то вовсе необязательно представлять число 2 в виде дроби и выполнять вычитание дробей с разными знаменателями. Число 2 можно вообразить, как две целые пиццы и далее представить, как от одной из них отрезали две третьих (два куска из трёх)

Тогда от той пиццы, от которой отрезали останется пиццы. Плюс одна из пицц останется нетронутой. Получится одна целая пицца и треть пиццы:

Если на рисунке вы закроете рукой две третьих пиццы (она закрашена), то сразу всё поймёте.

Вычитание смешанных чисел

Встречаются задачи, в которых требуется вычесть из одного смешанного числа другое смешанное число. Например, найдём значение выражения:

Чтобы решить этот пример, нужно смешанные числа и перевести в неправильные дроби, затем выполнить вычитание дробей с разными знаменателями:

Если от трёх целых и половины пиццы вычесть две целые и треть пиццы, то останутся одна целая и одна шестая пиццы:

Пример 2. Найти значение выражения

Переводим смешанные числа и в неправильные дроби и выполняем вычитание дробей с разными знаменателями:

К вычитанию смешанных чисел мы ещё вернёмся. В вычитании дробей есть немало тонкостей, которым новичок пока не готов. Например, возможен случай, когда уменьшаемое может оказаться меньше вычитаемого. Это может вывести нас в мир отрицательных чисел, которых мы ещё не изучали.

А пока изучим умножение смешанных чисел. Благо оно не такое сложное, как сложение и вычитание.

Умножение целого числа на дробь

Чтобы целое число умножить на дробь, достаточно умножить это целое число на числитель дроби, а знаменатель оставить без изменения.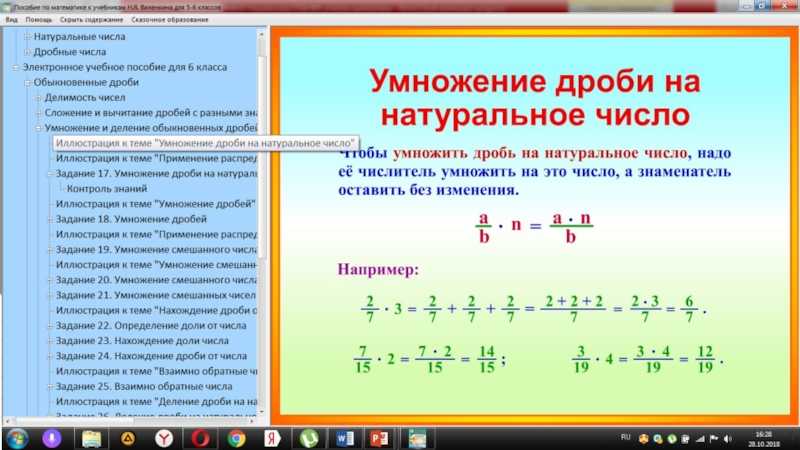

Например, умножим число 5 на дробь . Чтобы решить этот пример, нужно число 5 умножить на числитель дроби , а знаменатель оставить без изменения:

В ответе получилась неправильная дробь. Выделим в ней целую часть:

Если имеются пять целых пицц и мы возьмём от этого количества половину, то у нас окажется две целые пиццы и половина пиццы:

Пример 2. Найти значение выражения

Умножим число 3 на числитель дроби

В ответе получилась неправильная дробь , но мы выделили её целую часть и получили 2.

Также, можно было сократить эту дробь. Получился бы тот же результат. Выглядело бы это следующим образом:

Если имеются три целые пиццы и мы возьмём от этого количества две третьих, то у нас окажется две целые пиццы:

Пример 3. Найти значение выражения

Этот пример решается так же, как и предыдущие. Целое число и числитель дроби нужно перемножить:

Пример 4. Найти значение выражения

Умножим число 3 на числитель дроби

Умножение смешанного числа на дробь

Чтобы умножить смешанное число на дробь, нужно смешанное число перевести в неправильную дробь, затем выполнить перемножение обыкновенных дробей.

Пример 1. Найти значение выражения

Переведём смешанное число в неправильную дробь. После перевода это число превратится в дробь . Затем можно будет умножить эту дробь на

Допустим, имеются одна целая и половина пиццы:

Умножить эти куски на означает взять от них две трети. Чтобы взять от них две трети, сначала разделим их на три равные части. Разделим пополам ту пиццу, которая слева. Тогда у нас получится три равных куска:

Теперь если мы возьмем (два куска из трёх имеющихся), то получим одну целую пиццу. Для наглядности закрасим эти два куска:

Поэтому значение выражения было равно 1

Умножение смешанных чисел

Встречаются задачи, в которых требуется перемножить смешанные числа. Например, перемножить и . Чтобы решить этот пример, нужно перевести эти смешанные числа в неправильные дроби, затем выполнить умножение неправильных дробей:

Попробуем разобраться в этом примере с помощью рисунка. Допустим, имеются одна целая и половина пиццы:

Теперь разберемся со смешанным множителем . Этот множитель означает, что одну целую и половину пиццы нужно взять 2 раза и еще раза.

С множителем 2 всё понятно, он означает что одну целую и половину пиццы нужно взять два раза. Давайте возьмём два раза целую пиццу и половину:

Но ещё осталось взять от изначальной целой пиццы и половины, ведь множителем было смешанное число . Для этого вернёмся к изначальной одной целой и половине пиццы, и разделим их на равные части так, чтобы можно было взять от них ровно половину. А половину мы сможем взять, если разделим целую пиццу на четыре части, а половину на две части:

Мы разделили нашу целую пиццу и половину на равные части, и теперь можем сказать, что является половиной от этих кусков. Половиной от этих кусков является пиццы. Это можно хорошо увидеть, если мы упорядочим наши равные кусочки следующим образом:

А если смотреть на изначальную целую пиццу и половину с точки зрения такого порядка, как на этом рисунке, то половиной от них является пиццы.

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переводим смешанные числа в неправильные дроби и перемножаем эти неправильные дроби. Если в ответе получится неправильная дробь, выделим в ней целую часть:

Деление целого числа на дробь

Чтобы разделить целое число на дробь, нужно это целое число умножить на дробь, обратную делителю.

Например, разделим число 3 на дробь . Здесь число 3 — это делимое, а дробь — делитель.

Чтобы решить этот пример, нужно число 3 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 3 на дробь

Допустим, имеются три целые пиццы:

Если мы зададим вопрос «cколько раз (половина пиццы) содержится в трёх пиццах», то ответом будет «шесть раз».

Действительно, если мы разделим каждую пиццу пополам, то у нас получится шесть половинок:

Поэтому значение выражения равно 6.

Пример 2. Найти значение выражения

Чтобы решить этот пример, нужно число 2 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь

Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз пиццы содержится в этих двух пиццах?» Чтобы ответить на этот вопрос, выделим целую часть в дроби . После выделения целой части в этой дроби получим

Теперь поставим вопрос так: «Сколько раз (одна целая и половина пиццы) содержится в двух пиццах?».

Чтобы ответить на этот вопрос, нужно найти в двух пиццах такое количество пиццы, которое изображено на следующем рисунке:

В двух пиццах одна целая и половина пиццы содержится один раз. Это можно увидеть, если вторую пиццу разделить пополам:

А оставшаяся половина это треть от , которая не вместилась. Третью она является по той причине, что в одной целой и половине пиццы целую часть пиццы можно разделить пополам. Тогда каждый кусок будет третью от этого количества:

Поэтому значение выражения равно

Пример 3. Найти значение выражения

Чтобы решить этот пример, нужно число 5 умножить на дробь, обратную дроби . А обратная дробь для дроби это дробь . Поэтому умножаем число 5 на

Дробь это 2 целых и . Проще говоря, две целые и четверть пиццы:

А выражение определяет сколько раз содержится в пяти целых пиццах. Ответом было смешанное число .

То есть пиццы содержится в пяти целых пиццах раза.

Давайте нащупаем в пяти пиццах два раза по

Белым цветом осталось не выделено две четверти. Эти две четверти представляют собой от , которые не вместились. Двумя девятыми они являются по той причине, что в пиццы каждую целую пиццу можно разделить на четыре части. Тогда каждый кусок будет девятой частью от этого количества, а два куска соответственно двумя из девяти:

Поэтому значение выражения равно

Деление дроби на целое число

Чтобы разделить дробь на целое число, нужно данную дробь умножить на число, обратное делителю. Таким делением мы занимались в прошлом уроке. Вспомним ещё раз.

Пример 1. Разделим дробь на число 2

Чтобы разделить дробь на 2, нужно данную дробь умножить на число, обратное числу 2. А обратное числу 2 это дробь

Пусть имеется половина пиццы:

Разделим её поровну на две части. Тогда каждая получившаяся часть будет одной четвертой пиццы:

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Чтобы решить этот пример, нужно дробь умножить на число, обратное числу 2. Обратное числу 2 это дробь

Пример 3. Найти значение выражения

Умножаем первую дробь на число, обратное числу 3. Обратное числу 3 это дробь

Деление целого числа на смешанное число

Встречаются задачи, в которых требуется разделить целое число на смешанное число. Например, разделим 2 на .

Чтобы решить этот пример, нужно делитель перевести в неправильную дробь. Затем умножить число 2 на дробь, обратную делителю.

Переведём делитель в неправильную дробь, получим . Затем умножим 2 на дробь, обратную дроби . Обратная для дроби это дробь

Допустим, имеются две целые пиццы:

Зададим вопрос «Сколько раз (одна целая и половина пиццы) содержится в двух целых пиццах?». Похожий пример мы решали ранее, когда учились делить целое число на дробь.

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переводим делитель в неправильную дробь, получаем . Теперь умножаем число 5 на дробь, обратную дроби . Обратная для дроби это дробь

Сначала мы получили ответ , затем сократили эту дробь на 5, и получили , но этот ответ нас тоже не устроил, поскольку он представлял собой неправильную дробь. Мы выделили в этой неправильной дроби целую часть. В результате получили ответ

Деление смешанного числа на целое число

Чтобы разделить смешанное число на целое число, нужно смешанное число перевести в неправильную дробь, затем умножить эту дробь на число, обратное делителю.

Например, разделим на 2. Чтобы решить этот пример, нужно делимое перевести в неправильную дробь. Затем умножить эту дробь на число, обратное делителю 2.

Переведём смешанное число в неправильную дробь, получим .

Теперь умножаем на число, обратное числу 2. Обратное числу 2 это дробь

Допустим, имеется одна целая и половина пиццы:

Разделим это количество пиццы поровну на две части. Для этого сначала разделим на две части целую пиццу:

Затем разделим поровну на две части и половину:

Теперь если мы сгруппируем эти кусочки на две группы, то получим по пиццы в каждой группе:

Поэтому значение выражения равно

Пример 2. Найти значение выражения

Переведём делимое в неправильную дробь, получим . Теперь умножаем на число, обратное числу 4. Обратное числу 4 это дробь .

Деление смешанных чисел

Чтобы разделить смешанные числа, нужно перевести их в неправильные дроби, затем выполнить обычное деление дробей. То есть умножить первую дробь на дробь, обратную второй.

Пример 1. Найти значение выражения

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

Как решать дальше мы уже знаем. Первую дробь нужно умножить на дробь, обратную второй. Обратная для второй дроби это дробь .

Дорешаем данный пример до конца:

Допустим, имеются две целые и половина пиццы:

Если зададим вопрос «Сколько раз (одна целая и четверть пиццы) содержится в двух целых и половине пиццы», то ответом будет «два раза»:

Пример 2. Найти значение выражения

Переведём смешанные числа в неправильные дроби. Получим следующее выражение:

Теперь умножаем первую дробь на дробь, обратную второй. Обратная для дроби это дробь

Сначала мы получили дробь. Эту дробь мы сократили на 9. В результате получили дробь , но такой ответ нас тоже не устроил и мы выделили в дроби целую часть. В результате получили окончательный ответ .

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Показать решение

Задание 2. Найдите значение выражения:

Решение:

Показать решение

Задание 3. Найдите значение выражения:

Решение:

Показать решение

Задание 4. Найдите значение выражения:

Решение:

Показать решение

Задание 5. Найдите значение выражения:

Решение:

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано Автор

Сложение и вычитание смешанных чисел с разными знаменателями

Содержание

На этом уроке мы разберём, как происходит сложение и вычитание смешанных чисел с разными знаменателями.

Пример задачи с смешанными числами, имеющими разные знаменатели

Образавр, Вообразавр и Иксератопс собирались на пикник. Договорились, что каждый принесёт угощение. Все они купили по две пиццы.

Но по дороге к месту пикника Вообразавру захотелось есть, и он съел четвертинку пиццы. У него осталось $1\frac{3}{4}$ пиццы.

Иксератопс тоже захотел полакомиться пиццей по дороге, он съел третью часть, и принёс $1\frac{2}{3}$ пиццы.

Когда Образавр увидел, что остальные не стерпели и начали есть пиццу без него, ему стало обидно, он взял и съел сразу половину от одной из своих пицц. И у него получилось $1\frac{1}{2}$ пиццы.
Вот стоят друзья и думают, сколько же пиццы получилось у них в итоге?

Сложение смешанных дробей

$$1\frac{3}{4} + 1\frac{2}{3} + 1\frac{1}{2}$$

Чтобы сложить смешанные дроби с разными знаменателями, нужно уметь

складывать смешанные дроби с одинаковыми знаменателями;
складывать обыкновенные дроби с разными знаменателями.

Подсказка

При сложении смешанных дробей удобно поменять местами слагаемые так, чтобы сначала сложить все целые числа, а затем уже дробные части.

При сложении дробных частей мы действуем так, словно это обыкновенные дроби:

Находим общий знаменатель
Приводим к общему знаменателю при помощи дополнительных множителей
Выполняем сложение

$$1\frac{3}{4} + 1\frac{2}{3} + 1\frac{1}{2} = 1 + 1 + 1 + \frac{3}{4} + \frac{2}{3} + \frac{1}{2}$$

Найдём НОК для чисел $4, 3, 2$

Рассмотрим числа, кратные числу $4$

$$4 \cdot 1 = 4$$

$$4 \cdot 2 = 8$$

$$4 \cdot 3 = 12$$

Дальше можно уже не умножать, так как мы нашли число, кратное $3$. Оно чётное, значит, делится также на $2$. Ни $4$, ни $8$ не делится на $3$, значит, $12$ – это наименьшее общее кратное.

Получаем вот такой пример, где сначала идут целые, а потом дробные части смешанных дробей:

У нас получилось $3 + \frac{23}{12}$. Но $\frac{23}{12}$ – неправильная дробь, нужно выделить из неё целое число. Получается $1\frac{11}{12}$. Следовательно, наш пример будет выглядеть теперь так:

$$3 + \frac{23}{12} = 3 + 1+ \frac{11}{12} = 4\frac{11}{12}$$

Если в результате сложения смешанных дробей у нас получилось целое число и неправильная дробь, следует выделить целую часть из неправильной дроби и прибавить её к целому числу.

{"questions":[{"instruction":"Вычислите","content":"$11\\frac{18}{28} + 3\\frac{3}{14} + \\frac{1}{7}$ = [[input-10]]","widgets":{"input-10":{"type":"input","inline":1,"answer":"15"}},"step":1,"hints":["Переставим слагаемые так, чтобы целые части смешанных чисел прибавлялись к целым, а дробные — к дробным:
$11\\frac{18}{28} + 3\\frac{3}{14} + \\frac{1}{7} = 11 + 3 + \\frac{18}{28} +\\frac{3}{14}+ \\frac{1}{7}$","Приведём дробные части к общему знаменателю и произведём вычисления: $14+\\frac{20+6+2}{28} = 14\\frac{28}{28}$","Дробная часть получилась неправильной дробью. Выделим целую часть: $14\\frac{28}{28}=15$"]}]}

Вычитание смешанных дробей

У Образавра, Вообразавра и Иксератопса было $4\frac{11}{12}$ пиццы. Они съели $2\frac{5}{8}$ пиццы и поняли, что вполне сыты. Сколько пиццы у них осталось?

Вычитание смешанных дробей проходит по тому же принципу, что и сложение.

При вычитании смешанных дробей нужно представить уменьшаемое и вычитаемое в виде суммы целых и дробных частей, из целой части уменьшаемого вычесть целую часть вычитаемого, и из дробной части уменьшаемого вычесть дробной часть вычитаемого. Если у дробных частей смешанных чисел разные знаменатели, требуется сначала привести дроби к общему знаменателю при помощи дополнительных множителей.

Таким образом,

$$4\frac{11}{12}-2\frac{5}{8} = 4-2+\frac{11}{12}-\frac{5}{8} = 2 + \frac{11}{12}-\frac{5}{8}$$

Видите, мы сгруппировали целые части чисел и вычислили разность. Нам осталось провести вычитание дробей с разными знаменателями.

Найдём НОК для $12$ и $8$.

Рассматриваем два разложения на множители. Берём множители от большего числа $(2 \cdot 3 \cdot 2)$ и множитель от числа $8$, которого не хватает в разложении числа $12$. Получается

$$2 \cdot 3 \cdot 2 \cdot 2 = 24$$

Продолжим вычисление.

{"questions":[{"instruction":"Вычислите","content":"$8\\frac{9}{10}-3\\frac{2}{5}$[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["$5\\frac{1}{2}$","$5\\frac{1}{10}$","$5\\frac{7}{10}$","$5\\frac{7}{5}$"],"answer":[0]}},"step":1,"hints":["Сначала запишем этот пример так, чтобы целые части чисел вычитались из целых, а дробные части — из дробных: $8\\frac{9}{10}-3\\frac{2}{5}= 8-3+\\frac{9}{10}-\\frac{2}{5}$","Приведём дробные части к общему знаменателю и произведём вычисления: $5+\\frac{9-2\\cdot 2}{10} = 5\\frac{5}{10}$","Полученную дробную часть можно сократить, разделив числитель и знаменатель на одно и то же число: $5\\frac{5}{10}=5\\frac{1}{2}$"]}]}

Заимствование единицы из уменьшаемого при вычитании смешанных чисел

Если при вычитании смешанных чисел дробная часть уменьшаемого меньше дробной части вычитаемого, из целой части уменьшаемого занимают единицу и переводят в дробную часть.

$$6\frac{3}{85}-3\frac{3}{34}$$

$\frac{3}{85}<\frac{3}{34}$, так как чем больше знаменатель, тем меньше значение дроби.

Представим данную разность следующим образом:

$$6\frac{3}{85}-3\frac{3}{34} = 5 + 1\frac{3}{85}-3\frac{3}{34}$$

$$5-3 + \frac{85+3}{85}-\frac{3}{34} = 2 + \frac{88}{85}-\frac{3}{34}$$

Нам нужно найти НОК для чисел $85$ и $34$.

Теперь умножим дроби на дополнительные множители и произведём вычисление.

{"questions":[{"instruction":"Соедините примеры с ответами","content":"[[matcher-38]]","widgets":{"matcher-38":{"type":"matcher","labels":["$7\\frac{1}{2}+1\\frac{3}{5}$","$3\\frac{1}{6}+6\\frac{3}{4}$","$11\\frac{7}{9}-2\\frac{2}{6}$"],"items":["$9\\frac{1}{10}$","$9\\frac{11}{12}$","$9\\frac{4}{9}$"]}},"hints":["$7\\frac{1}{2}+1\\frac{3}{5} = 7+1+\\frac{1 \\cdot 5 + 3 \\cdot 2}{10} = 8 + \\frac{11}{10} = 9\\frac{1}{10}$","$3\\frac{1}{6}+6\\frac{3}{4} = 3+6+\\frac{1 \\cdot 2 + 3 \\cdot 3}{12} = 9 + \\frac{11}{12} = 9\\frac{11}{12}$","$11\\frac{7}{9}-2\\frac{2}{6} = 11-2+\\frac{7 \\cdot 2-2 \\cdot 3}{18} = 9 + \\frac{8}{18} = 9\\frac{4}{9}$"]}]}

Сложение и вычитание дробей

ГДЗ 1 класс

ГДЗ 10 класс

: Категория: Математика

То, каким образом мы будем складывать или вычитать дроби, напрямую зависит от знаменателей этих дробей. Самое простое: сложение и вычитание дробей с одинаковыми знаменателями. С него и начнем.

Cложение и вычитание дробей с одинаковыми знаменателями

Вспоминаем законы сложения дробей из четвертого класса.

Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Чтобы вычесть друг из друга дроби с одинаковыми знаменателями, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить прежним.

Убедимся в справедливости этого высказывания на примере. Разделим круг на 5 равных частей. Возьмем из этих пяти 1-у часть и 2 части. Сложим. Вместе они составят 3 части. А поскольку изначально круг был разделен на 5 таких частей, то это 3/5 круга.

1/5 + 2/5 = 3/5

Уберем из целого круга 2 зеленые части (2/5). Останется 3 части (3/5).

5/5 — 2/5 = 3/5

Но если знаменатели разные, то ни сложить, ни вычесть такие дроби сразу нельзя.

Можно складывать и вычитать дроби только с одинаковыми знаменателями.

При сложении смешанных дробей отдельно складываются/вычитаются целые части, отдельно дробные, и опять же только при условии одинаковых знаменателей у дробных частей.

$5\frac27+3\frac17=(5+3)+(\frac27+\frac17)=8+\frac37=8\frac37$
$5\frac27-3\frac17=(5-3)+(\frac27-\frac17)=2+\frac17=2\frac17$

Если при вычитании смешанных дробей складывается такая ситуация, что числитель первой дробной части (уменьшаемое) меньше числителя второй (вычитаемого), то нужно взять единичку от целой части первого числа, представить ее в виде дроби с тем же знаменателем, что и у дробной части, и прибавить эту дробь к дробной части. Целая часть станет на единицу меньше, а дробная будет теперь представлять собой неправильную дробь (числитель больше знаменателя). Зато легко можно будет провести вычитание.

$5\frac17-3\frac27=\mathit4\mathit+\mathit1\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}\mathit=\mathit4\mathit+\frac{\mathit7}{\mathit7}\mathit+\frac{\mathit1}{\mathit7}\mathit-\mathit3\frac{\mathit2}{\mathit7}=4\frac87-3\frac27=(4-3)+(\frac87-\frac27)=1+\frac67=1\frac67$

Что же делать, если знаменатели разные? Разберемся. 1}{\cancel6_2}=\frac12$

Чтобы привести дроби к одинаковому знаменателю, принято находить наименьший общий знаменатель, а это то же самое, что наименьшее общее кратное (НОК) этих знаменателей. Вспомним, как находить НОК, статья по ссылке >>

$\frac59+\frac16=?$

9 | 3 6 | 2
3 | 3 3 | 3
1 | 1
НОК(6;9) = 3 * 3 * 2 = 18

$\frac59+\frac16=\frac{5\ast2}{9\ast2}+\frac{1\ast3}{6\ast3}=\frac{10}{18}+\frac3{18}=\frac{13}{18}$

Еще примеры:

Если в результате сложения или вычитания получается неправильная дробь, нужно перевести ее в смешанную. Если получается сократимая дробь, результат необходимо сократить.

Вспоминаем: чтобы сократить дробь, нужно разделить ее числитель и знаменатель на одно и то же число — наибольший общий делитель (НОД). Статья о том, как найти НОД по ссылке >>

Для дробей, как и для натуральных чисел, выполняются переместительное и сочетательное свойства сложения:

$\frac ab+\frac cd=\frac cd+\frac ab$
$(\frac ab+\frac cd)+\frac pq=\frac ab+(\frac cd+\frac pq)$

Их нужно применять в заданиях на нахождение наиболее простого способа сложения нескольких дробей.

Пример. Вычислите значение выражения наиболее удобным способом:

Если все равно что-то в теме не поняли, задавайте вопросы в комментариях.

Назад
Вперед

умножить наподелить на

Уроки
Математика

Сложение дробей (Сложение одинаковых и разных дробей с примерами)

Сложение дробей учит нас складывать две или более дроби с одинаковыми или разными знаменателями. Добавление дроби зависит от двух основных условий:

Те же знаменатели
Различные знаменатели

При сложении дробей, если знаменатели совпадают (такие дроби называются подобными дробям), то их можно складывать напрямую. Но если знаменатели разные, (такие дроби называются непохожими дробями), то надо сделать знаменатели одинаковыми, а затем сложить дроби. Узнайте, похожие или не похожие на дроби, здесь.

Содержание:

Сложение дробей с одинаковыми знаменателями
Сложение дробей с разными знаменателями
Сложение дроби и целого числа
Сложение дроби с взаимно простым знаменателем
Добавление смешанных фракций
Вычитание дробей
Решенные примеры
Практические вопросы
Часто задаваемые вопросы

Сложение дробей с одинаковыми знаменателями

Если знаменатели двух или более дробей совпадают, то мы можем напрямую сложить числители, сохраняя общий знаменатель.

Выполните следующие действия, чтобы сложить дроби с одинаковыми знаменателями:

Сложите числители, оставив общий знаменатель
Напишите упрощенную дробь

Например: Сложите дроби: 5/6 и 7/6.

Так как знаменатели одинаковы, мы можем напрямую сложить числители.

(5/6) + (7/6) = (5 + 7)/6 = 12/6

Упростить дробь

12/6 = 2

Следовательно, сумма ⅚ и 7/6 равна 2.

Сложение дробей с разными знаменателями

Когда две или более дроби с разными знаменателями складываются вместе, мы не можем напрямую вычислить числители.

Выполните следующие действия, чтобы сложить дроби с разными знаменателями:

Проверить знаменатели дробей.
Сделать знаменатели дробей одинаковыми, найдя НОК знаменателей и рационализировав их
Сложите числители дробей, оставив знаменатель общим
Упростите дробь, чтобы получить окончательную сумму

Например: Добавить 3/12 + 5/2

Решение: Обе дроби 3/12 и 5/2 имеют разные знаменатели.

Мы можем записать 3/12 = ¼ в упрощенной дроби.

Итак, ¼ и 5/2 — это две дроби.

LCM 2 и 4 = 4

Умножить 5/2 на 2/2.

5/2 х 2/2 = 10/4

Теперь добавьте 1/4 и 10/4

¼ + 10/4 = (1+10)/4 = 11/4

Следовательно, сумма 3/12 и 5/2 равна 11/4.

Сложение дробей с целыми числами

Сложите дробь и целое число в три простых шага:

Запишите заданное целое число в виде дроби (например, 3/1)
Сделайте знаменатели одинаковыми и сложите дроби
Упростите дробь

Например: сложите 7/2 + 4

Здесь 7/2 — дробь, а 4 — целое число.

Мы можем записать 4 как 4/1.

Теперь, приравняв знаменатели, получим;

7/2 и 4/1 х (2/2) = 8/2

Добавить 7/2 и 8/2

7/2 + 8/2 = 15/2

Следовательно, сумма 7/2 и 4 равна 15/2.

Сложение дробей с взаимно простыми знаменателями

Взаимопростые числа Знаменатели : Знаменатели, у которых нет общих делителей, кроме 1.

Давайте научимся складывать дроби с взаимно простыми знаменателями, выполнив следующие шаги:

Проверить, являются ли знаменатели взаимно простыми
Умножьте первую дробь (числитель и знаменатель) на знаменатель другой дроби, а вторую дробь (числитель и знаменатель) на знаменатель первой дроби.
Сложите полученные дроби и упростите

Например, сложение дробей 9/7 и 3/4 можно сделать следующим образом.

Знаменатели 7 и 4 взаимно просты, так как они имеют только один наибольший общий делитель 1.

Итак, (9/7) + (3/4) = [(9 × 4) + (3 × 7)]/ (7 × 4)

= (36 + 21)/28

= 57/28

Добавление смешанных фракций

Смешанная дробь — это комбинация целого числа и дроби. Чтобы сложить две смешанные дроби, нам нужно сначала преобразовать их в неправильные дроби, а затем сложить вместе.

Чтобы добавить смешанные числа, выполните следующие действия:

Преобразование заданной смешанной дроби в неправильную дробь
Проверить, совпадают или разные знаменатели
Если разные знаменатели, то рационализировать их
Сложите дроби и упростите

Давайте разберемся, как складывать смешанные дроби на примере:

Пример: Добавить : 3 ⅓ + 1 ¾

Решение:

Шаг 1: Преобразуйте заданные смешанные дроби в неправильные дроби.

3 ⅓ = 10/3

1 ¾ = 7/4

Шаг 2: Сделайте знаменатели одинаковыми, взяв НОК и умножив подходящие дроби для обоих.

LCM 3 и 4 равно 12.

Итак, 10/3 = (10/3) × (4/4) = 40/12

7/4 = (7/4) × (3/3) = 21/12

Шаг 3: Возьмите знаменатель как общий и добавьте числители. Затем напишите окончательный ответ.

(40/12) + (21/12) = (40 + 21)/12 = 61/12

Следовательно, 3 ⅓ + 1 ¾ = 61/12 = 5 1/12

Вычитание дробей

Как мы знаем, сложение и вычитание в математике являются аналогичными операциями. Кроме того, мы складываем два или более числа, тогда как при вычитании мы вычитаем одно число из другого. Следовательно, вычитание дробей также следует тому же правилу, что и сложение дробей.

Если у данных дробей знаменатели одинаковы, то мы можем напрямую вычесть числитель, оставив знаменатель таким же.

Если знаменатели дробей различны, нам нужно сначала их рационализировать, а затем выполнять вычитание.

Некоторые примеры:

Пример 1: Вычтите ⅓ из 8/3.

Решение: Нам нужно найти,

8/3 – ⅓ = ?

Так как знаменатель у двух дробей ⅓ и 8/3 общий, следовательно, мы можем их прямо вычесть:

8/3 – ⅓ = (8-1)/3 = 7/3

Пример 2: Вычтите ½ из ¾.

Решение: Нам нужно вычесть ½ из ¾, т.е.

¾ – ½ = ?

Поскольку знаменатели двух дробей различны, следовательно, нам нужно их рационализировать, взяв НОК.

ОКМ (4,2) = 4

Теперь умножьте ½ на 2/2, чтобы получить 2/4

Следовательно,

¾ – 2/4 = (3-2)/4 = ¼

Следовательно, ¾ – ½ = ¼

Видео урок по дробям

Решенные примеры

Давайте решим несколько задач на сложение дробей.

Вопрос 1: Добавьте 1/2 и 7/2.

Решение: Даны дроби: 1/2 и 7/2
Поскольку знаменатели одинаковы, мы можем просто сложить здесь числители, сохранив знаменатель как есть.

Следовательно,

1/2 + 7/2

= (1+7)/2

= 8/2

Q. 2: Добавьте 3/5 и 4.

Решение: мы можем записать 4 как 4/1

Теперь нужно добавить две дроби 3/5 и 4/1.

Так как знаменатели здесь другие, нам нужно сначала упростить знаменатели, прежде чем складывать дроби.

Следовательно,

3/5 + 4/1

Взяв LCM из 5 и 1, получим;

НОК(5,1) = 5

Следовательно, умножив вторую дробь 4/1 на 5 как в числителе, так и в знаменателе, получим;

(4×5)/((1×5) = 20/5

Теперь 3/5 и 20/5 имеют общий знаменатель, т.е. 5, следовательно, теперь складываем дроби;

3/5 + 20/5

= 23/5

Добавление рабочего листа дроби

Сложение дробей – одна из важных тем в 6, 7 и 8 классах. Здесь мы предоставили рабочий лист для сложения дробей. Попрактиковавшись в вопросах, данных в этом листе, вы сможете легко решать суммы сложения муравьиных дробей. Попрактикуйтесь в данной добавленной ссылке рабочего листа дроби здесь и получите хорошие оценки на экзаменах.

Практические вопросы

⅜ + ⅝ =
1(⅓) + 3(5/2) =
2(¾) + ___ = 7
⅖ + ⅔ =
3/7 + 2 + 4/3 = ?

Связанные статьи

Посетите BYJU’S, чтобы в интересной форме изучить другие математические темы.

Часто задаваемые вопросы – Часто задаваемые вопросы

Как сложить две дроби с разными знаменателями?

Чтобы сложить две дроби с разными знаменателями, нам нужно рационализировать знаменатели, убрав НОК и сделав знаменатель одинаковым. Затем сложите числители дробей, сохраняя общий знаменатель. Например, ½ + ⅗
НОК 2 и 5 = 10
= (5/5) x (½) + (⅗) x (2/2)
= (5+6)/10
= 11/10

Каковы правила складывать и вычитать дроби?

Есть два простых правила сложения и вычитания дробей. Если знаменатели совпадают, то мы можем напрямую складывать и вычитать дроби. Но если знаменатели разные, нам нужно рационализировать знаменатели, найдя НОК двух, а затем сложив дроби.

Как складывать целые числа и дроби?

Если мы складываем целое число и дробь, то сначала нужно записать целое число в виде дроби. Например, сложив 3 и ½, получим
3+½ = 3x(2/2) + ½ = 6/2 + ½ = 7/2

Как сложить крупные дроби?

Возьмем две дроби: 11/24 и 9/60
НОК 24 и 60 = 120
Следовательно,
= (11/24)х(5/5) + (9/60)х(2/2 )
= (55+18)/120
= 73/120

Как складывать дроби с одинаковыми знаменателями?

Допустим, ⅗ и 7/5 — две дроби. Поскольку ⅗ и 7/5 — две одинаковые дроби с одинаковым знаменателем, мы можем напрямую сложить числители.
Следовательно,
⅗ + 7/5 = (3+7)/5 = 10/5 = 2

Сложение дробей с разными знаменателями

Сложение дробей с разными знаменателями означает, что нам нужно сложить дроби с разными знаменателями. В этом случае мы преобразуем данные дроби в подобные дроби, чтобы получить общие знаменатели, чтобы их стало легче складывать. Это делается путем нахождения наименьшего общего кратного (НОК) заданных знаменателей. Преобразуем каждую дробь таким образом, чтобы у нас был общий знаменатель, а затем складываем числители, чтобы получить сумму.

В этой статье мы научимся поэтапно складывать дроби с разными знаменателями. Мы также обсудим добавление смешанных дробей с разными знаменателями вместе с несколькими решенными примерами для лучшего понимания концепции.

1.	Что такое сложение дробей с разными знаменателями?
2.	шагов для сложения дробей с разными знаменателями
3.	Как складывать дроби с разными знаменателями?
4.	Сложение смешанных чисел с разными знаменателями
5.	Часто задаваемые вопросы о сложении дробей с разными знаменателями

Что такое сложение дробей с разными знаменателями?

Когда знаменатели не совпадают, дроби называются непохожими дробями. Например, 3/5 и 6/7 называются разными дробями, потому что у них разные знаменатели. Чтобы сложить две или более заданные дроби, знаменатели которых различны или различны, нам нужно найти наименьшее общее кратное (НОК) знаменателей. После нахождения НОК умножаем данные дроби на такое число, чтобы их знаменатели оставались общими. Уравняв знаменатели, мы можем просто сложить числители.

шагов для сложения дробей с разными знаменателями

Следующие шаги показывают процедуру сложения дробей с разными знаменателями.

Шаг 1: Сначала мы находим наименьшее общее кратное (НОК) заданных знаменателей.
Шаг 2: Затем мы запишем каждую дробь в такой форме, чтобы НОК стал общим знаменателем. Для этого умножаем числитель и знаменатель на обычное число с помощью НОК.
Шаг 3: После этого шага мы складываем числители этих одинаковых дробей (у которых теперь есть общие знаменатели).
Шаг 4: Наконец, мы уменьшаем результирующую дробь до наименьшего члена, если это необходимо.

Эти шаги можно понять с помощью примера, приведенного в следующем разделе.

Как складывать дроби с разными знаменателями?

Теперь давайте научимся складывать дроби с разными знаменателями, выполнив шаги, указанные выше.

Пример: Сложить 5/6 + 7/3

Решение:

Шаг 1: Поскольку у дробей разные знаменатели, находим НОК 6 и 3. НОК 6 и 3 6.
Шаг 2: Теперь преобразуйте данные дроби в эквивалентные дроби так, чтобы НОК стал их общим знаменателем. Как мы видим, 5/6 уже имеет LCM в качестве знаменателя, поэтому мы изменим только дробь 7/3 и сделаем ее эквивалентной дробью, которая будет равна 14/6.
Шаг 3: После этого мы можем сложить числители обеих дробей, так как знаменатели одинаковы.
Шаг 4: 5/6 + 14/6 = (5 + 14)/6 = 19/6. Это можно преобразовать в смешанную дробь и записать как $3\dfrac{1}{6}$

Сложение трех дробей с разными знаменателями

Для сложения трех или более дробей с разными знаменателями мы применяем те же шаги, что и выше. Давайте научимся складывать 3 дроби с разными знаменателями на следующем примере.

Пример: Добавить 1/2 + 3/5 + 7/3

Шаг 1: Сначала мы найдем LCM 2, 5 и 3, что равно 30.
Шаг 2: Теперь мы сделаем каждую дробь эквивалентной дробью таким образом, чтобы НОК 30 стал знаменателем каждой дроби.
Шаг 3: Эквивалентные дроби со знаменателем 30: 15/30, 18/30 и 70/30.
Шаг 4: Сложите все числители (15 + 18 + 70)/30 = 103/30. Это можно преобразовать в смешанную дробь и записать как $3\dfrac{13}{30}$

Сложение смешанных чисел с разными знаменателями

Если нам нужно сложить смешанные числа с разными знаменателями, мы преобразуем смешанную дробь в неправильную дробь. После этого мы можем добавить дроби, выполнив шаги, указанные выше. Давайте разберемся в этом с помощью следующего примера.

Пример: Сложите $5\dfrac{1}{7}$ и $4\dfrac{1}{5}$

Сначала преобразуйте смешанное число в неправильную дробь.

$5\dfrac{1}{7}$ = 36/7

$4\dfrac{1}{5}$ = 21/5

Теперь добавьте 36/7 и 21/5

LCM 7 и 5 равно 35

Равные дроби

36/7 = 180/35

21/5 = 147/35

Теперь добавим числители,

(180 + 5/73 = 280 + 5 143) = $9\dfrac{12}{35}$

Важные замечания по сложению дробей с разными знаменателями

Для сложения дробей с разными знаменателями мы берем НОК разных знаменателей и преобразуем их в одинаковые дроби а затем добавить числители.
Для сложения смешанных дробей с разными знаменателями мы преобразуем их в неправильные дроби и затем складываем.

☛ Статьи по теме

Сложение дробей с разными знаменателями Рабочие листы
Сложение и вычитание дробей
Вычитание дробей с разными знаменателями
Добавление смешанных фракций

Сложение дробей с разными знаменателями Примеры

Пример 1: Сложить 8/9 + 1/3 + 7/6
Решение: Для сложения дробей с разными знаменателями сначала найдем НОК чисел 9, 3 и 6
НОК = 18
Теперь мы преобразуем каждую дробь в эквивалентные дроби, взяв знаменатель в качестве НОК. , мы можем добавить числители.
(16 + 6 + 21)/18 = 43/18. Это можно преобразовать в смешанную дробь $2\dfrac{7}{18}$
Пример 2: Сложить 5/8 + 1/5
Решение: Чтобы сложить дроби с разными знаменателями, сначала найдем НОК чисел 8 и 5
НОК = 40
Затем преобразует каждую дробь в эквивалентные дроби, взяв знаменатель в качестве НОК.
(25 + 8)/40 = 33/40
Итак, сумма 5/8 + 1/5 равна 33/40
Пример 3: Сложить смешанные дроби $3\dfrac{1}{4}$ и $2\dfrac{2}{3}$
Решение: Чтобы сложить данные смешанные дроби, мы сначала преобразуйте их в неправильные дроби.
$3\dfrac{1}{4}$ = 13/4 и $2\dfrac{2}{3}$ = 8/3
Теперь, поскольку знаменатели разные, возьмем НОК 3 и 4. НОК (3, 4) = 12. Теперь преобразуйте дроби в подобные дроби.
13/4 = 39/12 и 8/3 = 32/12. Теперь сложите две дроби.
39/12 + 32/12 = 71/12 = $5\dfrac{11}{12}$
Ответ: $3\dfrac{1}{4}$ + $2 \dfrac{2}{3}$ = $5\dfrac{11}{12}$

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Запись на бесплатный пробный урок

Сложение дробей с разными знаменателями Вопросы

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о сложении дробей с разными знаменателями

Как складывать дроби с разными знаменателями?

Сложение дробей с разными знаменателями означает, что необходимо сложить две дроби с разными знаменателями. В этом случае мы преобразуем данные дроби в подобные дроби, чтобы получить общие знаменатели, чтобы их стало легче складывать. Это делается путем нахождения наименьшего общего кратного (НОК) заданных знаменателей. Нам нужно преобразовать каждую дробь таким образом, чтобы у нас был общий знаменатель, и после этого мы складываем числители, чтобы получить сумму.

Каковы примеры сложения дробей с разными знаменателями?

Ниже приведен пример сложения дробей с разными знаменателями. Прибавим 1/3 + 6/5.

Мы видим, что знаменатели не совпадают, следовательно, нам нужно сделать знаменатели равными, после чего мы можем сложить дроби.
В этом примере 1/3 + 6/5 мы сначала найдем НОК знаменателей 3 и 5, который равен 15.
Затем мы умножим обе дроби на такое число, чтобы знаменатели остались прежними.
Получается (5 + 18)/15 = 23/15.
Теперь преобразуем неправильную дробь в смешанное число: 23/15 = $1\dfrac{8}{15}$

Какова стратегия сложения дробей с разными знаменателями?

Стратегия сложения дробей с разными знаменателями состоит в том, чтобы найти НОК заданных знаменателей и сделать каждую дробь эквивалентной дробью с НОК в качестве знаменателя.

Как сложить дроби с разными знаменателями?

Ниже приведены шаги для сложения дробей с разными знаменателями. Давайте разберем это на примере и добавим 1/5 + 1/10

Шаг 1: Сначала мы найдем LCM 5 и 10, что равно 10.
Шаг 2: Теперь превратите каждую дробь в эквивалентную дробь таким образом, чтобы НОК (10) стал знаменателем каждой дроби.
Шаг 3: Эквивалентные дроби со знаменателем 10 будут 2/10 и 1/10
Шаг 4: Добавьте часть числителя (2 + 1)/10 = 3/10

Можно ли складывать дроби с разными знаменателями без использования НОК?

Нет, мы не можем складывать дроби с разными знаменателями без НОК.

Каково правило сложения дробей с разными знаменателями?

Основное правило сложения дробей с разными знаменателями состоит в том, чтобы найти НОК разных знаменателей и преобразовать данные неодинаковые дроби в одинаковые дроби. Это можно сделать, изменив их знаменатели равными НОК. Как только знаменатели станут одинаковыми, можно добавить числители.

Как сложить 3 дроби с разными знаменателями?

Чтобы сложить 3 дроби с разными знаменателями, мы используем те же правила, что и для сложения 2 дробей с разными знаменателями. Например, давайте сложим 1/6 + 1/3 + 1/2

. Нам нужно найти НОК 6, 3 и 2, что равно 6. Теперь мы преобразуем каждую дробь в эквивалентную дробь, используя НОК как знаменатель.

1/6 = 1/6

1/3 = 2/6

1/2 = 3/6

Теперь сложите числители этих дробей: 1/6 + 2/6 + 3/ 6 = (1 + 2 + 3)/6 = 6/6. Эта дробь может быть дополнительно уменьшена до 1 после упрощения.

Как складывать и вычитать дроби с разными знаменателями?

Чтобы складывать и вычитать дроби с разными знаменателями, мы используем одни и те же правила. Нам нужно найти НОК различных знаменателей и преобразовать данные неодинаковые дроби в одинаковые дроби. После этого шага мы добавляем или вычитаем числители в соответствии с вопросом.

Как складывать дроби с целыми числами и разными знаменателями?

Чтобы складывать дроби с целыми числами и разными знаменателями, мы должны записать целое число в виде дроби, то есть записать 1 в качестве знаменателя, а затем сложить его по тем же правилам сложения дробей. Например, добавим 6 + 3/4 + 1/2.

В этом случае 6 — это целое число, и мы можем записать его как 6/1.
Итак, перепишем дроби как 6/1 + 3/4 + 1/2.
Затем найдем НОК знаменателей, чтобы они были преобразованы в одинаковые дроби. LCM 1, 4 и 2 будет 4.
Теперь дроби можно записать как 6/1 + 3/4 + 1/2 = (24 + 3 + 2)/4 = 29/4. Это можно преобразовать в смешанную дробь как $7\dfrac{1}{4}$

Как складывать неправильные дроби с разными знаменателями?

Для сложения неправильных дробей с разными знаменателями используются те же правила, что и для сложения дробей. Например, сложим эти неправильные дроби с разными знаменателями: 7/2 + 8/3.

Сначала найдем НОК знаменателей. LCM 2 и 3 равен 6.
Затем мы преобразуем данные дроби в эквивалентные дроби. Итак, 7/2 станет 21/6, а 8/3 станет 16/6.
Теперь мы можем сложить их, потому что их знаменатели совпадают. Это означает, что (21 + 16)/6 = 37/6 = $6\dfrac{1}{6}$

Скачать БЕСПЛАТНЫЕ учебные материалы

Сложение дробей с разными знаменателями

Как складывать дроби с одинаковыми знаменателями

Сопутствующие ресурсы: Бум-карты с добавлением фракций, Цифровые дроби, Учебное пособие для печати,

Что такое общий знаменатель?

Во-первых, давайте убедимся, что мы понимаем различные части дроби: числитель и знаменатель. Числитель — это первое число в верхней части дроби, а знаменатель — второе число в нижней части дроби.

Знаменатель дроби — это число равных частей, на которые разбито целое. Например, если дробь равна 1/6, это означает, что целое было разделено на 6 равных частей, и у вас есть 1 из 6 частей. Если дробь 3/4, это означает, что целое было разделено на 4 равные части, и у вас есть 3 из этих частей.

Когда мы говорим, что дроби имеют общий знаменатель, это означает, что у них одинаковые числа внизу. Когда две дроби имеют общий знаменатель, это означает, что оба целых числа были разделены на одинаковое количество равных частей.

Дроби 5/7 и 2/7 имеют общий знаменатель, потому что у них в знаменателе стоит цифра 7. Это также говорит нам о том, что для обеих дробей целое было разделено на 7 равных частей.

Важно отметить, что когда две дроби имеют общий знаменатель, равные части будут одного размера . Чем больше знаменатель, тем меньше будет каждая часть. Чем меньше знаменатель, тем больше каждая часть. Когда знаменатели одинаковы, куски имеют одинаковый размер.

Что такое знаменатель?

Общие знаменатели также иногда называют «подобными знаменателям». Итак, если вам говорят, что у двух дробей знаменателя, например , это просто означает, что у них одинаковое нижнее число.

Как складывать дроби?

Чтобы складывать дроби, дроби должны иметь общий знаменатель. Нам нужно, чтобы кусочки каждой фракции были одинакового размера, чтобы объединить их вместе.

Допустим, нам нужно сложить 2/7 и 3/7. Эти две дроби имеют одинаковый знаменатель, поэтому равные части, на которые разбито целое, имеют одинаковый размер. Поскольку все части имеют одинаковый размер, мы можем сложить эти две дроби вместе.

Добро пожаловать на уроки математики у Кейт!
Учителя, обязательно ознакомьтесь с учебными пособиями и заданиями.

Мы можем добавить 2/7 к 3/7, заполнив дополнительные 2 клетки на диаграмме. Мы видим, что это дает нам сумму 5/7. (2 части плюс еще 3 части равняются 5 частям из 7 всего)

Если вы складываете две дроби с общим знаменателем, вы можете объединить их вместе, сложив вместе числители (верхние числа). Знаменатель всегда будет оставаться одним и тем же, потому что размер равных частей не изменится, когда вы объедините две дроби вместе.

Допустим, у вас есть 1/10 + 6/10. У них одинаковый знаменатель, поэтому их можно объединить вместе. Сложите числители (1 + 6 = 7). Оставьте знаменатель прежним (нижнее число останется 10).

Помните, знаменатель не меняется, потому что размеры фигур остаются прежними. Вы просто подсчитываете общее количество частей, когда складываете две дроби.

Вот визуальный способ взглянуть на ту же проблему:

Добавление дробей Примеры

Попробуйте сложить эти дроби самостоятельно, а затем прокрутите вниз, чтобы убедиться, что вы правы! Если вы сомневаетесь, это может помочь нарисовать картинку, которая поможет вам визуализировать проблему.

Прежде чем складывать дроби, убедитесь, что у них одинаковые знаменатели! Если знаменатели разные, мы не можем их объединить, потому что кусочки не одного размера.

В первой задаче оба знаменателя равны 9, поэтому у них есть общий знаменатель. Мы можем сложить дроби 2/9 и 5/9, сложив числители и сохранив тот же знаменатель. Это дает нам дробь 7/9.

Во второй задаче обе дроби имеют общий знаменатель 5. Это означает, что мы можем сложить числители (1 и 3) и оставить тот же знаменатель (всего 5 частей). Это дает нам сумму 4/5.

Сложение дробей Распространенная ошибка

Распространенная ошибка, которую, как я вижу, совершают студенты при сложении дробей, заключается в том, что они случайно складывают и числители, и знаменатели. Не добавляйте нижние числа! Знаменатель говорит вам, сколько равных частей в целом, это число останется прежним, когда вы сложите дроби.

Видео

Хотите увидеть еще несколько примеров? Посмотрите короткое видео о добавлении дробей ниже.

Практика сложения дробей

Думаете, вы готовы попробовать складывать дроби самостоятельно? Нажмите кнопку СТАРТ ниже, чтобы пройти пробный тест.

Работает на Interact

Готовы научиться складывать и вычитать дроби с разными знаменателями?
Хотите научиться умножать или делить дроби на дроби?

Как упростить сложение и вычитание дробей

Содержание

Что такое дроби?
Типы фракций
Моделей для представления фракций
Как сделать добавление и вычитание фракций легкими
шагов для добавления и вычитания фракций
Добавление/вычитание фракций — общие ошибки
Teachlack с Splashlearn
часто задаваемые вопросы
с Splashlearn
часто задаются вопросы
.

Страх дробей!

Дробь — это новое понятие с совершенно другим обозначением, которое затрудняет понимание учащимися. Одной из причин, по которой студенты находят это утомительным, также является то, что они когда-либо работали только с целыми числами. Поэтому, естественно, дроби кажутся им незнакомыми.

Борьба и испытания с фракциями реальны.

В Национальной оценке образовательного прогресса, 2005 г. говорится, что «Литература по математическому образованию громогласна в своих выводах о том, что понимание дробей является сложной областью математики для североамериканских учащихся». Именно этот первоначальный страх перед дробями продвигает дальше и делает понимание сложения и вычитания дробей обременительным.

Эта статья поможет учащимся понять, как складывать и вычитать дроби с помощью простых шагов и визуальных моделей. Мы также рассмотрим некоторые приемы, позволяющие упростить сложение и вычитание дробей.

Читайте дальше, чтобы убедиться, что дроби — друзья ваших детей, а не враги!

Что такое дроби?

Большинство учебных программ фокусируются на дробях в виде заштрихованных областей или областей, но они выходят за рамки этого. Учащиеся часто рассматривают дроби как процесс деления и закрашивания частей фигур, поэтому они упускают из виду тот факт, что дроби — это числа между целыми числами.

Внимательно посмотрите на изображение линейки ниже. Маркировка между 0 и 1 представляет числа, которые отличаются от целых чисел. Они называются дробями.

SplashLearn пробуждает любознательность на протяжении всей жизни благодаря своей обучающей программе PreK-5, основанной на играх, которую полюбили более 40 миллионов детей. С более чем 4000 веселых игр и занятий, это идеальный баланс между обучением и игрой для вашего малыша.

Попробуйте бесплатно

Дроби чисел между целыми числами

   Связанное чтение:    Блестящие математические цитаты, чтобы поделиться со студентами, чтобы вдохновить их

Важно подчеркнуть, что дроби — это числа, которые помогают нам быть точными и точными с суммами . У нас не всегда есть один полный килограмм или один полный дюйм при измерении. Поэтому становится критически важным найти способ представления этих «частей», и именно здесь дроби берут на себя ответственность.

Дроби записываются как a/b, где «a» — это число сверху, которое называется числителем. В то время как «b» является числом внизу и называется знаменателем.

Например: Для дроби 1/2; 1 — числитель, 2 — знаменатель.

Студенты часто путают числитель со знаменателем и наоборот. Чтобы запомнить эти запутанные термины, проще всего запомнить их так: D — вниз и D – знаменатель. Так что знаменатель всегда идет вниз!

ТИПЫ ДРОБЕЙ:

Наиболее распространенные типы дробей:

Типы дробей

Наиболее часто используемые дроби при сложении и вычитании дробей:

Подобные и отличные дроби .

Дроби с одинаковыми знаменателями называются Подобными дробями.

Пример:

Подобные дроби

Дроби с различными знаменателями называются непохожими дробями .

Пример:

В отличие от дробей

Еще один тип дроби, который учащиеся должны знать перед тем, как научиться складывать и вычитать дроби: Эквивалентная дробь

Дроби, имеющие разные числители и знаменатели, но равные одному и тому же значению, называются эквивалентными Фракции.

Пример:

Все дроби 1/2, 2/4, 3/6 и 4/8 представляют одно и то же значение, равное «ПОЛОВИНА»

Поскольку дроби похожи на любые другие числа, их можно представить с помощью различных моделей. .

Модели для представления фракций:

Наиболее распространенные модели для представления фракций:

a) Модель площади:
.
Наборы круглых и прямоугольных дробей используются для понимания того, что дроби являются частями целого.
Примеры модели зоны:
модели зоны
b) Линейная модель:
В линейной модели дроби рассматриваются как длины, а не площади. Числовая линия является важной линейной моделью, позволяющей учащимся воспринимать дроби как числа.
Линейная модель для дроби ¾ будет:
Линейная модель
c) Дискретная модель:
В дискретной модели под целым понимается набор дискретных объектов. Подмножества этого целого составляют дробные части.
Например, половина класса, 1/3 лотка с яйцами. Счетчики, шарики, кубики или любой другой набор объектов, которые можно посчитать, можно использовать в качестве манипулятора для моделирования дробей.
Как упростить сложение и вычитание дробей ?
Работа с дробями > Изучение дробей

Первое и главное, что учащиеся должны сделать, изучая сложение и вычитание дробей, — это лучше понимать дроби. Им нужно практиковать дроби, чтобы установить связь с реальным миром, т. е. им нужно складывать листы бумаги, вырезать детали, раскрашивать фигуры и т. д.
Одна из основных проблем с дробями заключается в том, что они не всегда конкретны. Мы начинаем учить дроби с помощью наглядных материалов, но когда дело доходит до операций с дробями, мы переключаемся на правила и процедуры для того же. Механическое заучивание шагов приводит к еще большей путанице.
При сложении дроби мы складываем числители, но не знаменатели. Но при умножении дробей мы умножаем не только числители, но и знаменатели. Это еще больше озадачивает студентов.
Лучше всего использовать визуальные модели, чтобы показать добавление дробей, которые помогут учащимся понять шаги, а не грабить шаги без концептуальной ясности.
Связанное чтение: Наиболее важные математические символы, необходимые учащимся для решения задач
Упражнение:
Чтобы добавить 1/8 и 3/8, возьмите пиццу, разрезанную на 8 ломтиков. из 8 ломтиков,
Теперь, если мы сложим или сложим вместе обе дроби/кусочки пиццы, мы получим 3 ломтика из 8 ломтиков пиццы, что означает 3/8.
Конкретный -> Контекстный -> Вычислительный
Чтобы представить новое и сложное понятие, такое как дроби, очень важно предоставить учащимся широкие возможности для его конкретного усвоения. Это означает погружение учащихся в такие занятия, как вырезание бумаги, складывание бумаги, рисование, приготовление пиццы из бумаги, яблоки, шоколадные батончики и т. д. Только используя такой опыт, они смогут увидеть, потрогать и почувствовать концепцию дробей и сделать свои собственные открытия. .

Как только учащиеся получат достаточное количество этого конкретного воздействия, они начнут устанавливать связи между этими объектами и реальным миром.
Много времени должно быть потрачено на создание, изучение, складывание и визуализацию дробей, прежде чем переходить к задачам с дробями, связанными с голыми числами.
Например: Прежде чем спрашивать ¼ от 20 =? , мы можем представить реальный сценарий следующим образом:
«У Рона было 20 долларов. Он потратил ¼ из них. Сколько денег у него осталось?»
Это поможет даже учащемуся, плохо разбирающемуся в дробях, начать строить связи.
Покажите им, «ПОЧЕМУ» правила работают
Если представление о дробях как о числах развито хорошо, то легче понять и операции над дробями. Точно так же, как мы складываем и вычитаем числа, можно складывать и вычитать дроби. Важно подчеркнуть концептуальное понимание наряду с процедурным знанием шагов.
Например:
Мы знаем, что 1 яблоко + 1 яблоко = 2 яблока
Точно так же мы можем складывать дроби.
Мы также знаем, что 2 яблока + 3 яблока = 5 яблок
Точно так же мы можем складывать дроби:
Чтобы узнать сумму 2/6 и 3/6; считайте это двумя шестыми и тремя шестыми, которые в сумме дадут пять шестых точно так же, как мы складываем числа.
Теперь давайте рассмотрим пример с вычитанием:
Мы знаем, что 5 яблок – 2 яблока = 3 яблока
Аналогично мы можем вычитать дроби:
В случае «похожих дробей» мы можем просто сложить/вычесть числители и оставить знаменатель прежним. Но мы не можем складывать разные дроби, как складываем одинаковые дроби.
Причина этого очень проста.

Точно так же, как мы не можем сложить 2 яблока и 3 апельсина и сказать, что сумма равна 5 апплонгов , мы не можем складывать дроби с разными знаменателями. Таким образом, важно сначала определить сложение как комбинацию двух или более одинаковых величин. Точно так же вычитание отнимает подобные единицы количества.

Итак, как нам складывать/вычитать разные дроби? Давайте посмотрим на это дальше!
Шаги Для добавления и вычтения фракций

Теперь давайте посмотрим на шаги, которые мы можем следовать, чтобы добавить или вычитать фракции:

Шаг 1 : Добавить знаменатели одинаково

. или Вычтите числители (сохранив знаменатель)

Шаг 3 : Упростите дробь
Чтобы складывать или вычитать разные дроби, первым делом нужно сделать знаменатели одинаковыми, чтобы числители можно было складывать так же, как мы для подобных дробей.
ШАГ 1: ОДИНАКОВЫЕ ЗНАМЕНАТЕЛИ

Как сделать знаменатели одинаковыми?

В случае одинаковых дробей знаменатели уже будут одинаковыми, поэтому вы можете пропустить шаг 1 и перейти к шагу 2. кратное другому знаменателю
Пример: ½ + ¾
В этом случае – 4 кратно 2. Мы можем умножить 2 на 2, чтобы получить 4, и в результате знаменатели станут одинаковыми. Таким образом, большее число становится общим знаменателем.
Применение :

Таким образом, теперь задача принимает следующий вид:
Если один знаменатель кратен другому, мы можем умножить меньший знаменатель на число (скажем, k) , что даст больший знаменатель. Тогда больший знаменатель становится общим знаменателем.
ii) Если оба знаменателя не имеют общего делителя
Пример: ¼ + ⅗
Связанное чтение: Простые способы сделать математику увлекательной для детей
В этом случае числа 4 и 5 не имеют общих делителей. Мы можем просто перемножить знаменатели, чтобы получить общий знаменатель.
4 х 5 = 20, поэтому 20 является общим знаменателем для обеих дробей.

Если у обоих знаменателей нет общего множителя, то вы умножаете оба знаменателя, чтобы получить общий знаменатель.

Давайте посмотрим, как мы получим 20 в качестве общего знаменателя для обеих дробей:
Если мы умножим знаменатель, мы должны умножить и числитель, чтобы получить эквивалентную дробь.
Таким образом, задача теперь выглядит так:
ШАГ 2: СОБЛЮДЕНИЕ/ВЫЧИТАНИЕ ЧИСЛИТЕЛЕЙ
Этот шаг довольно прост и прямолинеен. Мы должны сложить/вычесть числители, и результатом их суммы/разности будет новый числитель. Общий знаменатель (как обсуждалось на шаге 1) остается прежним.

Возьмем наши предыдущие примеры и продолжим оттуда:
½ + ¾
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить два числителя вместе (2 + 3 = 5), чтобы получить новый числитель, в то время как знаменатель (4) остается прежним.
Таким образом, ответ будет 5/4.
  ¼ + ⅗.
После того, как знаменатели одинаковы, эта задача выглядит так:
Теперь нам нужно сложить числители вместе (5 + 12 = 17), чтобы получить новый числитель, в то время как знаменатель (20) остается прежним.
Таким образом, ответ будет 17/20.
ШАГ 3: УПРОЩЕНИЕ Дроби
Ответы, которые мы получили выше, верны, но мы можем упростить дробь до тех пор, пока в числителе и знаменателе не будет общих множителей, кроме 1.
Дробь можно привести к упрощенной форме, удалив общие факторы.

Продолжим наши предыдущие примеры:
И,
В приведенных выше случаях – 5/4 и 17/20 уже упрощенные дроби, так как числитель и знаменатель не имеют общих множителей.
Приведем несколько примеров дробей, которые можно упростить:
4/12 не упрощается.
4 является общим делителем как в числителе, так и в знаменателе, поэтому его можно привести к упрощенной форме следующим образом:
Обратите внимание: Мы не будем рассматривать смешанные числа как отдельный случай, поскольку также дроби, записанные в разной (смешанной) форме.
Подытожим эти шаги, взяв по одному примеру сложения и вычитания.
Время попрактиковаться во всех трех шагах вместе!
Задача на сложение: 3/4 + 1/12
Шаг 1: Приведите знаменатели к тому же

Знаменатели равны 4 и 12. 12 кратно 4, поэтому общий знаменатель будет равен 12.
2 Шаг 2: Сложите/вычтите числители (сохранив знаменатель)
Шаг 3: Упростите дробь

Чтобы упростить 10/12, общий делитель равен 2
Итак, 10/12= 5/6 (в упрощенной форме)
Следовательно, 3/4 + 1/12= 5/6
Теперь давайте рассмотрим задачу на вычитание:

Пример: 2/5 – 1/3

Шаг 1: Совместите знаменатели

Общий знаменатель будет 3 x 5 = 15
Шаг 2: Сложите/вычтите числитель 59007
Шаг 3: Упростите дробь
1/15 уже в упрощенной форме, так как 1 и 15 не имеют общих множителей.
Связанное чтение: Способы умножения чисел всего за секунды
Метод бабочки
Очень интересный и полезный метод быстрого сложения/вычитания дробей.
Источник
В этом методе мы рисуем крылья бабочки, чтобы понять, какие два числа нужно перемножить. Затем мы продолжаем записывать результат в соответствующую антенну. Знаменатели умножаются, а результат записывается внизу живота.
В конце мы просто добавляем/вычитаем антенну и пишем ее над брюшком, чтобы получить результат.
Сложение/вычитание дробей – распространенные ошибки
Учителя должны следить за тем, чтобы учащиеся постепенно переходили от конкретного к контекстуальному и вычислительному уровням.
Учащимся нужно дать много примеров, чтобы помочь им преодолеть некоторые распространенные ошибки и неправильные представления:
1. Сложение/вычитание числителей и знаменателей

При сложении/вычитании дробей важно обращать особое внимание на то, как учащиеся представляют их:
Наиболее распространенная ошибка при сложении дробей — сложение числителей и знаменателей по отдельности, как мы складываем целые числа.
Например: при сложении 2/3 и 1/4 распространенной ошибкой является представление каждой дроби, как показано выше, а затем сложение их вместе, чтобы получить 3/7 в качестве ответа.
Когда учащиеся складывают, комбинируют или находят сумму, складывая вместе целые числа и обе дробные части, кажется разумным, что они рассматривают каждую дробь независимо друг от друга.
Итак, важно подчеркнуть, что дробными частями нельзя манипулировать независимо от их целого.
Вот почему важно иметь общий знаменатель. В случае общего знаменателя дроби можно интерпретировать на одной диаграмме и объединять. Давайте посмотрим на этот же пример, но в целом.
В этом случае общий знаменатель для 2/3 и 1/4 будет равен 12.
Теперь рассмотрим целое, состоящее из 12 частей.
Теперь найдем ⅔ и ¼.

, чтобы найти 2/3 первого разделителя целого на 3 равных частей:
2/3 будет 2 из этих 3 равных частей:
2/3 = 8/12
Аналогично, чтобы найти 1/4, мы нужно разделить целое на 4 равные части:
1/4 будет:
                                                                        1/4 = 3/12
8 частей, сумма которых равна 4, и 1 части равны 2/2. 11 частей.
2/3 + 1/4 = 8/12+ 3/12 = 11/12
Точно такая же ошибка наблюдается и при вычитании дробей. И числители, и знаменатели вычитаются по отдельности, как вычитаются целые числа.
Например: 5/6 – 1/3 = (5-1)(6-3) = 4/3
Найдем правильный способ решения 5/6 – 1/3 =?

В этом случае общий знаменатель для 5/6 и 1/3 будет равен 6 (общее кратное).
Теперь рассмотрим целое, состоящее из 6 частей:
5/6 будет:
Для 1/3 мы разделим целое на 3 равные части:
1/3 будет одной из этих трех равных частей:
                                                                                                                       от 5/6 отнимем 1/3, от 5 частей одного и того же целого отнимем 2 части.
5/6 – 1/3 = 5/6 – 2/6 = 3/6
2. Сложение/вычитание числителей без учета знаменателей часто рассматривают их как целые числа.
12/13 + 7/8 = 19, потому что 12 + 7 = 19
12/13 – 7/8 = 5, потому что 12 – 7 = 5
Главное здесь – сделать их понимание дробей конкретным , с самого начала.
3. Сложение/вычитание знаменателей без учета числителей

Некоторые учащиеся складывают только знаменатели и игнорируют числители. Они смотрят на знаменатели как на два целых числа и складывают/вычитают их.
12/13 + 7/8 = 21, потому что 13 + 8 = 21
13/12 – 7/8 = 5, потому что 13 – 8 = 5
Интересные занятия по сложению и вычитанию дробей

Включите простые действия, такие как разрезание предметов из реального мира, чтобы развить интерес и лучше понять дроби. Такие действия, как крестики-нолики, БИНГО или сопоставление, могут быть выполнены, чтобы сделать дроби более увлекательными.
Дроби в повседневной жизни

Родители должны поощрять разговоры о дробях с детьми в повседневной жизни. Поощряйте детей применять дроби в повседневных задачах, таких как деление продуктов на равные доли, в измерениях или при приготовлении их любимых новых рецептов. Мы также можем использовать дроби, когда говорим о времени или оценках, которые дети набрали в школе!
Рассказывая о дробях, вы избавляетесь от страха, и детям больше нравится практиковать их.
Игры с дробями
Игры побуждают учащихся практиковаться в ответах на многие вопросы, которые им обычно не нравятся в других случаях. Ознакомьтесь с этими забавными играми с дробями на SplashLearn
Модели дробей/манипуляторы

Использование манипуляторов, таких как полоски дробей, модели площадей, кубики лего и числовые линии, делает дроби интересными и увлекательными для детей. Эти манипуляции помогают детям визуализировать дроби и, следовательно, лучше их понимать.
Проблемы со словами на дроби

Решение контекстных задач помогает учащимся связать изучение дробей с реальными жизненными ситуациями. Они понимают значение, необходимость и важность дробей и то, как их применять для решения задач. Вы можете проверить эти игры с дробными словами на SplashLearn и сделать дроби намного проще!

Подводя итог:
Учащимся важно понимать, что дроби нельзя закрасить и раскрасить.
Дроби — это числа, которые используются для представления чисел между любыми двумя последовательными целыми числами.
Помогите учащимся практиковать дроби, вырезая, вставляя и раскрашивая их, чтобы они лучше понимали дроби и весело проводили время с ними.
Используйте модели дробей, чтобы помочь им визуализировать и понять сложение и вычитание дробей.
Убедитесь, что они знают, почему шаги сложения/вычитания дробей работают, а не просто слепо применяют шаги.
Как родитель, используйте дроби в повседневных разговорах, связывайте дроби с контекстом реальной жизни и предоставляйте им примеры из повседневной деятельности, такой как приготовление пищи, выпечка, время и измерения.
Обучение дробям с помощью SplashLearn

Любимое более чем 40 миллионами родителей приложение SplashLearn — это универсальное решение для обучения детей математике и чтению. Вы можете заставить своих маленьких учеников играть в игры на сложение и вычитание дробей или учиться с помощью рабочих листов. Благодаря обучению, согласованному с учебной программой, SplashLearn обеспечивает персонализированный опыт, который адаптируется к потребностям каждого ребенка.
Родители, зарегистрируйтесь бесплатно!
Часто задаваемые вопросы (FAQ)
1. Что такое дроби?
Дроби — это числа между целыми числами (0,1,2,3,4). Они представляют собой часть/часть целого. Дробь состоит из двух частей – числителя и знаменателя.
2. Каковы шаги для сложения и вычитания дробей?
Шаг 1 : Сделать знаменатели одинаковыми
Шаг 2 : Сложить/вычесть числители (сохраняя знаменатель)
Шаг 3 : Упростить дробь
3. Как складывать и вычитать дроби с разными знаменателями?
Дроби с разными знаменателями можно складывать путем преобразования их в дроби с одинаковыми знаменателями с помощью эквивалентных дробей.
4. Как складывать и вычитать смешанные числа?
Сначала запишите смешанные числа в виде дробей. Теперь сложите/вычтите так же, как вы делаете это с дробями. В конце не забудьте преобразовать ответ (дробь) в смешанное число!
5. Как складывать и вычитать отрицательные дроби?
Отрицательные дроби можно рассматривать как дроби с отрицательными числителями. Шаги для сложения и вычитания отрицательных дробей остаются такими же, как и для дробей, за исключением того, что теперь детям нужно будет добавлять отрицательные или положительные числители.
Простое руководство по сложению дробей (включая разные знаменатели)
В этом руководстве показано, как складывать дроби с помощью сложения и вычитания. Мы также включили дроби с разными знаменателями, которые требуют немного больше работы.
Во-первых, давайте начнем с видео о том, как складывать и вычитать дроби:

Дроби — это не что иное, как отношение «части» к «целому». Дроби можно складывать, вычитать, умножать и делить, понимая структуру дроби и следуя нескольким простым правилам. Эта статья покажет вам, как это сделать, но сначала давайте рассмотрим основы терминологии дробей.
Представьте одну сторону магического куба, как показано ниже. Он разделен на маленькие квадраты разного цвета одинакового размера. Какова доля желтых квадратов?
Чтобы определить эту долю, нам нужно посчитать желтые квадраты и соотнести это значение с общим количеством квадратов. «Часть» в данном случае — это три желтых квадрата, которые известны как числитель дроби. Это значение делится на общее количество квадратов или «целое». Всего квадратов шестнадцать, и это значение знаменателя дроби.
При написании дроби деление обычно обозначается горизонтальной чертой, при этом числитель пишется вверху, а знаменатель — внизу.
Теперь попробуем записать другую дробь:
Какова доля красных квадратов?
Да, верно! Это $\frac{4}{16}$. Однако эту дробь можно упростить и записать как: $\frac{1}{4}$.
Пожалуйста, найдите минутку, чтобы просмотреть нашу подробную статью о том, как упростить дроби, чтобы при необходимости просмотреть эту концепцию!
Теперь, если вас спросят, какова доля красных и желтых квадратов вместе взятых, как бы вы ответили? Это так просто, как кажется: просто подсчитайте общее количество красных и желтых квадратов, чтобы получить числитель. Знаменатель остается прежним:
Всего красных и желтых квадратов: 3 + 4 = 7
Доля объединенных красных и желтых квадратов: $\frac{7}{16}$

Это означает, что если доля желтых квадраты добавляются к доле красных квадратов, ответ должен быть $\frac{7}{16}$.
Прежде чем мы решим другую задачу, вот список полезных вещей, которые следует запомнить:
При сложении и вычитании дробей знаменатели не меняются. Сложение или вычитание выполняется только с числителями.
Прежде чем вы сможете складывать или вычитать дроби, знаменатели ваших дробей должны совпадать друг с другом.
Всегда старайтесь упрощать дроби перед операцией с ними, чтобы числа, с которыми вы работаете, были как можно меньше.
Использование этих квадратов помогает визуализировать концепцию сложения дробей, но помните, что в большинстве случаев визуальные цифры недоступны. Итак, давайте уберем визуальные эффекты и проработаем математические шаги на нескольких примерах:
Предположим, у вас нет квадрата, доступного для просмотра, и вас просто просят добавить $\frac{3}{16}$ и $\frac{1}{4}$. Как видите, знаменатели этих дробей не совпадают. Это нужно исправить, прежде чем мы сможем двигаться дальше:
Шаг 1
Найдите НОК (наименьшее общее кратное) знаменателей обеих дробей. Обратите внимание, что при работе с дробями LCM также называется наименьшим общим знаменателем (LCD), потому что наша цель — сопоставить знаменатели дробей.
У нас есть полезная статья об определении GCF и LCM, которая может быть полезной для обзора, но мы также рассмотрим шаги здесь:
Мини-шаг 1. {4}\). Когда у числа не указана степень, оно просто имеет степень 1. 9{4}\) = 16
LCD = 16
Шаг 3
(А вот и сложная часть, обратите внимание!)
Нам нужно знать LCD каждой дроби. внесите корректировку в одну или обе исходные дроби. Давайте посмотрим на одну дробь за раз и ответим на следующий вопрос: соответствует ли знаменатель ЖК?
Первая дробь равна $\frac{3}{16}$, и ответ на вопрос — да! Знаменатель 16 равен LCD 16. Эту дробь не нужно корректировать.
Вторая дробь равна $\frac{1}{4}$. Ясно, что 4 не равно LCD, равному 16. Эту дробь необходимо скорректировать, чтобы получить эквивалентную дробь со знаменателем, равным 16. Но как?
Регулировка проста: определите число, на которое нужно умножить знаменатель 4, чтобы получить ЖК-дисплей. Для этого просто разделите ЖК на исходный знаменатель. В этом случае $16\дел 4=4$.
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на этот коэффициент 4, как показано:
$(\frac{4}{4}\times \frac{1}{4})=\frac{4\times 1}{4\times 4}=\frac{4}{16}$
Помните, что при умножении дробей выполняйте операцию «напрямую», то есть (числитель х числитель) и (знаменатель х знаменатель).
Это умножение на $\frac{4}{4}$ не меняет значение исходной дроби, поскольку $\frac{4}{4}$ = 1.
После эквивалентной дроби \ (\frac{4}{16}\) можно сложить дроби:
$\frac{3}{16}+\frac{4}{16}=\frac{3+4}{ 16}=\frac{7}{16}$
Как видите, именно это мы и получили, сложив доли желтых и красных квадратов!
Эти рисунки могут быть полезны для тех из вас, кто предпочитает наглядную демонстрацию определения ЖКИ перед сложением или вычитанием дробей:
Давайте рассмотрим еще один пример, где одна дробь является правильной дробью (числитель меньше знаменателя) и вторая — неправильная дробь (числитель больше знаменателя). Способ сложения тот же, и не имеет значения, правильная дробь или неправильная. 9{2} =36\)
LCD = 36
Шаг 3
Теперь пришло время выяснить, какие дроби нужно изменить, чтобы получить одинаковые знаменатели. Для каждой дроби спросите: «Соответствует ли знаменатель LCD?»
Первая дробь равна $\frac{1}{12}$, и мы видим, что 12 не равняется LCD 36, поэтому эту дробь нужно будет скорректировать. Как и прежде, разделите ЖК на исходный знаменатель. В этом случае $36\div 12=3$.
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на 3, как показано:
$(\frac{3}{3}\times \frac{1}{12})=\frac{3\times 1}{3\times 12}=\frac{3}{36}$
Вторая дробь, $\frac{19}{18}$, также должна быть скорректирована, так как 18 не соответствует ЖК-дисплею.
Разделите ЖК-дисплей на знаменатель 18: $36\дел 18=2$.
Умножьте числитель и знаменатель второй дроби на 2, как показано:
$(\frac{2}{2}\times \frac{19}{18})=\frac{2\times 19} {2\times 18}=\frac{38}{36}$
Теперь, когда каждый знаменатель соответствует ЖК-дисплею, можно сложить эквивалентные дроби:
$\frac{3}{36}+\frac{38}{36}=\frac{3+38}{36}=\frac{41}{36}$
Добавление более двух дроби
К этому моменту статьи мы надеемся, что вы освоили искусство сложения двух дробей. Если вам нужно добавить более двух фракций, процедура такая же. Давайте сделаем пример, чтобы проиллюстрировать это.
Добавить: $\frac{4}{5}+\frac{1}{2}+\frac{1}{4}$
Все эти дроби представлены в простейшей форме, так что давайте начнем процесс найти LCM и настроить каждую дробь так, чтобы знаменатели были одинаковыми. 9{2}\) × 5 = 20
LCD = 20
Шаг 3
Теперь пришло время выяснить, какие дроби нужно изменить, чтобы получить похожие знаменатели. Для каждой дроби спросите: «Соответствует ли знаменатель LCD?»
Первая дробь равна $\frac{4}{5}$, и мы видим, что 5 не равно 20. Как и прежде, разделите LD на исходный знаменатель. В этом случае $20\дел 5=4$.
Теперь исходную дробь можно изменить, умножив числитель и знаменатель на 4, как показано:
$(\frac{4}{4}\times \frac{4}{5})=\frac{4\times 4}{4\times 5}=\frac{16}{20}$
Вторая дробь, $\frac{1}{2}$, также должна быть скорректирована, так как 2 не соответствует ЖК-дисплею.
Разделите LCD на знаменатель, 2: $20\div 2=10$
Умножьте числитель и знаменатель второй дроби на 10, как показано:
$(\frac{10}{ 10}\times \frac{1}{2})=\frac{10\times 1}{10\times 2}=\frac{10}{20}$
Наконец, определите корректировку, которую необходимо преобразован в третью дробь, $\frac{1}{4}$.
Разделите ЖК-дисплей на знаменатель 4, чтобы получить коэффициент 5. Отрегулируйте третью дробь, умножив на $\frac{5}{5}$.
$(\frac{5}{5}\times \frac{1}{4})=\frac{5\times 1}{5\times 4}=\frac{5}{20}$
Теперь, когда каждый из трех знаменателей соответствует ЖК-дисплею, можно сложить эквивалентные дроби:
$\frac{16}{20}+\frac{10}{20}+\frac{5}{20} =\frac{16+10+5}{20}=\frac{31}{20}$
Сложение дробей и целых чисел
Еще одно важное понятие, о котором следует помнить при изучении сложения дробей, заключается в том, как добавлять дроби к целым числам. К счастью, любое целое число можно переписать так, чтобы оно «выглядело» как дробь, путем деления его на единицу. Например,
4 = $\frac{4}{1}$

30 = $\frac{30}{1}$
72 = $\frac{72}{ 1}$
После того, как целое число будет записано в виде доли от единицы, процесс сложения и вычитания аналогичен тому, что мы обсуждали в этой статье.
Вот несколько примеров:
Добавить: 3 + $\frac{3}{14}$
Этот вопрос можно переписать так: $\frac{3}{1}$ + \ (\frac{5}{14}\)
Шаг 1
Подумав, определите ЖК-дисплей. На какое наименьшее число можно разделить без остатка и 14, и 1?
Как насчет 14? Это наименьшее число, на которое можно разделить как 1, так и 14. Используйте его в качестве ЖК-дисплея для настройки первой «дроби», $\frac{3}{1}$.
Разделите LCD на знаменатель 1: $14\div 1=14$
Умножьте первую дробь на $\frac{14}{14}$.
$(\frac{14}{14}\times \frac{3}{1})=\frac{42}{14}$
Поскольку знаменатели совпадают, можно складывать дроби:
$\frac{42}{14}+\frac{3}{14}=\frac{42+3}{14}=\frac{ 45}{14}$
Заключительные мысли!
В этой статье мы узнали, как складывать дроби и как складывать целые числа в дроби. Это довольно полезный навык, который закладывает основу для некоторых сложных математических работ. Хотите сократить путь? Попробуйте наш калькулятор дробей! Посетите остальную часть нашего веб-сайта, чтобы узнать о других интересных и полезных математических понятиях, объясненных простым способом. Нужна дополнительная помощь, видеообзоры или практические вопросы? Кликните сюда!
Как сложить 3 дроби с разными знаменателями?
Дроби могут быть определены как числа, которые могут быть представлены в виде A/B , где A и B — целые числа, а B не должно быть равно нулю. В дроби верхняя часть называется Числитель , а нижняя часть называется Знаменатель.
Примеры: 1/2, 4/5, -2/3 и т. д.
Сложение дробей
Для сложения дробей существует правило, согласно которому знаменатели дробей должны быть равны. . Если знаменатели дроби не равны, сделайте их равными, взяв наименьшее общее кратное (НОК) знаменателей.
Как найти LCM?
Чтобы найти НОК чисел (здесь знаменатели), мы будем использовать метод деления .
Давайте разберемся с этим методом на примере, возьмем два числа 6 и 15 для нахождения НОК методом деления.
Шаг 1: Составьте таблицу, состоящую из левой и правой частей, в правой части укажите числа, НОК которых мы находим.
Шаг 2: Теперь начните с наименьшего числа (не 1) и проверьте, имеет ли любое число из заданных чисел это кратное. В примере 2 — это множитель 6, поэтому используйте его, чтобы разделить 6 в следующей строке.
Шаг 3: Теперь во втором ряду 3 осталось 15, только множитель 3 равен 3, поэтому разделите его на 3. 3 также является коэффициентом 15, так что разделите 15 также. В результате получается 1, 5.
Шаг 4: Теперь 5 является коэффициентом 5, поэтому делим 5, результат равен 1, 1.
Шаг 5: Процесс завершен, так как мы получаем 1 для всех чисел , теперь умножьте все числа в левой части, которые равны 2, 3, 5, так что кратное из них равно 30.
Сложение 3 дробей с разными знаменателями
Шаги для сложения дробей с разными знаменателями:
Шаг 1: Найдите НОК знаменателей.
Шаг 2: Разделите НОК на знаменатель каждого добавляемого числа.
Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как при простом сложении.
Шаг 5: Знаменатель будет LCM.
Возьмем 3 дроби с разными знаменателями, 1/2, 2/3, 3/4
Шаг 1: Нахождение НОК 2,3,4
Шаг 2: Разделим НОК на знаменатель каждого числа, которое нужно сложить.
LCM = 12, поэтому разделите его на каждое число (знаменатель)
12/2 = 6 частное 1
12/3 = 4 частное 2
12/4 = 3 частное 3
2
42
42 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числители 1, 2, 3, поэтому умножьте их на соответствующие частные.
1×6 = 6
2×4 = 8
3×3 = 9
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
6 + 8 + 9 = 23, что является числителем.
Шаг 5: В знаменателе будет LCM, то есть 12.
Ответ: 23/12
Метод перекрестного умножения , 3/4
Шаг 1: Возьмите две дроби за один раз, чтобы взять 1/2 и 2/3
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель первого числа. второе число, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×3 + 2×2 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
2×3 = 6, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/6.
Шаг 5: Повторите описанную выше процедуру, взяв новую дробь 7/6 и третью дробь 3/4.
Наконец, мы получили ответ, который совпадает с найденным выше.
Примеры вопросов
Вопрос 1. Сложите данные дроби 1/7, 2/7, 3/7.
Ответ:
В данном вопросе знаменатели равны, поэтому просто сложите числители, и знаменатель будет равен 7. 6/7.
Вопрос 2: Найдите LCM 7, 3, 12.
Ответ:
Вопрос 3: Добавить данную дробь, 2/7, 5/12, 1, 1. /3.
Ответ:
Шаг 1: Находим НОК 7,12,3
НОК, мы получили 84.
Шаг 2: .
LCM = 84, поэтому разделите его на каждое число (знаменатель)
84/7 = 12 частное 1
84/12 = 7 частное 2
84/4 = 21 частное 3
2 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числитель 2, 5, 1, поэтому умножьте их на соответствующие частные.
2×12 = 24
5×7 = 35
1×21 = 21
Шаг 4: Сложите числители, которые мы получаем после умножения с частными, как простое сложение.
24 + 35 + 21 = 80, что является числителем.
Шаг 5: В знаменателе будет НОК, то есть 84.
Ответ: 80/84
Вопрос 4: Сложите данные дроби, 4/5, 3/10, 1/3.
Ответ:
Шаг 1: Нахождение МОК 5,10,3
МОК, которое мы получили, равно 30. быть добавлено.
LCM = 30, поэтому разделите его на каждое число (знаменатель)
30/5 = 6 частное 1
30/10 = 3 частное 2
30/3 = 10 частное 3
2 2 Шаг 3: Умножьте числитель на частное (найденное на предыдущем шаге).
Числители 4, 3, 1, поэтому умножьте их на соответствующие частные.
4×6 = 24
3×3 = 9
1×10 = 10
Шаг 4: Сложите числители, полученные после умножения на частные, как простое сложение.
24 + 9 + 10 = 43, что является числителем.
Шаг 5: В знаменателе будет НОК, поэтому будет 30.
Ответ: 43/300005
Ответ:
Вопрос 6: Сложите данные дроби 1/3, 1/4, 1/2 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмем две дроби за раз, так что возьмем 1/3 и 1/4 первое число со знаменателем второго числа, и аналогичным образом мы умножим числитель второго числа на знаменатель первого числа и сложим оба члена, чтобы получить числитель.
1×4 + 1×3 = 7, что является числителем
Шаг 3: Теперь давайте найдем знаменатель, для этого умножьте знаменатель первого члена на знаменатель второго члена, чтобы получить член знаменателя.
3×4 = 12, что является знаменателем.
Шаг 4: Мы находим новый член, который представляет собой сложение двух дробей, в данном случае новая дробь 7/12.
Шаг 5: Снова возьмите 7/12 и третью дробь, которая равна 1/2.
Шаг 6: Нахождение числителя
7×2 + 1×12 = 26, что является числителем
Шаг 7: Нахождение знаменателя
12×2 = 24, что является знаменателем
7
6/2 равно 4 9 теперь упростив его, мы получим 13/12.
Вопрос 7: Сложите данные дроби 1/5, 2/5, 3/10 методом перекрестного умножения.
Ответ:
Шаг 1: Возьмите две дроби за один раз, так что возьмите 1/5 и 2/5
Шаг 2: Сначала мы найдем члены числителя, поэтому мы умножим числитель первого числа на знаменатель второго числа и аналогичным образом умножим числитель второго числа на знаменатель первого числа и сложим оба термина, чтобы получить числитель.

§ Сложение дробей с разными знаменателями. Как найти общий знаменатель

Темы уроков

Сложение дробей с одинаковыми знаменателями

Сложение дробей с разными знаменателями

Как найти общий знаменатель

Сложение смешанных чисел

Смешанные числа. Сложение и вычитание

Смешанные числа: определения, примеры

Сложение смешанных чисел

Сложение смешанного числа и натурального числа

Сложение смешанного числа со смешанным числом

Сложение смешанного числа и правильной дроби

Вычитание смешанных чисел

Вычитание одного смешанного числа из другого

Вычитание смешанного числа из натурального числа

Умножение смешанных чисел

Умножение смешанного числа на смешанное число

Умножение смешанного числа на обыкновенную дробь

Умножение целого числа на дробь

Деление смешанных чисел

Деление смешанного числа на смешанное число

Деление смешанного числа на целое число

Деление целого числа на смешанное число

Деление смешанного числа на обыкновенную дробь

Сложение и вычитание дробей с разными, одинаковыми знаменателями. Вычитание смешанных дробей в 2023 году

Сложение дробей с одинаковыми знаменателями

Сложение дробей с разными знаменателями

Сложение обыкновенной дроби и натурального числа

Сложение смешанных чисел

Вычитание дробей с одинаковыми знаменателями

Вычитание дробей с разными знаменателями

Вычитание смешанных дробей (смешаных чисел) с разными знаменателями

Вычитание дроби из натурального числа

Вычитание натурального числа из обычной дроби: как отнять целое число из дроби

Смешанные числа

Умножение смешанного числа на дробь

Задания для самостоятельного решения

Сложение и вычитание смешанных чисел с разными знаменателями

Пример задачи с смешанными числами, имеющими разные знаменатели

Сложение смешанных дробей

Вычитание смешанных дробей

Заимствование единицы из уменьшаемого при вычитании смешанных чисел

Сложение и вычитание дробей

Cложение и вычитание дробей с одинаковыми знаменателями

Вам может пригодиться:

Сложение дробей (Сложение одинаковых и разных дробей с примерами)

Сложение дробей с одинаковыми знаменателями

Сложение дробей с разными знаменателями

Сложение дробей с целыми числами

Сложение дробей с взаимно простыми знаменателями

Добавление смешанных фракций

Вычитание дробей

Видео урок по дробям

Решенные примеры

Добавление рабочего листа дроби

Практические вопросы

Связанные статьи

Часто задаваемые вопросы – Часто задаваемые вопросы

Как сложить две дроби с разными знаменателями?

Каковы правила складывать и вычитать дроби?

Как складывать целые числа и дроби?

Как сложить крупные дроби?

Как складывать дроби с одинаковыми знаменателями?

Сложение дробей с разными знаменателями

Что такое сложение дробей с разными знаменателями?

шагов для сложения дробей с разными знаменателями

Как складывать дроби с разными знаменателями?

Сложение трех дробей с разными знаменателями

Сложение смешанных чисел с разными знаменателями

Сложение дробей с разными знаменателями Примеры

Сложение дробей с разными знаменателями Вопросы

Часто задаваемые вопросы о сложении дробей с разными знаменателями

Как складывать дроби с разными знаменателями?

Каковы примеры сложения дробей с разными знаменателями?

Какова стратегия сложения дробей с разными знаменателями?

Как сложить дроби с разными знаменателями?

Можно ли складывать дроби с разными знаменателями без использования НОК?

Каково правило сложения дробей с разными знаменателями?

Как сложить 3 дроби с разными знаменателями?

Как складывать и вычитать дроби с разными знаменателями?