Законы умножения: переместительный, сочетательный и распределительный
Переместительный закон умножения
Если множимое и множитель поменять местами, то произведение не изменится. Это можно легко проверить при подсчёте двумя способами числа звёздочек представленных на рисунке:
3 + 3 + 3 + 3 = 4 + 4 + 4
Так как множимое и множитель можно менять местами их ещё называют сомножителями или просто множителями.
Таким образом, для любых натуральных чисел a и b верно равенство:
a · b = b · a,
выражающее переместительный закон умножения:
От перестановки сомножителей произведение не меняется.
Сочетательный закон умножения
Произведение чисел 3, 2 и 4 не изменится, если из них какие-нибудь два числа заменить их произведением:
3 · 2 · 4 = 3 · (2 · 4) = 3 · 8 = 24,
3 · 2 · 4 = (3 · 2) · 4 = 6 · 4 = 24.
Таким образом, для любых натуральных чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательный закон умножения:
Произведение не изменится, если какую-либо группу сомножителей заменить их произведением.
Распределительный закон умножения
Для любых натуральных чисел верны равенства:
m · (a + b + …) = m · a + m · b + …
(a + b + …) · m = a · m + b · m + … ,
выражающие распределительный закон умножения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на число и полученные произведения сложить.
Распределительный закон умножения можно легко проверить при подсчёте двумя способами числа звёздочек, представленных на рисунке:
Первый: в каждом ряду расположено 3 жёлтых и 5 зелёных звёздочек, то есть всего в каждом ряду (3 + 5) звёздочек. В четырёх рядах всего (3 + 5) · 4 звёздочек.
Второй: жёлтые звёздочки расположены в четыре ряда по 3 звёздочки в каждом, то есть всего жёлтых звёздочек 3 · 4, а зелёных — 5 · 4. Всего звёздочек 3 · 4 + 5 · 4.
Кроме того, для любых натуральных чисел (если уменьшаемое больше или равно вычитаемому) верны равенства:
m · (a — b — …) = m · a — m · b — …
(a — b — …) · m = a ·
Например, 6 · (4 — 2) = 6 · 4 — 6 · 2.
Переход от умножения:
m · (a + b + …)
и
m · (a — b — . ..)
..)
соответственно к сложению и вычитанию:
m · a + m · b + …
и
m · a — m · b — …
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b + …
и
m · a — m · b — …
к умножению:
m · (a + b + …)
и
m · (a — b — …)
называется вынесением общего множителя за скобки.
Ответы к странице 36 №135-138 ГДЗ к учебнику Алгебра 7 класс Никольский
Ответы к теме 3.4. Основные свойства действительных чисел
Задание 135
Сформулируйте свойство транзитивности неравенств.Ответ
Свойство транзитивности неравенств: если a < b и b < с, то a < c.
Задание 136
Сохранится ли неравенство, если:
а) к обеим его частям прибавить действительное число;
б) обе его части умножить на положительное число;
в) обе его части умножить на нуль или отрицательное число?
Приведите примеры.
Решение
а) Если к обеим частям неравенства прибавить действительное число, то неравенство сохранится.
Например:
8 < 10 < 12
8 + 3 < 10 + 3 < 12 + 3
11 < 13 < 15 − верноб) Если обе части неравенства умножить на положительное число, то неравенство сохранится.
Например:
8 < 10 < 12
8 * 3 < 10 * 3 < 12 * 3
24 < 30 < 36 − вернов) Если обе части неравенства умножить на нуль или отрицательное число, то неравенство не сохранится.
Например:
1)
8 < 10 < 12
8 * 0 < 10 * 0 < 12 * 0
0 < 0 < 0 − неверно
2)
8 < 10 < 12
8 * (−1) < 10 * (−1) < 12 * (−1)
−8 < −10 < −12 − неверно
Задание 137
Сформулируйте:
а) переместительный закон сложения;
б) переместительный закон умножения;
в) сочетательный закон сложения;
г) сочетательный закон умножения;
д) распределительный закон.
Решение
а) переместительный закон сложения:
x + y = y + x для любых действительных чисел x и y.б) переместительный закон умножения:
x * y = y * x для любых действительных чисел x и y.в) сочетательный закон сложения:
(x + y) + z = x + (y + x) для любых действительных чисел x, y и z.г) сочетательный закон умножения:
(x * y) * z = x * (y * x) для любых действительных чисел x, y и z.д) распределительный закон:
(x + y) * z = x * z + y * z для любых действительных чисел x, y и z.
Задание 138
а) Что получится, если к числу прибавить 0?
б) Чему равна сумма противоположных чисел?
в) Можно ли разность a − b записать в виде суммы?
г) Что получится, если число умножить на 1; −1; 0?
д) Какое число называют обратным к числу a (a ≠ 0)?
е) Какие числа называют взаимно обратными?
ж) Чему равно произведение двух взаимно обратных чисел?
Решение
а) Если к числу прибавить 0, то число не изменится.
б) Сумма противоположных чисел равна 0.
в) Можно, так как a − b = a + (−b)
г) Если число умножить на 1, то получится данное число.
Если число умножить на −1, то получится противоположное данному число.
Если число умножить на 0, то получится 0.д) Число $\frac{1}{a}$ называют обратным к числу a (a ≠ 0).
е) Числа a и $\frac{1}{a}$ называют взаимно обратными.
ж) Произведение взаимно обратных чисел равно 1.
Законы математики
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Задание 2. Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Методическая разработка урока в 5-м классе по теме «Законы арифметических действий»
ЦЕЛИ:
- Повторить переместительный и сочетательный
законы сложения и умножения.

- Развивать умение пользоваться данными законами при решении примеров; объяснить распределительный закон.
- Развивать элементы творческой деятельности учащихся и умение контролировать свои действия.
ТИП УРОКА: Урок комплексного применения знаний, умений и навыков.
ВИД УРОКА: Урок теоретических, практических и самостоятельных работ.
ОБОРУДОВАНИЕ: проектор, карточки-задания.
ПЛАН УРОКА:
1. Организационный момент.
2. Проверка домашнего задания. Устная работа.
3. Изучение нового материала.
4. Работа с таблицей. Выполнение упражнений на закрепление.
5. Резерв — занимательный пример.
6. Задание на дом.
7. Подведение итогов урока.
Презентация.
ХОД УРОКА
1. Организационный момент.
Сегодня на уроке мы повторим переместительный и сочетательный законы сложения и умножения и познакомимся с ещё с одним законом
Запишем тему урока: Распределительный закон умножения.
2. Проверка домашнего задания. Устный счёт.
1) Слайд 2. Учащиеся самостоятельно выполняют вычисления, затем самопроверка.
2) 2 ученика выполняют индивидуальные задания, остальные работают устно.
Устная работа.
- Сформулируйте и запишите переместительный закон сложения.
- Сформулируйте и запишите переместительный закон умножения.
- Сформулируйте и запишите сочетательный закон сложения.
- Сформулируйте и запишите сочетательный закон умножения.
3. Изучение нового материала.
1) найдите площадь прямоугольника АВСД разными способами. Слайды14-18
Формулируется распределительное свойство
умножения относительно сложения.
2) найдите площадь прямоугольника АВМN разными способами. Слайды19-23
Формулируется распределительное свойство умножения относительно вычитания.
4. Закрепление.
1) Устная работа с таблицей на закрепление. Слайд 24
Перед вами таблица с номерами примеров и вариантами ответов и таблица с заданием на странице 67 учебника. У каждого ученика карточки с номерами от 1 до 4. После того, как я вам назову номер столбца, вы его вычисляете, находите верный ответ и показываете карточку с номером ответа, который считаете правильным
1 2 3 4 1 40 15 45 0 2 48 38 15 1 3 16 21 18 5 4 24 44 17 54 5 57 58 60 25
с 30 38 43 59 72 d 15 22 26 41 53 3(c-d) 3c-3d
Вопрос классу: надо ли было производить вычисления, чтобы заполнить вторую строчку?
2) Используя распределительный закон, письменно
найти значения выражений №220, №224. Ученики по
одному выходят к доске и решают по одному
примеру.
Ученики по
одному выходят к доске и решают по одному
примеру.
5. Физкультминутка.
6. Логическая задачка
Магия чисел
Цифры написаны на карточках и разложены в два ряда, как показано на доске. Поменяйте местами 2 карточки так, чтобы сумма четырёх чисел в каждой строке была одной и той же.
6. Задание на дом.
Выучить формулу и правило распределительного закона.
№225 (стр.67).
Творческое задание: придумать рекламу законам арифметических действий.
7. Подведение итогов урока.
- Что мы делали на уроке? Какие действия выполняли?
- Что нового вы узнали сегодня на уроке?
- С какими номерами примеров вам было тяжело справиться? А с какими легко?
Оценки за урок.
Конец формы
Основные свойства действий с рациональными числами
Данная статья посвящена обзору свойств действий с рациональными числами. Сначала рассмотрены основные свойства, а затем — те свойства, которые базируются на основных свойствах.
Сначала рассмотрены основные свойства, а затем — те свойства, которые базируются на основных свойствах.
Действия с рациональными числами. Основные свойства
Все свойства действий с рациональными числами базируются на основе свойств действий с целыми числами. Пусть a, b, c, d — некоторые произвольные рациональные числа. Перечисли оcновные свойства действий с ними.
- Коммутативное свойство сложения. Оно еще называется коммутативным или переместительным законом. a+b=b+a.
- Сочетательное свойство, или сочетательный закон сложения. a+(b+c)=(a+b)+c.
- Ноль — нейтральный элемент по сложению. Сложение нуля с любым числом не изменяет это число. a+0=a.
- Для любого рационального числа a существует такое противоположное число -a, что a+(-a)=0.
- Коммутативный (переместительный) закон умножения рациональных чисел. a·b=b·a.
- Сочетательный закон умножения.a·b·c=a·(b·c).
- Единица — нейтральный элемент по умножению. Умножение любого числа на единицу не изменяет этого числа.
 a·1=a.
a·1=a. - Для любого рационального числа a, отличного от ноля, существует такое обратное число a-1, что a·a-1=1.
- Распределительное свойство умножения относительно сложения. a·(b+c)=a·b+a·c.
Перечисленные выше свойства — основные свойства действий с рациональными числами. Остальные свойства являются следствием основных свойств.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеДругие свойства рациональных чисел
Кратко рассмотрим иные, наиболее часто используемые свойства действий с рациональными числами.
Умножение рациональных чисел с разными знаками. a·(-b)=-(a·b) или (-a)·b=-(a·b).
Умножение отрицательных рациональных чисел. (-a)·(-b)=a·b.
Умножение произвольного числа на ноль. a·0=0. Остановимся на доказательстве этого свойства. Пусть d — любое рациональное число. Справедливым будет равенство 0=d+(-d), которое можно переписать так: a·0=a·(d+(-d)). Теперь перепишем равенство с учетом распределительного свойства:
Теперь перепишем равенство с учетом распределительного свойства:
a·0=a·d+a·(-d)a·d+a·(-d)=a·d+(-a·d)
Сумма двух противоположных чисел a·d и (-a·d) дает ноль. Что и требовалось доказать.
Рассмотренные выше свойства — свойства умножения и сложения. Свойства вычитания и деления задаются как обратные свойства соответственно к сложению и умножению. Так, разность двух чисел a-b можно записать в виде суммы a+(-b), а частное ab есть не что иное, как произведение a·b-1.
С учетом свойств умножения и сложения можно доказать любые свойства действий с рациональными числами. Для примера, возьмем распределительное свойство умножения относительно вычитания:
a·(b-c)=a·b-a·ca·(b-c)=a·(b+(-c))=a·b+a·(-c)=a·b+(-a·c)=a·b-a·c
Запишите в буквенном виде переместительное, сочетательное и распределительное свойства умножения
Виды углов и их градусные меры.
Угол, стороны которого образуют прямую, называют развернутым (180°)
Угол, равный половине развернутого угла, называют прямым углом (90°)
Угол, меньший прямого, называется острым (<90°)
Угол, больший прямого, но меньше развёрнутого, называется тупым(90°< >180°)
2. Какие многоугольники называют равными? Какие фигуры называют равными?
Какие многоугольники называют равными? Какие фигуры называют равными?
Простая замкнутая ломаная вместе со своей внутренней областью называется многоугольником.
Два многоугольника называются равными, если они совпадают при наложении.
Две фигуры называют равными, если они совпадают при наложении.
Классификация треугольников по виду углов.
Треугольник с прямым углом называется прямоугольным треугольником
Треугольник с тупым углом называется тупоугольным треугольником
Треугольник, у которого все углы острые, называется остроугольным треугольником
Классификация треугольников по числу равных сторон.
Треугольник, две стороны которого равны, называется равнобедренным
Треугольник, все стороны которого равны, называется равносторонним
Треугольник, все стороны которого различны, называется разносторонним
Дайте определение прямоугольника. Сформулируйте свойство прямоугольника. Запишите формулу периметра прямоугольника.
Сформулируйте свойство прямоугольника. Запишите формулу периметра прямоугольника.
Четырёхугольник, все углы которого прямые, называется прямоугольником.
У прямоугольника противоположные стороны равны. Диагонали прямоугольника также равны и делятся точкой пересечения пополам.
Р=2а+2б
6. Что называют произведением числа а на натуральное число b, не равное 1? Как в равенстве a называют число а? Число b? Число с? Выражение a b?
Произведением числа А на натуральное число Б, не равное 1, называют сумму, состоящую из Б слагаемых, каждое из которых равно А
В равенстве а*б=с числа а и б называют множителями, а число с и запись а*б- произведением
Запишите в буквенном виде переместительное, сочетательное и распределительное свойства умножения.
Переместительный закон: а*б=б*а
От перестановки множителей произведение не изменяется
Сочетательный закон: (а*б)*с=а*(б*с)
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего числа.
Распределительный закон умножения:
Чтобы сумму двух чисел умножить на третье число, можно умножить на это число каждое слагаемое и полученные результаты сложить.
(а + б)*с=а*с + б*с
Чтобы умножить число на сумму двух чисел, можно умножить это число на каждое из слагаемых и полученные произведения сложить
а*(б + с)=а*б + а*с
8. Как в равенстве a называют число а? Число b? Число с? Выражение а : b? Что показывает частное двух чисел?
В равенстве а : б=с число А называют делимым, число Б- делителем, число С и запись а : б- частным
Частное А:Б показывает, во сколько число А больше числа Б или во сколько раз число Б меньше числа А
Конспект урока. Тема: «Умножение. Переместительный закон умножения». | План-конспект урока по алгебре (5 класс) по теме:
Урок №1. Тема: «Умножение. Переместительный закон умножения».
Цели урока:
- Изучение правила умножения натуральных чисел, переместительного закона умножения; формирование элементарных умений выполнять умножения натуральных чисел;
- развитие основных умений выполнять умножение натуральных чисел по основному алгоритму; развитие внимания, логического мышления;
- воспитание интереса к изучению предмета, умений работать в группах.

Ход урока.
1. Организационный момент.
Друзья мои, я очень рада
Войти в приветливый наш класс.
И для меня уже награда
Внимание ваших умных глаз.
Я знаю, каждый в классе гений,
Но без труда талант не впрок.
Возьмём же ручки и мелок
И вместе сочиним урок.
2. Мотивация урока.
Сегодня на уроке, ребята, нам предстоит выполнить серьёзную работу. От вас потребуется усидчивость, стремление, внимание, последовательность и правильность выполнения заданий. Вам уже известны правила сложения, вычитания натуральных чисел. Сегодня мы познакомимся с правилом умножения натуральных чисел.
3. Актуализация опорных знаний.
Нам предстоит познакомиться и дать определение ещё одному арифметическому действию, которое называется « УМНОЖЕНИЕ», что это такое и как производятся вычисления, попробуйте объяснить сами.
Математический диктант:
2*7, 10*5, 35*2, 7*9, 4*7, 5*6, 4*25, 3*1, 4*0.
Самопроверка.
4. Изучение нового материала.
Изучение нового материала.
С действием умножения вы знакомы из начальной школы. Поэтому для изучения нового материала вспомним то, что изучали ранее.
9+9+9+9
100+100+100+100+100
— Сосчитайте, сколько получится в каждом выражении? — Как вы думаете можно ли сделать вычисление этих выражений более быстрым? — Сколько раз в выражении 9+9+9+9 повторилось слагаемое? (4 раза) — Значит можно записать так: 9+9+9+9=9*4 — Сколько раз в выражении 100+100+100+100+100 повторилось слагаемое? (5 раза) — Значит можно записать так: 100+100+100+100+100=100*5 — А кто из вас, ребята, знает, как же называется арифметическое действие, которое помогает быстро сосчитать одинаковые слагаемые? (умножение) Правильно – УМНОЖЕНИЕ. Произведение m*n есть сумма n слагаемых, каждое из которых равно m. Умножением натуральных чисел называется действие, при котором находится сумма одинаковых слагаемых.
Если а и b – натуральные числа, то
При этом а и b называются множителями, с – произведением. А как же запомнить правильные ответы действия умножения? (надо знать таблицу умножения)
А как же запомнить правильные ответы действия умножения? (надо знать таблицу умножения)
Умножение обладает следующими свойствами.
1. Произведение двух чисел не изменяется при перестановке множителей. Это свойство умножения называют переместительным. С помощью букв его записывают так: а∙в=в∙а
2. Сумма п слагаемых, каждое из которых равно 1 , равен п . Поэтому верно равенство 1∙п=п.
3. Сумма п слагаемых, каждое из которых равно нулю, равна нулю. Поэтому верно равенство 0∙п=0.
5. Физкультминутка
-Давайте немножко взбодрим наше тело. Встаньте, пожалуйста, около своих парт и повторяйте за мной:
Руки подняли и помахали
Это деревья шумят.
В стороны руки и помахали
Это к нам птицы летят.
Быстро присели, руки сложили
В норке зверюшки сидят.
Встали и тихо за парты все сели.
Дети учиться хотят.
6. Закрепление нового материала.
Решить № 396, 397, 399(1, 3), 401.
7. Самостоятельная работа.
Решить № 403.
8. Итоги урока. Д/з.
Рефлексия.
— Что нового узнали на уроке?
— Чему научились?
— Оцените свои знания по таблице:
Знаю: (что такое умножение)
Сомневаюсь:
Не знаю:
- Что значит умножить одно натуральное число на другое?
- Как называются числа, которые перемножают?
- Как называют результат умножения?
- Сформулируйте переместительное свойство умножения. Запишите его с помощью букв.
- Чему равно произведение m ∙ 1?
- Чему равно произведение n ∙ 0?
Выучить п. 15, вопросы №395. Решить № 400(3, 4), 404, 402.
В труде умноженье поможет.
Чтоб дельной работа была,
Стократ трудолюбье умножим –
Умножатся наши дела.
— Спасибо за урок!
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.

- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Получение закона смещения Вина из закона Планка
Закон смещения Вина утверждает, что кривая излучения черного тела для различных температур достигает пика на длине волны, обратно пропорциональной температуре. Смещение этого пика является прямым следствием закона излучения Планка, который описывает спектральную яркость излучения черного тела как функцию длины волны при любой заданной температуре. Однако это было обнаружено Вильгельмом Вином за несколько лет до того, как Макс Планк разработал это более общее уравнение, описывающее полный сдвиг спектра излучения черного тела в сторону более коротких волн при повышении температуры.{10} Гц / К) \, T \ end {align} \]
В результате форма функции излучения абсолютно черного тела будет пропорционально изменяться по частоте с температурой. Когда Макс Планк позже сформулировал правильную функцию излучения черного тела, она не включала в явном виде постоянную Вина. Скорее, постоянная Планка h была создана и введена в его новую формулу. Из постоянной Планка h и постоянной Больцмана k можно получить постоянную Вина (уравнение \ ref {eq20}).
Когда Макс Планк позже сформулировал правильную функцию излучения черного тела, она не включала в явном виде постоянную Вина. Скорее, постоянная Планка h была создана и введена в его новую формулу. Из постоянной Планка h и постоянной Больцмана k можно получить постоянную Вина (уравнение \ ref {eq20}).
Авторы и авторство
(PDF) Определение истинной температуры испускаемых радиационных тел по обобщенному закону смещения Вина
J. Phys. D: Прил. Phys. 32 (1999) 1–4. Отпечатано в Великобритании PII: S0022-3727 (99) 05648-X
Определение истинной температуры
испускаемых радиационных тел из
обобщенный закон смещения Вина
А.И. Фисенко † § и С.Н.Ивашов ‡
† Центр экологии Онтарио , Пр-т Горта 4, Suite 1, Торонто, Онтарио M8W 3Y5, Канада
‡ Одесский государственный университет, 270100, Одесса, Дворянская улица, 2, Украина,
E-mail: [email protected]
Восход солнца
Маркированное доказательство
D / 105648 / PAP
17262ae
Отпечатано 10. 07.99
07.99
14.05
Поступило 5 июля 1999 г., окончательная форма 2 сентября 1999 г.
Реферат. Исследована температурная зависимость «обобщенного» закона смещения Вина для тантала
и светящихся пламени.Показано, что излучаемое тепловое излучение тантала
относится к тому же классу универсальности, что и вольфрам и цирконий
и карбиды титана. Испускаемое тепловое излучение светящихся пламен относится к классу универсальности
как у черного тела. Определены истинные температуры исследуемого вещества
.
1. Введение
Определение истинной температуры тела, имеющего непрерывные излучаемые спектры
, является важной проблемой в технологии высокоскоростных температур
[1,2].Серия используемых в настоящее время контактных методов измерения не
позволяет нам определять истинную температуру тела
. Однако эти методы
ограничены измерением установившейся температуры
[3–6] и также имеют пределы применения [1–3].
При измерении температуры оптическими пирометрами
наиболее важная длина волны излучения принадлежит диапазонам
видимого и инфракрасного излучения. В результате методы оптического пирометра
ограничивают измерение установившейся температуры
более 2400 К.
Метод доплеровского уширения спектральных линий также
имеет ограничение. Неясно, как отделить эффекты
, связанные с доплеровским уширением, от эффектов, которые проявляются
из-за явления взаимодействующих молекул газа,
уширения Лоренца. По поводу других методов см. [1–3].
В [7–9] был предложен метод высокоскоростной спектроскопии для измерения излучательной способности
при высоких температурах
.Однако в этих методах температура исследуемых веществ
определялась оптическими пирометрами. Это
означает, что температурный режим стал устойчивым.
Общей особенностью хорошо известных методов измерения температуры в установившемся режиме
является то, что они не позволяют достичь высокой степени точности, а их применение
не может использоваться для быстрых измерений из-за
ограничения времени задержки [10]. Поэтому разработка новых,
Поэтому разработка новых,
более точных методов измерения температуры является реальной проблемой
.
В [11,12] предложен бесконтактный метод определения
истинной температуры тел. Этот метод
не имеет ограничений по применению и может быть применен к
§ Автор, ответственный за переписку.
задача определения истинной температуры тел
с использованием современной высокоскоростной температурной технологии.Общая идея этого метода
состоит в следующем: (1) спектральная плотность излучения
аппроксимируется асимптотическим рядом Эджворта
; (2) коэффициенты серии Эджворта
восстанавливаются через частотные моменты спектральной плотности излучения
; (3) частотные моменты
определяются через излучательную способность тел ε (ν, T); (4) истинная температура веществ
определяется положением
максимума спектральной плотности излучения (аналогично
закон смещения Вина). Точность этого метода
Точность этого метода
выше, когда определено большое количество частотных моментов
. Точность еще выше, если правильно измерить каждый из
моментов.
Этот метод был проверен на спектральной плотности излучения
карбида циркония, карбида титана [11] и вольфрама
[12]. Показано, что закон смещения Вина для
исследованных тел линейно убывает при повышении температуры
.Истинные температуры были определены на основе «обобщенного» закона смещения Вина
. Точность в
определения установившейся температуры в этих случаях не падает ниже 2%. Важно отметить, что
аналогичный закон связи между температурой
и положением максимума спектральной яркости был
, полученный для карбидов [11] и вольфрама [12]. Со временем
испускают непрерывное тепловое излучение тел, которые имеют
аналогичный закон взаимосвязи между температурой T
и положением максимума спектральной яркости νmax, и
будут идентифицированы как принадлежащие к тому же классу универсальности.
Данная статья посвящена дальнейшему развитию
бесконтактного метода определения истинной температуры
тел, предложенного ранее в [11,12]. На примере
«обобщенный» закон смещения Вина
исследуется для светящихся пламен и тантала. Классы универсальности
, к которым принадлежат исследуемые тела
0022-3727 / 99/010001 + 04 $ 19,50 © 1999 IOP Publishing Ltd 1
Часто используемые математические формулы
Это хранилище формул, которые мы используем в других статьях.Цель этого документа состоит в том, чтобы обобщить математические операторы и термины, а также их обозначения и некоторые полезные отношения между ними. Мы не будем демонстрировать, как их получить. Это выходит за рамки этого документа, и в Интернете есть много ресурсов по этому поводу.
Мы используем оператор «⋅» для обозначения умножения. Таким образом, если мы увидим термин «abxy» в математическом выражении, мы знаем, что он представляет собой одну сущность, а не, например, умножение терминов «ab» на «xy», и в этом случае мы будем использовать « ab⋅xy «.
В этих формулах оператор «==» используется в основном для того, чтобы показать два альтернативных способа выражения одного и того же.
В этих формулах символы с полужирным шрифтом (например, X ) представляют случайные величины, а символы с обычным (не полужирным) шрифтом представляют неслучайные величины (например, « c »).
Ожидаемая стоимость
Мы используем выражение Eva ( X ) для обозначения ожидаемого значения случайной величины X .Символ μ x представляет значение, полученное в результате этого выражения.
Формула 1.
символов Евы.
Ожидаемое значение неслучайной переменной, например константы, является значением самой этой неслучайной переменной:
Формула 2. Ева неслучайной величины.
Ожидаемое значение произведения двух независимых случайных величин равно произведению этих переменных Ожидаемое значение с:
Формула 3. Ева произведения независимых переменных.
Ева произведения независимых переменных.
Если переменная масштабируется константой (неслучайной величиной), ожидаемое значение масштабируется этой константой. Это прямое следствие двух предыдущих формул.
Формула 4. Ева масштабированной переменной.
Если две случайные величины коррелированы , это означает, что значение одной из них в некоторой степени определяет или влияет на значение другой. Ковариация — это мера того, насколько эти переменные коррелированы.
Например, курение коррелирует с вероятностью заболевания раком: чем больше вы курите, тем больше вероятность того, что вы в конечном итоге заболеете раком.
Ожидаемое значение произведения двух коррелированных случайных величин равно произведению этих переменных Ожидаемое значение с плюс ковариация из них:
Формула 5. Ева произведения двух коррелированных переменных.
Обратите внимание, что формула 3 является частным случаем предыдущей формулы: когда случайные величины независимы, член Ковариация равен нулю и исчезает.
Ожидаемое значение суммы любых случайных величин равно сумме ожидаемых значений с этих переменных. Это верно независимо от , являются ли эти случайные величины независимыми или нет.
Формула 6. Ева суммы двух случайных величин. Независимо от того, независимы они или нет.
Консолидация предыдущих отношений приводит к получению свойства Linearity оператора Expected Value ( Linearity of Expectation ), которое истинно независимо от того, случайные величины независимы или нет.
Формула 7. Линейность ожидания.
Коварианс
Мы используем выражение Cov ( X , Y ) для обозначения Ковариации двух случайных величин X и Y .
Формула 8. Символы ковариации.
Ковариация — это мера того, насколько значения каждой из двух коррелированных случайных величин определяют другую.Если обе переменные изменяются одинаково (например, когда — в общем — одна растет, другая тоже растет), Ковариация положительна, в противном случае она отрицательна (например, когда одна увеличивается, другая уменьшается).
Если переменные независимы , Ковариация равна нулю. Однако ковариация должна считаться нулевой или ненулевой со статистической точки зрения, что означает, что есть некоторый факт, который заставляет нас полагать, что значение Ковариация не может быть оправдано только на основе случайности.
Формула 9. Оценка ковариации по необработанным данным.
Если переменные независимы , их Ковариация равна нулю. Это можно ясно увидеть в следующей формуле, где, если бы обе переменные были независимы друг от друга, оба члена при вычитании стали одинаковыми, а ковариация стала равной нулю:
Формула 10.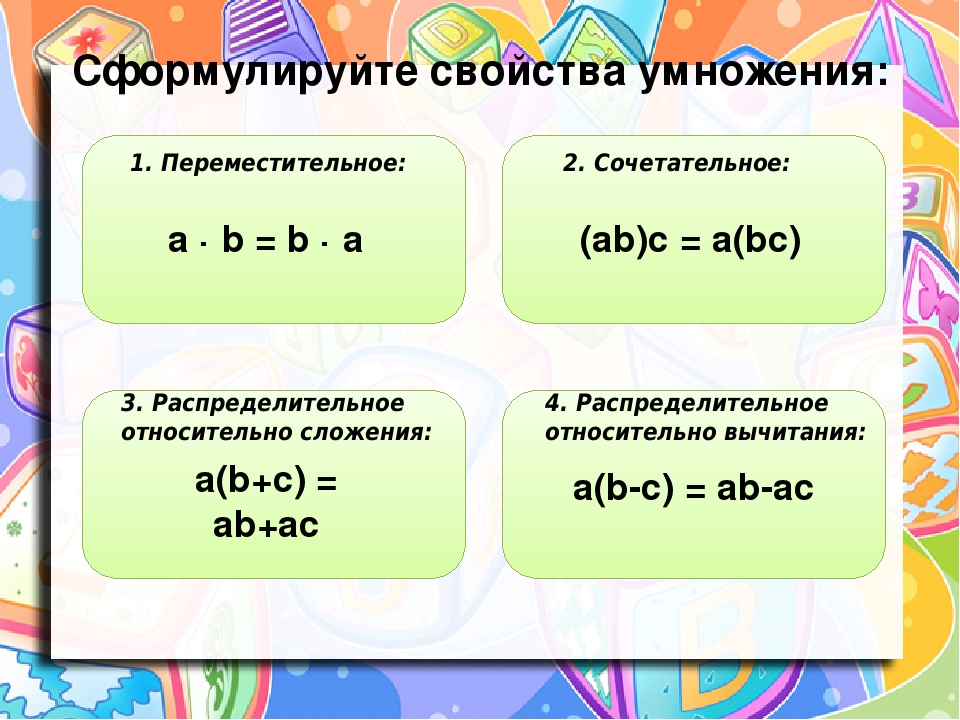 Оценка ковариации от ожидаемых значений.
Оценка ковариации от ожидаемых значений.
Однако обратное предыдущему правилу не всегда верно: если Ковариация равна нулю, это не обязательно означает , что случайные величины независимы.
Например, если X равномерно распределен в [-1, 1] , его ожидаемое значение и ожидаемое значение нечетных степеней (например, X ³) X приводят к нулю в [-1, 1] . По этой причине, если случайная величина Y определена как Y = X ², очевидно, что X и Y коррелируют . Однако их Ковариация численно равна нулю:
Формула 11.Если (независимые переменные) ==> (Ковариация == 0). Однако (Ковариация == 0) не обязательно означает, что эти переменные независимы.
Ковариация коммутативна.
Формула 12. Коммутативность ковариаций.
Коммутативность ковариаций.
Ковариация инвариантна к смещению одной или обеих переменных.
Формула 13. Ковариация инвариантна к смещению переменных.
Ковариация масштабируется по каждой шкале X и Y.
Формула 14. Масштаб каждой переменной увеличивает ковариацию.
Объединение двух последних уравнений:
Формула 15. Свойство нелинейности ковариации.
Разница
Вариация — это частный случай ковариации , когда обе переменные одинаковы.
Формула 16. Символы отклонения.
Дисперсия измеряет, насколько разбросаны значения случайной величины.Другими словами, насколько они разные между собой.
Формула 17. Оценка отклонения от исходных данных.
Мы можем вычислить отклонение из ожидаемых значений из X и его квадрата ( X ²).
Формула 18. Оценка отклонения от ожидаемых значений.
Дисперсия неслучайной переменной равна нулю.
Формула 19
Дисперсия инвариантна к смещению переменной.
Формула 20.
Смещение переменной прозрачно для дисперсии.
Если переменная масштабируется константой (неслучайной величиной), отклонение масштабируется на квадрат этой константы.
Формула 21.
Дисперсия также масштабируется константой, но квадратично.
Дисперсия суммы или разности двух коррелированных случайных величин составляет:
Формула 22.
Дисперсия суммы (и разности) двух случайных величин.
Если переменные независимы , ковариация равна нулю, а дисперсия суммы или разности одинакова:
Формула 23.
Когда ковариация равна нулю, дисперсия суммы равна дисперсии разности двух случайных величин. 2} = 0) $:
2} = 0) $:
Формула 26.Дисперсия произведения двух независимых переменных.
Другой способ получить произведение двух независимых случайных величин — это красивое уравнение:
Формула 27. Произведение двух независимых переменных.
Стандартное отклонение
Мы используем выражение StdDev (X) для обозначения стандартного отклонения случайной величины X .
Формула 28.
символов стандартного отклонения.
Стандартное отклонение — это квадратный корень из отклонения .
Формула 29. Стандартное отклонение — это (по определению) квадратный корень из отклонения .
Коэффициент корреляции
Коэффициент корреляции — это мера зависимости между двумя коррелированными случайными величинами.
Формула 30. Коэффициент корреляции.
Иногда вы можете измерить две выходные переменные из эксперимента, которые сильно коррелированы, потому что они происходят от двух функций общей переменной и того, что вы хотите знать об этих двух функциях. Если вы построите корреляционную формулу для связи между этими выходными переменными с помощью данных из многих экспериментов, вы сможете найти хорошее приближение этой корреляционной формулы. Однако возникает вопрос: как эта формула корреляции может пролить свет на функции, производящие эти выходные переменные?
Если вы построите корреляционную формулу для связи между этими выходными переменными с помощью данных из многих экспериментов, вы сможете найти хорошее приближение этой корреляционной формулы. Однако возникает вопрос: как эта формула корреляции может пролить свет на функции, производящие эти выходные переменные?
Предположим, у нас есть $ (f (x)) $ и $ (g (x)) $, оба оцениваются как $ (x_i) $ в $ ({x_1, x_2 … x_n}) $, что означает, что мы имеют точки $ ((f (x_i), g (x_i))) $. Теперь мы находим корреляцию по этим точкам.{-1} ({\ bf z})) \\ h ({\ bf z}) & = g \ left (\ frac {{\ bf z} — f_0} {f_1} \ right) \\ h ({\ bf z}) & = g_1 \ cdot \ left (\ frac {{\ bf z} — f_0} {f_1} \ right) + g_0 \\ \следовательно h ({\ bf z}) & = \ frac {g_1} {f_1} \ cdot {\ bf z} + \ left (g_0 — \ frac {g_1} {f_1} \ cdot f_0 \ right) \ tag {32} \ end {align *}
Формула 32. Аналитическая корреляция между двумя линейными функциями.
Это означает, что когда мы коррелируем две линейные функции, результирующая кривая также является линией, имеющей в качестве наклона один из $ (g (x)) $, деленный на один из $ (f (x)) $. Мы также знаем, что коррелированная линия пересекает ось $ (h) $ (когда $ (z = 0) $) в точке $ (h = (g_1 / f_1) \ cdot z + (g_0 — (g_1 / f_1) \ cdot f_0) ) $.
Мы также знаем, что коррелированная линия пересекает ось $ (h) $ (когда $ (z = 0) $) в точке $ (h = (g_1 / f_1) \ cdot z + (g_0 — (g_1 / f_1) \ cdot f_0) ) $.
Мы можем очень легко «подтвердить» этот случай. Предположим, наши линейные функции:
\ begin {align *} е (х) & = 2 \ cdot x + 13 \\ г (х) & = 3 \ cdot х + 5 \ end {align *}
Если мы построим эти функции для $ (x) $ в $ ({1, 2}) $, мы получим $ ((f, g) = {(15, 8), (17, 11)}) $. Зная, что эти точки принадлежат прямой, мы можем найти наклон как $ (\ Delta y / \ Delta x) $.Если наш предыдущий вывод верен, этот наклон должен быть равен $ (g_1 / f_1 = 3/2) $:
.\ begin {уравнение *} наклон = \ Delta y / \ Delta x = (11-8) / (17-15) = 3/2 \ end {уравнение *}
Что мы и думали!
Также согласно нашей последней формуле перехват коррелированной линии с $ (z = 0) $ должен происходить, когда h равно:
\ begin {align *}
h (0) & = (g_1 / f_1) \ cdot 0 + (g_0 — (g_1 / f_1) \ cdot f_0) \\
h & = 5 — (3/2) \ cdot 13 \\
h & = -14. 2 — \ frac {g_1} {f_1} \ cdot f_0 + g_0 \ cr
\ end {align *} \ tag {33}
2 — \ frac {g_1} {f_1} \ cdot f_0 + g_0 \ cr
\ end {align *} \ tag {33}
Формула 33.Аналитическая корреляция квадратичной функции с линейной.
РЕШЕНИЕ: (a) Вывести закон смещения Вина из Pl…
.Расшифровка стенограммы
В этом упражнении вы должны вывести закон Винса. То есть London max Times t равно Vince Constant, который составляет 2,9 температуры при минус трех ваттах, сэр. Эээ, метров отела. И для этого мы должны определить длину волны? Лямбда Макс. Такая, что интенсивность ягодного рыдания по закону панков I o off Lunda и T максимальна.Так что мне нужно будет помнить, что I от Линды и T согласно закону Планка, равно двум квадратам старшего возраста C здесь, Линда к пятому e к C над Линдой K t минус что? Хорошо. И нам нужно было найти максимум этого уравнения. И для этого вы знаете, что максимум будет найден, когда производная по Лунде равна нулю. Итак, что я собираюсь сделать, так это взять производную от I по отношению к Лондону. Итак, это просто константы. Остался такой же корабль я возраста С квадрат, и я собираюсь начать прибывать.Что происходит? Ах, в знаменателе. Итак, по правилу цепочки, я просто собираюсь, я просто собираюсь дифференцировать. Ах, древесина до 5-го 1-го. Итак, это будет минус пять по сравнению с Лондоном до шестого, и я умножу на то, что будет дальше. Что это за экспонента? Это производная. Первый член, Другая производная. Плюс, эм, нет, я оставлю еще одну. Ограничено пятью. Прыщик, и я выведу это экспоненту. Ах. Итак, сначала я собираюсь рассматривать экспоненту как переменную и выводить ее.Так что это будет минус термин экспоненциальный от си-ключа. Извини, это не К. Это должна быть Лунда. Кэти минус один в квадрате. Нет, я должен извлечь то, что внутри. Ах, термин здесь в квадрате, вот где. Здесь. Итак, у нас есть производная от экспоненты. Так что это сама экспонента. Умножает производную на аргумент экспоненты. И это минус тройка по сравнению с Кэти. Линда-сквер. Хорошо, помните, что я езжу относительно Лондона, вот почему мне пришлось трижды выводить второй срок.
Итак, это просто константы. Остался такой же корабль я возраста С квадрат, и я собираюсь начать прибывать.Что происходит? Ах, в знаменателе. Итак, по правилу цепочки, я просто собираюсь, я просто собираюсь дифференцировать. Ах, древесина до 5-го 1-го. Итак, это будет минус пять по сравнению с Лондоном до шестого, и я умножу на то, что будет дальше. Что это за экспонента? Это производная. Первый член, Другая производная. Плюс, эм, нет, я оставлю еще одну. Ограничено пятью. Прыщик, и я выведу это экспоненту. Ах. Итак, сначала я собираюсь рассматривать экспоненту как переменную и выводить ее.Так что это будет минус термин экспоненциальный от си-ключа. Извини, это не К. Это должна быть Лунда. Кэти минус один в квадрате. Нет, я должен извлечь то, что внутри. Ах, термин здесь в квадрате, вот где. Здесь. Итак, у нас есть производная от экспоненты. Так что это сама экспонента. Умножает производную на аргумент экспоненты. И это минус тройка по сравнению с Кэти. Линда-сквер. Хорошо, помните, что я езжу относительно Лондона, вот почему мне пришлось трижды выводить второй срок. Ладно, это слишком высокий квадрат возраста C. Я собираюсь повлиять на нее через окно до шестого и одного экспоненциального минус пять плюс H c. Над Лондоном, K T, умноженное на экспоненту Лунды агентства, Over. Линда Кэти закончила E до HC. Линда, К Т минус один. Ладно, у нас есть 30, чтобы интенсивность была максимальной. Это означает, что в квадратных скобках стоит ноль. Так что уже в возрасте. Смотри за бревнами, Кэти. Times E в ХК Руанды. Кэти закончила Е с сывороткой. Смотри, у меня 80 — ровно найти.Хорошо, я сделаю небольшой трюк. Я изменю переменную. Итак, ХК, над Линдой К т. Я собираюсь определить его как X. Итак, уравнение, которое мы должны решить для решения уравнения Триста Дентал, которое мы должны решить его ex times e x по e t ex miners, равно пяти, поэтому мы не можем решить его аналитически. Вы должны подключить его к какой-то программе, которая решает более поздние судебные уравнения. Так что я просто напишу здесь ответ. X равен четырем точкам 99 65 Это решение для at для X, и мы знаем, что X равно C и не учитывает T.
Ладно, это слишком высокий квадрат возраста C. Я собираюсь повлиять на нее через окно до шестого и одного экспоненциального минус пять плюс H c. Над Лондоном, K T, умноженное на экспоненту Лунды агентства, Over. Линда Кэти закончила E до HC. Линда, К Т минус один. Ладно, у нас есть 30, чтобы интенсивность была максимальной. Это означает, что в квадратных скобках стоит ноль. Так что уже в возрасте. Смотри за бревнами, Кэти. Times E в ХК Руанды. Кэти закончила Е с сывороткой. Смотри, у меня 80 — ровно найти.Хорошо, я сделаю небольшой трюк. Я изменю переменную. Итак, ХК, над Линдой К т. Я собираюсь определить его как X. Итак, уравнение, которое мы должны решить для решения уравнения Триста Дентал, которое мы должны решить его ex times e x по e t ex miners, равно пяти, поэтому мы не можем решить его аналитически. Вы должны подключить его к какой-то программе, которая решает более поздние судебные уравнения. Так что я просто напишу здесь ответ. X равен четырем точкам 99 65 Это решение для at для X, и мы знаем, что X равно C и не учитывает T. Итак, у нас есть то уравнение, которое мы хотели. Теперь мы можем изолировать любовь от чая здесь. Итак, у нас Лондон t равен C, умноженному на K, умноженному на 4,9 65 Хорошо. И это ответ на вопрос A, который один из нас хотел, чтобы мы нашли в этом упражнении, если мы должны вычислить Ah, Linda t как можно точнее. Так что я буду использовать H c. Ах, табличное значение для HC, которое составляет одно очко к 32 трем, 98 умноженное на 10 минус шесть голосов выборщиков. Метры. Это табличное значение для HC, деленное на K, это константы лодочника.Я также собираюсь использовать табличное значение восьмибалльного возраста для 8,6 173 раза минус пяти голосов выборщиков. Кальвин в минус один раз 4,967 65 Извините. Итак, это 2,8 девять семь умножить на 10 минус три метра Кальвина. Хорошо. И это константы Винса, поскольку вопрос хотел, чтобы мы нашли
Итак, у нас есть то уравнение, которое мы хотели. Теперь мы можем изолировать любовь от чая здесь. Итак, у нас Лондон t равен C, умноженному на K, умноженному на 4,9 65 Хорошо. И это ответ на вопрос A, который один из нас хотел, чтобы мы нашли в этом упражнении, если мы должны вычислить Ah, Linda t как можно точнее. Так что я буду использовать H c. Ах, табличное значение для HC, которое составляет одно очко к 32 трем, 98 умноженное на 10 минус шесть голосов выборщиков. Метры. Это табличное значение для HC, деленное на K, это константы лодочника.Я также собираюсь использовать табличное значение восьмибалльного возраста для 8,6 173 раза минус пяти голосов выборщиков. Кальвин в минус один раз 4,967 65 Извините. Итак, это 2,8 девять семь умножить на 10 минус три метра Кальвина. Хорошо. И это константы Винса, поскольку вопрос хотел, чтобы мы нашли
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатов
Предложения или отзывы?
13.
 5 законов движения планет Кеплера — University Physics Volume 1
5 законов движения планет Кеплера — University Physics Volume 1Цели обучения
К концу этого раздела вы сможете:
- Опишите конические сечения и их отношение к орбитальному движению
- Опишите, как орбитальная скорость связана с сохранением углового момента
- Определить период эллиптической орбиты от ее большой оси
Используя точные данные, собранные Тихо Браге, Иоганн Кеплер тщательно проанализировал положения на небе всех известных планет и Луны, обозначив их положения через равные промежутки времени.На основе этого анализа он сформулировал три закона, которые мы рассматриваем в этом разделе.
Первый закон Кеплера
Во времена Кеплера преобладала точка зрения, что все планетные орбиты были круговыми. Данные о Марсе представляли собой величайшую проблему для этой точки зрения, и это в конечном итоге побудило Кеплера отказаться от популярной идеи. Первый закон Кеплера гласит, что каждая планета движется по эллипсу, причем Солнце находится в фокусе эллипса. Эллипс определяется как набор всех точек, так что сумма расстояний от каждой точки до двух фокусов является постоянной.На рис. 13.16 показан эллипс и описан простой способ его создания.
Эллипс определяется как набор всех точек, так что сумма расстояний от каждой точки до двух фокусов является постоянной.На рис. 13.16 показан эллипс и описан простой способ его создания.
Для эллиптических орбит точка наибольшего сближения планеты с Солнцем называется перигелием. Она обозначена точкой A на рисунке 13.16. Самая дальняя точка — это афелий, обозначенная на рисунке точкой B . Для орбиты Луны вокруг Земли эти точки называются перигеем и апогеем соответственно.
Она обозначена точкой A на рисунке 13.16. Самая дальняя точка — это афелий, обозначенная на рисунке точкой B . Для орбиты Луны вокруг Земли эти точки называются перигеем и апогеем соответственно.
Эллипс имеет несколько математических форм, но все они являются частным случаем более общего уравнения для конических сечений. Есть четыре различных конических сечения, все из которых задаются уравнением
. αr = 1 + ecosθ.αr = 1 + ecosθ.13,10
Переменные r, и θθ показаны на рисунке 13.17 в случае эллипса. Константы αα и e определяются полной энергией и угловым моментом спутника в данной точке. Постоянная e называется эксцентриситетом.Значения αα и e определяют, какая из четырех конических секций представляет путь спутника.
Рис. 13.17 Как и раньше, расстояние между планетой и Солнцем составляет r , а угол, измеренный от оси x , которая проходит вдоль большой оси эллипса, составляет θθ.
Один из настоящих триумфов закона всемирного тяготения Ньютона с силой, обратной величине квадрата расстояния, заключается в том, что в сочетании с его вторым законом решение для пути любого спутника представляет собой коническое сечение.Каждый путь, пройденный м , является одним из четырех конических участков: круг или эллипс для ограниченных или замкнутых орбит или парабола или гипербола для неограниченных или открытых орбит. Эти конические сечения показаны на рис. 13.18.
Рисунок 13.18 Любое движение, вызванное силой, обратной квадрату, является одним из четырех конических сечений и определяется энергией и направлением движущегося тела.
Если полная энергия отрицательна, то 0≤e <10≤e <1, и уравнение 13.10 представляет ограниченную или замкнутую орбиту эллипса или круга, где e = 0e = 0.[Из уравнения 13.10 видно, что для e = 0e = 0, r = αr = α, и, следовательно, радиус постоянен.] Для эллипсов эксцентриситет связан с тем, насколько эллипс выглядит продолговатым. Круг имеет нулевой эксцентриситет, тогда как очень длинный вытянутый эллипс имеет эксцентриситет около единицы.
Круг имеет нулевой эксцентриситет, тогда как очень длинный вытянутый эллипс имеет эксцентриситет около единицы.
Если полная энергия точно равна нулю, то e = 1e = 1 и путь представляет собой параболу. Напомним, что спутник с нулевой полной энергией имеет именно убегающую скорость. (Парабола образуется только путем разрезания конуса параллельно касательной вдоль поверхности.) Наконец, если полная энергия положительна, то e> 1e> 1 и путь представляет собой гиперболу. Эти последние два пути представляют собой неограниченные орбиты, где m проходит мимо M один раз и только один раз. Такая ситуация наблюдалась для нескольких комет, которые приближаются к Солнцу, а затем уходят прочь, чтобы никогда не вернуться.
Мы ограничились случаем, когда меньшая масса (планета) вращается вокруг гораздо большей и, следовательно, стационарной массы (Солнца), но уравнение 13.10 также применимо к любым двум гравитационно взаимодействующим массам. Каждая масса образует коническое сечение той же формы, что и другая. Эта форма определяется полной энергией и угловым моментом системы, при этом центр масс системы находится в фокусе. Отношение размеров двух путей обратно отношению их масс.
Каждая масса образует коническое сечение той же формы, что и другая. Эта форма определяется полной энергией и угловым моментом системы, при этом центр масс системы находится в фокусе. Отношение размеров двух путей обратно отношению их масс.
Орбитальные передачи
С тех пор, как они были открыты, люди мечтали о путешествии к другим планетам нашей солнечной системы. Но как мы можем это сделать лучше всего? Самый эффективный метод был открыт в 1925 году Вальтером Хоманном, вдохновленным популярным научно-фантастическим романом того времени.Этот метод теперь называется переносом Хомана. В случае путешествия между двумя круговыми орбитами перемещение происходит по эллипсу «перехода», который идеально пересекает эти орбиты в афелии и перигелии эллипса. На рисунке 13.19 показан случай полета с орбиты Земли на орбиту Марса. Как и раньше, Солнце находится в фокусе эллипса.
Для любого эллипса большая полуось определяется как половина суммы перигелия и афелия. На рисунке 13.17 большая полуось — это расстояние от начала координат до обеих сторон эллипса по оси x , или только половина самой длинной оси (называемой большой осью).Следовательно, для перехода с одной круговой орбиты с радиусом r1r1 на другую круговую орбиту с радиусом r2r2 афелий переносного эллипса будет равен значению большей орбиты, а перигелий будет меньшей орбитой. Большая полуось, обозначенная a , поэтому задается как a = 12 (r1 + r2) a = 12 (r1 + r2).
На рисунке 13.17 большая полуось — это расстояние от начала координат до обеих сторон эллипса по оси x , или только половина самой длинной оси (называемой большой осью).Следовательно, для перехода с одной круговой орбиты с радиусом r1r1 на другую круговую орбиту с радиусом r2r2 афелий переносного эллипса будет равен значению большей орбиты, а перигелий будет меньшей орбитой. Большая полуось, обозначенная a , поэтому задается как a = 12 (r1 + r2) a = 12 (r1 + r2).
Рис. 13.19 Перигелий переходного эллипса находится на орбите Земли, а афелий — на орбите Марса.
Давайте возьмем случай путешествия с Земли на Марс.На данный момент мы игнорируем планеты и предполагаем, что мы одни на орбите Земли и хотим перейти на орбиту Марса. Из уравнения 13.9, выражения для полной энергии, мы можем видеть, что полная энергия для космического корабля на большей орбите (Марс) больше (менее отрицательно), чем для меньшей орбиты (Земля). Чтобы перейти на эллипс перехода с орбиты Земли, нам нужно будет увеличить нашу кинетическую энергию, то есть нам потребуется увеличение скорости. Самый эффективный метод — очень быстрое ускорение по круговой орбитальной траектории, которая также проходит по траектории эллипса в этой точке.(Фактически, ускорение должно быть мгновенным, чтобы круговая и эллиптическая орбиты совпадали во время ускорения. На практике конечное ускорение достаточно короткое, чтобы разница не принималась во внимание.) Как только вы вышли на орбиту Марса, вам понадобится еще один прирост скорости, чтобы перейти на эту орбиту, иначе вы останетесь на эллиптической орбите и просто вернетесь в перигелий, с которого начали. Для обратного пути вы просто выполняете обратный процесс с ретро-ускорением в каждой точке пересадки.
Чтобы перейти на эллипс перехода с орбиты Земли, нам нужно будет увеличить нашу кинетическую энергию, то есть нам потребуется увеличение скорости. Самый эффективный метод — очень быстрое ускорение по круговой орбитальной траектории, которая также проходит по траектории эллипса в этой точке.(Фактически, ускорение должно быть мгновенным, чтобы круговая и эллиптическая орбиты совпадали во время ускорения. На практике конечное ускорение достаточно короткое, чтобы разница не принималась во внимание.) Как только вы вышли на орбиту Марса, вам понадобится еще один прирост скорости, чтобы перейти на эту орбиту, иначе вы останетесь на эллиптической орбите и просто вернетесь в перигелий, с которого начали. Для обратного пути вы просто выполняете обратный процесс с ретро-ускорением в каждой точке пересадки.
Чтобы перейти на переносной эллипс, а затем снова выключиться, нам нужно знать каждую круговую орбитальную скорость и скорости переходной орбиты в перигелии и афелии. Требуемый прирост скорости — это просто разница между скоростью на круговой орбите и скоростью на эллиптической орбите в каждой точке. Мы можем найти круговые орбитальные скорости из уравнения 13.7. Чтобы определить скорости для эллипса, мы заявляем без доказательства (поскольку это выходит за рамки данного курса), что полная энергия для эллиптической орбиты составляет
Мы можем найти круговые орбитальные скорости из уравнения 13.7. Чтобы определить скорости для эллипса, мы заявляем без доказательства (поскольку это выходит за рамки данного курса), что полная энергия для эллиптической орбиты составляет
, где MSMS — масса Солнца, а — — большая полуось.Примечательно, что это то же самое, что и уравнение 13.9 для круговых орбит, но со значением большой полуоси, заменяющим радиус орбиты. Поскольку мы знаем потенциальную энергию из уравнения 13.4, мы можем найти кинетическую энергию и, следовательно, скорость, необходимую для каждой точки эллипса. Мы оставляем задачу найти эти скорости переноса для полета с Земли на Марс.
Мы заканчиваем это обсуждение указанием на несколько важных деталей. Во-первых, мы не учли гравитационную потенциальную энергию Земли и Марса или механику приземления на Марс.На практике это должно быть частью расчетов. Во-вторых, время решает все. Вы же не хотите прибыть на орбиту Марса и обнаружить, что его там нет. Мы должны покинуть Землю точно в правильное время, чтобы Марс оказался в афелии нашего переносного эллипса, как только мы прибудем. Такая возможность появляется каждые 2 года. И возвращение также требует правильного времени. Общая поездка займет чуть менее 3 лет! Есть и другие варианты, которые обеспечивают более быстрый транзит, в том числе облет Венеры с помощью гравитации.Но эти другие варианты сопряжены с дополнительными затратами энергии и опасны для космонавтов.
Мы должны покинуть Землю точно в правильное время, чтобы Марс оказался в афелии нашего переносного эллипса, как только мы прибудем. Такая возможность появляется каждые 2 года. И возвращение также требует правильного времени. Общая поездка займет чуть менее 3 лет! Есть и другие варианты, которые обеспечивают более быстрый транзит, в том числе облет Венеры с помощью гравитации.Но эти другие варианты сопряжены с дополнительными затратами энергии и опасны для космонавтов.
Второй закон Кеплера
Второй закон Кеплера гласит, что планета сметает равные площади за равное время, то есть площадь, разделенная во времени, называемая пространственной скоростью, постоянна. Взгляните на рисунок 13.20. Время, которое требуется планете, чтобы переместиться из позиции A в B , выметая область A1A1, в точности равно времени, необходимому для перемещения из позиции C в D , охват зоны A2A2, и перемещения из E С по F , зона подметания A3A3. Эти области одинаковы: A1 = A2 = A3A1 = A2 = A3.
Эти области одинаковы: A1 = A2 = A3A1 = A2 = A3.
Рисунок 13.20 Показанные заштрихованные области имеют равные площади и представляют один и тот же временной интервал.
Сравнивая площади на рисунке и расстояние, пройденное по эллипсу в каждом случае, мы видим, что для того, чтобы площади были равными, планета должна ускоряться по мере приближения к Солнцу и замедляться по мере удаления. . Такое поведение полностью соответствует нашему уравнению сохранения, уравнению 13.5. Но мы покажем, что второй закон Кеплера на самом деле является следствием сохранения углового момента, которое справедливо для любой системы, имеющей только радиальные силы.
Напомним определение углового момента из Angular Momentum, L → = r → × p → L → = r → × p →. Для случая орбитального движения L → L → — момент количества движения планеты относительно Солнца, r → r → — вектор положения планеты, отсчитываемый от Солнца, а p → = mv → p → = mv → — мгновенный импульс в любой точке орбиты. Поскольку планета движется по эллипсу, p → p → всегда касается эллипса.
Мы можем разделить импульс на две составляющие: радиальную составляющую p → radp → rad вдоль линии к Солнцу и составляющую p → perpp → perp, перпендикулярную r → r →.Перекрестное произведение для углового момента может быть записано как
L → = r → × p → = r → × (p → rad + p → perp) = r → × p → rad + r → × p → perpL → = r → × p → = r → × (p → рад + р → перп) = г → × р → рад + г → × р → перп.
Первый член справа равен нулю, потому что r → r → параллельно p → radp → rad, а во втором члене r → r → перпендикулярен p → perpp → perp, поэтому величина перекрестного произведения сводится к L = rpperp = rmvperpL = rpperp = rmvperp. Обратите внимание, что угловой момент , а не , зависит от pradprad. Поскольку сила тяжести действует только в радиальном направлении, она может изменять только pradprad, но не pperppperp; следовательно, угловой момент должен оставаться постоянным.
Теперь рассмотрим рисунок 13.21. Небольшая треугольная область ΔAΔA выметается за время ΔtΔt. Скорость идет вдоль пути и составляет угол θθ с радиальным направлением. Следовательно, перпендикулярная скорость определяется как vperp = vsinθvperp = vsinθ. Планета перемещается на расстояние Δs = vΔtsinθΔs = vΔtsinθ, спроецированное по направлению, перпендикулярному r . Поскольку площадь треугольника равна половине основания ( r ), умноженной на высоту (Δs) (Δs), для небольшого смещения площадь определяется как ΔA = 12rΔsΔA = 12rΔs.Подставляя ΔsΔs, умножая на м в числителе и знаменателе и переставляя, получаем
Скорость идет вдоль пути и составляет угол θθ с радиальным направлением. Следовательно, перпендикулярная скорость определяется как vperp = vsinθvperp = vsinθ. Планета перемещается на расстояние Δs = vΔtsinθΔs = vΔtsinθ, спроецированное по направлению, перпендикулярному r . Поскольку площадь треугольника равна половине основания ( r ), умноженной на высоту (Δs) (Δs), для небольшого смещения площадь определяется как ΔA = 12rΔsΔA = 12rΔs.Подставляя ΔsΔs, умножая на м в числителе и знаменателе и переставляя, получаем
Площадная скорость — это просто скорость изменения площади во времени, поэтому мы имеем
площадная скорость = ΔAΔt = L2m.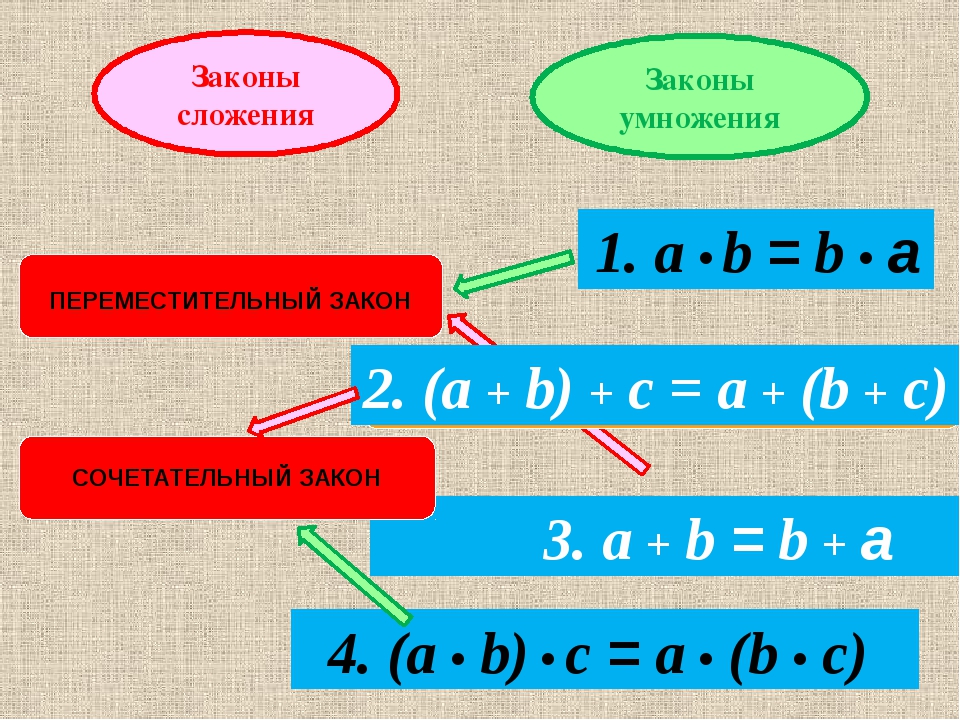 площадная скорость = ΔAΔt = L2m.
площадная скорость = ΔAΔt = L2m.Так как угловой момент постоянен, то должна быть постоянна и пространственная скорость. Это в точности второй закон Кеплера. Как и первый закон Кеплера, Ньютон показал, что это естественное следствие его закона всемирного тяготения.
Третий закон Кеплера
Третий закон Кеплера гласит, что квадрат периода пропорционален кубу большой полуоси орбиты. В работе «Спутниковые орбиты и энергия» мы вывели третий закон Кеплера для частного случая круговой орбиты.Уравнение 13.8 дает нам период круговой орбиты радиусом r вокруг Земли:
Для эллипса вспомним, что большая полуось составляет половину суммы перигелия и афелия. Для круговой орбиты большая полуось ( a ) совпадает с радиусом орбиты. Фактически, уравнение 13.8 дает нам третий закон Кеплера, если мы просто заменим r на a и возведем обе стороны в квадрат.
13,11
Мы изменили массу Земли на более общую M , поскольку это уравнение применимо к спутникам, вращающимся вокруг любой большой массы.
Пример 13.13
Орбита кометы Галлея
Определите большую полуось орбиты кометы Галлея, учитывая, что она достигает перигелия каждые 75,3 года. Если перигелий составляет 0,586 а.е., что такое афелий?Стратегия
Нам дан период, поэтому мы можем изменить уравнение 13.11, решив его для большой полуоси. Поскольку мы знаем значение перигелия, мы можем использовать определение большой полуоси, данное ранее в этом разделе, чтобы найти афелий.Отметим, что 1 астрономическая единица (AU) — это средний радиус орбиты Земли, который определяется как 1AU = 1,50 × 1011 м1AU = 1,50 × 1011 м.Решение
Преобразуя уравнение 13.11 и вставляя значения периода кометы Галлея и массы Солнца, мы имеем a = (GM4π2T2) 1/3 = ((6,67 × 10-11 Н · м2 / кг2) (2,00 × 1030 кг) 4π2 (75,3 года × 365 дней / год × 24 часа / день × 3600 сек / час) 2) 1 / 3. a = (GM4π2T2) 1/3 = ((6,67 × 10-11 Н · м2 / кг2) (2,00 × 1030 кг) 4π2 (75,3 года × 365 дней / год × 24 часа / день × 3600 сек / час) 2) 1/3.
a = (GM4π2T2) 1/3 = ((6,67 × 10-11 Н · м2 / кг2) (2,00 × 1030 кг) 4π2 (75,3 года × 365 дней / год × 24 часа / день × 3600 сек / час) 2) 1/3.Это дает значение 2,67 × 1012 м2.67 × 1012 м или 17,8 а.е. по большой полуоси.
Большая полуось составляет половину суммы афелия и перигелия, поэтому мы имеем
а = 12 (афелий + перигелий) афелий = 2а — перигелий. а = 12 (афелий + перигелий) афелий = 2а — перигелий.Подставляя значения, которые мы нашли для большой полуоси, и значение, данное для перигелия, мы находим, что значение афелия составляет 35,0 а.е.
Значение
Эдмонд Галлей, современник Ньютона, сначала подозревал, что три кометы, о которых сообщалось в 1531, 1607 и 1682 годах, на самом деле были одной и той же кометой.До того, как Тихо Браге провел измерения комет, считалось, что это были разовые события, возможно, возмущения в атмосфере, и что на них не влияло Солнце. Галлей использовал новую механику Ньютона, чтобы предсказать возвращение своей одноименной кометы в 1758 году.



 a·1=a.
a·1=a.
