Индивидуальная карточка по математике «Примеры с окошками, сложение и вычитание в пределах 10» | Учебно-методический материал по математике (1 класс) на тему:
Опубликовано 04.10.2014 — 20:53 — Тихонова Ольга Ивановна
Индивидуальная карточка содержит готовые примеры, достаточно записать ответ. Данный вид работы можно использовать на этапах повторения и закрепления.
Скачать:
Предварительный просмотр:
4 + = 9 | – 6 = 4 | 3 + = 5 | 4 + = 8 |
+ 1 = 9 | – 5 = 2 | + 1 =10 | + 7 = 9 |
+ 1 = 2 | 9 – = 1 | 4 + = 9 | 10 – = 7 |
– 3 = 4 | 1 + = 6 | – 3 = 5 | 9 + =10 |
6 + = 9 | – 3 = 7 | 7 + = 8 | – 6 = 3 |
– 8 =2 | + 6 = 10 | – 3 = 6 | 1 + = 8 |
4 + = 7 | 7 + = 9 | 9 – = 6 | – 3 = 2 |
3 + = 10 | – 2 = 4 | 3 + = 5 | 3 + = 9 |
5 + = 7 | – 6 = 3 | + 2 = 6 | – 4 = 1 |
– 8 = 1 | 8 – = 3 | 10 – =4 | – 3 =7 |
+ 6 = 9 | – 1 = 6 | – 5 = 2 | 3 + = 4 |
1 + = 6 | 6 + = 10 | 5 – = 4 | + 6 =10 |
– 4 = 3 | – 5 = 4 | + 7 = 9 | 9 + =10 |
+ 1 = 5 | 9 – = 4 | 8 + = 9 | – 1 = 7 |
1 + = 3 | 1 + = 4 | + 4 = 5 | – 4 = 6 |
+ 4 = 10 | – 2 = 2 | 1 + = 2 | 10 – =3 |
5 + = 6 | 6 – = 2 | – 5 = 1 | – 4 = 4 |
6 – = 1 | 2 + = 7 | 8 – = 1 | 8 – = 3 |
– 3 = 1 | – 7 = 2 | + 2 =10 | + 3 = 9 |
– 5 = 4 | 9 – = 8 | – 3 = 3 | 3 + = 8 |
– 3 = 3 | – 3 = 8 | 5 + =10 | – 6 = 2 |
5 + = 8 | – 4 = 3 | – 5 =5 | 2 + = 3 |
– 5 = 4 | 2 + = 8 | 6 + = 8 | + 3 = 8 |
5 + = 7 | 7 + = 10 | + 1 = 7 | 2 + = 6 |
8 – = 6 | – 4 = 3 | – 8 =2 | – 4 = 3 |
3 + = 9 | 10 – =8 | 6 – = 2 | 6 – = 2 |
+ 2 = 4 | + 5 = 10 | + 5 =10 | – 9 =1 |
… + 3 = 6 | 6 + = 10 | – 1 = 2 | + 1 = 8 |
… + 1 = 8 | – 4 = 1 | – 3 = 1 | 3 + = 7 |
… + 3 = 6 | 5 + = 9 | 8 – = 2 | – 5 = 2 |
… – 3 = 5 | + 1 = 8 | + 5 = 7 | 5 + = 9 |
По теме: методические разработки, презентации и конспекты
Индивидуальные работы для 1 класса по теме Сложение и вычитание в пределах 10
Индивидуальные работы для 1 класса по теме Сложение и вычитание в пределах 10 предназначено для повторения и закрепления материала.
В данный вид работы входят такие темы: 1. Счет в пределах 10. 2. Зап…
Карточки по математике «Сложение и вычитание в пределах 10»
В работе 8 вариантов карточек с примерами сложения и вычитания в пределах 10. ребенок прикладывает к карточке подписанный листок в клетку и записывает только ответы. Быстрая и удобная проверка….
Карточки по математике 1 класс. Сложение и вычитание в пределах 10.
Карточки по математике 1 класс. Сложение и вычитание в пределах 10….
Индивидуальные карточки по математике 2 класс.(для отработки вычислительных навыков сложения и вычитания в пределах ста)
Данный вид работы будет интересен учителям начальных классов для отработки вычислительных навыков в пределах ста. Карточки составлены согласнопрохождения тем и соответствуют программным требованиям. П…
Индивидуальные карточки для 3 класса по теме ПИСЬМЕННЫЕ ПРИЁМЫ СЛОЖЕНИЯ И ВЫЧИТАНИЯ В ПРЕДЕЛАХ 1000
В медодическом материале представлено множество математических примеров по теме: Письменные приемы сложения и вычитания в пределах 100.
…
Карточки для отработки контроля усвоения сложения и вычитания в пределах 10 и 20.
На этапе устного счета на уроке каждому ученику выдается карточка с 20 выражениями на определенную тему, например, сложение и вычитание двух. За 2 минуты обучающимся необходимо решить эти примеры. Пос…
Сложение и вычитание в пределах 20 КАРТОЧКИ ДЛЯ ИНДИВИДУАЛЬНОЙ РАБОТЫ ПО МАТЕМАТИКЕ «СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕЛЕЛАХ 20»
Сложение и вычитание в пределах 20 КАРТОЧКИ ДЛЯ ИНДИВИДУАЛЬНОЙ РАБОТЫ ПО МАТЕМАТИКЕ «СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕЛЕЛАХ 20"…
Поделиться:
10% компенсация на депозиты в тенге
- Главная /
- Депозиты /
- 10% компенсация на депозиты в тенге
не удалять
Вклады физических лиц в тенге, открытые в Halyk Bank, участвуют в Программе защиты тенговых вкладов, которая разработана Национальным банком совместно с правительством РК.
В рамках данной Программы предусмотрена выплата компенсации (премии) в размере 10% по вкладам физических лиц, соответствующим условиям Программы.
Для получения компенсации необходимо наличие действующего вклада в тенге
Компенсация будет выплачена вкладчикам, подтвердившим свое согласие не позднее 1 января 2023.
Заявления можно подать через мобильное приложение Halyk Homebank в разделе «Гос. услуги». При отсутствии приложения необходимо его установить и зарегистрироваться.
Утвержденные условия программы
- Важно не закрывать вклад до 24 февраля 2023 года*.
- При досрочном закрытии вклада до 24 февраля 2023 года, вклад автоматически исключается из участия в Программе.
- При автоматическом закрытии вклада по сроку допускается открытие нового вклада(-ов) в срок до 1 октября 2022 г. включительно, при условии, что новый вклад будет открыт за счет суммы закрытого вклада (с того же текущего/карточного счета, куда зачислена сумма закрытого вклада).
- Допускается частичное изъятие вклада, при этом расчет премии будет произведен на минимальный остаток, образовавшийся за период с 24.02.2022 г. по 23.02.2023 г. включительно.
- Пополнение вклада не ограничено, при этом сумма пополнений при расчете суммы компенсации не учитывается.
- Компенсация в размере 10% выплачивается каждому вкладчику по всем его вкладам единоразово, но не более 2 000 000 тенге.
- Выплата компенсации вкладчикам будет осуществлена на общую сумму вклада(-ов) в пределах 20 000 000 тенге.
- Компенсация будет зачислена на текущий либо карточный счет, подвязанный к договору банковского вклада.
- Компенсации будет выплачена в марте 2023 года.
* Вклады, по которым срок действия договора заканчивается до 24.02.2023 г. автоматически пролонгируются на условиях, действующих на момент пролонгации вклада.
Условия Программы размещены на официальном сайте «Открытые НПА»
Примеры расчета компенсации
Пример №1
Сумма по вашему вкладу на 23 февраля 2022 года составила 500 000 тенге. В течение года вы производили частичное снятие со вклада, и минимальная сумма остатка вклада составила 100 000 тенге. Премия будет рассчитана на наименьшую сумму вклада, образовавшуюся за период с 24 февраля 2022 года по 23 февраля 2023 года включительно.
Вам будет начислено 10% на сумму 100 000 тенге, размер премии составит 10 000 тенге
Пример №2
Сумма по вашему вкладу на конец операционного дня 23 февраля 2022 года составила 500 000 тенге. В течение года вы производили частичное снятие и пополняли вклад, сумма вклада на 24 февраля 2023 года составила 800 000 тенге.
Вам будет начислена компенсация в размере 10% на минимальный остаток с учетом произведенных частичных снятий в период с 24 февраля 2022 по 23 февраля 2023 года включительно. В случае, если минимальный остаток не был ниже 500 000 тенге, то вам будет начислена компенсация в размере 10% на сумму 500 000 тенге. Это составит 50 000 тенге. В случае, если минимальный остаток был ниже 500 000 тенге, то вам будет начислена компенсация в размере 10% на сумму минимального остатка.
Пример №3
Если у вас несколько вкладов на общую сумму 30 000 000 тенге, то компенсация будет рассчитана на сумму вкладов в пределах 20 000 000 тенге, на 10 000 000 тенге компенсация не предусмотрена.
Пример №4
Сумма вклада на 23 февраля 2022 года составила 2 900 000 тенге. 14 марта 2022 г. ваш указанный вклад закрывается по сроку на сумму 2 950 000 тенге с зачислением суммы вклада на ваш текущий счет, подвязанный к вкладу (входящий остаток по текущему счету равен 0 тенге).
Как получить 10% компенсацию по депозитам в Halyk Homebank
Считай, смекай, отгадывай — Белоиванова Марина Александровна
Прямая, луч, отрезок
Leave a comment
Если мы остро отточенным карандашом прикоснемся к листу бумаги, то на нём останется круглый след, который называют точкой.
В качестве имени точкам присваивают заглавные латинские буквы: А, В, С и т.д. При объединении множества точек получаются геометрическая фигура. Например, если точки выстроятся вдоль натянутого шнура, то получившаяся фигура даёт представление о прямой линии. С той лишь разницей, что прямая линия является бесконечной, то есть она неограниченно распространяется как в одну,…
Движение вдогонку
Leave a comment
Рассмотрим задачу, в которой объекты, двигаясь в одном направлении, будут сближаться. Жаба, обнаружила пропажу Дюймовочки, и бросилась догонять уносимый быстрым течением лист кувшинки, на котором сидела девочка. Чтобы определить, как ежесекундно изменялось расстояние между ними, то есть их относительная скорость, заполним таблицу зависимости координат Жабы и Дюймовочки от времени, где x1 — координата Дюймовочки, x2 — координата Жабы, d — расстояние между ними.
Расстояние между объектами уменьшалось каждую…
Read More >>
Движение с отставанием
Leave a comment
Чтобы понять, от чего зависит относительная скорость объектов, двигающихся в одном направлении, необходимо учесть, что при этом они могут сближаться, но могут и удаляться. Например, рассмотрим такую задачу. Волк объяснил Красной Шапочке, как пройти в бабушкину деревню. Девочка остановилась на полянке с координатой равной пяти и стала собирать для бабушки ягодки и цветочки. Когда она отправилась к бабушке, Волк был уже в точке с координатой 20. И Красная Шапочка, и…
Read More >>
Движение в противоположных направлениях
Leave a comment
Проиллюстрируем движение объектов в противоположных направлениях на следующей задаче.
На вопрос серого Волка: «В какую сторону побежал Заяц?» – Белочка указала противоположное направление. Волк бежал со скоростью 6 км/ч, а Заяц удалялся в противоположном направлении со скоростью 2 км/ч. Если заполнить таблицу зависимости координат Волка и Зайца от времени, где t – время их движения, x1 – координата Волка, x2 – координата Зайца, то можно заметить, как ежечасно изменялось расстояние…
Read More >>
Встречное движение
Leave a comment
Рассмотрим такую задачу. Курочка бежит навстречу к своему цыплёнку со скоростью 2 м/с. А цыплёнок приближается к курице со скоростью 1 м/с. Если заполнить таблицу зависимости координат курицы и цыплёнка от времени, где t – время их совместного встречного движения, x1 – соответствующая координата курицы, x2 – координата цыплёнка, то можно заметить, как ежесекундно изменялось расстояние d между ними.
Расстояние, на которое приближаются объекты друг к другу за единицу времени,…
Read More >>
Скорость, время, расстояние
Leave a comment
Быстрота передвижения Окружающий нас мир находится в постоянном развитии и движении. И людям часто приходится оценивать быстроту перемещения различных объектов наблюдения. Проще это делать, указывая пройденные ими расстояния за равные промежутки времени. Скорость Например, заяц может пробежать за один час 60 км, страус за час – 80 км, гепард за час – 120 км. Говорят, что скорость зайца 60 км в час, страуса – 80 км в час, гепарда –…
Read More >>
Единицы времени
Leave a comment
Год, месяц, неделя и сутки – это общеизвестные меры времени.
Как они возникли? Посмотрите пояснения на рисунках. Месяцы имеют разную длину. Как определить длину месяца? Почему происходит смена дня и ночи? А как же исчисляется время в течение суток? На циферблате часов расположены числа от 1 до 12, а в сутках 24 часа. Чтобы различить о каком времени суток идёт речь, обычно уточняют: семь часов утра или семь часов вечера….
Read More >>
Задание на лето
Leave a comment
Память имеет уникальное свойство вытеснять информацию, которой мы длительное время не пользуемся. Из-за этого каждый год в сентябре и дети, и учителя испытывают огромные трудности, поскольку приходится много времени уделять повторению. При этом текущая программа требует продолжения изучения новых тем. Но всё повторить невозможно, поэтому у многих учеников образуются белые пятна в знаниях или так называемые пробелы.
Особенно это заметно в математике, где новые навыки вырабатываются на имеющейся у ребенка…
Read More >>
Разрядные слагаемые
Leave a comment
Если начать считать предметы по порядку: один, два, три, четыре, пять и т. д., то есть, добавляя по единичке к каждому предыдущему числу, чтобы перейти к последующему, то дойдя до последнего однозначного числа 9, мы далее получим наименьшее двузначное число – 10. У двузначных чисел мы имеем две позиции для цифр: справа – разряд единиц, слева – разряд десятков. При счёте каждые 10 единичек объединяются в десяток, 10 десятков –…
Read More >>
Деление с остатком
Leave a comment
Сказка о том, как Белка к зиме готовилась Собрала как-то белка 16 грибов и решила посушить их на зиму.
«Развешу я их поровну на этих трёх ветках, – подумала она. – Красиво будет». Буду действовать так. Сначала на каждую веточку нанижу по одному грибочку, потом по два, потом по три, четыре, пять. У меня останется 1 грибок, но веток 3. Значит, дальше поровну распределить грибы не получится. Развешено по 5…
Read More >>
Площади
Leave a comment
Сегодня мы познакомимся с понятием площади, со способами сравнения площадей и их единицами измерения. В математике площадь – это часть плоскости, ограниченная замкнутой ломаной или кривой линией, занимающая какое-то место. В быту под словом площадь подразумевают большое и ровное место. Например, в городе или в селе площадь – это незастроенное пространство, от которого обычно расходятся в разные стороны улицы.
Посевная площадь – это пространство, предназначенное для посева, жилая площадь –…
Read More >>
Виды треугольников
Leave a comment
Какие же треугольники все разные! Есть ли какие-нибудь свойства, по которым можно было бы их различать? Да, их различают по особенностям углов и длинам сторон. Построение треугольника Как же получить эту фигуру? Поставим три точки на листе бумаги так, чтобы через них нельзя было провести одну прямую линию. Назовём эти точки, например, буквами А, К, М. Обычно точки обозначают заглавными латинскими буквами. Соединим эти точки кусочками прямых линий. Говорят –…
Read More >>
Родительское собрание
Leave a comment
Уважаемые родители! Наше родительское собрание посвящается итогам 2 четверти 2020/2021 учебного года.
Повестка дня 1.Итоги успеваемости и посещаемости занятий Правила поведения на утреннике Инструктажи по ТБ на зимних каникулах 4.Профилактика ковид-19 5.Горячее питание 6.О выборе программы обучения по ОРКЭС в 4х классах в 2021/2022 уч.году 7.Режим работы школы Ход собрания 1. ПРИМЕРНАЯ ВЕДОМОСТЬ 2 ЧЕТВЕРТЬ Русск.яз. Литер.чт. Род.(рус.) язык Род.(рус) лит.чт. Англ.яз. Математ. Окр.мир Музыка…
Read More >>
Образование и сравнение долей
Leave a comment
Разделим апельсин, например, на 8 равных частей. Эти равные части называются долями (апельсиновыми дольками). В нашем случае каждый кусочек – восьмая доля апельсина. Если взять три кусочка – будет три доли. Все, что мы проделали, записывается с помощью чисел, разделенных черточкой.
Эту запись назвали обыкновенной дробью: 3/8. Читают дробь так: три восьмых. Запись дробей Для того чтобы записать взятые доли, нужно выполнять действия по следующему правилу: посчитать, на сколько равных долей…
Read More >>
Функция СЧЁТЕСЛИ
Используйте СЧЁТЕСЛИ, одну из статистических функций, для подсчёта количества ячеек, соответствующих критерию; например, чтобы подсчитать, сколько раз конкретный город появляется в списке клиентов.
В своей простейшей форме СЧЁТЕСЛИ говорят:
.Например:
СЧЁТЕСЛИ(диапазон, критерии)
Имя аргумента | Описание |
|---|---|
диапазон (обязательно) | Группа ячеек, которую вы хотите подсчитать. Узнайте, как выбирать диапазоны на листе. |
критерии (обязательно) | Число, выражение, ссылка на ячейку или текстовая строка, определяющая, какие ячейки будут подсчитываться. Например, вы можете использовать число, например 32, сравнение, например «>32», ячейку, например B4, или слово, например «яблоки». COUNTIF использует только один критерий. Используйте СЧЁТЕСЛИМН, если вы хотите использовать несколько критериев. |
Диапазон может содержать числа, массивы, именованный диапазон или ссылки, содержащие числа. Пустые и текстовые значения игнорируются.Примеры
Чтобы использовать эти примеры в Excel, скопируйте данные из приведенной ниже таблицы и вставьте их в ячейку A1 нового рабочего листа.
Данные | Данные |
|---|---|
яблока | 32 |
апельсина | 54 |
персики | 75 |
яблока | 86 |
Формула | Описание |
=СЧЁТЕСЛИ(A2:A5;»яблоки») | Подсчитывает количество ячеек с яблоками в ячейках с A2 по A5. |
=СЧЁТЕСЛИ(A2:A5,A4) | Подсчитывает количество ячеек с персиками (значение в A4) в ячейках от A2 до A5. Результат 1. |
=СЧЁТЕСЛИ(A2:A5,A2)+СЧЁТЕСЛИ(A2:A5,A3) | Подсчитывает количество яблок (значение в A2) и апельсинов (значение в A3) в ячейках с A2 по A5. Результат равен 3. В этой формуле дважды используется СЧЁТЕСЛИ, чтобы указать несколько критериев, по одному критерию на выражение. Вы также можете использовать функцию СЧЁТЕСЛИМН. |
=СЧЁТЕСЛИ(B2:B5;»>55″) | Подсчитывает количество ячеек со значением больше 55 в ячейках с B2 по B5. |
=СЧЁТЕСЛИ(B2:B5,»<>«&B4) | Подсчитывает количество ячеек со значением, отличным от 75, в ячейках с B2 по B5. Амперсанд (&) объединяет оператор сравнения для не равно (<>) и значение в B4 для чтения =СЧЁТЕСЛИ(B2:B5,»<>75″). Результат 3. |
=СЧЁТЕСЛИ(B2:B5,»>=32″)-СЧЁТЕСЛИ(B2:B5,»<=85") | Подсчитывает количество ячеек со значением больше (>) или равным (=) 32 и меньшим (<) или равным (=) 85 в ячейках с B2 по B5. Результат 1. |
=СЧЁТЕСЛИ(A2:A5;»*») | Подсчитывает количество ячеек, содержащих любой текст в ячейках с A2 по A5. |
=СЧЁТЕСЛИ(A2:A5;»?????es») | Подсчитывает количество ячеек, содержащих ровно 7 символов и заканчивающихся буквами «es» в ячейках с A2 по A5. Знак вопроса (?) используется в качестве подстановочного знака для соответствия отдельным символам. Результат 2. |
Результат 2.
Результат 2.
Звездочка (*) используется в качестве подстановочного знака для соответствия любому символу. Результат 4.Общие проблемы
Проблема | Что пошло не так |
|---|---|
Для длинных строк возвращено неверное значение. | Функция СЧЁТЕСЛИ возвращает неправильные результаты, когда вы используете её для сопоставления строк длиннее 255 символов. Чтобы сопоставить строки длиннее 255 символов, используйте функцию СЦЕПИТЬ или оператор объединения &. Например, =СЧЁТЕСЛИ(A2:A5,»длинная строка»&»еще одна длинная строка»). |
Значение не возвращено, когда вы ожидаете значение. | Не забудьте заключить аргумент критерии в кавычки. |
Формула СЧЁТЕСЛИ получает ошибку #ЗНАЧ! ошибка при обращении к другому рабочему листу. | Эта ошибка возникает, когда формула, содержащая функцию, ссылается на ячейки или диапазон в закрытой книге, а ячейки вычисляются. |
Чтобы эта функция работала, другая книга должна быть открыта.Лучшие практики
Сделай это | Почему |
|---|---|
Имейте в виду, что СЧЁТЕСЛИ игнорирует верхний и нижний регистр в текстовых строках. | Критерии не чувствительны к регистру. Другими словами, строка «яблоки» и строка «ЯБЛОКИ» будут соответствовать одним и тем же ячейкам. |
Использовать подстановочные знаки. | Подстановочные знаки — вопросительный знак (?) и звездочка (*) — могут использоваться в критериях . Знак вопроса соответствует любому одиночному символу. Звездочка соответствует любой последовательности символов. Если вы хотите найти фактический вопросительный знак или звездочку, введите тильду (~) перед символом. Например, =СЧЁТЕСЛИ(A2:A5,»яблоко?») будут подсчитаны все экземпляры слова «яблоко» с последней буквой, которая может меняться. |
Убедитесь, что ваши данные не содержат ошибочных символов. | При подсчете текстовых значений убедитесь, что данные не содержат начальных и конечных пробелов, непоследовательного использования прямых и фигурных кавычек или непечатаемых символов. В этих случаях функция СЧЁТЕСЛИ может вернуть непредвиденное значение. Попробуйте использовать функцию CLEAN или TRIM. |
Для удобства используйте именованные диапазоны | СЧЁТЕСЛИ поддерживает именованные диапазоны в формуле (например, =СЧЁТЕСЛИ( фруктов ,»>=32″)-СЧЁТЕСЛИ( фруктов ,»>85″). Именованный диапазон может находиться на текущем рабочем листе, другой рабочий лист на той же рабочей книги или из другой рабочей книги. Чтобы ссылаться на другую рабочую книгу, эта вторая рабочая книга также должна быть открыта. |
Примечание. Функция СЧЁТЕСЛИ не будет подсчитывать ячейки на основе фона ячейки или цвета шрифта. Однако Excel поддерживает определяемые пользователем функции (UDF) с использованием операций Microsoft Visual Basic для приложений (VBA) над ячейками на основе цвета фона или шрифта.
Вот пример того, как вы можете подсчитать количество ячеек с определенным цветом ячейки с помощью VBA.
Нужна дополнительная помощь?
Вы всегда можете обратиться к эксперту в техническом сообществе Excel или получить поддержку в сообществе ответов.
См. также
Чтобы подсчитать непустые ячейки, используйте функцию СЧЕТЧИК
Для подсчета ячеек по нескольким критериям используйте функцию СЧЁТЕСЛИМН.
Посмотрите видео о том, как использовать функцию СЧЁТЕСЛИМН
Функция СУММЕСЛИ складывает только те значения, которые соответствуют одному критерию.
Функция СУММЕСЛИМН складывает только те значения, которые соответствуют нескольким критериям.
Функция IFS (Microsoft 365, Excel 2016 и более поздние версии)
Используйте функцию TRIM, чтобы удалить начальные и конечные пробелы из ячеек.
Используйте функцию CLEAN для удаления непечатаемых символов из ячеек.
Обзор формул в Excel
Как избежать неработающих формул
Обнаружение ошибок в формулах
Статистические функции
Функции Excel (по алфавиту)
Функции Excel (по категориям)
Использование СУММЕСЛИ, СЧЁТЕСЛИ и связанных функций для быстрого анализа данных (бесплатная предварительная версия)
Пропустить счет до 10 — Математика с мамой
Что такое пропуск счета до 10?
Пропустить счет до 10 означает считать десятками, каждый раз прибавляя десять. Не произносите числа между ними. Пропустить счет десятками очень важно, потому что это позволяет нам считать быстрее, чем считать единицами.
Например, пропустив счет десятками от нуля, мы получим 10, 20, 30, 40, 50, 60, 70, 80, 90 и 100.
Ниже приведен пример пустой рабочей таблицы гусеницы для подсчета пропусков, которую вы можете использовать, чтобы попрактиковаться в подсчете пропусков. Мы будем считать десятками, чтобы собрать гусеницу, записывая число в каждом сегменте.
Вот готовый пример гусеницы.
Как пропустить счет до 10
Чтобы пропустить счет до 10, добавьте 10, чтобы перейти к следующему числу. Проще всего это сделать, увеличив цифру в десятках числа на 1. Например, пропустим счет десятками от 7, получим 7, 17, 27, 37, 47, 57, 67, 77, 87, 97.
Цифра десятков просто увеличивается с 1 на 2, на 3 и т.д.
Альтернативный метод пропуска подсчета до 10 — использовать числовую сетку до 100 и перемещаться вниз на одну строку каждый раз, когда вы добавляете 10.
Имеем: 7, 17, 27, 37, 47, 57, 67, 77, 87 и 97.
Мы останавливаемся на 97, потому что это последнее число в паттерне перед 100, но мы могли бы продолжать считать, если бы нам было нужно.
Мы видим, что все числа заканчиваются той же цифрой, что и число, с которого мы начали.
Все числа заканчиваются на 7, потому что мы пропускаем счет десятками, начиная с 7.
Мы просто добавляем еще 1 к разряду десятков с каждым добавлением 10.
Счет в десятках от любого числа
Чтобы считать десятками от любого числа, добавьте 10, чтобы перейти к следующему числу. Самый простой способ сделать это — каждый раз увеличивать цифру в столбце десятков на 1. Например, начиная с 1, у нас есть 11, 21, 31, 41, 51, 61, 71, 81 и 91.
Чтобы пропустить счет десятками из любого числа, просто каждый раз добавляйте единицу к разряду десятков. Числа всегда будут заканчиваться одной и той же цифрой в столбце единиц.
Помните, что чтобы добавить 10 в числовую сетку, просто переместитесь на одну клетку вниз.
Вместо того, чтобы начинать с нуля, мы начинаем с «1».
Перемещение на одну клетку вниз по сетке каждый раз добавляет десять. У нас есть:
1, 11, 21, 31, 41, 51, 61, 71, 81 и 91.
Мы могли бы и дальше пропускать счет десятками, если бы это было необходимо.
Мы можем начать с любого числа в числовой сетке и двигаться вниз по столбцу, чтобы пропустить счет десятками. Помните, что эта числовая сетка может быть полезным учебным пособием, помогающим практиковать счет десятками.
Мы можем выбрать любое число в числовой сетке, от которого будем считать десятками.
Например, вот 46. Будем считать десятками от 46.
Мы начнем с 46 и будем двигаться вниз от квадрата к квадрату, каждый раз прибавляя десять.
Снова мы просто увеличиваем цифру десятков на единицу каждый раз от 46 до 56, до 66 и так далее.
Число 46 заканчивается цифрой «6» в столбце единиц измерения, поэтому другие числа в нашем шаблоне счета с пропусками также заканчиваются на «6».
Вот заготовка гусеница-счетчик, которую мы будем собирать вместе, пропускаем счет десятками от 11.
11 заканчивается цифрой единиц «1», поэтому другие числа в шаблоне также будут заканчиваться на «1».
В следующем примере мы считаем десятками, начиная с 3.
Все следующие числа в шаблоне также оканчиваются на 3.
Обучение пропуску счета до 10
Для обучения счету десятками полезно использовать числовую сетку. Чтобы добавить десять в числовую сетку, нужно просто переместиться на одну строку вниз от исходного числа. Используя числовую сетку, можно легче замечать закономерности, показывая, как цифра в столбце десятков каждый раз увеличивается на 1.
Чтобы пропустить счет десятками, продолжайте добавлять десять, чтобы перейти к следующему числу. Чтобы легко пропустить счет до десяти, каждый раз увеличивайте цифру десятков на единицу. Все числа будут заканчиваться одной и той же цифрой в столбце единиц измерения.
Счет с пропусками — более быстрый способ счета, чем счет единицами.
При обучении счету до 10 в первый раз может быть полезно использовать числовую сетку до 100, чтобы помочь визуализировать закономерности в числах.
Начиная с нуля, мы можем добавить десять, чтобы получить 10.
Продолжаем каждый раз прибавлять по 10 и получаем: 20, 30, 40, 50, 60, 70, 80, 90 и 100.
Мы видим, что каждый раз, когда мы прибавляем десять к числу в числовой сетке, мы перемещаемся на одну клетку вниз.
Мы начали с «0» и считали десятками. При пропуске счета на 10 от нуля все числа находятся в таблице десятикратного умножения.
Мы видим шаблон, в котором все числа заканчиваются одной и той же цифрой в столбце единиц. Все числа заканчиваются на ноль.
При обучении счету с пропуском до 10 важно отметить, что добавление десяти к числу каждый раз увеличивает цифру десятков на 1.
Мы можем видеть закономерность в цифрах десятков, увеличивающихся от 1 до 2, до 3 и так далее.
100 это 10 десятков.
Пропустить счет на 10 назад
Чтобы пропустить счет назад на 10, каждый раз вычитайте 10. Вычитание 10 в числовой сетке приводит к перемещению на одну клетку вверх каждый раз. Каждый раз цифра в столбце десятков будет уменьшаться на 1.
Например, из 42, считая в обратном порядке, мы получаем 42, 32, 22, 12 и 2. Цифра в столбце десятков каждый раз уменьшается на 1 от 4 до 3, затем от 2 до 1 и до 0.
Мы можем найти 42 на сетке чисел до 100.
Чтобы вычесть 10 из числовой сетки, мы перемещаемся вверх по сетке к квадрату прямо над числом, в котором мы сейчас находимся.
42 оканчивается на «2», поэтому другие числа в шаблоне также оканчиваются на «2».
Считая в обратном порядке, получаем 42, 32, 22, 12 и 2.
Мы не продолжаем вычитать 10, потому что 2 меньше 10, а на числовой сетке нет других квадратов, показанных выше 2.
Вот еще один пример.
Пропустите обратный счет десятками, начиная со 100, у нас будет 100, 90, 80, 70, 60, 50, 40, 30, 20, 10, 0.
Чтобы пропустить обратный счет десятками, вычтите десять, чтобы перейти к следующему новому числу. Столбец единиц останется прежним, а столбец десятков будет каждый раз уменьшаться на единицу. Все числа будут заканчиваться на одну и ту же цифру.
Мы можем использовать рабочие листы гусеницы с пропуском счета, чтобы попрактиковаться в обратном счете.
Вот пустой пример для пропуска обратного отсчета.
Вот рабочий лист гусеницы, который заполняется пропуском обратного счета десятками.
Мы видим, что числа в рабочем листе гусеницы для обратного счета совпадают с числами для прямого счета. Пропустить счет в обратном направлении может быть полезно для отработки моделей, наблюдаемых при пропуске счета в прямом направлении.
При обучении счету с пропусками важно сначала попрактиковаться в счете в прямом порядке, прежде чем переходить к счету в обратном порядке, используя те же числа.
Вот еще один рабочий лист для подсчета пропусков, в котором мы считаем в обратном порядке десятками от 99.
При обучении счету с пропуском до 10 полезно произносить числа, когда вы считаете вперед и назад, подчеркивая числа, которые остаются неизменными в каждом образце.
В чем смысл подсчета пропусков?
Счет с пропусками помогает нам искать закономерности в числах и лучше понимать относительный размер чисел. Подсчет пропусков — это форма повторного сложения, когда ответы образуют таблицу умножения. Таким образом, подсчёт помогает нам выучить таблицу умножения. Изучение того, как прибавлять и вычитать, пропуская счет вперед и назад, также укрепляет нашу способность выполнять сложение и вычитание.
В общем, пропуск счета укрепляет нашу уверенность при работе с числами. Умножение, деление, сложение и вычитание улучшаются, если сначала научиться пропускать счет вперед и назад на диапазон различных чисел.
Вот пример пропуска обратного счета на 10 из 92.
Мы просто вычитаем десять, чтобы получить каждое число, что равносильно уменьшению цифры десятков на 1 каждый раз.
92 заканчивается цифрой «2» в столбце единиц измерения. Следующие числа в скороговорке также будут заканчиваться на «2», но цифра в столбце десятков каждый раз будет уменьшаться на 1.
Образец, усвоенный в ходе этого процесса, позволяет нам затем научиться вычитать десять из любого числа.
Это помогает нам понять, как разные числа соотносятся друг с другом по размеру.
Глава 5
Цели
К концу этого урока вы сможете…
- решать задачи на счет с помощью правила умножения
- решать задачи на счет с помощью перестановок
- решать задачи на счет с помощью комбинаций
- решить задачи на подсчет, связанные с перестановками с неразличимыми элементами
- вычислить вероятности с участием перестановок и комбинаций
Для быстрого ознакомления с этим разделом посмотрите этот краткий видеообзор:
Помните классический метод расчета вероятностей из раздела 5.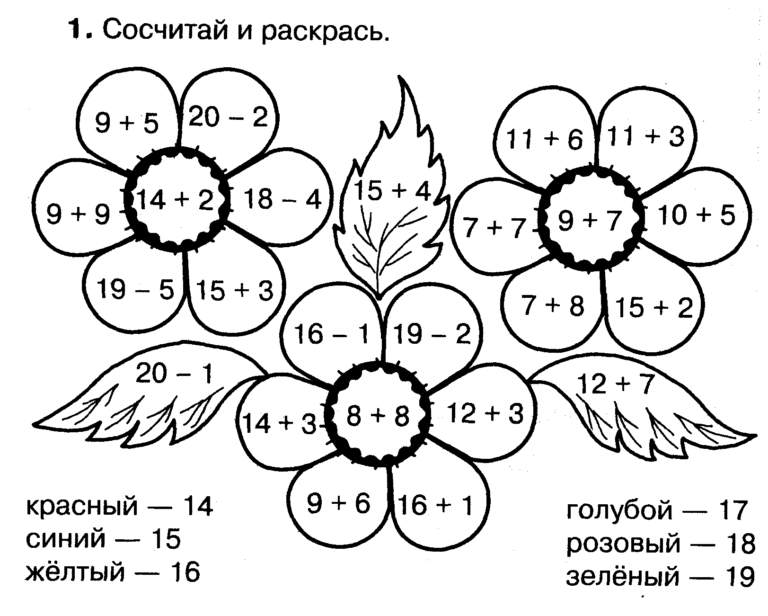
1?
| P(E) = | количество способов появления E | = | С(В) |
| общее количество возможных исходов | Н(С) |
Что ж, иногда подсчет «количества возможных событий E» или «общего количества возможных исходов» может быть довольно сложным. В этом разделе мы изучим несколько методов подсчета, которые помогут нам рассчитать некоторые из более сложных вероятностей.
Правило счета умножения
Предположим, вы готовитесь к свадьбе и вам нужно выбрать смокинги для жениха. На складе мужских смокингов есть функция Build-A-Tux, которая позволяет вам просматривать определенные комбинации и создавать свой смокинг онлайн. Предположим, у вас есть компоненты, сузившиеся до двух жакетов, двух комбинаций жилета и галстука и трех цветов рубашки.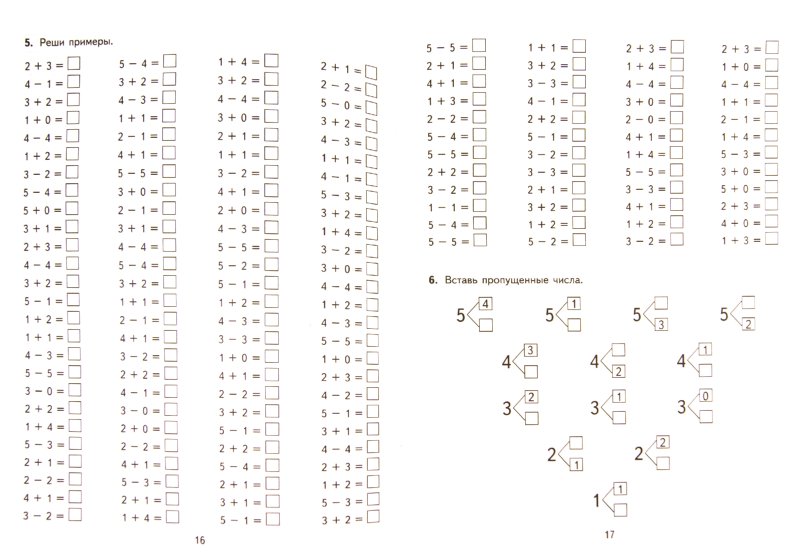
Сколько всего комбинаций может быть?
Хорошим способом помочь понять ситуацию такого типа является так называемая древовидная диаграмма . Мы начинаем с выбора жакета, а затем каждый жакет «разветвляется» на две комбинации жилета и галстука, а затем каждая из них «разветвляется» на три комбинации рубашки. Это может выглядеть примерно так:
Всего у нас есть 12 возможных комбинаций курток, жилетов и рубашек. (Конечно, некоторые могут не соответствовать вашему вкусу, но это уже другой вопрос…)
Нет ли более простого способа сделать это? Почему да, есть! Подумайте об этом так: для каждого варианта куртки есть два варианта жилета и галстука. Это дает нам 4 комбинации пиджака и жилета/галстука. Затем для каждого из этих есть три варианта выбора рубашки, что дает нам в общей сложности 12.
В общем, мы умножаем количество способов сделать каждый выбор, так что…
общее количество нарядов = (количество курток)•(количество жилетов/галстуков)•(количество рубашек)
Это приводит нас к правилу подсчета умножения:
Правилу подсчета умножения
Если задача состоит из последовательности вариантов выбора, в которой есть p способов сделать первый выбор, q способов сделать второй второй и т.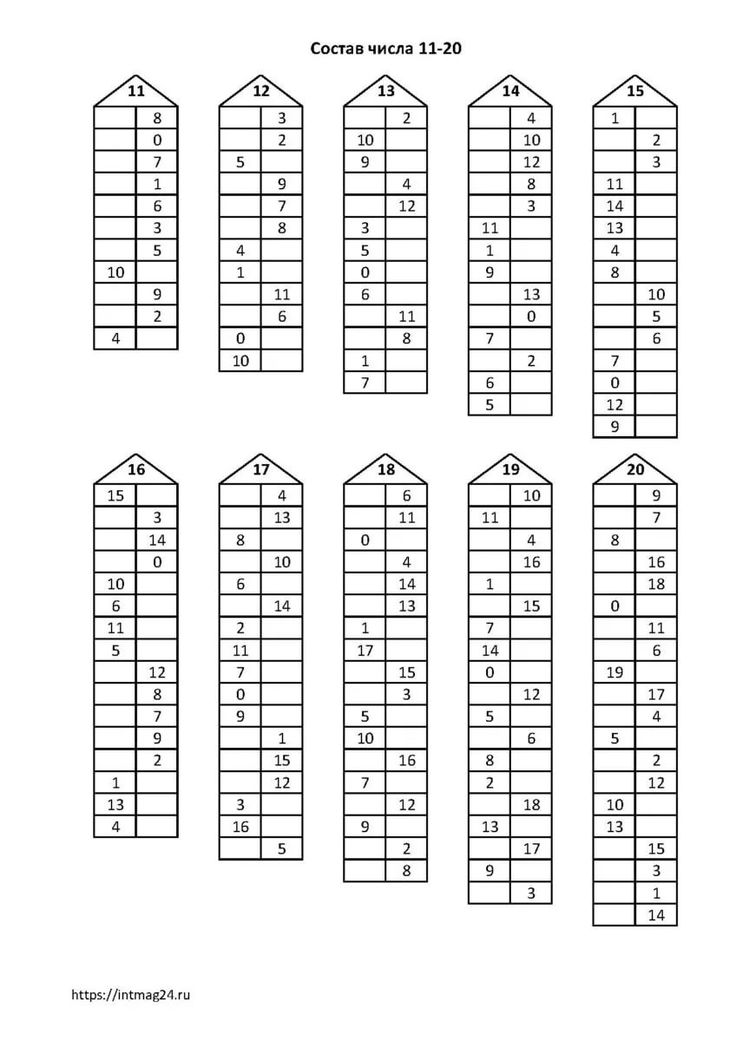
д., то задачу можно выполнить
p•q•r• …
разными способами.
Давайте попробуем несколько примеров.
Пример 1
Сколько 7-значных номерных знаков возможно, если первые три символа должны быть буквами, а последние четыре должны быть цифрами от 0 до 9, а повторяющиеся символы разрешены?
[ раскрыть ответ ]
Общее количество номерных знаков будет:
(# вариантов для 1-го символа)• (# вариантов для 2-го символа) • и т. д..
= 26•26•26•10• 10•10•10 = 175 760 000
Пример 2
Источник: Sears
На многих гаражных воротах снаружи двери есть пульт дистанционного управления. Предположим, вор подходит к определенному гаражу и замечает, что четыре конкретных числа используются хорошо. Если предположить, что код использует все четыре числа ровно один раз, сколько 4-значных кодов должен попробовать вор?
[ раскрыть ответ ]
Не очень много!
общее количество кодов = (# вариантов для 1-й цифры)•(# для 2-й цифры) • и т.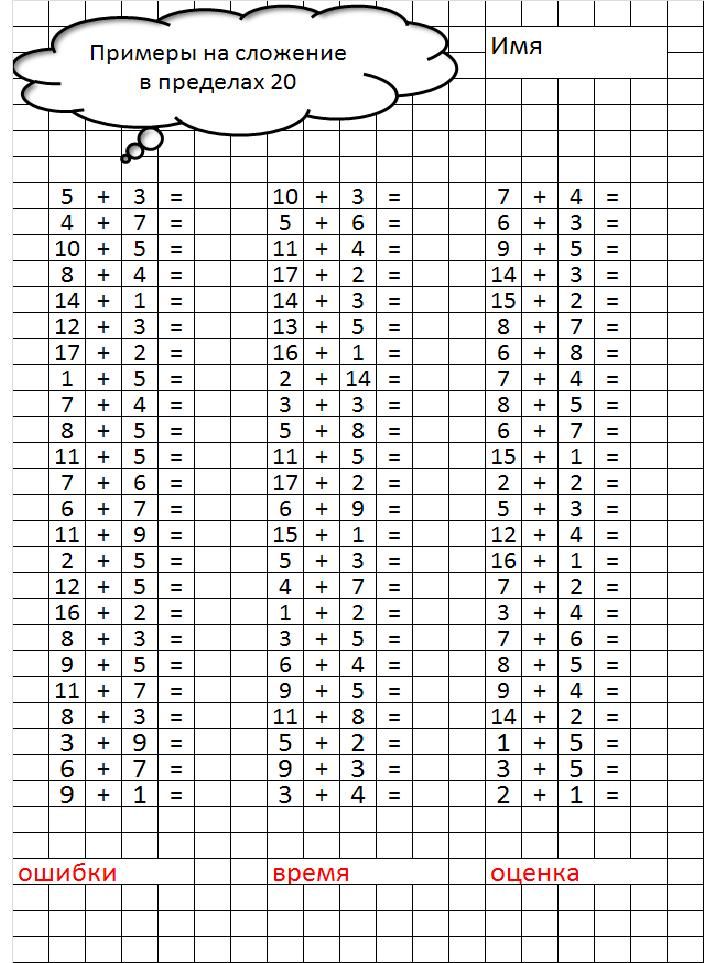
д.
= 4•3•2•1 = 24
Обратите внимание, что количество вариантов уменьшилось на единицу для каждой цифры, поскольку четыре числа использовались только один раз. Вы часто будете видеть, что это описывается либо как число, выбранное «без замены», либо как «повторение не разрешено».
Пример 2 из предыдущего раздела является примером особой техники подсчета, называемой перестановка . Вместо того, чтобы давать вам формулы и примеры, я хотел бы еще раз сослаться на некоторые материалы с одного из моих любимых веб-сайтов BetterExplained. Вот что пишет о перестановках автор Калид Азад:
Перестановки: волосатые подробности
Начнем с перестановок, или всех возможных способов что-то сделать. Мы используем модный термин «перестановка», поэтому позаботимся о каждой детали, включая порядок элементов. Допустим, у нас есть 8 человек:
- Алиса
- Боб
- Чарли
- Дэвид
- Ева
- Фрэнк
- Джордж
- Горацио
Сколькими способами мы можем получить золотую, серебряную и бронзовую медаль для «Лучшего друга в мире»?
Мы собираемся использовать перестановки, так как порядок, в котором мы раздаем эти медали, имеет значение.
Вот как это происходит:
- Золотая медаль: 8 вариантов: A B C D E F G H (Умно, как я сопоставил имена с буквами, а?). Допустим, А выигрывает золото.
- Серебряная медаль: 7 вариантов: B C D E F G H. Допустим, B выиграет серебро.
- Бронзовая медаль: 6 вариантов: C D E F G H. Допустим… C выигрывает бронзу.
Мы выбрали определенных людей для победы, но детали не имеют значения: сначала у нас было 8 вариантов, затем 7, затем 6. Всего вариантов было 8 * 7 * 6 = 336.
Давайте посмотрим на детали. Пришлось заказывать 3 человека из 8. Для этого мы начинали со всех вариантов (8) потом забирали их по одному (7, потом 6) пока не кончились медали.
Мы знаем, что факториал:
К сожалению, это слишком много! Нам нужно только 8 * 7 * 6. Как мы можем «остановить» факториал на 5?
Вот где перестановки становятся крутыми: обратите внимание, как мы хотим избавиться от 5*4*3*2*1. Какое другое название для этого? 5 факториал!
Итак, если мы сделаем 8!/5! получаем:
А почему мы использовали цифру 5? Потому что она осталась после того, как мы взяли 3 медали из 8.
Таким образом, лучше написать это так:
, где 8!/(8-3)! — это просто причудливый способ сказать: «Используйте первые 3 числа из 8!». Если у нас всего 90 655 n 90 656 предметов и мы хотим выбрать 90 655 k 90 656 в определенном порядке, мы получим:
просто означает «Используйте первые k чисел из n!»
А вот и причудливая формула перестановки: у вас есть n предметов, и вы хотите найти число способов k позиций можно заказать:
Источник: BetterExplained,
Калид Азад
Артикул: Легкие перестановки и комбинации
Используется с разрешения.
Кстати, в вашем тексте используется обозначение n P k , а не P(n,k) Калида. Я видел, как используются оба, хотя последний, как правило, более распространен на уроках математики более высокого уровня. Мы будем придерживаться версии учебника, просто чтобы быть последовательными.
Перестановки
n различных объектов, взятых r одновременноКоличество комбинаций r объектов, выбранных из n объектов в котором
- n объектов различны,
- повторы не допускаются,
- порядок имеет значение,
находится по формуле .
Хорошо, попробуем пару.
Пример 3
Предположим, организация избирает своих должностных лиц из попечительского совета. Если есть 30 попечителей, сколькими способами правление может избрать президента, вице-президента, секретаря и казначея?
[ раскрыть ответ ]
В этом примере у нас есть 30 «предметов» (доверенных лиц), из которых мы выбираем 4. Используя обозначения из вашего текста, мы хотим вычислить 30 P 4 , или
| 30 P 4 = | 30! | = | 30! | 90 635 = 30•29•28•27 = 657 720
| (30-4)! | 26! |
Пример 4
Предположим, вам дали список из 100 десертов и вас попросили оценить ваши 3 лучших. Сколько существует возможных списков «3 лучших»?
[ раскрыть ответ ]
| 100 P 3 = | 100! | = | 100! | = 100•99•98 = 970 200 |
| (100-3)! | 97! |
На предыдущей странице мы говорили о количестве способов выбрать 90 664 k 90 665 объектов из 90 664 n 90 665, если порядок имел значение — например, вручение медалей, избрание офицеров или маринование любимых десертов.
Что, если порядок не имеет значения, как выбор членов комитета?
Опять же, я позволю Калиду Азаду объяснить.
Комбинации, Хо!
Комбинации очень просты. Порядок не имеет значения. Вы можете смешать это, и это будет выглядеть так же. Допустим, я скряга и не могу позволить себе отдельные золотые, серебряные и бронзовые медали. На самом деле, я могу позволить себе только пустые жестяные банки.
Сколькими способами я могу раздать 3 консервные банки 8 людям?
Ну, в данном случае порядок, в котором мы выбираем людей, не имеет значения. Если я даю банку Алисе, Бобу, а затем Чарли, это то же самое, что дать Чарли, Алисе, а затем Бобу. В любом случае, они будут одинаково разочарованы.
Это поднимает и интересный момент — у нас здесь есть некоторые излишества. Элис Боб Чарли = Чарли Боб Элис. На минутку давайте просто выясним, сколькими способами мы можем переставить 3 человек.
Итак, у нас есть 3 варианта для первого человека, 2 для второго и только 1 для последнего.
Итак, у нас есть 3*2*1 способа переставить 3 человека.
Минуточку… это немного похоже на перестановку! Ты обманул меня!
Действительно. Если у вас есть N человек, и вы хотите знать, сколько аранжировок существует для 90 655 всех 90 656 из них, это просто N факториал или N!
Итак, если у нас есть 3 жестяных банки для раздачи, их будет 3! или 6 вариантов для каждого выбора, который мы выбираем. Если мы хотим выяснить, сколько комбинаций у нас есть, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56,9.0003
Общая формула:
, что означает «Найдите все способы выбрать k людей из n и разделите на k! варианты». Записав это, мы получим нашу формулу комбинации , или количество способов объединить k элементов из набора n:
Источник: BetterExplained,
Калид Азад
Артикул: Легкие перестановки и комбинации
Используется с разрешения.
В качестве примечания: в вашем тексте используется обозначение n C k , а не C(n,k) Калида. Как и в случае с перестановками, мы будем придерживаться версии из учебника, просто чтобы быть последовательными.
Комбинации
N Отличительные объекты, взятые R за времяКоличество соглашений N Объектов с использованием R ≤ N из них, в котором
≤ N из них 611111064 ≤ N из них ≤ n , в I, в котором ≤ n , в I, в котором ≤ n , в I, в котором . ,находится по формуле .
Хорошо, давайте попробуем этот новый.
Пример 5
Рассмотрим снова попечительский совет из 30 членов. Сколькими способами правление может избрать четырех членов финансового комитета?
[ раскрыть ответ ]
В этом примере у нас есть 30 «элементов» (доверенных лиц), из которых мы выбираем 4.
В отличие от примера 3, в этом примере порядок не имеет значения, поэтому мы рассматриваем комбинация, а не перестановка.
| 30 С 4 = | 30! | = | 30! | = | 30•29•28•27 | 90 635 = 27 405
| (30-4)!•4! | 26!4! | 4•3•2•1 |
Вы можете заметить, что это число немного меньше, чем в примере 3. Причина в том, что сейчас нас не волнует порядок, поэтому выбор попечителей A, B, C и D для комитета ничем не отличается от избрание попечителей B, C, A и D. Это отличается от примера 3, где мы избирали их на определенные должности.
Пример 6
Источник: stock.
xchng
Предположим, вы организатор волейбольного турнира. На турнир зарегистрировалось 10 команд, и кажется хорошей идеей, чтобы каждая команда сыграла с каждой командой по круговой системе, прежде чем выйти в плей-офф. Сколько игр возможно, если каждая команда сыграет с каждой другой командой один раз?
[ раскрыть ответ ]
На первый взгляд это может показаться не комбинацией, но давайте посмотрим поближе. У нас есть 10 «предметов» (команд), из которых мы выбираем 2. Порядок нам не важен, так как команда А играет с командой Б так же, как команда Б играет с командой А. Это именно комбинация!
| 10 С 2 = | 10! | = | 10! | = | 10•9 | = 45 |
| (10-2)!•2! | 8!2! | 2•1 |
Ух ты, сколько игр! Вот почему большинство турниров имеют структуру «пула» и разбивают турнир на два «пула» по 5 игроков.
0003
Подробнее о круговой системе турниров можно узнать в Википедии.
Второй тип встречается реже. Что, если мы хотим узнать, сколько способов упорядочить n объектов, но не все они различны? Вот пример для иллюстрации:
Пример 7
Сколькими способами можно переставить буквы в слове СТАТИСТИКА?
Ответ немного сложен. Думайте о переставленных словах как о местах для букв. Что-то вроде этого:
В СТАТИСТИКЕ у нас есть следующие буквы:
3 S
3 т
2 я
1 А
1 C
На самом деле мы не можем сказать, что есть 4 варианта выбора первой буквы и исходить оттуда, так как количество вариантов выбора второй буквы зависит от того, какая буква была выбрана для первой.
Вместо этого мы выбираем точки для каждой из букв. Сначала выберите 3 из 10 мест для буквы S. Мы можем сделать это в 10 C 3 способов. Затем выберите 3 места для 3 Т. Мы можем сделать это 7 C 3 способами.
Точно так же мы можем выбрать места для букв I, A и C способами 4 C 2 , 2 C 1 и 1 C 1 соответственно. Итого, значит переставляем буквы так:
10 C 3 • 7 C 3 • 4 C 2 • 3 •
3 2 12 1 C 1 способыЭто может быть только я, это действительно грязный. Как ни странно, выписывание комбинаций показывает хороший способ их упростить:
| 10! | • | 7! | • | 4! | • | 2! | • | 1! | = | 10! |
| 7!•3! | 4!•3! | 2!•2! | 1!•1! | 1!•0! | 3!•3!•2!•1!•1! |
Перестановки с неразличимыми элементами
Число перестановок n объектов, где имеется n1 объектов 1-го типа, n2 объектов 2-го типа и т.