Карточка 1 1. Реши примеры. 4-2+7-4= 9-2-4-3= 2+5-3+4= 2+2+5-2= 3+2+5-3= 4+5-5+9= | Карточка 2 1. Реши примеры. 7+2-8+2= 8+2-4+3= 8+2-9-1= 4+2-5+2= 6-5+9-3= 6+3-5+4= |
Карточка 3 1. Реши примеры. 10-4-3-2= 2+0+6-5= 6-2-3+7= 3+2+3+2= 9-4-2-2= 9-4+3-6= | Карточка 4 1. Реши примеры. 8-2-2-2= 3+6-2+3= 7-4-2+7= 1+9-3-2= 5+2+3-6= 9-2-5-2= |
Карточка 5 1. Реши примеры. 8-2-6+2= 2+4-3+2= 7-5+2-2= 3+2-4+2= 8-6-2+2= 3+4-6+2= | Карточка 6 1. Реши примеры. 5+3-4+3= 3+4-2-3= 7-3-2-2= 7-2+3-4= 4+3+2-7= 6+2-8+2= |
Карточка 7 1. Реши примеры. 8-4-2+3= 10-2-6+2= 10-5-3-2= 4+2-3-2= 4+2-3+6= 4+3-5+3= | Карточка 8 1. Реши примеры. 8-2-3+2= 7-2-2-2= 2+6+2-3= 4+3+3-5= 2+4+2+2= 2+3+2+3= |
Карточка 9 1. Реши примеры. 2+5+2-3= 2+4+4-2= 9-5-3+7= 7+3-2-5= 7-5-2+3= 10-8+7-2= | Карточка 10 1. Реши примеры. 9-5+3-2= 8-2+3-4= 7+2+1-4= 6+2+2-5= 2+3+2+3= 4+4+2-9= |
Счет в пределах 10 для детей от 5-6 лет
Здесь мы подготовили для вас математические примеры — Счет в пределах 10 — для максимальной тренировки детей, готовящихся к поступлению в школу или уже учащихся в 1-2 классах.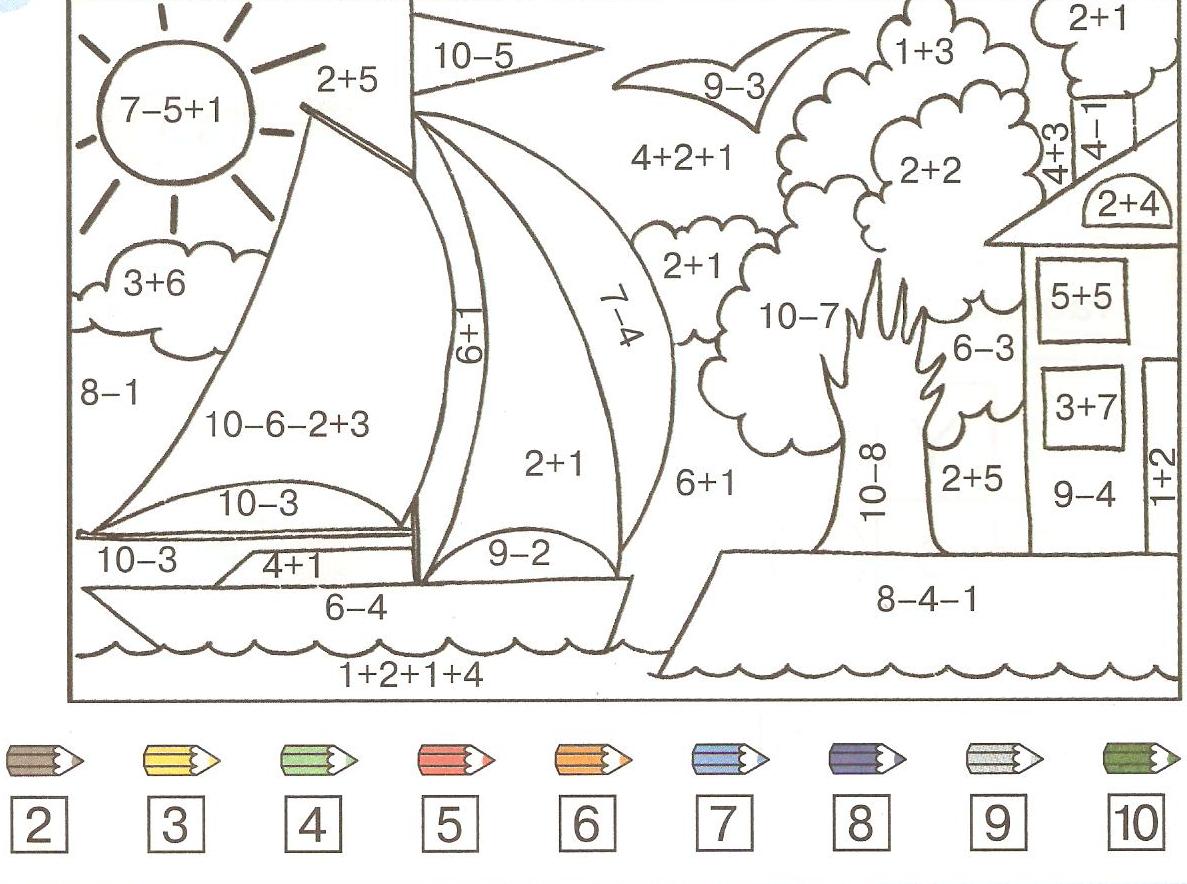
Скачайте примеры во вложениях, распечатайте все листы на принтере и попросите ребенка решить примеры, объяснив ему условия.
Математические примеры — Счет в пределах 10 на скорость:
Примеры нужно решать на скорость. Каждый лист поделен на 2 части — правая и левая половины. Для каждой части внизу даны пустые клетки, в которых нужно вписать время, за которое ребенок решил все примеры этой половины листа. Справа от клеток вы увидите оценку результатов ребенка. Если ребенок затратил на выполнение задания более 4 минут, то его оценка — грустный смайлик, если он успел правильно решить примеры менее, чем за 4 минуты — улыбающийся смайлик. Ну а если он справился менее, чем за 3 минуты — смайлик очень радостный — это высшая оценка!
Математические примеры — Счет в пределах 10 в количестве 8 страниц (то есть 16 заданий), находятся во вложениях внизу страницы.
Похожие задания, обучающие счету до 10, вы можете найти и в других материалах:
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
Считаем до 20 — Задания в картинках для печати
Считаем до 20 с помощью веселых игровых заданий для распечатки! Все, что вам нужно — это выбрать любой набор задачек в картинках, скачать их во вложениях и распечатать на принтере.
Устный счет в пределах 10 — Картинки с заданиями
Здесь мы подготовили для вас устный счет в пределах 10 в виде математических заданий в картинках. Данные задания формируют у детей навыки счета и способствуют более эффективному обучению простых математических действий.
Раскраски с заданиями на счет в пределах 10Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями. Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.
Задания с раскрасками — Порядковый счет до 10
В этих интересных заданиях дети узнают, что такое порядковый счет до 10. А те, кто уже знакомы с этим понятием, могут показать свои знания с помощью данного упражнения.
Счет до 5 — Картинки с заданиями для малышей
Здесь мы выложили для вас счет до 5 — картинки с математическими заданиями для малышей, благодаря которым ваши дети потренируют не только свои навыки счета, но и умение читать, писать, различать геометрические фигуры, рисовать и раскрашивать.
Прописи-цифры от 1 до 10 для распечатки — Скачай и обводи
Здесь вы можете скачать прописи цифры, распечатать их на принтере и использовать в домашнем обучении для подготовки детей к школе
А также в развивающих математических играх от лисенка Бибуши:
Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
Игра «Найди числа на картинке» для малышей от 4 лет
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
Математическая игра «Найди наибольшее и наименьшее число»
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое. После правильного ответа он услышит порядковый счет до этого числа.
Игра «Сложение и вычитание до 10» — Задачки в картинках
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши, в которой малыш сможет решить восемь новых задачек на счет до 10.
Задачи-примеры для малышей в картинках
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.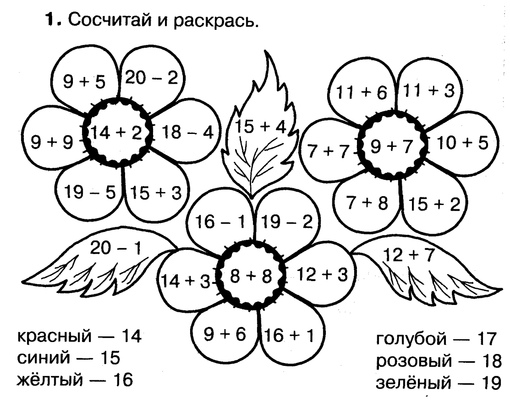
В трех уровнях игры ребенок будет решать задачи на вычитание, а в пяти — складывать заданные предметы.
Примеры по математике — 1 класс
Здесь вы можете найти примеры по математике (1 класс), распечатать на принтере и использовать в качестве учебного материала на уроках математики или в детских садах на этапе подготовки к поступлению в школу. Очень удобно проводить такие занятия с группой детей, так как для этого не нужно покупать каждому ребенку специальные рабочие тетради — достаточно только распечатать нужное количество экземпляров заданий на каждого ребенка.
Примеры по математике 1 класс — Распечатать и решать
Чтобы распечатать примеры по математике (1 класс) вам понадобится цветной принтер. В крайнем случае можно использовать черно-белый принтер, но дети гораздо лучше усваивают учебный материал, когда он подается в ярких образах и красивых иллюстрациях. Это способствует восприятию урока, как игры, и ребенок не чувствует напряжения.
- В первом задании нужно вставить числа в пустые клетки лепестков, чтобы в результате решения образованного примера получилось число в центре цветка.
- Во втором задании мы снова тренируем умение детей считать до 10. Необходимо нарисовать в каждой картинке указанное количество ягод.
Скачать примеры по математике (1 класс) вы можете во вложениях внизу страницы.
Распечатать кроссворды-примеры для 1 класса по математике
Здесь вы можете скачать и распечатать необычные кроссворды-примеры для 1 класса по математике. Обычные примеры решать скучно не интересно. Поэтому мы решили их немного приукрасить, сделав их в виде увлекательных чайнвордов. В первом задании сетка кроссвордов сделана таким образом, что все ответы в примерах должны совпадать при пересечении. Во втором задании все гораздо проще — здесь необходимо решать примеры змейкой, начиная с верхней точки (10 — 8 =). Если в конце змейки у вас получилась 10 — значит, чайнворд решен верно!
Скачать кроссворды примеры для 1 класса по математике вы можете во вложениях.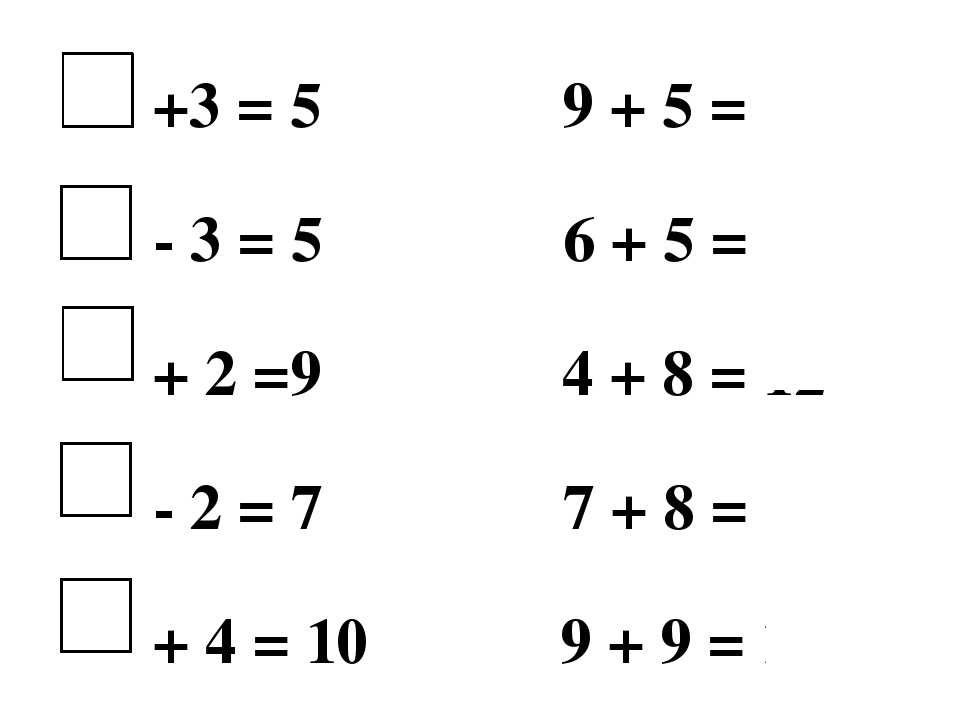
Веселые математические примеры-раскраски для первоклашек
Очень помогают в обучении детей задания с раскрасками. Дети с удовольствием раскрашивают картинки, предварительно выполняя указанные задания. В этом материале вы можете скачать примеры-раскраски по математике для первоклассников и дошкольников.
- В первом задании нужно решить пример в облачке и найти нужный самолет с ответом. Затем раскрасить его.
- Во втором задании ответ на пример находится в одной из бабочек. Ее нужно поймать и раскрасить.
Можно добавить еще несколько заданий для большей эффективности занятия. Например, при раскрашивании пусть ребенок сначала раскрасит самолетик с самым маленьким числом, затем с самым большим, а потом уже все остальные. Либо можно предложить ребенку раскрасить все самолетики (или бабочки) по порядку изображенных на них чисел.
Скачать математические примеры-раскраски для первоклассников вы можете во вложениях.
Решаем примеры по математике — В гостях у сказки
В этих сказочных сюжетах заключены настоящие примеры по математике, решив которые можно узнать кое-что о наших героях. Например в первом задании можно узнать, кто где живет. Для этого нужно решить все примеры. Ответы на примеры являются номером домика, в котором живет сказочный герой. Пусть ребенок назовет, кто у кого находится в гостях. А во втором задании, если ребенок решит правильно все примеры, то узнает, какой из сказочных героев едет в поезде не оплатив проезд.
Скачать примеры со сказочными героями вы можете во вложениях.
Примеры и счет до 10 по математике — Любимые мультяшки
Решать примеры по математике в 1 классе — не очень интересное занятие для детей, которые еще совсем недавно носились по детской площадке, взахлеб смотрели мультики и не думали ни о какой школе. Чтобы сгладить впечатление детей от скучных учебников, распечатывайте ему красочные картинки с заданиями, которые богаты иллюстрациями и любимыми мяльтяшными героями.
Обучение должно доставлять радость!
- В первом задании нужно решить все примеры по математике, нарисованные на тачках. Тачка, в решении примера которой получится самый большой ответ — считается самой быстрой на уличных гонках!
- Во втором задании ребенку необходимо посчитать количество сбежавших животных.
Скачать задания — Примеры и счет до 10 по математике вы можете во вложениях.
Обведи картинки, реши примеры по математике и раскрась
Здесь вы встретите очень интересные обучающие картинки, в которых детям предстоит выполнить несколько развивающих заданий. Для их выполнения ребенок должен уметь считать до 20 и решать простые примеры на сложение и вычитание.
Скачайте во вложениях картинки с заданиями, распечатайте на принтере и дайте ребенку вместе с цветными карандашами. Также подготовьте простой карандаш и ластик (для обведения по точкам). Затем объясните ребенку условия заданий:
В первом и втором задании сначала нужно обвести по точкам картинки (клоуна с мячом и куклу с мячом). Затем нужно раскрасить обе картинки определенным образом: каждый элемент раскраски содержит в себе математический пример. Ты должен решить этот пример и ответ, который у тебя получится в результате, подскажет тебе цвет, которым нужно раскрасить эту деталь. Справа нарисованы цветные кружки с числами. Это и есть числа-ответы. Будь внимателен!
Скачать задание с примерами, точками и раскрасками вы можете во вложениях.
Умные раскраски с примерами и заданиями по математике
Продолжаем решать примеры по математике с учащимися первых классов и дошкольников, готовящихся к школе. Опять вас ждут умные раскраски, которые смогут раскрашивать только те дети, которые умеют прибавлять и отнимать до 10. Также здесь есть еще одно математическое задание, в котором дети повторят знание четных и нечетных чисел, а также умение делить предметы поровну.
Если с третьим заданием возникают сложности, то пусть ребенок повторит еще раз пройденный материал на нашем сайте — Четные и нечетные числа до 20, а также Разделить поровну предметы.
- В первом задании нужно раскрасить цветочки определенным образом: каждому примеру соответствует определенный цвет. Нужно решить пример, посмотреть какому цвету относится полученный ответ-число и раскрасить в этот цвет. Так следует поступить со всеми примерами цветков.
- Во втором задании необходимо выполнить цепочку математических действий (прибавлений и отниманий) по порядку стрелочек. Каждый квадратик с числом нужно раскрасить в тот цвет, в который раскрашен воздушный шарик с данным числом.
- В третьем задании нужно поделить овощи, фрукты и предметы между зайчатами поровну. Для этого ребенок должен понимать, что поровну можно разделить только четное количество предметов. После этого предметы нужно раскрасить, как указано в задании.
Скачать умные раскраски с примерами и заданиями по математике вы можете во вложениях.
Раскраска — Реши простые примеры и узнай, чья это шапка
В этом задании-раскраске ребенок должен отгадать, чью шапку держит птичка. Но, как известно, математика — это точная наука, в ней не бывает отгадываний и предположение. Поэтому, тот кто умеет решать примеры — обязательно узнает, кому принадлежит шапка.
Для этого ребенок должен решить примеры возле каждого животного. Тот пример, в результате решения которого получится число, как на шапке — является ответом к задаче. Значит животное рядом с этим примером является полноправным владельцем шапки. Затем картинку с животными нужно раскрасить. В детском саду или школе можно выполнять это задание с группой детей. В таком случае один из детей окажется победителем, если первым скажет правильный ответ. Раскрашивать необходимо в свободной форме, без соревнований (дети должны приучаться к аккуратности, а скорость — не лучший помощник в этом).
Скачать раскраску с примерами вы можете во вложениях
Настольная игра «Математическое колесо» — Примеры
В этой настольной игре дети потренируются решать примеры по математике, руководствуясь не только умением прибавлять и отнимать числа, но и пространственным и логическим мышлением.
Чтобы начать играть в игру, необходимо изготовить ее с помощью картинок для скачивания (во вложениях) и нашей инструкции.
Приготовьте скачанные на нашем сайте и распечатанные картинки с математическим колесом, ножницы или канцелярский нож. Вырежьте два круга на каждом бланке (маленький и большой). Все, теперь можно приступать к игре.
Положите на стол вырезанный большой круг и внутри него маленький круг. Ребенок должен крутить маленький круг до тех пор, пока все примеры совпадут правильно.
Скачать 2 бланка настольной игры с примерами «Математическое колесо» вы можете во вложениях.
Бланк №1
Бланк №2
Задания-примеры по математике для 1 класса — Заплатка на коврик
Еще одна настольная игра, в которой нужно решать примеры по математике для 1 класса. Здесь нужно будет вырезать из скачанных и распечатанных бланков коврик и фрагменты-заплатки к нему. Начинать нужно с бланка №1 и дальше по порядку, так как задания усложняются. Затем можно начинать игру.
Объясните ребенку, что перед ним лежит специальный математический коврик, в котором отсутствует один фрагмент. Благодаря умению решать примеры, ребенок может найти отсутствующий фрагмент среди пяти предложенных вариантов и поставит заплатку на коврик. Когда ребенок выберет правильный вариант, пусть приклеит деталь к коврику.
Скачать задания-примеры по математике для 1 класса — Заплатка на коврик вы можете во вложениях.
Бланк №1
Бланк №2
Бланк №3
Фруктовые примеры — Умеешь ли ты логически мыслить?
Здесь вы можете скачать оригинальные фруктовые примеры, решить которые будет не так уж просто! Ведь прежде, чем их решать, нужно хорошо подумать, в чем заключается смысл условия задания. Пусть ребенок подольше рассмотрит картинки и подумает сам, как ему найти числовое значение фрукта возле которого стоит знак вопроса (в первом задании — яблоко, во втором — лимон).
Объясните ребенку так: На этой картинке необычные примеры. В них фрукты скрыли некоторые числа. То есть, под каждым фруктом запрятано какое-то число. Тебе нужно решить, какое число запрятано под яблоком. Для этого ты должен внимательно посмотреть как прибавляются и отнимаются фрукты в примерах и какие числа получаются в результате. Если ты узнаешь числа, скрытые под разными фруктами, то сможешь узнать и то число, которое скрыто под яблоком.
Занятие интересно проводить с группой детей — на перегонки.
Скачать фруктовые примеры вы можете во вложениях внизу страницы
Также вы можете скачать и другие математические задания в картинках:
Задания по математике для дошкольников — В картинках
Задания по математике для дошкольников, представленные в этом материале, помогут вам разнообразить свои занятия с детьми, обучая их самым основным математическим понятиям.
Соседи числа — Математические задания для детей
Соседи числа — это математические задания на закрепление знания порядкового счета. В этих заданиях ребенку нужно будет определить соседей для заданных чисел
Математические задания для 1 класса — В картинках для печати
Математические задания для 1 класса — это яркие красочные картинки с развивающими упражнениями по математике, включающие в себя разнообразные игровые задания для детей.
Задачи по математике — 1 класс. Распечатать в картинках
Здесь вы найдете увлекательные задачи по математике (1 класс) в картинках, которые научат детей мыслить логически и выполнять простые математические действия.
Разделить поровну предметы — Математические картинки
Здесь вы можете посмотреть и скачать красочные картинки задания, в которых нужно разделить поровну различные предметы. Такие занятия подготавливают детей к одному из сложных математических выражений — делению.
Раскраски с заданиями на счет в пределах 10
Чтобы дети могли быстро и с интересом освоить счет в пределах 10, мы подготовили для вас веселые раскраски с заданиями.
Каждое задание содержит в себе картинки для раскрашивания — это стимулирует ребенка правильно выполнить задание.
Четные и нечетные числа от 1 до 20 — Задания в картинках
В этом материале дети узнают, что такое четные и нечетные числа от 1 до 20 и научатся различать их, выполняя различные задания в картинках.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
А еще вы можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Счет от 1 до 10 — Посчитай картинки и выбери число»
В этой игре малыш должен посчитать количество предметов на игровом экране и нажать на соответствующее число. После этого он увидит и услышит порядковый счет до данного числа.
Игра «Найди числа на картинке» для малышей от 4 лет
Здесь ребенку нужно быть внимательным, чтобы найти все спрятанные числа на картинке. В игре также используется порядковый счет.
Математическая игра «Найди наибольшее и наименьшее число»
В этой игре ребенку необходимо выбрать среди предложенных чисел самое большое или самое маленькое.
Игра «Сложение и вычитание до 10» — Задачки в картинках
Представляем вашему вниманию еще одну развивающую математическую игру «Сложение и вычитание до 10» для детей раннего возраста от Лисенка Бибуши
Задачи-примеры для малышей в картинках
Математическая онлайн игра «Задачи-примеры для малышей в картинках» состоит из восьми задачек и подойдет детям, которые учатся считать до 10.
Карточки » Счет в пределах 10″
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
+3=9 6+ =8
+1=8 1+ =5
+2=7 0+ =7
+0=10 3+ =9
+1=6 5+ =6
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенную цифру.
— 3 =5 8 — = 1
— 0 =7 4 — = 0
— 3 =2 9 — = 2
— 4 =3 8 — = 3
— 4 =4 9 — = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Вставь пропущенный знак «+» или «-».
8 1 = 7 3 5 = 8
5 3 = 8 4 0 = 4
7 2 = 9 1 9 =10
8 4 = 4 6 6 = 0
1 5 = 6 2 5 = 7
Реши примеры.
4 + 3 – 5 =
10 – 6 + 2 =
2 – 1 + 8 =
10 – 10 + 5 =
8 – 1 + 3 =
Реши примеры.
9 – 3 – 3 =
8 – 3 + 4 =
2 + 4 + 4 =
6 – 5 + 1 =
8 + 2 – 5 =
Реши примеры.
8 – 3 + 5 =
3 + 4 – 2 =
9 + 1 – 6 =
2 + 6 – 3 =
8 – 3 + 4 =
Реши примеры.
10 – 5 – 2 =
7 + 2 – 4 =
10 – 2 – 7 =
1 + 9 – 10 =
6 – 4 – 2 =
Реши примеры.
0 + 6 + 3 =
5 + 1 – 4 =
7 – 5 + 5 =
4 – 3 + 9 =
3 + 6 – 9 =
Реши примеры.
4 + 3 + 2 =
8 – 6 + 4 =
6 + 3 – 7 =
1 + 6 – 4 =
4 + 5 – 7 =
Реши примеры.
9 – 0 + 1 =
5 + 3 – 6 =
4 + 4 – 5 =
8 – 5 + 2 =
10 – 4 – 5 =
Реши примеры.
4 + 3 – 5 =
10 – 6 + 2 =
2 – 1 + 8 =
10 – 10 + 5 =
8 – 1 + 3 =
Реши примеры.
9 – 3 – 3 =
8 – 3 + 4 =
2 + 4 + 4 =
6 – 5 + 1 =
8 + 2 – 5 =
Реши примеры.
8 – 3 + 5 =
3 + 4 – 2 =
9 + 1 – 6 =
2 + 6 – 3 =
8 – 3 + 4 =
Реши примеры.
10 – 5 – 2 =
7 + 2 – 4 =
10 – 2 – 7 =
1 + 9 – 10 =
6 – 4 – 2 =
Реши примеры.
0 + 6 + 3 =
5 + 1 – 4 =
7 – 5 + 5 =
4 – 3 + 9 =
3 + 6 – 9 =
Реши примеры.
4 + 3 + 2 =
8 – 6 + 4 =
6 + 3 – 7 =
1 + 6 – 4 =
4 + 5 – 7 =
Реши примеры.
9 – 0 + 1 =
5 + 3 – 6 =
4 + 4 – 5 =
8 – 5 + 2 =
10 – 4 – 5 =
Реши примеры.
4 + 3 – 5 =
10 – 6 + 2 =
2 – 1 + 8 =
10 – 10 + 5 =
8 – 1 + 3 =
Реши примеры.
9 – 3 – 3 =
8 – 3 + 4 =
2 + 4 + 4 =
6 – 5 + 1 =
8 + 2 – 5 =
Реши примеры.
8 – 3 + 5 =
3 + 4 – 2 =
9 + 1 – 6 =
2 + 6 – 3 =
8 – 3 + 4 =
Реши примеры.
10 – 5 – 2 =
7 + 2 – 4 =
10 – 2 – 7 =
1 + 9 – 10 =
6 – 4 – 2 =
Реши примеры.
0 + 6 + 3 =
5 + 1 – 4 =
7 – 5 + 5 =
4 – 3 + 9 =
3 + 6 – 9 =
Реши примеры.
4 + 3 + 2 =
8 – 6 + 4 =
6 + 3 – 7 =
1 + 6 – 4 =
4 + 5 – 7 =
Реши примеры.
9 – 0 + 1 =
5 + 3 – 6 =
4 + 4 – 5 =
8 – 5 + 2 =
10 – 4 – 5 =
Страница 102 — ГДЗ Математика 1 класс. Моро, Волкова. Учебник часть 2
Вернуться к содержанию учебника
Что узнали, чему научились в 1 классе?
Вопрос
1. Запиши ответы.
| 6 + 2 | 8 + 2 | 4 + 4 | 1 + 7 | 3 + 6 |
| 7 + 2 | 7 + 3 | 5 + 4 | 2 + 8 | 4 + 5 |
| 8 + 2 | 6 + 4 | 6 + 4 | 3 + 7 | 1 + 8 |
Проверь себя по таблице сложения на обороте обложки.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2.
Вспомни, суммой каких двух слагаемых можно заменить каждое из чисел от 2 до 10.
Например: 5 = 4 + 1, 5 = 1 + 4,
5 = 2 + 3, 5 = 3 + 2.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
3. Объясни, какие примеры на вычитание можно составить, используя эти равенства.
| 6 + 2 = 8 | 5 + 2 = 7 |
| 9 + 1 = 10 | 1 + 6 = 7 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
4. Составь и реши по два примера на вычитание числа 6; 7; 8; 5.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
5. Составь и реши по два примера на сложение и вычитание с ответом 5; 8; 7; 6.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6.
Реши примеры в два действия.
| 9 — 3 + 2 | 6 + 4 — 7 | 10 — 8 + 7 |
| 8 — 5 + 4 | 7 + 2 — 6 | 10 — 6 + 5 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
7.
| 8 + 2 + 3 | 16 — 6 — 3 | 7 + 3 + 5 |
| 9 + 1 + 3 | 12 — 2 — 4 | 6 + 4 + 5 |
Сколько всего прибавили к числу или вычли из числа в каждом примере?
Подсказка
В нашем справочнике повтори состав чисел от 1 до 10.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
8. Дополни до 10 каждое число: 7, 6, 8, 9.
Подсказка
В нашем справочнике повтори состав числа 10.
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
© budu5.
com, 2021
Пользовательское соглашение
Copyright
Конспект открытого урока математики «Число 10. Решение примеров в пределах 10» 1 класс
Конспект открытого урока математики
«Число 10. Решение примеров в пределах 10» 1 класс
Цель:
закрепление умения детей числа 10, учить решать примеры на сложение и вычитание в пределах 10.
Задачи урока:
• Закрепить знания письменного сложения и вычитания в пределах 10;
• Развитие психических процессов: внимания, памяти, мышления, эмоционально-волевой сферы;
• Воспитание аккуратности, доброжелательности, взаимопомощи, вежливости.
Оборудование:
1. тетрадь,
2. линейка,
3. карандаш,
4. ручка,
5. карточки с изображением сказочных персонажей с заданиями.
6. мультимедийная система.
Ход урока.
1. Организационный момент.
Здравствуйте, ребята, гости!
Ребята, посмотрите, что у меня в руках? Круг, квадрат, прямоугольник, треугольник.
Правильно. А как они вместе называются? Геометрические фигуры.
У вас на столах лежат предметные картинки по форме похожие на геометрические фигуры. Сейчас сядет тот, чья предметная картинка, напоминает форму круга, треугольника, квадрата.
С каким числом мы познакомились на прошлых уроках? Мы познакомились с числом 10.
Тема нашего урока: «Число 10.
Решение примеров на сложение и вычитание в пределах 10».
Ребята к нам в гости пришла гостья, а кто это отгадайте из загадки:
Прыгает зверюшка
Не рот, а ловушка.
Попадут в ловушку
И комар, и мушка. Лягушка
Правильно, а в каких еще сказках встречается персонаж лягушка?
Верно.
А поможет нам на уроке сказка «Царевна-лягушка».
Давайте посмотрим на экран, кого мы видим? Давайте посчитаем, сколько цыплят изображено на экране?
А сейчас посмотрим на экран, правильно ли мы посчитали?
А теперь вспомним, как пишется число 10.
А теперь открываем тетради. От сегодняшнего числа отступаем вниз 2 клеточки, пропишем одну строчку числа 10.
2. Устный счет.
А теперь сказка. У царя было три сына. И велел царь сыновьям, пока совсем не состарился, жениться. Вывел он их в чисто поле и велел пустить стрелы, куда упадет стрела, значит там их и судьба. Но стрелы, ребята, не простые, а с заданиями. Чтобы стрелы долетели до места, поможем сыновьям царя выполнить задания?
Задания: Посмотрите у меня в руках картинка, что на ней изображено? Какая это птица? Посчитайте и покажите мне цифрой. Как вы думаете, грачи уже прилетели?
А это, что за птицы? Посчитайте и покажите цифрой, сколько изображено скворцов. Скоро на уроках мы будем знакомиться с этими птицами.
Молодцы, ребята. Стрелы долетели до места: одна – до барского дома. Другая – до купеческого. А третья – на болото к лягушке.
А мы попадем с вами на весеннюю полянку. Смотрите глазками на движущие предметы. (Электроннаяфизминутка для глаз).
3. Арифметический диктант.
Царь женил сыновей, дал задание невесткам – испечь хлеб.
Ребята, поможем испечь хлеб Царевне-лягушке. Для этого нужно выполнить игровые задания. Я буду называть числовой ряд и пропускать числа, а вы должны показать, что я пропустила:
4 … 6, 7, 8
6 … 8, 9, 10
10, 9, 8, 7 … 5
назовите предыдущее 10, последующее 9,
назовите соседей числа 9.
Молодцы! Вы помогли испечь хлеб Царевне.
Царю понравилось.
4.Физминутка
Под пение весенних птиц, изображаем полет птиц (релаксация)
5. Изучение нового материала.
Следующим заданием царя было – соткать ковер. Чтобы он получился красивым, мы должны его украсить. Для этого нужно решить пример, найти ответ с рисунком. И пример на ковре заменить узором.
Сильный уровень:
6+4
10-5
8+2
Средний уровень
7+2
6 -6
8 -3
Молодцы, ребята, справились с заданием, помогли Царевне. Царю очень понравился ковер.
Царь пригласил всех на бал. Мы тоже с вами давайте отдохнем.
6. Физминутка.
Как живешь?
Как бежишь?
Вдаль глядишь?
Ждешь обед?
Машешь вслед?
Ночью спишь?
А шалишь?
7. Закрепление изученного материала.
Понравилась Василиса Ивану-Царевичу, взял он и сжег её шкурку. Улетела голубкой Василиса и велела искать её (у кого?). У Кощея Бессмертного.
Пошел Иван искать Василису.
Шел, шел и увидел избушку на курьих ножках, а в ней Баба-Яга сидит и говорит:
-Если решишь мою задачу, дам тебе за это клубок, который покажет тебе дорогу. Поможем Ивану решить задачу?
У пенечков 7 грибочков
И под елкой 3
Ребята, подумайте и выложите на партах в кассах решение этой задачи.
Сколько будет всех грибочков,
Ну-ка, посмотри?
Сколько грибочков всего? Как вы узнали?
Молодцы, справились с заданием. Отдала Баба-Яга клубок Ивану- Царевичу и он пошел спасать Василису.
А мы с вами пойдем по другой дорожке. Посмотрите, что начерчено на доске. Как называется эта линия? Прямая линия.
Отступите вниз две клетки, начертите прямую линию.
Молодцы! С заданием справились.
И прямая дорожка привела нас к дубу, где находится смерть Кощея.
Ребята, давайте снимем сундук.
А для этого нужно выполнить неравенство:
Слабый уровень
8…10
Поймали зайца. Теперь поймаем утку:
9…2
А из утки выкатилось яйцо. Давайте его разобьем:
5…5
Разбилось яйцо, достали мы иголку. Давайте сломаем её:
10…0
Молодцы, ребята. Вы помогли Ивану спасти Василису. Она вам очень благодарна, что вы ее спасли. Были активными, смелыми, дружными.
8. Итог урока.
Чем мы сегодня занимались на уроке?
Что вам понравилось?
Какие задания вызывали у вас трудности?
Задания по математике. 3 класс
Задания для домашних работ для 3 класса (3 четверть)
1. Реши примеры.
а) 5 * 6 + 64 : 8 = | б) 18 : 9 + 37 * 2= | в) 31 * 3 — 56 : 8 = | г) 70 — 51 : 3 * 4 = |
д) 9 * 4 — 28 : 7 = | е) 7 * 16 — 80 : 8 = | ж) 11 * 5 — 49 : 7 = | з) 68 — 19 + 30 : 2 = |
2. Реши задачу.
В ящик помещается 12 пачек печенья. Сколько всего пачек печенья помещается в 5 ящиков?
3. Реши задачу.
В книжный магазин привезли 88 учебников, которые упакованы в коробки. Сколько коробок с книгами привезли, если в каждой коробке находится 11 учебников?
4. Реши примеры.
а) 17 * 0= | б) 12 : 1= |
в) 24 * 1 = | г) 21 : 1 = |
д) 0 * 32 = | е) 0 : 15 = |
5. Реши задачу.
В пекарне из 15 кг муки испекли 45 тортов. Сколько килограмм муки необходимо, чтобы испечь 60 тортов?
6. Реши задачу.
На складе находилось 45 кг сахара. Дополнительно привезли 4 мешка по 8 кг сахара в каждом, а затем со склада увезли 10 кг сахара. Сколько килограмм сахара осталось на складе?
7. Реши примеры и проверь операцию деления умножением.
а) 48 : 6 = | б) 12 : 4= |
в) 24 : 8 = | г) 21 : 7 = |
д) 15 : 3 = | е) 0 : 15 = |
8. Реши уравнения.
а) X * 18 = 72 | б) 90 : Y = 30 | в) 21 : X = 3 | г) Y * 6 = 42 |
9. Реши ЗАДАНИЯ по геометрии.
a) Начерти c помощью линейки 3 отрезка. Длина первого отрезка равна 5 см, второй отрезок на 3 см длиннее первого, а третий отрезок в 2 раза короче второго.
б) Найди и выпиши все прямые, тупые и острые углы у фигур, изображённых на рисунке.
в) Найди периметр и площадь прямоугольника, изображённого на рисунке.
10. Реши примеры.
а) 17 * 3 = | б) 52 : 4 = |
в) 19 * 4 = | г) 48 : 2 = |
д) 12 * 5 = | е) 69 : 3 = |
ж) 22 * 3 = | з) 17 * 4 = |
к) 13 * 5 = | л) 75 : 5 = |
м) 96 : 4 = | н) 69 : 3 = |
11. Реши задачу.
Школьная бригада собрала в саду 36 кг яблок и 20 кг груш. Весь урожай разложили в ящики по 4 кг. Сколько ящиков понадобилось?
Задания для домашней работы для 3 класса (4 четверть)
1. Реши примеры.
а) 210 * 4 = | б) 840 : 4 = |
в) 6 * 120 = | г) 660 : 3 = |
д) 220 * 4 = | е) 490 : 7 = |
ж) 190 * 3 = | з) 360 : 6 = |
к) 3 * 280 = | л) 140 : 2 = |
м) 110 * 7 = | н) 640 : 4 = |
2. Реши примеры.
а) 970 — 50 = | б) 320 + 50 = |
в) 520 — 10 = | г) 630 + 90 = |
д) 320 — 30 = | е) 230 + 90 = |
ж) 220 — 20 = | з) 590 + 50 = |
3.
Реши задачу.
Для ремонта школы привезли 160 мешков цемента и 440 мешков песка. Сколько мешков строительного материала потребовалось для ремонта, если после ремонта осталось 250 мешков?
4. Реши задачу.
Фермер вырастил 230 ц картофеля и 140 ц капусты. 360 ц овощей отправили в школьную столовую. Сколько центнеров овощей осталось у фермера?
5. Реши уравнения.
а) 7 * х = 490
б) у : 9 = 70
в) a — 560 = 120
г) b + 380 = 960
6. Реши задачу.
На автостоянке стояло 84 легковых и несколько грузовых машин, которых было на 63 машины меньше, чем легковых. Во сколько раз грузовых машин меньше, чем легковых стояло на автостоянке?
7. Реши примеры столбиком.
а) 984 — 159 = | б) 523 + 369 = |
в) 523 — 459 = | г) 374 + 579 = |
д) 319 — 198 = | е) 130 + 379 = |
8. Реши примеры.
а) 24 * 8 + 336 : 6 + 88 =
б) 16 * 9 + 342 : 2 — 146 =
9. Реши задачу.
На продуктовом складе находилось 64 мешка с сахаром и несколько мешков с мукой, которых было на 56 штук меньше, чем мешков с сахаром. Во сколько раз мешков с мукой меньше, чем мешков с сахаром находилось на складе?
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/363108-zadanija-po-matematike-3-klass
Задач со словами — Полный курс алгебры
10
Примеры
Проблемы
ЗАДАЧИ СО СЛОВАМИ требует практики в переводе словесного языка на алгебраический язык. См. Урок 1, Задача 8. Тем не менее, проблемы со словами делятся на разные типы. Ниже приведены некоторые примеры.
Пример 1. ax ± b = c . Все проблемы, подобные следующей, в конечном итоге приводят к уравнению в такой простой форме.
Джейн потратила 42 доллара на обувь. Это было на 14 долларов меньше, чем вдвое, чем она потратила на блузку.
Сколько была кофточка?
Решение. У каждой проблемы со словом неизвестный номер. В этой проблеме цена кофточки. Всегда позволяйте x представлять неизвестное число. То есть пусть на вопрос ответит x .
Пусть тогда x будет, сколько она потратила на блузку. В задаче указано, что «Это», то есть 42 доллара, было на 14 долларов меньше, чем двукратное значение x .
Вот уравнение:
| 2 x — 14 | = | 42. |
| 2 x | = | 42 + 14 (Урок 9) |
| = | 56. | |
| x | = | 56 2 |
| = | 28. | |
Блузка стоила 28 долларов.
Пример 2. Всего в классе б мальчиков. Это в три раза больше, чем в четыре раза девушек. Сколько девочек в классе?
Решение. Опять же, пусть x представляет неизвестное число, которое вас просят найти: Пусть x будет количеством девушек.
(Хотя b неизвестно — это произвольная константа — это не то, что вас просят найти.)
В задаче указано, что «Это» — b — в три раза больше, чем в четыре раза x :
| 4 x + 3 | = | б . | ||
| Следовательно, | ||||
| 4 x | = | б — 3 | ||
| x | = | б — 3 4 | . | |
Решение здесь не число, потому что оно будет зависеть от значения b .
Это тип «буквального» уравнения, очень распространенного в алгебре.
Пример 3. Целое равно сумме частей.
Сумма двух чисел равна 84, и одно из них на 12 больше, чем другое. Какие два числа?
Решение. В этой задаче нам предлагается найти два числа.Следовательно, мы должны позволить x быть одним из них. Тогда пусть x будет первым числом.
Нам говорят, что другое число — еще 12, x + 12.
В задаче указано, что их сумма равна 84:
= 84
Линия над x + 12 представляет собой символ группировки, называемый vinculum . Это избавляет нас от написания скобок.
У нас:
| 2 x | = | 84–12 |
| = | 72. | |
| x | = | 72 2 |
| = | 36. | |
Это первое число. Следовательно, другой номер —
.x + 12 = 36 + 12 = 48.
Сумма 36 + 48 дает 84.
Пример 4.Сумма двух последовательных чисел составляет 37. Какие они?
Решение . Два последовательных числа равны 8 и 9 или 51 и 52.
Пусть тогда x будет первым числом. Тогда число после него будет x + 1.
.В задаче указано, что их сумма равна 37:
= 37
| 2 x | = | 37 — 1 |
| = | 36. | |
| x | = | 36 2 |
| = | 18. | |
Два числа — 18 и 19.
Пример 5. Одно число на 10 больше другого. Сумма, состоящая из удвоенного меньшего и трехкратного большего, равна 55.Какие два числа?
Решение. Пусть x будет меньшим числом.
Тогда большее число на 10 больше: x + 10.
Состояние проблемы:
| 2 x + 3 ( x + 10) | = | 55. |
| Это означает | ||
| 2 x + 3 x + 30 | = | 55.Урок 14. | .
| 5 x | = | 55 — 30 = 25. |
| x | = | 5. |
Это меньшее число. Чем больше число, тем больше на 10: 15.
Пример 6. Разделите 80 долларов между тремя людьми так, чтобы у второго было вдвое больше, чем у первого, а у третьего было на 5 долларов меньше, чем у второго.
Решение . Опять же, нас просят найти более одного числа. Мы должны начать с того, что допустим, что x будет тем, сколько получает первый человек.
Затем второй получает вдвое больше, 2 x .
А третий получает на 5 долларов меньше, 2 x — 5.
Их сумма 80 $:
| 5 x | = | 80 + 5 |
| x | = | 85 5 |
| = | 17. | |
Вот сколько получает первый человек. Следовательно, второй получает
| 2 x | = | 34. |
| А третий получает | ||
| 2 x -5 | = | 29. |
Сумма 17, 34 и 29 фактически равна 80.
Пример 7.Нечетные числа. Сумма двух подряд идущих нечетных чисел равна 52. Какие два нечетных числа?
Решение . Во-первых, четное число кратно 2: 2, 4, 6, 8 и так далее. В алгебре принято представлять четное число как 2 n , где при вызове переменной « n » подразумевается, что n будет принимать целочисленные значения: n = 0, 1, 2 , 3, 4 и т. Д.
Нечетное число на 1 больше (или на 1 меньше) четного.Итак, представим нечетное число как 2 n + 1.
Пусть 2 n + 1 будет первым нечетным числом. Далее будет еще 2 — это будет 2 n + 3. Задача утверждает, что их сумма 52:
| 2 n + 1 + 2 n + 3 | = | 52. |
Теперь мы решим это уравнение для n , а затем заменим решение в 2 n + 1, чтобы найти первое нечетное число.У нас:
| 4 n + 4 | = | 52 |
| 4 n | = | 48 |
| n | = | 12. |
Следовательно, первое нечетное число 2 · 12 + 1 = 25.Итак, следующее 27. Их сумма 52.
Проблемы
Задача 1. У Джули 50 долларов, что на восемь долларов больше, чем у Джона. Сколько у Джона? (Сравните Пример 1.)
Во-первых, что вы позволите представить в формате x ?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
Неизвестный номер — сколько у Джона.
Что такое уравнение?
2 x + 8 = 50.
Вот решение:
x = 21
долларов СШАПроблема 2. Карлотта потратила на рынке 35 долларов. Это было на семь долларов меньше, чем в три раза больше, чем она потратила в книжном магазине; сколько она там потратила?
Вот уравнение.
3 x — 7 = 35
Вот решение:
x = 14
долларов СШАПроблема 3.Есть b черный мрамор. Это на четыре больше, чем в два раза больше красных шариков. Сколько там красных шариков? (Сравните Пример 2.)
Вот уравнение.
2 x + 4 = b
Вот решение:
Проблема 4. Джанет потратила 100 долларов на книги. Это было на тыс. долларов меньше, чем в пять раз больше, чем она потратила на обед.Сколько она потратила на обед?
Вот уравнение.
5 x — к = 100
Вот решение:
Задача 5. Целое равно сумме частей.
Сумма двух чисел равна 99, и одно из них на 17 больше другого. Какие два числа? (Сравните Пример 3.)
Вот уравнение.
Вот решение:
Задача 6. Класс из 50 учеников делится на две группы; в одной группе на восемь меньше, чем в другой; сколько в каждой группе?
Вот уравнение.
Вот решение:
Проблема 7.Сумма двух чисел равна 72, и одно из них в пять раз больше другого; какие два числа?
Вот уравнение.
x + 5 x = 72.
Вот решение:
x = 12. 5 x = 60.
Задача 8. Сумма трех последовательных чисел 87; кто они такие? (Сравните Пример 4.)
Вот уравнение.
Вот решение:
28, 29, 30.
Задача 9. Группа из 266 человек состоит из мужчин, женщин и детей. Мужчин в четыре раза больше, чем детей, а женщин в два раза больше, чем детей. Сколько их там?
(Чему вы положите x — количеству мужчин, женщин или детей?)
| Пусть x | = | Количество детей.Тогда |
| 4 x | = | Количество мужчин. И |
| 2 x | = | Количество женщин. |
| Вот уравнение: | ||
x + 4 x + 2 x = 266
Вот решение:
х = 38.4 x = 152. 2 x = 76.
Задача 10. Разделите 79 долларов между тремя людьми так, чтобы у второго было в три раза больше, чем у первого, а у третьего было на два доллара больше, чем у второго. (Сравните Пример 6.)
Вот уравнение.
Вот решение:
11, 33, 35 долларов.
Задача 11. Разделите 15,20 доллара между тремя людьми так, чтобы у второго было на доллар больше, чем у первого, а у третьего — на 2,70 доллара больше, чем у второго.
Вот уравнение.
Вот решение:
3,50 доллара США, 4,50 доллара США, 7,20 доллара США.
Задача 12. Два последовательных нечетных числа таковы, что три раза первое будет на 5 больше, чем в два раза больше второго.Что это за два нечетных числа?
(см. Пример 7, где мы представляем нечетное число как 2 n + 1.)
Решение . Пусть первое нечетное число будет 2 n + 1.
Тогда следующий 2 n + 3 — потому что будет еще 2.
Задача состоит в следующем:
| 3 (2 n + 1) | = | 2 (2 n + 3) + 5. | |
| Это означает: | |||
| 6 n + 3 | = | 4 n + 6 + 5. | |
| 2 n | = | 8. | |
| n | = | 4. | |
Следовательно, первое нечетное число — 2 · 4 + 1 = 9. Следующее — 11.
И это верное решение, потому что в соответствии с проблемой:
3 · 9 = 2 · 11 + 5.
Следующий урок: Неравенство
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Как найти решение Набор
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как как ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Решение вопросов Word
МНОГО примеров!
В алгебре мы часто задаем словесные вопросы, например:
Пример: Сэм и Алекс играют в теннис.
В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр.
Сколько игр сыграл Алекс?
Как мы их решаем?
Уловка состоит в том, чтобы разбить решение на две части:
Превратите английский в алгебру.
Затем решите с помощью алгебры.
Превращение английского в алгебру
Превратить английский в алгебру помогает:
- Прочтите сначала все
- Сделайте эскиз , если возможно
- Присвойте букву значениям
- Найдите или разработайте формулы
Вам также следует записать , что на самом деле запрашивается для , чтобы вы знали, куда вы собираетесь и когда приедете!
Также ищите ключевые слова:
| Когда вы видите | Думаю | |
|---|---|---|
сложить, итого, сумма, увеличить, больше, вместе, вместе, плюс, более | + | |
минус, меньше, разница, меньше, уменьшилась, уменьшилась | – | |
умноженное, умноженное на произведение, множитель | × | |
разделенное, частное, на, из, соотношение, соотношение, процент, ставка | ÷ | |
| увеличить или уменьшить | геометрия формулы | |
| Скорость, скорость | расстояние формулы | |
| Сколько дней, часов, минут, секунд | время |
Ясное мышление
Некоторые формулировки могут быть сложными, из-за чего трудно думать «правильно», например:
$
Пример: У Сэма на 2 доллара меньше, чем у Алекса.Как это записать в виде уравнения?
- Пусть S = долларов, у Сэма
- Пусть A = долларов у Алекса
Теперь … вот что: S — 2 = A
или должно быть: S = A — 2
или должно быть: S = 2 — A
Правильный ответ: S = A — 2
( S — 2 = A — распространенная ошибка, так как в вопросе написано «Сэм … на 2 меньше … Алекс»)
Пример: на нашей улице собак вдвое больше, чем кошек.Как это записать в виде уравнения?
- Пусть D = количество собак
- Пусть C = количество кошек
Теперь … это то, что: 2D = C
или должно быть: D = 2C
Подумайте внимательно!
Правильный ответ: D = 2C
( 2D = C — распространенная ошибка, так как в вопросе написано «дважды … собаки … кошки»)
Примеры
Давайте начнем с очень простого примера , чтобы увидеть, как это делается:
Пример: прямоугольный сад размером 12 м на 5 м, какова его площадь?
Превратите английский в алгебру:
Эскиз:
.Письма:
- Используйте w для ширины прямоугольника: w = 12 м
- Используйте h для высоты прямоугольника: h = 5 м
Формула для площади прямоугольника: A = w × h
Нас спрашивают о Районе.
Решить:
A = ш × в = 12 × 5 = 60 м 2
Площадь 60 кв.м .
Теперь попробуем пример сверху страницы:
Пример: Сэм и Алекс играют в теннис. В выходные Сэм сыграл на 4 игры больше, чем Алекс, а вместе они сыграли 12 игр. Сколько игр сыграл Алекс?
Превратите английский в алгебру:
Письма:
- Используйте S , чтобы узнать, сколько игр Сэм сыграл
- Используйте A , чтобы узнать, сколько игр сыграл Алекс.
Мы знаем, что Сэм сыграл на 4 игры больше, чем Алекс, поэтому: S = A + 4
И мы знаем, что вместе они сыграли 12 игр: S + A = 12
Нас спрашивают, сколько игр сыграл Алекс: A
Решить:
Начать с: S + A = 12
S = A + 4 , поэтому мы можем
заменить S на «A + 4»: (A + 4) + A = 12
Упростить: 2A + 4 = 12
Вычтем 4 с обеих сторон: 2A = 12 — 4
Упростить: 2A = 8
Разделите обе части на 2: A = 4
Это означает, что Алекс сыграл 4 игры в теннис.
Проверка: Сэм сыграл на 4 игры больше, чем Алекс, поэтому Сэм сыграл 8 игр. Вместе они сыграли 8 + 4 = 12 игр. Да!
Немного более сложный пример:
Пример: Алекс и Сэм также создают таблицы.
Вместе они делают 10 столов за 12 дней.
Алекс, работая в одиночку, может заработать 10 за 30 дней.
Сколько времени потребуется Сэму, работая в одиночку, чтобы сделать 10 столов?
Превратите английский в алгебру:
Письма:
- Используйте a для скорости работы Алекса
- Используйте с для скорости работы Сэма
12 дней Алекса и Сэма — это 10 столов, поэтому: 12a + 12s = 10
30 дней одного Алекса — это тоже 10 столов: 30a = 10
Нас спрашивают, сколько времени потребуется Сэму, чтобы сделать 10 столов.
Решить:
30a = 10 , поэтому ставка Алекса (столов в день) составляет: a = 10/30 = 1/3
Начать с: 12a + 12s = 10
Положите «1/3» для a: 12 (1/3) + 12s = 10
.Упростить: 4 + 12s = 10
Вычтем 4 с обеих сторон: 12s = 6
Разделите обе стороны на 12: s = 6/12
Упростить: с = 1/2
Это означает, что ставка Сэма — половина стола в день (быстрее, чем у Алекса!)
Итак, 10 столов займет у Сэма всего 20 дней.
Интересно, стоит ли Сэму платить больше?
И еще пример «подстановки»:
Пример: Дженна усиленно тренируется, чтобы пройти квалификацию к Национальным играм.
У нее обычный еженедельный распорядок дня: в одни дни тренируется по пять часов в день, а в другие — по 3 часа в день.
В общей сложности она тренируется 27 часов в семидневную неделю. Сколько дней она тренируется по пять часов?
Письма:
- Количество «5 часовых» дней: d
- Количество «3-х часовых» дней: e
Мы знаем, что в неделе семь дней, поэтому: d + e = 7
И она тренируется 27 часов в неделю, из которых d 5 часов в день и e 3 часа в день: 5d + 3e = 27
Нас спрашивают, сколько дней она тренируется по 5 часов: d
Решить:
d + e = 7
Итак: e = 7 — d
Положим в 5d + 3e = 27 5d + 3 (7 − d) = 27
Упростить: 5d + 21 — 3d = 27
Вычтем 21 с обеих сторон: 5d — 3d = 6
Упростить: 2d = 6
Разделим обе части на 2: d = 3
Количество «5 часовых» дней — 3
Проверка : Она тренируется по 5 часов 3 дня в неделю, поэтому она должна тренироваться по 3 часа в день в остальные 4 дня недели.
3 × 5 часов = 15 часов, плюс 4 × 3 часа = 12 часов дает в сумме 27 часов
Некоторые примеры из Geometry:
Пример: круг имеет площадь 12 мм
2 , каков его радиус?Письма:
- Используйте A для площади: A = 12 мм 2
- Используйте r для радиуса
И формула для площади: A = π r 2
У нас спрашивают радиус.
Решить:
Нам нужно переставить формулу, чтобы найти площадь
Начать с: A = π r 2
Поменять местами стороны: π r 2 = A
Разделим обе части на π : r 2 = A / π
Извлечь квадратный корень из обеих частей: r = √ (A / π)
Теперь мы можем использовать формулу: r = √ (12/ π)
И получаем: r = 1.954 (до 3-х мест)
Пример: куб имеет объем 125 мм
3 , какова его площадь поверхности?Сделайте быстрый набросок:
Письма:
- Используйте V для объема
- Используйте A для Area
- Используйте s для длины стороны куба
Формулы:
- Объем куба: В = с 3
- Площадь куба: A = 6s 2
У нас спрашивают площадь.
Решить:
Первая тренировка с по формуле объема:
Начать с: В = с 3
Поменять местами стороны: с 3 = V
Извлечь кубический корень с обеих сторон: s = ∛ (V )
И получаем: s = ∛ (125 ) = 5
Теперь мы можем рассчитать площадь поверхности:
Начать с: A = 6s 2
И получаем: A = 6 (5) 2
A = 6 × 25 = 150 мм 2
Пример о деньгах:
Пример: Джоэл работает в местной пиццерии.Когда он работает сверхурочно, он зарабатывает в 1¼ раза больше обычного.
Одну неделю Джоэл проработал 40 часов по обычной ставке, а также 12 часов сверхурочно. Если Джоэл заработал за эту неделю 660 долларов, какова его нормальная ставка заработной платы?
Письма:
- Обычная ставка оплаты труда Джоэла: N $ в час
Формулы:
- Джоэл работает 40 часов по цене N долларов в час = 40 долларов N
- Когда Джоэл работает сверхурочно, он зарабатывает в 1¼ раза больше обычной ставки = 1 доллар.25N в час
- Джоэл работает 12 часов по цене 1,25 доллара США в час = (12 × 1 доллар США) = 15 долларов США доллара США
- А вместе он заработал 660 долларов, итак:
$ 40N + $ (12 × 1¼N) = 660 $
У нас спрашивают нормальную ставку зарплаты Джоэла в $ N.
Решить:
Начните с $ 40N + $ (12 × 1¼N) = 660 $
Упростить: 40N + 15N = 660 USD
Еще более упростите: 55 долларов США = 660 долларов США
Разделите обе стороны на 55: $ N = 12 $
Итак, обычная ставка оплаты труда Джоэла составляет 12 долларов в час.
Чек
Обычная ставка оплаты труда Джоэла составляет 12 долларов в час, поэтому его сверхурочная работа составляет 1¼ × 12 долларов в час = 15 долларов в час.Таким образом, его обычная заработная плата 40 × 12 = 480 долларов плюс его сверхурочная работа в размере 12 × 15 долларов = 180 долларов дает нам в общей сложности 660 долларов
.Подробнее о деньгах на этих двух примерах, связанных со сложным процентом
Пример: Алекс вкладывает 2000 долларов в банк под 11% годовых. Сколько это будет стоить через 3 года?
Это формула сложных процентов:
Итак, мы будем использовать эти буквы:
- Текущая стоимость PV = 2000 долларов США
- Процентная ставка (в десятичном формате): r = 0.11
- Количество периодов: n = 3
- Future Value (значение, которое мы хотим): FV
Нас спрашивают о будущей стоимости: FV
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: FV = $ 2000 × (1 + 0,11) 3
Вычислить: FV = $ 2000 × 1,367631
Вычислим: FV = 2735 долларов.26 (с точностью до цента)
Пример: Роджер положил 1000 долларов на сберегательный счет. На заработанные деньги ежегодно начислялись проценты по той же ставке. Через девять лет депозит Роджера вырос до 1 551,33 доллара США
Какова была годовая процентная ставка по сберегательному счету?
Формула сложных процентов:
с:
- Текущая стоимость PV = 1000 долларов США
- Процентная ставка (желаемое значение): р.
- Количество периодов: n = 9
- Будущая стоимость: FV = 1551 доллар.33
Нас спрашивают о процентной ставке: r
Решить:
Начать с: FV = PV × (1 + r) n
Добавьте то, что мы знаем: 1551,33 доллара = 1000 долларов × (1 + r) 9
Поменять стороны: 1000 $ × (1 + r) 9 = 1551,33 $
Разделите обе стороны на 1000: (1 + r) 9 = 1551,33 доллара США / 1000 долларов США
Упростить: (1 + r) 9 = 1.55133
Корень 9-й степени: 1 + r = 1,55133 (1/9)
Вычислить: 1 + r = 1.05
Вычислить: r = 0,05 = 5%
Таким образом, годовая процентная ставка составляет 5%
Чек : 1000 долларов × (1,05) 9 = 1000 долларов × 1,55133 = 1551,33 доллара
И пример вопроса о соотношении:
Пример: В начале года соотношение мальчиков и девочек в классе составляет 2: 1
Но теперь, полгода спустя, четыре мальчика покинули класс и появились две новые девочки.Соотношение мальчиков и девочек сейчас составляет 4: 3
Сколько всего студентов сейчас?
Письма:
- Кол-во мальчиков сейчас: б
- Количество девочек сейчас: г
Коэффициент текущей ликвидности 4: 3
b г = 4 3
который можно переставить на 3b = 4g
На начало года насчитывалось (b + 4) мальчиков и (g — 2) девочек, и соотношение составляло 2: 1
b + 4 г — 2 = 2 1
, который можно переставить на b + 4 = 2 (g — 2)
Нас спрашивают, сколько всего сейчас студентов: b + g
Решить:
Начать с: b + 4 = 2 (г — 2)
Упростить: b + 4 = 2g — 4
Вычтем 4 с обеих сторон: b = 2g — 8
Умножаем обе стороны на 3 (получаем 3b): 3b = 6g — 24
Помните 3b = 4g : 4g = 6g — 24
Вычтем 6g с обеих сторон : −2g = -24
Разделим обе части на −2: г = 12
Есть 12 девушек !
И 3b = 4g , поэтому b = 4g / 3 = 4 × 12/3 = 16 , так что есть 16 мальчиков
Итак, сейчас в классе 12 девочек и 16 мальчиков, всего человек. 28 учеников — человека.
Чек
Сейчас 16 мальчиков и 12 девочек, поэтому соотношение мальчиков и девочек составляет 16: 12 = 4: 3
В начале года было 20 мальчиков и 10 девочек, поэтому соотношение было 20: 10 = 2: 1
А теперь несколько квадратных уравнений:
Пример: произведение двух последовательных четных целых чисел равно 168. Что такое целые числа?
Последовательный означает один за другим. И это , даже , так что они могут быть 2 и 4, или 4 и 6 и т. Д.
Мы назовем меньшее целое число n , поэтому большее целое число должно быть n + 2
И нам говорят, что произведение (то, что мы получаем после умножения) равно 168, поэтому мы знаем:
п (п + 2) = 168
Нас спрашивают целые числа
Решить:
Начать с: n (n + 2) = 168
Развернуть: n 2 + 2n = 168
Вычтем 168 с обеих сторон: n 2 + 2n — 168 = 0
Это квадратное уравнение, и есть много способов его решить.Используя метод решения квадратного уравнения, мы получаем −14 и 12.
Проверка −14: −14 (−14 + 2) = (−14) × (−12) = 168 ДА
Проверка 12: 12 (12 + 2) = 12 × 14 = 168 ДА
Итак, есть два решения: -14 и -12 — одно, 12 и 14 — другое.
Примечание: мы также могли попробовать «угадать и проверить»:
- Мы могли бы попробовать, скажем, n = 10: 10 (12) = 120 NO (слишком мало)
- Затем мы могли бы попробовать n = 12: 12 (14) = 168 ДА
Но если мы не вспомним, что умножение двух отрицаний дает положительный результат, мы можем пропустить другое решение (−14) × (−12).
А:
Пример: вы архитектор. Вашему клиенту нужна комната вдвое больше ширины. Им также нужна веранда шириной 3 метра по длинной стороне.
У вашего клиента 56 квадратных метров красивой мраморной плитки для покрытия всей площади.
Какой должна быть длина комнаты?
Давайте сначала сделаем набросок, чтобы все было правильно !:
Письма:
- Длина помещения: L
- ширина помещения: Вт
- Общая площадь с верандой: А,
Мы знаем:
- ширина комнаты равна половине ее длины: W = ½L
- общая площадь равна (ширина комнаты + 3), умноженная на длину: A = (W + 3) × L = 56
Нас спрашивают о длине комнаты: L
Решить:
Начать с: (Ш + 3) × Д = 56
Заменитель W = ½L : (½L + 3) × L = 56
Упростить: ½L 2 + 3L = 56
Умножьте все члены на 2: L 2 + 6L = 112
Вычесть 112 с обеих сторон : L 2 + 6L — 112 = 0
Это квадратное уравнение , есть много способов его решить, на этот раз воспользуемся факторизацией:
Начать с: L 2 + 6L — 112 = 0
Два числа, которые умножаются, чтобы получить ac = -112,
и
сложить, чтобы получить b = 6, получится 14 и −8: L 2 + 14L — 8L — 112 = 0
Группа: L (L +14) — 8 (L + 14) = 0
Группа: (L — 8) (L + 14) = 0
Итак, L = 8 или -14
Есть два решения квадратного уравнения, но только одно из них возможно, так как длина комнаты не может быть отрицательной!
Итак, длина помещения 8 м
Чек
L = 8, поэтому W = ½L = 4
Итак, площадь прямоугольника = (W + 3) × L = 7 × 8 = 56
Вот и мы…
… Я надеюсь, что эти примеры помогут вам понять, как отвечать на словесные вопросы. А как насчет практики?
Графический метод решения линейных уравнений с двумя переменными
Графический метод решения линейных уравнений с двумя переменными Пусть система пары линейных уравнений имеет вид
a 1 x + b 1 y = c 1 …. (1)
a 2 x + b 2 y = c 2 ….(2)
Мы знаем, что при наличии двух прямых на плоскости возможна только одна из следующих трех возможностей —
(i) Две прямые пересекаются в одной точке.
(ii) Две прямые не будут пересекаться, как бы далеко они ни были вытянуты, т. Е. Параллельны.
(iii) Две линии совпадают.
Типы решений:
Есть три типа решений
- Уникальное решение.
- Бесконечное множество решений
- Нет решения.
Подробнее:
(A) Согласованный: Если система одновременных линейных уравнений имеет хотя бы одно решение, то система называется согласованной.
(i) Согласованные уравнения с единственным решением: Графики двух уравнений пересекаются в единственной точке.
Для примера Рассмотрим
x + 2y = 4
7x + 4y = 18
Графики (линии) этих уравнений пересекаются друг с другом в точке (2, 1), т.е. x = 2, y = 1.
Следовательно, уравнения согласуются с единственным решением.
(ii) Согласованные уравнения с бесконечным числом решений: Графики (линии) двух уравнений будут совпадать.
Для примера Рассмотрим 2x + 4y = 9 ⇒ 3x + 6y = 27/2
Графики приведенных выше уравнений совпадают. Координаты каждой точки на прямых являются решениями уравнений. Следовательно, данные уравнения согласованы с бесконечным множеством решений.
(B) Несогласованное уравнение: Если система одновременных линейных уравнений не имеет решения, то система называется несовместимой.
Нет Решение: График (линии) двух уравнений параллельны.
Для примера Рассмотрим
4x + 2y = 10
6x + 3y = 6
Графики (линии) данных уравнений параллельны. Они никогда не встретятся в какой-то момент. Итак, решения нет. Следовательно, уравнения несовместимы.
Из приведенной выше таблицы видно, что если строка a 1 x + b 1 y + c 1 = 0 и a 2 x + b 2 y + c 2 = 0 — это
Примеры графических методов
Пример 1: Путь шоссе номер 1 задается уравнением x + y = 7, а номер шоссе 2 задается уравнением 5х + 2у = 20.Представьте эти уравнения геометрически.
Сол. Имеем x + y = 7
⇒ y = 7 — x…. (1)
В табличной форме
и 5x + 2y = 20
⇒ y = \ (\ frac {20-5x} {2} \ )…. (2)
В табличной форме
Постройте точки A (1, 6), B (4, 3) и соедините их, чтобы образовать линию AB.
Аналогичным образом постройте точки C (2, 5). D (4, 0) и присоединитесь к ним, чтобы получить линейный компакт-диск. Ясно, что две прямые пересекаются в точке C. Теперь каждая точка на прямой AB дает нам решение уравнения (1).Каждая точка на CD дает нам решение уравнения (2).
Пример 2: Отец говорит своей дочери: «Семь лет назад я был в семь раз старше тебя. Кроме того, через три года я буду в три раза старше тебя ». Представьте эту ситуацию алгебраически и графически.
Сол. Пусть нынешний возраст отца равен x лет, а возраст дочери = y лет
Семь лет назад возраст отца = (x — 7) лет
Семь лет назад возраст дочери = (y — 7) лет
Согласно задаче
( x — 7) = 7 (y — 7) или x — 7y = — 42….(1)
Через 3 года возраст отца = (x + 3) лет
Через 3 года возраст дочери = (y + 3) лет
Согласно условию, указанному в вопросе
x + 3 = 3 (y + 3) или x — 3y = 6…. (2)
x — 7y = –42 ⇒ \ (y = \ frac {x + 42} {7} \)
x — 3y = 6 ⇒ \ (y = \ frac {x -6} {3} \)
Постройте точки A (0, 6), B (7, 7), C (14, 8) и соедините их, чтобы получить прямую линию ABC. Аналогичным образом постройте точки D (6, 0), E (12, 2) и F (18, 4) и соедините их, чтобы получить прямую линию DEF.
Пример 3: 10 учеников класса X приняли участие в викторине по математике. Если девочек на 4 больше, чем мальчиков, найдите количество мальчиков и девочек, принявших участие в викторине.
Сол. Пусть количество мальчиков равно x, а количество девочек равно y.
Тогда формируются уравнения:
x + y = 10…. (1)
и y = x + 4…. (2)
Нарисуем графики уравнений (1) и (2), найдя по два решения для каждого уравнений.Приведены
решений уравнений.
x + y = 10 ⇒ y = 10 — x
y = x + 4
Рисуя эти точки, мы проводим линии AB и CE, проходящие через них, чтобы представить уравнения. Две прямые AB и Ce пересекаются в точке E (3, 7). Итак, x = 3 и y = 7 — искомое решение пары линейных уравнений.
т.е. количество мальчиков = 3
количество девочек = 7.
Проверка:
Подставляя x = 3 и y = 7 в (1), получаем
L.H.S. = 3 + 7 = 10 = R.H.S., (1) проверяется.
Положив x = 3 и y = 7 в (2), мы получим
7 = 3 + 4 = 7, (2) проверено.
Следовательно, оба уравнения удовлетворяются.
Пример 4: Половина периметра сада, длина которого на 4 больше, чем его ширина 36м. Найдите размеры сада.
Сол. Пусть длина сада равна x, а ширина сада равна y.
Тогда формируется уравнение:
x = y + 4…. (1)
Полупериметр = 36
x + y = 36….(2)
y = x — 4
y = 36 — x
Отрисовывая эти точки, мы проводим прямые AB и CD, проходящие через них, чтобы представить уравнения.
Две прямые AB и CD пересекаются в точке (20, 16). Итак, x = 20 и y = 16 — необходимое решение пары линейных уравнений, т.е. длина сада составляет 20 м, а ширина сада. составляет 16 м.
Проверка:
Подставляем x = 20 и y = 16 в (1). Получаем
20 = 16 + 4 = 20, (1) проверяется.
Полагаем x = 20 и y = 16 в (2).получаем
20 + 16 = 36
36 = 36, (2) проверяется.
Следовательно, оба уравнения удовлетворяются.
Пример 5: Нарисуйте графики уравнений x — y + 1 = 0 и 3x + 2y — 12 = 0. Определите координаты вершин треугольника, образованного этими линиями и осью x, и заштрихуйте треугольная область.
Сол. Пара линейных уравнений:
x — y + 1 = 0…. (1)
3x + 2y — 12 = 0…. (2)
x — y + 1 = 0 ⇒ y = x + 1
3x + 2y — 12 = 0 ⇒ y = \ (\ frac {12-3x} {2} \)
Постройте точки A (0, 1), B (4, 5) и соедините их, чтобы получить прямую AB.Аналогичным образом постройте точки C (0, 6), D (2, 3) и соедините их, чтобы образовать линию CD.
Очевидно, две прямые пересекаются в точке D (2, 3). Следовательно, x = 2 и y = 3 является решением данной пары уравнений
.
Линия CD пересекает ось x в точке
E (4, 0), а линия AB пересекает ось x в точке F (–1, 0).
Следовательно, координаты вершин треугольника равны; D (2, 3), E (4, 0), F (–1, 0).
Проверка:
Оба уравнения (1) и (2) удовлетворяются при x = 2 и y = 3.Следовательно, Verified.
Пример 6: Графически показать, что система уравнений
x — 4y + 14 = 0; 3x + 2y — 14 = 0 согласуется с единственным решением.
Сол. Данная система уравнений:
x — 4y + 14 = 0…. (1)
3x + 2y — 14 = 0…. (2)
x — 4y + 14 = 0 ⇒ y = \ (\ frac {x + 14} {4} \)
3x + 2y — 14 = 0 ⇒ y = \ (\ frac {-3x + 14} {2} \)
Данные уравнения, представляющие две прямые, пересекаются друг с другом единственная точка (2, 4).Следовательно, уравнения согласуются с единственным решением.
Пример 7: Графически покажите, что система уравнений
2x + 5y = 16; \ (3x + \ frac {15} {2} = 24 \) имеет бесконечно много решений.
Сол. Данная система уравнений:
2x + 5y = 16…. (1)
\ (3x + \ frac {15} {2} = 24 \)…. (2)
2x + 5y = 16 ⇒ y = \ ( \ frac {16-2x} {5} \)
\ (3x + \ frac {15} {2} = 24 \) ⇒ y = \ (\ frac {48-6x} {15} \)
строки двух уравнений совпадают.Координаты каждой точки на этой линии являются решением.
Следовательно, данные уравнения совместимы с бесконечным множеством решений.
Пример 8: Графически покажите, что система уравнений
2x + 3y = 10, 4x + 6y = 12 не имеет решения.
Сол. Данные уравнения:
2x + 3y = 10 ⇒ y = \ (\ frac {10-2x} {3} \)
4x + 6y = 12 ⇒ y = \ (\ frac {12-4x} {6} \)
Постройте точки A (–4, 6), B (2, 2) и соедините их, чтобы образовать линию AB.Аналогичным образом постройте точки C (–3, 4), D (3, 0) и соедините их, чтобы получить линию CD.
Ясно, что графики данных уравнений представляют собой параллельные линии. Поскольку у них нет общей точки, нет и общего решения. Следовательно, данная система уравнений не имеет решения.
Пример 9: Учитывая линейное уравнение 2x + 3y — 8 = 0, запишите другое линейное уравнение с двумя переменными так, чтобы геометрическое представление
пары, образованной таким образом, было:
(i) пересекающиеся линии
(ii) параллельные линии
(iii) совпадающие линии
Sol. У нас есть, 2x + 3y — 8 = 0
(i) Другое линейное уравнение с двумя переменными, такое, что геометрическое представление пары, образованной таким образом, представляет собой пересекающиеся прямые:
3x — 2y — 8 = 0
(ii) Другие параллельные прямые до строки выше
4x + 6y — 22 = 0
(iii) Другая совпадающая линия с строкой выше
6x + 9y — 24 = 0
Пример 10: Решите следующую систему линейных уравнений графически;
3х + у — 11 = 0; x — y — 1 = 0
Закрасьте область, ограниченную этими линиями, а также осью y.Затем определите области области, ограниченные этими линиями и осью y.
Сол. Имеем,
3x + y — 11 = 0 и x — y — 1 = 0
(a) График уравнения 3x + y — 11 = 0
Мы имеем, 3x + y — 11 = 0
⇒ y = — 3x + 11
When, x = 2, y = –3 × 2 + 11 = 5
When, x = 3, y = — 3 × 3 + 11 = 2
Нанесение точек P (2, 5) и Q (3, 2) на миллиметровой бумаге и проведя линию, соединяющую их, мы получим график уравнения 3x + y — 11 = 0, как показано на рис.
(b) График уравнения x — y — 1 = 0
Мы имеем,
x — y — 1 = 0
y = x — 1
Когда, x = — 1, y = –2
Когда, x = 3, y = 2
Изобразив точки R (–1, –2) и S (3, 2) на одной миллиметровой бумаге и проведя линию, соединяющую их, мы получим график уравнения x — y — 1 = 0, как показано на рис.
Вы можете заметить, что две прямые пересекаются в точке
Q (3, 2). Итак, x = 3 и y = 2. Область, ограниченная линиями, представленными данными уравнениями, а также ось y заштрихована.
Итак, замкнутая область = Площадь заштрихованной части
= Площадь ∆QUT = 1/2 × основание × высота
= 1/2 × (TU × VQ) = 1/2 × (TO + OU) × VQ
= 1/2 (11 + 1) 3 = 1/2 × 12 × 3 = 18 кв. Единиц.
Следовательно, необходимая площадь составляет 18 кв.
Пример 11: Нарисуйте графики следующих уравнений
2x — 3y = — 6; 2х + 3у = 18; y = 2
Найдите вершины образовавшихся треугольников, а также площадь треугольника.
Сол. (а) График уравнения 2x — 3y = — 6;
Мы имеем, 2x — 3y = — 6 ⇒ y = \ (\ frac {2x + 6} {3} \)
When, x = 0, y = 2
When, x = 3, y = 4
Построение графика точки P (0, 2) и Q (3, 4) на миллиметровой бумаге и проведя линию, соединяющую их, мы получим график уравнения 2x — 3y = — 6, как показано на рис.
(б) График уравнения 2x + 3y = 18;
У нас есть 2x + 3y = 18 ⇒ y = \ (\ frac {-2x + 18} {3} \)
When, x = 0, y = 6
When, x = — 3, y = 8
Построение графика точки R (0, 6) и S (–3, 8) на одной миллиметровой бумаге и проведя линию, соединяющую их, мы получим график уравнения 2x + 3y = 18, как показано на рис.
(c) График уравнения y = 2
Ясно, что y = 2 для любого значения x. Мы можем взять точки T (3, 2), U (6, 2) или любые другие значения.
Построив точки T (3, 2) и U (6, 2) на одной миллиметровой бумаге и проведя линию, соединяющую их, мы получим график уравнения y = 2, как показано на рис.
Из рисунка видно, что пары, взятые попарно, пересекают друг друга в точках Q (3, 4), U (6, 2) и P (0, 2). Они образуют три вершины треугольника PQU.
Чтобы найти площадь треугольника, сформированного таким образом
Треугольник, сформированный таким образом, равен PQU (см. Рис.)
В ∆PQU
QT (высота) = 2 единицы
и PU (основание) = 6 единиц
, поэтому площадь ∆ PQU = (основание × высота)
= 1/2 (PU × QT) = 1/2 × 6 × 2 кв.Untis
= 6 кв. единиц.
Пример 12: При сравнении соотношений \ (\ frac {{{a} _ {1}}} {{{a} _ {2}}}, \ frac {{{b} _ {1}}) } {{{b} _ {2}}} и \ frac {{{c} _ {1}}} {{{c} _ {2}}} \) и, не рисуя их, выясните, соответствуют ли линии, представляющие следующие пары линейных уравнений пересекаются в точке, параллельны или совпадают.
(i) 5x — 4y + 8 = 0, 7x + 6y — 9 = 0
(ii) 9x + 3y + 12 = 0, 18x + 6y + 24 = 0
(iii) 6x — 3y + 10 = 0, 2x — y + 9 = 0
Сол. Сравнивая данные уравнения со стандартными формами уравнений a 1 x + b 1 y + c 1 = 0 и
a 2 x + b 2 y + c 2 = 0 имеем ,
(i) a1 = 5, b 1 = — 4, c 1 = 8;
a 2 = 7, b 2 = 6, c 2 = — 9
\ (\ frac {{{a} _ {1}}} {{{a} _ {2}}} = \ frac {5} {7}, \ frac {{{b} _ {1}}} {{{b} _ {2}}} = \ frac {-4} {6} \)
\ (\ Rightarrow \ frac {{{a} _ {1}}} {{{a} _ {2}}} \ ne \ frac {{{b} _ {1}}} {{{b} _ {2}}} \)
Таким образом, прямые, представляющие пару линейных уравнений, пересекаются.
(ii) a1 = 9, b 1 = 3, c 1 = 12;
a 2 = 18, b 2 = 6, c 2 = 24
\ (\ frac {{{a} _ {1}}} {{{a} _ {2}}} = \ frac {9} {18} = \ frac {1} {2}, \ frac {{{b} _ {1}}} {{{b} _ {2}}} = \ frac {3} {6} = \ frac {1} {2} и \ frac {{{c} _ {1}}} {{{c} _ {2}}} = \ frac {12} {24} = \ frac {1} { 2} \)
\ (\ Rightarrow \ frac {{{a} _ {1}}} {{{a} _ {2}}} = \ frac {{{b} _ {1}}} {{{ b} _ {2}}} = \ frac {{{c} _ {1}}} {{{c} _ {2}}} \)
Таким образом, линии, представляющие пару линейных уравнений, совпадают.
(iii) a1 = 6, b 1 = — 3, c 1 = 10;
a 2 = 2, b 2 = — 6, c 2 = 9
\ (\ frac {{{a} _ {1}}} {{{a} _ {2}}} = \ frac {6} {2} = 3, \ frac {{{b} _ {1}}} {{{b} _ {2}}} = \ frac {-3} {- 1} = 3и \ frac {{{c} _ {1}}} {{{c} _ {2}}} = \ frac {10} {9} \)
\ (\ Rightarrow \ frac {{{a} _ {1}} } {{{a} _ {2}}} = \ frac {{{b} _ {1}}} {{{b} _ {2}}} \ ne \ frac {{{c} _ {1} }} {{{c} _ {2}}} \)
Таким образом, прямые, представляющие пару линейных уравнений, параллельны.
Что такое сложение? — Определение, факты и примеры
ДополнениеПри сложении два или более чисел складываются вместе, то есть получается общая сумма двух или более чисел.
Пример:
Сколько всего яблок?
В одной корзине 7 яблок, в другой 4 яблока. Итак, складываем 7 и 4, чтобы найти общее количество яблок.
Чтобы сложить 7 и 4, мы можем отсчитать 4 шага вперед от 7
Символ, используемый для обозначения сложения, — это + (символ плюс).
Итак, 7 и 4 можно записать как 7 + 4
Дополнение
Предложение сложения — это математическое выражение, которое показывает два или более значений, сложенных вместе, и их сумму.
Мы можем записать математическое выражение для 7 плюс 4 равняется 11 как:
Сложенные числа называются слагаемыми, а ответ на сложение называется суммой. В дополнительном предложении добавляются слагаемые, чтобы получить сумму.
Добавлять маленькие числа можно и пальцами.
Примеры:
Числовые диаграммы — еще один способ сложения чисел.
Пример: Складываем 57 и 16, используя сетку сотен.
Шаг 1: Отметьте большее число. (Здесь отметка 57) Шаг 2: Если добавляемое число больше 10, разбейте его на десятки и единицы. (Здесь 16 = 10 + 6) Шаг 3: Перейти на десятки, как во втором числе. (Здесь 57 + 10 = 67) Шаг 4: Переместитесь вперед на столько единиц, сколько во втором числе. (Здесь 67 + 6 = 73) Достигнутое число и есть ответ. Итак, 57 + 16 = 73 |
Сложение по вертикали
Номера также можно складывать по вертикали.
Складываем 57 и 16 по вертикали.
Шаг 1: Напишите числа друг под другом в соответствии с местами цифр. | Шаг 2: Начните сложение с разряда единиц. Напишите сумму под цифрой из единиц. Если сумма разряда единиц больше 9, запишите цифру единиц суммы под единицами и перенесите ее цифру десятков в столбец десятков. | Шаг 3: Сложите цифры десятков. (если была цифра переноса, добавьте ее) |
Числа, содержащие более двух цифр, также можно складывать по вертикали.Мы всегда начинаем складывать с разряда единиц и движемся к цифрам в самом высоком месте.
Пример 1: Мари купила дизайнерскую сумочку за 231 доллар и пояс за 199 долларов. Сколько она потратила на оба?
Чтобы найти общую стоимость, нам нужно добавить 231 и 199
Мы можем складывать числа по вертикали как:
Итак, Мари потратила 430 долларов
Пример 2: На стадионе 2415 синих мест и 2770 красных мест.Сколько всего мест синих и красных?
Общее количество мест = 2415 + 2770
= 5185 мест
Интересные факты
|
Решение систем уравнений (одновременные уравнения)
Если у вас есть два разных уравнения с одинаковыми двумя неизвестными в каждом, вы можете решить для обеих неизвестных.Существует три распространенных метода решения: сложение / вычитание, подстановка и построение графика.
Метод сложения / вычитания
Этот метод также известен как метод исключения.
Чтобы использовать метод сложения / вычитания, выполните следующие действия:
Умножьте одно или оба уравнения на некоторое число (а), чтобы число перед одной из букв (неизвестных) в каждом уравнении было одинаковым или прямо противоположным.
Сложите или вычтите два уравнения, чтобы исключить одну букву.
Решите оставшееся неизвестное.
Решите для другого неизвестного, вставив значение неизвестного, найденного в одно из исходных уравнений.
Пример 1
Решите для x и y .
При добавлении уравнений исключаются термины и .
Теперь добавление 5 для x в первое уравнение дает следующее:
Ответ: x = 5, y = 2
Заменяя каждое x на 5 и каждое y на 2 в исходных уравнениях, вы можете увидеть, что каждое уравнение станет истинным.
В примере и пример , существовал уникальный ответ для x и y , который делал каждое предложение одновременно истинным. В некоторых ситуациях вы не получаете однозначных ответов или вообще не получаете ответов. Вы должны знать об этом, когда используете метод сложения / вычитания.
Пример 2
Решите для x и y.
Сначала умножьте нижнее уравнение на 3. Теперь перед y стоит 3 в каждом уравнении.
Уравнения можно вычесть, исключив члены y .
Вставьте x = 5 в одно из исходных уравнений, чтобы найти y .
Ответ: x = 5, y = 3
Конечно, если число перед буквой уже одно и то же в каждом уравнении, вам не нужно изменять ни одно уравнение. Просто сложите или вычтите.
Чтобы проверить решение, замените каждое x в каждом уравнении на 5 и замените каждое y в каждом уравнении на 3.
Пример 3
Решите для a и b .
Умножьте верхнее уравнение на 2. Обратите внимание на то, что происходит.
Теперь, если вы вычтете одно уравнение из другого, результат будет 0 = 0.
Это утверждение всегда верно .
Когда это происходит, система уравнений не имеет единственного решения. Фактически, любая замена a и b , которая делает одно из уравнений истинным, также делает истинным другое уравнение.Например, если a = –6 и b = 5, то оба уравнения выполняются.
[3 (- 6) + 4 (5) = 2 И 6 (- 6) + 8 (5) = 4]
В действительности мы имеем только одно уравнение, записанное двумя разными способами. В этом случае второе уравнение фактически является первым уравнением, умноженным на 2. Решением этой ситуации является либо исходное уравнение, либо упрощенная форма любого уравнения.
Пример 4
Решите для x и y .
Умножьте верхнее уравнение на 2. Обратите внимание на то, что происходит.
Теперь, если вы вычтите нижнее уравнение из верхнего уравнения, результат будет 0 = 1. Это утверждение не соответствует действительности . Когда это происходит, система уравнений не имеет решения.
В примерах 1–4 только одно уравнение было умножено на число, чтобы числа перед буквой были одинаковыми или противоположными. Иногда каждое уравнение необходимо умножить на разные числа, чтобы числа перед буквой были одинаковыми или противоположными.
Решите для x и y .
Обратите внимание, что не существует простого числа, на которое можно умножить любое уравнение, чтобы получить числа перед x или y , чтобы они стали одинаковыми или противоположными. В этом случае сделайте следующее:
Выберите букву, которую нужно удалить.
Используйте две цифры слева от этой буквы. Найдите наименьшее общее кратное этого значения как желаемое число перед каждой буквой.
Определите, на какое значение необходимо умножить каждое уравнение, чтобы получить это значение, и умножьте уравнение на это число.
Предположим, вы хотите исключить x . Наименьшее общее кратное 3 и 5, число перед x , равно 15. Первое уравнение нужно умножить на 5, чтобы получить 15 перед x . Второе уравнение нужно умножить на 3, чтобы получить 15 перед x .
Теперь вычтите второе уравнение из первого, чтобы получить следующее:
На этом этапе вы можете либо заменить y на и решить для x (метод 1, который следует ниже), либо начать с двух исходных уравнений и исключить y , чтобы решить для x (метод 2, который следует).
Метод 1
Используя верхнее уравнение: замените y на и решите относительно x .
Метод 2
Исключите y и решите для x .
Наименьшее общее кратное 4 и 6 равно 12. Умножьте верхнее уравнение на 3, а нижнее уравнение на 2.
Теперь сложите два уравнения, чтобы исключить y .
Решение: x = 1 и.
Метод замещения
Иногда система легче решается методом подстановки . Этот метод включает замену одного уравнения в другое.
Пример 6
Решите для x и y.
Из первого уравнения замените ( y + 8) на x во втором уравнении.
( y + 8) + 3 y = 48
Теперь решите г. Упростите, объединив и .
Теперь вставьте значение y , 10, в одно из исходных уравнений.
Ответ: y = 10, x = 18
Проверьте решение.
Пример 7
Решите для x и y , используя метод подстановки.
Сначала найдите уравнение, в котором перед буквой стоит цифра «1» или «- 1». Решите эту букву с точки зрения другой буквы.
Затем действуйте как в примере 6.
В этом примере в нижнем уравнении перед числами y стоит «1».
Решите относительно y в терминах x .
Замените 4 x -17 вместо y в верхнем уравнении, а затем решите относительно x .
Замените x на 4 в уравнении y — 4 x = –17 и решите относительно y .
Решение: x = 4, y = –1.
Проверьте решение:
Метод построения графика
Другой метод решения уравнений — это графического отображения каждого уравнения на координатном графике. Координаты перекрестка будут решением системы. Если вы не знакомы с построением координатных графиков, внимательно просмотрите статьи по координатной геометрии, прежде чем пытаться использовать этот метод.
Пример 8
Решите систему, построив график.
Сначала найдите три значения для x и y , которые удовлетворяют каждому уравнению. (Хотя для определения прямой необходимы только две точки, поиск третьей точки — хороший способ проверки.) Ниже приведены таблицы значений x и y :
Теперь изобразите две линии на координатной плоскости, как показано на рисунке 1.
Точка пересечения двух линий (4, 0) — это решение системы.
Если линии параллельны, они не пересекаются, и, следовательно, для этой системы нет решения.
Рис. 1. График из линий x = 4 + y и x — 3 y = 4, обозначающих решение.
Пример 9
Решите систему, построив график.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению.
3 x + 4 y = 2 6 x + 8 y = 4
Ниже приведены таблицы значений x и y .См. Рисунок 2.
х | л |
|---|---|
0 | |
2 | — 1 |
4 |
х | л |
|---|---|
0 | |
2 | — 1 |
4 |
Обратите внимание, что одинаковые точки удовлетворяют каждому уравнению.Эти уравнения представляют собой одну и ту же линию.
Следовательно, решение не единственное. Решение — это все точки на линии.
Следовательно, решением является любое уравнение прямой, поскольку они оба представляют одну и ту же линию.
Это похоже на пример когда это было сделано с использованием метода сложения / вычитания.
Рис. 2. График из линий 3 x + 4 y = 2 и 6 x + 8 y = 4, указывающих решение.
Пример 10
Решите систему, построив график.
Найдите три значения для x и y , которые удовлетворяют каждому уравнению. См. Следующие таблицы значений x и y :
х | л |
|---|---|
0 | 1 |
2 | |
4 | -2 |
х | л |
|---|---|
0 | 2 |
2 | |
4 | –1 |
Обратите внимание на то, что на рисунке 3 два графика параллельны.Они никогда не встретятся. Следовательно, у этой системы уравнений нет решения.
Для этой системы уравнений не существует решения.
Это похоже на пример выполняется методом сложения / вычитания.
Рисунок 3. График из линий 3 x + 4 y = 4 и 6 x + 8 y = 16, указывающих решение.
неравенств | Безграничная алгебра
Введение в неравенство
Неравенства используются для демонстрации отношений между числами или выражениями.
Цели обучения
Объясните, что представляет собой неравенство и как оно используется
Основные выводы
Ключевые моменты
- Неравенство описывает взаимосвязь между двумя разными значениями.
- Обозначение [latex] a b [/ latex] ] означает, что [latex] a [/ latex] строго больше, чем [latex] b [/ latex].
- Понятие [латекс] a \ leq b [/ latex] означает, что [latex] a [/ latex] меньше или равно [latex] b [/ latex], а обозначение [latex] a \ geq b [ / latex] означает, что [latex] a [/ latex] больше или равно [latex] b [/ latex].
- Неравенства особенно полезны для решения проблем, связанных с минимальными или максимальными возможными значениями.
Ключевые термины
- числовая строка : визуальное представление набора действительных чисел в виде ряда точек.
- неравенство : Утверждение, что из двух величин одно определенно меньше или больше другого.
В математике неравенства используются для сравнения относительного размера значений.Их можно использовать для сравнения целых чисел, переменных и различных других алгебраических выражений. Ниже приводится описание различных типов неравенств.
Строгое неравенство
Строгое неравенство — это отношение между двумя значениями, когда они различны. Точно так же, как в уравнениях используется знак равенства =, чтобы показать, что два значения равны, в неравенствах используются знаки, чтобы показать, что два значения не равны, и описать их взаимосвязь. Символы строгого неравенства: [latex] <[/ latex] и [latex]> [/ latex].
Строгие неравенства отличаются от обозначения [latex] a \ neq b [/ latex], что означает, что a не равно [latex] b [/ latex]. Символ [latex] \ neq [/ latex] не говорит о том, что одно значение больше другого или даже о том, что их можно сравнить по размеру.
В двух типах строгих неравенств [latex] a [/ latex] не равно [latex] b [/ latex]. Для сравнения размеров значений существует два типа отношений:
- Обозначение [латекс] a
- Обозначение [латекс] a> b [/ latex] означает, что [latex] a [/ latex] больше, чем [latex] b [/ latex].
Значение этих символов можно легко запомнить, заметив, что «большая» сторона символа неравенства (открытая сторона) обращена к большему числу. «Меньшая» сторона символа (точка) обращена к меньшему числу.
Указанные выше отношения можно продемонстрировать на числовой прямой. Вспомните, что значения на числовой строке увеличиваются по мере продвижения вправо.Следовательно, следующее представляет отношение [латекс] a [/ латекс] меньше, чем [латекс] b [/ латекс]:
[латекс] a
[латекс] a [/ latex] находится слева от [latex] b [/ latex] в этой числовой строке.
и следующее демонстрирует, что [латекс] a [/ latex] больше, чем [latex] b [/ latex]:
[латекс] a> b [/ латекс]
[латекс] a [/ latex] находится справа от [latex] b [/ latex] в этой числовой строке.
В целом обратите внимание, что:
- [латекс] a a [/ latex]; например, [latex] 7 <11 [/ latex] эквивалентно [latex] 11> 7 [/ latex].
- [латекс] a> b [/ latex] эквивалентен [латексу] b 6 [/ латекс].
Другое неравенство
В отличие от строгих неравенств, существуют два типа отношений неравенства, которые не являются строгими:
- Обозначение [латекс] a \ leq b [/ latex] означает, что [latex] a [/ latex] меньше или равно [latex] b [/ latex] (или, что эквивалентно, «максимум» [латекс] б [/ латекс]).
- Обозначение [латекс] a \ geq b [/ latex] означает, что [latex] a [/ latex] больше или равно [latex] b [/ latex] (или, что то же самое, «как минимум» [ латекс] б [/ латекс]).
Неравенства с переменными
В дополнение к отображению отношений между целыми числами, неравенства могут использоваться для отображения отношений между переменными и целыми числами.
Например, рассмотрим [латекс] x> 5 [/ латекс]. Это будет читаться как «[latex] x [/ latex] больше 5 ″ и означает, что неизвестная переменная [latex] x [/ latex] может иметь любое значение больше 5, но не 5 сама по себе.Для визуализации этого см. Числовую строку ниже:
[латекс] x> 5 [/ латекс]
Обратите внимание, что кружок над цифрой 5 не заполнен, что означает, что 5 не входит в возможные значения [latex] x [/ latex].
В качестве другого примера рассмотрим [латекс] x \ leq 3 [/ латекс]. Это будет читаться как «[latex] x [/ latex] меньше или равно 3 ″ и указывает, что неизвестная переменная [latex] x [/ latex] может иметь значение 3 или любое значение меньше 3. Для визуализации это, см. числовую строку ниже:
[латекс] x \ leq 3 [/ латекс]
Обратите внимание, что кружок над цифрой 3 закрашен, что означает, что 3 входит в возможные значения [latex] x [/ latex].
Неравенства демонстрируются раскрашиванием стрелки в соответствующем диапазоне числовой линии, чтобы указать возможные значения [latex] x [/ latex]. Обратите внимание, что открытый кружок используется, если неравенство строгое (т. Е. Для неравенств, использующих [latex]> [/ latex] или [latex] <[/ latex]), а закрашенный кружок используется, если неравенство не является строгим ( т.е. для неравенств с использованием [latex] \ geq [/ latex] или [latex] \ leq [/ latex]).
Решение проблем с неравенствами
Напомним, что уравнения могут использоваться для демонстрации равенства математических выражений, включающих различные операции (например: [latex] x + 5 = 9 [/ latex]).Точно так же неравенства можно использовать для демонстрации взаимосвязи между различными выражениями.
Например, рассмотрим следующие неравенства:
- [латекс] x — 7> 12 [/ латекс]
- [латекс] 2x + 4 \ leq 25 [/ латекс]
- [латекс] 2x
Каждое из них представляет отношение между двумя разными выражениями.
Одно из полезных применений неравенств, подобных этому, — в задачах, связанных с максимальными или минимальными значениями.
Пример 1
У Джареда есть лодка, максимальная масса которой составляет 2500 фунтов. Он хочет взять на лодку как можно больше друзей и предполагает, что он и его друзья в среднем весят 160 фунтов. Сколько людей могут одновременно кататься на его лодке?
Эту проблему можно смоделировать с помощью следующего неравенства:
[латекс] 160n \ leq 2500 [/ латекс]
где [latex] n [/ latex] — это количество людей, которые Джаред может взять на лодку. Чтобы понять, почему это так, рассмотрим левую часть неравенства.Он представляет собой общий вес [латексных] n [/ латексных] людей весом 160 фунтов каждый. Неравенство гласит, что общий вес Джареда и его друзей должен быть на меньше или равен максимальному весу 2500, который является пределом веса лодки.
Есть шаги, которые можно выполнить, чтобы решить такое неравенство. На данный момент важно просто понять значение таких утверждений и случаев, в которых они могут быть применимы.
Правила устранения неравенств
Арифметические операции могут использоваться для решения неравенств для всех возможных значений переменной.
Цели обучения
Решите неравенства, используя правила работы с ними
Основные выводы
Ключевые моменты
- Когда вы выполняете алгебраические операции с неравенствами, важно выполнять одну и ту же операцию с обеими сторонами, чтобы сохранить истинность утверждения.
- Если обе части неравенства умножаются или делятся на одно и то же положительное значение, результирующее неравенство истинно.
- Если обе стороны умножаются или делятся на одно и то же отрицательное значение, направление неравенства изменяется.
- Неравенства, связанные с переменными, можно решить, чтобы получить все возможные значения переменной, которые делают утверждение истинным.
Ключевые термины
- неравенство : Утверждение, что из двух величин одно определенно меньше или больше другого.
Операции с неравенствами
Когда вы выполняете алгебраические операции с неравенствами, важно проводить точно такие же операции с обеих сторон, чтобы сохранить истинность утверждения.
Каждая арифметическая операция подчиняется определенным правилам:
Сложение и вычитание
Любое значение [латекс] c [/ латекс] может быть добавлено или вычтено из обеих сторон неравенства. То есть для любых действительных чисел [латекс] a [/ latex], [latex] b [/ latex] и [latex] c [/ latex]:
- Если [латекс] a \ leq b [/ латекс], то [латекс] a + c \ leq b + c [/ латекс] и [латекс] a — c \ leq b — c [/ латекс].
- Если [латекс] a \ geq b [/ латекс], то [латекс] a + c \ geq b + c [/ латекс] и [латекс] a — c \ geq b — c [/ латекс].
Пока одна и та же стоимость добавляется или вычитается с обеих сторон, результирующее неравенство остается верным.
Например, рассмотрим следующее неравенство:
[латекс] 12 <15 [/ латекс]
Давайте применим описанные выше правила, вычтя 3 с обеих сторон:
[латекс] \ begin {align} 12 — 3 & <15 - 3 \\ 9 & <12 \ end {align} [/ latex]
Это утверждение все еще верно.
Умножение и деление
В свойствах, связанных с умножением и делением, указано, что для любых действительных чисел [latex] a [/ latex], [latex] b [/ latex] и ненулевое [latex] c [/ latex]:
Если [latex] c [/ latex] положительное значение, то умножение или деление на [latex] c [/ latex] не меняет неравенства:
- Если [latex] a \ geq b [/ latex] и [latex] c> 0 [/ latex], то [latex] ac \ geq bc [/ latex] и [latex] \ dfrac {a} {c} \ geq \ dfrac {b} {c} [/ latex].
- Если [latex] a \ leq b [/ latex] и [latex] c> 0 [/ latex], то [latex] ac \ leq bc [/ latex] и [latex] \ dfrac {a} {c} \ leq \ dfrac {b} {c} [/ латекс].
Если [latex] c [/ latex] отрицательно, то умножение или деление на [latex] c [/ latex] меняет неравенство:
- Если [latex] a \ geq b [/ latex] и [latex] c <0 [/ latex], то [latex] ac \ leq bc [/ latex] и [latex] \ dfrac {a} {c} \ leq \ dfrac {b} {c} [/ латекс].
- Если [latex] a \ leq b [/ latex] и [latex] c <0 [/ latex], то [latex] ac \ geq bc [/ latex] и [latex] \ dfrac {a} {c} \ geq \ dfrac {b} {c} [/ латекс].
Обратите внимание, что умножение или деление неравенства на отрицательное число изменяет направление неравенства. Другими словами, символ больше становится символом меньше, и наоборот.
Чтобы увидеть применение этих правил, рассмотрим следующее неравенство:
[латекс] 5> -3 [/ латекс]
Умножение обеих сторон на 3 дает:
[латекс] \ begin {align} 5 (3) &> -3 (3) \\ 15 &> -9 \ end {align} [/ latex]
Мы видим, что это верное утверждение, потому что 15 больше 9.
Теперь умножьте то же неравенство на -3 (не забудьте изменить направление символа, потому что мы умножаем на отрицательное число):
[латекс] \ begin {align} 5 (-3) & <-3 (-3) \\ -15 & <9 \ end {align} [/ latex]
Это утверждение также верно. Это демонстрирует, насколько важно изменить направление символа «больше» или «меньше» при умножении или делении на отрицательное число.
Устранение неравенств
Решение неравенства, которое включает переменную, дает все возможные значения, которые может принимать переменная, которые делают неравенство истинным.Решение неравенства означает преобразование его таким образом, чтобы переменная находилась с одной стороны символа, а число или выражение — с другой. Часто для преобразования неравенства таким образом требуется несколько операций.
Сложение и вычитание
Чтобы увидеть, как правила сложения и вычитания применяются к решению неравенств, рассмотрим следующее:
[латекс] x — 8 \ leq 17 [/ латекс]
Сначала выделите [латекс] x [/ латекс]:
[латекс] \ begin {align} x — 8 + 8 & \ leq 17 + 8 \\ x & \ leq 25 \ end {align} [/ latex]
Следовательно, [латекс] x \ leq 25 [/ latex] является решением [латекса] x — 8 \ leq 17 [/ latex].Другими словами, [latex] x — 8 \ leq 17 [/ latex] верно для любого значения [latex] x [/ latex], которое меньше или равно 25.
Умножение и деление
Чтобы увидеть, как применяются правила умножения и деления, рассмотрим следующее неравенство:
[латекс] 2x> 8 [/ латекс]
Делим обе стороны на 2, получаем:
[латекс] \ begin {align} \ dfrac {2x} {2} &> \ dfrac {8} {2} \\ x &> \ dfrac {8} {2} \\ x &> 4 \ end {align } [/ латекс]
Таким образом, выражение [latex] x> 4 [/ latex] является решением для [latex] 2x> 8 [/ latex].Другими словами, [latex] 2x> 8 [/ latex] верно для любого значения [latex] x [/ latex] больше 4.
Теперь рассмотрим другое неравенство:
[латекс] — \ dfrac {y} {3} \ leq 7 [/ латекс]
Поскольку используется отрицательный знак, мы должны умножить его на отрицательное число, чтобы найти [латекс] y [/ latex]. Это означает, что мы также должны изменить направление символа:
[латекс] \ begin {align} \ displaystyle -3 \ left (- \ frac {y} {3} \ right) & \ geq -3 (7) \\ y & \ geq -3 (7) \\ y & \ geq -21 \ end {align} [/ латекс]
Следовательно, решение [latex] — \ frac {y} {3} \ leq 7 [/ latex] — [latex] y \ geq -21 [/ latex].Таким образом, данное утверждение верно для любого значения [latex] y [/ latex], большего или равного [latex] -21 [/ latex].
Пример
Решите следующее неравенство:
[латекс] 3л — 17 \ geq 19 [/ латекс]
Сначала прибавьте 17 к обеим сторонам:
[латекс] \ begin {align} 3y — 17 + 17 & \ geq 19 + 17 \\ 3y & \ geq 36 \ end {align} [/ latex]
Затем разделите обе стороны на 3:
[латекс] \ begin {align} \ dfrac {3y} {3} & \ geq \ dfrac {36} {3} \\ y & \ geq \ dfrac {36} {3} \\ y & \ geq 12 \ конец {align} [/ latex]
Особые соображения
Обратите внимание: если мы попытаемся умножить или разделить обе части неравенства на неизвестную переменную, возникнут проблемы.Если какая-либо переменная [latex] x [/ latex] неизвестна, мы не можем определить, имеет ли она положительное или отрицательное значение. Поскольку правила умножения или деления положительных и отрицательных чисел различаются, мы не можем следовать этому же правилу при умножении или делении неравенств на переменные. Однако переменные можно складывать или вычитать с обеих сторон неравенства.
Сложные неравенства
Составное неравенство включает в себя три выражения, а не два, но также может быть решено, чтобы найти возможные значения переменной.
Цели обучения
Решите сложное неравенство, уравновесив все три компонента неравенства
Основные выводы
Ключевые моменты
- Составное неравенство имеет следующий вид: [латекс] a
- В составном неравенстве входят два утверждения. Первый оператор [латекс] a
- Пример составного неравенства: [латекс] 4
- Составное неравенство может содержать такое выражение, как [латекс] 1
- В составном неравенстве входят два утверждения. Первый оператор [латекс] a
Ключевые термины
- составное неравенство : Неравенство, состоящее из двух других неравенств в форме [латекс] a
- неравенство : Утверждение, что из двух величин одно определенно меньше или больше другого.
Определение сложных неравенств
Сложное неравенство имеет следующий вид:
[латекс] a На самом деле здесь есть два утверждения. Первый оператор [латекс] a Составное неравенство [латекс] a Рассмотрим [латекс] 4 Указанное выше неравенство по числовой прямой. Аналогичным образом рассмотрим [латекс] -2 Указанное выше неравенство по числовой прямой. Теперь рассмотрим [латекс] 1 Утверждение [латекс] 1 Чтобы найти возможные значения [latex] x [/ latex], нам нужно получить [latex] x [/ latex] отдельно: [латекс] 1 — 6 [латекс] -5 Следовательно, мы обнаруживаем, что если [latex] x [/ latex] — любое число строго между -5 и 2, утверждение [latex] 1 Решите [латекс] -3 <\ dfrac {-2x-7} {5} <7 [/ latex]. Умножьте каждую часть, чтобы удалить знаменатель из среднего выражения: [латекс] -3 \ cdot (5) <\ dfrac {-2x-7} {5} \ cdot (5) <7 \ cdot (5) [/ латекс] [латекс] -15 <-2x-7 <35 [/ латекс] Изолировать [латекс] x [/ латекс] в середине неравенства: [латекс] — 15 + 7 <-2x -7 + 7 <35 + 7 [/ латекс] [латекс] — 8 <-2x <42 [/ латекс] Теперь разделите каждую часть на -2 (и не забудьте изменить направление символа неравенства!): [латекс] \ displaystyle \ frac {-8} {- 2}> \ frac {-2x} {- 2}> \ frac {42} {- 2} [/ латекс] [латекс] 4> x> -21 [/ латекс] Наконец, принято (хотя и не обязательно) писать неравенство так, чтобы стрелки неравенства указывали влево (т.е., чтобы числа шли от наименьшего к наибольшему): [латекс] -21 Неравенства с абсолютными значениями можно решить, рассматривая абсолютное значение как расстояние от 0 до числа на числовой прямой. Решите неравенства с абсолютным значением Рассмотрим следующее неравенство, которое включает абсолютное значение: [латекс] | x | <10 [/ латекс] Зная, что решение [latex] \ left | x \ right | = 10 [/ latex] — это [latex] x = ± 10 [/ latex], многие студенты отвечают на этот вопрос [latex] x <± 10 [/ latex ].Однако это неверно. Вот два разных, но оба совершенно правильных подхода к решению этой проблемы. Какие номера работают? То есть, для каких чисел [латекс] \ left | x \ right | <10 [/ latex] верное утверждение? Давай попробуем. 4 работы. -4 тоже. 13 не работает. Как насчет -13? Нет: Если [латекс] x = -13 [/ латекс], то [латекс] \ left | x \ right | = 13 [/ latex], что не менее 10. Играя с числами таким образом, вы сможете убедить себя, что работающие числа должны быть где-то между -10 и 10.Это один из подходов к поиску ответа. Другой способ — думать об абсолютном значении как о расстоянии от 0. [latex] \ left | 5 \ right | [/ latex] и [latex] \ left | -5 \ right | [/ latex] равны 5, потому что оба числа на 5 от 0. В данном случае [латекс] \ left | x \ right | <10 [/ latex] означает «расстояние между [latex] x [/ latex] и 0 меньше 10». Другими словами, вы находитесь в пределах 10 единиц от нуля в любом направлении.Еще раз делаем вывод, что ответ должен быть между -10 и 10. Этот ответ можно визуализировать в числовой строке, как показано ниже, в которой выделены все числа, абсолютное значение которых меньше 10. Решение для [латекса] \ left | x \ right | <10 [/ latex]: Все числа, абсолютное значение которых меньше 10. Нет необходимости использовать оба этих метода; используйте тот метод, который вам легче понять. К более сложным задачам абсолютного значения следует подходить так же, как к уравнениям с абсолютными значениями: алгебраически выделить абсолютное значение, а затем алгебраически решить для [латекс] x [/ латекс]. Например, рассмотрим следующее неравенство: [латекс] \ влево | 2x \ вправо | + 3> 8 [/ латекс] Трудно сразу представить себе значение этого абсолютного значения, не говоря уже о самом значении [latex] x [/ latex]. Необходимо сначала выделить неравенство: [латекс] \ begin {align} \ left | 2x \ right | + 3 — 3 &> 8 — 3 \\ \ left | 2x \ right | &> 8 \ end {align} [/ латекс] А теперь подумайте о числовой прямой. В этих терминах это утверждение означает, что выражение [latex] 2x [/ latex] должно находиться более чем в 8 разрядах от 0.Следовательно, оно должно быть больше 8 или меньше -8. Выражая это неравенствами, имеем: [латекс] 2x> 8 [/ латекс] или [латекс] 2x <-8 [/ латекс] Теперь у нас есть 2 отдельных неравенства. [латекс] 4
[латекс] -2
[латекс] [/ латекс] Решение сложных неравенств
Пример 1
Неравенства с абсолютным значением
Цели обучения
Основные выводы
Ключевые моменты
Ключевые термины
Пробная версия и ошибка
Абсолютное значение как расстояние
Решение неравенств с абсолютным значением