Урок математики по теме «Счет в пределах 10. Решение примеров на сложение и вычитание» (1-й класс)

Цель урока:

• закрепить счёт в пределах 10 в прямом и обратном порядке;
• закрепить вычислительные навыки первого десятка.

Оборудование:

• геометрический самолёт;
• круг, треугольник, квадрат;
• рисунки бабочек, облаков, шариков, птиц, батона;
• сигнальный светофор;
• фуражка пирата-капитана;
• ножницы.

ХОД УРОКА

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

II. УСТНЫЙ СЧЕТ.

Сегодня наш урок будет немного необычен. Мы с вами будем путешествовать по стране “Математика”. А вот на чем, отгадайте сами:

Смело в небе проплывает,
Обгоняя птиц полет
Человек им управляет —
Что такое? (Самолет)

— Какая геометрическая фигура использована? (Треугольник)

— Сколько их? (9)

— Почему эту фигуру так назвали? (3 угла)

— Прежде чем отправиться в полет, мы должны сказать волшебные слова:

В небо, в небо поднимись!
Выше, выше полети!

— Ребята, когда мы с вами поднимались в небо на самолете, бабочки, которые сидели на полянке разлетелись. И мне, кажется, что они где-то у вас. Посмотрите! Нашли? Как хорошо! Так берите же скорей бабочек и выставляйте их на наборное полотно.

— Сколько всего бабочек? (6)

— У каждой бабочки есть свое число. Давайте прочитаем числа на них. (7, 10, 5, 8, 6, 9)

— Какие это числа? (Числа первого десятка)

— По порядку ли они расположены? (Нет)

— Поставьте их так, чтобы они расположились по порядку: от 5 до 10.

— Какое число следует за 7? (8) За 9? (10)

— Какое число стоит перед 10? (9) Перед 6? (5)

— Назовите соседей 7 (6, 8) , 9 (8, 10)

— Какое число больше, чем 6 на 3? (9) Меньше, чем 10 на 4? (6)

— Каких чисел не хватает в ряду? (1, 2, 3, 4)

Бабочки помогли нам поработать над числовым рядом. Давайте их выпустим на свободу.

Итак, мы с вами сегодня будем летчиками. Но для того, чтобы стать настоящими летчиками нам предстоит преодолеть много трудностей и препятствий.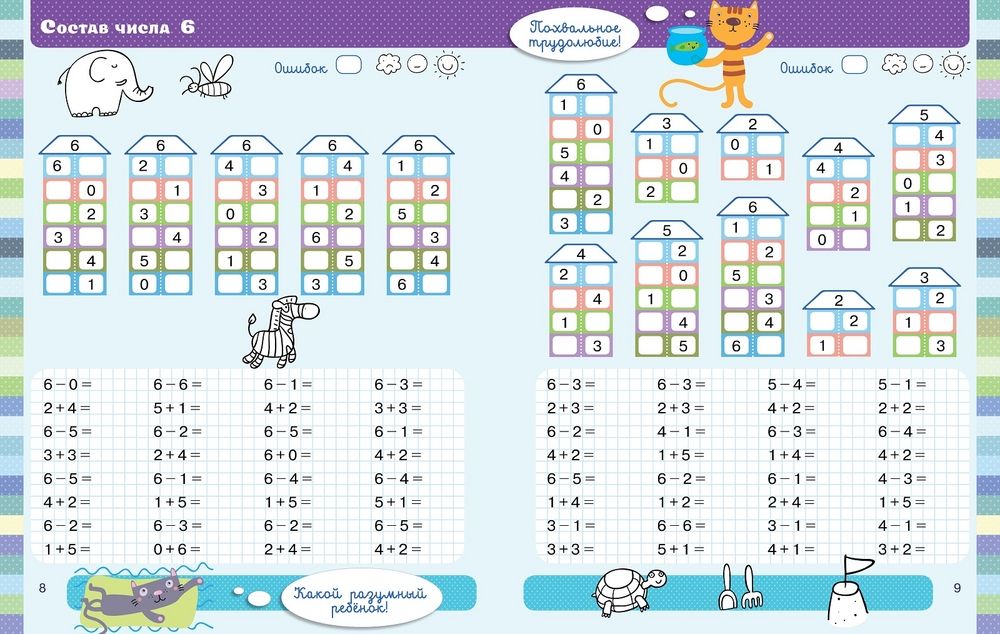 Летчики должны быть очень внимательными.

III. “ФОТОГРАФИРОВАНИЕ”.

— Какие фигуры? (Квадрат, круг, треугольник)

— Сколько их? (3)

— Какого цвета? (Жёлтый, красный, зелёный)

— Будьте внимательны. Что изменилось? (Порядок: красный, жёлтый, зелёный)

Посмотрите в небе летают арифметические облака. Составьте и решите задачи по выражениям:

Мы уже далеко от родной земли. Какое здесь темное небо! И много самолетов. Видимо была гроза и самолеты сбились с пути. Надо помочь провести каждый самолет точно по курсу. А кто быстро и правильно выполнит задание, тот становится капитаном нашего экипажа.

10 – 4 =   9– 5 =   8 + 2 =

6 + 3 =   1 + 7 =    10 – 3 =

Чтобы летчиком стать,
Чтобы в небо взлетать,
Надо многое знать
Надо много уметь.
И при этом, и при этом,
Вы заметьте-ка,
Летчикам помогает арифметика!

(Остальные дети проверяют с помощью светофоров)

IV. ЗАКРЕПЛЕНИЕ ПРОЙДЕННОГО.

1) У летчика должно быть хорошо развито воображение. Для этого вам предлагается следующее задание:

— На что похожа эта фигура? (Листик, яблоко)

— Из каких цифр она состоит? (3, 1, 5)

— Напишите эти цифры в порядке возрастания. В порядке убывания. (1, 3, 5; 5, 3, 1)

— Какие это числа? (Однозначные)

— Какую закономерность вы увидели? (Числа идут через один)

— На следующей строке продолжите этот ряд до 9. (1, 3, 5, 7, 9)

Посмотрите в иллюминатор, там пролетают воздушные шарики. На каждом из них записано число. Сейчас мы определим кто у нас самый ловкий. Угадайте, какой пример записан на другой стороне шарика.

V. ФИЗМИНУТКА.

Руки вставим все в разлёт,
Появился самолет.
Мах крылом туда-сюда
Делай “раз” и делай “два”
Раз и два, раз и два,
Опустили руки вниз,
И на место все садись!

VI. ПОВТОРЕНИЕ ПРОЙДЕННОГО.

Пока мы с вами делали зарядку, немного проголодались. Сколько раз надо разрезать батон, чтобы досталось по 1 части 5 ребятам? (4)

Давайте с помощью ножниц это проверим.

— Капитан, все ли спокойно на борту самолета? Мне, кажется, там кто-то выглядывает? Кто там? Воздушный пират. Он хочет на нас напасть!

Приготовьтесь к бою! Взяли оружие! А им является ум, быстрота и смелость.

Правильно решим пример — отобьемся от пиратов (№ 8, стр. 6, самостоятельно).

Прочитать пример, в ответе которого получилось число 1, 8, 10, 9, 2.

К сожалению, наше путешествие подходит к концу и нужно возвращаться на землю. А на земле, посмотрите, нас встречает кто? (Птицы)

— Какие это птицы? (Воробьи, вороны, синицы, снегири)

— Как их можно назвать? (Зимующие)

— Чем мы можем помочь птицам зимой? (Ставить кормушки, подкармливать)

— Составьте задачу.

— К какой схеме подходит эта задача?

Одну из задач записать и решить.

А сейчас нам нужно в бортжурналах начертить маршрут нашего путешествия. Приготовьте линейки и простые карандаши.

1-й отрезок — 7 клеток.

2-й отрезок — на 4 клетки меньше.

А 3-й отрезок — на 2 клетки больше, чем 2-й отрезок.

VII. ИТОГ УРОКА.

«Закрепление счёта и навыков сложения и вычитанияв пределах десяти»

Цель:

закрепление знаний, умений, навыков счёта и вычислительных навыков сложения и вычитания в пределах 10

Задачи:

1. Повторить прямой и обратный счёт от 0 до 10, закрепить понятия «рядом. между, после, перед; закрепить знание соседних чисел в числовом ряду, умения вычислять число на больше, на меньше; повторить состав чисел; закрепить навыки сложения, вычитания, сравнения чисел первого десятка и решения простой задачи на нахождение суммы;

2. Способствовать формированию логического мышления- учить операциям анализа, сравнения обобщения, исключения лишнего понятия из группы; развивать речь, память, внимание;

3. Способствовать формированию коммуникативной компетенции учащихся, учить культуре учебного труда, повышать познавательные интересы детей.

Оборудование:

Проектор, доска, мультимедийная презентация, дидактический раздаточный материал (конверты с карточками чисел, карточки для инд. работы ученикам продвинутого уровня), карточки для оценки учеников, ободок-кошачьи ушки.

Ход урока.

1. Организация класса

Необычный день у нас.

Гости к нам пожаловали в класс.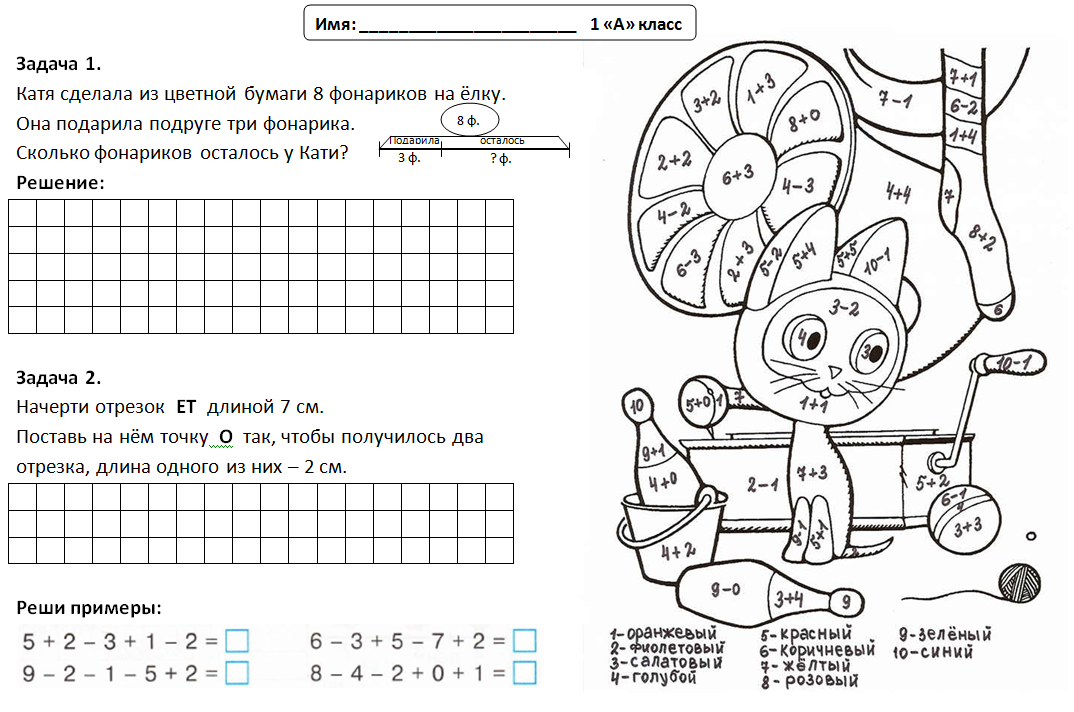

Что гостям сказать нам надо?

(Видеть Вас мы очень рады!)

Психологический настрой на урок. Игра «Вот так!»

(На каждый вопрос дети хором отвечают: “Вот так!” и жестом показывают нужное действие.

— Как живёте?

— Вот так! (Показать большой палец)

— Как идёте?

— Вот так! (Прошагать 2 пальцами одной руки по ладошке другой)

— Как бежите?

— Вот так! (Согнуть руки в локтях и показать, как работают ими при беге)

— Ночью спите?

— Вот так! (Руки “ лодочкой” под щёку и положить на них голову)

— Как берёте?

— Вот так!

— А даёте?

— Вот так!

— Как шалите?

— Вот так! (Произвольные движения)

— А грозите?

— Вот так! (Погрозить пальчиком)

— Как сидите?

— Вот так! (Руки на стол)

1. Целеполагание

-Ребята, сегодня у нас необычный урок. Мы изучаем основы математики уже половину учебного года. И научились многому. На уроке мы будем применять наши знания, умения и покажем, чему вы научились, как хорошо умеете считать, вычислять, отвечать, поднимая руку. Вести себя на уроке, как настоящие ученики.

Начнём. Для начала отгадаем загадки:

У неё косички,
Длинные реснички,
Юбочка с воланами,
Платьице с карманами.
Кто же это: белочка,
Мальчик или девочка? (девочка)

(слайд с девочкой )

Машинки катают,

Играют в танчики,

Игрушки разбросают

Озорные…( мальчики ).

(на экране появляется мальчик)

-Наш урок будет необычным, он пройдёт в форме соревнования между командами «Мальчики» и «Девочки». Посмотрим, кто же из вас более внимательный и умелый математик? Кто лучше считает? Кто умеет слышать учителя и одноклассников? И умеет правильно вести себя на уроке. За правильные и быстрые ответы вы будете получать «5». В конце урока победит та команда, у кого пятёрок больше.

1. Работа по закреплению пройденного материала

1. Лента чисел (работа с карточками)

-Работать сейчас будем в парах. По 2 ученика за партой. Кто умеет дружно работать, получит звёздочку.

Задание: Откройте конверт и положите числа по порядку от 0 до 10 на парту. Вместе постройте числовой ряд.

-Проверим, у кого правильные числовые ряды. Посчитайте вслух от 0 до 10, от 10 до нуля. (несколько детей считают)

-Ребята, числа так обрадовались, что вы хорошо умеете считать, что пришли на наш урок. Посмотрите, вот они на экране (видеоролик «Синий трактор. Счёт 1-5»)

-Ребята, сколько чисел было на экране?

— Каких чисел не хватает, чтобы досчитать до 10?

-Назовите их.

-Кто умеет считать и далее, после 10? (дети считают-1-2 ученика)

-На экране числовой ряд. Все числа написаны синим цветом. Подумайте, почему число 10 выделено красным цветом? Какое оно? Почему число 10 называют двузначным?

-Ну а теперь проверим, знаете ли вы место чисел в ряду?

Отвечать надо не голосом. А показывать карточку с правильным ответом.

Задание: Покажите соседей числа 4.А теперь назовите их.

Покажите соседа слева числу 6? Соседа справа числу 6?

Покажите число, предыдущее при счёте числу 2?

Последующее при счёте за числом 9?( дети показывают карточки, комментируют ответы)

Молодцы, получите звёздочки за правильные ответы.

1. Игра « Злая волшебница»

-Закройте глаза. Пока вы заснули, прилетела злая волшебница и перепутала все числа.

-Откройте глаза, и скажите ,что изменилось? (ответы детей)

-Заполните прямой и обратный числовые ряды на своём листке.

1. Игра « Запретное число»

А теперь встаньте, поиграем в «запретное число».

Я вразнобой буду называть числа, а вы показывайте эти числа на пальцах. Но показывать запретное число нельзя.

Сейчас запретное число 2.

4,6,5,8,1.

1. Игра «Мальчики на 1 больше, девочки на 1 меньше»

Задание: показать на пальцах число- мальчики на 1 больше, девочки на 1 меньше.

А теперь заполните таблицу в ваших листках.

Мальчики:

1	3	5	7	9

Девочки:

3	5	7	9	11

1. Устный счёт

За правильные ответы вы получите звёздочки.

1. Работа над задачей.

За правильный ответ-звёздочка.

(на экране рисунок к задаче)

-Составьте задачу по рисунку.

(ответы детей)

-А теперь решим задачу и запишем её решение. (ответы детей)

А теперь посмотрите на рисунок и внимательно послушайте.

Во дворе гуляли мальчики и девочки. Сколько детей всего?

Это задача? Почему?

Во дворе гуляли 4 мальчика и 3 девочки. У кого из них есть мишка?

Это задача? Почему?

Во дворе гуляли 4 мальчика и 3 девочки. Кого из них больше? На сколько?

Это задача? Почему?

1. Игра: « Кто погладит кошку?»

К доске выходит пара детей. Один игрок-кошка, он отходит несколько шагов от своего партнёра и говорит второму:

-Сколько до меня больших шагов?

Или

-Сколько до меня шагов-лилипутов?

А второй должен прикинуть. назвать число шагов, потом пройти сколько назвал-и дотянуться до игрока-кошки и погладить его.

Потом игроки меняются ролями.

то ответит правильно и погладит кошку-получит звёздочку.

-Из каких геометрических фигур этот котёнок?

1. Игра «Покажите вместе 5»

Игра на пальцах.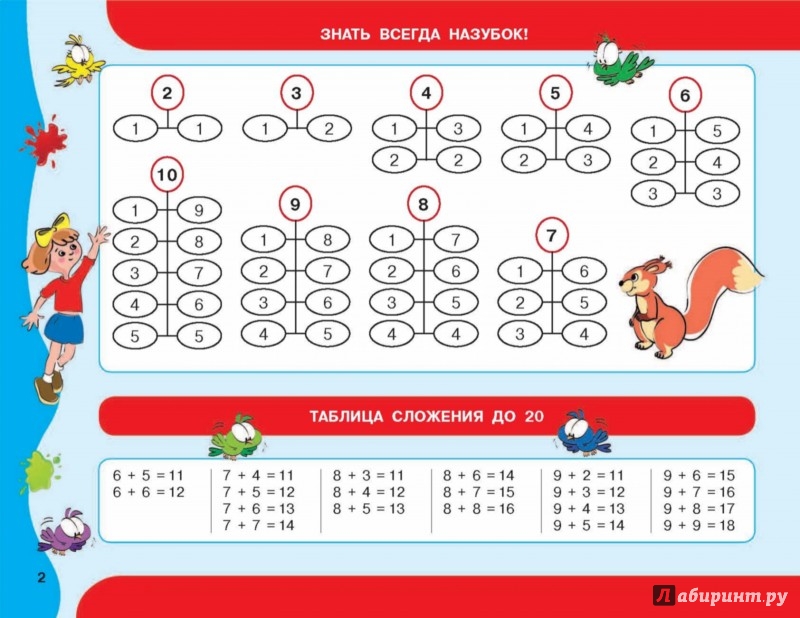 Я покажу на пальцах число от 0 до 5, а вы должны будете добавить от 0 до 5 пальцев-чтобы вместе они показывали ровно 5.

1. Работа над закреплением состава чисел.

-Расскажите состав чисел 2,3,4,5. Кто знает состав числа 6? Состав числа 7? И т.д.

Выполните задание на вашем листочке, впишите числа в домики состава чисел.

Проверка. (На экране появляются числа в домиках)

1. Сравнение чисел

Пьёт бензин, как молоко,

Может бегать далеко,

Возит грузы и людей.

Ты знаком, конечно, с ней.

Четыре колеса,

Резиновые шины,

Мотор и тормоза…

Как она называется? (Машина)

— Конечно, это любимая игрушка наших мальчиков.

А теперь послушайте загадку и постарайтесь ее отгадать.

Она на вид одна большая,

Но в ней сестра сидит вторая,

А третью во второй найдешь.

Их друг за дружкой разбирая,

До самой маленькой дойдешь.

Внутри их всех – малютка, крошка.

Все вместе – сувенир… (матрешка).

— Правильно, матрешка!

-Сравним количество предметов. А теперь выполните задания на листке. За быстрые правильные ответы-звёздочка.

Задание на листочках:

11. Физминутка «Пальчики»

У детишек-шалунишек, девочек и мальчиков

Знаем мы, на каждой ручке пять весёлых пальчиков

На другую посмотри, тоже пять. Не два, не три

Сложим пальцы вместе. Сколько пальцев? (10)

1. Конкурс «Быстрый счёт»

Ну а теперь проверим, кто же быстро умеет решать примеры. У девочек примеры на сложение. У мальчиков-на вычитание.

Решите примеры на карточках. Кто решит быстро и правильно, получит звёздочку.

1. Логические задания (резерв)

Найдите лишнее. Объясните свой выбор.

1. Итог урока

Подсчёт звёздочек.

Победители соревнования.

Рефлексия.

-Что мы умеем? Чему научились в школе?

(Счёт 0-10 прямой и обратный, место числа в ряду, соседи чисел, сравнение чисел, состав чисел, решение задач, выполнение логических заданий.)

Награждение медалями самых активных учеников.

Награждение медалями за стремление к знаниям.

Теперь ваши тетради будут украшены медалями.

9

Что такое числовое предложение? Определения Факты и примеры

Что такое числовое предложение?

Числовое предложение — это математическое предложение, состоящее из чисел и символов, как показано ниже.

Термин «числовое предложение» вводится на уровне начальной школы. Однако применение этих предложений выходит за рамки начальной школы, поскольку включает уравнения и неравенства. Эти предложения также можно описать как язык математики. Как показано ниже, предложение объединяет два выражения с символом отношения $(=, \gt, \lt, \text{etc. })$.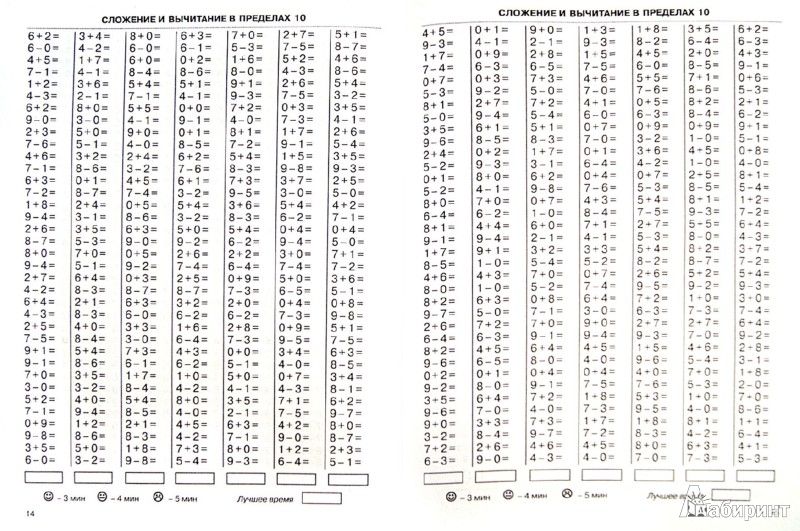

Эти предложения показывают отношения равенства или неравенства с использованием различных математических операций, таких как сложение, вычитание, умножение и деление.

Знак равенства и неравенства важен, так как предложение неполное и без них не имеет смысла.

10 $ + 8 \gt 15 $ — это пример числового предложения. Однако если мы напишем $10 + 8$  $15$, это не будет иметь никакого смысла.

Математическое предложение может быть истинным или ложным в зависимости от предоставленной информации.

Математическое предложение, которое дает всю информацию и известно, является ли оно истинным или ложным, как показано в примере ниже.

Применение числовых предложений

Математические задачи на предложения могут проявляться в виде задач со словами, в которых учащимся предлагается написать числовое предложение.

Например: У Мэри 10 ягод клубники. Если Дэн даст ей 15 ягод клубники, сколько всего клубник будет у Мэри?

Итак, у Мэри есть 10 долл.  США + 15 = 25 долл. клубники.

Почему учащиеся должны свободно произносить математические предложения?

1. Математические предложения помогают учащимся понять алгебру. Это включает в себя вплетение алгебраического мышления в математику начальной и средней школы.
2. Математические предложения обеспечивают гибкость решения задачи по сравнению с базовыми алгоритмами. Используя предложения, учащиеся могут разбить числа, чтобы увидеть значение каждой цифры. Они могут составлять и разлагать числа по разрядному значению или использовать другие стратегии, развивая свои навыки рассуждения и ментальной математики, как показано в примере ниже.

Интересный факт!

Числовые предложения — это просто числовое выражение словесной задачи.

Решенные примеры

Пример 1. Определите, является ли следующее предложение истинным или ложным.

$12 + 12 + 12 \lt 4 \times 12$

Решение:

Выражение в правой части знака неравенства (меньше) равно $12 + 12 + 12$, что равно 36

Решая выражения в правой части знака неравенства (меньше), получаем $4 \times 12$ или 48,

Поскольку $36 \lt 48$, мы можем сказать, что данное предложение $12 + 12 + 12 \lt 4 \times 12$ истинно.

Пример 2: Завершите математическое предложение так, чтобы оно было верным.

$6 + 7 = 9$ $+$ $\underline{}$

Решение:

$6 + 7 = 13$

Итак, чтобы сделать предложение верным, $9$ $+$ $\underline {}$ должен быть равен 13. Следовательно, пропущенное число должно быть $13$ $–$ $9$ или 4.

Пример 3. Подставьте значение в переменную (x) и укажите, является ли полученное предложение истинным или ЛОЖЬ.

$12 –$ x $= 9$ , подставьте 4 вместо x

Решение:

что неверно, поскольку $12$ $–$ $4 = 8 ≠ 9$.

Пример 4: Найдите значение x, чтобы следующее предложение было истинным.

$\text{x}$ $–$ $24 = 10$

Решение:

Добавление одного и того же числа к обеим сторонам знака равенства сделает предложение верным.

Чтобы найти значение x, мы можем добавить 24 к обеим сторонам знака равенства.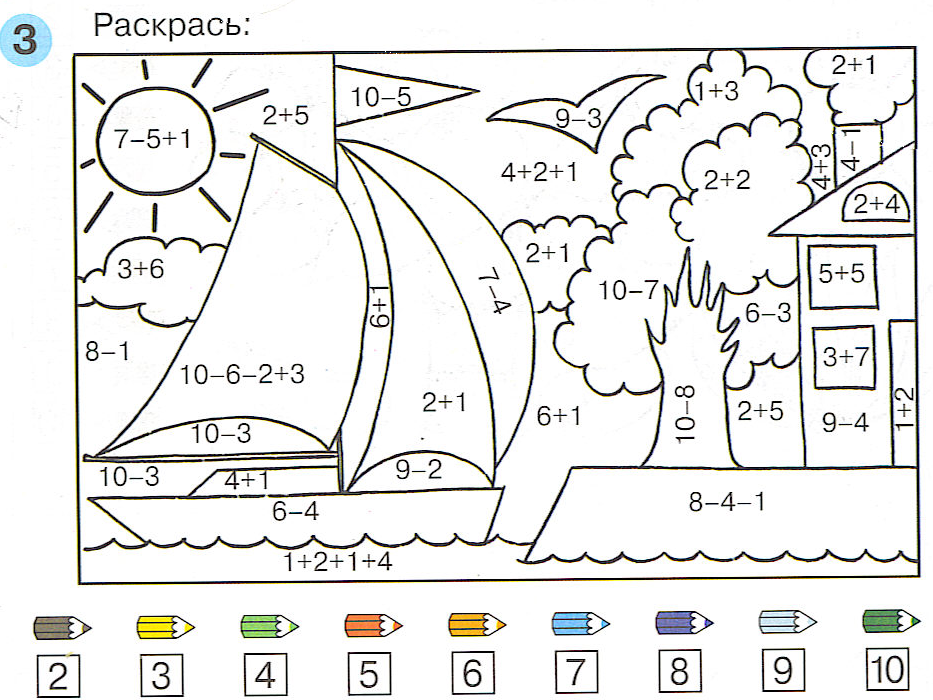

$\text{x}$ $–$ $24 + 24 = 10 + 24$

Следовательно, $\text{x}$ $= 34$

Практические задачи

1

Что из следующего не является числовое предложение?

$45 + 30 = 75$

$30 + 20 \gt 40$

$66 + 30$

$40 + 40 \lt 100$

Правильный ответ: $66 + 30$
Математическое предложение должно показывать отношение между двумя выражениями с такими символами, как $= , \lt \text{или} \gt$. Таким образом, $66 + 30$ — это не приговор.

2

Выберите правильное утверждение для предложений, данных ниже.

$40 + 30 = 70$
$90 + 1000 = 1900$

Верно только 1

Верно только 2 верно
$40 + 30 = 70, \text{но} 90 + 1000 = 1090 ≠ 1900$

3

Определите символ, который может заполнить пропуск, чтобы сделать предложение верным?

90 ◯ 20 = 70

$-$

$+$

$\times$

$\div$

Правильный ответ: $-$
$90$ $–$ $20 = 70$

Часто задаваемые вопросы

число предложение, чтобы быть правдой?

Математическое предложение не обязательно должно быть истинным.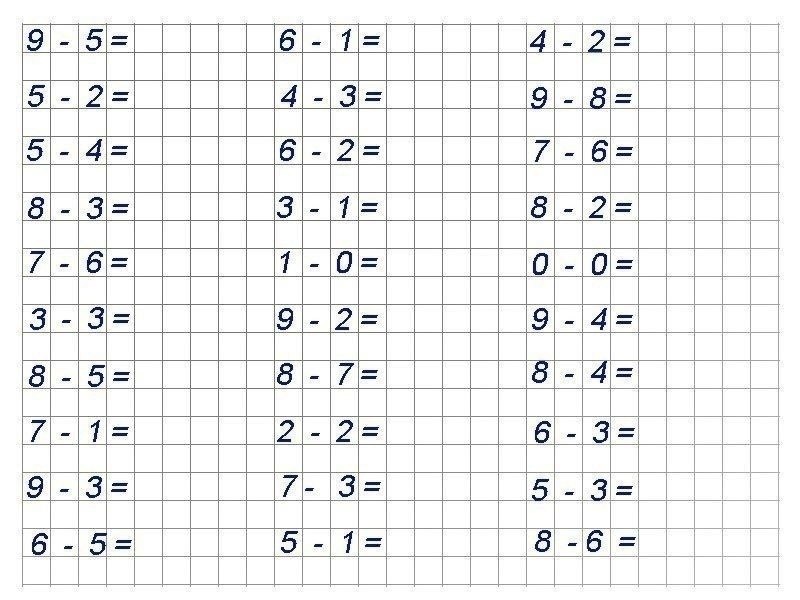 Однако каждое предложение дает нам информацию, и на основе предоставленной информации можно изменить утверждение с ложного на истинное.

В чем разница между уравнениями и неравенствами?

Уравнение — это математическое предложение, показывающее равное значение двух выражений, а неравенство — это предложение, показывающее, что одно выражение меньше или больше другого.

Можно ли дробные числа записать в виде числового предложения?

Да, дробные числа можно записать в виде предложения. Например,

$\frac{3}{4}+\frac{5}{4} = \frac{8}{4}$

Попрактикуйтесь в решении задач на смесь!

Объяснение

Purplemath

Обычно эти «смешанные» упражнения довольно легко решить, если вы нашли уравнения.

Чтобы помочь вам понять, как получить данную информацию, выбрать переменные, создать таблицу, чтобы организовать все, а затем создать уравнения, ниже приведены еще несколько задач с их сетками (но не их решения; я оставил эту часть для вас сделать).

Содержимое продолжается ниже

MathHelp.com

Задачи на смешанные слова

• Сколько литров 70-процентного спиртового раствора нужно добавить к 50 литрам 40-процентного спиртового раствора, чтобы получить 50-процентный спиртовой раствор?

Вы будете смешивать более сильный раствор с более слабым раствором. Количество литров более сильного раствора в настоящее время неизвестно; Я буду использовать s для обозначения количества литров более крепкого раствора. Тогда количество литров приготовленной вами смеси будет

s  + 50.

Составьте таблицу, в столбцах которой указаны количества литров растворов, процентное содержание спирта в каждом растворе (это ваша «норма «), и количество литров фактического спирта в каждом растворе.

	литр раствор	процент спирт	Всего литров Алкоголь
70% раствор	с	0,70	0,70 с
40% раствор	50	0,40	0,40(50) = 20
50% раствор	с + 50	0,50	0,50( с + 50)

Из последнего столбца вы получите уравнение:

0,7 с + 20 = 0,50( с + 50)

Найдите значение переменной.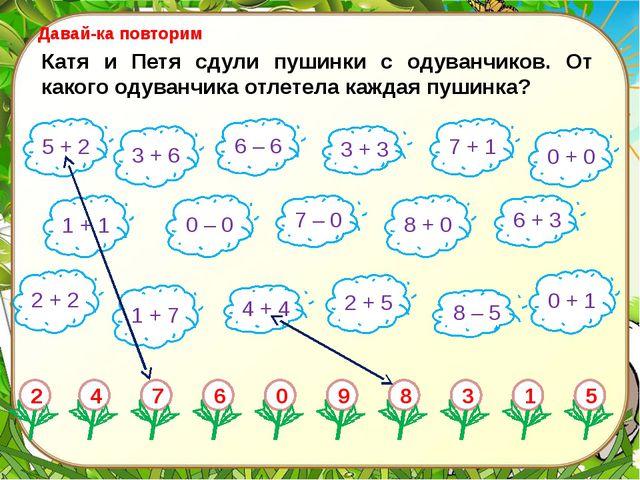 Не забудьте указать соответствующие единицы измерения (в данном случае «литры») в своем ответе.

Поскольку 40 % ближе к 50 %, чем к 70 %, следует ожидать, что в конечном итоге вы израсходуете больше литров 40 % раствора, чем 50 литров 70 % раствора.

---

• Сколько унций чистой воды нужно добавить к 50 унциям 15% солевого раствора, чтобы получить солевой раствор, содержащий 10% соли?

Я буду использовать w для обозначения необходимого количества унций воды. А так как в чистой воде нет соли, то процент воды, которая является солью, равен нулю, и количество унций соли также равно нулю.

	унция жидкость	процент соль	унция соль
вода	ш	0	0
15% раствор	50	0,15	0,15(50) = 7,5
10% раствор	50 + ш	0,10	0,10(50 + с )

Из последнего столбца вы получите уравнение:

7,5 = 0,10(50 + w )

Найдите w . Не забудьте указать соответствующие единицы измерения (в данном случае «унции») в своем ответе.

Примечание. Это упражнение типично для курсов алгебры и используется для обучения навыкам решения задач на уроках алгебры. Но, в реальной жизни, фактический процесс отличается. (Пример) Если вы находитесь в химической лаборатории, ожидайте, что измерение и смешивание будут работать по-другому.

---

• Найдите продажную цену за фунт кофейной смеси, приготовленной из 8 фунтов кофе, которая продается по цене 9,20 доллара за фунт, и 12 фунтов кофе по цене 5,50 доллара за фунт.

В этом упражнении нам предлагается сделать неявное допущение о том, что цена продажи смеси основана только на цене продажи (и количествах) вводимых ресурсов. Конечно, в реальной жизни продажная цена смеси была бы наценкой на стоимость смеси, а стоимость смеси была бы связана со стоимостью вводимых ресурсов плюс дополнительными затратами, связанными с смешиванием и переработкой. расфасовка. Но это алгебра, а не реальная жизнь.

Цена за фунт — это «ставка» для этого упражнения. Предполагается, что сумма цен на ресурсы равна общей цене смеси.

	фунтов кофе	стоимость за фунта	общая стоимость кофе
дорогой	8	9,20	8(9,20) = 73,60
дешевый	12	5,50	12(5,50) = 66
смесь	8 + 12 = 20	?	73,60 + 66 = 139,60

Из последней строки вы видите, что у вас есть 20 фунтов кофейной смеси. Эта смесь будет продаваться по цене $139,60. Чтобы найти продажную цену за фунт смеси, разделите (139,60 долл. США) на (20 фунтов). Упростите деление, чтобы найти удельную скорость.

Не забудьте указать соответствующие единицы измерения (в данном случае «доллары за фунт») в своем ответе.

Обратите внимание, что в данном случае переменная не нужна. Но если бы вы выбрали переменную для замены метки запроса (то есть «?» в нижней строке), это тоже было бы нормально.

---

• Сколько фунтов лимской фасоли стоимостью 0,90 доллара США за фунт нужно смешать с 16 фунтами кукурузы стоимостью 0,50 доллара США за фунт, чтобы приготовить смесь овощей, которая стоит 0,65 доллара США за фунт?

Цена за фунт – это «ставка» для этого упражнения.

Вам дано количество фунтов кукурузы, но не количество фунтов бобов. Я буду использовать b для обозначения этой суммы.

	фунтов овощей	стоимость за фунта	общая стоимость овощей
фасоль	б	0,90	0,90 б
кукуруза	16	0,50	16(0,50) = 8
смесь	б + 16	0,65	( б + 16)(0,65)

Стоимость исходных материалов добавляется к стоимости смеси, что (из крайнего правого столбца) дает уравнение: для значения переменной.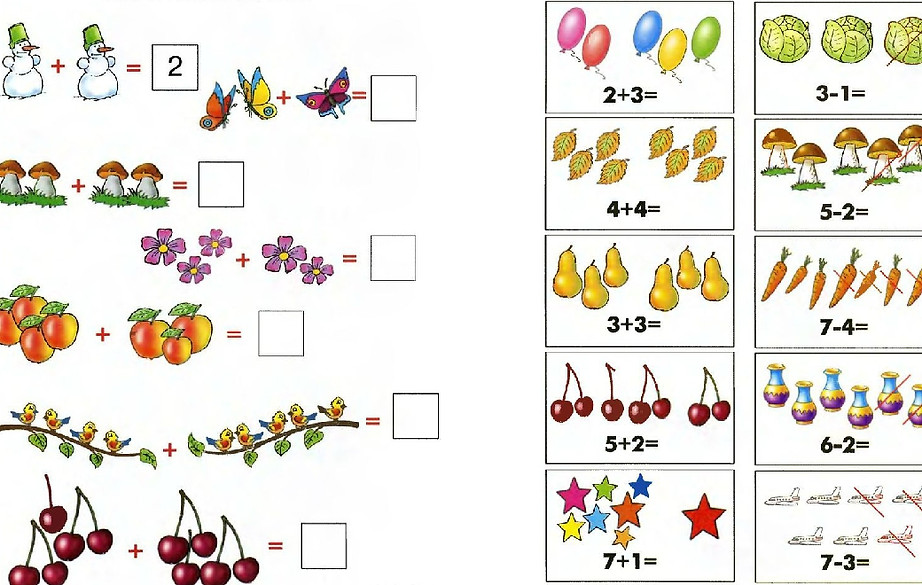 Не забудьте указать соответствующие единицы измерения (в данном случае «фунты») в своем ответе.

---

• Двести литров пунша, содержащего 35% фруктового сока, смешивают с 300 литрами (л) другого пунша. Полученный фруктовый пунш состоит из 20% фруктового сока. Найдите процент фруктового сока в 300 л пунша.

Процент удара, полученного от настоящих фруктов, является «нормой» для этого упражнения. Поскольку в упражнении запрашивается процент, я буду использовать переменную f .

	пробойник, L	% сок	сок, л
35% сок	200	0,35	0,35(200) = 70
прочие соки	300	р	300 р
смесь	200 + 300 = 500	0,20	0,20(500) = 100

Сумма введенных количеств сока будет равна общему количеству сока в смеси. Вы можете использовать последний столбец, чтобы создать уравнение:

70 + 300 p = 100

Или вы можете просто посмотреть на суммы и заметить, что 300 p должно равняться 30. В любом случае выполните деление, чтобы найти значение переменной. Помните, что вы ищете проценты, поэтому вам нужно преобразовать десятичное решение в процентную форму.

---

• Десять граммов сахара добавляют к 40-граммовой порции хлопьев для завтрака, состоящих на 30% из сахара. Какова процентная доля сахара в полученной смеси?

Обратите внимание, что, поскольку сахар состоит из 100% сахара, процентное содержание сахара в том, что добавляется в чашу, в десятичной форме равно 1,00.

Я буду использовать переменную s для обозначения процентного содержания сахара в смеси.

	грамм в миске	процент сахар	грамм сахар
сахар	10	1,00	10(1,00) = 10
крупа	40	0,30	40(0,30) = 12
смесь	10 + 40 = 50	с	10 + 12 = 22

Из нижнего ряда видно, что в 50 граммах в миске 22 грамма сахара, или ²² / ₅₀ .