‎App Store: Математика: решение примеров

Описание

Игра + обучение математике + таблица умножения в одном приложении!

Режим «Обучение» подойдет детям 1,2,3, 4 класса. Выбирайте операции которые нужно подтянуть (умножение, деление, сложение, вычитание) и пройдите большой арифметический тест, в конце теста будут наглядно показаны ошибке в виде таблицы результатов, с указанием правильных ответов. Ответы во время обучения вводить можно как в формате «выбери правильный вариант», так и в режиме ручного ввода цифр.

Режим «Игра» подойдет для детей и взрослых. Решать примеры нужно не только правильно но и быстро. Тут тебе придется показать все свои знания по математике и таблице умножения, чтобы решить арифметические примеры на сложение, вычитание, умножение и деление. Любая математическая игра на счет это настоящая тренировка для мозга. Но когда время на решение примера ограничено, этот навык развивается на более высоком уровне. Решение примеров на время развивает скорость мышления и отлично подходит в качестве тренировки для мозга.

В конце каждой игры ты увидишь подробную статистику твоих математических навыков. А также сравнишь свои очки в таблице лидеров.

Особенности:
• Образовательная игра: развивает арифметические навыки, знание таблицы умножения
• Математика для всех возрастов, для детей и взрослых
• Выбор операций: сложение, вычитание, умножение, деление
• Таблица лидеров
• Интуитивное управление
• Приятная графика
• Переводы: Русский, Английский, Французский, Немецкий, Испанский, Индонезийский, Японский, Китайский, Корейский

27 авг. 2021 г.

Версия 3.53

Улучшения в дизайне.
Новая возможность устанавливать время ответа в режиме обучение математики.

Оценки и отзывы

Оценок: 545

Оплата

Сейчас возможности отключить рекламы нет, не как не заплатить)

👎

Очень слабая игра не зитает ошибки и с временем не плодки

Вопрос по отключению рекламы

Приложение годное, приятно и понятно оформлено. Но… количество рекламы — адское. С одной стороны можно отключить за небольшую денежку, с другой — непонятно, это разово или по принципу подписки? Разъясните пожалуйста

Разработчик Sergey Kharitonov указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Данные, используе­мые для отслежи­вания информации

Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:

Связанные с пользова­телем данные

Может вестись сбор следующих данных, которые связаны с личностью пользователя:

• Покупки
• Геопозиция
• Идентифика­торы
• Данные об использова­нии
• Диагностика
• Другие данные

Не связанные с пользова­телем данные

Может вестись сбор следующих данных, которые не связаны с личностью пользователя:

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов.

Подробнее

Информация

Провайдер

Sergey Kharitonov

Размер

47,2 МБ

Категория

Образование

Возраст

4+

Copyright

© 2015 ИП Харитонов С.А.

Цена

Бесплатно

• Сайт разработчика
• Поддержка приложения
• Политика конфиденциальности

Поддерживается

Другие приложения этого разработчика

Вам может понравиться

Умножения и деление отрицательных чисел.

Решение примеров.

• Альфашкола
• Статьи
• Умножения и деление отрицательных чисел

 

 

В этой статье мы будем изучать умножение и деление отрицательных чисел. Существуют определенные правила умножения отрицательных чисел.

• \(«—«-\) при умножении минус на минус результат становится положительным;
• \(«-+»-\) при умножении минуса на плюс результат становится отрицательным;
•  \(«+-«-\) при умножении плюса на минус результат становится отрицательным;
• \(«++»-\)  при умножении плюса на плюс результат становится положительным.

---

Примеры умножения отрицательных чисел.  

Задача 1. Вычислить: \((-4)*(-4)\) и \((-6)*(-5).\)

Решение.

Отрицательное число при умножении на отрицательное станет положительным согласно правилу.

1. \((-4)*(-4)=16\)
2. \((-6)*(-5)=30\)

Ответ: \(16;30.\)

Задача 2. Вычислить: \((-10)*12\) и \((-7)*4.\)

Решение.

Отрицательное при умножении на положительное число станет отрицательным согласно правилу.

-10 * 12= -120

(-7)*4=-28

 

Ответ: \(-120; -28\)

---

Задача 3. Вычислить: \(11*(-11)\) и \(13*(-6).\)

Решение.

Положительное при умножении на отрицательное число станет отрицательным согласно правилу.

1. \(11*(-11)=-121\)
2. \(13*(-6)=-78\)

Ответ: \(-121;-78.\)

Деление отрицательных чисел

 

При делении действуют те же правила знаков, что и при умножении. Делить на ноль нельзя.

• ​\(«—«-\)​ при делении минус на минус результат становится положительным;
•  ​\(«-+»-\)​при делении минуса на плюс результат становится отрицательным;
•  \(«+-«-\)при делении плюса на минус результат становится отрицательным;
• \(«++»-\) при делении плюса на плюс результат становится положительным.

Задача 4. Вычислить: \((-16)*(-4)\) и \((-6)*(-2)\).

Решение.

1. \(-16:(-4)=4\)
2. \((-6):-2=3\)

Ответ: \(4;3.\)

Задача 5. Вычислить: \((-10):5\) и \((-12):6\).

Решение.

1.  \((-10):5=-2\)
2. \((-12):6=-2\)

Ответ: \(-2;-2.\)

Задача 3. Вычислить:  \(121:(-11)\) и  \(169:(-13)\).

Решение.

1.  \(121:(-11)=-11\)
2.  \(169:(-13)=-13\)

Ответ: \(-11;-13.\)

 

 

 

 

 

 

 

 

 

 

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Наши преподаватели

Владимир Валерьевич Ковалев

Репетитор по математике

Стаж (лет)

Образование:

Пятигорский государственный педагогический институт иностранных языков

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по французскому языку для 7-11 классов. Французский язык для меня — это «любовь с первого взгляда и на всю жизнь». В нём — красота и пластичность, математическая логика и дипломатичность, простота и невероятные связи с русским. Не было ни одного дня, чтобы я не совершенствовался в нём, и всякий раз нахожу что-то новое. За 40 прошлых лет были и более 20 лет преподавания в высшей школе, и более 10 лет переводческой работы, подготовка переводчиков к Всемирной шахматной Олимпиаде, Олимпиаде в Сочи и чемпионату мира по футболу-2018. Примерно 25 лет назад во Франции была разработана методика преподавания французского, как иностранного. С тех пор я применял её, как на группах, так и индивидуально, на разных возрастных группах, и, главное — на своих детях. Во всех случаях методика била по эффективности все ВУЗовские программы. Многократно подтверждено: 350 часов занятий, и ученик понимает и говорит на любые общебытовые темы.»

Виктория Анатольевна Шилова

Репетитор по математике

Стаж (лет)

Образование:

Северо-Казахстанский государственный университет имени Козыбаева

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по русскому языку 5-11 классов, подготовка к ОГЭ и ЕГЭ. Также репетитор по истории и обществознанию 5-11 классы, готовлю к ВПР/ОГЭ/ЕГЭ. Скорочтение для 5-11 классов. Я преподаю по авторской методике. Она включает в себя разные подходы и методы преподавания. Все мои ученики сдают выпускные экзамены .Всегда настраиваю на позитивное мышление, мотивирую на успех. Индивидуальный подход к каждому ученику.

Сергей Александрович Москвин

Репетитор по математике

Стаж (лет)

Образование:

Костромской государственный университет им. Н.А. Некрасова

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по русскому языку 2-9 классов, готовлю к ОГЭ. Репетитор по французскому языку 5-11 классы. Магистр филологических наук. Объясняю понятным языком, чтобы ребёнок усвоил правило. Мой ученик набрал за ОГЭ 100 баллов. Если Вашему ребёнку требуется улучшить русский язык, или подготовиться к экзамену, готов Вам помочь.

Похожие статьи

• Объем куба
• Дуга окружности. Центральный угол
• Примеры решения уравнений: логарифм с переменным основанием
• Как решать уравнения смешанного типа?
• Финансовый Университет при Правительстве РФ: Управление Персоналом
• И снова про логарифмические неравенства
• ОГЭ по математике, базовый уровень. Системы неравенств
• Лучшие идеи декора на Хэллоуин своими руками

Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности

Как научиться быстро считать в уме любые числа: техники устного счета

Устный счет – занятие, которым в наше время себя утруждает все меньшее количество людей. Гораздо проще достать калькулятор на телефоне и вычислить любой пример.

Но так ли это на самом деле? В этой статье мы представим математические лайфхаки, которые помогут научиться быстро складывать, вычитать, умножать и делить числа в уме. Причем оперируя не единицами и десятками, а  минимум двухзначными и трехзначными числами.

После освоения методов из этой статьи идея лезть в телефон за калькулятором уже не покажется такой хорошей. Ведь можно не тратить время и посчитать все в уме гораздо быстрее, а заодно размять мозги и произвести впечатление на окружающих (противоположного пола).

Итак, добро пожаловать в увлекательный мир вычислений! Мы собрали советы от наших авторов о том, как улучшить устный счет и стать математическим героем и гением. Кстати, если вам интересна математика, вы можете почитать статью «Пределы для чайников» в нашем блоге.

Предупреждаем! Если вы обычный человек, а не вундеркинд, то для развития навыка счета в уме понадобятся тренировки и практика, концентрация внимания и терпение. Сначала все может получаться медленно, но потом дело пойдет на лад, и вы сможете быстро считать в уме любые числа.

Гаусс и устный счет

 

Карл Фридрих Гаусс

 

Одним из математиков с феноменальной скоростью устного счета был знаменитый Карл Фридрих Гаусс (1777-1855). Да-да, тот самый Гаусс, который придумал нормальное распределение.

По его собственным словам, он научился считать раньше, чем говорить.  Когда Гауссу было 3 года, мальчик взглянул на платежную ведомость своего отца и заявил: «Подсчеты неверны». После того как взрослые все перепроверили, выяснилось, что маленький Гаусс был прав.

В дальнейшем этот математик достиг немалых высот, а его труды до сих пор активно используются в теоретических и прикладных науках. До самой смерти большую часть вычислений Гаусс производил в уме.

Здесь мы не будем заниматься сложными расчетами, а начнем с самого простого.

Сложение чисел в уме

Чтобы научиться складывать в уме большие числа, нужно уметь безошибочно складывать числа до 10. В конечном счете любая сложная задача сводится к выполнению нескольких тривиальных действий.

Чаще всего проблемы и ошибки возникают при сложении чисел с «переходом через 10». При сложении (да и при вычитании) удобно применять технику «опоры на десяток». Что это? Сначала мы мысленно спрашиваем себя, сколько одному из слагаемых не хватает до 10, а потом прибавляем к 10 оставшуюся до второго слагаемого разность.

Например, сложим числа 8 и 6. Чтобы из 8 получить 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В итоге получаем: 8+6=(8+2)+4=10+4=14

Основная хитрость со сложением больших чисел – разбить их на разрядные части, а потом сложить эти части между собой.

Пусть нам нужно сложить два числа: 356 и 728. Число 356 можно представить как 300+50+6.  Аналогично, 728 будет иметь вид 700+20+8. Теперь складываем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание чисел в уме

Вычитание чисел тоже будет даваться легко. Но в отличие от сложения, где каждое число разбивается на разрядные части, при вычитании «разбить» нужно только то число, которое мы отнимаем.

Например, сколько будет 528-321? Разбиваем число 321 на разрядные части и получаем: 321=300+20+1.

Теперь считаем: 528-300-20-1=228-20-1=208-1=207

Попробуйте визуализировать процессы сложения и вычитания. В школе всех учили считать в столбик, то есть сверху вниз. Один из способов перестроить мышление и ускорить счет – считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме

Умножение – это многократное повторение числа. Если нужно умножить 8 на 4, это значит, что число 8 нужно повторить 4 раза.

8*4=8+8+8+8=32

Так как все сложные задачи сводятся к более простым, нужно уметь умножать все однозначные числа. Для этого существует отличный инструмент – таблица умножения. Если вы не знаете эту таблицу на зубок, то мы настоятельно рекомендуем первым делом выучить ее и только потом приниматься за практику устного счета. К тому же учить там, по сути, нечего.

 

Таблица умножения

 

Умножение многозначных чисел на однозначные

Сначала потренируйтесь в умножении многозначных чисел на однозначные. Пусть нужно умножить 528 на 6. Разбиваем число 528 на разряды и идем от старшего к младшему. Сначала умножаем, а потом складываем результаты.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Умножение двузначных чисел

Здесь тоже нет ничего сложного, только нагрузка на краткосрочную память немного больше.

Перемножим 28 и 32. Для этого сведем всю операцию к умножению на однозначные числа. Представим 32 как 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Еще один пример. Умножим 79 на 57. Это значит, что на нужно взять число «79» 57 раз. Разобьем всю операцию на этапы. Сначала умножим 79 на 50, а потом – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950
• 79*7=(70+9)*7=490+63=553
• 3950+553=4503

Умножение на 11

Вот хитрый прием быстрого устного счета, который поможет умножить любое двузначное число на 11 с феноменальной скоростью.

Чтобы умножить двузначное число на 11, две цифры числа складываем друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в итоге трехзначное число — результат умножения исходного числа на 11.

Проверим и умножим 54 на 11.

• 5+4=9
• 54*11=594

Возьмите любое двузначное число, умножьте его на 11 и убедитесь сами — эта хитрость работает!

Возведение в квадрат

С помощью другого интересного приема устного счета можно легко и быстро возводить двузначные числа в квадрат. Особенно просто это делать с числами, которые заканчиваются на 5.

Результат начинается с произведения первой цифры числа на следующую за ней по иерархии. То есть, если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Проверим! Возведем в квадрат число 75.

• 7*8=56
• 5*5=25
• 75*75=5625

 

Раньше все считали без калькуляторов

 

Деление чисел в уме

Осталось разобраться с делением. По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно – ведь есть таблица умножения, которую вы знаете на зубок.

Деление на однозначное число

При делении многозначных чисел на однозначное необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Например, есть число 6144, которое нужно разделить на 8. Вспоминаем таблицу умножения и понимаем, что на 8 будет делиться число 5600. Представим пример в виде:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

При делении на двузначное число нужно пользоваться правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр этих чисел.

Например, умножим 1325 на 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, вооружившись этой ценной информацией, рассмотрим деление на двузначное число.

Сколько будет 4424:56?

Первоначально будем пользоваться методом «подгона» и найдем пределы, в которых лежит результат. Нам нужно найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Ее произведение на 6 должно заканчиваться цифрой 4. Согласно таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления  может быть либо число 74, либо 79. Проверяем:

79*56=4424

Готово, решение найдено! Если бы не подошло число 79, второй вариант обязательно оказался бы верным.

 

Картина Н.П. Богданова-Бельского «Устный счёт. В народной школе С. А. Рачинского»

 

Полезные советы

В заключение приведем несколько полезных советов, которые помогут быстро научиться устному счету:

• Не забывайте тренироваться каждый день;
• не бросайте тренировки, если результат не приходит так быстро, как хотелось бы;
• скачайте мобильное приложение для устного счета: так вам не придется самостоятельно придумывать себе примеры;
• почитайте книги по методикам быстрого устного счета. Существуют разные техники устного счета, и вы сможете овладеть той, которая лучше всего подходит именно вам.

Польза устного счета неоспорима. Тренируйтесь, и с каждым днем вы будете считать все быстрее и быстрее. А если вам понадобится помощь в решении более сложных и многоуровневых задач, обращайтесь к специалистам студенческого сервиса за быстрой и квалифицированной помощью!

Как объяснить ребенку умножение и деление?

Развитие ребенка

Как объяснить ребенку умножение и деление?

30 октября 2019 30 781 просмотр

Екатерина Ушахина

Можно заставить ребенка просто решать скучные примеры (и ему будет совсем неинтересно), а можно предложить ему решить забавные текстовые задачки в тетради Kumon или сразиться в межпланетном рыцарском турнире на звание лучшего знатока дробей. Второй подход определенно занимательнее: ребенку гораздо больше понравится учить математику в игре.

Ребятам постарше также по душе будут игровые моменты в обучении. Ведь гораздо веселее изучать математику через яркое домино, чем читать длинные главы в учебнике.

Подготовили для вас несколько советов и подборку книг, которые помогут разложить умножение и деление по полочкам.

Умножаем

Что такое умножение? При умножении второе число показывает, сколько раз нужно сложить первое число с самим собой. На рисунке в каждой шеренге стоят 13 человек, а всего шеренг 9. Чтобы подсчитать общее количество людей, нужно число 13 сложить само с собой 9 раз. Это и будет произведением чисел 13 на 9.

Не имеет значения, в каком порядке перемножаются числа: ответ будет одинаковым. Ниже показаны два способа, как можно вычислить произведение.

Умножение на 10, 100, 1000 Для того чтобы умножить целое число на 10, 100, 1000 и т. д., нужно просто дописать справа от этого числа один нуль (0), два нуля (00), три нуля (000) и т. д.

Приемы умножения. Некоторые числа легко умножать, зная особые приемы. В таблице показаны приемы быстрого умножения на 2, 5, 6, 9, 12 и 20.

Делим

Деление позволяет найти, сколько раз одно число содержится в другом. Процесс деления можно представить, например, так: если 10 монет раздать 2 людям, то каждый получит по 5 монет. Или так: 10 монет, разложенные в стопки по 2 монеты, дадут 5 стопок.

Как выполняется деление? Деление одного числа (делимого) на другое (делитель) показывает, сколько делителей содержится в делимом. Например, при делении 10 на 2 мы находим, сколько чисел 2 содержится в числе 10. Результат деления называется частным.

Деление как распределение. Распределение чего-либо — это, по сути, операция деления. Так, если поровну распределить четыре конфеты между двумя людьми, у каждого из них будет по две конфеты.

Как деление связано с умножением? Деление — это операция, обратная умножению. Если вы знаете результат деления, то можете записать соответствующее произведение, и наоборот.

Если 10 (делимое) поделить на 2 (делитель), то получится 5 (частное). Умножая частное (5) на делитель (2), мы получаем значение исходного делимого (10).

Другой подход к делению. Деление также показывает, сколько раз в делимом встречаются группы, равные делителю. Ответом будет то же самое частное. Получилось ровно 10 групп по 3 мяча (без остатка), поэтому 30 : 3 = 10. В этом примере 30 футбольных мячей делятся на группы по 3 мяча.

Книги и тетради, которые помогут закрепить навыки

Арифметикум

Домино, с которым ребенок научится хорошо складывать, вычитать, умножать и делить числа до 100. Игрок должен разместить карточку так, чтобы на оказавшихся рядом клеточках был написан пример и правильный ответ или два примера, в результате решения которых получится одно число.

Вокруг любой клеточки можно расположить сразу несколько карточек: по одной у каждой свободной стороны. Проверить вычисления игроки могут по цветным узорам: если узоры совпадают, ход сделан правильно.

Умножариум

Веселая игра поможет освоить математику

Это домино создано специально для легкого и увлекательного изучения таблицы умножения детьми: вместо традиционных точек на каждой карточке нанесены математические примеры и цифры.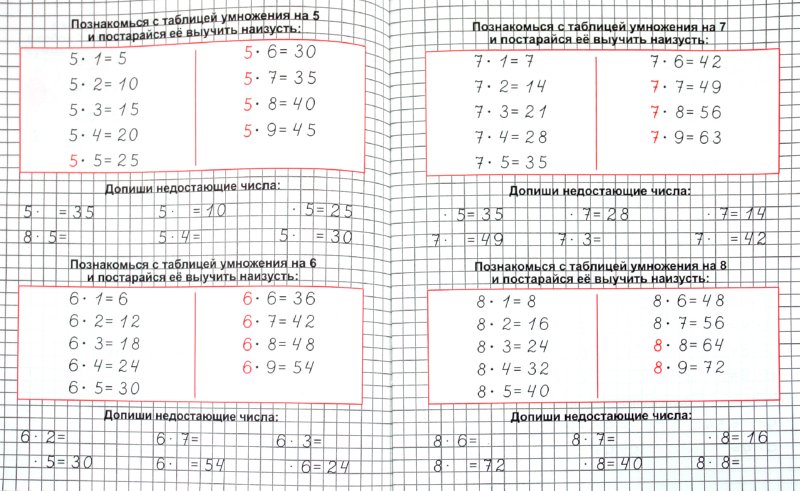 Совмещая клетку с примером (например, 5×8) и результат умножения (40), ребенок сразу видит, правильно ли он посчитал пример, благодаря цветовому паттерну, который должен совпасть на двух клетках.

Kumon спешит на помощь

У нас есть множество тетрадей разных уровней сложности, которые помогут выучить таблицу умножения на зубок.

KUMON. Математика. Умножение. Уровень 4

Эта яркая тетрадка научит ребенка умножать многозначные числа в столбик. Шаг за шагом он будет осваивать этот навык, его ждут примеры, которые будут постепенно усложняться, полезные подсказки и, конечно, ключи с ответами в конце тетради для самоконтроля.

Простые задачки научат умножать. Пример из тетради

Kumon. Математика. Деление. Уровень 4

Выполняя задания в этой тетради, ваш ребёнок научится делить многозначные числа в столбик с остатком и без него. Продвигаясь вперёд небольшими последовательными шажками, он обретёт не только математические знания, но и уверенность в своих силах.

Межпланетный рыцарский турнир

Решая примеры из этой книги, ребенок примет участие в настоящем межпланетном состязании! Каждый правильный ответ — ты успешно атаковал противника, каждая ошибка — противник успешно атаковал тебя. Для убедительности в книге есть изображения персонажей, за которых нужно сыграть юному математику, и их соперников, а также фантастические истории про инопланетян. Всех героев можно раскрасить!

Успешных занятий!

Табличное умножение и деление. Закрепление. 3-й класс

Цель: закрепить знания таблицы умножения и деления с числами 2, 3, 4.

Задачи:

• создавать условия для закрепления знаний таблицы умножения и деления с числами 2, 3, 4;
• создавать условия для формирования вычислительных навыков, умения решать задачи в 2 действия;
• создавать условия для развития умения сравнивать, доказывать, и делать выводы;
• создавать условия для формирования навыков самоанализа, самопонимания;
• показать связь математики с экологией;
• помочь учащимся научиться строить своё поведение в природе на основе знаний взаимосвязей в ней и соответствующей оценке возможных последствий своих поступков;
• содействовать воспитанию культуры поведения, бережного отношения к природе, чувства ответственности при решении экологических проблем.

Ход урока

Учитель: Ребята! Как всегда мы начинаем наш урок с минутки настроения. Сегодня показателем вашего настроения будут листья клёна. На партах у вас листья клёна различного цвета. Выберите и покажите.

– С каким настроением вы начинаете урок?

Радостное – жёлтый
Спокойное – зелёный
Тревожное – красный

– Какое у тебя настроение?
– В классе преобладает спокойное настроение (поместить) дерево, а на нём в основном зелёные листья
– Спасибо. У меня есть возможность на уроке помочь и быть полезной вам.

Чтоб в мир природы окунуться,
Поможет нам сейчас урок,
И мы отправимся все вместе….
В лес, в гости на часок (открыть)

– Но, чтобы отправиться в путешествие надо определить тему урока.

5 * 2 = 10
4 * 2 = 8
5 + 9 = 14
12 : 4 = 3
15 : 5 = 3

– Найдите лишний пример.

(5 + 9 = 14, этот пример из таблицы сложения в пределах 20, а остальные из таблицы умножения и деления.)

– Догадались ли вы, какова тема урока?
– Давайте мы её сформулируем

Табличное умножение и деление (открыть)

– Давайте решим эти примеры
– Что помогло тебе быстро справиться с заданием? (Знание таблицы умножения и деления с числами 2, 3, 4.)
– Чем мы будем заниматься? (Решать примеры и задачи с использованием знаний таблицы умножения и деления с числами 2, 3, 4.)
– Сегодня мы закрепим знания таблицы умножения и деления с числами 2, 3, 4.

1. Для путешествия нам необходимо собрать рюкзак, собирать его будете, объединившись в группы.

– У каждой группы есть только часть рюкзака, но вы можете принести его только тогда, когда правильно выполните задание.
– Чтобы справиться с заданием, вам нужно работать в группе дружно, слаженно и помнить правила работы в группе.
– Вспомните таблицу умножения деления вашего числа и заполните пропуски.

Работа в группах.

3 * 2 = 6
10 : 2 = 5
2 * 6 = 12
20 : 2 = 10
3 * 3 = 9

– Вы успешно справились с заданием.
– Рюкзак для путешествия готов! (Вернулись на места.)
– Подумайте, довольны ли вы результатом выполнения своей работы?
– Поднимите выбранный вами лист (помещаю на другое дерево)
– Для чего необходимо знать таблицу умножения деления? (чтобы быстро и правильно решать примеры и задачи на табличное умножение и деление)
– Молодцы! Вы прекрасно справились с заданием. Рюкзаки собраны. А теперь – в путь! (иллюстрация леса, туда прикрепляю детей с рюкзаками)
– Давайте внимательно послушаем звуки леса, нас встречает лесной житель. Да это дятел! (иллюстрация леса, туда прикрепляю после ответа детей дятла)
– А где мы можем взять информацию о дятле? (в энциклопедии и т. д.)
– Вот и я попросила Костю найти информацию.

Дятел – лесной доктор. Он избавляет деревья от насекомых – короедов. Так вот, один дятел за день съедает 753 паука-короеда. Добывая себе корм, он делает в деревьях выемки, их охотно используют для своих гнезд маленькие птички. Получается такая связь: деревья дятел птички.

(Иллюстрация деревья дятел птички)

– Из этой схемы видно, что растительный и животный мир в лесу связаны невидимыми нитями и составляют природное сообщество.

2. – А какая наука занимается изучением этих взаимоотношений, мы узнаем, когда решим примеры.

Игра “Сорбонки”

– Кто справился без ошибок?
– Поднимите выбранный вами лист (помещаю на другое дерево)
– Почему тебе удалось? Почему у тебя получилось?
– Что тебе нужно сделать, чтобы справиться в следующий раз? (повторить таблицу умножения и деления с числами 2, 3, 4).
– У кого количество правильных ответов увеличилось по сравнению со вчерашним днём?
– Я думаю, что в следующий раз таких ребят будет больше.
Вы прекрасно справились с заданием, поэтому мы можем открыть слово.

(Открываю, на доске запись: ЭКОЛОГИЯ)

– На каком уроке нам это понятие уже встречалось? (На окружающем мире.)
– Давайте вспомним, что такое экология?

По-гречески “экос” – “дом”, “логос” – “наука”. Экология – наука о доме, о месте жительства. Наука о доме – для мыши и журавля, для червя и бабочки, для деревьев, цветов и грибов. Дом этот очень большой: вся Земля является домом для всех на ней живущих.

Учитель: Экология – это наука о связях между живыми существами и окружающей средой, между человеком и природой.

3. – А как вы думаете, связана ли математика с экологией? Приведите примеры (поход до полного разложения бумаги нужно более 2-х лет; консервной банки – более 90 лет; полиэтиленовому кульку – 200 лет; стеклу – 1000 лет.)

Хозяйственная деятельность человека часто приводит к загрязнению воды, воздуха, гибели живой природы, а это, прежде всего, вредит его собственному здоровью, так как человек пьёт воду, дышит, использует в пищу разнообразных животных и растения. А чтобы этого не происходило необходимо вести подсчёты и контролировать деятельность человека.

Давайте убедимся на примере решения заданий.
У вас на партах лежат карточка с заданиями.
– Прочитайте задание 1.

Обычно на одном дереве дятел уничтожает 9 личинок. Сколько всего личинок может истребить дятел на 2 деревьях? на 4 деревьях? (по вариантам)

Можем мы сразу ответить на вопрос задачи? (Да.)

Кто может решить задачу самостоятельно? (решайте), кому нужна помощь?

1в. – отвечает на 1 вопрос, 2в. – отвечает на 2 вопрос, кто сделает быстро, может ответить на вопрос другого варианта.

А Костя, Лера, Аня, Таня ответят на дополнительный вопрос.

– На сколько личинок больше истребил дятел с 4 деревьев, чем с 2? (36-18=18(л.)) Оценки

Ребята, которые решали вперёд, проверьте решение. Проверка (на маркерных досках, 2 человека по вариантам) Оценки

Подумайте, чтобы произошло в природе, если бы дятлы исчезли? (стало бы больше насекомых вредителей, которые бы уничтожили деревья, которые дают пищу животным, выделяют кислород и т. д.)

В природе всё взаимосвязано. Поэтому то, что человек делает в природе, должно быть всегда хорошо продумано. Если люди не продумают заранее свои поступки в природе, не просчитают убытки, они могут нанести ей очень большой вред.

Математические знания могут пригодиться в решении экологических проблем? (Да. Мы на примере этой задачи узнали, сколько пользы приносит дятел)

Чтобы как можно меньше не только дятлов, но птиц исчезало, что необходимо делать?

Веди себя в лесу спокойно.
Не играй в шумные игры и не слушай громко музыку.
Не разоряй птичьи гнезда.
Не бери птенцов в руки (поместить на доску)

Подумайте, довольны ли вы результатом выполнения своей работы?
Поднимите выбранный вами лист (помещаю на другое дерево)

Физкультминутка

В лесу

Солнечным погожим днем
Мы с друзьями в лес идем.
Мы с собой несем корзинки.
Вот хорошая тропинка! (Ходьба на месте.)
Песни птиц звучат повсюду,
Шумом их пугать не буду,
Здесь отличные места,
Ах, какая красота (Наклоны вперед, назад.)
Снова мы идем по лесу.
А вокруг – так интересно!
(Повороты вправо-влево)
Отдохнуть пора, дружок. (Потягивания – руки в стороны.)
Мы присядем. Вот ручеек. (Дети садятся за парты.)

4.– Прочитайте задание 2.

Ученики 4-го класса, гуляя на поляне, сорвали 24 цветка, а ученики 3 класса – 16. Сколько бабочек останется без обеда, если 1 бабочка в среднем, чтобы быть сытой, должна попробовать нектар 4 цветков?

– Кто может решить задачу самостоятельно? (решайте), кому нужна помощь?

– Ребята, которые решали вперёд, проверьте решение (решение проверяем на маркерных досках 1способ один ученик, 2 способ другой ученик)

Подумайте, довольны ли вы результатом выполнения своей работы?

Поднимите выбранный вами лист (помещаю на другое дерево)

На Земле исчезают цветы,
С каждым годом заметнее это.
Меньше радости и красоты
Оставляет нам каждое лето.

Представьте на минуту, закрыв глаза, что все растения Земли вдруг исчезли.

Они поглощают из воздуха вредные для жизни человека газы, задерживают пыль на поверхности листьев, значит нам нечем будет дышать, растения служат для кого-то кормом, опыляют цветы и просто дают красоту,

Чтобы как можно меньше растений исчезало, что необходимо делать?

– Не ломай ветки деревьев.
– Не срывай цветы.

Физкультминутка

– Закройте глаза, прислушайтесь, вы непременно услышите чудесные звуки Земли.

5. – Ну что ж, ребята, идём дальше. Что же мы видим? Вам открылась неведомая лесная тропинка, по которой надо пройти (иллюстрация леса с лесной тропинкой)

– Но пройти по ней можно только по одному. Все вы поняли, какое большое значение имеет наука экология. Но если вы заметили, она очень тесно связана с математикой: ведь во всем нужны числовые подсчеты. Поэтому, чтобы стать настоящими экологами, мы сначала должны поупражняться в вычислениях самостоятельно.

– Вам необходимо каждому найти правильный ответ (ответы пишут на маркерных досках)

1 вариант

1. Выбери пример с ответом 10.

а) 3 * 2
б) 3 * 3
в) 3 * 4
г) 2 * 5

2. 1 множитель 2, произведение 14.Чему равен второй множитель?

а) 7
б) 14
в) 18
г) 9

3. Делимое 21, делитель 7.Чему равно частное?

а) 4
б) 3
в) 14
г) 30

4. Выбери пример с ответом 2.

а) 20 : 2
б) 12 : 3
в) 6 : 3
г) 9 : 3

2 вариант

Выбери пример с ответом 12.

а) 3 * 3
б) 9 * 1
в) 2 * 5
г) 2 * 6

2. 1 множитель 3, произведение 15.Чему равен второй множитель?

а) 5
б) 6
в) 15
г) 9

3. Делимое 12, делитель 2.Чему равно частное?

а) 3
б) 6
в) 24
г) 14

4. Выбери пример с ответом 3.

а) 8 : 4
б) 12 : 3
в) 9 : 3
г) 6 : 3

Проверка: сверяют с доской. Кто справился без ошибок? Почему тебе удалось? Почему у тебя получилось?

Подумайте, довольны ли вы результатом выполнения своей работы?
Поднимите выбранный вами лист (помещаю на другое дерево)
Что тебе нужно сделать, чтобы справиться в следующий раз? (повторить таблицу умножения и деления с числами 2, 3, 4).
– Молодцы, ребята, вы справились со всеми заданиями. Целый день мы бродили по лесу. Нам пора возвращаться обратно.
В процессе нашего путешествия мы записывали как вести себя в лесу.
В итоге у нас получилась общая памятка “Правила поведения в лесу” (повесить запись “Правила поведения в лесу”)
Может, вы хотите, что-то добавить?
– Не оставляй в лесу после себя мусор.
– Всегда слушай, как звучит лес, и твое настроение будет радостным.
Выполняя, эти правила вы также участвуете в охране природы

Зелёный цвет – это символ нашей планеты, символ жизни. Поэтому слово “экология” я выделила зелёным. Экологией сейчас занимаются многие учёные во всём мире. Наш природный дом в опасности. Чтобы его сберечь, каждый человек должен стать хотя бы немного экологом. Тогда и всё общество будет жить в согласии с природой.

Чему мы учились? Что помогло нам в этом?
Что мы нового узнали? (О связи математики и экологии. )
Где пригодятся эти знания?
Что показалось трудным? Удалось ли справиться?
А какое задание было интересным?
С каким настроением вы заканчиваете урок? Поднимите выбранный вами лист (помещаю на другое дерево)
Давайте вспомним, с каким настроением мы начинали урок?
А с каким заканчиваем?
Вот какое дерево у нас получилось. Настоящее, осеннее.

С давних времен 14 октября на Руси отмечался Покров-день, как день перелома в годичном круговороте жизни. С этого дня, по представлениям людей начиналась зима.

А мы провожая осень и встречая зиму, показали свою силу не только в математике, но и то что мы можем сделать для улучшения экологической обстановки, а значит для защиты собственного здоровья.

Умножение и деление в столбик: примеры

Математика сродни головоломкам. Особенно это касается деления и умножения в столбик. В школе эти действия изучаются от простого к сложному. Поэтому непременно полагается хорошо усвоить алгоритм выполнения названных операций на простых примерах. Чтобы потом не возникло трудностей с делением десятичных дробей в столбик. Ведь это самый сложный вариант подобных заданий.

Советы тем, кто хочет хорошо знать математику

Этот предмет требует последовательного изучения. Пробелы в знаниях здесь недопустимы. Такой принцип должен усвоить каждый ученик уже в первом классе. Поэтому при пропуске нескольких уроков подряд материал придется освоить самостоятельно. Иначе позже возникнут проблемы не только с математикой, но и другими предметами, связанными с ней.

Второе обязательное условие успешного изучения математики — переходить к примерам на деление в столбик только после того, как освоены сложение, вычитание и умножение.

Ребенку будет трудно делить, если он не выучил таблицу умножения. Кстати, ее лучше учить по таблице Пифагора. Там нет ничего лишнего, да и усваивается умножение в таком случае проще.

Как умножаются в столбик натуральные числа?

Если возникает затруднение в решении примеров в столбик на деление и умножение, то начинать устранять проблему полагается с умножения. Поскольку деление является обратной операцией умножению:

1. До того как перемножать два числа, на них нужно внимательно посмотреть. Выбрать то, в котором больше разрядов (длиннее), записать его первым. Под ним разместить второе. Причем цифры соответствующего разряда должны оказаться под тем же разрядом. То есть самая правая цифра первого числа должна быть над самой правой второго.
2. Умножьте крайнюю правую цифру нижнего числа на каждую цифру верхнего, начиная справа. Запишите ответ под чертой так, чтобы его последняя цифра была под той на которую умножали.
3. То же повторите с другой цифой нижнего числа. Но результат от умножения при этом нужно сместить на одну цифру влево. При этом его последняя цифра окажется под той, на которую умножали.

Продолжать такое умножение в столбик до тех пор, пока не закончатся цифры во втором множителе. Теперь их нужно сложить. Это и будет искомый ответ.

Алгоритм умножения в столбик десятичных дробей

Сначала полагается представить, что даны не десятичные дроби, а натуральные. То есть убрать из них запятые и далее действовать так, как описано в предыдущем случае.

Отличие начинается, когда записывается ответ. В этот момент необходимо сосчитать все цифры, которые стоят после запятых в обеих дробях. Именно столько их нужно отсчитать от конца ответа и там поставить запятую.

Удобно проиллюстрировать этот алгоритм на примере: 0,25 х 0,33:

• Записать эти дроби нужно так, чтобы число 33 было под 25.
• Теперь правую тройку нужно умножить на 25. Получится 75. Записать его полагается так, чтобы пятерка оказалась под тройкой, на которую выполнялось умножение.
• Потом умножать 25 на первую 3. Опять будет 75, но написано оно будет так, чтобы 5 оказалось под 7 предыдущего числа.
• После сложения этих двух чисел получается 825. В десятичных дробях запятыми отделены 4 цифры. Поэтому в ответе нужно отделить запятой тоже 4 цифры. Но их всего три. Для этого перед 8 придется написать 0, поставить запятую, перед ней еще один 0.
• Ответом в примере окажется число 0,0825.

С чего начать обучение делению?

До того как решать примеры на деление в столбик, полагается запомнить названия чисел, которые стоят в примере на деление. Первое из них (то, которое делится) — делимое. Второе (на него делят) — делитель. Ответ — частное.

После этого на простом бытовом примере объясним суть этой математической операции. Например, если взять 10 конфет, то поделить их поровну между мамой и папой легко. А как быть, если нужно раздать их родителям и брату?

После этого можно знакомиться с правилами деления и осваивать их на конкретных примерах. Сначала простых, а потом переходить ко все более сложным.

Алгоритм деления чисел в столбик

Вначале представим порядок действий для натуральных чисел, делящихся на однозначное число. Они будут основой и для многозначных делителей или десятичных дробей. Только тогда полагается внести небольшие изменения, но об этом позже:

• До того как делать деление в столбик, нужно выяснить, где делимое и делитель.
• Записать делимое. Справа от него — делитель.
• Прочертить слева и снизу около последнего уголок.
• Определить неполное делимое, то есть число, которое будет минимальным для деления. Обычно оно состоит из одной цифры, максимум из двух.
• Подобрать число, которое будет первым записано в ответ. Оно должно быть таким, сколько раз делитель помещается в делимом.
• Записать результат от умножения этого числа на делитель.
• Написать его под неполным делимом. Выполнить вычитание.
• Снести к остатку первую цифру после той части, которая уже разделена.
• Снова подобрать число для ответа.
• Повторить умножение и вычитание. Если остаток равен нулю и делимое закончилось, то пример сделан. В противном случае повторить действия: снести цифру, подобрать число, умножить, вычесть.

Как решать деление в столбик, если в делителе больше одной цифры?

Сам алгоритм полностью совпадает с тем, что был описан выше. Отличием будет количество цифр в неполном делимом. Их теперь минимум должно быть две, но если они оказываются меньше делителя, то работать полагается с первыми тремя цифрами.

Существует еще один нюанс в таком делении. Дело в том, что остаток и снесенная к нему цифра иногда не делятся на делитель. Тогда полагается приписать еще одну цифру по порядку. Но при этом в ответ необходимо поставить ноль. Если осуществляется деление трехзначных чисел в столбик, то может потребоваться снести больше двух цифр. Тогда вводится правило: нолей в ответе должно быть на один меньше, чем количество снесенных цифр.

Рассмотреть такое деление можно на примере — 12082 : 863.

• Неполным делимым в нем оказывается число 1208. В него число 863 помещается только один раз. Поэтому в ответ полагается поставить 1, а под 1208 записать 863.
• После вычитания получается остаток 345.
• К нему нужно снести цифру 2.
• В числе 3452 четыре раза умещается 863.
• Четверку необходимо записать в ответ. Причем при умножении на 4 получается именно это число.
• Остаток после вычитания равен нулю. То есть деление закончено.

Ответом в примере будет число 14.

Как быть, если делимое заканчивается на ноль?

Или несколько нолей? В этом случае нулевой остаток получается, а в делимом еще стоят нули. Отчаиваться не стоит, все проще, чем может показаться. Достаточно просто приписать к ответу все нули, которые остались не разделенными.

Например, нужно поделить 400 на 5. Неполное делимое 40. В него 8 раз помещается пятерка. Значит, в ответ полагается записать 8. При вычитании остатка не остается. То есть деление закончено, но в делимом остался ноль. Его придется приписать к ответу. Таким образом, при делении 400 на 5 получается 80.

Что делать, если разделить нужно десятичную дробь

Опять же, это число похоже на натуральное, если бы не запятая, отделяющая целую часть от дробной. Это наводит на мысль о том, что деление десятичных дробей в столбик подобно тому, которое было описано выше.

Единственным отличием будет пункт с запятой. Ее полагается поставить в ответ сразу, как только снесена первая цифра из дробной части. По-другому это можно сказать так: закончилось деление целой части — поставь запятую и продолжай решение дальше.

Во время решения примеров на деление в столбик с десятичными дробями нужно помнить, что в части после запятой можно приписать любое количество нолей. Иногда это нужно для того, чтобы доделить числа до конца.

Деление двух десятичных дробей

Оно может показаться сложным. Но только вначале. Ведь то, как выполнить деление в столбик дробей на натуральное число, уже понятно. Значит, нужно свести этот пример к уже привычному виду.

Сделать это легко. Нужно умножить обе дроби на 10, 100, 1 000 или 10 000, а может быть, на миллион, если этого требует задача. Множитель полагается выбирать исходя из того, сколько нолей стоит в десятичной части делителя. То есть в результате получится, что делить придется дробь на натуральное число.

Причем это будет в худшем случае. Ведь может получиться так, что делимое от этой операции станет целым числом. Тогда решение примера с делением в столбик дробей сведется к самому простому варианту: операции с натуральными числами.

В качестве примера: 28,4 делим на 3,2:

• Сначала их необходимо умножить на 10, поскольку во втором числе после запятой стоит только одна цифра. Умножение даст 284 и 32.
• Их полагается разделить. Причем сразу все число 284 на 32.
• Первым подобранным числом для ответа является 8. От его умножения получается 256. Остатком будет 28.
• Деление целой части закончилось, и в ответ полагается поставить запятую.
• Снести к остатку 0.
• Снова взять по 8.
• Остаток: 24. К нему приписать еще один 0.
• Теперь брать нужно 7.
• Результат умножения — 224, остаток — 16.
• Снести еще один 0. Взять по 5 и получится как раз 160. Остаток — 0.

Деление закончено. Результат примера 28,4:3,2 равен 8,875.

Что делать, если делитель равен 10, 100, 0,1, или 0,01?

Так же как и с умножением, деление в столбик здесь не понадобится. Достаточно просто переносить запятую в нужную сторону на определенное количество цифр. Причем по этому принципу можно решать примеры как с целыми числами, так и с десятичными дробями.

Итак, если нужно делить на 10, 100 или 1 000, то запятая переносится влево на такое количество цифр, сколько нулей в делителе. То есть, когда число делится на 100, запятая должна сместиться влево на две цифры. Если делимое — натуральное число, то подразумевается, что запятая стоит в его конце.

Это действие дает такой же результат, как если бы число было необходимо умножить на 0,1, 0,01 или 0,001. В этих примерах запятая тоже переносится влево на количество цифр, равное длине дробной части.

При делении на 0,1 (и т. д.) или умножении на 10 (и т. д.) запятая должна переместиться вправо на одну цифру (или две, три, в зависимости от количества нулей или длины дробной части).

Стоит отметить, что количества цифр, данных в делимом, может быть недостаточным. Тогда слева (в целой части) или справа (после запятой) можно приписать недостающие нули.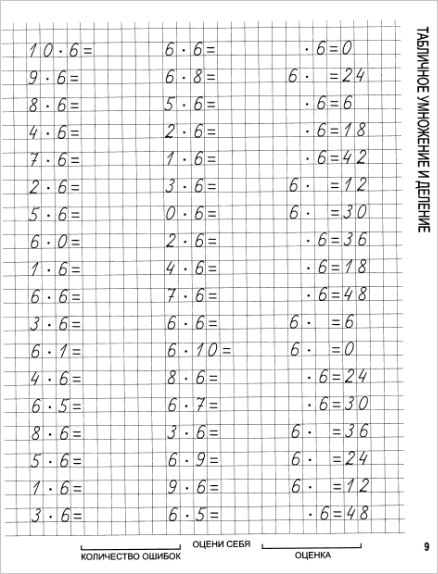

Деление периодических дробей

В этом случае не удастся получить точный ответ при делении в столбик. Как решать пример, если встретилась дробь с периодом? Здесь полагается переходить к обыкновенным дробям. А потом выполнять их деление по изученным ранее правилам.

Например разделить нужно 0,(3) на 0,6. Первая дробь — периодическая. Она преобразуется в дробь 3/9, которая после сокращения даст 1/3. Вторая дробь — конечная десятичная. Ее записать обыкновенной еще проще: 6/10, что равно 3/5. Правило деления обыкновенных дробей предписывает заменять деление умножением и делитель — обратным числом. То есть пример сводится к умножению 1/3 на 5/3. Ответом будет 5/9.

Если в примере разные дроби…

Тогда возможны несколько вариантов решения. Во-первых, обыкновенную дробь можно попытаться перевести в десятичную. Потом делить уже две десятичные по указанному выше алгоритму.

Во-вторых, каждая конечная десятичная дробь может быть записана в виде обыкновенной.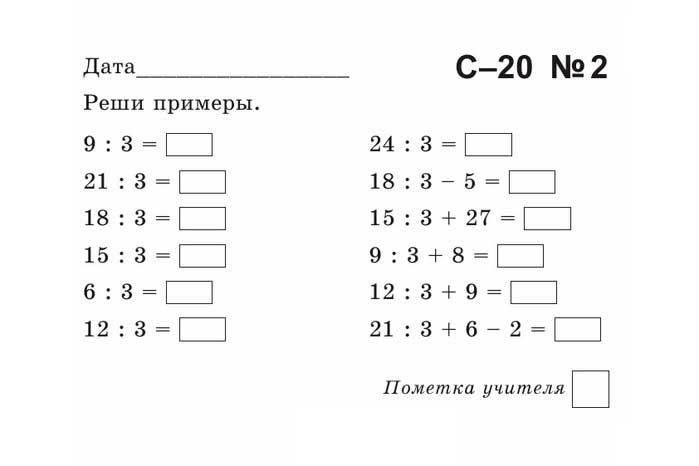 Только это не всегда удобно. Чаще всего такие дроби оказываются огромными. Да и ответы получаются громоздкими. Поэтому первый подход считается более предпочтительным.

Представлять и решать задачи на умножение и деление

32 из 85 Обучение ресурсы для моментов «ага»

• учебные ресурсы

  CUBES Доска объявлений и набор закладок

  Решайте задачи со словами с помощью этой доски объявлений CUBES для решения задач и набора закладок.

  1 страница 1 — 6

• учебное пособие

  Умножение с массивами – Учебная презентация

  Научите своих учеников связывать умножение с массивами с помощью этой учебной презентации из 16 слайдов.

  1 страница 2 — 3

• учебное пособие

  Карточки с заданиями Отдела благодарения

  Используйте различные стратегии для решения задач на деление слов с набором карточек с заданиями на День Благодарения.

  1 страница 3 — 5

• учебное пособие

  Цвет по фактору — рабочий лист

  Решите уравнения с отсутствующими факторами и раскрасьте картинку в соответствии с цветовой шкалой.

  2 страницы 3 — 4

• учебное пособие

  Карточки с задачами на умножение и деление слов (факты 1-12)

  Используйте ряд стратегий для решения задач на умножение и деление для фактов таблицы умножения 1-12.

  8 страниц 3

• учебное пособие

  Карточки с задачами на умножение и деление (факты 2, 5 и 10)

  Используйте ряд стратегий для решения задач на умножение и деление с таблицами умножения на 2, 5 и 10.

  8 страниц 3

• учебный ресурс

  Карточки задач массивов

  Попрактикуйтесь в умножении массивов, используя этот набор из 20 карточек с заданиями различными способами.

  7 страниц 2 — 3

• учебное пособие

  Рабочий лист «Умножение с использованием массивов»

  Попрактикуйтесь в умножении с использованием массивов с помощью этого двухстраничного рабочего листа, в котором учащиеся строят массивы и записывают их в виде предложений по умножению.

  4 страницы 3 — 4

• учебный ресурс

  Решение задач — Рабочий лист умножения и деления

  Потренируйтесь решать текстовые задачи, используя одношаговое деление и умножение.

  2 страницы 3 — 4

• учебное пособие

  Рабочий лист отдела с моделями

  Решите 8 задач на деление, представляя дивиденды в виде чисел, картинок и числовых предложений.

  4 страницы 2 — 3

• учебное пособие

  Активность сопоставления массивов

  Эта игра на умножение массивов включает 15 наборов карточек из 3 разных категорий: массивы, факты умножения и произведения.

  15 страниц 3

• учебное пособие

  Рабочий лист умножения с моделями

  Рабочий лист для практики работы с различными представлениями умножения.

  4 страницы 3

• учебное пособие

  Дракон дивизии – рабочий лист

  Набор супер крутых рабочих листов для деления!

  6 страниц 3 — 5

• учебное пособие

  Заполните шаблоны для живота

  Коллекция больших картинок, которые будут использоваться для демонстрации в начале обсуждения умножения.

  3 страницы 3 — 4

• учебное пособие

  Шаблон задач на умножение

  Шаблон для использования в качестве основы, помогающей учащимся решать задачи на умножение слов.

  3 страницы 3 — 4

• учебный ресурс

  Введение в умножение PowerPoint

  Обучающая презентация из 33 слайдов для ознакомления с навыками умножения.

  33 страницы 3 — 4

• учебное пособие

  Головоломки на умножение

  Упражнение на сопоставление, чтобы помочь учащимся понять задачи на умножение слов.

  8 страниц 3

• учебное пособие

  Рабочие листы по умножению и делению – Факты из 10

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 10.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – факты из 9

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 9.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – факты из 8

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 8.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – факты из 7

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 7.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – факты из 6

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 6.

  4 страницы 3 — 6

• учебный ресурс

  Рабочие листы по умножению и делению – Факты из 5

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 5.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – факты из 4

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты из 4.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы по умножению и делению – Факты 3

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 3.

  4 страницы 3 — 6

• учебное пособие

  Рабочие листы умножения и деления — факты 2

  Набор рабочих листов, которые помогут учащимся быстро и точно вспомнить факты 2.

  4 страницы 3 — 6

• учебное пособие

  Раскладывание умножения

  Увлекательный способ для учащихся попрактиковаться в представлении умножения различными способами

  2 страницы 2 — 3

• учебное пособие

  Таблица умножения — настольный размер

  Набор из 4 настольных таблиц умножения.

  1 страница 3 — 6

• учебное пособие

  Части числового предложения — умножение и деление

  Набор из 4 плакатов, поясняющих числа, связанные с умножением и делением числа.

  4 страницы 2 — 5

• учебное пособие

  Пакет плакатов с полосовой диаграммой (модель бара)

  Ленточные диаграммы (также известные как стержневые модели) — это стратегия решения проблем, которую можно применять ко всем операциям.

  20 страниц 2 — 6

• учебное пособие

  Умножение и деление — что это за операция? – Интерактивная презентация PowerPoint

  Интерактивный PowerPoint из 64 слайдов, который можно использовать при обучении решению задач на умножение и деление слов.

  64 страницы 2 — 4

• учебное пособие

  Crazy Boxes — Факты умножения от 1 до 12

  Забавный рабочий лист по умножению, на котором учащиеся создают цветовой узор, используя факты умножения от 1 до 12.

  2 страницы 3 — 6

Решение задач на умножение и деление слов

Использование манипуляций для моделирования умножения и деления

«Сегодня мы собираемся обсудить, как взять реальные проблемные ситуации и записать их в виде числовых предложений. Затем мы решим числовые предложения. Начнем с некоторых манипуляций. Я собираюсь раздать несколько цветных плиток. Найти партнера. Каждая пара учеников получит около 40 цветных плиток».

Для выполнения этого задания учащиеся должны работать в парах. Раздайте каждой паре учащихся не менее 40 цветных плиток.

Раздайте каждому учащемуся копию листа решения задач (M-3-5-1_Problem Solving и KEY.docx).

Попросите добровольца, «Кто-нибудь, пожалуйста, прочитайте вслух первый пример?» После того, как учащийся прочитает задачу, попросите учащихся объяснить ситуацию. «Кто-нибудь может объяснить проблему вслух?» Скорее всего, учащиеся смогут объяснить хотя бы некоторые аспекты проблемы. Задавайте учащимся наводящие вопросы до тех пор, пока не будет изложена важная информация (кто и что), и запишите эту информацию на доске, используя короткие фразы, как показано ниже.

 

            Есть трое детей. У каждого ребенка по 6 машин. Сколько машин всего?

 

Попросите учащихся смоделировать эту задачу. «Вместе с партнером смоделируйте эту задачу с помощью цветных плиток».

Когда учащиеся закончат, попросите одну пару учащихся показать, как они смоделировали задачу, используя цветные плитки. Затем продемонстрируйте, как нарисовать изображение модели. Попросите учащихся нарисовать модель на рабочем листе. (Вы можете нарисовать человека рядом с каждой группой, чтобы представить 3 детей.)

 

 

Теперь спросите учащихся «Какое числовое предложение мы можем написать для этой задачи?» Вероятно, некоторые учащиеся предложат  или . Важно сосредоточиться на предложении с числом умножения и напомнить учащимся, что это альтернативный способ представления повторяющегося сложения.

Также напомните учащимся, что числовое предложение  уместно, потому что его можно прочитать как «3 группы по 6 равны 18» . Хотя  по свойству коммутативности числовое предложение  не подходит, поскольку не существует шести групп по три автомобиля. Если мы поможем учащимся прочитать умножение как 3 группы по 6, они смогут использовать это значение умножения, чтобы различать задачи на умножение и деление.

«А теперь давайте немного изменим задачу. Вместо этого предположим, что мы знаем, что есть 18 игрушечных машин, которые нужно разделить поровну между тремя детьми. Какое числовое предложение мы можем написать для этой задачи?» Подведите учащихся к осознанию того, что в этой ситуации используется деление (18 ÷ 3 = 6), потому что мы делим определенное число на равные группы. Также подчеркните противоположную связь между исходной задачей на умножение () и новой задачей на деление (18 ÷ 3 = 6).

Попросите учащихся работать в парах, чтобы заполнить лист решения задач (M-3-5-1_Problem Solving и KEY. docx).

Когда учащиеся заполнили рабочий лист, попросите пару учащихся смоделировать каждую задачу и написать соответствующее числовое предложение. Когда учащиеся решают реальные задачи, им часто трудно определить, какую операцию использовать для решения задачи. Для каждой задачи обязательно спросите у пары учеников или у всего класса : «Как вы узнали, какую операцию использовать? Как узнать, нужно ли умножать или делить, чтобы решить задачу?» ( Я использовал умножение, когда было многократное сложение; я использовал деление, когда мне нужно было разделить число на равные группы .) Язык для описания этих различий включает в себя тот факт, что умножение используется, когда есть несколько групп, равных по размеру, и вы хотите найти общую сумму, а деление используется, когда есть одна большая группа и вы хотите разделить его на несколько равных по размеру групп.

Преобразование слов в задачи на умножение или деление

При решении практических задач учащимся часто труднее всего перевести предложения в математические символы. Это задание направлено на то, чтобы помочь учащимся научиться определять ключевые термины, обозначающие умножение или деление.

Распространить копию Умножить или Разделить? рабочий лист (M-3-5-1_Multiply or Divide и KEY.docx) всем учащимся.

Познакомить с рабочим листом. «Обратите внимание, что на листе есть два столбца. В колонке слева задачи написаны словами. Числовые предложения находятся в правом столбце. Пожалуйста, поработайте снова в парах. Сопоставьте словесную проблему с правильным числовым предложением. Будь осторожен. Обратите внимание, что многие числовые предложения выглядят одинаково, например, . Цель состоит в том, чтобы решить, является ли задача задачей умножения или деления. Давайте посмотрим на первый вместе». Начните следующим образом: «Как вы думаете, какое числовое предложение представляет число 1?» ( B, ) «Как вы думаете, почему число 1 — это задача на умножение?» ( Есть 15 кругов или групп, в каждом круге или группе по 3 яблока, и цель состоит в том, чтобы определить общее количество яблок во всех пирогах . ) Помогите учащимся сосредоточиться на умножении как определении суммы, когда есть количество равных групп. Убедитесь, что учащиеся по-прежнему имеют доступ к цветным плиткам из предыдущего занятия. Некоторые студенты могут захотеть использовать плитки для моделирования проблемы, чтобы определить, требует ли задача умножения или деления. «Теперь поработайте со своими партнерами, чтобы заполнить рабочий лист».

После того, как учащиеся закончат практическую работу, важно, чтобы пары учащихся объяснили каждую задачу. Основное внимание должно быть сосредоточено на том, как они определили, требуется ли умножение или деление.

Продолжайте просить учащихся объяснить правильное числовое выражение для каждой задачи. Ниже приводится краткое изложение того, как вы можете обсудить число 3, так как это задача на первое деление. «Как вы думаете, какое числовое предложение представляет число 3?» Многие группы, скорее всего, скажут G, что означает . «Как вы думаете, почему число 3 — это задача на деление?» Попросите учащегося или пару учащихся объяснить. Студенты, вероятно, скажут: «Всего 14 бананов, и общее количество бананов должно быть разделено на 2 равные группы для 2 обезьян; цель состоит в том, чтобы определить, сколько бананов съедает каждая обезьяна». Помогите учащимся сосредоточиться на делении, начав с общей суммы и разделив ее на равные группы.

[Примечание: деление может происходить двумя способами. Один из способов разделения состоит в том, что общее количество делится на определенное количество групп, и цель состоит в том, чтобы найти, сколько их в каждой группе. Именно это произошло в задаче об обезьянах. Всего было 14 бананов, их поделили на 2 равные группы, и ответом было количество бананов в каждой группе. Второй способ разделения состоит в том, что общая сумма делится на группы определенного размера, и цель состоит в том, чтобы решить, сколько групп может быть создано. Номер 8 — это тип проблемы. Всего есть 8 карандашей, карандаши разбиты на группы по 2, и цель состоит в том, чтобы определить, сколько групп будет. Если учащиеся сосредоточатся на делении как на задании общей суммы и разделении ее на равные группы, они будут готовы к обоим типам деления, даже не понимая тонкую разницу в том, как деление может быть представлено.]

Раздайте копии рабочего листа Zero and Eight (M-3-5-1_Zero and Eight and KEY.docx) всем учащимся. Попросите учащихся заполнить этот лист в классе или дома. Используйте рабочий лист, чтобы оценить способность учащихся переводить и решать реальные задачи на умножение и деление.

Добавочный номер:

Используйте приведенные ниже предложения, чтобы изменить урок по мере необходимости. В разделе «Рутина» представлены идеи для пересмотра концепций урока в течение года. Секция малых групп предлагает дополнительные возможности для практики для студентов, которым они могут быть полезны. Раздел «Расширение» дает возможности учащимся, готовым к испытаниям, выходящим за рамки требований стандарта.

• Обычный: В течение учебного года попросите учащихся составить реальные задачи на умножение и деление. Например, если есть 24 студента и 48 файлов cookie, сколько файлов cookie может быть у каждого студента?
• Небольшая группа: Учащиеся, которым требуется дополнительная практика, могут быть объединены в небольшие группы для работы над использованием манипуляторов для моделирования действий в текстовых задачах. Сосредоточьтесь на том, чтобы помочь учащимся определить действие «объединения равных групп» как умножение и «разделение на равные группы» как деление. Этот веб-сайт содержит дополнительные задачи на умножение и деление, которые можно использовать в малых группах.

http://www.beaconlearningcenter.com/WebLessons/CameronsTrip/default.htm

• Расширение: Три перечисленных ниже веб-сайта предлагаются учащимся, которые ищут более сложные задачи. Все они включают в себя многошаговые задачи реального мира, которые учащиеся должны решить. Многие также требуют, чтобы студенты использовали две операции. http://www.prongo.com/farm/game.html

http://www.studyzone.org/testprep/math5/d/twostep4p.cfm http://www.mathplayground.com/WordProblemsWithKatie2.html

Умножение и деление KS2

One Wasn’t Square

Возраст от 7 до 11 лет

Уровень сложности

Миссис Морган, классная учительница, приколола номера на спины троих детей. Используйте информацию, чтобы узнать, что это были за три числа.

Все цифры

Возраст от 7 до 11 лет

Уровень сложности

В этом умножении каждая цифра от 0 до 9 используется один раз и только один раз. Используя предоставленную информацию, можете ли вы заменить звездочки в расчетах цифрами?

Велосипедные квадраты

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы составить цикл из пар, которые складываются в квадрат, используя все числа в поле ниже, один раз и только один раз?

Треблинг

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы заменить буквы цифрами? В каждом случае есть только одно решение?

Квадрат умножения Пазл

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы собрать эту мозаику квадрата умножения?

Shape Times Shape

Возраст от 7 до 11 лет

Уровень сложности

Каждая из этих одиннадцати фигур обозначает разные числа. Можете ли вы использовать числовые предложения, чтобы понять, что они собой представляют?

Что тебе нужно?

Возраст от 7 до 11 лет

Уровень испытания

Четыре из этих подсказок необходимы, чтобы найти выбранное число в этой сетке, и четыре верны, но ничего не делают, чтобы помочь найти число. Сможете ли вы разобраться в подсказках и найти число?

Three Dice

Возраст от 7 до 11 лет

Уровень испытания

Исследуйте сумму чисел на верхней и нижней гранях линии из трех игральных костей. Что ты заметил?

Как ты это делаешь?

Возраст от 7 до 11 лет

Уровень сложности

Это групповое задание побудит вас поделиться стратегиями расчета и подумать о том, какая стратегия может быть наиболее эффективной.

Настольные шаблоны сходят с ума!

Возраст от 7 до 11 лет

Уровень испытания

Почти все мы делали шаблоны таблиц на сто квадратов, то есть 10 на 10 сеток. В этой задаче рассматриваются узоры на квадратных сетках разного размера.

Путешествия в Стране чисел

Возраст от 7 до 11 лет

Уровень испытаний

Том и Бен посетили Страну чисел. Используйте карты, чтобы определить количество очков, которое набирает каждый из их маршрутов.

Заказ карточек

Возраст от 5 до 11 лет

Уровень сложности

Эта задача предназначена для того, чтобы помочь детям выучить и использовать таблицы умножения на два и три.

Давайте разделимся!

Возраст от 7 до 11 лет

Уровень испытания

Посмотрите на разные способы разделения вещей. Что они имеют в виду? Как бы вы могли показать их на картинке, с вещами, цифрами и символами?

Камешки

Возраст от 7 до 11 лет

Уровень испытания

Поместите четыре камешка на песок в форме квадрата. Продолжайте добавлять столько камешков, сколько необходимо, чтобы удвоить площадь. Сколько дополнительных камешков добавляется каждый раз?

Конфеты в коробке

Возраст от 7 до 11 лет

Уровень сложности

Сколько коробок различной формы вы можете создать для 36 конфет в один слой? Сможешь ли ты расположить конфеты так, чтобы конфеты одного цвета не стояли рядом друг с другом в любом направлении?

Круг и круг

Возраст от 7 до 11 лет

Уровень испытания

Что произойдет, если вы присоединитесь к каждой второй точке этого круга? Как насчет каждой третьей точки? Попробуйте разные шаги и посмотрите, сможете ли вы предсказать, что произойдет.

Самый высокий и самый низкий

Возраст от 7 до 11 лет

Уровень сложности

Поместите знаки операций между числами 3 4 5 6, чтобы получить максимально возможное число и наименьшее возможное число.

Zios and Zepts

Возраст от 7 до 11 лет

Уровень испытания

На планете Вув есть два вида существ. У Zios 3 ноги, а у Zepts 7 ног. Великий исследователь планет Нико насчитал 52 ноги. Сколько Зио и сколько Зептов было?

Обильные числа

Возраст от 7 до 11 лет

Уровень сложности

48 называется обильным числом, потому что оно меньше суммы своих множителей (без самого себя). Можете ли вы найти более обильные числа?

Сделать 100

Возраст от 7 до 11 лет

Уровень сложности

Найдите хотя бы один способ вставить некоторые знаки операции (+ — x ÷), чтобы эти цифры достигли 100.

Мигающие огни

Возраст от 7 до 11 лет

Уровень испытания

Норри видит, как одновременно мигают две лампочки, затем одна из них мигает каждую 4-ю секунду, а другая — каждую 5-ю секунду. Сколько раз они мигают вместе в течение целой минуты?

Луны Вувва

Возраст от 7 до 11 лет

Уровень испытания

У планеты Вувв семь лун. Можете ли вы определить, сколько времени проходит между каждым суперзатмением?

Загадочная матрица

Возраст от 7 до 11 лет

Уровень испытания

Сможете ли вы заполнить эту квадратную таблицу? Числа от 2 до 12 использовались для его генерации, причем только одно число использовалось дважды.

Four Goodness Sake

Возраст от 7 до 11 лет

Уровень испытания

Используйте 4 четыре раза, выполняя простые операции, чтобы получить ответ 12. Сможете ли вы сделать 15, 16 и 17 тоже?

Квадраты умножения

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы определить расположение цифр в квадрате так, чтобы данные произведения были правильными? Цифры от 1 до 9 можно использовать один раз и только один раз.

Факторные строки

Возраст от 7 до 14 лет

Challenge Level

Расположите четыре карточки с числами на сетке в соответствии с правилами, чтобы получилась диагональная, вертикальная или горизонтальная линия.

Два простых числа составляют один квадрат

Возраст от 7 до 11 лет

Уровень сложности

Можете ли вы составить квадратные числа, складывая два простых числа вместе?

Кубики внутри кубов

Возраст от 7 до 14 лет

Уровень сложности

Мы начинаем с одного желтого куба и строим вокруг него куб 3x3x3 с красными кубиками. Затем мы строим вокруг этого красного куба синие кубы и так далее. Сколько кубиков каждого цвета мы использовали?

Остатки

Возраст от 7 до 14 лет

Уровень сложности

Я думаю о числе. Мое число одновременно кратно 5 и кратно 6. Каким может быть мое число?

Что быстрее?

Возраст от 7 до 11 лет

Уровень сложности

Что быстрее: считать до 30 единицами или считать до 300 десятками? Почему?

Квадрат чисел

Возраст от 7 до 11 лет

Уровень испытания

Сможете ли вы поместить числа от 1 до 8 в круги так, чтобы четыре вычисления были правильными?

Нечетные квадраты

Возраст от 7 до 11 лет

Уровень сложности

Задумайте число, возведите его в квадрат и вычтите начальное число. Оставшееся число нечетное или четное? Как изображения помогают объяснить это?

Лестницы вверх и вниз

Возраст от 7 до 11 лет

Уровень сложности

Один блок необходим, чтобы построить лестницу вверх и вниз с одной ступенькой вверх и одной ступенькой вниз. Сколько блоков потребуется, чтобы построить подъемно-спусковую лестницу с 5 ступенями вверх и 5 ступенями вниз?

Карточки для переноски

Возраст от 7 до 11 лет

Уровень испытания

Эти шестнадцать детей стоят в четыре ряда по четыре человека, один за другим. У каждого в руках карточка с номером. Можете ли вы работать пропущенные числа?

Простой способ умножить на 10?

Возраст от 7 до 11 лет

Уровень сложности

Согласны ли вы с утверждениями Бэджера? Являются ли рассуждения Бэджера «непроницаемыми»? Почему или почему нет?

Многократная сетка

Возраст от 7 до 11 лет

Уровень испытания

Что общего у чисел, заштрихованных синим цветом на этой сотке? Что вы заметили в розовых числах? Как насчет заштрихованных чисел в других квадратах?

Игра «Факторы и кратные»

Возраст от 7 до 16 лет

Уровень сложности

Эта игра может заменить стандартные практические упражнения по нахождению множителей и кратных.

Музыка для моих ушей

Возраст от 7 до 11 лет

Уровень испытания

Можете ли вы предсказать, когда вы будете хлопать и когда вы будете щелкать, если вы начнете этот ритм? Как насчет того, чтобы друг в это же время начал новый ритм?

Что в коробке?

Возраст от 7 до 11 лет

Уровень испытания

Эта большая коробка умножает все, что находится внутри, на одно и то же число. Если вы знаете числа, которые выпадают, какое умножение может происходить в коробке?

Многофакторные цепочки

Возраст от 7 до 11 лет

Уровень сложности

Вы видите, как работают эти цепочки с несколькими факторами? Найдите цепочку, которая содержит наименьшие возможные числа. Как насчет максимально возможных чисел?

Four Go

Возраст от 7 до 11 лет

Уровень испытания

Это испытание представляет собой игру для двух игроков. Выберите два числа для умножения или деления, затем отметьте свой ответ в числовой строке. Можете ли вы получить четыре подряд?

Представьте себе пирамиду…

Возраст от 7 до 11 лет

Уровень испытания

Представьте себе пирамиду, построенную из квадратных слоев маленьких кубиков. Если мы пронумеруем кубики сверху, начиная с 1, можете ли вы представить себе, какие кубики находятся непосредственно под этим первым кубом?

Игра «Остатки»

Возраст от 7 до 14 лет

Уровень испытания

Сыграйте в эту игру и посмотрите, сможете ли вы угадать число, выбранное компьютером.

Какой символ?

Возраст от 7 до 11 лет

Уровень испытания

Выберите символ, который нужно вставить в числовое предложение.

Таблица умножения Сдвиги

Возраст от 7 до 11 лет

Уровень сложности

В этом упражнении компьютер выбирает таблицу умножения и сдвигает ее. Можете ли вы каждый раз отрабатывать стол и смену?

Счетные шестеренки

Возраст от 7 до 14 лет

Уровень сложности

Какие пары шестерен позволяют цветному зубу касаться каждого зубца другой шестеренки? Какие пары не допускают этого? Почему?

Зажги свет снова

Возраст от 7 до 11 лет

Challenge Level

Каждый свет в этом интерактивном режиме включается в соответствии с правилом. Что происходит, когда вы вводите разные числа? Сможете ли вы найти наименьшее число, при котором загораются все четыре лампочки?

Следуй за цифрами

Возраст от 7 до 11 лет

Уровень сложности

Что произойдет, если сложить цифры числа, затем умножить результат на 2 и продолжать это делать? Вы можете попробовать разные числа и разные правила.

Любопытный номер 9От 7 до 11 лет ?

Факторная дорожка

Возраст от 7 до 14 лет

Уровень испытания

Факторная дорожка — это не гонка, а игра на ловкость. Идея состоит в том, чтобы пройти трассу за как можно меньше ходов, соблюдая правила.

Время пришло!

Возраст от 7 до 14 лет

Challenge Level

Как вы решите, какой способ переворачивания и/или поворота сетки даст вам наибольшую сумму?

Вычитание квадратов

Возраст от 7 до 11 лет

Уровень задания

Посмотрите, что получится, если взять число, возвести его в квадрат и вычесть ответ. Какой номер у вас получится? Ты можешь доказать это?

Этот Крысолов из Гамельна

Возраст от 7 до 11 лет

Уровень испытания

Исследуйте разное количество людей и крыс, если вы знаете, сколько всего ног!

Multiply Multiples 1

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы выполнить этот расчет, вписав пропущенные числа? Сколькими различными способами вы можете это сделать?

Multiply Multiples 2

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы придумать разные способы сбалансировать это уравнение?

Multiply Multiples 3

Возраст от 7 до 11 лет

Уровень сложности

Попробуйте сбалансировать это уравнение. Можете ли вы найти различные способы сделать это?

Правила дивизиона

Возраст от 7 до 11 лет

Уровень задания

В этом задании вам предлагается изучить деление трехзначного числа на однозначное число.

Всегда, иногда или никогда? Номер

Возраст от 7 до 11 лет

Уровень сложности

Всегда ли эти утверждения верны, иногда верны или никогда не верны?

Удовлетворение четырем утверждениям

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы найти двузначные числа, удовлетворяющие всем этим утверждениям?

Представьте свой метод

Возраст от 7 до 11 лет

Уровень сложности

Сможете ли вы сопоставить эти методы расчета с их визуальным представлением?

Сравните расчеты

Возраст от 7 до 11 лет

Уровень сложности

Можете ли вы расположить эти четыре расчета в порядке сложности? Как вы решили?

Dicey Array

Возраст от 5 до 11 лет

Уровень испытания

Посмотрите видеозапись этой игры. Можете ли вы разработать правила? Какие суммы кубиков лучше всего получить и почему?

 
Y Вас также может заинтересовать этот набор заданий на веб-сайте STEM Learning, который дополняет действия NRICH, описанные выше.

Решение задач на умножение и деление дробей и смешанных чисел

Форма поиска

Поиск

Задачи на дробное слово с интерактивными упражнениями

Пример 1. Если для изготовления платья требуется 5/6 ярдов ткани, то сколько ярдов потребуется, чтобы сшить 8 платьев?

Анализ: Чтобы решить эту задачу, мы преобразуем целое число в неправильную дробь. Затем мы умножим две дроби.

Решение:

Ответ: Чтобы сшить 8 платьев, потребуется 6 и 2/3 ярда ткани.

---

Пример 2: У Рене была коробка кексов, половину которых она отдала своему другу Хуану. Хуан отдал 3/4 своей доли своей подруге Елене. Какую часть первоначальной коробки кексов получила Елена?

Анализ: Чтобы решить эту задачу, мы умножим эти две дроби.

Решение:

Ответ: Елена получила 3/8 оригинальной коробки кексов.

---

Пример 3: Класс математики Нины имеет размеры 6 и 4/5 метра в длину и 1 и 3/8 метра в ширину. Какова площадь классной комнаты?

Анализ: Чтобы решить эту задачу, мы умножим эти смешанные числа. Но сначала мы должны преобразовать каждое смешанное число в неправильную дробь.

Решение:

Ответ: Площадь классной комнаты равна 9и 7/20 кв.

---

Пример 4: Плитка шоколада имеет длину 3/4 дюйма. Если его разделить на части длиной 3/8 дюйма, то сколько частей получится?

Анализ: Чтобы решить эту задачу, разделим первую дробь на вторую.

Решение:

Ответ: 2 шт.

---

Пример 5: У электрика есть кусок провода длиной 4 и 3/8 сантиметра. Она делит проволоку на куски длиной 1 и 2/3 сантиметра. Сколько штук у нее?

Анализ: Чтобы решить эту задачу, мы разделим первое смешанное число на второе.

Решение:

Ответ: У электрика 2 и 5/8 отрезка провода.

---

Пример 6: На складе имеется лента 1 и 3/10 метра. Если они разделят ленту на куски длиной 5/8 метров, то сколько кусков у них будет?

Анализ: Чтобы решить эту задачу, мы разделим первое смешанное число на второе. Сначала мы преобразуем каждое смешанное число в неправильную дробь.

Решение:

Ответ: На складе будет 2 и 2/25 куска ленты.

---

Резюме: На этом уроке мы узнали, как решать текстовые задачи на умножение и деление дробей и смешанных чисел.

---

Упражнения  

Указания: Вычтите смешанные числа в каждом приведенном ниже упражнении. При необходимости обязательно упростите результат. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ.

Примечание. Чтобы написать смешанное число четыре и две трети, введите 4, пробел, а затем 2/3 в форму.

1.	Одна партия печенья содержит 1 и 3/4 чашки растопленного шоколада. Сколько чашек растопленного шоколада нужно, чтобы приготовить 8 порций печенья? ОКНО ОТВЕТОВ:  чашки    ОКНО РЕЗУЛЬТАТОВ:

2.	Тодд выпил 5/8 банки сока на 24 унции. Лайла выпила в три раза меньше сока, чем Тодд. Сколько унций выпила Лила? ОТВЕТЫ:   унция. ОКНО РЕЗУЛЬТАТОВ:

3.	Прямоугольный ковер имеет длину 3 и 2/3 фута и ширину 2 и 3/4 фута. Какова площадь коврика? ОКНО ОТВЕТОВ:   кв. фут    ОКНО РЕЗУЛЬТАТОВ:

4.	Джанет имеет 5 и 3/4 сантиметра солодки. Она делит солодку на кусочки длиной 1 и 7/8 сантиметров. Сколько кусочков лакрицы у нее будет? ЯЩИК ОТВЕТОВ:   штук    ЯЩИК РЕЗУЛЬТАТОВ:

5.	Кусок дерева имеет длину 15 футов. Сколько 3/4-футовых секций можно отрезать от него? БЛОК ОТВЕТОВ:   разделы     БЛОК РЕЗУЛЬТАТОВ:

 

Уроки умножения и деления дробей и смешанных чисел
1.	Умножение дробей
2.	Умножение дробей путем исключения общих множителей
3.	Умножение смешанных чисел
4.	Обратные связи
5.	Деление дробей
6.	Разделение смешанных чисел
6.	Решение словесных задач
7.	Практические упражнения
8.	Упражнения с вызовом
9.	Решения

Подпишитесь на нашу БЕСПЛАТНУЮ рассылку!

Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!

Адрес электронной почты *

Умножение и деление дробей и смешанных чисел |

Форма поиска

Поиск

Инструкции: Выполните необходимые операции в каждом упражнении ниже. При необходимости обязательно упростите результат. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ.

Примечание: Чтобы записать дробь три четверти, введите 3/4 в форму. Чтобы написать смешанное число четыре и две трети, введите 4, пробел, а затем 2/3 в форму.

1.	Шоколадный батончик имеет длину 9/15 дюйма. Если его разделить на части длиной 1/5 дюйма, то сколько частей получится?
	ЯЩИК ОТВЕТОВ:   штук    ЯЩИК РЕЗУЛЬТАТОВ:

2.	Джастин отдал 2/3 своей пиццы 8 друзьям, которые разделили пиццу поровну. Какую часть первоначальной пиццы получил каждый друг?
	ОКНО ОТВЕТОВ:    ОКНО РЕЗУЛЬТАТОВ:

3.
	ОКНО ОТВЕТОВ:    ОКНО РЕЗУЛЬТАТОВ:

4.	Сад Марси имеет размеры 3 и 4/5 метра в длину и 2 и 7/8 метра в ширину. Какова площадь сада?
	ОКНО ОТВЕТОВ:  m 2     ОКНО РЕЗУЛЬТАТОВ:

5.
	ОКНО ОТВЕТОВ:    ОКНО РЕЗУЛЬТАТОВ:

6.	Плитка шоколада имеет длину 11/12 дюйма. Если его разделить на части длиной 5/8 дюйма, то сколько частей получится?
	ЯЩИК ОТВЕТОВ:   штук    ЯЩИК РЕЗУЛЬТАТОВ:

7.	У маляра в корыте было 22 литра краски. Если каждое ведро вмещает по 2 и 3/4 литра, то сколько ведер краски можно вылить из корыта?
	ОКНО ОТВЕТОВ:   ведра    ОКНО РЕЗУЛЬТАТОВ:

8.
	ОКНО ОТВЕТОВ:    ОКНО РЕЗУЛЬТАТОВ:

9.	У Фрэнка 8 и 2/3 фута веревки. Если он разделит веревку на куски длиной 1 и 4/9 фута, то сколько кусков веревки у него останется?
	ЯЩИК ОТВЕТОВ:  штук     ЯЩИК РЕЗУЛЬТАТОВ:

10.	Класс Кэти имеет площадь 15 и 5/6 квадратных футов. Если длина 8 и 3/4 фута, то какова ширина ее класса?
	ОКНО ОТВЕТОВ:  футы    ОКНО РЕЗУЛЬТАТОВ:

Уроки умножения и деления дробей и смешанных чисел
1.	Умножение дробей
2.	Умножение дробей путем исключения общих множителей
3.	Умножение смешанных чисел
4.	Обратные связи
5.	Деление дробей
6.	Разделение смешанных чисел
6.	Решение словесных задач
7.	Практические упражнения
8.	Упражнения с вызовом
9.	Решения

Подпишитесь на нашу БЕСПЛАТНУЮ рассылку!

Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!

Адрес электронной почты *

Использование умножения для решения задач на деление — Рабочие листы по математике

Использование умножения для решения задач на деление — Рабочие листы по математике — SplashLearn

Главная > Рабочие листы > Рабочие листы по математике > Используйте умножение для решения задач на деление

Сосредоточьтесь на основных математических навыках, используя умножение для решения задач на деление.

Распечатать

Присвоить классу

ПРЕДМЕТЫ И ТЕМЫ

Узнайте больше об использовании умножения для решения задач на деление. Рабочие листы

Помогите своему ребенку стать экспертом в делении с помощью этого листа. Рабочий лист предлагает учащимся решить задачи на деление, используя факты умножения. Что может быть лучше для вашего юного математика, чем развлекаться во время учебы? Этот рабочий лист будет стимулировать их ум и сделает обучение более увлекательным и живым!

Explore Amazing Worksheets on Division

Просмотреть все 158 рабочих листов

• Раздел

  Представляет Равную Группу

  Раскройте секреты математического волшебства, потренировавшись представлять равные группы.

  ПОДРОБНЕЕ

• Раздел

  Представление равных групп объектов

  Распечатайте этот рабочий лист, чтобы попрактиковаться в представлении равных групп объектов, как математическую легенду!

  ПОДРОБНЕЕ

• Подразделение

  Представление равного распределения

  Погрузитесь в этот увлекательный печатный лист, потренировавшись изображать равное распределение.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

• Деление

  Представление равного количества объектов

  В этом рабочем листе учащиеся должны представить равное количество объектов.

  ПОДРОБНЕЕ

• Деление

  Умножение и деление предложений

  Погрузитесь в этот увлекательный печатный лист, потренировавшись в умножении и делении предложений.

  ПОДРОБНЕЕ

• Отдел

  Завершите предложения по умножению и делению

  Оцените свои математические навыки, выполнив предложения по умножению и делению в этом рабочем листе.

  ПОДРОБНЕЕ

• Деление

  Свяжите умножение и деление для групп

  Закрепите математические понятия, потренировавшись связывать умножение и деление для групп.

  ПОДРОБНЕЕ

• Деление

  Связать умножение и деление для массивов

  Дети должны объяснить умножение и деление массивов в этом занимательном листе.

  ПОДРОБНЕЕ

• Деление

  Запись предложений с умножением и делением

  Раскройте секреты математического волшебства, потренировавшись писать предложения с умножением и делением.

  ПОДРОБНЕЕ

• Деление

  Создание предложений на умножение и деление

  Сосредоточьтесь на основных математических навыках с помощью этого забавного рабочего листа, создавая предложения на умножение и деление.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

• Division

  Определить верный факт

  Будьте на пути к тому, чтобы стать математиком, устанавливая верный факт.

  ПОДРОБНЕЕ

• Деление

  Разделить, используя факты умножения

  В этом рабочем листе учащиеся получат возможность разделить, используя факты умножения.

  ПОДРОБНЕЕ

• Раздел

  Представляет Равную Группу как Раздел

  Повысьте свою способность представлять равные группы как деления, распечатав этот забавный рабочий лист.

  ПОДРОБНЕЕ

• Деление

  Деление предложений для равных групп

  Оцените свои математические навыки, потренировавшись в делении предложений для равных групп в этом рабочем листе.

  ПОДРОБНЕЕ

• Division

  Завершите предложение о делении

  Разбавьте время занятий математикой, закончив предложение о делении.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

Родственные игры

Просмотреть все 109 Игры

• Деление

  Деление с использованием связанного факта

  Проявите себя в мире математики, научившись делить с помощью связанного факта.

  ПОДРОБНЕЕ

• Дивизион

  Завершите шаблоны деления

  Попрактикуйтесь в суперсиле деления, научившись составлять шаблоны деления.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

• Деление

  Разделение чисел, кратных 10, на однозначные числа

  Попросите вашего малыша разделить числа, кратные 10, на однозначные числа, чтобы сыграть в эту игру.

  ПОДРОБНЕЕ

• Отдел

  Раздел 10 фактов

  Исследуйте раздел 10 фактов с этой игрой.

  ПОДРОБНЕЕ

• Деление

  Раздели на 10 и закончи предложения деления

  Разделите на 10 и закончите предложения деления, чтобы попрактиковаться в делении.

  ПОДРОБНЕЕ

• Division

  Используйте факты из числа 10, чтобы найти пропавшее число

  Насладитесь чудом математической мультивселенной, исследуя, как использовать факты из числа 10, чтобы найти пропавшее число.

  ПОДРОБНЕЕ

• Деление

  Использование умножения для деления на 2

  Погрузитесь в мир математики, используя умножение для деления на 2.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

• Деление

  Завершите шаблоны деления

  Окунитесь в безумие математической мультивселенной, изучая способы завершения шаблонов деления.

  ПОДРОБНЕЕ

• Division

  Факты о делении 2

  Устройте собственную математическую вечеринку, изучив факты о делении 2.

  ПОДРОБНЕЕ

• Деление

  Раздели на 2 и закончи предложения деления

  Разделите на 2 и закончите предложения деления, чтобы играть.

  ПОДРОБНЕЕ

• Деление

  Поиск пропущенных чисел в предложениях с делением

  Наслаждайтесь чудом математики, научившись находить пропущенные числа в предложениях с делением.

  ПОДРОБНЕЕ

• Деление

  Разделить на 3, используя факты умножения 3

  Научиться делить на 3, используя факты умножения 3.

  ПОСМОТРЕТЬ ПОДРОБНОСТИ

• Деление

  Разделите на 3, чтобы завершить схемы деления

  Раскройте мудрость математики, научившись делить на 3, чтобы завершить схемы деления.