Порядок составления слова по составу. Составление слов по схемам
ПЛАН-КОНСПЕКТ УРОКА «СОСТАВЛЕНИЕ СЛОВ ПО СХЕМАМ. ПОРЯДОК РАЗБОРА СЛОВА ПО СОСТАВУ».
Ход урока.
1. Мотивация к учебной деятельности.
— Улыбнитесь друг другу и садитесь за рабочие места.
-Прочитайте пословицу, записанную на доске: «Любишь кататься – люби и саночки возить.»
—Постарайтесь объяснить её смысл.
— Что нужно делать, если хочешь получить новое знание, приобрести новое умение на уроке? (Трудиться самому, работать самому ,не лениться.)
— Я желаю вам преодолеть все трудности на уроке и сделать для себя новое открытие.
2. Актуализация знаний.
— Откроем тетради и запишем число.
— Какие опасности вас подстерегают в его написании? Объясните орфограммы.
Орфографическая разминка.
— Запишем предложение с объяснением орфограмм.
* Подул резкий ветер, и закачалась гибкая рябина.
(Комментирование предложения одним из учеников у доски. Остальные дети высказывают свои согласие или несогласие при помощи цвета: красный карандаш — «да», зелёный — «нет», предлагают свои варианты проверочных слов.)
— Зачем нужно учиться объяснять орфограммы? (Быть грамотными.)
Вопросы к ученику, выполнявшему работу у доски (для самооценки):
— Что тебе нужно было сделать?
-Ты сделал всё правильно или были недочёты?
— Ты сделал всё сам или с чьей-то помощью?
— Какие знания тебе пригодились?
-Какую отметку ты бы себе поставил?
-Мы с… учились оценивать свою работу.
Повторение основных понятий темы.
— Повторим то, что важно для урока.
Слайд №1. Примечание: при нажатии на «понятие» на слайде – «лишнее»
исчезнет, относящееся к теме выделится цветом.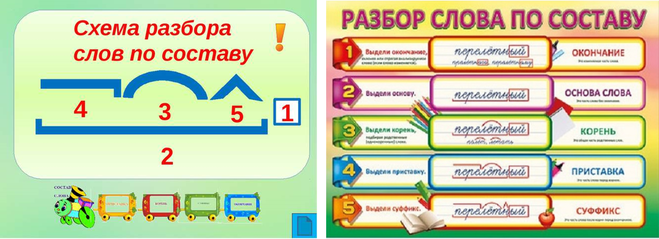
— Какие понятия «лишние»? (Предлог, глагол) Почему? (Не являются частями слова.)
— Расскажите, что вы знаете о каждой части слова. (Дети фронтально дают определение каждой части слова, приводят примеры, «сигналят» цветом о своём согласии или несогласии.)
3.Формулирование проблемы, планирование деятельности. Открытие нового знания.
Игра «Молчанка».
(На доске записаны слова в 3 столбика, по количеству рядов в классе. Одновременно по одному ученику от каждого ряда выходят к доске и, молча выделяют в словах части: окончание, основу, корень, приставку, суффикс.)
1 ряд 2 ряд 3 ряд
Грязный часовой капустная
Перегородка подорожник завязка
( Если допущены ошибки, то их исправляют,
сидящие на этом ряду дети. Остальные сигнализируют цветом. )
)
-Что мы сейчас делали? (Разбирали слова по составу.)
-В каком порядке вы его проводили? (Дети предлагают разные варианты.)
-Испытали ли затруднения? Какие?
-Как вы думаете, что важно знать при разборе слова по составу? (Порядок.)
-Попробуйте сформулировать тему сегодняшнего урока. (Порядок разбора слова по составу.)
-Чему же вы научитесь на уроке? ( Разбирать слова по составу в определённом порядке.)
-А что для этого нужно сделать? (Составить алгоритм разбора слова по составу и научиться им пользоваться на примерах.)
Освоение алгоритма разбора слова по составу.
1.Самостоятельное выведение алгоритма учениками на основе наблюдений и рассуждений.
-Запишите слова в столбик:
* берёзка * бежит *дошкольный
-Их надо разобрать по составу.
-С чего начать? Какая единственная часть в
слове изменяется? (Окончание.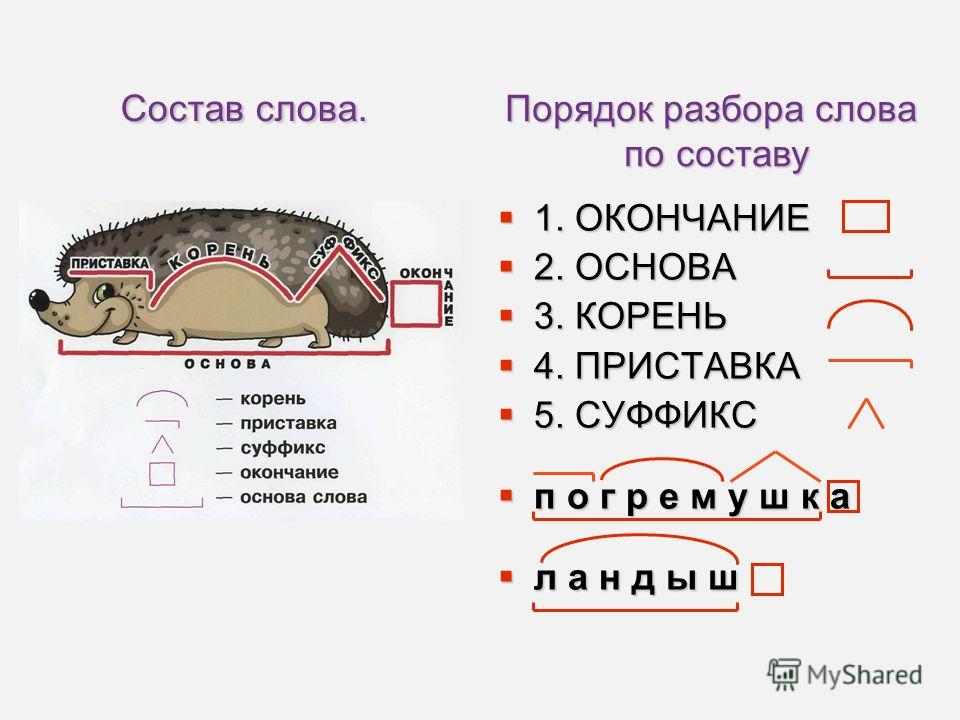 )
)
-Изменим слова и выделим окончания в них.
-Что теперь легко найти? (Основу.) Почему? (Основа – часть слова без окончания.) – Находим основу в словах.
— Что входит в основу обязательно? (Корень.) – Как выделить корень? (Подобрать как можно больше однокоренных слов, найти общую часть.)
— Какие части слова осталось выделить? (Приставку и суффикс, где они есть.)
— Сделайте вывод:
— В каком порядке нужно разбирать слово по составу? Составим опорный конспект. Повторите последовательность разбора, опираясь на предыдущее упражнение.
Слайд №2
1.Прочитайте слово.
2.Выделите окончание.
3.Выделите основу.
4.Выделите корень.
5.Выделите приставку и суффикс.
(Дети переворачивают памятки, заранее выложенные на их партах.)
2.Развитие умений работать по алгоритму. * Упр. №201
1,2 столбики – в
учебнике (фронтально) (Дети вслух проговаривают этапы разбора, следуя образцу. )
)
3 столбик – в тетрадь (1 вариант) — самостоятельно
4 столбик – в тетрадь (2 вариант) – самостоятельно
2 ученика работают у доски.
Самопроверка (Слайд№3)
-У кого задание не вызвало затруднений, разбор выполнен верно? Какой кружок себе нарисуете? (Полностью раскрашенный зелёным.)
-У кого возникли затруднения при выполнении задания? С какими словами? (Разбор затруднений.) Какой кружок себе нарисуете? (Не полностью раскрашенный зелёным.) Значит нужно ещё потренироваться в разборе по составу.
Вопросы к ученикам, выполнявших работу у доски (для самооценки):
-Справились?
-Самостоятельно работали?
-Верно выполнили задание?
-Какую отметку себе поставите?
Творческое задание. (Работа в парах.)
Слайд №4.
-Подберите слова к схемам:
1ряд 2ряд 3ряд
лис полос сказ
-Проверяем. Какие у вас подобраны слова к 1-ой
схеме, ко 2-ой, к 3-ей? Почему к каждой из схем удалось подобрать по несколько
вариантов слов? (1ряд — лисица, лисонька, лисёнок… 2 ряд — полоска,
полосочка, полосатый… 1 ряд — подсказка, рассказчик,присказка…)
Какие у вас подобраны слова к 1-ой
схеме, ко 2-ой, к 3-ей? Почему к каждой из схем удалось подобрать по несколько
вариантов слов? (1ряд — лисица, лисонька, лисёнок… 2 ряд — полоска,
полосочка, полосатый… 1 ряд — подсказка, рассказчик,присказка…)
-Кому было комфортно работать в паре?
4. Итог урока.
-Откройте рабочие тетради с печатной основой. Найдите тему №6 – задание №5. Каков правильный вариант ответа? В чём ошибка в других вариантах?
-Какую цель ставили перед собой на уроке?
— Удалось ли достичь цели?
— Что у вас получилось сегодня лучше всего?
— В чём испытали затруднения?
— Предлагаю оценить свою работу на уроке.
Слайд №5. (Самооценка работы на уроке и выбор дифференцированного домашнего задания.)Памятки по разбору слова по составу сохранить в папке и выучить порядок разбора.
5. Универсальные учебные действия, формируемые на данном уроке.
Познавательные УУД
1. Развиваем умения извлекать информацию из схем, иллюстраций, текстов.
Развиваем умения извлекать информацию из схем, иллюстраций, текстов.
2. Представлять информацию в виде схемы.
3. Выявлять сущность, особенности объектов.
4. На основе анализа объектов делать выводы.
5. Обобщать и классифицировать по признакам.
6. Ориентироваться на развороте учебника.
7. Находить ответы на вопросы в иллюстрации.
Регулятивные УУД
1. Развиваем умение высказывать своё предположение на основе работы с материалом учебника.
2. Оценивать учебные действия в соответствии с поставленной задачей.
3. Прогнозировать предстоящую работу (составлять план).
4. Осуществлять познавательную и личностную рефлексию.
Коммуникативные УУД
1. Развиваем умение
слушать и понимать других.
Развиваем умение
слушать и понимать других.
2. Строить речевое высказывание в соответствии с поставленными задачами.
3. Оформлять свои мысли в устной форме.
4. Умение работать в паре.
Личностные результаты
1. Развиваем умения выказывать своё отношение к героям, выражать свои эмоции.
2. Оценивать поступки в соответствии с определённой ситуацией.
3. Формируем мотивацию к обучению и целенаправленной познавательной деятельности.
6. Домашнее задание
Разгадай шарады, ответы запиши в тетрадь и разбери по составу.
Корень тот же, что и в слове сказка,
Суффикс тот же, что и в слове извозчик,
Приставка та же, что и в
слове расход.
Суффикс и окончание ищи в слове терпеливый,
Приставку — в слове выписать.
Корень – в слове преподносить.
Корень мой находится в цене,
В очерке найди приставку мне,
Суффикс мой в тетрадке все встречали,
Вся же – в дневнике я и в журнале.
Корень тот же, что и в слове отдавать,
Приставка взята из слова отличник,
Суффиксы взяты из слов мужество, откровенный, смелость.
Морфологический разбор слова «окомелок»
Слово можно разобрать в 2 вариантах, в зависимости от того, в каком контексте оно используется.
1 вариант разбора
Часть речи: Существительное
ОКОМЕЛОК — неодушевленное
Начальная форма слова: «ОКОМЕЛОК»
| Слово | Морфологические признаки |
|---|---|
| ОКОМЕЛОК |
|
| ОКОМЕЛОК |
|
Все формы слова ОКОМЕЛОК
ОКОМЕЛОК, ОКОМЕЛКА, ОКОМЕЛКУ, ОКОМЕЛКОМ, ОКОМЕЛКЕ, ОКОМЕЛКИ, ОКОМЕЛКОВ, ОКОМЕЛКАМ, ОКОМЕЛКАМИ, ОКОМЕЛКАХ
2 вариант разбора
Часть речи: Краткое прилагательное
ОКОМЕЛОК — слово может быть как одушевленное так и неодушевленное, смотрите по предложению в котором оно используется.
Начальная форма слова: «ОКОМЕЛКИЙ»
| Слово | Морфологические признаки |
|---|---|
| ОКОМЕЛОК |
|
Все формы слова ОКОМЕЛОК
ОКОМЕЛКИЙ, ОКОМЕЛКОГО, ОКОМЕЛКОМУ, ОКОМЕЛКИМ, ОКОМЕЛКОМ, ОКОМЕЛКАЯ, ОКОМЕЛКОЙ, ОКОМЕЛКУЮ, ОКОМЕЛКОЮ, ОКОМЕЛКОЕ, ОКОМЕЛКИЕ, ОКОМЕЛКИХ, ОКОМЕЛКИМИ, ОКОМЕЛОК, ОКОМЕЛКА, ОКОМЕЛКО, ОКОМЕЛКИ, ОКОМЕЛЬЧЕ, ПООКОМЕЛЬЧЕ, ОКОМЕЛЬЧАЙШИЙ, ОКОМЕЛЬЧАЙШЕГО, ОКОМЕЛЬЧАЙШЕМУ, ОКОМЕЛЬЧАЙШИМ, ОКОМЕЛЬЧАЙШЕМ, ОКОМЕЛЬЧАЙШАЯ, ОКОМЕЛЬЧАЙШЕЙ, ОКОМЕЛЬЧАЙШУЮ, ОКОМЕЛЬЧАЙШЕЮ, ОКОМЕЛЬЧАЙШЕЕ, ОКОМЕЛЬЧАЙШИЕ, ОКОМЕЛЬЧАЙШИХ, ОКОМЕЛЬЧАЙШИМИ
Разбор слова в тексте или предложении
Если вы хотите разобрать слово «ОКОМЕЛОК» в конкретном предложении или тексте, то лучше использовать
морфологический разбор текста.
Найти синонимы к слову «окомелок»
Примеры предложений со словом «окомелок»
1
На дворе Ротман поставил на березовый окомелок пустую бутылку, отмерил двадцать шагов, дал в руки сосновый дрын.
Миледи Ротман, Владимир Владимирович Личутин
2
Так окомелком в дыхало и залеплю, чтоб зубаревых детей во рту недосчитался.
Где зреют апельсины. Юмористическое описание путешествия супругов Николая Ивановича и Глафиры Семеновны Ивановых по Ривьере и Италии, Николай Лейкин, 1897г.
Найти еще примеры предложений со словом ОКОМЕЛОК
Композиция функций: свойства, вычисления и примеры
К настоящему времени вы, вероятно, знаете, что функции представляют собой математические выражения, которые принимают входные данные и возвращают выходные данные. Но что, если бы вы использовали одну функцию в качестве входных данных для другой функции? Ну, тогда вы использовали композицию функций . Когда вы используете одну функцию в качестве входных данных для другой, вы создаете совершенно новую функцию. Составная функция .
Но что, если бы вы использовали одну функцию в качестве входных данных для другой функции? Ну, тогда вы использовали композицию функций . Когда вы используете одну функцию в качестве входных данных для другой, вы создаете совершенно новую функцию. Составная функция .
Определение состава функций
Композиция функций — это метод использования одной функции в качестве входных данных для другой функции, в результате чего получается новая уникальная функция.
Как именно это выражается математически? Хорошо, если составная функция просто принимает одну функцию в качестве входных данных для другой, вы можете выразить это так:
\[ h(x) = f(g(x)) \]
где \(h(x)\ ) — составная функция, а \(f(x)\) и \(g(x)\) — составляющие ее функции.
В качестве альтернативы мы можем использовать обозначение круга для обозначения композиции функций
\[ h(x) = (f \circ g)(x) \]
где \(h(x)\) — составная функция, а \( f(x) \) и \(g( х)\) — составляющие его функции.
Давайте посмотрим, как можно использовать этот метод для формирования составных функций.
Формирование составных функций
Это все хорошо, но как именно формировать эти составные функции? Ну на самом деле это совсем не сложно!
Возьмем функции \(f(x) = 2x\) и \(g(x) = x + 2\). Чтобы найти составную функцию \(h(x) = f(g(x))\), вы просто подставляете \(g(x)\) в \(f(x)\) везде, где вы видите \(x\) .
\[ \begin {align} h(x) &= f(g(x))\\ &= 2g(x)\\ & = 2(x + 2)\\ & = 2x + 4.\end {align} \]
Ниже приведен график, показывающий графики функций \(f(x)\) и \(g(x)\) и результирующей составной функции \(h(x)\). На графике видно, что, составив две наши исходные функции, вы получите новую и уникальную функцию.
Рис. 1. График функций \(f(x)\), \(g(x)\) и сложной функции \(h(x)\).
Давайте посмотрим на другой пример, чтобы убедиться, что вы поняли это!
Рассмотрим функции \( f(x) = 3x + 2 \) и \( g(x) = 5x + 4 \). Найдите функцию \( h(x) = (f \circ g)(x) \).
Найдите функцию \( h(x) = (f \circ g)(x) \).
Решение:
Чтобы найти составное, замените каждое \( x \) в функции \( f(x) \) на функцию \( g(x) \).
\[ \begin{align} h(x) &= (f \circ g)(x) \\ &= 3g(x) + 2 \\ &= 3(5x + 4) + 2 . \end{align}\]
Тогда это просто случай упрощения путем раскрытия скобок и сбора одинаковых терминов.
\[ \begin{align} h(x) &= 3(5x + 4) + 2 \\ &=15x + 12 + 2 \\ &= 15x + 14 . \end{align} \]
Не слишком сложно, верно? Ну, помните, функции — это нечто большее, чем просто само выражение. При формировании составных функций часто приходится останавливаться и учитывать также домен функции. Давайте посмотрим, как это работает.
Области составных функций
Чтобы функция выполнялась, входные данные для этой функции должны находиться в пределах области определения функции.
Домен функции представляет собой набор всех возможных входных данных для этой функции.
Это в равной степени верно и для составных функций. Из этого вы можете сделать вывод, что для того, чтобы составная функция оставалась истинной, выходные данные внутренней функции должны находиться в пределах домена внешней функции.
Давайте рассмотрим пример, чтобы было немного понятнее.
Учитывая функции
\[ f(x) = \frac{1}{x-2}, \quad \{ x \in \mathbb{R} | х \neq 2 \} \]
и
\[ g(x) = x + 2, \quad \{ x \in \mathbb{R} \}, \]
какова область определения сложной функции \( f(g(x)) )\)?
Помните, что \(\{ x \in \mathbb{R} \}\) означает, что \(x\) является действительным числом, и что \( \{ x \in \mathbb{R} | x \neq 2 \} \) означает, что \(x\) может быть любым вещественным числом, кроме \(2\).
Решение:
Выходы функции \( g(x) \) должны попадать в область определения \( f(x) \), поэтому они должны быть подразделом множества всех действительных чисел.
\[ \{ x \in \mathbb{R}\}\]
Вы также знаете, что результат функции \( g(x) \) не должен быть равен \( 2 \).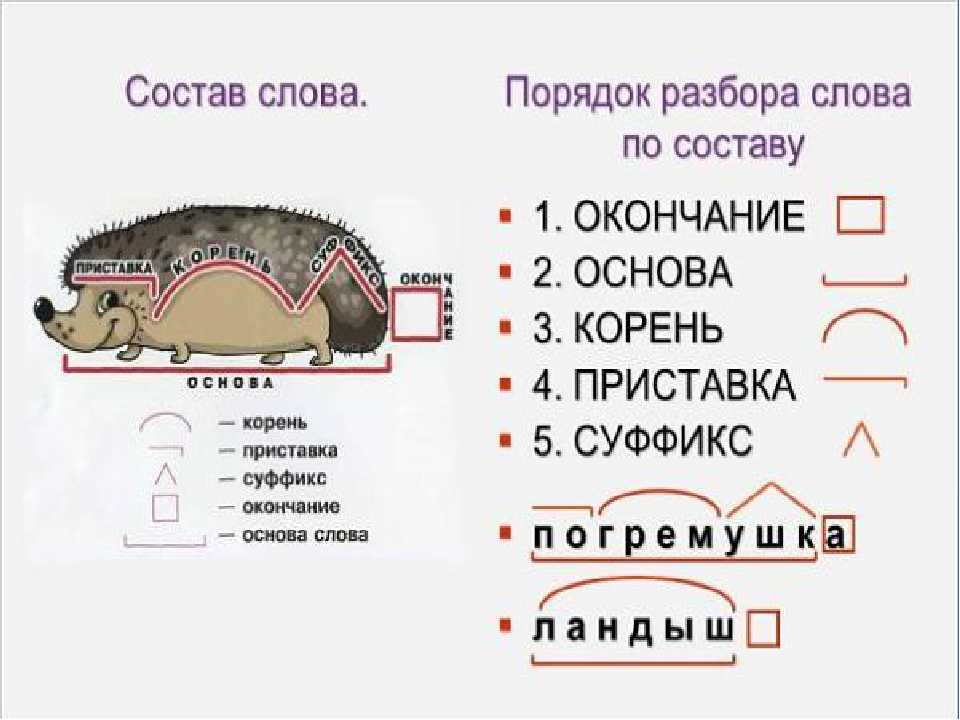
\[ g(x) \neq 2 \]
\[ \frac{1}{x-2} \neq 2 \]
\[ x \neq 2.5\]
Поэтому область определения функции \( f(g(x)) \) все, кроме \(2.5\), или другими словами
\[ \{ x \in \mathbb{R} | х \neq 2.5 \}. \]
Что происходит, когда вы составляете функции из дробей?
Композиция функций с дробями
Когда вы составляете функции, и одна из них имеет квадратный корень или дробь (например, рациональная функция), вам нужно быть осторожным с доменом. Давайте посмотрим на пример.
Возьмем функции \( g(x) = \sqrt{x}\) и
\[ f(x) = \frac{1}{x-2}.\]
Найти \( (f \ circ g)(x) \) и область определения сложной функции.
Решение:
Обратите внимание, что функция \(g(x)\) представляет собой квадратный корень, поэтому ее область определения равна \([0, \infty)\. Итак, вы уже знаете, что областью определения функции композиции являются не все действительные числа. Если вы делаете композицию,
\[ (f \circ g) (x) = \frac{1}{\sqrt{x}-2}.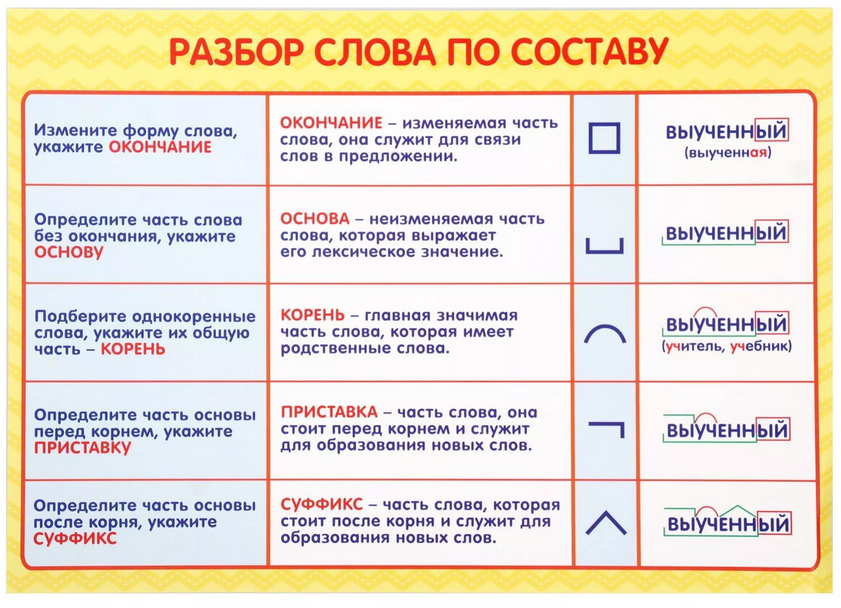 \]
\]
Вы знаете, что в знаменателе не может быть нуля, поэтому домен из \(f \circ g\) должно быть
\[ \sqrt{x} — 2 \not= 0,\]
, что означает
\[ \sqrt{x} \not= 2,\]
so
\[ x \not= 4.\]
Объединение ограничений на домен \(g(x)\) с ограничением \(x \not= 4\) дает вам, что композиция \( (f \circ g)(x)\) имеет область определения \( [0, 4) \cup (4, \infty)\).
Композиция функций с несколькими переменными
Композиция функций может выполняться в функциях с несколькими переменными так же, как и с одной переменной. Эти переменные могут быть как общими, так и не общими для отдельных функций, процесс во многом остается тем же.
Однако важно отметить, что окончательная составная функция будет содержать только переменные, присутствующие во внутренней функции.
Давайте рассмотрим пример, чтобы увидеть, как это работает.
Сначала рассмотрим две функции с разными переменными. Рассмотрим функции
\[ f(x) = \sqrt{x + 2} \]
и
\[ g(y) = 10y.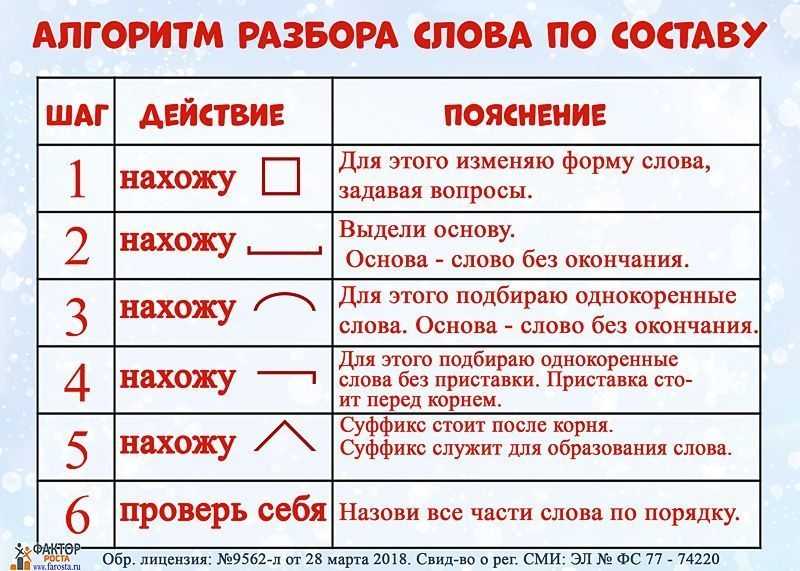 \]
\]
Найдем композицию этих функций \( f(g(y)) \). Обратите внимание, что составная функция является функцией только \( y \) , , а не \( x \) .
Решение:
Как и раньше, вы подставляете значение \( g(y) \) вместо \( x \) в \( f(x) \) , чтобы найти результирующую составную функцию.
\[ f(g(y)) = \sqrt{10y + 2} \]
Область определения этой составной функции также будет выражена \( y \) . Поскольку вы не можете извлечь квадратный корень из отрицательного значения (предположим, что вы пренебрегаете мнимыми числами), домен выглядит следующим образом:
\[ \begin{align} 10y + 2 &> 0\\ 10y &> -2 \\ y & >-0,2 . \end{align}\]
Таким образом, вся составная функция, включая домен функции, равна
\[f(g(y)) = \sqrt{10y + 2}, \quad\{y \in \mathbb{R}, y > -0,2 \}. \]
Оценка композиций функций
После того, как составная функция сформирована, ее оценка для заданного входа выполняется просто. {-1}(x)\right) \): 92 + 4 \\ &= h(x). \end{align}\]
{-1}(x)\right) \): 92 + 4 \\ &= h(x). \end{align}\]
Следовательно, вы нашли правильное разложение.
Составление функций Примеры
Давайте рассмотрим несколько примеров вопросов, чтобы увидеть, сможете ли вы использовать все, что узнали.
Рассмотрим ракету, движущуюся в пространстве с равномерным ускорением, \( a \) и массы, \( m \), с начальной скоростью, \( u \). Учитывая, что его скорость в момент времени \( t \) описывается формулой \( v = u + at \) 92 ,\]
найдите выражение для кинетической энергии ракеты в момент времени \(t\).
Решение:
Каждое из этих уравнений можно переписать в виде функций, учитывая, что \( u \) , \( a \) , и \( m \) все константы, \( t \) и \( v \) две ваши независимые переменные, а \( v \) и \( E_K \) ваши зависимые переменные. Таким образом, в функциональной записи:
\[ \begin{align} &v(t) = u + at \\ & E_K(v) = \frac{1}{2} mv^2 . \end{align}\] 92 + 6x + 9}, \quad \{ x \in \mathbb{N} | x \neq 3 \} \]
\end{align}\] 92 + 6x + 9}, \quad \{ x \in \mathbb{N} | x \neq 3 \} \]
и
\[ g(x) = \sqrt{x}, \quad \{ x \in \mathbb{R}, \quad x\ge 0 \} ,\] какова область определения сложной функции \(f(g(x))\)?
Решение:
Результат \( g(x) \) должен находиться в области определения \( f(x) \). Поэтому выходы \( g(x) \) должны принадлежать множеству \( \mathbb{N}\setminus \{3 \} \).
Это означает, что вывод \( g(x) \) не может быть \( 3 \), так как вывод \(g(x)\) должен находиться в области определения \(f(x)\) и область определения \(f(x)\) не включает \(3\). Поэтому
\[ g(x) \neq 3, \]
так
\[ 3 \neq \sqrt{x} ,\]
что означает
\[ x \neq 9. \]
вывод \( g(x) \) должен быть натуральным числом, поэтому вывод также должен быть больше нуля. Поэтому
\[ \begin{align} & g(x) > 0 \\ & \sqrt{x} > 0\\ & x > 0. \end{align} \]
Это на самом деле не дает вам много новой информации, поскольку вы уже знали, что на выходе должно быть натуральное число!
Собирая все вместе, ваш окончательный домен для \( f(g(x) \) равен
\[ \{ x \in \mathbb{N} | x \neq 9 \}. \]
\]
Что насчет
Давайте рассмотрим две функции с несколькими общими переменными. Рассмотрим функции
\[ f(x,y) = 2x + 9y \]
и
\[ g(x,y) = \frac {15x}{y — 10} .\]
Найдем составную функцию \( f(g(x,y),y) \).
Решение:
В этом случае \(y \) во втором месте \( f(g(x,y),y) \) говорит вам, что должны произойти две вещи:
- значение \( g(x,y) \) подставляется в \( f(x,y) \) где любой \( x \) присутствует; и
- \(y\) остается там, где присутствует любой \( y \) .
Выполнение этих двух шагов дает вам
\[ f(g(x,y),y) = 2 \left( \frac{15x}{y-10} \right) + 9y. \]
Теперь упростим, раскрыв скобки и собрав похожие члены:
\[ \begin{align} f(g(x,y), y) &= \frac{30x}{y-10} + 9y \ \ &= \frac{30x}{y-10} + \frac{92. \]
Композиция функций — основные выводы
- Новая функция может быть сформирована путем использования одной функции в качестве входных данных для другой, это называется составной функцией.

- При рассмотрении области определения композиции двух функций важно учитывать область определения всей функции, а не только составляющих ее функций.
- Функции можно разложить на две или более составляющие функции.
- Предел сложной функции в точке — это внешняя функция, оцениваемая в пределе внутренней функции, приближающейся к этой точке.
Композиция функций — определение, свойства и примеры
В математике композиция функции — это операция, при которой две функции, говорящие f и g, порождают новую функцию, говорящую h, таким образом, что h(x) = g( ф (х)). Это означает, что здесь функция g применяется к функции x. Итак, в основном функция применяется к результату другой функции.
Давайте посмотрим на определение составной функции .
Составные функции Определение
Пусть f : A → B и g : B → C — две функции. Тогда композиция f и g, обозначаемая g ∘ f, определяется как функция g ∘ f : A → C, заданная формулой g ∘ f (x) = g(f (x)), ∀ x ∈ A.
На приведенном ниже рисунке показано представление составных функций .
Порядок функции важен при работе с композицией функций, поскольку (f ∘ g) (x) не равно (g ∘ f) (x).
Отношение и функция являются важной концепцией классов 11 и 12. См. ниже символ композиции функции и домен с примером.
Символ: Также обозначается как (g∘f)(x), где ∘ — маленький кружок. Мы не можем заменить ∘ точкой (.), потому что это будет отображаться как произведение двух функций, таких как (g.f)(x).
Домен: f(g(x)) читается как f от g от x. В композиции (f o g) (x) область определения функции f становится g(x). Домен — это набор всех значений, которые входят в функцию.
Пример: Если f(x) = 3x+1 и g(x) = x 2 , то f от g от x, f(g(x)) = f(x 2 ) = 3x 2 +1.
Если мы реверсируем операцию функции, например, f от f от x, g(f(x)) = g(3x+1) = (3x+1) 2
Также читайте:
Свойства функциональных композиций
Ассоциативное свойство: Согласно ассоциативному свойству композиции функций, если есть три функции f, g и h, то они называются ассоциативными тогда и только тогда, когда;
ж ∘ (г ∘ ч) = (ж ∘ г) ∘ ч
Переместительное свойство: Две функции f и g называются коммутирующими друг с другом тогда и только тогда, когда;
г ∘ ж = ж ∘ г
Еще несколько свойств:
- Композиция функции «один к одному» всегда один к одному.

- Функциональная композиция из двух функций onon всегда находится на
- Обратная композиция двух функций f и g равна композиции обратной обеих функций, например (f ∘ g) -1 = ( g -1 ∘ f -1 ).
Как решать составные функции
В математике решение сложной функции означает получение композиции двух функций. Маленький кружок (∘) используется для обозначения композиции функции.
Выполните приведенные ниже шаги, чтобы понять, как решить данную составную функцию.
Шаг 1: Сначала запишите данную композицию другим способом.
Рассмотрим f(x) = x 2 и g(x) = 3x
Сейчас,
(f ∘ g) (x) можно записать как f[g(x)].
Шаг 2: Замените переменную x, находящуюся во внешней функции, на внутреннюю функцию, взяв за основу отдельные функции.
Значит,
(f ∘ g)(x) = f(3x) {поскольку g(x) = 3x}
Шаг 3: Наконец, упростим полученную функцию.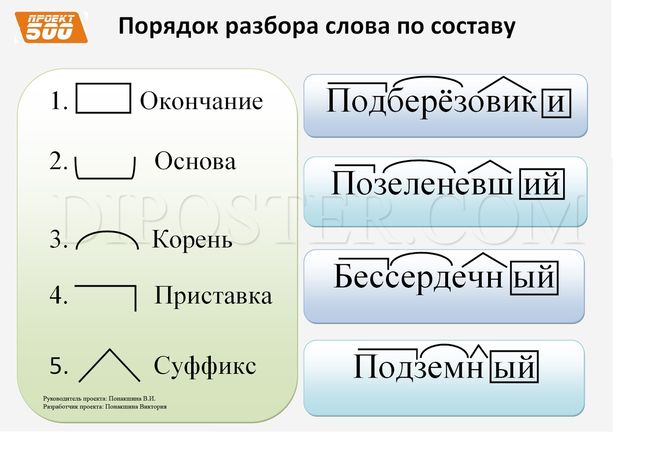
(f ∘ g)(x) = f(3x) = (3x) 2 {поскольку f(x) = x 2 }
= 9x 2
Функциональная композиция сама с собой
Можно составить функцию с самой собой. Предположим, что f — функция, тогда композиция функции f с самой собой будет
(f∘f)(x) = f(f(x))
Разберем это на примере:
Пример: Если f(x) = 3x 2 , то найти (f∘f)(x).
Решение: Дано: f(x) = 3x 2
(f∘f)(x) = f(f(x))
= f (3x 2 )
= 3(3x) 2
= 3,9 х 2
= 27 х 2
Пример композиции функций
Q.1: Если f (x) = 2x и g(x) = x+1, то найти (f∘g)(x), если x = 1.
Решение: Дано, f(x) = 2x
г(х) = х+ 1
Следовательно, композиция f из g будет;
(f∘g)(x) = f(g(x)) = f(x+1) = 2(x+1)
Теперь подставляем значение x = 1
f(g(1)) = 2(1+1) = 2 (2) = 4
Q.

