Разбор слов по составу
Разбор слова по составу
Тип лингвистического анализа, в результате которого определяется структура слова, а также его состав, называется морфемным анализом.
Виды морфем
В русском языке используются следующие морфемы:
— Корень. В нем заключается значение самого слова. Слова, у которых есть общий корень, считаются однокоренными. Иногда слово может иметь два и даже три корня.
— Суффикс. Обычно идет после корня и служит инструментом для образования других слов. К примеру, «гриб» и «грибник». В слове может быть несколько суффиксов, а может не быть совсем.
— Приставка. Находится перед корнем. Может отсутствовать.
— Окончание. Та часть слова, которая изменяется при склонении или спряжении.
— Основа. Часть слова, к которой относятся все морфемы, кроме окончания.
Важность морфемного разбора
В русском языке разбор слова по составу очень важен, ведь нередко для правильного написания слова необходимо точно знать, частью какой морфемы является проверяемая буква.
Пример
В качестве примера можно взять два слова: «чёрный» и «червячок». Почему в первом случае на месте ударной гласной мы пишем «ё», а не «о», как в слове «червячок»? Нужно вспомнить правило написания букв «ё», «е», «о» после шипящих, стоящих в корне слова. Если возможно поменять форму слова либо подобрать родственное ему так, чтобы «ё» чередовалась с «е», тогда следует ставить букву «ё» (чёрный — чернеть). Если чередование отсутствует, тогда ставится буква «о» (например, чокаться, шорты).
В случае же со словом «червячок» «-ок-» — это суффикс. Правило заключается в том, что в суффиксах, если стоящая после шипящих букв гласная находится под ударением, всегда пишется «о» (зрачок, снежок), в безударном случае — «е» (платочек, кармашек).
Как разобрать слово по составу
Для помощи начинающим существуют морфемно-орфографические словари. Можно выделить книги таких авторов, как Тихонов А.Н.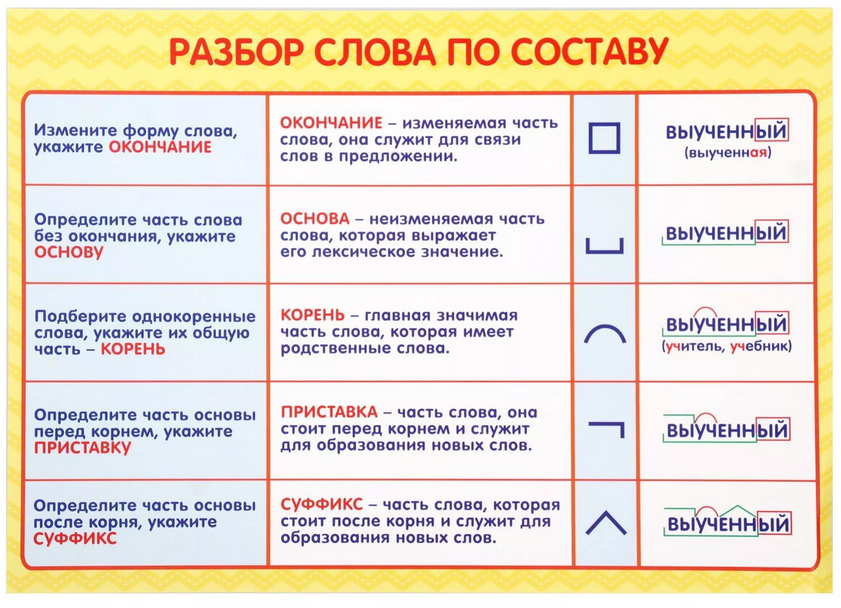
В любом слове непременно должны присутствовать корень и основа. Остальных морфем может и не быть. Иногда слово целиком может состоять из корня (или основы): «гриб», «чай» и т.д.
Этапы морфемного анализа
Чтобы морфемный разбор слов было легче осуществить, следует придерживаться определенного алгоритма:
— Сначала нужно определить часть речи, задав вопрос к слову. Для прилагательного это будет вопрос «какой?», для существительного — «что?» или «кто?».
— Затем нужно выделить окончание. Чтобы его найти, слово нужно просклонять по падежам, если часть речи это позволяет. Например, наречие изменить никак нельзя, поэтому у него не будет окончания.
— Далее нужно выделить основу у слова. Все, кроме окончания, — основа.
— Потом следует определить корень, подобрав родственные однокоренные слова.
Особенности разбора
Иногда подход к морфемному разбору в программах университета и школы может отличаться.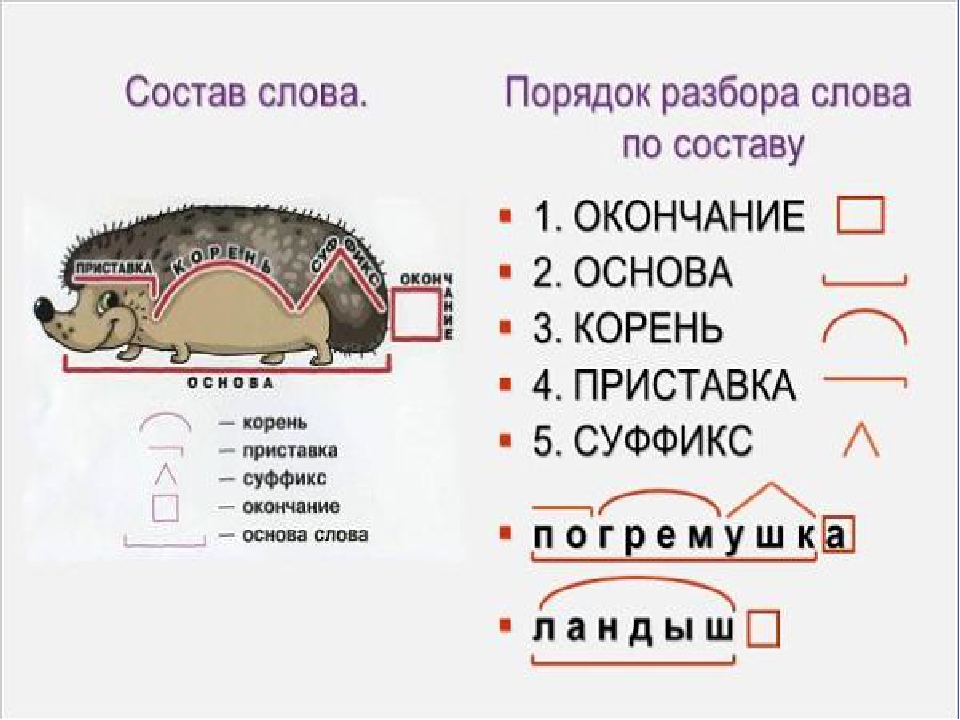 Во всех случаях различия аргументированы и имеют право на существование. Поэтому стоит ориентироваться на морфемный словарь, рекомендованный в конкретном учебном заведении.
Во всех случаях различия аргументированы и имеют право на существование. Поэтому стоит ориентироваться на морфемный словарь, рекомендованный в конкретном учебном заведении.
Только что искали: плутос сейчас о с й т у п сейчас ступень 1 секунда назад компас 1 секунда назад нурай 1 секунда назад у я н и ш т к е ц 1 секунда назад проетроа 1 секунда назад подделка 1 секунда назад сосннен 1 секунда назад боузръедл 1 секунда назад б р и г а д а 2 секунды назад кристалл 2 секунды назад ш о ё а р т 2 секунды назад у и н м о л к и с 2 секунды назад лескапи 2 секунды назад
Морфологический разбор слова «умножение»
Часть речи: Существительное
УМНОЖЕНИЕ — неодушевленное
Начальная форма слова: «УМНОЖЕНИЕ»
| Слово | Морфологические признаки |
|---|---|
| УМНОЖЕНИЕ |
|
| УМНОЖЕНИЕ |
|
Все формы слова УМНОЖЕНИЕ
УМНОЖЕНИЕ, УМНОЖЕНЬЕ, УМНОЖЕНИЯ, УМНОЖЕНЬЯ, УМНОЖЕНИЮ, УМНОЖЕНЬЮ, УМНОЖЕНИЕМ, УМНОЖЕНЬЕМ, УМНОЖЕНИИ, УМНОЖЕНЬИ, УМНОЖЕНИЙ, УМНОЖЕНИЯМ, УМНОЖЕНЬЯМ, УМНОЖЕНИЯМИ, УМНОЖЕНЬЯМИ, УМНОЖЕНИЯХ, УМНОЖЕНЬЯХ
Разбор слова по составу умножение
умножени
е
| Основа слова | умножени |
|---|---|
| Приставка | у |
| Корень | множ |
| Суффикс | ени |
| Окончание | е |
Разобрать другие слова
Разбор слова в тексте или предложении
Если вы хотите разобрать слово «УМНОЖЕНИЕ» в конкретном предложении или тексте, то лучше использовать
морфологический разбор текста.
Найти синонимы к слову «умножение»
Примеры предложений со словом «умножение»
1
гордо говорит служанка, – А ещё, я учу таблицу умножения и уже прохожу умножение на цифру четыре!
Хуже уже не будет! Фантастическое приключение. Часть 4, Олег Михайлович Янгулов
2
На счётах умножение и деление, только костяшки отскакивают, делает, а ты в четвёртом классе таблицу умножения не можешь выучить.
Купола в солнечном просторе, Сергей Николаевич Прокопьев, 2020г.
3
Умножение детей уменьшало в Прохоре Абрамовиче интерес к себе;
Чевенгур, Андрей Платонов, 1929г.
4
Потому ты таблицу умножения знаешь, а мы на место тебя пришлем нового, молодого, который таблицы умножения не знает!
Люди сороковых годов, Алексей Феофилактович Писемский, 1869г.
5
Два из них – сложение и умножение – считала хорошими и к ним стремилась.
Авантюрный роман, Надежда Тэффи
Найти еще примеры предложений со словом УМНОЖЕНИЕ
Математика — Понятие умножения — 1161 слов
При понимании умножения учащимся необходимо понимать правила сложения, так как они тесно взаимосвязаны. Умножение иногда называют повторным сложением, применение которого происходит быстрее и эффективнее.
Например, вместо сложения 4+4+4=12 умножение упрощает его до 4*3=12. Если, например, есть три ученика, у каждого из которых по четыре линейки, это можно показать, разложив четыре линейки в три группы и позволив ученику сосчитать их индивидуально. В результате будет получен тот же самый ответ. Это указывает на то, что сложение включает в себя использование фактического количества раз, которое нужно умножить на число, чтобы добавить его.
Если, например, есть три ученика, у каждого из которых по четыре линейки, это можно показать, разложив четыре линейки в три группы и позволив ученику сосчитать их индивидуально. В результате будет получен тот же самый ответ. Это указывает на то, что сложение включает в себя использование фактического количества раз, которое нужно умножить на число, чтобы добавить его.
Например, 4*5= 4+4+4+4+4= 5+5+5+5= 20, с другой стороны, умножение предполагает работу со многими группами одинакового размера или группами с одинаковым количеством предметы в каждой группе. Умение считать количество групп и предметов необходимо для того, чтобы уметь их умножать. Затем это показывает, что сложение является инициатором умножения, когда можно решить задачу на умножение путем многократного сложения.
Это позволяет учащимся понять концепции сложения, которые включают манипулирование группами для получения общего продукта. Кроме того, это помогает учащимся узнать количество или размер предметов в нескольких группах одинакового размера.
Например, если в пачке восемь карандашей и человек решил купить пять таких упаковок, то можно узнать, сколько у него карандашей. Эту проблему можно решить с помощью метода сложения 8+8+8+8+8=40, который представляет собой повторяющееся сложение, заменяемое методом умножения 8*5=40. Кроме того, учащиеся могут понять, что математика заключается в том, как формулировать и решать задачи, а не в запоминании или чтении.
Это позволяет учащимся вместо заучивания математических формул, таких как 4*8=32; вместо этого они считают, что тот же ответ можно получить другими методами, такими как 4 * 8 = 8 + 8 + 8 + 8 = 24 + 8 = 32. Это хороший метод, который наглядно показывает отношения умножения и сложения. Кроме того, учащийся может манипулировать группами и заданием, чтобы получить аналогичный ответ, например, 6*7= 3*7+3*7= 21+21= 42 — аспект, который дает творческий метод изучения таблицы умножения, точная работа математики.
Коммутативное свойство — это операция, возникающая при изменении порядка задействованных элементов без изменения результатов. Например, 3-2 не равно 2-3. Примеры коммутативного сложения и умножения: x+y=y+x или 12+13=13+12; и x*y=y*x, или 9*5=5*9. Ассоциативность — это процесс, при котором числа можно перегруппировать любым способом без изменения ответа. В этом свойстве ответ не зависит от того, как комбинируются числа.
Например, 3-2 не равно 2-3. Примеры коммутативного сложения и умножения: x+y=y+x или 12+13=13+12; и x*y=y*x, или 9*5=5*9. Ассоциативность — это процесс, при котором числа можно перегруппировать любым способом без изменения ответа. В этом свойстве ответ не зависит от того, как комбинируются числа.
Например, (x+y) +z= x+(y+z). или 3+(5+4)= (3+5)+4=3+(9)=(8)+4= 12; и x*(y*z)= (x*y)*z или 3*(5*4)=(3*5)*4=60. С другой стороны, в распределительном свойстве число способно умножаться на сумму двух других чисел или распределяться на эти числа по отдельности и давать тот же ответ. Например, x*(y+z) =x*y+x*z или 4*(3+2)=4*(5)=20 или 4*3+4*2=12+8=20.
Эти свойства помогают учащимся в запоминании, позволяя им понять свойства, связанные с включением шаблонов и стратегий, таких как пятерки и девятки.
Например, счет с пропусками помогает учащимся находить числа, кратные двум и пяти, путем осознания того, что они уже знают. Например, массив может быть предоставлен для чтения 2 строк и 6 столбцов, которые можно интерпретировать как 6 столбцов по 2 или 2 строки по 6, перевернув его. То же самое относится к трем строкам по 5, которые учащийся может интерпретировать как 15, помещенных в 3 строки, что дает 5 столбцов или 5 в каждой строке.
То же самое относится к трем строкам по 5, которые учащийся может интерпретировать как 15, помещенных в 3 строки, что дает 5 столбцов или 5 в каждой строке.
В распределительной собственности стратегия личного изобретения используется при попытке вспомнить один из нескольких фактов умножения. Например, ученик может понять, что 7*9сложно, и решите добавить еще 2 семерки к уже известному кратному 7: 49, чтобы получить 63, что упрощает знание 7 * 9 = 63. Кроме того, он позволяет использовать факты пяти, чтобы получить шестерки. Например, в задачах 6*3 ученик может подумать, что это означает 5 групп по 3 и еще одну группу по 3. То есть 6*3= (5*3)+(1*3)=18.
Однако учащиеся допускают некоторые концептуальные ошибки, наиболее распространенными из которых являются забывание ранее изученных знаний. Например, учащиеся часто забывают правила сложения и умножения. Например, правило 4*3 означает, что группу из 4 предметов считают три раза, а вместо этого добавляют две цифры.
Здесь важно, чтобы учителя повторили некоторую важную информацию из предыдущей темы, чтобы активизировать память учащихся и вспомнить, что они узнали об этих правилах. Это ошибка, вызванная тем, что математика является кумулятивным предметом.
Это ошибка, вызванная тем, что математика является кумулятивным предметом.
Кроме того, учащиеся путаются из-за смены знаков при одновременном выполнении сложения или умножения. Например, в такой задаче, как 3 * 7 + 3 * 7, ученик может решить ее, сначала занимаясь сложением, а затем умножением, то есть 3 * (10) * 7 = 210 вместо 21 + 21 = 42. Это связано с путаницей правил применения знаков по порядку (какой из них идет первым).
Здесь обучая учащегося ПРАВИЛУ БОДМАСА, он обеспечит эффективное решение задач, содержащих более одного знака, применяя сначала первый знак. Кроме того, иллюстрируя разные знаки и предостерегая учащихся, чтобы они понимали, когда имеют дело с умножением, а не сложением, они смогут справиться с этой проблемой.
Другая концептуальная ошибка возникает из-за смешения ассоциативных правил с правилами свойств распределения. Студенты забывают эти правила, и во многих случаях они забывают интерпретировать знаки, что приводит к неправильному решению задач.
Например, если учащемуся предлагается задача на 4+ (3+5), они иногда путают ее с 4*(3+5) и вместо решения как 4+(8)=12 получают (12)+(20)= 32. Здесь объяснение учащемуся, как знак перед скобкой влияет на числа в скобках, позволит им, когда это необходимо для распределения, а когда нет. Также это требует интенсивной практики и повторения, чтобы выработать у ученика привычку.
Понимание того, что математика является запутанным предметом для многих учащихся, важно для родителей, учителей и воспитателей. Это потому, что математика содержит множество правил, а также формул, которые нужно запоминать и вспоминать. Один из способов помочь учащимся запомнить эти правила и формулы — соотнести их с примерами из реальной жизни.
Это создаст основания для формул, что позволит учащимся выявить в них проблемы. Например, при умножении длины и ширины для получения площади это можно сопоставить с примерами из реальной жизни, когда нужно нанести такое количество краски на стену в классе.
С другой стороны, если дважды добавить длину и дважды ширину, чтобы получить периметр прямоугольника, это можно соотнести с измерением забора вокруг участка земли. Таким образом, математика станет менее опасной для ученика, поскольку он будет рассматривать ее как явление реальной жизни. Кроме того, объединение примеров с умножением и сложением поможет учащимся укрепить эти понятия.
Это эссе по математике — понятие умножения было написано и представлено вашим коллегой ученик. Вы можете использовать его для исследовательских и справочных целей, чтобы написать свою собственную статью; однако ты должны цитировать его соответственно.
Запрос на удаление
Если вы являетесь владельцем авторских прав на эту статью и больше не хотите, чтобы ваша работа публиковалась на IvyPanda.
Запросить удаление
словесные задачи | нул
Это руководство по решению текстовых задач!
Перед тем, как начать решать текстовые задачи, важно понять, что такое текстовые задачи. Словесная задача — это математическое упражнение в форме гипотетического вопроса, требующего математического анализа и решения уравнений. Хороший способ решать текстовые задачи — использовать метод под названием «GRASS». GRASS — это аббревиатура от «Дано», «Требуется», «Анализ», «Решение» и «Утверждение». Вы можете использовать GRASS шаг за шагом, чтобы разбить задачу на слова, чтобы упростить ее решение.
Словесная задача — это математическое упражнение в форме гипотетического вопроса, требующего математического анализа и решения уравнений. Хороший способ решать текстовые задачи — использовать метод под названием «GRASS». GRASS — это аббревиатура от «Дано», «Требуется», «Анализ», «Решение» и «Утверждение». Вы можете использовать GRASS шаг за шагом, чтобы разбить задачу на слова, чтобы упростить ее решение.
Дано : Определите данную информацию в вопросе. Какие значения даны и что они представляют? Может быть полезно знать следующие термины, которые иногда используются в математических задачах, и их значение:
| . Срок | Значение |
Сумма | + (дополнение) |
Разница | — (вычитание) |
Продукт | * (умножение) |
Коэффициент | / (отдел) |
Обязательно : Посмотрите, что на самом деле просит вас найти вопрос. Что бы это ни было, представьте его с помощью переменной, например, x.
Что бы это ни было, представьте его с помощью переменной, например, x.
Анализ : Если применимо, нарисуйте эскиз, если он еще не предоставлен. Определитесь с подходящими математическими методами и формулами, связывающими различные интересующие величины. По возможности используйте только одну переменную. Например, если вы ищете два числа, отличающиеся на 5, пусть x и x+5 (или x и x-5) представляют два числа, а НЕ x и y. В качестве альтернативы вы можете использовать некоторую информацию, представленную в вопросе, чтобы помочь вам переписать уравнение только с одной переменной.
Решение : Решите уравнение или найдите ответ, который вы ищете. Вам придется хорошо подумать о различных математических методах, которые вы изучили на курсах, чтобы выяснить, какие из них подходят для этого конкретного вопроса. Убедитесь, что ваши решения имеют смысл в контексте приложения — например, отрицательная область не имеет никакого смысла.
Утверждение : Завершите заключительным утверждением, чтобы прояснить ответ на вопрос. Если применимо, включите единицы измерения в свой ответ.
Если применимо, включите единицы измерения в свой ответ.
Вот простой пример, показывающий, как GRASS используется для решения текстовой задачи.
Пример :
Периметр прямоугольного парка составляет 26 м. Если длина парка 5 м, то какова его ширина?
Дано : В этом вопросе периметр прямоугольного парка равен 26 м. Нам также говорят, что длина парка составляет 5 м. Итак, P = 26 м и L = 5 м.
Требуется : Вопрос спрашивает: «Какова ширина парка?» Отсюда мы знаем, что нам нужно найти ширину. Найти: ш = ?
Анализ : Мы можем нарисовать набросок прямоугольного парка, чтобы узнать, какие формулы нам, возможно, придется использовать для определения ширины.
Примечание. Более длинные стороны соответствуют длине, а более короткие — ширине.
Из этого наброска видно, что нам нужна формула для периметра прямоугольника.
P= 2L + 2w
Если мы переформулируем уравнение для w, то получим
w = (P – 2L) ÷ 2
Упрощенное уравнение:
w = P/2 — L
Решение .