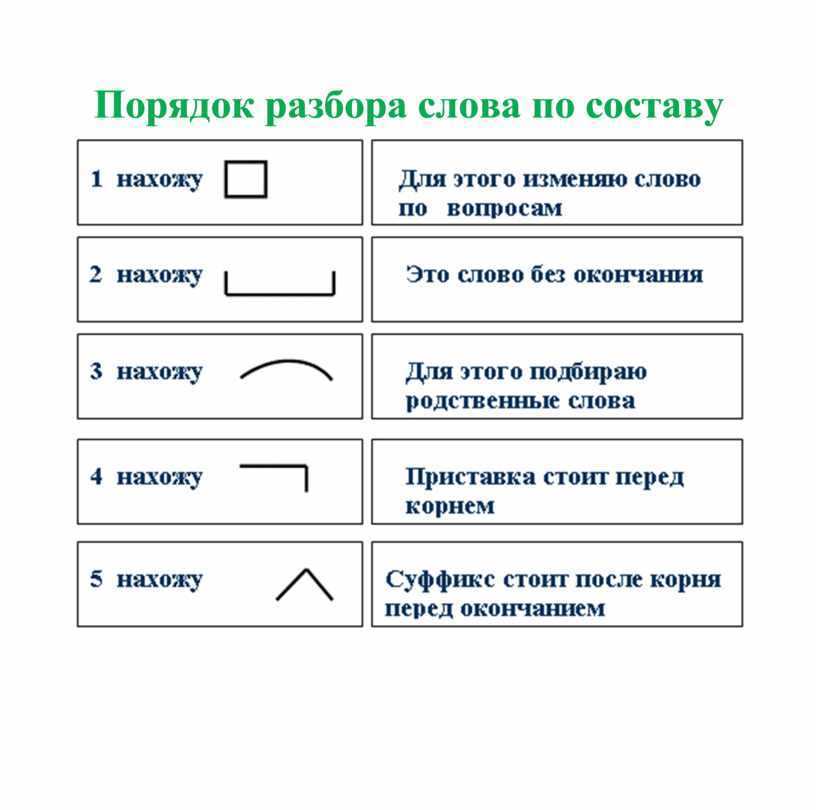
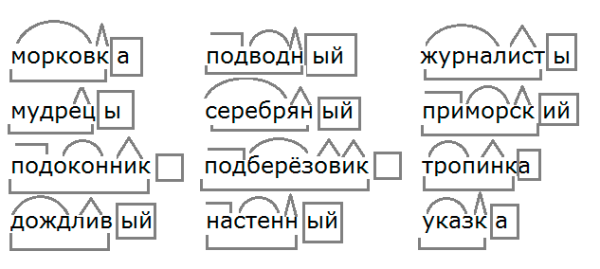
Слова «цепочка» морфологический и фонетический разбор
Объяснение правил деление (разбивки) слова «цепочка» на слоги для переноса.
Онлайн словарь Soosle.ru поможет: фонетический и морфологический разобрать слово «цепочка» по составу, правильно делить на слоги по провилам русского языка, выделить части слова, поставить ударение, укажет значение, синонимы, антонимы и сочетаемость к слову «цепочка».
Содержимое:
- 1 Слоги в слове «цепочка» деление на слоги
- 2 Как перенести слово «цепочка»
- 3 Морфологический разбор слова «цепочка»
- 4 Разбор слова «цепочка» по составу
- 5 Сходные по морфемному строению слова «цепочка»
- 6 Синонимы слова «цепочка»
- 7 Ударение в слове «цепочка»
- 8 Фонетическая транскрипция слова «цепочка»
- 9 Фонетический разбор слова «цепочка» на буквы и звуки (Звуко-буквенный)
- 10 Предложения со словом «цепочка»
- 11 Сочетаемость слова «цепочка»
- 12 Значение слова «цепочка»
- 13 Склонение слова «цепочка» по подежам
- 14 Как правильно пишется слово «цепочка»
- 15 Ассоциации к слову «цепочка»
Слоги в слове «цепочка» деление на слоги
Количество слогов: 3
По слогам: це-по-чка
По правилам школьной программы слово «цепочка» можно поделить на слоги разными способами.
Допускается вариативность, то есть все варианты правильные. Например, такой:
це-поч-ка
По программе института слоги выделяются на основе восходящей звучности:
це-по-чка
Ниже перечислены виды слогов и объяснено деление с учётом программы института и школ с углублённым изучением русского языка.
ч примыкает к этому слогу, а не к предыдущему, так как не является сонорной (непарной звонкой согласной)
Как перенести слово «цепочка»
це—почка
цепо—чка
цепоч—ка
Морфологический разбор слова «цепочка»
Часть речи:
Имя существительное
Грамматика:
часть речи: имя существительное;
одушевлённость: неодушевлённое;
род: женский;
число: единственное;
падеж: именительный;
отвечает на вопрос: (есть) Что?
Начальная форма:
цепочка
Разбор слова «цепочка» по составу
| цеп | корень |
| очк | суффикс |
| а | окончание |
цепочка
Сходные по морфемному строению слова «цепочка»
Сходные по морфемному строению слова
Синонимы слова «цепочка»
1.
рустов
2. цепь
3. вереница
4. ряд
5. цепка
6. череда
7. чреда
8. смычок
9. шатлен
10. змейка
11. ланцы
12. удавка
Ударение в слове «цепочка»
цепо́чка — ударение падает на 2-й слог
Фонетическая транскрипция слова «цепочка»
[цып`оч’ка]
Фонетический разбор слова «цепочка» на буквы и звуки (Звуко-буквенный)
| Буква | Звук | Характеристики звука | Цвет |
|---|---|---|---|
| ц | [ц] | согласный, глухой непарный, твёрдый, шумный | ц |
| е | [ы] | гласный, безударный | е |
| п | [п] | согласный, глухой парный, твёрдый, шумный | п |
| о | [`о] | гласный, ударный | о |
| ч | [ч’] | согласный, глухой непарный, мягкий, шипящий | ч |
| к | [к] | согласный, глухой парный, твёрдый, шумный | к |
| а | [а] | гласный, безударный | а |
Число букв и звуков:
На основе сделанного разбора делаем вывод, что в слове 7 букв и 7 звуков.
Буквы: 3 гласных буквы, 4 согласных букв.
Звуки: 3 гласных звука, 4 согласных звука.
Предложения со словом «цепочка»
У девочки был мобильный телефон и золотая цепочка.
Источник: И. С. Прокопенко, Код бессмертия. Правда и мифы о вечной жизни, 2016.
Выпрямился и замер над кругом, спустив кристалл на длинной цепочке почти до самого пола.
Источник: Е. М. Малиновская, Ритуалы экзорцизма, 2015.
Когда знания выстроились в логическую цепочку, оставалось только удивляться силе, сноровке и многофункциональности снабжённого крыльями тела.
Источник: Юрий Иванович, Невменяемый дракон, 2008.
Сочетаемость слова «цепочка»
1. золотая цепочка
2.
логическая цепочка
3. серебряная цепочка
4. цепочка следов
5. цепочка событий
6. цепочка людей
7. конец цепочки
8. звенья цепочки
9. длина цепочки
10. цепочка порвалась
11. цепочка оборвалась
12. цепочка замкнулась
13. снять цепочку
14. выстроиться в цепочку
15. выстроить логическую цепочку
16. (полная таблица сочетаемости)
Значение слова «цепочка»
ЦЕПО́ЧКА , -и, род. мн. -чек, дат. -чкам, ж. 1. Маленькая и тонкая цепь. (Малый академический словарь, МАС)
Склонение слова «цепочка» по подежам
| Падеж | Вопрос | Единственное числоЕд.ч. | Множественное числоМн.ч. |
|---|---|---|---|
| ИменительныйИм. | что? | цепочка | цепочки |
| РодительныйРод. | чего? | цепочки | цепочек |
ДательныйДат. | чему? | цепочке | цепочкам |
| ВинительныйВин. | что? | цепочку | цепочки |
| ТворительныйТв. | чем? | цепочкой, цепочкою | цепочками |
| ПредложныйПред. | о чём? | цепочке | цепочках |
Как правильно пишется слово «цепочка»
Правописание слова «цепочка»
Орфография слова «цепочка»
Правильно слово пишется: цепо́чка
Нумерация букв в слове
Номера букв в слове «цепочка» в прямом и обратном порядке:
- 7
ц
1 - 6
е
2 - 5
п
3 - 4
о
4 - 3
ч
5 - 2
к
6 - 1
а
7
Ассоциации к слову «цепочка»
Медальон
Крестик
Звено
Подвеска
Ключик
Жилетка
Днк
Браслет
Амулет
Серьга
Жилет
Сердечко
Колечко
Умозаключение
Брошь
Шея
Распятие
Ложбинка
Щеколда
Бусы
Кармашек
Оправа
Перстень
Пенсне
Бачок
Змейка
Жетон
Наручник
Засов
Молекула
Колье
Ожерелье
Задвижка
Украшение
Вырез
Ошейник
Свисток
Бриллиант
Запястье
Сапфир
Муравьев
Изумруд
Кольцо
Булавка
Верблюдов
Талисман
Рубин
Логический
Платиновый
Пищевой
Золотой
Серебряный
Витой
Тоненький
Карманный
Брюшной
Шейный
Обручальный
Молекулярный
Бриллиантовый
Рубиновый
-
Последовательный
Технологический
Выстраиваться
Выстраивать
Выстроиться
Замыкать
Растянуться
Позвякивать
Протянуться
Приоткрыться
Обвивать
Свисать
Выстроить
Звякнуть
Подвесить
Поигрывать
Болтаться
Свешиваться
Вытянуться
Прицепить
Отстегнуть
Висеть
Накинуть
Прикрепить
Тянуться
Натянуться
Вытягиваться
Теребить
Застегнуть
Крепиться
Обрываться
Расстегнуть
Передавать
Намотать
Поблескивать
Опоясывать
Пристегнуть
Позолотить
Страница не найдена
wordmap
Данная страница не найдена или была удалена.
Только что искали:
ладквка 1 секунда назад
париться 1 секунда назад
мастикар 2 секунды назад
акмуср 2 секунды назад
ламти 2 секунды назад
душегрею 3 секунды назад
перешнырнула 4 секунды назад
накопировало 5 секунд назад
паркан 5 секунд назад
схвативший за глотку 6 секунд назад
рбоан 7 секунд назад
взявший за яйца 9 секунд назад
прижавший к ногтю 10 секунд назад
амтади 11 секунд назад
спортигра 12 секунд назад
Последние игры в словабалдучепуху
| Имя | Слово | Угадано | Время | Откуда |
|---|---|---|---|---|
| Игрок 1 | безударность | 80 слов | 3 минуты назад | 95.29.166.229 |
| Игрок 2 | безударность | 141 слово | 4 часа назад | 91.132.23.36 |
| Игрок 3 | мультивалент | 35 слов | 4 часа назад | 91. 132.23.36 |
| Игрок 4 | руни | 0 слов | 8 часов назад | 178.45.158.215 |
| Игрок 5 | монотипистка | 13 слов | 8 часов назад | 178.34.184.168 |
| Игрок 6 | гидроэлектростанция | 20 слов | 9 часов назад | 188.254.127.56 |
| Игрок 7 | бобыч | 0 слов | 9 часов назад | 92.37.142.103 |
| Играть в Слова! | ||||
| Имя | Слово | Счет | Откуда | |
|---|---|---|---|---|
| Игрок 1 | шланг | 53:51 | 1 час назад | 93.170.175.250 |
| Игрок 2 | товар | 44:52 | 1 час назад | 93. 170.175.250 |
| Игрок 3 | дулеб | 45:44 | 1 час назад | 176.59.116.179 |
| Игрок 4 | совет | 18:25 | 1 час назад | 93.170.175.250 |
| Игрок 5 | струп | 4:5 | 1 час назад | 93.170.175.250 |
| Игрок 6 | гнома | 18:22 | 1 час назад | 93.170.175.250 |
| Игрок 7 | лазок | 48:45 | 1 час назад | 46.249.29.37 |
| Играть в Балду! | ||||
| Имя | Игра | Вопросы | Откуда | |
|---|---|---|---|---|
| Данил | На одного | 10 вопросов | 5 часов назад | 46. 147.152.47 |
| Нннн | На одного | 10 вопросов | 9 часов назад | 213.211.104.168 |
| Anna | На двоих | 10 вопросов | 1 день назад | 178.64.157.200 |
| Хуй | На одного | 10 вопросов | 1 день назад | 217.112.2.72 |
| Хуй | На одного | 10 вопросов | 1 день назад | 217.112.2.72 |
| Кирка | На одного | 5 вопросов | 1 день назад | 185.54.236.23 |
| Игорь | На одного | 10 вопросов | 1 день назад | 188.170.76.170 |
| Играть в Чепуху! | ||||
Идея цепного правила
Цепное правило позволяет вычислить производную композиции функций, такой как композиция $f(g(x))$ функций $f$ и $g$.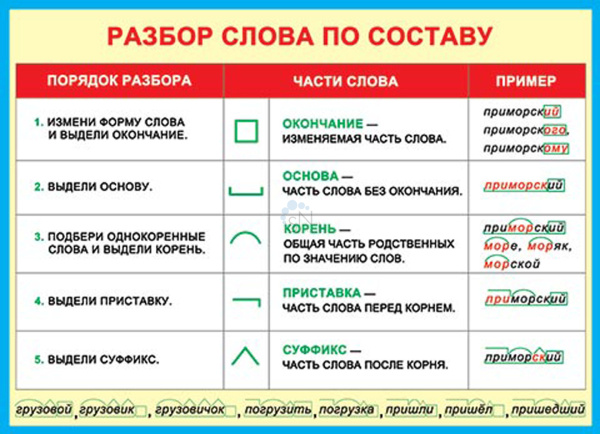
Правильное применение цепного правила может быть сложным, тем более, что со сложным выражением может потребоваться использовать цепное правило несколько раз. Тем не менее, идея цепного правила может быть понята довольно просто.
В следующем видео представлена основная идея цепного правила. В оставшейся части этой страницы мы проиллюстрируем идею цепного правила тремя способами. Во-первых, мы проиллюстрируем концепцию с помощью функциональных машин. Во-вторых, мы показываем, что для линейных функций цепное правило — это просто произведение наклонов графиков функций. В-третьих, мы показываем, что для нелинейных функций цепное правило — это просто произведение наклонов касательных линий к графикам функций. Примеры цепного правила приведены на другой странице.
Видео введение
Идея цепного правила.
Подробнее о видео.
Цепное правило функциональных машин
Композицию $f(g(x))$ двух функций $f$ и $g$ можно визуализировать как соединение двух функциональных машин так, чтобы выход $g$ стал ввод $f$.
Назовем объединенную функцию $h(x)$ так, чтобы $h(x)=f(g(x))$. (Иногда мы записываем композицию как $h=f \circ g$, так что большая функциональная машина ниже, обозначенная как $f \circ g$, иллюстрирует $h$.)
На приведенной выше иллюстрации функциональных машин $h$ — это функция, которая полностью преобразует сферу, введенную сверху, в ограненную сферу на выходе внизу. Входные данные для $h$ — это входные данные для $g$, а выходные данные для $h$ — это выходные данные для $f$. Производная от $h$ говорит нам, насколько изменится выход $h$, если мы немного изменим его вход, т. е. это отношение изменения выхода $h$ к изменению его входа (эквивалентно , отношение изменения выпуска $f$ к изменению входа $g$). Перефразируя предельное определение производной, мы могли бы записать это как
\начать{выравнивать*}
h’ &= \lim_{\text{небольшие изменения}}\frac{\text{изменение на выходе $h$}}{\text{изменение на входе на $h$}}\\
&= \lim_{\text{небольшие изменения}}\frac{\text{изменение на выходе $f$}}{\text{изменение на входе на $g$}}.
\конец{выравнивание*}
Цепное правило вычисляет эту производную, следуя цепочке событий, которые происходят, когда мы меняем входные данные на $g$ и наблюдаем результирующее изменение выходных данных $f$. Изменение входных данных $g$ (сферы) сначала вызывает изменение выходных данных $g$ (куба). Это приводит к такому же изменению входа в $f$ (тот же куб), что в конечном итоге приводит к изменению выхода $f$ (ограненной сферы).
В представлении функциональной машины производная от $h$ представляет собой отношение между изменением ограненной сферы и изменением сферы. Производная от $g$ – это отношение изменения куба к изменению сферы, а производная $f$ – отношение изменения грани сферы к изменению куба. Если мы умножим отношения, соответствующие производным от $g$ и $f$, множители, соответствующие изменению куба, сокращаются, и мы получим отношение, соответствующее производной от $h$. Если мы подумаем о $d$ в обозначении производной как об обозначении «изменения», мы можем записать результат цепного правила в терминах входов и выходов функциональной машины следующим образом.
В терминах производных функций мы можем записать цепное правило как $$h’ = f’ \cdot g’.$$ Нам нужно быть осторожными, чтобы вычислять производные в правильных точках. Если мы обозначим вход в $g$ как $x$ (сфера), то мы должны вычислить производную от $g$ в $x$, используя $g'(x)$. Поскольку вход в $g$ является входом в $h$, мы также должны вычислить производную от $h$ как $x$, используя $h'(x)$. Однако сфера (или $x$) — это не то, что входит в машину $f$. Вместо этого куб входит в машину $f$. Следовательно, мы должны вычислить производную от $f$ в кубе. Что такое куб? Куб — это результат работы машины $g$, когда мы помещаем в нее сферу (или $x$). Результатом $g$ является $g(x)$, поэтому мы должны вычислить производную от $f$ в $g(x)$, используя $f'(g(x))$ в нашей формуле цепного правила. Таким образом, результирующая цепная формула имеет вид \начать{собирать} h'(x) = f'(g(x))g'(x). \label{chain_rule_formula} \конец{собрать}
Цепное правило для линейных функций
Производная функции основана на линейной аппроксимации: касательной к графику функции.
По этой причине мы часто можем получить интуитивное представление о свойствах производной, просто взглянув на линейные функции. Цепное правило, в частности, очень просто для линейных функций. Как мы увидим, одна важная тонкость цепного правила отсутствует у линейных функций, поэтому они служат хорошей отправной точкой для получения интуитивных сведений о цепном правиле.
Простая форма
Если $g$ и $f$ — линейные функции, мы можем записать их как
\начать{выравнивать*}
г(х) &= ах+б\\
f(x) &= cx + d\\
\конец{выравнивание*}
где $a$, $b$, $c$ и $d$ — параметры, определяющие наклоны и точки пересечения функций по вертикали. См. левую панель апплета ниже, где $g$ и $f$ обозначены толстыми синими и тонкими голубыми линиями соответственно. Композиция $f$ и $g$ есть
\начать{выравнивать*}
ч (х) &= е (г (х)) \\
&= f(ax+b)\\
&= с(ах+б)+d\\
&=acx+bc+d.
\конец{выравнивание*}
График $h$ представляет собой линию с наклоном $ac$ и пересечением по вертикали $bc+d$, график показан толстой зеленой линией на правой панели в апплете ниже.
Поскольку $f$, $g$ и $h$ являются линейными функциями, их производные (т. е. наклоны их касательных) просто равны наклонам самих прямых. Другими словами, $f'(x)=c$, $g'(x)=a$ и $h'(x)=ac$ не зависят от значения $x$. В этом случае несложно заметить, что производная $h'(x)$ равна произведению производных $f’$ и $g’$.
На самом деле производные не зависят от точек пересечения $b$ и $d$, поэтому представьте частный случай, когда $b=d=0$. В этом случае $g(x)=ax$, поэтому входные данные $x$ умножаются на наклон $a$. Функция $f(x)=cx$ умножает свои входные данные на наклон $c$. Наконец, в этом особом случае $h$ просто умножает свои входные данные как на $a$, так и на $c$, так что его наклон равен $ac$. Что может быть проще? Цепное правило просто утверждает тот очевидный факт, что умножение на $a$ с последующим умножением на $c$ — это то же самое, что и умножение на одно число $ac$.
Даже если $b \ne 0$ или $d \ne 0$, цепное правило не намного сложнее, так как эти числа не влияют на наклоны.
Мы по-прежнему просто умножаем производную $a$ на производную $c$, чтобы получить производную композиции $ac$.
Предостережение
Причина простой формы цепного правила для линейных функций заключается в том, что производные были константами, не зависящими от входных значений функций. Экспериментируя с линейными функциями, можно ошибочно предположить, что производная $h'(x)$ композиции $h(x)=f(g(x))$ может быть равна произведению производной $f'( x)$, умноженное на производную $g'(x)$. Фактическое цепное правило уравнения \eqref{chain_rule_formula} имеет важное отличие. При использовании цепного правила нужно быть осторожным, чтобы вычислить производную от $f$ в $g'(x)$ и использовать действительное цепное правило $h'(x)=f'(g(x))g'( х)$.
Следующий апплет иллюстрирует цепное правило для линейных функций. Хотя это не имеет значения для линейных функций, апплет графически показывает правильные точки (зеленые символы), где нужно вычислять производные от $f$ и $g$. Если вы понимаете, как рассчитываются эти точки, вы будете правильно вычислять цепное правило даже для нелинейных функций.
Поскольку почти каждый случай, когда мы хотим использовать цепное правило, будет включать нелинейные функции, оценка производных в правильных точках является важным шагом.
Красные стрелки на левой панели показывают, как графически вычислить $h(x)=f(g(x))$, где $x=x_0$. Соглашения почти идентичны тем, которые используются для создания паутины решения итерации функций.
Начиная с красной точки для $x_0$, нужно двигаться вертикально, чтобы вычислить $g(x_0)$, которая будет высотой точки (зеленый ромб), где мы попадаем на график $g$. Чтобы перевести $g(x_0)$ с вертикальной оси на горизонтальную, нужно перейти по горизонтали к графику диагонали $y=x$. В этот момент значения горизонтальной координаты и вертикальной координаты совпадают; обе координаты равны $g(x_0)$. Затем, чтобы вычислить $h(x_0)=f(g(x_0))$, нужно просто двигаться вертикально к графику $f$. Вертикальная координата этой точки (зеленый треугольник) и есть искомая $f(g(x_0))$.
Поскольку для вычисления $h(x_0)$ функция $g$ оценивается в $x_0$, а функция $f$ оценивается в $g(x_0)$, в этих местах необходимо вычислить производные $g$ и $f$ соответственно.
Несмотря на то, что производная для случая линейных функций не зависит от этих точек, можно использовать апплет, чтобы помнить, что $h'(x_0)=f'(g(x_0))g'(x_0).$
Цепное правило для линейных функций. Линейные функции $g(x)=ax+b$ (толстая синяя линия слева) и $f(x)=cx+d$ (тонкая голубая линия слева) складываются в линейную функцию $h( x)=f(g(x))=c(ax+b)+d=cax+cb+d$ (зеленая линия справа). В этом линейном случае производные от $f$, $g$ и $h$ представляют собой просто наклоны прямых: $f'(x)=c$, $g'(x)=a$ и $h ‘$ — это просто произведение $f’$ и $g’$: $h'(x)=ac$. В этом случае линейных функций цепное правило довольно простое, поскольку наклоны не зависят от точек, в которых они оцениваются. Тем не менее, чтобы подготовиться к нелинейному случаю, когда наклоны зависят от местоположения, соответствующие наклоны для расчета $h'(x)$ при $x=x_0$ (представленные красными точками на оси X) отслеживаются зеленым цветом. точки на графиках функций. Зеленая точка на графике $h$ на правой панели иллюстрирует точку на графике, высота которой равна $h(x_0)$, как указано на вертикальной оси.
На левой панели показаны точки на графиках $f$ и $g$, необходимые для вычисления $h(x_0)=f(g(x_0))$. Сначала оценивается $g(x_0)$, показанный зеленым ромбом на графике $g$. Затем оценивается $f(x)$ как $x=g(x_0)$. Значение $g(x_0)$ — это высота зеленого ромба, показанная точкой на вертикальной оси. Чтобы перевести значение $g(x_0)$ с вертикальной на горизонтальную ось, можно сдвинуться по горизонтали к точке $(g(x_0),g(x_0))$ на линии $x=y$ (серая диагональная линия). Затем нужно просто перейти вертикально к графику $f$, чтобы вычислить $h(x_0)=f(g(x_0))$, который отмечен на вертикальной оси. Соответствующие наклоны $g$ и $f$ рассчитываются в точках, необходимых для оценки $f(g(x_0))$, т. е. наклон $g$ при $x=x_0$ и наклон $f $ при $x=g(x_0)$. Таким образом, производная $h$ при $x=x_0$ является произведением этих наклонов: $h'(x_0) = f'(g(x_0)) g'(x_0)$. Вы можете изменить значения параметров, введя значения в поля; вы также можете изменить $x_0$, перетащив одну из красных точек на осях $x$.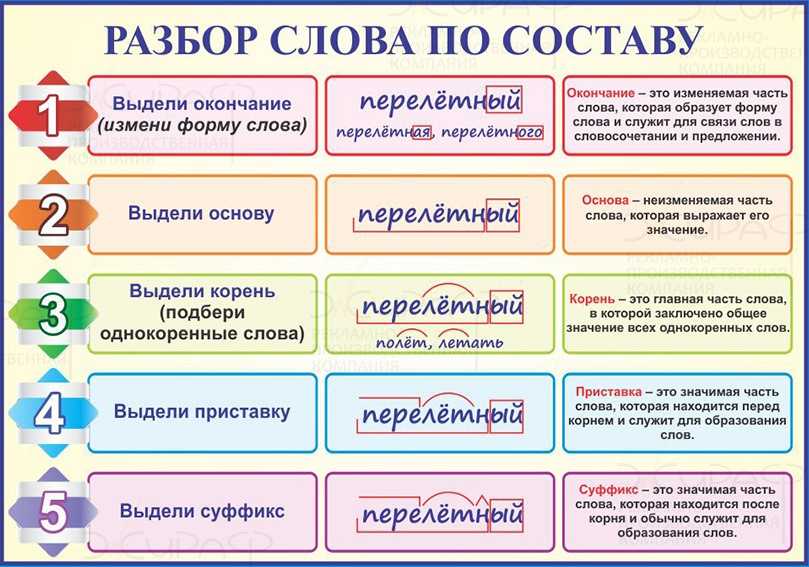
Вы можете увеличивать, уменьшать или перемещать оси, нажимая соответствующие кнопки.
Дополнительная информация об апплете.
Цепное правило нелинейных функций
Если вы понимаете цепное правило для линейных функций, в том числе, где вычислять производную, то для понимания цепного правила для нелинейных функций нужно немногое. Единственное отличие состоит в том, что касательная к графику нелинейной функции зависит от точки, в которой вы вычисляете касательную. Как и выше, если вы понимаете, что для вычисления $h(x_0)$ нужно вычислить $g$ в $x_0$ и $f$ в $g(x_0)$, тогда имеет смысл, что $h'(x_0)= f'(g(x_0)) g'(x_0)$.
Следующий апплет использует те же соглашения, что и предыдущий апплет. Просто это намного сложнее, чем приведенная выше линейная версия, потому что нам нужно построить касательные линии, которые зависят от точек, в которых мы оцениваем функции. Апплет дает понять, что мы получим неправильный ответ, если будем исследовать наклон $f$ в $x_0$, а не в $g(x_0)$.
Апплет не показывает неправильную касательную с наклоном $f'(x_0)$ (это сделало бы его слишком запутанным). Но вы можете видеть, что функция $f$ в целом имеет другой наклон выше точки $x_0$, чем в зеленом треугольнике.
Цепное правило как умножение уклонов. Цепное правило для производной композиции $h(x)=f(g(x))$ двух функций $f$ и $g$ можно рассматривать как произведение наклонов касательной. Хитрость заключается в том, чтобы оценить наклоны в правильных точках функций $f$ и $g$. Правильные точки, обозначенные зелеными символами на графиках функций, — это точки, в которых функции оцениваются для вычисления $f(g(x))$. Чтобы вычислить состав $h(x)$ при $x=x_0$ (красные точки на оси $x$ на обеих панелях), нужно сначала вычислить $g$ при $x=x_0$, как показано зеленым ромб на графике $g$ (толстая синяя кривая на левой панели). Затем оценивается $f$ в $g(x_0)$. Для графического переноса значения $g(x_0)$ с вертикальной оси на горизонтальную ось сдвигают по горизонтали от зеленого ромба к линии $x=y$ (серая линия), достигая точки $(g(x_0) ),г(х_0))$.
Двигаясь по вертикали к графику $f$ (тонкая голубая кривая), можно получить $f(g(x_0))$ — вертикальную координату зеленого треугольника. На графике композиции $h(x)=f(g(x))$ (зеленая кривая на правой панели) вычисление $h(x_0)$ просто соответствует перемещению по вертикали от красной точки, представляющей $x_0$, к зеленый кружок на графике $h$, что дает вертикальную координату $h(x_0)$. Наклон касательной в зеленом кружке на графике $h$ — это просто произведение наклона касательной к $g$ в зеленом ромбе и наклона касательной к $f$ в точке зеленый треугольник, как и в случае линейных функций. Наклоны показаны рядом с зелеными символами, а касательные показаны тонкими линиями того же цвета, что и графики функций. Таким образом, формула цепного правила для производной $h$, оцениваемой при $x=x_0$, выглядит следующим образом: $h'(x_0)=f'(g(x_0))g'(x_0)$. Вы можете изменить функции и $x_0$, введя выражения в поля; вы также можете изменить $x_0$, перетащив одну из красных точек на осях $x$. Вы можете увеличивать, уменьшать или перемещать оси, нажимая соответствующие кнопки.
Дополнительная информация об апплете.
Эта страница посвящена исключительно идее цепного правила. Конечно, знать общую идею и точно пользоваться цепным правилом — разные вещи. Если вы новичок в цепном правиле, ознакомьтесь с несколькими простыми примерами цепного правила. Если вы хотите увидеть более сложные примеры, взгляните на страницу правил цепочки из Calculus Refresher.
Статистические меры несходства последовательностей ДНК в рамках моделей цепи Маркова по составу оснований
Сравнительное исследование
. 2001 г., июнь; 57 (2): 441-8.
doi: 10.1111/j.0006-341x.2001.00441.x.
Т.Дж. Ву 1 , YC Hsieh, L A Li
принадлежность
- 1 Департамент статистики, Национальный университет Чэн-Кинг, Тайнань, Тайвань.
[email protected]
- PMID: 11414568
- DOI: 10.1111/j.0006-341x.2001.00441.x
Сравнительное исследование
T J Wu et al. Биометрия. 2001 июнь
. 2001 г., июнь; 57 (2): 441-8.
doi: 10.1111/j.0006-341x.2001.00441.x.
Авторы
Т.Дж. Ву 1 , YC Hsieh, L A Li
принадлежность
- 1 Департамент статистики, Национальный университет Чэн-Кинг, Тайнань, Тайвань. [email protected]
- PMID: 11414568
- DOI: 10.1111/j.0006-341x.2001.00441.x
Абстрактный
В молекулярной биологии очень важен вопрос количественной оценки сходства между двумя биологическими последовательностями. Прошлые исследования показали, что инструменты поиска на основе слов эффективны в вычислительном отношении и могут находить некоторые новые функциональные сходства или различия, невидимые для других алгоритмов, таких как FASTA. Недавно в рамках независимой модели базовой композиции Ву, Берк и Дэвисон (1997, Biometrics 53, 1431 1439) охарактеризовал семейство мер несходства на основе слов, которые определяли расстояние между двумя последовательностями путем одновременного сравнения частот всех подпоследовательностей n соседних букв (т.
Е. n-слов) в двух последовательностях. В частности, они ввели использование расстояния Махаланобиса и стандартизированного евклидова расстояния в изучение несходства последовательностей ДНК. Они показали, что оба расстояния имеют лучшую чувствительность и селективность, чем обычно используемое евклидово расстояние. Цель этой статьи состоит в том, чтобы распространить Махаланобиса и стандартизированные евклидовы расстояния на модели цепей Маркова с композицией оснований. Кроме того, вводится новая мера несходства, основанная на расхождении Кульбака-Лейблера между частотами всех n-слов в двух последовательностях. Применение к реальным данным показывает, что расхождение Кульбака-Лейблера дает лучшую производительность, чем евклидово расстояние. Кроме того, в модели цепи Маркова порядка kQ для базовой композиции, где kQ — это предполагаемый порядок, основанный на последовательности запроса, стандартизированное евклидово расстояние работает очень хорошо. В такой модели оно работает так же, как расстояние Махаланобиса, и лучше, чем несоответствие Кульбака-Лейблера и евклидово расстояние.
Поскольку стандартизированное евклидово расстояние вычисляется значительно быстрее, чем расстояние Махаланобиса, в обычной вычислительной среде рабочей станции/ПК обычно рекомендуется использовать стандартизированное евклидово расстояние в модели цепи Маркова порядка kQ базовой композиции. Однако, если пользователя очень заботит вычислительная эффективность, рекомендуется использовать невязку Кульбака-Лейблера, которая может быть вычислена так же быстро, как евклидово расстояние. Это может значительно улучшить текущую технологию сравнения больших наборов данных последовательностей ДНК.
Похожие статьи
Мера несхожести последовательностей ДНК, основанная на расстоянии Махаланобиса между частотами слов.
Ву Т.Дж., Берк Дж.П., Дэвисон Д.Б. Ву Т.Дж. и соавт. Биометрия. 1997 декабрь; 53 (4): 1431-9. Биометрия. 1997. PMID: 9423258
Оптимальные размеры слов для измерения несходства и оценки степени несходства между последовательностями ДНК.
Ву Т.Дж., Хуан Ю.Х., Ли Л.А. Ву Т.Дж. и соавт. Биоинформатика. 2005 15 ноября; 21 (22): 4125-32. doi: 10.1093/биоинформатика/bti658. Epub 2005 6 сентября. Биоинформатика. 2005. PMID: 16144805
Взвешенная относительная энтропия для сравнения последовательностей без выравнивания на основе марковской модели.
Чанг Г., Ван Т. Чанг Г и др. J Biomol Struct Dyn. 2011 фев; 28 (4): 545-55. дои: 10.1080/07391102.2011.10508594. J Biomol Struct Dyn. 2011. PMID: 21142223
Усовершенствованная модель филогенетического анализа всего генома с помощью преобразования Фурье.
Инь С., Яу С.С. Инь С. и др. Дж Теор Биол. 2015 7 октября; 382: 99-110. doi: 10.1016/j.jtbi.2015.06.033. Epub 2015 4 июля.
Дж Теор Биол. 2015.
PMID: 26151589Мера непохожести последовательностей ДНК, основанная на свободной энергии взаимодействия ближайших соседей.
Чжан Ю, Чен В. Чжан И и др. J Biomol Struct Dyn. 2011 фев; 28 (4): 557-65. дои: 10.1080/07391102.2011.10508595. J Biomol Struct Dyn. 2011. PMID: 21142215
Дж Теор Биол. 2015.
PMID: 26151589Посмотреть все похожие статьи
Цитируется
Заметка об анализе ДНК и редизайне с использованием цепи Маркова.
Zakarczemny M, Zajęcka M. Закарземный М. и соавт. Гены (Базель). 2022 21 марта; 13 (3): 554. doi: 10.3390/genes13030554. Гены (Базель). 2022. PMID: 35328107 Бесплатная статья ЧВК.
Анализ последовательности без выравнивания и приложения.
Рен Дж., Бай С., Лу Й.Ю., Тан К., Ван И., Райнерт Г., Сун Ф. Рен Дж. и др. Annu Rev Biomed Data Sci. 2018 июль;1:93-114. doi: 10.1146/annurev-biodatasci-080917-013431. Epub 2018 25 апр. Annu Rev Biomed Data Sci. 2018. PMID: 31828235 Бесплатная статья ЧВК.
Инструмент машинного обучения на основе k-mer с открытым исходным кодом для быстрого и точного подтипирования геномов ВИЧ-1.
Солис-Рейес С., Авино М., Пун А., Кари Л. Солис-Рейес С. и соавт. ПЛОС Один. 14 ноября 2018 г .; 13 (11): e0206409. doi: 10.1371/journal.pone.0206409. Электронная коллекция 2018. ПЛОС Один. 2018. PMID: 30427878 Бесплатная статья ЧВК.
SSAW: новый метод анализа подобия последовательностей, основанный на стационарном дискретном вейвлет-преобразовании.
