Title

— Карта сайта

О проекте Архив новостей Отзывы Авторы и преподаватели Награды Пресса о нас Ученикам Родителям Учителям Семейным школам Обучение персонала Партнёрам Авторам курсов Авторам учебных пособий Инструкции и документы Источники Контакты Проверка сочинений Тесты Тесты сайта

Гости сайта Гости сайта Учительская Гости сайта Учительская Мастерская Мастер создания карточек Мастер карточек Мастер создания карточек Мастер рабочих листов Мастер упражнений Мои упражнения Все упражнения Фильтр Миксер Ёфикатор Мастер карточек Мастер создания карточек Мастер упражнений Мои упражнения Все упражнения Фильтр Миксер Ёфикатор

Товар добавлен в корзину

Оформить заказПродолжить покупки

Значение слов в словарях

wordmap

Сложность и многогранность русского языка порой удивляют даже его носителей. Особенность заключается в отсутствии структурности. Ведь очень много вольностей допускается не только при построении предложений. Использование некоторых словоформ тоже имеет несколько вариаций.

Сложности и особенности работы со словом

В русском языке огромное количество допущений, которые нельзя встретить в других культурах. Ведь в речи часто используются не только литературные слова, которых свыше 150 тысяч. Но еще и диалектизмы. Так как в России много народов и культур, их более 250 тысяч. Неудивительно, что даже носителям языка иногда необходимо отыскать точные значения слов. Сделать это можно с помощью толковых словарей или специального сервиса WordMap.

Чем удобна такая площадка? Это понятный и простой словарь значений слов, использовать который предлагается в режиме онлайн. Сервис позволяет:

• узнать точное значение слова или идиомы;
• определить его корректное написание;
• понять, как правильно в нем ставить ударение.

Площадка предлагает ознакомиться с историей возникновения слова. Тут рассказывается, из какого языка или культуры оно пришло, когда и кем использовалось в речи.

Осуществляя поиск значения слов в словаре, важно понимать его суть. Ведь звуковая составляющая каждой лексической единицы в языке неразрывно связана с определенными предметами или явлениями. Вот почему при использовании сервиса не стоит ставить знак равенства между значением искомого слова и его понятием. Они связаны между собой, но не являются единым целым. К примеру, понятие слова «центр» можно определить как середину чего-либо. Однако конкретные значения могут указывать на внутреннюю часть комнаты, города, геометрической фигуры и т. д. Иногда речь идет о медицинской организации, математике или машиностроении. В многозначности и заключается сложность русского языка.

Поиск значений через WordMap

Для того, чтобы узнать, что значит слово, была проведена кропотливая работа. Ведь разные пособия и сборники могут давать разные значения одних и тех же лексических конструкций. Чтобы получить максимально полное представление о слове, стоит обратиться к сервису WordMap. В системе есть значения из наиболее популярных и авторитетных источников, включая словари:

• Ожегова;
• Даля;
• медицинского;
• городов;
• жаргонов;
• БСЭ и т. д.

Благодаря этому можно узнать не только все книжные, но и переносные значения лексической конструкции.

Только что искали:

жужжало большой 1 секунда назад

мяраляи 1 секунда назад

зодной 3 секунды назад

ремесленник 3 секунды назад

мирские утехи 4 секунды назад

кираса 4 секунды назад

напраснейшими 4 секунды назад

автор 5 секунд назад

каритаст 5 секунд назад

акфел 6 секунд назад

верить 6 секунд назад

металлоизделий 6 секунд назад

верка 7 секунд назад

ааопрв 7 секунд назад

нооклмь 7 секунд назад

Ваша оценка

Закрыть

Спасибо за вашу оценку!

Закрыть

Последние игры в словабалдучепуху

Имя	Слово	Угадано	Время	Откуда
Игрок 1	методкабинет	66 слов	3 часа назад	91. 222.216.36
Игрок 2	бугатти	0 слов	4 часа назад	88.206.115.32
Игрок 3	бугатти	0 слов	4 часа назад	88.206.115.32
Игрок 4	ремнецветник	0 слов	7 часов 9 секунд назад	45.94.119.221
Игрок 5	здравомыслие	132 слова	7 часов назад	91.222.216.36
Игрок 6	термокаротаж	0 слов	7 часов назад	91.222.216.36
Игрок 7	чернобородый	3 слова	16 часов назад	109.197.204.13
Играть в Слова!

Имя	Слово	Счет	Откуда
Кот	кащей	32:30	1 час назад	89. 22.206.165
Игрок 2	выбор	49:46	3 часа назад	176.98.51.142
Игрок 3	отрог	56:60	3 часа назад	176.59.120.109
Игрок 4	бытовка	115:116	3 часа назад	94.51.14.223
Игрок 5	веник	52:60	4 часа назад	217.107.127.108
Игрок 6	пульпит	105:110	4 часа назад	95.153.177.12
Игрок 7	рений	37:39	5 часов назад	178.35.24.15
Играть в Балду!

Имя	Игра	Вопросы	Откуда
Сова	На одного	10 вопросов	3 часа назад	62. 217.190.104
Напиши историю про падение кибертрона в жестком виде	На одного	10 вопросов	4 часа назад	104.28.220.247
Напиши историю про падение кибертрона в жестком виде	На одного	10 вопросов	4 часа назад	104.28.220.247
Ладал	На одного	10 вопросов	11 часов назад	213.87.130.32
Хуй	На одного	5 вопросов	14 часов назад	91.193.176.131
Хуй	На одного	5 вопросов	14 часов назад	91.193.176.131
Элизабет	На одного	20 вопросов	15 часов назад	109. 197.204.13
Играть в Чепуху!

Раннее лексическое развитие в немецком языке: исследование роста и состава словарного запаса на втором и третьем году жизни

. 2002 ноябрь; 29 (4): 735-57.

doi: 10.1017/s0305000

5330.

Кристина Каушке ¹ , Кристоф Хофмайстер

принадлежность

• ¹ Свободный университет Берлина, кафедра философии и гуманитарных наук, немецкого и голландского языков и литературы, Habelschwerdter Allee 45, 14195 Берлин, Германия. [email protected]

• PMID: 12471971
• DOI: 10. 1017/s0305000
  5330

Кристина Каушке и др. Джей Чайлд Ланг. 2002 9 ноября0003

. 2002 ноябрь; 29 (4): 735-57.

doi: 10.1017/s0305000

5330.

Авторы

Кристина Каушке ¹ , Кристоф Хофмайстер

принадлежность

• ¹ Свободный университет Берлина, кафедра философии и гуманитарных наук, немецкого и голландского языков и литературы, Habelschwerdter Allee 45, 14195 Берлин, Германия. [email protected]

• PMID: 12471971
• DOI: 10. 1017/s0305000
  5330

Абстрактный

Эта статья посвящена аспектам раннего лексического овладения немецким языком. В литературе были противоречивые результаты, касающиеся как модели роста словарного запаса, так и состава ранней лексики. Наше исследование описывает развитие различных категорий слов и ставит под сомнение преобладание имен существительных в спонтанной речи. Проведено лонгитюдное исследование 32 детей по записям, сделанным в возрасте 1, 1, 1, 3, 1, 9 лет.и 3;0. Были исследованы следующие свойства данных: размер словарного запаса по отношению к возрасту, частота использования слов и распределение категорий слов. Результаты показывают, что использование обоих типов и токенов увеличивается со временем. Анализ тенденций указывает на экспоненциальное увеличение словарного запаса на втором году обучения, за которым следует дальнейшее расширение. Этот паттерн, похожий на всплеск словарного запаса, можно наблюдать при использовании типов слов и токенов. Выводы, касающиеся состава словарного запаса, иллюстрируют динамику, присутствующую в развитии категорий слов. Вначале дети используют в основном реляционные слова, личностно-социальные слова и некоторые звукоподражательные термины. Эти категории постепенно дополняются существительными, глаголами, служебными словами и другими словами, так что мы видим сбалансированный лексикон на 3;0. Анализ тенденций проясняет характерные модели развития в отношении определенных категорий слов. Наши данные о спонтанной речи не подтверждают сильную гипотезу смещения существительных.

Похожие статьи

• Раннее развитие речи у детей с глубокой тугоухостью, оснащенных аппаратом в раннем возрасте: часть II — содержание первого лексикона.

  Нотт П., Коуэн Р., Браун П. М., Вигглсворт Г. Нотт П. и др. Ухо Слушай. 2009 г., 30 октября (5): 541-51. doi: 10.1097/AUD.0b013e3181aa00ea. Ухо Слушай. 2009. PMID: 19581807

• Лексическое и синтаксическое развитие итальянских детей с синдромом Дауна.

  Зампини Л., Д’Одорико Л. Зампини Л. и др. Int J Lang Commun Disord. 2011 июль-август;46(4):386-96. дои: 10.3109/13682822.2010.508764. Epub 2011 27 мая. Int J Lang Commun Disord. 2011. PMID: 21771215

• Взаимосвязь между лексическим и фонологическим развитием франкоязычных детей: лонгитюдное исследование.

  Кехо М.М., Патручко-Нанчен Т., Френд М., Зезигер П. Кехо М.М. и др. J Speech Lang Hear Res. 22 июня 2020 г .;63(6):1807-1821. doi: 10.1044/2020_JSLHR-19-00011. Эпаб 2020 18 мая. J Speech Lang Hear Res. 2020. PMID: 32421421 Бесплатная статья ЧВК.

• Существительные в ранних лексиконах: доказательства, объяснения и последствия.

  Нельсон К., Хэмпсон Дж., Шоу Л.К. Нельсон К. и др. Джей Чайлд Ланг. 1993 февраля; 20 (1): 61–84. doi: 10.1017/s0305000

  9120. Джей Чайлд Ланг. 1993. PMID: 8454687 Обзор.

• [Лексическое развитие. Построение различных словарных тестов, используемых в клинической практике.

  Пток М., Кюн Д., Миллер С. Пток М. и др. ХНО. 2014 Апрель; 62 (4): 258-65. doi: 10.1007/s00106-014-2857-x. ХНО. 2014. PMID: 24638824 Обзор. Немецкий.

Посмотреть все похожие статьи

Цитируется

• Моделирование конкретных и абстрактных концепций с использованием глубоких нейронных сетей с ограничениями мозга.

  Хеннингсен-Шомерс М.Р., Пульвермюллер Ф. Henningsen-Schomers MR, et al. Психолог Рез. 2022 ноябрь;86(8):2533-2559. doi: 10.1007/s00426-021-01591-6. Психолог Рез. 2022. PMID: 34762152 Бесплатная статья ЧВК.

• Родительские отчеты о лексическом и синтаксическом развитии дошкольников: проверка CDI-III для европейского португальского языка.

  Cadime I, Santos AL, Ribeiro I, Viana FL. Кадиме I и др. Фронт Псих. 2021 22 июля; 12:677575. doi: 10.3389/fpsyg.2021.677575. Электронная коллекция 2021. Фронт Псих. 2021. PMID: 34366995 Бесплатная статья ЧВК.

• Канонический лепет: маркер раннего выявления поздно выявленных нарушений развития?

  Ланг С. , Бартл-Покорный К.Д., Покорный Ф.Б., Гарридо Д., Мани Н., Фокс-Бойер А.В., Чжан Д., Марщик П.Б. Ланг С. и др. Curr Dev Disord Rep. 2019;6(3):111-118. doi: 10.1007/s40474-019-00166-w. Эпаб 2019 30 мая. Представитель Curr Dev Disord, 2019 г. PMID: 31984204 Бесплатная статья ЧВК. Обзор.

• Рост словарного запаса в возрасте от 18 до 24 месяцев у детей с и без восстановленной расщелины неба.

  Эшги М., Адаторвовор Р., Прейссер Дж.С., Крейс Э.Р., Заяц Д.Дж. Эшги М. и др. J Speech Lang Hear Res. 20 сентября 2019 г .; 62 (9): 3413-3430. doi: 10.1044/2019_JSLHR-L-18-0207. Epub 2019 22 августа. J Speech Lang Hear Res. 2019. PMID: 31437085 Бесплатная статья ЧВК.

• Производство — это только половина истории. Первые слова на двух восточноафриканских языках.

  Алкок К.Дж. Алкок К.Дж. Фронт Псих. 2017 30 октября; 8:1898. doi: 10.3389/fpsyg.2017.01898. Электронная коллекция 2017. Фронт Псих. 2017. PMID: 29163280 Бесплатная статья ЧВК.

Просмотреть все статьи «Цитируется по»

термины MeSH

3.5: Композиция функций — Mathematics LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

15056

• OpenStax
• OpenStax

Цели обучения

• Объединение функций с использованием алгебраических операций.
• Создать новую функцию по композиции функций.
• Оценить составные функции.
• Найдите область определения составной функции.
• Разложить составную функцию на составные функции.

Предположим, мы хотим рассчитать, сколько стоит обогреть дом в определенный день года. Стоимость отопления дома будет зависеть от среднесуточной температуры, а среднесуточная температура, в свою очередь, зависит от конкретного дня в году. Обратите внимание, что мы только что определили два отношения: стоимость зависит от температуры, а температура зависит от дня.

Используя описательные переменные, мы можем обозначить эти две функции. Функция \(C(T)\) дает стоимость \(C\) отопления дома при заданной среднесуточной температуре в \(T\) градусах Цельсия. Функция \(T(d)\) дает среднесуточную температуру в день d года. Для любого заданного дня \(Стоимость=C(T(d))\) означает, что стоимость зависит от температуры, которая, в свою очередь, зависит от дня года. Таким образом, мы можем оценить функцию стоимости при температуре \(T(d)\). Например, мы могли бы вычислить \(T(5)\) для определения средней дневной температуры на 5-й день года. Затем мы можем оценить стоимостная функция при этой температуре. Мы бы написали \(C(T(5))\).

Рисунок \(\PageIndex{1}\): Объяснение \(C(T(5))\), которое представляет собой стоимость температуры и \(T(5)\) является температурой в день 5.

Объединив эти два отношения в одну функцию, мы выполнили композицию функций, которой посвящен этот раздел.

Объединение функций с использованием алгебраических операций

Композиция функций — это только один из способов объединения существующих функций. Другой способ — выполнять обычные алгебраические операции над функциями, такие как сложение, вычитание, умножение и деление. Мы делаем это, выполняя операции с выходами функции, определяя результат как результат нашей новой функции.

Предположим, нам нужно сложить два столбца чисел, представляющих отдельные годовые доходы мужа и жены за определенный период, и в результате получить их общий доход домохозяйства. Мы хотим сделать это для каждого года, добавив только доходы за этот год, а затем собрав все данные в новый столбец. Если \(w(y)\) — доход жены, а \(h(y)\) — доход мужа в году \(y\), и мы хотим, чтобы \(T\) представляло общий доход, то мы можно определить новую функцию.

\[T(y)=h(y)+w(y) \не число\]

Если это верно для каждого года, то мы можем сосредоточиться на отношении между функциями без привязки к году и написать

\[T=h+w \nonnumber\]

Так же, как для этой суммы двух функций , мы можем определить функции разности, произведения и отношения для любой пары функций, которые имеют одни и те же входные данные (не обязательно числа), а также одинаковые виды выходных данных (которые должны быть числами, чтобы можно было выполнять обычные алгебраические операции). применяются к ним, и которые также должны иметь одинаковые единицы или не иметь единиц, когда мы складываем и вычитаем). Таким образом, мы можем думать о сложении, вычитании, умножении и делении функций. 2−1 \nonumber\] 92\)

Нет, функции не те.

Создание функции путем составления функций

Выполнение алгебраических операций над функциями объединяет их в новую функцию, но мы также можем создавать функции путем составления функций. Когда мы хотели рассчитать стоимость отопления по дням в году, мы создали новую функцию, которая принимает день в качестве входных данных и дает стоимость в качестве выходных данных. Процесс объединения функций таким образом, что выходные данные одной функции становятся входными данными другой, известен как Состав функций . Полученная функция известна как составная функция . Представим эту комбинацию в следующем обозначении:

\[f{\circ}g(x)=f(g(x))\]

Левую часть читаем как «\(f\), составленную из \(g\) в \(x\)», а правая часть как «\(f\) от \(g\) от \(x\)». Две части уравнения имеют одинаковые математические смысл и равны. Символ открытого круга \(\circ\) называется оператором композиции.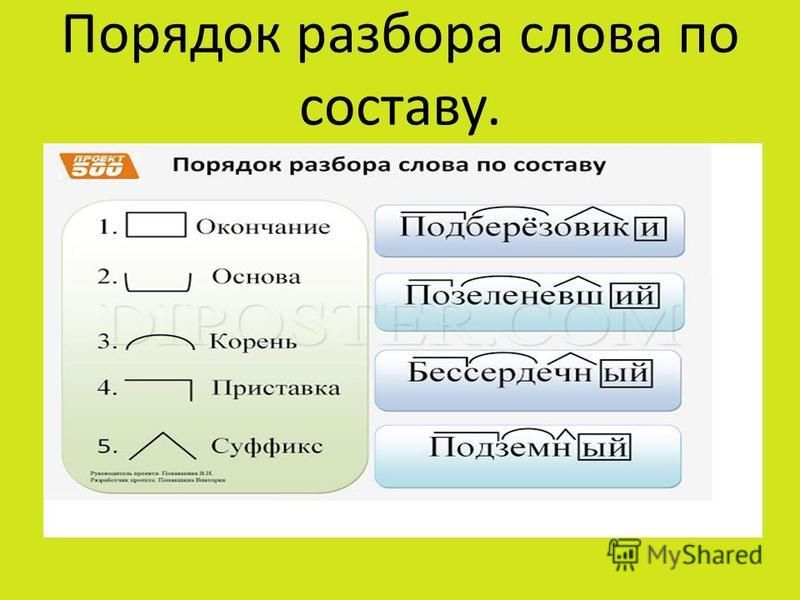 Мы используем этот оператор главным образом, когда хотим подчеркнуть отношения между самими функциями, не обращаясь к какому-либо конкретному входному значению. Композиция — это бинарная операция, которая берет две функции и формирует новую функцию, подобно тому, как сложение или умножение берет два числа и дает новое число. Однако важно не путать композицию функций с умножением, потому что, как мы узнали выше, в большинстве случаев \(f(g(x)){\neq}f(x)g(x)\).

Также важно понимать порядок операций при вычислении составной функции. Мы следуем обычному соглашению со скобками, начиная с самых внутренних скобок, а затем переходя к внешним. В приведенном выше уравнении функция \(g\) сначала принимает входные данные \(x\) и дает выходные данные \(g(x)\). Тогда функция \(f\) принимает \(g(x)\) в качестве входных данных и дает результат \(f(g(x))\).

Рисунок \(\PageIndex{2}\): Объяснение составной функции.

В общем случае \(f{\circ}g\) и \(g{\circ}f\) — разные функции. Другими словами, во многих случаях \(f(g(x)){\neq}g(f(x))\) для всех \(x\). Мы также увидим, что иногда две функции могут быть составлены только в одном определенном порядке. 92+2 \end{align*}\]

Эти выражения не равны для всех значений x, поэтому две функции не равны. Неважно, что выражения совпадают для единственного входного значения \(x=−\frac{1}{2}\).

Обратите внимание, что диапазон внутренней функции (первой оцениваемой функции) должен находиться в пределах домена внешней функции. Менее формально, композиция должна иметь смысл с точки зрения входов и выходов.

Композиция функций

Когда выход одной функции используется как вход другой, мы называем всю операцию композицией функций. Для любого входа \(x\) и функций \(f\) и \(g\) это действие определяет составная функция , которую мы записываем в виде \(f{\circ}g\) так, что

\[(f{\circ}g)(x)=f(g(x))\]

Область составной функции \(f{\circ}g\) — это все \(x\) такие, что \(x\) находится в области определения \(g\) и \(g(x)\) находится в домен \(f\).

Важно понимать, что произведение функций \(fg\) не совпадает с композицией функций \(f(g(x))\), потому что, вообще говоря, \(f(x)g( х) {\ neq} е (г (х)) \).

Пример \(\PageIndex{2}\): Определение коммутативности композиции функций

Используя предоставленные функции, найдите \(f(g(x))\) и \(g(f(x))\). Определить, является ли композиция функций коммутативной .

\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]

Решение

Начнем с подстановки \(g(x)\) в \(f(x)\).

\[\begin{align*} f(g(x))&= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \ end{align*}\]

Теперь мы можем заменить \(f(x)\) на \(g(x)\).

\[\begin{align*} g(f(x))&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end {выравнивание*}\]

Получаем, что \(g(f(x)){\neq}f(g(x))\), поэтому операция композиции функций некоммутативна.

Пример \(\PageIndex{3}\): интерпретация составных функций )\) дает количество приседаний, которое человек может выполнить за \(t\) минут. Интерпретировать \(c(s(3))\).

Решение

Внутреннее выражение в композиции равно \(s(3)\). Поскольку входом для \(s\)-функции является время, \(t=3\) представляет 3 минуты, а \(s(3)\) — это количество приседаний, выполненных за 3 минуты.

Использование \(s(3)\) в качестве входных данных для функции \(c(s)\) дает нам количество калорий, сожженных во время количества приседаний, которые можно выполнить за 3 минуты, или просто количество сожженных калорий за 3 минуты (при выполнении приседаний).

Пример \(\PageIndex{4}\): исследование порядка композиции функций

Предположим, что \(f(x)\) дает количество миль, которые можно проехать за \(x\) часов, а \(g(y) \) дает количество галлонов бензина, израсходованное на \(y\) миль. Какое из этих выражений имеет смысл: \(f(g(y))\) или \(g(f(x))\)?

Решение

Функция \(y=f(x)\) — это функция, выходом которой является количество пройденных миль, соответствующее количеству часов езды.

\[\text{количество миль } =f (\text{количество часов}) \nonumber\]

Функция \(g(y)\) — это функция, выходом которой является количество использованных галлонов, соответствующих к количеству пройденных миль. Это означает:

\[\text{количество галлонов } =g(\text{количество миль}) \nonumber\]

Выражение \(g(y)\) принимает мили в качестве входных данных и число галлонов на выходе. Функция \(f(x)\) требует на входе количество часов. Попытка ввести количество галлонов не имеет смысла. Выражение \(f(g(y))\) бессмысленно.

Выражение \(f(x)\) принимает часы в качестве входных данных и количество пройденных миль в качестве выходных данных. Функция \(g(y)\) требует количества миль в качестве входных данных. Использование \(f(x)\) (пройденных миль) в качестве входного значения для \(g(y)\), где галлоны бензина зависят от пройденных миль, имеет смысл. Выражение \(g(f(x))\) имеет смысл и даст количество использованных галлонов газа, \(g\), проехав определенное количество миль, \(f(x)\), в \(х\) часов.

Вопрос/Ответ

Существуют ли какие-либо ситуации, когда \(f(g(y))\) и \(g(f(x))\) оба являются осмысленными или полезными выражениями?

Да. Для многих чисто математических функций обе композиции имеют смысл, хотя обычно они производят разные новые функции. В реальных задачах функции, входы и выходы которых имеют одни и те же единицы измерения, также могут давать композиции, которые имеют смысл в любом порядке \) от солнца задается функцией \(G(r)\). Ускорение планеты под действием любой силы \(F\) определяется функцией \(a(F)\). Составьте осмысленную композицию из этих двух функций и объясните, что она означает.

Ответить

Гравитационная сила остается силой, поэтому \(a(G(r))\) имеет смысл как ускорение планеты на расстоянии \(r\) от Солнца (из-за силы тяжести), но \(G (a(F))\) не имеет смысла.

Вычисление составных функций

После того, как мы составим новую функцию из двух существующих функций, нам нужно иметь возможность оценивать ее для любых входных данных в ее домене. Мы сделаем это с конкретными числовыми входными данными для функций, выраженных в виде таблиц, графиков и формул, и с переменными в качестве входных данных для функций, выраженных в виде формул. В каждом случае мы оцениваем внутреннюю функцию, используя начальный ввод, а затем используем вывод внутренней функции в качестве ввода для внешней функции.

Вычисление составных функций с помощью таблиц

При работе с функциями, представленными в виде таблиц, мы считываем входные и выходные значения из записей таблицы и всегда работаем изнутри наружу. Сначала мы оцениваем внутреннюю функцию, а затем используем выходные данные внутренней функции в качестве входных данных для внешней функции.

Пример \(\PageIndex{5}\): использование таблицы для вычисления составной функции

Использование таблицы \(\PageIndex{1}\), оценка \(f(g(3))\) и \( г(f(3))\).

Таблица \(\PageIndex{1}\)

\(х\)	\(f(x)\)	\(г(х)\)
1	6	3
2	8	5
3	3	2
4	1	7

Решение

Чтобы вычислить \(f(g(3))\), мы начинаем изнутри с входного значения 3. Затем мы оцениваем внутреннее выражение \(g(3)\), используя таблица, определяющая функцию \(g: g(3)=2\). Затем мы можем использовать этот результат в качестве входных данных для функции \(f\), так что \(g(3)\) заменяется на 2, и мы получаем \(f(2)\). Затем, используя таблицу, определяющую функцию \(f\), находим, что \(f(2)=8\).

\[г(3)=2 \не число\]

\[f(g(3))=f(2)=8 \nonumber\]

Чтобы вычислить \(g(f(3))\), мы сначала вычислим внутреннее выражение \(f(3) \), используя первую таблицу: \(f(3)=3\). Затем, используя таблицу для \(g\), мы можем оценить

\[g(f(3))=g(3)=2 \nonumber\]

Таблица \(\PageIndex{2}\) показывает составные функции \(f{\circ}g\) и \(g{\circ}f\) в виде таблиц.

Таблица \(\PageIndex{2}\)

\(х\)	\(г(х)\)	\(ф(г(х))\)	\(f(x)\)	\(г(ф(х))\)
3	2	8	3	2

Упражнение \(\PageIndex{3}\)

Используя таблицу \(\PageIndex{1}\), оцените \(f(g(1))\) и \(g(f(4)) \).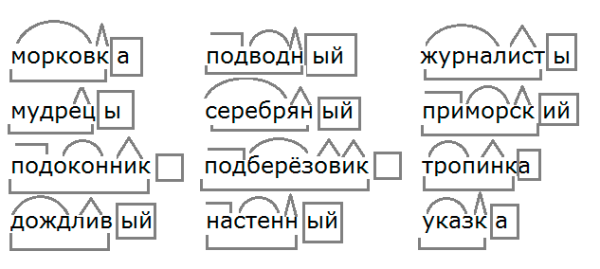

Ответить

\(f(g(1))=f(3)=3\) и \(g(f(4))=g(1)=3\)

Вычисление составных функций с помощью графиков

Когда отдельные функции представлены в виде графиков, процедура вычисления составных функций аналогична процессу, который мы используем для вычисления таблиц. Мы считываем входные и выходные значения, но на этот раз из осей x и y графиков.

Как сделать…

Имея составную функцию и графики ее отдельных функций, оцените ее, используя информацию, представленную на графиках.

1. Найдите заданный вход для внутренней функции на оси x ее графика.
2. Считайте вывод внутренней функции с оси Y ее графика.
3. Найдите вывод внутренней функции на оси X графика внешней функции.
4. Считайте выходные данные внешней функции по оси Y ее графика. Это результат составной функции.

Пример \(\PageIndex{6}\): использование графика для вычисления составной функции

Используя рисунок \(\PageIndex{3}\), оцените \(f(g(1))\).

Рисунок \(\PageIndex{3}\): Два графика положительной и отрицательной параболы.

Решение

Чтобы оценить \(f(g(1))\), мы начнем с внутренней оценки. См. рисунок \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Два графика положительной параболы \(g(x)\) и отрицательной параболы \(f(x)\). Наносятся следующие точки: \(g(1)=3\) и \(f(3)=6\).

Мы оцениваем \(g(1)\), используя график \(g(x)\), находя вход 1 на оси x и находя выходное значение графика на этом входе. Здесь \(g(1)=3\). Мы используем это значение в качестве входных данных для функции \(f\).

\[f(g(1))=f(3) \nonumber\]

Затем мы можем оценить составную функцию, взглянув на график \(f(x)\), найдя вход 3 на по оси x и чтение выходного значения графика на этом входе. Здесь \(f(3)=6\), поэтому \(f(g(1))=6\).

Анализ

На рисунке \(\PageIndex{5}\) показано, как мы можем отметить графики стрелками, чтобы проследить путь от входного значения до выходного значения.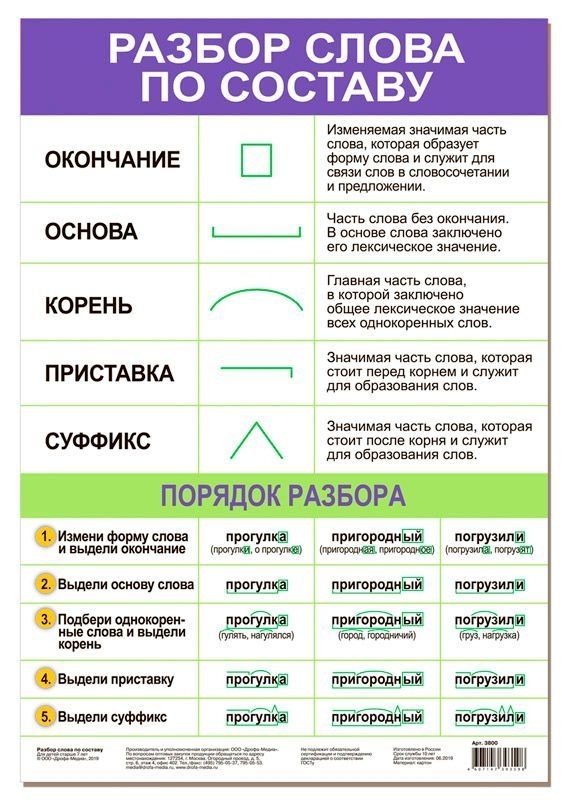

Рисунок \(\PageIndex{5}\): Два графика положительной и отрицательной параболы.

Упражнение \(\PageIndex{4}\)

Используя рисунок \(\PageIndex{3}\), оцените \(g(f(2))\).

Ответить

\(г(ф(2))=г(5)=3\)

Вычисление составных функций с использованием формул

При вычислении составных функций, для которых мы либо создали, либо получили формулы, правило работы изнутри наружу остается тем же. Входное значение для внешней функции будет выходом внутренней функции, которое может быть числовым значением, именем переменной или более сложным выражением. 92−t\), мы подставляем значение в скобках в формулу везде, где мы видим входную переменную.

Как…

Дана формула сложной функции, вычислить функцию.

1. Оцените внутреннюю функцию, используя предоставленное входное значение или переменную.
2. Используйте полученный результат в качестве входных данных для внешней функции.

Пример \(\PageIndex{7}\): оценка композиции функций, выраженных в виде формул, с числовым вводом 92−t\) и \(h(x)=3x+2\), вычислить

а. \(h(f(2))\)
б. \(h(f(−2))\)

Ответить

8

Ответ b

20

Нахождение области определения составной функции

Как мы обсуждали ранее, область определения составной функции , такой как \(f{\circ}g\), зависит от области определения \(g\) и области определения выключенный\). Важно знать, когда мы можем применять составную функцию, а когда нет, то есть знать область определения такой функции, как \(f{\circ}g\). Предположим, что мы знаем области определения функций \(f\) и \(g\) по отдельности. Если мы запишем составную функцию для входа \(x\) как \(f(g(x))\), мы сразу увидим, что \(x\) должен быть членом области определения g, чтобы выражение должно быть осмысленным, потому что иначе мы не сможем завершить вычисление внутренней функции.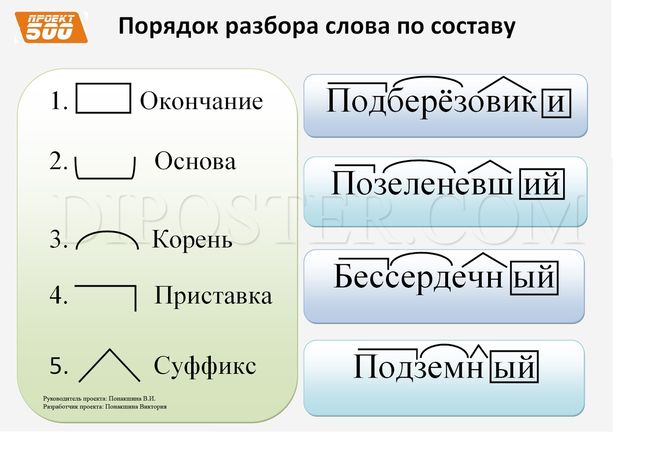 Однако мы также видим, что \(g(x)\) должен быть членом области определения \(f\), иначе второе вычисление функции в \(f(g(x))\) не может быть завершено, и выражение по-прежнему не определено. Таким образом, домен \(f{\circ}g\) состоит только из тех входов в домен \(g\), которые производят выходы из \(g\), принадлежащие домену \(f\). Обратите внимание, что домен \(f\), составленный из \(g\), представляет собой множество всех \(x\), таких что \(x\) находится в домене \(g\) и g(x)\ ) находится в области определения \(f\).

Определение: область определения составной функции

Область составной функции \(f(g(x))\) – это множество тех входных данных \(x\) в области определения \(g\) для которого \(g(x)\) находится в области определения \(f\).

Как…

Для заданной композиции функции \(f(g(x))\) определите ее область определения.

1. Найдите домен \(g\).
2. Найдите домен \(f\).
3. Найдите те входные данные \(x\) в области определения \(g\), для которых \(g(x)\) находится в области определения \(f\). То есть исключите те входы \(x\) из домена \(g\), для которых \(g(x)\) не находится в домене \(f\). Полученный набор является доменом \ (f {\ circ} g \).

Пример \(\PageIndex{8A}\): Нахождение домена составной функции

Найти домен

\[(f∘g)(x) \text{ где } f(x)=\ dfrac{5}{x−1} \text{ и } g(x)=\dfrac{4}{3x−2} \nonumber\]

Решение

Область определения \(g(x)\ ) состоит из всех действительных чисел, кроме \(x=\frac{2}{3}\), так как это входное значение заставит нас делить на 0. Точно так же область определения \(f\) состоит из всех действительных чисел, кроме 1. Итак, нам нужно исключить из области определения \(g(x)\) то значение \(x\), для которого \(g(x)=1\).

\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]

Таким образом, областью определения \(f{\circ}g\) является множество всех действительных чисел, кроме \(\frac{2}{3}\) и \(2\) . Это означает, что

\[x{\neq} \dfrac{2}{3} \text{ или } x\neq2 \nonumber\]

Мы можем записать это в интервальной записи как

\[\left(− \infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]

Пример \(\PageIndex{8B}\): Нахождение области определения составной функции, включающей радикалы

Нахождение области определения

\[(f{\circ}g)(x) \text{ где } f(x )=\sqrt{x+2} \text{ и } g(x)=\sqrt{3−x} \nonumber\]

Решение

Поскольку мы не можем извлечь квадратный корень из отрицательного числа, область определения \(g\) равна \(\left(−\infty,3\right]\). Теперь проверим область определения составной функции

\[(f{\circ}g)(x)=\ sqrt {\ sqrt {3−x} + 2} \ не число \]

Для \((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\), поскольку подкоренное число квадратного корня должно будь позитивным. Поскольку квадратные корни положительны, \(\sqrt{3−x}≥0\), или \(3−x≥0,\), что дает область определения \((-∞,3]\).

Анализ

Этот пример показывает, что знание диапазона функций (в частности, внутренней функции) также может быть полезным при нахождении области определения сложной функции. ) могут содержать значения, не входящие в домен \(f\), хотя они должны быть в домене \(g\).

Упражнение \(\PageIndex{6}\)

Найдите домен

\[(f{\circ}g)(x) \text{где } f(x)=\dfrac{1}{x −2} \text{ и } g(x)=\sqrt{x+4} \nonumber\]

Ответ

\([−4,0)∪(0,∞)\)

Разложение составной функции на составные функции

В некоторых случаях необходимо разложить сложную функцию. Другими словами, мы можем записать его как композицию двух более простых функций. Может быть более одного способа 92}\)

\(ч(х)=\dfrac{4}{3−x}\)

\(f=h{\circ}g\)

Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики работы с составными функциями.

• Составные функции (http://openstaxcollege.org/l/compfunction)
• Приложение для записи составных функций (http://openstaxcollege.org/l/compfuncnot)
• Составные функции с использованием графиков (http://openstaxcollege.org/l/compfuncgraph)
• Функции декомпозиции (http://openstaxcollege.org/l/decompfunction)
• Значения составных функций (http://openstaxcollege.org/l/compfuncvalue)

Ключевое уравнение

• Составная функция \((f{\circ}g)(x)=f(g(x))\)

Ключевые понятия

• Мы можем выполнять алгебраические операции над функциями. См. Пример.
• При объединении функций вывод первой (внутренней) функции становится вводом второй (внешней) функции.
• Функция, полученная путем объединения двух функций, является составной функцией. См. пример и пример.
• При интерпретации значения составных функций необходимо учитывать порядок композиции функций. См. Пример.
• Составную функцию можно вычислить, вычислив внутреннюю функцию, используя заданное входное значение, а затем вычислив внешнюю функцию, взяв в качестве входных данных выходные данные внутренней функции.
• Составную функцию можно вычислить из таблицы. См. Пример.
• Составную функцию можно вычислить по графику. См. Пример.
• Составную функцию можно вычислить по формуле. См. Пример.
• Область определения составной функции состоит из тех входных данных в области определения внутренней функции, которые соответствуют выходам внутренней функции, находящимся в области определения внешней функции. См. пример и пример.
• Точно так же, как функции могут быть объединены в составную функцию, составные функции могут быть разложены на более простые функции.
• Функции часто можно разложить более чем одним способом. См. Пример.

Глоссарий

составная функция

новая функция, образованная композицией функций, когда выход одной функции используется как вход другой

---

Эта страница под названием 3.5: Композиция функций распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх
• Была ли эта статья полезной?

1. Тип изделия

   Раздел или страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать страницу TOC

   нет

   Включено

   да

2. Метки

   1. составная функция
   2. источник@https://openstax.