Глава 16. Фазовые равновесия в многокомпонентных системах
16.1. Метод физико-химического анализа
16.2. Общая характеристика диаграмм состояния двухкомпонентных систем
16.3. Диаграмма состояния двухкомпонентной системы с простой эвтектикой и с полиморфными превращениями компонентов
16.4. Диаграмма состояния двухкомпонентной системы с образованием химического соединения, плавящимся без разложения (конгруэнтно)
16.5. Диаграмма состояния двухкомпонентной системы с образованием химического соединения, которое плавиться инконгруэнтно
16.6. Диаграмма состояния двухкомпонентной системы с ликвацией
16.7. Диаграмма состояния двухкомпонентных систем с образованием твердых растворов
16.8. Диаграммы состояния трехкомпонентных систем. Основные понятия и определения. Треугольник Гиббса
16.9. Диаграмма состояния трехкомпонентной системы с простой эвтектикой
16.10. Диаграмма состояния трехкомпонентной системы с химическими соединениями, плавящимися конгруэнтно
 1. Метод физико-химического анализа
1. Метод физико-химического анализаМетод физико-химического анализа основан на изучении зависимости физических свойств системы от параметров, определяющих ее равновесие. В качестве изучаемых свойств могут быть выбраны тепловые, объемные, электрические, магнитные, оптические и другие свойства системы. Нас будет интересовать агрегатное состояние системы при изменении состава и температуры системы. Анализ системы будем делать с помощью диаграммы состояния. Диаграмма состояния (или фазовая диаграмма) представляет собой графическое изображение зависимости между параметрами состояния системы и фазовыми превращениями в системе. Диаграммы состояния или строят на основании экспериментальных данных в координатах [температура, состав системы] или рассчитывают. Анализ диаграмм состояния позволяет установить протекающие в системе качественные изменения, характер взаимодействия между компонентами, области существования и составы равновесных фаз.
Рассмотрим один из методов получения диаграммы состояния двухкомпонентной системы в координатах [состав расплава — температура образца] (рис.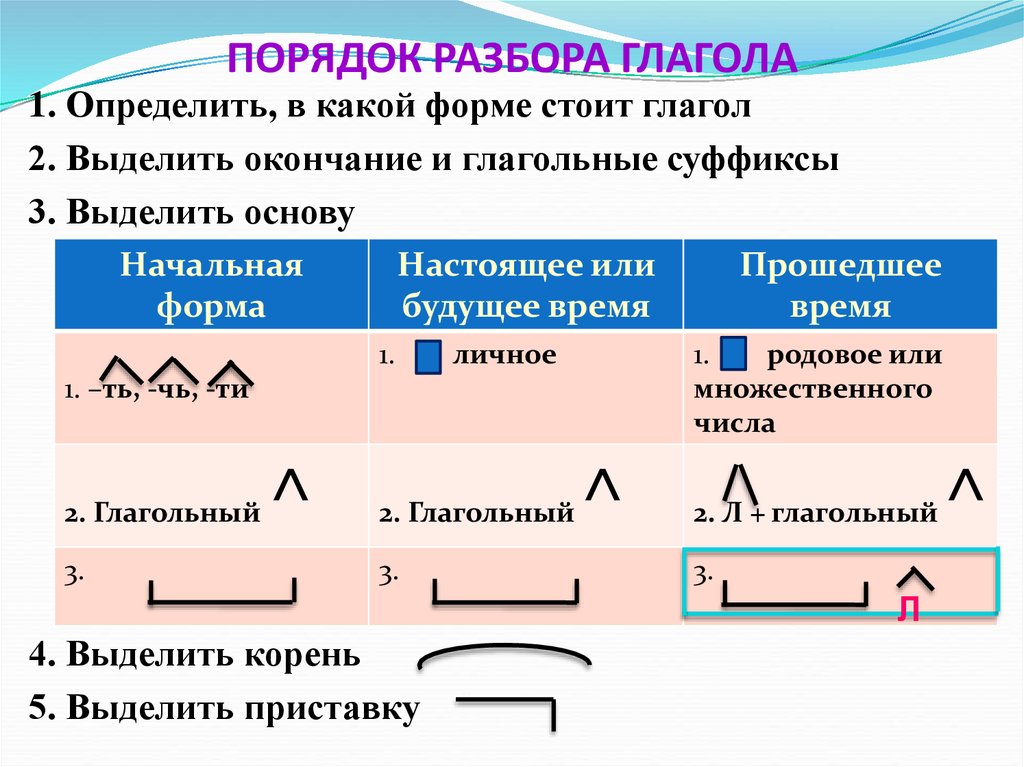
Рис. 16.1. Кривые охлаждения расплава
Рис. 16.2. Диаграмма состояния двухкомпонентной системы
16.2. Диаграмма состояния двухкомпонентной системы
Ступенька на кривой 10 соответствует температуре эвтектики на диаграмме состояния (см. раздел 2.1). Отметим, что на кривой охлаждения расплава 40 нет точки перегиба. Это означает, что при охлаждении данного расплава кристаллизация веществ А и В из расплава происходит при одной температуре.
16.2. Общая характеристика диаграмм состояния двухкомпонентных систем
Для двухкомпонентных систем, без учета давления как переменного параметра, правило фаз приобретает вид: С = К – Ф + 1. Диаграмма состояния двухкомпонентной системы (см. рис. 16.2) получена на основании анализа кривых охлаждения образцов (см. рис. 16.1). Из анализа кривых А и В получены температуры кристаллизации веществ А и В (Т0А и Т0В ). Точки перегиба на кривых 10, 20, 30 соответствуют температурам кристаллизации вещества А из расплава. Точки перегиба на кривых 60, 80 — кристаллизации вещества В из расплава. Температура Т = 200 °С — это температура эвтектики Тэв.

16.3. Диаграмма состояния двухкомпонентной системы с простой эвтектикой и с полиморфными превращениями компонентов
Рассмотрим диаграмму состояния с простой эвтектикой на примере системы лейцит [Lc](KAlSi2O6) — анортит [An](СaAl2Si2O8) (рис. 16.3). Система двухкомпонентная, компонент А — лейцит, компонент В — анортит. По оси ОХ отложена мольная доля анортита, xAn. Сделаем анализ диаграммы состояния для образца, в котором мольная доля анортита 0,2, мольная доля лейцита 0,8. Диаграмма состояния — эвтектического типа. Правило фаз Гиббса: С = К – Ф + 1 = 2 – Ф + 1 = 3 – Ф. TLc = 1958 °К — температура кристаллизации лейцита, TAn = 1823 °К — температура кристаллизации анортита, Tэв = 1686 °К — температура эвтектики. В области выше линии ликвидуса (например, для нашего образца состава xAn = 0,2, xLc = 0,8, при температуре Т1) в системе одна фаза — расплав. Для нашего образца система однофазная (расплав) для всех Т > Т2 (Т2 — температура, которая соответствует точке 2 на диаграмме).
 По окончании кристаллизации эвтектического расплава температура системы может быть понижена и при Т < T4, в системе будет эвтектическая смесь кристаллов анортита и лейцита; например, при Т = Т5). Анализ образца, в котором изначально xAn > 0,48 делается аналогично. Если изначально образец будет состава xAn = 0,48, при охлаждении расплава данного образца мы сразу попадаем в точку с, в которой начнет выделятся из расплава эвтектическая смесь кристаллов анортита и лейцита. Итак, после того, как мы приготовили образец заданного состава (в нашем случае образец был состава xAn = 0,2, xLc = 0.8) мы нагреваем образец до температуры T = T1, при которой в системе одна фаза — расплав и, читая диаграмму состояния, имеем возможность определить температуру фазовых превращений, составы равновесных фаз и их относительное содержание при охлаждении образца. Например, на основании правила рычага в фигуративной точке 3 системе с мольной долей анортита xAn = 0,2 отвечает расплав а состава х31 и кристаллы лейцита.
По окончании кристаллизации эвтектического расплава температура системы может быть понижена и при Т < T4, в системе будет эвтектическая смесь кристаллов анортита и лейцита; например, при Т = Т5). Анализ образца, в котором изначально xAn > 0,48 делается аналогично. Если изначально образец будет состава xAn = 0,48, при охлаждении расплава данного образца мы сразу попадаем в точку с, в которой начнет выделятся из расплава эвтектическая смесь кристаллов анортита и лейцита. Итак, после того, как мы приготовили образец заданного состава (в нашем случае образец был состава xAn = 0,2, xLc = 0.8) мы нагреваем образец до температуры T = T1, при которой в системе одна фаза — расплав и, читая диаграмму состояния, имеем возможность определить температуру фазовых превращений, составы равновесных фаз и их относительное содержание при охлаждении образца. Например, на основании правила рычага в фигуративной точке 3 системе с мольной долей анортита xAn = 0,2 отвечает расплав а состава х31 и кристаллы лейцита.
16.4. Диаграмма состояния двухкомпонентной системы с образованием химического соединения, плавящимся без разложения (конгруэнтно)
При охлаждении бинарного расплава в системе возможно образование химического соединения. Если это соединение плавится конгруэнтно AmBn = mA + nB, то будет образовываться эвтектика как с компонентом А, так и с компонентом В, а на диаграмме появится вертикальная линия и температурный максимум (рис. 16.4). Вертикальная линия определяет состав вновь образовавшегося соединения и делит диаграмму на две части, каждая из которых может рассматриваться как самостоятельная двойная система. Температурный максимум определяет верхний температурный предел устойчивости вещества AmBn.
Рис. 16.4. Система волластонит глинозем
Сделаем анализ диаграммы состояния волластонит + глинозем, (см. рис. 16.4). Особенность процесса охлаждения расплава: при охлаждении расплава волластонита в присутствии глинозема (алюмината кальция) происходит образование геленита, т. е. образуется вещество, которое отсутствовало в начальном состоянии системы. При температуре Т1, соответствующей фигуративной точке 1, в системе одна фаза — расплав, в котором мольная доля глинозема хСа = 0,4. При температуре Т2, в результате реакции между волластонитом и глиноземом, начнется кристаллизация геленита:
рис. 16.4). Особенность процесса охлаждения расплава: при охлаждении расплава волластонита в присутствии глинозема (алюмината кальция) происходит образование геленита, т. е. образуется вещество, которое отсутствовало в начальном состоянии системы. При температуре Т1, соответствующей фигуративной точке 1, в системе одна фаза — расплав, в котором мольная доля глинозема хСа = 0,4. При температуре Т2, в результате реакции между волластонитом и глиноземом, начнется кристаллизация геленита:
CaAl2O4 = | Ca2Al2SiO7. | |
волластонит | глинозем | геленит |
При Т = Т3 продолжается образование геленита в расплаве состава: мольная доля глинозема Хса = 0,3; мольная доля волластонита 0,7.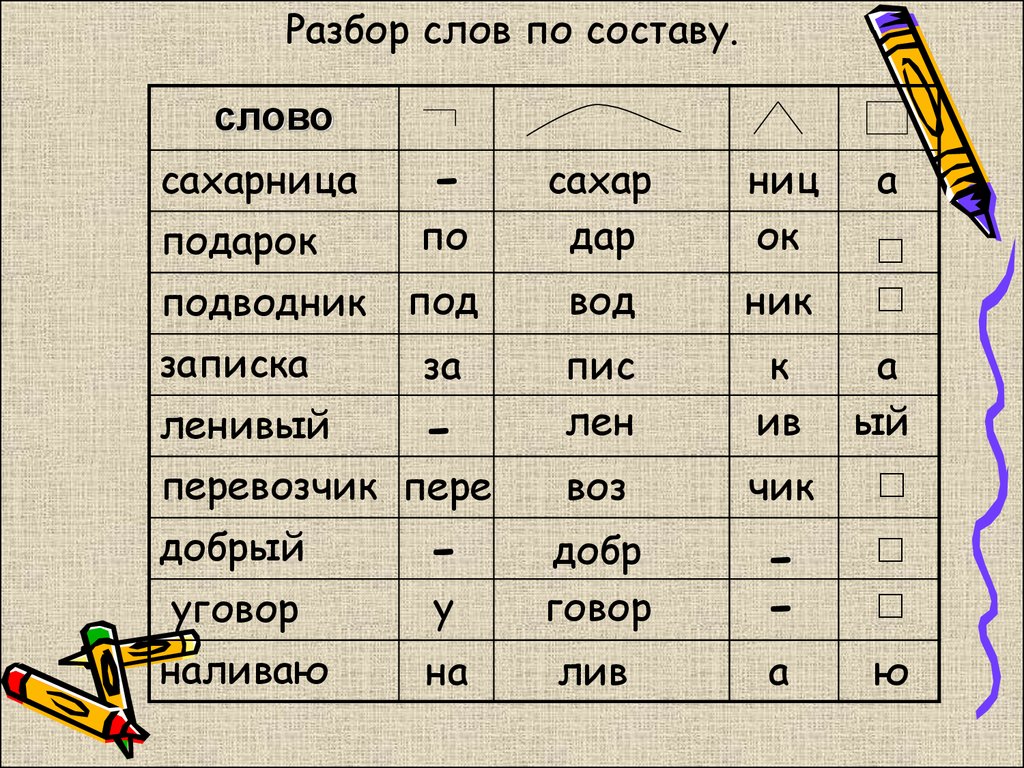 При Т = Т4 = Тэв1 из расплава начнет выделятся волластонит; в системе три фазы: расплав, в котором мольная доля глинозема 0,2, кристаллы геленита и волластонита. При понижении температуры образца ниже Tэв1 образуется эвтектическая твердая фаза из кристаллов α-волластонита и геленита. Отметим важную особенность анализируемой системы: наличие полиморфного превращения волластонита: при Т < 1106 °С α-волластонит превращается в β-волластонит. Далее: геленит не может существовать в виде жидкой фазы. При нагревании выше 1596 оС геленит разлагается на волластонит и глинозем (конгруэнтное плавление геленита).
При Т = Т4 = Тэв1 из расплава начнет выделятся волластонит; в системе три фазы: расплав, в котором мольная доля глинозема 0,2, кристаллы геленита и волластонита. При понижении температуры образца ниже Tэв1 образуется эвтектическая твердая фаза из кристаллов α-волластонита и геленита. Отметим важную особенность анализируемой системы: наличие полиморфного превращения волластонита: при Т < 1106 °С α-волластонит превращается в β-волластонит. Далее: геленит не может существовать в виде жидкой фазы. При нагревании выше 1596 оС геленит разлагается на волластонит и глинозем (конгруэнтное плавление геленита).
16.5. Диаграмма состояния двухкомпонентной системы с образованием химического соединения, которое плавиться инконгруэнтно
Пусть при охлаждении двухкомпонентного расплава, в результате химической реакции mA + nB = AmBn, образуется вещество AmBn. Плавление вещества АmВn называется инконгруэнтным, если разложение вещества АВ сопровождается выделением кристаллов А или В: АmВn = А + расплав, или АmВn = В + расплав.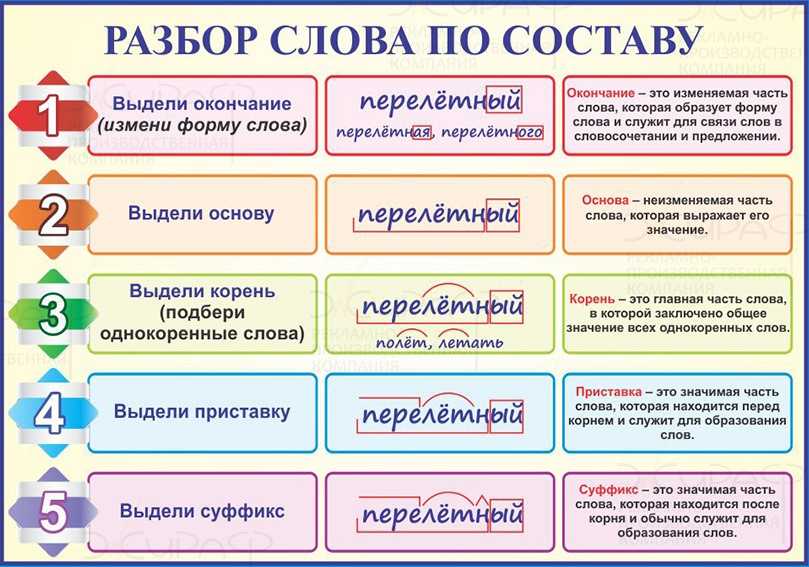 На диаграмме состояния системы с образованием вещества, которое плавится инконгруэтно, рис. 16.5, линия ликвидуса [c, k, P, d, TB] имеет излом в точке Р и «скрытый» максимум, точка e. Участок пунктирной кривой Реf, который формально является продолжением линии ликвидуса сkР, неосуществим. Это связано с тем, что при нагревании вещества АmВn до температуры TP > 800 °C, оно разлагается, выделяя кристалл В: АmВn = В + расплав. Точка Р, характеризующая состав расплава при разложении АmВn, называется точкой перитектики. Линия MN отвечает составу образовавшегося вещества AmBn. Максимальная температура существования АmВn равна ТP = 800 °C. Проведем анализ диаграммы состояния для образца, начальный состав которого xB = 0,8, xA = 0,2. На диаграмме (рис. 16.5) по оси ОХ отложена мольная доля компонента В в системе. ТА и ТВ температуры плавления компонентов А и В соответственно. Тэв = 200 °С — температура эвтектики. Нагреем образец до температуры, выше линии ликвидуса [c, P, TB], например, до температуры Т1, которая соответствует фигуративной точке 1 диаграммы.
На диаграмме состояния системы с образованием вещества, которое плавится инконгруэтно, рис. 16.5, линия ликвидуса [c, k, P, d, TB] имеет излом в точке Р и «скрытый» максимум, точка e. Участок пунктирной кривой Реf, который формально является продолжением линии ликвидуса сkР, неосуществим. Это связано с тем, что при нагревании вещества АmВn до температуры TP > 800 °C, оно разлагается, выделяя кристалл В: АmВn = В + расплав. Точка Р, характеризующая состав расплава при разложении АmВn, называется точкой перитектики. Линия MN отвечает составу образовавшегося вещества AmBn. Максимальная температура существования АmВn равна ТP = 800 °C. Проведем анализ диаграммы состояния для образца, начальный состав которого xB = 0,8, xA = 0,2. На диаграмме (рис. 16.5) по оси ОХ отложена мольная доля компонента В в системе. ТА и ТВ температуры плавления компонентов А и В соответственно. Тэв = 200 °С — температура эвтектики. Нагреем образец до температуры, выше линии ликвидуса [c, P, TB], например, до температуры Т1, которая соответствует фигуративной точке 1 диаграммы.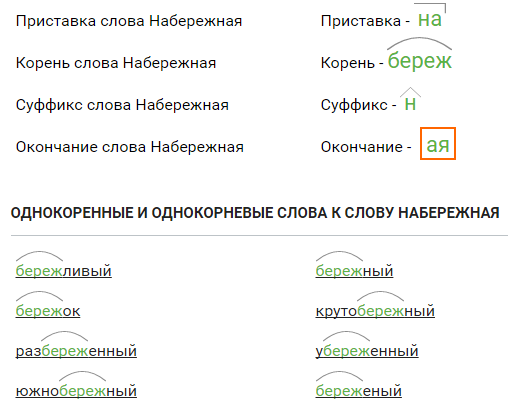 В системе будет одна фаза, расплав, в котором мольная доля В (xb = 0,8), число степеней свободы системы С = 3 – Ф = 2. При охлаждении расплава до Т = Т2 начнется выделение кристаллов В из расплава. При дальнейшем понижении температуры расплава мы будем двигаться по кривой ликвидуса от фигуративной точки 2 к точке d и дальше к точке Р. При температуре расплава Т = Т3 (которая соответствует фигуративной точке d) в системе продолжается выделение кристаллов В из расплава; в системе две фазы: расплав, в котором мольная доля В равна xd и кристаллы вещества В. При дальнейшем понижении температуры мы будем двигаться по кривой ликвидуса до точки Р.
В системе будет одна фаза, расплав, в котором мольная доля В (xb = 0,8), число степеней свободы системы С = 3 – Ф = 2. При охлаждении расплава до Т = Т2 начнется выделение кристаллов В из расплава. При дальнейшем понижении температуры расплава мы будем двигаться по кривой ликвидуса от фигуративной точки 2 к точке d и дальше к точке Р. При температуре расплава Т = Т3 (которая соответствует фигуративной точке d) в системе продолжается выделение кристаллов В из расплава; в системе две фазы: расплав, в котором мольная доля В равна xd и кристаллы вещества В. При дальнейшем понижении температуры мы будем двигаться по кривой ликвидуса до точки Р.
Рис. 16.5. Диаграмма состояния двухкомпонентной системы
с химической реакцией между компонентами
При температуре, соответствующей точке Р, ТР = Т4 = 800 °С из расплава начнут выделятся кристаллы вещества AmBn, которые образуются в результате химической реакции mA + nB = AmBn. Таким образом, при Т = Т4 = 800 °С в системе три фазы: расплав, с мольной долей В, равной 0,5, кристаллы вещества AmBn и кристаллы вещества В. После того, как закончится процесс кристаллизации расплава, при Т < T4 (например при Т = Т5) в системе две фазы: кристаллы вещества В и кристаллы вещества АmВn. Разобранная диаграмма соответствует, например, системе кальцит (компонент А) + нефелин (компонент В). Компоненту AmBn соответствует канкринит Ne3CaCO3 (Ne — нефелин).
Таким образом, при Т = Т4 = 800 °С в системе три фазы: расплав, с мольной долей В, равной 0,5, кристаллы вещества AmBn и кристаллы вещества В. После того, как закончится процесс кристаллизации расплава, при Т < T4 (например при Т = Т5) в системе две фазы: кристаллы вещества В и кристаллы вещества АmВn. Разобранная диаграмма соответствует, например, системе кальцит (компонент А) + нефелин (компонент В). Компоненту AmBn соответствует канкринит Ne3CaCO3 (Ne — нефелин).
16.6. Диаграмма состояния двухкомпонентной системы с ликвацией
При охлаждении расплава может произойти расслоение в жидкой фазе, т. е. образование жидкостей, не смешивающихся друг с другом. Это явление называется ликвацией. На рисунке 16.6 приведена диаграмма состояния двухкомпонентной системы (А и В) с ликвацией.
Рис. 16.6. Диаграмма состояния двухкомпонентной
системы с ликвацией
На диаграмме по оси ОХ отложена мольная доля компонента В в системе. ТА и ТВ — температуры кристаллизации компонентов А и В соответственно. Ликвация (область диаграммы [eLfe] будет иметь место только для системы, в которой изначально мольная доля компонента В в системе будет лежать в пределах 0,2 < xb < 0,7. Сделаем анализ диаграммы состояния для образца, в котором xВ = 0,3. Нагреем образец до температуры выше линии ликвидуса, например, до температуры Т = Т1 = 800 °С, которая соответствует фигуративной точке 1. При температуре Т1 в системе одна фаза — двухкомпонентный расплав, в котором мольная доля компонента А xА = 0.7, xВ = 0,3. При охлаждении образца, при температуре Т2, произойдет расслоение расплава, появится вторая жидкая фаза (расплав), в которой xВ = 0,66. При последующем охлаждении расплава мы будем двигаться по кривой ликвидуса от точки 2 к точке d, затем к точке e, n и c. При температуре Т = Т3 (которая соответствует фигуративной точке d) в системе две жидкие фазы — два несмешивающихся расплава: первый расплав, в котором мольная доля компонента В равна xd1 и второй расплав состава xB = xd2.
ТА и ТВ — температуры кристаллизации компонентов А и В соответственно. Ликвация (область диаграммы [eLfe] будет иметь место только для системы, в которой изначально мольная доля компонента В в системе будет лежать в пределах 0,2 < xb < 0,7. Сделаем анализ диаграммы состояния для образца, в котором xВ = 0,3. Нагреем образец до температуры выше линии ликвидуса, например, до температуры Т = Т1 = 800 °С, которая соответствует фигуративной точке 1. При температуре Т1 в системе одна фаза — двухкомпонентный расплав, в котором мольная доля компонента А xА = 0.7, xВ = 0,3. При охлаждении образца, при температуре Т2, произойдет расслоение расплава, появится вторая жидкая фаза (расплав), в которой xВ = 0,66. При последующем охлаждении расплава мы будем двигаться по кривой ликвидуса от точки 2 к точке d, затем к точке e, n и c. При температуре Т = Т3 (которая соответствует фигуративной точке d) в системе две жидкие фазы — два несмешивающихся расплава: первый расплав, в котором мольная доля компонента В равна xd1 и второй расплав состава xB = xd2. При Т = Т4 (температура эвтектики Тэв2) в системе три фазы: из жидкой фазы начнется выделение кристаллов В; расплав, в котором xВ = 0,2 и расплав, в котором xВ = 0,7. При Т < Т4 жидкая фаза опять будет однородной (ликвация отсутствует). В точке n (которой соответствует температура Т = Т5) в системе две фазы: кристаллы В и расплав, в котором xВ = xn = 0,25. В точке эвтектики с (при Т = Т6 = Тэв1) в системе три фазы: кристаллы А, кристаллы В и расплав с xВ = 0,1. При последующем охлаждении, когда исчезнет расплав, при Т < Т6 в системе образуется эвтектическая смесь кристаллов веществ А и В.
При Т = Т4 (температура эвтектики Тэв2) в системе три фазы: из жидкой фазы начнется выделение кристаллов В; расплав, в котором xВ = 0,2 и расплав, в котором xВ = 0,7. При Т < Т4 жидкая фаза опять будет однородной (ликвация отсутствует). В точке n (которой соответствует температура Т = Т5) в системе две фазы: кристаллы В и расплав, в котором xВ = xn = 0,25. В точке эвтектики с (при Т = Т6 = Тэв1) в системе три фазы: кристаллы А, кристаллы В и расплав с xВ = 0,1. При последующем охлаждении, когда исчезнет расплав, при Т < Т6 в системе образуется эвтектическая смесь кристаллов веществ А и В.
16.7. Диаграмма состояния двухкомпонентных систем с образованием твердых растворов
При охлаждении двухкомпонентного расплава возможно образование твердых растворов (см. главу 10). Если содержащиеся в твердом растворе компоненты растворяются друг в друге в любых соотношениях, то образуется непрерывный ряд твердых растворов. Если же компоненты растворяются лишь до определенных пределов концентрации, то такой раствор называется твердым раствором с ограниченной растворимостью. На рисунке 16.7 приведена диаграмма состояния двухкомпонентной системы с образованием непрерывного ряда твердых растворов. Данного типа диаграмма состояния характерна, например, для системы анортит (СаО×Al2О3×2SiО2) и альбит (Na2O×Al2O3×6SiO2). При охлаждении расплава этих компонентов образуется непрерывный ряд твердых растворов — плагиоклазы. Геленит (СаO×Al2O3×SiO2) с окерманитом (2СаО×МgО×2SiО2) дает непрерывный ряд твердых растворов мелилиты.
На рисунке 16.7 приведена диаграмма состояния двухкомпонентной системы с образованием непрерывного ряда твердых растворов. Данного типа диаграмма состояния характерна, например, для системы анортит (СаО×Al2О3×2SiО2) и альбит (Na2O×Al2O3×6SiO2). При охлаждении расплава этих компонентов образуется непрерывный ряд твердых растворов — плагиоклазы. Геленит (СаO×Al2O3×SiO2) с окерманитом (2СаО×МgО×2SiО2) дает непрерывный ряд твердых растворов мелилиты.
Рис. 16.7. Диаграмма состояния двухкомпонентной системы
с образованием твердых растворов
Проведем анализ диаграммы состояния на рисунке 16.7. Верхняя кривая на диаграмме — линия ликвидуса, с помощью которой можно определить состав расплава в системе, нижняя кривая — линия солидуса, с помощью которой можно определить состав твердого раствора при заданной температуре в системе. По оси ОХ отложена мольная доля компонента В. ТА и ТВ температуры кристаллизации компонентов А и В соответственно. Приготовим образец, в котором мольная доля компонента В хВ = 0,4. Нагреем образец до температуры выше линии ликвидуса, например до Т = Т1 = 925 °С (данная температура соответствует фигуративной точке 1 диаграммы). Если расплав (xВ = 0,4) охлаждать от температуры Т1 до Т2, при Т = Т2 из расплава начнут выделятся кристаллы твердого раствора состава xВ = 0,92, xА = 0,08 (твердый раствор состава А08В92). При охлаждении расплава от Т2 до Т4 мы будем перемещаться по линии ликвидуса от точки m точке n и далее к точке TA. В этом случае будет иметь место выделение из расплава кристаллов твердого раствора, состав которого зависит от температуры расплава. Например, при Т = Т3, расплав (xВ ≈ 0,12) находится в равновесии с твердым раствором, А30В70. При Т < Т4 в системе одна фаза — твердый раствор, в котором мольная доля компонента В, xВ = 0,4 (твердый раствор состава А60В40).
Приготовим образец, в котором мольная доля компонента В хВ = 0,4. Нагреем образец до температуры выше линии ликвидуса, например до Т = Т1 = 925 °С (данная температура соответствует фигуративной точке 1 диаграммы). Если расплав (xВ = 0,4) охлаждать от температуры Т1 до Т2, при Т = Т2 из расплава начнут выделятся кристаллы твердого раствора состава xВ = 0,92, xА = 0,08 (твердый раствор состава А08В92). При охлаждении расплава от Т2 до Т4 мы будем перемещаться по линии ликвидуса от точки m точке n и далее к точке TA. В этом случае будет иметь место выделение из расплава кристаллов твердого раствора, состав которого зависит от температуры расплава. Например, при Т = Т3, расплав (xВ ≈ 0,12) находится в равновесии с твердым раствором, А30В70. При Т < Т4 в системе одна фаза — твердый раствор, в котором мольная доля компонента В, xВ = 0,4 (твердый раствор состава А60В40).
16.8. Диаграммы состояния трехкомпонентных систем. Основные понятия и определения. Треугольник Гиббса
Диаграмма состояния трехкомпонентной системы даже при условии, что давление в системе постоянно — это трехмерная картинка. Как правило — это треугольная призма, грани которой представляют собой диаграммы состояния двойных систем. При изучении тройных систем обычно пользуются проекциями пространственных фигур на основание призмы. При использовании проекций диаграмм состояния на плоскость основания призмы для каждой точки проекции указывается температура образца.
Как правило — это треугольная призма, грани которой представляют собой диаграммы состояния двойных систем. При изучении тройных систем обычно пользуются проекциями пространственных фигур на основание призмы. При использовании проекций диаграмм состояния на плоскость основания призмы для каждой точки проекции указывается температура образца.
Для определения состава расплава или твердого раствора пользуются методом расчета состава, предложенный Гиббсом (треугольник Гиббса). Если в основание призмы положить равносторонний треугольник АВС и ВН = Н — высота треугольника (рис. 16.8), то легко показать, что для любой точки треугольника сумма отношений перпендикуляров, опущенных из этой точки на стороны треугольника к высоте треугольника Н, равна единице. Например, для точки а: hа/H + hв/H + hс/H = 1. Если положить, что отношение ha/H пропорционально мольной доле компонента А в расплаве, а hb/H и hс/H — мольной доле В и С соответственно, то мы получаем возможность определить состав расплава для любой точки ΔАВС. Отметим, что при построении диаграмм состояния трехкомпонентных систем используют и другие методы определения состава расплава. Например, стороны треугольника делят на десять равных частей и проводят линии, параллельные сторонам треугольника.
Отметим, что при построении диаграмм состояния трехкомпонентных систем используют и другие методы определения состава расплава. Например, стороны треугольника делят на десять равных частей и проводят линии, параллельные сторонам треугольника.
Рис. 16.8. Треугольник Гиббса
16.9. Диаграмма состояния трехкомпонентной системы с простой эвтектикой
На рис.16.9 приведена диаграмма состояния трехкомпонентной системы с простой эвтектикой. Пусть температура системы такова, что в точке b две фазы: кристаллы вещества В находятся в равновесии с расплавом, в котором мольная доля В xb = hb/H, мольная доля, А xa = ha/H и xc = hc/H (Н — высота ΔАВС). При охлаждении расплава мы будем двигаться по прямой В-b-d, при этом будет продолжаться выделение кристаллов В из расплава, а состав расплава будет соответствовать координатам прямой b — d. В точке d начнется выделение кристаллов c из расплава.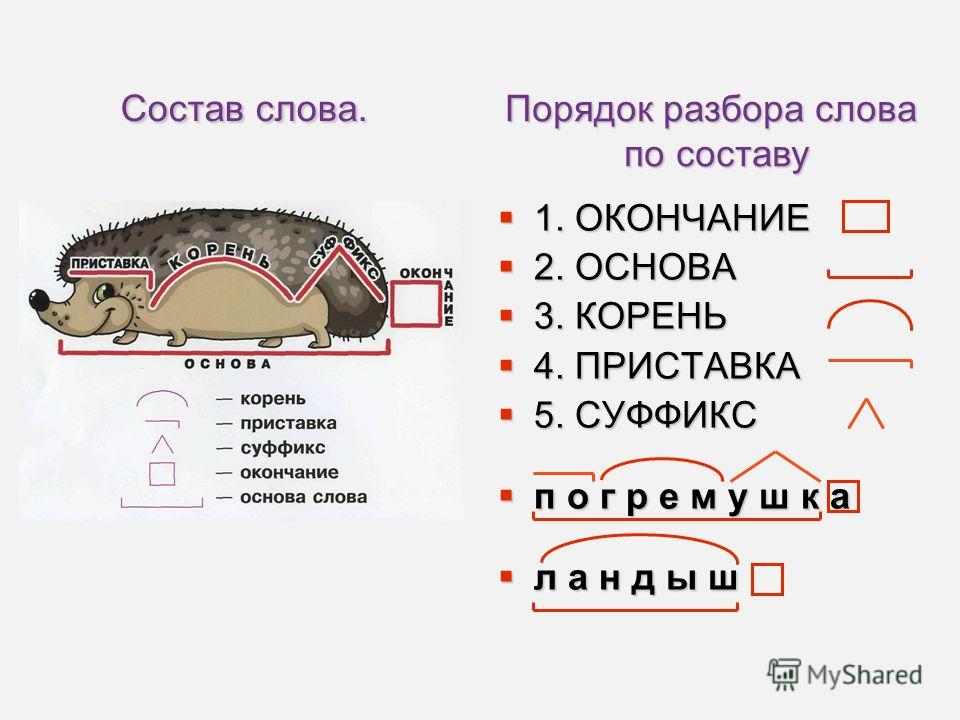 При дальнейшем понижении температуры мы будем двигаться к точке тройной эвтектики — Э (рис. 16.9).
При дальнейшем понижении температуры мы будем двигаться к точке тройной эвтектики — Э (рис. 16.9).
При температуре расплава, соответствующей точке Э в системе четыре фазы: кристаллы В, кристаллы А, кристаллы С и эвтектический расплав, состав которого соответствует координате точки Э. При дальнейшем понижении температуры образца, при Т < Тэв (когда исчезнет расплав), в системе эвтектическая смесь кристаллов А, В, и С. Координаты точек ЭАВ, ЭВС, ЭАС соответствуют температуре и расплавам двойных эвтектик. В общем случае диаграммы состояния трехкомпонентных систем — очень сложные и содержат большое количество взаимнопересекающихся линий, которые разграничивают области равновесного состояния различных фаз системы.
Рис. 16.9. Диаграмма состояния трехкомпонентной
системы с простой эвтектикой
16.10. Диаграмма состояния трехкомпонентной системы с химическими соединениями,
плавящимися конгруэнтно
В системе LiF + NaF + MgF2 при охлаждении расплава образуется двойное соединение состава NaMgF3, которое плавится конгруэнтно. На рисунке 16.10 приведена диаграмма состояния данной системы. Определим одно важное понятие, которое часто используется при анализе диаграмм состояния тройных систем: линия Алькемаде или бинодаль Нода, или конода; это все одно и то же. Линия Алькемаде — это прямая линия, соединяющая точки составов двух фаз, первичные поля кристаллизации которых имеют общую пограничную кривую. Например, поля первичной кристаллизации (см. рис. 16.10) LiF и NaF разделены граничной кривой АВ. Следовательно, сторона треугольника составов, соединяющая LiF и NaF, является линией Алькемаде. Линия LiF — C — NaMgF3 — линия Алькемаде или конода. Теорема Алькемаде утверждает, что пересечение коноды с соответствующей пограничной кривой происходит в точке температурного максимума; точка С на коноде LiF — NaMgF3 — точка максимума температуры на граничной кривой. Стрелками на граничных кривых показаны направления понижения температуры при охлаждении расплава.
На рисунке 16.10 приведена диаграмма состояния данной системы. Определим одно важное понятие, которое часто используется при анализе диаграмм состояния тройных систем: линия Алькемаде или бинодаль Нода, или конода; это все одно и то же. Линия Алькемаде — это прямая линия, соединяющая точки составов двух фаз, первичные поля кристаллизации которых имеют общую пограничную кривую. Например, поля первичной кристаллизации (см. рис. 16.10) LiF и NaF разделены граничной кривой АВ. Следовательно, сторона треугольника составов, соединяющая LiF и NaF, является линией Алькемаде. Линия LiF — C — NaMgF3 — линия Алькемаде или конода. Теорема Алькемаде утверждает, что пересечение коноды с соответствующей пограничной кривой происходит в точке температурного максимума; точка С на коноде LiF — NaMgF3 — точка максимума температуры на граничной кривой. Стрелками на граничных кривых показаны направления понижения температуры при охлаждении расплава.
Рис. 16.10. Диаграмма состояния трехкомпонентной системы
16.10. Диаграмма состояния трехкомпонентной системы
с образованием двойного соединения,
которое плавится конгруэнтно
Разбор слова по составу презентация, доклад
ThePresentationru
- Регистрация |
- Вход
- Загрузить
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Страхование
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Презентация на тему Разбор слова по составу, предмет презентации: Разное.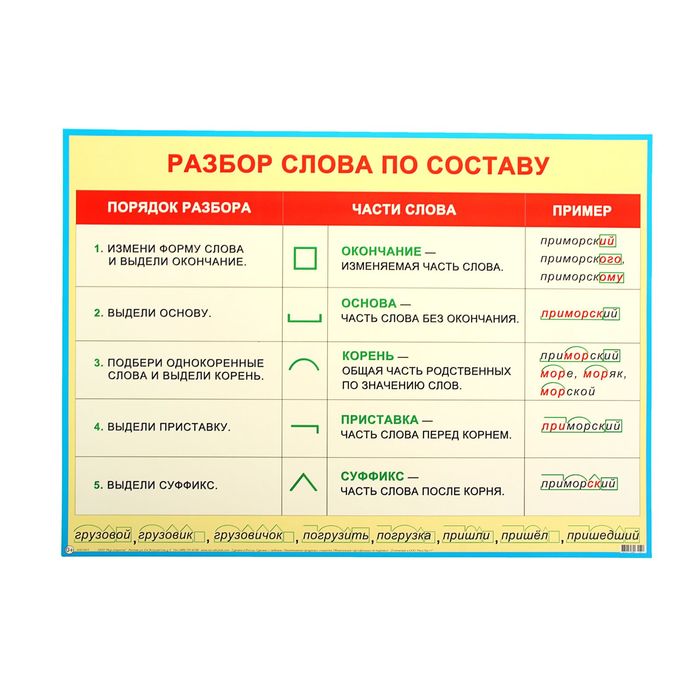 Этот материал содержит 5 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
Этот материал содержит 5 слайдов. Красочные слайды и илюстрации помогут Вам заинтересовать свою аудиторию. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций ThePresentation.ru в закладки!
группа № 1
Разбор слова по составу
Подготовили учащиеся 8б класса МОУ Борской СОШ №2 «Образовательный центр»
группа №1
Маслина Л.
Мокшина И.
Жаркова М.
Гребенникова Л.
Порядок разбора слова по составу
Выделить окончание.
Выделить основу.
Найти корень.
Выделить приставки и суффиксы.
группа № 1
Разбор по составу некоторых частей речи:
группа № 1
Попробуйте найти корень в словах:
Разуть
Заснуть
Воткнутый
Начнут
Ушла
Переел
Сожжение
Навсегда
Вынуть
Доить
Драчливый
группа № 1
Проверьте себя:
Разуть
Заснуть
Воткнутый
Начнут
Ушла
Переел
Сожжение
Навсегда
Вынуть
Доить
Драчливый
Скачать презентацию
Обратная связь
Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте.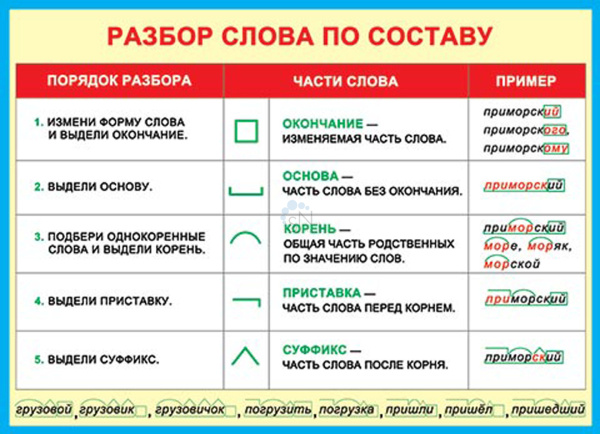 Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:
Email: Нажмите что бы посмотреть
Что такое ThePresentation.ru?
Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.
Для правообладателей
Риторический анализ – сочинение первого года обучения
риторический анализ потребуется:
- фокус на конкретном тексте
- изучить отдельные риторические элементы
- обсудить назначение и действие этих элементов
- оценить эффективность сообщения
Что такое риторический анализ? Эссе по риторическому анализу оценивает эффективность сообщения текста, исследуя, насколько хорошо риторические элементы работают вместе, чтобы достичь целевой аудитории. Риторические элементы включают ряд элементов, таких как дикция, тон, источники, структура и даже способы убеждения, этос, логос и пафос. Цель эссе по риторическому анализу — обсудить, как эти отдельные элементы функционируют в тексте и как они работают вместе, чтобы успешно донести сообщение до конкретной аудитории.
Риторические элементы включают ряд элементов, таких как дикция, тон, источники, структура и даже способы убеждения, этос, логос и пафос. Цель эссе по риторическому анализу — обсудить, как эти отдельные элементы функционируют в тексте и как они работают вместе, чтобы успешно донести сообщение до конкретной аудитории.
Одним из ключей к написанию риторического анализа является сосредоточение внимания на отдельных элементах, а не на общей теме текста. С таким типом эссе очень легко сойти с пути и обсудить проблему, поскольку большинство людей хотят присоединиться к разговору, а не анализировать конкретные элементы. Однако постарайтесь сосредоточиться на каждом риторическом элементе в отдельности; оценить, как этот элемент функционирует в тексте, и оценить, как он действует в отношении целевой аудитории. Обратитесь к главе Что такое риторика? для дальнейших объяснений и примеров того, что такое риторика и, что не менее важно, чем риторика не является. В этой главе также представлены эвристики для анализа автора, аудитории, сеттинга и контекста, цели, среды, позиционирования и идентификации, а также риторических ошибок, которые являются хорошей отправной точкой для написания эссе по риторическому анализу.
Какие существуют другие подходы к написанию риторического анализа? Писатели могут выбирать из многих подходов к анализу текста, таких как метод Тулмина (см. «Анализ утверждений (т. е. метод Тулмина)» для аргументации, риторическая ситуация Битцера (см. «Другой подход к аргументации» в разделе «Альтернативные или культурные методы и подходы»). для аргументации или даже способов убеждения логоса, этоса или пафоса (см. «Письмо с апелляциями» для аргументации).
Нужно больше?
Университет Жизни разместил это полезное видео «Центр письма: риторический анализ».
Эвристики анализа намерений автора см. в документе Excelsior Online Reading Lab «Оценка намерений автора».
Оценка замысла автора
Если вам нужна дополнительная информация о риторических стратегиях, посмотрите «Общие риторические приемы» на YouTube.
Каковы некоторые примеры этого жанра?
- «Не совсем чистая зачистка: риторические стратегии в книге Гроуза «Очистка: последний феминистский рубеж»» Гарриет Кларк
- Образец риторического анализа: риторический анализ высказывания Аддисона «Два года лучше, чем четыре»
Урок по анализу заблуждений находится в дополнительном разделе.
архивный анализ | english 015: введение в риторику и сочинение
Memo Propossial Due сентября 29 / Грубовой проект срок октября 8 / Окончательный проект срок октября. Следующие три задания в нашем классе предназначены не только для того, чтобы дать вам возможность попрактиковаться в создании конкретных аргументов, но и для того, чтобы тщательно выработать набор сильных исследовательских навыков. Во-первых, в документе «Архивный анализ» вы создадите аргумент на основе первичного исследования, описав и проанализировав артефакты из университетских архивов. Это возможность узнать больше о штате Пенсильвания и районе Государственного колледжа, поскольку вы развиваете аргументацию по теме, которая вас действительно интересует. Вместо того, чтобы начинать с твердой убежденности и чувства аргументации, мы начнем с чувства любопытства. Тем не менее, помните обо всех трех шагах, когда вы выбираете тему для исследования. Знание того, что вашей последней задачей является написание предложения, должно помочь вам провести мозговой штурм по теме. Какие проблемы стоят сегодня перед нашим кампусом или сообществом? Как историческая перспектива может помочь вам понять эту проблему? Вероятно, во время посещения архивов вы просмотрите множество артефактов. 1) Опишите выбранный вами артефакт(ы). 2) Оцените важность для нашего представления об истории штата Пенсильвания сегодня. Почему важно, чтобы мы понимали информацию, которую вы раскрыли? 3) Проанализируйте содержимое вашего артефакта таким образом, чтобы подтвердить свою оценку его важности. Что такого в артефакте и его содержимом, что делает его ценным? 4) Разработайте аргумент о вашем артефакте. Хотя этот проект в конечном счете приведет к аргументации предложения, ваши аргументы на этом этапе могут принимать разные формы. Убедите ли вы свою аудиторию в том, что артефакт действительно важен? Вы приводите аргумент в пользу того, как Пенн Стейт изменился с течением времени? Используете ли вы этот фрагмент истории, чтобы привлечь внимание к текущему вопросу или проблеме? Не волнуйтесь, если у вас нет конкретной аудитории/цели/аргумента перед началом проекта. Во-вторых, в аннотированной библиографии вы создадите корпус вторичных исследований, чтобы дополнить и поддержать эти первичные источники. Наконец, вы объедините эти усилия, чтобы написать аргументацию предложения, которая свяжет ваше историческое исследование с текущей проблемой, стоящей перед нашим кампусом.
Во-вторых, в аннотированной библиографии вы создадите корпус вторичных исследований, чтобы дополнить и поддержать эти первичные источники. Наконец, вы объедините эти усилия, чтобы написать аргументацию предложения, которая свяжет ваше историческое исследование с текущей проблемой, стоящей перед нашим кампусом. Вы сможете использовать информацию из нескольких источников в своей статье, но я хотел бы, чтобы вы выделили один или два из этих артефактов в своей статье. Это может быть письмо или служебная записка, официальный документ или запись, справочник, заметки из личного дела, фотография и т. д. Выберите артефакт, который действительно привлечет ваше внимание и который, в свою очередь, будет интересен вашей аудитории. Выберите конкретную аудиторию (в этом случае ваша аудитория, скорее всего, будет связана с Пенсильванским университетом) и используйте этот текст как возможность проинформировать их о вашей теме и ваших артефактах. Развивая свою аргументацию, подумайте, как сделать эту информацию актуальной, интересной и важной для современной аудитории. Кому нужно понять эту историю? Почему? По сути, ваша статья должна отражать ценность первоисточников — ваша аудитория должна видеть, откуда взялась ваша информация и почему она важна. Вам понадобится:
Вы сможете использовать информацию из нескольких источников в своей статье, но я хотел бы, чтобы вы выделили один или два из этих артефактов в своей статье. Это может быть письмо или служебная записка, официальный документ или запись, справочник, заметки из личного дела, фотография и т. д. Выберите артефакт, который действительно привлечет ваше внимание и который, в свою очередь, будет интересен вашей аудитории. Выберите конкретную аудиторию (в этом случае ваша аудитория, скорее всего, будет связана с Пенсильванским университетом) и используйте этот текст как возможность проинформировать их о вашей теме и ваших артефактах. Развивая свою аргументацию, подумайте, как сделать эту информацию актуальной, интересной и важной для современной аудитории. Кому нужно понять эту историю? Почему? По сути, ваша статья должна отражать ценность первоисточников — ваша аудитория должна видеть, откуда взялась ваша информация и почему она важна. Вам понадобится: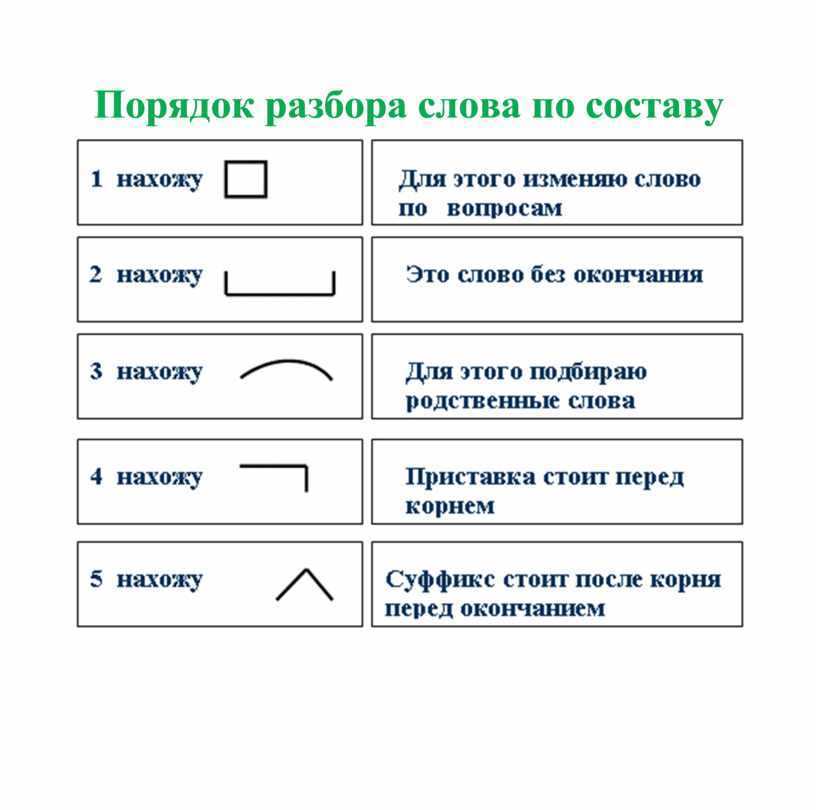 Что именно вы смотрите? Какую информацию вы получили из своего артефакта?
Что именно вы смотрите? Какую информацию вы получили из своего артефакта?