Тема урока | «Распределительный закон умножения» |
Предмет | математика |
Класс | 5 |
Автор урока (ФИО, должность) | Кирпичёва Елена Евгеньевна, учитель математики |
Образовательное учреждение | МОУ СОШ №172, г. Нижний Новгород |
Республика/край, город/поселение | Нижегородская область, г. Нижний Новгород |
Методическая информация | |
Тип урока | систематизация и обобщения знаний |
Цели урока | 1) образовательные: систематизировать, расширить и углубить знания, формировать умение применять распределительный закон умножения при решении задач, продолжить выявление пробелов в знаниях и ликвидировать их. 2) развивающие: способствовать развитию наблюдательности, умения находить наиболее рациональные пути решения задач, развивать вычислительные навыки, продолжить формирование у учащихся умения самостоятельно работать. 3) воспитательные: воспитание чувства ответственности за результат, воспитывать культуру умственного труда, развивать коммуникативные качества личности, развивать способность самооценки. |
Задачи урока |
|
Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока | Закрепление знаний по теме: «Распределительный закон умножения». Продолжение выработки умений применять распределительный закон умножения при упрощении выражений, путем вынесения общего множителя за скобки, для более рационального счета, решать уравнения и составлять их при решении текстовых задач. |
Необходимое оборудование и материалы | Слайдовая презентация урок «Распределительный закон умножения», классная доска, ноутбук, 1экран, 1медиапроектор, учебник «Математика, 5» автор Н.Я. Виленкин, В.И. Жохов, индивидуальные оценочны листы, карточки с проверочными заданиями тестами, рабочие тетради. |
Мотивация учащихся | Цель каждого ученика во время урока –игры набрать максимальное число баллов и получить отличную оценку, хорошо подготовиться к контрольной работе. |
Ход и содержание урока | см. ниже |
Проверка и оценивание ЗУНКов | На каждом этапе урока происходит либо самопроверка, либо взаимопроверка. |
Рефлексия деятельности на уроке | Осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения , как они были устранены, и что чувствовал ученик при этом. |
Домашнее задание | 1 уровень. Подобрать 8 примеров и 2 задачи на применение распределительного закона умножения из дополнительной литературы: дидактические материалы, сборники задач. 2 уровень. «Придумай задачу другу» — придумать и решить тоже количество заданий. |
Дополнительная необходимая информация | |
В помощь учителю | |
Использованные источники и литература (если имеются) | учебник: Математика, 5» автор Н. В.И. Жохов |
Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить | Наглядность, удобство в применении, экономия времени учителя, обратная связь, выявление пробелов и их ликвидация, заинтересованность учащихся |
Советы по логическому переходу от данного урока к последующим | После урока обобщения следует проведение контрольной работы |
Другое | |
Цель/задачи этапа | Деятельность учителя | Деятельность ученика | Компетенции/ аспекты компетенции/ УУД | Оценивание/ формы контроля | Результат | |||||||||||||||||
I этап: мотивация к учебной деятельности — 2 мин. | ||||||||||||||||||||||
Мотивировать обучающихся к учебной деятельности на уроке, определить содержательные рамки урока. | Обеспечивает мотивацию, создаёт условия для возникновения у обучающихся внутренней потребности включения в учебную деятельность. Я сегодня хочу начать урок с таких слов, которые будут сегодня девизом нашего урока: «Считайте несчастным тот день и тот час, в который ты не усвоил ничего нового, ничего не прибавил к своему образованию» Я. | Проявляют интерес к изучению материала. Объясняют, как они понимают эту фразу | Коммуникативная/ диалог. | Самоконтроль, словесное поощрение учителя. | Внутренняя и внешняя готовность обучающихся к учебной деятельности на уроке. | |||||||||||||||||
II этап: актуализация и фиксирование индивидуального затруднения в пробном учебном действии — 5 мин. | ||||||||||||||||||||||
Актуализировать изученные способы действий, активизировать мыслительные операции; зафиксировать затруднения. | Организует деятельность по актуализации фиксации индивидуального затруднения.
25+65+75 5∙12∙4 34+17+83 25∙8∙4 27+123+16+234 50(346∙2) 76∙5∙2 Ребята! Почему мы такие трудные примеры решили очень быстро? Записываем формулы на доске. a+b=b+a ab=ba a(bc)=(ab)c a+(b+c)=(a+b)+c Дома вы выучили формулировки законов ,проверьте. 2. Предлагаю вам ещё решить примеры устно:
| Актуализируют способы действия, выполняют пробное учебное действие и фиксируют собственное затруднение. Отвечают на вопросы Изучили переместительный и сочетательные законы сложения и умножения Данные примеры, на первый взгляд устно вычислить невозможно. Значит для выполнения данного задания не хватает знаний. Возникает проблемная ситуация. | Коммуникатив-ная (умение строить речевое высказывание в соответствии с поставленными задачами) Учебно-познавательная/ использование информации для решения учебных задач. | Внешний контроль, самоконтроль, взаимоконт-роль | Актуализация изученных способов действия; выполнение пробного учебного действия, фиксация затруднений. | |||||||||||||||||
III этап: Постановка учебной задачи — 5 мин. | ||||||||||||||||||||||
Обсуждение затруднений | Почему возникли затруднения? Чего мы ещё не знаем? Можем ли мы использовать имеющиеся формулы для выполнения поставленной задачи? | Возникает проблемная ситуация. Пытаются решить примеры, высказывают свои мнения. Приходят к выводу, что мы не знаем ещё какой-то закон, который нам поможет решать такие примеры устно. | Коммуникатив-ная /взаимодействие Регулятивные /умение определять цель деятельности на уроке Учебно-познавательная/ использование информации для решения учебной задачи, планирование. | Самоконт-роль, внешний контроль | Готовность к восприятию новых знаний | |||||||||||||||||
IV этап: Открытие нового знания (построение проекта выхода из затруднения) — 8 мин. | ||||||||||||||||||||||
Организовать коммуникатив-ное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения; зафиксировать новый способ действия в знаковой, вербальной форме. | Организуется работа в парах. Каждая пара получает задачу , которую необходимо решить различными способами: (прямоугольники из картона. Измерить, найти площадь двумя способами, вывести общую формулу). Перейдем к обсуждению проделанной нами работы и ее результатов. Сколько разных способов рассмотрели? Обсудим 1 способрешения задачи. Сравним полученные выражения при 2 способе решения задачи. Что в них общего? Сравните ответы – результаты задачи при решении первым и вторым способом. В таких случаях говорят, что числовое значение первого выражения равно числовому значению второго выражения. Какой вывод можно сделать из этого факта? Верно! Запишите соответствующие равенства к задаче. Сколько различных букв нам необходимо для записи буквенного выражения? Что можно записать при помощи буквенного выражения? Так, наверное, у нас тоже получился какой-то закон? Как его прочитать? Попробуйте перевести его с математического языка на русский. Это свойство назвали распределительным свойством умножения относительно сложения. Как вы думаете, почему его назвали распределительным? | Устанавливают закономерности; делают выводы; формулируют правило (эталон), фиксируют преодоление возникшего ранее затруднения. перерабатывают информацию. Отвечают на вопросы, обсуждают. Рассмотрели 2 способа решения. Задачи мы решали с помощью составления выражения. В задаче в первом способе, выражение содержит скобки и два действия: сложение и умножение. При втором способе решения выражение содержит три действия: два действия на умножение и одно на сложение. Ответы – результаты одинаковые. Можно сделать такой вывод: в задаче первое выражение равно второму выражению. Записывают полученные числовые равенства. Три разных числа, значит букв необходимо 3. (a+b)*c=ac+ab Свойство или правила. Чтобы умножить сумму на число, можно сначала умножить это число на первое слагаемое, затем на второе слагаемое и сложить полученные произведения. | Учебно – познавательная/ исследовательс-кая деятельность. Коммуникатив-ная/ работа в парах, взаимодействие Информационная/ сбор информации, обработка и передача. | Самоконт-роль. Оценка учителем работы групп. | Выводят Формулу закона и его словесную формулировку. Затем его читают по учебнику | |||||||||||||||||
V этап: первичное закрепление с комментированием во внешней речи — 7 мин. | ||||||||||||||||||||||
Организовать усвоение детьми нового способа действий при решении задач с проговариванием во внешней речи. | Организует работу обучающихся по первичному закреплению знаний обучающихся. А чем нам может быть полезен этот закон? Поможет ли он нам вычислить устно примеры, данные в начале урока? | Выполняют комментированное письмо с проговариванием способов действий. Выполняют задание в тетради, работая вместе с классом. | Учебно-познавательная/ использование информации для решения учебной задачи. Коммуникатив-ная/ фронтальная работа с подробным объяснением решения. 138*48+138*52=(48+52)*138=13800 67*149+149*33=(67+33)*149=14900 62*126+38*126=(62+38)*126=12600 150*6=(100+50)*6=600+300=6=900 520*4=(500+20)*4=2000+80=2080 | Внешний контроль, взаимоконт-роль,. | Усвоение нового способа действий при решении примеров | |||||||||||||||||
Физминутка (музыкальная). VI этап: Включение нового знания в систему знаний, повторение и контроль — 13 мин. | ||||||||||||||||||||||
Организовать самостоятельное выполнение каждым обучающимся заданий на новый способ действий; организовать самопроверку обучающимися своих решений. | Организует ситуацию решения учебной задачи; предоставляет возможность выявления причин ошибок и их устранения (индивидуальная коррекционная деятельность)
№219 (а-г) №222(а,б) №223 (а, в) — Какой вывод можно сделать? 2. Математический диктант. (презентация) Критерии: оценка «5» — 5 заданий Оценка «4» — 4 задания Оценка «3» — 3 задания Оценка «2» — менее 3 заданий. | Ученики решают предложенные задания, возникает проблемная ситуация №223(а, в). Так значит распределительный закон есть и относительно вычитания! Меняются тетрадями и выставляют оценки соседу по парте. | Учебно-познавательная / самоконтроль и самооценка Информационная/ переработка, использование информации для решения учебной задачи. | Самооценка. | Определение уровня усвоения нового способа действий | |||||||||||||||||
VII этап: рефлексия учебной деятельности на уроке. Итог урока — 3 мин. | ||||||||||||||||||||||
Организовать рефлексию и самооценку обучающихся | Организует рефлексию и самооценку, объясняет домашнее задание. Вопросы: — Какую задачу ставили на уроке? — Удалось решить поставленную задачу? — Каким способом? — Какие получили результаты? — Что нужно сделать еще? — Где можно применить новые знания? — Что на уроке у вас хорошо получилось? — Над чем еще надо поработать? Оцените свою работу на уроке и отношение к новой теме. Нарисуйте один из предложенных знаков и смайлик. (презентация) Объявление оценок за урок. | Дети соотносят цель учебной деятельности и её результаты, фиксируют степень её соответствия, оценивают уровень достижения поставленной цели и намечают цели дальнейшей деятельности. Отвечают на поставленные вопросы. Проводят самооценку. | Учебно-познавательная/ самооценка , взаимооценка. Информационная / обработка и передача информации. | Самоконт-роль, взаимоконт-роль, внешний контроль | Осознание обучающимися своей учебной деятельности; самооценка результатов своей деятельности. | |||||||||||||||||
VIII этап: информация о домашнем задании – 2 мин. | ||||||||||||||||||||||
Обсудить и записать домашнее задание. | Стр27. правило запомнить, №108(д — з), №114 (б, г) СПАСИБО всем за урок! | Воспринимают информацию, записывают в дневники домашнее задание | ||||||||||||||||||||
Распределительный закон умножения 5 класс
Вы можете ознакомиться и скачать презентацию на тему Распределительный закон умножения 5 класс. Доклад-сообщение содержит 21 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
«Распределительный
закон умножения». 5 класс.
5 класс.
Описание слайда:
Три пути ведут к знанию: путь размышления — это путь самый благородный, путь подражания — это путь самый легкий и путь опыта — это путь самый горький. Конфуций
Слайд 3
Описание слайда:
Цели урока: Систематизировать, расширить и углубить знания по данной теме. Развивать наблюдательность, умение анализировать, вычислительные навыки. Искать наиболее рациональные пути решения задач.
Слайд 4
Описание слайда:
Этапы урока:
1.
Слайд 5
Описание слайда:
Накопительная оценка: Максимум — 41 балл, от 37 до 41 — оценка «5», от 29 до 35 — оценка «4», от 20 до 28 — оценка «3», менее 20 баллов — оценка «2».
Слайд 6
Описание слайда:
ЭТАП №1. Домашнее задание.
№1. Упростите выражение:
а) 46а + 54а – а – 2а = 97а;
б) 23m – 14m + 48 = 9m + 48;
в) 56в + 14в – 70в = 0;
г) 37х — 17х + 34х – 54х + 100 = 100.
Слайд 7
Описание слайда:
Этап №2. «Разминка» — тест. Задание №1.
Соедините линиями соответствующие законы
умножения:
а) a · b = b · а А) Распределительный
б) (a · b) · с = а · (b · с) Б) Переместительный
в) а · b + а · с = а · (b + с) В) Сочетательный
Задание №1.
Соедините линиями соответствующие законы
умножения:
а) a · b = b · а А) Распределительный
б) (a · b) · с = а · (b · с) Б) Переместительный
в) а · b + а · с = а · (b + с) В) Сочетательный
Слайд 8
Описание слайда:
Задание №2. Отметить знаком «+» верно выполненные выражения. а) 37у + 62у – 31у = 68у; + б) 108х – 28х – х = 80х; - в) 39m + 51m + 100 = 190m; - г) 44k – 4k – 20 = 40k – 20. +
Слайд 9
Описание слайда:
Задание №3. Составьте уравнение к задаче и решите его.
Ученик задумал число, умножил его на 8, затем это же число отдельно умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик?
Уравнение: 8х + 15х = 276,
х = 12.
Ответ: ученик задумал число 12.
Составьте уравнение к задаче и решите его.
Ученик задумал число, умножил его на 8, затем это же число отдельно умножил на 15 и результаты сложил. В сумме получилось 276. Какое число задумал ученик?
Уравнение: 8х + 15х = 276,
х = 12.
Ответ: ученик задумал число 12.
Слайд 10
Описание слайда:
Этап №3. «Математическая эстафета».
1 ряд 2 ряд 3 ряд____
1) 25х + 87х = 336; 1) 66у – 29у = 74; 1) 54х + 41х = 190;
2) 41у – 21у + у; 2) 92х + х — 33х; 2) 63а + а — 51а;
3) 16а – 9а + 5 = 75; 3) 25k – 16k + 5 = 86; 3) 39х – 27х + 15 = 63;
4) 45b + 24b – 69b; 4) 74с + 47с – 121с; 4) 45у + 31у — 76у;
5) 18х + 62х – 15=145; 5) 16а + 73а – 26 =152; 5) 58х + 96х – 54 =100;
6) 99k – 19 k + k – 81; 6) 46d — 24d + d — 23; 6) 61k – 57k + k – 5;
7) 44х – 22х = 880; 7) 77у – 55у = 660; 7) 99d – 11d = 176;
8) n + 2n – 3n + 2008; 8) 9t – 5t – 4t + 2009; 8) х + 5х — 6х + 2010;
9) 55х – 13х – 17х = 625.
Слайд 11
Описание слайда:
Этап 3. «Математическая эстафета» Ответы: 1 ряд 2ряд 3 ряд 1. x = 3 1. y = 2 1. x=2 2. 21y 2. 60x 2. 13a 3. a = 10 3. k = 9 3. x = 4 4. 0 4. 0 4. 0 5. x = 2 5. a = 2 5. x = 1 6. 81k – 81 6. 23d – 23 6. 5k – 5 7. x = 40 7. y = 30 7. d =2 8. 2008 8. 2009 8. 2010 9. x = 25 9. y = 9 9. y = 6
Слайд 12
Этап №4. «Решение задач с помощью уравнений».
1 ряд. Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба?
_________________________________________________________________
2 ряд. В лесу жили хамелеоны. Синих хамелеонов было в 7 раз больше, чем красных, а красных в 5 раз больше, зеленых. Сколько хамелеонов каждого цвета жило в лесу, если всего их было насчитано 123?
_______________________________________________________
3 ряд. В зоопарке жили хищные животные. Тигров было в 2 раза больше, чем ягуаров и в 4 раза меньше, чем пантер. Сколько хищников каждого вида жило в зоопарке, если всего насчитывалось 55 животных?
Маша, Оля и Таня пошли в лес за грибами. Маша собрала в 3 раза больше грибов, чем Таня, а Оля в 2 раза больше, чем Таня. Сколько грибов собрала каждая девочка, если всего они собрали 84 гриба?
_________________________________________________________________
2 ряд. В лесу жили хамелеоны. Синих хамелеонов было в 7 раз больше, чем красных, а красных в 5 раз больше, зеленых. Сколько хамелеонов каждого цвета жило в лесу, если всего их было насчитано 123?
_______________________________________________________
3 ряд. В зоопарке жили хищные животные. Тигров было в 2 раза больше, чем ягуаров и в 4 раза меньше, чем пантер. Сколько хищников каждого вида жило в зоопарке, если всего насчитывалось 55 животных?
Слайд 13
Описание слайда:
Этап №4. Ответы к задачам.
1 ряд. х – грибов собрала Таня.
Уравнение: х + 2х + 3х = 84.
х = 14.
Ответ: 42, 28 и 14 грибов.
_____________________________________________
2 ряд. х – зеленых хамелеонов жило в лесу.
Уравнение: х + 5х + 35х = 123
х = 3.
Ответ: 105, 15 и 3 хамелеона.
_____________________________________________
3 ряд. х – ягуаров жило в зоопарке.
Уравнение: 2х + х + 8х = 55,
х = 5.
Ответ: 10, 5 и 40 животных.
Ответы к задачам.
1 ряд. х – грибов собрала Таня.
Уравнение: х + 2х + 3х = 84.
х = 14.
Ответ: 42, 28 и 14 грибов.
_____________________________________________
2 ряд. х – зеленых хамелеонов жило в лесу.
Уравнение: х + 5х + 35х = 123
х = 3.
Ответ: 105, 15 и 3 хамелеона.
_____________________________________________
3 ряд. х – ягуаров жило в зоопарке.
Уравнение: 2х + х + 8х = 55,
х = 5.
Ответ: 10, 5 и 40 животных.
Слайд 14
Описание слайда:
Этап №5. Самостоятельная работа.
1 уровень.
№1. Упростите выражение. Заполните пропуски.
а) 15x + 20x + x = ( + +)∙ x = ∙x,
б) 24a – 12a – 78 = ( — ) ∙ а — 78 = ∙а — ,
в) y + 55y – 56y + 45 = ( + — ) ∙ y + = y + = ,
№2. Решите уравнение.
а) 78x + 92x = 340 б) 49y – 27y + 34 = 100
( + ) ∙ x = 340 ( — )∙y + 34 = 100
∙ x = 340 y = 100 34
x = 340 : y =
x = y = :
Ответ: y =
Ответ:
№3. По данной к задаче таблице составь уравнение:
Собрали яблок:
Петя 4х яблок
Галя х яблок
Коля 7х яблок
Вместе дети собрали — 72 яблока.
Самостоятельная работа.
1 уровень.
№1. Упростите выражение. Заполните пропуски.
а) 15x + 20x + x = ( + +)∙ x = ∙x,
б) 24a – 12a – 78 = ( — ) ∙ а — 78 = ∙а — ,
в) y + 55y – 56y + 45 = ( + — ) ∙ y + = y + = ,
№2. Решите уравнение.
а) 78x + 92x = 340 б) 49y – 27y + 34 = 100
( + ) ∙ x = 340 ( — )∙y + 34 = 100
∙ x = 340 y = 100 34
x = 340 : y =
x = y = :
Ответ: y =
Ответ:
№3. По данной к задаче таблице составь уравнение:
Собрали яблок:
Петя 4х яблок
Галя х яблок
Коля 7х яблок
Вместе дети собрали — 72 яблока.
Слайд 15
Описание слайда:
2 уровень. №1. Упростите выражение. а) 46х + 87х – 38х; б) 84y — 37y + 41y – 124; в) 65а + 36а – а – 100; №2. Решите уравнение: а) 43х + 2 ∙ 3х = 98; б) 59а – 38а – 95 = 10. №3. Решите задачу. условия Выразить через «х» сколько животных кенгуру в 5 раз больше, чем пони пони в 2 раза больше, чем бегемотов бегемоты Всего в зоопарке было 26 животных. Составим и решим уравнение.
Слайд 16
Описание слайда:
3 уровень. №1. Вычислить как можно более простым способом:
а) 5 ∙ 2 + 5 ∙ 22 + 5 ∙ 222 + 5 ∙ 2222;
б) 33 ∙ 25 – 25 ∙ 23 + 10 ∙15 – 40 ∙ 5
№2. Решите уравнение.
(((7х – 2∙2х) + 6х) – 7х) + 2 ∙ 4х = 1000.
№3. Решите задачу.
Условия Выразить через «х»
сорок в 2 раза больше, чем синиц и
в 3 раза меньше, чем снегирей
синиц
снегирей
Всего на дереве сидело- 18 птиц.
Составляем и решаем уравнение.
№1. Вычислить как можно более простым способом:
а) 5 ∙ 2 + 5 ∙ 22 + 5 ∙ 222 + 5 ∙ 2222;
б) 33 ∙ 25 – 25 ∙ 23 + 10 ∙15 – 40 ∙ 5
№2. Решите уравнение.
(((7х – 2∙2х) + 6х) – 7х) + 2 ∙ 4х = 1000.
№3. Решите задачу.
Условия Выразить через «х»
сорок в 2 раза больше, чем синиц и
в 3 раза меньше, чем снегирей
синиц
снегирей
Всего на дереве сидело- 18 птиц.
Составляем и решаем уравнение.
Слайд 17
Описание слайда:
Этап 5. 1 уровень. 1. 36х 2. 12а – 78 3. 45 4. x = 2 5. y = 3 6. 4x + x + 7x = 72.
Слайд 18
Описание слайда:
2 уровень. 1. 95х
2. 88y – 124
3. 100a – 100
4. x = 2
5. a = 5
6. x + 2x +5 ∙ 2x = 26,
x = 2;
20, 4 и 2 животных.
1. 95х
2. 88y – 124
3. 100a – 100
4. x = 2
5. a = 5
6. x + 2x +5 ∙ 2x = 26,
x = 2;
20, 4 и 2 животных.
Слайд 19
Описание слайда:
3 уровень. 1. 12340 2. 200 3. х =100 4. 2х + х + 2 ∙ 3х = 18, х = 2; 4, 2 и 12 птиц.
Слайд 20
Описание слайда:
Оцени свои знания: Максимум — 41 балл, от 37 до 41 — оценка «5», от 29 до 35 — оценка «4», от 20 до 28 — оценка «3», менее 20 баллов — оценка «2».
Слайд 21
Описание слайда:
Спасибо за урок, дети!
Распределительный закон умножения — javatpoint
следующий → ← предыдущая Закон дистрибутивности гласит, что если мы умножаем число на группу чисел, которые складываются/вычитаются вместе, то будет получен тот же результат, если мы будем выполнять каждое умножение отдельно. Например: 5 * (3 + 7) = 5 * 3 + 5 * 7 5 * (10) = 15 + 35 50 = 50 Таким образом, результаты обоих способов одинаковы. Распределительный закон является одним из наиболее часто используемых законов в дискретной математике. Есть еще два важных закона: Ассоциативное право и Коммутативное право. Мы можем легко упростить арифметические вычисления, а также алгебраические выражения с помощью различных типов свойств, которые есть в Math. В этом разделе мы узнаем об одном свойстве, которое является Распределяющим свойством. Очень легко запомнить распределительный закон. Мы изучим определение, формулу и различные примеры распределенного закона. Определение распределительного права Распределительный закон является разновидностью алгебраического закона. В дистрибутивном законе мы умножаем одно значение на два или более значений в наборе скобок. Согласно этому закону, когда множитель умножается на сумму двух слагаемых, необходимо умножить каждое из двух слагаемых на множитель, а затем выполнить операцию сложения. Х (У + Z) = ХУ + ХZ Здесь X, Y и Z используются для обозначения трех разных значений. Чтобы понять это, возьмем простой пример, т. е. 9 (5 + 1). Мы видим, что бином «5 + 1» стоит в скобках. Порядок работы описывает, что мы сначала узнаем значение 5+1, а уже после этого умножим его на 9. После умножения получим результирующее значение 54. Распределительный закон с переменнымиЧтобы понять это, возьмем пример, 5(6 + 8x) В этом примере мы видим, что скобки содержат два значения, которые нельзя добавить, потому что эти значения не похожи на другие термины. Поэтому мы не можем еще больше упростить его. Для этого нам понадобится метод другого типа. В это время мы можем использовать закон распределения. Итак, если мы применим закон распределения, то получим следующее: 5*6+5*8х Здесь мы видим, что скобки больше нет, и число 5 умножается на каждый член. Теперь мы упростим умножение отдельных терминов следующим образом: 30 + 40х С помощью распределительного закона умножения мы можем упростить выражение, в котором мы умножаем число на разность или сумму. Этот закон гласит, что произведение суммы/разности чисел и суммы/разности произведений равны друг другу. В дискретной математике мы можем использовать закон распределения для двух арифметических операций, которые описываются следующим образом:0006
Распределительный закон умноженияМы можем использовать только сложение и вычитание, чтобы выразить закон распределения умножения. Согласно этому свойству операция существует внутри скобки. Это означает, что внутри скобки и между числами должен быть символ сложения или вычитания. Теперь разберемся сложением и вычитанием отдельно в законе распределения. 1. Распределительный закон умножения по сложению Когда есть случай, когда мы хотим умножить значение на сумму, в этом случае мы будем применять свойство умножения вместо сложения. Есть два случая выполнения распределения умножения над сложением. Случай 1: В первом случае мы сначала добавим числа. После этого умножим прибавленное число на 5. Таким образом, 7 * (9 + 4) = 7 * (13) = 91 Случай 2: Во втором случае мы сначала решим скобку. Это означает, что мы сначала умножим каждое число на 5. Это можно назвать распределением 5, а после этого мы добавим продукты. Итак, перед сложением мы выполним умножение 7(9) и 7(4) следующим образом: 7(9) + 7(4) = 63 + 28 = 91 Как мы видим, результат обоих способов одинаков. Оба метода подробно описываются приведенными ниже уравнениями. В левой части (слева) происходит сложение чисел 9 и 4, а затем оно умножается на 5. Выражение правой части переписывается путем применения распределения, в котором мы сначала распределяем 5, а затем умножаем их на 5, и, наконец, мы добавим результаты. 7(9 + 4) = 7(9) + 7(4) 7(13) = 63 + 28 65 = 65 2. Распределительный закон умножения над вычитаниемКогда есть случай, когда мы хотим умножить значение вычитанием, в этом случае мы будем применять свойство умножения вместо вычитания. Например, : Здесь мы умножим число 5 на вычитание 10 и 3, то есть (10 — 3). Есть два случая выполнения распределения умножения над вычитанием. Случай 1: В первом случае мы сначала вычтем числа. После этого вычитаемое число умножим на 7. Таким образом, 7 * (9 — 4) = 7 * (5) = 35 Случай 2: Во втором случае мы сначала решим скобку. Это означает, что мы сначала умножим каждое число на 7. Это можно назвать распределением 7, а после этого мы будем вычитать произведения. 7(9) — 7(4) = 63 — 28 = 35 Как видим, результат в обоих случаях одинаков. Мы также можем использовать распределительный закон сложения и вычитания для перезаписи выражений для различных целей. Распределительное право отделаБольшое число можно разделить на более мелкие множители, разбив эти числа с помощью закона распределения. Разберемся в этом на примере, который описывается так: Пример: В этом примере мы должны разделить 84 на 6. Решение: Число 84 можно записать как 60 + 24. Следовательно, 84/6 можно записать как .(60 + 24) / 6 Теперь мы применим операцию деления распределения к каждому фактору в приведенной выше скобке, и тогда мы получим следующее: (60/6) + (24/6) = 10 + 4 = 14 Примеры закона о распределении:Существуют различные примеры закона распределения, которые описываются следующим образом: Пример 1: В этом примере мы должны решить выражение 4 * (2x 4 + 7x) с помощью закона распределения. Решение: Согласно распределительному закону: X * (Y + Z) = XY + XZ После расстановки значений получим следующие 4 * (2x 4 + 7x) = 4 * 2x 4 + 4 * 7x = 8x 4 + 28x Пример 2: В этом примере мы должны решить выражение 4 * (8xy + 12yx) с помощью закона распределения. Решение: Согласно распределительному закону: X * (Y + Z) = XY + XZ После подстановки значений получим следующее 4 * (8xy + 12yx) = 4 * 8xy + 4 * 12yx = 32xy + 48xy = 80xy Пример 3: В этом примере мы должны решить выражение 5 * (20 — 8) с помощью закона распределения. Решение: Согласно распределительному закону: Х * (Y — Z) = XY — XZ После подстановки значений получим следующее 5 * (20 — 8) = 5 * 20 — 5 * 8 = 100 — 40 = 60 Пример 4: В этом примере мы должны решить выражение 6x * (x 3 + у) с помощью распределительного закона. Решение: Согласно распределительному закону: X * (Y + Z) = XY + XZ После подстановки значений получим следующее 6х * (х 3 + у) = 6х * х 3 + 6х * у = 6x 4 + 6xy Почему не деление и умножениеМы не можем выполнить распределительный закон умножения над делением и умножением. Теперь разберемся в этом с помощью некоторых примеров, которые описываются следующим образом: Распределение закона умножения над умножением Предположим, что есть три целых числа 5, 9 и 3. Теперь предположим, что мы можем применить распределительный закон к умножению. Таким образом, это условие должно выполняться: Х (У * Z) = ХУ * ХZ Решим это выражение, сначала перемножив числа в скобках, а затем умножив умноженное число на 5. Таким образом, мы получим следующее: 5 (4 * 8) = 5 * 32 = 160 Теперь мы сначала решим скобку. (5*4)*(5*8) = 20*40 = 800 Как мы видим, оба результата не совпадают. Таким образом, доказано, что распределительный закон умножения не может быть применен к умножению. Распределительный закон умножения по делению Предположим, что есть три целых числа 5, 9 и 3. Теперь предположим, что мы можем применить закон распределения к делению. Таким образом, это условие должно выполняться: Х (Y/Z) = XY/XZ Решим это выражение, сначала разделив числа, а затем умножив разделенное число на 5. Таким образом, мы получим следующее: 5 (9/3) = 5*3 = 15 Теперь мы сначала решим скобку. Это означает, что мы умножим каждое число на 5. После этого мы выполним операцию деления. (5*9)/(5*3) = 45/15 = 3 Как мы видим, оба результата не совпадают. Таким образом, доказано, что распределительный закон умножения над делением и умножением не может быть применен. Следующая темаДоказательство от противоречия в дискретной математике ← предыдущая следующий → |
Распределительное свойство
Умножение — одна из четырех операционных функций математики, остальные три — сложение, вычитание и деление. И студенты, изучающие математику, должны понимать все аспекты этой операционной функции. Теперь, переходя к свойствам, есть три основных типа свойств числа: коммутативное, которое может быть достигнуто с помощью операций сложения и умножения, затем есть ассоциативное свойство, которое имеет дело с бинарными функциями числа, а затем есть Распределительное свойство, также известное как распределительный закон умножения.
Понимание свойства распределения
Свойство распределения используется, когда вам нужно умножить заданное число на сумму двух чисел. В таких случаях вы обычно делаете, следуя правилу порядка операций, — сначала складываете числа, а затем умножаете их на заданное число. Например, если вам нужно умножить число 5 на сумму 10 + 5, то вы можете представить его таким образом, 5 (10 + 5), теперь по правилу порядка действий вы должны сначала найти сумма 10 + 5, которая становится 15, а затем вы должны умножить 15 на 5. Все решение может выглядеть так,
В таких случаях вы обычно делаете, следуя правилу порядка операций, — сначала складываете числа, а затем умножаете их на заданное число. Например, если вам нужно умножить число 5 на сумму 10 + 5, то вы можете представить его таким образом, 5 (10 + 5), теперь по правилу порядка действий вы должны сначала найти сумма 10 + 5, которая становится 15, а затем вы должны умножить 15 на 5. Все решение может выглядеть так,
5(10 + 5)
= 5(15)
= 75
Но согласно распределительному закону умножения вам нужно сначала распределить сумму, а затем умножить ее на заданное число, а затем вы должны добавить результаты обоих. Возьмем еще раз тот же пример, который был 5 (10 + 5). Теперь вам нужно сначала умножить 5 на 10, что равно 50, а затем умножить 5 на 5, ответ равен 25, теперь добавьте 50 и 25 вместе, у вас есть 75. Полное решение выглядит так:
5(10 + 5)
= 5(10) + 5(5)
= 50 + 25
= 75
Распределительное свойство может быть представлено в виде уравнения как:
Одна вещь, которую вы должны Имейте в виду, что распределительный закон умножения остается тем же, даже когда переменные внутри скобки суммы увеличиваются. То есть, если вопрос 5 (10 + 5 + 5), то правило остается тем же, оно выглядит так: 5 (10) + 5 (5) + 5 (5), что становится 50 + 25. + 25, и сумма становится 100.
То есть, если вопрос 5 (10 + 5 + 5), то правило остается тем же, оно выглядит так: 5 (10) + 5 (5) + 5 (5), что становится 50 + 25. + 25, и сумма становится 100.
Шаги, которые необходимо выполнить в Распределительной Собственности
Всегда лучше иметь краткое изложение шагов, чтобы еще лучше понять распределительный закон Умножения, и, следовательно, следующие шаги являются одними и теми же.
Самым первым шагом в свойстве Распределение является умножение числа, находящегося вне скобок или круглых скобок, на первое число, указанное внутри круглых скобок.
Теперь умножьте число, указанное вне скобок, на второе число, указанное в скобках.
Наконец, вы должны сложить оба результата.
Типы распределительных свойств
Наиболее широко используются три свойства чисел. Они коммутативны, ассоциативны и дистрибутивны. Распределительное свойство также известно как распределительный закон умножения. Распределительное свойство является наиболее часто используемым свойством в математике. Распределять означает, само название предполагает, что что-то делить.
Они коммутативны, ассоциативны и дистрибутивны. Распределительное свойство также известно как распределительный закон умножения. Распределительное свойство является наиболее часто используемым свойством в математике. Распределять означает, само название предполагает, что что-то делить.
Распределительное свойство означает деление заданных операций на числа так, чтобы уравнение стало легче решать. Итак, давайте изучим определение распределительного свойства, формулу распределительного свойства, пример распределительного свойства и распределительное свойство с переменными
Определение распределительного свойства
Распределительное свойство применяется к умножению числа на сумму или разность двух чисел, т.е. распределительное свойство справедливо для умножения над сложением и вычитанием.
Определение распределительного свойства просто гласит, что «умножение распределяется по сложению».
Например, возьмем уравнение
Формула распределения свойств
(Изображение будет загружено в ближайшее время)
Давайте разберемся с этой концепцией на примерах свойств распределения
Например, 3 ( 2 + 3) = 3 ( 2 + 3 ) 6) = 18
или
По распределительному праву
\ [3 (2 + 4) = 3 \ Times 2 + 3 \ Times 4 \]
= 6 + 12
= 18
ЗДЕСЬ. равномерно между 2 и 4. Мы замечаем, что независимо от того, следуем ли мы порядку операции или дистрибутивному закону, результат один и тот же.
Распределительное свойство с переменными
Закон распределительного свойства можно также использовать при умножении или делении алгебраических выражений, включающих вещественные числа и переменные, которые называются распределительным свойством с переменными.
Выражение может быть мономиальным, биномиальным или полиномиальным.
Вы можете умножить многочлен на моном, используя закон распределения, следующим образом:
Первый шаг — умножить внешний член на первый член в скобках.
Затем умножьте внешний член на второй член в скобках с заданной операцией между ними.
Теперь выполните данную операцию. 9{2}\]
Свойство распределения также позволяет нам упростить алгебраическое уравнение и найти значения неизвестных переменных.
Использование распределительного свойства для поиска значений неизвестных переменных
Умножение внешних членов на внутренние члены в скобках.

Затем объедините подобные термины.
Расположите члены так, чтобы переменные и константы стояли напротив знака равенства.
Решите уравнение и упростите его, чтобы получить неизвестные значения.
. = 8/4
x = 2
В математике распределительное свойство применяется к различным операциям, таким как
Распределительное свойство сложения
Распределительное свойство вычитания
Распределительное свойство умножения
Распределительное свойство деления
Распределительное свойство сложения Складываем два или более их числа
90. Распределительное свойство говорит нам, что сумма двух чисел, умноженная на третье число, равна сумме каждого сложения, умноженного на третье число. Распределительное свойство сложения представлено как
Распределительное свойство говорит нам, что сумма двух чисел, умноженная на третье число, равна сумме каждого сложения, умноженного на третье число. Распределительное свойство сложения представлено как\[(p + q) \times r = (p \times q) + (p \times q)\]
Распределительное свойство вычитания
Распределительное свойство вычитания такое же, как и распределительное свойство сложения. И представляется как:
\[(p — q) \times r = (p \times q) — (p \times q)\]
Распределительное свойство умножения
Когда мы хотим умножить любое число с суммой числа мы обычно сначала складываем числа, а затем умножаем на число.
Например, 6( 2+ 3) = 6(5) = 30
Но по закону распределительного свойства умножения мы сначала умножаем число на каждое слагаемое, а затем выполняем сложение произведений.

AS, 6 (2 + 3)
= \ [6 \ Times 2 + 6 \ Times 3 \]
= 12 + 18
= 30
3
= 30
333333. что результаты операций одинаковы.
Распределительное свойство деления
Деление больших чисел требует немного времени, поэтому распределительное свойство позволяет упростить задачу, разбивая эти числа на более мелкие множители, а затем распределяя операцию деления между ними.
Например, Divide 96 8
Решение: мы можем написать 96 = 80 + 16
(80 + 16) 8
Теперь Распределение Распределения. ,
( 80 ÷ 8) + (16 ÷ 8)
= 10 + 2
= 12
6
Давайте разберемся с этой концепцией на дополнительных примерах свойств распределения.
9{2} + 18ab \] Примеры решения = 32x + 16
Примеры решения = 32x + 16Время викторины
Применение закона о распределении
7A (5A + 2)
\ правило — Полный курс алгебры
Навыки
в
A L G E B R AСодержание | Дом
14
м ( а + б ) = мА + мб
«Чтобы умножить сумму на число,
умножьте каждый член суммы.»Это называется распределительным правилом. m умножает на , затем на умножается. Мы говорим, что мы «раздали» 90 644 m 90 645 на 90 644 90 645 и 90 644 b 90 645 .
(Сравните урок 9 арифметики.)
Пример 1. 2( x + y + z ) = 2 x + 2 y + 2 z .

Мы распределили 2 до x , y и z . Мы «размножились».
Example 2. 3 x 4 ( x 2 − 5 x + 1) = 3 x 6 − 15 x 5 + 3 x 4 .
То есть
3 x 4 · x 2 = 3 x 6 , Правило 1 степени 3 x 4 · −5 x = −15 x 5 , Правило знаков 3 x 4 · 1 = 3 x 4 . Всякий раз, когда степень x является множителем — 3 x 4 — это множитель — и он умножает степени x , то всегда добавляйте экспоненты.

Задача 1. −1( a − b + c − d )
Каков будет эффект умножения на -1?
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!Каждый знак изменится.
−1( a − b + c − d ) = − a + b − c + d
Отсюда следует, что мы можем менять все знаки в обеих частях уравнения .
Это уравнение
− x + а − б = с эквивалентно этому: x − а + б = − с . 
Теоретически мы умножили обе части на −1.
Задача 2. Умножить.
а) 5( x + 4) = 5 x + 20 б) 5( х — 4) = 5 х — 20 в) x ( x + 1) = x 2 + x г) 2 x (3 x 2 + 5 x − 6) = 6 x 3 + 10 x 2 − 12 x д) 3 x 2 (4 x 3 − 3 x 2 + 5 x − 8) = 12 x 5 − 9 x 4 + 15 x 3 − 24 x 2 е) −5 x 4 ( x 3 — 4 x 2 + 2 x — 6) = –5 4 x x — 6) = –5 4 x x — 6) = — 5 + 2 x — 6).  10 x 5 + 30 x 4
10 x 5 + 30 x 4 г) 2 x г ( x 2 − 3 x г + г 5 2) = 2 x 3 y — 6 x 2 y 2 + 2 x 4 + 2 x Y 3 44444444449 3 444 4. .
h) −4 x y 2 ( x 3 y − 6 x y 2 − 2 x + 3 y + 1)
= −4 x 4 y 3 + 24 x 2 y 4 + 8 x 2 y 2 − 12 x y 3 − 4 x у 2
Задача 3. Умножьте и упростите, то есть добавьте одинаковые члены.
a) 2(4 x + 5 y ) + 3(5 x − y ) = 8 x + 10 у + 15 x − 3 у = 23 x + 7 у б) 4(2 х — 1) — 5( х — 2) = 8 x — 4 — 5 x + 10 = 3 x + 6 c) 3 x (3 x − 2 y ) − 2 y ( x − y) = 9 x 2 − 6 xy − 2 yx + 2 y 2 = 9 x 2 − 8 xy + 2 y 2 г) x ( x 2 − 10 х + 25) — 5( х 2 — 10 х + 25) = х 3 − 10 х 2 + 25 х − 5 х 2 + 50 50 2 6445 х = x 3 − 15 x 2 + 75 x − 125 д) a ( a 2 − 2 ab + b 2 ) − b ( a 2 − 2 ab + b 2 ) = a 3 − 2 a 2 b + A B 2 — B A 2 + 2 A B 2 – 444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. 
= A 3 — 3 A 2 B + 3 A B 2 — B 2 — B 2 — B . Сумма по сумме
( a + b + c )( x + y + z )
Сначала распределите a на x , y и z .
Затем распределите b .
Затем раздайте c .
( a + b + c )( x + y + z )
= a x + a y + a z + b x + b y + b z + c x + c y + c z .
Задача 4. Умножьте ( p − q )( x − y + z ).
 Соблюдайте Правило знаков (Урок 4).
Соблюдайте Правило знаков (Урок 4).( p − q )( x − y + z ) = px − py + pz − qx + qy − qz
Пример 3. Умножить ( 90 644 x 90 645 − 2) ( 90 644 x 90 645 + 3). Упростите, добавив подобные термины.
Решение . Сначала распределите x , затем распределите −2:
( х — 2)( х + 3) = x · x + x · 3 − 2 · x − 2 · 8 = x 2 + 3 x − 2 x − 6 = х 2 + х — 6. Учащийся не должен писать первую строку выше, но должен быть в состоянии написать вторую строку —
x 2 + 3 x − 2 x − 6
— немедленно.

(В Уроке 15 мы увидим более искусный способ получить ответ.)
Следует избегать вертикального умножения, как это делается в арифметике. Возможно, все в порядке, когда алгебра является завершающим курсом, а учитель заинтересован только в том, чтобы студенты сдали тест, а навыки не являются проблемой. Но для студентов, которые продолжат заниматься исчислением, эта привычка будет трудно побороть. Учащийся никогда не увидит вертикальное умножение ни в одном тексте по математическому анализу или в любом тексте по физике, а ученику, привыкшему видеть вертикальное умножение, будет трудно читать эти тексты. Учитель, допускающий вертикальное умножение, не делает этим ученикам никакой пользы.
То же самое можно сказать и об обучении любому методу решения уравнений, кроме транспонирования, и общему методу обратных операций.
Задача 5. Умножить. Всегда упрощайте, добавляя похожие термины.
а) ( x + 5)( x + 2) = x 2 + 2 x + 5 x + 10 = x 2 + 7 x + 10 б) ( x + 5)( x − 2) = х 2 − 2 х + 5 х − 10 = x 2 + 3 x − 10 c) ( x − 5)( x − 2) = x 2 − 2 x − 5 x + 10 = х 2 − 7 х + 10 d) (2 x − 1)( x + 4) = 2 х 2 + 8 х — х — 4 = 2 x 2 + 7 x − 4 e) (3 x + 2)(4 x − 5) = 12 x 2 − 15 x + 8 x − 10 = 12 x 2 − 7 x − 10 Задача 6.
 Умножить.
Умножить.а) ( x − 5) 2 = ( х — 5) ( х — 5) = x 2 − 5 x − 5 x + 25 = х 2 − 10 x + 25. б) ( x − 5)( x + 5) = x 2 + 5 x − 5 x − 25 = x 2 − 25. Пример 4. ( x − 4)( x 2 + 3 х — 10) = x 3 + 3 x 2 − 10 x − 4 x 2 − 12 х + 40 = x 3 − x 2 − 22 х + 40. 
Обратите внимание: При распространении −4 мы предусмотрели одинаковые термины, выровняв их. Однако это не является строго необходимым.
Задача 7. Умножить.
а) ( x + 2)( x 2 + 4 x − 5) = x 3 + 4 x 2 − 5 x + 2 x 2 + 8 х — 10 = x 3 + 6 x 2 + 3 х — 10 Примечание: Эффект умножения на x заключается в простом увеличении каждого показателя степени на 1.
b) ( x − 3)( x 2 − 6 x + 9) = x 3 − 6 x 2 + 9 х − 3 x 2 + 18 х — 27 = x 3 − 9 x 2 + 27 х — 27 c) (3 x − 4)( x 2 − 7 x − 2) = 3 x 3 − 21 x 2 − 6 x − 4 x 2 + 28 х + 8 = 3 x 3 − 25 x 2 + 22 х + 8 d) ( x − 1)( x 3 + x 2 7 + x2 + 8) = x 4 + x 3 + х 2 + х − x 3 – х 2 – х – 1 = х 4 − 1 Примечание: Умножение на −1 просто меняет знаки.




 Я. Виленкин,
Я. Виленкин,
 Создать условия для того, чтобы учащиеся могли применять их на
Создать условия для того, чтобы учащиеся могли применять их на




 Затем команды обмениваются листами с
Затем команды обмениваются листами с Уравнения и ответы высвечиваются на экране.
Уравнения и ответы высвечиваются на экране.
 Рефлексия: осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения , как они были устранены, и что чувствовал ученик при этом.
Рефлексия: осознание учеником деятельности: того как, каким способом получен результат, какие при этом встречались затруднения , как они были устранены, и что чувствовал ученик при этом. Выставляет
Выставляет С, Сологуб В.А.
С, Сологуб В.А.
 Работа в парах, группах по 8-9 человек помогает развивать коммуникативные качества учащихся, умение высказывать свое мнение, выслушивать способы решения других и выбирать наиболее рациональные из них.
Работа в парах, группах по 8-9 человек помогает развивать коммуникативные качества учащихся, умение высказывать свое мнение, выслушивать способы решения других и выбирать наиболее рациональные из них. Развитие находчивости, активности при решении математических задач, способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Развитие находчивости, активности при решении математических задач, способности к эмоциональному восприятию математических объектов, задач, решений, рассуждений
 А. Коменский
А. Коменский


 Давайте составим буквенное выражение для задачи, для этого разные числа заменим разными буквами.
Давайте составим буквенное выражение для задачи, для этого разные числа заменим разными буквами.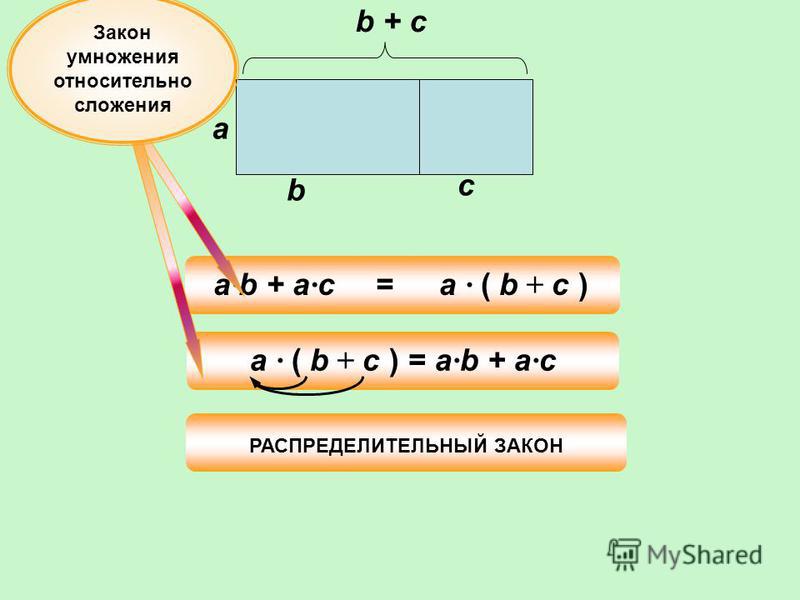




 edu.ru/catalog/rubr/608887c4-68f4-410f-bbd4-618ad7929e22/113934/?interface=pupil&class=47&subject=16
edu.ru/catalog/rubr/608887c4-68f4-410f-bbd4-618ad7929e22/113934/?interface=pupil&class=47&subject=16
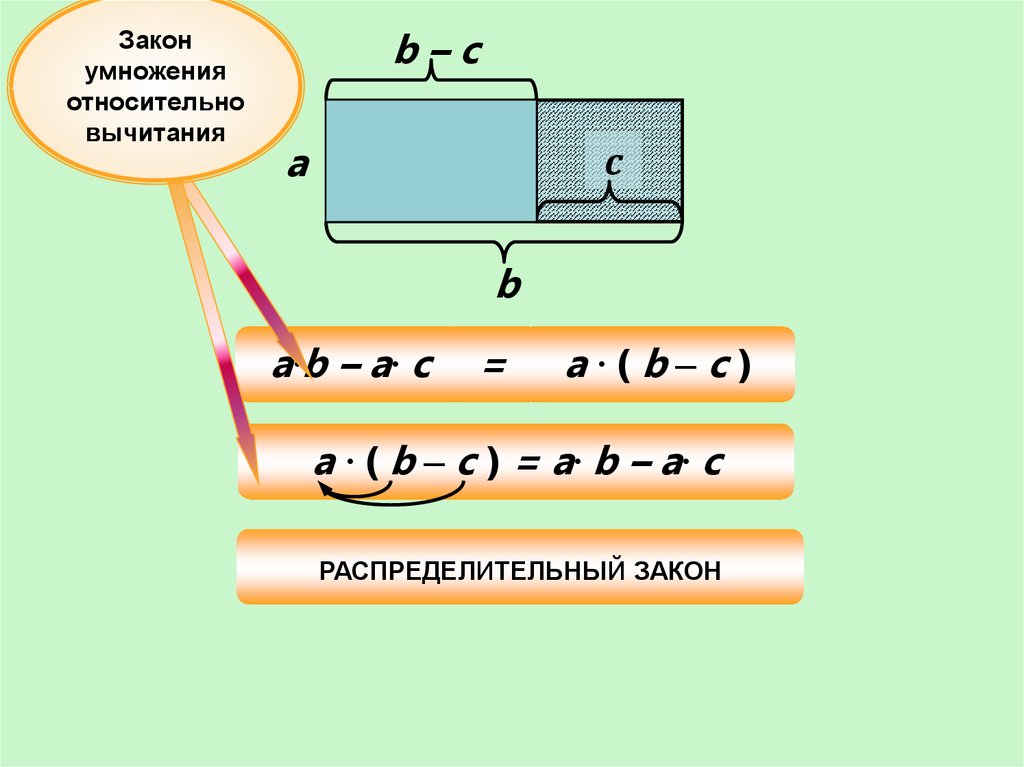
 В символической форме распределительный закон можно представить следующим образом:
В символической форме распределительный закон можно представить следующим образом:
 Например: Здесь мы умножим число 7 на сумму 9 + 4.
Например: Здесь мы умножим число 7 на сумму 9 + 4. В результатах мы увидим, что результаты обеих сторон одинаковы.
В результатах мы увидим, что результаты обеих сторон одинаковы. Когда у нас есть случай, когда мы умножаем число на сумму, это означает, что мы можем сначала выполнить сложение, а затем умножение. Мы также можем сначала умножить каждое слагаемое, а затем добавить произведения. Тот же процесс можно применить и для вычитания. В каждом случае мы воздействуем внешним множителем на каждое значение, содержащееся в скобках, так что перед сложением или вычитанием умножение может происходить с каждым значением.
Когда у нас есть случай, когда мы умножаем число на сумму, это означает, что мы можем сначала выполнить сложение, а затем умножение. Мы также можем сначала умножить каждое слагаемое, а затем добавить произведения. Тот же процесс можно применить и для вычитания. В каждом случае мы воздействуем внешним множителем на каждое значение, содержащееся в скобках, так что перед сложением или вычитанием умножение может происходить с каждым значением.
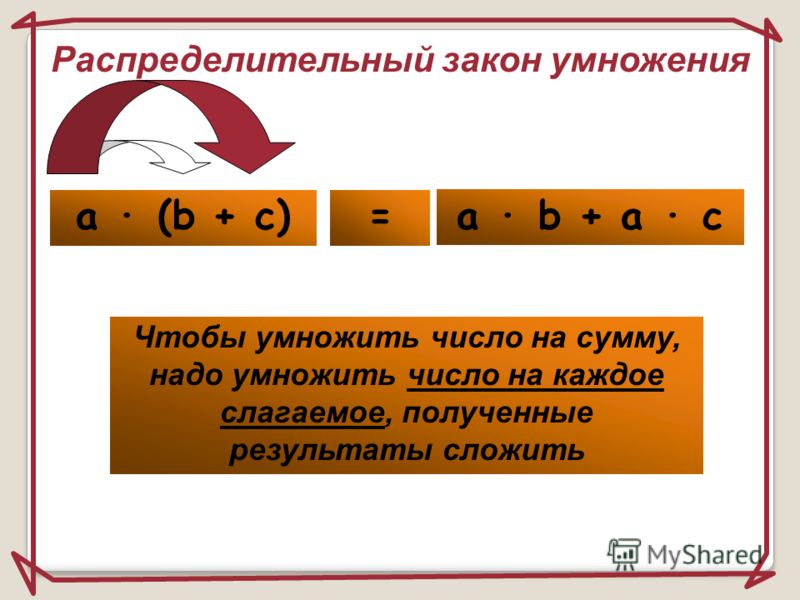
 Это означает, что мы будем умножать каждое число на 5. После этого мы выполним операцию умножения.
Это означает, что мы будем умножать каждое число на 5. После этого мы выполним операцию умножения.

 Распределительное свойство говорит нам, что сумма двух чисел, умноженная на третье число, равна сумме каждого сложения, умноженного на третье число. Распределительное свойство сложения представлено как
Распределительное свойство говорит нам, что сумма двух чисел, умноженная на третье число, равна сумме каждого сложения, умноженного на третье число. Распределительное свойство сложения представлено как
 Примеры решения = 32x + 16
Примеры решения = 32x + 16


 10 x 5 + 30 x 4
10 x 5 + 30 x 4 
 Соблюдайте Правило знаков (Урок 4).
Соблюдайте Правило знаков (Урок 4).
 Умножить.
Умножить.
