Распределительное переместительное сочетательное свойства: Переместительное свойство умножения – определение (5 класс, математика)

Содержание

Сочетательное и распределительное свойства умножения

Представим себе такую историю…

– 3 умножить на 2 и умножить на 12… так, так, так… Получается 72, – считал Саша.

– Саша, что ты там считаешь? – спросил у друга Паша.

– Папа привёз мне 3 коробки с шоколадными плитками, в каждой коробке по 2 плитки, а в каждой плитке по 12 долек. Мне стало так интересно, это же сколько шоколадных долек я съем. Представляешь, получилось 72 шоколадные дольки, – радовался Саша.

– Здорово! – сказал Паша. – Но я бы посчитал дольки по-другому. Смотри, у тебя есть 3 коробки, а в каждой коробке 2 шоколадные плитки по 12 шоколадных долек каждая… Посчитаем… тоже получается, что у тебя 72 шоколадные дольки.

– Как же это так? – задумался Саша. – Мы с тобой считали совсем по-разному, а количество долек получилось одинаковое. Разве может быть такое?

– Не знаю, – ответил Паша, – но точно знаю, кто может нам помочь!

– Ребята, прежде чем я вам объясню, почему у вас получилось одинаковое количество шоколадных долек, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– А теперь вернёмся к вашему вопросу, – продолжил Электроша. – Чтобы посчитать количество шоколадных долек, Саша 3 умножил на 2 и тем самым выяснил сколько шоколадных плиток ему привёз папа. А так как в каждой шоколадной плитке по 12 долек, то Саша полученное произведение умножил на 12. И получил, что всего у него 72 шоколадные дольки.

– Точно, Электроша! Я так и считал, – подтвердил Саша.

– В свою очередь, Паша решил посчитать количество шоколадных долек другим способом. Он 3 умножил на произведение 2 и 12, так как в трёх коробках будет по 2 умножить на 12 шоколадных долек. И тоже получил, что всего 72 шоколадные дольки.

– Да, именно таким способом я считал, – сказал Паша.

– Вы заметили, что способы подсчёта разные, а в результате получается одно и то же число – 72, – продолжил Электроша. – А почему так случилось? Да потому, что оба способа подсчёта верны и показывают нам очередное свойство умножения, которое называется сочетательное свойство умножения.

Запомните! Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.

В буквенном виде это свойство записывают так: .

Сочетательное свойство умножения разрешает в произведении ставить скобки и объединять множители как удобнее.

– Вот, например, давайте найдём значение выражения: , – предложил ребятам Электроша.

– Электроша, это сложный пример, – задумались мальчишки, – в уме нам такой не решить. Сначала нужно умножить 737 на 25, а потом ещё и на 4. Без калькулятора тут нам не обойтись.

– Ребята, пример кажется сложным только на первый взгляд, – подбодрил ребят Электроша. – Давайте применим сочетательное свойство умножения и возьмём в скобки множители 25 и 4. Смотрите, произведение 25 и 4 совсем не сложно найти в уме, оно равно 100. Останется посчитать, чему будет равно произведение 737 и 100.

– Получится 73 700, – сказали мальчишки.

– Молодцы! – похвалил ребят Электроша. – Вы заметили, как быстро мы справились с решением примера?

– Да… мы решили его за 5 секунд, – радовались мальчишки.

– Польза от сочетательного свойства умножения будет ещё больше, если применить его вместе с переместительным свойством. И помните, прежде чем начать вычисления, нужно всегда подумать, как это сделать проще!

– Давайте решим вот такой пример: .

– Сначала воспользуемся переместительным свойством умножения и переставим местами множители 5 и 824, – начал Паша. – А потом применим сочетательное свойство умножения и заключим в скобки множители 5 и 20.

– 5 умноженное на 20 равно 100, – продолжил Саша. – А теперь 824 умножим на 100. Получим 82 400.

– Молодцы! – похвалил ребят Электроша. – А теперь давайте решим вот такую задачку: Саша за 1 минуту может решить 3 примера, а Паша за это же время может решить 4 примера. Сколько примеров решат за 5 минут Саша и Паша вместе?

– Электроша, это же задача про нас! – обрадовались ребята.

– В задаче сказано, что я могу решить 3 примера за 1 минуту, – начал Саша. – Значит, за 5 минут я могу решить 5 умножить на 3 примеров.

– А я за 1 минуту могу решить 4 примера, – продолжил Паша. – Тогда за 5 минут я смогу решить 5 умножить на 4 примеров.

– Осталось сложить наши решённые примеры, – сказали мальчишки. – И получим, что за 5 минут мы вместе можем решить 35 примеров.

– Молодцы! – похвалил ребят Электроша. – Но эту же задачу можно было решить и другим способом. Смотрите, за 1 минуту вы можете вместе решить 3 + 4 примеров. Тогда за 5 минут вы вместе решите 5 умноженное на сумму 3 и 4. Посчитаем… тоже получаем 35 примеров.

Посмотрите, правые части наших равенств равны, значит, будут равны и левые части. Получаем равенство, которое иллюстрирует распределительное свойство умножения относительно сложения.

Запомните! Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое из слагаемых и полученные произведения сложить.

В буквенном виде это свойство записывают так: .

Из распределительного свойства умножения относительно сложения следует, что это равенство справедливо и справа налево: .

Кстати, распределительное свойство умножения относительно сложения справедливо для трёх и более слагаемых.

– Напомните мне, какую формулу мы применяем для нахождения периметра прямоугольника, – спросил у ребят Электроша.

– , – ответили мальчишки.

– Молодцы! Применяя распределительное свойство умножения относительно сложения, формулу для нахождения периметра прямоугольника можно записать и в таком виде: 𝑃=2𝑎+2𝑏=2(𝑎+𝑏).

– Распределительное свойство умножения действует и относительно вычитания, – продолжил Электроша.

Запомните! Чтобы число умножить на разность двух чисел, можно это число умножить на уменьшаемое и вычитаемое и из первого произведения вычесть второе.

В буквенном виде это свойство записывают так: .

Равенства справедливы для всех натуральных чисел при или .

– Давайте решим вот такой пример: , – предложил Электроша.

– Электроша, но тут какие-то сложные вычисления получаются, – расстроился Саша.

– Тут совсем нет ничего сложного, – подбодрил Сашу Электроша. – Применяя распределительное свойство умножения относительно вычитания, мы можем записать это выражение как 4 умножить на 250 минус 4 умножить на 25. Ну а теперь вы можете вычислить?

– Да, – обрадовались мальчишки. – Первое произведение равно 1000, второе – 100. Тогда разность произведений будет равна 900.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.

Задание первое: вычислите наиболее удобным способом:

а) ;

б) ;

в) .

Решение: первое выражение: . Применим переместительное свойство умножения и поменяем местами второй и третий множители. Затем применим сочетательное свойство умножения и заключим в скобки первый и второй множители.

Тогда в скобках получим 10. Осталось 10 умножить на 497. В результате получим 4970.

Следующее выражение: . Применим распределительное свойство умножения относительно сложения (справа налево). Получим произведение 209 и суммы чисел 19 и 81. В скобках получаем 100. 209 умножим на 100. В результате получим 20 900.

И последнее выражение: . Применим распределительное свойство умножения относительно вычитания. Получим произведение 28 и разности чисел 160 и 60. В скобках получаем 100. Тогда 28 умножим на 100. В результате получим 2800.

переместительное, сочетательное и распределительное — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7

Содержание

Свойства умножения: переместительное, сочетательное и распределительное

Переместительное свойство умножения

От перестановки сомножителей местами произведение не меняется.

Следовательно, для любых чисел a и b верно равенство:

a · b = b · a,

выражающее переместительное свойство умножения.

Примеры:

6 · 7 = 7 · 6 = 42;

4 · 2 · 3 = 3 · 2 · 4 = 24.

Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.

Сочетательное свойство умножения

Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.

Следовательно, для любых чисел a, b и c верно равенство:

a · b · c = (a · b) · c = a · (b · c),

выражающее сочетательное свойство умножения

Пример:

3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30

или

3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.

Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:

25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.

В данном случае можно было вычислить всё последовательно:

25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,

но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.

Распределительное свойство умножения

Сначала рассмотрим распределительное свойство умножения относительно сложения:

Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Следовательно, для любых чисел a

, b и m верно равенство:

m · (a + b) = m · a + m · b,

выражающее распределительное свойство умножения.

Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.

Следовательно, для любых чисел a, b и m верно равенство:

(a + b) · m = a · m + b · m.

Теперь рассмотрим распределительное свойство умножения относительно вычитания:

Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

m · (a — b) = m · a — m · b.

Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:

Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.

Следовательно, для любых чисел a, b и m верно равенство:

(a — b) · m = a · m — b · m.

Переход от умножения:

m · (a + b) и m · (a — b)

соответственно к сложению и вычитанию:

m · a + m · b и m · a — m · b

называется раскрытием скобок.

Переход от сложения и вычитания:

m · a + m · b и m · a — m · b

к умножению:

m · (a + b) и m · (a — b)

называется вынесением общего множителя за скобки.

Сочетательное и распределительное свойства умножения

Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.

Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.

Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).

Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).

Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.

В буквенном виде это свойство записывают так:

(ab)c = a(bc)

Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.

Например, верны равенства:

abc = cba,

17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).

На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.

Подсчитаем количество квадратов со стороной 1 см двумя способами.

С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).

Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.

Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.

В буквенном виде это свойство записывают так:

a(b + c) = ab + ac

Из распределительного свойства умножения относительно сложения следует, что

ab + ac = a(b + c).

Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:

P = 2(a + b).

Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:

a(m + n + p + q) = am + an + ap + aq.

Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то

a(b − c) = ab − ac

Пример 1. Вычислите удобным способом:

1) 25 * 867 * 4;

2) 329 * 75 + 329 * 246.

Решение.

1) Используем переместительное, а затме сочетательное свойства умножения:

25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.

2) Имеем:

329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.

Пример 2. Упростите выражение:

1) 4a * 3b;

2) 18m − 13m.

Решение.

1) Используя переместительное и сочетательное свойства умножения, получаем:

4a * 3b = (4 * 3) * ab = 12ab.

2) Используя распределительное свойство умножения относительно вычитания, получаем:

18m − 13m = m(18 − 13) = m * 5 = 5m.

Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.

Решение.

Согласно распределительному свойству умножения относительно сложения имеем:

5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.

Такое преобразование называют раскрытием скобок.

Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.

Решение. Имеем:

125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.

Пример 5. Выполните умножение: 3 сут 18 ч * 6.

Решение. Имеем:

3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.

При решении примера было использовано распределительное свойство умножения относительно сложения:

3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.

Сочетательное и распределительное свойства умножения

Представим себе такую историю…

– 3 умножить на 2 и умножить на 12… так, так, так… Получается 72, – считал Саша.

– Саша, что ты там считаешь? – спросил у друга Паша.

– Не знаю, – ответил Паша, – но точно знаю, кто может нам помочь!

– Давайте сверимся! Посмотрите, что у вас должно было получиться!

– Точно, Электроша! Я так и считал, – подтвердил Саша.

– Да, именно таким способом я считал, – сказал Паша.

В буквенном виде это свойство записывают так: .

– Вот, например, давайте найдём значение выражения: , – предложил ребятам Электроша.

– Получится 73 700, – сказали мальчишки.

– Молодцы! – похвалил ребят Электроша. – Вы заметили, как быстро мы справились с решением примера?

– Да… мы решили его за 5 секунд, – радовались мальчишки.

– Давайте решим вот такой пример: .

– 5 умноженное на 20 равно 100, – продолжил Саша. – А теперь 824 умножим на 100. Получим 82 400.

– Электроша, это же задача про нас! – обрадовались ребята.

В буквенном виде это свойство записывают так: .

Кстати, распределительное свойство умножения относительно сложения справедливо для трёх и более слагаемых.

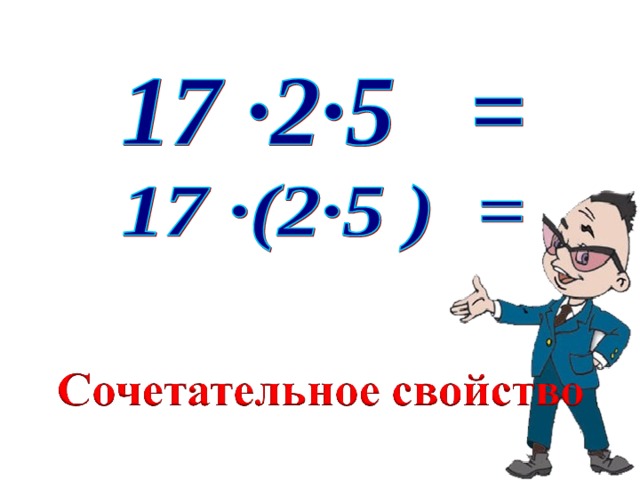
– , – ответили мальчишки.

– Распределительное свойство умножения действует и относительно вычитания, – продолжил Электроша.

В буквенном виде это свойство записывают так: . Равенства справедливы для всех натуральных чисел при или .

– Давайте решим вот такой пример: , – предложил Электроша.

– Электроша, но тут какие-то сложные вычисления получаются, – расстроился Саша.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним задание.

Задание первое: вычислите наиболее удобным способом:

а) ;

б) ;

в) .

« Переместительное, сочетательное и распределительное свойства сложения и умножения». ( 5 класс)

Тема: « Переместительное, сочетательное и распределительное свойства сложения и умножения». ФИ___________________________

1 вариант

Сформулируй и запиши распределительное свойство относительно сложения.

_________________________________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________

Запиши.

Сочетательное свойство сложения_______________________________

Переместительное свойство умножения__________________________

Запишите выражение и вычислите, равное данному, используя сочетательное

и переместительное свойства сложения и умножения

(68 + 36) + 44= ___________________________________________________________________

(48 + 27) + 3= _____________________________________________________________________

(8 ·5) · 2=_________________________________________________________________________

(30 ·9)· 3= _________________________________________________________________________

2·31·4·50·25=____________________________________________________________

Вычислите наиболее удобным способом:

28 · 160 — 28 ·60= ________________________________________________________

_______________________________________________________________________

209 · 19 + 209 · 81 = ______________________________________________________

_______________________________________________________________________

405 • 82 + 405 • 18 =______________________________________________________

_______________________________________________________________________

497 • 38 – 496 • 38 = ______________________________________________________

_______________________________________________________________________

479 ∙ 28 + 479 ∙ 72=_______________________________________________________

_______________________________________________________________________

Тема: « Переместительное, сочетательное и распределительное свойства сложения и умножения». ФИ_________________________

Вариант

Сформулируй и запиши распределительное свойство относительно вычитания.

_________________________________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________

Запиши.

Сочетательное свойство умножения___________________________

Переместительное свойство сложения_________________________

Запишите выражение и вычислите , равное данному, используя сочетательное переместительное свойства сложения и умножения.

(7 ·2) ·3= ___________________________________________

(2 ·46)·5= ________________________________________

(1700 + 624) + 376= ______________________________

(254+86) + 14= _____________________________________

4·27·25·2·50=________________________________________

Вычислите наиболее удобным способом:

32·45 — 25·32 =___________________________________________________________

_______________________________________________________________________

27·413 + 413·73 =_________________________________________________________

_______________________________________________________________________

344 • 92 + 344 • 108 =_____________________________________________________

_______________________________________________________________________

13 • 48 – 35 • 13 = ________________________________________________________

_______________________________________________________________________

657 ∙ 29 – 557 ∙ 29=_______________________________________________________

_______________________________________________________________________

Ответы:

1 вариант

Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
Сочетательное свойство сложения: (a+b)+c=a+(b+c)

Переместительное свойство умножения: a·b=b·a

(68 + 36) + 44=68 + (36 + 44)= 68+80=148

(48 + 27) + 3=48 + (27+ 3)=48+30=78

(8 ·5) · 2=8 ·(5 · 2)=8·10=80

(30 ·9)· 3=(30 ·3)· 9=90·9=810

28 · 160 — 28 · 60 = (160-60)·28=100·28=2800

209 · 19 + 209 · 81 = (19+81)·209=100·209=20900

405 • 82 + 405 • 18 =(82+18)·405=100·405=40500

497 • 38 – 496 • 38 =(497-496)·38=1·38=38

479 ∙ 28 + 479 ∙ 72=(28+72)·479=100·479=47900

5*. 318+264=582 495-126=369 108·7=756

Вариант

Чтобы умножить число на разность двух чисел, можно умножить это число на уменьшаемое и на вычитаемое, и из первого произведения вычесть второе.
Сочетательное свойство умножения: (a·b) · c=a· (b·c)

Переместительное свойство сложения: a+b=b+a

(7 ·2) ·3= 7·(2·3)=7·6=56

(2 ·46)·5= (2 ·5) ·46=10·46=460

(1700 + 624) + 376= 1700+(624+376)=1700+1000=2700

(254+86) + 14= 254+(86 + 14)=254+100=354

4·27·25·2·50=(4·25) · (2·50)·31=100·100·31=310000

32·45 — 25·32 =(45-25) · 32=20·32=640

27·413 + 413·73 =(27+73) ·413=100·413=41300

344 • 92 + 344 • 108 =(92+108) ·344=200·344=68800

13 • 48 – 35 • 13 =(48-35) ·13=13·13=13²=169

657 ∙ 29 – 557 ∙ 29=(657-557) ·29=100·29=2900

5*. 3785244+8424632=12209876 28656545-252934=28403611

Задание

балы

Критерии оценивания:

Балы

менее 6

от 6 до 8

от 9 до 10

от 11 до 12

оценка

Сочетательное и распределительное свойства умножения

Ключевые слова: алгоритм, умножение, математическая задача, переместительное свойство

Учебник: Математика 5 класс. Учебник для учащихся общеобразовательных организаций. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.

Тип урока: урок применения и закрепления знаний.

Целевые установки на достижение результата:

личностные: развивать навыки самостоятельной работы, ответственного отношения к учению, готовности к саморазвитию, умение контролировать процесс и результат учебной и математической деятельности;

метапредметные: учить использовать приобретенные знания в практической деятельности, действовать по алгоритму, видеть математическую задачу в окружающей жизни, строить логические рассуждения и делать выводы;

предметные: закрепить навыки умножения натуральных чисел и применения сочетательного и переместительного свойств умножения натуральных чисел, записывать эти свойства в виде формул, углубит навыки решения задач.

Формы организации работы: фронтальная, парная, индивидуальная.

Оборудование: компьютер, проектор, учебник.

Этапы урока

1 этап. Организация. (3 мин.)

Приветствие, проверка готовности к уроку. Эмоциональный настрой детей на учебную деятельность. Учащиеся сдают тетради с домашними работами.

2 этап. Устный опрос (индивидуальный). (4 мин.)

— Сформулируйте сочетательное свойство умножения. Записать на доске буквенную форму.

— Сформулируйте распределительное свойство умножения. Записать на доске буквенную форму.

3 этап. Закрепление теории и актуализация знаний. (Презентация. Слайд 2–6). (13 мин.)

Дополнительное прочтение/запись свойств умножения, разбор примеров для подтверждения достоверности данный свойств. Приведение жизненных примеров из личного опыта учащихся.

4 этап. Физкультминутка. (1 мин.)

5 этап. Закрепление теории практикой. (19 мин.)

Работа в парах (слайд 7). Ребята выполняют задания, после выполнения меняются тетрадями для проверки соседа. (9 мин.).

Индивидуальная работа. Номера в учебнике – 430, 432. Стр. 118. (10 мин.).

6 этап. Подведение итогов. Рефлексия. Запись домашнего задания. (5 мин.)

Ученики записывают в дневник домашнее задание. На отдельных листочках записывают продолжения высказываний (слайд 8) и оставляют на партах.

Свойства умножения и деления. Распределительное и переместительное свойство

Свойства умножения

Умножение — арифметическое действие, в котором участвуют два аргумента: множимый и множитель. Результат их умножения называется произведением.

Узнаем, какие бывают свойства умножения и как их применять.

Переместительное свойство умножения

От перестановки мест множителей произведение не меняется.

То есть, для любых чисел a и b верно равенство: a * b = b * a.

Это свойство можно применять к произведениям, в которых больше двух множителей.

Примеры:

6 * 5 = 5 * 6 = 30;
4 * 2 * 3 = 3 * 2 * 4 = 24.

Сочетательное свойство умножения

Произведение трех и более множителей не изменится, если какую-то группу множителей заменить их произведением.

То есть, для любых чисел a, b и c верно равенство: a * b * c = (a * b) * c = a * (b * c).

Пример:

3 * 2 * 5 = 3 * (2 * 5) = 3 * 10 = 30

или

3 * 2 * 5 = (3 * 2) * 5 = 6 * 5 = 30.

Сочетательное свойство можно использовать, чтобы упростить вычисления при умножении. Например: 25 * 15 * 4 = (25 * 4) * 15 = 100 * 15 = 1500.

Если не применять сочетательное свойство и вычислять последовательно, решение будет значительно сложнее: 25 * 15 * 4 = (25 * 15) * 4 = 375 * 4 = 1500.

Распределительное свойство умножения относительно сложения

Чтобы умножить сумму на число, нужно умножить на это число каждое слагаемое и сложить полученные результаты.

То есть, для любых чисел a, b и c верно равенство: (a + b) * c = a * c + b * c.

Это свойство работает с любым количеством слагаемых: (a + b + с + d) * k = a * k + b * k + c * k + d * k.

В обратную сторону распределительное свойство умножения относительно сложения звучит так:

Чтобы число умножить на сумму чисел, нужно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.

Распределительное свойство умножения относительно вычитания

Чтобы умножить разность на число, нужно умножить на это число сначала уменьшаемое, затем вычитаемое, и из первого произведения вычесть второе.

То есть, для любых чисел a, b и c верно равенство: (a − b) * c = a * c − b * c.

В обратную сторону распределительное свойство умножения относительно вычитания звучит так:

Чтобы число умножить на разность чисел, нужно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.

Свойство нуля при умножении

Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

То есть, для любых чисел a, b и c верно равенство:
0 * a * b * c = 0.

Свойство единицы при умножении

Если умножить любое целое число на единицу, то в результате получится это же число.

То есть, умножение на единицу не изменяет умножаемое число: a * 1 = a.

Свойства деления

Деление — арифметическое действие обратное умножению. В результате деления получается число (частное), которое при умножении на делитель дает делимое.

Основные свойства деления целых чисел

Деление на нуль невозможно.
Деление нуля на число: 0 : a = 0.
Деление равных чисел: a : a = 1.
Деление на единицу: a : 1 = a.
Для деления переместительное свойства не выполняется: a : b ≠ b : a.
Деление суммы и разности на число: (a ± b) : c = (a : c) ± (b : c).
Деление произведения на число:
(a * b) : c = (a : c) * b, если a делится на c;
(a * b) : c = a * (b : с), если b делится на c;
(a * b) : c = a * (b : с) = (a : c) * b, если a и b делятся на c.
Деление числа на произведение:
a : (b * c) = (a : b) * (1 : c) = (a : c) * (1 : b).

И еще одно важное свойство деления, которое проходят в 5 классе:

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

В буквенной форме это свойство выглядит так: a : b = (a * k) : (b * k), где k — любое натуральное число.

Применим свойства деления на практике.

Пример 1

Мама купила 6 кг конфет и разложила их в три пакета. Сколько килограммов конфет в каждом пакете?

Как решаем:

Так как в каждом пакете одинаковое количество конфет, разделим 6 кг на три равные части: 6 : 3 = 2. Значит в каждом пакете по 2 кг конфет.

Ответ: 2 кг

Пример 2

Вычислить: 500 * (100 : 5).

Как решаем: 500 * (100 : 5) = (500 * 100) : 5 = 50000 : 5 = 10000.

Ответ: 500 * (100 : 5) = 10000.

Пример 3

Упростить выражение: 27a – 16a.

Как решаем: 27a – 16a = a * 27 – a * 16 = a * (27 — 16) = a * 11 = 11a.

Ответ: 11a.

Свойства умножения и деления помогают упрощать выражения. То есть, если запомнить эти свойства и научиться их применять, то решать задачки можно быстрее.

Развить математическое мышление помогут интерактивные уроки в Skysmart. Ученики занимаются по индивидуальной программе и в комфортном темпе. А внимательные учителя помогают подготовиться к контрольной и найти ответ на любой — даже самый неловкий — вопрос.

Приходите на бесплатный вводный урок вместе с ребенком: познакомимся, порешаем задачки и вдохновим на учебу!

Умножение натуральных чисел: свойства, примеры

Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.

Переместительное свойство умножения натуральных чисел

Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:

Переместительный закон умножения

От перемены мест множителей произведение не меняется.

В буквенном виде переместительное свойство записывается так: a·b=b·a

a и b — любые натуральные числа.

Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2·6. По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2·6=2+2+2+2+2+2=12. Теперь поменяем множители местами. 6·2=6+6=12. Очевидно, переместительный закон выполняется.

На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.

Сочетательное свойство умножения натуральных чисел

Второе название для сочетательного свойства умножения — ассоциативный закон, или ассоциативное свойство. Вот его формулировка.

Сочетательный закон умножения

Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c.

Приведем формулировку в буквенном виде:

a·b·c=a·b·c

a, b, c — любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.

Для наглядности приведем пример. Сначала вычислим значение 4·3·2.

4·3·2=4·6=4+4+4+4+4+4=24

Теперь переставим скобки и вычислим значение 4·3·2.

4·3·2=12·2=12+12=24

4·3·2=4·3·2

Как видим, теория совпадает с практикой, и свойство справедливо.

Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.

Распределительное свойство относительно умножения

Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.

Распределительное свойство умножения относительно сложения

Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c.

Запишем в форме буквенного выражения:

a·b+c=a·b+a·c

a, b, c — любые натуральные числа.

Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4·3+2.

4·3+2=4·3+4·2=12+8=20

С другой стороны 4·3+2=4·5=20. Справедливость распределительного свойства умножения относительно сложения показана наглядно.

Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

Распределительное свойство умножения относительно вычитания

Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.

Распределительное свойство умножения относительно вычитания

Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c.

Запишем в форме буквенного выражения:

a·b-c=a·b-a·c

a, b, c — любые натуральные числа.

В предыдущем примере заменим «плюс» на «минус» и запишем:

4·3-2=4·3-4·2=12-8=4

С другой стороны 4·3-2=4·1=4. Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.

Умножение единицы на натуральное число

Умножение единицы на любое натуральное число в результате дает данное число.

1·a=a

По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.

1·a=∑i=1a1

Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a. Таким образом, переместительное свойство умножения остается справедливым:

1·a=a·1=a

Умножение нуля на натуральное число

Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.

Умножение нуля на натуральное число

Произведение числа 0 и любого натурального числа a равно числу 0.

0·a=0.

По определению, произведение 0·a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.

В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.

Напимер: 0·498=0; 0·9638854785885=0

Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a·0=0.

Как идентифицировать 6 типов химических реакций

Обновлено 26 марта 2020 г.

Лан Луо

Проверено: Lana Bandoim, B.S.

Химические реакции являются неотъемлемой частью технологий, участвуя в различных видах человеческой деятельности, которые являются частью нашей повседневной жизни. Примеры химических реакций, с которыми мы сталкиваемся каждый день, включают сжигание топлива и изготовление вина и пива. Химические реакции также широко распространены в природе, от химического выветривания горных пород, фотосинтеза в растениях и процесса дыхания у животных.

В более широком аспекте существует трех типов реакций : физическая, химическая и ядерная. Химические реакции можно разделить на множество категорий. Шесть распространенных типов химических реакций : синтез, разложение, одинарное вытеснение, двойное вытеснение, горение и кислотно-основные реакции. Ученые классифицируют их на основе того, что происходит при переходе от реагентов к продуктам. Это помогает прогнозировать реакционную способность реагентов и продуктов, образующихся в результате реакций.

Типы реакций

Химическая реакция — это процесс, в котором одно или несколько веществ, реагентов, подвергаются химическому превращению с образованием одного или нескольких различных веществ, продуктов. Это процесс, который включает перегруппировку составляющих атомов реагентов с образованием продуктов без изменения ядер атомов.

Например, в процессе производства соды и сельтерской воды диоксид углерода барботируется в воду в условиях повышенного давления и образует новое соединение, известное как угольная кислота (H ₂ CO ₃). По этому уравнению вы знаете, что произошла химическая реакция.

CO ₂ (г) + H ₂ O (л) -> H ₂ CO ₃ (водн.)

Физическая реакция отличается от химической реакции. Физические изменения включают только изменение состояния, например, замерзание воды до льда и сублимацию сухого льда до диоксида углерода. В обоих сценариях химическая идентичность реагентов, H ₂ O и CO ₂, не изменилась.Продукты по-прежнему состоят из тех же соединений, что и реагенты.

Ядерная реакция также отличается от химической реакции. Он включает столкновение двух ядер с образованием одного или нескольких нуклидов, отличных от родительских ядер. Например, Эрнест Резерфорд выполнил первую искусственную трансмутацию, подвергнув газообразный азот воздействию альфа-частиц, образуя изотоп ¹⁷ O и выбрасывая протон в этом процессе. Элемент в реагенте изменился, таким образом, произошла реакция.

Типы химических реакций

Наиболее распространенными типами химических реакций являются синтез, разложение, одинарное вытеснение, двойное вытеснение, горение и кислотно-основные реакции. Однако такая категоризация не является исключительной. Например, кислотно-основная реакция также может быть классифицирована как реакция двойного замещения.

Реакция синтеза

Реакция синтеза — это реакция, в которой два или более вещества объединяются с образованием более сложного.Химическое уравнение для общей формы реакции синтеза выглядит следующим образом:

Одним из примеров реакции синтеза является комбинация железа (Fe) и серы (S) с образованием сульфида железа.

Другим примером является объединение газообразного натрия и хлора с образованием более сложной молекулы — хлорида натрия.

2Na (s) + Cl ₂ (g) -> 2NaCl (s)

Реакция разложения

Реакция разложения работает прямо противоположно реакции синтеза. Это реакция, в которой более сложное вещество распадается на на более простые. Общая форма реакции разложения может быть записана как:

Примером реакции разложения является электролиз воды с образованием водорода и газообразного кислорода.

H ₂ O (l) -> H ₂ (g) + O ₂ (g)

Разложение также может быть термическим, например превращение угольной кислоты в воду и диоксид углерода в условиях нагревания .Обычно встречается в газированных напитках.

H ₂ CO ₃ (водн.) -> H ₂ O (л) + CO ₂ (г)

Реакция одинарного вытеснения

Также известна как реакция одиночного замещения, реакция одиночного вытеснения это когда чистый элемент меняется местами с другим элементом в соединении. Он имеет общую форму:

Многие металлы могут реагировать с сильной кислотой. Например, магний реагирует с соляной кислотой с образованием газообразного водорода и хлорида магния. В этой реакции магний меняется местами с водородом в соляной кислоте.

Mg (s) + 2HCl (водный) -> H ₂ (g) + MgCl ₂ (водный)

Магний также может реагировать с водой с образованием гидроксида магния и газообразного водорода.

Mg (s) + 2H ₂ O (l) -> H ₂ (g) + Mg (OH) ₂ (aq)

Двойное вытеснение

Другой тип химических реакций — двойное вытеснение, в котором катионы двух реагентов меняются местами, образуя два совершенно разных продукта.Общая форма этой реакции:

Одним из примеров реакции двойного замещения является реакция хлорида бария с сульфатом магния с образованием сульфата бария и хлорида магния. В этой реакции катионы бария и магния в реагентах меняются местами на новые соединения бария и магния.

BaCl ₂ + MgSO ₄ -> BaSO ₄ + MgCl ₂

Другой пример — реакция нитрата свинца с иодидом калия с образованием иодида свинца и нитрата калия.

Pb (NO ₃) ₂ + 2KI _{-> PbI ₂ + 2KNO ₃}

В обоих случаях в результате реакции образуется осадок (BaSO ₄ и PbI ₂) из двух растворимые реагенты, поэтому они также группируются по реакциям осаждения.

Реакция горения

Реакция горения — это экзотермическая окислительно-восстановительная химическая реакция , при которой топливо реагирует с кислородом с образованием газообразных продуктов. Хотя обычно это инициируется какой-либо формой энергии, такой как использование зажженной спички для зажигания огня, выделяемое тепло обеспечивает энергию для поддержания реакции.

Полная реакция сгорания происходит при наличии избытка кислорода и дает в основном обычные оксиды, такие как диоксид углерода и диоксид серы. Для обеспечения полного сгорания содержание кислорода должно быть в два или три раза больше теоретического количества, рассчитанного по стехиометрии. Полное сгорание углеводорода можно выразить в виде:

4C _x H _y + (4x + y) O ₂ -> 4xCO ₂ + 2yH ₂ O + heat

Горение метана, который является насыщенным углеводородом, выделяет значительное количество тепла (891 кДж / моль), и его можно суммировать следующим уравнением:

CH ₄ + 2O ₂ -> CO ₂ + 2H ₂ O + heat

Нафталин — еще один пример углеводорода, при его полном сгорании также выделяется углекислый газ, вода и тепло.

C ₁₀ H ₈ + 12O ₂ -> 10CO ₂ + 4H ₂ O + heat

Спирты также могут служить источником топлива для горения, например, метанол.

CH ₃ OH + O ₂ -> CO ₂ + 2H ₂ O + heat

Неполное сгорание происходит, когда недостаточно кислорода для полной реакции с топливом с образованием диоксида углерода и воды. Таким примером является сжигание метана при ограниченном количестве кислорода для получения комбинации монооксида углерода, диоксида углерода, углеродной золы и воды.Это может быть выражено приведенными ниже уравнениями в зависимости от количества присутствующего кислорода.

2CH ₄ + 3O ₂ -> 2CO + 4H ₂ O

Больше, но недостаточно кислорода:

4CH ₄ + 7O ₂ -> 2CO + 2CO ₂ + 8H ₂ O

Слишком большое количество оксида углерода может привести к отравлению воздуха, поскольку он соединяется с гемоглобином с образованием карбоксигемоглобина и снижает его способность доставлять кислород.Поэтому важно обеспечить полное сгорание топлива для бытовых и промышленных нужд.

Кислотно-основная реакция

Кислотно-основная реакция — это реакция между кислотой и основанием, одним из продуктов которой является вода. Это особый тип реакции двойного вытеснения (местами переключения A и B), и эти примеры химических реакций записываются как:

Простой пример кислотно-основной реакции — это когда антацид (гидроксид кальция) нейтрализует желудочную кислоту (соляная кислота). ).

Ca (OH) ₂ + 2HCl -> CaCl ₂ + 2H ₂ O

Другой пример — реакция уксуса (уксусной кислоты) с пищевой содой (бикарбонатом натрия). В этом процессе образуются вода и углекислый газ, но не выделяется тепло, поэтому это не реакция горения.

CH ₃ COOH + NaHCO ₃ -> CH ₃ COONa + H ₂ O + CO ₂

Исследование смещения зоны стыковки поперечно прокатанных серийно расположенных гибридных деталей

1 .

Assunção E, Quintino L, Miranda R (2009) Сравнительное исследование лазерной сварки индивидуальных заготовок в автомобильной промышленности. Int J Adv Manuf Technol 49 (1-4): 123–131. https://doi.org/10.1007/s00170-009-2385-0

Артикул Google Scholar

Бабич З., Александрович С., Стефанович М., Сливич М. (2008) Определение характеристик пластичности сварных заготовок по индивидуальному заказу. Журнал технологии пластичности 33: 39–47

Han SW, Hwang TW, Oh IY, Moon YH (2018) Технико-экономическое обоснование изготовления заготовок по индивидуальному заказу путем прокатки частично сложенных заготовок. J Mech Sci Technol 32 (4): 15–75. https://doi.org/10.1007/s12206-018-0312-8

Артикул Google Scholar

Каче Х., Стонис М., Беренс Б.А. (2013) Hybridschmieden. Monoprozessuales Umformen und Fügen Metallischer Blech- und Massivelemente wt Werkstatttechnik online, vol 103, pp 257–262

Google Scholar

Wesling V, Treutler K, Bick T, Stonis M, Langner J, Kriwall M (2018) Характеристики соединения и гибридной композитной ковки твердых алюминиевых деталей и оцинкованных стальных листов. Conf Ser: Mater Sci Eng 373: 012026. https://doi.org/10.1088/1757-899X/373/1/012026

Артикул Google Scholar

Blohm T et al (2017) Исследование зоны соединения гибридных деталей, сваренных лазерной сваркой, и поперечно-клиновых прокатных деталей. Форма Int J Mater.https://doi. org/10.1007/s12289-017-1393-0

Pater Z (2014) Поперечно-клиновая прокатка. В кн .: Комплексная обработка материалов. С. 211–279. https://doi.org/10.1016/B978-0-08-096532-1.00315-0

Google Scholar

Li Q, Lovell M (2008) Механизмы разрушения поперечно-клиновой прокатки и промышленное применение. Int J Adv Manuf Technol 37 (3–4): 265–278. https://doi.org/10.1007/s00170-007-0979-y

Артикул Google Scholar

Blohm T, Stonis M, Behrens BA (2015) Исследование параметров моделирования поперечно-клиновой прокатки титана и стали бейнитного класса. J Appl Mech Mater 736: 165–170

Артикул Google Scholar

10.

Knust J, Stonis M, Behrens BA (2016) Оптимизация преформ для процессов горячей штамповки с использованием адаптивного количества вспышек в зависимости от сложности формы поперечного сечения. Прод Eng 10 (6). https://doi.org/10.1007/s11740-016-0702-7

11.

Knust J, Podszus F, Stonis M, Behrens BA, Overmeyer L, Ullmann G (2016) Оптимизация преформ для процессов горячей штамповки с использованием генетических алгоритмов. Int J Adv Manuf Technol 85 (5-8). https://doi.org/10.1007/s00170-016-9209-9

12.

Blohm T, Langner J, Stonis M, Behrens BA (2017) Базовое исследование постепенного формования серийно расположенных гибридных деталей с использованием поперечно-клиновой прокатки. https://doi.org/10.1016/j.proeng.2017.10.921

13.

Sun B, Xu J, Peng W, Shu X, Yin A, Huang G (2018) Экспериментальное исследование поперечно-клиновой прокатки многослойного вала из композита 42CrMo / Q235.Int J Adv Manuf Technol 96 (1-4): 895–903. https://doi. org/10.1007/s00170-017-1537-x

Артикул Google Scholar

14.

Патер З., Томчак Дж., Булзак Т. (2017) Новые возможности штамповки в процессах поперечно-клиновой прокатки. Архив строительства и машиностроения 18 (1). https://doi.org/10.1016/j.acme.2017.06.005

15.

Pater Z, Tomczak J (2012) Экспериментальные испытания поперечно-клиновой прокатки поковок из сплавов цветных металлов.Arch Metall Mater 4 (4): 919–928. https://doi.org/10.2478/v10172-012-0101-9

Артикул Google Scholar

16.

Li J, Wang B, Ji H, Huang X, Tang X, Ma W (2017) Влияние параметров поперечно-клиновой прокатки на формуемость сплава Ti – 6Al – 4V. Int J Adv Manuf Technol 92 (5–8): 2217–2229. https://doi.org/10.1007/s00170-017-0263-8

Артикул Google Scholar

17.

akırcalı M, Kılıçaslan C, Güden M, Kıranlı E, Shchukin V, Petronko V (2013) Поперечная клиновая прокатка сплава Ti6Al4V (ELI): экспериментальные исследования и моделирование деформации и разрушения методом конечных элементов. Int J Adv Manuf Technol 65 (9–12): 1273–1287. https://doi.org/10.1007/s00170-012-4256-3

Артикул Google Scholar

18.

Wensheng Y, Wang L, Tingxiang Y (2015) Экспериментальное исследование процессов поперечно-клиновой прокатки алюминиевого сплава.В кн .: Известия. Международная конференция по передовым инженерным материалам и технологиям. Гуанчжоу, Китай, p 2015

Google Scholar

19.

Кожевникова Г.В. (2012) Поперечно-клиновая прокатка — физико-технический институт. Rue Publishing House

20.

Li Q (2003) Характеристика механизмов разрушения при поперечно-клиновой прокатке. Диссертация, Университет Питтсбурга

21.

B.-A.Беренс, А. Чугреев, М. Селински и Т. Маттиас (2019) Оптимизация формы зоны соединения для гибридных компонентов из алюминия и стали посредством геометрически согласованных поверхностей соединения в процессе сварки трением

хлор | Использование, свойства и факты

Хлор (Cl) , химический элемент, второй по легкости член галогенных элементов или Группа 17 (Группа VIIa) периодической таблицы. Хлор — это токсичный едкий газ зеленовато-желтого цвета, раздражающий глаза и дыхательную систему.

Британская викторина

118 Названия и символы из таблицы Менделеева

Периодическая таблица Менделеева состоит из 118 элементов. Насколько хорошо вы знаете их символы? В этой викторине вам будут показаны все 118 химических символов, и вам нужно будет выбрать название химического элемента, который представляет каждый из них.

9039 −34 ° C (−29 ° F)

Свойства элемента
атомный номер	17
атомный вес	от 35,446 до 35,457
точка плавления	−103 ° C (−153 ° F)
плотность (1 атм, 0 ° C или 32 ° F)	3,214 г / литр (0,429 унции / галлон)
степени окисления	−1, +1, +3, +5, +7
электронная конфигурация	1 с ² 2 с ² 2 с ⁶ 3 с ² 3 с ⁵

История

Каменная соль (поваренная соль или хлорид натрия) известна уже несколько тысяч лет.Это основной компонент солей, растворенных в морской воде, из которых он был получен в Древнем Египте путем испарения. В римские времена солдатам частично платили солью ( salarium , корень современного слова salarium ). В 1648 году немецкий химик Иоганн Рудольф Глаубер получил сильную кислоту, которую он назвал спиртом соли, путем нагревания влажной соли в угольной печи и конденсации паров в приемнике. Позже он получил тот же самый продукт, теперь известный как соляная кислота, путем нагревания соли с серной кислотой.

ионная связь: хлорид натрия или поваренная соль
Ионная связь в хлориде натрия. Атом натрия (Na) отдает один из своих электронов атому хлора (Cl) в химической реакции, в результате чего положительный ион (Na ⁺) и отрицательный ион (Cl ^—) образуют стабильное ионное соединение. (хлорид натрия; поваренная соль) на основе этой ионной связи.
Encyclopædia Britannica, Inc.
В 1774 году шведский химик Карл Вильгельм Шееле обработал порошкообразный черный оксид марганца соляной кислотой и получил зеленовато-желтоватый газ, который он не смог распознать как элемент. Истинная природа газа как элемента была признана в 1810 году английским химиком Хамфри Дэви, который позже назвал его хлором (от греческого chloros , что означает «желтовато-зеленый») и объяснил его отбеливающее действие.
Возникновение и распространение
Помимо очень небольшого количества свободного хлора (Cl) в вулканических газах, хлор обычно находится только в форме химических соединений. Он составляет 0,017 процента земной коры. Природный хлор представляет собой смесь двух стабильных изотопов: хлора-35 (75.53 процента) и хлор-37 (24,47 процента). Наиболее распространенным соединением хлора является хлорид натрия, который в природе встречается в виде кристаллической каменной соли, часто обесцвеченной из-за примесей. Хлорид натрия также присутствует в морской воде, средняя концентрация которой составляет около 2 процентов от этой соли. Некоторые моря, не имеющие выхода к морю, такие как Каспийское море, Мертвое море и Большое соленое озеро в штате Юта, содержат до 33 процентов растворенной соли. В крови и молоке присутствует небольшое количество хлорида натрия.Другими хлорсодержащими минералами являются сильвит (хлорид калия [KCl]), бишофит (MgCl ₂ ∙ 6H ₂ O), карналлит (KCl ∙ MgCl ₂ ∙ 6H ₂ O) и каинит (KCl ∙ MgSO ₄ ∙ 3H ₂ O). Он содержится в минералах эвапорита, таких как хлорапатит и содалит. В желудке присутствует свободная соляная кислота.
Мертвый Море
Солевые месторождения на юго-западном берегу Мертвого моря недалеко от Масады, Израиль.
З. Радован, Иерусалим Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.Подпишись сейчас
Современные солевые отложения, должно быть, образовались в результате испарения доисторических морей, сначала кристаллизовались соли с наименьшей растворимостью в воде, а затем соли с большей растворимостью. Поскольку хлорид калия более растворим в воде, чем хлорид натрия, некоторые отложения каменной соли, например, в Штассфурте, Германия, были покрыты слоем хлорида калия. Чтобы получить доступ к хлориду натрия, сначала удаляют калиевую соль, важную как удобрение.
RAM Рабочий процесс подъема несущей системы — RAM | STAAD Wiki — RAM | STAAD
Откидные стены представляют собой тонкие бетонные панели. Когда тонкая стенка подвергается осевому сжатию и изгибу вне плоскости, необходимо учитывать эффекты второго порядка. ACI 318 допускает усиленный подход первого порядка, упругий подход второго порядка или неупругий подход второго порядка. ACI 318 также предоставляет альтернативный анализ тонких стен, который представляет собой усиленный подход первого порядка и является основой ACI 551.2R. RAM Structural System реализовала упругий анализ второго порядка для решения проблемы тонкой стены.
В дополнение к упругому анализу второго порядка, были реализованы несколько функций для облегчения анализа на месте и проектирования наклонных конструкций в 3D-модели.
Распределенная стенка с собственным весом
Зазоры (стыки) могут быть назначены для обеспечения аналитического разделения от соседних панелей
Назначение параметра эксцентриситета для автоматического применения внеплоскостных моментов силы тяжести
Давление на стены
Механизм изоляции отклонения от плоскости
Асимметричное армирование стен для различного покрытия на внутренней и внешней стороне
Рассмотрение раздела нетто за обнаружение
По умолчанию собственный вес стен рассчитывается по этажам и применяется к верхней части элемента. Это консервативно, но может привести к чрезмерным эффектам отклонения от плоскости 2 ^и порядков в тонких стенах. В RAM Manager — Criteria — Self Weight была добавлена опция для распределения собственного веса стены по сетке конечных элементов. Вместо того, чтобы прикладывать собственный вес к верхней части физической стены, собственный вес применяется к верхней части каждого конечного элемента оболочки внутри стены.
Поскольку анализ наклонных стен выполняется в RAM Frame, все наклонные стены, которые будут учитываться при анализе, должны быть смоделированы как боковые стены.Чтобы отличать наклонные бетонные стены от монолитных бетонных стен (предположение по умолчанию), в диалоговые окна компоновки стен и изменения свойств было добавлено свойство типа. Когда выбран наклон вверх, свойства зазора доступны и могут быть назначены любому концу. Воздействие назначается граням стены и воздействует на покрытие арматуры в RAM Concrete Wall.
При моделировании наклонных стен, которые имеют физическое соединение между панелями, назначение зазора используется для обеспечения аналитического разделения между стенами, а не физического моделирования разделения. Промежутки отображаются на плане в виде оранжевых прямоугольников с хвостами, указывающими на стену, на которой они моделируются. На фасаде зазоры отображаются в виде жирных оранжевых линий с вкладками, указывающими на внутреннюю часть стены, в которой они моделируются. Зазор необходимо назначить только одному концу стены на стыке, но его можно назначить обоим концам стены, чтобы облегчить быстрое моделирование. . Однако это может привести к неоднозначным условиям для поддерживаемых элементов в соединениях. RAM Modeler — Integrity — DataCheck помечает эти условия как ошибки, когда они возникают.
Когда стена моделируется на компоновке этажа, i-конец стены — это конец, имеющий меньшую координату X или меньшую координату Y, если координата X одинакова, независимо от того, какая точка нажимается первой при моделировании. стена. Основная поверхность стены находится с правой стороны, если вы идете от конца i к концу стены. Когда вы смотрите на стену на возвышении, вы всегда смотрите на основную грань. RAM Modeler — Параметры — Показать стену позволяет включить основные свойства лица и экспозиции на графическом дисплее.Стрелка первичной грани указывает от основной грани. Ярлыки для назначений внешней и внутренней экспозиции отображаются на соответствующем лице.
При анализе упругости второго порядка необходимо учитывать области трещин на стене. Жесткость после растрескивания является функцией внутренних сил и размещения арматуры. Армирование стены не определяется до тех пор, пока анализ не будет выполнен и спроектирован в RAM Concrete Wall. Таким образом, анализ каркаса RAM основан на коэффициенте растрескивания, присвоенном стене, который применяется ко всем конечным элементам, чтобы приблизиться к эффектам растрескивания.Фактор трещин (изгиб), показанный в диалоговом окне «Добавить бетонную стену» выше, изменяет внеплоскостную жесткость стены в анализе RAM Frame.
ACI 318 позволяет использовать уменьшенный момент инерции с анализом упругости второго порядка для учета растрескивания. ACI 551.2R утверждает, что панель в условиях предельной нагрузки обычно демонстрирует трещины на большей части высоты, и что испытания и аналитические исследования подтверждают, что допущение Ec Icr по всей панели тесно коррелирует с результатами испытаний.Альтернативный анализ ACI 318 для тонких стен дает уравнение для момента инерции трещины, который обычно составляет менее 0,35 Ig.
Коэффициент растрескивания (изгиба) требует инженерной оценки. Он должен представлять эффективный момент инерции вне плоскости для анализа факторизованной нагрузки (условия при разрушении прочности) с уменьшением неопределенности. Инженеру рекомендуется начинать с консервативного коэффициента трещин, чтобы избежать недооценки эффектов порядка 2 ^и, а затем уточнять коэффициент трещин, если требуется более высокая точность.
Таблицу DA Tilt-Up Tools можно использовать для определения того, соответствует ли коэффициент трещин, назначенный в Modeler, альтернативному методу ACI 318 для тонких стен.
Эксцентриситет стены назначается автоматически при моделировании стены на основе критериев по умолчанию, указанных в RAM Modeler — Set Defaults — Eccentricities. После того, как стена была смоделирована, назначение эксцентриситета можно изменить с помощью команды «Макет — Стена — Изменить эксцентриситет». Обратите внимание, что эксцентриситет стены применяется ко всем стенам, но в настоящее время моменты из-за эксцентриситета учитываются только на боковых стенах в анализах RAM Frame.Эксцентриситет измеряется перпендикулярно плоскости стены и применяется ко всем нагрузкам от одностороннего настила и поддерживаемых гравитационных балок / балок. Если жесткая связь назначена гравитационной балке, поддерживаемой стеной, жесткая связь имеет приоритет над назначением эксцентриситета.
Давление на стену добавляется в режиме подъема в RAM Modeler. Вариант поперечной нагрузки создается в Таблице стоек — Варианты боковых нагрузок. Существует опция «Блокировать смещения диафрагмы», которая является отдельным свойством для каждого варианта нагружения. Когда выбрана эта опция, диафрагма не будет смещаться при анализе рамы RAM при анализе случая нагружения. Цель этой опции — изолировать поведение вне плоскости от поведения в плоскости. Например, давление ветра, вызывающее изгиб стены вне плоскости, часто является нагрузкой на компоненты и облицовку, которые не обязательно учитывать для основной системы сопротивления поперечной силе. Предотвращая смещение диафрагмы, инженер может смоделировать компоненты и давление ветра на обшивку на всех стенах в одном случае нагрузки, и никакие силы в плоскости не будут создаваться в 3D-анализе.Этот вариант малоэффективен для гибкой диафрагмы.
Свойства давления создаются в Таблице стоек — Боковые нагрузки — Нагрузки от давления на стену. Давление всегда прикладывают перпендикулярно плоскости стены. Следовательно, вы определяете величину давления и то, будет ли оно действовать по направлению к основной поверхности или от нее. В режиме фасада вы смотрите на главную поверхность стены. Направление к находится в экране. Давление может быть явно определено как верхнее и нижнее давления (линейно изменяющееся между верхним и нижним в зависимости от высоты) или как сила инерции, основанная на весе стенки и доле силы тяжести, которую необходимо учитывать.
После определения варианта боковой нагрузки и давления можно назначить давления, указав вариант нагрузки, выбрав свойство нагрузки и применив его к стенам. Отобразятся штриховка и метки с назначениями.
Проемы в стенах имеют свойство распределения, определяющее, как справиться с той частью давления в стене, которая существует над проемом. Давление может быть распределено по вертикальной или горизонтальной сторонам проема или полностью игнорироваться.Проемы создаются и изменяются в режиме высот в RAM Modeler.
По умолчанию в RAM Frame игнорируется внеплоскостная жесткость стены. Жесткость вне плоскости можно изменить в RAM Frame Analysis — Criteria — General. Обычно откидные стены прикрепляются к основанию штифтами, чтобы они не находились в плоскости, поэтому также следует выбрать вариант фиксации при повороте. Сходимость теоретических результатов происходит по мере уменьшения размеров сетки и может потребоваться уменьшение максимального расстояния между узлами по умолчанию.Однако уменьшение размера ячейки увеличит время анализа.
Когда к стенам прикладываются моменты силы тяжести из-за эксцентриситета и бокового давления, диафрагмы не могут быть отнесены к гибким или псевдогибким, поскольку это не условия для диафрагмы. Без диафрагмы стене не к чему опереться при анализе методом конечных элементов. Если есть моменты силы тяжести из-за эксцентриситета, вы столкнетесь с нестабильностью в анализе или массивными смещениями.Точно так же давление на стену будет вызывать чрезмерные смещения, если смещения диафрагмы не заблокированы (не применимо к гибким диафрагмам), если только вы не собираетесь смотреть на консольные стены с фиксированными основаниями.
Создание сценариев силовых нагрузок для анализа в плоскости в RAM Frame и анализ отдельных загружений ничем не отличается от предыдущих версий RAM Structural System. После анализа случаев нагружения выполняется упругий анализ второго порядка в режиме RAM Frame Analysis — сочетания нагрузок.В меню «Комбинации» есть «Пользовательские», «Сила» и «Комбинации услуг». Пользовательские комбинации — это результаты наложенного загружения, которые не анализируются. Комбинации «Сила» и «Служба» рассматриваются в расширенном анализе. Инженер должен создавать комбинации расширенного анализа только для условий, в которых требуется итеративный анализ. Например, предположим, что один случай давления ветра был создан для компонентов и сил оболочки, которые будут контролировать внеплоскостную конструкцию, а сгенерированные случаи ветрового давления были созданы для основной системы сопротивления силе в плоскости.Малые p-дельта-эффекты пренебрежимо малы для конструкции в плоскости, а реализация P-дельта в режиме нагрузок анализа рамы подходит для любых больших p-дельта-эффектов, которые влияют на поведение в плоскости. Следовательно, комбинации расширенного анализа могут включать только комбинации, которые включают случай внеплоскостного давления, как показано ниже.
Критерии, определенные в режиме загружений, также используются в анализе сочетания нагрузок. Некоторые критерии приведут к тому, что аналитическая модель для случая гравитации будет отличаться от случая боковой нагрузки.Это может создать проблему для анализа комбинации нагрузок, содержащей оба случая. При возникновении этих условий будут выданы ошибки. Пользователь должен будет изменить выбор в режиме загружений, прежде чем продолжить анализ сочетания нагрузок.
Дополнительные критерии, относящиеся только к эластичному анализу второго порядка, существуют в RAM Frame Analysis — режиме комбинаций нагрузок — Criteria — Advanced Analysis. Как обсуждалось ранее, коэффициенты сечения трещин, введенные в RAM Modeler, предназначены для использования для анализа прочности.При анализе условий эксплуатации факторы трещин могут быть ослаблены. Вместо того, чтобы вводить отдельные коэффициенты взлома для комбинаций прочности и услуг, для комбинаций услуг вводится один модификатор фактора взлома (см. Раздел Анализ услуг ниже). Снижение динамической нагрузки можно включить или отключить. Критерии поиска неисправностей для итеративного анализа доступны, чтобы помочь в достижении сходимости.
Расширенный анализ выполняется путем перехода в раздел «Процесс — расширенный анализ», выбора комбинаций для рассмотрения и нажатия кнопки «ОК».Если расширенные комбинации не определены или не выбраны допустимые комбинации, тип комбинации будет иметь красный индикатор состояния.
Для просмотра и составления отчета о результатах анализа сочетания нагрузок необходимо выбрать подходящий тип сочетания нагрузок. В отчетах и результатах на экране учитывается только тип комбинации нагрузки активного режима вывода. Аналогичным образом, модуль «Силы стенок сдвига рамы» имеет диалоговое окно для выбора типа комбинации для результатов огибающей.
Анализ комбинации сервисов в режиме сочетания нагрузок анализа кадров RAM — это эластичный анализ 2-го порядка, который масштабирует факторы взлома, назначенные в RAM Modeler с помощью множителя сервиса в Критерии — Расширенный анализ. Сервисный анализ в Альтернативном методе ACI для анализа изогнутых стенок вне плоскости представляет собой итеративную билинейную интерполяцию, которая учитывает смещение в момент образования трещин с учетом полного момента инерции и смещение в номинальный момент с учетом момента инерции трещины.Смещения вне плоскости в RAM Frame будут больше, чем смещения, рассчитанные с использованием тонкой стены ACI для практических моментов. Если максимальное узловое смещение в RAM Frame для сервисной комбинации превышает пределы смещения, перед изменением жесткости стены следует выполнить более подробный анализ.
Во-первых, повторно запустите сервисный анализ, используя полный момент инерции. Чтобы в сервисном анализе использовался полный момент инерции, модификатор сервиса в критериях расширенного анализа должен быть больше единицы, деленной на коэффициент трещин при изгибе, назначенный в RAM Modeler.Программа ограничит жесткость в 1,0 раза больше полного момента инерции при анализе. Если максимальный рабочий момент в стене с учетом эффектов 2-го порядка ниже 2/3 момента растрескивания, то стена остается неповрежденной для служебной комбинации на тонкую стену ACI. Предположение об использовании полного момента инерции было верным.
Если стены треснули, повторно запустите анализ сервиса с модификатором сервиса, который переводит фактор взлома, назначенный в RAM Modeler, в состояние сервиса (например,грамм. 1.4). Если фактор взлома в Modeler представляет собой полностью взломанный раздел, результаты RAM Frame консервативны и при желании могут использоваться напрямую. Если смещения превышают пределы прогиба, модификатор обслуживания обычно может быть увеличен, потому что моменты обслуживания меньше момента, который снижает жесткость до полного растрескивания. Однако это решение требует инженерной экспертизы.
Электронная таблица DA Tilt-Up Tools может быть использована для анализа услуг.
RAM Concrete Shear Wall был переименован в RAM Concrete Wall в версии 17.00. Программа была усовершенствована, чтобы позволить размещать арматуру асимметрично и учитывать откосы. Кроме того, было добавлено рассмотрение комбинаций прочности для расширенного анализа и наклона арматурной крышки.
Сгенерированные и пользовательские сочетания нагрузок накладывают результаты загружения для создания силы сочетания нагрузок. Предполагая, что анализ порядка 2 ^и был выполнен только для сил вне плоскости, сгенерированные и пользовательские комбинации должны учитывать только случаи в плоскости.Комбинации силовых нагрузок, учитываемые в анализе заказа на упругость 2 ^и, могут быть выбраны для расчета в RAM Concrete Wall — Комбинации нагрузок — Advanced. Все выбранные комбинации учитываются при оформлении всех разрезов.
В разделе «Бетонная стена — Критерии — Критерии проектирования» есть параметры для размещения покрытия и перемычки на поверхности стены. Откидные стены используют минимальные требования к покрытию для сборных железобетонных изделий. Наружные поверхности предполагают воздействие погодных условий, что требует дополнительного укрытия в соответствии с ACI 318.RAM Concrete Wall — Assign — Прозрачная крышка стеновой панели позволяет инженеру игнорировать общие критерии покрытия. Наклонные стены обычно имеют вертикальные стержни, расположенные ближе всего к поверхности стены, чтобы максимизировать изгибную способность вне плоскости для стены, проходящей по вертикали. Предыдущие версии предполагали, что вертикальные полосы находились внутри горизонтальных полос. Таким образом, существуют отдельные варианты размещения для монолитных стен и стен с откидным верхом.
Бетонная стена — Назначить — Глубина раскрытия стеновых панелей позволяет указать глубину, которая влияет на размещение стержней и бетонное сечение, учитываемое при проектировании.Например, если толщина стены составляет 10 дюймов с 1 дюймовой прозрачной крышкой, а на первичной поверхности имеется выступ 0,75 дюйма, покрытие до стержней, ближайших к первичной поверхности, измеряется изнутри глубины выемки. Если вертикальные стержни находятся ближе всего к грани, расстояние от грани 10-дюймовой стены до края вертикальной кромки арматуры составляет 1,75 дюйма. Глубина откоса применяется ко всем прорезям в стеновой панели. Бетонное сечение, учитываемое при расчетах на прочность, исключает откосы.
Критические горизонтальные сечения для сил в плоскости обычно возникают в нижней части стен и проемов.При проектировании вне плоскости критические горизонтальные сечения часто возникают на средней высоте, где момент отклонения от плоскости является наибольшим. Программа не пытается определить максимальный момент вне плоскости и добавить разрез в этом месте. Инженер должен добавить разрезы там, где их нужно проверить. Если неочевидно, где будет возникать критическое сечение изгиба вне плоскости по высоте стены, инженер может использовать параметры максимального шага разреза в генераторе разрезов, чтобы создать несколько разрезов по высоте стены.Однако увеличение количества разрезов увеличивает время проектирования.
Диалоговое окно «Бетонная стена — Процесс — Просмотр / обновление» и сводный отчет по расчету разрезов включают проверку на сдвиг вне плоскости. Выявить местоположения и точное размещение стержней можно визуализировать в разрезе. Взаимодействие осевого изгиба всегда рассматривало слабые осевые моменты в стене. Чистый изгиб вне плоскости происходит при бета-угле 90 или 270 градусов.
Джентрификация и перемещение культур в американских городах »NCRC
[mashshare]
Джейсон Ричардсон , директор по исследованиям и оценке, NCRC
Брюс Митчелл , Ph.Н. крайним и ненужным культурным перемещением. ^[1] Хотя джентрификация увеличивает стоимость собственности в районах, пострадавших от длительного изъятия инвестиций, она также приводит к росту арендной платы, стоимости домов и имущества.Поскольку эти растущие расходы сокращают предложение доступного жилья, существующие жители, которые часто являются чернокожими или латиноамериканцами, перемещаются. Это не позволяет им получить выгоду от экономического роста и большей доступности услуг, которые связаны с увеличением инвестиций. Джентрификация представляет собой проблему для сообществ ^[2], которые пытаются достичь экономического возрождения без разрушения, связанного с перемещением населения.
Это исследование показало, что с 2000 по 2013 год произошло следующее:
Джентрификация и перемещение давних жителей были наиболее интенсивными в крупнейших городах страны и редкими в большинстве других мест.
Джентрификация была сконцентрирована в крупных городах с динамично развивающейся экономикой, но также появилась и в небольших городах, где она часто оказывала влияние на наиболее благоустроенные районы вблизи центральных деловых районов.
Перемещение чернокожих и испаноязычных жителей сопровождалось джентрификацией во многих местах и затронуло не менее 135 000 человек в период нашего исследования. В Вашингтоне, округ Колумбия, 20 000 чернокожих жителей были перемещены, а в Портленде, штат Орегон, за десять лет были перемещены 13 процентов чернокожего населения.
На семь городов приходится почти половина общенациональной джентрификации: Нью-Йорк, Лос-Анджелес, Вашингтон, округ Колумбия, Филадельфия, Балтимор, Сан-Диего и Чикаго.
Вашингтон, округ Колумбия, был самым джентрифицированным городом по проценту подходящих кварталов, которые испытали джентрификацию; Нью-Йорк был самым облагороженным по объему. Считалось, что микрорайоны имеют право на джентрификацию, если в 2000 году они относились к 40% ниже стоимости дома и доходов семьи в этом мегаполисе.
Исследование придает вес тому, что критики называют концентрацией не только богатства, но и инвестиций в создание богатства, лишь в горстке крупнейших мегаполисов страны, в то время как другие регионы страны находятся в упадке.
Строгие тесты для джентрификации и перемещения в этом исследовании и ограничения доступных данных, вероятно, занижены случаи джентрификации и перемещения.
Большинство районов с низким и средним доходом не подвергались джентрификации или возрождению в течение периода нашего исследования.Они оставались обнищавшими, не затронутыми инвестициями и строительным бумом, которые произошли в крупных городах, и уязвимы для будущего джентрификации и перемещения.
[optin-monster-shortcode id = ”pp9hbd0oskt3h64b5asb”]
Крупные преобразования происходят в самых процветающих американских городах. Многие из более чем 600 организаций-членов Национальной коалиции за реинвестирование сообществ (NCRC) выразили озабоченность по поводу джентрификации, перемещения и преобразований в своих сообществах.Мы хотели лучше понять, где происходили джентрификация и перемещение, и как их измерять и контролировать. Означает ли джентрификация также перемещение?
Используя Бюро переписи населения США и экономические данные, NCRC обнаружил, что во многих крупных американских городах в период с 2000 по 2013 год наблюдались признаки джентрификации и некоторого расового перемещения. Центром джентрификации были оживленные деловые районы в центре города, и примерно в четверти случаев она сопровождалась по расовому перемещению.Перемещение непропорционально сильно повлияло на чернокожих и испаноязычных жителей, которых оттолкнули, прежде чем они смогли извлечь выгоду из возросшей стоимости собственности и возможностей в обновленных кварталах. Это усугубило кризис доступности в центре наших крупнейших городов.
Джентрификация была наиболее интенсивной в крупнейших прибрежных городах страны, но в средних и малых городах внутри страны она была редкой: большинство городов страны не испытали джентрификации, как оценивалось в этом исследовании.
Районы облагораживаются, когда приток инвестиций и изменения в застроенной среде приводят к росту стоимости дома, доходов семьи и уровня образования жителей. Культурное перемещение происходит, когда в районах проживания меньшинств наблюдается быстрое сокращение своей численности по мере того, как богатые белые джентрификаторы заменяют нынешних жителей.
В этом исследовании районы считались имеющими право на джентрификацию, если в 2000 году они находились в пределах 40 процентов ниже стоимости дома и доходов семьи в этом мегаполисе.
Измерение джентрификации и перемещения чревато спорами, поскольку люди, на которых влияют экономические и социальные преобразования в своих кварталах, напрямую ощущают разрушение общественных связей. Это исследование измеряло джентрификацию и перемещение с использованием эмпирических методов и данных, что имеет свои недостатки и ограничения. Во-первых, хотя использование данных переписи населения США повышает достоверность результатов исследования, оно также ограничивает анализ населения периодом времени с 2000 по 2010 год, в то время как социальные и экономические данные собирались в соответствии с U.Программа S. Census American Community Survey (ACS), охватывающая период с 2000 г. по 2009-2013 гг., Пятилетняя консолидация социальных и экономических данных. Это ограничивает наши открытия недалеким прошлым. Однако районы с более поздней динамикой джентрификации и перемещения не могли быть охвачены. Во-вторых, использование переписных участков, в которых проживает в среднем около 4000 жителей, в качестве заместителя для микрорайонов может замаскировать изменения в микрорайонах, происходящие в сообществах меньшего размера.Вследствие этих ограничений по срокам и масштабу исследования не следует подразумевать, что другие районы не испытали таких же эффектов до, во время или после периода исследования. Вместо этого исследование предназначено для выявления случаев джентрификации и перемещения, которые можно измерить с высокой степенью уверенности, и избежания ложного указания на джентрификацию там, где ее не было, но оно не может охватить полноценную реальность жителей в джентрифицированных районах.
Отказ от инвестиций в сообществах с низким и средним доходом является результатом долгой истории дискриминации в области кредитования, жилья и исключительной расовой практики, известной как красная линия ^[3]. Недавнее исследование, проведенное Федеральным резервным банком Чикаго, напрямую увязало сокращение инвестиций сообщества с исторической практикой «красной черты», очевидной на картах жилищной безопасности («красной черты») Корпорации жилищного кредитования (HOLC), составленных для всех крупных городов США 80 лет назад ^{[ 4]}.Исследование, проведенное NCRC в 2018 году, показало, что три из четырех районов, отмеченных инспекторами HOLC как «опасные» в 1930-х годах, все еще испытывают экономические трудности, с более низкими доходами и более высокой долей жителей из числа меньшинств. Экономические результаты для чернокожих и латиноамериканских семей, проживающих в лишенных инвестиций районах, часто сдерживаются более низкими доходами, меньшим количеством предприятий и меньшими возможностями для создания богатства. Эта история заложила основу для джентрификации и перемещения.
Местные адвокаты и должностные лица должны проводить политику, которая поощряет инвестиции, одновременно повышая способность существующих жителей оставаться и извлекать выгоду из восстановления.В нашем документе от 2016 года, Закон о реинвестировании сообществ: Как CRA может способствовать интеграции и предотвращать перемещение в джентрифицированных районах , мы определили несколько способов, с помощью которых местные заинтересованные стороны могут способствовать возрождению в интересах более широкого сообщества, например, партнерство между банками и сообществом. -основанные организации для поощрения справедливого развития; кооперативы с ограниченной долей участия и общинные земельные трасты; предоставление существующим арендаторам права преимущественной покупки при переоборудовании квартир в сочетании с программами финансирования для малообеспеченных и впервые покупаемых; правила инклюзивного зонирования; и раздельные налоговые ставки для действующих резидентов облагораживающихся кварталов. Кроме того, процесс HUD по обеспечению справедливого жилищного строительства (AFFH) дает возможность группам населения взаимодействовать с муниципальным руководством в процессе планирования. AFFH предоставляет механизм для определения областей, которые уязвимы для джентрификации или могут находиться на ранних стадиях джентрификации. Затем общественные группы могут работать над разработкой стратегий, направленных на предотвращение перемещения действующих жителей за счет привлечения инвестиций и предоставления доступного жилья.
Крупные и мелкие местные банки также могут сыграть свою роль, поддерживая развитие жилищного строительства и вариантов финансирования, которые позволяют удерживать семьи с низким и средним доходом в сообществе, а не исключать их.Органы банковского регулирования должны признать проинтегративное банковское финансирование как отвечающее потребностям сообщества, кредитуя банки за эти усилия в их экзаменах CRA. Стратегии, подобные тем, которые продвигаются посредством правила AFFH HUD, продвигающего инвестиции в инклюзивные и разнообразные районы, должны иметь право на рассмотрение CRA. Очень важно, чтобы программы, способствующие экономическому процветанию традиционных жителей джентрифицированных кварталов, обсуждались в публичных оценках, выпущенных после экзамена CRA, чтобы документально подтвердить их эффективность и побудить другие банки применять сопоставимые инвестиционные стратегии на своих рынках.
ВВЕДЕНИЕ
Любое обсуждение джентрификации, вероятно, вызовет ряд откликов. Разговор с членом NCRC, живущим в бедном районе с высоким уровнем преступности в Балтиморе, штат Мэриленд, завершается мольбой: «Когда мы сможем получить часть этого (джентрификации) в моем районе?» Другой член NCRC из Портленда, штат Орегон, переживает джентрификацию как разрушение общественных связей, поскольку арендная плата растет, а семьи перемещаются. В Арлингтоне, штат Вирджиния, большое арендное сообщество из 3000 иммигрантов преимущественно латиноамериканского происхождения, привлеченное энергичным Вашингтоном Д.C. экономия исчезает, когда собственность продается, сносится бульдозером и заменяется смесью роскошных и доступных квартир, которые не являются ни по-настоящему доступными, ни изобильными для бывших арендаторов ^[5]. В быстро облагораживающемся районе Шоу в Вашингтоне, округ Колумбия, Объединенная церковь Христа в храме Линкольна, община, существовавшая с 1860-х годов и являвшаяся вехой в борьбе за гражданские права, вынуждена распустить в 2018 году, так как ее членство сокращается до 20 прихожане ^[6].Джентрификация вызывает споры, потому что она затрагивает людей на уровне района, она может нарушить знакомые и устоявшиеся связи места, создавая дезориентирующую новую местность. Для людей, перемещенных из-за того, что район становится недоступным, это больше, чем просто ностальгия или дискомфорт по незнакомому. Часто они вынуждены мириться с более длительными поездками на работу и нарушением структур поддержки, предоставляемых их старыми соседями и семьей. В этих случаях под джентрификацией понимается конечная стадия исключения меньшинств (обычно чернокожих) жителей из доступного жилья внутри города.Меры государственной политики, начавшиеся с «расчистки трущоб» в 1930-х и 1940-х годах, затем стали «обновлением городов» (Collins & Shester 2012; Hyra 2012) и строительством системы автомагистралей, которые разделили общины в 1950-х, 1960-х и 1970-х годах (Mohl 2004: Карась 2015), который затем превратился в «редевелопмент» в 1980-х и 1990-х годах. Теперь остатки этих сообществ сталкиваются с кризисом доступности, поскольку богатые, обычно белые джентрификаторы, имеющие доступ к кредитам, въезжают и трансформируют экономическую и социальную динамику сообщества.
В то время как общественное мнение о джентрификации варьируется от надежды на улучшение условий жизни до беспокойства и даже враждебности, исследования по джентрификации расходятся во мнениях относительно того, является ли перемещение неизбежным результатом. Некоторые исследователи утверждают, что джентрификация, сопутствующая перемещению, является сложной проблемой, и, хотя показатели мобильности жителей с низким доходом эквивалентны в джентрификационных и негентрифицирующих районах, семьи с низким доходом не могут позволить себе переехать и заменить покинутые семьи по мере роста стоимости жилья. (Динг, Хван и Дивринги, 2015 г.).Другие исследователи обнаружили, что перемещение происходило редко (Ellen and O’Regan, 2011; Freeman 2005), в то время как другие комментируют его распространенность (Newman and Wyly, 2006). Это расхождение во мнениях может быть связано с тем, что масштабы и тип джентрификации варьируются от места к месту. Городская форма или модели землепользования в городах США значительно различаются по размеру и структуре, и процесс джентрификации может вовлекать районы в быстрый процесс изменений или разворачиваться в течение десятилетий в более крупных районах. Кроме того, хотя жилые и коммерческие аспекты сообщества взаимосвязаны, джентрификация жилых и коммерческих районов имеет несколько разную динамику (Meltzer 2016).Перемещение также может принимать различные формы: расовые / этнические, классовые и культурные. Наконец, Маркузе (1986) утверждает, что во многих случаях перемещение из-за систематического сокращения инвестиций в города, которое привело к отказу от многих кварталов в центре города, часто предшествует джентрификации. По всем этим причинам полезно иметь четкое представление о рассматриваемом типе джентрификации, о том, как он изучается и в течение какого периода.
Основное внимание в этом отчете уделяется джентрификации жилых домов и перемещению по расовому и этническому признаку во всех городских районах США. S. Это всесторонний анализ джентрификации и перемещения на национальном уровне в 935 мегаполисах. Цель состояла в том, чтобы определить, насколько широко распространена джентрификация в городских районах США, а затем определить районы, где джентрификация и перемещение происходили одновременно. Первый шаг этого анализа — найти районы с признаками джентрификации. Используя методологию, разработанную профессором Колумбийского университета Лэнсом Фриманом, в исследовании исследуется повышение уровня образования, стоимости дома и дохода как определяющих критериев того, произошла ли джентрификация в районе (2005 г.).Мы определяем, в каких кварталах (переписных участках) наблюдаются признаки джентрификации за период 2000-2013 гг. На участках с признаками джентрификации проводится второй анализ, чтобы выяснить, произошло ли расовое / этническое перемещение в течение того же периода времени. В этом исследовании рассматриваются следующие вопросы: 1) Насколько распространена джентрификация и последующее перемещение? 2) Есть ли региональные различия в джентрификации и перемещении? 3) Какие переменные переписи связаны с джентрификацией по всей стране?
ОБЗОР ЛИТЕРАТУРЫ
Термин «джентрификация» был впервые введен в употребление в 1960-х годах британским социологом Рут Гласс (1964) для описания вытеснения рабочего класса жителей лондонских кварталов пришельцами из среднего класса. С самого начала джентрификация понималась как форма изменения района, приводящая к вытеснению нынешних жителей одного социального класса и культуры другим, более состоятельным классом, что связано с увеличением стоимости собственности. В случае Соединенных Штатов сегрегированная жилая структура американских городов создает условия, при которых джентрификация часто происходит по расовому признаку. В этих случаях джентрификации и расового перемещения зажиточные белые прибывшие часто вытесняют нынешних жителей из числа меньшинств.
Джентрификация — это сложная форма смены соседства. На уровне улиц это проявляется в улучшении застроенной структуры кварталов, поскольку дома ремонтируются и создаются предприятия (Krase, 2012; Kreager, Lyons and Hays, 2011; Papachristos et al. 2011). Хотя самое базовое понимание джентрификации включает в себя перемещение людей и инвестиций, чтобы повлиять на изменение района, оно также включает более широкие политические и экономические силы. Политические решения правительства влияют как на транспорт, так и на доступность услуг и удобств в сообществе. Взаимодействие между правительством и общественностью при принятии решений относительно зонирования и распределения государственных ресурсов в сочетании с решениями частных застройщиков об инвестировании капитала сильно влияют на желательность района (Zuk et al. 2015). Силы, приводящие к изменениям в районе, такие как джентрификация, также включают взаимодействие между перемещением людей, решениями государственной политики и доступностью капитала. Следовательно, джентрификация — это предмет, требующий анализа социальных, политических и экономических обстоятельств.
Экономические движущие силы изменения соседства включают динамику предложения государственных инвестиций и стоимость земли в контексте более широкой столичной экономики. Работая над докторской степенью в Университете Джона Хопкинса, покойный Нил Смит наблюдал за облагораживанием внутренней гавани Балтимора (1979). Это побудило его определить движущие силы, которые приводят к джентрификации с точки зрения арендной платы за землю — износ и физический износ старых построек, а также увеличение потенциальной прибыли от земли, на которой они были построены. Когда потенциальный доход от аренды земли превышает восприятие риска инвесторами, районы становятся вероятными кандидатами на перепланировку. Хотя экономика объясняет потоки капитала в облагораживающие коммерческие и жилые районы, существуют более широкие культурные факторы, которые изменили взгляды на желательность городского образа жизни и увеличили спрос на районы в центре города.
Жизненные предпочтения, связанные с жизнью в районе, всегда играли важную роль в установлении желательности различных городских районов.В послевоенную эпоху произошли сдвиги как в федеральной политике, так и в культуре потребления, которые оказали огромное влияние на структуру городского жилья (Cohen 2004). Экономические условия эпохи депрессии и производственные приоритеты во время Второй мировой войны препятствовали строительству нового жилья более десяти лет. Это способствовало появлению устаревшего городского жилья, предложение которого было слишком маленьким, чтобы удовлетворить потребности растущего и все более богатого населения в послевоенную эпоху. Доступность ипотечного финансирования через Закон о жилищном строительстве 1949 года вызвала строительный бум.Большая часть жилья была построена в пригородах, где застройщики, используя эффект масштаба, могли найти большие неосвоенные участки для массивных новых застроек. Это ускорило реконфигурацию американской городской системы, поскольку белые жители среднего класса переселялись в пригороды, перемещая население и столицу из центральных районов (Jackson 1987). Часто это оставляло центральные районы городов с высокой долей меньшинств и жителей с низкими доходами, что приводило к сокращению базы доходов и увеличению спроса на городские услуги.Этот сдвиг в экономическом процветании и населении от центральных районов городов получил широкое признание как теория послевоенного упадка городов; тем не менее, городское развитие сильно различается по стране, и его не следует рассматривать как единственное объяснение послевоенного городского развития (Beauregard 1993). В нынешнюю эпоху стареющий жилой фонд пригородов внутреннего кольца стал менее желательным, поскольку требования поездок на работу и привлекательность центра города сместили спрос на жилье ближе к центральному деловому району (CBD) городских районов.
На вопрос «кто джентрифицирует?» зависит от демографии и класса. Многие авторы ссылаются на роль молодых миллениалов в джентрификации (Hwang & Lin 2016; Baum-Snow & Hartley 2016; Couture & Handbury 2016; Ding, Hwang & Divringi 2015). Миллениалы реже испытывают расовую и этническую вражду, чем предыдущие поколения (Freeman & Cai, 2015; Owens, 2012; Glaeser & Vigdor, 2012). Во многих центральных районах городов за последние два десятилетия также произошло сокращение насильственных преступлений, что может сделать некоторые районы с низким доходом привлекательными для новичков (Ellen, Horn & Reed, 2016).Увеличение рабочего времени и сокращение свободного времени также создали потребность в сокращении времени в пути и работе ближе к дому (Edlund, Machade, & Sviatchi, 2016). Решения государственной политики также имеют влияние. Некоторые исследователи указывают на роль программы HOPE VI в сносе аварийного государственного жилья (Goetz 2013; Vale & Gray 2013). Изменения в расходах на уровне города на жилые комплексы, парки и велосипеды со смешанным доходом повышают привлекательность центра города (Buehler and Stowe, 2016; Hyra 2012; Tissot, 2011).Наконец, многие городские лидеры действовали по совету влиятельных градостроителей, таких как Эдвард Глезер и Ричард Флорида, которые популяризировали идею о том, что удобства в центральных районах городов привлекают представителей поколения X и миллениалов, которые являются частью состоятельного «креативного класса». », Который оживляет кварталы (Clark, 2011; Флорида, 2014; Glaeser & Shapiro, 2003). Сочетание недооцененной собственности и меняющихся культурных представлений о желательности городской жизни увеличивает спрос на жилье в центральных районах многих США.С. города.
Хотя джентрификация неявно подразумевает экономический переход, поскольку более состоятельный класс заменяет нынешних жителей, многие исследователи также отмечают, что эта форма изменения соседства имеет культурные и расовые аспекты. Представления миллениалов о расе изменились по сравнению с предыдущими поколениями, так что районы меньшинств теперь считаются «крутыми и резкими» (Hyra, 2016), но это не обязательно означает, что они остаются привлекательными или доступными для нынешних жителей.Несколько исследователей обнаружили, что районы, переходящие в состояние изобилия, создают новую социальную напряженность, которая влияет на взаимодействия, что часто может приводить к сегрегации на микроуровне (Chaskin & Joseph, 2015; Tach, 2014; Hyra 2015). Новые жители могут сместить фокус внимания сообщества и динамику политической власти, включая черных и белых джентрификаторов среднего класса, обладающих политическим влиянием в местных инициативах, которые иногда выступают против расширения доступного жилья в их новых районах (Boyd 2005; Hyra 2008; Паттилло 2007).
Несмотря на множество исследований по этому вопросу, остается важный вопрос, означает ли джентрификация также перемещение? Экономика джентрификации прямо заявляет, что стоимость соседской собственности увеличивается, уменьшая предложение доступного жилья, доступного для жителей с низкими доходами, которые затем становятся перемещенными лицами, поскольку стоимость жизни в этом районе увеличивается. Однако несколько исследований показывают, что уровень мобильности людей с низким доходом эквивалентен джентрификации и более стабильным районам с низким доходом (Ding, Hwang & Divringi, 2015; Ellen & O’Regan, 2011; Freeman, 2005; Freeman & Braconi, 2004; Маккинниш, Уолш и Уайт, 2010).Некоторые ссылаются на это как на доказательство того, что массового перемещения не происходит. Однако Хайра (2016) утверждает, что это неверная интерпретация, которая просто показывает, что уровень мобильности для людей с низким доходом одинаково высок во всех типах районов. Дело не в том, что перемещение не происходит в джентрифицированных районах, а в том, что в целом люди с низкими доходами переезжают чаще. Кроме того, перемещение других жителей с низкими доходами обратно в районы для джентрификации сдерживается нехваткой доступного жилья (Ding, Hwang & Divringi, 2015).Со временем в районе происходит чистая потеря жителей с низкими доходами, поскольку стоимость жилья растет, и район становится все менее и менее доступным. Этот переход в экономическом статусе кварталов часто происходит по расовому признаку, поскольку нынешние чернокожие и латиноамериканские жители с низким доходом переезжают и заменяются белыми джентрификаторами с более высокими доходами. Фриман (2005) обнаружил всплеск движения белых в районы чернокожих с 2000 года.
Приток богатых белых джентрификаторов в районы, где раньше проживали малообеспеченные меньшинства, можно рассматривать как форму расового исключения из городских районов с динамично развивающейся экономикой.Из-за расового неравенства в доступе к жилищному кредитованию нынешние чернокожие домовладельцы все чаще отказываются от джентрификации кварталов. В период с 1993 по 2000 год у чернокожих и испаноязычных претендентов на ипотеку в джентрифицированных районах вероятность отказа в кредите была в 2,32 и 1,96 раза выше, чем у белых неиспаноязычных претендентов (Wyly & Hammel 2004). Различия в доступе к ипотечным кредитам на уровне соседства имеют давнюю историю и были задокументированы в нескольких городах NCRC (Richardson et al. 2015 и 2016). Ротштейн (2017) документирует историю красной линии, восходящую к началу 20-го века. Сочетание местной политики, связанной с зонированием, ограничительными условиями, запретом кредитования в «опасных» районах и неформальной сегрегационной практикой, такой как управление жилищным фондом и социальное давление, не позволяло жителям кварталов с низкими доходами и меньшинствами получить доступ к кредитам. Такая модель отказа от инвестиций подготовила почву для джентрификации и переселения во многих районах (Marcuse 1986).Джентрификация, которая снижает предложение доступного жилья, в сочетании с политикой сноса государственного жилья (Goetz 2013) привели к перемещению расовых меньшинств и жителей с низкими доходами в некоторых городах.
МЕТОДЫ
Это исследование было направлено на количественную оценку изменений в перемещении в городских районах США путем оценки изменений на уровне переписного участка (района) с использованием общенациональных данных переписи населения США, нормализованных базой данных продольных трактов (LTDB) ^[7]. Нормализация данных переписи необходима, поскольку границы участков могут со временем меняться, что приводит к неточностям. Мы проанализировали данные LTDB о социально-экономических изменениях в период с 2000 по 2013 год для всех 50 штатов США. Изменения численности населения оценивались с использованием данных десятилетних переписей за 2000 и 2010 годы, которые были нормализованы LTDB.
Исследователи использовали несколько различных методов, чтобы определить районы, которые, по-видимому, переживают джентрификацию, и затем оценить темпы изменения жилья.В исследовании использовалась методология, разработанная Фриманом (2005) и использованная Федеральной резервной системой Филадельфии (Ding, Hwang & Divringi, 2015) и Go Governance.com (2015) для определения местоположения джентрифицированных районов. Этот метод включает оценку уровня образования и экономического статуса жителей, а также стоимости собственности в районе в начале периода переписи, а затем оценку изменений в следующей переписи населения США. Это включает в себя несколько проверок:
Право на участие определяется участками в основной статистической области (CBSA), которые ниже 40 ^— процентилей как по медианному доходу домохозяйства, так и по средней стоимости дома.Кроме того, в начале периода население должно составлять 500 жителей или больше.
Возможная джентрификация определяется путем включения всех подходящих участков и последующего определения участков, которые входили в верхний 60 ^-й процентиль для увеличения как средней стоимости дома, так и процента выпускников колледжей.
Последней проверкой является определение увеличения медианного дохода домохозяйства на уровне района с 2000-2013 гг. С поправкой на инфляцию.
Участки переписи, отвечающие всем вышеперечисленным критериям, были затем определены как проходящие или подвергшиеся джентрификации.
Все критерии джентрификации указывают на то, что социально-экономический статус жителей урочища изменился. Затем мы рассмотрели каждый тракт на предмет изменений в населении расовых подгрупп ^[8]. Эти изменения оценивались по двум критериям;
Снизилась ли доля расовой группы в населении более чем на два стандартных отклонения от среднего значения по всем переписным участкам? ^[9]
Уменьшилось ли абсолютное число жителей этой расовой группы по крайней мере на пять процентов?
Если переписной участок был облагорожен и соответствовал обоим этим критериям, мы определили, что он пережил культурное перемещение ^[10] (Рисунок 1).Культурное смещение происходит, когда вкусы, нормы и желания новичков вытесняют и заменяют вкусы действующих жителей (Zukin 2010). Поскольку такую культурную трансформацию кварталов трудно измерить напрямую, сокращение численности меньшинств использовалось в качестве косвенного показателя. Сдвиги населения были изучены с использованием данных переписи населения за десятилетие 2000 и 2010 годов.
Рисунок 1: Критерии джентрификации и перемещения на уровне переписных участков с использованием десятилетних переписей 2000 и 2010 годов и пятилетних ACS 2009-2013 годов.
РЕЗУЛЬТАТЫ
Национальные изменения — Джентрификация
На национальном уровне 90,7 процента или 67 153 переписных участков имеют статус микрополитена или мегаполиса и относятся к городской зоне. Из этих городских участков 16,7% или 11 196 участков соответствовали критериям права на джентрификацию в 2000 году, в начале периода проверки (Рисунок 2). В общей сложности 1049 переписных участков соответствовали всем трем проверкам на джентрификацию: увеличение средней стоимости дома, уровень образования и рост доходов к 2013 году.Это составляет девять процентов подходящих городских участков для переписи населения в США. Хотя это, кажется, указывает на то, что джентрификация встречается редко, критерии отбора были строгими и ограничивались относительно коротким периодом времени. Джентрификация, по-видимому, сосредоточена в частях крупных и экономически динамичных городов, которые находятся недалеко от центральных деловых районов. Жителей привлекает близость к работодателям, а также наличие множества удобств и услуг, связанных с городским образом жизни.Наконец, перемещение было отмечено в 232, или 22 процентах джентрифицированных участков.
Диаграмма 2: Количество городских переписных участков, отвечающих критериям приемлемости, джентрификации и переселения на национальном уровне. Около девяти процентов подходящих участков были облагорожены, и 17 процентов из них также имели признаки расового / этнического перемещения.
Хотя джентрификация затронула меньшую часть переписных участков в городах США, она была в значительной степени сконцентрирована в крупнейших городских районах. На национальном уровне почти четверть (24 процента) всех городских территорий, или CBSA, подверглась джентрификации по крайней мере одного тракта в период с 2000 по 2013 год (Таблица 1).CBSA — это городские районы с населением не менее 10 000 человек, которые включают небольшие микрополитены, аналогичные городам, и более крупные статистические районы метрополий (MSA) или города. В 13% поселков облагорожен только один урочище. Более умеренные уровни джентрификации, от двух до 10 участков, произошли в восьми процентах городов. Интенсивная джентрификация, когда в период с 2000 по 2013 год было джентрифицировано более 10 участков, произошла в трех процентах городов по стране.
Таблица 1: Города США (CBSA) с количеством участков переписи, облагороженных за период 2000-2013 гг.
Мы оценили численность населения городов, в которых происходила джентрификация. Джентрификация была сосредоточена в крупнейших городских районах. CBSA с населением более одного миллиона человек содержали 79 процентов участков для джентрификации. Еще семь процентов составили города с населением от 500 000 до 1 миллиона человек. В городах с населением от 100 000 до 500 000 человек находилось 10 процентов джентрификационных участков.Самые маленькие города и поселки с населением менее 50 000 человек содержали только четыре процента джентрифицированных территорий в национальном масштабе (рис. 3). Карта показывает, что, хотя в прибрежных городах было наибольшее количество участков, подвергшихся джентрификации, большие города во внутренних районах, такие как Атланта, Даллас, Денвер, Миннеаполис и Питтсбург, также подверглись обширной джентрификации.
Рисунок 3: Национальное распределение городов по количеству участков (кварталов), подвергшихся джентрификации в 2000-2013 гг.
Города с самыми высокими показателями джентрификации включают Нью-Йорк, Лос-Анджелес, Вашингтон, округ Колумбия.C., Филадельфия, Балтимор, Сан-Диего и Чикаго (рис. 4). На эти семь городов приходится почти половина от общего объема джентрификации в стране, или 501 участок из 1049. Удивительно, что муниципальные районы Балтимора и Филадельфии входят в первую десятку списка, занимая четвертое и пятое место по количеству джентрифицированных районов в исследовании, поскольку эти города не считаются одними из самых экономически динамичных городов страны. Различные модели джентрификации очевидны для трех крупнейших городов (Нью-Йорк, Лос-Анджелес, Чикаго) по сравнению со следующими тремя крупнейшими городами (Вашингтон, округ Колумбия). С., Филадельфия, Балтимор).
Рисунок 4: Города по количеству джентрифицированных участков в 2000-2013 гг.
Три крупнейших городских района (Нью-Йорк, Лос-Анджелес, Чикаго) входят в первую семерку по количеству джентрифицированных кварталов на Рисунке 4. Города верхнего уровня по численности населения имеют гораздо больше районов и могут быть более экономически динамичными. чем города второго и третьего уровня. Изучение городов по доле кварталов, отвечающих критериям отбора в 2000 г. и которые действительно были джентрифицированы в течение следующих 10 лет, дает более значимое представление о темпах джентрификации в некоторых районах (таблица 5).Вашингтон, округ Колумбия, был городом с самым высоким процентом джентрификации кварталов, при этом Сан-Диего, Нью-Йорк, Атланта, Балтимор и Портленд также имели как большое количество участков, так и высокие темпы джентрификации.
Таблица 2: Города с высокой долей подходящих для джентрификации кварталов 2000-2013
Изучение карт разных городов выявляет закономерности концентрированной джентрификации в одних и более размытые в других. Анализ карты Балтимора (рис. 5f) показывает концентрацию джентрификации вокруг Внутренней гавани, которая затем простирается от центра города на север до Университета Джонса Хопкинса.Балтимор, Филадельфия и Вашингтон, округ Колумбия, демонстрируют концентрированную джентрификацию вокруг своих центральных деловых районов, тогда как модель джентрификации более разбросана в трех крупнейших городах: Чикаго, Лос-Анджелесе и Нью-Йорке (рисунки 5a-f).
Рис. 5a-f: Джентрификация и перемещение населения в Нью-Йорке, Лос-Анджелесе, Чикаго, Филадельфии, Вашингтоне, округ Колумбия, и Балтиморе. Три крупнейших города (Чикаго, Лос-Анджелес, Нью-Йорк) имеют разбросанный и размытый образец джентрификации, в то время как Балтимор, Филадельфия и Вашингтон, округ Колумбия.C., демонстрируют большую концентрацию деятельности по джентрификации вокруг центральной части города.
Национальные изменения — перемещение
Культурное перемещение было изучено путем расчета сокращения числа чернокожих и испаноязычных жителей в районах переписи. На национальном уровне 187 джентрифицированных участков показали некоторый уровень смещения чернокожих, а 45 участков показали смещение латиноамериканцев (Таблица 3). Это затронуло более 135 000 человек по всей стране. В то время как количество белых жителей увеличивалось в большинстве районов, были случаи, когда численность азиатского и латиноамериканского населения увеличивалась в районах, подвергающихся джентрификации, а численность чернокожего населения уменьшалась.
Таблица 3: Демографический переход территорий с большой потерей жилья чернокожих и латиноамериканцев, 2000-2010 гг.
Затем мы вычислили средние потери в городских районах, которые испытали джентрификацию и потерю постоянного чернокожего или латиноамериканского населения. В случае переселения чернокожего населения средний ущерб на один участок составлял 593 чернокожих жителя (Таблица 4). Самый средний ущерб понес в Новом Орлеане, 1075 чернокожих жителей на каждый участок, в основном из-за массового перемещения районов, вызванного катастрофой урагана Катрина в 2005 году. Потери жилья чернокожих в Вашингтоне, округ Колумбия, Нью-Йорке и Филадельфии были особенно острыми из-за большого количества затронутых участков и большого числа перемещенных лиц. Более 20 000 чернокожих жителей Вашингтона, округ Колумбия, почти 15 000 в Нью-Йорке и 12 000 в Филадельфии переехали из жилых кварталов.
Таблица 4: Районы метро, в которых более двух районов испытали джентрификацию и потерю чернокожего населения в течение 2000-2010 гг. Приведено общее количество участков и среднее количество жителей, потерянных на участках с перемещением.
Участков с признаками перемещения латиноамериканцев было намного меньше, чем участков с признаками перемещения чернокожих, хотя среднее количество перемещенных жителей на один участок было схожим. В 45 районах с признаками переселения латиноамериканцев среднее уменьшение количества жителей составило 542. В Денвере и Остине было самое высокое среднее уменьшение числа жителей латиноамериканского происхождения в районах джентрификации с 1054 и 1039 соответственно (Таблица 5).
Таблица 5: Районы метро, в которых более чем один район испытали джентрификацию и потерю латиноамериканского населения в течение 2000-2010 гг.Приведено общее количество участков и среднее количество жителей на один участок.
Чтобы изучить региональные различия в перемещении чернокожих и латиноамериканцев из джентрифицированных участков, мы рассчитали процент джентрификации участков и участков с признаками перемещения. Города с самым высоким уровнем перемещения чернокожих в период с 2000 по 2010 год были сконцентрированы на юге, при этом девять из 16 городов с высоким уровнем перемещения чернокожих располагались там (Рисунок 6). Ричмонд, Шарлоттсвилль, Вашингтон, Д.C. и Новый Орлеан имели самый высокий процент смещения черных на уровне трактов (рис. 6). В то время как в Ричмонде и Шарлоттсвилле был умеренный уровень джентрификации, по крайней мере, половина районов джентрификации в этих городах также испытали перемещение.
Рис. 6: Районы метро с высоким уровнем вытеснения черных на уровне участков с количеством участков, квалифицируемых как джентрифицированные.
Перемещение латиноамериканцев произошло в меньшем количестве городов, чем перемещение чернокожих, и затронуло 45 переписных участков на национальном уровне.Городом с наибольшим количеством пострадавших участков был Нью-Йорк, где на девяти участках были нанесены убытки, свидетельствующие о перемещении латиноамериканцев. За исключением Нью-Йорка, перемещение латиноамериканцев было наиболее интенсивным на Западе, при этом наибольший процент приходился на Денвер, Остин, Хьюстон и Даллас, затем следовал Лос-Анджелес (Рисунок 7). Однако количество пораженных участков было небольшим: пять в Денвере; четыре в Остине, Далласе и Хьюстоне; и восемь в Лос-Анджелесе. Эта разница в скорости перемещения латиноамериканцев и чернокожих может быть связана с высоким уровнем пригородов для латиноамериканского населения этих городов, поскольку в национальном масштабе 45 процентов испаноязычных жителей живут в районах за пределами центра города. Показатели субурбанизации чернокожих жителей ниже — 39 процентов (Massey & Tannen, 2018). Уровни сегрегации от неиспаноязычных белых также сильно различаются для этих двух демографических групп. Наиболее распространенным показателем сегрегации является индекс несходства, который измеряет равномерность распределения жителей между двумя группами. На национальном уровне этот индекс намного выше для белых неиспаноязычных и чернокожих жилых районов — 0,60, чем для белых неиспаноязычных и испаноязычных жилых районов на.40. Латиноамериканское население также довольно быстро увеличивалось за период исследования, увеличившись с 12,5 процента населения в 2000 году до 16,3 процента в 2010 году. Процент чернокожего населения увеличился меньше, с 12,9 процента в 2000 году до 13,6 процента в 2010 году. более низкие уровни демографического перемещения латиноамериканских жителей могут быть связаны с сочетанием роста населения, меньшей сегрегацией по сравнению с неиспаноязычными белыми и / или уменьшением частоты джентрификации в районах проживания латиноамериканского большинства, которые с большей вероятностью будут расположены в пригородах, чем чернокожие -мажоритарные участки.
Рисунок 7: Джентрификация и перемещение латиноамериканцев в национальном масштабе, на котором более 2 участков были облагорожены в период с 2000 по 2013 год. Рисунок 8: Количество участков с признаками перемещения чернокожих и латиноамериканцев в период с 2000 по 2013 год. Латиноамериканское перемещение сконцентрировано на Западе, а перемещение чернокожих — на Востоке и Среднем Западе.
Критики джентрификации иногда утверждают, что длительное сокращение инвестиций и депопуляция районов создали экономические и социальные условия для последующего культурного перемещения (Marcuse 1986).Чтобы проверить это, мы исследовали города с большим количеством участков с переселенцами чернокожих на предмет долгосрочных демографических сдвигов между 1990 и 2010 годами (Таблица 6). Двадцатилетний период исследования был выбран для отражения влияния демографических изменений, происходящих в течение более длительного периода времени, чем джентрификация, особенно в тех случаях, когда перемещение фактически предшествовало джентрификации. В большинстве случаев в облагораживаемых районах наблюдалась картина уменьшения процента чернокожих и увеличения процента белых жителей.Эта картина уменьшения количества чернокожих и роста числа белых жителей на уровне трактата была особенно распространена в Вашингтоне, округ Колумбия, Сан-Франциско-Окленде, Атланте, Новом Орлеане и Ричмонде. Многие участки также показали, что имела место долгосрочная потеря населения, что указывает на покинутость территории или снижение плотности проживания до или во время демографического перехода. Эта тенденция была очевидна в Балтиморе, но особенно серьезна в Новом Орлеане, где катастрофа урагана «Катрина» вызвала массовое покидание районов.В Филадельфии и Вашингтоне, округ Колумбия, были гораздо более низкие уровни потери населения в районах джентрификации. В городах Даллас, Ричмонд, Нью-Йорк и особенно в Атланте и Сан-Франциско наблюдались высокие темпы прироста населения.
Таблица 6: Участки с указанием переселения чернокожих и проценты общей убыли населения, затем проценты смены жилья черных и белых в джентрифицированных районах города.
Также в период с 1990 по 2010 год во многих городах произошло заметное сокращение латиноамериканского населения и рост белого населения.Исключением были Лос-Анджелес и Сан-Диего (Таблица 7), где как белое, так и испаноязычное население сократилось в джентрифицированных районах. Связь между потерей населения на уровне трактов и демографическими изменениями была очевидна в Денвере, Далласе, Сан-Диего и Чикаго. Области перемещения латиноамериканцев в Денвере, Хьюстоне, Остине и Далласе показаны на рисунках 8 a-d. Во всех этих городах также были урочища, пережившие перемещение чернокожих.
Таблица 7: Территории с указанием переселения латиноамериканцев и процентной доли латиноамериканского и неиспаноязычного белого проживания во всех джентрифицированных районах города.Рисунок 9a-d: Джентрификация и латиноамериканское перемещение. В Денвере, Хьюстоне, Остине и Далласе в CBSA наблюдались самые высокие темпы перемещения латиноамериканцев в течение 2000-2013 гг. Во всех случаях в мегаполисах также были признаки переселения чернокожих жителей.
ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
В прошлых исследованиях джентрификации и перемещения измерялись изменения в районе путем оценки степени мобильности существующих жителей с низкими доходами в джентрифицированных районах. В целом, результаты показали высокие, но сопоставимые показатели мобильности жителей с низкими доходами в джентрифицированных и негентрифицирующих районах, но с низкими показателями замены малоимущих в джентрифицированных районах.Следовательно, этот метод анализа не позволяет напрямую измерять расовое / этническое перемещение. В этом исследовании использовался другой подход, изучались сдвиги в расовом / этническом составе территорий в 2000 и 2010 годах, чтобы определить, где джентрификация и демографические изменения свидетельствовали о перемещении. Национальные темпы джентрификации низкие в малых и малых городах, при этом 76 процентов городских территорий не подвергаются джентрификации в соответствии с нашими критериями. Это может быть консервативная оценка из-за требования абсолютного увеличения дохода домохозяйства.Еще 13 процентов испытали джентрификацию только в одном районе, в то время как 8 процентов городов США испытали умеренную джентрификацию. Тем не менее, в крупнейших населенных пунктах произошла интенсивная джентрификация: 3 процента городов демонстрируют признаки джентрификации в 10 или более районах, а 79 процентов районов джентрификации находятся в городах с населением один миллион или более человек. Хотя джентрификация может быть относительно редкой на национальном уровне, она может быть интенсивной в крупнейших городах с динамично развивающейся экономикой.Прибрежные города испытали самые высокие темпы джентрификации: семь из 10 крупнейших городов по общему количеству джентрифицированных городов расположены на восточном или западном побережье.
Закон о сокращении налогов и занятости от 2017 года создал 8000 зон возможностей по всей стране для привлечения инвестиций в неблагополучные районы. Хотя эти зоны возможностей не были определены, когда началось это исследование, предварительный анализ показывает, что 70 процентов джентрифицированных кварталов находятся в пределах Зоны возможностей или прилегают к ней.Тем не менее, большинство зон возможностей, похоже, не было джентрифицировано в течение периода исследования.
Некоторые вопросы для исследования в будущем: Будут ли инвестиции в зону возможностей концентрироваться в основном в быстрорастущих районах и пропускать многие другие, как мы обнаружили в случае джентрификации. Будут ли инвестиции поступать в основном в зоны возможностей, которые уже джентрифицированы или прилегают к джентрифицированным районам?
Это исследование показывает, что перемещение меньшинств действительно происходит во многих городах, где оно часто концентрируется в районах, прилегающих к центральному деловому району.Перемещение групп меньшинств было высоким в джентрификационных районах, причем 22 процента имели признаки высокого уровня потери жилья чернокожими или латиноамериканцами. В то время как более крупные города испытали более высокий уровень джентрификации, перемещение также соответствовало региональному расположению. Южные города испытали большую интенсивность перемещения чернокожих, в то время как западные города испытали большую интенсивность перемещения латиноамериканцев. Кроме того, Вашингтон, округ Колумбия, и Филадельфия отличались высоким уровнем смещения чернокожих, в то время как Денвер и Остин имели высокий уровень смещения латиноамериканцев.Эти результаты показывают, что джентрификация часто сопровождается высоким уровнем культурного перемещения. Поскольку часть этого исследования, посвященная перемещению, была ограничена десятилетиями до 2010 года, трудно оценить долю районов проживания меньшинств, которые имеют признаки перемещения, которое приведет к расовой и этнической интеграции или со временем перегруппируется и превратится в районы белого большинства. Очень важно изучить экономические и демографические изменения, возникающие в результате джентрификации, на предмет их влияния на равенство на уровне микрорайонов.
ССЫЛКИ
Баум-Сноу, Н. и Хартли, Д., 2016, май. Причины и последствия изменения центрального соседства, 1970–2010 гг. В Research Symposium on Gentrification and Neighborhood Change (стр. 57-85).
Борегар, Р.А., 2001. Федеральная политика и послевоенный упадок городов: случай соучастия правительства ?. Обсуждение жилищной политики , 12 (1), стр. 129-151.
Бойд, М., 2005. Обратная сторона расового подъема: значение джентрификации в афроамериканском районе. Город и общество , 17 (2), стр 265-288.
Бюлер Р. и Стоу Дж., 2016 г. Велосипед в регионе Вашингтона. Дилемма капитала: рост и неравенство в Вашингтоне, округ Колумбия , стр. 180-206.
Часкин, Р.Дж. и Иосиф, М.Л., 2015. оспариваемая пространство: принципы построения и нормативно-правовые режимы в сообществах смешанного дохода в Чикаго. Журнал Американской академии политических и социальных наук , 660 (1), стр. 136-154.
Коэн, Л., 2004. Республика потребителей: политика массового потребления в послевоенной Америке. Journal of Consumer Research , 31 (1), стр 236-239.
Коллинз В.Дж. и Шестер К.Л., 2013. Расчистка трущоб и обновление городов в Соединенных Штатах. Американский экономический журнал: прикладная экономика , 5 (1), стр 239-73.
Couture, V. и Handbury, J., 2017. Городское возрождение в Америке, 2000–2010 годы (№ w24084). Национальное бюро экономических исследований.
Дин, Л., Хван, Дж. И Дивринги, В., 2015. Джентрификация и мобильность в жилых помещениях в Филадельфии. Документы для обсуждения Федерального резервного банка Филадельфии. Октябрь. файл. C: / Пользователи / winifred / Загрузки / дискуссионная бумага_ джентрификация и жилая мобильность. pdf (по состоянию на 20 ноября 2015 г.) .
Эдлунд, Л., Мачадо, К. и Святски, М., 2017. Джентрификация и повышение отдачи от навыков. https://www.gc. cuny.edu/CUNY_GC/media/CUNY-Graduate-Center/PDF/Programs/Economics/Other%20docs/GAll2017x11x13_1.pdf
Эллен, И.Г. и О’Реган, К.М., 2011. Как меняются районы с низким доходом: вход, выход и развитие. Региональная наука и городская экономика , 41 (2), стр. 89-97.
Эллен, И.Г., Мертенс Хорн, К. и Рид, Д., 2016. Привлекает ли падение преступности к джентрификации? Центр Фурмана Нью-Йоркского университета. http://furmancenter.org/files/NYUFurmanCenter_WhitePaper_FallingCrimeGentrification_18OCT2016.pdf
Флорида, Р., 2014. Творческий класс и экономическое развитие. Экономическое развитие ежеквартально , 28 (3), стр. 196-205.
Фримен, Л., 2005. Смещение или наследование? Жилая мобильность в облагороженных кварталах. Urban Affairs Review , 40 (4), стр. 463-491.
Фриман, Л., 2009. Разнообразие микрорайонов, сегрегация мегаполисов и джентрификация: каковы связи в США ?. Городские исследования , 46 (10), стр. 2079-2101.
Фриман, Л. и Бракони, Ф., 2004.Джентрификация и перемещение Нью-Йорка в 1990-е годы. Журнал Американской ассоциации планирования , 70 (1), стр. 39-52.
Фримен, Л. и Цай, Т., 2015. Вхождение белых в кварталы чернокожих: наступление новой эры ?. Анналы Американской академии политических и социальных наук , 660 (1), стр. 302-318.
Glaeser, E.L. и Шапиро, Дж. М., 2003. Рост городов в 1990-е годы: город снова оживает ?. Региональный журнал , 43 (1), стр.139-165.
Глезер, Э. и Вигдор, Дж., 2012. Конец сегрегированного века. Манхэттенский институт политических исследований, январь , стр. 23–26.
Гласс Р., 1964. Аспекты изменений. The Gentrification Debates: Reader , pp.19-30.
Гетц, Э.Г., 2013. Руины Нового курса: раса, экономическая справедливость и государственная жилищная политика . Издательство Корнельского университета.
Хван Дж. И Лин Дж., 2016. Что мы узнали о причинах недавней джентрификации ?. Городской пейзаж , 18 (3), стр.9-26.
Хайра, Д.С., 2008. Новое городское обновление: экономическая трансформация Гарлема и Бронзевилля . Издательство Чикагского университета.
Хайра, Д.С., 2012. Осмысление нового городского обновления: сравнение прошлого с настоящим. Urban Affairs Review , 48 (4), стр. 498-527.
Хайра, Д., 2015. Движение «Назад в город»: реконструкция района и процессы политического и культурного вытеснения. Городские исследования , 52 (10), стр 1753-1773.
Хайра, Д., 2016. Комментарий: Причины и последствия джентрификации и будущее политики справедливого развития. Городской пейзаж , 18 (3), стр 169-178.
Джексон, К.Т., 1987. Граница Крэбграсс: субурбанизация Соединенных Штатов . Издательство Оксфордского университета.
Карас, Д., 2015. Дорога к неравенству: неодинаковое влияние системы межгосударственных автомагистралей на бедные и меньшинства в американских городах. New Visions for Public Affairs , 7 , pp.9-21.
Крегер, Д.А., Лион, С.Дж. и Хейс, З.Р., 2011. Оживление городов и преступность в Сиэтле, 1982–2000 гг. Социальные проблемы , 58 (4), стр. 615-639.
Мэсси, Д.С. и Таннен, Дж., 2018. Субурбанизация и сегрегация в Соединенных Штатах: 1970–2010 годы. Этнические и расовые исследования , 41 (9), стр. 1594-1611.
Маркузе, П., 1986. Начало строительства государственного жилья в Нью-Йорке. Журнал городской истории , 12 (4), стр. 353-390.
Ли, Б.А. и Вуд, П. Б., 1991. Зависит ли соседская расовая преемственность от места проживания? Демография , 28 (1), стр.21-40.
Маркузе, П., (1986) Брошенность, джентрификация и перемещение: связи в Нью-Йорке, в Смит, Н. и Уильямс, П. (ред.) Джентрификация города, Лондон: Анвин Хайман.
Маккинниш, Т., Уолш, Р. и Уайт, Т.К., 2010. Кто облагораживает кварталы с низкими доходами ?. Журнал экономики города , 67 (2), стр. 180-193.
Мельцер, Р., 2016. Джентрификация и малый бизнес: угроза или возможность ?. Городской пейзаж , 18 (3), стр. 57-86.
Mohl, R.A., 2004. Остановите дорогу: восстания на автострадах в американских городах. Журнал городской истории , 30 (5), стр.674-706.
Ньюман К. и Уайли Е.К., 2006. Повторный визит к джентрификации и вытеснению. Исследовательский бюллетень .
Оуэнс, А., 2012. Районы на подъеме: Типология кварталов, переживающих социально-экономический подъем. Город и сообщество , 11 (4), стр 345-369.
Папахристос, А.В., Смит, К.М., Шерер, М.Л. и Фуджиеро, М.А., 2011. Больше кофе, меньше преступности? Связь между джентрификацией и уровнем преступности в районе Чикаго, 1991–2005 гг. Город и сообщество , 10 (3), стр. 215–240.
Паттильо, М., 2017. Черный на блоке. В Расовая структура и радикальная политика в африканской диаспоре (стр. 21-52). Рутледж.
Ричардсон, Дж., Митчелл, Б., Уэст, Н., 2015. Ипотека и кредитование малого бизнеса в Балтиморе и прилегающих районах, NCRC https://ncrc.org/wp-content/uploads/2015/11/ncrc_baltimore_lending_analysis_web .pdf
____________________________, 2016. Ипотечное жилищное кредитование в Сент-Луисе, Милуоки, Миннеаполисе и прилегающих районах, NCRC https://ncrc.org/wp-content/uploads/2018/01/Home-Mortgage-Lending2.pdf
Rothstein, R., 2017. Цвет закона: забытая история того, как наше правительство разделило Америку .Liveright Publishing.
Смит, Н., 1979. К теории джентрификации возврат к городу движение капитала, а не людей. Журнал Американской ассоциации планирования , 45 (4), стр. 538-548.
Тач, Л.М., 2014. Разнообразие, неравенство и микросегрегация: динамика включения и исключения в расово и экономически разнообразном сообществе. Городской пейзаж , 16 (3), стр. 13-46.
Tissot, S., 2011. О собаках и людях: создание пространственных границ в элитном районе. City & Community , 10 (3), стр. 265-284.
Вейл, Л. и Грей, А., 2013. Десятиборье смещения. Журнал Места . https://placesjournal.org/article/the-displacement-decathlon/
Wyly, E.K. и Хаммел, Д.Дж., 2004. Джентрификация, сегрегация и дискриминация в американской городской системе. Окружающая среда и планирование A , 36 (7), стр. 1215-1241.
Zuk, M., Bierbaum, A.H., Chapple, K., Gorska, K., Loukaitou-Sideris, A., Онг, П. и Томас, Т., 2015, август. Джентрификация, вытеснение и роль государственных инвестиций: обзор литературы. В Федеральный резервный банк Сан-Франциско (том 79).
Зукин, С., 2010. Голый город: Смерть и жизнь подлинных городских мест, Нью-Йорк. Oxford University Press
^[1] Культурное перемещение происходит, когда вкусы, нормы и желания новоприбывших вытесняют и заменяют вкусы нынешних жителей, а также может повлечь за собой утрату исторически и культурно значимых институтов. сообщество.
^[2] В этом отчете мы использовали слова «сообщество», «город» и «район метро» как синонимы. Во многих случаях мы также использовали переписной участок в качестве прокси для соседства, и эти слова следует рассматривать как синонимы для наших целей.
^[3] См. Отчет NCRC о HOLC и редлайнинге https://ncrc.org/holc/
^[4] https://www.chicagofed.org/publications/working-papers/2017/wp2017 -12
^[5] Arna Valley Apartments https: // www.usatoday.com/story/news/nation/2014/11/10/niversity-virginia-diversity-race/18079525/
^[6] https://www.washingtoncitypaper.com/news/city-desk/article / 21023685 / после-150-лет-линкольн-храм-объединенная-церковь-христа провела свою последнюю службу
^[7] https://s4.ad.brown.edu/projects /diversity/Researcher/Bridging.htm
^[8] Использовались данные о следующих расовых и этнических подгруппах; неиспаноязычные белые, черные, испаноязычные и азиатские. Только десятилетняя перепись предлагает достаточно низкую ошибку выборки, чтобы ее можно было использовать, ограничивая наше исследование данными переписей 2000 и 2010 годов.
^[9] Изменение численности населения на уровне переписных участков имеет нормальное распределение.
^[10] Хайра, Д., 2015. Движение «Назад в город»: реконструкция района и процессы политического и культурного вытеснения. Городские исследования , 52 (10), стр 1753-1773.
Фотография Jami с Wikicommons.
Закон Планка и закон смещения Вина
Закон Планка описывает излучение, испускаемое черными телами, а закон смещения Вина — максимум спектральной интенсивности этого излучения.Узнайте больше об этом в этой статье.
Эта статья, в частности, дает ответы на следующие вопросы:
Как можно математически описать спектр излучаемой длины волны?
Что утверждает закон Стефана Больцмана?
Как можно вывести закон Стефана-Больцмана из закона Планка?
Что гласит закон Вены о перемещении?
Излучение черного тела
Спектр излучаемых длин волн черного тела, показанный на рисунке ниже, долгое время не мог быть объяснен. До этого всегда предполагалось, что энергия будет распределяться непрерывно. Только введя дискретные уровни энергии, физику Максу Планку удалось математически описать излучение абсолютно черного тела. Хотя сначала он не знал, как физически интерпретировать введение дискретных уровней энергии, он заложил основы квантовой механики.
Планк смог получить следующую формулу для распределения спектральной интенсивности \ (I_s \) как функции длины волны \ (\ lambda \).5} \ cdot \ frac {1} {\ exp \ left (\ dfrac {hc} {\ lambda k_B T} \ right) -1}} ~~~ \ text {Закон Планка (форма длины волны)} \\ [5px ]
\ end {align}
Интенсивность означает мощность излучения черного тела, излучаемого на единицу площади ( поверхностная плотность мощности ). Если, как в этом случае, интенсивность связана с интервалом длин волн, в пределах которого излучается мощность, это называется спектральной интенсивностью . Если спектральная интенсивность нанесена по длине волны, то на такой диаграмме площадь под кривой соответствует излучаемой интенсивности в рассматриваемом диапазоне длин волн. 2} \ cdot \ frac {1} {\ exp \ left (\ dfrac {hf} {k_B T} \ right) -1}} ~~~ \ text {Закон Планка (частотная форма)} \\ [5px]
\ end {align}
В статье «Различные формы закона Планка», вывод этой частотной формы из формы длины волны и другие формы закона Планка обсуждаются подробно.
Закон Стефана-Больцмана
Как уже упоминалось, излучаемая интенсивность определяется площадью под спектральным распределением интенсивности. Следовательно, закон Планка должен быть интегрирован по всему диапазону длин волн или частотному диапазону.3} {\ exp \ left (\ dfrac {hf} {k_B T} \ right) -1} ~ \ text {d} f \\ [5px]
\ end {align}
Этот интеграл можно решить, заменив аргумент \ (\ frac {hf} {k_BT} \) экспоненциальной функции на \ (x \) (интегрирование подстановкой). Таким образом, между переменной \ (x \) и переменной \ (f \) применяются следующие отношения:
\ begin {align}
& x: = \ frac {hf} {k_B T} ~~~ \ Rightarrow \ boxed {\ color {red} {f = \ frac {x k_B T} {h}}} \\ [ 5px]
& \ frac {\ text {d} x} {\ text {d} f} = \ frac {h} {k_B T} ~~~ \ Rightarrow \ boxed {\ color {blue} {\ text {d } f = \ frac {k_B T} {h} \ text {d} x}} \\ [5px]
\ end {align}
Если эти отношения используются в уравнении (\ ref {her}), то получается:
\ begin {align}
& I = \ frac {2 \ pi h} {c ^ 2} \ cdot \ int_ {0} ^ {\ infty} \ frac {\ left (\ color {red} {\ frac {x k_B T} {h}} \ right) ^ 3} {\ exp \ left (\ color {red} {x} \ right) -1} ~ \ color {blue} {\ frac {k_B T} {h} \ текст {d} x} \\ [5px]
& I = \ frac {2 \ pi h} {c ^ 2} \ cdot \ int_ {0} ^ {\ infty} \ frac {k_B ^ 3 T ^ 3} { h ^ 3} \ frac {x ^ 3} {\ exp \ left (x \ right) -1} ~ \ frac {k_B T} {h} \ text {d} x \\ [5px]
& I = \ frac {2 \ pi h} {c ^ 2} \ cdot \ frac {k_B ^ 3 T ^ 3} {h ^ 3} \ cdot \ frac {k_B T} {h} \ cdot \ int_ {0} ^ {\ infty } \ frac {x ^ 3} {\ exp \ left (x \ right) -1} ~ \ text {d} x \\ [5px]
& I = \ frac {2 \ pi k_B ^ 4} {h ^ 3 c ^ 2} T ^ 4 \ int_ {0} ^ {\ infty} \ frac {x ^ 3} {\ exp \ left (x \ right) -1} ~ \ text {d} x \\ [5px]
\ end {align}
Интеграл \ (\ int_ {0} ^ {\ infty} \ frac {x ^ 3} {\ exp \ left (x \ right) -1} ~ \ text {d} x \) не может быть решен так легко в обычным способом. 4} \\ [5px]
\ end {align}
Для неметаллических поверхностей коэффициент излучения во многих случаях превышает 0.9. Поэтому многие объекты можно рассматривать как черные тела в очень хорошем приближении в отношении испускаемого излучения. Это позволяет относительно легко определять температуру реальных объектов с помощью тепловизора или пирометра, так как свойства поверхности имеют довольно незначительное влияние (если только поверхности не обладают высокой отражающей способностью).
Закон Вены о перемещении
Теперь необходимо более внимательно изучить спектральное распределение как функцию температуры.Оказывается, максимум кривой смещается с повышением температуры в сторону все более коротких длин волн. Зависимость этой длины волны \ (\ lambda_ {max} \) от температуры определяется следующим уравнением. Это уравнение также известно как закон смещения Вина .
\ begin {align}
& \ boxed {\ lambda_ {max} = \ frac {2897,8 \ text {мкм K}} {T}} ~~~ \ text {Закон смещения Вина} \\ [5px]
\ end {align}
Рисунок: Закон смещения Вина
Закон смещения Вина может быть получен путем определения максимумов закона Планка. 6 \ cdot \ left [\ exp \ left (\ frac {hc} {k_B T \ lambda} \ right) -1 \ right]}} _ {> 0} \ underbrace {\ left (\ frac {hc} {k_B T \ lambda} \ cdot \ frac {\ exp \ left (\ frac {hc} {k_B T \ lambda} \ right)} {\ exp \ left (\ frac {hc} {k_B T \ lambda} \ right) — 1} — 5 \ right)} _ {= 0} = 0
\ end {align}
Это уравнение будет равно нулю, только если член в круглой скобке станет нулем:
\ begin {align}
& \ frac {hc} {k_B T \ lambda} \ cdot \ frac {\ exp \ left (\ frac {hc} {k_B T \ lambda} \ right)} {\ exp \ left ( \ frac {hc} {k_B T \ lambda} \ right) -1} — 5 = 0 \\ [5px]
\ end {align}
С заменой, приведенной ниже, это уравнение можно упростить:
\ begin {align}
\ label {max}
& \ boxed {x: = \ frac {hc} {\ lambda k_B T}} ~~~ \ Rightarrow ~~~ x \ cdot \ frac {\ exp \ left (x \ right)} {\ exp \ left (x \ right) -1} — 5 = 0 \\ [5px]
\ end {align}
Это уравнение может быть решено только численно, например.грамм. методом Ньютона. Результат будет x = 4,9651. С этим результатом длина волны \ (\ lambda_ {max} \) может быть определена как функция температуры путем преобразования уравнения (\ ref {max}):
\ begin {align}
& \ lambda_ {max} = \ frac {hc} {x k_B T} = \ frac {\ tfrac {hc} {x k_B}} {T} = \ frac {0,0028978 \ text {m K}} {T} = \ frac {2897,8 \ text {µm K}} {T} \\ [5px]
\ end {align}
\ begin {align}
& \ boxed {\ lambda_ {max} = \ frac {2897,8 \ text {мкм K}} {T}} \\ [5px]
\ end {align}
Максимум спектральной интенсивности также можно определить для частотной формы \ (I_s (f) \).{10} \ tfrac {\ text {Hz}} {\ text {K}} \ cdot T}
\ end {align}
Обратите внимание, что закон смещения Вина указывает длину волны \ (\ lambda_ {max} \), на которой спектральная интенсивность имеет максимум. Этот максимум нельзя приравнивать к максимуму самой интенсивности или максимуму мощности излучения! Это приводит, например, к тому, что, хотя общее соотношение \ (f = \ frac {c} {\ lambda} \) применимо, оно не применяется в данном конкретном случае \ (f_ {max} = \ frac {c} { \ lambda_ {max}} \)!
Это связано с тем, что спектральная интенсивность — это величина, связанная с длиной волны. Один измеряет мощность излучения в определенном интервале длин волн \ (\ text {d} \ lambda \) и называет его мощностью излучения. Таким образом, сравнение различных значений мощности излучения возможно только в том случае, если всегда учитываются одни и те же интервалы длин волн. Поскольку частота не пропорциональна длине волны, а обратно пропорциональна, эквидистантные интервалы длин волн также не означают эквидистантные интервалы частот!
Простым примером является диапазон длин волн от 1 до 10 мкм, который разделен на интервалы по 1 мкм каждый.В результате получается следующая эквидистантная серия:
\ begin {align}
& 1-2-3-4-5-6-7-8-9-10 \\ [5px]
\ end {align}
Обратные значения этого, которые в переносном смысле имеют значение частоты как обратной величины длины волны, больше не приводят к эквидистантному ряду:
\ begin {align}
& \ frac {1} {1} — \ frac {1} {2} — \ frac {1} {3} — \ frac {1} {4} — \ frac {1} { 5} — \ frac {1} {6} — \ frac {1} {7} — \ frac {1} {8} — \ frac {1} {9} — \ frac {1} {10} \\ [ 5px]
& 1-0,5-0,333-0,25-0,25-0,2-0,167-0,143-0,125-0,111-0,1 \\ [5px]
\ end {align}
Таким образом, нельзя сравнивать эквидистантные интервалы длин волн с эквидистантными частотными интервалами. Следовательно, частота \ (f_ {max} \), отличная от той, которую можно было ожидать из формулы \ (f_ {max} = \ frac {c} {\ lambda_ {max}} \), получается при использовании частотной формы спектрального интенсивность.
Суперпозиция волн
Суперпозиция волн
Дэниел А. Рассел , аспирантура по акустике, Государственный университет Пенсильвании
Эта работа Дэна Рассела находится под международной лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 4.0.
На основе работы на http://www.acs.psu.edu/drussell/demos.html. Дополнительная информация об использовании этого содержимого доступна по адресу http://www.acs.psu.edu/drussell/Demos/copyright.html.
Содержание этой страницы было первоначально опубликовано 25 июля 1996 г. . HTML-код был изменен для соответствия HTML5 27 января 2014 г.
Принцип суперпозиции может применяться к волнам, когда две (или более) волны проходят через одну и ту же среду одновременно. Волны проходят сквозь друг друга, не беспокоясь. Чистое смещение среды в любой точке пространства или времени — это просто сумма смещений отдельных волн. Это верно для волн конечной длины (волновые импульсы) или непрерывных синусоидальных волн.
Наложение двух волновых импульсов противоположного направления
Анимация слева показывает, что два гауссовых волновых импульса распространяются в одной среде, но в противоположных направлениях. Две волны проходят друг через друга без помех, и чистое смещение является суммой двух отдельных смещений.
Следует также отметить, что эта среда является недисперсной (все частоты распространяются с одинаковой скоростью), поскольку импульсы гауссовой волны не меняют свою форму при распространении. Если бы среда была дисперсной, то волны меняли бы свою форму.
Солитоны — это примеры нелинейных волн, которые не подчиняются принципу суперпозиции при взаимодействии друг с другом.
Конструктивное и разрушительное вмешательство
Две волны (с одинаковой амплитудой, частотой и длиной волны) распространяются в одном направлении. o \)), они интерферируют деструктивно и нейтрализуют друг друга.
Анимация слева показывает, как две синусоидальные волны с одинаковой амплитудой и частотой могут складываться либо деструктивно, либо конструктивно в зависимости от их относительной фазы. (ПРИМЕЧАНИЕ: эта анимация не изображает распространение реальных волн в среде — она служит только для иллюстрации эффекта изменения фазового сдвига между двумя волнами и результирующей конструктивной или деструктивной интерференции). Разность фаз между двумя волнами увеличивается со временем, так что можно увидеть эффекты как конструктивной, так и деструктивной интерференции.Когда две отдельные волны точно совпадают по фазе, в результате получается большая амплитуда. Когда две серые волны становятся точно не в фазе, суммарная волна равна нулю.
Две синусоидальные волны, распространяющиеся в противоположных направлениях, создают стоячую волну
Бегущая волна перемещается из одного места в другое, тогда как стоячая волна , кажется, стоит на месте, колеблясь на месте. В этой анимации две волны (с одинаковой амплитудой, частотой и длиной волны) движутся в противоположных направлениях.Используя принцип суперпозиции, результирующую амплитуду волны можно записать как:
$$ y (x, t) = y_m \ sin (kx — \ omega t) + y_m \ sin (kx + \ omega t) = 2 y_m \ cos (\ omega t) \ sin (kx) $$
Эта волна больше не является бегущей волной, потому что зависимости положения и времени были разделены. Амплитуда волны как функция положения равна \ (2y_m \ sin (kx) \). Эта амплитуда не перемещается, а остается неподвижной и колеблется вверх и вниз согласно \ (\ cos (\ omega t) \). Для стоячих волн характерны места с максимальным смещением ( пучностей, ) и места с нулевым смещением ( узлов, ).
Фильм слева показывает, как стоячая волна может быть создана из двух бегущих волн. Если две синусоидальные волны, имеющие одинаковую частоту (и длину волны) и одинаковую амплитуду, распространяются в противоположных направлениях в одной и той же среде, то при использовании суперпозиции чистое смещение среды является суммой двух волн. Как показано в фильме, когда две волны не совпадают по фазе на 180 ° друг с другом, они нейтрализуются, а когда они точно синфазны друг с другом, они складываются.Когда две волны проходят друг через друга, конечный результат меняется от нуля до некоторой максимальной амплитуды. Однако этот паттерн просто колеблется; она не движется ни вправо, ни влево, и поэтому называется «стоячей волной ».
Я поставил на веревке две точки: одну в пучности, а другую в узле. Что есть что?
Посмотрите мою связанную анимацию, чтобы увидеть, как в среде могут возникать стоячие волны из-за отражения волны от границы.
Две синусоидальные волны с разными частотами: удары
Две волны одинаковой амплитуды движутся в одном направлении. Две волны имеют разные частоты и длины волн, но обе движутся с одинаковой скоростью волны. Используя принцип суперпозиции, результирующее смещение частицы можно записать как:
$$ y (x, t) = y_m \ sin (k_1 x — \ omega_1 t) + y_m \ sin (k_2 x + \ omega_2 t) = 2y_m \ cos \ bigg [\ frac {k_1-k_2} {2} x — \ гидроразрыв {\ omega_1- \ omega_2} {2} t \ bigg] \ sin \ bigg [\ frac {k_1 + k_2} {2} x — \ frac {\ omega_1 + \ omega_2} {2} t \ bigg] $$
Это результирующее движение частицы является произведением двух бегущих волн . Одна часть представляет собой синусоидальную волну, которая колеблется со средней частотой f = ½ ( f ₁ + f ₂). Это частота, которую воспринимает слушатель. Другая часть представляет собой косинусоидальную волну, которая колеблется с разностной частотой f = ½ ( f ₁ — f ₂). Этот термин контролирует амплитуду «огибающей» волны и вызывает восприятие «биений». Частота биений на самом деле в два раза больше разностной частоты, f _биений = ( f ₁ — f ₂).
На анимации слева направо движутся две волны с немного разными частотами. Поскольку две волны движутся в одной и той же среде, они движутся с одинаковой скоростью.
Сочетательное и распределительное свойства умножения доклад, проект
Главная

Разное

Образование

Спорт

Естествознание

Природоведение

Религиоведение

Французский язык

Черчение

Английский язык

Астрономия

Алгебра

Биология

География

Геометрия

Детские презентации

Информатика

История

Литература

Математика

Музыка

МХК

Немецкий язык

ОБЖ

Обществознание

Окружающий мир

Педагогика

Русский язык

Технология

Физика

Философия

Химия

Шаблоны, фоны, картинки для презентаций

Экология

Экономика

Презентация на тему Сочетательное и распределительное свойства умножения, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 14 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Слайд 1Текст слайда:
Тема: Сочетательное и распределительное свойства умножения
Учитель математики:
Назарова Анна Георгиевна
Слайд 2Текст слайда:
Цели урока:
Сформулировать сочетательное и распределительное свойства умножения;
Научить применять свойства при решение выражений, задач;
Развивать умение работать в коллективе;
Воспитывать познавательный интерес к предмету.
Слайд 3Текст слайда:
1. Что называют произведением числа а на натуральное число b не равное нулю? 2. Сформулируйте переместительное свойство умножение? 3.Как записывают в буквенном виде переместительное свойство умножения?
Слайд 4Текст слайда:
Вычислите: 693*100= 974*1000= 540*40= 120*400= 214*10= 100*328=
Слайд 5Текст слайда:
Сочетательное свойство умножение.
Чтобы произведение двух чисел умножить на третье число,можно первое число умножить на произведение второго и третьего чисел.
(ав)с=а(вс)
Слайд 6Текст слайда:
Из переместительного и сочетательного свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений
Слайд 7Текст слайда:
Например:
17*2*3*5 = (17*3)*(2*5)
(3+4)+7=(7+3)+4
Слайд 8Текст слайда:
Распределительное свойство
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
а(в+с)=ав+ас
Слайд 9Текст слайда:
Так же справедливо распределительное свойство умножения относительно вычитания

а(в-с)=ав-ас
Слайд 10Текст слайда:
Например:
Р=2(а+в)
5(2м+7)=10м+35
18п+7п=п(18+7)
Слайд 11Текст слайда:
Работа по учебнику. Письменно. № 420, 422,424
Слайд 12Текст слайда:
Итоги урока.
Сформулируйте сочетательное свойство умножения?
Как записывают в буквенном виде сочетательное свойство умножения?
Сформулируйте распределительное свойство умножения?
Как записывают в буквенном виде распределительное свойство умножения.
Слайд 13Текст слайда:
Рефлексия.
Что нового узнали на уроке…
Что больше понравилось на уроке….
Что было трудным на уроке….
Все ли было легко….
Слайд 14Текст слайда:
Домашнее задание.
Параграф 17, № 421,423,425.
Скачать презентацию
Что такое shareslide.ru?
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Распределительное свойство сложения и умножения. Основные свойства умножения целых чисел
Цели урока:
Получить равенства, выражающие распределительное свойство умножения относительно сложения и вычитания.
Научить учащихся применять это свойство слева направо.
Показать важное практическое значение этого свойства.
Развивать у учащихся логическое мышление. Закрепить навыки работы на компьютере.
Оборудование: компьютеры, плакаты со свойствами умножения, с изображениями машин и яблок, карточки.
Ход урока
1. Вступительное слово учителя.
Сегодня на уроке мы рассмотрим ещё одно свойство умножения, которое имеет важное практическое значение, помогает быстро производить умножение многозначных чисел. Повторим ранее изученные свойства умножения. По ходу изучения новой темы проверим домашнее задание.
2. Решение устных упражнений.
I . На доске запись:
1 – понедельник
2 – вторник
3 – среда
4 – четверг
5 – пятница
6 – суббота
7 – воскресенье
Задание. Задумайте день недели. Умножить номер задуманного дня на 2. Прибавить к произведению 5. Умножить сумму на 5. Увеличить произведение в 10 раз. Назвать результат. Вы загадали… день.
(№ * 2 + 5) * 5 * 10
II . Задание из электронного учебника «Математика 5-11кл. Новые возможности для усвоения курса математики. Практикум». ООО «Дрофа» 2004, ООО «ДОС» 2004, CD – ROM, НФПК». Раздел «Математика. Натуральные числа». Задание №8. Экспресс-контроль. Заполните пустые клетки в цепочке. Вариант 1.
III . На доске:
a + b
(a + b) * c
m – n
m * c – n * c
2) Упростить:
5 * x * 6 * y
3 * 2 * а
а * 8 * 7
3 * а * b
3) При каких значениях x равенство обращается в верное:
x + 3 = 3 + x
407 * x = x * 407? Почему?
Какие свойства умножения применялись?
3. Изучение нового материала.
На доске плакат с изображениями машин.
Рисунок 1.
Задание для 1 группы учащихся (мальчиков).
В гараже в 2-х рядах стоят грузовые и легковые машины. Записать выражения.
Сколько грузовых машин в 1-ом ряду? Сколько легковых?
Сколько грузовых машин во 2-ом ряду? Сколько легковых?
Сколько машин всего в гараже?
Сколько грузовых машин в 1-ом ряду? Сколько грузовых машин в двух рядах?
Сколько легковых машин в 1-ом ряду? Сколько легковых машин в двух рядах?
Сколько всего машин в гараже?
Найти значения выражений 3 и 6. Сравнить эти значения. Записать выражения в тетрадь. Прочитать равенство.
Задание для 2 группы учащихся (мальчиков).
В гараже в 2-х рядах стоят грузовые и легковые машины. Что означают выражения:
4 – 3
4 * 2
3 * 2
(4 – 3) * 2
4 * 2 – 3 * 2
Найти значения двух последних выражений.
Значит, между этими выражениями можно поставить знак =.
Прочитаем равенство: (4 – 3) * 2 = 4 * 2 – 3 * 2.
Плакат с изображениями красных и зелёных яблок.
Рисунок 2.
Задание для 3 группы учащихся (девочек).
Составить выражения.
Какова масса одного красного и одного зелёного яблока вместе?
Какова масса всех яблок вместе?
Какова масса всех красных яблок вместе?
Какова масса всех зелёных яблок вместе?
Какова масса всех яблок?
Найти значения выражений 2 и 5 и сравнить их. Записать это выражение в тетрадь. Прочитать.
Задание для 4 группы учащихся (девочек).
Масса одного красного яблока 100 г, одного зелёного 80 г.
Составить выражения.
На сколько г масса одного красного яблока больше, чем зелёного?
Какова масса всех красных яблок?
Какова масса всех зелёных яблок?
На сколько г масса всех красных яблок больше, чем зелёных?
Найти значения выражений 2 и 5.Сравнить их. Прочитать равенство. Только ли для этих чисел верны равенства?
4. Проверка домашнего задания.
Задание. По краткой записи условия задачи поставить главный вопрос, составить выражение и найти его значение при данных значениях переменных.
1 группа
Найти значение выражения при а = 82,b = 21, c = 2.
2 группа
Найти значение выражения при а = 82, b = 21, с= 2.
3 группа
Найти значение выражения при а = 60, b = 40, с = 3.
4 группа
Найти значение выражения при а = 60, b =40, с = 3.
Работа в классе.
Сравнить значения выражений.
Для 1 и 2 групп:(а + b) * с и а * с + b * с
Для 3 и 4 групп:(а – b) * с и а * с – b * с
(а + b) * с = а * с + b * с
(а – b) * с = а * с – b * с
Итак, для любых чисел а, b, с верно:
При умножении суммы на число можно умножить на это число каждое слагаемое и сложить полученные произведения.
При умножении разности на число можно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе.
При умножении суммы или разности на число умножение распределяется на каждое число, заключённое в скобках. Поэтому это свойство умножения называется распределительным свойством умножения относительно сложения и вычитания.
Прочитаем формулировку свойства по учебнику.
5. Закрепление нового материала.
Выполнить №548. Примените распределительное свойство умножения.
(68 + а) * 2
17 * (14 – x)
(b – 7) * 5
13 * (2 + y)
1) Выбирай задания на оценку.
Задания на оценку «5».
Пример 1. Найдём значение произведения 42 * 50. Представим число 42 в виде суммы чисел 40 и 2.
Получим: 42 * 50 = (40 + 2) * 50. Теперь применим распределительное свойство:
42 * 50 = (40 + 2) * 50 = 40 * 50 + 2 * 50 = 2 000 +100 = 2 100.
Аналогично решить №546:
а) 91 * 8
в) 6 * 52
д) 202 * 3
ж) 24 * 11
з) 35 * 12
и) 4 * 505
Представить числа 91,52, 202, 11, 12, 505 в виде суммы десятков и единиц и применить распределительное свойство умножения относительно сложения.
Пример 2. Найдём значение произведения 39 * 80.
Представим число 39 в виде разности 40 и 1.
Получим: 39 * 80 = (40 – 1) = 40 * 80 – 1 * 80 = 3 200 – 80 = 3 120.
Решить из №546:
б) 7 * 59
е) 397 * 5
г) 198 * 4
к) 25 * 399
Представить числа 59, 397, 198, 399 в виде разности десятков и единиц и применить распределительное свойство умножения относительно вычитания.
Задания на оценку «4».
Решить из №546 (а, в, д, ж, з, и). Применить распределительное свойство умножения относительно сложения.
Решить из № 546 (б, г, е, к). Применить распределительное свойство умножения относительно вычитания.
Задания на оценку «3».
Решить №546 (а, в, д, ж, з, и). Применить распределительное свойство умножения относительно сложения.
Решить №546 (б, г, е, к).
Для решения задачи №552 составить выражение и выполнить рисунок.
Расстояние между двумя сёлами 18 км. Из них выехали в разные стороны два велосипедиста. Один проезжает в час m км, а другой n км. Какое расстояние будет между ними через 4 ч?
(Устно. Примеры записаны на обратной стороне доски.)
Вместо поставьте пропущенные цифры:
Задание из электронного учебника «Математика 5-11кл. Новые возможности для усвоения курса математики. Практикум». ООО «Дрофа» 2004, ООО «ДОС» 2004, CD – ROM, НФПК». Раздел «Математика. Натуральные числа». Задание №7. Экспресс-контроль. Восстановите пропавшие цифры.
6. Подведение итогов урока.
Итак, мы рассмотрели распределительное свойство умножения относительно сложения и вычитания. Повторим формулировку свойства, прочитаем равенства, выражающие свойство. Применение распределительного свойства умножения слева направо можно выразить условием «раскрыть скобки», т. к. в левой части равенства выражение было заключено в скобки, а в правой скобок нет. При решении устных упражнений на отгадывание дня недели мы тоже использовали распределительное свойство умножения относительно сложения.
(№ * 2 + 5) * 5 * 10 = 100 * № + 250, а затем решали уравнение вида:
100 * № + 250 = а
Мы определили сложение, умножение, вычитание и деление целых чисел. Эти действия (операции) обладают рядом характерных результатов, которые называются свойствами. В этой статье мы рассмотрим основные свойства сложения и умножения целых чисел, из которых следуют все остальные свойства этих действий, а также свойства вычитания и деления целых чисел.
Навигация по странице.
Для сложения целых чисел характерны еще несколько очень важных свойств.
Одно из них связано с существованием нуля. Это свойство сложения целых чисел утверждает, что прибавление к любому целому числу нуля не изменяет это число . Запишем данное свойство сложения с помощью букв: a+0=a и 0+a=a (это равенство справедливо в силу переместительного свойства сложения), a – любое целое число. Можно услышать, что целое число нуль называют нейтральным элементом по сложению. Приведем пару примеров. Сумма целого числа −78 и нуля равна −78 ; если к нулю прибавить целое положительное число 999 , то в результате получим число 999 .
Сейчас мы дадим формулировку еще одного свойства сложения целых чисел, которое связано с существованием противоположного числа для любого целого числа. Сумма любого целого числа с противоположным ему числом равна нулю . Приведем буквенную форму записи этого свойства: a+(−a)=0 , где a и −a – противоположные целые числа. Например, сумма 901+(−901) равна нулю; аналогично сумма противоположных целых чисел −97 и 97 равна нулю.
Основные свойства умножения целых чисел
Умножению целых чисел присущи все свойства умножения натуральных чисел . Перечислим основные из этих свойств.
Также как нуль является нейтральным целым числом относительно сложения, единица является нейтральным целым числом относительно умножения целых чисел. То есть, умножение любого целого числа на единицу не изменяет умножаемое число . Так 1·a=a , где a – любое целое число. Последнее равенство можно переписать в виде a·1=a , это нам позволяет сделать переместительное свойство умножения. Приведем два примера. Произведение целого числа 556 на 1 равно 556 ; произведение единицы и целого отрицательного числа −78 равно −78 .
Следующее свойство умножения целых чисел связано с умножением на нуль. Результат умножения любого целого числа a на нуль равен нулю , то есть, a·0=0 . Также справедливо равенство 0·a=0 в силу переместительного свойства умножения целых чисел. В частном случае при a=0 произведение нуля на нуль равно нулю.
Для умножения целых чисел также справедливо свойство, обратное к предыдущему. Оно утверждает, что произведение двух целых чисел равно нулю, если хотя бы один из множителей равен нулю . В буквенном виде это свойство можно записать так: a·b=0 , если либо a=0 , либо b=0 , либо и a и b равны нулю одновременно.
Распределительное свойство умножения целых чисел относительно сложения
Совместно сложение и умножение целых чисел нам позволяет рассматривать распределительное свойство умножения относительно сложения, которое связывает два указанных действия. Использование сложения и умножения совместно открывает дополнительные возможности, которых мы были бы лишены, рассматривая сложение отдельно от умножения.
Итак, распределительное свойство умножения относительно сложения гласит, что произведение целого числа a на сумму двух целых чисел a и b равно сумме произведений a·b и a·c , то есть, a·(b+c)=a·b+a·c . Это же свойство можно записать в другом виде: (a+b)·c=a·c+b·c .
Распределительное свойство умножения целых чисел относительно сложения вместе с сочетательным свойством сложения позволяют определить умножение целого числа на сумму трех и большего количества целых чисел, а далее – и умножение суммы целых чисел на сумму.
Также заметим, что все остальные свойства сложения и умножения целых чисел могут быть получены из указанных нами свойств, то есть, они являются следствиями указанных выше свойств.
Свойства вычитания целых чисел
Из полученного равенства, а также из свойств сложения и умножения целых чисел вытекают следующие свойства вычитания целых чисел (a , b и c – произвольные целые числа):
Вычитание целых чисел в общем случае НЕ обладает переместительным свойством: a−b≠b−a .
Разность равных целых чисел равна нулю: a−a=0 .
Свойство вычитания суммы двух целых чисел из данного целого числа: a−(b+c)=(a−b)−c .
Свойство вычитания целого числа из суммы двух целых чисел: (a+b)−c=(a−c)+b=a+(b−c) .
Распределительное свойство умножения относительно вычитания: a·(b−c)=a·b−a·c и (a−b)·c=a·c−b·c .
И все другие свойства вычитания целых чисел.
Свойства деления целых чисел
Рассуждая о смысле деления целых чисел , мы выяснили, что деление целых чисел – это действие, обратное умножению. Мы дали такое определение: деление целых чисел – это нахождение неизвестного множителя по известному произведению и известному множителю. То есть, целое число c мы называем частным от деления целого числа a на целое число b , когда произведение c·b равно a .
Данное определение, а также все рассмотренные выше свойства операций над целыми числами позволяют установить справедливость следующих свойств деления целых чисел:
Никакое целое число нельзя делить на нуль.
Свойство деления нуля на произвольное целое число a , отличное от нуля: 0:a=0 .
Свойство деления равных целых чисел: a:a=1 , где a – любое целое число, отличное от нуля.
Свойство деления произвольного целого числа a на единицу: a:1=a .
В общем случае деление целых чисел НЕ обладает переместительным свойством: a:b≠b:a .
Свойства деления суммы и разности двух целых чисел на целое число: (a+b):c=a:c+b:c и (a−b):c=a:c−b:c , где a , b , и c такие целые числа, что и a и b делится на c , и c отлично от нуля.
Свойство деления произведения двух целых чисел a и b на целое число c , отличное от нуля: (a·b):c=(a:c)·b , если a делится на c ; (a·b):c=a·(b:c) , если b делится на c ; (a·b):c=(a:c)·b=a·(b:c) , если и a и b делятся на c .
Свойство деления целого числа a на произведение двух целых чисел b и c (числа a , b и c такие, что деление a на b·c возможно): a:(b·c)=(a:b)·c=(a:c)·b .
Любые другие свойства деления целых чисел.
Рассмотрим пример, подтверждающий справедливость переместительного свойства умножения двух натуральных чисел. Отталкиваясь от смысла умножения двух натуральных чисел , вычислим произведение чисел 2 и 6 , а также произведение чисел 6 и 2 , и проверим равенство результатов умножения. Произведение чисел 6 и 2 равно сумме 6+6 , из таблицы сложения находим 6+6=12 . А произведение чисел 2 и 6 равно сумме 2+2+2+2+2+2 , которая равна 12 (при необходимости смотрите материал статьи сложение трех и большего количества чисел). Следовательно, 6·2=2·6 .
Приведем рисунок, иллюстрирующий переместительное свойство умножения двух натуральных чисел.
Сочетательное свойство умножения натуральных чисел.
Озвучим сочетательное свойство умножения натуральных чисел: умножить данное число на данное произведение двух чисел – это то же самое, что умножить данное число на первый множитель, и полученный результат умножить на второй множитель . То есть, a·(b·c)=(a·b)·c , где a , b и c могут быть любыми натуральными числами (в круглые скобки заключены выражения, значения которых вычисляются в первую очередь).
Приведем пример для подтверждения сочетательного свойства умножения натуральных чисел. Вычислим произведение 4·(3·2) . По смыслу умножения имеем 3·2=3+3=6 , тогда 4·(3·2)=4·6=4+4+4+4+4+4=24 . А теперь выполним умножение (4·3)·2 . Так как 4·3=4+4+4=12 , то (4·3)·2=12·2=12+12=24 . Таким образом, справедливо равенство 4·(3·2)=(4·3)·2 , подтверждающее справедливость рассматриваемого свойства.
Покажем рисунок, иллюстрирующий сочетательное свойство умножения натуральных чисел.

В заключении этого пункта отметим, что сочетательное свойство умножения позволяет однозначно определить умножение трех и большего количества натуральных чисел .
Распределительное свойство умножения относительно сложения.
Следующее свойство связывает сложение и умножение. Оно формулируется так: умножить данную сумму двух чисел на данное число – это то же самое, что сложить произведение первого слагаемого и данного числа с произведением второго слагаемого и данного числа . Это так называемое распределительное свойство умножения относительно сложения.
С помощью букв распределительное свойство умножения относительно сложения записывается как (a+b)·c=a·c+b·c (в выражении a·c+b·c сначала выполняется умножение, после чего – сложение, подробнее об этом написано в статье ), где a , b и c – произвольные натуральные числа. Отметим, что силу переместительного свойства умножения, распределительное свойство умножения можно записать в следующем виде: a·(b+c)=a·b+a·c .
Приведем пример, подтверждающий распределительное свойство умножения натуральных чисел. Проверим справедливость равенства (3+4)·2=3·2+4·2 . Имеем (3+4)·2=7·2=7+7=14 , а 3·2+4·2=(3+3)+(4+4)=6+8=14 , следовательно, равенство (3+4)·2=3·2+4·2 верно.
Покажем рисунок, соответствующий распределительному свойству умножения относительно сложения.

Распределительное свойство умножения относительно вычитания.
Если придерживаться смысла умножения, то произведение 0·n , где n – произвольное натуральное число, большее единицы, представляет собой сумму n слагаемых, каждое из которых равно нулю. Таким образом, . Свойства сложения позволяют нам утверждать, что последняя сумма равна нулю.
Таким образом, для любого натурального числа n выполняется равенство 0·n=0 .
Чтобы оставалось справедливым переместительное свойство умножения примем также справедливость равенства n·0=0 для любого натурального числа n .
Итак, произведение нуля и натурального числа равно нулю , то есть 0·n=0 и n·0=0 , где n – произвольное натуральное число. Последнее утверждение представляет собой формулировку свойства умножения натурального числа и нуля.
В заключении приведем пару примеров, связанных с разобранным в этом пункте свойством умножения. Произведение чисел 45 и 0 равно нулю. Если умножить 0 на 45 970 , то тоже получим нуль.
Теперь можно смело начинать изучение правил, по которым проводится умножение натуральных чисел .
Список литературы.
Математика. Любые учебники для 1, 2, 3, 4 классов общеобразовательных учреждений.
Математика. Любые учебники для 5 классов общеобразовательных учреждений.
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143 ). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3 . Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3 ) * 4 .
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4 ).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4 . Имеем: (5 * 3 ) * 4 = 5 * (3 * 4 ).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений .
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3 ) * (2 * 5 ).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2 . Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2 ).
Равенсто 3 * (3 + 2 ) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения .
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2 a + 2 b для нахождения периметра прямоугольника записать в таком виде:
P = 2 (a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1 . Вычислите удобным способом:
1 ) 25 * 867 * 4 ;
2 ) 329 * 75 + 329 * 246 .
1 ) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * (25 * 4 ) = 867 * 100 = 86 700 .
2 ) Имеем:
329 * 754 + 329 * 246 = 329 * (754 + 246 ) = 329 * 1 000 = 329 000 .
Пример 2 . Упростите выражение:
1 ) 4 a * 3 b;
2 ) 18 m − 13 m.
1 ) Используя переместительное и сочетательное свойства умножения, получаем:
4 a * 3 b = (4 * 3 ) * ab = 12 ab.
2 ) Используя распределительное свойство умножения относительно вычитания, получаем:
18 m − 13 m = m(18 − 13 ) = m * 5 = 5 m.
Пример 3 . Запишите выражение 5 (2 m + 7 ) так, чтобы оно не содержало скобок.
Согласно распределительному свойству умножения относительно сложения имеем:
5 (2 m + 7 ) = 5 * 2 m + 5 * 7 = 10 m + 35 .
Такое преобразование называют раскрытием скобок .
Пример 4 . Вычислите удобным способом значение выражения 125 * 24 * 283 .
Решение. Имеем:
125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8 ) * (3 * 283 ) = 1 000 * 849 = 849 000 .
Пример 5 . Выполните умножение: 3 сут 18 ч * 6 .
Решение. Имеем:
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
Технологическая карта открытого урока по математике на тему «Сочетательное и распределительное свойство умножения». 5-й класс
org/Person»> Петрухина Александра Вадимовна
Разделы: Математика
Класс: 5
Ключевые слова: свойство умножения
Базовый учебник: А.Г.Мерзляк, В.Б.Полонский, М.С.Якир Математика: Учебник для 5 класса общеобразовательных учреждений / А.Г. и др. — 2-е изд., перераб. – М. :Вентана Граф, 2018.
Тип урока: Комбинированный урок.
Цели:
Образовательные: создать условия для организации деятельности учащихся, направленной на формирование компетенций.
Развивающие: способствовать развитию критического мышления, математической грамотности, внимания, умения сравнивать и обобщать понятия.
Воспитательные: обеспечить условия для взаимодействия в команде, интереса к предмету.
Предметные: закрепить навыки применения сочетательного и распределительного свойств умножения для рациональных способов вычислений и преобразований.
Личностные: формировать умение контролировать процесс и результат учебной и математической деятельности.
Метапредметные: формировать умение строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы, развивать способность к самопроверке, взаимопроверке
Планируемые результаты: учащиеся научатся применять сочетательное и распределительное свойства умножения для выбора наиболее рациональных способов вычислений.
Основные понятия: Сочетательное свойство умножения, распределительное свойство умножения относительно сложения, распределительное свойство умножения относительно вычитания.
Формы работы учащихся: фронтальная, групповая, парная, индивидуальная.
Оборудование: компьютер, проектор, раздаточный материал, презентация
№
Этапы организации учебной деятельности
Цель
этапа
Деятельность учителя
Деятельность учащихся
Формируемые универсальные учебные действия (УУД)
1.
Организационный этап
(3 мин.)
Постановка цели и задач урока. Мотивация учебной деятельности учащихся.
Проговариваю цель урока, ставлю учебную задачу.
Интерактивная работа с приложением www. menti.com.
Учащимся необходимо записать при помощи своих мобильных устройств, слова, выражения, которые им приходят на ум при использовании термина Свойство.
Уточняю понимание учащимися поставленных целей.
Выполняют задание.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: целеполагание, планирование.
Познавательные: самостоятельное выделение и формулирование познавательной цели.
Коммуникативные: умения слушать, осознанно строить речевое высказывание, воспринимать ответы учащихся.
2.
Этап актуализации знаний
(5 мин.)
Организовать познавательную деятельность учащихся.
Организую работу по рядам у доски, (соревновательный момент), необходимо записать свойства умножения.
— Переместительное свойство;
— Сочетательное свойство;
— Распределительное свойство относительно сложения;
— Распределительное свойство относительно вычитания;
— Свойство умножения на единицу;
— Свойство умножения на нуль.
Проговорить свойства в парах.
Выходят к доске по очереди, друг за другом, 6 человек от каждого ряда и записывают свойства умножения

Проговаривают свойства в парах.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: волевая саморегуляция.
Познавательные: поиск и выделение необходимой информации, смысловое чтение.
Коммуникативные: умения слушать, осознанно строить речевое высказывание, воспринимать ответы учащихся.
3.
Этап закрепления изученного материала
(8 мин. )
Организовать деятельность учащихся по закреплению знаний.
Формулирую задание. (На основе заранее подготовленного домашнего задания. Учащимся необходимо было составить математические задачи, и иллюстрации к ним). Учащимся, необходимо поменяться друг с другом задачами и выполнить решение в тетради.
Выполняют задание, работают индивидуально, решая задачи в тетрадях, осуществляют проверку.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: волевая саморегуляция, контроль.
Познавательные: умение осознанно и произвольно строить речевое высказывание.
Коммуникативные: умение участвовать в коллективном обсуждении, умение выражать свои мысли.
4.
Изучение нового материала
(7 мин).
Показать новый способ решения примеров с буквенной частью.
Подсказки:
Приготовить несколько непонятных примеров. Показать ученикам без объяснений, что это и зачем это нужно. Попросить угадать, верно решенный пример, давая подсказки, термины.
Логически, на основании полученных знаний, подсказки учителя, находят верно решенные примеры. Выявляют новый способ рационального решения примеров.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: волевая саморегуляция, контроль, коррекция.
Познавательные: умение выбрать наиболее эффективные способы решения.
Коммуникативные: способность сохранять доброжелательное отношение друг к другу.
5.
Этап первичного закрепления изученного материала.
(13 мин.)
Закрепить изученный материал.
Заполнить все:
Подготовить задания по теме урока с пропущенными полями. Раздать ученикам и попросить заполнить поля. В конце обсудить, что осталось незаполненным. Попросить озвучить, что получилось.
Выполняют задания, работая в парах на раздаточном материале, затем комментируют, проговаривая получившиеся результаты.
Сравнивают, устраняют ошибки.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: волевая саморегуляция, контроль, коррекция.
Познавательные: умение выбрать наиболее эффективные способы решения, рефлексия.
Коммуникативные: способность сохранять доброжелательное отношение друг к другу, умение договариваться, слушать и вступать в диалог.
6.
Рефлексия.
(3 мин.)
Провести самооценку.
Какова была тема урока?
Какую цель надо было достигнуть?
При помощи мобильных устройств и приложения www.menti.com осуществляют оценку урока и самооценку.
Проговаривают тему и цель урока.
Осуществляют самооценку.
Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности.
Регулятивные: контроль, коррекция, оценка.
Познавательные: умение осознанно и произвольно строить речевое высказывание в устной и письменной форме.
Коммуникативные: способность сохранять доброжелательное отношение друг к другу, умение слушать.
7.
Домашнее задание.
(1 мин.)
Разъяснить методику выполнения домашнего задания.
§17, упр. 429, 432, 435
Записывают домашнее задание.
Личностные: развитие ответственности.
Регулятивные: волевая саморегуляция.
Познавательные: умение выбрать наиболее эффективные способы решения
Коммуникативные: умение слушать.
14.10.2020
Свойства умножения и деления кратко Арифметика
Привет, мой друг, тебе интересно узнать все про свойства умножения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое свойства умножения, свойства деления , настоятельно рекомендую прочитать все из категории Арифметика.
свойства умножения
Переместительное свойство умножения
От перестановки множителей произведение не меняется.

a • b = b • a
Сочетательное свойство умножения
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.

a • (b • c) = (a • b) • c
Переместительное и сочетательное свойства умноженияпозволяют сформулировать правило преобразования произведений.
При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.

a • 0 = 0
0 • a • b • c = 0
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.

(a + b) • c = a • c + b • c
Это свойство справедливо для любого количества слагаемых.

(a + b + с + d) • k = a • k + b • k + c • k + d • k
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так:

(a — b) • c = a • c — b • c
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
свойства деления
Ни одно число нельзя делить на нуль.

При делении нуля на число получается нуль.
0 : a = 0

При делении любого числа на 1 получается это же число.
b : 1 = b

Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.

a : b = (a • k) : (b • k), где k — любое натуральное число.
Обратите внимание, что именно свойство деления выше позволяет намсокращать дроби.
Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений.
Задача
У Короля есть 45 мешков с золотыми монетами, в каждом мешке по 108 золотых монет.
Он хочет разделить эти деньги поровну между своими тремя сыновьями.
Сколько золотых монет достанется каждому из принцев?
Решение 1

1)45:3=15(мешков) достанется мешков каждому принцу

2)15*108=1620(монет) достанется монет каждому принцу

Решение 2

1)45*108=4860(монет) всего монет у короля

2)4860:3=1620(монет) достанется монет каждому принцу

Решение 3

1)108:3=36(монет) каждому принцу, если делить один мешок

2)36*45=1620(монет) достанется монет каждому принцу

См . Об этом говорит сайт https://intellect.icu . также
десятичные дроби ,

умножение в столбик ,

как читать десятичные дроби ,

перевод обыкновенной дроби в десятичную ,

нахождение обыкновенной дроби от числа ,

деление обыкновенных дробей ,

умножение обыкновенных дробей ,

вычитание обыкновенных дробей ,

взаимно обратные числа , взаимно обратные дроби ,

сравнение обыкновенных дробей ,

периодическая дробь ,

сложение обыкновенных дробей , общий знаменатель ,

сокращение обыкновенных дробей ,

смешанные числа , выделение целой части обыкновенной дроби ,

Как ты считаеешь, будет ли теория про свойства умножения улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое свойства умножения, свойства деления и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Из статьи мы узнали кратко, но емко про свойства умножения
Объяснение коммутативных, ассоциативных и дистрибутивных свойств
Коммутативные, ассоциативные и дистрибутивные свойства или законы лежат в основе алгебры и впервые знакомятся с детьми, в очень общих чертах, в начальной школе. В нашем руководстве для родителей мы объясняем, как ваш ребенок начнет понимать основы высшей математики.
или Зарегистрируйтесь, чтобы добавить к своим сохраненным ресурсам
Что такое коммутативное, ассоциативное и дистрибутивное свойство?
Коммутативность, ассоциативность и дистрибутивность используются в алгебре для решения задач с числами.
Коммутативное свойство, объясненное для родителей
Слово «коммутативный» происходит от «коммутировать» или «перемещаться», поэтому коммутативное свойство относится к способности перемещать числа внутри числовых предложений .
Например: 2 + 3 дает ответ 5, и если мы переставим числа так, чтобы получилось 3 + 2, мы все равно получим ответ 5. Точно так же с умножением: 6 x 4 = 24, так же как 4 x 6 = 24.
В алгебре мы записали бы свойство коммутативности как:
a + b = b + a
a × b = b × a
Свойство перестановочности применимо к сложению и умножению, но не к вычитанию или делению.

Дети начальной школы вряд ли услышат слова «переместительное свойство», но детей 2-го класса учат, что сложение чисел можно выполнять в любом порядке, а вычитание чисел нельзя .
Объяснение ассоциативного свойства для родителей
Ассоциативное свойство говорит о том, что когда мы складываем или умножаем числа, не имеет значения, как мы их группируем.
Это правило применяется к числам, сгруппированным в скобках, например: 2 + (3 + 4) или 5 х (2 х 3).
Мы заключаем расчеты в скобки, когда хотим, чтобы кто-то первым сделал эти расчеты. Однако, когда речь идет о группе чисел, которые нужно добавить, не имеет значения, куда идут скобки, ответ все равно будет тот же. Точно так же и с группой чисел, которые нужно перемножить, ответ будет одинаковым вне зависимости от того, как сгруппированы числа.
В алгебре ассоциативное свойство записывается следующим образом:
(a + b) + c = a + (b + c)
(a × b) × c = a × (b × c)
ассоциативное свойство относится к сложению и умножению, но не к вычитанию или делению.
Маловероятно, что дети услышат термин «ассоциативное свойство» в начальной школе, но их могут попросить решить задачу, например следующую, где применяется правило:
Три друга собрали сосновые шишки и собирают их в контейнер. Мэри и Пол собирают по 20 сосновых шишек. Джон добавляет в коллекцию еще 15. Сколько их всего?
При решении приведенной выше задачи со словами (20 + 20) + 15 = 20 + (20 + 15)
<noscript><img loading='lazy' src='' /></noscript> youtube.com/embed/81NfQ350vw8?rel=0″/>
Распределительное свойство, объясненное для родителей .
Например: если мы хотим выполнить следующее умножение 2(5 +3), это означает, что мы вычисляем, сколько будет 2 лотов по 5, плюс 2 лота по 3, так что 2x можно «распределить» по 5 + 3 в 2 x 5 и 2 x 3. Это можно записать в виде следующей формулы:
a × (b + c) = a × b + a × c
Опять же, термин «распределительное свойство» не будет использоваться в начальной школе явно, однако детей могут попросить решить аналогичную задачу на следующий:
В Березовом классе 25 детей, в Каштановом классе 28 детей. Каждый ребенок в обоих классах должен принести пару перчаток в школу в понедельник. Сколько всего индивидуальных перчаток будет доставлено?
Здесь ребенку нужно понять, что он может решить это как:
25 + 28 = 53
2 x 53 = 106
Или они могут сделать:
2 x 25 = 50
2 x 28 = 56
50 + 56 = 106
09
91004
.
Как преподается алгебра в KS2
Дети начнут изучать алгебру в 6 классе, где они узнают, как использовать простые формулы и находить пропущенные числа в уравнениях.
В национальной учебной программе не указано, что дети KS2 должны знать об использовании скобок в расчетах. Однако возможно, что более способные дети 6-х классов познакомятся с использованием скобок; правила о порядке выполнения вычислений преподаются как BODMAS (скобки, прочее/индексы, деление, умножение, сложение и вычитание).
Больше похоже на это
Что такое числовое предложение?
Что такое БОДМАС?
Математика для 6 класса: чему учит ваш ребенок
Глоссарий для родителей по основам счета
Что такое формула?
Что такое уравнения?
Введение в алгебру
Вербальные рассуждения: Введение в математические уравнения
Вербальные рассуждения: практика алгебры
9.
3.1: Ассоциативные, коммутативные и дистрибутивные свойства
Последнее обновление
Сохранить как PDF
Идентификатор страницы
64043
Проект NROC
Цели обучения
Определение и использование коммутативных свойств для сложения и умножения.
Определите и используйте ассоциативные свойства для сложения и умножения.
Определение и использование свойства дистрибутива.
Введение
В алгебре много раз нужно упростить выражение. Свойства действительных чисел предоставляют инструменты, которые помогут вам взять сложное выражение и упростить его.
Ассоциативные, коммутативные и дистрибутивные свойства алгебры чаще всего используются для упрощения алгебраических выражений. Вы захотите иметь хорошее представление об этих свойствах, чтобы упростить решение задач по алгебре.
Коммутативные свойства сложения и умножения
Вы можете столкнуться с повседневными делами, в которых порядок задач может быть изменен без изменения результата. Например, подумайте о том, чтобы налить утром чашку кофе. Вы получите ту же вкусную чашку кофе, если вы добавите ингредиенты одним из следующих способов:
Налейте 12 унций кофе в кружку, затем добавьте немного молока.
Добавьте немного молока в кружку, затем добавьте 12 унций кофе.
Порядок добавления ингредиентов не имеет значения. Точно так же не имеет значения, надеваете ли вы сначала левый или правый ботинок, прежде чем отправиться на работу. Если вы выходите из дома в обеих туфлях, вы на правильном пути!
В математике мы говорим, что эти ситуации коммутативны — результат будет одинаковым (кофе приготовлен по вашему вкусу, вы выходите из дома в обеих туфлях) независимо от порядка выполнения задач.
Аналогично, коммутативное свойство сложения утверждает, что при сложении двух чисел их порядок можно изменить, не влияя на сумму. Например, $\ 30+25$ имеет ту же сумму, что и $\ 25+30$.
$\ 30+25=55$
$\ 25+30=55$
Аналогично умножение. Коммутативное свойство умножения гласит, что при умножении двух чисел их порядок можно изменить, не влияя на произведение. Например, $\ 7 \cdot 12$ имеет тот же продукт, что и $\ 12 \cdot 7$.
$\ 7 \cdot 12=84$
$\ 12 \cdot 7=84$
Эти свойства применимы ко всем действительным числам. Рассмотрим несколько примеров сложения.
Исходное уравнение Переписанное уравнение
$\ 1,2+3,8=5$ $\ 3,8+1,2=5$
$\ \frac{1}{2}+\frac{1}{8}=\frac{5}{8}$ $\ \frac{1}{8}+\frac{1}{2}=\frac{5}{8}$
$\ 14+(-10)=4$ $\ (-10)+14=4$
$\ \frac{1}{3}+\left(-1 \frac{2}{3}\right)=-1 \frac{1}{3}$ $\ \left(-1 \frac{2}{3}\right)+\frac{1}{3}=-1 \frac{1}{3}$
$\ (-5,2)+(-3,6)=-8,8$ $\ (-3,6)+(-5,2)=-8,8$
Переместительное свойство сложения
Для любых действительных чисел $\ a$ и $\ b$, $\ a+b=b+a$.
Вычитание не является коммутативным. Например, $\ 4-7$ отличается от $\ 7-4$. Знак $\-$ здесь означает вычитание.
Однако напомним, что $\ 4-7$ можно переписать как $\ 4+(-7)$, поскольку вычитание числа равносильно сложению противоположного числа. Применяя здесь свойство коммутативности для сложения, можно сказать, что $\ 4+(-7)$ то же самое, что $\ (-7)+4$. Обратите внимание, как это выражение сильно отличается от $\ 7-4$.
Теперь посмотрим на несколько примеров умножения.
Исходное уравнение Переписанное уравнение
$\ 4.5 \cdot 2=9$ $\ 2 \cdot 4.5=9$
$\ (-5) \cdot 3=-15$ $\ 3 \cdot(-5)=-15$
$\ \frac{1}{5} \cdot 5=1$ $\ 5 \cdot \frac{1}{5}=1$
$\ \left(-\frac{1}{4}\right) \cdot\left(-\frac{8}{10}\right)=\frac{1}{5}$ $\ \left(-\frac{8}{10}\right) \cdot\left(-\frac{1}{4}\right)=\frac{1}{5}$
Коммутативное свойство умножения
Для любых действительных чисел $\ a$ и $\ b$, $\ a \cdot b=b \cdot a$.
Порядок не имеет значения, пока две величины перемножаются. Это свойство работает для действительных чисел и для переменных, представляющих действительные числа.
Как вычитание не коммутативно, так и деление не коммутативно. $\ 4 \div 2$ не имеет того же частного, что и $\ 2 \div 4$.
Пример
Запишите выражение $\ (-15,5)+35,5$ другим способом, используя свойство коммутативности сложения, и покажите, что оба выражения дают один и тот же ответ.
Раствор
$\ (-15,5)+35,5=20$ Добавление.
$\ 35,5+(-15,5)$ Используя свойство коммутативности, вы можете поменять местами -15,5 и 35,5, чтобы они располагались в другом порядке.
$\ \begin{array}{c}
35,5+(-15,5) \\
35,5-15,5=20
\end{массив}$ Сложение 35,5 и -15,5 равносильно вычитанию 15,5 из 35,5. Сумма 20.
$\ (-15,5)+35,5=20$ и $\ 35,5+(-15,5)=20$
Упражнение
Перепишем $\ 52 \cdot y$ по-другому , используя свойство коммутативности умножения. Обратите внимание, что $\ y$ представляет собой действительное число.
$\ 5 лет \cdot 2$
$\ 52 года$
$\ 26 \cdot 2 \cdot y$
$\ у \cdot 52$
Ответить
Неверно. Вы не можете переключить одну цифру из 52 и присоединить ее к переменной $\y$. Правильный ответ: $\y\cdot 52$.
Неверно. Это еще один способ переписать $\ 52 \cdot y$, но свойство коммутативности не использовалось. Правильный ответ: $\y\cdot 52$.
Неверно. Вам не нужно множить 52 на $\ 26 \cdot 2$. Правильный ответ: $\y\cdot 52$.
Правильно. Порядок факторов обратный.
Ассоциативные свойства сложения и умножения
Ассоциативное свойство сложения утверждает, что числа в выражении сложения можно группировать различными способами без изменения суммы. Вы можете запомнить значение ассоциативного свойства, вспомнив, что когда вы связывает с членами семьи, друзьями и коллегами, в конечном итоге вы формируете с ними группы.
Ниже приведены два способа упрощения одной и той же задачи на сложение. В первом примере 4 сгруппировано с 5 и $\ 4+5=9$.
$\ 4+5+6=9+6=15$
Здесь та же проблема решается сначала группировкой 5 и 6, $\ 5+6=11$.
$\ 4+5+6=4+11=15$
В обоих случаях сумма одинакова. Это показывает, что изменение группировки чисел при сложении дает ту же сумму.
Математики часто используют круглые скобки, чтобы указать, какая операция должна быть выполнена первой в алгебраическом уравнении. Приведенные выше задачи на сложение переписаны здесь, на этот раз с использованием круглых скобок для обозначения ассоциативной группировки.
$\ (4+5)+6=9+6=15$
$\ 4+(5+6)=4+11=15$
Понятно, что скобки не повлиять на сумму; сумма одинакова независимо от того, где расположены скобки.
Ассоциативное свойство дополнения
Для любых действительных чисел $\ a$, $\ b$ и $\ c$,
$\ (a+b)+c=a+(b+c)$.
В приведенном ниже примере показано, как свойство ассоциативности можно использовать для упрощения выражений с вещественными числами.
Пример
Перепишите $\ 7+2+8,5-3,5$ двумя разными способами, используя ассоциативное свойство сложения. Покажите, что выражения дают один и тот же ответ.
Решение
$\ \begin{массив}{r}
7+2+8.5-3.5 \\
7+2+8.5+(-3.5)
\end{массив}$
Свойство ассоциативности не применяется к выражениям, включающим вычитание. Итак, перепишем выражение как сложение отрицательного числа.
$\ \begin{array}{r}
(7+2)+8,5+(-3,5) \\
9+8,5+(-3,5) \\
17,5+(-3,5) \\
17,5-3,5=14
\end{массив}$
Группа 7 и 2 и сложите их вместе. Затем прибавьте к этой сумме 8,5. Наконец, добавьте -3,5, что равносильно вычитанию 3,5.
Вычесть 3.5. Сумма 14.
$\ \begin{array}{r}
7+2+(8.5+(-3.5)) \\
7+2+5 \\
9+5
\end{массив}$
Сложите 8,5 и -3,5 и сложите их вместе, чтобы получить 5. Затем сложите 7 и 2 и прибавьте эту сумму к 5.
Сумма равна 14.
$\ (7+2)+8,5-3,5=14$ и $\ 7+2+(8,5+(-3,5))=14$
Умножение имеет ассоциативное свойство, которое действует точно так же, как и свойство сложения. Ассоциативное свойство умножения утверждает, что числа в выражении умножения можно перегруппировать с помощью круглых скобок. Например, приведенное ниже выражение можно переписать двумя разными способами, используя свойство ассоциативности.
Исходное выражение: $\ -\frac{5}{2} \cdot 6 \cdot 4$
Выражение 1: $\ \left(-\frac{5}{2} \cdot 6\right ) \cdot 4=\left(-\frac{30}{2}\right) \cdot 4=-15 \cdot 4=-60$
Выражение 2: $\ -\frac{5}{2} \cdot(6 \cdot 4)=-\frac{5}{2} \cdot 24=-\frac{120}{2}=- 60$
Скобки не влияют на произведение. Произведение одно и то же независимо от того, где стоят скобки.
Ассоциативное свойство умножения
Для любых действительных чисел $\ a$, $\ b$ и $\ c$, $\ (a \cdot b) \cdot c=a \cdot (б \cdot c)$.
Упражнение
Перепишите $\ \frac{1}{2} \cdot\left(\frac{5}{6} \cdot 6\right)$, используя только ассоциативное свойство.
$\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$
$\ \left(\frac{5}{6} \cdot 6\right) \cdot \frac{1}{2}$
$\ 6 \cdot\left(\frac{5}{6} \cdot \frac{1}{2}\right)$
$\ \frac{1}{2} \cdot 5$
Ответить
Правильно. Здесь числа перегруппированы. Теперь $\ \frac{1}{2}$ и $\ \frac{5}{6}$ сгруппированы в скобках вместо $\ \frac{5}{6}$ и $ \6$.
Неверно. Порядок чисел не меняется, когда вы переписываете выражение, используя ассоциативное свойство умножения. То, как они сгруппированы , должно измениться. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.
Неверно. Порядок чисел не меняется, когда вы переписываете выражение, используя ассоциативное свойство умножения. Только как они сгруппированы должен измениться. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.
Неверно. Умножение в круглых скобках не является применением свойства. Правильный ответ: $\ \left(\frac{1}{2} \cdot \frac{5}{6}\right) \cdot 6$.
Использование ассоциативных и коммутативных свойств
Вы обнаружите, что ассоциативные и коммутативные свойства являются полезными инструментами в алгебре, особенно при вычислении выражений. Используя коммутативные и ассоциативные свойства, вы можете переупорядочивать термины в выражении так, чтобы совместимые числа располагались рядом друг с другом и группировались вместе. Совместимые числа — это числа, которые легко вычислить, например $\ 5+5$, или $\ 3 \cdot 10$, или $\ 12-2$, или $\ 100 \ раздел 20$. (Основным критерием совместимых чисел является то, что они «хорошо работают» вместе.) Два приведенных ниже примера показывают, как это делается.
Пример
Оцените выражение $\ 4 \cdot(x \cdot 27)$, когда $\ x=-\frac{3}{4}$.
Решение
$\ 4 \cdot(x \cdot 27)$ Исходное выражение.
$\ 4 \cdot\left(\left(-\frac{3}{4}\right) \cdot 27\right)$ Замените $\ -\frac{3}{4}$ на $\ x$.
$\ \begin{array}{r}
\left(4 \cdot\left(-\frac{3}{4}\right)\right) \cdot 27 \\
\left(-\frac{12}{4}\right) \cdot 27
\end{массив}$
Используйте ассоциативное свойство умножения, чтобы перегруппировать множители так, чтобы $\ 4$ и $\ -\frac{3}{4}$ находились рядом друг с другом.
Умножение $\ 4$ на $\ -\frac{3}{4}$ делает вычисление выражения немного проще, чем умножение $\ -\frac{3}{4}$ на \ (\ 27\).
$\ -3 \cdot 27=-81$ Умножить. $\ 4$ раз $\ -\frac{3}{4}=-3$, а $\ -3$ раз $\ 27$ равно $\ -81$.
$\ 4 \cdot(x \cdot 27)=-81$ когда $\ x=\left(-\frac{3}{4}\right)$
Пример
Упростить: $\ 4+12+3+4-8$
Решение
$\ 4+12+3+4-8$ Исходное выражение.
$\ 12+3+4+4+(-8)$ Определите совместимые номера. $\ 4+4$ равно $\ 8$, и есть $\ -8$. подарок. Вспомните, что вы можете думать о $\ -8$ как о $\ +(-8)$. Используйте свойство коммутативности сложения, чтобы сгруппировать их вместе.
$\ 12+3+(4+4+(-8))$ Используйте ассоциативное свойство для группировки $\ 4+4+(-8)$.
$\ 12+3+0$ Добавить $\ 4+4+(-8)$.
$\ 12+3+0=15$ Добавьте остальные условия.
$\ 4+12+3+4-8=15$
Упражнение
Упростите выражение: $\ -5+25-15+2+8$
5
15
30
55
Ответить
Неверно. Когда вы используете свойство коммутативности для перестановки слагаемых, убедитесь, что отрицательные слагаемые имеют свои отрицательные знаки. Правильный ответ 15.
Правильно. Используйте свойство коммутативности, чтобы изменить выражение так, чтобы совместимые числа располагались рядом друг с другом, а затем используйте свойство ассоциативности, чтобы сгруппировать их.
Неверно. Проверьте свое сложение и вычитание и подумайте о порядке, в котором вы складываете эти числа. Используйте свойство коммутативности, чтобы переставить слагаемые так, чтобы совместимые числа располагались рядом друг с другом. Правильный ответ 15.
Неверно. Похоже, вы проигнорировали отрицательные знаки здесь. Когда вы используете свойство коммутативности для перестановки слагаемых, убедитесь, что отрицательные слагаемые имеют свои отрицательные знаки. Правильный ответ 15.
Распределительное свойство
Распределительное свойство умножения — это очень полезное свойство, которое позволяет вам переписывать выражения, в которых вы умножаете число на сумму или разность. Свойство утверждает, что произведение суммы или разности, например $\ 6(5-2)$, равно сумме или разности произведений, в данном случае $\ 6(5)-6( 2)$.
$\ \begin{array}{l}
6(5-2)=6(3)=18 \\
6(5)-6(2)=30-12=18
\end{array}$
Распределительное свойство умножения можно использовать при умножении числа на сумму. Например, предположим, что вы хотите умножить 3 на сумму $\ 10+2$.
$\ 3(10+2)=?$
В соответствии с этим свойством вы можете сначала сложить числа 10 и 2, а затем умножить на 3, как показано здесь: $\ 3(10+2) =3(12)=36$. В качестве альтернативы вы можете сначала умножить каждое слагаемое на 3 (это называется распределением на 3), а затем вы можете сложить продукты. Этот процесс показан здесь.
$\ \begin{array}{l}
3(10+2)=3(12)=36 \\
3(10)+3(2)=30+6=36
\end {массив}$
Продукты одинаковые.
Поскольку умножение является коммутативным, вы можете использовать распределительное свойство независимо от порядка множителей.
Распределительные свойства
Для любых действительных чисел $\ a$, $\ b$ и $\ c$:
Умножение распределяется над сложением:
$\ a(b +в)=а б+а в$
Умножение распределяет по вычитанию:
$\ a(b-c)=a b-a c$
Упражнение
Перепишите выражение $\ 10(9-6)$, используя свойство распределения.
$\ 10(6)-10(9)$
$\ 10(3)$
$\ 10(6-9)$
$\ 10(9)-10(6)$
Ответить
Неверно. Поскольку вычитание не является коммутативным, вы не можете изменить порядок. Правильный ответ: $\ 10(9)-10(6)$.
Неверно. Это правильный способ найти ответ. Но вопрос просил вас переписать задачу, используя свойство дистрибутивности. Правильный ответ: $\ 10(9)-10(6)$
Неверно. Вы изменили порядок чисел 6 и 9. Обратите внимание, что вычитание не является коммутативным, и вы не использовали свойство дистрибутивности. Правильный ответ: $\ 10(9)-10(6)$.
Правильно. 10 правильно распределены, так что они используются для умножения 9и 6 отдельно.
Распределение с переменными
Пока переменные представляют действительные числа, свойство распределения может использоваться с переменными. Свойство дистрибутивности важно в алгебре, и вы часто будете встречать такие выражения: $\ 3(x-5)$. Если вас попросят расширить это выражение, вы можете применить распределительное свойство точно так же, как если бы вы работали с целыми числами.
Помните, что когда вы умножаете число и переменную, вы можете просто написать их рядом, чтобы выразить умноженное количество. Таким образом, выражение «тройная переменная $\ x$» может быть записано несколькими способами: $\ 3 x$, $\ 3(x)$ или $\ 3 \cdot Икс$.
Пример
Используйте свойство распределения для расширения выражения $\ 9(4+x)$.
Раствор
$\ 9(4+x)$ Исходное выражение.
$\ 9(4)+9(х)$ Распредели 9 и умножь.
$\ 36+9 х$ Умножить.
$\ 9(4+х)=36+9 х$
Пример
Используйте свойство распределения для вычисления выражения $\ 5(2 x-3)$, когда $\ x=2$.
Раствор
$\ 5(2 x-3)$ Исходное выражение.
$\ 5(2 х)-5(3)$ Раздать 5.
$\10 х-15$ Умножить.
$\ 10(2)-15$
$\ 20-15=5$
Подставьте 2 вместо $\ x$ и оцените.
Когда $\ х=2,5(2 х-3)=5$.
Как вы думаете, что произойдет в приведенном выше примере, если вы подставите $\ x=2$ перед распределением 5? Получили бы вы такой же ответ 5? В приведенном ниже примере показано, что произойдет.
Пример
Используйте свойство распределения для вычисления выражения $\ 5(2 x-3)$, когда $\ x=2$.
Раствор
$\ 5(2 x-3)$ Исходное выражение.
$\ 5(2(2)-3)$ Замените $\ x$ на 2.
$\ \begin{array}{c}
5(4-3) \\
5(4)-5(3)
\end{массив}$ Умножить.
$\ 20-15=5$ Вычитание и оценка.
Когда $\ x=2,5(2 x-3)=5$.
Объединение одинаковых терминов
Распределительное свойство также может помочь вам понять фундаментальную идею алгебры: такие величины, как $\ 3x$ и $\ 12x$, можно складывать и вычитать так же, как числа 3 и 12. Давайте рассмотрим один пример и посмотрим, как это можно сделать.
Пример
Добавить: $\ 3 x+12 x$
Решение
$\ 3(x)+12(x)$ $\ 3 x$ равно 3 раза $\ x$, а $\ 12 x$ равно 12 раз $\ x$
$\ х(3+12)$ Изучая свойство дистрибутивности (а также используя свойство коммутативности), вы знаете, что $\ x(3+12)$ совпадает с $\ 3(x)+12(x)$.
$\ \begin{array}{c}
x(15) \\
\text { or } \\
15 x
\end{массив}$ Объедините члены в скобках: $\ 3+12=15$.
$\ 3 x+12 x=15 x$
Видите, что произошло? Думая о $\ x$ как о распределенной величине, вы можете увидеть, что $\ 3x+12x=15x$. (Если вы не уверены в этом, попробуйте подставить любое число в это выражение… вы обнаружите, что это верно!)
Группы терминов, состоящие из коэффициента, умноженного на одну и ту же переменную, называются «подобными терминами». В приведенной ниже таблице показаны различные группы похожих терминов:
Группы похожих терминов
$\ 3 х, 7 х, -8 х, -0,5 х$
$\ -1,1 г, -4 г, -8 г$
$\ 12 т, 25 т, 100 т, 1 т$
$\ 4 а Ь,-8 а Ь, 2 а Ь$
Всякий раз, когда вы видите одинаковые члены в алгебраическом выражении или уравнении, вы можете складывать или вычитать их точно так же, как если бы вы складывали или вычитали действительные числа. Так, например,
$\ 10 y+12 y=22 y$ и $\ 8 x-3 x-2 x=3 x$.
Будьте осторожны, чтобы не комбинировать термины, которые не имеют одной и той же переменной: $\ 4 x+2 y$ не равно $\ 6 x y$!
Пример
Упрощение: $\ 10 y+5 y+9 x-6 x-x$.
Раствор
$\ 10 у+5 у+9 х-6 х-х$ В этом выражении есть похожие члены, так как все они состоят из коэффициента, умноженного на переменную $\ x$ или $\ y$. Обратите внимание, что $\ -x$ совпадает с $\ (-1) x$.
$\ 15 у+2 х$ Добавить похожие термины. $\ 10 y+5 y=15 y$ и $\ 9 x-6 x-x=2 x$.
$\ 10 y+5 y+9 x-6 x-x=15 y+2 x$
Упражнение
Упростите: $\ 12 x-x+2 x-8 x$.
$\ 23 х$
$\ 5$
$\ 5 х$
$\х$
Ответить
Неверно. Похоже, вы добавили все термины. Обратите внимание, что $\ -x$ и $\ -8 x$ отрицательны. Правильный ответ: $\ 5 х$.
Неверно. Вы правильно объединили целые числа, но не забудьте также включить переменную! Правильный ответ: $\ 5x$.
Правильно. Когда вы объединяете эти похожие термины, вы получаете сумму $\ 5x$
Неверно. Похоже, вы вычли все члены из $\ 12x$. Обратите внимание, что $\ -x$ и $\ -8 x$ отрицательны, а $\ 2 x$ положительны. Правильный ответ: $\ 5 х$.
Резюме
Коммутативные, ассоциативные и дистрибутивные свойства помогают преобразовать сложное алгебраическое выражение в более простое. Когда вы переписываете выражение с помощью коммутативного свойства, вы меняете порядок сложения или умножения чисел. Когда вы переписываете выражение, используя ассоциативное свойство, вы группируете другую пару чисел вместе, используя круглые скобки. Вы можете использовать коммутативные и ассоциативные свойства для перегруппировки и изменения порядка любого числа в выражении, если выражение полностью состоит из слагаемых или множителей (а не из их комбинации). Распределительное свойство можно использовать для перезаписи выражений для различных целей. Когда вы умножаете число на сумму, вы можете складывать, а затем умножать. Вы также можете сначала умножить каждое слагаемое, а затем сложить продукты вместе. Тот же принцип применяется, если вы умножаете число на разницу.
Эта страница под названием 9.3.1: Ассоциативные, коммутативные и дистрибутивные свойства распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована проектом NROC с помощью исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
Проект NROC
Лицензия
СС BY-NC-SA
Версия лицензии
4,0
Метки
source@https://content. nroc.org/DevelopmentalMath.HTML5/Common/toc/toc_en.html
Укажите коммутативность, ассоциативность и дистрибутивность рациональных чисел.
Система счисления включает в себя различные типы чисел, например, простые числа, нечетные числа, четные числа, рациональные числа, целые числа и т. д. Эти числа могут быть выражены в виде цифр или слов соответственно. Например, такие числа, как 40 и 65, выраженные в виде цифр, также могут быть записаны как сорок и шестьдесят пять.
A Система счисления или Система счисления определяется как элементарная система для выражения чисел и цифр. Это единственный способ представления чисел в арифметической и алгебраической структуре.
Числа используются в различных арифметических значениях, применимых для выполнения различных арифметических операций, таких как сложение, вычитание, умножение и т. д., которые применяются в повседневной жизни для целей вычислений. Значение числа определяется цифрой, ее разрядностью в числе и основанием системы счисления.
Числа обычно также известны как цифры и представляют собой математические значения, используемые для счета, измерений, маркировки и измерения основных величин.
Числа – это математические значения или цифры, используемые для измерения или вычисления величин. Оно представлено цифрами как 2,4,7 и т. д. Примерами чисел являются целые числа, целые числа, натуральные числа, рациональные и иррациональные числа и т. д.
Типы чисел
В реальной системе счисления существуют различные типы чисел, которые подразделяются на наборы. Типы описаны ниже:
Натуральные числа: Натуральные числа — это положительные числа, которые считаются от 1 до бесконечности. Набор натуральных чисел представлен ‘N’ . Это числа, которые мы обычно используем для счета. Набор натуральных чисел может быть представлен как N = 1, 2, 3, 4, 5, 6, 7,…
Целые числа: Целые числа — это положительные числа, включая ноль, который считается от 0 до бесконечности. Целые числа не включают дроби или десятичные дроби. Множество целых чисел представлено цифрой 9.0015 ‘В’. Набор может быть представлен как W = 0, 1, 2, 3, 4, 5,…
Целые числа: Целые числа представляют собой набор чисел, включающий все положительные счетные числа, ноль, а также все отрицательные счетные числа, которые считать от отрицательной бесконечности до положительной бесконечности. В наборе нет дробей и десятичных знаков. Набор целых чисел обозначается ‘Z’ . Множество целых чисел можно представить в виде Z = …..,-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5,…
Десятичные числа : Любое числовое значение, состоящее из десятичной точки, является десятичным числом. Его можно выразить как 2,5, 0,567 и т. д.
Вещественное число: Вещественные числа — это заданные числа, не содержащие мнимых значений. Он включает в себя все положительные целые числа, отрицательные целые числа, дроби и десятичные значения. Обычно он обозначается «R».
Комплексное число: Комплексные числа — это набор чисел, включающий мнимые числа. Его можно выразить как a+bi, где «a» и «b» — действительные числа. Обозначается цифрой «С».
Рациональные числа: Рациональные числа — это числа, которые можно представить как отношение двух целых чисел. Он включает в себя все целые числа и может быть выражен в виде дробей или десятичных знаков. Обозначается ‘Q’.
Иррациональные числа: Иррациональные числа — это числа, которые не могут быть выражены дробями или отношениями целых чисел. Он может быть записан десятичными знаками и иметь бесконечные неповторяющиеся цифры после запятой. Обозначается цифрой «П».
Что такое рациональные числа?
Рациональные числа имеют форму p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел.
При делении рационального числа выходные данные представляются в десятичной форме, которая может быть либо оканчивающейся, либо повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.
свойства рациональных чисел
Основные свойства чисел:
Собственность закрытия
Commutative Property
СОБСТВЕННАЯ ПЕРЕДА.
Свойство обратного элемента
Свойство замыкания
В этом свойстве действительных чисел мы можем сложить или умножить любые два действительных числа, что также даст вещественное число.
Пример:
2 + 5 = 7 и 80 + 40 = 120 для сложения
6 × 5 = 30 для умножения
Коммутативное свойство число не имеет значения, каков порядок, он даст нам тот же результат даже после замены или изменения их положения.
Или мы можем сказать, что место сложения или умножения чисел может быть изменено, но это даст тот же результат.
Это свойство действительно для сложения и умножения, но не для вычитания и деления.
x + y = y + x или x.y = y.x
Пример:
Если мы добавим 6 в 2 или 2 в 6 результатов будут одинаковыми, если мы умножаем оба числа
7 + 2 = 9 = 2 + 7 7 × 5 = 35 = 5 × 7
Ассоциативное свойство
Это свойство утверждает, что при сложении (или умножении) трех или более чисел сумма (или произведение) остается одинаковой независимо от группировки слагаемых (или множимых).
Порядок выполнения операций сложения или умножения не имеет значения, пока не меняется последовательность чисел. Это определяется как ассоциативное свойство.
То есть перестановка чисел таким образом, что их значение не изменится.
(x + y) + z = x + (y + z) и (x. y) .z = x. (Y.z)
Пример: (8 + 5) + 6 = 8 + (5 + 6) (8 × 5) × 6 = 8 × (5 × 6)
19 = 19 240 = 240
, как вы можете увидеть даже после изменения их порядка, он также дает тот же результат в обоих операциях, которые также добавляют как умножение.
Распределительное свойство
Это свойство помогает нам упростить умножение числа на сумму или разность. Он распределяет выражение, поскольку упрощает расчет.
x × (y + z) = x × y + x × z и x × (y — z) = x × y — x × z
Пример:
Упрощение 20 × (5 + 6)
= 20 × 5 + 20 × 6
= 100 + 120
= 220
То же самое относится и к вычитанию.
Свойство элемента идентификации
Это элемент, который оставляет другие элементы неизменными при объединении с ними. Элемент идентичности для операции сложения равен 0, а для умножения равен 1.
Для сложения a + 0 = a и для умножения a.0 = 0
Пример:
Для сложения, если a = 6
а + 0 = 6 + 0 = 6
и для умножения, если a = 6
a.0 = 6.0 = 0
Обратный элемент
Обратное число для числа «a» , обозначаемое числом 01/a, которое равно 01/a. при умножении на «а» дает мультипликативное тождество 1 .
Мультипликативная обратная дробь: a/b равна b/a
Аддитивная обратная число «a» — это число, которое при сложении с «a» дает результат ноль . Это число также известно как аддитивное обратное или противоположное (число), изменение знака и отрицание.
Или мы можем сказать, что действительное число меняет знак с положительного числа на отрицательное и с отрицательного числа на положительное. Нуль сам по себе является аддитивным обратным.
Пример: обратная 9 равна 1/9, а аддитивная обратная 9 равна -9
Укажите коммутативность, ассоциативные и распределительные свойства рациональных чисел. Кроме того, проверьте a × b = b × a и a + b = b + a для a = ½ и b = ¾
Решение:
Как мы объяснили выше все свойства рационального числа, которые также включают коммутативность, ассоциативные и дистрибутивные свойства 3/4
Следовательно,
В соответствии со свойством коммутативности: в нем говорится, что операция сложения или умножения числа не имеет значения, каков порядок, она даст нам тот же результат даже после замены или изменения их положения.
a + b = b + a or a.b = b.a
Теперь у нас есть a = 1/2 и b = 3/4
Итак, 1/2 + 3/4 = 3/4 + 1// 2 или 1/2 . 3/4 = 3/4. 1/2
5/4 = 5/4 3/8 = 3/8
Следовательно, доказано
Аналогичные вопросы
Вопрос 1. Докажите ассоциативность при одинаковых значениях a = 1/2, b = 3/4 и c = 2/3?
Решение:
Согласно ассоциативному свойству
Это свойство утверждает, что при сложении (или умножении) трех или более чисел или сумме (или произведении) они одинаковы независимо от группировки слагаемых ( или множители).
Порядок выполнения операций сложения или умножения не имеет значения, пока не меняется последовательность чисел. Это определяется как ассоциативное свойство.
(a + b) + c = a + (b + c) и (a.b) .c = a. (B.c)
Теперь у нас есть a = 1/2 и b = 3/4 и c = 2/3
(1/2 + 3/4 ) + 2/3 = 1/2 + (3/4 + 2/3) или (1/2 . 3/4 ). 2/3 = 1/2. (3/4 . 2/3)
5/4 + 2/3 = 1/2 + 17/12 . 3/8 2/3 = 1/2. 2/4
23/12 = 23/12 2/8 = 2/8
1/4 = 1/4
Следовательно, доказано
Вопрос 2: с одинаковым значением A = 1/2 и b = 3/4 и c = 2/3, докажите распределительное свойство?
Решение:
В соответствии с распределительным свойством
Это свойство помогает нам упростить умножение числа на сумму или разность. Он распределяет выражение, поскольку упрощает расчет.
A × (B + C) = A × B + A × C и A × (B — C) = A × B — A × C
Теперь у нас есть A = 1/2 и B = 3// 4 и c = 2/3
1/2 × (3/4 + 2/3) = (1/2 × 3/4) + (1/2 × 2/3) и 1/2 × (3/ 4 – 2/3) = 1/2 × 3/4 – 1/2 × 2/3
1/2 × 17/12 = 3/8 + 2/6 1/2 × 1/12 = 3/8 — 2/6
17/24 = 17/24 1/24 = 1/24
Отсюда доказано

Ассоциативные, дистрибутивные и коммутативные свойства — Практика использования этих свойств
К сожалению, в прошлом году рекламный блок начал отключать загрузку почти всех изображений на нашем сайте, что привело к тому, что mathwarehouse стало непригодным для использования пользователями adlbock.
Все вместе на 1 странице!
Чтобы узнать больше о любом из перечисленных ниже свойств, посетите отдельную страницу этого свойства.
Распределительное свойство
Ассоциативное свойство
Коммутативное свойство
Свойства и Операции
Давайте посмотрим, как (и если) эти свойства работают со сложением, умножением, вычитанием и делением.
Дополнение
Имущество Пример с дополнением
Распределительное свойство
Ассоциативный
Коммутативный
Резюме: Все 3 из этих свойств применимы к сложению.
Умножение
Имущество Пример с умножением
Распределительное свойство Распределительное свойство — это применение умножения (поэтому здесь нечего показывать).
Ассоциативный
Коммутативный
Резюме: Все 3 из этих свойств применимы к умножению.
Вычитание
Имущество Пример с вычитанием
Распределительное свойство
Ассоциативный
Коммутативный
Резюме: Распределительное свойство — единственное, которое применимо к вычитанию.
Подразделение
Имущество Пример с вычитанием
Распределительное свойство
Ассоциативный
Коммутативный
Сводка: Ни одно из этих свойств не относится к делению.
Практика Проблемы
Какие из следующих утверждений иллюстрируют распределительное, ассоциированное и коммутативное свойство?
Направления: Нажмите на каждую кнопку ответа, чтобы увидеть, какое свойство соответствует утверждению слева .
Заявление Свойство
7 + 2 = 2 + 7
Коммутативное свойство
6 + (2 + 11) = (6 + 2) + 11
Ассоциативное свойство
5 (2 + 4) = 5 • 2 + 5 • 4
Распределительное свойство
(12 • 44) • 13 • 5 = 12 • 44 • (13 • 5)
Ассоциативное свойство
5 • 3 • 11 = 11 • 5 • 3
Коммутативное свойство
6 (3 + 11 + 4) = 6 • 3 + 6 • 11 + 6 • 4
Распределительное свойство
Все три из этих свойств также могут быть применены к алгебраическим выражениям.
Какие из следующих утверждений иллюстрируют распределительное, ассоциированное и коммутативное свойство?
Направления: Нажмите на каждую кнопку ответа, чтобы увидеть, какое свойство соответствует утверждению слева .
Заявление Свойство
а + с = с + а
Коммутативное свойство
а (х + у + г) = а • х + а • у + а • г
Распределительное свойство
(а • у) • х • г = а • у • (х • г)
Ассоциативное свойство
Распределительное свойство
Ассоциативное свойство
Коммутативное свойство
Закрытие, Ассоциативный, Распределительный и др.
0
Сохранить
Скачать публикацию в формате PDF
Свойства целых чисел важны для понимания целых чисел. Целые числа являются частью системы счисления. Основные свойства целых чисел перечислены ниже: свойство замыкания, коммутативное свойство, ассоциативное свойство, распределительное свойство, мультипликативное свойство и аддитивное свойство. Понимание целых чисел является базовой математикой и важной темой алгебры. Целые числа — это группа положительных и отрицательных счетных целых чисел, а также нуль, не имеющий дробной части. Пример: 1, -1, 0, 101 и -101.
В этой статье мы узнаем о целочисленных свойствах натуральных чисел, таких как замыкание, коммутативность, ассоциативность, дистрибутивность, мультипликативность и аддитивность, с примерами решения и часто задаваемыми вопросами.
Свойства целых чисел
Все натуральные числа и целые числа являются целыми числами с начальной точкой 1 и 0 соответственно до бесконечности. Следовательно, их свойства схожи. Ниже приведены важные свойства целых чисел:
Свойство замыкания
Commutative Property
Associative Property
Identity Property
Distributive Property
9
Integer Property Addition Multiplication Subtraction Division
Свойство замыкания a + b ∈ Z a × b ∈ Z a – b ∈ Z a ÷ b ∉ Z (b + c) = (a + b) + c a × (b × c) = (a × b) × c (a – b) – c ≠ a – (b – c) ( a ÷ b) ÷ c ≠ a ÷ (b ÷ c)
Свойство идентичности a + 0 = a = 0 + a a × 1 = a = 1 × a a – 0 = a ≠ 0 – а а ÷ 1 = а ≠ 1 ÷ а
Распределительное имущество a × (b + c) = a × b + a × c
a × (b − c) = a × b − a × c свойство замыкания означает, что множество закрыто для некоторой математической операции. То есть, если операцию всегда можно выполнить с элементами множества, множество замкнуто по отношению к этой операции. В результате множество либо замкнуто, либо открыто по отношению к определенной операции.
Сложение целых чисел: Сумма двух целых чисел всегда является целым числом. Если a и b — любые два целых числа, то a + b = также является целым числом. Например: 19 + 23 = 42.
Вычитание целых чисел: Разница между двумя целыми числами всегда является целым числом. Если a и b — любые два целых числа, то a — b = также является целым числом. Например: 19 – 23 = -4.
Умножение целых чисел: Произведение двух целых чисел всегда является целым числом. Если a и b — любые два целых числа, то a x b = также является целым числом. Например: 3 x 4 = 12,9.0024
Деление целых чисел: Деление двух целых чисел всегда является целым числом. Если a и b — любые два целых числа, то $\frac{a}{b}$ = также является целым числом. Пример: $\frac{4}{2}$= 2.
Узнайте о свойствах рациональных чисел здесь.
Переместительное свойство
Переместительное свойство — это математическое правило, которое гласит, что порядок, в котором мы складываем, умножаем, вычитаем или делим числа, не меняет произведение.
Сложение целых чисел: Сложение двух целых чисел коммутативно по своей природе. Если a и b — любые два целых числа, то a + b = b + a Например: 2 + 4 = 6 и 4 + 2 = 6 Итак, 2 + 4 = 4 + 2.
Вычитание целых чисел: Вычитание двух целые числа не коммутативны по своей природе. Если a и b — любые два целых числа, то a — b ≠ b — a Например: 2 — 4 = -2 и 4 — 2 = 4 Итак, 2 — 4 ≠ 4 — 2.
Умножение целых чисел: Умножение двух целых чисел коммутативна по своей природе. Если a и b — любые два целых числа, то a x b = b x a Например: 3 x 4 = 12 & 4 x 3 = 12 Итак, 3 x 4 = 4 x 3
Деление целых чисел: Деление двух целых чисел не является коммутативным по своей природе. Если a и b любые два целых числа, то $\frac{a}{b} \neq \frac{b}{a}$ Пример: $\frac{4}{2} = 2$ и \ (\frac{2}{4} = 0,5\), поэтому $\frac{4}{2} \neq \frac{2}{4}$
Узнайте о типах чисел здесь.
Ассоциативное свойство
Этот закон просто гласит, что при сложении и умножении чисел можно изменить группировку чисел в задаче, и это не повлияет на ответ.
Сложение целых чисел: Сложение целых чисел носит ассоциативный характер. Если a, b и c — любые три целых числа, то a + (b + c) = (a + b) + c
Пример: 2 + (4 + 1) = 2 + 5 = 7 и (2 + 4) + 1 = 6 + 1 = 7 Итак, 2 + (4 + 1) = (2 + 4) + 1 с использованием ассоциативного свойства сложения.
Вычитание целых чисел: Вычитание целых чисел не является ассоциативным по своей природе. Если a, b и c — любые три целых числа, то a — (b — c) = (a — b) — c Пример: 2 — (4 — 1) = 2 — 3 = -1 и (2 — 4) — 1 = -2 – 1 = -3 Итак, 2 – (4 – 1) ≠ (2 – 4) – 1
Умножение целых чисел: Умножение целых чисел носит ассоциативный характер. Если a, b и c — любые три целых числа, то a x (b x c) = (a x b) x c. Пример: 2 x (4 x 1) = 2 x 4 = 8 и (2 x 4) x 1 = 8 x 1 = 8. Итак, 2 x (4 x 1) = (2 x 4) x 1
Деление целых чисел: Деление двух целых чисел не является коммутативным по своей природе. Если a и b — любые два целых числа, то $\frac{a}{b} \neq \frac{b}{a}$ Пример: $\frac{8}{2} = 4$ и \ (\frac{2}{8} = 0,25\), поэтому $\frac{8}{2} \neq \frac{2}{8}$
Свойство идентичности
Индивидуальность — это число, которое при сложении, вычитании, умножении или делении с любым числом (назовем это число n) позволяет n оставаться неизменным. Это также свойство целых чисел
Аддитивное тождество: Сумма любого целого числа и нуля является рациональным числом. Если a — любое целое число, то a + 0 = 0 + a = a как ноль — это аддитивная идентичность для рациональных чисел. Например: 2 + 0 = 0 + 2 = 2
Идентификатор умножения: Произведение любого целого числа на 1 и есть само целое число. «Единица» — это мультипликативная идентичность для целых чисел. Если a представляет собой любое целое число, то a x 1 = 1 x a = a Например: 5 x 1 = 1 x 5 = 5
Читайте о двоичных числах здесь.
Распределяющее свойство
Распределяющее свойство используется для простого решения выражений путем распределения числа на числа, указанные в скобках.
Распределительное свойство умножения над сложением: Умножение целых чисел является распределительным над сложением. Если a, b и c — любые три рациональных числа, то a x (b + c) = a x b + a x c Например, 1 x (2 + 1) = 1 x 3 = 1, тогда 1 x 2 + 1 x 1 = 2 + 1 = (2 + 1) = 3 Следовательно, умножение дистрибутивно над сложением.
Распределительное свойство умножения над вычитанием: Умножение целых чисел является распределительным над вычитанием. Если a, b и c — любые три рациональных числа, то a x (b — c) = a x b — a x c Например: 1 x (2 — 1) = 1 x 1 = 1 Следовательно, 1 x 2 — 1 x 1 = 2 — 1 = (2 – 1) = 1 Итак, 1 х (2 – 1) = 1 х 2 – 1 х 1 Следовательно, умножение является дистрибутивным по отношению к вычитанию.
Подробнее о взаимно простых числах
Решенные примеры свойств целых чисел
Давайте посмотрим на некоторые примеры свойств целых чисел, которые встречаются на экзаменах.
Решено Пример 1: Найдите два последовательных целых числа, сумма которых равна 129.
Решение: Пусть x и x + 1 (последовательные целые числа отличаются на 1) будут двумя числами. Используйте тот факт, что их сумма равна 129, чтобы написать уравнение.
x + (x + 1) = 129
Найдите x, чтобы получить
x = 64
Два числа:
x = 64 и x + 1 = 65
Мы видим, что сумма двух чисел равна 129.
Решено Пример 2: Сумма трех последовательных четных целых чисел равна 84. Найдите эти числа.
Решение: Разница между двумя четными целыми числами равна 2. Пусть x, x + 2 и x + 4 — три числа. Их сумма равна 84, следовательно,
x + (x + 2) + (x + 4) = 84
Решите x и найдите три числа
x = 26, x + 2 = 28 и x + 4. = 30
Все три числа четные. Убедитесь, что их сумма равна 84.
Надеюсь, что эта статья о свойствах целых чисел была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Часто задаваемые вопросы о свойствах целых чисел
В.1 Что такое распределительное свойство целых чисел?
Ответ 1 Распределительное свойство умножения над сложением: Умножение целых чисел дистрибутивно над сложением. Если a, b и c — любые три рациональных числа, то a x (b + c) = a x b + a x c Пример: 1 x (2 + 1) = 1 x 3 = 1, т. е. 1 x 2 + 1 x 1 = 2 + 1 = (2 + 1) = 3. Следовательно, умножение дистрибутивно над сложением. Распределительное свойство умножения над вычитанием: умножение целых чисел является распределительным над вычитанием. Если a, b и c — любые три рациональных числа, то a x (b — c) = a x b — a x c. Пример: 1 x (2 – 1) = 1 x 1 = 1, т.е. 1 x 2 – 1 x 1 = 2 – 1 = (2 – 1) = 1, т.е. 1 x (2 – 1) = 1 x 2 – 1 x 1. Следовательно, умножение является дистрибутивным по отношению к вычитанию.
Q.2 Что такое целые числа?
Ответ 2 Целое число — это целое, а не дробное число, которое может быть положительным, отрицательным или нулевым. Любое число, содержащееся в наборе комбинаций всех вышеперечисленных числовых категорий, называется целым числом. Целочисленный набор — это тот, который содержит все натуральные числа, целые числа и отрицательные числа. В результате каждое натуральное число, каждое целое число и каждое отрицательное число являются целыми числами. Дроби (в форме p/q) и десятичные числа не входят в набор целых чисел. Множество целых чисел бесконечно, то есть у него нет ни начала, ни конца ни с одной стороны. Это потому, что всегда есть другое число с увеличением или уменьшением на 1 для каждого числа как с положительной, так и с отрицательной стороны. Следовательно, множество целых чисел не может быть ограничено и поэтому неисчерпаемо.
Q.3 Как рисовать целые числа на числовой прямой?
Ответ 3 Множество положительных и отрицательных целых чисел, включая ноль, называется целым числом. Визуальное представление целых чисел в числовой строке известно как целые числа в числовой строке. В числовой строке целые числа помогают нам выполнять различные арифметические операции. Как представить целые числа в числовой строке Шаг 1: Сначала нарисуйте длинную горизонтальную линию. Шаг 2: Отметьте ноль в середине. Шаг 3: Отметьте все положительные числа справа. Шаг 4: Отметьте все положительные числа слева.
Q.4 Каковы применения целых чисел?
Ответ 4 Целые числа обычно используются для представления двух противоположных обстоятельств. Это не просто цифры; к ним прикреплены знаки. Положительные и отрицательные числа можно использовать по-разному. Наибольшее практическое применение целых чисел — измерение температуры. Положительные и отрицательные характеристики температуры позволяют нам понять, сравнить и количественно оценить изменение температуры. В дополнение к определению температуры банки используют целые числа для расчета кредитов и дебетов. Целые числа помогают в лучшей количественной оценке данных. Отрицательные целые числа широко используются для описания температуры ниже точки замерзания, денежного кредита, высоты ниже уровня моря, уровня лифта, когда он ниже уровня земли, отрицательных результатов экзаменов и, среди прочего, в качестве штрафа в викторинах / играх.
Q.5 Является ли ноль целым числом?
Ответ 5 Ноль — это целое число, обозначенное 0, которое при использовании в качестве счетного числа означает отсутствие объектов. Это единственное целое число (и, соответственно, единственное действительное число), которое не является ни отрицательным, ни положительным. Nonzero относится к числу, отличному от нуля. Нуль функции также известен как корень функции. Ноль — это целое число, как и целое число. Он известен как нейтральное целое число, потому что он не является ни отрицательным, ни положительным. 0 — это целое число, потому что это целое число, которое можно выразить без остатка.
Q.6 Каковы свойства целых чисел?
Ответ 6 Свойства целых чисел: свойство замыкания, ассоциативное свойство, коммутативное свойство, распределительное свойство и свойство тождества
Скачать публикацию в формате PDF
Подробнее с testbook.com
5 902 902 Свойства целых чисел | Замыкание, коммутативность, ассоциативная, дистрибутивность
Свойства целых чисел, имеет дело с различными понятиями, которые приведены ниже:
Замыкание свойств целых чисел
Коммутативное свойство целых чисел
Ассоциативное свойство целых чисел
Распределительное свойство целых чисел
Аддитивный идентификатор
Мультипликативное тождество целых чисел
Свойство замыкания целых чисел
Свойство замыкания при сложении целых чисел
Если мы складываем любые два целых числа, результат, полученный при сложении двух целых чисел, всегда является целым числом. Таким образом, мы можем сказать, что целые числа замкнуты относительно сложения.
Допустим, «a» и «b» – два целых числа , положительное или отрицательное. Когда мы складываем два целых числа, их результатом всегда будет целое число, то есть (a + b) всегда будет целым числом.
Пример –
Укажите, замыкается ли (– 11) + 2 при сложении
Решение
– 11 + 2
– 9
2 т. е. (-9) также является целым числом, можно сказать, что целые числа замкнуты относительно сложения.
Свойство замыкания при вычитании целых чисел
Если мы вычтем любые два целых числа, результатом всегда будет целое число, поэтому мы можем сказать, что целые числа замкнуты при вычитании.
Допустим, «a» и «b» — два целых числа, положительные или отрицательные, их результат всегда должен быть целым числом, т. е. (a + b) всегда будет целым числом.
Пример –
Укажите, замыкается ли (24 – 12) при вычитании
Решение –
24 – 12
12
Поскольку и 24, и -12 являются целыми числами, а их разность, т. е. (12), также является целым числом, мы можем сказать, что целые числа замкнуты при вычитании.
Свойство замыкания при умножении целых чисел :
Если мы умножаем любые два целых числа, результатом всегда будет целое число, поэтому мы можем сказать, что целые числа замыкаются при умножении.
Допустим, «a» и «b» — два целых числа, положительные или отрицательные, и если их умножить, их результат всегда должен быть целым числом, т. е. [(-a) x b] и [a x (–b)] будет всегда быть целым числом.
Пример –
Покажите, что (-30) x 11 закрыто при умножении
Решение –
– 30 x 11
-330
, а их произведение целые, так как 1 -30003
являются целыми числами, т. е. (-330) также является целым числом, можно сказать, что целые числа замкнуты относительно умножения.
Свойство замыкания при делении целых чисел :
Если мы разделим любые два целых числа, результат не обязательно будет целым числом, поэтому мы можем сказать, что целые числа не замыкаются при делении.
Допустим, «a» и «b» — два целых числа, и если мы их разделим, их результат ( a ÷ b ) не обязательно будет целым числом.
Пример –
Укажите, замыкается ли (14) ÷ 5 при делении.
Решение –
(14) ÷ 5
8
Поскольку и 14, и 5 являются целыми числами, но (14) ÷ 5 = 2,8, что не является целым числом. Следовательно, можно сказать, что целые числа не замкнуты относительно деления.
Переместительное свойство целых чисел
Переместительное свойство при сложении целых чисел:
Если мы сложим два целых числа, скажем, ‘a’ и ‘b’, ответ всегда будет одинаковым, т.е. если мы добавим (2+3) = ( 3+2) = 5. Итак, целые числа коммутативны при сложении. Точно так же, если мы применим это к целым числам, (-5 + 3) = (3 + (-5)) = -2, это также верно для всех целых чисел. Таким образом, мы можем сказать, что свойство коммутативности выполняется при сложении для всех целых чисел.
В обобщенной форме для любых двух целых чисел «a» и «b»
а + б = б + а
Пример –
Покажите, что -32 и 23 следуют свойству коммутативности при сложении.
Раствор –
Л.С.Ш = -32 + 23 = – 9
П.С.С = 23 + (-32) = 23 – 32 = – 9
Это означает, что два целых числа следуют свойству коммутативности при сложении.
Переместительное свойство при вычитании целых чисел :
Противоречиво, коммутативное свойство не будет выполняться при вычитании целого числа, скажем, (5 – 6) не равно (6 – 5). Рассмотрим для целых чисел (4) и (-1), разность двух чисел не всегда одинакова.
{4 — (-1) = 4 + 1 = 5} и {(-1) — 4 = — 1 — 4 = -5}, поэтому разница двух целых чисел равна 5 и (-5), которые не равны поэтому мы можем сказать, что свойство коммутативности не будет выполняться для вычитания целых чисел.
В обобщенной форме для любых двух целых чисел «a» и «b»
(а – б) ≠ (б – а)
Пример –
Проверить, следуют ли -88 и 22 коммутативному свойству при вычитании.
Решение –
L.H.S = -88 – 22 = – 110
R.H.S = 22 – (-88) = 22 + 88 = 110 коммутативность при вычитании.
Переместительное свойство при умножении целых чисел :
Если мы умножим два целых числа, скажем, «а» и «б», ответ всегда будет одинаковым, т. е. если мы умножим (2×3) = (3×2) = 6. Таким образом, целые числа коммутативны при умножении. Точно так же, если мы применим это к целым числам, (-5 × 3) = (3x (-5)) = -6, это также верно для всех целых чисел. Таким образом, мы можем сказать, что свойство коммутативности выполняется при умножении для всех целых чисел.
В обобщенной форме для любых двух целых чисел «a» и «b»
a x b = b x a
Пример –
Покажите, что любые два целых числа следуют свойству коммутативности при умножении.
Предположим, что два целых числа равны (-12) и 20. , LHS = RHS, т. е. ‘a x b’ = ‘b x a’
Это означает, что два целых числа следуют коммутативному свойству при умножении.
Переместительное свойство при делении целых чисел :
Свойство коммутативности не будет выполняться при делении целого числа, скажем, (12 ÷ 6) не равно (6 ÷ 12). Давайте рассмотрим для целых чисел, скажем, (-14) и (7), деление двух чисел не всегда одинаково.
[(-14) ÷ 7 = -2] и [7 ÷ (-14) = -0,5}, поэтому результат деления двух целых чисел не равен, поэтому мы можем сказать, что свойство коммутативности не будет выполняться для деления целых чисел .
В обобщенной форме для любых двух целых чисел «a» и «b»
(a ÷ b) ≠ (b ÷ a)
Пример –
Укажите, следуют ли (-12) и (-3) коммутативному закону при делении?
Решение –
Л.С.П. = (-12) ÷ (-3) = 4
П.С.С = (-3) ÷ (-12) = 25
Итак, Л.С.С ≠ П.С. то есть (a ÷ b) ≠ (b ÷ a)
Это означает, что два целых числа не следуют коммутативному свойству при делении.
Ассоциативное свойство целых чисел
Ассоциативное свойство при сложении целых чисел :
Поскольку свойство коммутативности выполняется для сложения, аналогично свойство ассоциативности также выполняется для сложения.
В обобщенной форме для любых трех целых чисел скажем «a», «b» и «c»
a + (b + c) = (a + b) + c
Пример –
Покажите, что (-6), (-1) и (3) ассоциативны относительно сложения.
Решение –
Л.С.С = – 6 + (-1 + 3)
= – 6 + 2
= – 4
Справа = (- 6 + (-1)) + 3
= (- 6 – 1) + 3
= -7 + 3
= -4
Итак, L.H.S = R.H.S, т.е. a + (b + c) = (a + b) + c
Это означает, что все три целых числа следуют ассоциативному свойству при сложении.
Ассоциативное свойство при вычитании целых чисел :
Противоречит этому, поскольку свойство коммутативности не выполняется для вычитания, аналогично свойство ассоциативности также не выполняется для вычитания целых чисел.
В обобщенной форме для любых трех целых чисел укажите «a», «b» и «c»
а – (б – в) ≠ (а – б) – в
Пример –
Проверить, следуют ли (-6), (-1) и 3 ассоциативному свойству при вычитании.
Решение –
Л.С.С = -6 – (-1 -3)
= -6 – (-4)
= -6 +4
= -2
С.С. = (-6 – -1)) – 3
= (-6 +1) – 3
= -5 -3
= -8
Итак, LHS ≠ RHS
Это означает, что все три целых числа не следуют ассоциативному свойству при вычитании .
Ассоциативное свойство при умножении целых чисел :
Поскольку коммутативное свойство верно для умножения, аналогично ассоциативное свойство также верно для умножения.
Ассоциативность умножения не зависит от группировки целых чисел.
В обобщенной форме для любых трех целых чисел скажем «a», «b» и «c»
a x (b x c) = (a x b) x c
Пример –
Показать, что (-2), (-3) и 4 обладают ассоциативным свойством для умножения
Решение –
L.H.S = (-2) x (-3 x 4)
= -2 x -12
= 24
П.С.С = (-2 x -3) x 4
= 6 x 4
= 24
Итак, Л. С.С = П.С.; то есть a x (b x c) = (a x b) x c
Это означает, что все три целых числа следуют ассоциативному свойству при умножении.
Распределительное свойство целых чисел :
Распределительные свойства умножения целых чисел делятся на две категории: над сложением и над вычитанием.
1. Дистрибутивность умножения над сложением верна для всех целых чисел.
В обобщенной форме для любых трех целых чисел скажем «a», «b» и «c»
a x (b + c) = (a x b) + (a x c)
Пример –
Покажите, что (-2), 3 и 5 следуют дистрибутивному свойству умножения над сложением.
Решение –
Л.В.С. = -2 x (3 + 5)
= -2 x 8
= -16 -6 + (-10)
= -6 -10
= -16
Таким образом, Л.В.С = П.В.С; т. е. a x (b + c) = (a x b) + (a x c)
Это означает, что распределительное свойство умножения над сложением выполняется для всех целых чисел.
2. Дистрибутивность умножения над вычитанием верна для всех целых чисел.
В обобщенной форме для любых трех целых чисел укажите «a», «b» и «c»
a x (b – c) = (a x b) – (a x c)
Пример –
Покажите, что (-5), (-4) и (-2) следуют дистрибутивному свойству умножения над вычитанием.
Л.Г.С = -5 x (-4 – (-2))
= -5 x (-4 + 2)
= -5 x -2
= 10
П.Г.С = (-5 x -4 ) – (-5 x -2)
= 20 – 10
= 10
Итак, Л.В.С = П.В.С; т. е. a x (b – c) = (a x b) – (a x c)
Это означает, что распределительное свойство умножения над вычитанием выполняется для всех целых чисел.
Аддитивная идентичность :
Когда мы добавляем ноль к любому целому числу, мы получаем одно и то же число, поэтому ноль является аддитивной идентичностью для целых чисел. Точно так же, если мы добавим ноль к любому целому числу, мы получим одно и то же целое число, независимо от того, положительное оно или отрицательное.

admin
Навигация по записям
Мужские имена с отчеством романович: Имена подходящие к отчеству Романович
Википедия писатель бунин: HTTP status 402 — payment required, требуется оплата
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Рубрики
Воспитывать
Дети
Подросток
Правильно
Разное
Рекомендации
Советы
2024 © Все права защищены.

Семейные советы
Как правильно ?
Дети
Воспитание

Формула прибыли: различные формулы расчета прибыли с определением и примерами
Формула себестоимости: изучите C.P. Формула прибыли и убытков с примерами
Свойства натуральных чисел, объясненные в примерах решения
Длинное деление, исследование с символом, шагами, делением многочлена и примерами решения
Операции над вещественными числами, свойства, примеры решения и часто задаваемые вопросы

Исходное уравнение	Переписанное уравнение
\(\ 1,2+3,8=5\)	\(\ 3,8+1,2=5\)
\(\ \frac{1}{2}+\frac{1}{8}=\frac{5}{8}\)	\(\ \frac{1}{8}+\frac{1}{2}=\frac{5}{8}\)
\(\ 14+(-10)=4\)	\(\ (-10)+14=4\)
\(\ \frac{1}{3}+\left(-1 \frac{2}{3}\right)=-1 \frac{1}{3}\)	\(\ \left(-1 \frac{2}{3}\right)+\frac{1}{3}=-1 \frac{1}{3}\)
\(\ (-5,2)+(-3,6)=-8,8\)	\(\ (-3,6)+(-5,2)=-8,8\)

Исходное уравнение	Переписанное уравнение
\(\ 4.5 \cdot 2=9\)	\(\ 2 \cdot 4.5=9\)
\(\ (-5) \cdot 3=-15\)	\(\ 3 \cdot(-5)=-15\)
\(\ \frac{1}{5} \cdot 5=1\)	\(\ 5 \cdot \frac{1}{5}=1\)
\(\ \left(-\frac{1}{4}\right) \cdot\left(-\frac{8}{10}\right)=\frac{1}{5}\)	\(\ \left(-\frac{8}{10}\right) \cdot\left(-\frac{1}{4}\right)=\frac{1}{5}\)

\(\ 4 \cdot(x \cdot 27)\)	Исходное выражение.
\(\ 4 \cdot\left(\left(-\frac{3}{4}\right) \cdot 27\right)\)	Замените \(\ -\frac{3}{4}\) на \(\ x\).
\(\ \begin{array}{r} \left(4 \cdot\left(-\frac{3}{4}\right)\right) \cdot 27 \\ \left(-\frac{12}{4}\right) \cdot 27 \end{массив}\)	Используйте ассоциативное свойство умножения, чтобы перегруппировать множители так, чтобы \(\ 4\) и \(\ -\frac{3}{4}\) находились рядом друг с другом. Умножение \(\ 4\) на \(\ -\frac{3}{4}\) делает вычисление выражения немного проще, чем умножение \(\ -\frac{3}{4}\) на \ (\ 27\).
\(\ -3 \cdot 27=-81\)	Умножить. \(\ 4\) раз \(\ -\frac{3}{4}=-3\), а \(\ -3\) раз \(\ 27\) равно \(\ -81\).

\(\ 4+12+3+4-8\)	Исходное выражение.
\(\ 12+3+4+4+(-8)\)	Определите совместимые номера. \(\ 4+4\) равно \(\ 8\), и есть \(\ -8\). подарок. Вспомните, что вы можете думать о \(\ -8\) как о \(\ +(-8)\). Используйте свойство коммутативности сложения, чтобы сгруппировать их вместе.
\(\ 12+3+(4+4+(-8))\)	Используйте ассоциативное свойство для группировки \(\ 4+4+(-8)\).
\(\ 12+3+0\)	Добавить \(\ 4+4+(-8)\).
\(\ 12+3+0=15\)	Добавьте остальные условия.

\(\ 5(2 x-3)\)	Исходное выражение.
\(\ 5(2 х)-5(3)\)	Раздать 5.
\(\10 х-15\)	Умножить.
\(\ 10(2)-15\) \(\ 20-15=5\)	Подставьте 2 вместо \(\ x\) и оцените.

№	Этапы организации учебной деятельности	Цель этапа	Деятельность учителя	Деятельность учащихся	Формируемые универсальные учебные действия (УУД)
1.	Организационный этап (3 мин.)	Постановка цели и задач урока. Мотивация учебной деятельности учащихся.	Проговариваю цель урока, ставлю учебную задачу. Интерактивная работа с приложением www. menti.com. Учащимся необходимо записать при помощи своих мобильных устройств, слова, выражения, которые им приходят на ум при использовании термина Свойство. Уточняю понимание учащимися поставленных целей.	Выполняют задание.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: целеполагание, планирование. Познавательные: самостоятельное выделение и формулирование познавательной цели. Коммуникативные: умения слушать, осознанно строить речевое высказывание, воспринимать ответы учащихся.
2.	Этап актуализации знаний (5 мин.)	Организовать познавательную деятельность учащихся.	Организую работу по рядам у доски, (соревновательный момент), необходимо записать свойства умножения. — Переместительное свойство; — Сочетательное свойство; — Распределительное свойство относительно сложения; — Распределительное свойство относительно вычитания; — Свойство умножения на единицу; — Свойство умножения на нуль. Проговорить свойства в парах.	Выходят к доске по очереди, друг за другом, 6 человек от каждого ряда и записывают свойства умножения Проговаривают свойства в парах.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: волевая саморегуляция. Познавательные: поиск и выделение необходимой информации, смысловое чтение. Коммуникативные: умения слушать, осознанно строить речевое высказывание, воспринимать ответы учащихся.
3.	Этап закрепления изученного материала (8 мин. )	Организовать деятельность учащихся по закреплению знаний.	Формулирую задание. (На основе заранее подготовленного домашнего задания. Учащимся необходимо было составить математические задачи, и иллюстрации к ним). Учащимся, необходимо поменяться друг с другом задачами и выполнить решение в тетради.	Выполняют задание, работают индивидуально, решая задачи в тетрадях, осуществляют проверку.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: волевая саморегуляция, контроль. Познавательные: умение осознанно и произвольно строить речевое высказывание. Коммуникативные: умение участвовать в коллективном обсуждении, умение выражать свои мысли.
4.	Изучение нового материала (7 мин).	Показать новый способ решения примеров с буквенной частью.	Подсказки: Приготовить несколько непонятных примеров. Показать ученикам без объяснений, что это и зачем это нужно. Попросить угадать, верно решенный пример, давая подсказки, термины.	Логически, на основании полученных знаний, подсказки учителя, находят верно решенные примеры. Выявляют новый способ рационального решения примеров.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: волевая саморегуляция, контроль, коррекция. Познавательные: умение выбрать наиболее эффективные способы решения. Коммуникативные: способность сохранять доброжелательное отношение друг к другу.
5.	Этап первичного закрепления изученного материала. (13 мин.)	Закрепить изученный материал.	Заполнить все: Подготовить задания по теме урока с пропущенными полями. Раздать ученикам и попросить заполнить поля. В конце обсудить, что осталось незаполненным. Попросить озвучить, что получилось.	Выполняют задания, работая в парах на раздаточном материале, затем комментируют, проговаривая получившиеся результаты. Сравнивают, устраняют ошибки.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: волевая саморегуляция, контроль, коррекция. Познавательные: умение выбрать наиболее эффективные способы решения, рефлексия. Коммуникативные: способность сохранять доброжелательное отношение друг к другу, умение договариваться, слушать и вступать в диалог.
6.	Рефлексия. (3 мин.)	Провести самооценку.	Какова была тема урока? Какую цель надо было достигнуть? При помощи мобильных устройств и приложения www.menti.com осуществляют оценку урока и самооценку.	Проговаривают тему и цель урока. Осуществляют самооценку.	Личностные: развитие доброжелательности, готовности к сотрудничеству, ответственности. Регулятивные: контроль, коррекция, оценка. Познавательные: умение осознанно и произвольно строить речевое высказывание в устной и письменной форме. Коммуникативные: способность сохранять доброжелательное отношение друг к другу, умение слушать.
7.	Домашнее задание. (1 мин.)	Разъяснить методику выполнения домашнего задания.	§17, упр. 429, 432, 435	Записывают домашнее задание.	Личностные: развитие ответственности. Регулятивные: волевая саморегуляция. Познавательные: умение выбрать наиболее эффективные способы решения Коммуникативные: умение слушать.

\(\ (-15,5)+35,5=20\)	Добавление.
\(\ 35,5+(-15,5)\)	Используя свойство коммутативности, вы можете поменять местами -15,5 и 35,5, чтобы они располагались в другом порядке.
\(\ \begin{array}{c} 35,5+(-15,5) \\ 35,5-15,5=20 \end{массив}\)	Сложение 35,5 и -15,5 равносильно вычитанию 15,5 из 35,5. Сумма 20.

\(\ 9(4+x)\)	Исходное выражение.
\(\ 9(4)+9(х)\)	Распредели 9 и умножь.
\(\ 36+9 х\)	Умножить.

\(\ 5(2 x-3)\)	Исходное выражение.
\(\ 5(2(2)-3)\)	Замените \(\ x\) на 2.
\(\ \begin{array}{c} 5(4-3) \\ 5(4)-5(3) \end{массив}\)	Умножить.
\(\ 20-15=5\)	Вычитание и оценка.

\(\ 3(x)+12(x)\)	\(\ 3 x\) равно 3 раза \(\ x\), а \(\ 12 x\) равно 12 раз \(\ x\)
\(\ х(3+12)\)	Изучая свойство дистрибутивности (а также используя свойство коммутативности), вы знаете, что \(\ x(3+12)\) совпадает с \(\ 3(x)+12(x)\).
\(\ \begin{array}{c} x(15) \\ \text { or } \\ 15 x \end{массив}\)	Объедините члены в скобках: \(\ 3+12=15\).

\(\ 10 у+5 у+9 х-6 х-х\)	В этом выражении есть похожие члены, так как все они состоят из коэффициента, умноженного на переменную \(\ x\) или \(\ y\). Обратите внимание, что \(\ -x\) совпадает с \(\ (-1) x\).
\(\ 15 у+2 х\)	Добавить похожие термины. \(\ 10 y+5 y=15 y\) и \(\ 9 x-6 x-x=2 x\).

Имущество	Пример с дополнением
Распределительное свойство
Ассоциативный
Коммутативный
Резюме: Все 3 из этих свойств применимы к сложению.

Имущество	Пример с умножением
Распределительное свойство	Распределительное свойство — это применение умножения (поэтому здесь нечего показывать).
Ассоциативный
Коммутативный
Резюме: Все 3 из этих свойств применимы к умножению.

Заявление	Свойство
7 + 2 = 2 + 7	Коммутативное свойство
6 + (2 + 11) = (6 + 2) + 11	Ассоциативное свойство
5 (2 + 4) = 5 • 2 + 5 • 4	Распределительное свойство
(12 • 44) • 13 • 5 = 12 • 44 • (13 • 5)	Ассоциативное свойство
5 • 3 • 11 = 11 • 5 • 3	Коммутативное свойство
6 (3 + 11 + 4) = 6 • 3 + 6 • 11 + 6 • 4	Распределительное свойство

Заявление	Свойство
а + с = с + а	Коммутативное свойство
а (х + у + г) = а • х + а • у + а • г	Распределительное свойство
(а • у) • х • г = а • у • (х • г)	Ассоциативное свойство