Виды задач в 1 классе. Простые задачи на сложение и вычитание.
Простые задачи на сложение и вычитание
Нахождение
суммы двух слагаемых
Нахождение
неизвестного слагаемого
Нахождение
неизвестного слагаемого
В коробке лежало 3 простых и 4 цветных карандаша. Сколько всего карандашей было в коробке?
3+4=7 (шт.)
Ответ: 7 карандашей в коробке.
В коробке всего лежало 7 карандашей. Из них 3 простых. Остальные — цветные. Сколько цветных карандашей в коробке?
7-3=4 (шт.)
Ответ: 4 цветных карандаша в коробке.
В коробке всего лежало 7 карандашей. Из них 4 цветных. Остальные — простые. Сколько простых карандашей в коробке?
7-4=3 (шт.
)
Ответ: 3 простых карандаша в коробке.
Нахождение разности (остатка)
Нахождение неизвестного уменьшаемого
Нахождение неизвестного вычитаемого
Мама купила 7 пирожных. 3 пирожных съели. Сколько осталось?
Было — 7 п.
Съели — 3 п.
Осталось — ? п.
7-3=4 (п.)
Ответ: 4 пирожных осталось.
Мама купила пирожные. После того, как 3 съели, осталось 4. Сколько пирожных купили?
Было — ? п.
Съели — 3 п.
Осталось — 4 п.
3+4=7 (п.)
Ответ: 7 пирожных купили.
Мама купила 7 пирожных. После того, как несколько съели, осталось 4. Сколько пирожных съели?
Было — 7 п.
Съели — ? п.
Осталось — 4 п.
7-4=3 (п.)
Ответ: 3 пирожных съели.
Увеличение
на несколько единиц
Уменьшение
на несколько единиц
Разностное сравнение
В коробке лежало 3 простых карандаша, а цветных на 2 больше. Сколько цветных карандашей лежало в коробке?
3+2=5 (шт.)
Ответ: 5 цветных карандашей лежало в коробке.
В коробке лежало 5 цветных карандашей, а простых на 2 меньше. Сколько простых карандашей лежало в коробке?
5-2=3 (шт.)
Ответ: 3 простых карандаша лежало в коробке.
В коробке лежало 5 цветных и 3 простых карандаша. На сколько больше было цветных карандашей, чем простых?
5-3=2 (шт.)
Ответ: на 2 карандаша больше цветных, чем простых.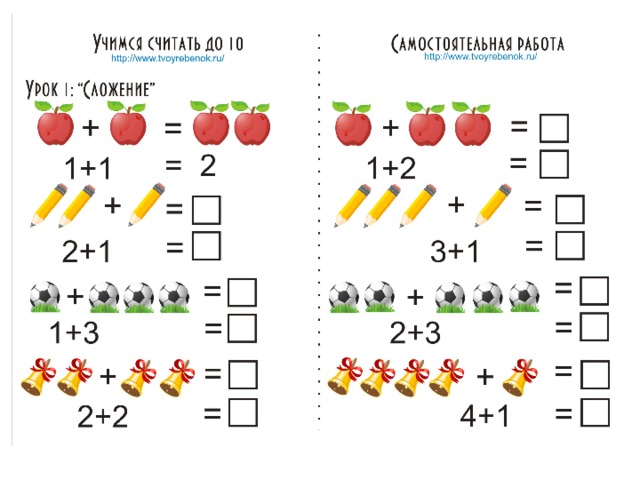
Прием рассмотрения задач с недостающими или лишними данными. Например:
У кормушки было 6 серых и 5 белых голубей. Один белый голубь улетел. Сколько белых голубей стало у кормушки?
Анализ текста показывает, что одно из данных лишнее – 6 серых голубей. Для ответа на вопрос оно не нужно. После решения задачи учитель предлагает внести в текст задачи такие изменения, чтобы данное понадобилось. Это приводит к составной задаче:
У кормушки было 6 серых и 5 белых голубей. Один голубь улетел. Сколько голубей у кормушки?
Эти изменения условия повлекут за собой необходимость выполнять два действия: (6+5) -1 или (6-1)+5 или (5-1)+6.
Таким образом простая задача «достраивается» до составной.
Методические приемы преобразования задач в начальной школе.
Преобразование задач – это изменение связи между числовыми данными в некотором тексте.
Изменение связи между числовыми данными может быть следующих видов:
изменение связи между числовыми данными условия и требования.
Например, дана задача: «На одном столе лежало 5 книг, на другом столе на 2 книги больше. Сколько книг лежало на втором столе?»
Сделаем краткую запись:
I стол — 5 кн.
II стол — ?, на 2 кн. больше
Преобразуем задачу.
Например: «На одном столе лежало 5 книг, на другом столе на 2 книги больше. Сколько книг лежало на двух столах?»
Сделаем краткую запись:
I стол — 5 кн.
II стол — ?, на 2 кн. Больше
Таким образом, мы преобразовали простую задачу в составную.
изменение связи между числовыми данными в условии.
Например, дана задача: «В красной вазе стояло 7 роз, а в зеленой на 4 меньше. Сколько роз стояло в двух вазах?»
Составим краткую запись:
Крас. ваза – 7 роз
Зел. ваза — ?, на 4 меньше
Преобразуем задачу.
Например: «В красной вазе стояло 7 роз, а в зеленой на 4 больше. Сколько роз стояло в двух вазах?»
Составим краткую запись:
Крас. ваза – 7 роз
Зел. ваза — ?, на 4 больше
Таким образом, преобразовав задачу, мы изменили отношения между объектами задачи с «меньше на» на «больше на».
изменение связи между числовыми данными в условии и числовыми данными условия и требования.
Первый этап — подготовительный. Основная цель этого этапа — организовать систему упражнений по выполнению операций над множествами. Так, подготовкой к решению задач на сложение являются упражнения по объединению множеств. Упражнения на выделение части множества проводятся для подготовки детей к решению задач на вычитание. С помощью операций над множествами раскрывается отношение “часть — целое”, доводится до понимания смысл выражений “больше на…”, “меньше на…”, вопросов: “Что известно?”, “Что нужно узнать?”
ГДЗ(дүж) решения для учебника Математика Абылкасымова 5 класс 2017 KZGDZ.COM
Глава 1. НАТУРАЛЬНЫЕ ЧИСЛА И НУЛЬ
§ 1. Запись натуральных чисел
Упражнение
12345678910111213
§ 2. Координатный луч
Упражнение
14151617181920212223242526
§ 3. Сравнение натуральных чисел
Упражнение
2728293031323334353637383940
§ 4.
Арифметические действия е натуральными числамиУпражнение
4142434445464748495051525354555657585960
§ 5. Числовые и буквенные выражения. Упрощение выражений
Упражнение
61626364656667686970717273747576777879
§ 6. Уравнения
Упражнение
808182838485868788899091
§ 7. Формулы. Вычисления по формулам
Упражнение
9293949596979899100101102
§ 8. Решение текстовых задач
Упражнение
103104105106107108109110111112113114115116117118119120121122
§ 9. Последовательность из натуральных чисел
Упражнение
123124125126127128129130131132
Глава 2. ДЕЛИМОСТЬ НАТУРАЛЬНЫХ ЧИСЕЛ
§ 10. Делители и кратные натуральных чисел. Простые и составные числа
Упражнение
133134135136137138139140141142143144145146147148149150151152153
§11.
Основные свойства делимостиУпражнение
154155156157158159
160161162163164165166167168169170
§ 12. Признаки делимости на числа 2. 3, 5, 9.
Упражнение
171172173174175176177178179180181182183184185186187188189190191192193194
§13. Степень
Упражнение
195196197198199200201202203204205206207208209210211212
§14. Разложение натурального числа на простые множители
Упражнение
213214215216217218219220221222223224225226227228229230231232233
§15. Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
Упражнение
234235236237238239
240241242243244245246247248249250251252253254255256257258259
Глава 3. ОБЫКНОВЕННЫЕ ДРОБИ И ДЕЙСТВИЯ НАД НИМИ
§ 16. Обыкновенная дробь.
Чтение и запись обыкновенных дробейУпражнение
260261262263264265266267268269270271272273274275276277278279280281282283284285286
§ 17. Основное свойство обыкновенной дроби
Упражнение
287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319
320321322323324325
§ 18. Правильные и неправильные обыкновенные дроби. Смешанные числа
Упражнение
326327328329330331332333334335336337338339340341342343344345
§19. Перевод неправильной обыкновенной дроби в смешанное число и смешанного числа в неправильную обыкновенную дробь
Упражнение
346347348349350351352353354355356357358359360361362363364
§ 20. Изображение обыкновенных дробен и смешанных чисел на координатном луче
Упражнение
365366367368369370371372373374375376377378379380381
§ 21.
Приведение обыкновенных дробей к общему знаменателюУпражнение
382383385386387388389390391392393394395396397398
§ 22. Сравнение обыкновенных дробей и смешанных чисел
Упражнение
399400
401402403404405406407408409410411412413414415416417418419420
§ 23. Сложение и вычитание обыкновенных дробей
Упражнение
421422423424425426427428429430431432433434435436437438439440441442443444445446447448449450451452453454
§ 24. Сложение смешанных чисел
Упражнение
455456457458459460461462463464465466467468469470471472473474475476477478
§ 25. Вычитание смешанных чисел
Упражнение
479480
481482483484485486487488489490491492493494495496497498499500501502503
§ 26. Умножение обыкновенных дробей и смешанных чисел
Упражнение
504505506507508509510511512513514515516517518519
§ 27.
Деление обыкновенных дробей и смешанных чиселУпражнение
520521522523524525526527528529530531532533534535536537
§ 28. Действия с обыкновенными дробями, нулем, натуральными и смешанными числами
Упражнение
538539540541542543544545546547548549550551552553554555556
Глава 4. ТЕКСТОВЫЕ ЗАДАЧИ
§ 29. Нахождение дроби от числа и числа по его дроби
Упражнение
557558559560
561562563564565566567568569570571572573574575576577578
§ 30. Задачи на совместную работу
Упражнение
579580581582583584585586587588589590591592593
Глава 5. ДЕСЯТИЧНЫЕ ДРОБИ II ДЕЙСТВИЯ НАД НИМИ
§ 31. Десятичная дробь. Чтение и запись десятичных дробей
Упражнение
594595596597598599600601602603604606607
§ 32. Перевод десятичной дроби в обыкновенную дробь
Упражнение
608609610611612613614615616617
§ 33.
Изображение десятичных дробей на координатном луче. Сравнение десятичных дробейУпражнение
618619620621622623624625626627628629630631632633
§ 34. Сложение и вычитание десятичных дробей
Упражнение
634635636637638639640641
642643644645646647648649650
§ 35. Умножение десятичной дроби на натуральное число
Упражнение
651652653654655656657658659660661662663664665666667668669
§ 36. Умножение десятичных дробей
Упражнение
670671672673674675676677678679680681682683684685
§ 37. Деление десятичной дроби на натуральное число
Упражнение
686687688689690691692693694695696697698699700701
§ 38. Деление десятичных дробей
Упражнение
702703704705706707708709710711712713714715716717718719720
§ 39.
Умножение и деление десятичных дробей на 10. 100. 1000. … и на 0.1. 0,01, 0,001Упражнение
721
722723724725726727728729730731732733734735736
§ 40. Действия с десятичными и обыкновенными дробями
Упражнение
737738739740741742743744745746747748749750751752753754755756757
§41. Округление чисел
Упражнение
758759760761762763764765
§ 42. Решение текстовых задач
Упражнение
766767768769770771772773774775776777778779
Глава 6. МНОЖЕСТВА
§ 43. Множество. Элементы множества. Изображение множеств
Упражнение
780781782783784785787
§ 44. Отношения между множествами. Подмножества
Упражнение
788789790791792793794795
§ 45. Объединение и пересечение множеств
Упражнение
796797798799800
§ 46.
Решение текстовых задачУпражнение
801802
803804805806807808
Глава 7. ПРОЦЕНТЫ
§ 47. Процент
Упражнение
809810811812813815816817818819820821822823824825826828829830831
§ 48. Нахождение процентов от числа и числа по его процентам
Упражнение
832833834835836837838839840841842843
§ 49. Решение текстовых задач
Упражнение
844845846847848849850851852853854855856857858859860861862863864865866867868869
Глава 8. УГЛЫ. МНОГОУГОЛЬНИКИ
§ 50. Угол
Упражнение
870871872873874875876877878880881
§ 51. Многоугольники
Упражнение
882883884885
886887888889890
Глава 9. ДИАГРАММЫ
§ 52. Окружность. Крут
Упражнение
891892893894895896897898899901902
§ 53.
Диаграмма. Представление статистических данных с помощью диаграммУпражнение
903904906907908909910911912913915916917919920921
Глава 10. РАЗВЕРТКИ ПРОСТРАНСТВЕННЫХ ФИГУР
§ 54. Прямоугольный параллелепипед (куб) и его развертка
Упражнение
922923924926
§ 55. Задачи на разрезание фигур. Задачи на складывание фигур
Упражнение
929930931932933934
Глава 11. УПРАЖНЕНИЯ ДЛЯ ПОВТОРНЕИЯ
Упражнение
937938939940941942943944945946947948949950951952953954955956957958959960961962963964965966967968969970971972973974
975976977978979980
Математика — древнейшая, основополагающая дисциплина. Сталкиваемся мы с ней каждый день, сами это не подозревая. Грамотность школьника напрямую зависит от успеваемости в школе. Не спешите огорчаться, если материал, данный учителем вам непонятен, в решебнике есть вся информация, изложенная понятным для пятиклассника языком.
Гранит науки грызть не всем под силу, а родители, зачастую, не могут правильно и доходчиво объяснить сложные понятия и формулы.
В сборнике готовых домашних заданий по математике за 5 класс от авторов А.Е. Абылкасымова, Т.П. Кучер, З.Э. Жумагулова 2017 г. собраны решения и ответы по всему задачнику. Ученики овладеют навыком работы с числами, порядком их исчисления, разберут уравнения и задачи на логику, родители смогут проверить и объяснить ребенку что-то более подробно.
Как преподавать задачи на сложение и вычитание
Мои ученики мучились с тем, как решать задачи на сложение и вычитание , казалось, целую вечность. Они могли подчеркнуть вопрос и найти числа. В большинстве случаев мои ученики просто складывали два числа вместе, не понимая смысла задачи.
Тьфу.
Вы можете рассказать?
Ниже приведены пять стратегий решения математических задач, которые можно использовать при обучении словесным задачам на сложение и вычитание с использованием любого ресурса.
Итак, как мне учить текстовые задачи? Это довольно сложно, но так весело, как только вы войдете в него.
Как преподавать задачи на сложение и вычитание
Основные компоненты обучения задачам на сложение и вычитание включают:
- Обучение соотношению чисел s – Как учитель, знайте тип задач и помогайте учащимся решать действие в задаче
- Дифференцируйте числа – Дайте учащимся только правильные числа, чтобы они могли прочитать задачу, не увязая в вычислениях
- Используйте академический словарь — и будьте последовательны в том, что вы используете.
- Остановить поиск «Ответа» — дело не в ответе; речь идет о процессе
- Различие между моделями и стратегиями – одна связана с отношениями между числами, а другая – с тем, как учащиеся «решают» или вычисляют задачу.
Я большой сторонник НЕ изучения списков ключевых слов.
Это просто не работает последовательно во всех проблемах. Это короткий путь, ведущий к сбоям в математическом мышлении. Вы также не должны просто давать учащимся рабочие листы с текстовыми задачами и заставлять их искать ключевые слова для текстовых задач. Я более подробно рассказываю о том, почему это не работает, в статье «Проблема с использованием ключевых слов для решения текстовых задач».
Научите соотношению чисел в математических задачах со словами
Один из способов помочь вашим ученикам решать задачи со словами — научить их отношениям между числами. Другими словами, помогите им понять, что числа в задаче каким-то образом связаны друг с другом.
Я учу текстовые задачи, убирая числа. Звучит странно, верно?
Устранение отвлекающих факторов на числа помогает учащимся сосредоточиться на проблемной ситуации и понять действие или взаимосвязь чисел. Это также удерживает учащихся от решения задачи до того, как мы поговорим о взаимосвязи чисел.
Когда я преподаю текстовые задачи, я даю ученикам задачи с пробелами и без чисел.
___ + ___ = неизвестно
Хотите бесплатный образец текстовых задач, которые я использую в своем классе? Щелкните ссылку или изображение ниже. БЕСПЛАТНЫЙ образец текстовых задач по типу задачи
Различие чисел в задачах Word
Только после того, как мы обсудим задачу, я даю ученикам числа. Я различаю числа в зависимости от потребностей учащихся. В начале года мы все делаем одни и те же числа, чтобы я мог убедиться, что ученики понимают процесс.
После того, как учащиеся ознакомятся с процессом, я начинаю давать разным учащимся разные числа в зависимости от их уровня математического мышления.
Я также меняю номера в течение года с однозначных на двузначные.
Прелесть пустых мест в том, что я могу вставить в задачу любые числа, которые захочу, чтобы попрактиковаться в стратегиях, над которыми мы работали в классе.
В какой-то момент мы создаем список слов, но не список ключевых слов. Мы создаем список действий или глаголов и определяем, соединяют ли эти действия что-то или разделяют. Сколько вы можете придумать?
Вот несколько идей:
Присоединяйтесь: положил, получил, взял, купил, сделал
Разделить: съел, потерял, положил, уронил, использовал
Не бойтесь использовать академическую лексику при обучении словесным задачам
Я учу своих учеников определять начало проблемы, изменение проблемы и результат проблемы. Я учу их искать неизвестных .
Все эти слова мы используем при решении задач, и мы изучаем структуру словесной задачи через словарный запас и взаимосвязь чисел.
На самом деле, использование одного и того же словаря для разных типов задач помогает учащимся увидеть взаимосвязь чисел на более глубоком уровне.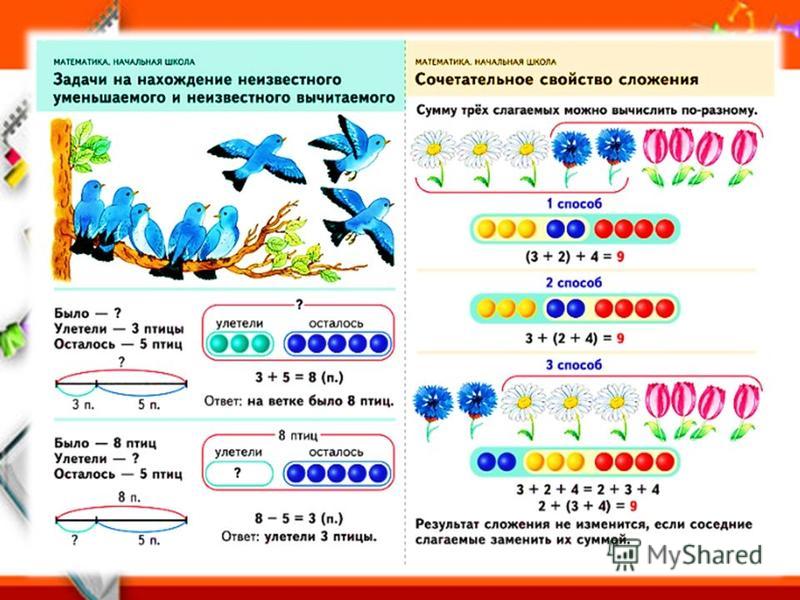
Возьмите эти примеры, можете ли вы определить запуск, изменение и результат в каждой проблеме? Подсказка: посмотрите на код, используемый для типа проблемы в правом нижнем углу.
Для сравнения задач мы используем термины больше , меньше , больше и меньше . Попробуйте решить эти задачи и посмотрите, сможете ли вы определить компоненты словесных задач.
Перестаньте искать «ответ» при решении текстовых задач
Это заблуждение труднее всего разрушить.
Учащиеся не решают словесную задачу, чтобы найти «ответ». Хотя ответ помогает мне, учителю, понять, понял ли ученик взаимосвязь чисел, , я хочу, чтобы ученики могли объяснить свой процесс и понять глубину словесных задач.
Ладно, это первоклассники и второклассники. Я знаю.
Мои студенты все еще могут объяснить после обучения, что они начинают изд с одной цифры.
Проблема результат ed в прочем другой номер. Затем учащиеся узнают, что они ищут замену на между этими двумя числами.
Все дело в отношениях.
Различие между моделями и стратегиями
Пару лет назад я наткнулся на эту статью о необходимости помочь учащимся разработать адекватные модели для понимания связи чисел в задаче.
У меня в голове взорвалась лампочка. Мне нужно было провести различие между модели, которые студенты используют для понимания соотношения чисел в задаче, и стратегии для решения вычислений в задаче. Модели и стратегии работают в тандеме, но очень разные.
Модели — это визуальные способы представления проблем. Стратегии — это способы, которыми учащийся решает задачу, складывая и разбирая числа.
Самое главное в моделях — отойти от них. Я знаю, это звучит странно.
Вы так долго обучаете студентов пользоваться моделями, а потом не хотите, чтобы они использовали модели.
Ну, на самом деле, вы хотите, чтобы студенты двигались к эффективности.
Младшие школьники разыгрывают задачи, рисуют задачи с изображениями и рисуют задачи с кругами или линиями. Направьте учащихся к эффективности. По мере того, как числа становятся больше, модель должна представлять отношение чисел
Это яркий пример перехода от модели перевернутой v к модели столбцов.
Ученик переходит от рисования кругов к использованию перевернутой буквы v.
Учащиеся должны полностью использовать одну модель, прежде чем переходить на другую. Они могут даже использовать два одновременно, пока выясняют сходство между моделями.
Студенты также должны иметь возможность создавать свои собственные модели. Вы увидите, как я иногда давал студентам копии модели, которые они могли вклеить в свои тетради, а иногда студенты рисовали свою собственную модель. Они должны нести ответственность за выбор того, что лучше всего подходит для них. Начните обучение с конкретных моделей, а затем позвольте учащимся выбрать одну из них для использования.
Всегда подталкивайте учащихся к более эффективным моделям.
То же самое касается стратегий для вычислений. Сначала обучайте стратегиям с помощью математических фактов, а затем применяйте их к текстовым задачам, чтобы учащиеся понимали стратегии и могли быстро выбрать одну из них для использования. При обучении сосредоточьтесь на одной или двух стратегиях. Как только учащиеся овладеют некоторыми стратегиями, попросите их выбрать стратегии, которые работают для решения различных задач.
Какие числа вы вставляете в пробелы?
Будьте целеустремленны в числах, которые вы выбираете для своих текстовых задач. Разные наборы чисел подходят для разных стратегий и разных моделей. Используйте числовые наборы, которые учащиеся уже использовали в вычислениях.
Если вас учили составлять 10, используйте числа, которые составляют 10. Если вы работаете над сложением без перегруппировки, используйте эти наборы чисел. Чем больше связей вы сможете установить между вычислениями и решением задачи, тем лучше.
Приведенные выше примеры в основном предназначены для задач объединения и разделения. Неудивительно, что у наших студентов такие трудности с задачами на сравнение, поскольку мы не учим их в той же степени, что и задачи на соединение и разделение.
Нашим ученикам нужно еще больше практиковаться в решении подобных задач, потому что отношение чисел более абстрактно. Однако я собираюсь оставить это для другого поста в блоге.
Вы хотите получить БЕСПЛАТНЫЙ образец ресурса, который я использую для обучения задачам на сложение и вычитание по типу задач ? Нажмите на эту ссылку или изображение ниже.
Как приобрести задачи на сложение и вычитание
Полный ресурс также доступен для покупки в моем магазине и на сайте Teachers Pay Teachers.
Другие идеи для обучения словесным задачам
Рассказы. Рабочие листы и учебные пособия по математике Второй класс.
Числа и операции (NCTM)
Понимать числа, способы представления чисел, отношения между числами и системы счисления.
Развивать чувство целых чисел, представлять и использовать их гибкими способами, включая связывание, составление и разложение чисел.
Соедините числовые слова и цифры с величинами, которые они представляют, используя различные физические модели и представления.
Понимать значения операций и их взаимосвязь.
Понимать различные значения сложения и вычитания целых чисел и связь между этими двумя операциями.
Понимание эффектов сложения и вычитания целых чисел.
Свободно считать и делать разумные оценки.
Разработка и использование стратегий для вычисления целых чисел с упором на сложение и вычитание.
Развивайте беглость с основными комбинациями чисел для сложения и вычитания.
Алгебра (NCTM)
Представление и анализ математических ситуаций и структур с использованием алгебраических символов.
Используйте конкретные, графические и словесные представления, чтобы развить понимание изобретенных и общепринятых символических обозначений.
Используйте математические модели для представления и понимания количественных отношений.
Моделируйте ситуации, связанные со сложением и вычитанием целых чисел, используя предметы, изображения и символы.
Измерение (NCTM)
Понимать измеримые атрибуты объектов и единиц, систем и процессов измерения.
Распознавать атрибуты длины, объема, веса, площади и времени.
Координаторы учебной программы 2 класса (NCTM)
Числа и действия и алгебра: Развитие быстрого запоминания фактов сложения и связанных с ними фактов вычитания и беглость с многозначным сложением и вычитанием
Дети используют свое понимание сложения, чтобы развивать быстрое запоминание основные факты сложения и связанные с ними факты вычитания. Они решают арифметические задачи, применяя свое понимание моделей сложения и вычитания (таких как объединение или разделение множеств или использование числовых линий), отношений и свойств числа (таких как разрядное значение) и свойств сложения (коммутативность и ассоциативность).
Связи с Фокусными точками 2-го уровня (NCTM)
Числа и операции: Дети используют разрядность и свойства операций для создания эквивалентных представлений заданных чисел (например, 35 представлено 35 единицами, 3 десятками и 5 единицами или 2 десятки и 15 единиц), а также писать, сравнивать и упорядочивать многозначные числа. Они используют эти идеи для составления и разложения многозначных чисел. Дети складывают и вычитают, чтобы решить множество задач, включая приложения, связанные с измерением, геометрией и данными, а также нестандартные задачи.