Произведение это умножение а деление: Произведение (математика) | это… Что такое Произведение (математика)?

admin

Содержание

Умножение степеней, деление, таблица

Что такое степень числа

Алгебра дает нам такое определение: 

«Степенью n числа а является произведение множителей величиной а n-раз подряд»

  • an — степень, где

a — основание степени

n — показатель степени

Соответственно:

Читается такое выражение, как a в степени n

Если говорить проще то, степень, а точнее показатель степени (n), говорит нам о том, сколько раз следует умножить это число (основание степени) на само себя.

А значит, если у нас есть задачка, где спрашивают, как возвести число в степень, например, число — она решается довольно просто:

  • 23 = 2·2·2, где

2 — основание степени

3 — показатель степени

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Таблица степеней

Здесь мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3). Не важно, в какой класс перешел ребенок — таблица пригодится всегда.

Число

Вторая степень

Третья степень

1

1

1

2

4

8

3

9

27

4

16

64

5

25

125

6

36

216

7

49

343

8

64

512

9

81

729

10

100

1000

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Свойства степеней: когда складывать, а когда вычитать

Степень в математике с натуральным показателем имеет несколько важных свойств, которые позволяют упрощать вычисления. Рассмотрим основные из них.

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

am · an = am+n

a — основание степени

m, n — показатели степени, любые натуральные числа.

Раз

35 · 32 = 35+3 = 38 = 6 561

Два

28 · 81= 28 · 23 = 211 = 2048

Свойство 2: частное степеней

Когда мы делим степени с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

, где

a — любое число, не равное нулю

m, n — любые натуральные числа такие, что m > n

Раз

Два: записать частное в виде степени

Свойство 3: возведение степени в степень

Когда возводим степень в степень, то основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

(an)m = an· m 

a — основание степени (не равное нулю)

m, n — показатели степени, натуральное число

Свойство 4: возведение произведения в степень

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a · b)n = an · bn

a, b — основания, не равные нулю

n — показатель степени, натуральное число

Свойство 5: возведение частного в степень

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)n = an : bn

a, b — основания степени, не равные нулю

n — показатель степени, натуральное число

Бесплатные занятия по английскому с носителем

Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику.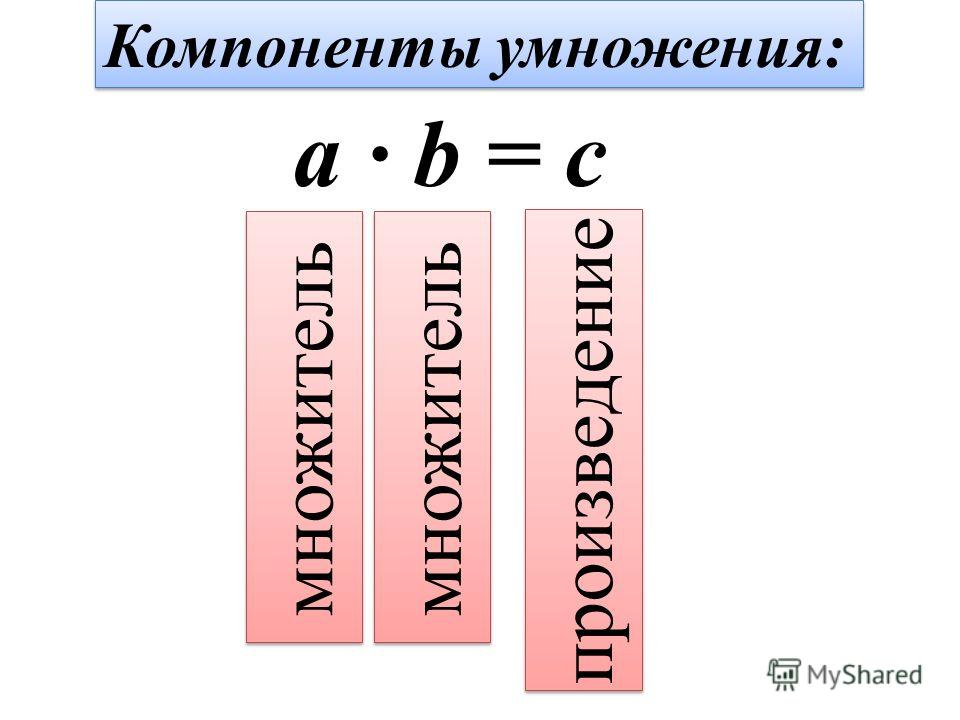 Сделайте язык частью жизни.

Умножение степеней с одинаковым показателем

Для того, чтобы произвести умножение степеней с одинаковыми показателями, нужно перемножить основания, а показатель степени оставить неизменным:

an · bn = (a · b)n , где

a, b — основания степени (не равные нулю)

n — показатель степени, натуральное число

  • a5 · b5 = (a·a·a·a·a) ·(b·b·b·b·b) = (ab)·(ab)·(ab)·(ab)·(ab) = (ab)5
  • 35 · 45 = (3·4)5 = 125 = 248 832
  • 16a2 = 42·a2 = (4a)2

Деление чисел с одинаковыми степенями

При делении степеней с одинаковыми показателями результат частного этих чисел возводится в степень:

an : bn = (a : b)n, где 

a, b — основания степени (не равные нулю), любые рациональные числа, b ≠ 0, 

n — показатель степени, натуральное число

Как Разделить Число на Произведение

Основные определения

Давайте для начала вспомним, что такое деление, умножение и, как их правильно записывать.

 

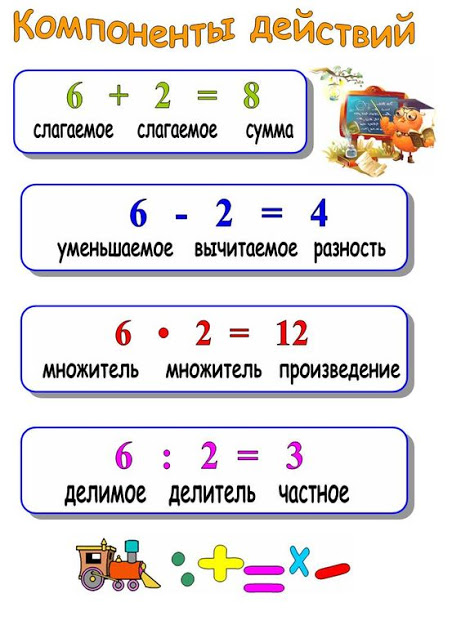
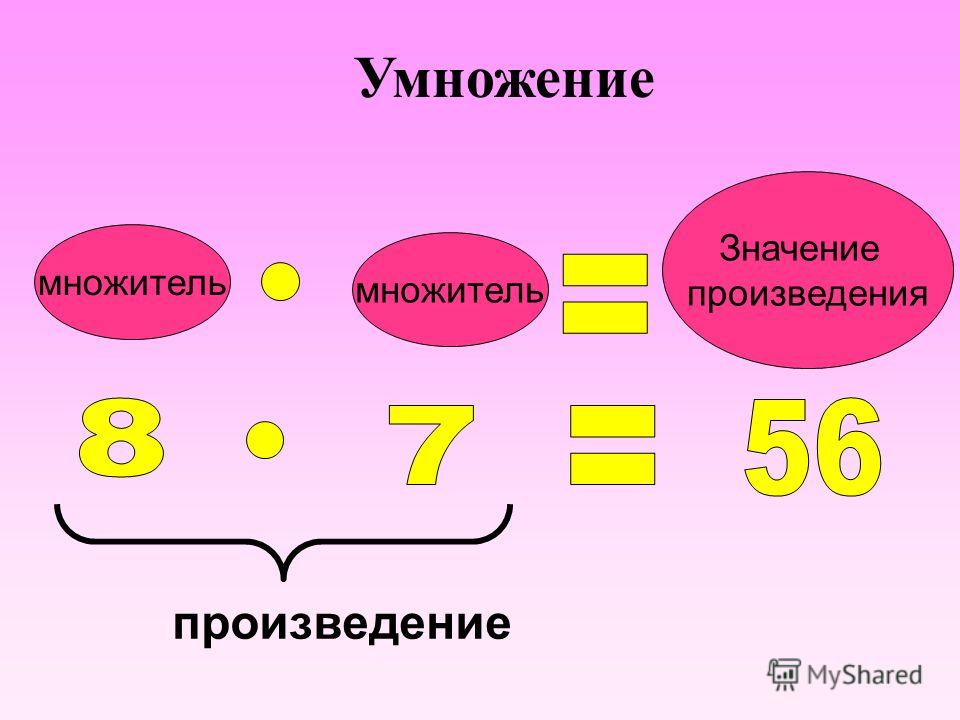
Умножение — арифметическое действие в виде краткой записи суммы одинаковых слагаемых.

  • Запись: 2 * 3 = 6, где 2 — множимое, 3 — множитель, 6 — произведение.
  • 2 * 3 = 3 + 3 = 6

В случае, если множимое и множитель поменять ролями, произведение остается одним и тем же.

  • Например: 3 * 2 = 2 + 2 + 2 = 6.

Поэтому и множитель, и множимое называют сомножителями.

Деление — арифметическое действие обратное умножению.

  • Запись: 20 : 5 = 4 или 20/5 = 4, где 20 — делимое, 5 — делитель, 4 — частное.

В этом случае произведение делителя 5 и частного 4, в качестве проверки, дает делимое 20.

Если в результате деления, частное является не целым числом, то его можно представить в виде дроби. 

Свойства деления в виде формул:

Распределительные свойства

(a + b) : c = a : c + b : c

(a — b) : c = a : c — b : c

(a * b) : c = (a : c) * b = (b : c) * a

a : (b * c) = (a : b) : c = (a : c) : b

Действия с единицей и нулём

a : 1 = a

a : a = 1

0 : a = 0 (a ≠ 0)

на нуль делить нельзя

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Способы деления числа на произведение

Число можно разделить на произведение двумя способами. Сформулируем правило деления числа на произведение для каждого способа и попрактикуемся на примерах.

1 способ

Чтобы разделить число на произведение, нужно сначала выполнить умножение в скобках, а затем разделить число на полученный результат.

Так, например, чтобы найти значение выражения: 666 : (3 * 2), нужно сначала перемножить то, что находится в скобках: 3 * 2 = 6.

Затем и разделить 666 на полученный результат: 666 : 6 = 111. Значит 666 : (3 * 2) = 666 : 6 = 111.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение — можно воспользоваться вторым способом.

2 способ

Чтобы разделить число на произведение, нужно разделить это число на первый сомножитель, а полученный результат разделить на второй сомножитель.

Например, чтобы найти значение выражения: 120 : (5 * 6), нужно сначала разделить  120 на 5: 120 : 5 = 24. Далее, полученное частное 24 разделить на 6: 24 : 6 = 4. А Теперь 120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4.

Так как от перестановки множителей произведение не меняется, то множители можно легко поменять местами: 120 : (6 * 5) и разделить 120 сначала на 6, а затем полученный результат разделить на 5: 120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.

Проще говоря, не важно на какой множитель первым делить число — результат будет одинаковым. Проверим:

120 : (5 * 6) = (120 : 5) : 6 = 24 : 6 = 4

тоже самое, что и

120 : (6 * 5) = (120 : 6) : 5 = 20 : 5 = 4.

Из этого примера делаем вывод, что значение частного не изменится от порядка выполнения действий.

Эти правила иногда называют свойствами деления числа на произведение. Но, по сути, неважно, как это называть. Главное — как это работает. Далее попрактикуемся на примерах.

Примеры деления числа на произведение

Пример 1. Применить правило деления числа на произведение двух чисел:
24 : ( 3 * 4).

Как рассуждаем:

 

  1. Чтобы разделить число на произведение, вычислим сначала произведение в скобках: 3 * 4 = 12.

  2. Подставляем полученное число в выражение:

24 : ( 3 * 4) = 24 : 12 = 2.

Вот и ответ. А теперь решим это же выражение другим способом.

 

  1. Чтобы разделить число на произведение чисел, нужно сначала число 24 разделить на первый множитель 3. А после, разделить полученный на второй множитель 8:

24 : ( 3 * 4) = 24 : 3 : 4 = 8 : 4 = 2.

А как можно еще решить это выражение?

 

  1. Чтобы число разделить на произведение, нужно сначала число 24 разделить на второй множитель 4. И полученный результат разделить на первый множитель 3:

24 : ( 3 * 4) = 24 : 4 : 3 = 6 : 3 = 2.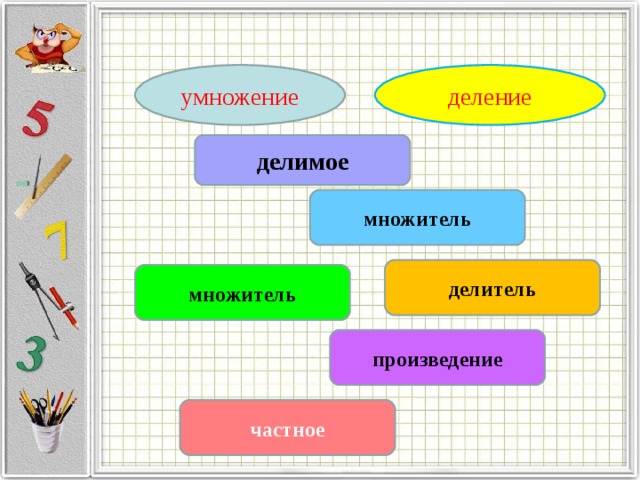

Вот, как это работает! Мы нашли значение выражения разными способами, при этом результаты получились одинаковыми.

Пример 2. Вычислить: тысячу разделить на произведение двадцати и пяти.

Ответ:

1000 : (20 * 5) = 1000 : 100 = 100

1000 : (20 * 5) = 1000 : 20 : 5 = 50 : 5 = 10

1000 : (20 * 5) = 1000 : 5 : 2 = 200 : 2 = 10

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Свойства деления. Деление произведения, суммы и разности на число

  • Деление произведения на число
  • Деление числа на произведение
  • Деление суммы на число
  • Деление разности на число
  • Общие формулы свойств деления

Деление произведения на число

Произведение можно разделить на число двумя способами:

1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(12 · 5) : 3,

можно сначала умножить  12  на  5:

12 · 5 = 60

и полученное произведение разделить на  3:

60 : 3 = 20,

значит  (12 · 5) : 3 = 60 : 3 = 20.

Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.

2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.

Например, чтобы найти значение выражения:

(8 · 20) : 4,

можно сначала разделить любой из сомножителей  (8  или  20)  на  4:

8 : 4 = 2

и полученное частное умножить на другой сомножитель:

2 · 20 = 40,

значит  (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.

Данное выражение можно решить ещё так:

(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.

Деление числа на произведение

Число можно разделить на произведение двумя способами:

1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.

Например, чтобы найти значение выражения:

60 : (3 · 2),

можно сначала умножить  3  на  2:

3 · 2 = 6

и разделить  60  на полученный результат:

60 : 6 = 10,

значит  60 : (3 · 2) = 60 : 6 = 10.

Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.

2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.

Например, чтобы найти значение выражения:

120 : (5 · 3),

можно сначала разделить  120  на  5:

120 : 5 = 24,

а теперь, полученное частное  24  разделить на  3:

24 : 3 = 8,

значит  120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8.

Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:

120 : (3 · 5)

и разделить  120  сначала на  3,  а затем полученный результат разделить на  5:

120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8.

Получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:

120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8

тоже самое, что и

120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8.

Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.

Деление суммы на число

Сумму можно разделить на число двумя способами:

1) Чтобы разделить сумму на какое-нибудь число, можно сначала вычислить значение суммы (выполнить сложение) и полученный результат разделить.

Например, чтобы найти значение выражения:

(15 + 12) : 3,

можно сначала сложить числа  15  и  12:

15 + 12 = 27

и полученную сумму разделить на  3:

27 : 3 = 9,

значит  (15 + 12) : 3 = 27 : 3 = 9.

Если все слагаемые в записи суммы делятся на число, на которое надо разделить сумму, то можно воспользоваться вторым способом нахождения частного от деления суммы на число.

2) Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.

Например, чтобы найти значение выражения:

(42 + 28 + 70) : 7,

можно каждое слагаемое разделить на число  7:

42 : 7 = 6,    28 : 7 = 4   и   70 : 7 = 10;

и полученные частные  (6,  4  и  10)  сложить:

6 + 4 + 10 = 20,

значит  (42 + 28 + 70) : 7 = 42 : 7 + 28 : 7 + 70 : 7 = 6 + 4 + 10 = 20.

Деление разности на число

Разность можно разделить на число двумя способами:

1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.

Например, чтобы найти значение выражения:

(24 — 8) : 2,

можно сначала вычесть из  24  число  8:

24 — 8 = 16,

и полученную разность разделить на  2:

16 : 2 = 8,

значит  (24 — 8) : 2 = 16 : 2 = 8.

Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.

2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.

Например, чтобы найти значение выражения:

(42 — 28) : 7,

можно отдельно уменьшаемое и вычитаемое разделить на число  7:

42 : 7 = 6,   28 : 7 = 4

и найти разность полученных частных:

6 — 4 = 2,

значит  (42 — 28) : 7 = 42 : 7 — 28 : 7 = 6 — 4 = 2.

Общие формулы свойств деления

Все свойства деления можно представить в виде формул:

Распределительные свойства
(a + b) : c = a : c + b : c
(a — b) : c = a : c — b : c
(a · b) : c = (a : c) · b = (b : c) · a
a : (b · c) = (a : b) : c = (a : c) : b
Действия с единицей и нулём
a : 1 = a
a : a = 1
0 : a = 0 (a ≠ 0)
На нуль делить нельзя

Что означает произведение слов в математике?

Обновлено 19 декабря 2020 г.

Автор: Берт Маркграф

Произведение — это результат выполнения математической операции умножения. Когда вы перемножаете числа вместе, вы получаете их произведение. Другими основными арифметическими операциями являются сложение, вычитание и деление, а их результаты называются соответственно суммой, разностью и частным. Каждая операция также имеет специальные свойства, определяющие порядок расположения и комбинирования чисел. Для умножения важно знать об этих свойствах, чтобы вы могли умножать числа и комбинировать умножение с другими операциями, чтобы получить правильный ответ.

TL;DR (слишком длинно, не читал)

Значение произведения в математике — это результат умножения двух или более чисел. Чтобы получить правильный продукт, важны следующие свойства:

  • Порядок чисел не имеет значения.
  • Группировка чисел скобками не действует.
  • Умножение двух чисел на множитель и последующее сложение их равносильно умножению их суммы на множитель.
  • Умножение на 1 оставляет число без изменений.

Значение произведения числа

Произведение числа на одно или несколько других чисел — это значение, полученное при умножении чисел. Например, произведение 2, 5 и 7 равно

2 × 5 × 7 = 70

Хотя произведение, полученное путем умножения определенных чисел, всегда одно и то же, произведения не уникальны. Произведение 6 и 4 всегда равно 24, как и произведение 2 и 12 или 8 и 3. Независимо от того, какие числа вы умножаете, чтобы получить произведение, операция умножения имеет четыре свойства, которые отличают ее от других основных арифметических операций. , Сложение, вычитание и деление имеют некоторые из этих свойств, но каждое из них имеет уникальную комбинацию.

Арифметическое свойство коммутации

Коммутация означает, что условия операции можно менять местами, и последовательность чисел не влияет на ответ. Когда вы получаете произведение путем умножения, порядок, в котором вы умножаете числа, не имеет значения. То же самое и с дополнением. Вы можете умножить 8 × 2, чтобы получить 16, и вы получите тот же ответ, если 2 × 8. Аналогично, 8 + 2 дает 10, тот же ответ, что и 2 + 8.

Вычитание и деление не обладают свойством коммутация. Если вы измените порядок чисел, вы получите другой ответ. Например,

8 ÷ 2 = 4 \text{ но } 2 ÷ 8 = 0,25

Для вычитания

8 — 2 = 6 \text{ но } 2 — 8 = -6

Деление и вычитание не являются коммутативными операциями.

Распределительное свойство

Распределение в математике означает, что умножение суммы на множитель дает тот же ответ, что и умножение отдельных чисел суммы на множитель с последующим сложением. Например,

3 × (4 + 2) = 18 \text{, и } (3 × 4) + (3 × 2) = 18

Сложение перед умножением дает тот же ответ, что и распределение множителя между числами, которые нужно сложить, и затем умножение перед сложением.

Деление и вычитание не обладают распределительным свойством. Например,

3 ÷ (4 — 2) = 1,5 \текст{ но } (3 ÷ 4) — (3 ÷ 2) = -0,75

Вычитание перед делением дает другой ответ, чем деление перед вычитанием.

Свойство ассоциативности для произведений и сумм

Свойство ассоциативности означает, что если вы выполняете арифметическую операцию более чем с двумя числами, вы можете связать два числа или заключить их в скобки, не влияя на ответ. Произведения и суммы обладают свойством ассоциативности, а разности и частные — нет.

Например, если произвести арифметическую операцию над числами 12, 4 и 2, то сумма может быть рассчитана как

(12 + 4) + 2 = 18 \text{ или } 12 + (4 + 2) = 18

Пример произведения:

(12 × 4) × 2 = 96 \text{ или } 12 × (4 × 2) = 96

Но для частных

\frac{12 ÷ 4}{2} = 1.5 \text{ while } \frac{12}{4 ÷ 2} = 6

и для разностей

(12 — 4) — 2 = 6 \text{ while } 12 — (4 — 2) = 10

Умножение и сложение обладают ассоциативным свойством, а деление и вычитание — нет.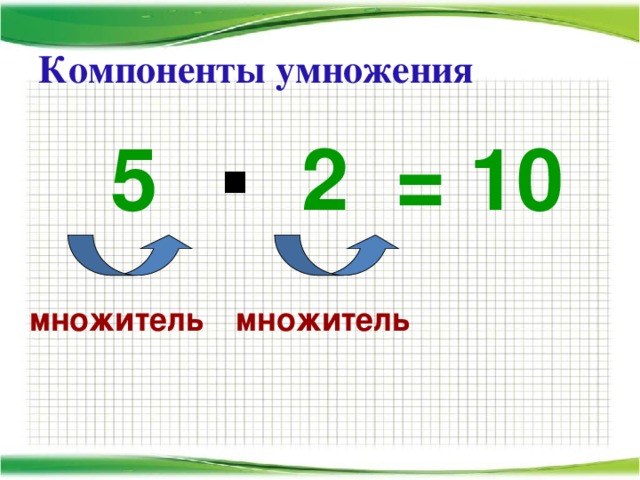

Операционные тождества — разница и сумма по сравнению с произведением и частным

Если вы выполняете арифметическую операцию над числом и операционным тождеством, число остается неизменным. Все четыре основные арифметические операции тождественны, но не совпадают. Для вычитания и сложения идентичность равна нулю. Для умножения и деления тождество одно.

Например, для разницы 8 − 0 = 8. Число остается одинаковым. То же верно и для суммы 8 + 0 = 8. Для произведения 8 × 1 = 8 и для частного 8 ÷ 1 = 8. Произведения и суммы имеют одни и те же основные свойства, за исключением того, что они имеют разные операционные тождества. В результате умножение и его произведения обладают уникальным набором свойств, которые необходимо знать, чтобы получить правильные ответы.

Продукт

(справочник Simulink) Продукт

(справочник Simulink)
Ссылка Simulink    
Продукт

Умножить или разделить входы

Библиотека

Simulink Math Operations and Blockset Math с фиксированной точкой

Описание


Блок Product выполняет умножение или деление своих входных данных.

Этот блок производит выходные данные, используя либо поэлементное, либо матричное умножение, в зависимости от значения Умножение параметра . Вы указываете операции с параметром Число входов . Символы умножения ( * ) и деления ( / ) указывают операции, которые необходимо выполнить на входах:

  • Если входов два или более, то количество символов должно равняться количеству входов. Например, « */* » требует трех входных данных. В этом примере, если для параметра Умножение установлено значение Поэлементно блок делит элементы первого (верхнего) входа на элементы второго (среднего) входа, а затем умножает на элементы третьего (нижнего) входа. В этом случае все нескалярные входные параметры этого блока должны иметь одинаковые размерности.
  • Если, однако, параметр Умножение установлен на Матрица , выход блока представляет собой матричное произведение входов, помеченных « * «, и инверсию входов, помеченных «/«, с порядком операций после входа в Количество входов параметр. Размерности входных данных должны быть такими, чтобы матричный продукт был определен.
  • Если требуется только умножение входов, то вместо символов » * » можно указать числовое значение параметра, равное количеству входов. Это может использоваться в сочетании с поэлементным или матричным умножением.
  • Если вводится один вектор и для параметра Умножение установлено значение Поэлементно , то одно « * » заставит блок выводить скалярное произведение векторных элементов. Одно «/» заставит блок выводить обратное значение скалярного произведения элементов вектора.
  • Если вводится одна матрица и параметр Умножение установлен на Поэлементно , то одиночное « * » или «/» вызовет ошибку блока. Однако, если параметр Умножение установлен на Matrix , то одиночное « * » заставит блок выводить матрицу без изменений, а одно «/» заставит блок выводить обратную матрицу.

Когда установлен флажок Показать дополнительные параметры , некоторые параметры, которые становятся видимыми, являются общими для многих блоков. Для подробного описания этих параметров обратитесь к Block Parameters в документации Fixed-Point Blockset.

Поддержка типов данных

Блок Product принимает сигналы любой сложности и типа данных, включая типы данных с фиксированной точкой, кроме int64 и uint64 . Все входные сигналы должны быть одного типа данных.

Параметры и диалоговое окно

Количество входов
Введите количество входов или комбинацию символов « * » и «/«. См. Описание выше для полного обсуждения этого параметра.
Умножение
Укажите поэлементное или матричное умножение. См. Описание выше для полного обсуждения этого параметра.
Показать дополнительные параметры
Если выбрано, дополнительные параметры, характерные для реализации блока, становятся видимыми, как показано.

Требовать, чтобы все входы имели одинаковый тип данных
Выберите этот параметр, чтобы требовать, чтобы все входы имели один и тот же тип данных.
Режим типа выходных данных
Укажите тип выходных данных и масштабирование, чтобы они совпадали с первыми входными данными, или наследуйте тип данных и масштабирование по внутреннему правилу или обратному распространению. Вы также можете выбрать встроенный тип данных из раскрывающегося списка. Наконец, если вы выберете Указать в диалоговом окне , Тип выходных данных , Значение масштабирования вывода и Заблокировать масштабирование вывода от изменений с помощью параметров инструмента автомасштабирования станут видимыми.
Если вы выберете Наследовать через внутреннее правило для этого параметра, Simulink выберет комбинацию масштабирования вывода и типа данных, которая требует наименьшего объема памяти, совместимого с размещением диапазона вывода и поддержанием точности вывода (и избегая потери значимости в случае дивизионные операции). Если для параметра Производственные характеристики оборудования на панели Advanced диалогового окна Simulation Parameters установлено значение Неограниченные целочисленные размеры , Simulink выбирает тип данных без учета аппаратных ограничений. Если параметр установлен на Microprocessor , Simulink выбирает наименьший доступный аппаратный тип данных, способный соответствовать ограничениям диапазона, точности и потери значимости. Например, если блок умножает входные данные типа int8 и int16 и Указаны неограниченные целочисленные размеры , тип выходных данных будет sfix24 . Если Микропроцессор , а микропроцессор поддерживает 8-битные, 16-битные и 32-битные слова, тип выходных данных — int32 . Если ни одна из длин слов, предоставленных целевым микропроцессором, не может разместить выходной диапазон, Simulink отображает сообщение об ошибке в Simulink Diagnostic Viewer.
Тип выходных данных
Укажите любой тип данных, включая типы данных с фиксированной точкой. Этот параметр виден, только если Указать в диалоговом окне выбрано для Параметр режима типа выходных данных .
Значение масштабирования выхода
Установите выходное масштабирование с использованием только точек счисления или масштабирования [Slope Bias]. Этот параметр виден только в том случае, если для параметра Режим типа выходных данных выбрано значение Задать в диалоговом окне .
Блокировка масштабирования вывода от изменений с помощью инструмента автомасштабирования
Если выбрано, Масштабирование вывода заблокировано. Этот параметр виден, только если Задать в диалоговом окне выбрано для параметра Режим типа выходных данных.
Округление целых чисел до
Выберите режим округления для вывода с фиксированной точкой.
Насыщение при целочисленном переполнении
Если выбрано, переполнения насыщаются.

Преобразования и операции

Блок Product сначала выполняет указанные операции умножения или деления на входах, а затем преобразует результаты в тип выходных данных, используя заданные режимы округления и переполнения. Обратитесь к Правилам для Арифметических Операций в документации Fixed-Point Blockset для получения дополнительной информации о правилах, которым этот блок подчиняется при выполнении операций с фиксированной точкой.

Характеристики

Размеры
Да
Прямой ввод
Да
Время выборки
Унаследовано от приводного блока
Скалярное расширение
Да
Пересечение нуля
№

Предварительный поиск по индексу Зонд

Как вычислить умножение и деление двух чисел с помощью JavaScript?

Посмотреть обсуждение

Улучшить статью

Сохранить статью

  • Последнее обновление: 31 мар, 2021

  • Читать
  • Обсудить

    • Посмотреть обсуждение

    Улучшить статью

    Сохранить статью

    Арифметическая операция работает с двумя числами, а числа называются операндами.

    Умножение Оператор умножения (*) умножает два или более чисел.

    Пример: 

    вар а =1 5;
вар б = 12;
вар с = а × б;

    Подход: Создайте html-форму для получения ввода от пользователя для выполнения операции умножения. Добавьте код javascript внутри html для выполнения логики умножения. Свойство Document.getElementById(id).value возвращает значение атрибута value текстового поля.

    Below is the implementation of the above approach:

    HTML

    < html >

       

    < head >

    < Стиль Тип = "Текст/CSS" > 9000 3

    59595959595959595959595959595959595959595959595 9. " " " " ".0134

           поле: 30 пикселей;

         }

       style >

    head >

       

    < body >

       < форма >

         1-й номер: < input type = "text"  

         id = "firstNumber" />< br >

         2nd Number: < Вход Тип = "Текст"

    ID = "Secondnmanmer" = " = " = " = " = " = " = " = "0134

         < input type = "button" onClick = "multiplyBy()"  

         Value = "Multiply" />< br >

       form >

       

       < p >The Result is : < br >

        < span id = "result" > span >

       p >

       

       

       < script >

    Функция умножна ()

    {

    num1 = документ. GetlelementByID (

  • num1 = документ. GetlelementByID ( 9000

    555555555555555555559555555555555555555555555555555555555555555595559. .

           num2 = document.getElementById(

             "secondNumber").value;

           document.getElementById(

             "результат").innerHTML = число1 * число2;

         }

       script >

    body >

       

    html >

    • Вывод:

    Умножение 2 чисел

    Деление Оператор деления (/) делит два или более чисел.

    Пример: 

    вар а = 50;
вар б = 20;
вар с = а/б;

    Подход: Создайте html-форму, чтобы принять ввод от пользователя для выполнения операции деления. Добавьте код JavaScript внутри html для выполнения логики деления. Свойство Document.getElementById(id).value возвращает значение атрибута value текстового поля.

    Ниже приведена реализация вышеуказанного подхода:

    HTML

    < html >

       

    < head >

       < style type = "text/css" >

         body {

           margin: 30px;

         }

       style >

    head >

       

    < body >

       < form >

    1 -й номер: < Вход Тип = "

    "0133 id = "firstNumber" />< br >

         2nd Number: < input type = "text"  

         ID = "Secondnumber" /> < BR >

    <

    <

    <

    <

    <

    <

    <

    . 0134 onClick = "divideBy()"  

          Value = "Divide" />

       form >

     

       < p >The Result is : < br >

         < span id = "result" > span >

       p >

       

       

       < Скрипт >

    Функция Divideby ()

    {

    334134

    33334.

    admin

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    2024 © Все права защищены.