Примеры вычитание сложение: Примеры на сложение и вычитание для 1-4 классов и дошкольников

Содержание

Сложение и вычитание целых чисел. Вычитание и сложение чисел с переходом через десяток Сложение вычитание 1

Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.

Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа.

Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве.

Есть возможность разрезать А4 пополам и получить 2 листа с заданиями, если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.

Решаем столбик, отмечаем успехи: тучка — не очень хорошо решили, смайлик — хорошо, солнышко — замечательно!

Сложение и вычитание в пределах 10

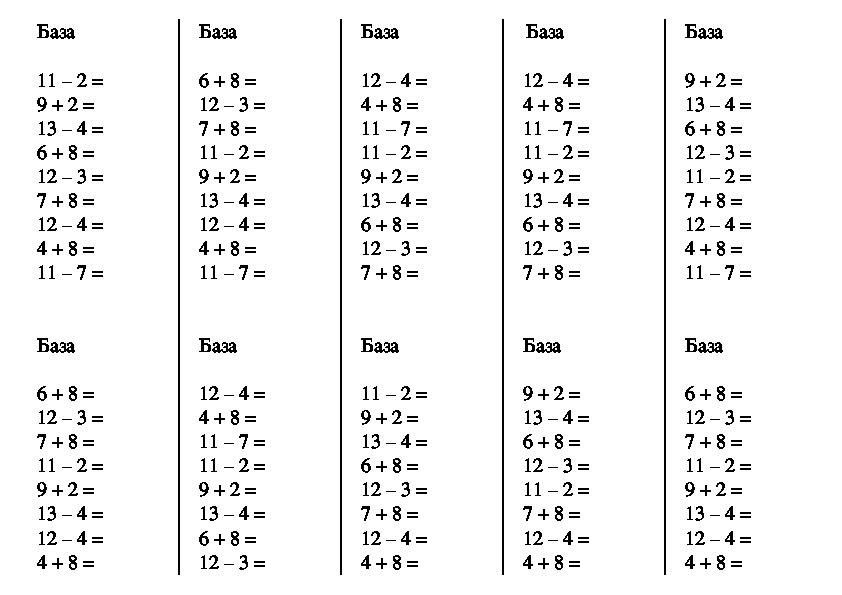
А теперь вразброс!

И с пропусками (окошками):

Примеры на сложение и вычитание в пределах 20

К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц.

При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .

Примеры для печати без перехода через десяток вперемешку:

Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы.

Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания):

Цель: в ходе практической работы и наблюдений развить умение прибавлять и вычитать число 1.

Планируемые результаты:

учащиеся научатся выполнять сложение и вычитание вида +1, – 1; моделировать действия сложения и вычитания с помощью предметов, рисунков, числового отрезка; устанавливать аналогии и причинно – следственные связи, делать выводы; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.

Ход урока

1. Организационный момент.

Давайте, ребята, учиться считать:
Делить, умножать, прибавлять, вычитать.
Запомните все, что без точного счета
Не сдвинется с места любая работа.
Без счета не будет на улице света,
Без счета не сможет подняться ракета.
Беритесь, ребята, скорей за работу!
Учитесь считать, чтоб не сбиться со счету!

2. Актуализация знаний.

1) Логическая разминка.

Сколько на рисунке (Рисунок 1) треугольников? (3.)

Рисунок 1

Решите задачи:

Саша грустнее, чем Толик. Толик грустнее, чем Алик. Кто веселее всех? (Алик.)
Ира аккуратнее, чем Лиза. Лиза аккуратнее, чем Оля. Кто всех аккуратнее? (Ира.)

2) Индивидуальная работа.

(У доски работают три ученика.)

2 5		2 + 1 3		6 5
6 9		6 – 1 6		4 1

Вопросы остальным учащимся:

Сосчитайте от 2 до 7, от 8 до 4.

Назовите:

соседей чисел 5, 8;
число, которое на 1 больше, чем 3;
число, которое на 2 меньше, чем 8;
соседей числа 7;
число, которое стоит между числами 4 и 6.

3) Устный счет.

Игра «Кто быстрее».
На доске два перемешанных магнитных набора чисел от 1 до 10. По команде первая колонка расставляет числа в порядке возрастания, а вторая – в порядке убывания.

Игра «Молчанка».
Учитель молча показывает пропуск, учащиеся – карточку с цифрой или знаком.

3 + = 4		2 – = 1
4 – = 3		2 2 = 4
1 3 = 4		3 1 = 2

3.

Самоопределение к деятельности.

Игра «Где мое место?»
К доске выходят десять учеников, каждый получает карточку с числом от 1 до 10 (карточки раздаются произвольно). Дети должны быстро построиться по порядку номеров у доски.

Правильно ли построились ребята?

Первый, второй, третий, четвертый, пятый – шаг вперед. Сколько здесь ребят? (5.)

Прибавим к этому числу 1. Какой ученик сделает шаг вперед? (Шестой.)

К 5 прибавили 1 и получили 6. А если к 6 прибавим 1, ученик, с какой карточкой сделает шаг вперед? (7.)

По аналогии рассматриваются случаи 7 + 1, 8 + 1, 9 + 1.

Сделайте вывод: какое число мы получаем, если прибавляем к числу 1? (Если прибавляем к числу 1, получается следующее число.)

Вывод повторяют несколько учеников друг за другом.

Сколько было учеников? (10.)

Сколько учеников село на место? (1.)

Сколько учеников осталось? (9.)

Как это записать? (10 – 1 = 9. )

Аналогично рассматриваются случаи 9 – 1,8 – 1,7 – 1 и т.д.

Кто догадался, чему мы научимся на уроке? (Прибавлять и вычитать число 1.)

Правильно, сегодня мы с вами вспомним, как прибавлять и вычитать число 1, узнаем, как это можно сделать при помощи числового отрезка.

4. Работа по теме урока.

Работа по учебнику

Откройте учебник на с. 80. Посмотрите, правильно ли мы определили, чем будем заниматься на уроке.

Прочитайте в учебнике предложение, котором говориться о том, как прибавить число 1.

Кто может закончить следующее предложение? (Чтобы вычесть из числа… (надо назвать предыдущее число.))

Посмотрите на таблицы и рисунок, приведенные ниже. Каким видом спорта занимаются лягушата? (Прыжками в воду.)

Сколько всего лягушат? (10.)

Сколько лягушат уже в воде? (1.)

В воде 1 лягушонок, и еще один уже прыгнул с мостика. Сколько лягушат сейчас будет в воде? (2. )

Как это записать? (1 + 1 = 2.)

Сколько всего лягушат было на вышке? (10.)

Сколько лягушат прыгнуло? (1.)

Сколько осталось? (9.)

Как это записать? (10 – 1=9.)

Сделайте вывод. Как прибавить или вычесть число 1? (Чтобы прибавить 1, нужно назвать следующее число. Чтобы вычесть из числа 1, надо назвать предыдущее число.)

5. Физкультурная минутка.

Утором бабочка проснулась,
Улыбнулась, потянулась.
Раз – росой она умылась,
Два – изящно покружилась,
Три – нагнулась и присела,
На четыре – улетела.

6. Закрепление изученного материала.

1) Работа с электронным приложением к учебнику «Математика» М.И. Моро.

Тема «Числа от 1 до 10». Сложение и вычитание. Прибавить и вычесть 1.

2) Практическая работа.

Раздать детям карточки с числами от 0 до 10, они строят числовой ряд.

2 + 1 – с какого деления начнете движение? В каком направлении пойдете? Сколько шагов сделаете? Возле какого числа вы остановились? Какой ответ в примере?

3) Работа по учебнику №2 (с. 81).

Рассмотрите рисунки. Составьте по ним выражения и объясните, что они означают.

Работа в парах. Учащиеся соотносят число, рисунок и количество точек на костяшках домино.

4) Работа в тетради с печатной основой (с.29).

Расскажите, что вы видите на первом рисунке. (Было 3 воробья, к ним прилетел еще 1 воробей.)

Какое равенство можно составить? (3 + 1 = 4.)

Самостоятельно составьте равенство по второму рисунку. (Проверка.)

Самостоятельное выполнение следующего задания. Проверка. Учащиеся хором читают состав каждого числа.

Прочитайте следующее задание. Вычислите.

Какую закономерность вы обнаружили в первом столбике? (Первое число становится меньше на 1, вычитаем везде 1. Ответ уменьшается на 1.)

Назовите закономерность во втором столбике. (Первое число увеличивается на 1, прибавляем везде 1. Ответ становится больше на 1.)

Чем интересен первый столбик? (И первое, и второе числа уменьшаются на 1. Ответ везде равен 0.)

7. Рефлексия.

«Проверь себя» (учебник, с. 81). Работа в парах.

8. Подведение итогов урока.

Что вы запомнили на этом уроке? (Чтобы прибавить 1, нужно назвать следующее число. Чтобы вычесть из числа 1, надо назвать предыдущее число.)

В этом уроке мы изучим сложение и вычитание целых чисел , а также правила для их сложения и вычитания.

Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:

−3, −2, −1, 0, 1, 2, 3

Положительные числа легко , и . К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.

Содержание урока

Примеры сложения и вычитания целых чисел

Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, и где положительные.

Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:

Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:

Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Пример 2. Найдём значение выражения 1 − 3.

Значение данного выражения равно −2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:

Знак минуса в выражении 1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.

Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.

Пример 3. Найти значение выражения −2 + 4

Значение данного выражения равно 2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.

Знак плюса в выражении −2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Пример 4. Найти значение выражения −1 − 3

Значение данного выражения равно −4

Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4

Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.

Знак минуса в выражении −1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.

Пример 5. Найти значение выражения −2 + 2

Значение данного выражения равно 0

Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.

Знак плюса в выражении −2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Правила сложения и вычитания целых чисел

Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.

Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.

Пример 1. Найти значение выражения −2 + 5

Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:

Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.

Итак, посмотрим какой модуль больше:

Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.

У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть ответ будет положительным:

−2 + 5 = 5 − 2 = 3

Обычно записывают покороче: −2 + 5 = 3

Пример 2. Найти значение выражения 3 + (−2)

Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3+−2.

Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:

3 + (−2) = |3| − |−2| = 3 − 2 = 1

Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть ответ положительный.

Обычно записывают покороче 3 + (−2) = 1

Пример 3. Найти значение выражения 3 − 7

В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:

Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.

3 − 7 = 7 − 3 = −4

В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.

Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4

Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.

Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:

3 − 7 = − (7 − 3) = − (4) = −4

В этом случае равенство будет соблюдаться на каждом этапе:

После того, как выражение вычислено, скобки можно убрать, что мы и сделали.

Поэтому, чтобы быть более точным, решение должно выглядеть так:

3 − 7 = − (7 − 3) = − (4) = − 4

Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:

a − b = − (b − a)

Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.

На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.

Итак, знакомимся с новым правилом:

Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.

Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:

Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет вычитаемому.

На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:

А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:

5 + (−3) = |5| − |−3| = 5 − 3 = 2

Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.

Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.

Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.

А стало быть, для наглядности данное выражение можно записать следующим образом:

(+3) − (+1)

Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.

В выражении (+3) − (+1) в ычитаемое это число (+1), а противоположное ему число это (−1).

Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)

(+3) − (+1) = (+3) + (−1)

Дальнейшее вычисление не составит особого труда.

(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2

На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.

Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.

У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:

Заменим вычитание сложением:

(+3) − (+7) = (+3) + (−7)

Дальнейшее вычисление не составляет труда:

(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4

Пример 7. Найти значение выражения −4 − 5

Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).

(−4) − (+5) = (−4) + (−5)

Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:

Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.

Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:

(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9

Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:

(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9

Решение для данного примера можно записать покороче:

−4 − 5 = −(4 + 5) = −9

или ещё короче:

−4 − 5 = −9

Пример 8. Найти значение выражения −3 − 5 − 7 − 9

Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:

(−3) − (+5) − (+7) − (+9)

Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:

(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)

Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:

(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =

= −(|−3| + |−5| + |−7| + |−9|) = −(3 + 5 + 7 + 9) = −(24) = −24

Решение данного примера можно записать покороче:

−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24

или ещё короче:

−3 − 5 − 7 − 9 = −24

Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7

Приведём выражение к понятному виду:

(−10) + (+6) − (+15) + (+11) − (+7)

Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:

(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)

Соблюдая , выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:

Первое действие:

(−10) + (+6) = − (10 − 6) = − (4) = − 4

Второе действие:

(−4) + (−15) = − (4 + 15) = − (19) = − 19

Третье действие:

(−19) + (+11) = − (19 − 11) = − (8) = −8

Четвёртое действие:

(−8) + (−7) = − (8 + 7) = − (15) = − 15

Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15

Примечание . Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.

Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:

Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

На данном уроке вы вспомните, как складывать и вычитать числа с переходом через десяток. Решая интересные задания, вы повторите алгоритм сложения и вычитания чисел с переходом через десяток. У вас будет возможность попрактиковать изученный ранее материал вместе с веселыми пчелками.

Тема: Повторение

Урок: Вычитание и сложение чисел с переходом через десяток

Посмотрите на числовой ряд. (рис. 1)

Рис. 1

Как связаны пары чисел между собой? В сумме они дают 10.

Запомните эти пары. (рис. 2)

Рис. 2

Это свойство чисел нам пригодится при решении задач.

Выполним сложение по частям, для этого разбиваем второе слагаемое 6 на две части так, чтобы первая часть дополняла число 9 до десяти. (рис. 3)

Рис. 3

Первая часть — число 1, вторая часть — все что осталось — 5. (рис. 4)

Рис. 4

Значит, 9 + 6 = 15.

1. Читаю пример

Первое слагаемое …

Второе слагаемое …

2. Нахожу число, которое дополнит первое слагаемое до 10. Это число …

3. Разбиваю второе слагаемое на 2 части … и …

4. Дополняю первое слагаемое до 10 и прибавляю оставшиеся единицы. 10 + …

5. Читаю ответ …

Потренируемся в счёте.

Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар. (рис. 5)

Рис. 5

Решение представлено на рисунке. (рис. 6)

Рис. 6

Если у вас возникли затруднения, повторите состав чисел, это вам обязательно поможет.

А теперь рассмотрим пример на вычитание.

Находим количество единиц в уменьшаемом — число 11 состоит из 1 десятка и 1 единицы. Разбиваем вычитаемое 6 на две части: первая равна количеству единиц уменьшаемого — 1, вторая — оставшихся единиц — 5. (рис. 7)

Рис. 8

Значит, 11 — 6 = 5

1. Читаю пример

Уменьшаемое …

Вычитаемое …

2. В разряде единиц уменьшаемого число …

3. Разбиваю вычитаемое на две части … и …

4. Вычитаю первую часть …, получаю 10, вычитаю из 10 вторую часть …

5. Читаю ответ.

Закрепим новое знание.

У нас три кошки: рыжая, белая и чёрная. (рис. 9)

Рис. 9

У них родились котята. Хотите узнать сколько? Тогда правильно решите примеры и назовите цвет кошки, у которой больше всего котят. (рис. 10)

Рис. 10

Следовательно, больше всех котят у рыжей кошки.

На данном уроке вы вспомнили алгоритм сложения и вычитания чисел с переходом через десяток. Вы закрепили изученный ранее материал, решая веселые задачи, что поможет вам в дальнейшем изучении математики.

Список литературы

Александрова Л. А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
Башмаков М.И., Нефедова М.Г. Математика. 1 класс. — М: Астрель, 2012.
Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.

Пособия для начальной школы ().
Социальная сеть работников образования ().
5klass.net ().

Домашнее задание

1. Вспомните алгоритм сложения и вычитания чисел с переходом через десяток.

2. Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар.

3. Решите примеры:

Сложение и вычитание чисел — Excel для Mac

Сложение нескольких чисел в одной ячейке

Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите несколько чисел, разделенных знаком «плюс» (+).

Например: 50+10+5+3.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 68.

Примечания:
- Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Сложение чисел с помощью ссылок на ячейки

Ссылка на ячейку представляет собой букву столбца и номер строки, например А1 или F345. При использовании в формуле ссылки на ячейку вместо значения ячейки можно изменить значение, не меняя формулу.

Введите число, например 5, в ячейку C1. Затем введите другое число, например 3, в ячейку D1.
В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите C1+D1.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 8.

Примечания:
- Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.
- Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Быстрое суммирование чисел в строке или столбце

Введите несколько чисел в столбец или строку, а затем выделите заполненный диапазон ячеек.
На строка состояния, посмотрите на значение рядом с sum. Общее количество — 86.

Вычитание нескольких чисел в одной ячейке

Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите несколько чисел, разделенных знаком «минус» (–).

Например: 50-10-5-3.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 32.

Вычитание чисел с помощью ссылок на ячейки

Введите числа в ячейки C1 и D1.

Например, введите 5 и 3.
В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите C1-D1.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 2.

Примечания:
- Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.
- Если вместо ожидаемого результата отображается дата, выделите ячейку и на вкладке Главная выберите пункт Общий.

Сложение нескольких чисел в одной ячейке

Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите несколько чисел, разделенных знаком «плюс» (+).

Например: 50+10+5+3.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 68.

Примечание: Если вместо ожидаемого результата вы видите дату, выберите ячейку, а затем на вкладке «Главная» в области «Число» выберите во всплывающее меню пункт «Общие».

Сложение чисел с помощью ссылок на ячейки

Введите число, например 5, в ячейку C1. Затем введите другое число, например 3, в ячейку D1.
В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите C1+D1.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 8.

Примечания:
- Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.
- Если вместо ожидаемого результата вы видите дату, выберите ячейку, а затем на вкладке «Главная» в области «Число» выберите во всплывающее меню пункт «Общие».

Быстрое суммирование чисел в строке или столбце

Введите несколько чисел в столбец или строку, а затем выделите заполненный диапазон ячеек.
На строка состояния посмотрите на значение рядом с sum=. Общее количество — 86.

Если строка состояния не отображается, в меню Вид выберите пункт Строка состояния.

Вычитание нескольких чисел в одной ячейке

Щелкните любую пустую ячейку и введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите несколько чисел, разделенных знаком «минус» (–).

Например: 50-10-5-3.
Нажмите клавишу RETURN.

Если использовать числа из примера, получается результат 32.

Вычитание чисел с помощью ссылок на ячейки

Введите числа в ячейки C1 и D1.

Например, введите 5 и 3.
В ячейке E1 введите знак равенства (=), чтобы начать ввод формулы.
После знака равенства введите C1-D1.
Нажмите клавишу RETURN.

Если вы использовали числа из примера, результат будет -2.

Примечания:
- Если изменить значение в ячейке C1 или D1 и нажать клавишу RETURN, значение ячейки E1 изменится, даже если формула осталась неизменной.
- Если вместо ожидаемого результата вы видите дату, выберите ячейку, а затем на вкладке «Главная» в области «Число» выберите во всплывающее меню пункт «Общие».

Вычитание чисел с разными знаками

В курсе арифметики установлено, что вычитание есть действие, обратное сложению, при помощи которого по данной сумме и по одному слагаемому находят другое слагаемое.

Пользуясь этим определением, мы должны разобрать, как надо выполнять вычитание относительных чисел.

Пусть надо из (+8) вычесть (–3), т. е. пусть надо

Первое данное число выражает данную сумму, второе – данное слагаемое, а над найти другое слагаемое (для него оставлено место после знака равенства), т. е. надо решить вопрос: какое число надо сложить с (–3), чтобы в сумме получилось (+8)? Этот вопрос запишем в такой форме:

(?) + (–3) = +8.

Но сразу этот вопрос решить трудно, а поэтому сначала решим более простой, вспомогательный вопрос: какое число надо сложить с (–3), чтобы в сумме получился нуль ?, т. е.

(?) + (–3) = 0.

На этот вопрос ответ ясен: надо взять для неизвестного слагаемого число, имеющее ту же абсолютную величину, как и данное слагаемое, но обратный знак, – в данном случае надо для неизвестного слагаемого взять число +3. Теперь перейдем к решению главного вопроса: мы взяли для неизвестного слагаемого число + 3 и в сумме получился нуль, но нам надо получить в сумме число +8, поэтому надо чтобы и в другое слагаемое вошло это же число +8. Следовательно, неизвестное слагаемое должно состоять: 1) из +3, чтобы в сумме получился нуль и 2) из +8, чтобы эту сумму «нуль» довести до требуемой +8. Поэтому на месте неизвестного слагаемого пишем + 3 + 8:

(+ 8) – (– 3) = + 3 + 8 = + 11.

Последнее (= + 11) написано на том основании, что числа + 3 и + 8 надо соединить в одно или сложить.

Вот еще примеры:

(– 7) – (+ 5) = – 5 – 7 = – 12.

Искомое слагаемое должно состоять: 1) из –5, чтобы в сумме получился нуль и 2) из –7, чтобы дополнить этот нуль до требуемой суммы, до –7. Сложив числа –5 и –7, получим –12.

(– 3) – (– 8) = + 8 – 3 = + 5.

Искомое слагаемое должно состоять: 1) из +8, чтобы в сумме получился нуль и 2) из –3, чтобы дополнить этот нуль до требуемой суммы, до –3. Сложив числа +8 и –3, получим +5.

(+7) – (+9) = –9 + 7 = –2.

Искомое слагаемое должно состоять: 1) из –9, чтобы в сумме получился нуль и 2) +7, чтобы дополнить этот нуль до требуемой суммы, до +7; сложив числа –9 и +7, получим –2.

Из этих примеров видим, что вычитание в алгебре состоит лишь в умении раскрывать скобки: надо второе число (данное слагаемое или вычитаемое) написать с обратным знаком, а первое число (данную сумму или уменьшаемое) написать с тем же знаком. После того, как это сделано, т. е., когда скобки раскрыты, дело сводится к сложению, так как написаны числа рядом с их знаками, напр., в последнем примере: – 9 + 7.

Так как сумма не изменяется от перестановки слагаемых, то можно числа, полученные в разобранных примерах после раскрытия скобок, переставить, чтобы порядок был согласен с порядком данных чисел:

(+ 8) – (– 3) = + 8 + 3; (– 7) – (+ 5) = – 7 – 5;
– 3 – (– 8) = – 3 + 8; (+ 7) – (+ 9) = + 7 – 9.

Итак,

чтобы раскрыть скобки при вычитании, надо первое число (уменьшаемое) написать без изменения и приписать к нему второе число (вычитаемое) с обратным знаком.

Заметим еще, что при обозначении вычитания первое число пишется часто без скобок, а если оно положительное, то, как уже известно, знак + можно впереди не писать.

Например,

– 3 – (– 5) = – 3 + 5 = + 2; 1 – (– 6) = 1 + 6 = 7;
3 – (+ 3) = 3 – 3 = 0.

14. Примеры на сложение и вычитание. Пусть требуется вычислить:

1 – {3 + [5 – (3 – 5 – 6)]}.

Мы станем руководствоваться следующим порядком: если внутри какой-либо пары скобок нет других скобок и нет действия, то эти скобки можно раскрыть; если же внутри этих скобок есть действие (сложение), то надо сначала его выполнить. В нашем примере такой порядок: сначала выполним сложение чисел, написанных внутри маленьких скобок, потом надо эти скобки раскрыт, выполнить сложение внутри квадратных скобок, раскрыть квадратные скобки, выполнить сложение внутри витых скобок, раскрыть эти скобки и, наконец, сложить полученные числа:

1 – {3 + [5 – (3 – 5 – 6)]} = 1 – {3 + [5 – (– 8)]} = 1 – {3 + [5 + 8]} =
= 1 – {3 + [+13]} = 1 – {3 + 13} = 1 – {+ 16} = 1 – 16 = – 15.

Конечно, при навыке можно сразу выполнять несколько действий и, следовательно, укоротить вычисление.
Еще пример:

Пусть еще требуется вычислить выражение:

a – {(b – c) – [d + (e + f)]} при a = – 3; b = 1; c = 4; d = – 5; e = – 7; f = 2.

Выполним вычисления по действиям:

1) b – c = + 1 – (+ 4) = 1 – 4 = – 3;

2) e + f = (– 7) + (+ 2) = – 7 + 2 = – 5;

3) d + (– 5) = – 5 + (– 5) = – 5 – 5 = – 10;

4) (– 3) – (– 10) = – 3 + 10 = + 7;

5) – 3 – (+ 7) = – 3 – 7 = – 10.

Примеры для упражнений:

Если взять число нуль и прибавлять к нему по +1, то получим ряд постепенно увеличивающихся целых чисел:

0, +1, +2, +3, +4, +5, …..

Этот ряд совпадает (см. конец п. 10) с натуральным рядом чисел, т. е. с

0, 1, 2, 3, 4, 5 …..

Если мы, взяв число нуль, вычтем из него (+1), затем еще раз вычтем (+1) и т. д., то, согласно с тем, как мы это понимали в арифметике по отношению к натуральному ряду чисел, мы теперь признаем, что и здесь станем получать все уменьшающиеся целые числа:

1) 0 – (+ 1) = – 1; 2) (– 1) – (+ 1) = – 1 – 1 = – 2;
3) (– 2) – (+ 1) = – 3 и т. д.

Получим, идя от нуля налево, ряд уменьшающихся относительных чисел:

….., – 5, – 4, – 3, – 2, – 1, 0.

Соединяя этот ряд с предыдущим, получим полный ряд относительных чисел:

….., – 6, – 5, – 4, – 3, – 2, – 1, 0, +1, +2, +3, +4, +5, +6 …..

Этот ряд и вправо и влево идет без конца.

Всякое число в этом ряду больше другого, которое стоит левее и меньше любого, стоящего правее его. Так +1 > –3; 0 > –6; –5 < 0; –3 < +2 и т. д.

В промежутках между целыми числами этого ряда можно вставить бесконечно много дробных чисел.

Сложение и вычитание столбиком

Когда мы считаем, используя арабские цифры, то первое, что следует сделать, – это запомнить суммы чисел от нуля до девяти. Как мы учимся считать? Сначала запоминаем, что 1+1=2, 2+3=5, 4+5=9, 6+7=13 и так далее. Очень важно также усвоить, что 0+0=0.

Когда мы считаем на счетах, запоминать ничего не надо. Необходимо только научиться считать от одного до десяти. На этом этапе преимущества расчетов при помощи чисел, записанных на бумаге, еще незаметны. Кажется, что счеты удобнее.

А теперь попробуем сложить два больших числа, например 5894 и 2578. Все, что для этого нужно, – это уметь складывать числа в пределах десяти. Сначала разобьем числа на единицы, десятки, сотни и тысячи, то есть на разряды.

	5000	и	800	и	90	и	4
плюс	2000	и	500	и	70	и	8
	7000	и	1300	и	160	и	12

Теперь разобьем число 1300 на 1000 и 300, 160 на 100 и 60, а 12 на 10 и 2. Теперь надо просто прибавить тысячи к тысячам, сотни к сотням, десятки к десяткам. В результате получаем: 8000 и 400 и 70 и 2, то есть 8472.

Упрощенно процесс сложения можно изобразить так:

Упрощение заключается в том, что мы не записываем «нули» и переносим «единицы» в следующий разряд, то есть десятки переносим в колонку десятков и так далее.

Вычитание – это процесс, обратный сложению. Предположим, надо из 531 вычесть 298. Мы также разбиваем числа на разряды:

	500	и	30	и	1
минус	200	и	90	и	8

Вначале может показаться, что нам придется вычитать 8 из 1, и 90 из 30. Но это не так, мы ведь можем занять один десяток и одну сотню из следующих разрядов. Перепишем таблицу в новом виде:

	400	и	120	и	11
минус	200	и	90	и	8
	200	и	30	и	3

Таким образом, получаем ответ: 233.

Когда мы производим вычитание в столбик, то следуем именно этому принципу, хотя форма записи более упрощенная.

Человек, привыкший считать на счетах, сможет произвести эту операцию гораздо быстрее, чем средний ученик, вычисляющий разность этих двух чисел на бумаге. Однако счеты требуют, кроме всего прочего, наработки чисто механических навыков.

В то же время, когда мы считаем в столбик, мы записываем все этапы, и легко проверить правильность расчетов. Используя счеты, этого сделать нельзя. Метод подсчета в столбик настолько же эффективнее подсчета на счетах, насколько изображение чисел на счетах эффективнее, чем показывать числа на пальцах.

Материалы по теме:

Поделиться с друзьями:

Загрузка…

Сложение и вычитание многочленов: алгоритм и правило, примеры

Алгоритмы сложения и вычитания многочленов

Чтобы сложить два многочлена , достаточно между ними поставить знак «+».2-x+18 $

Урок математики в 6 классе «Сложение и вычитание в пределах 1000 с переходом через разряд».

Тема урока: Сложение и вычитание в пределах 1000 с переходом через разряд.

Цель урока:

Закрепление у учащихся умения выполнять сложение и вычитание чисел в пределах 1000 с переходом через разряд. Формирование навыка использования полученных знаний в новых условиях.

Задачи урока:

Образовательная:

Повторение знания нумерации в пределах 1000,

закрепление умения пользоваться приемами устных и письменных вычислений,закрепление умения складывать и вычитать числа в пределах 1000 с переходом через разряд.

Коррекционная:

развитие процессов анализа, сравнения, обобщения, коррекция произвольного внимания, развитие пространственных представлений, развитие умения контролировать свою работу.

Воспитательная:

воспитание самостоятельности, самоконтроля, умения планировать свою деятельность, воспитание интереса к предмету, аккуратности ведения записи в тетради. Соблюдение здоровьесберегающего режима на уроке.

План урока:

1.Организационный момент.

2. Общекоррекционная работа.

3.Постановка темы и задач предстоящего урока.

4. Устный счет (нумерация в пределах 1000)

5.Закрепление и повторение изученных знаний

1) Работа с учебником:

— решение примеров у доски (на сложение в столбик)

– решение задачи;

— решение примеров у доски(на вычитание в столбик)

2) Физкультминутка.

3)Выполнение дифференцированных заданий по карточкам.

6.Домашнее задание.

7.Итог урока, оценка работы учащихся

8.Рефлексия

Ход урока:

1.Организационный момент.

— Рапорт дежурного.

— Проверка готовности учащихся к уроку

(тетрадь, учебник, дневник, ручка, карандаш, линейка).

2.Общекоррекционная работа.

— Какой сегодня день недели?(вторник).

—какой день был вчера? Будет завтра?

— Какое сейчас время года? (зима)

— Назовите зимние месяцы. (декабрь, январь, февраль)

Какой самый главный праздник мы все ждём? На Новый год принято дарить подарки и мы с вами вместе подарим этот урок всем гостям.

3.Сообщение темы и цели урока.

Сегодня на уроке мы будем считать устно, решать примеры, задачи, а так же на самостоятельной работе проверим ваши умения складывать и вычитать в столбик. Но основная наша цель в процессе урока закрепление умения складывать и вычитать числа с переходом через разряд в пределах 1000.

Введение в сюжет урока.

Отгадайте-ка, ребятки,

Месяц в этой вот загадке.

Дни его всех дней короче.

Всех ночей длиннее ночи.

На поля и на луга

До весны легли снега.

О каком месяце говорится в загадке? (о декабре)

Декабрь уже наступил, и снега уже легли на поля и на луга. Первому снегу рады все: и взрослые, и дети. У детей появляется много игр.

Во что вы любите играть зимой?

4.Устный счет.

А давайте и мы с вами тоже слепим снеговика.

Чтобы скатать первый снежный ком, нужно ответить на вопрос.

Какое из чисел лишнее в ряду?

100,200,900,30

356,392,367,453

600,72,431,569.

Чтобы получился второй ком, расположите числа в порядке возрастания.

500,420,440,450,470,480, 400,430,460,410,490.

3)Голова у снеговика появится, если вы верно решите примеры в игре « Сложи снежные комки в свое ведро»

160-110= 30+40= 260-190= 300-250= 160-120= 190-150=

360-320= 280-110= 100-60= 480-310= 360-310= 460-50=

Чего не хватает у нашего снеговика? (морковки)

Смотрите-ка, а на ней загадка?

На деревья, на кусты

С неба падают цветы.

Белые пушистые,

Только не душистые.

Что это?

(Снежинка)

Физкультминутка для глаз.

Сосчитайте сколько мальчиков в классе за метелку для снеговика.

5.Закрепление сложения и вычитания по учебнику: достраиваем снеговика за верно выполненные задания.

1. Стр 100 №376 ( по столбику)

Глаза , рот, руки, пуговицы.

Задача.

Дедушка Мороз приготовил для нашей школы 150 подарков, а для соседней школы на 40 подарков меньше. Сколько всего подарков приготовил Дед Мороз?

6.Закрепление и повторение изученных знаний

1)Выполнение дифференцированных заданий по карточкам (решение примеров на сложение и вычитание трёхзначных чисел с переходом через разряд самостоятельно.

В-1 Карточка №1

Реши примеры:

216 + 527 = 837 – 254 =

394 +425 = 766 – 329 =

В-2 Карточка №1

Реши примеры:

116+235= 637-254=

_—

384+125= 749-311=

7.Домашнее задание: с. 100 № 374

8.Итог урока, оценка работы учащихся.

9.Рефлексия.

Определи свое настроение.

Встаньте, пожалуйста, те,

кто устал на уроке;

— кому было трудно;

— кто был уверен в себе;

— у кого осталось отличное настроение.

Молодцы! Спасибо всем за урок!

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

ПероваМ.Н., КапустинаГ.М., Математика 5 класс, учебник для специальных (коррекционных) образовательных учреждений VIIIвида, Москва «Просвещение», 2010.
Библиотечка «Первого сентября» Серия «Математика» Выпуск 35, 2010 г., с.24

Использованные материалы и Интернет-ресурсы

1. http://images.yandex.ru

Математика 2 класс Богданович М. В. Устное сложение и вычитание двузначных чисел с переходом через десяток.

Категория: —>> Математика 2 класс Богданович
Задание: —>> 478 — 497 498 — 517 518 — 537 538 — 557 558 — 582

наверх

Задание 478.

Реши примеры.

Решение:

30 + 40 = 70

60 + 20 = 80

30 + 30 = 60

10 + 60 = 70

Задание 479.

Решение:

60 + 17 = 77
60 + 13 = 73
60 + 16 = 76

7 + 4 = 11
7 + 8 = 15
7 + 9 = 16

Задание 480.

Реши примеры, применяя переместительное свойство действия сложения.

20 + 4 + 60 + 5

30 + 8 + 40 + 9

Решение:

20 + 60 + 5 + 4 = 89

30 + 40 + 9 + 8 = 87

Задание 481.

Рассмотри записи и прочитай объяснение.

20 + 50 = 70

8 + 9 = 17

70 + 17 = 87

Объяснение: 20 и 50 — семьдесят, 8 и 9 — семнадцать, к 70 прибавить 17, будет 87.

Задание 482.

Рассмотри запись и объясни решение.
35 + 48 = 30 + 5 + 40 + 8 = 70 + 13 = 83

Решение:

Объяснение: 30 и 40 — семьдесят, 5 и 8 — тринадцать, к 70 прибавить 13, будет 83.

Задание 483.

1) У мальчика было 85 к. Он купил булочку за 45 к. Сколько денег осталось у мальчика?
2) У мальчика было 85 к. Он купил булочку за 45 к. и конфету за 28 к. Сколько денег осталось у мальчика?

Решение:

1) 85 — 45 = 40
Ответ: 40 к.

1) 45 + 28 = 73
2) 85 — 73 = 12
Выражение: 85 — (45 + 28) = 12
Ответ: 12 к.

Задание 484.

Найди сумму 75 + 19 устно, а потом проверь ответ письменно.

Решение:

75 + 19 = 94
Проверка: 94 — 19 = 75

Задание 485.

Реши примеры.

Решение:

17 + 25 = 42

36 + 36 = 72

54 + 38 = 92

42 + 49 = 91

Задание 486.

Курица за месяц снесла 23 яйца, а индюшка — на 8 яиц меньше. 6 индюшиных яиц использовали для приготовления печенья, а остальные сдали в инкубатор. Сколько индюшиных яиц сдали в инкубатор?

Решение:

1) 23 — 8 = 15
2) 15 — 6 = 9
Выражение: 23 — 8 — 6 = 9
Ответ: 9 яиц.

Задание 487.

Реши примеры.

Решение:

25 + 67 = 92

56 + 18 = 74

77 + 14 = 91

43 + 38 = 81

Задание 488.

Найди сумму 20 + a, если a = 10, a = 17.

Решение:

1) a = 10 20 + 10 = 30
2) a = 17 20 + 17 = 37

Задание 489.

Реши примеры

Решение:

17 + 18 = 35

10 + 14 = 24

18 + 19 = 37

10 + 15 = 25

Задание 490.

2 медвежонка стоят спиной друг к другу на расстоянии 20 шагов. Какое расстояние будет между медвежатами, если каждый сделает вперёд 27 шагов?

Решение:

1) 27 + 27 = 54
2) 20 + 54 = 74
Выражение: 20 + 27 + 27 = 74
Ответ: 74 шага.

Задание 491.

Чтобы приготовить раствор для укладки кирпичей, взяли 13 кг цемента, песка — на 39 кг большее, а остальное составляла вода. Сколько всего килограммов цемента и песка израсходовали? Какова масса раствора, если воды взяли 15 кг?

Решение:

1) 13 + 39 = 52
2) 13 + 52 = 65
3) 65 + 15 = 80
Выражение: (13 + 39 + 13) + 15 = 80
Ответ: 65 кг цемента и песка израсходовали, 80 кг масса раствора.

Задание 492.

Устно реши пример 48 + 27 и объясни решение.

Решение:

48 + 27 = 40 + 20 + 8 + 7 = 75
Объяснение: 40 и 20 — шестьдесят, 8 и 7 — пятнадцать, к 60 прибавить 15, будет 75.

Задание 493.

В швейной мастерской 18 катушек серых ниток, белых на 26 больше, чем серых, а черных на 37 больше, чем белых. Сколько катушек чёрных ниток в мастерской?

Решение:

1) 18 + 26 = 44
2) 44 + 37 = 81
Выражение: 18 + 26 + 37 = 81
Ответ: 81 катушка.

Задание 494.

1) Увеличь на 12: 60, 0, 20, 33, 65, 14.
Уменьш на 30: 90, 45, 100, 30, 31, 48.

Решение:

12 + 60 = 72
12 + 0 = 12
12 + 20 = 32
12 + 33 = 45
12 + 65 = 77
12 + 14 = 26

90 — 30 = 60
45 — 30 = 15
100 — 30 = 70
30 — 30 = 0
31 — 30 = 1
48 — 30 = 18

Задание 495.

Решение:

50 + 14 = 64
50 + 11 = 61
50 + 17 = 67

4 + 9 = 13
4 + 5 = 9
4 + 7 = 11

Задание 496.

Рассмотри запись и объясни решение.

Решение:

Объяснение: складываем сначала единицы 8 и 4, получаем 12, 12 прибавляем к 30 получаем 42.

Задание 497.

Устно объясни, как найти сумму 67 + 6.

Решение:

67 + 6 = 73
Объяснение: складываем сначала единицы 7 и 6, получаем 13, 13 прибавляем к 60 получаем 73.

Задание: —>> 478 — 497 498 — 517 518 — 537 538 — 557 558 — 582

Сложение и вычитание положительных и отрицательных чисел

Числа могут быть положительными или отрицательными

Это числовая строка:


Отрицательные числа (-)	Положительные числа (+)


«-» — отрицательный знак.	«+» — положительный знак

Отсутствие знака означает положительный результат

Если число имеет без знака , это обычно означает, что это положительное число .

Воздушные шары и гиря

Давайте подумаем о числах как о воздушных шарах (положительных) и весах (отрицательных):

К этой корзине привязаны воздушные шары и гирьки:

Добавление положительного числа

Сложение положительных чисел — это просто сложение.

Мы можем добавить шары (мы добавляем положительное значение )

корзина тянется вверх (положительно)

Пример: 2 + 3 = 5

на самом деле говорит

«Положительное 2 плюс Положительное 3 равно Положительное 5»

Мы могли бы записать это как (+2) + (+3) = (+5)

Вычитание положительного числа

Вычитание положительных чисел — это просто вычитание.

Воздушные шары можно забрать ( вычитаем положительное значение )

корзина тянется вниз (минус)

Пример: 6 — 3 = 3

на самом деле говорит

«Положительное 6 минус Положительное 3 равно Положительное 3»

Мы могли бы записать это как (+6) — (+3) = (+3)

Добавление отрицательного числа

Теперь посмотрим, как выглядит сложение и вычитание отрицательных чисел :

Мы можем добавлять веса (мы добавляем отрицательные значения )

корзина тянется вниз (минус)

Пример: 6 + (−3) = 3

на самом деле говорит

«Положительные 6 плюс отрицательные 3 равны положительным 3»

Мы могли бы записать это как (+6) + (−3) = (+3)

Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного числа) или прибавление веса (добавление отрицательного числа) заставляют корзину опускаться.

Значит, результат тот же :

(+6) — (+3) = (+3)
(+6) + (−3) = (+3)

Другими словами, вычитание положительного аналогично добавлению отрицательного .

Вычитание отрицательного числа

Наконец, мы можем убрать веса (мы вычитаем отрицательных значений )

корзина тянется вверх (положительно)

Пример: Что такое 6 — (−3)?

6 — (- 3) = 6 + 3 = 9

Да, действительно! Вычесть отрицание — это то же самое, что и сложить!

Два отрицания дают положительный результат

Что мы нашли?

Добавление положительного числа — это простое сложение…

Добавление положительного значения Добавление

Положительное и отрицательное вместе …

Вычитание положительного
или
Добавление отрицательного
равно
Вычитание

Пример: Что такое 6 — (+3)?

6 — (+ 3) = 6 — 3 = 3

Пример: Что такое 5 + (−7)?

5 + (- 7) = 5 — 7 = −2

Вычитание негатива…

Вычитание отрицательного числа аналогично добавлению

Пример: Что такое 14 — (−4)?

14 — (- 4) = 14 + 4 = 18

Правила:

Все это можно поместить в два правила :

	Правило	Пример
+ (+)	Два одинаковых знака превращаются в знак плюс	3 + (+ 2) = 3 + 2 = 5
— (-)	Два одинаковых знака превращаются в знак плюс	6 — (- 3) = 6 + 3 = 9

+ (-)	Два непохожих знака превращаются в знак минуса	7 + (- 2) = 7 — 2 = 5
— (+)	Два непохожих знака превращаются в знак минуса	8 — (+ 2) = 8 — 2 = 6

Они «как знаки», когда они похожи друг на друга (другими словами: одинаковые).

Итак, все, что вам нужно запомнить, это:

Два знака типа становятся положительным знаком

Два знака , отличных от , становятся отрицательным знаком

Пример: Что такое 5 + (- 2)?

+ (-) — это в отличие от знаков (они не совпадают), поэтому они становятся отрицательным знаком .

5 + (- 2) = 5 — 2 = 3

Пример: Что такое 25 — (- 4)?

— (-) — это , как знак , поэтому они становятся положительным знаком .

25 — (- 4) = 25 + 4 = 29

Пример: Что такое −6 + (+ 3)?

+ (+) — это , как и знак , поэтому они становятся положительным знаком .

−6 + (+ 3) = −6 + 3 = −3

Начните с −6 на числовой прямой, двигайтесь вперед на 3, и вы получите −3

А теперь поиграйте!

Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха!

Объяснение здравого смысла

И есть объяснение «здравого смысла»:

Если я скажу «Ешь!» Я призываю вас поесть (положительный результат)

Если я скажу «Не ешьте!» Я говорю об обратном (отрицательном).

Теперь, если я скажу: « НЕ, не ешьте!», Я говорю, что не хочу, чтобы вы умерли с голоду, поэтому я снова говорю: «Ешь!» (положительный).

Итак, два отрицания дают положительный результат, и если это вас устраивает, тогда вы сделали!

Другое объяснение здравого смысла

Друг +, враг —

+ + ⇒ +		друг друга мой друг
+ — ⇒ —		друг врага — мой враг
— + ⇒ —		враг друга — мой враг
— — ⇒ +		враг врага мой друг

Пример банка

Пример: В прошлом году банк по ошибке снял с вашего счета 10 долларов, и они хотят это исправить.

Итак, банк должен забрать отрицательные 10 долларов.

Допустим, ваш текущий баланс составляет 80 долларов США, поэтому у вас будет:

80 долларов — (- 10 долларов) = 80 долларов + 10 долларов = 90 долларов

Итак, вы получаете на свой счет долларов, еще 10 .

Длинный пример, который вам может понравиться

Очки союзника

Элли может быть непослушным или милым. Так родители Элли сказали

«Если вы будете любезны, мы добавим 3 балла (+3).
Если вы непослушны, снимаем 3 балла (−3).
Когда вы набираете 30 очков, вы получаете игрушку. »

Союзник начинает день с 9 очками:		9
Мама Элли обнаруживает пролитое молоко:		9 — 3 = 6
Тогда папа признается, что пролил молоко и пишет «отменить». Как «отменить» минус 3? Мы добавляем 3 снова!
Итак, мама считает:		6 — (−3) = 6 + 3 = 9

Итак, когда мы вычитаем отрицательное, мы получаем
баллов (т.е.е. так же, как добавление очков).

Таким образом, вычитание отрицательного числа аналогично добавлению

Несколько дней спустя. У Элли 12 очков.

Мама добавляет 3 очка, потому что комната Элли чистая.		12 + 3 = 15

Папа говорит: «Я убрал эту комнату» и пишет «отменить» на диаграмме.Мама считает:		15 — (+3) = 12

Папа видит, как Элли чистит собаку. Пишет на графике «+3». Мама считает:		12 + (+3) = 15

Элли бросает камень в окно. Папа пишет на диаграмме «−3».Мама считает:		15 + (−3) = 12

См .: как « 15 — (+3) », так и « 15 + (−3) » дают 12.

Итак:

Неважно, вычтете ли вы положительные
баллов или добавите отрицательные,
вы все равно потеряете баллы.

Таким образом, вычитание положительного
или
Добавление отрицательного
равно
Вычитание

Попробуйте эти упражнения…

Теперь попробуйте этот лист и посмотрите, как у вас дела.

А еще попробуйте эти вопросы:

Вычитание целых чисел — ChiliMath

Если вы умеете складывать целые числа, я уверен, что вы также можете вычитать целые числа. Ключевым шагом является преобразование задачи вычитания целых чисел в задачу сложения целых чисел. Процесс очень прост. Вот как:

Шаги по вычитанию целых чисел

Шаг 1 : Преобразуйте задачу вычитания целых чисел в задачу сложения целых чисел.Вот как:

Во-первых, сохраните первое число (известное как minuend).
Во-вторых, измените операцию с вычитания на сложение.
В-третьих, получите знак, противоположный второму числу (известное как вычитаемое)
Наконец, продолжите обычное сложение целых чисел.

Шаг 2 : Продолжайте обычное сложение целых чисел.

⊗ Обратите внимание, что в конечном итоге вы добавите целые числа. Итак, для вашего удобства, вот краткое изложение правил добавления целых чисел.

Случай 1 : сложение двух целых чисел с одинаковым знаком

Сложите их абсолютные значения и сохраните общий знак.

Случай 2 : сложение двух целых чисел с разными знаками

Вычтите их абсолютные значения (большее абсолютное значение минус меньшее абсолютное значение), затем возьмите знак числа с большим абсолютным значением.

Примеры целочисленного вычитания

Пример 1 : Вычтите указанные ниже целые числа.

Решение:

Нам нужно будет преобразовать задачу от вычитания к сложению. Для этого мы сохраняем первое число, равное –13, меняем операцию с вычитания на сложение, затем меняем знак ^₊ 4 на ^— 4.

Последний шаг — продолжить регулярное добавление. Сложите их абсолютные значения. Затем определяем знак окончательного ответа. Поскольку мы добавляем целые числа с одинаковым знаком, мы сохраняем общий знак, который в данном случае отрицательный.

Пример 2 : Вычтите целые числа, указанные ниже.

Решение:

Как и раньше, преобразуйте задачу вычитания в задачу сложения. Остается положительное 9, переключите операцию с «минус» на «плюс», затем получите противоположный знак вычитания (второе число) с отрицательного на положительный.

А теперь добавим их. Мы складываем два положительных целых числа, поэтому ожидаем, что ответ также будет положительным, потому что общий знак положительный.

Пример 3 : Найдите разность двух целых чисел.

Решение:

Надеюсь, вы уже разбираетесь в этом. Давайте сначала сделаем это задачей сложения целых чисел, а затем приступим к регулярному сложению целых чисел с разными знаками.

Итак, мы сначала вычитаем их абсолютные значения, а затем получаем знак числа с большим абсолютным значением.

Вычитая абсолютные значения, получаем 24 минус 19, что дает нам +5. Но окончательный ответ — ^— 5, потому что знак идет от ^— 24.

Практика с рабочими листами

Возможно, вас заинтересует:

Целочисленное сложение
Целочисленное умножение
Целочисленное деление

Правила сложения и вычитания

целых чисел

Сложение и вычитание целых чисел является битовой сложностью. Сложение и вычитание — две функции, которые являются основными математическими функциями. В целых числах эта математическая функция немного сложна из-за наличие определенного знака перед числом i.е. ‘-‘ и ~ ez_lsquo + ez_rsquo ~. Однако, когда вы добавляете или вычитаете два числа с одним и тем же знаком, которые вы делаете, как указано, но если числа имеют разные знаки, то это разные.
Если между положительным и отрицательным числом производится вычитание, то производится сложение.

Правила сложения и вычитания целых чисел

Правила сложения и вычитания целых чисел:
1) Если два числа имеют разный знак, например положительный и отрицательный, вычтите два числа и дайте знак большему числу.
2) Если два числа имеют одинаковый знак, т.е. положительные или отрицательные знаки, сложите два числа и дайте общий знак.
3) (положительный) x (положительный) = положительный знак продукта.
4) (отрицательный) x (отрицательный) = отрицательный знак продукта.
5) (положительный) x (отрицательный) = отрицательный знак продукта. Число
положительное, следовательно, знак продукта положительный.
6) (отрицательный) x (положительный) = знак продукта отрицательный. Примечание: ответ сложения или вычитания между двумя числами будет иметь знак большего числа.
Решенные примеры:
1. вычесть: (-4) — (-3)
(отрицательный) x (отрицательный 3) = + 3
= -4 + 3
= -1.
Здесь я поставил знак числа большего значения, например (- 4).
2. Сложение: -8 + 10
= -8 + 10
= 2
3. Вычесть: -9 — (+9)
(отрицательное) x (положительное 9) = — 9
= -9 — 9
= — 18

Практикуйтесь в правилах сложения и вычитания целых чисел

1. Вычесть: 6 — (-9)
2. Вычесть: 10 — (10)
3. Вычесть: 10 — (8)
4.Вычесть: 34 — (-9)
5. Вычесть: 73 — (88)
6. Вычесть: 19 — (-29)
7. Вычесть: 15 — (23)
8. Вычесть: 54– (-34)
9. Вычесть: 0 — (38)
10. Вычесть: -34– (-18)
11. Сложение: 78+ (-12)
12. Сложение: 68 + (-56)
13. Сложение: 36 + (9)
14. Дополнение: 94 + (-99)
15. Дополнение: -63 + (0)
16. Дополнение: 20 + (-6)
17. Дополнение: -37 + (73)
18 Сложение: 48 + (-12)
19. Сложение: 78 + (-67)
20. Сложение: 5 + (23) Целочисленные правила сложения и вычитания
Целочисленные правила на домашней странице математики 6-го класса

Covid-19 привел мир к феноменальному переходу.

За электронным обучением будущее уже сегодня.

Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!

Covid-19 повлиял на физическое взаимодействие между людьми.

Не позволяйте этому влиять на ваше обучение.

Типы задач сложения и вычитания В примерах используются целые числа

Вернитесь назад Обзор

Задачи соединения
Отдельные проблемы
Проблемы части-части-целого
Сравнить или устранить проблемы
Образцы к классу

Задачи объединения

(начальный номер + номер изменения = сумма или результат)

Отсутствующая сумма или неизвестный результат

(начальный номер + номер изменения = ____________)

У Пита было 3 яблока.Энн дала Питу еще 5 яблок. Сколько яблок у Пита сейчас?
У Санди было 7 центов. Майк дал ей еще 4. Сколько всего десять центов у Сэнди?

Отсутствующее изменение: добавление Неизвестно

(начальный номер + ____________ = сумма или результат)

У Кэти было 5 карандашей. Сколько еще карандашей ей нужно положить, чтобы у нее было всего 7 карандашей?
У Санди 7 центов.Майк дал ей еще. Теперь у Сэнди 11 центов. Сколько дал ей Майк?

Отсутствует начало или начальное добавление Неизвестно

(____________ + номер изменения = сумма или результат)

Боб получил 2 печенья. Теперь у него 5 печенек. Сколько файлов cookie было у Боба вначале?
У Санди есть десять центов. Майк дал ей еще 4. Теперь у Сэнди 11 центов. Сколько центов было у Сэнди для начала?

Отдельные проблемы

(начало — изменение = разница или сумма или результат)

Результирующая разница или сумма неизвестна

(начальный номер + номер изменения = ____________)

У Сэнди 11 центов.Она дала Майку 4 цента. Сколько десять центов у Сэнди сейчас?
У Джо было 8 шариков. Затем он дал Тому 5 шариков. Сколько шариков сейчас у Джо?

Недостающее изменение Добавление / вычитание Неизвестно

(начальный номер + ____________ = разница или сумма)

У Санди было 11 центов. Она дала Майку. Теперь у нее 7 центов. Сколько она дала Майку?
У Фреда было 11 конфет.Он потерял некоторые части. Теперь у него 4 леденца. Сколько конфет потерял Фред?

Начальное добавление / минус Неизвестно

(____________ + номер изменения = разница или сумма)

У Санди было несколько десятицентовиков. Она дала 4 Майку. Теперь у Сэнди осталось 7 центов. Сколько центов было у Сэнди для начала?
У Карен были проблемы со словами. Она решила 2 из них. У нее все еще есть проблемы с тремя словами. Сколько словесных проблем у нее было в начале?

Часть — Часть — Проблемы целиком

(часть + часть = целое)

Целая или сумма отсутствует

(часть + часть = ____________

В волейбольной команде 6 мальчиков и 8 девочек.Сколько детей в команде?
У Бобби 3 десятицентовика, а у Аззи 5. Если сложить их вместе, сколько у них получится?
У Майка 5 пенсов и 10 центов. Сколько у него монет?
У Майка 5 центов, а у Сэнди 10 центов. Они кладут туда копейки в копилку. Сколько центов они положили в банк?
У Сары 6 сахарных пончиков и 9 простых пончиков. Затем она кладет их все на тарелку. Сколько пончиков на тарелке?

Отсутствующая часть неизвестна

(часть + ____________ = целое) или
(____________ + часть = целое)

У Карлоса в кармане было 8 четвертей.Он протягивает руку и вытаскивает четыре. Сколько еще в его кармане?
У Брайана 14 цветов. Восемь из них красные, остальные желтые. Сколько желтых цветов у Брайана?
Бобби и Санди положили 12 центов в кошелек мелочи. Сэнди вставила 8. Сколько положила Бобби? или Майк и Сэнди положили 11 центов в копилку. Майк вложил 7 центов. Сколько центов вложил Санди?
У Майка 10 монет. 7 его монет — десять центов, остальные — пенни.Сколько грошей?
У Джо и Тома получается 8 шариков, когда они складывают все шарики вместе. У Джо 3 шарика. Сколько шариков у Тома?

Проблемы сравнения или выравнивания

(одно значение + или — разница = второе значение)

Разница неизвестна

(одно значение + или — разница = второе значение)
(одно значение — второе значение = разница)

У Джо 3 воздушных шара.У его сестры Конни 5 воздушных шаров. Насколько больше воздушных шаров у Конни, чем у Джо?
У Дженис 8 жевательных резинок. У Тома 2 жевательной резинки. У Тома на сколько палочек меньше, чем у Дженис?
У Майка 11 центов, а у Сэнди 5. На сколько центов больше у Майка, чем у Сэнди?
У Майка 11 центов. У Сэнди 5 центов. На сколько центов меньше у Сэнди, чем у Майка?

Больше Неизвестно

(одно значение + разница = второе значение)
(второе значение — разница = первое значение)

У Луиса 6 золотых рыбок.У Карлы на 2 золотых больше, чем у Луиса. Сколько золотых рыбок у Карлы?
Папа купил 18 бутылок молока в воскресенье, а в понедельник принес на 6 бутылок меньше. Сколько бутылок он принес в понедельник?
У Майка на 4 цента больше, чем у Сэнди. У Сэнди 7 центов. Сколько десять центов у Майка?
У Сэнди на 4 цента меньше, чем у Майка. У Сэнди 7 центов. Сколько десять центов у Майка?
У Джейн 7 кукол. У Энн 3 куклы. Сколько кукол нужно проиграть Джейн, чтобы иметь столько же, сколько Энн?
У Конни 13 шариков.Если Джим выиграет 5 шариков, у него будет такое же количество шариков, что и у Конни. Сколько шариков у Джима?

Меньшее Неизвестно

(одно значение + разница = второе значение)
(второе значение — разница = первое значение)

У Максин 9 свитеров. У нее на 5 свитеров больше, чем у Сью. Сколько свитеров у Сью?
У Джима 5 шариков. У него на 8 шариков меньше, чем у Конни. Сколько шариков у Конни?
У Сэнди на 4 цента меньше, чем у Майка.У Майка 11 центов. Сколько центов у Сэнди?
У Майка на 4 цента больше, чем у Сэнди. У Майка 11 центов. Сколько центов у Сэнди? У Сьюзан 8 шариков.
У Фреда 5 шариков. Сколько еще шариков нужно Фреду, чтобы у него было столько же шариков, сколько у Сьюзен?

Куда бы вы это положили?

В футбольной команде было 6 мальчиков. К команде присоединились еще два мальчика. Сейчас в команде столько же мальчиков, сколько девочек.Сколько девушек в команде?
На столе было 11 стаканов. Я убираю 4 из них, чтобы на столе было столько же стаканов, сколько тарелок. Сколько тарелок было на столе?
В танцевальной группе было несколько девушек. Четверо из них сели, чтобы у каждого мальчика был партнер. В танцевальной группе 7 мальчиков. Сколько девушек в танцевальной группе?
У Джима 7 четвертей. У Энн 3 квартала. Сколько четвертей нужно потратить Джиму, чтобы иметь столько же, сколько Энн?

Идеи возникли из: Исследования сложения и вычитания целых чисел .Карен К. Фусон в Справочнике по исследованиям в области преподавания и обучения математике . Эд. Дуглас А. Гроуз. Macmillan Publishing Co., 1992.

Заметки доктора Роберта Свитленда
[Домашняя страница: thehob.net]

Как сложение и вычитание можно применять в нашей повседневной жизни

Математические вычисления повсеместно используются дома, в обществе и на работе. Овладев основами, такими как сложение и вычитание, вы будете чувствовать себя более уверенно в различных настройках, требующих быстрого вычисления чисел в вашей голове, таких как подсчет сдачи в проходном ресторане.Прочная основа функциональной математики также полезна для более сложных операций, таких как сложение или вычитание десятичных знаков, дробей или футов и дюймов, для которых может потребоваться калькулятор или карандаш и бумага.

Домашние обязанности

От первой чашки кофе до ночного гуляния с собакой — математика необходима для повседневных домашних дел. Например, вы можете проснуться с желанием выпить две чашки кофе вместо одной. Если вы обычно добавляете 1½ столовых ложки кофе в перколятор, чтобы приготовить одну чашку объемом 8 унций, вам нужно добавить 1½ плюс 1,5, чтобы знать, что требуются три столовые ложки кофе.Вам также потребуется удвоить количество воды в перколяторе. В течение дня математика играет важную роль, если вы должны проверить оставшиеся минуты работы мобильного телефона, измерить окна для занавесок, испечь половину партии печенья, сократить семейный бюджет или определить, в какое время выпускать собаку, если вы хотите восемь часов сна. до того, как прозвучит ваш будильник утром.

Покупка и продажа

Каждый раз, когда вы используете кредитную или дебетовую карту, полезно проверять свою банковскую выписку и личную книгу чековых книжек на точность.Например, если ваш начальный баланс составлял 1000 долларов, а вы купили продуктов на 200 долларов, ваш конечный баланс должен составлять 800 долларов. Когда вы заходите в продуктовый магазин за несколькими товарами, полезно подсчитать предполагаемые покупки перед выездом, чтобы убедиться, что у вас достаточно наличных денег или денег на текущем счете. Другие распространенные денежные операции, включающие сложение и вычитание, включают расчет чаевых, заполнение налоговых деклараций и оценку налога с продаж по объектам налогообложения.

Job Success

Большинство работ требует определенного уровня математических способностей, от базовой арифметики до векторного исчисления.Примеры работ, которые включают в себя обширное сложение и вычитание, включают кассиров в банках, бухгалтеров, кассиров, официантов и операторов платных пунктов. Если вы занимаетесь плотником, вы измеряете доски и укорачиваете их пилой до нужной длины. Даже если ваша работа не требует математики, начальник может ожидать, что вы закажете расходные материалы или заполните табели учета рабочего времени, суммируя часы и вычитая время отпуска. Вас также могут попросить отслеживать данные, такие как увеличение количества ежедневных звонков, полученных после показа рекламной рекламы.

Воспитание детей

Знание математики удобно, если дети в вашей семье обращаются к вам за помощью с домашним заданием. Согласно книге «Что я могу сделать, чтобы помочь своему ребенку с математикой, когда я никого не знаю», родители должны указать на то, что математика практична и является требованием для колледжа и многих высокооплачиваемых профессий. Вы можете быть хорошим примером для подражания, сохраняя позитивный настрой, помогая детям складывать и вычитать. Родители и опекуны также добавляют или вычитают при определении правильной дозировки лекарств с учетом веса ребенка, измерении роста ребенка, помощи в подсчете монет в копилке или ведении счета во время бейсбольных игр.

Сложение и вычитание с деньгами

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Сложение и вычитание целых чисел

В сегодняшнем сообщении блога мы рассмотрим целые числа : , что они собой представляют и как их складывать и вычитать.

Давайте начнем с понимания того, что на самом деле представляют собой целые числа:

Целые числа — это числа, не являющиеся дробными и десятичными.Эти числа включают натуральные числа (1, 2, 3…), отрицательные числа (-1, -2, -3…) и ноль (0).

Целые числа могут быть представлены в числовой строке. Справа от нуля — натуральные числа, а слева — отрицательные числа.

Сложение и вычитание отрицательных чисел

Чтобы научиться складывать или вычитать целые числа, мы будем использовать числовую строку.

Нам нужно найти первое число в числовой строке.
Если мы складываем, мы считаем, сколько значений стоит второе число справа.
Если мы вычитаем, мы считаем, сколько значений стоит второе число слева.

Например: 5–9

Итак, нам нужно найти первое число в строке.

Если мы складываем, мы считаем, сколько значений стоит второе число справа. Если мы вычитаем, мы считаем, сколько значений стоит второе число слева.

В этой задаче мы вычитаем, что означает, что нам нужно считать влево. Второе число — 9, поэтому мы считаем 9 значений слева от 5.

Итак, 5-9 = — 4

Уловка:

Я покажу вам небольшой трюк. Надеюсь, это поможет вам легче складывать и вычитать.

Если два числа имеют одинаковый знак , мы складываем два числа, не обращая внимания на знак, и после сложения приклеиваем знак, который был у чисел, на окончательный ответ.Например: — 2-5

Оба числа имеют одинаковый знак, поэтому мы складываем их: 2 + 5 = 7. Теперь мы просто добавляем знак, с которого должны были начинаться два числа, то есть отрицательный знак (-). Тогда окончательный ответ -7.

Если у двух чисел разный знак , мы просто вычитаем их: большее число минус меньшее. После этого мы добавляем к ответу тот знак, который был у большого числа. Например: 3-7

Оба числа имеют разные знаки, поэтому мы вычитаем меньшее из большего: 7 — 3 = 4.