| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Деление в столбик
Деление многозначных или многоразрядных чисел удобно производить письменно в столбик.
Давайте разберем, как это делать. Начнем с деления многоразрядного числа на одноразрядное, и постепенно увеличим разрядность делимого.
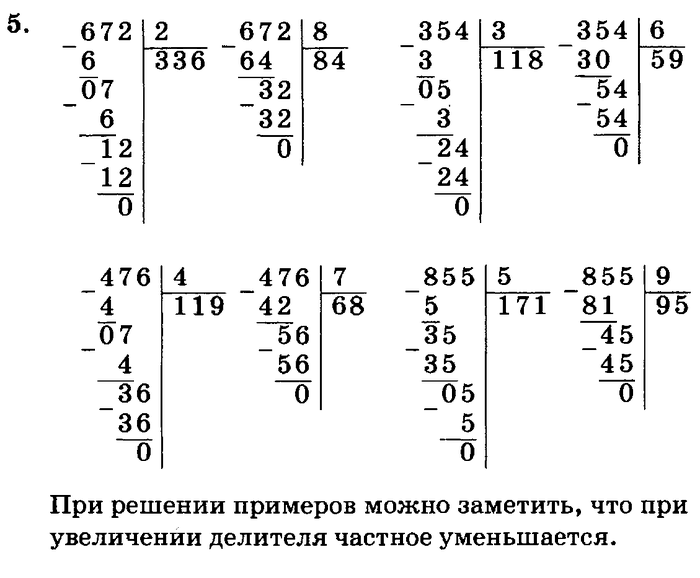
Итак, поделим 354 на 2 . Для начала разместим эти числа как показано на рисунке:
Делимое размещаем слева, делитель справа, а частное будем записывать под делителем.
Теперь начинаем делить делимое на делитель поразрядно слева на право. Находим первое неполное делимое, для этого берем первый слева разряд, в нашем случае 3 и сравниваем с делителем.
3 больше 2 , значит 3 и есть неполное делимое. Ставим точку в частном и определяем, сколько ещё разрядов будет в частном – столько же, сколько осталось в делимом после выделения неполного делимого. В нашем случае в частном столько же разрядов, сколько в делимом, то есть старшим разрядом будут сотни:
Для того чтобы 3 разделить на 2 вспоминаем таблицу умножения на 2 и находим число при умножении которого на 2 получим наибольшее произведение, которое меньше 3.
2 × 1 = 2 (2 < 3)
2 × 2 = 4 (4 > 3)
2 меньше 3 , а 4 больше, значит, берем первый пример и множитель 1 .
Записываем 1 в частное на место первой точки (в разряд сотен), а найденное произведение записываем под делимым:
Теперь находим разность, между первым неполным делимым и произведением найденного разряда частного и делителем:
Далее находим второе неполное делимое, для этого значение следующего разряда делимого опускаем к разности:
Полученное значение сравниваем с делителем. 15 больше 2 , значит, мы нашли второе неполное делимое. Для того чтобы найти результат деления 15 на 2 вновь вспоминаем таблицу умножения на 2 и находим наибольшее произведение, которое меньше 15 :
2 × 7 = 14 (14 < 15)
2 × 8 = 16 (16 > 15)
Искомый множитель 7 , записываем его в частное на место второй точки (в десятки).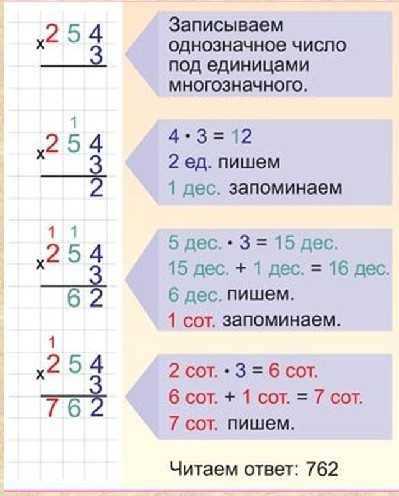
Находим разность между вторым неполным делимым и произведением найденного разряда частного и делителя:
Продолжаем деление, для чего находим третье неполное делимое. Спускаем следующий разряд делимого:
Делим неполное делимое на 2, полученное значение ставим в разряд единиц частного. Проверим правильность деления:
2 × 7 = 14
Результат деления третьего неполного делимого на делитель пишем в частное, находим разность:
Разность мы получили равную нулю, значит деление произведено правильно.
Усложним задачу и приведем другой пример:
1020 ÷ 5
Запишем наш пример в столбик и определим первое неполное частное:
Разряд тысяч делимого составляет 1 , сравниваем с делителем:
1 < 5
Добавляем в неполное делимое разряд сотен и сравниваем:
10 > 5 – мы нашли неполное делимое.
Делим 10 на 5 , получаем 2 , записываем результат в частное.
Разность между неполным делимым и результатом умножения делителя и найденного разряда частного.
10 – 10 = 0
0 мы не пишем, опускаем следующий разряд делимого – разряд десятков:
Сравниваем второе неполное делимое с делителем.
2 < 5
Нам следует добавить в неполное делимое ещё один разряд, для этого в частное, на разряд десятков ставим 0 :
20 ÷ 5 = 4
Записываем ответ в разряд единиц частного и проверяем: записываем произведение под второе неполное делимое и вычисляем разность. Получаем 0 , значит пример решён правильно.
И ещё 2 правила деления в столбик:
1. Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить, например:
Сколько нулей в младшем разряде делимого мы убираем, столько же нулей убираем в младших разрядах делителя.
2. Если в делимом после деления остались нули, то их следует перенести в частное:
Итак, сформулируем последовательность действий при делении в столбик.
- Размещаем делимое слева, делитель справа. Помним, что делимое мы делим, поразрядно выделяя неполные делимые и деля их последовательно на делитель. Разряды в неполное делимое выделяются слева направо от старших к младшим.
- Если в делимом и делителе в младших разрядах стоят нули, то перед делением их можно сократить.
- Определяем первый неполный делитель:
а) выделяем в неполный делитель старший разряд делимого;
б) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (в), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
в) добавляем в неполное делимое следующий разряд и переходим к пункту (б).
- Определяем сколько разрядов будет в частном, и ставим столько точек на месте частного (под делителем) сколько будет в нем разрядов. Одна точка (один разряд) за все первое неполное делимое и остальных точек (разрядов) столько же, сколько осталось разрядов в делимом после выделения неполного делимого.
- Делим неполное делимое на делитель, для этого находим число, при умножении которого на делитель получилось бы число либо равное неполному делимому, либо меньше его.
- Найденное число записываем на место очередного разряда частного (точки), а результат умножения его на делитель записываем под неполным делимым и находим их разность.
- Если найденная разность меньше или равна неполному делимому значит, мы правильно поделили неполное делимое на делитель.
- Если в делимом остались еще разряды, то продолжаем деление, иначе переходим к пункту 10.
- Опускаем к разности следующий разряд делимого и получаем очередное неполное делимое:
а) сравниваем неполное делимое с делителем, если делитель больше, то переходим к пункту (б), если меньше, значит, мы нашли неполное делимое и можем переходить к пункту 4;
б) добавляем к неполному делимому следующий разряд делимого, при этом в частное на место следующего разряда (точки) пишем 0;
в) переходим к пункту (а).
10. Если мы выполняли деление без остатка и последняя найденная разность равна 0 , то мы правильно выполнили деление.
Мы говорили о делении многоразрядного числа на одноразрядное. В случае, когда разрядность делителя больше, деление выполняется аналогично:
Синтетический отдел | Колледж Алгебра
Результаты обучения
- Используйте синтетическое деление для деления многочленов.
Как мы уже видели, деление многочленов в длину может включать много шагов и быть весьма громоздким. Синтетическое деление — это сокращенный метод деления многочленов для особого случая деления на линейный множитель, старший коэффициент которого равен 1.
Чтобы проиллюстрировать процесс, вспомните пример в начале раздела. 9{2}+4x+5[/latex] на [latex]x+2[/latex] с использованием алгоритма длинного деления.
Окончательный вид процесса выглядел так:
В таблице много повторений. Если мы не будем записывать переменные, а вместо этого выстроим их коэффициенты в столбцы под знаком деления, а также исключим частичные произведения, мы уже получим более простую версию всей задачи.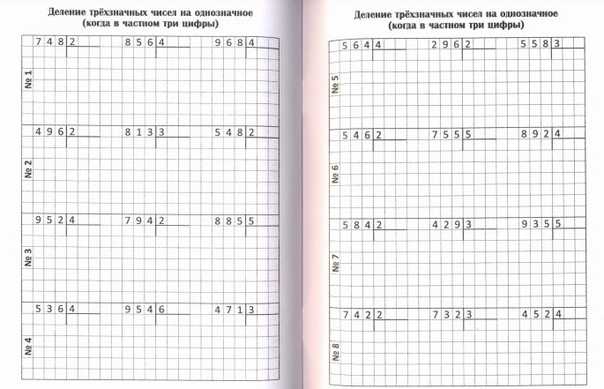
Синтетическое деление несет в себе это упрощение еще на несколько шагов. Сверните таблицу, переместив каждую из строк вверх, чтобы заполнить все свободные места. Кроме того, вместо деления на 2, как при делении целых чисел, а затем умножения и вычитания среднего произведения, мы меняем знак «делителя» на -2, умножаем и складываем. Процесс начинается с уменьшения старшего коэффициента. 92} -7x+18[/latex], а остаток равен –31. Процесс будет более понятен в следующих примерах.
A Общее примечание: синтетическое деление
Синтетическое деление — это сокращение, которое можно использовать, когда делитель представляет собой двучлен в форме x — k . В синтетическом делении в процессе деления используются только коэффициенты.
Как сделать: Имея два многочлена, используйте синтетическое деление для деления
- Напишите k для делителя.
- Запишите коэффициенты делимого.
- Уменьшить старший коэффициент.
- Умножить старший коэффициент на k . Напишите произведение в следующем столбце.
- Добавьте условия второго столбца.
- Умножьте результат на k . Напишите произведение в следующем столбце.
- Повторите шаги 5 и 6 для остальных столбцов.
- Используйте нижние числа, чтобы записать частное. Число в последнем столбце является остатком и имеет степень 0, следующее число справа имеет степень 1, следующее число справа имеет степень 2 и так далее. 9{3}-3x+40[/latex] на [latex]x+7[/latex].
Показать решение
https://www.myopenmath.com/multiembedq.php?id=29483&theme=oea&iframe_resize_id=mom1
Полиномиальное деление можно использовать для решения различных прикладных задач, связанных с выражениями для площади и объема. Мы рассмотрели приложение в начале этого раздела. Теперь мы решим эту задачу на следующем примере.
Пример: использование полиномиального деления в прикладной задаче
9{2}-23x+6[/латекс]. Ширина прямоугольника равна x + 6. Найдите выражение для длины прямоугольника.Показать решение
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
2.4: Значимые цифры в расчетах
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 47449
- Правильно использовать значащие цифры в арифметических операциях.
- 23,096 × 90,300
- 125 × 9.000
- 13,77 + 908.226
- 1027 + 611 + 363,06
- 2(1,008 г) + 15,99 г
- 137,3 с + 2(35,45 с)
- \( {118,7 г\более 2} — 35,5 г\)
- 5(1,008 с) — 10,66 с
- 99,0 см+ 2(5,56 см)
- Ответить на
- -5,62 с
- Ответ б
- 110,2 см
- Округление
- Если отбрасываемое число больше или равно 5, увеличьте число слева от него на 1 (например, 2,9699, округленное до трех значащих цифр, равно 2,97).
- Если отбрасываемое число меньше 5, изменений нет (например, 4,00443, округленное до четырех значащих цифр, равно 4,004).
- Правило умножения и деления состоит в том, что в окончательном ответе должно быть столько же значащих цифр, сколько в числе с наименьшим количеством значащих цифр.
Ширина прямоугольника равна x + 6. Найдите выражение для длины прямоугольника.Цели обучения
Округление
Прежде чем разбираться с особенностями правил определения значащих цифр в вычисляемом результате, нужно уметь правильно округлять числа. до округлить число до , сначала решить, сколько значащих цифр должно быть в числе.
Как только вы это узнаете, округлите до указанного количества цифр, начиная слева. Если число непосредственно справа от последней значащей цифры меньше 5, оно отбрасывается, а значение последней значащей цифры остается прежним. Если число непосредственно справа от последней значащей цифры больше или равно 5, последняя значащая цифра увеличивается на 1.
Рассмотрим измерение \(207,518 \: \text{m}\). Прямо сейчас измерение содержит шесть значащих цифр. Как бы мы последовательно округляли его до все меньшего и меньшего числа значащих цифр? Следуйте процессу, указанному в таблице \(\PageIndex{1}\).
| Количество значащих цифр | Округленное значение | Рассуждение |
|---|---|---|
| 6 | 207,518 | Все цифры значащие |
| 5 | 207,52 | 8 раундов от 1 до 2 |
| 4 | 207,5 | 2 выпадает |
| 3 | 208 | 5 раундов от 7 до 8 |
| 2 | 210 | 8 заменяется на 0 и округляет 0 до 1 |
| 1 | 200 | 1 заменяется на 0 |
Обратите внимание, что чем больше округление сделано, тем менее надежна цифра.
Приблизительного значения может быть достаточно для некоторых целей, но научная работа требует гораздо более высокого уровня детализации.
При математических операциях с числами важно помнить о значащих цифрах. Например, деление 125 на 307 на калькуляторе дает 0,4071661238… с бесконечным числом цифр. Но имеют ли цифры в этом ответе какое-либо практическое значение, особенно когда вы начинаете с чисел, каждое из которых имеет только три значащих цифры? При выполнении математических операций существует два правила ограничения количества значащих цифр в ответе: одно правило для сложения и вычитания, а другое правило для умножения и деления.
В операциях со значащими цифрами ответ сообщается таким образом, чтобы он отражал надежность наименее точной операции . Ответ не более точен, чем наименее точное число, использованное для получения ответа.
Умножение и деление
Для умножения или деления правило состоит в том, чтобы подсчитать количество значащих цифр в каждом умножаемом или делимом числе, а затем ограничить значащие цифры в ответе наименьшим числом.
Например:
Окончательный ответ, ограниченный четырьмя значащими цифрами, равен 4094. Первая отброшенная цифра — 1, поэтому мы не округляем.
Экспоненциальное представление обеспечивает способ передачи значащих цифр без двусмысленности. Вы просто включаете все значащие цифры в начальное число. Например, число 450 имеет две значащие цифры и будет записано в научной записи как 4,5 × 10 2 , тогда как число 450,0 имеет четыре значащих цифры и будет записано как 4,500 × 10 9 .0236 2 . В экспоненциальном представлении все значащие цифры указаны явно.
Пример \(\PageIndex{1}\)
Напишите ответ для каждого выражения в экспоненциальном представлении с соответствующим количеством значащих цифр.
Решение
a
Второй столбец помечен как «Ответ», а под ним в строке находится ответ. 93\)b
| Пояснение | Ответить |
|---|---|
| Калькулятор дает ответ 1125, но мы ограничиваем его тремя значащими цифрами. 93\) |
Сложение и вычитание
Как значащие числа обрабатываются в вычислениях? Это зависит от того, какой тип расчета выполняется. Если вычисление представляет собой сложение или вычитание, правило следующее: ограничьте сообщаемый ответ крайним правым столбцом, в котором все числа имеют общие значащие цифры. Например, если вы должны сложить 1,2 и 4,71, мы заметим, что первое число останавливает свои значащие цифры в столбце десятых, а второе число останавливает свои значащие цифры в столбце сотых.
Поэтому мы ограничиваем наш ответ десятым столбцом.
Мы опускаем последнюю цифру — 1 — потому что она не имеет значения для окончательного ответа.
Отбрасывание позиций в суммах и разностях поднимает тему округления. Несмотря на некоторые соглашения, в этом тексте мы примем следующее правило: окончательный ответ следует округлить в большую сторону, если первая пропущенная цифра 5 или больше, и округлить в меньшую сторону, если первая пропущенная цифра меньше 5.
Пример \(\PageIndex{2}\)
Решение
a
| Пояснение | Ответить |
|---|---|
| Ответ калькулятора: 92\) |
b
| Пояснение | Ответить | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Калькулятор дает в качестве ответа 2001,06, но поскольку 611 и 1027 имеют крайнюю правую значащую цифру в разряде единиц, окончательный ответ должен быть ограничен разрядом единиц. 90\) Помните, что калькуляторы не понимают значащие цифры. Вы тот, кто должен применить правила значащих цифр к результату вашего калькулятора. Вычисления, связанные с умножением/делением и сложением/вычитанием На практике химики обычно работают с калькулятором и переносят все цифры в последующих вычислениях. Однако при работе на бумаге мы часто хотим свести к минимуму количество цифр, которые нам приходится записывать. В рабочих примерах в этом тексте мы часто будем показывать результаты промежуточных шагов расчета. При этом мы покажем результаты только для правильного количества значащих цифр, разрешенных для этого шага, фактически рассматривая каждый шаг как отдельный расчет. Пример \(\PageIndex{3}\)Раствора.
б.
в.
Упражнение \(\PageIndex{3}\)Выполните вычисления и запишите свои ответы, используя правильное количество значащих цифр. Сводка |
Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
Поскольку последовательное округление может усугубить неточности, промежуточное округление должно выполняться правильно. При работе на бумаге всегда округляйте промежуточный результат, чтобы сохранить хотя бы на одну цифру больше, чем можно оправдать, и переносите это число на следующий шаг в расчетах. Затем окончательный ответ округляется до правильного количества значащих цифр в самом конце.
Эта процедура предназначена для закрепления правил определения количества значащих цифр, но в некоторых случаях она может давать окончательный ответ, отличающийся последней цифрой от полученного с помощью калькулятора, где все цифры переносятся на последний шаг.
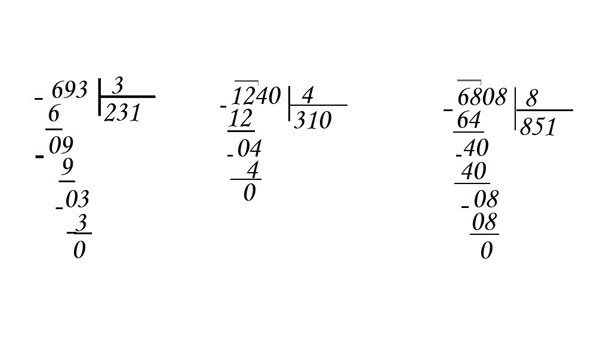
Первый столбец слева помечен как «Объяснение», а под ним в строке находится объяснение первого деления. Второй столбец помечен как «Ответ», а под ним в строке находится ответ.
