Умножение: по-японски, по-итальянски и методом майя
- Аналия Йоренте
- BBC Mundo
Подпишитесь на нашу рассылку ”Контекст”: она поможет вам разобраться в событиях.
Автор фото, Getty Images
Подпись к фото,Не заболела бы голова…
«Математика такая трудная…» Вы наверняка не раз слышали эту фразу, а, может быть, даже сами ее произносили вслух.
Для многих математические вычисления — дело непростое, но вот вам три несложных способа, которые помогут выполнить хотя бы одно арифметическое действие — умножение. Без калькулятора.
Вполне вероятно, что в школе вы познакомились с наиболее традиционным способом умножения: сначала вы выучили на память таблицу умножения, а уж затем стали в столбик перемножать каждую из цифр, которыми записываются многозначные числа.
Если вам надо перемножить многозначные числа, то, чтобы найти ответ, потребуется большой лист бумаги.
Но если от этого длинного набора идущих одна под другой строчек с цифрами у вас голова идет кругом, то есть и другие, более наглядные методы, которые могут вам помочь в этом деле.
Но тут пригодятся некоторые художественные навыки.
Давайте порисуем!
Как минимум три способа умножения связаны с рисованием пересекающихся линий.
1. Способ индейцев майя, или японский метод
Относительно происхождения этого способа существует несколько версий.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Попробуйте метод майя и японцев
Пропустить Подкаст и продолжить чтение.
Подкаст
Что это было?
Мы быстро, просто и понятно объясняем, что случилось, почему это важно и что будет дальше.
эпизоды
Конец истории Подкаст
Некоторые говорят, что его придумали индейцы цивилизации майя, населявшие районы Центральной Америки до прибытия туда конкистадоров в XVI веке. Он также известен как японский метод умножения, поскольку учителя в Японии используют именно этот визуальный способ, когда учат младших школьников умножению.
Суть в том, что параллельные и перпендикулярные линии представляют цифры тех чисел, которые нужно перемножить.
Давайте умножим 23 на 41.
Для этого нам надо нарисовать две параллельные линии, представляющие 2, и, немного отступя, еще три линии, представляющие 3.
Затем, перпендикулярно к этим линиям мы нарисуем четыре параллельные линии, представляющие 4 и, чуть отступя, еще одну линию для 1.
Теперь нам надо пересчитать все точки пересечения этих линий. Именно так мы и получаем наш результат — 943, как если бы мы умножали в столбик.
Ну как, неужели трудно?
2. Индийский способ, или итальянское умножение «решеткой» — «джелозия»
Происхождение этого способа умножения тоже не ясно, однако он хорошо известен по всей Азии.
«Алгоритм «джелозия» передавался из Индии в Китай, затем в Аравию, а оттуда в Италию в XIV-XV веках, где он получил название «джелозия», поскольку внешне был похож на венецианские решетчатые ставни», — пишет Марио Роберто Каналес Виллануэва в своей книге, посвященной различным способам умножения.
Автор фото, Getty Images
Подпись к фото,Индийская или итальянская система умножения похожа на венецианские жалюзи
Давайте снова возьмем пример с умножением 23 на 41.
Теперь нам потребуется начертить таблицу из четырех клеток — по клетке на цифру. Подпишем сверху у каждой клетки соответствующую цифру — 2,3,4,1.
Затем надо разделить каждую клетку надвое по диагонали, чтобы получились треугольники.
Теперь мы сначала умножим первые цифры каждого числа, то есть 2 на 4, и запишем в первом треугольнике 0, а во втором 8.
Потом перемножим 3×4 и запишем 1 в первом треугольнике, а 2 во втором.
Проделаем то же самое и с другими двумя цифрами.
Когда все клетки нашей таблицы будут заполнены, мы складываем цифры в такой последовательности, как показано на видео, и записываем получившийся результат.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Попробуйте индийский метод
Первая цифра у нас будет 0, вторая 9, третья 4, четвертая 3. Таким образом, результат получился: 943.
Как вам показалось, проще этот способ или нет?
Давайте попробуем еще один метод умножения с помощью рисунка.
3. «Массив», или метод таблицы
Как и в предыдущем случае, для этого потребуется нарисовать таблицу.
Возьмем тот же пример: 23 x 41.
Тут нам надо разделить наши числа на десятки и единицы, поэтому 23 мы запишем как 20 в одной колонке, и 3 в другой.
По вертикали мы запишем наверху 40, а внизу 1 .
Затем мы перемножим числа по горизонтали и вертикали.
Для просмотра этого контента вам надо включить JavaScript или использовать другой браузер
Подпись к видео,Трудно умножать в уме? Нарисуйте таблицу.
Но вместо того чтобы умножать 20 на 40, мы отбросим нули и просто перемножим 2 x 4, получив 8.
То же самое сделаем, умножая 3 на 40. Мы удерживаем в скобках 0 и умножаем 3 на 4 и получаем 12.
Проделаем то же самое с нижним рядом.
Теперь добавим нули: в левой верхней клетке у нас получилось 8, но мы отбросили два нуля — теперь мы их допишем и получится 800.
В правой верхней клетке, когда мы умножали 3 на 4(0), у нас получилось 12; теперь мы допишем ноль и получим 120.
Сделаем так же со всеми прочими удержанными нулями.
И наконец, мы складываем все четыре числа, полученных умножением в таблице.
Результат? 943. Ну как, помогло?
Важно разнообразие
Автор фото, Getty Images
Подпись к фото,Все способы хороши, главное — чтобы ответ сошелся
Что точно можно утверждать, — так это то, что все эти разные способы дали нам один и тот же результат!
Нам все-таки пришлось кое-что перемножить в процессе, но каждый шаг был проще, чем при умножении традиционным способом, и гораздо более наглядный.
Так почему же мало где в мире в обычных школах учат этим методам вычисления?
Одной из причин может быть упор на обучение «вычислениям в уме» — чтобы развивать умственные способности.
Однако Дэвид Уиз, учитель математики из Канады, работающий в государственных школах в Нью-Йорке, объясняет это иначе.
«Недавно я прочитал, что причина, по которой используется традиционный метод умножения, — это экономия бумаги и чернил. Этот метод не был придуман как самый простой для использования, но как самый экономный с точки зрения ресурсов, поскольку чернила и бумага были в дефиците», — объясняет Уиз.
Автор фото, Getty Images
Подпись к фото,Для некоторых методов вычисления только головы недостаточно, нужны еще и фломастеры
Невзирая на это, он полагает, что альтернативные методы умножения очень полезны.
«Я не думаю, что это полезно — сразу учить школьников умножению, заставляя их выучивать таблицу умножения, но не объясняя им при этом, откуда она взялась. Поскольку если они забудут одно число, то как они смогут продвинуться в решении задачи? Метод майя или японский метод необходим, потому что с его помощью вы можете понять общую структуру умножения, а это хорошее начало», — полагает Уиз.
Существует и ряд других способов умножения, например, русский или египетский, они не требуют дополнительных навыков рисования.
Как говорят специалисты, с которыми мы беседовали, все эти методы помогают лучше понять процесс умножения.
«Понятно, что все идет на пользу. Математика в сегодняшнем мире открыта как внутри, так и снаружи классной комнаты», — резюмирует Андреа Васкес, учительница математики из Аргентины.
Страница 35 — ГДЗ Математика 4 класс. Моро, Бантова. Учебник часть 2
- Главная
- ГДЗ
- 4 класс
- Математика
- Моро, Бантова. Учебник
- Что узнали. Чему научились
- Страница 35. Часть 2
Вернуться к содержанию учебника
Что узнали. Чему научились
Вопрос
1.
| 84 • 10 — 40 | 10 • (920 — 20) | 184 • 100 — 300 |
| 78 • 10 — 700 | 8 • (720 — 700) | 100 • 391 — 3000 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
2.
| 50 : 50 • 100 | 15 • 2 • 100 | 25 • 4 • 100 | 180 : 2 + 210 • 4 |
| 24 • 10 : 8 | 48 : 3 • 10 | 100 : 2 : 10 | 150 : 3 + 250 • 4 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
3.
| 107 • 7 | 250 • 4 | 320 • 3 | 125 • 4 | 182 • 2 |
| 206 • 4 | 105 • 8 | 430 • 2 | 125 • 8 | 316 • 3 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
4. Выполни деление с остатком.
Выполни деление с остатком.
| 327 : 10 | 1684 : 100 | 15928 : 100 | 135628 : 10 |
| 358 : 10 | 1605 : 10 | 15862 : 10 | 36704 : 10 |
| 615 : 100 | 1730 : 100 | 34518 : 100 | 52080 : 100 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
5. Вычисли удобным способом.
| 45 • (2 • 7) | 720 : (9 • 2) | 67 • (4 • 25) | 17 • 2 • 8 • 125 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
6.
| 213 • 90 | 1872 • 60 | 529 • 800 | 905 • 200 |
| 487 • 40 | 6097 • 70 | 674 • 500 | 708 • 600 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
7.
| 3800 • 40 | 1090 • 700 | 600 • 580 | 3070 • 80 |
| 4200 • 60 | 2900 • 300 | 700 • 402 | 40300 • 20 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
8.
| 6510 : 30 | 46800 : 600 | 38960 : 80 | 34500 : 300 |
| 2280 : 50 | 395000 : 500 | 81720 : 90 | 52200 : 600 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
9.
| 100520 — 470 • 50 + 13980 | 400000 — 867 • 400 |
| 14110 + 801000 : 900 — 7604 | 9805 + 146510 : 70 |
| 734600 : 50 + 454 • 40 | 8213 • 30 — 12240 : 30 |
| (560 — 12240 : 30) + 145 | 11140 : (2076 — 2056) |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
10.
| 463700 : 50 + 546 • 40 | 8130 : 30 — 2640 : 10 |
| 55440 : 90 — 10460 : 20 | 900100 — (735 — 184) • 80 |
| 41090 : 70 + 11950 : 50 | 60997 + (6012 + 6228) : 30 |
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
11. Какими могут быть длины сторон прямоугольника, периметр которого равен 26 см, а площадь — 40 см2?
Какими могут быть длины сторон прямоугольника, периметр которого равен 26 см, а площадь — 40 см2?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
12. Вычислительная машина работает так:
Какой ответ будет получаться на выходе из машины, если на входе будет число 47; 53; 28; 94?
Ответ
Поделись с друзьями в социальных сетях:
Вопрос
Сравни площади фигур
Ответ
Поделись с друзьями в социальных сетях:
Вернуться к содержанию учебника
Умножение в столбик.
 Умножение и деление столбиком
Умножение и деление столбикомВ третьем классе начальной школы дети начинают изучать внетабличные случаи умножения и деления. Числа в пределах тысячи – материал, на котором происходит овладение темой. Программа рекомендует операции деления и умножения трехзначных и двузначных чисел производить на примере однозначных. В ходе работы над темой учитель начинает формировать у детей такой важный навык, как умножение и деление столбиком. В четвертом классе отработка навыка продолжается, но используется числовой материал в пределах миллиона. Деление и умножение в столбик выполняется на многозначные числа.
Что является основой умножения
Главные положения, на которых строится алгоритм умножения многозначного числа на многозначное, являются теми же, что при действиях на однозначное. Правил, которыми пользуются дети, существует несколько. Они были «раскрыты» школьниками еще в третьем классе.
Первым правилом является поразрядность операций. Второе заключается в использовании таблицы умножения в каждом разряде.
Необходимо учесть, что эти основные положения усложняются при выполнении действий с многозначными числами.
Записанный ниже пример позволит понять, о чем идет речь. Допустим, необходимо 80 х 5 и 80 х 50.
В первом случае ученик рассуждает так: 8 десятков необходимо повторить 5 раз, получатся тоже десятки, и их будет 40, так как 8 х 5 = 40, 40 десятков – это 400, значит, 80 х 5 = 400. Алгоритм рассуждения прост и понятен ребенку. В случае затруднения он легко может найти результат, воспользовавшись действием сложения. Способ замены умножения сложением можно применять и для проверки правильности собственных вычислений.
Чтобы найти значение второго выражения, тоже необходимо воспользоваться табличным случаем и 8 х 5. Но какому разряду будут принадлежать полученные 40 единиц? Вопрос для большинства детей остается открытым. Прием замены умножения действием сложения в данном случае нерационален, так как сумма будет иметь 50 слагаемых, поэтому воспользоваться им для нахождения результата невозможно. Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
Становится понятно, что знаний для решения примера недостаточно. Видимо, существуют еще какие-то правила умножения многозначных чисел. И их нужно выявить.
В результате совместных усилий педагога и детей становится ясно, что для умножения многозначного числа на многозначное необходимо умение применять сочетательный закон, при котором один из множителей заменяется произведением (80 х 50 = 80 х 5 х 10 = 400 х 10 = 4000)
Кроме того, возможен путь, когда используется распределительный закон умножения относительно сложения или вычитания. В этом случае один из множителей необходимо заменить суммой двух или более слагаемых.
Исследовательская работа детей
Ученикам предлагается достаточно большое количество примеров подобного вида. Дети каждый раз пытаются найти более простой и быстрый способ решения, но при этом от них все время требуется развернутая запись хода решения или подробные устные объяснения.
Учитель делает это, преследуя две цели. Во-первых, дети осознают, отрабатывают основные пути выполнения операции умножения на многозначное число. Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Во-вторых, приходит понимание того, что способ записи таких выражений в строчку очень неудобен. Наступает момент, когда сами ученики предлагают записывать умножение в столбик.
Этапы изучения умножения на многозначное число.
В методических рекомендациях изучение указанной темы происходит в несколько этапов. Они должны следовать один за другим, давая возможность школьникам понять весь смысл изучаемого действия. Перечень этапов открывает учителю общую картину процесса подачи материала детям:
- самостоятельный поиск учениками способов нахождения значения произведения многозначных множителей;
- для решения поставленной задачи используется сочетательное свойство, а также умножение на единицу с нулями;
- отработка навыка умножения на круглые числа;
- использование при вычислениях распределительного свойства умножения относительно сложения и вычитания;
- операции с многозначными числами и умножение в столбик.
Следуя указанным этапам, учитель постоянно должен обращать внимание детей на тесные логические связи ранее изученного материала с тем, что осваивается в новой теме. Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Школьники не только занимаются умножением, но и учатся сопоставлять, делать выводы, принимать решения.
Задачи изучения умножения в курсе начальной школы
Учитель, преподавая математику, точно знает, что наступит момент, когда у четвероклассников возникнет вопрос о том, как решать столбиком умножение многозначных чисел. И если он вместе с учениками на протяжении трех лет обучения – во 2, 3, и 4 классах – целенаправленно и вдумчиво изучал конкретный смысл умножения и все вопросы, которые связаны с этой операцией, то трудностей в освоении рассматриваемой темы у детей возникнуть не должно.
Какие же задачи ранее были решены учениками и их преподавателем?
- Освоение табличных случаев умножения, то есть получение результата в один шаг. Обязательным требованием программы является доведение навыка до автоматизма.
- Умножение многозначного числа на однозначное. Результат получается путем многократного повторения шага, которым дети уже владеют в совершенстве.
- Умножение многозначного числа на многозначное осуществляется благодаря повторению шагов, обозначенных в пункте 1 и 2.
 Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Использование свойств умножения
Перед тем как на последующих страницах учебников начнут появятся примеры умножения столбиком, 4 класс должен очень хорошо научиться пользоваться для рационализации вычислений сочетательным и распределительным свойством.
Путем наблюдений и сопоставлений ученики приходят к выводу, что сочетательное свойство умножения для нахождения произведения многозначных чисел используется только тогда, когда один из множителей можно заменить произведением однозначных чисел. А это возможно не всегда.
Распределительное свойство умножения в этом случае выступает как универсальное. Дети замечают, что множитель всегда можно заменить суммой или разностью, поэтому свойство используется для решения любого примера на умножение многозначных чисел.
Алгоритм записи действия умножения в столбик
Запись умножения столбиком является самой компактной из всех существующих.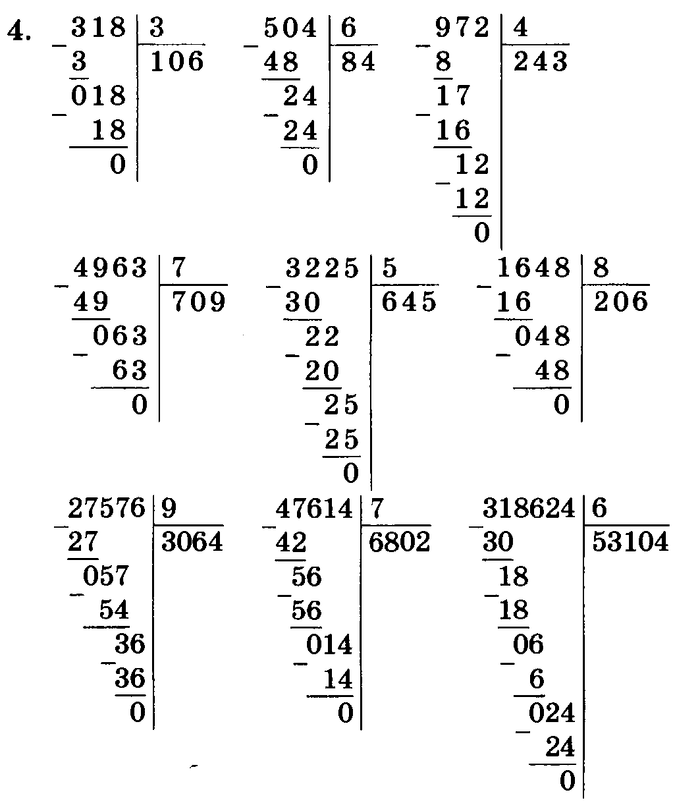 Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Обучение детей этому виду оформления начинается с варианта умножения многозначного числа на двузначное.
Детям предлагается самостоятельно составить последовательность действий при выполнении умножения. Знание этого алгоритма станет залогом успешного формирования навыка. Поэтому учителю не нужно жалеть времени, а постараться приложить максимум усилий к тому, чтобы порядок выполнения действий при умножении в столбик был усвоен детьми на «отлично».
Упражнения для формирования навыка
Прежде всего нужно отметить, что примеры умножения в столбик, предлагаемые детям, от урока к уроку усложняются. После знакомства с умножением на двузначное число дети учатся выполнять действия с трехзначными, четырехзначными числами.
Для отработки навыка предлагаются примеры с готовым решением, но среди них преднамеренно размещают записи с ошибками. Задача учеников состоит в том, чтобы обнаружить неточности, объяснить причину их появления и исправить записи.
Теперь при решении задач, уравнений и всех других заданий, где надо выполнять умножение многозначных чисел, от учеников требуется оформление записи столбиком.
Развитие познавательных УУД при изучении темы «Умножение чисел в столбик»
Большое внимание на уроках, посвященных изучению указанной темы, уделяется развитию таких познавательных действий, как нахождение разных способов решения поставленной задачи, выбор наиболее рационального приема.
Использование схем для проведения рассуждений, установление причинно-следственных связей, анализ наблюдаемых объектов на основе выделенных существенных признаков – еще одна группа формируемых познавательных умений при изучении темы «Умножение в столбик».
Обучение детей способам деления многозначных чисел и оформлению записи столбиком осуществляется только после того, как дети научатся умножать.
Банк вопросов по математике для 4-го класса Умножение и деление Умножение и деление
вопрос_ответ 1)
В зале было 240 рядов стульев. Если в каждом ряду 170 стульев, сколько человек может разместиться в зале?
А)
40800
Б)
408
В)
41000
Г)
410
Посмотреть решение play_arrowвопрос_ответ 2)
Определите недостающее число.
| \[\mathbf{163}\times \mathbf{38}=(\mathbf{160}+\mathbf{3})\times \,\,[\,\,\,\,\,\, ]\] |
А)
\[\text{35}-\text{3}\]
B)
\[\text{3}0+\text{3}\]
C)
\[\text{35}+\text{3}\]
D)
\[~\text{3}0+\text{5}\]
Посмотреть решение play_arrowвопрос_ответ 3)
Найдите произведение, которое получится, если разность между 12030 и 8107 умножить на 37.
A)
\[\text{3923}\times \text{3}0-\text{3923}\times \text{7}\]
\[\text{(39}00+\text{23)}\times \text{(4}0-\text{3)}\]
C)
\[\text{3923}\times \text{4}0+\text{3923}\times \text{3}\]
Г)
3923
Посмотреть решение play_arrowвопрос_ответ 4)
Найдите произведение 684 и 43, округленное до ближайших 100.
А)
30600
Б)
29400
В)
29500
Г)
29000
Посмотреть решение play_arrowвопрос_ответ 5)
Общий вес 4 словарей и 1079 тетрадей 75 кг. Если каждая тетрадь весит 68 г, каков вес каждого словаря?
А)
0,407 г
Б)
407 кг
В)
1628г
D)
0,407 кг
Посмотреть решение play_arrowвопрос_ответ 6)
Стоимость велосипеда рупий. 797. Сколько стоят 8 велосипедов?
797. Сколько стоят 8 велосипедов?
А)
рупий. 7978
B)
рупий. 6376
C)
рупий. 7376
D)
рупий. 6386
Посмотреть решение play_arrowвопрос_ответ 7)
Какое число будет в [ ], если \[8\times 6=2\times [\,\,\,\,\,]\times 8?\]
А)
32
Б)
4
В)
3
Г)
2
Посмотреть решение play_arrowquestion_answer 8)
Сумант экономит рупий.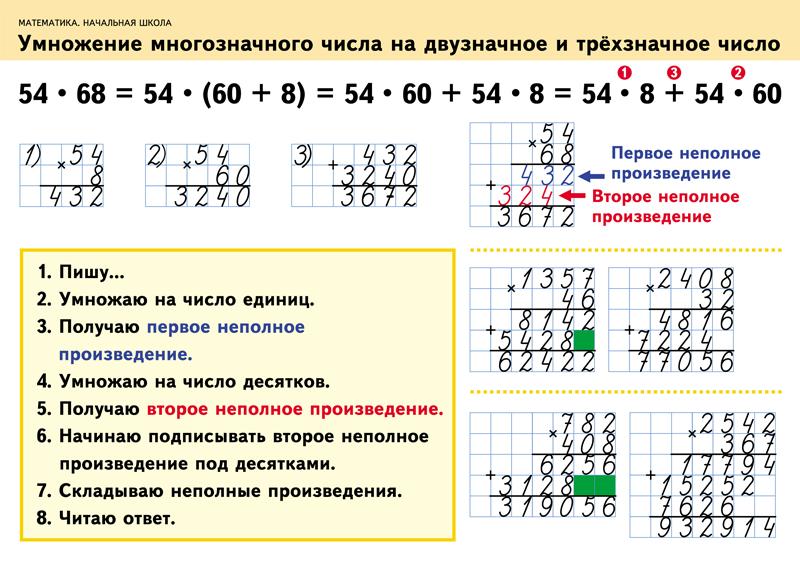 250 каждый месяц. Сколько денег он сэкономит за год?
250 каждый месяц. Сколько денег он сэкономит за год?
А)
рупий. 2600
B)
рупий. 3000
C)
рупий. 2500
D)
рупий. 3500
Посмотреть решение play_arrowвопрос_ответ 9)
Какую цифру нужно поставить в [ ], чтобы следующее умножение было правильным?
А)
1
Б)
3
В)
4
Г)
7
Посмотреть решение play_arrowвопрос_ответ 10)
В школьном клубе 525 членов. Если каждый участник платит рупий. 11 как членский взнос, сколько денег собирается?
Если каждый участник платит рупий. 11 как членский взнос, сколько денег собирается?
А)
рупий. 5725
B)
рупий. 5775
C)
рупий. 52511
D)
рупий. 6775
Посмотреть решение play_arrowвопрос_ответ 11)
Если стоимость 1 упаковки печенья ТИГР составляет \[\times \text{ 5},\], сколько пакетов я могу получить за \[\times \text{ 3}0\] с БЕСПЛАТНЫМ ПРЕДЛОЖЕНИЕМ, показанным здесь?
А)
6
B)
9
C)
10
D)
12
Посмотреть решение play_arrowвопрос_ответ 12)
Если Означает 30, какое число будет означать?
А)
60
Б)
70
В)
80
Г)
75
Посмотреть решение play_arrowвопрос_ответ 13)
Изучите данные уравнения. Если эти числовые предложения верны, что из следующего верно?
Если эти числовые предложения верны, что из следующего верно?
А)
Б)
В)
Г)
Посмотреть решение play_arrow
вопрос_ответ 14)
Навя хочет прочитать книгу, в которой всего 340 страниц. Из них 16 страниц содержат только рисунки, а еще 6 страниц содержат примечания автора, содержание и т. д. Если на каждой оставшейся странице около 30 строк печати, сколько всего строк придется прочитать Навье?
А)
9540
Б)
9660
В)
6540
Г)
9840
Посмотреть решение play_arrowвопрос_ответ 15)
Дважды определенное число равно 42. Сколько в шесть раз больше этого числа?
Сколько в шесть раз больше этого числа?
А)
\[\text{6}\times \text{42}\]
B)
\[\text{6}+\text{42}\]
В)
\[\text{3}\times \text{42}\]
D)
\[\text{12}\times \text{42}\]
Посмотреть решение play_arrowвопрос_ответ 16)
Если произведение всех трех чисел в любой строке, столбце или диагонали одинаково, найдите пропущенное число в данном квадрате.
| 12 | 1 | 18 |
| 9 | ? | 4 |
| 2 | 36 | 3 |
А)
6
Б)
8
В)
12
Г)
5
Посмотреть решение play_arrowвопрос_ответ 17)
A Что такое значение \[\text{(137}\times \text{137)}-(\text{136}\times \text{136})\]?
А)
493
Б)
1869
В)
273
Г)
869
Посмотреть решение play_arrowвопрос_ответ 18)
В данном умножении произведение 11418 неверно из-за ошибки в одной из цифр.
A)
Найдите неправильную цифру. 0
Б)
3
В)
8
Г)
5
Посмотреть решение play_arrowвопрос_ответ 19)
Если найти произведение \[\text{11111 }\times \text{ 11111}\].
А)
12345432
Б)
123454321
C)
12345621
Г)
1111111
Посмотреть решение play_arrowquestion_answer 20)
Изучите следующую диаграмму и найдите пропущенный член.
А)
5
Б)
15
В)
25
Г)
40
Посмотреть решение play_arrowвопрос_ответ 21)
Найдите пропущенный член в следующем.
А)
5
Б)
6
В)
25
Г)
12
Посмотреть решение play_arrowвопрос_ответ 22)
Если найти произведение \[\text{55555}\times \text{5}\].
А)
2757575
Б)
277777
В)
27775
Г)
277775
Посмотреть решение play_arrowвопрос_ответ 23)
Указание: На основе следующей таблицы ответьте на следующие вопросы.
|
How many children does each represent?
А)
500
Б)
600
В)
1000
Г)
800
Посмотреть решение play_arrowвопрос_ответ 24)
Направление: На основе следующей таблицы ответьте на следующие вопросы.
|
Какой из следующих детей является правильным представлением в Дели?
А)
Б)
В)
Г)
Посмотреть решение play_arrowвопрос_ответ 25)
Как можно написать \[\text{2}0\text{5}\times \text{6}\]?
A)
\[\text{(2}00+\text{5}0\text{)}\times \text{6}\]
B)
\[\text{(2}0+\text{5)}\times \text{6}\]
C)
\[\text{(2}00-\text{5)}\times \text{6}\]
D)
\[\text{200 }\!\!\times\!\!\text{ 6 }+\text{ 5 }\times \text{ 6}\]
Посмотреть решение play_arrowвопрос_ответ 26)
Направление: На основании следующих цифр и данной таблицы видно, какое количество квадратов образуется по количеству точек. ? и так далее. ? и так далее.
How many squares are formed к 49точки? А) 25 Б) 36 В) 49 Г) 64 Посмотреть решение play_arrowвопрос_ответ 28) Соблюдая следующие операции умножения, найдите произведение \[707\умножить на 707. А) 499864 Б) 494949 В) 499849 Г) 499649 Посмотреть решение play_arrowвопрос_ответ 29) Определите произведение \[\text{15}\times \text{31}\times \text{78}\], округлив каждое число до ближайших десяти. А) 24000 Б) 48000 В) 42000 Г) 21000 Посмотреть решение play_arrowвопрос_ответ 30) Чему равно произведение разрядов числа «5», как показано на счетах? А) 50000 Б) 25000 В) 250000 Г) 500000 Посмотреть решение play_arrowвопрос_ответ 31) Сколько минут было в феврале 2004 года? А) \[\text{28}\times \text{24}\times \text{6}0\] B) \[30\умножить на 24\умножить на 60\] C) \[\text{31}\times \text{24}\times \text{6}0\] D) \[\text{29}\times \text{24}\times \text{6}0\] Посмотреть решение play_arrowвопрос_ответ 32) Панду и Рагху написали два двузначных числа, каждое из которых имеет цифру 7 только один раз и в указанном месте.
А) 990 Б) 6790 В) 6887 Г) 7663 Посмотреть решение play_arrowquestion_answer 33) Найдите произведение чисел, изображенных на счетах с шипами. А) 26838 Б) 27838 C) 24938 D) 26848 Посмотреть решение play_arrowвопрос_ответ 34) Фабрика производит 1617 пар обуви в неделю. Сколько обуви она производит в день? А) 2301 Б) 231 В) 16175 Г) 230 Посмотреть решение play_arrowвопрос_ответ 35) Произведение двух чисел равно 476. А) 104 Б) 14 В) 24 Г) 442 Посмотреть решение play_arrowвопрос_ответ 36) Если 5 транзисторов стоят рупий. 1525, найдите стоимость каждого транзистора. А) рупий. 350 B) рупий. 35 C) рупий. 305 D) рупий. 303 Посмотреть решение play_arrowвопрос_ответ 37) Мадху разделил 3250 на 18 и получил частное 179 и остаток от 28. A) Проверить, если частное \[\times \] Делитель Остаток = Делимое, B) Проверьте его расчеты \[\text{18}\times \text{1},\text{18}\times \text{7}\] и \[\text{18}\times \ текст{9}\]. C) Проверить, если остаток < делимого. D) Проверить, равен ли остаток делителю. Посмотреть решение play_arrowquestion_answer 38) Изучите предложения с заданным числом. Если эти числовые предложения верны, что из следующего может быть правильным? A)
B)
C)
D) Посмотреть решение play_arrow question_answer 39) Точная стоимость доллара по отношению к индийской рупии меняется изо дня в день. А) 8 Б) 9 В) 10 Г) 12 Посмотреть решение play_arrowвопрос_ответ 40) Мурали расположил несколько шариков, как показано на рисунке. Какой из следующих фактов деления лучше всего представлен группировкой шариков? (Необходимо учитывать все шарики) A) \[\text{21}\div \text{5}\] дает частное 4 и остаток 1 B) \[\text{21}\div \text{7}\] дает частное 3 C) \[\text{2}0\div \text{5}\] дает частное 4 D) \[\text{5}\div \text{4}\] дает частное 1 и остаток 1 Посмотреть решение play_arrowвопрос_ответ 41) Если обозначает 30, что будет означать? А) 6 Б) 10 C) 12 Г) 26 Посмотреть решение play_arrowвопрос_ответ 42) Какая пара вычислений дает два разных ответа? А) \[(\text{16}+\text{9})\] и \[(\text{9}+\text{16})\] B) \[(\text{9}\div \text{3})\] и \[(\text{3}\div \text{9})\] C) \[(\text{7}\times \text{3})\] и \[(\text{3}\times \text{7})\] D) \[(\text{5}+\text{4}+\text{11})\]и\[(\text{4}+\text{11}+\text{5} )\] Посмотреть решение play_arrowвопрос_ответ 43) 10 учеников посадили 530 саженцев. A) \[\text{53}0\div \text{1}0\] B) \[\text{53}0\times \text{1}0\] C) \[\text{53}0-\text{1}0\] D) \[\text{53}0+\text{1}0\] Посмотреть решение play_arrowвопрос_ответ 44) Если Каково значение \[\text{777 }\div \text{21}\] ? А) 12 Б) 17 В) 27 Г) 37 Посмотреть решение play_arrowquestion_answer 45) Приведенный на рисунке кувшин можно заполнить наполовину, налив в него 5 полных стаканов молока из мерного стакана. A) \[\text{100 mZ}\] B) \[\text{125 mZ}\] C) \[~\text{2}00\text{ mZ}\] D) \[\text{25}0\text{ mZ}\] Посмотреть решение play_arrowвопрос_ответ 46) Найдите пропущенный термин в следующем квадрате. ____
А) 7 Б) 9 В) 11 Г) 13 Посмотреть решение play_arrowвопрос_ответ 47) Каково значение \[\text{13}+\text{6}-\text{2}+\text{5}\times \text{4}\]? А) 36 Б) 45 В) 25 Г) 28 Посмотреть решение play_arrowвопрос_ответ 48) Какое из следующих утверждений верно при делении числа на 100? A) Частное получается удалением цифры единиц. B) Частное получается удалением цифры десятков. C) Частное получается удалением десятков и единиц. D) Частное – это цифра единиц. Посмотреть решение play_arrowquestion_answer 49) Учитель приносит пакет с мелками, чтобы раздать их классу из 30 детей. Если она планирует дать каждому ребенку по 1 набору из 8 мелков и у нее нет лишних мелков, то сколько мелков должно быть в сумке? А) 38 Б) 240 В) 39 Г) 30 Посмотреть решение play_arrowquestion_answer 50) Дана рассадка учащихся в классе, где каждый ящик соответствует одному стулу. A) Занято на два стула больше, чем пусто. B) Девять стульев заняты. C) Количество занятых стульев = (Количество свободных стульев-\[\div 2\]) + 3 D) У каждого ученика рядом с ним сидит партнер. Посмотреть решение play_arrowвопрос_ответ 51) Соблюдайте заданную закономерность.
A) Поделите 64 на 2. B) Умножьте 64 на 2. C) Добавьте 2 к 64. D) Поделите 64 на 16. Посмотреть решение play_arrowвопрос_ответ 52) Каково значение \[\text{(abab) }\!\!\div\!\!\text{ ab?}\] ? Если ab представляет любое двузначное число. А) 101 Б) 11 В) 10 D) 1001 Посмотреть решение play_arrowвопрос_ответ 53) На следующем рисунке каждое число в левом овале имеет определенную простую связь со своей парой в правом овале. А) 11 Б) 13 В) 17 D) 26 Посмотреть решение play_arrowвопрос_ответ 54) Найдите частное деления чисел, представленных данными счетами. А) 112 Б) 132 В) 142 D) 122 Посмотреть решение play_arrowвопрос_ответ 55) Каждое выражение в поле имеет одинаковое значение.
A) \[\text{72}-\text{12}\] B) \[\text{72}-\text{9}\] C) \[~\text{72}-\text{8}\] D) \[\text{72}-\text{6}\] Посмотреть решение play_arrowвопрос_ответ 56) Птица летит n км в одну сторону. Какое из следующих выражений показывает 2 поездки туда и обратно? (Помните, что поездка туда и обратно – это поездка до места и обратно. A) \[\text{(4}-\text{n) км}\] B) \[(\text{2}-\text{n) км}\] C) \[\text{(2n) км}\] D) \[\text{(4n) км}\] Посмотреть решение play_arrowвопрос_ответ 57) Каждая буква от A до F соответствует данным цифрам соответственно.
A) \[\text{(C }\!\!\times\!\!\text{ D) + E}\] B) \[\text{(C }\!\!\times\!\!\text{ C) + F}\] C) \[\text{(C }\!\!\times\!\!\text{ D) + B}\] D) \[\text{D }\!\!\times\!\!\text{ E}\] Посмотреть решение play_arrowquestion_answer 58) В сумке 12 книг. А) 12 Б) 13 В) 24 Г) 36 Посмотреть решение play_arrowвопрос_ответ 59) Показанная числовая машина использует правило для замены каждого введенного в нее числа другим числом. Каждый раз используется одно и то же правило. В приведенной таблице показаны результаты, когда в числовую машину были введены три различных числа.
А) 1 Б) 2 В) 3 Г) 4 Посмотреть решение play_arrowЭффективные стратегии обучения многозначному умножению Многозначное умножение — сложная концепция для обучения. В качестве альтернативы, если вы ищете ресурс, где вся работа выполняется за вас, вас может заинтересовать эта Станция многозначного умножения, где учащиеся работают с различными стратегиями в своем собственном темпе, осваивая каждую из них по мере они идут. Стратегии интегрированы стратегическим образом, гарантируя, что учащиеся постепенно наращивают свое понимание. См. Станцию многозначного умножения ЗДЕСЬ.
Итак, с чего начать обучение многозначному умножению? Важно начать со стратегий, которые помогут учащимся решать многозначные уравнения в уме.
1. Коммутативные и ассоциативные свойства . В первую очередь важно, чтобы учащиеся запомнили эти свойства. Свойство коммутативности утверждает, что порядок множителей не меняет произведения. Например, 4 × 3 и 3 × 4 равны 12. Ассоциативное свойство утверждает, что факторы могут быть сгруппированы по-разному. Например, (7×2)x5 дает тот же результат, что и (2×5)x7. Эти свойства помогают учащимся понять, что они могут манипулировать уравнениями, чтобы упростить их решение. 2. Использование коэффициентов. Это отличный способ научить учащихся тому, что числами можно манипулировать, чтобы упростить решение уравнения. Когда мы учим многозначному умножению, наша цель не всегда состоит в том, чтобы как можно быстрее получить правильный ответ. Иногда наша цель состоит в том, чтобы уметь мыслить творчески, когда дело доходит до числа. 3. Умножение на 10, 100 и 1000, а также кратное 10, 100 и 1000. аккуратно, по частям. Когда вы обучаете этой концепции, важно сосредоточиться на правилах разрядности, прежде чем обучать таким приемам, как прием «добавление нулей». Например, когда учащиеся сталкиваются с уравнением 45×100, они должны понимать, что разрядные значения увеличиваются на 2 разряда, чтобы получилось 4500. Точно так же при умножении уравнения типа 3×1000 разрядные значения увеличиваются на 3. мест, чтобы получить 3000. После того, как учащиеся усвоили эту концепцию, мы можем научить их тому, что когда в множителях есть 2 нуля, мы добавляем 2 нуля к произведению. Имейте в виду, что этим трюкам следует обучать только ПОСЛЕ того, как ученики отлично разбираются в математике, лежащей в основе концепции. 4. Разделение чисел. Это одна из самых полезных математических стратегий в уме. Он включает в себя разбиение одного из факторов, умножение на группы, а затем сложение этих групп вместе. Вот пример: в этом примере мы разбиваем 12 на 10 и 2, а затем умножаем на части. Таким образом, 12×30 становится (10×30) + (2×30). Это гораздо проще решить! Мы также можем использовать эту стратегию для умножения больших чисел, например 103×9. Мы можем разбить 103 на 100 и 3, а затем умножить по частям, например так: (100×9) + (3×9). 5. Метод окна/окна. Мне нравится метод «ящик/окно», потому что он использует расширенную форму каждого фактора, что делает его отличной стратегией для закрепления концепций восприятия чисел. Чтобы использовать эту стратегию, мы рисуем прямоугольник (количество столбцов и строк зависит от количества цифр в факторах), а затем записываем развернутые формы факторов сверху и сбоку. Затем мы умножаем каждую часть и складываем части вместе, когда закончим. 6. Частичные продукты. Это одна из самых важных стратегий обучения в качестве альтернативы длинному умножению. В частичных произведениях уравнение настроено так же, как и в традиционном длинном умножении, но способ умножения отличается. Например, для уравнения 35×3 мы сначала умножаем 3×5, чтобы получить 15. Затем мы умножаем 3×30, чтобы получить 90. Обратите внимание, что мы умножаем на ТРИДЦАТЬ, а не на три. Это потому, что 3 представляет 30. Это дает нам 90. Теперь мы складываем 15 и 9.0 вместе, чтобы получить 105. Если вам нужен более подробный учебник по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок. Стратегии, которые я изложил выше, являются НАИБОЛЕЕ важными для обучения многозначному умножению. Все эти стратегии делают упор на понимание чисел и гарантируют, что учащиеся действительно понимают, что означают числа в каждом уравнении. Это спорная тема. Некоторые учителя считают, что наше обучение должно быть сосредоточено ТОЛЬКО на чувстве числа, поэтому мы не обучаем стратегиям, которые не фокусируются на понимании числа. Эти учителя, как правило, используют такие стратегии, как частичные произведения, в течение всего года как очень эффективную альтернативу традиционному длинному умножению. Другие учителя считают, что мы должны учить так, как много лет назад учили умножению. Тогда это работало, так почему бы не работать сейчас?! Эти учителя, как правило, больше сосредотачиваются на стратегиях, таких как традиционное длинное умножение, и меньше на более современных методах, таких как ящик/окно или частичные произведения.
Я здесь не для того, чтобы говорить вам, какой способ лучше 🙂 Это зависит от вас и ваших учеников. Тем не менее, я скажу вам свое личное убеждение. Лично я склонен не впадать ни в одну крайность. Я большой сторонник стратегий, которые способствуют пониманию числа. Следующие стратегии в меньшей степени ориентированы на числовое восприятие, но они могут стать интересным способом умножения для тех учащихся, которые готовы к испытаниям.
8 раз (8x) Генератор рабочих листов таблицы умноженияПримечание. Эта страница содержит устаревшие ресурсы, которые больше не поддерживаются. Вы можете продолжать использовать эти материалы, но мы можем поддерживать только наши текущие рабочие листы, доступные как часть нашего членского предложения. Приведенный выше ресурс умножения и деления соответствует (полностью или частично) стандарту 3OA07, взятому из Общего базового стандарта по математике (см. отрывок ниже). Различные ресурсы, перечисленные ниже, соответствуют одному стандарту. Свободно умножайте и делите в пределах 100, используя такие стратегии, как отношение между умножением и делением (например, зная, что 8 x 5 = 40, известно, что 40 ÷ 5 = 8) или свойства операций. ЗанятиеКарточки
ТаблицаТаблицы умножения
Таблицы умножения
Пример/рекомендация
Флэш-карта
Карточки
ИграИгры Build The Answer
Игра «Угадай число»
Целевая игра
Числовая строка
ГоловоломкаКроссворд
Ящики умножения
Квадраты умножения
Таблица
Таблицы делений
|
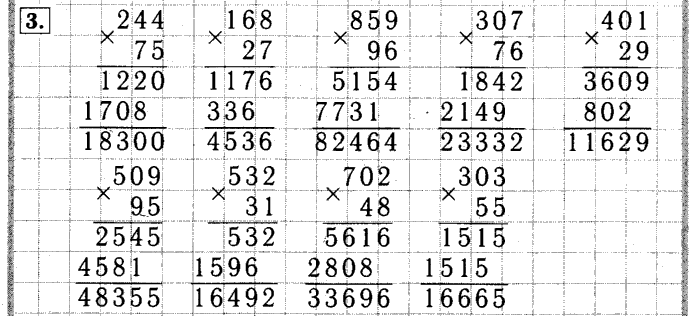 Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами.
Окончательный результат будет получен путем объединения промежуточных значений и соотнесения неполных произведений с разрядами. 0040
0040 ? и так далее.
? и так далее. \]
\] 

 Если одно число равно 34, то какое другое число?
Если одно число равно 34, то какое другое число? Какая из этих проверок поможет Мадху обнаружить его ошибки?
Какая из этих проверок поможет Мадху обнаружить его ошибки? В определенный день руб. 288 стоил 6 долларов. Сколько долларов будет рупий. 480 стоили в тот день?
В определенный день руб. 288 стоил 6 долларов. Сколько долларов будет рупий. 480 стоили в тот день? Если каждый ученик посадил одинаковое количество саженцев, сколько саженцев посадил каждый ученик?
Если каждый ученик посадил одинаковое количество саженцев, сколько саженцев посадил каждый ученик? Сколько молока вмещает полная чашка?
Сколько молока вмещает полная чашка?
 Стулья с крестиком заняты. Что из этого верно?
Стулья с крестиком заняты. Что из этого верно?
 На основе соотношения найдите пропущенное число.
На основе соотношения найдите пропущенное число.
 )
)  Сколько пакетов нужно для 144 книг?
Сколько пакетов нужно для 144 книг?
 Давно прошли те времена, когда мы обучали одному методу, такому как длинное умножение, и просто *надеялись*, что все наши ученики поймут и смогут эффективно использовать этот метод. Сегодня мы знаем, как важно обучать многозначному умножению более стратегически. Это гарантирует, что каждый ученик в вашем классе сможет добиться успеха в той или иной степени. Это также гарантирует, что знания учащихся построены на стратегической основе и что они действительно ПОНИМАЮТ процесс многозначного умножения.
Давно прошли те времена, когда мы обучали одному методу, такому как длинное умножение, и просто *надеялись*, что все наши ученики поймут и смогут эффективно использовать этот метод. Сегодня мы знаем, как важно обучать многозначному умножению более стратегически. Это гарантирует, что каждый ученик в вашем классе сможет добиться успеха в той или иной степени. Это также гарантирует, что знания учащихся построены на стратегической основе и что они действительно ПОНИМАЮТ процесс многозначного умножения. Вместо того, чтобы сразу переходить к длинному умножению или эффективной альтернативе, начните со следующего:
Вместо того, чтобы сразу переходить к длинному умножению или эффективной альтернативе, начните со следующего: Это один из таких случаев. Мы могли бы взять уравнение 4×15 и разбить 15 на его множители, 3 и 5. Теперь у нас есть это уравнение: 4×3×5. Теперь мы можем решить это так: (4×3)x5 -> 12×5 -> 60. Это просто для того, чтобы показать, что существует не только один правильный способ решения этого уравнения.
Это один из таких случаев. Мы могли бы взять уравнение 4×15 и разбить 15 на его множители, 3 и 5. Теперь у нас есть это уравнение: 4×3×5. Теперь мы можем решить это так: (4×3)x5 -> 12×5 -> 60. Это просто для того, чтобы показать, что существует не только один правильный способ решения этого уравнения.
 Если вам нужно более подробное руководство по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок.
Если вам нужно более подробное руководство по этой стратегии, см. ЭТО сообщение в блоге, которое также включает видеоурок. Но как насчет таких стратегий, как традиционное длинное умножение?
Но как насчет таких стратегий, как традиционное длинное умножение? Однако я также считаю, что для НЕКОТОРЫХ ваших учеников есть место традиционным методам. Вам придется быть судьей здесь. Если у вас есть ученики, которые борются с многозначным умножением, вы, вероятно, решите, чтобы они сосредоточились на частичных произведениях и коробках/окнах, и остановитесь на этом. Зачем добавлять еще больше путаницы? Они могут быть очень успешными с этими стратегиями. ОДНАКО, у вас могут быть ученики, которые отлично понимают то, чему вы учили до сих пор, и готовы к более сложной задаче! Эти учащиеся могут преуспеть в других, менее ориентированных на числа методах, поскольку они уже хорошо разбираются в математических концепциях. Для этих студентов я собираюсь рассказать о нескольких других стратегиях.
Однако я также считаю, что для НЕКОТОРЫХ ваших учеников есть место традиционным методам. Вам придется быть судьей здесь. Если у вас есть ученики, которые борются с многозначным умножением, вы, вероятно, решите, чтобы они сосредоточились на частичных произведениях и коробках/окнах, и остановитесь на этом. Зачем добавлять еще больше путаницы? Они могут быть очень успешными с этими стратегиями. ОДНАКО, у вас могут быть ученики, которые отлично понимают то, чему вы учили до сих пор, и готовы к более сложной задаче! Эти учащиеся могут преуспеть в других, менее ориентированных на числа методах, поскольку они уже хорошо разбираются в математических концепциях. Для этих студентов я собираюсь рассказать о нескольких других стратегиях. Некоторые учителя считают, что учащимся, использующим этот метод, легче переносить числа, потому что числа расположены диагональными рядами, поэтому легче увидеть, где их нужно добавить. Объяснение этой стратегии требует некоторого времени, поэтому, пожалуйста, просмотрите ЭТУ запись в блоге, которая также включает видеоурок по стратегии.
Некоторые учителя считают, что учащимся, использующим этот метод, легче переносить числа, потому что числа расположены диагональными рядами, поэтому легче увидеть, где их нужно добавить. Объяснение этой стратегии требует некоторого времени, поэтому, пожалуйста, просмотрите ЭТУ запись в блоге, которая также включает видеоурок по стратегии.
 К концу 3 класса знать наизусть все произведения двух однозначных чисел.
К концу 3 класса знать наизусть все произведения двух однозначных чисел.  1 x 1 до 12 x 12
1 x 1 до 12 x 12 45) x 9)
45) x 9)