Комплект карточек (10) «Обучающий калейдоскоп. Сложение и вычитание в пределах 10»

Навигация:Главная›Для школ›Учебно-наглядные пособия и оборудование›Начальная школа›Математика›Раздаточные пособия›Комплект карточек (10) «Обучающий калейдоскоп. Сложение и вычитание в пределах 10»

В избранномВ избранное Артикул: 10685 Цена: предоставляется по запросу Задать вопрос по оборудованию

Назначение  Комплект карточек предназначен для использования на уроках математики в начальной школе. Учитель может использовать карточки в качестве основного вида деятельности на уроке, а также во внеурочной деятельности, в группах продленного дня и математических кружках. Используется вместе с наглядно-дидактическим пособием «Обучающий калейдоскоп»  Технические характеристики и комплектность  Габаритные размеры в упаковке (дл. *шир.*выс.), см 14*28*1 Вес, кг, не более 0,2 В комплект входят: карточки с заданиями 10 шт. руководство по эксплуатации 1 шт. 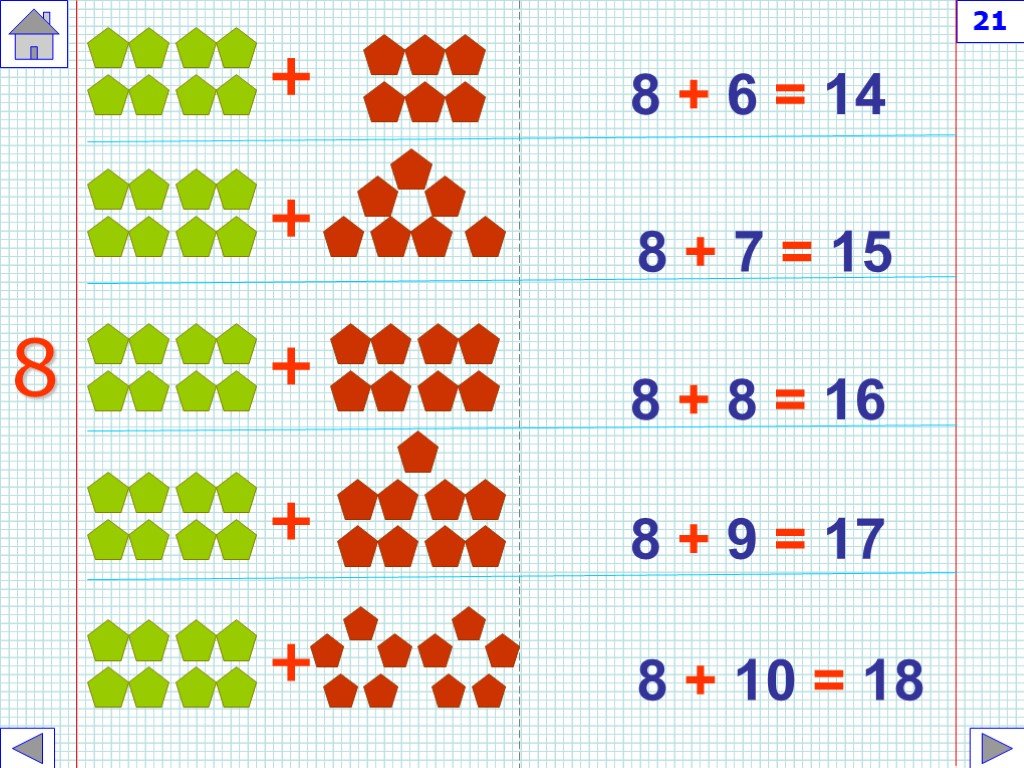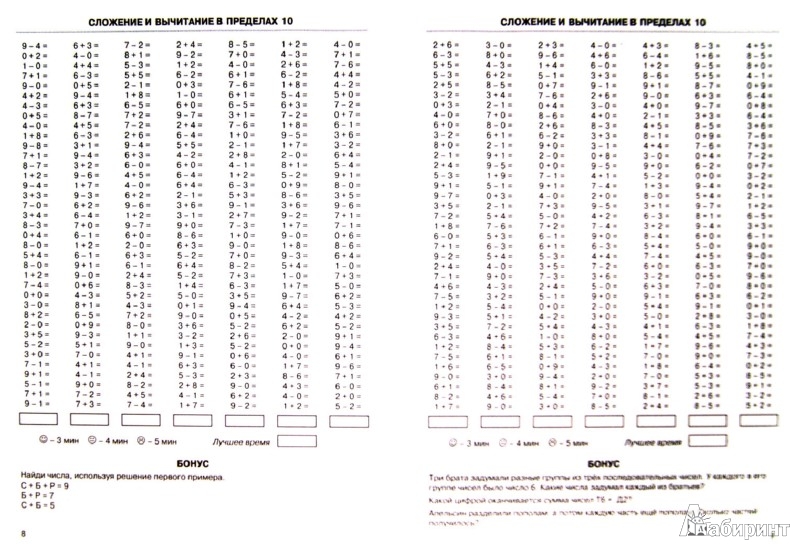Пособие состоит из 10 полноцветных, напечатанных на картоне и ламинированных пленкой карточек. Карточки снабжены маркировкой, где буква обозначает предмет, первая цифра – код темы, вторая цифра – порядковый номер (тему) карточки в серии, последняя цифра – вариант (I или II). М2.1.I, М2.1.II. Состав числа первого десятка в схемах, где число представлено двумя слагаемыми, одно из которых неизвестно. Учитель может предложить учащимся самим сформулировать задание: «Из каких двух слагаемых состоит число 9, если одно из них 3?» и записать в тетрадь эти схемы в виде примеров. М2.2.I .  Формируется умение понимать смысл выражений «уменьши на …». При работе с данными карточками рекомендуется записать математи-ческие выражения в тетрадь. М2.2.II. Формируется умение понимать математические действия сло-жения и вычитания, выраженные словами. Закрепляются понятия «слагаемое», «уменьшаемое», «вычитаемое», «сумма», «разность», навыки сложения и вычитания в пределах 10.  Рекомендуется использовать карточку для устных вычислений. Можно использовать в качестве проверочной работы. М2.3.I. Задачи в картинках. Учат сложению и вычитанию в пределах 10, пониманию условий задач и математических действий, обозначенных словами «съели», «добавили», «принесли», «разбили» и т.д. М2.3.II. Решение задач. Формируется умение понимать условия задач, решать простые задачи на сложение и вычитание в пределах 10. Возможно как устное, так и письменное решение данных задач. М2.4.I, М2.4.II. Простые примеры на сложение и вычитание в пределах 10. Формируется представление о последовательности действий. М2.5.I, М2.5.II. Измерение длины отрезка в сантиметрах линейкой. Знакомство учащихся с обозначением отрезков, буквами, которыми могут обозначаться отрезки. Закрепляется навык сложения и вычитания в пределах 10. Рекомендуется записывать длины отрезков в тетрадь. ← Назад

Инженерные классы

Образовательные робототехнические модули

WS Junior — Мехатроника Festo

Учебно-наглядные пособия и оборудование

• Анатомия
• Биология
• География
• ИЗО, МХК
• Иностранный язык
• История
• Литература
• Математика
• Начальная школа
• НВП
• ОБЖ
• Русский язык
• Труд
• Физика
• Химия
• Музыка
• Черчение
• Астрономия
• Информатика
• Физическая культура

Точки роста

Мультимедийное оборудование

3D Принтеры

Учебное оборудование Phywe.

Учебные лаборатории ФГОС.

Инновационное оборудование. Переносные лаборатории

Инновационное оборудование. Цифровые учебные лаборатории

Национальный проект «Образование»

Сложение и вычитание в пределах

Главная » Ментальная Арифметика

15.04.202113.09.2017

Сложение и вычитание в пределах 10.

При вычислениях вспоминай  состав числа.
4+2.  4 и 2 это 6. Значит 4+2=6
5-3.  5 состоит из 3 и 2. Если вычислить 3. То остается 2.
Значит, 5-3-2.

Примеры:

Сложение и вычитание в пределах 20 (без перехода через десяток)

13  + 4. Число 13 раскладываю на сумму разрядных слагаемых  10 и 3. Единицы   складываю  с   единицами:   3  +  4   =   7. Потом к  10 прибавляю  7,  получаю  17.  Значит,   13   +  4  =  17.

13  —  2.   Число   13   раскладываю   на  сумму   разрядных  слагаемых 10  и  3.   Единицы   вычитаю   из   единиц:   3-2 = 1.   Потом к  10 прибавляю 1.  Значит, 13   — 2  =   11.

Примеры:

Сложение и вычитание в пределах 20 (с переходом через десяток)

6 + 5, Удобнее прибавлять к круглому числу (к 10). Число 5 раскладываю на сумму удобных слагаемых, так, чтобы 6 до­полнить до 10. Потом прибавляю остальное. 6 + 5 = 6 + (4 + 1) = = (6 + 4) + 1 = 10 + 1 = 11. Значит, 6+5=11.

13-5. Удобнее вычитать из круглого числа (из 10), Число 5 раскладываю на сумму удобных слагаемых, так, чтобы 13 уменьшить до 10. Потом вычитаю остальное, 13 — 5 = 13 -(3 + 2) = (13 — 3) — 2 =  10 — 2 = 8. Значит,   13-5-8.

Примеры:

Сложение и вычитание типа 10 + 7, 17 — 7, 15 — 10

10 + 7. Если к 1 десятку прибавить 7 единиц, то получится число, состоящее из I десятка и 7 единиц, то есть число 17. Значит, 10 + 7 = 17.

15 — 10. Число 15 раскладываю на сумму разрядных сла­гаемых 10 и 5. Десятки вычитаю из десятков: 10 — 10 = 0. Осталось 5 единиц. 15 — 10 — (10 + 5) — 10 = (10 — 10) + 5 = 5. Значит. 15-10=5

17-7. Число 17 раскладываю на сумму разрядных слагае­мых 10 и 7. Единицы вычитаю из единиц: 7-7 =0. Остался 1 десяток. 17 — 7 = (10 + 7) — 7 = 10 + (7 — 7) = 10 + 0 -10. Значит. 17 — 7 = 10

Примеры:

Сложение и вычитание типа 36 + 3, 53 — 2

36 + 3. Число 36 раскладываю на сумму разрядных слагаемых 30 и 6. Единицы складываю с единицами: 6 + 3 = 9. Потом к 30 прибавляю 9, получаю 39. Значит, 36 + 3=39.

53-2. Число 53 раскладываю на сумму разрядных слагае­мых 50 и 3. Единицы вычитаю из единиц: 3 — 2 = 1. Потом к 50 прибавляю   I, получаю 51. Значит,   53   — 2 = 51

Примеры:

Вычитание типа 60-2.

Число 60 складываем на сумму удобных слагаемых 50  и 10. Удобнее вычислять 2 из 10, и полученный результат, 8, прибавить  к 50. 60-2=(50+10) -2=50 +(10- 2)= 50 +8 =58. Значит 60 -2= 58.

Примеры:

Сложение и вычитание типа 65 + 1, 65 — 1
65 + 1 Прибавить 1 — значит, назвать следующее число. За числом 65 стоит число 66. Следовательно, 65 + 1 » 66 65-1.

Вычесть 1 — значит назвать предыдущее число. Перед числом 65 стоит число 64. Следовательно. 65 — 1 =64

Примеры:

Сложение и  вычитание типа 20 + 6, 26 — 20, 26-6.

20 + 6. Если к 2 десяткам прибавить 6 единиц, то получится число, состоящее из 2 десятков и 6 единиц, то есть число 26.  Значит,  20  +  6  =  26.

26 — 20. Число 26 раскладываю на сумму разрядных слагаемых 20 и 6. Десятки вычитаю из десятков: 20 — 20 = 0.Осталось 6 единиц.  Значит,  26 —  20 = 6.

26  —  6.  Число 26 раскладываю на сумму разрядных слагаемых 20   и  6,   Единицы  вычитаю   из   единиц:   6-6 =   0,   Осталось  2 десятка,  26  — 6 = (20   + 6)  — 6 = 20  + (6 — 6) = 20  + 0  = 20. Значит,  26  —  6 «  20.

Примеры:

Скачать задания- математический счет.

Вычитание сложением (метод дополнений)

(также называется методом дополнений)

Здесь мы видим, как выполнять вычитание с помощью сложения!

(Я не рекомендую это для обычной работы с вычитанием, но это все еще допустимый и интересный способ вычитания.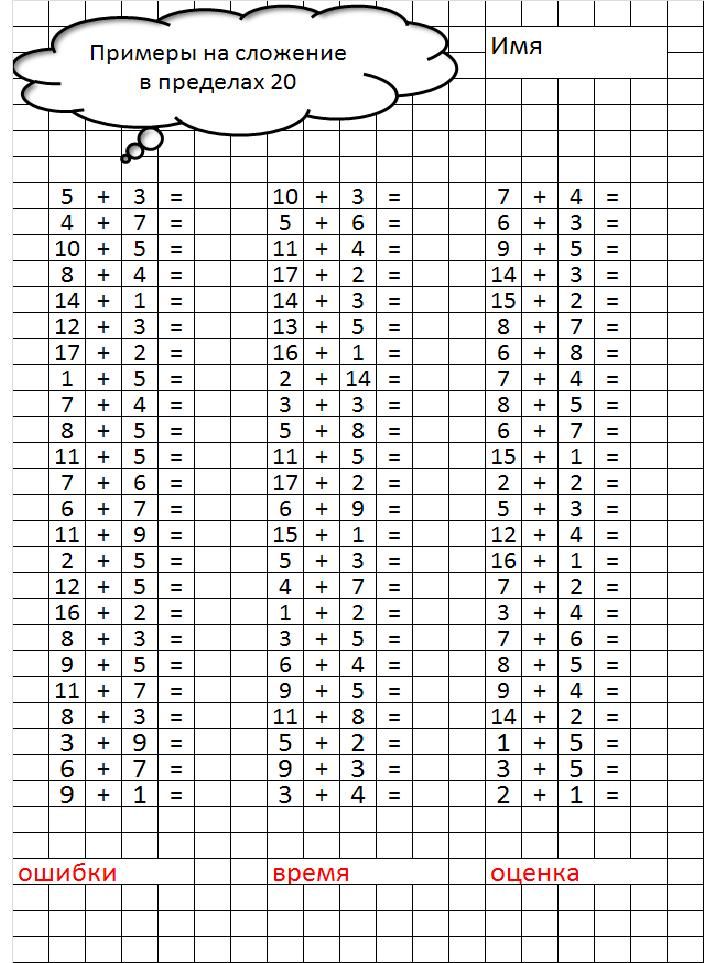 И в некоторых случаях он может сэкономить время.)

Шаги

Выполните следующие шаги:

• возьмите « дополнение » числа, которое мы вычитаем из (посмотрим как скоро)
• прибавьте к числу, которое мы вычитаем из
• отбросить лишнюю «1» слева

Дополнение

«Дополнение» — это число , к которому нужно добавить , чтобы получить 10 (или 100, 1000 и т. д., в зависимости от того, сколько у нас цифр) 7=10 (мы добавляем 7 , чтобы получить 10)

Пример: дополнение 85 равно 15 , потому что 85+15=100

Пример: дополнение числа 111 равно 889 , потому что 111+889=1000

Вычисление дополнения

Дополнение легко найти!

Основная идея состоит в том, чтобы найти разность между каждой цифрой и 9 . Это приведет нас к «999…», так что нам нужно только добавить 1, чтобы получить «1000…»

На практике легко следовать этому методу:

• Начните с «единиц» позиция
• Пропустить любые нули
• Тогда:

Для первой цифры , отличной от нуля:		найти, что делает его 10
Для все остальные цифры :		найти, что делает его 9

Вот два примера:

(Вы можете проверить, работает ли это, добавив число и его дополнение, 9Например, 0102

372+628=1000 )

С небольшим опытом «что прибавляется к 10» или «что прибавляется к 9» становится автоматическим, и получение дополнения становится быстрым и легким.

Вот еще один пример, где мы должны пропустить некоторые нули:

Пример: Каково дополнение 1700 ?

• Пропустить два нуля
• Дополнение «10» к 7 равно 3 ,
• Дополнение «9» к 1 равно 8 ,

Итак, ответ:

8300

(Проверьте: 1700+8300 = 10000 )

Теперь добавьте их!

Теперь добавьте два числа (используя сложение столбцов), но не забудьте отбросить лишнюю «1» слева.

Вот 3 шага ( дополнить , добавить , отбросить ):

И мы нашли, что 653 − 372 = 281 (проверьте, если хотите!)

Что, если число, которое мы вычитаем имеет меньше цифр?

Как мы можем, например, сделать 4567 − 56 ?

После взятия дополнения мы просто заполняем все недостающие места девятками.

Пример: 4567 − 56

Что ж, дополнение 56 равно 44 , но нам нужно «дополнить его» до 4 цифр, чтобы получилось 9944. Теперь мы складываем их:

 4567
+9944

2

2 14511

Затем отбросьте лишнюю «1» слева, и ответ будет таким:

4511

В этом случае было бы проще использовать быстрое вычитание, но оно показывает, как это « дополнить , добавить , отбросить «метод работает.

Теперь вы можете попрактиковаться с этими таблицами вычитания. меньшие числа в простой форме представления Любое число может быть представлено в этой научной нотации таким образом, что число находится между 1 (один) и 10 (десять) и умножается на степень 10.

Пример: 7200000 (72 лакха) может быть представлен в научной форме как 7,2 × 10 ⁶

Здесь 7200000 представлен как 7,2, умноженные на 10 до мощности 6.

9

20000.

Мы можем выполнить сложение между двумя или более числами, представленными в экспоненциальном представлении. Чтобы объяснить, как выполнить сложение в экспоненциальном представлении, рассмотрим пример

2 × 10 ² + 3 × 10 ²

Прежде чем приступить к решению вышеуказанной задачи, спросите себя, каков результат 2t+3t?

Ответ 5t, потому что в этих двух числах есть одна и та же переменная «t», поэтому мы добавляем коэффициент двух чисел, то есть 2,3, и добавляем к результату переменную «t».

Здесь также при выполнении сложения нужно проверить, одинакова ли степень числа 10 или нет.

Шаг 1: Здесь степень 10 для обоих чисел одинакова, т. е. 2. Если степени 10 одинаковы, то сразу переходите к Шагу 3, пропустив Шаг 2

Шаг 2: Если степени 10 не совпадают, преобразуйте число так, чтобы степени 10 двух чисел стали одинаковыми.

Шаг 3: Просто добавьте коэффициенты и степени.

2+3 = 5 × 10 ²

Чтобы получить больше информации об этом дополнении, давайте рассмотрим несколько примеров.

Пример 1. Выполните сложение между 4 × 10 ³ и 5 × 10 ² .

Решение:

4 × 10 ³ + 5 × 10 ²

Шаг 1: Здесь степени 10 для двух чисел не совпадают. Поэтому нам нужно преобразовать эти силы в одинаковые, либо увеличив одну, либо уменьшив другую.

Шаг 2: Здесь мы увеличиваем степень второго числа, уменьшая коэффициент.

5 × 10 ² можно преобразовать в 0,5 × 10 ³

Шаг 3: Поскольку степени 10 для двух чисел одинаковы, теперь мы можем добавить часть коэффициента, чтобы получить результат.

4 × 10 ³ + 0,5 × 10 ³ = 4,5 × 10 ³

9

Пример 2: Выступление 2:

9

. ×   10 ⁵ .

Решение:

11 × 10 ² + 5 × 10 ⁵

Шаг 1: Здесь степени 10 не совпадают. Поэтому нам нужно преобразовать эти силы в одинаковые, либо увеличив одну, либо уменьшив другую.

Шаг 2: Здесь мы увеличиваем степень первого числа с 2 до 5, уменьшая коэффициент.

11 × 10 ² => 1,1 × 10 ³ => 0,11 × 10 ⁴ => 0,011 × 10 ⁵

11 × 10 ² можно обратиться к 0,01111111111111111195 ² .

Шаг 3: Поскольку степени 10 для двух чисел одинаковы, теперь мы можем добавить часть коэффициента, чтобы получить результат.

0,011 × 10 ⁵ + 5 × 10 ⁵ = 5,011 ×   10 ⁵

Вычитание в научной нотации

при выполнении сложения.

Рассмотрим несколько примеров

Пример 1. Вычитание между 5 ×   10 ³ и 2 ×   10 ³ .

Решение:

5 × 10 ³ – 2 × 10 ³

Шаг 1: Здесь две степени числа 10 равны. Таким образом, мы можем пропустить часть шага 2 и перейти к шагу 3 и выполнить вычитание между коэффициентами.

Шаг 2: Равные степени 10, если не равны.

Шаг 3: Поскольку степени 10 для двух чисел одинаковы, нет, мы можем вычесть части коэффициента, чтобы получить результат.

5 × 10 ³ — 2 × 10 ³ = 3 × 10 ³

Пример 2: Найти ценность

. Пример 2: Найти ценность

. 2 ×   10 ²

Решение:

Шаг 1: Здесь степени 10 для двух чисел не совпадают. Итак, нам нужно увеличить/уменьшить степень числа 10 так, чтобы обе степени были равны.

Шаг 2: Здесь мы уменьшаем степень первого числа, представленного в научном представлении, от степени 3 до степени 2 путем увеличения коэффициента.

1 × 10 ³ => 10 × 10 ²

Шаг 3: Поскольку степени 10 для двух чисел одинаковы, мы можем вычесть коэффициенты, чтобы получить результат.