Карточки на умножение столбиком трёхзначных чисел | Материал по математике (3 класс):
Дидактический материал
по математике к учебнику Л.Г. Петерсон
3 класс
Учитель начальных классов
МБОУ Гимназия им. А.И.Яковлева:
Мерц Н.В.
Г.Урай
2019 г.
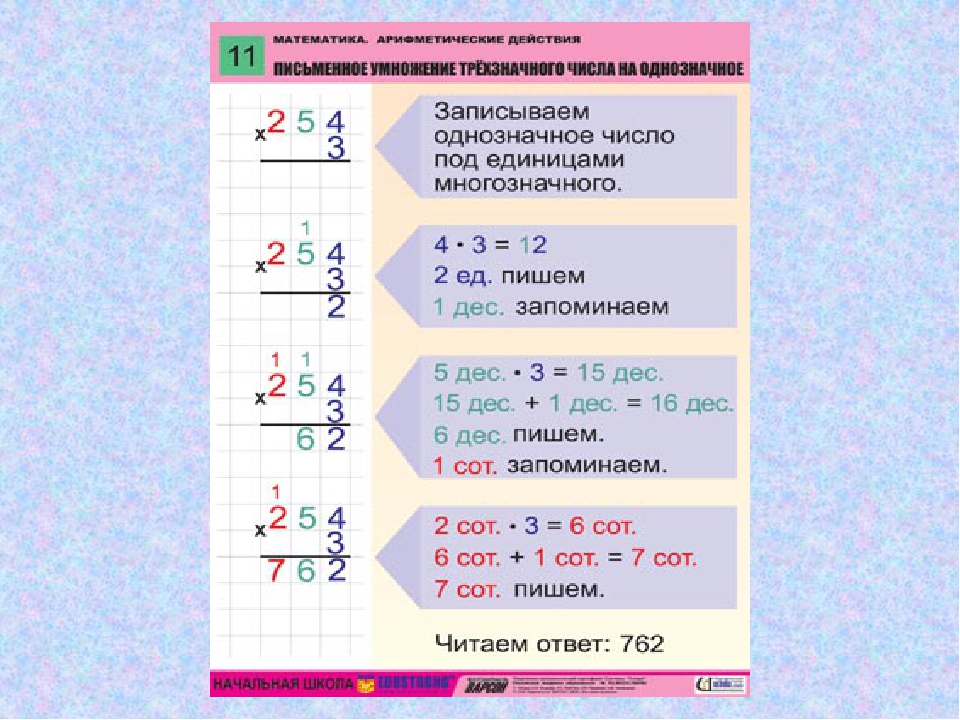
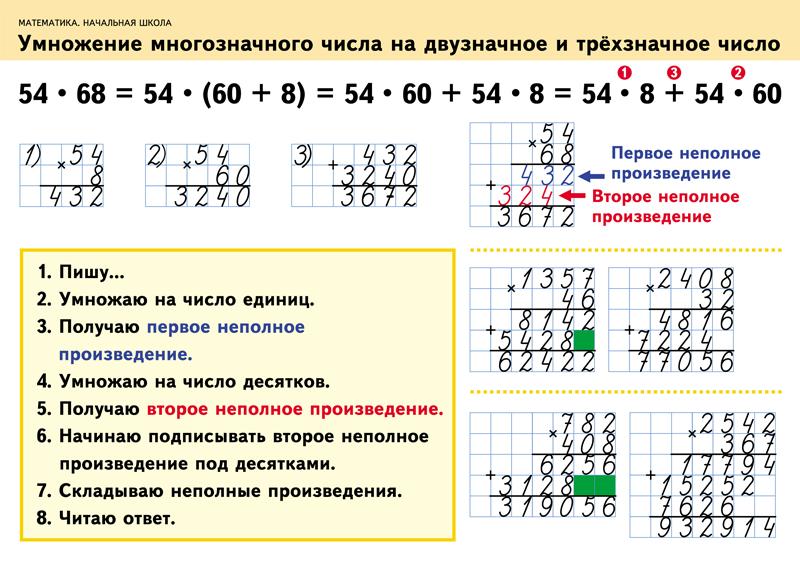
Цель: помочь детям освоить запись столбиком, алгоритм вычислений умножения многозначного числа на однозначное .
Задачи:
— на примере умножения трёхзначного числа на однозначное помочь детям постепенно в индивидуальном темпе освоить новый приём вычисления;
-активизировать образовательную деятельность обучающихся;
-создать ситуацию успеха, поддержать ученика
-использовать обратную связь для диагностики ошибок с последующим их устранением.
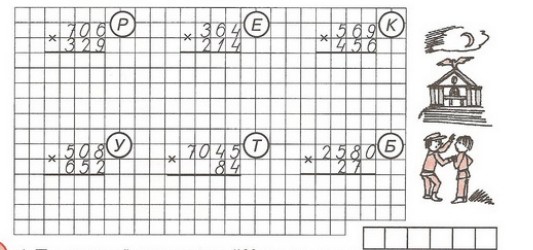
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
183 · 4 177 · 4 149 · 5 285 · 3
153 · 5 168 · 5 231 · 4 234 · 4
Ф.
И.________________________ вар – 2. Решите примеры, записывая их столбиком
160 · 6 220 · 5 360 · 4 340 · 6
450·3 130·7 570·4 430 · 3
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
183 · 4 177 · 4 149 · 5 285 · 3
153 · 5 168 · 5 231 · 4 234 · 4
Ф.И.________________________ вар – 2. Решите примеры, записывая их столбиком
160 · 6 220 · 5 360 · 4 340 · 6
450·3 130·7 570·4 430 · 3
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
231· 4 960 · 2 234 · 4 241 · 4
250· 3 330 · 7 270 · 4 560 · 2
Ф.
И.________________________ вар – 2. Решите примеры, записывая их столбиком
298 · 2 231 · 3 397 · 4 219 · 4
250 · 3 360 · 2 430 · 7 370 · 4
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
231· 4 960 · 2 234 · 4 241 · 4
250· 3 330 · 7 270 · 4 560 · 2
Ф.И.________________________ вар – 2. Решите примеры, записывая их столбиком
298 · 2 231 · 3 397 · 4 219 · 4
250 · 3 360 · 2 430 · 7 370 · 4
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
245 • 3 257 • 3 752 • 2 364 • 2
250 • 3 360 • 2 470 • 2 190 • 3
Ф.
И.________________________ вар – 2. Решите примеры, записывая их столбиком
257 • 3 298 • 3 195 • 3 264 • 2
290 • 3 520 • 2 240 • 4 730 • 2
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
245 • 3 257 • 3 752 • 2 364 • 2
250 • 3 360 • 2 470 • 2 190 • 3
Ф.И.________________________ вар – 2. Решите примеры, записывая их столбиком
257 • 3 298 • 3 195 • 3 264 • 2
290 • 3 520 • 2 240 • 4 730 • 2
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
305 • 3 357 • 3 602 • 3 462 • 2
451 • 3 460 • 2 670 • 2 480 • 3
Ф.
И.________________________ вар – 2. Решите примеры, записывая их столбиком
407 • 3 463 • 3 605 • 3 463 • 2
341 • 3 540 • 2 680 • 2 470 • 3
Ф.И.________________________ вар – 1. Решите примеры, записывая их столбиком
305 • 3 357 • 3 602 • 3 462 • 2
451 • 3 460 • 2 670 • 2 480 • 3
Ф.И.________________________ вар – 2. Решите примеры, записывая их столбиком
407 • 3 463 • 3 605 • 3 463 • 2
341 • 3 540 • 2 680 • 2 470 • 3
Калькулятор НОД и НОК с решением онлайн
| 0 | ||||
| AC | +/- | ÷ | ||
| 7 | 8 | 9 | × | |
| 4 | 5 | 6 | — | |
| 1 | 2 | 3 | + | |
| 0 | 00 | , | = | |
При помощи данного калькулятора вы можете легко найти наибольший общий делитель НОД и наименьшее общее кратное НОК благодаря подробно расписанному решению.
Вы можете найти НОД и НОК для двух, трех и четырех чиселВыберите количество чисел для НОД и НОК
| 2 числа | 3 числа | 4 числа |
Вы так же можете воспользоваться:
калькулятором нахождения НОД и НОК по алгоритму Евклида калькулятором нахождения НОД и НОК для любого количества чисел
Наибольший общий делитель НОД
Наибольший общий делитель НОД(a, b) – это наибольшее натуральной число, на которое можно разделить без остатка числа a и b.
Если числа имеют только один общий делитель – единицу, то такие числа называют взаимно простыми.
Наибольший общий делитель НОД обозначают: НОД(a, b), (a, b), gcd(a, b), hcf(a, b).
Свойства НОД
- Наибольший общий делитель чисел a и b делится на любой общий делитель этих чисел.
Данное свойство означает, что если найти все общие делители чисел a и b, то НОД(a, b) будет делится на любой из этих делителей.
Например, возьмём два числа 15 и 30 и найдем все общие делители этих чисел: 1, 3, 5, 15. Наибольший из этих делителей – число 15. Тогда число 15 делится на 1, 3, 5, 15. - Если число a делится на b, то НОД(a, b) = b.
Например, число 20 делится на число 10, тогда НОД(20, 10) = 10. - При помощи наибольшего общего делителя можно привести дроби к несократимому виду.
Например, дробь 5/30 можно привести к несократимому виду, если найти НОД(30, 5). НОД(30, 5) = 5, следовательно число 5 – самое больше число из возможных делителей числа 30 и 5 на которое можно разделить эти числа, тогда 30:5 = 6, 5:5 = 1. Получаем дробь 5/30 = 1/6.
Любые действия с дробями и развернутое поэтапное решение можно вычислить, используя калькулятор дробей.
Как найти наибольший общий делитель НОД
Чтобы найти наибольший общий делитель НОД двух, трех и более чисел, необходимо:
- Разложить числа на простые множители.
- Найти общие множители чисел – такие числа, которые есть в разложении всех чисел и вычеркнуть их.
- Перемножить оставшиеся множители.
Приведем пример, найдем наибольший общий делитель двух чисел 24 и 58.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
58 — составное число
Разложим число 24 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
24 : 2 = 12 — делится на простое число 2
12 : 2 = 6 — делится на простое число 2
6 : 2 = 3 — делится на простое число 2.
Завершаем деление, так как 3 простое числоРазложим число 58 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
58 : 2 = 29 — делится на простое число 2.
Завершаем деление, так как 29 простое число - Выделим синим цветом и выпишем общие множители.
24 = 2 ⋅ 2 ⋅ 2 ⋅ 3
58 = 2 ⋅ 29У чисел (24, 58) только один общий множитель — 2 и он и будет наибольшим общим делителем этих чисел
Ответ: НОД (24, 58) = 2
Способ №2
- Найдем все возможные делители чисел (24, 58). Для этого поочередно разделим число 24 на делители от 1 до 24, число 58 на делители от 1 до 58. Если число делится без остатка, то делитель запишем в список делителей.
Для числа 24 выпишем все случаи, когда оно делится без остатка:
24 : 1 = 24;
24 : 2 = 12;
24 : 4 = 6;
24 : 6 = 4;
24 : 8 = 3;
24 : 12 = 2;
24 : 24 = 1;Для числа 58 выпишем все случаи, когда оно делится без остатка:
58 : 1 = 58;
58 : 2 = 29;
58 : 29 = 2;
58 : 58 = 1; - Выпишем все общие делители чисел (24, 58) и выделим зеленым цветом самый большой, это и будет наибольший общий делитель НОД чисел (24, 58)
Общие делители чисел (24, 58): 1, 2
Ответ: НОД (24, 58) = 2
Наименьшее общее кратное НОК
Наименьшее общее кратное НОК(a, b) – это наименьшее число, которое можно разделить на числа a и b без остатка.
Наименьшее общее кратное НОК обозначается: НОК(a, b), [a, b], LCM(a, b), lcm(a, b).
Как найти наименьшее общее кратное НОК
Чтобы найти НОК двух, трех и более чисел необходимо:
- Разложить эти числа на простые множители.
- Выписать множители одного из чисел и добавить к ним множители из разложения остальных чисел, которых нет в разложении.
- Умножить получившиеся множители.
Приведем пример, найдем наименьшее общее кратное НОК для чисел 30 и 225.
Способ №1
- Разложим числа на простые множители. Для этого проверим, является ли каждое из чисел простым (если число простое, то его нельзя разложить на простые множители, и оно само является своим разложением).
225 — составное число
30 — составное числоРазложим число 225 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
225 : 3 = 75 — делится на простое число 3
75 : 3 = 25 — делится на простое число 3
25 : 5 = 5 — делится на простое число 5.
Завершаем деление, так как 5 простое числоРазложим число 30 на простые множители и выделим их зелены цветом. Начинаем подбирать делитель из простых чисел, начиная с самого маленького простого числа 2, до тех пор, пока частное не окажется простым числом
30 : 2 = 15 — делится на простое число 2
15 : 3 = 5 — делится на простое число 3.
Завершаем деление, так как 5 простое число - Прежде всего запишем множители самого большого числа, а затем меньшего числа. Найдем недостающие множители, выделим синим цветом в разложении меньшего числа множители, которые не вошли в разложение большего числа.
225 = 3 ∙ 3 ∙ 5 ∙ 5
30 = 2 ∙ 3 ∙ 53) Теперь, чтобы найти НОК нужно перемножить множители большего числа с недостающими множителями, которые выделены синим цветом
НОК (225 ; 30) = 3 ∙ 3 ∙ 5 ∙ 5 ∙ 2 = 450
Способ №2
- Найдем все возможные кратные чисел (225 ; 30). Для этого поочередно умножим число 225 на числа от 1 до 30, число 30 на числа от 1 до 225.
Выделим все кратные числа 225 зеленым цветом:
зеленым цветом:
225 ∙ 1 = 225; 225 ∙ 2 = 450; 225 ∙ 3 = 675; 225 ∙ 4 = 900;
225 ∙ 5 = 1125; 225 ∙ 6 = 1350; 225 ∙ 7 = 1575; 225 ∙ 8 = 1800;
225 ∙ 9 = 2025; 225 ∙ 10 = 2250; 225 ∙ 11 = 2475; 225 ∙ 12 = 2700;
225 ∙ 13 = 2925; 225 ∙ 14 = 3150; 225 ∙ 15 = 3375; 225 ∙ 16 = 3600;
225 ∙ 17 = 3825; 225 ∙ 18 = 4050; 225 ∙ 19 = 4275; 225 ∙ 20 = 4500;
225 ∙ 21 = 4725; 225 ∙ 22 = 4950; 225 ∙ 23 = 5175; 225 ∙ 24 = 5400;
225 ∙ 25 = 5625; 225 ∙ 26 = 5850; 225 ∙ 27 = 6075; 225 ∙ 28 = 6300;
225 ∙ 29 = 6525; 225 ∙ 30 = 6750;Выделим все кратные числа 30 зеленым цветом:
30 ∙ 1 = 30; 30 ∙ 2 = 60; 30 ∙ 3 = 90; 30 ∙ 4 = 120;
30 ∙ 5 = 150; 30 ∙ 6 = 180; 30 ∙ 7 = 210; 30 ∙ 8 = 240;
30 ∙ 9 = 270; 30 ∙ 10 = 300; 30 ∙ 11 = 330; 30 ∙ 12 = 360;
30 ∙ 13 = 390; 30 ∙ 14 = 420; 30 ∙ 15 = 450; 30 ∙ 16 = 480;
30 ∙ 17 = 510; 30 ∙ 18 = 540; 30 ∙ 19 = 570; 30 ∙ 20 = 600;
30 ∙ 25 = 750; 30 ∙ 26 = 780; 30 ∙ 27 = 810; 30 ∙ 28 = 840;
30 ∙ 29 = 870; 30 ∙ 30 = 900; 30 ∙ 31 = 930; 30 ∙ 32 = 960;
30 ∙ 33 = 990; 30 ∙ 34 = 1020; 30 ∙ 35 = 1050; 30 ∙ 36 = 1080;
30 ∙ 37 = 1110; 30 ∙ 38 = 1140; 30 ∙ 39 = 1170; 30 ∙ 40 = 1200;
30 ∙ 41 = 1230; 30 ∙ 42 = 1260; 30 ∙ 43 = 1290; 30 ∙ 44 = 1320;
30 ∙ 45 = 1350; 30 ∙ 46 = 1380; 30 ∙ 47 = 1410; 30 ∙ 48 = 1440;
30 ∙ 49 = 1470; 30 ∙ 50 = 1500; 30 ∙ 51 = 1530; 30 ∙ 52 = 1560;
30 ∙ 53 = 1590; 30 ∙ 54 = 1620; 30 ∙ 55 = 1650; 30 ∙ 56 = 1680;
30 ∙ 57 = 1710; 30 ∙ 58 = 1740; 30 ∙ 59 = 1770; 30 ∙ 60 = 1800;
30 ∙ 61 = 1830; 30 ∙ 62 = 1860; 30 ∙ 63 = 1890; 30 ∙ 64 = 1920;
30 ∙ 65 = 1950; 30 ∙ 66 = 1980; 30 ∙ 67 = 2010; 30 ∙ 68 = 2040;
30 ∙ 69 = 2070; 30 ∙ 70 = 2100; 30 ∙ 71 = 2130; 30 ∙ 72 = 2160;
30 ∙ 73 = 2190; 30 ∙ 74 = 2220; 30 ∙ 75 = 2250; 30 ∙ 76 = 2280;
30 ∙ 77 = 2310; 30 ∙ 78 = 2340; 30 ∙ 79 = 2370; 30 ∙ 80 = 2400;
30 ∙ 81 = 2430; 30 ∙ 82 = 2460; 30 ∙ 83 = 2490; 30 ∙ 84 = 2520;
30 ∙ 85 = 2550; 30 ∙ 86 = 2580; 30 ∙ 87 = 2610; 30 ∙ 88 = 2640;
30 ∙ 89 = 2670; 30 ∙ 90 = 2700; 30 ∙ 91 = 2730; 30 ∙ 92 = 2760;
30 ∙ 93 = 2790; 30 ∙ 94 = 2820; 30 ∙ 95 = 2850; 30 ∙ 96 = 2880;
30 ∙ 97 = 2910; 30 ∙ 98 = 2940; 30 ∙ 99 = 2970; 30 ∙ 100 = 3000;
30 ∙ 101 = 3030; 30 ∙ 102 = 3060; 30 ∙ 103 = 3090; 30 ∙ 104 = 3120;
30 ∙ 105 = 3150; 30 ∙ 106 = 3180; 30 ∙ 107 = 3210; 30 ∙ 108 = 3240;
30 ∙ 109 = 3270; 30 ∙ 110 = 3300; 30 ∙ 111 = 3330; 30 ∙ 112 = 3360;
30 ∙ 113 = 3390; 30 ∙ 114 = 3420; 30 ∙ 115 = 3450; 30 ∙ 116 = 3480;
30 ∙ 117 = 3510; 30 ∙ 118 = 3540; 30 ∙ 119 = 3570; 30 ∙ 120 = 3600;
30 ∙ 121 = 3630; 30 ∙ 122 = 3660; 30 ∙ 123 = 3690; 30 ∙ 124 = 3720;
30 ∙ 125 = 3750; 30 ∙ 126 = 3780; 30 ∙ 127 = 3810; 30 ∙ 128 = 3840;
30 ∙ 133 = 3990; 30 ∙ 134 = 4020; 30 ∙ 135 = 4050; 30 ∙ 136 = 4080;
30 ∙ 137 = 4110; 30 ∙ 138 = 4140; 30 ∙ 139 = 4170; 30 ∙ 140 = 4200;
30 ∙ 141 = 4230; 30 ∙ 142 = 4260; 30 ∙ 143 = 4290; 30 ∙ 144 = 4320;
30 ∙ 145 = 4350; 30 ∙ 146 = 4380; 30 ∙ 147 = 4410; 30 ∙ 148 = 4440;
30 ∙ 149 = 4470; 30 ∙ 150 = 4500; 30 ∙ 151 = 4530; 30 ∙ 152 = 4560;
30 ∙ 153 = 4590; 30 ∙ 154 = 4620; 30 ∙ 155 = 4650; 30 ∙ 156 = 4680;
30 ∙ 157 = 4710; 30 ∙ 158 = 4740; 30 ∙ 159 = 4770; 30 ∙ 160 = 4800;
30 ∙ 161 = 4830; 30 ∙ 162 = 4860; 30 ∙ 163 = 4890; 30 ∙ 164 = 4920;
30 ∙ 165 = 4950; 30 ∙ 166 = 4980; 30 ∙ 167 = 5010; 30 ∙ 168 = 5040;
30 ∙ 169 = 5070; 30 ∙ 170 = 5100; 30 ∙ 171 = 5130; 30 ∙ 172 = 5160;
30 ∙ 173 = 5190; 30 ∙ 174 = 5220; 30 ∙ 175 = 5250; 30 ∙ 176 = 5280;
30 ∙ 177 = 5310; 30 ∙ 178 = 5340; 30 ∙ 179 = 5370; 30 ∙ 180 = 5400;
30 ∙ 181 = 5430; 30 ∙ 182 = 5460; 30 ∙ 183 = 5490; 30 ∙ 184 = 5520;
30 ∙ 185 = 5550; 30 ∙ 186 = 5580; 30 ∙ 187 = 5610; 30 ∙ 188 = 5640;
30 ∙ 189 = 5670; 30 ∙ 190 = 5700; 30 ∙ 191 = 5730; 30 ∙ 192 = 5760;
30 ∙ 193 = 5790; 30 ∙ 194 = 5820; 30 ∙ 195 = 5850; 30 ∙ 196 = 5880;
30 ∙ 197 = 5910; 30 ∙ 198 = 5940; 30 ∙ 199 = 5970; 30 ∙ 200 = 6000;
30 ∙ 201 = 6030; 30 ∙ 202 = 6060; 30 ∙ 203 = 6090; 30 ∙ 204 = 6120;
30 ∙ 205 = 6150; 30 ∙ 206 = 6180; 30 ∙ 207 = 6210; 30 ∙ 208 = 6240;
30 ∙ 209 = 6270; 30 ∙ 210 = 6300; 30 ∙ 211 = 6330; 30 ∙ 212 = 6360;
30 ∙ 213 = 6390; 30 ∙ 214 = 6420; 30 ∙ 215 = 6450; 30 ∙ 216 = 6480;
30 ∙ 217 = 6510; 30 ∙ 218 = 6540; 30 ∙ 219 = 6570; 30 ∙ 220 = 6600;
30 ∙ 221 = 6630; 30 ∙ 222 = 6660; 30 ∙ 223 = 6690; 30 ∙ 224 = 6720;
30 ∙ 225 = 6750; - Выпишем все общие кратные чисел (225 ; 30) и выделим зеленым цветом самое маленькое, это и будет наименьшим общим кратным чисел (225 ; 30).
Общие кратные чисел (225 ; 30): 450, 900, 1350, 1800, 2250, 2700, 3150, 3600, 4050, 4500, 4950, 5400, 5850, 6300, 6750
Ответ: НОК (225 ; 30) = 450
Выделим все кратные числа 225 зеленым цветом:
зеленым цветом:
| Вам могут также быть полезны следующие сервисы |
| Калькуляторы (Теория чисел) |
| Калькулятор выражений |
| Калькулятор со скобками |
| Калькулятор разложения числа на простые множители |
| Калькулятор НОД и НОК |
| Калькулятор НОД и НОК по алгоритму Евклида |
| Калькулятор НОД и НОК для любого количества чисел |
| Представление многозначных чисел в виде суммы разрядных слагаемых |
| Калькулятор деления числа в данном отношении |
| Калькулятор процентов |
| Калькулятор перевода числа с Е в десятичное |
| Калькулятор экспоненциальной записи чисел |
| Калькулятор нахождения факториала числа |
| Калькулятор нахождения логарифма числа |
| Калькулятор квадратных уравнений |
| Калькулятор остатка от деления |
| Калькулятор корней с решением |
| Калькулятор нахождения периода десятичной дроби |
| Калькулятор больших чисел |
| Калькулятор округления числа |
| Калькулятор свойств корней и степеней |
| Калькулятор комплексных чисел |
| Калькулятор среднего арифметического |
| Калькулятор арифметической прогрессии |
| Калькулятор геометрической прогрессии |
| Калькулятор модуля числа |
| Калькулятор абсолютной погрешности приближения |
| Калькулятор абсолютной погрешности |
| Калькулятор относительной погрешности |
| Дроби |
| Калькулятор интервальных повторений |
| Учим дроби наглядно |
| Калькулятор сокращения дробей |
| Калькулятор преобразования неправильной дроби в смешанную |
| Калькулятор преобразования смешанной дроби в неправильную |
| Калькулятор сложения, вычитания, умножения и деления дробей |
| Калькулятор возведения дроби в степень |
| Калькулятор перевода десятичной дроби в обыкновенную |
| Калькулятор перевода обыкновенной дроби в десятичную |
| Калькулятор сравнения дробей |
| Калькулятор приведения дробей к общему знаменателю |
| Калькуляторы (тригонометрия) |
| Калькулятор синуса угла |
| Калькулятор косинуса угла |
| Калькулятор тангенса угла |
| Калькулятор котангенса угла |
| Калькулятор секанса угла |
| Калькулятор косеканса угла |
| Калькулятор арксинуса угла |
| Калькулятор арккосинуса угла |
| Калькулятор арктангенса угла |
| Калькулятор арккотангенса угла |
| Калькулятор арксеканса угла |
| Калькулятор арккосеканса угла |
| Калькулятор нахождения наименьшего угла |
| Калькулятор определения вида угла |
| Калькулятор смежных углов |
| Калькуляторы систем счисления |
| Калькулятор перевода чисел из арабских в римские и из римских в арабские |
| Калькулятор перевода чисел в различные системы счисления |
| Калькулятор сложения, вычитания, умножения и деления двоичных чисел |
| Системы счисления теория |
| N2 | Двоичная система счисления |
| N3 | Троичная система счисления |
| N4 | Четырехичная система счисления |
| N5 | Пятеричная система счисления |
| N6 | Шестеричная система счисления |
| N7 | Семеричная система счисления |
| N8 | Восьмеричная система счисления |
| N9 | Девятеричная система счисления |
| N11 | Одиннадцатиричная система счисления |
| N12 | Двенадцатеричная система счисления |
| N13 | Тринадцатеричная система счисления |
| N14 | Четырнадцатеричная система счисления |
| N15 | Пятнадцатеричная система счисления |
| N16 | Шестнадцатеричная система счисления |
| N17 | Семнадцатеричная система счисления |
| N18 | Восемнадцатеричная система счисления |
| N19 | Девятнадцатеричная система счисления |
| N20 | Двадцатеричная система счисления |
| N21 | Двадцатиодноричная система счисления |
| N22 | Двадцатидвухричная система счисления |
| N23 | Двадцатитрехричная система счисления |
| N24 | Двадцатичетырехричная система счисления |
| N25 | Двадцатипятеричная система счисления |
| N26 | Двадцатишестеричная система счисления |
| N27 | Двадцатисемеричная система счисления |
| N28 | Двадцативосьмеричная система счисления |
| N29 | Двадцатидевятиричная система счисления |
| N30 | Тридцатиричная система счисления |
| N31 | Тридцатиодноричная система счисления |
| N32 | Тридцатидвухричная система счисления |
| N33 | Тридцатитрехричная система счисления |
| N34 | Тридцатичетырехричная система счисления |
| N35 | Тридцатипятиричная система счисления |
| N36 | Тридцатишестиричная система счисления |
| Калькуляторы площади геометрических фигур |
| Площадь квадрата |
| Площадь прямоугольника |
| КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ |
| Калькуляторы (Комбинаторика) |
| Калькулятор нахождения числа перестановок из n элементов |
| Калькулятор нахождения числа сочетаний из n элементов |
| Калькулятор нахождения числа размещений из n элементов |
| Калькуляторы линейная алгебра и аналитическая геометрия |
| Калькулятор сложения и вычитания матриц |
| Калькулятор умножения матриц |
| Калькулятор транспонирование матрицы |
| Калькулятор нахождения определителя (детерминанта) матрицы |
| Калькулятор нахождения обратной матрицы |
Длина отрезка. Онлайн калькулятор расстояния между точками |
| Онлайн калькулятор нахождения координат вектора по двум точкам |
| Калькулятор нахождения модуля (длины) вектора |
| Калькулятор сложения и вычитания векторов |
| Калькулятор скалярного произведения векторов через длину и косинус угла между векторами |
| Калькулятор скалярного произведения векторов через координаты |
| Калькулятор векторного произведения векторов через координаты |
| Калькулятор смешанного произведения векторов |
| Калькулятор умножения вектора на число |
| Калькулятор нахождения угла между векторами |
| Калькулятор проверки коллинеарности векторов |
| Калькулятор проверки компланарности векторов |
| Генератор Pdf с примерами |
| Тренажёры решения примеров |
| Тренажёр таблицы умножения |
| Тренажер счета для дошкольников |
| Тренажер счета на внимательность для дошкольников |
Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ. |
| Тренажер решения примеров с разными действиями |
| Тренажёры решения столбиком |
| Тренажёр сложения столбиком |
| Тренажёр вычитания столбиком |
| Тренажёр умножения столбиком |
| Тренажёр деления столбиком с остатком |
| Калькуляторы решения столбиком |
| Калькулятор сложения, вычитания, умножения и деления столбиком |
| Калькулятор деления столбиком с остатком |
| Конвертеры величин |
| Конвертер единиц длины |
| Конвертер единиц скорости |
| Конвертер единиц ускорения |
| Цифры в текст |
| Калькуляторы (физика) |
Механика |
| Калькулятор вычисления скорости, времени и расстояния |
| Калькулятор вычисления ускорения, скорости и перемещения |
| Калькулятор вычисления времени движения |
| Калькулятор времени |
Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения. |
| Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния. |
| Импульс тела. Калькулятор вычисления импульса, массы и скорости |
| Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы. |
| Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения |
Оптика |
| Калькулятор отражения и преломления света |
Электричество и магнетизм |
| Калькулятор Закона Ома |
| Калькулятор Закона Кулона |
| Калькулятор напряженности E электрического поля |
| Калькулятор нахождения точечного электрического заряда Q |
| Калькулятор нахождения силы F действующей на заряд q |
| Калькулятор вычисления расстояния r от заряда q |
| Калькулятор вычисления потенциальной энергии W заряда q |
| Калькулятор вычисления потенциала φ электростатического поля |
| Калькулятор вычисления электроемкости C проводника и сферы |
Конденсаторы |
| Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе |
| Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе |
| Калькулятор вычисления энергии W заряженного конденсатора |
Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов |
| Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов |
| Калькуляторы по астрономии |
| Вес тела на других планетах |
| Ускорение свободного падения на планетах Солнечной системы и их спутниках |
| Генераторы |
| Генератор примеров по математике |
| Генератор случайных чисел |
| Генератор паролей |
Дочь заставляет внука самостоятельно делать домашние задания, хотя он без помощи взрослых не справляется
Совершенно не понимаю свою дочь. Она зациклилась на идее вырастить своего сына самостоятельной личностью, поэтому наотрез отказывается помогать ему с уроками. Не спорю, самостоятельность — это хорошо, но, как говорится, “всему свое время”.
А моему внуку только восемь лет и без помощи взрослых ему не обойтись.
Тем более, сейчас школьная программа — «мама не горюй». Ну как маленький ребенок должен сам разбираться со всеми этими запутанными заданиями?
К тому же, внук, окончив первый класс, не очень хорошо считал и писал, пока я не вмешалась. А почерк по-прежнему оставляет желать лучшего. Однако мою дочь не переубедить. Она, почему-то, твердо убеждена, что всему должны научить в школе, а уроки он прекрасно сделает один.
Когда-то в школе действительно учили так, что большинство детей хорошо усваивало полученные знания, но сейчас — совершенно иная ситуация. Если судить по опыту многих моих знакомых, учителя стараются разобрать в классе как можно больше тем.
Вот только делают это очень поверхностно. А то, что не успели изучить на уроке, эти нерадивые педагоги задают на дом. Так что родителям по-любому приходится активно участвовать в образовательном процессе.
Моя же дочь махнула на все рукой. Как вернется с работы, так первым делом принимается за домашние дела, а остаток вечера сидит в телефоне.
Про зятя вообще молчу — этот увалень в свободное время только и делает, что ест, валяется на диване и тоже увлеченно смотрит на экран смартфона.
А все его общение с ребенком ограничивается вопросами «как дела» и «чем занята мама». Ну, может иногда отвести его в школу — и то, если очень попросить. Вот внук и вынужден в одиночку биться над домашними заданиями, пока его родители бьют баклуши. Естественно, получается у него из рук вон плохо.
Конечно, я помогаю внуку по мере возможности, как бы дочь ни сопротивлялась. Стараюсь подробно объяснить ему суть того или иного задания. Часто задаю наводящие вопросы, а для закрепления материала даю еще парочку аналогичных упражнений. И, главное, тогда внук начинает делать успехи.
Правда, чтобы он и дальше хорошо учился, надо заниматься систематически. А я не всегда могу брать внука к себе домой или приезжать к дочери. Ведь я сама работаю. К тому же, готовку и уборку никто не отменял, да и муж скучает.
Если же я пытаюсь поговорить об этом с дочерью, она неизменно упирает руки в боки.
«Мам, я же много раз просила тебя не лезть со своей помощью! Учеба Алешки касается только его самого. А ты этого понять не можешь, да еще и жалуешься на нехватку времени. Сама виновата!».
Интересно, в чем же моя вина? Наверное, в том, что мне небезразлично развитие внука, в отличие от его родителей. У них-то есть дела поважнее — посмотреть видеоролики да пообщаться с друзьями. Не ясно, зачем вообще рожали при таком отношении к родительским обязанностям.
Когда задаю дочери этот вопрос, она начинает оправдываться занятостью на работе. «Пойми, мы очень устаем и вечером хотим отдохнуть, а не корпеть над учебниками вместе с Алешей. Он должен справляться сам. Ну сколько я могу это повторять?!».
Вообще-то, мы с мужем в свое время и поболее вкалывали. Однако всегда находили время на то, чтобы помочь дочери с уроками.
И ничего, не развалились. Дочери же особенно уставать не с чего — сидит себе в комфортном офисе да нажимает кнопочки на компьютере. Зять тоже не перетруждается.
Так почему бы не потратить хоть пару часов на своего же ребенка? А дочь повторяет как попугай, что не будет с ним заниматься. «Я прекрасно помню, как вы валились с ног после работы, но все равно делали со мной домашку. Не хочу себе такой же участи!».
Вот так, одной фразой, она обесценила наши с мужем старания. А ведь если бы не мы, дочь перебивалась бы с тройки на двойку и пошла бы в ПТУ после девятого класса. Однако и я, и муж приложили максимум усилий, чтобы она стала уверенной хорошисткой и поступила в приличный вуз на бесплатной основе.
Хотя учебная программа в то время и не успела настолько испоганиться, как сейчас, мы все равно «держали руку на пульсе» даже в старших классах. Только поэтому дочь и попала на бюджет.
Видимо, ей отшибло память, раз заставляет внука самостоятельно делать домашние задания.
И у нее есть еще одна «железная» отговорка. «Алеша ходит на продленку. Там у них наверняка проверяют домашку. Зря мы что ли деньги за это платим?».
Судя по количеству ошибок и помарок в тетрадях внука, в этой школе никто даже мельком не смотрит на выполненные домашние задания. А обязанности педагогов, ведущих продленку, ограничиваются простым присмотром за детьми. Это не дело, конечно, но «ничего не попишешь».
Дочка, как будто, вообще не в курсе школьной жизни Алеши. Тот же дневник проверяет лишь после многочисленных напоминаний со стороны учительницы. Я более чем уверена, что у них был не один разговор на тему успеваемости моего внука. А дочь об этом старательно молчит, как мне кажется.
Хорошо, что я за лето успела освежить в памяти внука программу первого класса и немного подготовила его ко второму, пока он гостил у меня на даче. Однако я с ужасом жду нового учебного года, поскольку дочь и ее муж опять пустят все на самотек, полагая, что «оценки на будущее не влияют, а троечники часто успешнее отличников».
Я с их подходом в корне не согласна, а потому буду дальше бороться за внука. Не хочу, чтобы он пополнил ряды неучей, которых и так хватает в наши дни.
В рубрике «Мнение читателей» публикуются материалы от читателей.
Матрицы умножения — примеры
М. Борна
На этой странице вы можете увидеть множество примеров умножения матриц.
Вы можете перезагружать эту страницу сколько угодно раз и каждый раз получать новый набор чисел и матриц. Вы также можете выбрать матрицы разного размера (внизу страницы).
(Если вам сначала нужна справочная информация о матрицах, вернитесь к разделу «Введение в матрицы» и «4. Умножение матриц»).
Перемножить матрицы A и B .
|
|
Ответить
Чтобы сэкономить работу, мы сначала проверяем, можно ли их умножить.
У нас есть (4×4) × (4×4) и поскольку количество столбцов в A такое же, как количество строк в B (в данном случае два средних числа равны 4), мы можем продолжить и умножить эти матрицы. Нашим результатом будет матрица (4×4).
Первым шагом является запись двух матриц рядом следующим образом:
|
|
Мы умножаем отдельные элементы в первой строке матрицы A на соответствующие элементы в первом столбце матрицы B и складываем результаты.
Это дает нам число, которое нам нужно поместить в первую строку, позицию первого столбца в матрице ответов.
|
|
1×13 + 0×0 + 2×5 + 3×4 = 35
После этого умножаем элементы по первой строке матрицы A с соответствующими элементами вниз по второму столбцу матрицы B , затем добавьте результаты.
Это дает нам ответ, который нам нужно поместить в первую строку, второй столбец матрицы ответов.
|
|
1×14 + 0×3 + 2×2 + 3×7 = 39
Продолжаем по строкам и столбцам следующим образом:
|
|
| = | 1×13 + 0×0 + 2×5 + 3×4 | 1×14 + 0×3 + 2×2 + 3×7 | 1×15 + 0×-2 + 2×-4 + 3×8 | 1×-1 + 0×1 + 2×6 + 3×9 | ||
| 4×13 + 5×0 + -2×5 + 6×4 | 4×14 + 5×3 + -2×2 + 6×7 | 4×15 + 5×-2 + -2×-4 + 6×8 | 4×-1 + 5×1 + -2×6 + 6×9 | |||
| -4×13 + 7×0 + 8×5 + 9×4 | -4×14 + 7×3 + 8×2 + 9×7 | -4×15 + 7×-2 + 8×-4 + 9×8 | -4×-1 + 7×1 + 8×6 + 9×9 | |||
| 10×13 + 11×0 + 12×5 + -3×4 | 10×14 + 11×3 + 12×2 + -3×7 | 10×15 + 11×-2 + 12×-4 + -3×8 | 10×-1 + 11×1 + 12×6 + -3×9 |
| = | 35 | 39 | 31 | 38 | ||
| 66 | 109 | 106 | 43 | |||
| 24 | 44 | -34 | 140 | |||
| 178 | 176 | 56 | 46 |
См.
другой пример?Вы можете обновить эту страницу, чтобы увидеть другой пример с матрицами другого размера и другими числами; ИЛИ
Выберите интересующие вас размеры матрицы и нажмите кнопку .
матрица 3×3 умножить на матрицу 3×3матрица 2×3 умножить на матрицу 3×4
матрица 1×4 умножить на матрицу 4×1
матрица 4×2 умножить на матрицу 2×3
4. Умножение матриц
Важно: Мы можем перемножать матрицы, только если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
а) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно и дает в качестве ответа матрицу 2 × 4.
b) Умножение матрицы 7 × 1 на матрицу 1 × 2 допустимо; это дает матрицу 7 × 2
c) Матрица 4 × 3, умноженная на матрицу 2 × 3, НЕвозможна.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы понять, что происходит. После этого мы увидим пример с числами.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы работаем через 1-й строки первой матрицы, умножая на 1-го столбца второй матрицы, элемент за элементом. Мы добавить полученных продуктов. Наш ответ занимает позицию a 11 (вверху слева) матрицы ответов.
Проделываем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается в позицию a 12 .
Теперь о 2-й -й строке первой матрицы и 1-м -м столбце второй матрицы. Результат помещается в позицию а 21 .
Наконец, делаем 2-ю строку первой матрицы и 2-й столбец второй матрицы. Результат помещается в позицию a 22 .
Таким образом, результат умножения двух наших матриц выглядит следующим образом:
`[(a,b,c),(d,e,f)][(u,v),(w,x),(y,z)]` `=[(au+bw+cy,av +bx+cz),(du+ew+fy,dv+ex+fz)]`
Теперь давайте рассмотрим числовой пример.
Пользователи телефона
ПРИМЕЧАНИЕ. Если вы разговариваете по телефону, вы можете прокручивать любые широкие матрицы на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0,-1,2),(4,11,2))((3,-1),(1,2),(6,1))`
Ответить
Это 2×3 умножить на 3×2, что даст нам 2×2 отвечать.
`((0,-1,2),(4,11,2)) ((3,-1),(1,2),(6,1))`
`=((0xx3+ — 1xx1 + 2xx6,0xx-1+ -1xx2 + 2xx1), (4xx3+11xx1+2xx6,4xx -1 + 11xx2 + 2xx1))`
` = ((0-1+12,0-2+2), (12+11+12,-4+22+2))`
` = ((11,0),(35,20)) `
Наш ответ — матрица 2×2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем по строк первой матрицы и по столбцам второй матрицы, поэлементно. Затем мы добавляем продукты:
`((a,b),(c,d))((e,f),(g,h))` `=((ae+bg,af+bh),(ce+dg,cf+dh ))`
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9),(5,-1))((-2,3),(4,0))`
Ответить
` ((8,9),(5,-1))((-2,3),(4,0)) `
`= ((8 xx -2+9xx4,8xx3+9xx0),( 5xx-2+ -1xx4,5xx3 + -1xx0))`
` = ((-16+36,24+0),(-10+ -4,15 + 0)) `
` = ((20 ,24),(-14,15)) `
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя матричное умножение.
Пример 4
Система уравнений
−3 х + у = 1
6 х — 3 у = -4
можно записать как:
`((-3,1),(6,-3))((x),(y))=((1),(-4))`
Матрицы идеально подходят для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру для решения системы требуются только первая и последняя матрицы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 — Обозначение
Уход с записью умножение матриц.
Следующие выражения имеют различных значений:
AB это умножение матриц
A × B является произведением перекрестного , которое возвращает вектор
A * B используется в компьютерной записи, но не на бумаге
А • B произведение точек , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. в главе «Вектор».]
Примечание 2. Коммутативность умножения матриц
`AB = BA`?
Давайте посмотрим, так ли это на примере.
Пример 5
Если
`А=((0,-1,2),(4,11,2))`
и
`В=((3,-1),(1,2),(6,1))`
найти AB и ВА.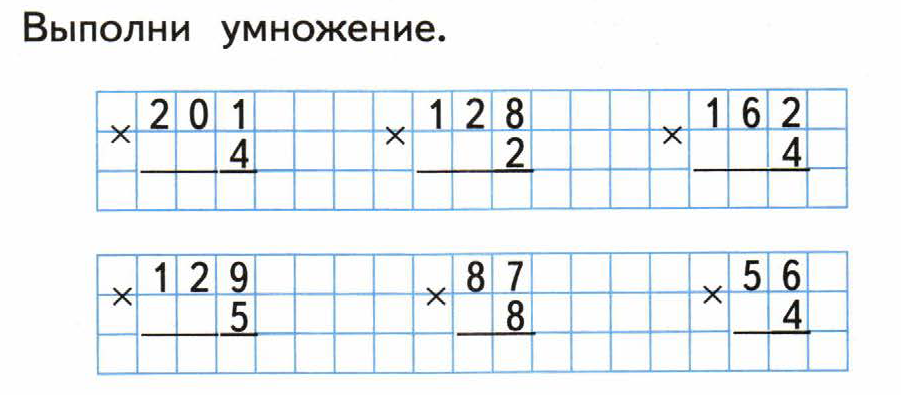
Ответить
Мы выполнили AB выше, и ответ был:
`AB = ((0,-1,2),(4,11,2)) ((3,-1),(1,2), (6,1))`
` = ( (11,0),(35,20) )`
Теперь BA равно (3 × 2)(2 × 3), что даст 3 × 3:
`BA= ((3,-1),(1,2),(6,1))((0,-1,2),(4,11,2))`
`= ((0 -4,-3-11,6-2),(0+8,-1+22,2+4),(0+4,-6+11,12+2))`
` = (( -4,-14,4),(8,21,6),(4,5,14)) `
Итак, в этом случае AB НЕ равно BA.
Фактически, для большинства матриц нельзя изменить порядок умножения на обратный и получить тот же результат.
В общем случае при перемножении матриц перестановочный закон не выполняется, т. е. AB ≠ BA . Есть два общих исключения из этого:
- Матрица идентичности: IA = AI = A .
- , обратная матрицы: A -1 А = АА -1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6. Умножение на матрицу идентичности
Учитывая, что
`А=((-3,1,6),(3,-1,0),(4,2,5))`
найти AI .
Ответить
`AI = ((-3,1,6),(3,-1,0),(4,2,5)) ((1,0,0),(0,1,0),(0 ,0,1))`
`=((-3+0+0,0+1+0,0+0+6),(3+0+0,0+ -1+0,0+0 +0),(4+0+0,0+2+0,0+0+5))`
` =((-3,1,6),(3,-1,0),(4,2,5))`
`=A`
Мы видим, что умножение на единичную матрицу не изменить значение исходной матрицы.
То есть
АИ = А
Упражнения
1. Если возможно, найдите BA и AB .
`А=((-2,1,7),(3,-1,0),(0,2,-1))`
`В=(4\\-1\\\5)`
Ответить
`BA=(4\ \ -1\ \ \ 5)((-2,1,7),(3,-1,0),(0,2,-1))`
`=(-8+(-3)+0\ \ \ 4+1+10\ \ \ 28+0+(-5))`
`=(-11\ \ 15\ \ 23)`
AB невозможно. (3 × 3) × (1 × 3).
2. Определить, если B = A -1 , учитывая:
`А=((3,-4),(5,-7))`
`В=((7,4),(5,3))`
Ответить
Если B = A -1 , то `AB = I`.
`AB=((3,-4),(5,-7))((7,4),(5,3))`
`=((21-20,12-12),( 35-35,20-21))`
`=((1,0),(0,-1))`
` !=I`
Таким образом, B НЕ является обратным A.
3. При изучении движения электронов, одна из спиновых матриц Паули равна
`s=((0,-j),(j,0))`
где
`j=sqrt(-1)`
Покажите, что с 2 = I.
[Если вы никогда раньше не видели j , перейдите к разделу, посвященному комплексным числам].
92+0))``= ((1,0),(0,1))`
`=I`
4. Оцените следующее матричное умножение, которое используется при управлении движением роботизированного механизма .
`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`
Ответить
`( (cos\ 60° ,-sin\ 60° ,0),(sin\ 60°, cos\ 60°,0),(0,0,1))((2),(4),( 0))`
`=((2(0,5)-4(0,866)+0),(2(0,866)+4(0,5)+0),(0+0+0))`
`= ((-2.
464),(3.732),(0))`
Интерпретация этого заключается в том, что рука робота перемещается из позиции (2, 4, 0) в позицию (-2,46, 3,73, 0). То есть это движется в x-y плоскость, но ее высота остается равной z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят ему, на сколько градусов двигаться.
Интерактивы Matrix Multiplication
- Другие примеры умножения матриц
- Интерактивные операции с матрицами
Умножение матриц — ChiliMath
ПоискУмножение матриц — это «беспорядочный тип», потому что вам нужно будет выполнить определенный набор процедур, чтобы сделать это правильно. Это «грязный тип», потому что процесс более сложный. Однако позже, после прохождения процедуры и некоторых примеров, вы поймете, что необходимые шаги выполнимы. Не волнуйся, я помогу тебе в этом!
Но сначала нам нужно убедиться, что две матрицы «разрешено» перемножать. В противном случае данные две матрицы «несовместимы» для перемножения.
В этом случае говорят, что решение не определено.
Всегда помните об этом!
Чтобы умножение матриц работало, количество столбцов левой матрицы ДОЛЖНО РАВНО количеству строк правой матрицы.
Предположим, нам даны матрицы A и B, найдите AB (выполните умножение матриц, если применимо). Определите, какая из них является левой и правой матрицами, исходя из их расположения. Это очень важный шаг.
Чтобы определить, могу ли я умножить две заданные матрицы, мне нужно обратить внимание на количество столбцов матрицы A и количество строк матрицы B. Если они равны, то я могу приступить к умножению матриц. В противном случае я сделаю вывод, что ответ не определен!
Поскольку матрица A имеет количество столбцов 2 , а матрица B имеет количество строк 3 , и они не равны (2 ≠ 3) , я заключаю, что AB = undefined . Это означает, что их продукт не может быть найден.
Примеры умножения матриц, также известного как «беспорядочный тип»
Указания : Имея следующие матрицы, выполните указанную операцию.
Пример 1 : Вычислите, если возможно, произведение B и E.
Чтобы матрицы B и E имели произведение, количество столбцов левой матрицы B должно равняться количеству строк правой матрицы E.
- Матрица B (слева)
количество столбцов = 3
- Матрица E (справа)
количество строк = 3
Поскольку это так, то их можно умножать вместе. Вот шаги:
Шаг 1: Поместите их рядом.
Шаг 2: Умножьте строки B на столбцы E путем умножения соответствующих элементов каждой строки на каждый элемент столбца, а затем сложите их вместе.
Пожалуйста, внимательно посмотрите анимированное решение.
Если у вас не хватает терпения смотреть анимированное решение выше о том, как выполнить умножение матриц, вы можете просмотреть обычное решение, которое я включил ниже.
Пример 2 : Рассчитайте, если возможно, произведение E и F.
Сначала проверьте, существует ли произведение двух матриц, убедившись, что количество столбцов левой матрицы E равно строк правой матрицы F.
- Матрица E (слева)
Количество столбцов = 2
- Матрица F (справа)
Количество Rows = 2
9098. E равно количеству строк матрицы F. Это означает, что произведение EF определено, поэтому мы можем продолжить и выполнить матричное умножение. Ниже показано анимированное пошаговое решение умножения матриц.Пример 3 : Рассчитайте, если возможно, произведение F и E.
В нашем предыдущем примере мы успешно получили произведение EF. На этот раз мы хотим выяснить, сможем ли мы найти произведение E[латекс] и [латекс]F в таком порядке.
Напомню, что действительные числа коммутативны при умножении, что означает, что порядок умножения не влияет на конечный продукт.
Например…
Таким образом, возникает большой вопрос, работает ли это также при умножении матриц?
Проверим, равно ли количество столбцов матрицы F количеству строк матрицы E.
- Матрица F (слева)
количество столбцов = 2
- Матрица E (справа) 9096
количество строк = 3
Очевидно, что количество столбцов матрицы F не равно количеству строк матрицы E. Отсюда следует, что произведение КЭ не может быть вычислено, а значит, не определено!
В общем случае умножение матриц не является коммутативным.
Пример 4 : Рассчитайте, если возможно, произведение AE.
Стандартный способ описания размера или размерности матрицы:…
(указать количество строк) x (указать количество столбцов)
…читается как «количество строк в Число столбцов».
3 x 3 (матрица три на три)
3 x 2 (матрица три на два)
Поскольку количество столбцов матрицы A равно количество строк матрицы E , то делаем вывод, что произведение AE определено.