Урок 43. приём деления для случаев вида 87 : 29, 66 : 22 — Математика — 3 класс

Математика, 3 класс

Урок № 43. Приём деления для случаев вида 87 : 29, 66 : 22

Перечень вопросов, рассматриваемых в теме:

1. Как разделить двузначное число на двузначное?

2. Как выполнить деление вида 87 : 29, 66 : 22?

3. Как проверить правильность результата деления?

Глоссарий по теме:

Деление – это обратное действие умножению

Умножение – это сложение одинаковых слагаемых.

Метод подбора – это способ деления двузначного числа на двузначное, при котором частное подбираем последовательно и проверяем умножением.

Обязательная и дополнительная литература:

1. Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для общеобразовательных организаций М.; Просвещение, 2017, C-18.

2. Петерсон Л. Г. Математика 3 класс. Часть 2. – М.: Ювента, 2013– 96 C., С-86.

3. Марченко И.С. Справочник школьника по математике: 1 – 4 классы. – М.: Эксмо, 2014. С. 160, (Светлячок) С. 50.

Теоретический материал для самостоятельного изучения

Рассмотрим решение задачи.

Высота дома тридцать два метра, а высота дерева – шестнадцать метров. Во сколько раз дом выше дерева?

Чтобы узнать во сколько раз дом выше, надо тридцать два разделить на шестнадцать. Получится два, в два раза. Выполнить такое деление можно

используя взаимосвязь умножения и деления. Это поможет научиться делить двузначное число на двузначное методом подбора частного.

Рассмотрим пример 48 : 12

Пробуем в частном два и проверяем. Двенадцать умножить на два получится двадцать четыре — не подходит. Пробуем- три. Двенадцать умножить на три равно тридцать шесть, тоже не подходит. Пробуем четыре. Двенадцать умножаем на четыре, получается сорок восемь, подходит. Значит, сорок восемь разделить на двенадцать получится четыре.

48 : 12

12 ∙ 2 = 24 не подходит

12 ∙ 3 = 36 не подходит

12 ∙ 4 = 48 подходит

Значит,

48 : 12 = 4

В случае деления числа шестьдесят шесть на двадцать два, подбираем число, на которое надо умножить двадцать два, чтобы получилось шестьдесят шесть. Это число три.

66 : 22

22 ∙ 3 = 66

66 : 22 = 3, так как 22 ∙ 3 = 66

Умножение нужно использовать для проверки правильности вычислений.

88 : 11 = 8, так как 11 ∙ 8 = 88

Чтобы делать меньше проб при подборе частного, нужно обратить внимание на последнюю цифру в делимом и делителе. В делимом цифра один , в делителе — цифра семь. В таблице умножения на семь находим число двадцать один (ведь один последняя цифра в делимом). Чтобы получить двадцать один, нужно семь умножить на три. Три – пробное число. Выполняем проверку.

81 : 27 = 3

Делимое 81 — последняя цифра 1

Делитель 27 — последняя цифра 7

7 ∙ 3 = 21 Проверка: 27 ∙ 3 = 81

Частное найдено, верно.

Выполним тренировочные задания

Вставьте пропущенные числа:

54 : 27 = ____ , так как 27 ∙ ___ = 54;

Ответ: 54 : 27 = 2 , так как 27∙ 2 = 54.

Зачеркните пример с ошибкой:

38 : 19 = 2

42 : 14 = 2

64 : 16 = 3

Ошибка в примере 42 : 14 = 2 и 64 : 16 = 3

Расшифруйте, расставляя ответы в порядке возрастания, название одного из самых высоких деревьев в мире:

Я 78 : 26

С 99 : 33

В 78 : 13

Й 64 : 16

К 84: 12

О 70 : 14

Е 88 : 11

Ответ:

11 8 7 6 5 4 3

С Е К В О Й Я

Как быстро умножать двузначные числа в уме?

Умение мгновенно считать в уме может стать бесценным подспорьем в работе и в условиях скоростных темпов жизни современного человека.

Как быстро умножать большие числа, как овладеть такими полезными навыками? У большинства вызывает затруднения устное перемножение двузначных чисел на однозначные. А о сложных арифметических расчетах и говорить нечего. Но при желании способности, заложенные в каждом человеке, можно развить. Регулярные тренировки, немного усилий и применение, разработанных учеными, эффективных методик позволят достичь потрясающих результатов.

Выбираем традиционные методы

Проверенные десятилетиями способы перемножения двузначных чисел не теряют своей актуальности. Простейшие приемы помогают миллионам обычных школьников, учащихся специализированных ВУЗов и лицеев, а также людям, занимающимся саморазвитием, усовершенствовать вычислительное мастерство.

Умножение с помощью разложения чисел

Наиболее легким способом, как быстро научиться умножать большие числа в уме, является перемножение десятков и единиц. Сначала умножаются десятки двух чисел, затем поочередно единицы и десятки.

Четыре полученных числа суммируются. Для использования этого метода важно уметь запоминать результаты перемножения и складывать их в уме.

Например, для умножения 38 на 57 необходимо:

• разложить число на (30+8)*(50+7);
• 30*50 = 1500 – запомнить результат;
• 30*7 + 50*8 = 210 + 400 = 610 – запомнить;
• (1500 + 610) + 8*7 = 2110 + 56 = 2166

Естественно, необходимо отлично знать таблицу умножения, так как быстро умножать в уме этим способом не удастся без соответствующих умений.

Умножение в столбик в уме

Визуальное представление привычного перемножения в столбик многие используют при расчетах. Этот метод подойдет тем, кто умеет надолго запоминать вспомогательные числа и выполнять с ними арифметические действия. Но процесс значительно упрощается, если вы научились, как быстро умножать двузначные числа на однозначные. Для перемножения, например, 47*81 нужно:

• 47*1 = 47 – запомнить;
• 47*8 = 376 – запоминаем;
• 376*10 + 47 = 3807.

Запоминать промежуточные результаты поможет проговаривание их вслух с одновременным суммированием в уме. Несмотря на сложность мысленных вычислений, после непродолжительных тренировок этот метод станет вашим любимым.

Приведенные выше способы умножения универсальны. Но знание более эффективных алгоритмов для некоторых чисел намного сократит количество расчетов.

Умножение на 11

Это, пожалуй, самый простой способ, который используется для умножения любых двузначных чисел на 11.

Достаточно между цифрами множителя вставить их сумму:
13*11 = 1(1+3)3 = 143

Если в скобках получается число больше 10, то к первой цифре добавляется единица, а из суммы в скобках вычитается 10.
28*11 = 2 (2+8) 8 = 308

Умножение больших чисел

Очень удобно перемножать числа, близкие к 100 разложением их на составляющие. Например, необходимо умножить 87 на 91.

• Каждое число необходимо представить как разницу 100 и еще одного числа:
  (100 — 13)*(100 — 9)
  Ответ будет состоять из четырех цифр, две первые из которых – разница первого множителя и вычитаемого из второй скобки или наоборот – разница второго множителя и вычитаемого из первой скобки.
  
  87 – 9 = 78
  91 – 13 = 78
• Вторые две цифры ответа — результат перемножения вычитаемых из двух скобок.13*9 = 144
• В результате получаются числа 78 и 144. Если при записывании окончательного результата получается число из 5 цифр вторую и третью цифру суммируем. Результат: 87*91 = 7944.

Это самые простые способы перемножения. После многократного их применения, доведения вычислений до автоматизма можно осваивать более сложные техники. И через некоторое время проблема, как быстро умножить двузначные числа перестанет вас волновать, а память и логика существенно улучшатся.

3 класс — Умножение чисел в столбик. Двузначные на однозначные, задачи. Свойства и примеры

Дата публикации: 12 апреля 2017.

3 КЛАСС. ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.1

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.
	44		31		89		50		21
x	8	x	4	x	0	x	8	x	6
	…		…		…		…		…
	46		67		46		35		81
x	6	x	9	x	6	x	7	x	2
	…		…		…		…		…
	73		89		60		63		33
x	7	x	1	x	4	x	1	x	8
	…		…		…		…		…
	47		27		12		61		79
x	4	x	1	x	4	x	3	x	0
	…		…		…		…		…
	51		97		33		88		76
x	3	x	0	x	4	x	4	x	3
	…		…		…		…		…
	29		37		59		86		30
x	3	x	7	x	2	x	7	x	0
	…		…		…		…		…
	85		25		90		16		71
x	6	x	5	x	7	x	9	x	3
	…		…		…		…		…
	79		52		50		73		20
x	7	x	4	x	3	x	3	x	7
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.2

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.
	79		49		74		79		31
x	7	x	5	x	2	x	3	x	7
	…		…		…		…		…
	95		82		19		17		25
x	6	x	3	x	1	x	1	x	5
	…		…		…		…		…
	71		85		96		16		31
x	6	x	7	x	1	x	9	x	4
	…		…		…		…		…
	39		64		10		55		10
x	9	x	6	x	2	x	0	x	2
	…		…		…		…		…
	75		90		83		25		24
x	1	x	2	x	8	x	8	x	4
	…		…		…		…		…
	91		54		80		68		20
x	5	x	5	x	2	x	1	x	0
	…		…		…		…		…
	11		90		26		11		62
x	6	x	1	x	6	x	2	x	3
	…		…		…		…		…
	61		19		74		27		51
x	3	x	0	x	8	x	2	x	8
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.3

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.
	44		16		24		99		65
x	5	x	2	x	8	x	8	x	6
	…		…		…		…		…
	94		66		61		62		63
x	0	x	1	x	8	x	2	x	4
	…		…		…		…		…
	50		53		79		41		73
x	2	x	8	x	9	x	7	x	5
	…		…		…		…		…
	23		96		11		75		48
x	1	x	3	x	5	x	1	x	0
	…		…		…		…		…
	10		92		37		28		46
x	4	x	1	x	3	x	1	x	9
	…		…		…		…		…
	56		65		95		97		42
x	3	x	6	x	5	x	3	x	4
	…		…		…		…		…
	31		10		48		43		76
x	1	x	7	x	3	x	2	x	6
	…		…		…		…		…
	63		14		58		80		41
x	9	x	0	x	3	x	3	x	8
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.4

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.
	31		31		17		34		81
x	0	x	0	x	6	x	7	x	7
	…		…		…		…		…
	89		72		42		27		71
x	4	x	6	x	4	x	1	x	5
	…		…		…		…		…
	73		35		96		11		19
x	6	x	3	x	7	x	3	x	4
	…		…		…		…		…
	34		76		79		12		13
x	9	x	9	x	7	x	2	x	6
	…		…		…		…		…
	27		66		99		60		86
x	9	x	0	x	2	x	2	x	6
	…		…		…		…		…
	64		49		92		55		58
x	3	x	5	x	2	x	5	x	3
	…		…		…		…		…
	97		31		70		42		38
x	8	x	2	x	8	x	8	x	6
	…		…		…		…		…
	24		83		15		71		40
x	8	x	9	x	7	x	9	x	4
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.5

Дата: __________________ ФИО: ______________________________ Оценка:__________
Умножи числа в столбик. Двузначное на однозначное.
	40		45		41		26		41
x	8	x	1	x	3	x	5	x	9
	…		…		…		…		…
	67		58		37		83		82
x	4	x	2	x	5	x	9	x	7
	…		…		…		…		…
	79		15		81		33		19
x	6	x	0	x	6	x	5	x	7
	…		…		…		…		…
	95		46		34		21		35
x	9	x	5	x	2	x	0	x	2
	…		…		…		…		…
	46		25		91		57		68
x	4	x	9	x	3	x	4	x	7
	…		…		…		…		…
	86		13		73		81		20
x	9	x	2	x	8	x	4	x	3
	…		…		…		…		…
	31		74		63		60		49
x	4	x	0	x	2	x	4	x	1
	…		…		…		…		…
	35		22		37		28		17
x	8	x	7	x	2	x	7	x	1
	…		…		…		…		…

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.1
ANSWERS.

Умножи числа в столбик. Двузначное на однозначное.
	44		31		89		50		21
x	8	x	4	x	0	x	8	x	6
	352		124		0		400		126
	46		67		46		35		81
x	6	x	9	x	6	x	7	x	2
	276		603		276		245		162
	73		89		60		63		33
x	7	x	1	x	4	x	1	x	8
	511		89		240		63		264
	47		27		12		61		79
x	4	x	1	x	4	x	3	x	0
	188		27		48		183		0
	51		97		33		88		76
x	3	x	0	x	4	x	4	x	3
	153		0		132		352		228
	29		37		59		86		30
x	3	x	7	x	2	x	7	x	0
	87		259		118		602		0
	85		25		90		16		71
x	6	x	5	x	7	x	9	x	3
	510		125		630		144		213
	79		52		50		73		20
x	7	x	4	x	3	x	3	x	7
	553		208		150		219		140

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.2
ANSWERS.

Умножи числа в столбик. Двузначное на однозначное.
	79		49		74		79		31
x	7	x	5	x	2	x	3	x	7
	553		245		148		237		217
	95		82		19		17		25
x	6	x	3	x	1	x	1	x	5
	570		246		19		17		125
	71		85		96		16		31
x	6	x	7	x	1	x	9	x	4
	426		595		96		144		124
	39		64		10		55		10
x	9	x	6	x	2	x	0	x	2
	351		384		20		0		20
	75		90		83		25		24
x	1	x	2	x	8	x	8	x	4
	75		180		664		200		96
	91		54		80		68		20
x	5	x	5	x	2	x	1	x	0
	455		270		160		68		0
	11		90		26		11		62
x	6	x	1	x	6	x	2	x	3
	66		90		156		22		186
	61		19		74		27		51
x	3	x	0	x	8	x	2	x	8
	183		0		592		54		408

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.3
ANSWERS.

Умножи числа в столбик. Двузначное на однозначное.
	44		16		24		99		65
x	5	x	2	x	8	x	8	x	6
	220		32		192		792		390
	94		66		61		62		63
x	0	x	1	x	8	x	2	x	4
	0		66		488		124		252
	50		53		79		41		73
x	2	x	8	x	9	x	7	x	5
	100		424		711		287		365
	23		96		11		75		48
x	1	x	3	x	5	x	1	x	0
	23		288		55		75		0
	10		92		37		28		46
x	4	x	1	x	3	x	1	x	9
	40		92		111		28		414
	56		65		95		97		42
x	3	x	6	x	5	x	3	x	4
	168		390		475		291		168
	31		10		48		43		76
x	1	x	7	x	3	x	2	x	6
	31		70		144		86		456
	63		14		58		80		41
x	9	x	0	x	3	x	3	x	8
	567		0		174		240		328

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.4ANSWERS.

Умножи числа в столбик. Двузначное на однозначное.
	31		31		17		34		81
x	0	x	0	x	6	x	7	x	7
	0		0		102		238		567
	89		72		42		27		71
x	4	x	6	x	4	x	1	x	5
	356		432		168		27		355
	73		35		96		11		19
x	6	x	3	x	7	x	3	x	4
	438		105		672		33		76
	34		76		79		12		13
x	9	x	9	x	7	x	2	x	6
	306		684		553		24		78
	27		66		99		60		86
x	9	x	0	x	2	x	2	x	6
	243		0		198		120		516
	64		49		92		55		58
x	3	x	5	x	2	x	5	x	3
	192		245		184		275		174
	97		31		70		42		38
x	8	x	2	x	8	x	8	x	6
	776		62		560		336		228
	24		83		15		71		40
x	8	x	9	x	7	x	9	x	4
	192		747		105		639		160

3 КЛАСС.

ЗАДАНИЯ. УМНОЖЕНИЕ.Стр.5
ANSWERS.

Умножи числа в столбик. Двузначное на однозначное.
	40		45		41		26		41
x	8	x	1	x	3	x	5	x	9
	320		45		123		130		369
	67		58		37		83		82
x	4	x	2	x	5	x	9	x	7
	268		116		185		747		574
	79		15		81		33		19
x	6	x	0	x	6	x	5	x	7
	474		0		486		165		133
	95		46		34		21		35
x	9	x	5	x	2	x	0	x	2
	855		230		68		0		70
	46		25		91		57		68
x	4	x	9	x	3	x	4	x	7
	184		225		273		228		476
	86		13		73		81		20
x	9	x	2	x	8	x	4	x	3
	774		26		584		324		60
	31		74		63		60		49
x	4	x	0	x	2	x	4	x	1
	124		0		126		240		49
	35		22		37		28		17
x	8	x	7	x	2	x	7	x	1
	280		154		74		196		17

Письменное умножение на двузначное число

Привет, ребята!

На прошлом уроке мы с вами научились умножать на двузначное число, применяя распределительное свойство умножения.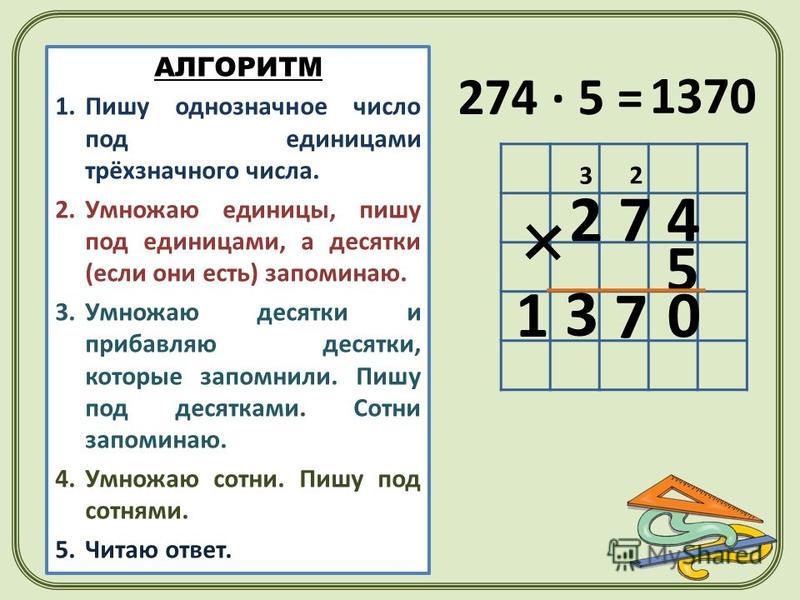 Помните, как это было? Допустим, надо перемножить числа семьдесят девять и сорок семь. Заменяем второй множитель суммой разрядных слагаемых, умножаем семьдесят девять на сорок и на семь. Складываем полученные результаты. Их ещё можно назвать неполными произведениями, потому что каждое из них – это часть всего произведения, которое равно трём тысячам семистам тринадцати.

79 · 47 = 79 · (40 + 7) = 79 · 40 + 79 · 7 = 3 160 + 553 = 3 713

Но согласитесь, что вычисление получилось не очень лёгким и довольно длинным. А ведь вы уже умеете выполнять письменный приём умножения на однозначное число. Давайте попробуем столбиком умножать и на двузначные числа.

Возьмём это же числовое выражение 79 · 47, но запишем его столбиком. Не забываем: единицы второго множителя пишем под единицами первого множителя, а десятки – под десятками. От этого правила мы отступаем только тогда, когда умножаем на числа, оканчивающиеся нулями.

Начинаем умножение. И здесь мы также воспользуемся распределительным свойством умножения. Хотя в записи столбиком есть кое-какие отличия в последовательности выполнения действий по сравнению с записью в строчку.

Во втором множителе четыре десятка и семь единиц. Умножать первый множитель сначала будем на единицы второго. Девятью семь – шестьдесят три. Три пишем, шесть запоминаем. Семь десятков умножаем на семь – сорок девять десятков, да ещё шесть десятков, которые запоминали – пятьдесят пять десятков. На единицы мы умножили. Первое неполное произведение равно пятистам пятидесяти трём.

Переходим к умножению на десятки. Теперь семьдесят девять будем умножать на четыре десятка, и поэтому записывать ответ начнём под десятками.

Девять умножаем на четыре десятка – тридцать шесть десятков. Шесть десятков пишем под десятками, а тридцать десятков, то есть три сотни, запоминаем. Семь десятков умножаем на четыре десятка – двадцать восемь, но уже сотен. Да ещё три сотни, которые запоминали, – тридцать одна сотня.

Второе неполное произведение – три тысячи, одна сотня и шесть десятков.

Теперь неполные произведения надо сложить. Единиц – три, десятков – одиннадцать. Один пишу и один запоминаю. Сотен – семь. Единиц тысяч – три. Произведение чисел семьдесят девять и сорок семь равно трём тысячам семистам тринадцати.

Ну что, ребята, вы поняли, как всё просто?! Конечно, если вы хорошо знаете таблицу умножения.

Так можно умножать не только двузначные, но и трёхзначные, четырёхзначные, любые многозначные числа на двузначные. Вот, например, хочу я умножить тысяча семьсот девятнадцать на двадцать четыре. Записываю выражение. Начинаю умножать на единицы. Девятью четыре – тридцать шесть. Шесть пишу, три десятка запоминаю. Один десяток умножить на четыре – четыре. Да ещё три – семь. Семью четыре – двадцать восемь. Восемь сотен пишу, два запоминаю. Одну тысячу умножить на четыре – четыре тысячи. Да ещё две – шесть тысяч. Первое неполное произведение – шесть тысяч восемьсот семьдесят шесть.

Умножаю тысяча семьсот девятнадцать на два десятка. Не забывайте: когда умножаем на десятки, запись начинаем под десятками.

Девять умножаем на два десятка – восемнадцать десятков. Восемь пишем под десятками, единицу запоминаем.

Один умножить на два – два. И добавляем один – три. Пишем под сотнями.

Семью два – четырнадцать. Четыре пишем под тысячами, единицу запоминаем. Один умножить на два – два, да ещё один – три. Второе неполное произведение – тридцать четыре тысячи, три сотни и восемь десятков.

Складываем неполные произведения. Получилось сорок одна тысяча двести пятьдесят шесть.

Ну что, поверим, как вы поняли способ письменного умножения на двузначное число?

Вот вам три примера. Жду вашего решения.

58 · 34; 726 · 78; 3 261 · 18

А теперь проверьте ваше решение.

Если у кого-то не такие ответы – не беда. Найдите причину своей ошибки, и тогда, я уверена, больше вы её не допустите.

Ну что, ребята, пришло время нам сегодня расстаться. Удачного дня и хороших отметок! Пока!

3 класс. Математика. Умножение суммы на число. — Умножение двузначного числа на однозначное.

Комментарии преподавателя

Если вас когда-нибудь интересовал вопрос, как можно умножить двузначное число на однозначное, если вы не поняли этот материал в школе и просто хотите самостоятельно научиться, тогда этот урок специально для вас. Мы познакомимся с приёмами, которые вам потребуются, чтобы произвести данную операцию. Также мы научимся умножать однозначное число на двузначное. Может, для этого нужны какие-то специальные навыки и умения? Давайте опровергнем или подтвердим это утверждение именно на этом уроке.

 Примеры № 1

Раз­де­лим дан­ные при­ме­ры на две груп­пы:

а)                     д) 

б)                       э) 

в)                    е) 

г)                     ё) 

После того как про­ана­ли­зи­ру­ем за­да­ние – видим, что в одном стол­би­ке будут при­ме­ры, где дву­знач­ные круг­лые числа умно­жа­ют на од­но­знач­ные. В дру­гом стол­би­ке будут про­из­ве­де­ния од­но­знач­ных чисел.

а)                     б)          

в)                    д) 

г)                     э) 

е)                     ё) 

Ре­ше­ние: 1. Для того чтобы вы­чис­лить про­из­ве­де­ния из пер­во­го стол­би­ка, можно за­ме­нить круг­лые числа их про­из­ве­де­ни­ем:

а) 

в)  

г) 

е) 

2. При­ме­ры из вто­ро­го стол­би­ка – это таб­лич­ное умно­же­ние:

б) 

д) 

э) 

ё) 

 Задача №1

Усло­вие: кот Мур­чик решал при­ме­ры (рис. 1) и раз­лич­ные ин­те­рес­ные за­да­ния. Но одно из за­да­ний не смог ре­шить:

По­мо­ги коту ре­шить при­мер.

Рис. 1. Кот Мур­чик (Ис­точ­ник)

Ре­ше­ние: 1. Кот Мур­чик не до­га­дал­ся, что число 23 можно за­ме­нить сум­мой чисел и тогда, умно­же­ние будет проще, по­то­му что при­ме­ним рас­пре­де­ли­тель­ный закон умно­же­ния:

.

2. После за­ме­ны числа 23 на сумму чисел 20 и 3, мы уви­де­ли, что, кроме таб­лич­но­го умно­же­ния, встре­ча­ет­ся ещё и умно­же­ние круг­ло­го числа, по­это­му по­сту­пим так. Круг­лое число пред­ста­вим в виде про­из­ве­де­ния:

.

3. Под­ста­вим дан­ное вы­ра­же­ние из вто­ро­го дей­ствия в фор­му­лу из пер­во­го дей­ствия и вы­пол­ним вы­чис­ле­ния:

.

 Примеры №2

а)                                б)                                в) 

Дей­ство­вать будем по ал­го­рит­му:

1. За­ме­ним боль­шое число сум­мой.

2. При­ме­ним рас­пре­де­ли­тель­ный закон умно­же­ния: про­из­ве­де­ние суммы равно сумме про­из­ве­де­ний.

3. Вы­чис­лим зна­че­ние

а) .

б) .

в) .

 Задание №1

Верно ли утвер­жде­ние, что зна­че­ния про­из­ве­де­ний в каж­дом стол­би­ке будут оди­на­ко­вы?

1.                                2. 

                         

                         

                                  

Ре­ше­ние: 1. Дву­знач­ное число за­ме­ня­ем сум­мой раз­ряд­ных сла­га­е­мых. Для пер­во­го при­ме­ра в пер­вом стол­би­ке – это де­сять и два:

.

Но число 12 можно за­ме­нить и дру­ги­ми сла­га­е­мы­ми: 8 и 4; 7 и 5. По­это­му в пер­вом стол­би­ке все зна­че­ния про­из­ве­де­ний будут оди­на­ко­вы.

2. По­смот­рим вни­ма­тель­но на вто­рой стол­бик. Для пер­во­го при­ме­ра из вто­ро­го стол­би­ка по­лу­чим сумму раз­ряд­ных сла­га­е­мых – де­сять и шесть:

.

Число 16 можно за­ме­нить дру­ги­ми сла­га­е­мы­ми, на­при­мер 7 и 9 или 8 и 8. По­это­му в этом стол­би­ке зна­че­ния про­из­ве­де­ний также будут сов­па­дать.

Можно сде­лать вывод ка­са­тель­но при­ме­ров из пер­во­го и вто­ро­го стол­би­ка – умно­жать сумму чисел легче, когда хотя бы одно из сла­га­е­мых – круг­лое число.

 Задание №2

За­ме­ни­те пер­вый дву­знач­ный мно­жи­тель в про­из­ве­де­нии  на раз­лич­ные сла­га­е­мые и вы­чис­ли­те про­из­ве­де­ние.

Ре­ше­ние: 1. При­ме­ня­ем рас­пре­де­ли­тель­ное свой­ство умно­же­ния

.

.

.

Источник конспекта: http://interneturok.ru/ru/school/matematika/3-klass/vnetablichnoe-umnozhenie-i-delenie/priyomy-umnozheniya-dlya-sluchaev-vida-23-h-4-i-4-h-23?seconds=0

Источник видео: https://www.youtube.com/watch?v=ZVmrQ-FlRxM

Деление двузначного числа на двузначное способом подбора. (3 класс)

1. ГБОУ «Гимназия №1592»СП №2043

Урок – путешествие
по математике в 3 «В» классе
по теме: Деление вида 87 : 29; 66 : 22
Учитель начальных классов: Мамедоразова Г.Н.

2. Цели и задачи урока:

Образовательные:
научить делить двузначное число на двузначное
способом подбора;
совершенствовать навыки решения задач изученных
видов;
формирование положительной мотивации учения.
Развивающие:
развивать вычислительные навыки, логическое
мышление, математическую речь.
Воспитательные:
воспитание в детях стремление вести здоровый образ
жизни.

3. Я умею думать, Я умею рассуждать. Что полезно для здоровья, То и буду выбирать.

5. Устный счет. 1). Составьте различные примеры на умножение и деление, используя только эти числа. 9, 24, 3, 8, 12, 48, 4, 6, 2, 18.

2). Прочитайте только те, которые делятся на 5, на 8, на 9.
36, 40, 6, 15, 9, 72, 45, 64, 30, 32, 27.
3) Решите задачи.
•В воскресенье в поход пошли 28 мальчиков, а девочек в 4 раза меньше.
Сколько девочек пошло в поход?
•В течение четырёх дней врач принимал каждый день по 10
больных, а на пятый день он принял 19 больных. Сколько больных
принял за 5 дней?
•Площадь листа квадратной формы 48 см2, чему равна одна ее
сторона?

6. Все отлично

Хорошо
Надо чутьчуть
постараться
Хорошее
настроение

7.

14  7 14 7=98
98 : 14=7
7 14=98
98 : 7=14

8. Работа с учебником. №1, с.18 24 : 12; 45 : 15; 88 : 44

2
3
2

9. Физкультминутка

Активный образ жизни

10. 1. Пираты поймали 81 рыбу. Решили засолить ее в бочки по 27 штук в каждой. Сколько бочек понадобилось?

Решение задач
2. На острове пираты с одной пальмы собрали
32 кг бананов, а с другой 48 кг. Разложили все
бананы по ящикам по 8 кг в каждом ящике.
Сколько всего ящиков потребовалось?
Рациональное
питание

11. Тренировочные задания

№ 2 (3 столбик), с 18 – стандарт «3»
№ 4, с.18
— хорошо «4»
№ 5, с.18
— отлично «5»

Приёмы быстрых вычислений

На олимпиаде Кенгуру и на Внешнем независимом тестировании запрещено пользоваться калькуляторами. Поэтому очень важно научиться тратить на вычисления как можно меньше времени, чтобы использовать его на обдумывание задач.

Умножение двузначного числа на 11

Чтобы двузначное число умножить на 11, сложите его первую и последнюю цифру. Если результат будет однозначным, впишите его между двумя цифрами первоначального числа, а если двузначным – прибавьте первую цифру результата к первой цифре первоначального числа, а вторую – впишите между цифрами.

Примеры:
45х11
Складываем 4+5=9. Поэтому результатом будет 495.

76х11
Складываем 7+6=13. Единицу прибавляем к семёрке, а тройку пишем в середину и получаем 836.

Математическое обоснование:
Пусть нужно двузначное число 10a+b. Умножить на 11. Результатом будет 110a+11b = 100a +10 (a+b) +b

Умножение и деление на 5 и 25

Чтобы число умножить число на 5, его нужно разделить на 2 и умножить на 10. Чтобы число разделить на 5, его нужно умножить на 2 и разделить на 10.

Аналогично, умножение/деление на 25 заменяется делением/умножением на 4 и умножением/делением на 100

Примеры:
36х5
Делим 36 на 2, получаем 18. Умножаем 18 на 10 и получаем 180.

3/5
Умножаем 3 на 2 и получаем 6. Делим 6 на 10 и получаем 0,6

45/25
Умножаем 45 на 4, получаем 180. Делим 180 на 100, получаем 1,8

84х25
Делим 84 на 4, получаем 21. Умножаем 21 на 100 и получаем 2100.

Математическое обоснование:
Поскольку 5=10/2, умножение/деление на 2 можно свести к более простым умножениям/делениям на 2 и 10.

Возведение в квадрат числа, оканчивающегося на 5

Чтобы возвести в квадрат число, оканчивающееся пятёркой, нужно умножить число, полученное отбрасыванием последней пятёрки на следующее в натуральном ряду, и к результату приписать 25.

Примеры:
65²
Умножаем 6 на 7, получаем 42. Приписываем 25, получаем 4225.

115²
Умножаем 11 на 12, получаем 132. Приписываем 25, получаем 13225.

Математическое обоснование:
Возведём в квадрат число 10n+5. (10n+5)² = 100n²+100n+25 = 100n(n+1)+25, откуда и следует данное правило.

Возведение в квадрат числа, близкого к круглому

Целесообразно воспользоваться формулами квадрата суммы или разности.

Примеры:
19² = (20-1)² = 400–40+1=361

42² = (40+2)² = 1600+160+4 = 1764

Математическое обоснование:
Формула квадрата суммы: (a+b)² = a²+2ab+b²
Формула квадрата разности: (a-b)² = a²–2ab+b²

Вычитание из степени десятки

Для вычитания числа из степени десятки, нужно последнюю его цифру заменить дополнением до десяти, а остальные (включая первые виртуальные нули) – дополнениями до девяти.

Примеры:
1000-725 = (9-7)(9-2)(10-5) = 275
100000 – 1237 = 100000 – 01237 = (9-0)(9-1)(9-2)(9-3)(10-7) = 98763

Математическое обоснование:
Правило следует из алгоритма вычитания столбиком.

Прибавление числа, близкого к степени десятки

Вместо прибавления числа, состоящего из девяток и оканчивающегося на 9 (8, 7, 6 и т.д.), прибавьте следующую большую степень десятки и вычтите 1 (2, 3, 4 и.т.д)

Примеры:
125+999 = 1125-1 = 1124
6528+996 =7258-4=7254

Математическое обоснование:
Для k-значного числа 99…9 = 100..00 – 1

Упрощённые признаки делимости на 4 и 8

Обычно для проверки делимости на 4 применяется следующий признак: Если двуциферное окончание числа делится на 4, то и само число делится на 4.

Однако, использовав обобщённый признак делимости, заметим, что число 10 даёт остаток 2 при делении на 4. Поэтому переформулируем правило так: Если сумма последней цифры с удвоенной предпоследней делится на 4, то и само число делится на 4.

Аналогично для делимости на 8. Вместо проверки на делимость трёхциферного окончания, можно выполнять проверку суммы последней, удвоенной предпоследней и учетверённой третьей с конца цифры.

Примеры:
Число 1324
4+2*2=8 – делится на 4.
4+2*2+3*4=20 – не делится на 8

Число 6328
8+2*2=12 – делится на 4.
8+2*2+3*4=24 – делится на 8

Математическое обоснование:
Обобщённый признак делимости подробно рассмотрен в отдельной статье.

NumberNut.com: Арифметика: Сложение: двузначные числа

Добавление двузначных чисел похоже на добавление однозначных значений, вы просто выполняете процесс сложения более одного раза. Когда вы складываете двузначные числа, вы складываете столбцов вместе, а не целые числа. Например, вы не захотите складывать в уме 78 и 57 как полные числа. Эти числа легче разбить на небольшие части. Вы должны начать с добавления чисел в столбце единиц , а затем перейти к сумме чисел в столбце десятков .Этот пример был немного сложным, потому что он включает в себя переноску. Давайте посмотрим на несколько простых примеров …

24 + 45 = 69
37 + 11 = 48
82 + 6 = 88

Вот еще один способ увидеть проблему. Вам будет легче решить их в формате по вертикали (вверх и вниз), когда вы начнете с сложения. Намного легче увидеть, как числа выстраиваются в столбцы. В этом примере столбец единиц добавляет до девяти (9), а столбец десятков добавляет до шести (6).

Не забывайте всегда работать влево. Вы запишете свои дополнения, выстроив те столбцы, которые выстроены в линию, а затем начнете добавлять. Если вы закончите с одним столбцом, в котором нет значения для десятков, это нормально. Просто представьте это как ноль. Любое число, добавленное к нулю, есть само.
Следующая задача при добавлении двузначных чисел состоит в том, что вы добавляете числа, которые включают с или с перегруппировкой . Мы уже немного говорили о переноске в предыдущем уроке. Если сумма из одного столбца больше девяти (9), вы переносите «1» в следующий столбец слева.

Что делать, если у вас проблема 78 + 57? Вы должны начать с столбца единиц (8 + 7 = 15). Запишите «5» в своем ответе и переместите «1» в столбец десятков. Следующим шагом будет сложение всех значений из столбца десятков (1 + 7 + 5). Это сумма «13», которую вы запишите в своем ответе. Ваша окончательная сумма будет «135».

Пример:

78 + 57 ? 1 78 + 57 5 78 + 57 13 5

Дополнительные примеры:
48 + 32 = 80
(8 + 2 = 10, напишите 0 и перенесите 1, 1 + 4 + 3 = 8)

29 + 29 = 58
(9 + 9 = 18, напишите 8 и перенесите 1, 1 + 2 + 2 = 5)

95 + 16 = 111
(5 + 6 = 11, напишите 1 и перенесите 1, 1 + 9 + 1 = 11)

75 + 87 = 162
(5 + 7 = 12, запишите 2 и перенесите 1, 1 + 7 + 8 = 16)

Сложение двух двузначных чисел с перегруппировкой — математика для 2-го класса

Научитесь складывать двузначные числа с перегруппировкой

Вы помните, как складывать двузначные числа? 🤔

Рассмотрим на примере.

33 + 21

Сначала напишите числа в форме столбца !

🤓 Совет: Напишите Единицы справа (👉).

Затем начните с добавления столбца Ones .

Затем добавьте столбец Десятки.

Отличная работа!

Теперь давайте посмотрим, что происходит, когда добавляемые числа становятся немного больше.

Перегруппировка

Давайте решим это уравнение:

16 + 78 =?

Сначала запишем уравнение в виде столбцов .

Затем мы сначала добавляем единицы.

Что такое 6 + 8?

6 + 8 = 14

Это 14!

Но вы не можете написать 14 вместо единицы. Есть место только для 1 цифры!

👍Нужно перегруппироваться!

Перегруппировка — это когда вы берете 10 единиц и превращаете их в 1 десятку!

Давайте создадим счетчики только для Единственных.

Что такое 6 + 8?

одна группа десятков

четыре единицы

Мы помещаем 4 в столбец «Единицы».

Мы помещаем 1 десятку в столбец «Десятки».

Теперь добавим Десятки.

Наш ответ — 94.

Молодец! 🙌

Другой пример

А теперь попробуем без счетчиков.

29 + 35 =?

Какой первый шаг?

Правильно, форма столбца !

Когда мы складываем Единицы, получаем 14.

Нам нужно перенести «1» в столбец Десятки.

Теперь мы можем добавить Десятки.

1 + 2 + 3 = 6

Отличная работа! 💪 Вы получили это!

Смотри и учись

А теперь пора практиковаться!

номеров до 2 цифр | Решенные примеры | Номера

В этом видео вы вместе с Ритой и Джоэлем подсчитываете палочки на ферме. Не упустите трюк, который использует Рита, когда палочек больше 10.

Содержание

Мы в Cuemath считаем, что математика — это жизненный навык.Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Учащиеся могут исследовать огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.

Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.

Концепт Видео по номерам

Посмотрите это видео о том, как числа знакомят детей Cuemath Way!

Давайте разберемся, почему? за что!

---

Введение в числа до 2-х цифр

Мы начинаем считать числа на пальцах наших рук в очень молодом возрасте, а затем переходим к использованию суперкомпьютеров для вычисления очень больших чисел.

Каким бы ни было количество цифр в числе, правильное расположение каждой цифры является наиболее важным.

Сегодня мы поговорим о двузначных числах, но перед этим познакомимся с однозначными числами.

Имеется 10 однозначных чисел — \ (0,1,2,3,4,5,6,7,8 \) и \ (9 \)

Все двузначные или двузначные числа, которые мы обсудим, являются комбинациями любых двух из девяти из этих десяти чисел.

Да, 0 не всегда считается, и мы вернемся к этому позже.

Посмотрите это моделирование, чтобы увидеть, как двузначное число представлено в блоках и стержнях.

10 блоков, соединенных вместе, образуют стержень.

10 единиц равно 1 десятке.

---

Большая идея: числа до 2-х цифр

Простая идея: разряды чисел

Каждое число, состоящее из более чем одной цифры, должно иметь разные цифры, описываемые их разрядами .

Разрядные значения, которые мы используем, — это единицы, десятки, сотни, тысячи, десять тысяч и так далее.

Вы заметите, что каждое из следующих подряд значений разряда в десять раз больше предыдущего.

Когда мы ограничиваемся 2-значными числами, мы имеем дело только с двумя разрядами — единиц и десятков .

Допустим, вы покупаете мороженое в магазине, и к вам на обед приходят 5 друзей.

Включая родителей, вам нужно 5 \ (+ \) You \ (+ \) Parents = 8 мороженого.

Вы можете пойти в магазин и купить 8 единиц мороженого.

Если вы пригласите весь класс домой, когда будете готовы бросить школу, у вас будет 33 друга \ (+ \) вы \ (+ \) ваши родители = 36 мороженого.

Итак, вы возьмете 3 ванны, чтобы получить эквивалент 30 мороженого.

Кроме того, вы возьмете 6 стаканчиков мороженого, всего получится 36 мороженых.

Именно это и происходит, когда мы создаем двузначные числа.

Присвоение значений мест

Итак, каждый набор из десяти единиц превращается в число с десятичной ценностью, точно так же, как продавец сделал 1 ванну, объединив 10 чашек мороженого.

Давайте посмотрим на 3 набора чисел, чтобы понять преобразование единиц в комбинацию единиц и десятков:

\ (\ begin {align} & {\ text {33 единицы: 3 десятки + 3 единицы}} \\ & {\ text {8 единиц: 1 десять + 8 единиц}} \\ & {\ text {27 единиц: 2 Десятки + 3 единицы}} \ end {align} \)

Я уверен, что вы смогли разобрать, что только первый правильный.

Во втором неверно разряжаются десятки, а в третьем — единицы.

Вот какие правильные комбинации будут для обоих наборов:

\ (\ begin {align} {3 \ text {Десятки} + 3 \ text {Units} \\ = (3 \ times 10) + (3 \ times 1) \\ = 30 + 3 = 33} \\ { 1 \ text {Десять} + 8 \ text {Единицы} \\ = (1 \ times 10) + (8 \ times 1) \\ = 10 + 8 = 18} \\ {\ text {2 Tens} + 3 \ текст {Единицы} \\ = (2 \ times 10) + (3 \ times 1) \\ = 20 + 3 = 23} \ end {align} \)

\ (\ begin {align} & 33 \ text {units:} \\ & (3 \ times 10) + (3 \ times 1) \\ & = 30 + 3 = 33 \\ & 8 \ text {units:} \\ & (0 \ times 10) + (8 \ times 1) \\ & = 0 + 8 = 8 \\ & 27 \ text {units:} \\ & (2 \ times 10) + (7 \ times 1 ) \\ & = 20 + 7 = 27 \ end {align} \)

Некоторые общие 2-значные числа

Посмотрим, знаете ли вы ответы на следующие 5 вопросов:

1. Сколько цифр в дюжине?
2. Что считается несчастливым числом?
3. Что такое оценка?
4. Сколько ярдов в длину поле для крикета?
5. Какое число составляет четверть века?

Ответы на приведенные выше вопросы по порядку: \ (12, 13, 20, 22 \) и \ (25. \) Все эти пять чисел являются двузначными числами.

Есть сомнения, что вы хотите очистить? Получите разъяснения с помощью простых решений на 2-значных числах от наших экспертов по математике в LIVE, персонализированных и интерактивных онлайн-классах Cuemath.

Сделайте своего ребенка экспертом по математике, Забронируйте БЕСПЛАТНЫЙ пробный урок сегодня!

---

Двухзначный номер

Всего 90 двузначных номеров, начиная с 10-99

Вот список всех 2-значных чисел от 10-99

---

Как найти количество цифр в числе?

Мы увидели, как с помощью руки можно считать числа от 1 до 10

Мы также можем использовать счетчики, блоки и стержни для подсчета и номеров кадров.

Однозначное число будет содержать только одну цифру от 0 до 9

Двухзначное число будет состоять из двух цифр: одно в разряде десятков, а другое — в разряде единиц.

Пример: 25 — это двухзначное число, где 2 в разряде десятков и 5 в разряде единиц.

Точно так же трехзначное число будет состоять из трех цифр.

Пример: 134 — это трехзначное число, где 1 в разряде сотен, 3 в разряде десятков и 4 в разряде единиц.

Можете ли вы сказать, сколько цифр будет в 5-значном числе?

---

Насколько это важно?

Значение (или иное) нуля в двузначных числах

Мы уже знаем, что двузначное число может быть образовано комбинацией двух из 10 цифр от 0 до 10

А как насчет тех чисел, у которых 0 в десятичном значении?

Давайте рассмотрим число, которое образовалось бы из нуля в разряде десятков и пяти в разряде единицы.

Число: \ (\ begin {align} (0 \ times 10) + (5 \ times 1) = 0 + 5 = 5 \ end {align} \)

Цифра десятков не может быть 0, потому что она фактически становится однозначным числом.

Но это не тот случай, когда ноль стоит на месте единицы.

Давайте на этот раз попробуем поменять числа и возьмем пять в разряде десятков и ноль в разрядах единиц.

Число: \ (\ begin {align} (5 \ times 10) + (0 \ times 1) = 50 + 0 = 50 \ end {align} \)

Итак, когда дело доходит до нуля, есть девять вариантов, в которых ноль вместо десяти, когда полученное число представляет собой однозначное число, независимо от того, какое число стоит на месте единицы.

Помогите детям воспринимать числа как гибкие величины.

Полезный совет — попросить студентов разбивать числа разными способами.

Напр. 15 — это 10 и еще 5.
При этом 15 — это тоже 14 и еще 1.
Также на 11 и 4 больше.

Часто играйте в эту игру с разными числами.
Начните с маленьких чисел, например 15 и 20, а затем переходите к большим числам, например 32 и 46

.

Помогите детям привыкнуть к счету пропусков по 10
Они должны иметь возможность пропускать счет на 10 из любого числа.
Начните с серии 10, 20, 30, . .. но затем создайте комфорт, попросив учащихся пропустить счет на 10 с любой другой начальной точки.
Например. с 23:23, 33, 43, 53, …

Перечислите числа по 10 в одной строке и по одной во второй строке.
Покажите образцы того, как можно составить числа от 11 до 99, комбинируя десятки и единицы.

Сложные вопросы

1. Я двузначное четное число больше 6 + 6 и меньше 15.Найди меня!
2. Я — двухзначное число от 50 до 60, и моя единица измерения — это количество сторон квадрата.
3. У меня двухзначное четное число больше 80 и меньше 90, а сумма моих цифр равна 12. Найди меня!

Распространенные ошибки или заблуждения

• Дети могут часто произносить все числа до 99 (или 100), но могут ошибаться , когда их просят найти большее число между двумя числами.
  Студенты иногда произносят числа от 1 до 100, как будто они запомнили буквы алфавита.
  Если это произойдет, то найти большее число 14 и 15 так же сложно, как найти большую букву между C и D.
  Дети должны понимать, что, в отличие от букв, числа связаны друг с другом.
  15 ровно на единицу больше 14
  Для этого используйте числовые линии, цветные счетчики, чтобы связать звук с количеством.

• Дети склонны к ошибаться при работе с числами, когда значение разряда десятков меняется на .
  Например. при переходе с 19 до 20, с 29 до 30, с 39 до 40 и т. д.
  Часто двузначные числа вводятся без ссылки на разрядные значения.
  Хотя это облегчает запоминание чисел, это, возможно, не лучшая стратегия, поскольку дети не видят числа, составленные из общего набора цифр — от 0 до 9
  Лучше всего использовать счеты для моделирования чисел и использовать блоки Base-10, чтобы помочь им визуализировать числа.

• Дети допускают ошибки при написании чисел .
  Особенно с одиннадцати до девятнадцати.
  Практике нет замены.
  Дети должны практиковаться в написании числовых имен.
  Как правило, эту ошибку можно легко исправить с помощью небольшой преднамеренной и целенаправленной практики.

Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь пройти тест сейчас.

---

Решенные примеры

Райан сказал: «В числе 100000 6 цифр». Можете ли вы посчитать количество цифр в номере и подтвердить, прав ли он?

Решение:

Подсчитав количество цифр в 100000, можно заметить, что в числе 5 нулей и 1 единица.

Таким образом, это шестизначное число.

\ (\ следовательно \) Райан прав

Номер состоит из двух цифр.

7 в разряде десятков и 5 разрядах.

Что это за номер и напишите его номер имя?

Решение:

Разместим числа в таблице значений разряда.

Десятки	Единицы Место
7	5

Число 75 или семьдесят пять.

\ (\ следовательно \) Номер 75

Обозначьте двузначные числа, представленные блоками и стержнями, показанными ниже.

Решение:

Синие стержни представляют место десятков, а желтые блоки — место единиц.

С. №	Десятки	Единицы Место	Число
а)	2	8	28
б)	2	1	21
в)	1	2	12
г)	3	0	30

\ (\ следовательно \) Цифры: a) 28 b) 21 c) 12 и d) 30

Найдите сумму наибольшего двузначного числа и наименьшего двузначного числа.

Найдите количество цифр в найденном числе

Решение:

Наибольшее двузначное число — 99, наименьшее двузначное число — 10

Их сумма равна \ (99 + 10 = 109 \)

109 состоит из 3 цифр, это 3-значное число.

\ (\ следовательно \) сумма 109 и трехзначное число

Что является предшественником и преемником разности наибольшего двузначного числа и числа 20?

Решение:

Наибольшее двузначное число = 99

Разница между 99 и 20 равна \ (99-20 = 79 \)

Предшественник 79 — 78, преемник 79 — 80

\ (\ следовательно \) Предшественник — 78, а преемник — 80

Найдите сумму чисел, показанных на счетах.

Решение:

Давайте сначала определим числа, а затем сложим их.

С. №	Десятки	Единицы Место	Число
1	3	3	33
2	2	8	28
3	1	3	13
Сумма			74

\ (\ следовательно \) сумма 74

---

Практические вопросы

Вот несколько занятий для вас.

Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Важные примечания

1. Наименьшее двузначное число — 10, а наибольшее двузначное число — 99.
2. Всего 90 двузначных чисел.
3. 10 единиц составляет 1 Десятку.
4. Двузначное число не может начинаться с 0, поэтому разряд десятков может иметь любое число от 1 до 9.

Образцы материалов олимпиады по математике

IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.

Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:

Чтобы узнать больше об олимпиаде по математике, вы можете нажмите здесь

---

Часто задаваемые вопросы (FAQ)

1.Сколько там двузначных чисел?

Всего 90 двузначных чисел.

2. Как складывать двузначные числа?

1. К разряду единиц второго числа прибавляем место единиц первого числа.
2. Складываем разряды десятков первого числа с разрядами десятков второго числа.
3. Если есть переходящий остаток на шаге — 1 прибавьте его к разряду десятков.

\ (\ begin {align}
& 29 \
+ & 34 \
& — \\
= \: & 6 3 \\
& —
\ end {align} \)

3.Какое двузначное число является наибольшим?

Наибольшее двузначное число — 99.

4. Какое первое двузначное число?

Первое двузначное число — 10.

Видеоурок: Сложение двухзначных чисел в столбцы

Стенограмма видео

Добавление двух цифр в столбец Номера

В этом видео мы узнаем как сложить два двузначных числа методом столбца.Вот два двузначных числа, 27 и 45. Цифра десятков в числе 27 — это два. 27 имеет две десятки. Мы можем смоделировать это с помощью числовой стоимости блоки. И цифра десятков в числе 45 это четверка. Мы можем смоделировать это с помощью четырех десятков блоки. Две десятки стоят 20. Четыре десятки стоят 40.

В двузначных числах также есть единицы. цифра. Цифра из единиц в числе 27 — это семь. Мы можем смоделировать семь из 27 используя блоки из семи единиц.И пять цифр в числе 45 стоит пять. Мы смоделировали это с помощью пяти блоки.

Когда мы складываем два числа, используя В столбце сложения пишем числа друг над другом. Сначала добавляем единицы, а затем десятки. Начнем с добавления единиц в тот столбец. Мы уже знаем, что 27 имеет семь единиц, а 45 — пять. Вот наши семь из номер 27.И мы можем добавить пять из число 45. Сколько у нас их все вместе? Семь плюс пять составляют 12. Можете ли вы заметить преднамеренное ошибка? Мы можем написать только одну цифру в один столбец. Как только мы достигнем 10 единиц, мы должны обменять их на один 10-секундный блок. Итак, у нас есть два в одном столбец. И мы должны написать 10, которые мы обменялись в столбце десятков. Мы написали это в квадрате над нашими двумя десятками и четырьмя десятками, чтобы не забыть добавить это, когда мы подойдем к добавление столбца десятков.

Теперь, когда мы закончили добавлять столбец единиц, нам нужно добавить десятки. У 27 две десятки, а у числа 45 имеет четыре десятки. Две десятки плюс четыре десятки дают нам всего шесть десятков. Но не забудьте добавить 10 мы обменялись. Шесть десятков плюс еще 10 дают нам всего семь десятков. 27 плюс 45 равно 72.

Итак, когда мы складываем два двузначных числа числа, используя метод сложения столбцов, сначала мы записываем наши числа в столбцы.Мы всегда сначала добавляем столбец единиц на случай, если нам нужно перегруппироваться. А потом складываем десятки. Давайте попробуем задать несколько вопросов, чтобы Помогите нам попрактиковаться в сложении двух двузначных чисел методом столбца.

Найдите 42 плюс 29. Подсказка: вам нужно перегруппировать их? сделать 10?

В этом вопросе мы должны найти сумма двух двузначных чисел 42 и 29. И мы видим, что Расчет проводился столбцовым методом.Мы видим, что 42 имеет четыре десятки и два. И мы добавляем 29, в котором два 10 и девять единиц. Мы всегда начинаем с добавления один столбец. Нам нужно добавить два и девять. Два и девять — это 11. Но мы можем записать только одну цифру в наша колонка. Мы знаем, что 11 это 10 и один более. Итак, мы записываем единичную цифру в один столбец и один 10 в столбце десятков. 11 — это одна 10 и одна одна. Мы обменяли 10 штук на одного 10.И мы написали это 10 над нашим другие десятки, чтобы напомнить нам, что нужно добавить их к другим десяткам, когда мы добавляем десятки столбец.

Теперь мы можем складывать десятки. У нас четыре десятки в числе 42 и две десятки в числе 29. Четыре десятки плюс две десятки дают нам всего шесть десятков. Но не будем забывать, что у нас есть еще 10, которые мы обменяли. Шесть десятков плюс одна десятка дают нам всего семь десятков. Мы добавили 42 и 29, чтобы получить ответ 71.Сначала мы добавили те, и мы их всего 11. Итак, нам пришлось перегруппировать 10 наших чтобы получить 10. Затем мы добавили наши десятки. У нас было шесть десятков, и мы добавили одну мы перегруппировались, что дало нам семь десятков. 42 плюс 29 равно 71.

Найдите сумму. Подсказка: добавьте те, а затем добавьте десятки. 52 плюс 17 равняется чему.

В этом вопросе мы должны найти сумма 52 и 17. И нам дается подсказка.Сначала мы должны добавить единицы, и затем нам нужно добавить десятки. Начнем с добавления единиц. 52 имеет две единицы, а число 17 их семь. Что такое два плюс семь? Два плюс семь — девять. Всего у нас девять единицы. Теперь нам нужно добавить десятки. У 52 пять десятков, а у числа 17 имеет одну 10. Пять десятков плюс одна десятка дает нам всего шесть десятков. Сумма 52 и 17 равна 69.

Найдите сумму.Подсказка: добавьте единицы, а затем десятки. Что происходит, когда их больше чем 10? 54 плюс 37 равняется чему.

В этом вопросе мы должны найти сумма двух двузначных чисел 54 и 37. Мы можем сказать по тому, как эта сумма Было указано, что мы должны использовать метод сложения столбцов. Мы должны начать с добавления единицы. 54 — четыре, а 37 — семь единицы. Четыре плюс семь дает нам в сумме 11 шт.И мы знаем, что число 11 — это состоит из одной 10 и одной. Таким образом, мы можем написать одно в единицах столбец. И мы должны перегруппировать 10 наших единицы и обменять их на 10.

В этом расчете мы написали 10 мы обменяли на другие десятки. Иногда мы пишем этот номер в верхняя часть остальных десятков. Где бы мы ни писали 10, мы поменяны, мы должны не забыть добавить его при добавлении в столбец десятков.Добавим десятки. 54 имеет пять десятков. 37 имеет три десятки. Пять десятков плюс три десятки дают нам Всего восемь десятков плюс одна, которую мы обменяли, дает нам в общей сложности девять. Пять плюс три плюс один равно девять. Сумма 54 и 37 дает 91.

Хлоя пролила на себя чернила домашнее задание. Найдите закрытые номера.

Первая сумма Хлои 28 плюс еще одно двузначное число. 28 плюс что-то равно 89. И мы видим, что у Хлои пролила чернила на одну из цифр в своем расчете.Если мы начнем с добавления единиц, восемь единиц плюс один дает нам девять единиц. Что Хлоя добавила к своим двум десяткам дать ей восемь десятков? Мы знаем, что две десятки плюс шесть десятков дает нам восемь десятков, потому что два плюс шесть равно восьми. Итак, недостающая цифра в десятках столбец — шестерка. 28 плюс 61 равно 89.

На вторую сумму Хлои пролились чернила на одной из цифр. Тридцать с чем-то плюс 23 равно 58.Так что нам просто нужно найти недостающее одна цифра. Что мы добавляем к трем, чтобы дать нам всего восемь? Мы знаем, что три плюс пять равно восемь. 35 плюс 23 равно 58. Таким образом, пропущенная цифра — пять. Пять плюс три равно восемь.

В последней сумме Хлои два цифры были покрыты чернилами. 64 плюс 79. Давайте начнем с размышлений о недостающая цифра.64 имеет четыре единицы, а у нас есть всего девять. Что нам нужно добавить к четырем к дайте нам девять? Мы знаем, что четыре плюс пять — это девять. Итак, недостающая цифра — это пять. Теперь найдем недостающие десятки цифра. 64 имеет шесть десятков, а у нас всего из семи десятков. Шесть плюс один равняется семи. Таким образом, недостающая цифра десятков — это один. Шесть 10 плюс одна 10 равняются семи 10сек.Итак, недостающий номер в этом вычисление 15. 64 плюс 15 равно 79.

Мы использовали метод сложения столбцов чтобы помочь нам найти недостающие цифры. Отсутствующий номер в первом сложение — шесть, второе недостающее число — пять, а третье недостающее число — 15.

Что мы узнали из этого видео? Мы научились складывать два двузначные числа с использованием добавления столбцов. Мы узнали, что сначала добавляем один столбец, а затем мы добавляем столбец десятков.

Практика с двузначными числами — бесплатное занятие по математике для 1 класса

Это примеры упражнений, которые помогают детям выучить двузначные числа и разряды с десятками и единицами в 1 классе.

1. Заполнить.

2. Добавьте десять, нарисовав еще один столбец из десяти. Вычтите десять, вычеркнув десятиколонный.

3. Объяснить своему учителю, как вы добавляете десять к числу или вычитаете десять.

а. 61 + 10 = ______ 61 — 10 = ______

г. 37 + 10 = ______ 37 — 10 = ______

г. 89 + 10 = ______ 89 — 10 = ______

4. Сопоставьте номер с его именем.

16 60 23 32 76 14 12 двенадцать четырнадцать шестнадцать тридцать два шестьдесят двадцать три семьдесят шесть

90 29 11 19 91 39 93 одиннадцать девятнадцать девяносто три девяносто один двадцать девять тридцать девять девяносто

5.Запишите каждое число как (десятки) + (единицы).

а. 91 = _____ + _____

г. 79 = _____ + _____

г. 58 = _____ + _____

6. Доп.

а. 20 + 6 = _______ 80 + 2 = _______

г. 60 + 7 = _______ 10 + 1 = _______

г. 6 + 50 = _______ 5 + 30 = _______

7. Заполнить.

Мне от 84 до 92. У меня их нет. Кто я?

---

Авторские права HomeschoolMath.net.

---

AAA Сейчас

• AAAKnow имеет полный набор из тысяч интерактивные уроки арифметики .
• не требует затрат или регистрации. требуется для практики. math на сайте AAAKnow.com.
• Неограниченная практика доступно по каждой теме, что позволяет доскональное владение концепциями.
• широкий спектр уроков (от детского сада до восьмого класса). level) позволяет обучению или обзору происходить на текущем уровне каждого человека.
• Немедленная обратная связь предотвращает неправильную практику и обучение методы, что является обычным результатом традиционных домашних заданий и рабочих листов. Практика может продолжаться сколько угодно долго в безопасном формате, который помогает повысить самооценку и уверенность в себе.
• Попробуйте уроки , нажав на один из оценки вверху или в области темы в левой части страницы.
• Не забудьте добавить сайт в «Любимые места» и рассказать другим о сайт. — отличный способ выучить или повторить математику .

Что нового в AAA Know?

Веб-сайт AAAMath.com начал свою работу в 2000 году и предлагал бесплатные интерактивные уроки математики по основам арифметики и связанным с ней темам математики для K-8.Мы считали, что этот подход лучше, чем традиционные рабочие листы, потому что он обеспечивает немедленную обратную связь, тогда как рабочие листы позволяют студентам неоднократно практиковать неправильные методы, прежде чем они будут оценены.

AAAKnow.com был зеркалом AAAMath.com, который использовался для обработки высоких нагрузок трафика. По сути, они были одинаковыми. Когда переписывание AAAMath.com в современный формат было завершено, мы решили разместить его на сайте AAAKnow.com. Таким образом люди все еще могли использовать AAAMath.com, если они предпочитают его, и могут опробовать и использовать новый формат, если они предпочитают его.

AAAMath.com

1. Использует старый веб-формат.
2. Оригинальные уроки
3. Не работает с мобильными устройствами
4. В основном для настольных компьютеров
5. Новые уроки будут ссылками на AAAKnow.com
6. Все уроки старого формата будут по-прежнему доступны
7. Интерактивные уроки математики
8. Без оплаты или регистрации
9. Неограниченная практика
10. Мгновенная обратная связь предотвращает отработку неправильных методов.
11. Отличный способ выучить математику
12. Может быть изменен на новый формат в будущем

AAA Сейчас.com

1. Использует современный веб-формат.
2. Практически идентичные уроки
3. Хорошо работает с мобильными устройствами
4. Для любого типа компьютера
5. На сайте будут разработаны новые уроки
6. Все уроки старого формата будут по-прежнему доступны
7. Интерактивные уроки математики
8. Без оплаты или регистрации
9. Неограниченная практика
10. Мгновенная обратная связь предотвращает отработку неправильных методов.
11. Отличный способ выучить математику
12. Будет и дальше развиваться

Пожалуйста, дайте нам знать, если у вас есть какие-либо предложения или комментарии о веб-сайте AAAKnow.com, используя форму обратной связи для анонимных комментариев.

Рабочие листы для сложения двух цифр

Сумма до 20

На этих листах для 1-го класса сложите двузначные и однозначные числа с суммой до 20.

Стандарт:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

с проблемами Word:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

• Загрузить все

2-значный плюс однозначный

Сложите двузначное и однозначное число, расположенное по вертикали. Эти распечатываемые двузначные таблицы сложения для 2-го класса помогут вам развить навыки перегруппировки, а не сложения перегруппировки.

Без перегруппировки:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Захвати все

Без перегруппировки с проблемами Word:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Захвати все

Перегруппировка:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Grab ’em All

Перегруппировка с проблемами Word:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Захвати все

• Загрузить все

Добавление 2-значных чисел с проблемами со словами

На каждом листе для 1-го и 2-го классов 12 стандартных 2-значных сложений и 2 задачи со словами.

Без перегруппировки:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Захвати все

Перегруппировка:

Лист 1 | Лист 2 | Лист 3 | Лист 4 | Лист 5

Захвати все

• Загрузить все

Упражнение по сложению двухзначных столбцов: без перегруппировки

В этом разделе содержатся упражнения по добавлению столбцов без дополнительных перегруппировок.

15 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

25 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

50 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

75 за страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

100 на страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

• Загрузить все

Упражнение по сложению 2-значного столбца: перегруппировка

Найдите сумму двухзначных слагаемых.Требуется перегруппировка (переноска). У вас есть дополнительные упражнения на выбор от 15 до 100 на страницу.

15 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

25 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

50 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

75 за страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

100 на страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

• Загрузить все

Горизонтальное двухзначное сложение: без перегруппировки

Развивайте свои математические навыки, решая эти задачи на сложение по горизонтали.

15 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

25 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

50 на странице:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

75 за страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

100 на страницу:

Лист 1 | Лист 2 | Лист 3 | Хватай их всех

• Загрузить все

Горизонтальное двухзначное сложение: перегруппировка

упражнений на сложение с двумя цифрами в этом разделе содержат перегруппированные рабочие листы сложения с добавлениями, расположенными вдоль ряда.