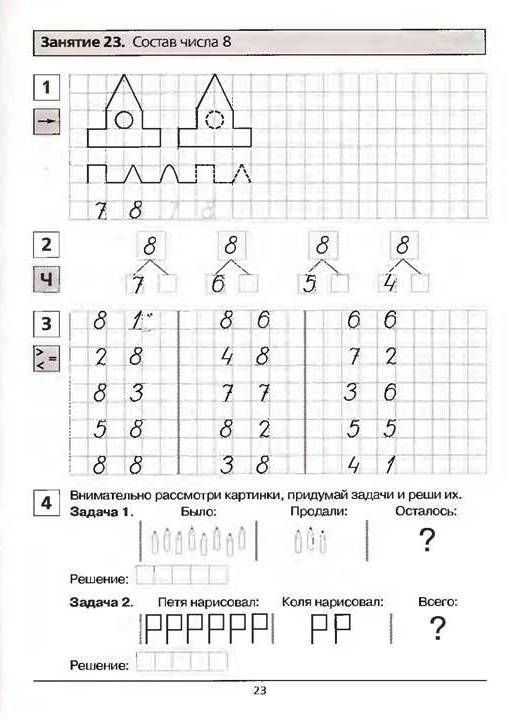
«Число и цифра 6. Состав числа 6»

Цели:

знать

1. Цифру 6 как знак, используемый для записи числа.

2. Название, последовательность чисел от 1 до 10.

3. Знаки сравнения

4. Ряд однозначных чисел и его состав.

уметь

1. Читать, записывать и сравнивать однозначные числа.

2. Выполнять действия сложения и вычитания с использованием 1 и 0.

3. Составлать, читать, записывать и находить значение числовых выражений содержащее одно действие.

4. Применять полученные знания на практике.

Визуальный инструментарий: карточки, схемы.

ХОД УРОКА

1. Эмоциональный настрой.

Ребята, сегодня урок математики пройдёт под девизом “Больше думай, меньше говори”. Итак, в течение всего урока мы должны думать, а отвлекаться и разговаривать как можно меньше.

А теперь давайте поприветствуем друг друга.

Доброе утро солнце!
Доброе утро небо!
Доброе утро я!
Доброе утро вся страна!

2. Актуализация знаний.

Учитель читает стихотворение.

Чтоб врачом, моряком или лётчиком стать,
Надо, прежде всего математику знать.
И на свете нет профессий, вы заметьте-ка,
Где бы вам не пригодилась – математика!

А теперь послушайте загадку.

Что за вишенка, дружок
Кверху загнут стебелёк?
Ты её попробуй съесть,
Эта вишня цифра …6.

Работа в прописи. Показ написания цифры 6, дети обводят по точкам, далее пишут самостоятельно. А как получается число 6? При помощи иллюстраций геометрических фигур ученики делают вывод, что

5 + 1 = 6

6 — 1 = 5

3. Закрепление.

— Устный счёт

Родились у мамы-кошки
Шесть котят, такие крошки!
Как котята подрастали,
Их ребятам раздавали.
Лишь двоих оставили пока.
Остальных котят с утра
Разобрала детвора.
Сколько маленьких котят
Оставалось у ребят?

6 – 4 = 2

На лесной опушке сидят
Три зайчихи-старушки
Да тут же возле них
Пляшут трое молодых.
Сосчитайте поскорей
Сколько было всех зверей?

3 + 3 = 6

(В.Н.Савичев)

— Найди соседей числа.

— Найди пропущенные числа

4. Пальчиковая игра.

Утро настало
Солнышко встало
(Вращательные движения ладонями рук)
(Левая рука зажата в кулак, правая рука разжимает пальцы левой)
Вставай большак,
Вставай указка,
Вставай серёдка,
Вставай сиротка.
И, ты крошечка-митрошечка,
Привет, ладошечка.
(Хлопок в ладоши)
Затем, тоже самое с правой рукой.

5. Индивидуальная работа (карточки).

— Дидактическая игра “Правильно–неправильно”

Цели: различать правильное и зеркальное изображение цифровых знаков.

— Цифра потерялась

— Найди ошибку.

0+6=0 6-1=0

1+5=6 6-6=0

4+2=5 6-3=2

6. Закрепление и повторение.

— Впиши последующее число

— Математический диктант. Запиши цифрами и геометрическими фигурами.

Шесть треугольников, три квадрата, четыре круга.

— Напиши цифры по порядку

3, 5, 4, 1, 6, 2, 0.

7. Физминутка.

Видишь, бабочка летает,
(Машем руками-крылышками)
На лугу цветы считает.
(Считаем пальчиком)
— Раз, два, три, четыре, пять.
(Хлопки в ладоши)
Ох, считать, не сосчитать!
(Прыжки на месте)
За день, за два и за месяц…
(Шагаем на месте)
Шесть, семь, восемь, девять, десять.

(Хлопки в ладоши)
Даже мудрая пчела
(Машем руками-крылышками.)
Сосчитать бы не смогла!
(Считаем пальчиком)

(Г.Виеру)

8. Работа в прописи.

Вставь пропущенные числа

9. Итог урока. Релаксация (фронтально).

А) — Назови шесть имён девочек.

— Шестой месяц года.

— Шестой день недели.

— Шестую букву алфавита.

— Шесть имён мальчиков.

Б) Прямой и обратный счёт.

— Назови числа от 1 до 10 по порядку.

— От 2 до 6, от 10 до 6.

— Какое число, следующее за 5, за 3, за 1.

— Какое число между 4 и 6, 3 и 5, 0 и 2.

В) Что лишнее?

— Понедельник, сентябрь, октябрь.

— Волк, собака, лиса.

Г) Засели домики.

10. Домашнее задание.

Реши примеры.

2 +4 = 6 – 1= 3 + 3=

6 – 0 = 6 – 6 = 1 + 5 =

— Что узнали нового?

— Понравился ли вам урок?

— Вы не забыли, под каким девизом мы работали?

Молодцы! На уроке математике мы с вами думали, а разговаривать старались меньше. За урок все получают звёздочки и квадратики.

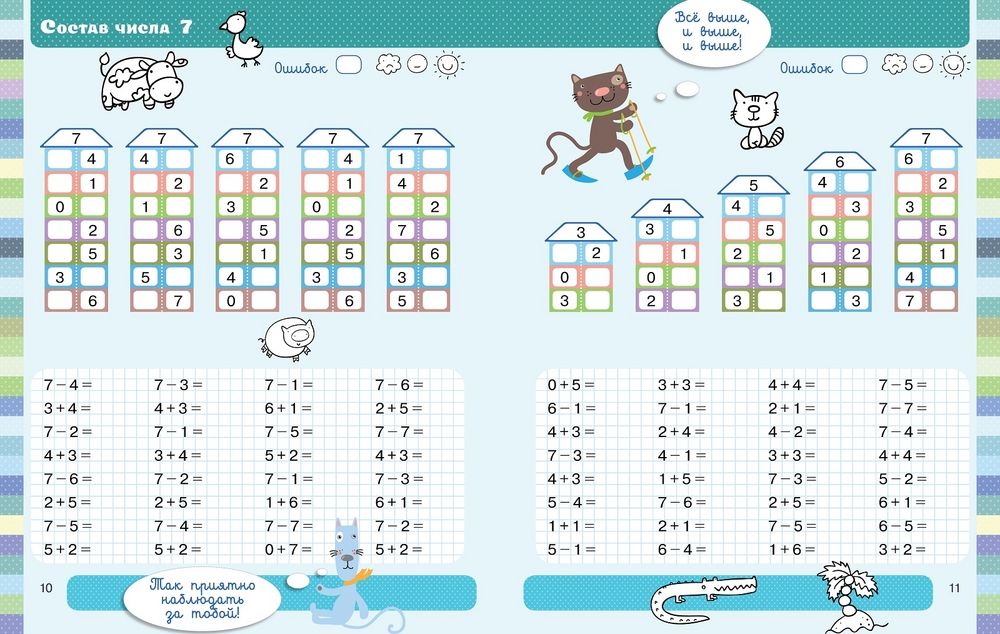
Состав числа 6, 7, 8, 9: урок математики в 1 классе

Цели и задачи урока:

• Совершенствовать навыки табличного сложения.

• Закрепить умения решать задачи.

• Развивать речь, память, внимание, логическое мышление, математические способности.

• Воспитывать гуманное отношение друг к другу, умению выслушивать мнения каждого.

УУД

Регулятивные: определяют план выполнения задания, применяют изученные способы действия для решения задач в различных ситуациях.

Познавательные: перерабатывают полученную информацию: сравнивают и группируют математические объекты: числа, числовые выражения, равенства и неравенства.

Коммуникативные: решают совместно с соседом по парте поставленную задачу, обдумывают, обмениваются своими мнениями.

Личностные: осваивают роль «хорошего» ученика, регулируют своё поведение на основе усвоенных норм и правил.

Формы работы: индивидуальная, самостоятельная, фронтальная.

ХОД УРОКА

Организационный момент

Цель ‒ настроить учащихся для плодотворной работы на уроке, организовать внимание учащихся.

Вход под весёлую музыку…

А ну-ка, дети, встаньте в ряд!

Готов к работе мой отряд?

Занимай свои места.

Математика сложна.

Но скажу с почтеньем

Математика нужна

Всем без исключения!

— Прежде чем начать, урок создадим себе и друг другу хорошее настроение. А хорошее настроение начинается с улыбки. Улыбнёмся друг другу. Думаю, что сегодняшний день принесёт нам радость и удачу.

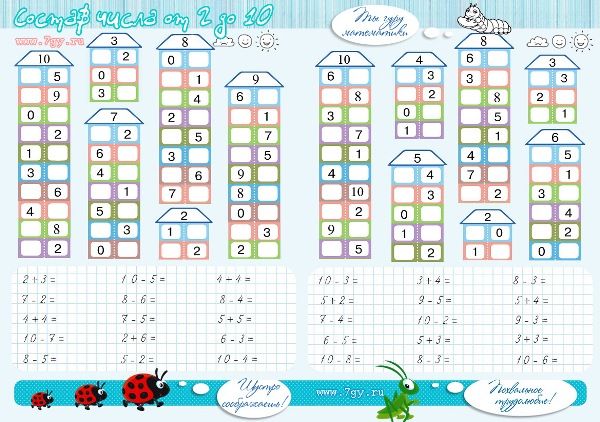
— Назовите тему сегодняшнего урока. (Состав числа 6, 7, 8, 9)

— Скажите, чему мы будем сегодня учиться? (Решать учебные задачи. Повторять составы изученных чисел.)

— Вам предстоит проявить свою находчивость, показать свои успехи в нашей теме, для того, чтобы в будущем уметь решать более сложные задачи и математические выражения.

— Ребята, отгадайте загадку.

Ветви белой краской разукрашу,

Брошу серебро на крышу вашу.

Тёплые весной придут ветра

И меня прогонят со двора.

Что это? (Зима)

— Сегодня 12-й день зимы. Назовите месяц. Сегодня 12 декабря. А какое число было вчера? Какое число будет завтра? В декабре мы встречаем самый радостный праздник, назовите его.

— Вы любите новый год?

— Ребята, у меня для вас сюрприз.

— Нам пришло звуковое письмо из города Великий Устюг (на слайде Родина Деда Мороза).

Послушайте его.

(Голос на магнитофоне)

«Дорогие ребята! Это пишу вам я, Дед Мороз. Прежде чем отправиться к вам в путь, я решил узнать, какие у вас успехи в учебе? Шлю вам мой морозный привет. До скорой встречи на новогоднем представлении! Ваш Дед Мороз.»

— Ребята, давайте покажем, что у нас отличные успехи…

— А поможет нам в работе …. Угадайте, кто это? (Загадка о снеговике)

Мы слепили снежный ком,

Шляпу сделали на нем,

Нос приделали и в миг Получился... Въезжает снеговик.

Актуализация знаний

Работа с натуральным рядом чисел.

Сегодня посланец Деда Мороза Снеговик предлагает математические задания.

Первое ‒ Поработать с числами.

— Ой, а где же наши числа, наверное их раздул по классу зимний ветер. Давайте соберём их. (По классу развешаны карточки с цифрами 5, 2, 8, 3, и др.) Дети собирают цифры и крепят на доску.

— Запишите числа в порядке возрастания.

Работа в тетради (Я тетрадочку открою…) Правила посадки!

Там, где точка через клетку.

Постановка проблемы.

— Давайте придумаем ещё задания с этими числами.

— Предлагаю сравнить числа.

— Клетку от написанного вниз запись сравнения, запись двух неравенств.

— Как вы думаете, используя только эти числа, можно ли составить числовые выражения?

— Запись в тетрадях. (2 выражения) Состав каких чисел повторили?

Снеговик доволен вашей работой. Предлагает отдохнуть.

Физминутка для глаз

Внимание! Послушайте загадку:

Колкую, зелёную

Срубили топором.

Красивую, зелёную

Принесли к нам в дом.

— Что же принесли в дом? (ёлку)

На слайдах природа зимнего леса.

Каждая ёлочка мечтает оказаться в праздничном зале.

Постановка учебной задачи на слайде «Наряди ёлочку».

А вот и наша гостья. Снеговик предлагает выполнить следующую учебную задачу. Нарядить ёлочку шарами. Но не всё так просто.

— Давайте исследуем, какие шары можно повесить на нашу зелёную красавицу. А для этого нам понадобятся наши знания. Ведь шары можно вешать только … зная состав чисел.

Игра «Наряди ёлочку»

Вывод…

(Молодцы, мы со Снеговиком довольны, как вы справились с заданием. Ребята, мы со Снеговиком увидели, что ещё не все ребята дают правильные ответы, некоторые путаются, но это не беда, потому что на следующих уроках мы продолжим совершенствовать свои знания.)

— Пока мы наряжали ёлочку, нам пришло по электронной почте письмо из Великого Устюга от Деда Мороза. (на слайде электронное письмо)

— Давайте прочитаем его содержание.

— Что нам предстоит выполнить? (решить логическую задачу)

Решение логической задачи.

На уроке технологии Миша вырезал несколько снежинок, а Маша столько же. Теперь у ребят 8 снежинок. Сколько вырезал каждый? (на слайде)

— Молодцы. Состав какого числа мы повторили?

Физпауза

Работа по учебнику.

— Напомните, мне чему мы учимся? (Повторяем составы изученных чисел)

— Новый год ‒ это праздник волшебства. Я предлагаю вам оказаться в роли волшебников. Откройте учебники на стр. 107, № 256 (1 столбик).

— Математические выражения заколдованы. Подумайте, какую работу предстоит выполнить? (вычислить) Для работы понадобится веер.

Молодцы!

Работа с геометрическим материалом.

— У вас в пакетиках геометрические фигуры. Достаньте их.

— Назовите фигуры. (Треугольник, круги, четырёхугольники. ) Снеговик предлагает провести эксперимент.

— «Кто самый внимательный?» Он просит из данных фигур выполнить портрет его друга. (на слайде снеговик из фигур) Даётся 15 сек.

Проверка.

— Какая фигура оказалась лишней?

— Молодцы! (убрали фигуры)

— Вы были внимательными. Такое задание тренирует вашу память, развивает мыслительную деятельность. Я довольна, что все справились с заданием.

Самостоятельная работа

— Наш Снеговик взял с собой волшебный сундучок. Что же в нём? Снежки. Не простые, а с заданиями. Подумайте, какую работу предстоит выполнить? (Вставить числа, что бы равенства были верные)

Проверка на слайде с правильными ответами.

— Давайте оценим свой успех по шкале правильности. У кого всё правильно?

— Ставим х возле верхней планки.

— Если 1-2 ошибки ‒ х посередине.

— Если больше 2 ошибок ‒ х внизу.

(Молодцы, я довольна вашими результатами.)

(Ничего страшного, на следующих урокам мы продолжим работу и у вас всё получится)

— Все задания на сегодняшнем уроке направлены на поверку знаний состава чисел. Без них мы бы не смогли выполнить одно из сложных заданий урока. Вы готовы с ним справиться?

Мультимедийная игра «Кроссворд»

Итог Молодцы! Приятно работать с такими замечательными детьми!

Рефлексия

Предлагаю оценить свою работу смайликами.

— Очень понравилось, всё понял.

— Буду внимательным, есть трудности.

— Что-то огорчило, не понял.

– Снеговик благодарит всех за работу! И Деду Морозу обязательно доложит о наших успехах!

– Спасибо за урок!

Составные числа — определение, список, свойства и примеры

В математике составные числа — это числа, имеющие более двух делителей. Эти номера также называются составными . Составные числа — это полная противоположность простым числам, у которых есть только два делителя, то есть 1 и само число. Все натуральные числа, не являющиеся простыми, являются составными числами, так как их можно разделить более чем на два числа. Например, 6 является составным числом, потому что оно делится на 1, 2, 3 и даже на 6. В этой статье мы узнаем определение составных чисел, свойства, наименьшее составное число, четные и нечетные составные числа, список составные числа и разница между простыми и составными числами, а также множество решенных примеров в деталях.

Содержание: Определение Примеры Свойства Список составных чисел Как найти составное число Типы составных номеров Нечетный Четный Наименьшее составное число Разница между простыми и составными числами Прост-факторизация составного числа Решенные примеры Практические вопросы Часто задаваемые вопросы

Что такое составные числа в математике?

Определение 1: В математике составными числами называются числа, имеющие более двух делителей.

Определение 2: Числа, которые могут быть получены путем умножения двух наименьших положительных целых чисел и содержат хотя бы один делитель, отличный от числа «1» и самого себя, называются составными числами. Эти числа всегда имеют более двух множителей.

Факт: Любое четное число, большее 2, является составным числом.

Является ли 0 составным числом?

Ноль (0) не считается ни простым, ни составным числом, поскольку у него нет делителей.

Примеры составных чисел

Примерами составных чисел являются 6, 14, 25, 30, 52 и т. д., например:

Составные номера	Факторы
6	1, 2, 3, 6
14	1, 2, 7, 14
25	1, 5, 25
30	1, 2, 3, 5, 6, 10, 15, 30
52	1, 2, 4, 13, 26, 52

Во всех приведенных выше примерах составные числа имеют более двух делителей. Есть ряд составных чисел, которые мы можем перечислить из набора натуральных чисел от 1 до 1000 и более. Давайте посмотрим список составных чисел в следующем разделе.

Свойства составных чисел

Свойства составных чисел легко запомнить.

• Составные числа имеют более двух делителей
• Составные числа делятся без остатка на свои множители
• Каждое составное число само по себе является множителем
• Наименьшее составное число 4
• Каждое составное число будет включать как минимум два простых числа в качестве множителей (например, 10 = 2 x 5, где 2 и 5 — простые числа)
• Составные числа также делятся на другие составные числа

Список составных номеров

Вот список составных чисел от 1 до 100 по математике. Учащиеся могут записать это, а также попытаться написать числа после 100 для практики, такие как составные от 1 до 200 или до 500.

Таблица составных чисел

Составные числа от 1 до 200

Целые положительные числа, имеющие более двух делителей, являются составными числами.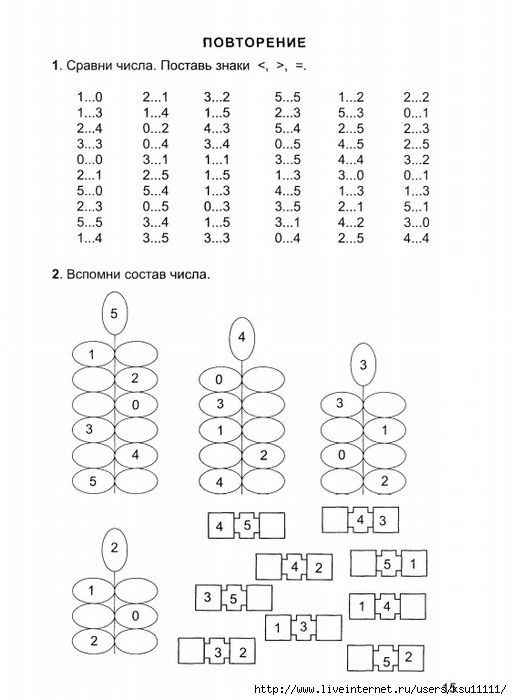 Список составных чисел от 1 до 200 приведен ниже в таблице.

4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 129, 130, 132, 133, 134, 135, 136, 138, 140, 141, 142, 143, 144, 145, 146, 147, 148, 150, 152, 154, 155, 156, 157, 158, 159, 160, 162, 164, 165, 166, 168, 170, 172, 174, 175, 176, 177, 178, 180, 182, 184, 185, 186, 187, 188, 189, 190, 192, 194, 195 , 196 и 198.

Как найти составной номер?

Процедуры определения того, является ли заданное число простым или составным:

• Найдите все делители натурального числа
• Число называется простым, если оно имеет только два делителя: 1 и само
.
• Если число имеет более двух делителей, то оно составное

Пример: Найдите, является ли 14 составным числом. Найдем множители числа 14. 14÷1 = 14 14÷2 = 7 14÷7 = 2 14÷14 = 1 Как мы видим, множители числа 14 равны 1,2,7 и 14, так что это составное число.

Типы составных чисел

В математике есть два основных типа составных чисел:

• Нечетные составные числа или составные нечетные числа
• Четные составные числа или Составные четные числа

Нечетные составные числа

Все нечетные целые числа, не являющиеся простыми, являются нечетными составными числами. Примеры составных нечетных чисел: 9, 15, 21, 25, 27, 31 и т. д.

.

Четные составные числа

Все четные целые числа, не являющиеся простыми, являются четными составными числами. Примеры четных составных чисел: 4, 6, 8, 10, 12, 14, 16 и т. д.

Наименьшее составное число

4 — наименьшее составное число.

Почему?

1 не является составным числом, потому что единственный делитель 1 равен 1. Целые положительные числа 2 и 3 являются простыми числами, потому что их можно разделить только на два множителя: единицу и само себя. Значит 2 и 3 не составные.

Но в случае с числом 4 у нас больше двух множителей. Делители 4 равны 1,2,4. Таким образом, это число удовлетворяет условию составного числа, как указано выше. После 4 6 является следующим составным положительным целым числом, которое имеет делители 1, 2, 3 и 6.

Следовательно, 4 — наименьшее составное число (доказано).

Важные примечания по составным номерам Наименьшее составное число = 4 Наименьшее простое число = 2 Наименьшее нечетное составное число = 9 Двузначное наименьшее составное число = 10

Разница между простыми и составными числами

Различия между простыми и составными числами в математике перечислены ниже:

Простые числа	Составные номера
Делится только на 1 и на себя, поэтому имеет только два множителя.	Имеет более двух факторов (1 и саму себя).
Можно записать только как произведение двух чисел	Можно записать как произведение двух или более чисел
Пример: 5 имеет делители 1 и 5	Пример: 4 имеет делители 1, 2 и 4

Простая факторизация составных чисел

Здесь приведен список составных числительных от 1 до 50 с их разложением на простые множители. Здесь вы можете увидеть, как составные части разложены на простые числа. Проверьте приведенную ниже таблицу, чтобы лучше понять. С помощью этой таблицы вы также можете найти составные числа за пределами 50 с их простой факторизацией.

Составные номера	Факторизация простых чисел
4	2 × 2
6	2 × 3
8	2 × 2 × 2
9	3 × 3
10	2 × 5
12	2 × 2 × 3
14	2 × 7
15	3 × 5
16	2 × 2 × 2 × 2
18	2 × 3 × 3
20	2 × 2 × 5
21	3 × 7
22	2 × 11
24	2 × 2 × 2 × 3
25	5 × 5
26	2 × 13
27	3 × 3 × 3
28	2 × 2 × 7
30	2 × 3 × 5
32	2 × 2 × 2 × 2 × 2
33	3 × 11
34	2 × 17
35	5 × 7
36	2 × 2 × 3 × 3
38	2 × 19
39	3  × 13
40	2 × 2 × 2 × 5
42	2 × 3 × 7
44 ​​	2 × 2 × 11
45	3 × 3 × 5
46	2 × 23
48	2 × 2 × 2 × 2 × 3
49	7 × 7
50	2 × 5 × 5

Видео урок о числах

Связанные статьи

• Простые и составные числа
• Простая факторизация
• Простые, составные и четные, нечетные числа

Решенные задачи на составные числа

Пример 1:

Определите, является ли 328 составным числом.

Решение:

Делители числа 328 равны 1, 2, 4, 8, 41, 82, 164, 328.

Следовательно, 328 — составное число.

Пример 2:

Какова простая факторизация числа 60?

Решение:

Разложение числа 60 на простые множители:

60 = 2 × 2 × 3 × 5.

Пример 3:

Перечислите составные числа из заданного набора чисел.

2, 4, 9, 11, 21, 31, 44, 53, 67, 88, 101, 108.

Решение:

Составные числа: 4, 9, 21, 44, 88, 108.

Пример 4:

Найдите произведение первых 5 составных чисел.

Решение:

Первые 5 составных чисел: 4, 6, 8, 9, 10.

Следовательно, произведение первых 5 составных чисел = 4 × 6 × 8 × 9 × 10

= 17280

Таким образом, произведение первых пяти составных чисел равно 17280.

Практические вопросы (рабочий лист)

1. Список составных чисел от 20 до 30.
2. Определите, является ли 85 составным числом.
3. Каковы простые делители числа 99?
4. Чему равна сумма делителей составного числа 18?
5. Найдите составные числа среди следующего набора чисел в данной таблице.

7	18	33	11
6	13	90	21
98	5	63	19
61	52	2	81

Чтобы узнать больше о различных типах чисел, загрузите BYJU’S -The Learning App из магазина Google Play и посмотрите интерактивные видеоролики.

Часто задаваемые вопросы о составных номерах

Что такое составной номер?

Составное число — это натуральное или положительное целое число, имеющее более двух делителей. Например, 15 имеет делители 1, 3, 5 и 15, следовательно, это составное число.

Является ли 2 составным числом?

Нет, 2 не является составным числом, потому что оно имеет только два делителя, то есть 1 и 2. Следовательно, это простое число.

Является ли 9 составным числом?

Да, 9 — составное число, потому что оно имеет более двух делителей, например 1, 3 и 9.

Какие составные числа от 1 до 100?

Список составных чисел от 1 до 100:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81,82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100.

Является ли число 19 простым или составным?

19 — простое число, потому что оно имеет только два делителя, то есть 1 и 19.

Является ли 1 составным числом?

Нет, потому что у 1 не более двух множителей, а только 1 множитель. Следовательно, оно не является ни простым, ни составным.

Сколько составных чисел от 1 до 10?

Есть четыре составных числа от 1 до 10. Это 4,6,8 и 9.

Является ли 49 составным числом?

Да, 49 — составное число, потому что оно содержит более 2 делителей. Делители 49 равны 1, 7 и 49.

Домен композиции | Колледж Алгебра

Результаты обучения

• Найдите область определения составной функции.
• Разложить составную функцию.

Как мы обсуждали ранее, домен составной функции , такой как [latex]f\circ g[/latex], зависит от домена [latex]g[/latex] и домена [latex]f [/латекс]. Важно знать, когда мы можем применять составную функцию, а когда нет, то есть знать область определения такой функции, как [latex]f\circ g[/latex]. Предположим, что мы знаем области определения функций [latex]f[/latex] и [latex]g[/latex] по отдельности. Если мы напишем составную функцию для ввода [латекс]x[/латекс] как [латекс]f\left(g\left(x\right)\right)[/латекс], мы сразу увидим, что [латекс] x[/latex] должен быть членом домена [latex]g[/latex] для того, чтобы выражение имело смысл, потому что в противном случае мы не сможем завершить вычисление внутренней функции.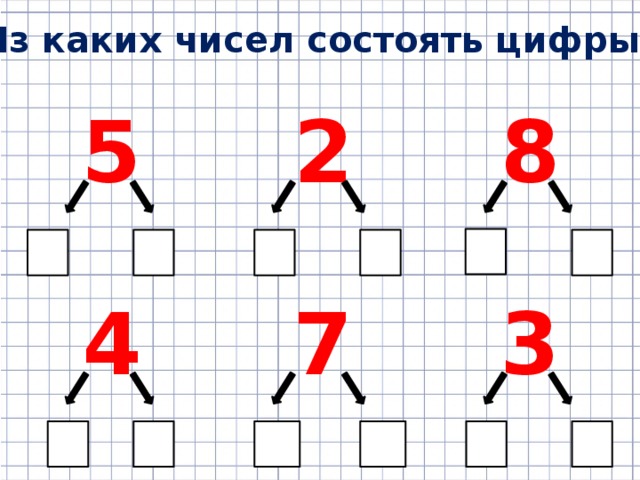 Однако мы также видим, что [latex]g\left(x\right)[/latex] должен быть членом домена [latex]f[/latex], иначе вычисление второй функции в [latex]f\left (g\left(x\right)\right)[/latex] не может быть завершено, и выражение по-прежнему не определено. Таким образом, домен [latex]f\circ g[/latex] состоит только из тех входных данных в домене [latex]g[/latex], которые производят выходные данные из [latex]g[/latex], принадлежащие домену [ латекс]ф[/латекс]. Обратите внимание, что домен [latex]f[/latex], составленный из [latex]g[/latex], представляет собой набор всех [latex]x[/latex], таких что [latex]x[/latex] находится в домене из [latex]g[/latex] и [latex]g\left(x\right)[/latex] находится в домене [latex]f[/latex].

Общее примечание. Область определения составной функции

Область определения составной функции [latex]f\left(g\left(x\right)\right)[/latex] — это набор этих входных данных [latex] x[/latex] в домене [latex]g[/latex], для которого [latex]g\left(x\right)[/latex] находится в домене [latex]f[/latex].

Как сделать: по заданной композиции функций [latex]f\left(g\left(x\right)\right)[/latex] определите ее область определения.

1. Найдите домен [latex]g[/latex].
2. Найдите домен [latex]f[/latex].
3. Найдите те входные данные, [latex]x[/latex], в домене [latex]g[/latex], для которых [latex]g(x)[/latex] находится в домене [latex]f[/ латекс]. То есть исключить из домена [latex]g[/latex] те входные данные, [latex]x[/latex], для которых [latex]g(x)[/latex] не входит в домен [latex]. ж[/латекс]. Полученный набор является доменом [latex]f\circ g[/latex].

Пример: нахождение области определения сложной функции справа)=\dfrac{5}{x — 1}\text{ и}g\left(x\right)=\dfrac{4}{3x — 2}[/latex]

Показать решение

Пример: нахождение области определения составной функции, включающей радикалы x\right)=\sqrt{x+2}\text{ и }g\left(x\right)=\sqrt{3-x}[/latex]

Показать решение

Попробуйте

Найдите домен

[latex]\left(f\circ g\right)\left(x\right)\text{где}f\left(x\right)=\dfrac{1 }{x — 2}\text{ и }g\left(x\right)=\sqrt{x+4}[/latex]

Показать решение

Попробуйте

Мы можем использовать графики, чтобы визуализировать домен, который является результатом композиции двух функций.