«Состав числа 4. Счёт до 4.»
МКОУ «Линевская школа- интернат для обучающихся с ОВЗ»
Конспект урока в 1 классе
по теме:
«Состав числа 4. Счёт до 4.»
Подготовила и провела:
учитель начальных классов
Игнатова Н.Н
р.п. Линёво
Конспект урока математики в 1 классе
Тема урока: Состав числа 4. Счёт до 4.
Цель урока: знакомство учащихся с составом числа 4.
Задачи урока:
научить как получить число 4 из двух более меньших чисел, называть предыдущие и последующие числа. Решать примеры в пределах 4;
развивать математическую речь, вычислительные навыки;
воспитывать положительную мотивацию к обучению; формировать социальные представления об окружающем мире.
ХОД УРОКА
Орг.
момент
Прозвенел, друзья, звонок,
Начинается урок
Вы проснуться все успели?
А теперь вперёд за дело
Математика нас ждёт,
Начинаем устный счёт.
Устный счёт
Счет от 1 до 10 в прямом и обратном порядке чисел
Назовите число, которое при счете идет за числом 2,3 ,перед числом 2,4.
Назовите соседей числа 2(1,3)Соседи числа 3(2,4)
Из норки выглянул барсук,
Уселась белочка на сук,
Вспорхнул на ветку воробей,
На тропку выполз муравей –
Все улыбнулись солнцу!
Сколько всего животных улыбнулись солнцу?
4. Однажды Леший с Водяным
Бродили по местам грибным.
И нашли под елью скоро
Два огромных мухомора.
Походили у осин и нашли ещё один.
Сколько грибов нашли друзья?
5. Мышка, лягушка, ёж, петушок
Строили в поле себе теремок.
Сделали крышу, крыльцо и окошки
И протоптали к дому дорожки.
Сколько животных строили теремок?
6.
Три зелёные лягушки
Сидели на опушке.
Одна им подмигнула
И в озеро нырнула.
Сколько лягушек осталось на опушке?
7.Четыре снегиря на ветке сидели.
Два снегиря от них улетели.
— Сколько ж осталось? – подумал медведь.
А ты сосчитал? Медведю ответь!
3. Сообщение темы и цели урока. Мотивация учебной деятельности.
—Сегодня будет необычный урок, а урок-сказка, которую мы составим вместе с вами. А кто будет героем нашей сказки, вы мне подскажете, когда отгадаете загадку.
Формой он похож на мяч. Был когда-то он горяч.
Спрыгнул со стола на пол, И от бабушки ушел.
У него румяный бок… Вы, узнали? (КОЛОБОК).
Точно, это был Колобок.
—Кто помнит, кого встретил Колобок во время своего путешествия, когда ушел от бабушки и дедушки? Назовите.
—Сколько всего зверей встретил Колобок?
—С числом и цифрой 4 мы уже знакомы, а сегодня мы узнаем, как получить число 4 из двух более меньших чисел, будем решать примеры, используя известные нам числа.
Все знания, полученные сегодня, пригодятся нам в дальнейшем на уроках математики, а так же в жизни.
В конце урока мы должны будем заселить домики, в котором живет цифра 4
Кто стоит первым?
—Перед лисой?
—После волка?
—Кто стоит вторым?
—А между медведем и зайцем?
2)—Кто мне сможет найти цифру 4 на наборном полотне?
—На что похожа цифра 4 — вспомним
«Ставим стульчик вверх ногами
И … «четвёрка» перед нами
4.Физминутка
Сколько ёлочек зелёных,
Столько выполним наклонов.
Сколько здесь у нас кружков,
Столько сделаем прыжков.
5.Работа по теме урока
Пальчиковая гимнастика
Минутка чистописания.
Чтоб уметь писать красиво надо правильно сидеть.
На пол ровно ножки ставить, Головою не вертеть.
Проверь рукою расстояние От парты до своей груди
Склони головку чуть-чуть на бок И ручку правильно держи.
Лежал Колобок на окошке, студился, взял и покатился.
Нарисуем дорожку, по которой покатился Колобок.
1.Работа в тетради:
—Найдите в тетрадях строчку с цифрой 4. Напишите сначала 4 цифры. Выберите самую красивую и подчеркните её. И также напишите другие до конца строки.
—Катится Колобок дальше, смотрит, сидит Заяц, сидит, горюет, не может сосчитать грибочки. Поможем зайчику…
—Катится Колобок, песни поет, цветами любуется, птиц слушает. Выкатился на поляну, видит – Медведь, Мне надо сосчитать цветы. А я совсем запутался.
—Да это же совсем не сложно — говорит Колобок, — Мы с ребятами тебе поможем. Правда, ребята?
—Сколько в первой вазе синих цветов? Какой цифрой обозначается это число —
— Сколько красных? Какой цифрой обозначается это число-
— Сколько всего? Какой цифрой обозначается это число-
— Как получили 4?
— Как с помощью этих цифр и математических знаков записать, как мы получили число-4? 1+3=4
Катится колобок дальше, а навстречу ему волк.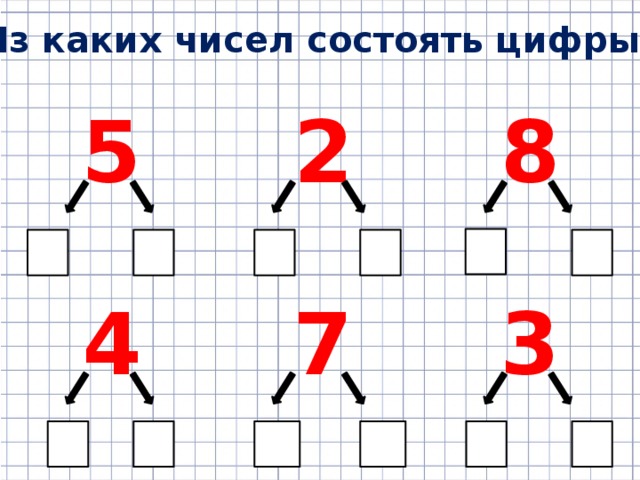
—Если выполнишь мое задание – не съем тебя! Поможем Колобку? Вы должны быть очень внимательны!!
3)—Нарисуйте 2 зеленых кружочка
— добавьте ещё 2 красный.
—Сколько получилось? Как получилось это число?
—Как это записать выражением? 2+2-4
—Запишите этот пример под рисунком
Катится по тропинке Колобок, вдруг из-за елки Лиса с тетрадью по математике. «Слушай, Колобок – говорит Лиса, выполнишь задание в тетради – домой вернешься, нет — съем тебя!»
— Ребята не допустим, чтобы Лиса съела Колобка?
обведите 3 клеточки, закрасьте синим цветом. 1 клеточку – оранжевым Сколько клеточек обвели? Записать пример.
— Вот и закончилась наша сказка. Вам понравилось?
пришло время заселить наш домики.
6. Итог
— Над составом какого числа работали?
— Как получить число 4?
Вычитаем и складываем Знакомство с составом числа примеры… (4-6л.) (мПапкаДошк) (папка)
63 ₽
42 ₽
+ до 9 баллов
Бонусная программа
Итоговая сумма бонусов может отличаться от указанной, если к заказу будут применены скидки.
Купить
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
В наличии больше 30 шт.
В наличии в 275 магазинах. Смотреть на карте
170
Цена на сайте может отличаться от цены в магазинах сети. Внешний вид книги может отличаться от изображения на сайте.
Предлагаем вашему вниманию серию папок для дошкольного образования «Солнечные ступеньки».
.»Солнечные ступеньки» предназначены для всестороннего развития способностей ребенка. Все задания соответствуют задачам умственного развития и воспитания, определенным «Типовой программой воспитания и обучения в детском саду».
.Папка дошкольника поможет ребенку:
.- закрепить состав числа;
.- сравнивать числа между собой;
.- решать простые математические задачи на сложение и вычитание.
.Цветной вкладыш необходимо разрезать по пунктирным линиям.
Описание
Характеристики
Предлагаем вашему вниманию серию папок для дошкольного образования «Солнечные ступеньки». .»Солнечные ступеньки» предназначены для всестороннего развития способностей ребенка. Все задания соответствуют задачам умственного развития и воспитания, определенным «Типовой программой воспитания и обучения в детском саду». .Папка дошкольника поможет ребенку: .- закрепить состав числа; .- сравнивать числа между собой; .- решать простые математические задачи на сложение и вычитание. .Цветной вкладыш необходимо разрезать по пунктирным линиям. Карточки с цифрами и картинками помогут ребенку самостоятельно составлять различные примеры и задачи.
Дакота
Как получить бонусы за отзыв о товаре
1
Сделайте заказ в интернет-магазине
2
Напишите развёрнутый отзыв от 300 символов только на то, что вы купили
3
Дождитесь, пока отзыв опубликуют.
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Если он окажется среди первых десяти, вы получите 30 бонусов на Карту Любимого Покупателя. Можно писать неограниченное количество отзывов к разным покупкам – мы начислим бонусы за каждый, опубликованный в первой десятке.
Правила начисления бонусов
Раскраска плюс математика
Плюсы
Как в старом добром учебнике советском задания
Бумага белая
Минусы
Нет
Книга «Вычитаем и складываем Знакомство с составом числа примеры… (4-6л.) (мПапкаДошк) (папка)» есть в наличии в интернет-магазине «Читай-город» по привлекательной цене.
Комбинации функций
Комбинации функций
|
Содержание: Эта страница соответствует
Предполагаемые проблемы из сообщения
р.
145 #1, 2, 5, 6, 9, 12, 13, 14, 19, 23, 24, 26, 31, 35, 36, 39, 41, 44, 45, 49, 52, 55, 57, 61, 62, 65,
68
Арифметические комбинации
Состав функций
Арифметические комбинации
Сумма, разность, произведение и частное двух функций f и g определяются следующим образом.
| Сумма | (f + g)(x) = f(x) + g(x) |
| Разница | (f — g)(x) = f(x) — g(x) |
| Продукт | (f * г) (х) = f (х) * г (х) |
| Частное | (f/g)(x) = f(x)/g(x) |
Пример 1. Пусть f(x) = x 2 + 3x -7 и g(x) = 4x +5.
(f + g)(3) = f(3) + g(3) = 11 + 17 = 28,
(f/g)(2) = f(2)/g(2) = 3/13,
Обратите внимание, что мы могли бы оценить функцию f + g при любом числе, вычисляя f и g по отдельности и добавляя
результаты, как мы сделали выше для 3.
Однако мы обычно упрощаем формулу для f + g, комбинируя аналогичные члены,
затем используйте эту новую формулу для вычисления функции суммы.
(f + g)(x) = f(x) + g(x) = (x 2 + 3x -7 ) + (4x +5) = x 2 + 7x — 2.
Итак, (f + g)(3) = 3 2 +7*3 -2 = 28, что согласуется с нашим предыдущим ответом.
Примечание о доменах:
Как правило, арифметическая комбинация двух функций f и g при любом x, находящемся в области определения как f, так и g, с одно исключение . Частное f/g не определено при значениях x, где g равно 0.
Например, если f(x) = 2x + 1 и g(x) = x — 3, то доамины f+g, f-g и f*g являются действительными числами. Область определения f/g — это набор всех действительных чисел, кроме 3, поскольку g(3) = 0..
.
Пример 2. Пусть f(x) = x 2 — 9 и g(x) = x — 3 .
Упрощать
формула для f/g.
(f / g)(x) = f(x) / g(x) = (x 2 — 9)/(x — 3) = (x + 3)(x — 3)/(x — 3) ) = х + 3.
Существует технический момент, относящийся к этому примеру, который часто игнорируется на уроках предварительного исчисления.
(f/g)(x) равно не равной функции h(x) = x + 3, так как f/g не определена при x = 3, а h является. На самом деле нет ничего плохого в том, чтобы думать о f / g как об одном и том же h, но это разные функции.
92-9)/(x-3) в поле f и введите x+3 в поле ч. В окне расчета введите h(3) и нажмите Enter. Возвращается ответ 6. Теперь оцените f в 3, набрав f(3) и нажав клавишу ввода.
Упражнение 1:
Найдите f + g, f — g, f * g и f / g для f(x) = x 2 — 3x + 2, g(x) = x — 2. Примечание: f можно разложить на множители. Мы рассмотрим факторинг многочленов в следующем разделе. Ответ
* часто не пишется для продуктов, поэтому вы увидите, что fg используется для обозначения продукта f*g.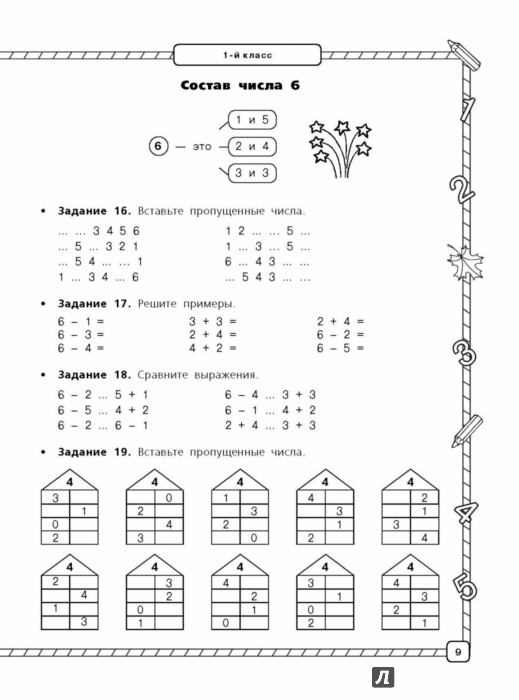
Вернуться к содержанию
Состав функций
Композиция двух функций f и g определяется формулой (f ° g)(x) = f(g(x)).
Пример 3. Пусть f(x) = x 2 — x + 1
(f°g)(5) = f(g(5)) = f(13) = 157.
(g ° f)(5) = g(f(5)) = g(21) = 61.
Примечания к составу:
Не путайте состав (f°g) с продуктом (f*g). Композиция (f°g)(x) означает «оценить g в x, затем оценить f в результате g(x)». Произведение (f*g)(x) означает «оценить f и g в x и умножить результаты».
Композиция не коммутативна. Другими словами, f°g вообще не равно g°f. (см. пример выше.)
В то время как (f ° g)(x) можно вычислить при любом x, вычислив g в x, а затем вычислив f в результате, мы часто
желаю упростить формулу композиции.
Пример 4 . Используйте те же функции, что и в последнем примере, f(x) = x 2 — x + 1 , и г(х) = 3х — 2 .
(f°g)(x) = f(3x — 2) = (3x — 2) 2 — (3x — 2) + 1 = (9x 2 -12x + 4)-(3x-2) +1 = 9x 2 — 15х + 7.
(g ° f)(x) = g(x 2 — x + 1) = 3(x 2 — x + 1) -2 = 3x 2 — 3x + 1.
Используя эти формулы, мы получаем те же результаты, что и в предыдущем примере:
(f°g)(5) = 9*25-15*5+7=157.
(г°ж)(5) = 3*25 -3*5 +1 = 61,
Упражнение 2:
Пусть f(x) = x 2 -3x + 4 и пусть g(x) = x + 1.
(a) Упростите формулу для f(g(x)).
(b) Проверьте свой ответ с помощью Java-калькулятора следующим образом:
Откройте калькулятор , введите формулы для f и g и в поле h.
Введите упрощенный формула для f(g(x)).
В окне вычислений оцените f(g(5)) и h(5). Если формула, которую вы ввели в h, является правильным упрощением f(g(x)), то эти два значения должны совпадать.
Попробуйте провести эксперимент с двумя значениями, отличными от 5.
Введите упрощенный
формула для f(g(x)).Вернуться к содержанию
|
Полное руководство – mathsathome.com
Видео-урок по составным функциям
Как найти составные функции
Чтобы найти составную функцию:
- Определите внешние и внутренние функции.
- Напишите внешнюю функцию.
- Замените каждую 𝑥 внутренней функцией.
- При необходимости упростите.
Например, если и , рассчитайте .
1. Определите внешнюю и внутреннюю функции
Для составной функции , находится внутри . Это вход в .
При записи в виде , внешняя функция — это та, что написана слева, а внутренняя функция — справа.
— это внутренняя функция и внешняя функция.
2. Напишем внешнюю функцию
Напишем внешнюю функцию .
3. Замените каждый 𝑥 внутренней функцией
Каждый найденный 𝑥 должен быть заменен внутренней функцией .
и так, заменяем 𝑥 на 𝑥 2 .
.
В следующем примере мы сохраним и на этот раз вычислим .
1. Определите внешнюю и внутреннюю функции
Для составной функции , находится внутри . Это вход в .
При записи в виде внешняя функция — это та, что написана слева, а внутренняя функция — справа.
— это внутренняя функция и внешняя функция.
2. Напишем внешнюю функцию
Напишем внешнюю функцию .
3. Замените каждый 𝑥 внутренней функцией
Каждый найденный 𝑥 должен быть заменен внутренней функцией .
и так, заменяем 𝑥 на 𝑥+3.
Мы должны возвести в квадрат все числа 𝑥+3, поэтому сначала заключаем их в скобки: (𝑥+3).
.
Порядок составных функций
Порядок составных функций имеет значение, поскольку другой порядок приводит к совершенно другой функции. Всегда заменяйте внутреннюю функцию справа внешней функцией слева. Например, если f( 𝑥) = 𝑥 +3 и g( 𝑥 )= 𝑥 2 , f(g( 𝑥))=𝑥 2 +3 и g(f( 𝑥))=( 𝑥+3) 2 .
Всегда заменяйте крайнюю правую функцию функцией слева от нее.
Например, означает, что подставляется в качестве ввода в .
означает, что подставляется как вход в .
Чтобы запомнить порядок составных функций, нарисуйте обратную стрелку от самой правой функции к самой левой.
Всегда заменяйте функцию справа на функцию слева.
Составные функции с числами
Составные функции могут быть вычислены, когда число является входом. Подставьте число в функции справа налево. Например, если f(𝑥)=2 𝑥 +1 и g( 𝑥)=𝑥 2 , то gf( 3) находится подстановкой 3 в 𝑑=f() 2 𝑥 +1 , чтобы получить 7. Затем подставьте 7 в 9.0038 g( 𝑥)=𝑥 2 чтобы получить 49. gf( 3) =49.
Когда входными данными составной функции являются числа, результирующий ответ также является числом.
Если входные данные составной функции равны 𝑥, результирующим ответом будет другая функция.
При вводе чисел в составную функцию важно оценивать каждую функцию справа налево.
В приведенном ниже примере мы сначала подставляем 4 в g(𝑥), чтобы получить 2, а затем подставляем полученное значение 2 в f(𝑥), чтобы получить 11.
Что такое составные функции?
Составная функция — это функция, которая находится внутри другой функции. Одна функция заменяется на вход другой функции. Например, f[ g(𝑥) ] означает, что g( 𝑥 ) заменяется на каждые 𝑥 в функции f( 𝑥 ). Составная функция f[g( 𝑥 ) ] произносится как «f of g of 𝑥».
Например, в приведенной ниже составной функции заменяется на для формы .
Составная функция отличается от функций, из которых она состоит.
Обозначение составной функции
Составные функции могут быть записаны в различных обозначениях.
Функция, подставленная в качестве входных данных для другой функции, может быть записана как:
В математике символ круга ∘ используется для обозначения состава функций.
Например, (f∘g)(𝑥) означает взять результат g и подставить его в f.
читается как «f из g», «f, составленный из g», «f круг g», «f вокруг g» или «f около g».
Диаграмма-стрелка составной функции
Диаграмма-стрелка может использоваться для объяснения составных функций. Входы первой функции перечислены слева. Стрелки соединяют эти входы с их выходами посередине. Эти выходные данные затем являются входными данными для следующей функции, выходные данные которой показаны справа.
Например, чтобы найти с помощью диаграммы со стрелкой ниже, введите 2, показанное красной стрелкой.
Первая стрелка показывает функцию . Когда мы возводим 2 в квадрат, мы получаем 4.
Вторая стрелка покидает 4 и достигает результата 7. Это потому, что функция говорит нам добавить три к предыдущему результату. 4 + 3 = 7.
Следовательно =7.
Свойства составных функций
Составные функции обладают следующими свойствами:
- Обратная композиция функций равна композиции обратной обеих функций. (ф∘г) -1 = г -1 ∘f -1 .
- Композиция функций «один к одному» также является взаимно однозначной.
- Композиция онто-функций также является онто-функцией.
- Составные функции ассоциативны. То есть f∘(g∘h) = (f∘g)∘h.
- Композиция функций, вообще говоря, некоммутативна. Нельзя предполагать, что f[g(x)] = g[f(x)].
- Составная функция, содержащая хотя бы одну четную функцию, будет четной.
- Составная функция, состоящая из совершенно нечетных функций, также будет нечетной.
(ф∘г) -1 = г -1 ∘f -1 .Составные функции с 3 функциями
Чтобы найти составную функцию, состоящую из трех функций, подставьте крайнюю правую функцию в среднюю функцию, а затем подставьте ее в крайнюю левую функцию. For example, if g(𝑥)= 𝑥 2 , f( 𝑥 )=3 𝑥+1 and h( 𝑥)= 1 / 𝑥 then h(g( f( 𝑥)))= 1 / (3𝑥+1) 2 .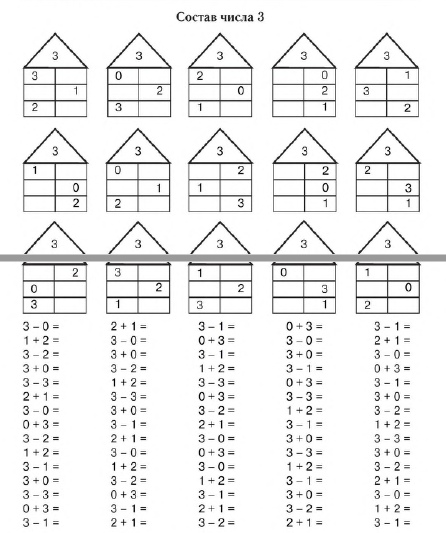
Стрелки можно рисовать справа налево, чтобы помочь запомнить порядок составных функций. В примере h(g(f(𝑥))) функция f заменяется на функцию g, чтобы сформировать g(f(𝑥)).
г(f(𝑥)) = (3𝑥-1) 2 .
Затем это подставляется в функцию h 1 / 𝑥 . Мы заменяем 𝑥 на (3𝑥-1) 2 .
ч(г(ж(𝑥))) = 1 / (3𝑥-1) 2 .
Примеры композитной функции
Пример композитной функции с квадратными корнями
IF G (𝑥) = 𝑥 2 + 5𝑥 и F (𝑥) = √ 𝑥, Вычисление G (F (8) = √ 𝑥, расчет G (F (8) = √ 𝑥, расчет G (8) = √ 𝑥, расчет G (8) = √ 𝑥, расчет G (8) = √ 𝑥, расчет G (8) = √ 𝑥, расчет G () = √ 𝑥. ). Подставьте √ 𝑥 во все 𝑥 , найденные в функции g( 𝑥 ) .
г(ж( 𝑥 )) = ( √ 𝑥 ) 2 +5 √ 𝑥 . Здесь √ 𝑥 и квадратная операция отменяется, чтобы оставить g(f( 𝑥 )) = 𝑥 +5 √ 𝑥 .
Пример композитной функции с фракциями
, если G ( 𝑥 ) = 1 / 𝑥 и F ( 𝑥) = 1- 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 𝑥 и F () = 1- 𝑥 𝑥 и F (). 𝑥 )). Замените функцию f на 𝑥 в функции g. г(f( 𝑥))= 1 / (1- 𝑥) . Эта составная функция записывается в виде дроби.
Пример составной функции с Sin(𝑥)
Если g(𝑥) = 2𝑥 + 1 и f(𝑥) = sin( 𝑥), вычислить f(g( 𝑥 )).
Подставьте 2 𝑥 +1 в каждое 𝑥 , найденное в функции f( 𝑥 ) . f(g( 𝑥 )) = sin(2 𝑥+1) .
Пример составной функции с e
𝑥 e 𝑥 и ln( 𝑥) являются обратными функциями. При записи в виде составной функции эти две функции компенсируют друг друга. Если g( 𝑥)=e 𝑥 и f( 𝑥)=ln( 𝑥 )- 𝑥, вычислить f(g( )6). Каждая 𝑥 в f( 𝑥) заменяется на e 𝑥 и, следовательно, f(g( 𝑥))=ln(e 𝑥 6 𝑥
. Это упрощается до 𝑥-e 𝑥 .
Функция, состоящая из самой себя
Функция, f( 𝑥 ) может быть составлена из самой себя, чтобы сформировать f(f( 𝑥)), которая также может90 быть записана как f00 ( 𝑥).
Это означает, что функция помещается как вход самой себе. Например, если f( 𝑥)=5 𝑥-2, то в f(f( 𝑥)), 𝑥 в f( 𝑥)=5 𝑥-2 будет заменено на 5 𝑥-2 . f(f( 𝑥)) =5 (5𝑥-2)-2, which simplifies to 25 𝑥 -12.
Область определения составных функций
Чтобы вычислить область определения составной функции gf(𝑥):
- Найдите значения, исключенные из области определения внешней функции g(𝑥).
- Установите f(𝑥) равным этим исключенным значениям и решите относительно 𝑥, чтобы найти значения, которые должны быть исключены из домена.
- Найдите любые другие значения, исключенные из области определения внутренней функции f(𝑥).
- Объедините эти результаты, чтобы сформировать общую область составной функции.
Например, если и , найдите домен .
Шаг 1. Найдите значения, которые исключены из области определения g(𝑥)
В функции g(𝑥) не может быть знаменателя, равного 0.
x≠0, так как мы не можем делить на 0
Шаг 2. Установите f(𝑥) равным этим исключенным значениям и найдите 𝑥
.
Мы решаем это для 𝑥, чтобы найти любые дополнительные значения, которые должны быть исключены из домена.
Возводим в квадрат обе части уравнения.
Затем мы видим, что .
Шаг 3. Найдите любые значения, которые исключены из внутренней функции, f( 𝑥 )
. Мы не можем извлекать корень из отрицательного числа.
Поэтому .
Шаг 4. Объедините эти результаты, чтобы определить область определения составной функции
В , областью является то .
Однако на шаге 2 мы сталкиваемся с проблемами, потому что это приводит к нулевому знаменателю составной функции.
Таким образом, конечный домен составной функции равен .
Составные функции из графиков
Чтобы найти значение составной функции из графика:
- Используйте ввод составной функции, чтобы считать вывод из графика внутренней функции.
- Используйте этот вывод как ввод графика внешней функции.
Например, функции f(𝑥) и g(𝑥) показаны ниже.
Используйте графики для расчета значения составной функции g(f(5)).
Шаг 1. Используйте вход составной функции для считывания вывода с графика внутренней функции
Входное число составной функции равно 5.
Мы читаем график внутренней функции f( 𝑥) в точке, где 𝑥 = 5.
Когда 𝑥 = 5, функция f(𝑥) имеет выход 4.
Шаг 2. Используйте этот выход как вход графика внешней функции
Мы используем выход 4 из первого графика в качестве входных данных для внешней функции g(𝑥).
Когда 𝑥 = 4, g(𝑥) имеет выход 5.
Следовательно, g(f(𝑥)) = 5.
Вот еще один пример.
Чтобы вычислить g(f(2)), мы сначала подставляем 2 в качестве входных данных в график f(𝑥).
Это дает нам результат 2 по оси Y.
Затем мы используем этот вывод 2 из графика f(𝑥) в качестве входных данных для графика g(𝑥).
Когда 𝑥 = 2, g(𝑥) имеет выход 7.
Следовательно, g(f(2)) = 7.
Составные функции с использованием таблицы
Чтобы вычислить значение составной функции из таблицы:
- Считайте выходные данные внутренней функции из ее таблицы по требуемому значению.
- Используйте этот вывод в качестве ввода в таблице внешней функции и прочитайте новый вывод.
