ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 16 вычти сумму чисел 8 и 6. К разности чисел 11 и 9 прибавить 9 | ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 15 вычти сумму чисел 5 и 6. К разности чисел 14 и 9 прибавить 2 | ||||||||
ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 16 вычти сумму чисел 8 и 6. К разности чисел 11 и 9 прибавить 9 | ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 15 вычти сумму чисел 5 и 6. К разности чисел 14 и 9 прибавить 2 | ||||||||
ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 16 вычти сумму чисел 8 и 6. К разности чисел 11 и 9 прибавить 9 | ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 15 вычти сумму чисел 5 и 6. К разности чисел 14 и 9 прибавить 2 | ||||||||
ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 16 вычти сумму чисел 8 и 6. К разности чисел 11 и 9 прибавить 9 | ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 15 вычти сумму чисел 5 и 6. К разности чисел 14 и 9 прибавить 2 | ||||||||
ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 16 вычти сумму чисел 8 и 6. К разности чисел 11 и 9 прибавить 9 | ВЫРАЖЕНИЯ СО СКОБКАМИ Составь из следующих предложений выражения со скобками и реши их. Из числа 15 вычти сумму чисел 5 и 6. К разности чисел 14 и 9 прибавить 2 | ||||||||
НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ:
| НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ: 10 + (8 – 5) = 17 – (5 +3) = (7 + 3) + 7 = (10 + 8) – 9 = 5+ (6 + 4) = (10 +9) – 3 = (9 +9) – 6 = 14 – (9 +1) = | ||||||||
НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ:
| НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ: 10 + (8 – 5) = 17 – (5 +3) = (7 + 3) + 7 = (10 + 8) – 9 = 5+ (6 + 4) = (10 +9) – 3 = (9 +9) – 6 = 14 – (9 +1) = | ||||||||
НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ:
| НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ: 10 + (8 – 5) = 17 – (5 +3) = (7 + 3) + 7 = (10 + 8) – 9 = 5+ (6 + 4) = (10 +9) – 3 = (9 +9) – 6 = 14 – (9 +1) = | ||||||||
НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ:
| НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ: 10 + (8 – 5) = 17 – (5 +3) = (7 + 3) + 7 = (10 + 8) – 9 = 5+ (6 + 4) = (10 +9) – 3 = (9 +9) – 6 = 14 – (9 +1) = | ||||||||
НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ:
| НАЙДИ ЗНАЧЕНИЯ ВЫРАЖЕНИЙ: 10 + (8 – 5) = 17 – (5 +3) = (7 + 3) + 7 = (10 + 8) – 9 = 5+ (6 + 4) = (10 +9) – 3 = (9 +9) – 6 = 14 – (9 +1) = |
Е | Н | Б | О | Е | У | В | |
а + 21 | |||||||
а : 8 | |||||||
А | К | Ч | Т | Р | Л | Х | |
Е | Н | Б | О | Е | У | В | |
а + 21 | 45 | 69 | 53 | 77 | 85 | 181 | 101 |
а : 8 | 3 | 6 | 4 | 7 | 8 | 20 | 10 |
А | К | Ч | Т | Р | Л | Х | 20 | 45 | 53 | 69 | 77 | 85 |
Х | Л | Е | Б | Н | О | Е | Количество рядов | Всего стульев |
Одинаковое | 3 р. | 24 ст. | |||||
Одинаковое | 2 р. | ? ст. |
Типы, использование, правило BODMAS, решенные проблемы и часто задаваемые вопросы
Первый вопрос, который студент получает по этой теме: «Как мы можем определить скобки». При вычислении выражения, содержащего заключенное в квадратные скобки подвыражение, скобки обозначают тип группировки, операторы в подвыражении имеют приоритет над окружающими его. Кроме того, для различных скобок существует множество применений и определений.
Типы кронштейнов
Часто используемые типы кронштейнов:
Круг ()
Квадратные кронштейны []
Куршивые кронштейны {}
Угловые скобки.
 являются наиболее часто используемым типом скобок. В математических задачах скобки в основном используются для группировки чисел. Используйте порядок операций для решения проблемы, когда мы видим несколько чисел и операций в скобках.
являются наиболее часто используемым типом скобок. В математических задачах скобки в основном используются для группировки чисел. Используйте порядок операций для решения проблемы, когда мы видим несколько чисел и операций в скобках.Скобки используются в математике по трем основным причинам:
Чтобы разделить числа для пояснения, можно использовать круглые скобки. Например, если у нас есть дополнительная проблема с отрицательным числом, чтобы различить два знака, будут использоваться круглые скобки. Чтобы отличить число от его показателей, также можно использовать круглые скобки. Как правило, это происходит, если мы поднимаем отрицательное число до контроля.
Квадратные скобки
В математике квадратные скобки [ ] используются в различных ситуациях:
Квадратные скобки иногда используются вместо скобок (или в дополнение к ним) в очень сложных выражениях, особенно в качестве знака группы вне внутреннего набора скобок.

Они могут означать то же, что и скобки, но предназначены для облегчения чтения. Все зависит от ситуации.
Квадратные скобки используются для включения номера, который он охватывает при работе с включением.
Их также можно использовать для обозначения наименьшего общего кратного
Фигурные скобки (также известные как фигурные скобки)
Левые фигурные скобки и правые фигурные скобки используются вместе в математических выражениях. Их можно заменить квадратными скобками или круглыми скобками. Во вложенной фразе с тремя уровнями группировки круглые скобки обычно используются в самых внутренних группировках. В группе следующего более высокого уровня используются квадратные скобки, в то время как фигурные скобки используются в самых внешних группах (см.
 « Вложенные выражения » для примера).
« Вложенные выражения » для примера).Угловые кронштейны
Внутреннее произведение двух функций представлено угловой скобкой, состоящей из бра и кет (бра+кет = скобка). Поскольку угловые скобки напоминают знаки «меньше» и «больше», некоторым учащимся они могут показаться запутанными. Но вы освоитесь, как только начнете время от времени использовать их в своей математической практике.
Для чего нужны скобки?
Пример: 5 * (2 + 4) равно 30, (5 * 3) + 2 равно 30.
Скобки часто используются в математических выражениях, чтобы обозначить группировку, где это уместно, чтобы предотвратить двусмысленность и повысить ясность.
В декартовой системе координат скобки используются для обозначения координат точки.
Пример: (4,8) обозначает точки в системе координат x-y, где координата x равна 4, а координата y равна 8.

Пример: f(x), g(x).
Пример: [0,8) обозначает полузамкнутый интервал, включающий все действительные числа, кроме 8 от 0 до 8.
Широкие круглые скобки вокруг двух чисел обозначают биномиальный коэффициент, один над другим.
Как и в (a,b,c), круглые скобки вокруг набора из двух или более чисел обозначают набор из n чисел, которые связаны определенным образом.
Матрица обозначается широкими скобками вокруг массива чисел.
Для обозначения наибольшего общего делителя используются круглые скобки.
Правило BODMAS
Скобки находят свое основное применение в правиле BODMAS или PEMDAS, где последовательность операций должна выполняться при разрешении выражения.
 BODMAS или PEMDAS означает:
BODMAS или PEMDAS означает:B — скобки, P — круглые скобки
O — порядок, E — показатели степени
D — деление
M — умножение
A — сложение
S — вычитание
выполнять до тех пор, пока выражение не будет разрешено. Согласно закону БОДМАСА, если в выражении есть скобки ((), {},), мы сначала должны преодолеть или упростить скобку, а затем порядок, затем делить, умножать, складывать и вычитать слева направо. В неправильном порядке решение проблемы приведет к неправильному ответу.
Проще говоря, четыре операции имеют решающее значение для обучения арифметике, и подростки, которые не знают, в какой последовательности их выполнять, не смогут двигаться вперед с годами.
Еще одна причина, по которой BODMAS преподается на уроках математики, заключается в том, что учащимся намного легче запомнить, какую операцию выполнять при столкновении со сложными уравнениями.

Основные задачи на скобки и их применение:
1) Решить (2 + 4) — (6 — 3)
Ответ: В данном выражении задействованы две круглые скобки. Мы можем решить обе из них по отдельности по правилу БОДМАСа, а затем объединить их результаты.
(2 + 4) = 6……….(1)
(6 — 3) = 3………..(2)
Теперь вычитая (1) с (2), получаем
( 2 + 4) — (6 — 3) = 6 — 3 = 3
2) Решите (3 + (5 * 4)) — ((4 * 6) — 10)
Ответ: задействовано четыре скобки в заданном выражении. Мы решим это, используя правило BODMAS, чтобы найти ответ.
Первые круглые скобки: (5 * 4) = 20………………………………..(1)
Вторые круглые скобки: (3 + (5*4))=(3 + 20) =23 ………(2)
Третья скобка (4 * 6) = 24……………………………(3)
Четвертая скобка ((4 * 6) — 10) = (24 — 10) = 14……(4)
Теперь вычитаем (2) и (4) получаем
(3+(5*4))-((4*6)-10)=23-14=9.

Что такое скобки в математике? Определение, типы, примеры и использование
Что такое скобки?
Вы, должно быть, видели в учебниках по математике различные символы, подобные этим: (, ), [ ], { и }. Эти символы называются скобками. Скобки в математике служат очень важной цели; эти символы помогают нам сгруппировать различные выражения или числа вместе. Скобки подразумевают, что вещь или выражение, заключенное в них, должно иметь более высокий приоритет по сравнению с другими вещами.
Различные виды скобок
Обычно в математике используются три вида скобок,
- Скобки или круглые скобки, ( )
- Фигурные скобки или фигурные скобки { }
- Квадратные или коробчатые скобы [ ]
Скобки Скобки
Они также известны как круглые скобки и записываются как ( ). Это самые распространенные виды брекетов. Они используются для группировки различных значений и уравнений вместе.
При использовании просто вокруг чисел круглые скобки обозначают умножение.
 9{-3}$
9{-3}$Примеры: (2 + 4), 5(111), 25 – (12 + 8) и т. д.
Фигурные скобки
Как и скобки, фигурные скобки также используются для группировки различных математических компонентов; однако фигурные скобки также используются для обозначения множеств или для написания вложенных выражений. Примеры:
[4 + [3 $\times$ (- 2)] – [{(4 $\times$ 6) + (14 $\div$ 7)} – (- 3)],
[{ 12 − (12 − 2) } + (5 − 7)] + 9 и т. д.
Квадратные скобки
Квадратные скобки обычно используются для различения подвыражений сложного математического выражения.
Примеры: [100 – (3 – 1) + (7 x 8)], 10 x [(4 – 2) x ( 4 x 2)] и т. д.
Порядок операций скобок
При оценке математическое выражение, состоящее из разных скобок, мы должны следовать определенным правилам. Это называется правилами работы или порядком работы скобок.
- Общий порядок работы скобки можно проиллюстрировать как [ { ( ) } ]; это означает, что в данной задаче вам придется сначала упростить значения в самой внутренней скобке.
 Это означает, что будут решены первые ( ) скобки, затем будут решены { } скобки и, наконец, [ ] скобки.
Это означает, что будут решены первые ( ) скобки, затем будут решены { } скобки и, наконец, [ ] скобки. - Вторым шагом в решении этих задач является поиск показателя степени; если есть, решите сначала.
- На третьем шаге ищем выражения с операторами умножения или деления. Если оба оператора присутствуют, мы проверяем выражение слева направо. Какой бы оператор ни пришел первым, мы сначала решим этот оператор.
Например, в выражении 10 6 ÷ 5 мы проверяем слева направо, поскольку сначала идет умножение, поэтому мы сначала решаем умножение, а затем деление.
10 $\times$ 6 ÷ 5
= 60 ÷ 5
= 12
- На четвертом и последнем шаге мы ищем числа, которые нужно сложить или вычесть. Мы следуем той же инструкции, если присутствуют оба оператора, мы смотрим слева направо в выражении, и какой бы оператор ни был первым, мы решаем это выражение первым. Но если операции в скобках, мы всегда сначала решаем скобки, так как скобки имеют наивысший приоритет.

Чтобы запомнить упомянутые выше шаги, мы можем использовать аббревиатуру PEMDAS,
P – Скобки,
E – Экспоненты
M – Умножение
D – Деление
A – Сложение
S – Вычитание.
давайте воспользуемся pemdas для вычисления выражения Следуйте порядку решения круглых скобок ( ), затем фигурных скобок { }, а затем квадратных скобок [ ].
= 100 − [(2) + (56)]
= 100 − 58
Шаг 2: В данном выражении нет показателя степени.
Шаг 3: В данном выражении нет ни умножения, ни деления.
Шаг 4: Решите вычитание.
= 100 − 58
= 42
Решенные примеры
Вопрос 1: Найдите значение выражения: (5 + 4) − (3 − 2).
Ответ: Данное выражение:
(5 + 4) − (3 − 2),
Шаг 1: Решение значений в скобках,
(5) (1),
Таким образом, ответ равен (9) − (1) = 8.

Вопрос 2: Найдите значение выражения: {(7 − 2) × 3} ÷ 5
Ответ : Заданное уравнение:
{(7 − 2) × 3} ÷ 5
Шаг 1: Решение скобок
{(7 − 2) × 3} ÷ 5
= {5 × 3} ÷ 5
Решение фигурной скобки
= {15} ÷ 5= 15 ÷ 5
= 3
Вопрос 3: Найдите значение выражения: (12 ÷ 6) × (4 − 2)
Решение:
Данное уравнение: 2) x (2)
Таким образом, ответ: (2) x (2) = 4
Вопрос 4: Найдите значение выражения: [120 + { (3 x 4) + (4 − 2) − 1 } + 20]
Ответ: Следуя правилу PEMDAS, сначала
Шаг 1: Найдем значения в скобках ( ),
[120 + { (3 x 4) + (4 − 2 ) — 1 } + 20 ]
= [ 120 + { (12 ) + ( 2 ) — 1 } + 20 ],
Теперь вычисляем значения в скобках { } ,
= [ 120 + { 13 } + 20 ],
Наконец, сложите все значения в скобках [ ],
Ответ: 153.
 2$ 9{2} = 4,096 $
2$ 9{2} = 4,096 $4
Решение этого выражения, 12 + (5 + 3),
18
20
16
8
Правильный ответ: 20
.
. Правильный ответ — 20.Часто задаваемые вопросы
Почему скобки важны в математике?
Скобки — очень важная часть математического уравнения; они отделяют разные математические выражения друг от друга и помогают установить приоритет для выражений, которые необходимо решить в первую очередь.
Является ли PEMDAS единственным методом решения проблем со скобами?
BODMAS — это другой аббревиатур от PEMDAS, где B означает скобки, O — числа или степени, D — деление, M — умножение, A — сложение и S — вычитание. Любое выражение считается правильно решенным, если оно соответствует правилу PEMDAS или BODMAS.
Есть ли еще виды кронштейнов?
Угловые скобки также используются в различных математических выражениях; они представлены с〈 〉.




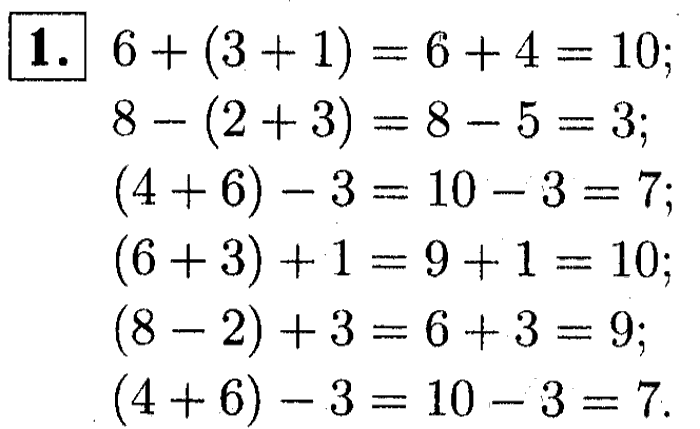 Тема: «Порядок выполнения действий».
Тема: «Порядок выполнения действий». Они записывают ответы в таблицу.)
Они записывают ответы в таблицу.) Хлебное дерево растёт в Азии и внешне напоминает дуб. Местные жители очень любят и ценят это замечательное дерево. Остаться голодным рядом с хлебным деревом невозможно. Его похожие на ананас плоды прокалывают и оставляют на ночь. К утру мякоть плода начинает бродить, и из неё можно печь хлеб, который имеет сладкий вкус. Одно дерево может прокормить семью из 4-5 человек.
Хлебное дерево растёт в Азии и внешне напоминает дуб. Местные жители очень любят и ценят это замечательное дерево. Остаться голодным рядом с хлебным деревом невозможно. Его похожие на ананас плоды прокалывают и оставляют на ночь. К утру мякоть плода начинает бродить, и из неё можно печь хлеб, который имеет сладкий вкус. Одно дерево может прокормить семью из 4-5 человек. Данные выражения содержат действия сложения, вычитания, умножения и деления.)
Данные выражения содержат действия сложения, вычитания, умножения и деления.)




