Примеры сложные по математике 1 класс: Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи

admin

Содержание

Тренажеры по математике 1 класс. Примеры на сложение и вычитание, задачи — «Семья и Школа»

Содержание

Примеры по математике на деление для 3 класса | контрольные, примеры для детей

Учим детей » Математика

Не все дети 3 класса хорошо понимают тему деления числа. Для того, чтобы ребенок лучше усвоил материал, нужно постоянно решать примеры на деление. Так он повторит правила на умножение и деление, а также приобретет навыки решения подобных примеров. На нашем сайте можно распечатать примеры на деления для 3 класса бесплатно.

Тема: Деление двухзначного числа на однозначное

1. Реши примеры на деление (для детей 3 класса)

28 : 7 =27 : 9 =28 : 4 =
54 : 9 =56 : 7 =56 : 8 =
36 : 6 =64 : 8 =63 : 9 =
45 : 5 =42 : 6 =25 : 5 =

примеры деление 3 класс

36 : 4 =27 : 9 =72 : 9 =
18 : 6 =36 : 3 =91 : 7 =
15 : 3 =10 : 10 =10 : 5 =
81 : 9 =9 : 3 =50 : 5 =

примеры деление 3 класс

2. Выполни деление и проверь результат умножением.

12 : 6 =24 : 4 =14 : 2 =
20 : 10 =60 : 15 =40 : 8 =

примеры деление 3 класс

2. Реши примеры. Внимательно выполняй последовательность действий.

72 : 9 + 22 * 5 — 28 : 7 =
36 — 81 : 9 + 12 : 2 * 7 =
20 + 7 * 5 — 48 : 12 =
90 : 30 — 34 + 11 * 4 =

3. Реши примеры на деление (для детей 3 класса)

90:3=
76:2=
46:3=
81:4=
100:25=
54:3=
74:2=
66:33=
90:30=
66:22=
36:2=
46:3=
99:11=
80:2=
88:4=
84:2=
100:20=
56:2=

4. Примеры с элементами деления. Запиши заданные предложения в виде примеров и реши их.

1. К числу 34 прибавь частное чисел 40 и 5.
3.2. К числу 33 прибавь частное чисел 33 и 11.
3.3. Из числа 42 вычти частное чисел 54 и 5.
3.3. Из числа 90 вычти частное чисел 64 и 8.

5.
Сравни выражения и поставь знак >, < или = :
7 * 3 + 7 (?) 7 * 53 * 5 — 5 (?) 3 * 4
8 * 4 — 8 (?) 8 * 33 * 6 + 6 (?) 3 * 5
6 * 5 — 6 (?) 6 * 47 * 2 + 7 (?) 7 * 4
6.

Реши сложные примеры на деление (тренажер деления)

40:20=
96:8=
46:2=
75:25=
80:2=
100:2=
78:6=
90:18=
34:17=
85:17=

85:17=
80:16=
84:7=
32:4=
99:9=
48:4=
72:3=
96:6=
26:2=
84:6=

7. Примеры для распечатки для урока 3 класса

Порядок действий в примерах со скобками: попробуйте решить простой пример

Англоязычный Twitter облетела старая задачка по математике, которая разделила пользователей на несколько враждующих лагерей. Однако, ничего удивительного здесь нет, ведь правильное решение примеров по действиям со скобками всегда непросто отыскать, особенно если вы давно закончили школу. Хватит ли у вас смекалки и знаний базовой математики, чтобы пройти это испытание, посильное для младшеклассника, но непреодолимое для взрослого?

Юлиана Качанова Отвечаю за тесты

Twitter: 1RealMir

Решить пример со скобками по действиям пытались многие комментаторы твиттера, при этом используя самые разные, в том числе и несуществующие, математические приемы.

Известный новозеландский актёр Тайка Вайтити, знакомый отечественным кинозрителям по фильму «Реальные упыри», принял участие в данном интернет-споре, но к сожалению, не стал «отличником», решившим задачу правильно. Его, как и большинство других участников, подвело знание порядка действий сложных примеров со скобками.

Если вы считаете что хорошо помните последовательность действий в примерах со скобками, то попробуйте дать правильный ответ:

Не торопитесь давать ответ: правила хотя бы вспомните!

ВОПРОС 1 ИЗ 1

3

17

21

Главное – не торопитесь! В математике порядок действий примеров со скобками имеет огромное значение. «Дорожная карта» для того, чтобы правильно решить тот, или иной пример выглядит следующим образом:

  • Внимательно посмотрите на пример и сначала произведите действие, которое указано в скобках.
  • Запомните: порядок выполнения действий в примерах со скобками отдаёт предпочтение умножению и делению. Их называют действиями первой ступени.
  • Последними выполняются сложение и вычитание. Это действия второй ступени.

Такая последовательность действий в примере со скобками выбрана не случайно и позволяет без особых затруднений получить правильный ответ.

Для закрепления рассмотрим следующий пример действия со скобками:

5+(7−2⋅3)⋅(6−4):2

В этом сложном примере со скобками порядок действий будет точно таким же.

Сначала мы вычислим значение первой скобки. Для этого сначала нужно выполнить умножение 2 на 3, как действие первой ступени, а затем вычесть из 7 полученное произведение. Получится 7-6=1
После этого мы переходим ко второй скобке. Если в первой скобке у нас был пример с умножением и вычитанием в ней, то здесь у нас только вычитание: 6-4=2

Давайте подставим решение примеров в скобках в первоначальное выражение:

5+(1)⋅(2):2 . 

Здесь уже сложных примеров со скобками нет, мы оставили их просто для визуального понимания, какое число по итогам наших манипуляций получилось.

Порядок действий в примерах со скобками (как впрочем и без них) требует от нас сначала выполнения умножения и деления, а затем сложения и вычитания. Продолжаем соблюдать его и получаем что сначала мы должны умножить 1 на 2, а затем поделив её на 2 прибавить разность к 5:

5+1⋅2:2=6

Таким образом первоначальный пример со скобками также будет равняться 6

5+(7−2⋅3)⋅(6−4):2=6.

ENG 1001: Предложения: простые, составные и сложные

Общим недостатком письменной речи является отсутствие разнообразных предложений. Осознание из трех основных типов предложений — простых, составных и сложных — может помочь вам варьировать предложения в вашем письме.

Самое эффективное письмо использует Разновидность типы предложений, описанные ниже.

1. Простые предложения

Простое предложение содержит самые основные элементы, которые делают его предложение: подлежащее, глагол и законченная мысль.

Примеры простых предложений включают следующее:

  1. Джо ждал поезда.
    «Джо» = подлежащее, «ждал» = глагол
     
  2. Поезд опоздал.
    «Поезд» = подлежащее, «был» = глагол
     
  3. Мэри и Саманта сели на автобус.
    «Мэри и Саманта» = составное подлежащее, «брал» = глагол
     
  4. Я искал Мэри и Саманту на автобусной остановке.
    «Я» = подлежащее, «посмотрел» = глагол
     
  5. Мэри и Саманта прибыли на автобусную станцию ​​рано, но ждали до полудня на автобусе.
    «Мэри и Саманта» = составное подлежащее, «прибыл» и «waited» = составной глагол  

Совет .

Если вы используете много простых предложений в эссе, подумайте над тем, чтобы пересмотреть некоторые из них. предложений в составные или сложные предложения (поясняется ниже).

использование составных подлежащих, составных глаголов, предложных фраз (таких как «на автовокзале») и другие элементы помогают удлинить простой предложения, но простые предложения часто бывают короткими. Использование слишком большого количества простых предложения могут сделать письмо «прерывистым» и могут помешать письму течет плавно.

Простое предложение может также называться самостоятельным предложением . Это называется «независимым», потому что, хотя он может быть частью составное или сложное предложение, оно также может стоять само по себе как полное предложение.
 

2. Составные предложения

Составное предложение относится к предложению, состоящему из двух независимых предложения (или полные предложения), связанные друг с другом с помощью

координирующего соединение . Сочинительные союзы легко запомнить, если подумать о слова «FAN BOYS»:

  • Ф или
  • А и
  • N или
  • Б ут
  • О р
  • Y и
  • С или

Примеры составных предложений включают следующее:

  1. Джо ждал поезд, но поезд опоздал.
     
  2. Я искал Мэри и Саманту на автовокзале, но они прибыли на вокзал раньше полдень и ушел на автобус до моего приезда.
     
  3. Мэри и Саманта прибыли на автовокзал до полудня, и они уехали на автобус до моего приезда.
     
  4. Мэри и Саманта ушли на автобус до моего приезда, так
    я их на автовокзале не видел.

Совет : Если в эссе вы часто используете сложные предложения, вам следует подумать о том, чтобы преобразовать некоторые из них в сложные предложения (поясняется ниже).

Сочинительные союзы полезны для соединения предложений, но составные предложения часто злоупотребляют. В то время как сочинительные союзы могут указывать на некоторые тип отношения между двумя независимыми частями в предложении, они иногда не указывают на большую часть отношений. Слово «и» для например, только добавляет одно независимое предложение к другому, не указывая, как две части предложения логически связаны. Слишком много сложных предложений, которые использование «и» может ослабить написание.

Более четкие и конкретные отношения могут быть установлены с помощью сложные предложения.
 

3. Сложные предложения

Сложное предложение состоит из независимого предложения и одного или нескольких связанных с ним зависимых пунктов

. А зависимое предложение похоже на независимое предложение или полное предложение, но в нем отсутствует один из элементов, которые сделали бы его законченным предложением.

Примеры зависимых статей включают следующее:

  • , потому что Мэри и Саманта прибыли на автовокзал до полудня
  • пока он ждал на вокзале
  • после того, как они уехали на автобусе

Зависимые предложения, подобные приведенным выше , не могут стоять отдельно как предложение, но их можно добавлять к независимое предложение, образующее сложное предложение.

Зависимые предложения начинаются с подчинительных союзов . Ниже приведены некоторые из наиболее распространенных подчинительных союзов:

  • после
  • хотя
  • как
  • потому что
  • до
  • хотя
  • если
  • с
  • хотя
  • кроме
  • до
  • когда
  • всякий раз, когда
  • тогда как
  • где
  • , а

Сложное предложение объединяет независимое предложение с одним или несколькими зависимыми предложениями.

Зависимое предложение может идти первым в предложении, за которым следует независимое предложение, как в следующем:

Совет : Когда зависимое предложение идет первым, для разделения двух предложений следует использовать запятую.

  1. Поскольку Мэри и Саманта прибыли на автовокзал до полудня, я не увидел их на вокзале.
  2. Ожидая на вокзале, Джо понял, что поезд опаздывает.
  3. Выехав на автобусе, Мэри и Саманта поняли, что Джо ждет их на вокзале.

И наоборот, независимые предложения могут идти первыми в предложении, а за ними — зависимое предложение, как в следующем примере:

Совет : Когда независимое предложение стоит первым, для разделения двух предложений следует использовать запятую , а не .

  1. Я не видел их на вокзале, потому что Мэри и Саманта прибыли на автовокзал до полудня.
  2. Джо понял, что поезд опаздывает, пока он ждал на вокзале.
  3. Мэри и Саманта поняли, что Джо ждал на вокзале после того, как они уехали в автобусе.

Сложные предложения часто более эффективны, чем сложные предложения, потому что сложное предложение указывает на более четкие и конкретные отношения между главными частями предложения. Слово «прежде» например, сообщает читателям, что одно происходит раньше другого. Такое слово, как «хотя» передает более сложные отношения, чем такое слово, как «и».

Термин периодическое предложение используется для обозначения сложного предложения, начинающегося с зависимого предложения и заканчивающийся независимым предложением, например: «Пока он ждал на вокзале, Джо понял, что поезд опаздывает».

Периодические предложения могут быть особенно эффективными, потому что завершенная мысль возникает в конец этому, так что первая часть предложения может доходить до значения, которое приходит в конце.

Предложения, начинающиеся с «И» или «Потому что»

Следует ли начинать предложение с «и» или «но» (или с одной из других координирующих союзы)?

Короткий ответ — «нет». Вы должны избегать начала предложения с «и», «или», «но» или другого сочинительные союзы. Эти слова обычно используются для соединения частей предложения, а не начинать новое предложение.

Однако такие предложения можно эффективно использовать. Поскольку предложения, начинающиеся с этих слов, выделяются, они иногда используются для выделения. Если вы используете предложения, начинающиеся с одного из сочинительных союзов, вы должны использовать эти предложения экономно и осторожно.

Следует ли начинать предложение со слова «потому что»?

Нет ничего плохого в том, чтобы начинать предложение со слова «потому что».

Возможно, некоторым учащимся говорят не начинать предложение со слова «потому что», чтобы избежать фрагментов предложения. (что-то вроде «Потому что Мэри и Саманта приехали на автовокзал до полудня» — это фрагмент предложения), но это совершенно верно. допустимо начинать предложение со слова «потому что», если предложение завершено (например, «Потому что Мэри и Саманта прибыли в автовокзала до полудня, я их на вокзале не видел».)

Смотри!

Комплексное число — определение, формула, свойства, примеры

Комплексные числа помогают найти квадратный корень из отрицательных чисел. Концепция комплексных чисел была впервые упомянута в I веке греческим математиком Героем Александрийским, когда он пытался найти квадратный корень из отрицательного числа. Но он просто изменил отрицательное значение на положительное и просто взял числовой корень. Кроме того, реальная идентичность комплексного числа была определена в 16 веке итальянским математиком Джероламо Кардано в процессе нахождения отрицательных корней кубических и квадратичных полиномиальных выражений.

Комплексные числа находят применение во многих научных исследованиях, обработке сигналов, электромагнетизме, гидродинамике, квантовой механике и анализе вибрации. Здесь мы можем понять определение, терминологию, визуализацию комплексных чисел, свойства и операции с комплексными числами.

1. Что такое комплексные числа?
2. График комплексных чисел
3. Свойства комплексных чисел
4. Операции над комплексными числами
5. Алгебраические тождества комплексных чисел
6. Решенные примеры
7. Практические вопросы
8. Часто задаваемые вопросы о комплексных числах

Что такое комплексные числа?

Комплексное число – это сумма действительного числа и мнимого числа. Комплексное число имеет вид a + ib и обычно обозначается буквой z. Здесь и a, и b – действительные числа. Величина «а» называется действительной частью, которая обозначается Re(z), а «b» называется мнимой частью Im(z). Также ib называют мнимым числом.

 

 

 

 

 

 

 

 

Примеры комплексных чисел: \(2+3i, -2-5i, \,\,\dfrac 1 2 + i\dfrac 3 2\) и т. д.

Степень of i

Алфавит i называется йотой и полезен для представления мнимой части комплексного числа. Кроме того, йота (i) очень полезна для нахождения квадратного корня из отрицательных чисел. У нас есть значение i 2  = -1, и оно используется для нахождения значения √-4 = √i 2 4 = 9.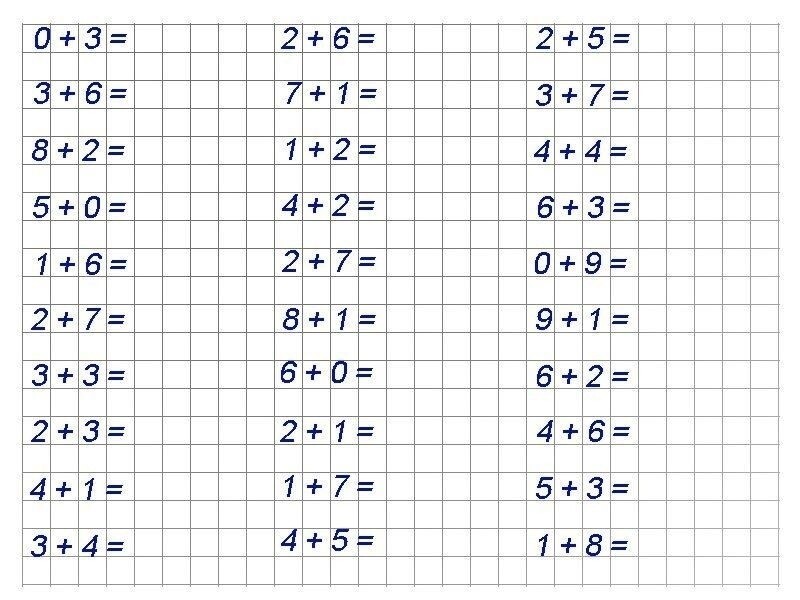 0337 + 2i Значение i 2  = -1 является основным аспектом комплексного числа. Давайте попробуем понять больше о возрастающих силах i.

  • я = √-1
  • я 2  = -1
  • i 3   = i.i 2  = i(-1) = -i
  • i 4  = (i 2 ) 2  = (-1) 2  = 1
  • i 4n  = 1
  • я 4n + 1  = я
  • i 4n + 2  = -1
  • i 4n + 3  = -i

Графики комплексных чисел

Комплексное число состоит из действительной и мнимой частей, которые можно рассматривать как упорядоченную пару (Re(z), Im(z)) и представлять в виде точек координат на евклидовой плоскости. Евклидова плоскость применительно к комплексным числам называется комплексной плоскостью или Плоскостью Аргана, названной в честь Жана-Роберта Аргана. Комплексное число z = a + ib представлено действительной частью — a относительно оси x и мнимой частью -ib относительно оси y.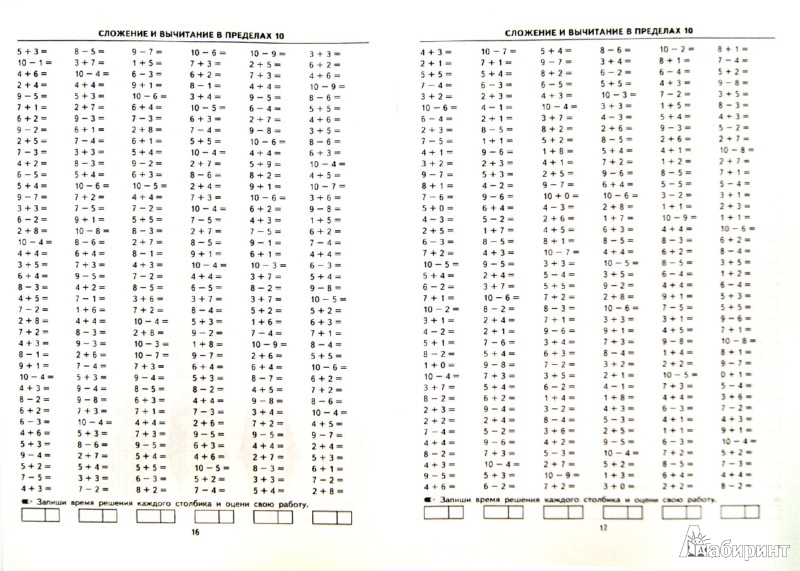 {-1}\frac{b}{a}\). 9{-1}\frac{b}{a}\)).

Свойства комплексного числа

Следующие свойства комплексных чисел помогают лучше понять комплексные числа, а также выполнять различные арифметические операции над комплексными числами.

Сопряжение комплексного числа

Сопряжение комплексного числа образуется путем взятия той же действительной части комплексного числа и замены мнимой части комплексного числа на ее аддитивную обратную. Если сумма и произведение двух комплексных чисел являются действительными числами, то они называются сопряженными комплексными числами. Для комплексного числа z = a + ib его сопряженным является \(\bar z\) = a — ib.

Сумма комплексного числа и его сопряженного равна \(z + \bar z\)  = (a + ib) + (a — ib) = 2a, а произведение этих комплексных чисел \(z.\bar z \) = (a + ib) × (a — ib) = a 2  + b 2 .

Обратная величина комплексного числа

Обратная величина комплексных чисел полезна в процессе деления одного комплексного числа на другое комплексное число. {-1}\).

Равенство комплексных чисел

Равенство комплексных чисел аналогично равенству действительных чисел. Два комплексных числа \(z_1 = a_1 + ib_1\) и \(z_2 = a_2 + ib_2 \) называются равными, если относительная часть обоих комплексных чисел равна \(a_1 = a_2\),  и мнимая части обоих комплексных чисел равны \(b_1 = b_2 \). Кроме того, два комплексных числа в полярной форме равны тогда и только тогда, когда они имеют одинаковую величину, а их аргумент (угол) отличается на целое кратное 2π.

Упорядочивание комплексных чисел

Упорядочивание комплексных чисел невозможно. Действительные числа и другие связанные системы счисления можно упорядочить, но нельзя упорядочить комплексные числа. Комплексные числа не имеют структуры упорядоченного поля, и нет упорядоченности комплексных чисел, совместимой со сложением и умножением. Также нетривиальная сумма квадратов в упорядоченном поле есть число \(\neq 0\), а в комплексном числе нетривиальная сумма квадратов равна i 2  + 1 2  = 0.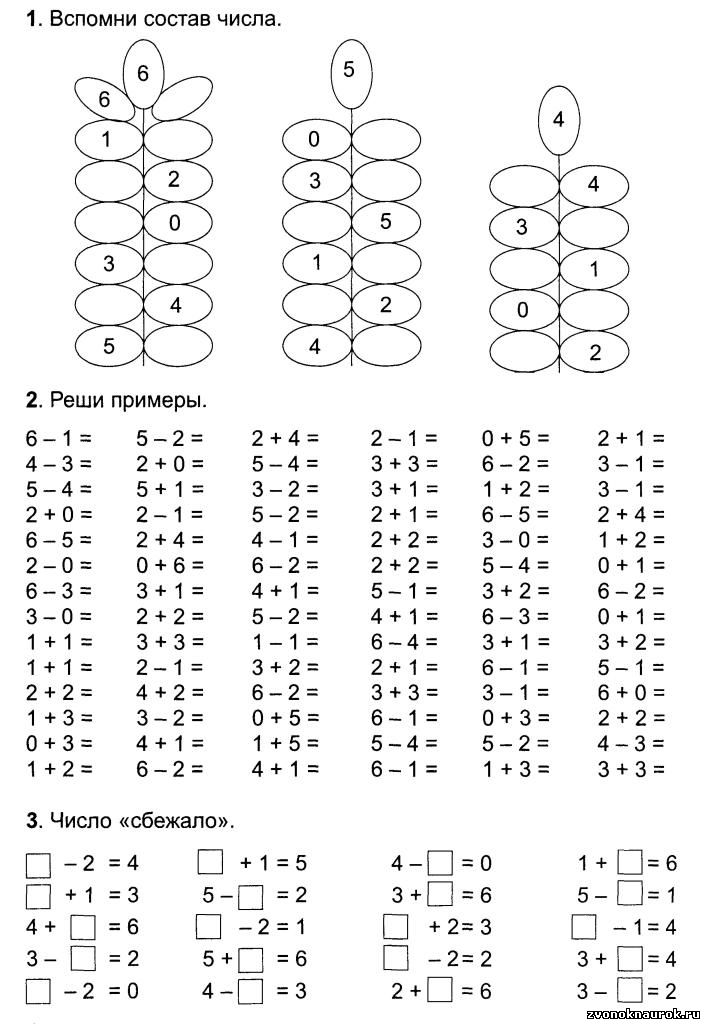 Комплексные числа можно измерить и представить на двумерной арграндовой плоскости по их величине, которая является расстоянием от начала координат.

Формула Эйлера: В соответствии с формулой Эйлера для любого действительного значения θ мы имеем e iθ  = Cosθ + iSinθ, и оно представляет комплексное число в координатной плоскости, где Cosθ – действительная часть, представленная относительно ось x, Sinθ – мнимая часть, представленная относительно оси y, θ – угол, образованный по отношению к оси x и воображаемой линии, соединяющей начало координат и комплексное число. Согласно формуле Эйлера и функциональному представлению x и y имеем e x + iy  = e x (уютный + isiny) = e x уютный + т.е. x Siny. Это разлагает экспоненциальную функцию на ее действительную и мнимую части.

Операции над комплексными числами

Различные операции сложения, вычитания, умножения, деления натуральных чисел можно выполнять и для комплексных чисел. Детали различных арифметических операций с комплексными числами заключаются в следующем.

Сложение комплексных чисел

Сложение комплексных чисел аналогично сложению натуральных чисел. Здесь в комплексных числах действительная часть добавляется к действительной части, а мнимая часть добавляется к мнимой части. Для двух комплексных чисел вида \(z_1 = a + id\) и \(z_2 = c + id\) сумма комплексных чисел \(z_1 + z_2 = (a + c) + i(b + d) \). Комплексные числа следуют всем следующим свойствам сложения.

  • Закон замыкания: Сумма двух комплексных чисел также является комплексным числом. Для двух комплексных чисел \(z_1\) и \(z_2\) сумма \(z_1 + z_2\) также является комплексным числом.
  • Коммутативный закон: Для двух комплексных чисел \(z_1\), \(z_2\) имеем \(z_1 + z_2 = z_2 + z_1\).
  • Ассоциативный закон: Для данных трех комплексных чисел \(z_1, z_2, z_3\) имеем \(z_1 + (z_2 + z_3) = (z_1 + z_2)+z_3 \). 2 = -1\). Для двух комплексных чисел \(z_1\) = a + ib, \(z_2\) = c + id произведение равно \(z_1.z_2\) = (ca — bd) + i(ad + bc).

    Умножение комплексных чисел в полярной форме немного отличается от упомянутой выше формы умножения. Здесь абсолютные значения двух комплексных чисел перемножаются, а их аргументы складываются для получения произведения комплексных чисел. Для комплексных чисел \(z_1 = r_1(Cos\theta_1 + iSin\theta_1)\) и  z 2  = \(z_2 = r_1(Cos\theta_2 + iSin\theta_2)\) произведение комплексные числа \(z_1.z_2 = r_1.r_2(Cos(\theta_1 + \theta_2) + iSin(\theta_1 + \theta_2))\). 92 + 2z_1z_2 +2z_2z_3 +2z_3z_1\)

Связанные темы:

  • Комплексное сопряжение
  • Калькулятор комплексных чисел
  • Тригонометрия
  • Координатная плоскость
  • Координатная геометрия
Комплексные числа Советы и подсказки:
  • Все действительные числа являются комплексными числами, но все комплексные числа не обязательно должны быть действительными числами.
  • Все мнимые числа являются комплексными числами, но все комплексные числа не обязательно должны быть мнимыми числами. 9{2}-4(1)(1)}}{2(1)} \\[0,2 см]
    &=\frac{-1 \pm \sqrt{-3}}{2}\\[0,2 см]
    \text{Здесь } &\sqrt{-3} = \sqrt{-1} \times \sqrt{3} = i \sqrt{3}\\[0,2 см]
    x&= \frac{-1 \pm i\sqrt{3}}{2}\\[0,2 см]
    \end{align} \]

    Таким образом, корнями данного квадратного уравнения являются: \(\frac{-1}{2}+ i\frac{\sqrt{3}}{2};\,\,\ , \frac{-1}{2}- i\frac{\sqrt{3}}{2}\)

  • Пример 2: Выразите сумму, разность, произведение и частное следующих комплексных чисел в виде комплексного числа.

    \[\begin{align} z_1&=-2+i\\[0.2cm]z_2&= 1-2i \end{align} \]

    Решение:

    Сумма:

    \[ \begin{ выровнять} z_1+z_2&= (-2+i)+(1-2i)\\[0,2 см] &=(-2+1)+ (i-2i)\\[0,2 см] &= -1-i \end{align}\]

    Разница:

    \[ \begin{align} z_1-z_2&= (-2+i)-(1-2i)\\[0,2 см] &=(-2-1) + (i+2i)\\[0,2 см] &= -3+3i \end{align}\]

    Продукт:

    \[ \begin{align} z_1\cdot z_2&= (-2+i)( 1-2i)\\[0,2см] &=-2+4i+i-2i^2\\[0,2см] &=-2+4i+i+2 \,\,\, [\потому что i^2 =-1]\\[0,2 см] &=5i \end{выравнивание}\] 92=-1]\\[0,2 см] &= \dfrac{-4-3i}{5}\\[0,2 см] &=- \dfrac{4}{5}- i \dfrac{3}{5 }\end{align}\]

    Следовательно, имеем:

    Сумма = -1 — i
    Разница = -3 + 3i
    Продукт = 5i
    Деление = -4/5 — 3i/5

    • перейти к слайдуперейти к слайду

    Разбивайте сложные концепции с помощью простых визуальных средств.

    Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

    Записаться на бесплатный пробный урок

    перейти к слайдуперейти к слайду

     

    Часто задаваемые вопросы о комплексных числах

    Что такое комплексные числа в математике?

    Комплексное число представляет собой комбинацию действительных и мнимых значений. Обозначается z = a + ib, где a, b — действительные числа, а i — мнимое число. i = \(\sqrt{-1}\) и никакое действительное значение не удовлетворяет уравнению i 2  = -1, поэтому I называется мнимым числом.

    Для чего используются комплексные числа?

    Комплексное число используется для простого нахождения квадратного корня из отрицательного числа. Здесь мы используем значение i 2  = -1 для представления отрицательного знака числа, что помогает легко находить квадратный корень. Здесь мы имеем √-4 = √i 2 4 = + 2i. {-1}\frac{b}{a} \)).

    Что такое действительные и комплексные числа?

    Комплексные числа являются частью действительных чисел. Некоторые действительные числа с отрицательным знаком трудно вычислить, и мы представляем отрицательный знак с помощью йоты «i», и такое представление чисел вместе с «i» называется комплексным числом. Дополнительные комплексные числа полезны для нахождения квадратного корня из отрицательного числа, а также для нахождения отрицательных корней квадратного или полиномиального выражения.

    Как делить комплексные числа? 92)}\).
    Как строить графики комплексных чисел?

    Комплексное число вида z = a + ib может быть представлено в плоскости арганда. Комплексное число z = a + ib может быть представлено в виде координат точки как (Re(z), Im(z)) = (a, ib). Здесь действительная часть представлена ​​относительно оси x, а мнимая часть представлена ​​относительно оси y.

    Как преобразовать комплексные числа в полярную форму?

    Комплексное число может быть легко преобразовано в полярную форму.

7 способов помочь младшему школьнику с математикой

Предположим, что математика уже в начальной школе ребёнка идёт туго, со скрипом. Трудно и скучно складывать и вычитать, не говоря уже о чём-то более сложном. Новые темы никак не хотят укладываться в голове. Писательница и мама троих детей Ксения Букша рассказывает, основываясь на собственном опыте, как помочь ребёнку освоить математику.

Раскладываем трудности по полочкам

На уровне 1–5-го классов неспособных к математике детей не бывает. Но бывают дети с конкретными трудностями, которые можно и нужно преодолеть. Подумаем, почему ребёнку трудно с математикой.

Вот возможные варианты или их комбинации.

  • Плохо считает, нет навыка счёта. Не очень хорошо знаком с числами.
  • Не может вникнуть в суть поставленной задачи, с трудом понимает, что надо делать. Пробует все варианты («Так неправильно? Тогда попробую разделить», «В три раза больше — здесь нужен плюс или минус?»).
  • Усваивает шаблонное решение, но не может его доработать. Столкнувшись с малейшим изменением условий, впадает в ступор.
  • Не умеет читать сложные тексты. В результате не понимает ни описания правил, ни текста задачи. Если на пальцах объяснить, что надо делать, сразу решает нормально.
  • В голове не укладываются концепции. С трудом их понимает и быстро забывает. Такой ребёнок может сто раз услышать объяснение, что такое икс (неизвестное), но так и не понять.
  • Не развит навык наглядного представления. Не может представить себе, нарисовать схематичную картинку, «увидеть в уме».
  • Короткое внимание: всё понимает, но делает кучу ошибок, особенно в длинных сложных примерах.

Как видим, математика раскладывается на множество разных навыков. Когда мы выяснили, в чём проблема, мы можем её решать. Заранее прошу прощения у учителей и методистов: я всего лишь родитель, а мои мысли по этому поводу — всего лишь частное мнение, хотя я стараюсь его обосновывать.

Ждём, пока созреет способность абстрактно мыслить

Мозг нейротипичного ребёнка дозревает до абстрагирования и обобщения далеко не сразу. У некоторых это происходит раньше, у других позже. Например, не все дети могут соотнести число и количество. Для очень многих и во 2–3-м классе есть только «15 яблок», а просто «15» нет.

При этом они как-то привыкают оперировать числами, и пробел в базовом понимании не очень заметен, пока речь не заходит о чуть более сложных вещах. Например, именно им трудновато понять, почему не может быть «полтора» в ответе на вопрос «сколько землекопов?». А уж когда начинаются проценты или задачи на скорость и расстояние, становится совсем сложно.

Стоит вернуться назад к конкретике. Возможно, для понимания дробей пока нужно проговаривать «в числителе арбузы, в знаменателе мальчики; 21 арбуз достался 42 мальчикам — каждому по половинке арбуза». Даже в пятом классе почти все концепции ещё можно заземлить до конкретики.

Развиваем навыки счёта

Просто учиться считать — это скучно. Нам помогут всевозможные игры с числами. Для начала — усложнённые ходилки с 2–3 кубиками (когда за один ход максимум — 18 очков, а не 6), потом — разнообразные игры в кости, где нужно считать очки.

Самая простая игра известна мне под названием «единичка»: игроки по очереди бросают один кубик (или два, или три), пытаясь добраться до сотни очков. Серия прерывается, когда у игрока выпадает хотя бы одна единичка: в этом случае очки за эту серию сгорают, и нужно уметь остановиться вовремя.

Очень рекомендую покер на костях. В этой игре есть ряд комбинаций, каждую из которых надо выбросить за три попытки. Эти попытки можно копить. Игроки делают ходы по очереди, выигрывает тот, кто первым выполнит все комбинации. Помимо простого навыка складывания очков, покер постепенно развивает тонкое понимание случайности и вероятности, просчитываемого риска и шансов. В такой покер может научиться играть даже шести- или семилетка.

Для отработки деления и умножения мы с дочкой говорили о числах как о «родственниках». Например, у числа 72 очень большая «семья»: у него есть «детки» 24 и 36, есть «внуки» — 2, 3, 4, 6, 12, 18. А вот число 37 не завело себе никакой «семьи», оно простое. Зато если «поженить» его с другим «одиночкой» — 41, у них получится вместе 78, теперь можно «заводить детей и внуков». Это хорошо помогает ориентироваться в таблице умножения.

Учим видеть и наглядно обобщать задачу

Чтобы хорошо схематизировать, надо уметь выделять именно то, что важно для условия задачи, и схематично изображать это на картинке. Сначала мы учимся выделению главного. Это знаменитые игры «что лишнее?», в которых может быть и несколько ответов. Арбуз, аист, абрикос, виноград — что лишнее? Смотря по какому признаку.

В учебнике Петерсон есть чудесные задачи, загромождённые кучей ненужных данных или лишённые необходимых условий. В задании автор просит найти и выделить только те условия, которые нужны для решения, а если их нет — указать, чего не хватает. Научившись видеть задачу, можно перейти к схематизации.

Многие дети вообще не понимают, зачем рисовать схемы к задачам и почему это проще. Всё потому, что схемы эти даны готовыми. Но по какому принципу они строятся? Почему, например, неважно, какой длины сам поезд, если он едет из А в Б? Как нарисовать «3 часа»? А «все груши, посаженные мальчиками»?

Можно вместе рисовать схемы разных задач, а потом предлагать ребёнку придумывать похожие. Такие задания есть и в учебниках, но там их мало. Для некоторых эта трудность вообще определяет все отношения с математикой, да и вообще с упорядочиванием данных, абстрагированием, обобщением, поиском решения.

Оттачиваем логику

Логика — один из инструментов, которые нужны всем. Нет людей, которые были бы не склонны к логике, есть те, у кого она «не поставлена». Это как умение орудовать шуруповёртом: научиться может каждый, у кого есть руки. Вы можете сами оценить, насколько железная у вас логика. Я очень люблю вот этот чудесный тест.

Человека с логикой не способна заморочить никакая пропаганда или реклама, его не запутает недобросовестный банк, он гораздо лучше ориентируется в окружающем мире.

С детьми можно начать с простых силлогизмов, которые иногда звучат смешно, но приводят к пониманию очень важных штук. Например, услышав от кого-нибудь сентенцию «мальчики не плачут», ребёнок может уточнить: «некоторые или все?»

Если дети не проходят понятие множества, стоит хоть немножко вместе с ним порисовать «кружочки» (не обязательно сразу вводить все понятия) и порешать соответствующие задачи: вот мальчики, вот коты, а вот те, кого зовут Вася. Где мальчики, которых зовут не Вася? А где тут девочки? А где кот Барсик?

Развиваем воображение

Воображение необходимо для всего, что связано с математикой и логикой. (Я даже не пишу «как ни странно», потому что это совершенно не странно.) Особенно умение мыслить образами.

Я очень люблю игру, в которой родитель и ребёнок по очереди задают друг другу «графические загадки», не имеющие точного ответа. Каждый рисует серию непонятных геометрических фигур или их комбинаций (точка в треугольнике, молния и круг, несколько кругов, касательные…), а другой дорисовывает их так, чтобы получилась картинка. Чем остроумнее решение, тем больше удовольствия получают оба игрока.

Существует много древних и новых игр, в которых нужно складывать узоры из деталей и фрагментов яйца (колумбово яйцо), квадрата, по-разному раскрашенных граней кубика («Сложи узор»). Есть и трёхмерные наборы, например «Пентамино». Речь не о том, чтобы выполнять задания, хотя все эти наборы можно использовать и так, но именно о творчестве из имеющихся деталей и об умении увидеть образ.

А можно ещё вырезать снежинки, дорисовывать симметричных бабочек и человечков, придумывать шифры, рисовать лабиринты и карты. Всё это и есть развитие математического воображения.

Учим ребёнка вычленять, чего конкретно он не понимает (метакогниция)

Я уже не раз писала про неё — и в связи с математикой, и в связи с сочинениями. Вкратце метакогниция — это умение «понимать, как я думаю», «знать, чего именно я не знаю», осознание своего мыслительного процесса. Именно этому почти никогда не учат в школе, а иногда даже портят уже развитую способность. Предполагается ведь, что есть простые и сложные способы решения той или иной задачи. Часто это так и есть, но порой гораздо ценнее умение идти самому и по шагам проверять себя: «Так нужно делать? Я прав?»

Совместные рассуждения (и я не про математику) ценны и тем, что сближают ребёнка и родителя, и тем, что мы показываем, как проходит процесс думания. Он не должен быть гладким и автоматическим. В нём есть тупики, неожиданные повороты. «Наше первоначальное предположение неверно, а это значит, что нужно идти не по дороге 1, а по дороге 2». Кстати, это пригодится и в школьной математике, когда нужно будет понимать доказательства теорем. Ведь хорошо запоминается только то, что прошёл сам своим умом, когда смог повторить чужие рассуждения и знаешь в них каждый поворот.

Самые непонятые математические стандарты в 1-м классе

Я был так взволнован, чтобы написать этот пост, потому что я провел более половины своей 23-летней преподавательской карьеры в 1--м -м классе. Мне нравится этот уровень обучения, и мне особенно нравится насыщенный математический контент, с которым ученики сталкиваются в течение года обучения!

Как я уже говорил в своем последнем посте, обучение математике в младших классах невероятно сложно, и стандарты могут быть легко неправильно поняты. Вот почему я изучал согласованные материалы, учился у Core Advocates и постоянно углублял свое собственное понимание математического содержания. Давайте погрузимся в некоторые примеры!

Стандарт Общая смещенная инструкция
1.OA.A.1 Используйте сложение и вычитание в пределах 20 для решения текстовых задач, связанных с ситуациями сложения, взятия, сложения, разъединения и сравнения с неизвестными во всех положениях, например, с использованием предметов, рисунков , и уравнения с символом неизвестного числа для представления проблемы. Инструкция включает не все типы задач из таблицы сложения и вычитания*.

В инструкциях по типам задач одним ситуациям уделяется больше внимания, чем другим, и сложение считается более важным, чем вычитание.

Инструкция включает в себя приемы получения ответов, такие как обучение ключевым словам, вместо поддержки математического мышления и осмысления.

*Обычные ситуации сложения и вычитания можно найти здесь .

1. OA.B.3 Применение свойств операций в качестве стратегий сложения и вычитания.*  Примеры: Если известно 8 + 3 = 11, то 3 + 8 = 11 также известно. (Переместительное свойство сложения.) Чтобы сложить 2 + 6 + 4, можно сложить вторые два числа, чтобы получить десятку, поэтому 2 + 6 + 4 = 2 + 10 = 12. (Ассоциативное свойство сложения.)

*Студентам не нужно использовать формальные термины для этих свойств.

 Инструкция фокусируется на процедурном обучении свойствам операций, а не на построении понимания свойств, почему они работают математически и как их можно использовать при сложении и вычитании.

Обучение делает акцент на изучении словарного запаса, преподавании только терминов и их определений, вместо понимания математических понятий и идей, лежащих в основе терминологии.

Примечание. Использование точного математического языка важно, но учащимся не нужно запоминать или запоминать термины. Акцент делается на понимании и использовании свойств операций.

1.OA.D.7 Понять значение знака равенства и определить, верны или нет уравнения сложения и вычитания. Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8 – 1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2, Инструкция упрощает значение знака равенства путем процедурных операций вместо того, чтобы формировать понимание учащимися того, что знак равенства означает одинаковость величин по обе стороны от знака равенства в уравнении (независимо от того, присутствует ли число или выражение).

Инструкция направлена ​​на то, чтобы всегда решать каждую сторону знака равенства, вместо того, чтобы иногда использовать стратегии или математические рассуждения, чтобы определить, является ли уравнение истинным или ложным.

1.NBT.B.3 Сравнивать двузначные числа по значениям разрядов десятков и единиц, записывая результаты сравнения с помощью символов >, = и <. Инструкция не связывает разрядное значение, понимая, что две цифры в двузначных числах представляют количество десятков и единиц для использования в сравнениях.

Инструкция фокусируется на процедурах сравнения чисел, а не на понимании количества двузначных чисел.

1.NBT.C.4 Сложение в пределах 100, включая двузначное число и однозначное число, а также сложение двузначного числа и числа, кратного 10, с использованием конкретных моделей или чертежей и стратегий в зависимости от места значение, свойства операций и/или взаимосвязь между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию. Поймите, что при сложении двузначных чисел складываются десятки и десятки, единицы и единицы; а иногда надо составить десятку. Инструкции и задачи, предлагаемые учащимся, ограничены задачами, в которых одно из двух слагаемых всегда является однозначной цифрой или десятичной цифрой.

Инструкция устремляется к стандартному алгоритму и не связывает конкретные и графические представления, основанные на понимании разрядности.

1.MD.A.2 Выразить длину объекта в виде целого числа единиц длины путем наложения нескольких копий более короткого объекта (единицы длины) встык; понимать, что измерение длины объекта — это количество единиц длины одинакового размера, которые охватывают его без промежутков или перекрытий. Ограничьтесь контекстами, в которых измеряемый объект охватывает целое число единиц длины без промежутков или перекрытий. Инструкция фокусируется на процедурах измерения, а не на построении понимания повторяющихся единиц длины при измерении (используйте одну единицу повторно, от начала до конца, без пробелов, начиная с одной конечной точки).

Инструкция включает измерения с использованием стандартных единиц измерения или стандартных измерительных инструментов, таких как линейки.

Давайте подробнее рассмотрим два ключевых стандарта: 1.OA.D.7 и 1.NBT.C.4. Оба эти стандарта представляют собой основную работу для 1 класса и играют важную роль в последовательном обучении математике в начальной школе. Как учитель я многому научился по этим стандартам!

1.OA.D.7

Поймите значение знака равенства и определите, верны или нет уравнения сложения и вычитания. Например, какие из следующих уравнений верны, а какие нет? 6 = 6, 7 = 8 – 1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2,

В своем классе, когда я ставил задачи на истину/ложь с выражением по обе стороны от знака равенства, я обычно учил студентов всегда решать сначала обе стороны. Я бы проследил это сравнением количеств: если количества были одинаковыми, то это было истинным, а если не одинаковым, то оно было ложным. Разговаривая с коллегами и посещая другие классы, я обнаружил, что многие учителя используют тот же метод. Узнав больше об этом стандарте, я понял, что превратил это обучение в процедуру, и в итоге студенты не стали лучше понимать знак равенства.

Аспект Строгости, требуемый в этом стандарте, — это концептуальное понимание. Цель обучения математике состоит в том, чтобы учащиеся поняли , что величины по обе стороны от знака равенства должны быть одинаковыми, иначе уравнение не имеет математического смысла. Знак равенства означает не получение ответа, а нечто гораздо более глубокое! Он показывает, что количества одинаковы или равны.

Я не только систематизировал то, что должно было стать концептуальным обучением, но и упустил возможность сделать акцент на рассуждениях и математическом мышлении, основанном на числах и операциях. Например, в задаче 4 + 4 = 3 + 9, учащиеся не должны ничего добавлять. Они должны уметь рассуждать, что 4 + 4 не больше 9, а 3 + 9 должно быть больше 9, поэтому без добавления чего-либо (кроме известного факта 4 + 4) это уравнение должно быть ложным. Всякий раз, когда мы можем сделать акцент на математическом осмыслении в нашем обучении, мы должны извлечь выгоду из этой возможности!!

1.NBT.C.4.

Сложение в пределах 100, включая двузначное число и однозначное число, а также сложение двузначного числа и числа, кратного 10, с использованием конкретных моделей или чертежей и стратегий, основанных на позиционном значении, свойствах операций, и/или отношения между сложением и вычитанием, свяжите стратегию с письменным методом и объясните используемую аргументацию. Поймите, что при сложении двузначных чисел складываются десятки и десятки, единицы и единицы; а иногда надо составить десятку.

Я выбрал этот стандарт, потому что я неправильно понимал его, будучи учителем первого класса, пока у меня не появилась возможность углубить свое понимание, изучив учебную программу, согласованную со стандартами. Я думал, что стандарт требует, чтобы все задачи, с которыми работают студенты, выглядели примерно так: 23 + 6 , 42 + 4 и 38 + 3 , или 23 + 60 , 42 + 40 и . 38 + 30 . Во всех этих примерах одно из слагаемых всегда либо однозначное число, либо кратное десяти. Как оказалось, я неправильно понял этот стандарт!

Изучая стандартную учебную программу в качестве учителя, я столкнулся со многими проблемами, такими как 23 + 36, 42 + 54 и 38 + 27. Так как же эти двузначные сложения могут соответствовать этому стандарту и способствовать работе, которая произойдет через 2 -й класс? Я также задавался вопросом, как избежать процедурных инструкций и вместо этого сосредоточиться на понимании значения с помощью операции сложения. Давайте посмотрим на 23 + 36 и воспользуемся приведенными ниже образцами студенческих работ:

Как видите, в одном примере учащийся разложил 36 на 30 и 6, затем добавил 23 + 6 в качестве первого шага, добавив единицы и единицы. . Далее студент добавил 29+ 30, прибавляя десятки и десятки, чтобы найти всю сумму. Этот метод соответствует стандарту.

В другом примере учащийся разложил оба числа в развернутую форму, затем отдельно прибавил единицы и десятки (20 + 30 и 3 + 6), а затем прибавил 50 + 9. В этом случае учащийся использовал графическое представление и связанные это к написанным уравнениям. Этот метод также соответствует стандарту.

Другая часть этого стандарта подразумевает понимание того, что «иногда необходимо составить десятку». Как первоклассник может решить задачу такого типа (например, 38 + 27), следуя стандарту? Опять же, давайте посмотрим на образцы студенческих работ ниже:

Как видите, один студент разложил 27 на 25 и 2, а затем добавил 38 + 2, создав эквивалентную задачу 40 + 25. Этот студент знал, что 2 нужно, чтобы получить число 40 в следующем десятилетии, и смог разложить 27 чтобы получить 2. С помощью этого метода студент составил новую десятку.

Другой учащийся сложил единицы с единицами, составляя новую десятку, затем складывал десятки с десятками, используя графическое представление на основе разрядности. Затем студент решил, добавив 50 + 15. Оба метода находятся в рамках стандарта.

Мне нравится та гибкость, которую допускают в этих задачах, закладывая основу для различных методов решения и различных типов мышления учащихся. Все методы решения основаны на позиционном значении и построены на быстром сложении в пределах 100 и сложении трехзначных чисел в степени 2 nd и являются основой для глубокого понимания будущих алгоритмов.

Я надеюсь, что этот пост помог вам по-другому взглянуть на сложное изучение математики, которое происходит в первом классе! Я хотел бы прочитать ваши комментарии или услышать от вас на Twitter! (@mrsmillergrade1). В этой серии блогов я также снижаю классы, так что следите за моим постом о детском саду, который выйдет следующим!

Об авторе: Энджи Миллер работает специалистом по обучению математике в школьном округе Анакортес в штате Вашингтон. До своей роли помощника учителей она преподавала в начальных классах и специальном образовании в течение 19 лет. Энджи неустанно выступает за справедливость в классе математики за счет улучшения учебной практики, углубления знаний и использования согласованных высококачественных учебных материалов. Благодаря своей работе с Вашингтонской ассоциацией образования, ведущими преподавателями и новыми лидерами она разработала профессиональное изучение математических смен Common Core State Standards для преподавателей по всей стране. Энджи работает в Институте стандартов UnboundEd по программе K-2 Math. Энджи является учителем, сертифицированным Национальным советом, и имеет сертификат по лидерству учителей Вашингтонского университета.

Комментарии по математике в табеле успеваемости

Обширный список описательных комментариев, фраз и предложений, которые помогут вам написать четкие и подходящие отзывы в табелях успеваемости по математике для родителей и учащихся. Сосредоточенный на наиболее распространенных и важных областях обучения математике (арифметика, чувство чисел, геометрия, измерения и т. д.), этот список содержит простые для понимания утверждения, написанные простым языком, которые помогут вам адаптировать и передать конкретные предложения для похвалы. , улучшение и проблемы.

Классы:

+ показать теги

ТИП:

Классные инструменты


Стратегии обучения:

Табель комментариев и фраз по всем предметам

Оценка


Добавить в избранное

СОЗДАТЬ НОВУЮ ПАПКУ