Математика. Сложение и вычитание «столбиком»
Главная > Образование > Математика > МАТЕМАТИКА «С НУЛЯ» (учебник) >
<< Назад | Оглавление | Далее >>
Как мы знаем, любое число можно записать с помощью десяти значков, которые называются (арабскими) цифрами. Это значит, что для выполнения любых письменных заданий по математике не нужно уметь считать больше, чем до десяти. Пусть нам, например, дано задание пересчитать огромное число песчинок, высыпанных на стол. Мы отсчитываем десять песчинок и складываем их в одну кучку. Потом отсчитываем еще десять песчинок и складываем их в другую кучку. И так далее, и так далее, пока только можно. Оставшиеся песчинки, не попавшие ни в одну из кучек (если такие будут), отодвигаем на дальний конец стола, чтобы не мешались. Перед нами остались только кучки-десятки. Их-то мы и начинаем пересчитывать. И принимаемся мы за дело точно так же, как и тогда, когда перед нами была лишь большая россыпь отдельных песчинок.
Кучки- | Кучки — | Кучки — | Кучки- | Кучки- | Кучки- | Отдельные |
В самую правую колонку надо занести количество отдельных песчинок, не попавших ни в какие кучки. По-научному, эта колонка таблицы называется разрядом единиц. Говорят также, что это самый младший разряд числа. Во вторую колонку справа (разряд десятков) следует поставить количество кучек-десятков. И так далее. При необходимости, слева к таблице можно приписать еще любое количество столбцов (старших разрядов), и не так уж важно, как они называются. Если же столбцов, наоборот, окажется слишком много, то лишние столбцы слева можно стереть. Задание по пересчету песчинок выполнено.
По-научному, эта колонка таблицы называется разрядом единиц. Говорят также, что это самый младший разряд числа. Во вторую колонку справа (разряд десятков) следует поставить количество кучек-десятков. И так далее. При необходимости, слева к таблице можно приписать еще любое количество столбцов (старших разрядов), и не так уж важно, как они называются. Если же столбцов, наоборот, окажется слишком много, то лишние столбцы слева можно стереть. Задание по пересчету песчинок выполнено.
Теперь рассмотрим, как можно сложить два больших числа, не пользуясь счетами. Допустим, к 1234 песчинкам требуется прибавить 2345 песчинок. Заносим оба числа в таблицу:
| Тысячи | Сотни | Десятки | Единицы |
1-е слагаемое | 1 | 2 | 3 | 4 |
2-е слагаемое | 2 | 3 | 4 | 5 |
Поскольку мы собрались складывать эти числа, то и назвали мы их слагаемыми.
| Тысячи | Сотни | Десятки | Единицы |
1-е слагаемое | 1 | 2 | 3 | 4 |
2-е слагаемое | 2 | 3 | 4 | 5 |
Сумма | 3 | 5 | 7 | 9 |
Заметим, что результат сложения по-научному называется суммой. Таким образом,
Таким образом,
1234 + 2345 = 3579.
К сожалению, не всегда всё получается так просто. Пусть надо вычислить
5678 + 6789.
Заносим слагаемые в таблицу, складываем по отдельности каждый разряд и получаем:
| Тысячи | Сотни | Десятки | Единицы |
1-е слагаемое | 5 | 6 | 7 | 8 |
2-е слагаемое | 6 | 7 | 8 | 9 |
Сумма | 11 | 13 | 15 | 17 |
Прямо скажем, вышло плохо. Вот, к примеру, в самом младшем разряде оказалось 17 песчинок. Из такого количества песчинок можно сделать одну полновесную кучку-десяток, и место этой кучке-десятку — в следующем по старшинству разряде. Придется переписать таблицу в другом виде, формируя по мере надобности новые кучки и сразу помещая их в правильный разряд. После этого остается еще раз выполнить сложение внутри каждого разряда, и только тогда получится правильный ответ:
Вот, к примеру, в самом младшем разряде оказалось 17 песчинок. Из такого количества песчинок можно сделать одну полновесную кучку-десяток, и место этой кучке-десятку — в следующем по старшинству разряде. Придется переписать таблицу в другом виде, формируя по мере надобности новые кучки и сразу помещая их в правильный разряд. После этого остается еще раз выполнить сложение внутри каждого разряда, и только тогда получится правильный ответ:
| Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
1-е слагаемое |
| 5 | 6 | 7 | 8 |
2-е слагаемое |
| 6 | 7 | 8 | 9 |
Вспомогательные | | | | 1 | 7 |
| Сумма | 1 | 2 | 4 | 6 | 7 |
Ну что ж, в принципе, так делать можно, но не всегда ответ получается быстро. Вот, например, какую длинную таблицу приходится составлять, чтобы сложить таким способом числа 9999 и 1:
Вот, например, какую длинную таблицу приходится составлять, чтобы сложить таким способом числа 9999 и 1:
| Десятки тысяч | Тысячи | Сотни | Десятки | Единицы |
1-е слагаемое |
| 9 | 9 | 9 | 9 |
2-е слагаемое |
|
|
|
| 1 |
Вспомогательные |
| | | 1 | 0 |
Вспомогательные |
| | 1 | 0 | 0 |
Вспомогательные |
| 1 | 0 | 0 | 0 |
Сумма | 1 | 0 | 0 | 0 | 0 |
Подумаем, нельзя ли обойтись более короткой записью. Давайте еще раз сложим числа 5678 и 6789 и постараемся быть по возможности краткими. Ну, во-первых, нет никакой необходимости так тщательно разлиновывать таблицу и выписывать заголовки столбцов и строк. Напишем слагаемые просто так:
Давайте еще раз сложим числа 5678 и 6789 и постараемся быть по возможности краткими. Ну, во-первых, нет никакой необходимости так тщательно разлиновывать таблицу и выписывать заголовки столбцов и строк. Напишем слагаемые просто так:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 |
Проделаем сперва сложение в разряде единиц:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
| 1 | 7 | ||
В результате такого сложения у нас образовалась дополнительная кучка-десяток, которую мы и записали в подходящий для нее разряд. Теперь, когда мы будем складывать кучки-десятки, мы учтем и эту дополнительную кучку тоже: 7 десятков + 8 десятков = 15 десятков; 15 десятков + 1 десяток = 16 десятков; 16 десятков = 1 сотня + 6 десятков. Значит, следует написать:
Теперь, когда мы будем складывать кучки-десятки, мы учтем и эту дополнительную кучку тоже: 7 десятков + 8 десятков = 15 десятков; 15 десятков + 1 десяток = 16 десятков; 16 десятков = 1 сотня + 6 десятков. Значит, следует написать:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
| 1 | 7 | ||
| 1 | 6 |
| |
Подобным же образом, вновь образованную кучку-сотню мы учитываем при выполнении сложения в разряде сотен:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
| 1 | 7 | ||
| 1 | 6 |
| |
| 1 | 4 |
| |
Наконец, осталось сложить всё, что оказалось в разряде тысяч (и, ради красоты, написать еще раз единицу из самого старшего разряда строчкой ниже):
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
| 1 | 7 | ||
| 1 | 6 |
| |
| 1 | 4 |
| |
1 | 2 |
| ||
1 |
| |||
Ответ-то мы получили, это число 12467, но записано оно как-то неудобно — лесенкой, идущей снизу вверх. Уж лучше писать лесенкой промежуточные результаты. Вот что получается, например, после сложения единиц:
Уж лучше писать лесенкой промежуточные результаты. Вот что получается, например, после сложения единиц:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
| 1 |
| ||
| 7 | |||
Продолжая писать такие маленькие лесенки, мы получим конечный ответ в виде:
+ | 5 | 6 | 7 | 8 |
6 | 7 | 8 | 9 | |
1 | 1 | 1 | 1 |
|
1 | 2 | 4 | 6 | 7 |
Это уже гораздо красивее. Однако и этом пути нас ожидают мелкие неудобства. Пусть надо сложить числа 5172 и 9284. Начинаем, как обычно, с разряда единиц:
Однако и этом пути нас ожидают мелкие неудобства. Пусть надо сложить числа 5172 и 9284. Начинаем, как обычно, с разряда единиц:
+ | 5 | 1 | 7 | 2 |
9 | 2 | 8 | 4 | |
| 6 | |||
Очередь за разрядом десятков. Складываем 7 и 8 и получаем 15. Ну, и куда теперь писать цифру 1, куда цифру 5? Мы же забыли оставить под чертой свободную строчку, откуда должны начинаться лесенки! Но, конечно, мы не будем ничего зачеркивать и переделывать. Мы просто запишем цифру 1 на самый верх таблицы. Важно лишь то, чтобы она попала в правильный разряд:
| 1 |
| ||
+ | 5 | 1 | 7 | 2 |
9 | 2 | 8 | 4 | |
| 5 | 6 | ||
Теперь вычисления легко довести до конца:
1 |
| 1 |
| |
+ | 5 | 1 | 7 | 2 |
9 | 2 | 8 | 4 | |
1 | 4 | 4 | 5 | 6 |
Наконец-то всё стало хорошо! Но можно сделать еще лучше.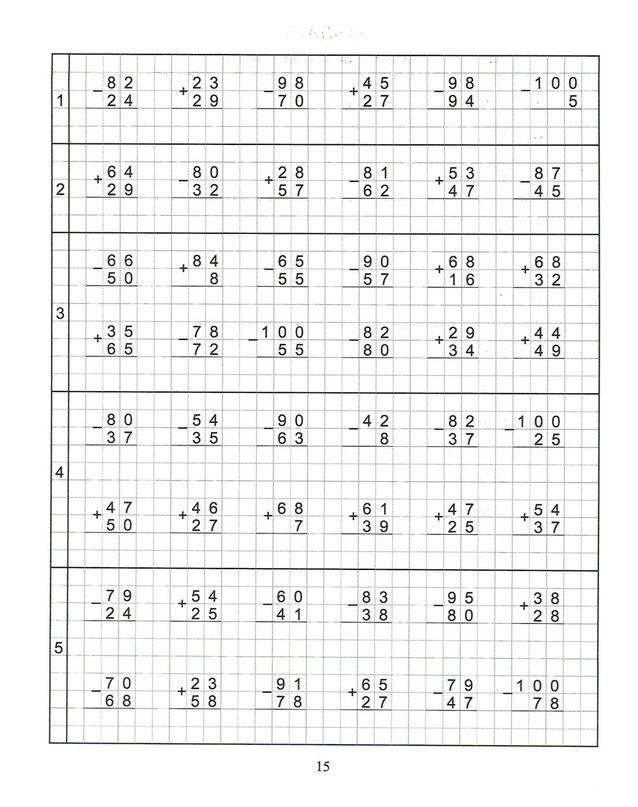 На самом верху всё равно ничего, кроме единичек, стоять не может. А значит, вовсе не обязательно эти единички так уж тщательно выписывать. Достаточно вместо этих единичек ставить небольшие аккуратные точки. Вот так:
На самом верху всё равно ничего, кроме единичек, стоять не может. А значит, вовсе не обязательно эти единички так уж тщательно выписывать. Достаточно вместо этих единичек ставить небольшие аккуратные точки. Вот так:
• |
| • |
| |
+ | 5 | 1 | 7 | 2 |
9 | 2 | 8 | 4 | |
1 | 4 | 4 | 5 | 6 |
Теперь мы всё знаем про то, как складывать «в столбик»! Осталось только тренироваться и тренироваться, чтобы научиться это делать быстро и без ошибок.
Пора осваивать вычитание. Пусть требуется вычислить
3579 − 1234.
Заготавливаем табличку:
− | 3 | 5 | 7 | 9 |
1 | 2 | 3 | 4 |
Проделываем вычитание в каждом разряде по отдельности и получаем ответ:
− | 3 | 5 | 7 | 9 |
1 | 2 | 3 | 4 | |
| 2 | 3 | 4 | 5 |
Ну а если из числа 12467 требуется вычесть число 5678? Начинаем как обычно:
− | 1 | 2 | 4 | 6 | 7 |
| 5 | 6 | 7 | 8 |
М-да… Ситуация в разряде единиц складывается очень неприятная. Из семи надо вычитать восемь. Но у нас уже есть кое-какой опыт. Мы знаем, как следует выходить из такого положения. Надо разбить кучку-десяток на отдельные песчинки, и всё тогда встанет на свои места. Записать это можно так:
Из семи надо вычитать восемь. Но у нас уже есть кое-какой опыт. Мы знаем, как следует выходить из такого положения. Надо разбить кучку-десяток на отдельные песчинки, и всё тогда встанет на свои места. Записать это можно так:
10 | |||||
− | 1 | 2 | 4 | 6 | 7 |
| 5 | 6 | 7 | 8 | |
| −1 |
| |||
Теперь вычисления в разряде единиц можно проделать очень легко: 10 + 7 = 17; 17 − 8 = 9. Заносим получившуюся девятку в таблицу:
10 | |||||
− | 1 | 2 | 4 | 6 | 7 |
| 5 | 6 | 7 | 8 | |
−1 |
| ||||
| 9 | ||||
Переходим к разряду десятков. Здесь нас тоже ожидает неприятность. Из шести надо вычесть семь, а потом вычесть еще одну единицу. Повторяем трюк с разбиением кучки из более старшего разряда:
Здесь нас тоже ожидает неприятность. Из шести надо вычесть семь, а потом вычесть еще одну единицу. Повторяем трюк с разбиением кучки из более старшего разряда:
10 | 10 | ||||
− | 1 | 2 | 4 | 6 | 7 |
| 5 | 6 | 7 | 8 | |
−1 | −1 |
| |||
| 9 | ||||
В разряде десятков теперь имеем: 10 + 6 = 16; 16 − 7 = 9; 9 − 1 = 8. Продолжаем так дальше и в конце концов получаем:
Продолжаем так дальше и в конце концов получаем:
10 | 10 | 10 | 10 | ||
− | 1 | 2 | 4 | 6 | 7 |
| 5 | 6 | 7 | 8 | |
−1 | −1 | −1 | −1 |
| |
| 6 | 7 | 8 | 9 | |
Всё бы хорошо, да только мы уже знаем, что подобная форма записи может привести к некоторым неудобствам. Попробуем вычислить
Попробуем вычислить
14456 − 5172.
В разряде единиц ситуация складывается очень удачно:
− | 1 | 4 | 4 | 5 | 6 |
| 5 | 1 | 7 | 2 | |
| 4 | ||||
Переходим к вычислениям в разряде десятков. А здесь не всё так уж гладко. Придется записать так:
| 10 |
| |||
| −1 |
| |||
− | 1 | 4 | 4 | 5 | 6 |
| 5 | 1 | 7 | 2 | |
| 8 | 4 | |||
Доводим вычисления до конца и получаем:
| 10 |
| 10 |
| |
| −1 |
| −1 |
| |
− | 1 | 4 | 4 | 5 | 6 |
| 5 | 1 | 7 | 2 | |
| 9 | 2 | 8 | 4 | |
Но, конечно, эту запись хорошо бы еще сократить. Вовсе необязательно выписывать в верхней части таблички такие лесенки:
Вовсе необязательно выписывать в верхней части таблички такие лесенки:
Всё это сооружение можно заменить на одну-единственную точку, которую удобно записать на месте «−1». В результате получается:
| • |
| • |
| |
− | 1 | 4 | 4 | 5 | 6 |
| 5 | 1 | 7 | 2 | |
| 9 | 2 | 8 | 4 | |
Таким образом, точка наверху таблицы как бы разбивает кучку своего разряда на десять кучек более младшего разряда.
В качестве заключительного примера вычислим 1000 − 1:
− | 1 | 0 | 0 | 0 |
| 1 | |||
Здесь, для того чтобы выполнить вычитание в разряде единиц, надо бы разбить кучку-десяток на отдельные песчинки, но и кучек-десятков у нас нет. Не беда! Мы немножко сфокусничаем. Сейчас мы как бы из воздуха позаимствуем одну кучку-десяток, но зато потом, когда мы будем проводить вычисления в разряде десятков, надо будет обязательно позаимствованную кучку вернуть. Смело ставим точку в разряд десятков. В разряде единиц получаем: 10 + 0 = 10; 10 − 1 = 9:
| • |
| ||
− | 1 | 0 | 0 | 0 |
| 1 | |||
| 9 | |||
Пришло время разбираться с разрядом десятков. Здесь у нас есть ноль кучек, да еще одну кучку надо вернуть, о чем нам напоминает точка сверху. Ставим точку в разряд сотен и не задумываемся о том, разбивается ли при этом на десять кучек настоящая кучка-сотня или такая кучка заимствуется «из воздуха». Теперь в разряде десятков у нас есть десять кучек. Одну из них возвращаем, остается девять:
Здесь у нас есть ноль кучек, да еще одну кучку надо вернуть, о чем нам напоминает точка сверху. Ставим точку в разряд сотен и не задумываемся о том, разбивается ли при этом на десять кучек настоящая кучка-сотня или такая кучка заимствуется «из воздуха». Теперь в разряде десятков у нас есть десять кучек. Одну из них возвращаем, остается девять:
| • | • |
| |
− | 1 | 0 | 0 | 0 |
| 1 | |||
| 9 | 9 | ||
Дальнейшие действия никакой сложности не представляют. Окончательный результат таков:
Окончательный результат таков:
| • | • | • |
|
− | 1 | 0 | 0 | 0 |
| 1 | |||
| 9 | 9 | 9 | |
Теперь и про вычитание нам всё известно. Осталось нарабатывать навык.
Примеры из «бесконечного» сборника типовых упражнений
Сложение и вычитание трехзначных чисел
Сложение и вычитание шестизначных натуральных чисел
Упражнения на переходы между разрядами
3 класс — сложение и вычитание трехзначных чисел и вычитание столбиком.
 Примеры
ПримерыДата публикации: .
Вычитание двузначных чисел (повторение)
1. Запиши заданные предложения в виде числовых выражений и реши их.
1.1. Из числа 78 вычти число 49.1.2. Из числа 92 вычти число 63.
1.3. Из числа 49 вычти число 38.
2. Реши примеры.
| 633 — 159 = | 272 — 174 = | 395 — 182 = | 799 — 527 = |
| 782 — 618 = | 509 — 456 = | 308 — 241 = | 579 — 258 = |
| 367 — 250 = | 885 — 663 = | 285 — 172 = | 789 — 252 = |
3. Вместо … поставь числа, чтобы выражение стало верным.
| 856 — … = 589 | 695 — … = 384 | 672 — … = 298 | 314 — … = 273 |
| … — 256 = 488 | … — 423 = 573 | … — 347 = 478 | … — 243 = 45 |
| 357 — … = 298 | … — 312 = 237 | 405 — … = 69 | . .. — 232 = 388 .. — 232 = 388 |
Вычитание трехзначных чисел
1. Запиши заданные предложения в виде числовых выражений и реши их.
1.1. Из числа 798 вычти число 647.1.2. Из числа 458 вычти число 412.
1.3. Из числа 599 вычти число 241.
2. Реши примеры.
| 936 — 287 = | 745 — 293 = | 366 — 182 = | 959 — 235 = |
| 862 — 192 = | 779 — 503 = | 848 — 472 = | 729 — 531 = |
| 374 — 233 = | 852 — 634 = | 773 — 117 = | 892 — 442 = |
Решение текстовых задач на вычитание
1. В школе учится 670 учеников, из них 370 – мальчики. Сколько девочек учится в школе?
2. На склад завезли 690 мешков с сахаром. В первый день увезли 130 мешков, а во второй день увезли ещё 357 мешков. Сколько всего мешков с сахаром осталось на складе после второго дня?
3. В библиотеку привезли 702 книги, из них 268 книг раздали 3 классу и 211 книг – 1 классу. Сколько книг осталось в библиотеке для 2 класса?
4. В цистерну было налито 869 литров бензина, 347 литров бензина было израсходовано. Сколько литров бензина осталось в цистерне?
В цистерну было налито 869 литров бензина, 347 литров бензина было израсходовано. Сколько литров бензина осталось в цистерне?
Табличное вычитание и проверка вычитания сложением
1. Выполни вычитание и проверь результат.
| 385 — 247 = | 164 — 95 = | 548 — 118 = | 338 — 144 = |
| 436 — 147 = | 235 — 215 = | 696 — 23 = | 985 — 566 = |
| 757 — 664 = | 347 — 164 = | 654 — 147 = | 179 — 155 = |
2. Запиши заданные предложения в виде числовых выражений, реши их и проверь результат.
2.1. Из числа 564 вычти число 18.2.2. Из числа 851 вычти число 676.
2.3. Из числа 352 вычти число 213.
2.4. Из числа четыреста шестнадцать вычти число триста тридцать пять.
Урок 10. сложение и вычитание чисел столбиком — Математика — 5 класс
Математика
5 класс
Урок № 10
Сложение и вычитание чисел столбиком
Перечень вопросов, рассматриваемых в теме:
— сложение натуральных чисел в столбик;
— вычитание натуральных чисел в столбик
Тезаурус
Сложение – арифметическое действие, посредством которого из двух или нескольких чисел получают новое, содержащее столько единиц, сколько было во всех данных числах вместе.
Сумма – результат сложения.
Сложение столбиком предполагает последовательное сложения цифр первого и второго числа, складывают числа справа налево, начиная с единиц, потом десятки, сотни и т.д.
Разность чисел a и b – это такое число, которое при сложении с числом b даёт число а.
Чтобы найти разность методом «вычитание столбиком» (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:
- поместить вычитаемое под уменьшаемое, записать единицы под единицами, десятки под десятками и т.д.;
- вычесть поразрядно.
Обязательная литература
- Никольский С. М. Математика: 5 класс. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. – М.: Просвещение, 2017 – 272 с.
- Потапов М. К. Математика. Книга для учителя. 5-6 классы. // М. К. Потапов, А. В. Шевкин. – М.: Просвещение, 2010 – 256 с.
Дополнительная литература
- Бурмистрова Т. А. Математика.
 Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с. - Потапов М. К. Математика: дидактические материалы. 6 класс. // М. К. Потапов, А. В. Шевкин – М.: Просвещение, 2010 – 118 с.
- Чесноков А. С. Дидактические материалы по математике 5 класс. // А. С. Чесноков, К. И. Нешков. – М.: Академкнига, 2014, – 124 с.
Теоретический материал для самостоятельного изучения
При сложении и вычитании чисел в пределах 20 удобно использовать таблицу.
Многозначные числа складывают и вычитают по разрядам, используя переместительный, сочетательный и распределительный законы.
Например, сложим 32 и 24. Разложим эти числа на разрядные слагаемые. Получим сумму тридцати, двух, двадцати и четырёх. Сложим попарно десятки и единицы, в результате получим сумму 50 и 6. Сложив эти числа, получим 56.
32 + 24 = 30 + 2 + 20 + 4 = (30 + 20) + (2 + 4) = 50 + 6 = 56
Рассмотрим разность 58 и 33. Представим эти числа в виде суммы разрядных слагаемых. Получим (50 + 8) – (30 + 3). Вычтем одноимённые разряды. От 50 отнимем 30, от 8 отнимем 3, сложив результаты, получим двадцать пять.
Получим (50 + 8) – (30 + 3). Вычтем одноимённые разряды. От 50 отнимем 30, от 8 отнимем 3, сложив результаты, получим двадцать пять.
58 – 33 = 50 + 8 – 30 – 3 = (50 – 30) + (8 – 3) = 20 + 5 = 25
Обычно сложение и вычитание многозначных чисел выполняют столбиком, записывая числа друг под другом так, чтобы цифры одинаковых разрядов стояли друг под другом, и начинают вычислять с разряда единиц.
Если сложение в каком-либо разряде даст в результате число, большее или равное 10, то десять единиц этого разряда заменяют единицей следующего разряда, прибавляя эту единицу к цифре следующего разряда (справа налево).
Вычислим 48 + 37.
Начинаем сложение с разрядов единиц: восемь и семь в сумме дают пятнадцать. Записываем в ответе цифру пять в разряд единиц, а единицу прибавляем к сумме разрядов десятков. Получаем восемь – эту цифру записываем в ответе в разряд десятков.
В итоге получили ответ – восемьдесят пять.
Если при вычитании в каком-либо разряде цифра уменьшаемого меньше цифры вычитаемого, то нужно «занять» одну единицу в следующем (справа налево) разряде уменьшаемого.
Вычтем 19 из 72.
Запишем это выражение в столбик и начнём вычитание с разряда единиц. Нам надо от 2 вычесть 9, это сделать нельзя, поэтому «займём» у семёрки 10, в итоге теперь нам надо от 12 вычесть 9, получаем 3, записываем это число в ответе в разряд единиц. Затем нам надо помнить, что у семёрки мы заняли один десяток, итого у нас осталось 6. Теперь из 6 вычитаем 1. Получаем 5. Записываем это число в разряд десятков.
Значит, разность 72 и 19 равна 53.
Разбор решения заданий тренировочного модуля
№ 1. Вычислите значение выражения 65789 + 45607.
Решение: запишем это выражение в столбик и выполним сложение по разрядам:
Ответ: 111396.
№ 2. На рынке в течение первого дня было продано 54 тонн фруктов, а завезено 76 тонн. Во второй день продали 65 тонн, а завезли 48 тонн. Увеличилась или уменьшилась масса фруктов на рынке, и на сколько? Выберите правильный ответ.
Варианты ответов:
- увеличилась на 5 тонн;
- уменьшилась на 5 тонн;
- увеличилась на 7 тонн;
- осталась без изменений.

Решение:
- Найдём, сколько фруктов было завезено в первый и второй дни: 76 + 48 = 124 (тонн).
- Найдём, сколько фруктов было продано за два дня: 54 + 65 = 119 (тонн).
- Сравним полученные числа 124 и 119, 124 > 119
- Найдём, насколько увеличилась масса фруктов: 124 – 119 = 5 (тонн).
Ответ: увеличилась на 5 тонн.
Как считать в столбик сложение и вычитание. Вычитание чисел, формула. Пример вычитания на числовой прямой
Чтобы найти разность методом «вычитание столбиком » (другими словами, как считать в столбик или столбиком вычитание), необходимо следовать таким шагам:
- поместить вычитаемое под уменьшаемое, записать единицы под единицами, десятки под десятками и т.д.
- вычесть поразрядно.
- если необходимо занять десяток из большего разряда, то над разрядом, в котором заняли, поставить точку. Над разрядом, для которого заняли, поставить 10.
- если в разряде, в котором заняли, стоит 0, тогда занимаем из следующего разряда уменьшаемого и над ним ставим точку.
 Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.
Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.
Ниже рассмотренные примеры покажут вам как происходит вычитание двухзначных, трехзначных и любых многозначных чисел столбиком.
Вычитание чисел в столбик очень помогает при вычитании больших чисел (как и сложение в столбик). Лучше всего научиться на примере.
Необходимо записать числа одно под другим таким образом, чтобы крайняя правая цифра 1-го числа стала под крайней правой цифрой 2-го числа. Число, которое больше (уменьшаемое) записываем сверху. Слева между числами ставим знак действия, здесь это «-» (вычитание).
2 — 1 = 1 . То, что у нас получается пишем под чертой:
10 + 3 = 13.
Из 13 вычтем девять.
13 — 9 = 4.
Так как мы заняли десяток у четверки, то она уменьшилось на 1. Для того, чтобы не забыть об этом у нас и стоит точка.
4 — 1 = 3.
Результат:
Вычитание столбиком из чисел, содержащих нули.

Опять же, разберем на примере:
Записываем числа в столбик. Которое больше — сверху. Начинаем вычитание справа налево по одной цифре. 9 — 3 = 6.
Из нуля вычесть 2 не получится, тогда опять занимаем у цифры слева. Это нуль. Ставим над нулем точку. И снова, у нуля занять не получится, тогда двигаемся дальше к следующей цифре. Занимаем у единицы. Ставим над ней точку.
Обратите внимание: когда в вычитании столбиком над 0 есть точка, нуль становится девяткой.
Над нашим нулем есть точка, значит, он стал девяткой. Вычитаем из нее 4. 9 — 4 = 5 . Над единицей есть точка, то есть она уменьшается на 1. 1 — 1 = 0. Полученный нуль не нужно записывать.
Существует удобный метод нахождения разности двух натуральных чисел – вычитание в столбик, или вычитание столбиком. Этот способ берет свое название от метода записи уменьшаемого и разности друг под другом. Так можно провести и основные, и промежуточные вычисления в соответствии с нужными разрядами чисел.
Этим методом удобно пользоваться, поскольку это очень просто, быстро и наглядно. Все сложные на первый взгляд подсчеты можно свести к сложению и вычитанию простых чисел.
Ниже мы рассмотрим, как именно пользоваться этим методом. Наши рассуждения будут подкреплены примерами для большей наглядности.
Что нужно повторить перед изучением вычитания столбиком?
Метод основан на некоторых простых действиях, которые мы уже разбирали ранее. Необходимо повторить, как правильно вычитать с помощью таблицы сложения. Также желательно знать основное свойство вычитания равных натуральных чисел (в буквенном виде оно записывается как a − a = 0). Нам понадобятся следующие из него равенства a − 0 = a и 0 − 0 = 0 , где a – любое произвольно взятое натуральное число (если требуется, посмотрите основные свойства нахождения разности целых чисел).
Кроме того, важно знать, как определять разряд натуральных чисел.
Главное на первом этапе – правильно записать исходные данные. Для начала записываем первое число, из которого будем вычитать. Под ним располагаем вычитаемое. Цифры должны быть расположены строго одна под другой с учетом разряда: десятки под десятками, сотни под сотнями, единицы под единицами. Запись читается справа налево. Далее ставим минус с левой стороны от столбика и подводим черту под обоими числами. Под ней будет записываться конечный результат.
Для начала записываем первое число, из которого будем вычитать. Под ним располагаем вычитаемое. Цифры должны быть расположены строго одна под другой с учетом разряда: десятки под десятками, сотни под сотнями, единицы под единицами. Запись читается справа налево. Далее ставим минус с левой стороны от столбика и подводим черту под обоими числами. Под ней будет записываться конечный результат.
Пример 1
Покажем на примере, какая запись подсчета является правильной:
С помощью первой мы можем найти, сколько будет 56 − 9 , с помощью второй – 3 004 − 1 670 , третьей – 203 604 500 − 56 777 .
Как видно, с помощью этого метода можно производить вычисления разной сложности.
Далее рассмотрим сам процесс нахождения разности. Для этого выполняем поочередное вычитание значений разрядов: сначала вычитаем единицы из единиц, потом десятки из десятков, потом сотни из сотен и т.д. Значения записываем под чертой, отделяющей исходные данные от результата. В итоге у нас должно получиться число, которое и будет верным ответом задачи, т. е. разностью исходных чисел.
е. разностью исходных чисел.
Как именно выполняются подсчеты, можно увидеть на этой схеме:
С общей картиной записи и подсчета мы разобрались. Однако в методе есть и некоторые моменты, нуждающиеся в уточнении. Для этого мы приведем конкретные примеры и поясним их. Начнем с простейших задач и будем постепенно наращивать сложность, пока наконец не разберем все нюансы.
Советуем внимательно прочитать все примеры, потому что каждый из них иллюстрирует отдельные непонятные моменты. Если вы дойдете до конца и запомните все объяснения, то подсчет разности натуральных чисел в дальнейшем не будет вызывать у вас ни малейших затруднений.
Пример 2
Условие: найдем разность 74 805 — 24 003 с помощью вычитания столбиком.
Решение:
Запишем эти числа одно под другим, правильно расположив разряды друг под другом, и подчеркнем их:
Вычитание начинается справа налево, то есть с единиц. Считаем: 5 — 3 = 2 (если нужно, повторите таблицы сложения натуральных чисел). Итог запишем под чертой там, где указаны единицы:
Итог запишем под чертой там, где указаны единицы:
Вычитаем десятки. Оба значения в нашем столбике нулевые, а вычитание нуля из нуля всегда дает нуль (как вы помните, мы упоминали, что нам в дальнейшем потребуется это свойство вычитания). Результат записываем в нужное место:
Следующий шаг – нахождение значения разности тысяч: 4 − 4 = 0 . Получившийся нуль записываем на положенное ему место и получаем в итоге:
У нас получилось 50 802 , которое и будет верным ответом для указанного выше примера. На этом вычисления завершены.
Ответ: 50 802 .
Возьмем другой пример:
Пример 3
Условие : подсчитаем, сколько будет 5 777 — 5 751 с помощью метода нахождения разности столбиком.
Решение:
Шаги, которые нам нужно сделать, мы уже приводили выше. Выполняем их последовательно для новых чисел и получаем в итоге:
В начале результата стоит два нуля. Т.к. они стоят первыми, то можно смело их отбросить и получить в ответе 26 . Это число и будет правильным ответом нашего примера.
Это число и будет правильным ответом нашего примера.
Ответ: 26 .
Если посмотреть на условия двух примеров, приведенных выше, легко заметить, что до сих пор мы брали только числа, равные по количеству знаков. Но метод столбика можно использовать и тогда, когда уменьшаемое включает в себя больше знаков, чем вычитаемое.
Пример 4
Условие: найдем разность 502 864 число 2 330 .
Решение
Запишем числа друг под другом, соблюдая нужную соотнесенность разрядов. Это будет выглядеть так:
Теперь поочередно вычисляем значения:
– единиц: 4 − 0 = 4 ;
– десятков: 6 − 3 = 3 ;
– сотен: 8 − 3 = 5 ;
– тысяч: 2 − 2 = 0 .
Запишем, что у нас получилось:
Вычитаемое имеет значения в месте десятков и сотен тысяч, а вот уменьшаемое нет. Что же делать? Вспомним, что пустота в математических примерах равнозначна нулю. Значит, нам нужно вычесть нули из исходных значений. Вычитание нуля из натурального числа всегда дает нуль, следовательно, все, что нам остается, – это переписать исходные значения разрядов в область ответа:
Наши подсчеты завершены. Мы получили итог: 502 864 — 2 330 = 500 534 .
Мы получили итог: 502 864 — 2 330 = 500 534 .
Ответ: 500 534 .
В наших примерах значения разрядов вычитаемого всегда оказывались меньше, чем значения уменьшаемого, поэтому никаких трудностей при подсчете это не вызывало. Что делать, если из значения верхней строки нельзя вычесть значение нижней, не уйдя при этом в минус? Тогда нам нужно «взять взаймы» значения более старших разрядов. Возьмем конкретный пример.
Пример 5
Условие: найдите разность 534 — 71 .
Пишем уже привычный нам столбик и делаем первый шаг вычислений: 4 — 1 = 3 . Получаем:
Далее нам надо перейти к подсчету десятков. Для этого нам надо из 3 вычесть 7 . Это действие с натуральными числами выполнить нельзя, ведь оно имеет смысл только при таком уменьшаемом, которое больше вычитаемого. Поэтому в данном примере нам нужно «занять» единицу из старшего разряда и тем самым «разменять» его. То есть 100 мы как бы меняем на 10 десяток и берем одну из них. Чтобы не забыть об этом, отметим нужный разряд точкой, а в десятках запишем 10 другим цветом.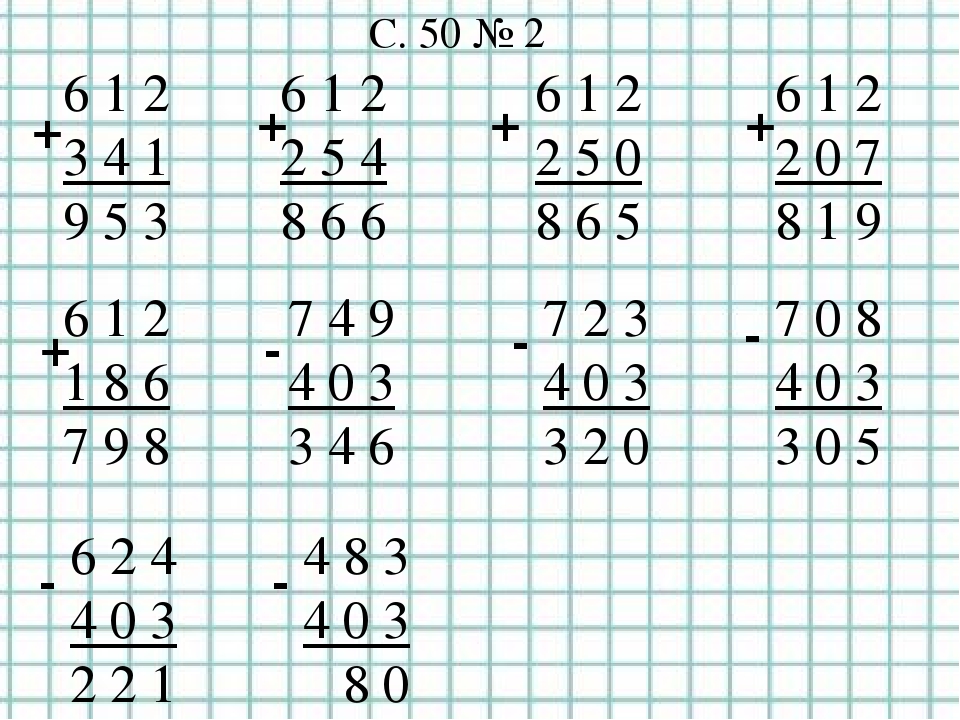 У нас получилась запись следующего вида:
У нас получилась запись следующего вида:
Получившийся результат пишем на нужном месте под чертой:
Нам осталось закончить подсчет, вычислив сотни. У нас стоит точка над числом 5: это значит, что мы отсюда брали десяток для предыдущего разряда. Тогда 5 − 1 = 4 . От четверки же ничего отнимать не нужно, поскольку вычитаемое в разряде сотен значений не имеет. Записываем 4 на место и получаем ответ:
Ответ : 463 .
Зачастую выполнять действие «размена» в рамках одного примера приходится несколько раз. Разберем такую задачу.
Пример 6
Условие: сколько будет 1 632 — 947 ?
Решение
В первом же этапе подсчета надо вычесть двойку из семерки, так что сразу «занимаем» десятку для размена на 10 единиц. Отмечаем это действие точкой и считаем 10 + 2 — 7 = 5 . Вот как выглядит наша запись с отметками:
Далее нам надо подсчитать десятки. Указанная точка означает, что для вычислений мы берем в этом разряде число на единицу меньше: 3 − 1 = 2 . Из двойки нам придется вычитать четверку, так что «размениваем» сотни. У нас получается (10 + 2) − 4 = 12 − 4 = 8 .
Из двойки нам придется вычитать четверку, так что «размениваем» сотни. У нас получается (10 + 2) − 4 = 12 − 4 = 8 .
Движемся дальше к подсчету сотен. Из шестерки мы уже занимали единицу, так что 6 − 1 = 5 . Из пятерки вычитаем девятку, для чего берем имеющуюся у нас тысячу и «размениваем» ее на 10 сотен. Таким образом, (10 + 5) − 9 = 15 − 9 = 6 . Теперь наша запись с примечаниями выглядит так:
Нам осталось сделать подсчеты в тысячном разряде. Одну единицу отсюда мы уже занимали, так что 1 − 1 = 0 . Пишем результат под итоговую черту и смотрим, что получилось:
На этом вычисления закончены. Нуль в начале можно отбросить. Значит, 1 632 − 947 = 685 .
Ответ: 685 .
Возьмем еще более сложный пример.
Удобно проводить особым методом, который получил название вычитание столбиком или вычитание в столбик . Этот способ вычитания оправдывает свое название, так как уменьшаемое, вычитаемое и разность записываются в столбик.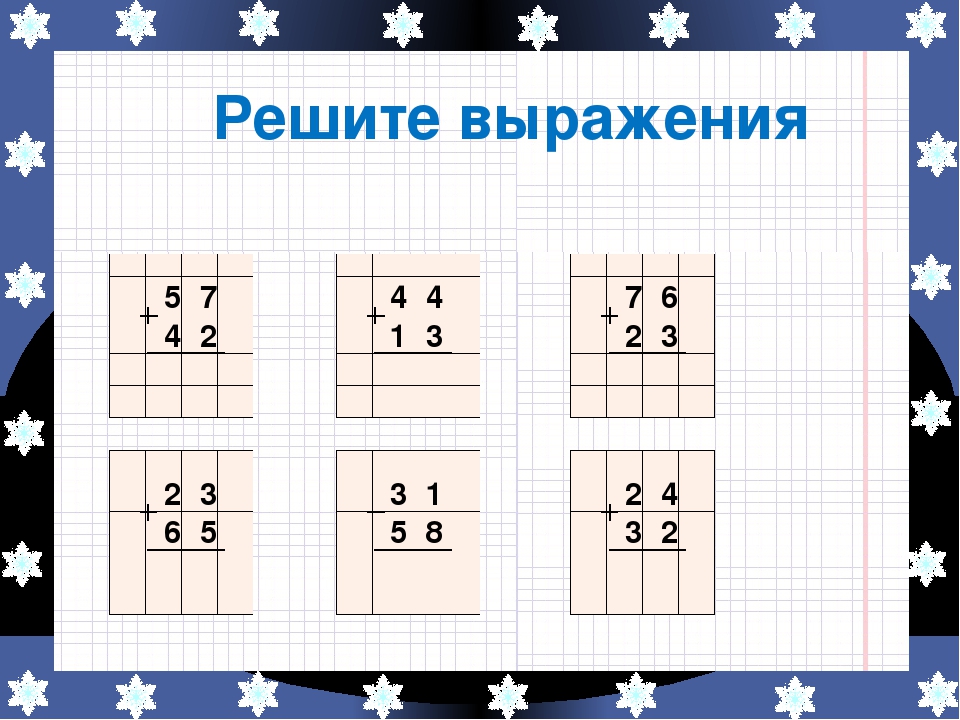 Промежуточные вычисления также проводятся в столбиках, соответствующих разрядам чисел.
Промежуточные вычисления также проводятся в столбиках, соответствующих разрядам чисел.
Удобство вычитания натуральных чисел столбиком заключается в простоте вычислений. Вычисления сводятся к использованию таблицы сложения и применению свойств вычитания.
Давайте разберемся, как выполняется вычитание столбиком. Процесс вычитания будем рассматривать вместе с решением примеров. Так будет понятнее.
Навигация по странице.
Что необходимо знать для вычитания столбиком?
Для вычитания натуральных чисел столбиком необходимо знать, во-первых, как выполняется вычитание с помощью таблицы сложения .
Наконец, не помешает повторить определение разряда натуральных чисел .
Вычитание столбиком на примерах.
Начнем с записи. Сначала записывается уменьшаемое. Под уменьшаемым располагается вычитаемое. Причем делается это так, что цифры оказываются одна под другой, начиная справа. Слева от записанных чисел ставится знак минус, а внизу проводится горизонтальная линия, под которой будет записан результат после проведения необходимых действий.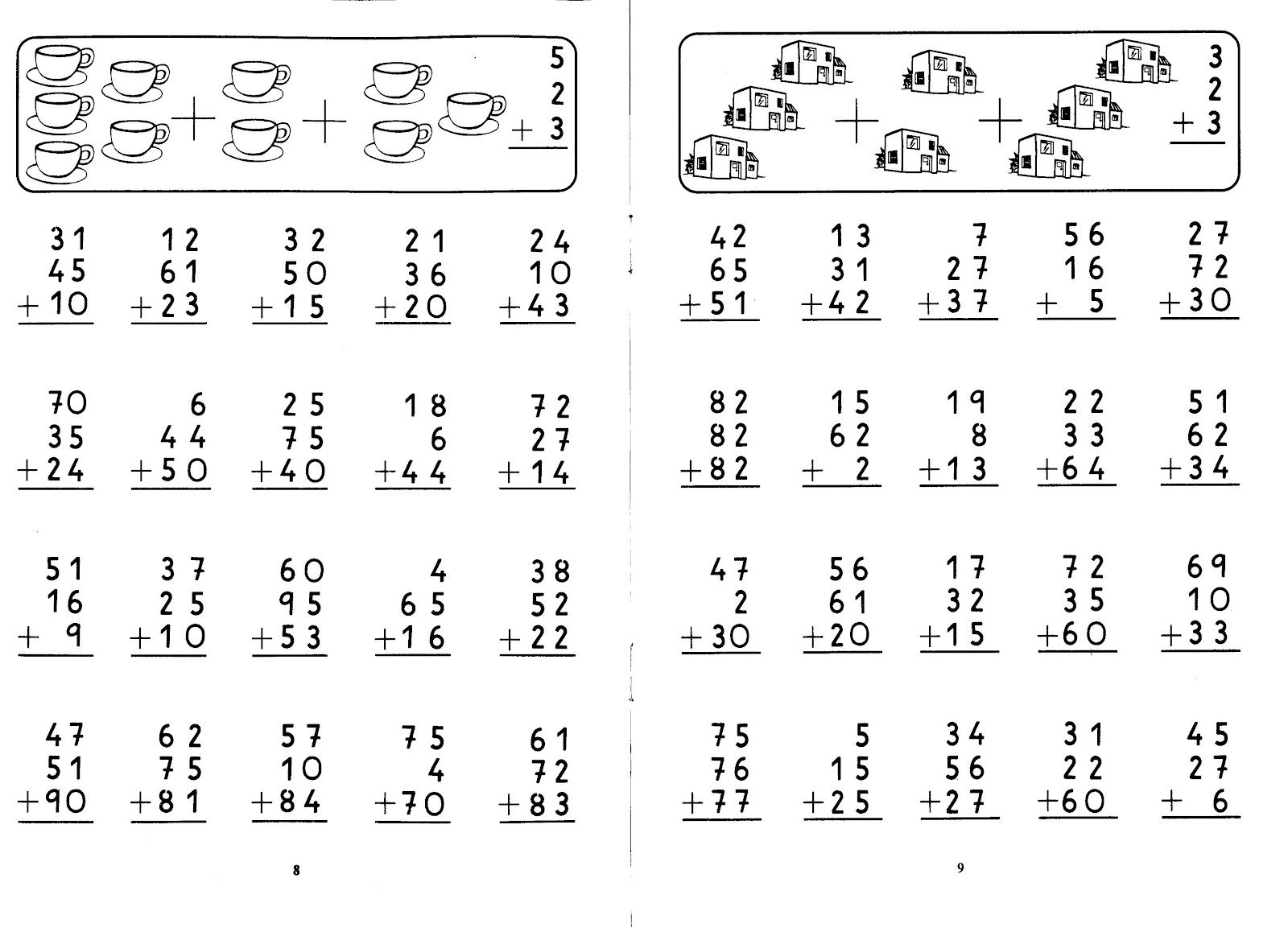
Приведем несколько примеров правильных записей при вычитании столбиком. Запишем в столбик разность 56−9 , разность 3 004−1 670 , а так же 203 604 500−56 777 .
Итак, с записью разобрались.
Переходим к описанию процесса вычитания столбиком. Его суть заключается в последовательном вычитании значений соответствующих разрядов. Сначала вычитаются значения разряда единиц, далее – значения разряда десятков, далее – значения разряда сотен и т.д. Результаты записываются под горизонтальной линией на соответствующих местах. Число, которое образуется под линией после завершения процесса, является искомым результатом вычитания двух исходных натуральных чисел.
Представим схему, иллюстрирующую процесс вычитания столбиком натуральных чисел.
Приведенная схема дает общую картину вычитания натуральных чисел столбиком, однако она не отражает всех тонкостей. С этими тонкостями разберемся при решении примеров. Начнем с самых простых случаев, а дальше будем постепенно продвигаться к более сложным случаям, пока не разберемся со всеми нюансами, которые могут встретиться при вычитании столбиком.
Пример.
Для начала вычтем столбиком из числа 74 805 число 24 003 .
Решение.
Запишем эти числа так, как этого требует метод вычитания столбиком:
Начинаем с вычитания значений разрядов единиц, то есть, вычитаем из числа 5 число 3 . Из таблицы сложения имеем 5−3=2 . Записываем полученные результат под горизонтальную черту в этом же столбике, в котором находятся числа 5 и 3 :
Теперь вычитаем значения разряда десятков (в нашем примере они равны нулю). Имеем 0−0=0 (это свойство вычитания мы упоминали в предыдущем пункте). Записываем полученный нуль под линию в том же столбике:
Идем дальше. Вычитаем значения разряда сотен: 8−0=8 (по свойству вычитания, озвученному в предыдущем пункте). Теперь наша запись примет следующий вид:
Переходим к вычитанию значений разряда тысяч: 4−4=0 (это свойств вычитания равных натуральных чисел). Имеем:
Осталось вычесть значения разряда десятков тысяч: 7−2=5 . Записываем полученное число под черту на нужное место:
Записываем полученное число под черту на нужное место:
На этом вычитание столбиком завершено. Число 50 802 , которое получилось внизу, является результатом вычитания исходных натуральных чисел 74 805 и 24 003 .
Рассмотрим следующий пример.
Пример.
Отнимем столбиком от числа 5 777 число 5 751 .
Решение.
Делаем все так же, как в предыдущем примере – вычитаем значения соответствующих разрядов. После завершения всех шагов запись примет следующий вид:
Под чертой получили число, в записи которого слева находятся цифры 0 . Если эти цифры 0 отбросить, то получим результат вычитания исходных натуральных чисел. В нашем случае отбрасываем две цифры 0 , получившиеся слева. Имеем: разность 5 777−5 751 равна 26 .
До этого момента мы вычитали натуральные числа, записи которых состоят из одинакового количества знаков. Сейчас на примере разберемся, как вычитаются столбиком натуральные числа, когда в записи уменьшаемого больше знаков, чем в записи вычитаемого.
Пример.
Вычтем из числа 502 864 число 2 330 .
Решение.
Записываем уменьшаемое и вычитаемое в столбик:
По очереди вычитаем значения разряда единиц: 4−0=4 ; далее – десятков: 6−3=3 ; далее – сотен: 8−3=5 ; далее – тысяч: 2−2=0 . Получаем:
Теперь, чтобы завершить вычитание столбиком, нам еще нужно вычесть значения разряда десятков тысяч, а дальше – значения разряда сотен тысяч. Но из значений этих разрядов (в нашем примере из чисел 0 и 5 ) нам вычитать нечего (так как вычитаемое число 2 330 не имеет цифр в этих разрядах). Как же быть? Очень просто – значения этих разрядов просто переписываются под горизонтальную линию:
На этом вычитание столбиком натуральных чисел 502 864 и 2 330 завершено. Разность равна 500 534 .
Осталось рассмотреть случаи, когда на некотором шаге вычитания столбиком значение разряда уменьшаемого числа меньше, чем значение соответствующего разряда вычитаемого. В этих случаях приходится «занимать» из старших разрядов. Давайте разберемся с этим на примерах.
В этих случаях приходится «занимать» из старших разрядов. Давайте разберемся с этим на примерах.
Пример.
Вычтем столбиком из числа 534 число 71 .
Решение.
На первом шаге вычитаем из 4 число 1 , получаем 3 . Имеем:
На следующем шаге нам нужно вычитать значения разряда десятков, то есть, из числа 3 нужно вычесть число 7 . Так как 3, то мы не можем выполнить вычитание этих натуральных чисел (вычитание натуральных чисел определяется лишь когда вычитаемое не больше, чем уменьшаемое). Что же делать? В этом случае мы берем 1 единицу из старшего разряда и «размениваем» ее. В нашем примере «размениваем» 1 сотню на 10 десятков. Чтобы наглядно отразить наши действия, поставим жирную точку над числом в разряде сотен, а над числом в разряде десятков запишем число 10 , используя другой цвет. Запись примет следующий вид:
Прибавляем полученные после «размена» 10 десятков к 3 имеющимся десяткам: 3+10=13 , и из этого числа вычитаем 7 .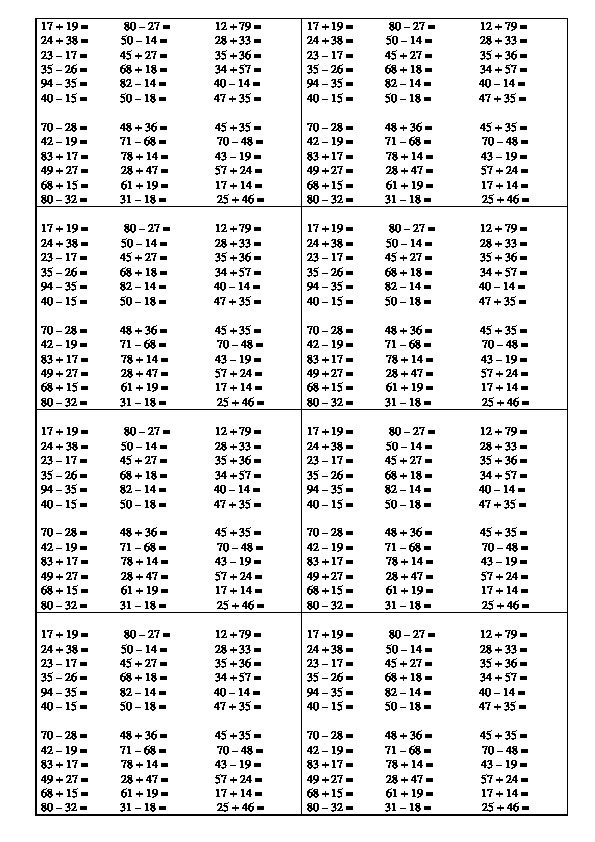 Имеем 13−7=6 . Это число 6 записываем под горизонтальной чертой на свое место:
Имеем 13−7=6 . Это число 6 записываем под горизонтальной чертой на свое место:
Переходим к вычитанию значений разряда сотен. Здесь мы видим над числом 5 точку, которая означает, что из этого числа мы брали единицу «на размен». То есть, сейчас мы имеем не 5 , а 5−1=4 . От числа 4 больше ничего отнимать не нужно (так как исходное вычитаемое число 71 не содержит цифр в разряде сотен). Таким образом, под горизонтальную черту записываем число 4 :
Итак, разность 534−71 равна 463 .
Иногда при вычитании столбиком «разменивать» единицы из старших разрядов приходится несколько раз. В подтверждение этих слов разберем решение следующего примера.
Пример.
Отнимем от натурального числа 1 632 число 947 столбиком.
Решение.
На первом же шаге нам нужно вычесть из числа 2 число 7 . Так как 2,то сразу приходится «разменивать» 1 десяток на 10 единиц. После этого из суммы 10+2 вычитаем число 7 , получаем (10+2)−7=12−7=5
:
После этого из суммы 10+2 вычитаем число 7 , получаем (10+2)−7=12−7=5
:
На следующем шаге нам нужно вычесть значения разряда десятков. Мы видим, что над числом 3 стоит точка, то есть, мы имеем не 3 , а 3−1=2 . И от этого числа 2 нам нужно отнять число 4 . Так как 2, то опять приходится прибегать к «размену». Но сейчас уже размениваем 1 сотню на 10 десятков. При этом имеем (10+2)−4=12−4=8
:
Теперь вычитаем значения разряда сотен. Из числа 6 была занята единица на предыдущем шаге, поэтому имеем 6−1=5 . От этого числа нам нужно отнять число 9 . Так как 5, то нам нужно «разменять» 1 тысячу на 10 сотен. Получаем (10+5)−9=15−9=6
:
Остался последний шаг. Из единицы в разряде тысяч мы занимали на предыдущем шаге, поэтому имеем 1−1=0 . От полученного числа нам ничего больше отнимать не нужно. Это число и записываем под горизонтальную черту:
Это нахождение одного из слагаемых по сумме и другому слагаемому.
Исходная сумма называется уменьшаемым , известное слагаемое — вычитаемым , а результат (т.е. искомое слагаемое) называется разностью .
Свойства вычитания чисел
1. a — (b + c) = (a — b) — c = (a — c) — b ;
2. (a + b) — c = (a — c) + b = a + (b — c) ;
3. a — (b — c) = (a — b) + c .
Для наглядного изображения арифметических операций (как сложения так и вычитания) можно использовать числовую прямую — это прямая, которая состоит из точки начала координат (эта точка соответствует нулю) и двух распространяющихся от нее лучей, один из которых соответствует положительным числам, а другой отрицательным.
Пример вычитания на числовой прямой
На этой числовой прямой можно увидеть, что числа находящиеся слева от 0 имеют отрицательное значение. Вычитая из отрицательного числа (в данном случае -1) единицу три раза, мы получим число -1.
Вычитая из положительного числа 4, положительное число 3 (или отрицательное число -1 три раза), получим единицу
Пример
| 4 — 3 = 1 ; | 3 — 4 = — 1 ; |
| -1 -3 = — 4 ; |
Вычитание чисел столбиком
Сначала вычитаются единицы, затем десятки, сотни и т. д. Разность каждого столбца записывается под ним. При необходимости из соседнего левого столбца (т.е. из старшего разряда) занимается 1 .
д. Разность каждого столбца записывается под ним. При необходимости из соседнего левого столбца (т.е. из старшего разряда) занимается 1 .
Рассмотрим несколько примеров вычитания в столбик, приведенных ниже.
Пример вычитания двузначных чисел столбиком
Пример вычитания трехзначных чисел столбиком
Принцип вычитания трехзначных чисел похож на метод вычитания двузначных чисел, в данном случае числа уже не десятки, а сотни.
Пример вычитания четырехзначных чисел столбиком
Принцип вычитания четырехзначных чисел похож на метод вычитания трехзначных чисел, в данном случае числа уже не сотни, а тысячи.
Сложение и вычитание столбиком: онлайн-курс
Курс для обучения сложению и вычитанию чисел столбиком.
На протяжении всего курса необходимо решать примеры на сложение и вычитание столбиком. Курс разбит на уроки по тематикам и степени сложности.
На главной странице курса представлен список из 9 уроков. Требуется решать примеры достаточно правильно (количество правильных ответов должно быть не менее 95%) и быстро (в зависимости от сложности примеров, каждый ответ должен занимать в среднем не более 4-9 секунд), чтобы завершить урок.
Чтобы начать курс и перейти к решению примеров необходимо нажать — «Начать / Продолжить урок» у Урока 1.
Будут показаваться примеры, нужно вводить ответ с помощью клавиатуры.
Ответ вводится справа на лево: сначала единицы, затем десятки, сотни и т.д. Поле, где появится следующая цифра ответа, обведено тонкой рамкой.
Если необходимо запомнить добавление или вычитание десятка из следующего столбика, можно нажать на верхнюю цифру в этом столбике. При сложении над этой цифрой появится маленькая единица в качестве напоминания, при вычитании — точка. Повторное нажатие на верхнюю цифру убирает напоминание.
Повторное нажатие на верхнюю цифру убирает напоминание.
Если ответ правильный, производится переход к следующему примеру. В случае неверного ответа показывается сообщение об ошибке и выводится правильный ответ.
Учитываются ошибки и время, за которое дан правильный ответ.
Для завершения урока необходимо решить не менее 100 примеров, но необходимое количество будет корректироваться в зависимости от количества ошибок и времени за которое дан правильный ответ (если оно больше допустимого).
Над примером расположена шкала (прогресс), показывающая, сколько процентов от полного материала урока пройдено.
Урок завершен, когда процент готовности по уроку 100%. В списке уроков этот урок помечается так
Через каждые 10 примеров тренажер переходит в режим «Паузы». Это необходимо чтобы отдохнуть и отвлечься, т.к. важно время, затраченное на пример. Здесь же ученику сообщается о том, насколько хорошо он справляется с заданием: в таблице приведены показатели текущей успеваемости по последней группе примеров — количество правильных ответов, ошибок, среднее время, затрачиваемое на ответ, а также среднее время, необходимое для того, чтобы материал считался усвоенным. Если среднее время ученика меньше указанного (в этом случае оно будет зеленым) — значит все в порядке.
Это необходимо чтобы отдохнуть и отвлечься, т.к. важно время, затраченное на пример. Здесь же ученику сообщается о том, насколько хорошо он справляется с заданием: в таблице приведены показатели текущей успеваемости по последней группе примеров — количество правильных ответов, ошибок, среднее время, затрачиваемое на ответ, а также среднее время, необходимое для того, чтобы материал считался усвоенным. Если среднее время ученика меньше указанного (в этом случае оно будет зеленым) — значит все в порядке.
После паузы можно продолжить или вернуться к списку уроков. При этом прогресс по уроку будет сохранен.
Сложение и вычитание величин | Математика
При сложении или вычитании однородных величин единицы измерения величин не меняются.
Чтобы найти сумму или разность однородных величин, надо произвести действия над их численными значениями и, к полученному результату, приписать единицу измерения величины.
Пример 1. Найти сумму 37 м + 12 м:
37 + 12 = 49 м.
Пример 2. Найти разность 108 км — 69 км:
108 — 69 = 39 км.
Если величины состоят из двух единиц измерения, то можно либо сразу произвести действия над их численными значениями, по необходимости переводя промежуточный результат из одной единицы измерения в другую. Либо сначала привести их к одной единице измерения, а потом произвести нужные вычисления.
Пример 1. Найти сумму величин:
12 кг 729 гр + 9 кг 435 гр.
Сложение будем производить столбиком. Напишем числа так, чтобы килограммы были записаны под килограммами, а граммы — под граммами.
Складываем единицы граммов: 9 + 5 = 14 (единиц граммов или 1 десяток граммов и 4 единицы). Пишем под единицами граммов цифру 4 и 1 десяток запоминаем.
Складываем десятки граммов: 2 + 3 = 5 (десятков граммов). К этим 5 десяткам надо прибавить ещё один, который мы получили при сложении единиц: 5 + 1 = 6 (десятков граммов). Пишем под десятками граммов цифру 6.
К этим 5 десяткам надо прибавить ещё один, который мы получили при сложении единиц: 5 + 1 = 6 (десятков граммов). Пишем под десятками граммов цифру 6.
Складываем сотни граммов: 7 + 4 = 11 (сотен граммов или 1 тысяча граммов и 1 сотня). Пишем под сотнями граммов цифру 1 и 1 тысячу запоминаем.
Складываем единицы килограммов: 2 + 9 = 11 (единиц килограммов). К этим 11 единицам надо прибавить ещё 1, которую мы получили при сложении сотен граммов: 11 + 1 = 12 (единиц килограммов или 1 десяток и 2 единицы). Пишем цифру 2 и 1 десяток запоминаем.
Складываем десятки килограммов: 1 + 0 = 1 (десяток килограммов). К этому десятку надо прибавить ещё один, который мы получили при сложении единиц килограммов: 1 + 1 = 2 (десятка килограммов). Пишем под десятками килограммов цифру 2.
Всего получили 22 кг 164 гр.
Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:
12 кг 729 гр = 12729 гр;
9 кг 435 гр = 9435 гр;
а затем численные значения величин можно сложить столбиком:
полученный результат, при необходимости, можно привести обратно к двум единицам измерения:
22164 гр = 22 кг 164 гр.
Пример 2. Найти разность величин:
9 км 528 м — 6 км 909 м.
Вычитание будем производить столбиком. Напишем числа так, чтобы километры были записаны под километрами, а метры — под метрами:
Всего получили 2 км 619 м.
Данное выражение можно вычислить по другому: сначала привести обе величины к одной единице измерения:
9 км 528 м = 9528 м;
6 км 909 м = 6909 м;
а затем выполнить вычитание столбиком:
полученный результат, при необходимости, можно привести обратно к двум единицам измерения:
2619 м = 2 км 619 м.
«Запись сложения и вычитания двузначных чисел в столбик».
Тема: «Запись сложения и вычитания двузначных чисел в столбик».
Тип урока: урок открытия новых знаний.
Цель:
1) Формировать умение выполнять письменное сложение и вычитание двузначных чисел «в столбик».
2) Тренировать умение применять известные способы сложения и вычитания двузначных чисел без перехода через разряд, решать задачи, выполнять действия с величинами.
Задачи:
— образовательные:
формировать у учащихся умение записывать выражение на сложение и вычитание столбиком.
— развивающие:
развивать мыслительные операции посредством наблюдений, сравнений, сопоставлений, обобщений.
развивать творческое мышление.
формировать умение видеть проблему и наметить пути ее решения.
— воспитательные:
воспитывать у учащихся навыки учебного труда.
формировать ответственность, чувство дружбы и уважения друг к другу.
Демонстрационный материал:
1) изображение гнома
2) таймер;
3) опорная схема сложения и вычитания двузначных чисел в столбик:
4) эталон «Построй свою математику». Тема: «Сложение и вычитание двузначных чисел столбиком»
Тема: «Сложение и вычитание двузначных чисел столбиком»
Раздаточный материал:
1) карточки с известными способами сложения:
Ход урока:
Содержание урокаСлайд электронной презентации
1.Организационный момент.
Цель этапа: настроить детей на предстоящую деятельность, создать положительный психологический настрой.
Учитель: Добрый день! Я рада вас видеть на уроке! Я очень хочу, что бы урок получился интересным, познавательным, что бы мы все вместе, повторили, закрепили и открыли новые секреты.
Готовы вы к уроку?
На вас надеюсь я, друзья!
Мы хороший дружный класс
Все получится у нас!
Слайд 7
2. Мотивация к учебной деятельности:
Мотивация к учебной деятельности:
Цель: создать условия для возникновения у учащихся потребности включения в учебную деятельность посредством создания ситуации удивления, при появлении на уроке математики героя гнома
– Сегодня на уроке у нас необычный гость. Отгадайте загадку:
Загадка
Он пришел из сказки к нам,
Постучал тихонько в дом,
В ярком красном колпачке —
ну, конечно, это …
– Как вы думаете, почему он решил прийти на урок математики? (…)
– Да, он очень любит общаться с детьми, помогать им в учёбе, любит, когда дети учатся, сам любит учиться. Гномик – мудрый человечек. И он, как и вы, знает, что значит учиться. Вы согласны принять его как гостя на уроке математики?
– Гномик знает, что ходить в гости с пустыми руками не принято, поэтому он принёс для вас несколько интересных заданий. Вот одно их них.
Вот одно их них.
45 40 35 30 25
36 32 28 24 20
92 87 82 77 72
– Посмотрите внимательно на все эти числа. Как называются эти числа? (Двузначные.)
– Что вы умеете делать с двузначными числами? (Складывать, вычитать, сравнивать.)
— Как вы думаете, чему будет посвящен наш урок?
Слайд 8-9
3. Актуализация и пробное учебное действие.
Цель: актуализировать способы сложения и вычитания двузначных чисел без перехода через разряд: с помощью моделей, по общему правилу, по частям, с помощью числовой прямой.
– Давайте порадуем нашего гостя своими знаниями. С чего начнём? (С повторения необходимых знаний.)
Устный счёт.
1) Способы сложения двузначных чисел без перехода через разряд.
– Посмотрите на второй ряд чисел и назовите самое большое число. (36.)
– Задуманное число больше 36 на 12. Какое число задумали? (48.)
– Как вы это узнали? (К 36 прибавили 12.)
– Какими способами можно сложить числа 36 и 12?
Дети указывают способы, которые вспомнят.
– Вы уверены, что вспомнили все способы сложения? Может, спросим у гномика? Ведь он, математик.
-Возьмите карточки со способами сложения.
– Посмотрите, оказывается, у гномика есть карточки, на которых написаны все известные вам способы сложения двузначных чисел. Проверьте по карточке, все ли способы вы перечислили.
– Объясните решение примера 36 + 12 всеми известными вам способами. Работаем на карточках гномика.
Работа в группах.
По одному аналитику с каждой группы с места с объяснением.
1.(По графическим моделям: к 3 (десяткам) прибавляем 1 (десяток), получаем 4 десятка.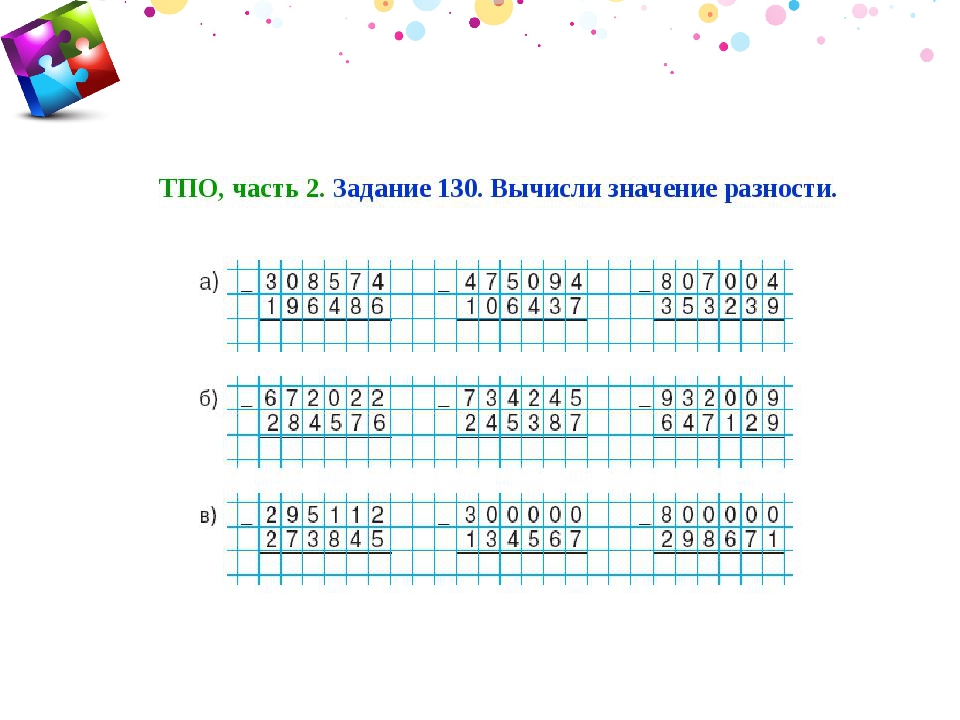 Рисуем 4 . К 6 точкам (единицам) прибавляем 2 точки (единицы), получаем 8 единиц. Рисуем 8 точек. Ответ: 4 десятка 8 единиц.)
Рисуем 4 . К 6 точкам (единицам) прибавляем 2 точки (единицы), получаем 8 единиц. Рисуем 8 точек. Ответ: 4 десятка 8 единиц.)
(2.По общему правилу: раскладываем 36, как 30 и 6; а 12, как 10 и 2. Сначала к 30 прибавляем 10, получаем 40. Затем к 6 прибавляем 2, получаем 8. 40 и 8 – 48.)
3.(По частям: раскладываем второе слагаемое 12, как 10 и 2. Сначала к 36 прибавляем 10, получаем 46, затем к 46 прибавляем 2, получаем 48.)
4.(По числовой прямой: находим на числовой прямой 36, вправо присчитываем 12, получаем 48.)
2) Способы вычитания двузначных чисел без перехода через разряд.
– Пользуясь удобным для вас способом, выполните следующее задание.
– Задуманное число меньше 36 на 12. Какое число задумали? (24.)
– Как вы узнали? (Из 36 вычли 12.)
– Какими способами можно вычесть из 36 12? (По графическим моделям; по общему правилу: из 3 десятков вычитаем 1 десяток, получаем 2 десятка, а из 6 единиц вычитаем 2 единицы, получаем 4 единицы. Ответ 24. По частям: сначала из 36 вычитаем 10, получаем 26, а потом еще 2, получаем 24. По числовому лучу.)
Ответ 24. По частям: сначала из 36 вычитаем 10, получаем 26, а потом еще 2, получаем 24. По числовому лучу.)
– Молодцы! А я знаю, что многим из вас и вычитать помогли волшебные карточки гномика. В чём же заключается их волшебство? Почему, посмотрев на них, можно вспомнить и способы вычитания? (Потому что способы вычитания такие же, как способы сложения.)
– Зачем надо знать так много способов сложения и вычитания двузначных чисел? (Чтобы выбрать удобный.)
– Подумайте, какой способ наиболее удобен для вас.
– Что важно помнить, складывая или вычитая двузначные числа? (Десятки прибавляем к десяткам, единицы к единицам. Из десятков вычитаем десятки, из единиц – единицы.)
3) Индивидуальное задание для пробного действия на подробную запись решения примеров.
– Что дальше? (Будет задание, в котором что-то новое.)
– Верно. Гномик знает, что должно быть такое задание, поэтому подготовил его для вас.
Решите примеры в тетради с подробной записью за 1 минуту:
23 + 14 37 – 5
58 – 4 36 + 42
39 + 50 31 + 68
– Вы такие примеры решали? (Да.)
– А подробную запись составлять умеете? (Умеем.)
– Что же в этом задании для вас ново? (Мы никогда не решали так много примеров с подробной записью за такое короткое время.)
– Но поскольку задание дано, значит, его можно выполнить за такое короткое время? (Можно.)
– Попробуете выполнить это задание? (Попробуем.)
Откройте тетради, запишите дату.
Стихотворение, предворяющее работу в тетради, содержит элементы здоровьесберегающих технологий.
Тетрадь с наклоном положу,
Ручку правильно держу.
Сяду прямо, не согнусь,
За работу я возьмусь.
Я тоже буду решать эти примеры с подробной записью вместе с вами за то же время.
– Внимание! Начали!
Я завожу таймер на 1 минуту.
Я на «крыле» доски решаю эти примеры, записывая их в столбик. Очень важно, чтобы дети видели, что заранее ничего не было записано, и учитель успеет за 1 минуту решить все эти примеры .
– Стоп!
– Вы успели выполнить задание до конца? (Нет.)
– А я успела.
(Пока не показываю детям решённые примеры).
– Чего же вы не смогли сделать? (Мы не смогли решить примеры с подробной записью быстро.)
4. Выявление места и причины затруднения.
Цель: организовать выявление и фиксацию учащимися места и причины затруднения.
– Расскажите, как вы действовали, выполняя это задание? (…)
– Почему же вы не успели? (Мало времени на подробную запись решения).
5.Физкультминутка:
Цель: избежать перегрузки и переутомления учащихся, сохранить мотивацию учения.
Потрудились, отдохнём.
Встанем, глубоко вздохнём.
Руки в стороны, вперёд,
Влево, вправо поворот,
Три наклона, прямо встать,
Руки вниз и вверх поднять,
Руки плавно опустили,
Всем улыбки подарили.
Слайд 10-16
Слайд
6. Построение проекта выхода из затруднения.
Цель: выбрать способ и средства для построения нового знания.
– Значит, подходят ли известные вам способы письменного объяснения? (Нет.)
– Что же делать? (Может быть, есть короткий способ письменного объяснения?)
– Да, – это запись примеров в столбик. Вы знаете, как записать и решить примеры в столбик? (Нет.)
– Сформулируйте цель урока. (Узнать способ записи и решения примеров в столбик)
– Зачем вам необходим этот способ? (Чтобы экономить время )
– Какова тема урока?
«Запись и решение примеров в столбик»
Слайд 17
7. Реализация построенного проекта.
Цель:
1) зафиксировать новые способы действий в речи, в виде алгоритма и опорного сигнала;
2) зафиксировать преодоление возникшего затруднения.
– Что значит запись в столбик? (Число под числом.)
Давайте запишем пример: 35+23
– Так как же записать числа в столбик? (Единицы под единицами, десятки под десятками.)
(Демонстрация эталона и раздаю детям урок №5: «Сложение двузначных чисел столбиком» из пособия «Построй свою математику»)
1 ученик у доски.
– Проверим ваши записи по эталону.
Работа в парах. Взаимопроверка. Работа по эталону.
А теперь проверьте друг у друга запись и решение этого примера и расскажите алгоритм сложения друг другу.
– Как записывать примеры в столбик, вы выяснили. Какую цель вы еще поставили? (Надо научиться решать примеры, записанные в столбик.
– Как дополнить наш эталон, чтобы сразу было видно, откуда начинать считать?
– Поставим стрелку над разрядом единиц.
Добавляю в опорный сигнал стрелку.
Теперь скажите, как же я так быстро справилась с заданием? (Вы решали примеры в столбик.)
(Открываю решённые примеры.)
– Какую из поставленных целей вы достигли? (Мы научились записывать примеры в столбик.
Слайд 18
Слайд 14
7. Первичное закрепление.
Цель: создать условия для выполнения учащимися типовых заданий на использование новых способов действий.
– А что дальше? (Надо потренироваться.)
1
Задание:
Рассмотри разные способы записи примеров на сложение и вычитание. Чем удобна запись примеров столбиком?
) № 2, стр. 8. Слайд
8. Слайд– Объясните, как записаны и решены примеры из № 2, стр. 8. (Запись примеров столбиком удобна тем, что соответствующие цифры при сложении и вычитании расположены рядом.)
Объяснение по одному ученику с места.
2) № 4, стр. 9.
– Молодцы! Теперь исправьте запись примеров из № 4, стр. 9, и решите их.
– Есть ли ошибки в записи примеров?
– Найдите эти ошибки и запишите примеры правильно.
По 1ученику у доски с комментированием записи, остальные – в учебнике.
– Как здорово у вас получается!
Слайд 19
Слайд
9. Самостоятельная работа с самопроверкой по эталону.
Слайд 18
Цель:
1) организовать самостоятельное выполнение учащимися заданий на запись и решение примеров в столбик;
2) создать ситуацию успеха для каждого ребёнка.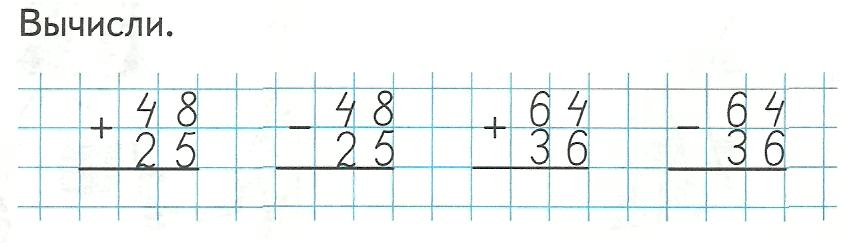 :
:
Самостоятельно:
№ 5 (1, 2, 3 столбик), стр. 9.
Задание:
Реши примеры, записав их в тетрадь столбиком:
54 + 2 63 – 21 26 + 13
54 – 2 63 + 21 26 – 13
– Что общего у примеров каждого столбика и чем они отличаются? (Общее: одинаковые числа, а отличаются действиями.)
– Проверьте.
Открыть на доске эталон для самопроверки:
Проговорить, как выполняли каждый пример.
– Что надо помнить, чтобы затруднений не было? (Пишем единицы под единицами, десятки под десятками, …)
– Гномик очень вами доволен и рад, что смог вам помочь.
Слайд 22-23
10. Гимнастика для глаз.
Слад 24
11. Включение в систему знаний и повторение.
Включение в систему знаний и повторение.
Цель:
тренировать способность к анализу и решению задач, к выполнению действий с величинами.
-Наш гномик решил в мебельном магазине купить кровать, только не знает какого размера нужно покупать кровать. Давайте поможем ему. Для этого нужно решить задачу №7,стр.9
Задание:
Рост гнома 43 см, а длина кровати 4 дм 8 см. Уместится ли гном на кровати?
Решение:
4 дм 8 см = 48 см
43 см < 48 см
Ответ: гном уместится на кровати.
– Прочтите задачу.
– О какой величине говорится в задаче? (О длине.)
– В каких единицах измерения выражена эта величина в тексте задачи? (В дециметрах и сантиметрах.)
– Что известно в задаче и что надо узнать? (Известен рост гнома – 43 см, и длина кровати – 4 дм 8 см. Надо узнать, уместится ли гном на кровати?)
– Продолжите анализ задачи. (Чтобы ответить на вопрос задачи, надо сравнить рост гнома и длину кровати. Сравнение величин возможно, когда они выражены в одинаковых единицах измерения, поэтому надо 4 дм 8 см перевести в см, а потом сравнить.
(Чтобы ответить на вопрос задачи, надо сравнить рост гнома и длину кровати. Сравнение величин возможно, когда они выражены в одинаковых единицах измерения, поэтому надо 4 дм 8 см перевести в см, а потом сравнить.
– Переведите и запишите это в тетрадь. 4 дм 8 см =48 см.
– А теперь сравните. 43 см < 48 см. Ответ: гном уместится на кровати.
Слайд 25-26
12. Рефлексия учебной деятельности на уроке.
Цель:
1) организовать самооценку учащимися своей учебной деятельности на уроке.
2) обсудить и записать домашнее задание
– Сегодня на уроке вы учились? Обоснуйте.
– Достигли вы цели? Докажите. (…
– С какими затруднениями вы столкнулись?
– Удалось ли их преодолеть?
– Над чем еще надо поработать?
— Поработаете дома?
Домашнее задание:
Цель:
сообщить учащимся домашнее задание, разъяснить методику выполнения.
Домашнее задание:
№ 5 (4–5 столбики ), №6 (2 уравнения на выбор)
☺
Спасибо за урок!
Слайд 27
Матрицы сложения и вычитания — ChiliMath
В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.
Если вы знаете, как складывать и вычитать действительные числа, эта тема должна быть действительно легкой. Единственное, что требуется для «легального» выполнения операций сложения или вычитания в «мире» матриц, — это убедиться, что данные матрицы должны иметь одинаковый размер или размерность.
Что означает, что данная матрица имеет одинаковый размер или размерность?
Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размерность, потому что у них одинаковое количество строк и столбцов.
Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:
количество строк x количество столбцов
Позвольте мне показать вам несколько примеров…
Последняя матрица размером 5 x 5 также считается «квадратной матрицей», потому что количество строк и количество столбцов равны.Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, — это то, что сначала она должна быть квадратной матрицей.
Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.
Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размер. В противном случае мы заключаем, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разные размеры или размеры, не определена!
Теперь давайте посмотрим на общее правило того, как складывать и вычитать матрицы, размеры или размеры которых совпадают.
Правила сложения и вычитания матриц одинакового размера или измерения
Предположим, что матрицы A и B имеют две строки и два столбца (2 × 2) с некоторыми произвольными элементами или записями…
«Формулы» для сложения и вычитания матриц показаны ниже…
- Добавить матрицы , добавив их соответствующие записи
- Вычесть матрицы путем вычитания их соответствующих записей
Давайте поработаем над некоторыми проблемами.
Примеры сложения и вычитания матриц
Пример 1 : Выполните указанную операцию для A + C.
Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «размерность», потому что их количество строк и столбцов одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне о том, что найти их сумму — это нормально.
Добавлю соответствующие записи и упрощу.
Вот как это просто!
Пример 2 : Выполните указанную операцию для B + F.
Обратите внимание, что матрица B имеет размерность , равную 2 × 3 , а матрица F имеет размерность , равную 2 × 2 .
Поскольку количество строк и столбцов не совпадает, тогда сумма матриц B и F не существует или не определена . Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.
Пример 3 : Выполните указанную операцию для E-B.
Последние два примера показали вам, как складывать матрицы. На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».
В этом примере нам нужно найти разницу между матрицей E и матрицей B.
Однако кажется, что это невозможно, поскольку они имеют различных размеров или размеров. Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.
Поскольку я не могу вычесть по входам, из-за того, что записи двух матриц не имеют прямого соответствия, я должен заявить, что НЕ возможно, найти их различие.Следовательно, наш ответ — undefined .
Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно добавлять или вычитать только матрицы с одинаковыми размерами или размерами. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы знаете, вы будете осторожны в следующий раз, когда столкнетесь с такой проблемой.
Пример 4 : Выполните указанную операцию для F-D.
При быстром просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов.Большой!
Для начала я вычту соответствующие записи F и D. Мое единственное предостережение — будьте очень осторожны при вычитании действительных чисел. Обычно здесь возникают общие ошибки. Помните, что два соседних отрицательных знака оказываются положительными.
Неплохо, правда?
Пример 5 : Выполните указанную операцию для C-A.
Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3 × 3). Это позволяет нам выполнять операцию вычитания.
Вычитая по входу, я получил…
Пример 6 : Выполните указанную операцию для (A + C) + (C-A).
Это отличный пример «многоступенчатой» задачи, которая включает в себя сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.
Чтобы пропустить некоторые шаги, просмотрите, как мы решили для (A + C) в примере 1 и C-A в примере 5.
Пока у нас есть эти частичные ответы…
Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.
Как видите, сложение и вычитание матриц очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как с этим справиться.
Пример 7 : Выполните указанную операцию для (A + C) + (C-A).
Это та же проблема, что и в примере 6. Но я хочу решить ее немного иначе, чтобы продемонстрировать тот факт, что есть другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.
Поехали…
Если вы рассматриваете выражение (A + C) + (C-A) как , объединяющее похожие или похожие термины, проблема типа , то имеет смысл, что мы можем быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.
Обратите внимание, что я могу объединить C-термины как 2C.
Теперь, члены A должны сокращаться, потому что они имеют противоположные знаки.
Наша исходная задача сводится к 2C, что составляет в два или в два раза больше матрицы C .
Это означает, что я собираюсь умножить каждый элемент матрицы C на 2. На самом деле это тема моего другого урока по алгебре, посвященного скалярному умножению матрицы.
С
, то 2C решается с помощью…
Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?
Практика с рабочими листами
Возможно, вас заинтересует:
Скалярное умножение
Умножение матриц
Изучите и практикуйте вертикальное добавление
В сегодняшнем посте мы рассмотрим вертикальное добавление , добавив .Как всегда, мы рассмотрим примеры, которые помогут нам понять, из чего он состоит и как это делается.
Но прежде чем начать, давайте рассмотрим математические кубики, которые мы собираемся использовать для сложения. Как представить число с помощью этих математических кубиков? Это просто! Мы собираемся использовать отдельные единицы как единицы. Они соответствуют номеру, например:
И, так что же нам для 10-ки? Полоски 10 упрощают представление чисел, поэтому нам не нужно использовать много отдельных единиц, вместо этого мы можем объединить их в полоску с 10 единицами.
Сложение по вертикали
Мы собираемся начать рассмотрение некоторых упражнений по вертикальному сложению. Чтобы убедиться, что мы действительно это понимаем, мы собираемся решить три задачи сложения:
21 + 34
42 + 6
37 + 8
Начнем с первой задачи. Решение требует двух шагов: первый шаг состоит в настройке чисел, которые мы собираемся сложить, а второй шаг — в фактическом сложении чисел.
- Установка проблемы
Чтобы добавить проблему по вертикали, нам нужно убедиться, что мы правильно установили числа.Для этого нам нужно правильно выровнять числовые столбцы. Итак, 1-е место совпадает с 1-м местом, 10-е место совпадает с 10-м местом и т. Д .:
Чтобы получить лучшее представление, воспользуемся математическими кубиками:
- Добавить
Теперь нам просто нужно прибавить к , имея в виду две очень важные вещи:
а) Мы всегда будем складывать числа, которые попадают в один столбец.
б) Мы начинаем со столбца с единицей, а оттуда переходим влево.
Итак, сначала мы добавляем столбец с единицей:
И после добавляем столбец десятков:
А что происходит, если в столбце нет числа? Мы делаем то же самое, что и раньше: выстраиваем числа в столбцы, идущие справа налево, и добавляем столбцы, начиная с столбца 1. Если в столбце только одно число, мы к нему ничего не добавляем.
Пример 1
42 + 6
Сначала мы добавляем столбец 1s:
А теперь переходим к столбцу 10.
Второе число имеет 0 в разряде 10, поэтому номер разряда 10 остается неизменным:
А что произойдет, если, сложив числа в столбце, мы получим число больше 9? Можно ли записать 2 цифры в один столбец? Точно нет! Если это произойдет, мы должны использовать перегруппировку.
Пример 2
37 + 8
Сначала мы добавляем столбец с единицами. Но 7 плюс 8 дает нам 2-значное число . Мы не можем записать два числа в один столбец, , поэтому мы разделяем сумму 15.Мы помещаем одну из цифр в столбец 10 и одну из них в столбец 1. Другими словами, мы оставляем 5 на месте 1, а переносим 1 в столбец с номером 10:
Теперь нам просто нужно добавить столбец 10.
На этом сегодня все закончилось. Что вы думаете об этом посте? Помогло ли понять, как добавить по вертикали? Если вы хотите попрактиковаться в других задачах сложения, щелкните следующие ссылки:
И помните, что для продолжения обучения вы можете создать учетную запись в Smartick и попробовать ее бесплатно.
Подробнее:
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Добавление матрицы
Как и в обычной алгебре, матричная алгебра имеет такие операции, как сложение и вычитание.
Как складывать и вычитать матрицы
Две матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые измерение; то есть в них должно быть одинаковое количество строк и столбцов.
Сложение или вычитание осуществляется путем сложения или вычитания. соответствующие элементы. Например, рассмотрим матрицу A и матрица B .
Обе матрицы имеют одинаковое количество строк и столбцов (2 строки и 3 столбца), поэтому их можно складывать и вычитать. Таким образом,
| A + B = |
|
А,
| A — B = |
|
И, наконец, обратите внимание, что порядок добавления матриц не важный; таким образом, A + B = В + А .
Проверьте свое понимание
Проблема 1
Рассмотрим представленные ниже матрицы — A , B , C и D
Какие из следующих утверждений верны?
I. A + B = C
II. B + C = D
III. B — C = D
(A) только я
Только
(B) II
Только
(C) III
(D) I и II
(E) I и III
Решение
Правильный ответ — (C), как показано ниже.
|
Обратите внимание, что матрицы A, и B нельзя добавить, потому что B имеет больше столбцов, чем A . Матрицы можно складывать или вычитать только в том случае, если они имеют одинаковые количество строк и такое же количество столбцов.
Как складывать и вычитать матрицы
Сложение и вычитание матриц
На этом этапе нашего курса линейной алгебры мы много работали с матрицами, мы выполняли операции со строками для решения систем линейных уравнений, представляя линейную систему в виде матрицы и используя их в наших интересах посредством сокращения строк и эшелонированных форм. Мы также научились понимать не только обозначения матриц, но и их элементы, их размеры, и теперь пора подумать о них в целом и узнать, какие операции могут быть выполнены с ними (обратите внимание: «с ними», НЕ «в их»).
На этом уроке мы познакомимся с первыми двумя из четырех основных операций, которые можно выполнить с парой (или более) матриц: сложение, вычитание, скалярное умножение и умножение. Мы знаем эти базовые операции из арифметики, поэтому нам просто нужно узнать, как они работают со всей структурой матриц и с результатами, которые они производят. Обратите внимание, что мы не упомянули деление матриц, потому что деления между матрицами не существует (или, по крайней мере, процесс еще не определен), единственное деление, которое мы можем сделать, — это разделить элементы в матрице на скаляр, но разделить матрицу на другую матрицу невозможно.
Сложение и вычитание матриц
Мы начинаем с работы с двумя основными операциями, известными нам с тех пор, как мы впервые познакомились с математикой в начальной школе: сложение и вычитание (или что-то «плюс» и «минус»). Чтобы проработать эти операции в этом уроке, давайте определим набор из двух матриц для сложения и вычитания. Итак, определяем матрицы A и B следующим образом:
Уравнение 1: матрицы A и BТеперь с ними мы настроены для работы через операции сложения и вычитания матриц.К операции будут применяться несколько правил, но мы поговорим о них в следующем разделе, а пока давайте быстро пройдемся по процессу, а затем мы сможем вернуться и проверить, насколько операции были возможны. Начнем с добавления A и B:
Уравнение 2: сложение матриц A и BМы закодировали каждый элемент в матрицах цветом, чтобы вы могли видеть, что было сделано для каждого элемента. Обратите внимание на то, как сложение двух матриц действует в случае отдельных элементов, требуя, чтобы у вас были точно такие же элементы в матрицах, участвующих в операции, и чтобы они распределялись одинаковым образом.
Мы вернемся к этой теме в следующем разделе, но пока вы должны помнить, что при добавлении матриц вы будете складывать элементы первой матрицы с соответствующей (той, которая находится в «том же месте», той же строке и столбце число) во второй матрице.
Теперь давайте посмотрим на матричное вычитание:
Уравнение 3: вычитание матрицы B из AГлядя на приведенное выше вычитание, мы можем легко заключить, что этот процесс очень похож на процесс сложения, поскольку вычитание вычисляется по отдельности для каждого из элементов матриц, таким образом давая результат для каждого соответствующего пространства элементов и в результате получается матрица с таким же количеством элементов в той же организации.
Проще говоря, сложение и вычитание матриц работают одинаково, единственная разница между ними — это арифметический знак, который вы используете для работы: знак плюс для сложения и знак минус для вычитания.
Крайне важно, чтобы вы поняли этот вывод, поскольку это может помочь вам не запутаться при работе с различной литературой по данной теме. Дело в том, что некоторые математики, книги или учебные материалы в целом могут относиться к операциям сложения и вычитания как к «сложению» в целом.Эта конкретная ссылка исходит из того факта, что вычитание эквивалентно сложению чисел, в которых хотя бы одно из них отрицательно. Если у вас есть какие-либо вопросы по этому поводу, помните, что вычитание в арифметике также называется «разницей», и все потому, что когда вы складываете числа с разными знаками, результатом становится разница между ними. Мы рассмотрели эту тему в нашем уроке по вычитанию целых чисел, который, хотя и не является частью этого курса линейной алгебры, вы можете проверить в любое время на веб-сайте StudyPug.Вы также можете проверить следующую статью о сложении и вычитании целых чисел, которая содержит дополнительные упражнения и некоторые графические изображения.
Вкратце: Как складывать матрицы? Мы добавляем каждый соответствующий элемент в задействованные матрицы, чтобы создать новую матрицу, в которой такие элементы будут занимать то же место, что и их предшественники. Как вычесть матрицы? Точно так же, как мы вычисляем сложение, за исключением того, что мы используем знак минус для работы вместо знака плюс.
Правила сложения и вычитания матриц
Матричное сложение и вычитание — это две операции, которые, хотя и несложны и просты для решения (как показано выше), у вас все же есть несколько правил, которым нужно следовать, чтобы работать.
Например, когда мы добавляли матрицу A к матрице B выше, сначала обратите внимание, что A и B — очень похожие матрицы, они имеют одинаковое количество строк и столбцов каждая и операция сложения применяется к каждому «соответствующему члену» в них. Это приводит к основному правилу сложения и вычитания матриц, которое соответствует размерам матриц, с которыми работают друг с другом.
Также обратите внимание, что вычитание матриц происходит в очень похожем режиме, на самом деле единственное изменение состоит в том, что вместо знака сложения между матрицами и соответствующими элементами в каждом матричном пространстве у вас есть знак вычитания.
С учетом всего этого правила сложения и вычитания матриц следующие:
- Вы можете складывать или вычитать только матрицы с одинаковыми размерами.
- Если подумать, это происходит из-за того, что добавление матриц с разными размерами создает проблему, потому что не все элементы в каждой матрице будут иметь соответствующий элемент для работы, и, следовательно, операцию невозможно завершить.
- Сложение матриц является коммутативным, но вычитание — нет, если сначала вы не примените знак минуса к матрице справа, таким образом сначала преобразуя операцию в сложение.
- Свойство коммутативности означает, что при добавлении двух матриц вы можете изменить порядок их добавления, и это не повлияет на результат.
- Это не так просто при вычитании. В уравнении 3 у нас есть пример вычитания матриц, обратите внимание, что если вы просто измените порядок матриц, не перемещая знак минус, результат не будет таким же, тогда как вычитание матриц может быть коммутативным? Вы должны применить отрицательный знак к матрице, которая вычитается первой! Проверьте процесс шаг за шагом ниже: Уравнение 4: Условие, чтобы сделать вычитание матрицы коммутативным = сначала преобразовать его в сложение! Обратите внимание, как для того, чтобы иметь возможность изменять порядок матриц, не влияя на результат, мы должны преобразовать вычитание в сложение, что просто означает, что вы должны сначала применить отрицательный знак ко второй матрице, тем самым сделав все отрицательные числа его элементов (которые произведут операцию вычитания, не беспокоясь о порядке элементов).Это единственный способ изменить порядок матриц при вычитании, поэтому помните об этом процессе при работе с еще более сложными проблемами: например, в случаях, когда у вас может быть более двух матриц и вы связываетесь в группах. Подробнее об ассоциации в следующем пункте.
- Матричное сложение и вычитание ассоциативны.
- Свойство ассоциативности используется в задачах, включающих более двух матриц, которые складываются или вычитаются друг из друга.Это свойство позволяет вам сначала работать с операцией между двумя матрицами, а затем использовать матрицу, полученную в результате такой операции, для выполнения второй операции под рукой. Повторяйте такой процесс до тех пор, пока не выполните все необходимые операции с участием всех матриц в задаче.
- При сложении или вычитании матриц результирующая матрица будет иметь те же размеры, что и матрица, которая ее создала.
- Это имеет смысл, поскольку каждый элемент в первой матрице будет работать с соответствующим элементом второй матрицы, таким образом производя результат для каждого пространства элементов.Такие результаты затем станут элементами новой матрицы.
Примеры сложения и вычитания
Далее мы покажем примеры сложения и вычитания матриц. В первом примере упражнения мы сосредоточимся на демонстрации условий, в которых такие операции возможны. Затем мы решаем несколько примеров матричных задач с пошаговым объяснением операций. В конце этого раздела мы решим матричные уравнения, которые включают либо сложение, либо вычитание матриц.
Пример 1
Можем ли мы сложить или вычесть следующие матрицы?
- Корпус 1: Уравнение 5: Можете ли вы сложить эти две матрицы вместе? (Дело 1) Обратите внимание, что размеры матриц, участвующих в сложении, не совпадают. Первая матрица имеет три строки и два столбца, таким образом, это матрица 3×2, а вторая содержит две строки и три столбца, что делает ее размер равным 2×3. Наличие таких различий означает, что, хотя они имеют одинаковое количество элементов, их позиции не соответствуют друг другу, и поэтому по правилам сложения матриц сложение невозможно.
- Случай 2: Уравнение 6: Можете ли вы сложить эти две матрицы вместе? (случай 2) Учитывая, что в этом случае мы будем добавлять матрицы 2×2 (явно; обе матрицы имеют одинаковую размерность 2×2), тогда да, добавление этих двух матриц возможно путем добавления каждого из элементов в первой матрице с соответствующим ему элементом из вторая матрица. Результирующая матрица также будет иметь размеры 2×2.
- Случай 3: Уравнение 7: Можете ли вы сложить эти две матрицы вместе? (случай 3) Как вы, возможно, уже подумали, добавление двух матриц, подобных приведенным выше, невозможно.Размеры этих матриц не совпадают (одна — матрица 3×3, а другая — 2×2), поэтому это добавление невозможно.
Пример 2
Складываем следующие две матрицы:
Уравнение 8: сложение двух матрицПри добавлении двух матриц каждый элемент добавляется к соответствующему элементу в другой матрице. Процесс прост и показан ниже:
Уравнение 9: Решение для сложения двух матрицВыполните те же действия в следующих двух упражнениях.
Пример 3
Складываем следующие две матрицы:
Уравнение 10: сложение двух матрицИтак, мы добавляем каждый элемент в матрицах к соответствующему элементу в другой матрице. Обратите внимание, что, как упоминалось ранее, матрицы должны иметь одинаковые размеры, чтобы возникло поэлементное соответствие:
Уравнение 11: Решение для сложения двух матрицПример 4
Складываем следующие две матрицы:
Уравнение 12: сложение трех матрицПри добавлении более двух матриц вы можете связать две, выполнив сначала их сложение, а затем добавив полученную матрицу к оставшейся матрице.Это то, что мы называем ассоциативным свойством сложения матриц, это и другие свойства сложения матриц будут объяснены в последующих уроках, а пока проверьте процесс решения этой проблемы ниже:
Уравнение 13: Решение для сложения трех матрицИтак, как вы можете видеть, первым шагом было добавление матриц 1 и 2, что привело к новой матрице, которая позже добавляется к третьей. Если добавление матриц содержит больше трех матриц, один и тот же процесс связывания можно повторять столько раз, сколько необходимо, чтобы упростить задачу, пока у вас не получится простая операция с двумя матрицами.
Пример 5
Вычтите следующие матрицы:
Уравнение 14: Вычитание двух матрицЕще раз обратите внимание, что матрицы, участвующие в вычитании, должны иметь одинаковые размеры, чтобы соблюдалось поэлементное соответствие.
Уравнение 15: Решение для вычитания двух матрицПример 6
Вычтите следующие матрицы:
Уравнение 16: Вычитание двух матрицНеважно, насколько велики матрицы, если они имеют одинаковые размеры, вы можете выполнить вычитание.
Уравнение 17: Решение для вычитания двух матрицПример 7
Вычтите следующие матрицы:
Уравнение 18: Вычитание трех матрицОбратите внимание, что для вычитания матриц с более чем двумя матрицами мы можем снова использовать свойство ассоциативности. Помните, что вычитание матриц не коммутативно (вы не можете изменить порядок матриц в операции и получить тот же результат).
Уравнение 19: Решение вычитания трех матрицПример 8
Решите следующее уравнение, содержащее добавление постоянной матрицы к переменной.
Уравнение 20: Найдите A в матричном уравнении (часть 1)Мы начинаем с вычитания матрицы в левой части к обеим частям уравнения, чтобы мы могли легко решить для A, выполнив вычитание матрицы:
Уравнение 21: Найдите A в матричном уравнении (часть 2)Пример 9
Решите следующие матричные уравнения
Уравнение 22: Найдите X в матричном уравнении (часть 1)В этом случае самый простой способ найти X — передать его в правую часть, добавив его к обеим частям уравнения, чтобы оно стало положительным.Мы также вычитаем матрицу, найденную в правой части уравнения, с обеих сторон, и, таким образом, получаем вычитание матрицы, определяющее X.
Уравнение 23: Найдите X в матричном уравнении (часть 2)Решая вычитание матриц, находим X.
Пример 10
Найдите значения элементов a, b, c, d, e и f, решив следующее матричное уравнение наиболее эффективным способом.
Уравнение 24: Нахождение значений элементов в самой левой матрицеВ этой задаче мы можем преобразовать элемент за элементом случай, уравнение, которое позволит нам получить значение каждого из элементов в первой матрице.
Другими словами, вы знаете, что элемент из первой строки и первого столбца (вверху слева) в первой матрице будет добавлен к элементу в первой строке и первом столбце второй матрицы, чтобы получить элемент в этом пространстве. в получившейся матрице справа. Другими словами, мы можем легко записать следующие уравнения для каждого пространства элементов:
Уравнение 25: Набор уравнений для каждой переменной, которую необходимо решитьИ из этого мы можем решить значение каждой переменной:
Уравнение 25: Решение переменных от a до fПосле того, как мы научимся складывать и вычитать матрицы, пришло время изучить другие операции: скалярное умножение матриц и умножение двух или более матриц будут объяснены в следующих двух уроках.
Мы завершаем наш урок на сегодня несколькими полезными ссылками: первая содержит краткий список основных правил сложения матриц и дополнительную лекцию по матричным операциям.
И это все, до встречи на нашем следующем уроке!Как складывать и вычитать в Microsoft Excel
Пришло время изучить Microsoft Excel. Возможно, вам нужно суммировать значения ячеек по нескольким строкам рабочего листа. Итак, как в Excel складывать или вычитать? Продолжай читать! (PS: вы также захотите знать, как умножать и делить.)
○ Это руководство содержит партнерские ссылки. Прочтите нашу политику раскрытия информации, чтобы узнать больше. ○Учебник KeynoteSupport.com
Прежде чем мы начнем, запомните одну важную вещь: все формулы Excel должны начинаться со знака равенства .
Как сложить два числа
Чтобы сложить два числа в Microsoft Excel, введите формулу = X + Y в ячейку, в которой вы хотите отобразить ответ. X и Y могут быть числами, адресами ячеек (например, G4) или формулами. Если вы введете = 4 + 2 в ячейку электронной таблицы, Excel вернет ответ 6.
На приведенном выше листе формула в ячейке C2 = B1 + B2 суммирует прибыль за 1-й и 2-й кварталы для расчета общей прибыли за первую половину. Мы набрали = b1 + b2, но Excel автоматически делает буквы заглавными ..
Как суммировать строку или столбец чисел
При суммировании строк, столбцов или любого диапазона ячеек с более чем несколькими ячейками гораздо более продуктивно использовать функцию СУММ в Excel. А это просто. В приведенном ниже примере наша формула в ячейке B5 равна = СУММ (B1: B4).
Начните формулу со знака равенства, а внутри скобок введите начальную ячейку диапазона и конечную ячейку , разделенные двоеточием . (Хотя формула (= B1 + B2 + B3 + B4) не так эффективна для пользователя, она даст тот же результат.)
Как вычесть два числа
Для вычитания чисел в Microsoft Excel используйте формулу = A − B, где A и B — числа, ссылки на ячейки или формулы, возвращающие числовое значение.Если вы введете = 4-1 в ячейку электронной таблицы, Excel вернет ответ 3.
В примере с рабочим листом мы хотим знать, какую прибыль мы получаем от каждого проданного товара, вычитая наши затраты из нашей продажной цены. Формула в ячейке D2: = B2-C2.
Полное руководство по математике в Excel см. В нашем учебном пособии «Основы математики в Excel: написание формул и выражений». Спасибо, что зашли. Ваше здоровье!
↑ Вернуться к началу
примеров двоичного вычитания
примеров двоичного вычитанияПримеры двоичного вычитания
Вот несколько примеров бинарного вычитания.Они вычисляются без учета слова размер, следовательно, не может быть смысла «переполнения» или «потери значимости». Работайте по столбцам справа налево, вычитая в каждом столбце. Если вы должны от нуля вычесть единицу, слева нужно «одолжить», так же, как при десятичном вычитании. • 1011011–10010
= 1001001:
|
 Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.
Сборник рабочих программ. 5-6 классы. // Составитель Т. А. Бурмистрова – М.: Просвещение, 2014.- 80 с.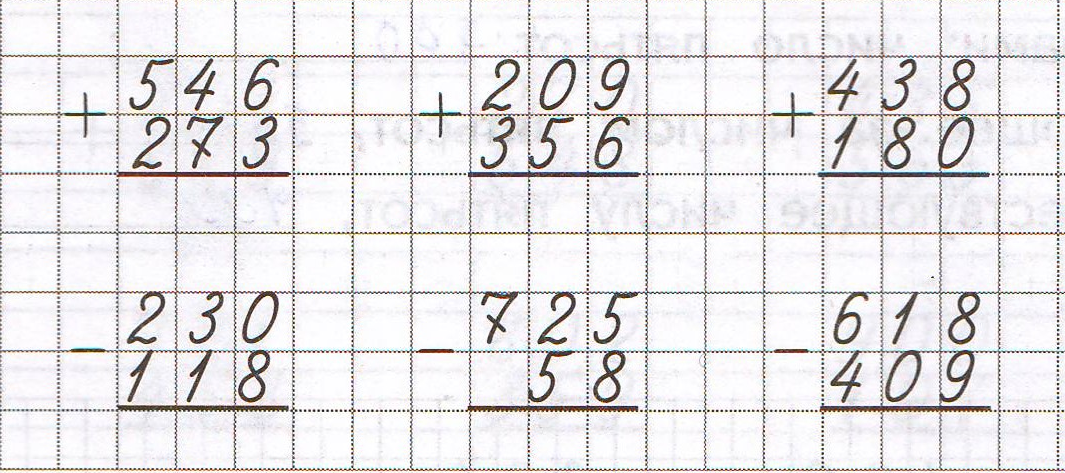
 Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.
Над разрядом, для которого заняли, поставить 9, т.к. один десяток занят.