Сложение и вычитание двузначных чисел – приемы с примерами
4.7
Средняя оценка: 4.7
Всего получено оценок: 301.
4.7
Средняя оценка: 4.7
Всего получено оценок: 301.
Двузначные числа достаточно часто встречаются в современной жизни, поэтому нужно уметь складывать и вычитать их практически мгновенно. Сегодня мы рассмотрим несколько приемов, которые позволят быстро посчитать, а потом проверить правильность расчетов при сложении и вычитании двухзначных чисел.
Система счисления
Для начала решим, какие числа в математики считаются двузначными. По слову сразу ясно, что это числа, которые содержат два значащих знака. Значащие позиции считаются от единиц вверх, по есть по готовому числу справа налево.
Сначала идут единицы, затем десятки, сотни и так далее. При этом знаки могут распространяться и +влево от единиц в виде десятичных дробей после запятой.
Такая система называется позиционной. Каждая цифра в ней меняет свое значение в зависимости от занимаемой позиции.
Отдельно стоит сказать, что значащей считается любая позиция, отличная от нуля. В любом числе незначащих позиций бесконечно много. Мы пишем 23, но понимаем, что в этом числе 0 сотен и тысяч, то есть можно записать его, как 0023.
Количество нулей перед числом может быть бесконечно большим, поэтому незначащие позиции перед числом не пишут.Сложение двузначных чисел
Сложение двузначных чисел это всем привычный процесс, который можно выполнить в столбик или посчитать строкой «в уме». Но при этом можно считать быстро и в строку.
Рассмотрим пример: 18+29 – посчитаем сначала единицы, а затем десятки, после чего сложим результаты. Похожий подход используют при вычислениях в столбик.
9+8=17
10+20=30
30+17=47 – такой расчет займет меньше минуты, что сэкономит время для решения куда более важных задач.
Этот вариант наиболее универсален, но бывают ситуации, когда можно еще больше увеличить скорость счета. Наиболее любимый составителями примеров вариант: единицы двузначных чисел в сумме дают 10.
18+12=10+10+(8+2)=30 – просто к сумме десятков двух чисел прибавляется 1
Еще один вариант это два числа, которые ученикам психологически сложно считать. Не известно почему, но некоторые сложения тяжело даются учащимся.
Как правило, это: 7+6 и 8+7. Со временем ребята привыкают к тому, что первое равняется 13, а второе 15. Но лучше заучить это и не забивать голову.
Используются эти знания примерно так: 17+16=10+10+7+16=20+13=33
Вычитание
Вычитать по тому же принципу, что и складывать не получится, потому что такое вычитание будет слишком громоздким для нетренированного разума. Поэтому используют следующий алгоритм:
- Смотрим, сколько десятков в вычитаемом
- Раскладываем уменьшаемое на три числа: в одном столько же десятков, сколько в вычитаемом, во втором все единицы, что были в уменьшаемом и 10, в следующем остаток.

- Считаем
На практике это выглядит так: 73-28=(20+13+40)-28=20+13+40-(20+8)=20+13+40-20-8=(20-20)+(13-8)+40=5+40. Это немного сложно для начала, но после тысяч и тысяч решенных примеров, ваш мозг будет все равно вычислять по этой схеме. Поэтому проще разобраться на двух-трех примерах и не тратить время
Если посмотреть в суть всех методов быстрого сложения и вычитания двузначных чисел, то это простое умение правильно сгруппировать числа. Просто методы предлагают пользоваться не начальными значениями, а раскладывать их на более удобные в работе числа.
Проверки
Для того, чтобы быстро проверить правильность результатов нужно помнить две вещи:
- Результатом сложения и вычитания могут быть отрицательные
- Результаты сложения и вычитания двухзначных чисел не могут быть больше 200 и меньше – 200. Дело в том, что максимальное целое двузначное число это 99, а минимальное – 99. Наименьшее значение можно получить, если сложить два минимальных значения.
 Максимальное значение это сумма двух максимальных значений. Вот и получается 99+99=198 и -99-99=-198. А дробные приставки не дадут в сумме больше 2.
Максимальное значение это сумма двух максимальных значений. Вот и получается 99+99=198 и -99-99=-198. А дробные приставки не дадут в сумме больше 2.
Что мы узнали?
Мы поговорили о сложении и вычитании двузначных чисел. Обговорили приемы сложения и вычитания двузначных чисел «в уме». Указали на методы определения грубых ошибок в вычислениях.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Оценка статьи
Средняя оценка: 4.7
Всего получено оценок: 301.
А какая ваша оценка?
Сложение двузначных чисел
Педагогам в школе не всегда хватает терпения и времени на индивидуальные занятия с каждым ребенком, чтобы убедиться в том, что материал усвоен качественно и ребенок действительно разобрался в теме. Иногда родителям приходится своими силами, не имея специальных навыков, использовать различные методики, позволяющие ребенку усвоить те или иные правила и принципы. В первую очередь это касается математики, поскольку в этом предмете упущение в одной из тем неизбежно приведет к отставанию по предмету, и в результате, к значительному снижению успеваемости в целом.
В первую очередь это касается математики, поскольку в этом предмете упущение в одной из тем неизбежно приведет к отставанию по предмету, и в результате, к значительному снижению успеваемости в целом.
Для того, чтобы ребенок усвоил азы процесса сложения и вычитания, необходимы совместные усилия как со стороны педагогического коллектива, так и со стороны родителей в процессе контроля за выполнением домашнего задания. Обучение проходит в несколько этапов:
- Сложение однозначных чисел.
- Сложение двузначных чисел в соседних десятках.
- Сложение двузначных чисел через десяток.
Именно последовательность этих этапов поможет ребенку легко усвоить принципы сложения. Кроме того, положительных результатов в обучении проще достичь, если предлагать ребенку материал в игровой форме. Когда малыш заинтересован, он намного быстрее схватывает новую для себя информацию.
Детям, как правило, намного легче понять сложение двузначных чисел, нежели вычитание. Особенно если речь идет о прибавлении в пределах следующего десятка. Если малышу тяжело сразу усвоить необходимую информацию, рекомендуется использование различных способов обучения, пока не будет достигнут желаемый результат. И, конечно, не стоит забывать об игровой форме обучения – можно сказать, что это уже половина успеха.
Особенно если речь идет о прибавлении в пределах следующего десятка. Если малышу тяжело сразу усвоить необходимую информацию, рекомендуется использование различных способов обучения, пока не будет достигнут желаемый результат. И, конечно, не стоит забывать об игровой форме обучения – можно сказать, что это уже половина успеха.
Разделение чисел
Для того, чтобы второкласснику проще было разобраться с тем, в чем заключается принцип сложения, рекомендуется разбивать числа на десятки и единицы. К примеру, чтобы сложить 26 и 35, необходимо написать 10+10+10+10+10+5+6. Как правило, детям очень легко дается такой принцип сложения и в будущем они используют его для ведения расчетов в уме.
Сложение в столбик
Такой способ считается одним из самых простых, базовых. Благодаря его изучению во 2 классе, как это заложено в школьной программе, для ребенка значительно упрощается восприятие десятков и единиц. Кроме того, такой способ предусматривает возможности для дополнительных пометок в случае необходимости, что также способствует визуализации. Примеры на сложение таким способом решаются быстро и приводят к правильному результату.
Примеры на сложение таким способом решаются быстро и приводят к правильному результату.
Помимо сложения, такой способ используется для вычитания. Специалисты в сфере образования рекомендуют начинать знакомство с таким способом именно со сложения, которое дается детям проще.
Онлайн-игры как инструмент обучения
В помощь родителям сегодня создано огромное количество мини-игр, которые также направлены на упрощение процесса обучения сложению двузначных чисел во 2 классе. Их применение помогает детям в кратчайшие сроки, а также с интересом освоить даже тот материал, понимание которого давалось с трудом. Это касается и примеров на сложение с переходом через разряд.
Такой способ упрощает понимание процесса для детей благодаря тому, что с каждым следующим заданием примеры становятся все сложнее. К примеру, начинают с упражнений на сложение в пределах 20 и переходят к более сложным. При таком способе происходит усиление нагрузки, а многократное повторение способствует закреплению материала. Сначала детям демонстрируются примеры, только потом предоставляется возможность решать задания самостоятельно. В некоторых упрощенных вариантах ребенку предлагаются варианты ответов. Это наталкивает ребенка на правильное решение, но с другой стороны, дети очень сообразительны и зачастую пытаются просто угадать ответ.
Сначала детям демонстрируются примеры, только потом предоставляется возможность решать задания самостоятельно. В некоторых упрощенных вариантах ребенку предлагаются варианты ответов. Это наталкивает ребенка на правильное решение, но с другой стороны, дети очень сообразительны и зачастую пытаются просто угадать ответ.
Если ребенок допустил ошибку, ни в коем случае не следует ругать его, даже если он не прилагал достаточно усилий. Следует объяснить ему, в чем именно заключается проблема, а также помочь справиться с задачей.
Примеры на сложение двузначных чисел в большинстве случаев не вызывают сложностей у школьников. Их изучение происходит поэтапно, и дети, благодаря своей любознательности, с легкостью усваивают новую для себя информацию.
Рабочие листы по вычитанию двузначных чисел | Сводка, примеры и типы
Рабочие листы / Математика / Рабочие листы на вычитание двойных цифр
Премиум
Не готовы приобрести подписку? Нажмите, чтобы загрузить бесплатную пробную версию Загрузить образец
Содержание
В вычитании двузначных чисел мы имеем дело с двузначными числами. Вычитание — очень простая операция в математике. Это помогает нам изучить и понять другие важные операции.
Вычитание — очень простая операция в математике. Это помогает нам изучить и понять другие важные операции.
См. файл фактов ниже для получения дополнительной информации о вычитании двузначных чисел или, в качестве альтернативы, вы можете загрузить наш 28-страничный пакет рабочих листов по вычитанию двузначных чисел для использования в классе или дома. Этот рабочий лист разбит на начальный, средний и продвинутый, что означает, что вы можете выбрать уровень сложности для своего ученика.
Ключевые факты и информация
Резюме:
- Вычитание означает вычитание числа из другого числа.
Пример: 11 – 10 = 1 - Когда мы вычитаем ноль из числа, число остается неизменным.
Пример: 20 – 0 = 20 - При вычитании двузначных чисел может быть два случая. Либо мы берем взаймы, либо не берем.
- Вычитание — очень простая операция в математике. Это помогает нам изучить и понять другие важные операции.
- Используется в повседневных задачах.

Что такое вычитание?
- Простейшее определение вычитания говорит нам, что вычитание числа из другого числа называется вычитанием.
- Мы знаем, что в математике есть четыре основных операции.
- Сложение и вычитание являются одними из самых основных операций и будут использоваться для понимания оставшихся двух операций.
- Мы используем вычитание каждый день. Иногда мы имеем дело с меньшими значениями, а иногда с большими значениями.
- Начнем с вычитания однозначных чисел, а затем перейдем к вычитанию двузначных.
- Символ или оператор вычитания «-».
Вычитание одной цифры
- Сначала мы вспомним вычитание однозначных чисел, а затем перейдем к вычитанию двузначных чисел.
- Вот несколько примеров вычитания однозначных чисел:
2 – 1 = 1
4 – 3 = 2
5 – 2 = 3
2 – 0 = 2
6 – 0 = 6
- Вычитание числа из самого себя дает 0, как показано ниже:
4 – 4 = 0
9 – 9 = 0
Вычитание двузначных чисел
- При вычитании двузначных чисел мы имеем дело с двузначными числами.

- Сначала мы размещаем числа друг над другом так, чтобы большее число оказалось сверху.
- Это можно объяснить на примере.
- Предположим, у нас есть два вычитаемых из следующих двузначных чисел:
24 – 12 = ?
- Переставляем их, как показано ниже:
- Числа располагаем так, чтобы цифры на одном месте были друг над другом, и точно так же цифры на десятках располагались друг над другом.
- Затем мы выполняем вычитание, начиная с разряда единиц, как показано ниже:
4 – 2 = 2
- Затем мы переходим к разряду десятков и выполняем вычитание, как показано ниже: 2 96 – 1 = 1
- Вот несколько простых примеров, когда заимствования не происходит.

- Вычитание здесь дает однозначное число.
- Для второго примера имеем:
- Мы видели, что, кроме того, мы использовали перенос в некоторых вопросах, где это необходимо.
- Аналогичным образом при вычитании мы заимствуем цифру, когда это необходимо.
- Это будет легче понять на примере:
- В этом примере мы расположим цифры так же, как в предыдущих примерах, как показано ниже:
- Теперь, когда мы пытаемся вычесть цифры из разряда единиц, мы видим, что 2 меньше 6, поэтому мы не можем вычесть 6 из 2.
- Здесь в этом случае мы заимствуем цифру из разряда десятков:
- Когда мы заимствуем цифру из разряда десятков, 2 в разряде единиц становится 2 + 10 = 12
- И 3 в разряде десятков становится 2.

- Итак, теперь, когда мы выполняем вычитание цифр в разряде единиц, мы есть:
- Когда мы вычитаем цифры на Tens Place.
- Так же, как сложение, вычитание используется в повседневной жизни.
- Мы постоянно имеем дело с числами.
- Когда мы считаем деньги, готовим или считаем что-то еще, нам может понадобиться вычитание.
- Вычитание помогает нам понять другие важные математические операции, такие как деление.
Пример:
- Решите следующие двузначные числа:
54 – 12 = ?
72 – 31 = ?- Расположим их и выполним следующие вычитания.
- для цифров в одном месте:
4 — 2 = 2
- для цифров на Tens Place:
5 — 1 = 4
SO, 54 — 12 = 42
SO, 54 — 12 = 42 9003
SO, 54 — 12 = 42
SO, 54 — 12 = 42 9003
.

- Для второй части:
- После аранжировки выполним следующие вычитания.
- для цифров в одном месте:
- для цифр на Tens Place:
- Решите следующие двузначные числа:
- Расположим эти числа по вертикали, как показано ниже:
- Заметим, что в этом случае мы должны заимствовать цифру, как показано:
- После заимствования 10 мы делаем следующие вычитания.
- для цифров в одном месте:
- для цифр на Tens Place:
- Рабочий лист 1 (для начинающих)
- Рабочий лист 2 (для начинающих)
- Рабочий лист 3 (для начинающих)
- Рабочий лист
- Рабочий лист 5 (промежуточный)
- Рабочий лист 6 (промежуточный)
- Рабочий лист 7 (промежуточный)
- Рабочий лист 8 (промежуточный)
- Рабочий лист 9 (Advance)
- Рабочий лист 10 (Advance)
- 4 (Advance)
- Рабочий лист 10 (Advance)
- 4 (Advance)
- .
- Worksheet 12 (Advance)
- Построить/вытянуть уменьшаемое (59) с основанием десять блоков.
- Отнять сумму вычитаемого (15). Удалите 5 блоков единиц и 1 блок десятков.

- Подсчитайте оставшиеся блоки и найдите разницу.
- Нарисуйте незамкнутую числовую линию.
- Напишите уменьшаемое в конце числовой строки. >>> 57
- Определите, сколько переходов и пропусков вам нужно выполнить.
- Вычитаемое равно 27. Вам нужно нарисовать 2 больших прыжка и 6 маленьких прыжков.
- Пропустить счет назад, чтобы найти разницу.
- 57-26=31
Таким образом, 24 – 12 = 12
При вычитании у нас может быть два случая:
Случай I (без перегруппировки / без заимствования)
14 – 12 = ?
28 – 16= ?
Итак, 14 – 12 = 2
Итак, 28 – 16 = 12
Случай II (перегруппировка / заимствование)
32 – 16 = ?
12 — 6 = 6
2 — 1 = 1
7 — 3 = 4
SO, 72 — 31 — 4193 9003
. Пример:61 – 22 = ?
11 — 2 =
5 — 2 = 3
SO, 61 — 22 = 39993
2
2
. Рабочие листы для вычитания двузначных чисел Это фантастический комплект, который включает в себя все, что вам нужно знать о вычитании двузначных чисел, на 28 подробных страницах. Если вы ссылаетесь на какой-либо контент этой страницы на своем собственном веб-сайте, пожалуйста, используйте приведенный ниже код, чтобы указать эту страницу как первоисточник. Рабочие листы по вычитанию двузначных чисел: https://kidskonnect.com — KidsKonnect, 6 марта 2019 г. Ссылка появится в виде рабочих листов для вычитания двузначных чисел: https://kidskonnect.com — KidsKonnect, 6 марта 2019 г. Вы можете использовать эти рабочие листы как есть или отредактировать их с помощью Google Slides, чтобы сделать их более конкретными для ваших собственных уровней способностей учащихся и стандартов учебной программы. Второй класс — очень важный год, когда речь идет о беглой речи. Это время, когда они учатся знакомиться с фактами сложения и вычитания двузначных чисел. В своем предыдущем посте я поделился четырьмя стратегиями сложения, на которых сосредоточился. Сегодня я расскажу о четырех стратегиях вычитания, используемых для введения двузначного вычитания без перегруппировки. Точно так же, как введение двузначного сложения, я знакомлю своих учеников с несколькими стратегиями и моделями, которые они могут использовать для решения задач на вычитание. Мы проводим много времени, сосредотачиваясь на ПОЧЕМУ что-то делается до того, как мы научим КАК что-то делается. Предоставление учащимся выбора в обучении путем предоставления им нескольких способов решения проблем помогает им добиться успеха. Гибкость является ключевым фактором, потому что каждый ребенок учится по-разному. Техасский TEK для вычитания двузначных чисел гласит: Общий базовый стандарт для состояний вычитания двузначных чисел: Обратите внимание: выделенный жирным шрифтом текст выше ничего не говорит о стандартном алгоритме, который мы выучили много лет назад. Продолжайте читать, чтобы узнать о четырех стратегиях вычитания, которые я представляю и которым обучаю своих студентов, сосредоточившись на вычитании двузначных чисел без перегруппировки. Также обратите внимание, что эти стратегии не будут сосредоточены на перегруппировке. Прежде чем приступить к выполнению этой задачи, учащиеся должны хорошо понимать разрядное значение И простое вычитание. В начале нашего блока вычитания я всегда делаю эту опорную диаграмму. Когда мы изучаем новую стратегию, такую как вычитание двузначного числа без перегруппировки, она добавляется ко всей нашей групповой таблице. Мои ученики хранят соответствующую копию в своих математических журналах, чтобы использовать их позже, когда им понадобится дополнительная поддержка. Прежде чем мы начнем, я хочу, чтобы вы ознакомились со словарем, который будет использоваться. В этом посте вы услышите термины минус , вычитаемое и разность . В задаче 67-33=34 67 — уменьшаемое , 33 — вычитаемое , а 34 — разность 9.0063 . При введении вычитания двузначного числа без перегруппировки я всегда начинаю с моделей с основанием 10. Помимо использования кубиков с основанием десять, я также учу их рисовать кубики на бумаге. Это связано с тем, что ученики не всегда будут иметь доступ к манипулятивным средствам, но у них будут карандаш и бумага. Я всегда даю своим ученикам коврик, помещенный в пластиковый чехол. Это позволяет учащимся также писать или рисовать с помощью сухостираемого маркера, и их можно использовать снова и снова. Вот как работает эта стратегия на примере 59.-15=44 Для студентов, чтобы нарисовать эту стратегию, она работает так же. Мы рисуем «палочки» для обозначения десятков и «точки» для обозначения единиц. Я также учу их отнимать или вычеркивать сначала единицы, а затем десятки. Это поможет, когда перегруппировка будет введена позже. Вторая стратегия вычитания, которую я представляю, это метод расширенной формы. Чтобы успешно использовать эту стратегию, вашим учащимся необходимо четкое понимание значения места и расширяющихся чисел. Уменьшаемое и вычитаемое в задаче на вычитание будут расширены и выстроены вертикально. Я всегда прошу своих учеников обвести знак минус, чтобы помочь им не забывать вычитать, а не прибавлять. Вот как это работает на примере 86-43. Расширить уменьшаемое. >>> 80+6 Разверните вычитаемое и напишите его вертикально под уменьшаемым. >>> 40+3 Обведите знак минус. Вычитание и решение по вертикали на основе разрядности, начиная с единиц, затем десятков. Найдите разницу. >>> 40+3=43 Стратегия вычитания модели числового ряда, как правило, более сложная для учащихся. Им нужно хорошее знание ментальной арифметики и пропуск счета, чтобы этот метод давался им легко. Я часто использую счет в качестве разминки перед нашим математическим блоком. Пример: Попросите учащихся встать в круг. Выберите учащегося, который будет идти первым, и пропустите счет на 10, начиная с числа 35. Первый человек говорит 35, следующий говорит 45 и так далее. Для тех, кто испытывает трудности, я часто даю им подержать в руках диаграмму сотен, чтобы помочь. Вы можете попросить их сделать это, считая вперед или назад. Еще один способ усовершенствовать практику счета — заставить их петь, пока они выстраиваются в очередь. Пример: Класс, давайте пропустим счет на 2, когда мы выстроимся в очередь. Я также обнаружил, что учащимся полезно записывать свои действия перед решением задачи. Вот как это работает на примере 57-26. Этот традиционный метод, вероятно, помог вам выучить двузначное вычитание в детстве, и с ним лучше всего знакомы родители наших детей. Для этой стратегии учащиеся должны выстроить оба числа вертикально друг под другом. Минухенд (большее число) идет сверху, а вычитаемое (меньшее число) идет снизу. Сначала они будут вычитать единицы, а затем десятки, чтобы найти разницу. Один совет, который может быть полезен при первом изучении этой стратегии, состоит в том, чтобы учащиеся использовали маркер, чтобы выделить разряд единиц, или сначала обвести числа в разряде единиц. Это помогает им визуализировать, с чего им нужно начать в первую очередь. Эта концепция может быть для них более сложной, чем мы думаем, потому что они обучены читать и писать слева направо. В конце нашего модуля мы всегда делаем эти брошюры по стратегиям вычитания, чтобы помочь нам повторить. Они могут сохранить их, чтобы использовать позже в качестве справочного материала, когда это необходимо. Ого! Это может показаться большим количеством информации для обработки. Мы все изучаем понятия по-разному, и стратегии вычитания, которыми я поделился, оказались полезными для моих учеников. Нет правильной или неправильной стратегии, когда дело доходит до решения задач на вычитание двузначных чисел. Позвольте своим учащимся выбрать наиболее подходящий для них метод и придерживайтесь его. Как только они нашли метод, который им удобен, важно предоставить им множество возможностей для практики. Ниже приведены некоторые ресурсы, которые могут быть вам полезны. Модуль «Сложение и вычитание без перегруппировки» Этот модуль включает в себя 10-дневные практические и увлекательные занятия для ваших учеников, чтобы отработать все стратегии вычитания для двузначного вычитания без перегруппировки, которые я перечислил выше. Есть ежедневные задачи на сложение и вычитание, интерактивные подсказки в блокноте, игры на вычитание без перегруппировки и многое другое. Хотите сохранить эти идеи стратегий вычитания на потом? Закрепите изображение ниже! Если бы вы спросили меня 10 или даже 20 лет назад, что я буду делать сегодня, я бы не сказал, что учебная программа Подробнее » Умение сравнивать числа требует глубокого понимания разрядности.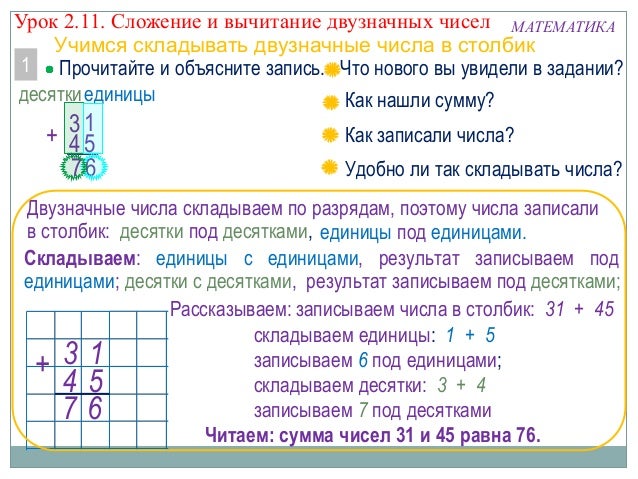 это готовых к использованию рабочих листов для вычитания двузначных чисел, которые идеально подходят для обучения студентов вычитанию двузначных чисел, в которых мы имеем дело с двузначными числами. Вычитание — очень простая операция в математике. Это помогает нам изучать и понимать другие важные операции
это готовых к использованию рабочих листов для вычитания двузначных чисел, которые идеально подходят для обучения студентов вычитанию двузначных чисел, в которых мы имеем дело с двузначными числами. Вычитание — очень простая операция в математике. Это помогает нам изучать и понимать другие важные операции
Полный список включенных рабочих листов
Ссылка/цитирование этой страницы
4 Методика обучения вычитанию двузначных чисел без перегруппировки

2.4B: Сложите до четырех двузначных чисел и вычтите двузначные числа, используя умственные стратегии и алгоритмы, основанные на разрядном значении и свойствах операций.
2.NBT.B.5: Свободное сложение и вычитание в пределах 100 с использованием стратегий, основанных на позиционном значении, свойствах операций и/или взаимосвязи между сложением и вычитанием. .
. 

 Мы начнем с числа 40 и посмотрим, как высоко мы можем считать. Когда все выстроятся правильно, мы остановимся. Стратегия числовой строки фокусируется на том, что учащиеся «прыгают» и «прыгают» назад по числовой строке, чтобы найти разницу в заданной задаче. Я называю 10-е прыжки, а 1-е — пропуски.
Мы начнем с числа 40 и посмотрим, как высоко мы можем считать. Когда все выстроятся правильно, мы остановимся. Стратегия числовой строки фокусируется на том, что учащиеся «прыгают» и «прыгают» назад по числовой строке, чтобы найти разницу в заданной задаче. Я называю 10-е прыжки, а 1-е — пропуски.
Стандартный алгоритм 
Вычитание двузначных чисел без перегруппировки Резюме:

10 неоспоримых причин, почему учителя лучшие: празднование 10-летия перехода во 2-й класс
Как легко научить сравнивать числа, используя стратегию точечного метода


 Максимальное значение это сумма двух максимальных значений. Вот и получается 99+99=198 и -99-99=-198. А дробные приставки не дадут в сумме больше 2.
Максимальное значение это сумма двух максимальных значений. Вот и получается 99+99=198 и -99-99=-198. А дробные приставки не дадут в сумме больше 2.