§ Вычитание десятичных дробей
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
Скрыть меню
На главную страницу
Войти при помощи
Темы уроков
Начальная школа
- Геометрия: начальная школа
- Действия в столбик
- Деление с остатком
- Законы арифметики
- Периметр
- Порядок действий
- Разряды и классы. Разрядные слагаемые
- Счет в пределах 10 и 20
Математика 5 класс
- Взаимно обратные числа и дроби
- Десятичные дроби
- Натуральные числа
- Нахождение НОД и НОК
- Обыкновенные дроби
- Округление чисел
- Перевод обыкновенной дроби в десятичную
- Площадь
- Проценты
- Свойства сложения, вычитания, умножения и деления
- Среднее арифметическое
- Упрощение выражений
- Уравнения 5 класс
- Числовые и буквенные выражения
Математика 6 класс
- Масштаб
- Модуль числа
- Окружность.
Площадь круга - Отношение чисел
- Отрицательные и положительные числа
- Периодическая дробь
- Признаки делимости
- Пропорции
- Рациональные числа
- Система координат
- Целые числа
Площадь кругаАлгебра 7 класс
- Алгебраические дроби
- Как применять формулы сокращённого умножения
- Многочлены
- Одночлены
- Системы уравнений
- Степени
- Уравнения
- Формулы сокращённого умножения
- Функция в математике
Геометрия 7 класс
- Точка, прямая и отрезок
- Что такое аксиома и теорема
Алгебра 8 класс
- Квадратичная функция. Парабола
- Квадратные неравенства
- Квадратные уравнения
- Квадратный корень
- Неравенства
- Системы неравенств
- Стандартный вид числа
- Теорема Виета
Алгебра 9 класс
- Возрастание и убывание функции
- Нули функции
- Область определения функции
- Отрицательная степень
- Среднее
геометрическое
Алгебра 10 класс
- Иррациональные числа
Алгебра 11 класс
- Факториал
Думать и творить, творить и думать — вот основа всякой мудрости.
на главную
Введите тему
Русский язык Поддержать сайт
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
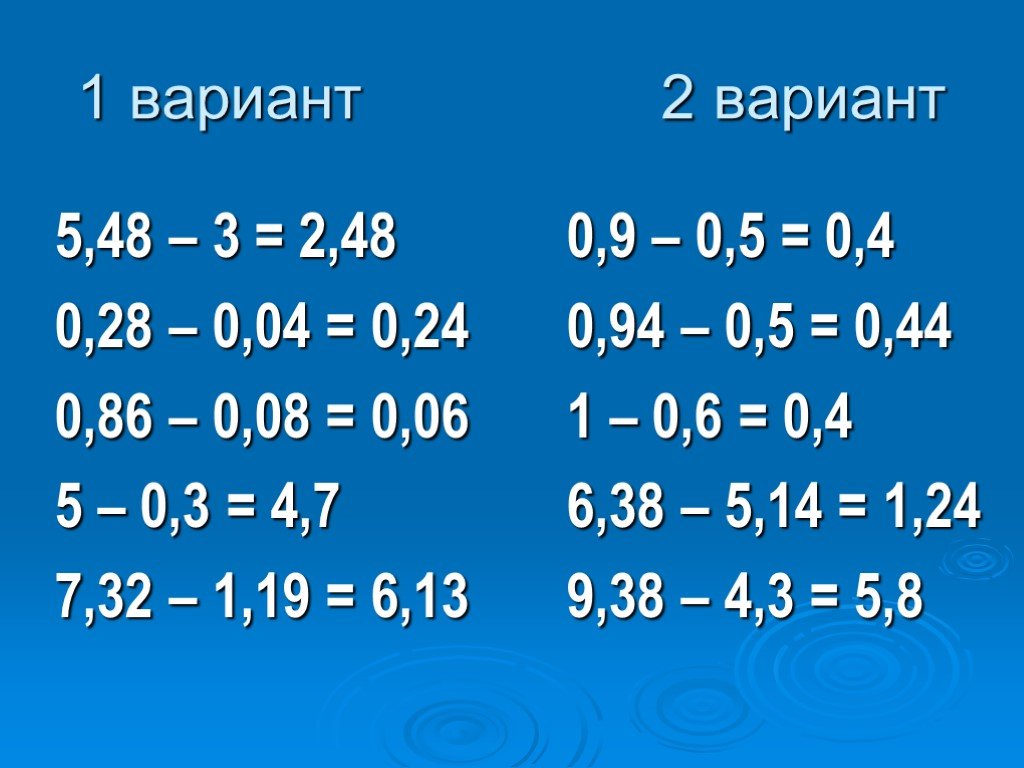
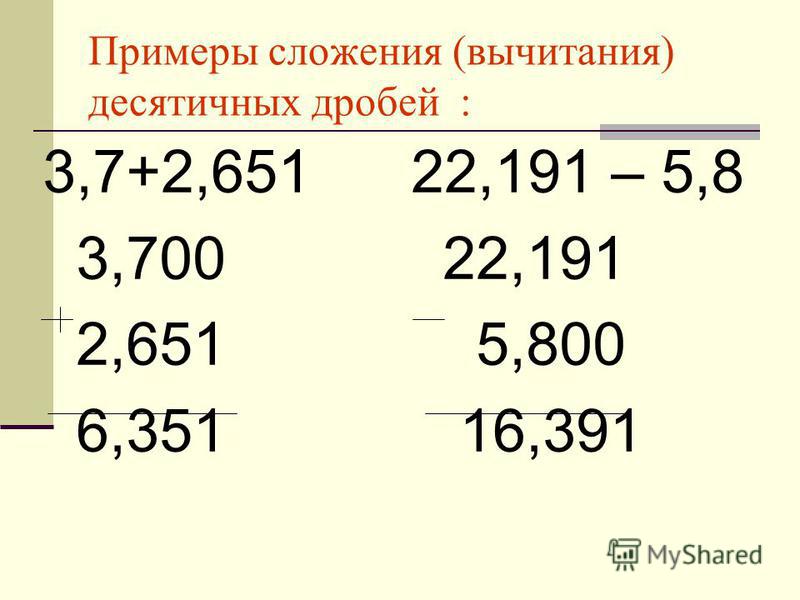
Также как и сложение, вычитание десятичных дробей производим по правилам вычитания в столбик натуральных чисел.
Основные правила вычитания десятичных дробей.
- Уравниваем количество знаков после запятой.
- Записываем десятичные дроби друг под другом так, чтобы запятые были друг под другом.
- Выполняем вычитание десятичных дробей, не обращая внимания на запятые, по правилам
вычитания в столбик натуральных чисел.
- Ставим в ответе запятую под запятыми.
Если вы чувствуете себя уверенно в десятичных дробях и хорошо понимаете, что называется десятыми, сотыми и т.д., предлагаем вам попробовать другой способ вычитания (сложения) десятичных дробей без их записи в столбик.
Другой способ вычитания десятичных дробей, как и сложение, основывается на трёх основных правилах.
Вычитают десятичные дроби справа налево. То есть, начиная с самой правой цифры после запятой.
Вычитать нужно по цифрам разрядов. Целые из целых, десятые из десятых, сотые из сотых, тысячные из тысячных и т.д.
При вычитании большей цифры из меньшей, у соседа слева меньшей цифры занимаем десяток.
Как обычно, рассмотрим пример:
Десятые вычитаем из десятых. 2 — в первом числе, 3 — во втором числе. Так как из 2 (меньшего) мы не можем вычесть 3 (большее), занимаем десяток у соседа слева для 2.
У нас это 5. Теперь мы не
из 2 вычитаем
3,
а из 12 вычитаем 3.12 − 3 = 9
На месте десятых нового числа пишем 9. Не забываем, что после занятия десятка из 5, мы должны вычесть из 5 единицу. Чтобы это не забыть ставим над 5 пустой кружок.И наконец, вычитаем целые части. 14 — в первом числе (не забудьте, что мы из 5 вычли 1), 8 — во втором числе.
14 − 8 = 6
У нас это 5. Теперь мы не
из 2 вычитаем
3, Десятые можно вычитать только из десятых, сотые из сотых, тысячные из тысячных и т.д. Если в одной из десятичных дробей, отсутствует цифра нужного разряда, вместо неё пишем ноль.
Во втором числе самая правая цифра это 2 (сотые),
а в первом числе сотых нет в явном виде. Поэтому, к
первому числу справа от 9 добавляем ноль и вычитаем согласно
основным правилам.
Десятичные дроби Как читать десятичные дроби Сложение десятичных дробей Вычитание десятичных дробей Умножение десятичных дробей Деление десятичных дробей Как сравнивать десятичные дроби
Правило сложения и вычитание десятичных дробей
Такие арифметические вычислительные действия, как сложение и вычитание десятичных дробей, необходимы для того, чтобы, оперируя дробными числами получать искомый результат. Особая важность проведения этих операций состоит в том, что во многих сферах деятельности человека меры многих сущностей представлены именно десятичными дробями. Поэтому для осуществления определенных действий со многими предметами материального мира требуется складывать или вычитать именно десятичные дроби. Следует заметить, что на практике эти операции используются практически повсеместно.
Процедуры сложения и вычитания десятичных дробей по своей математической сути осуществляется практически точно так же, как аналогичные операции для целых чисел.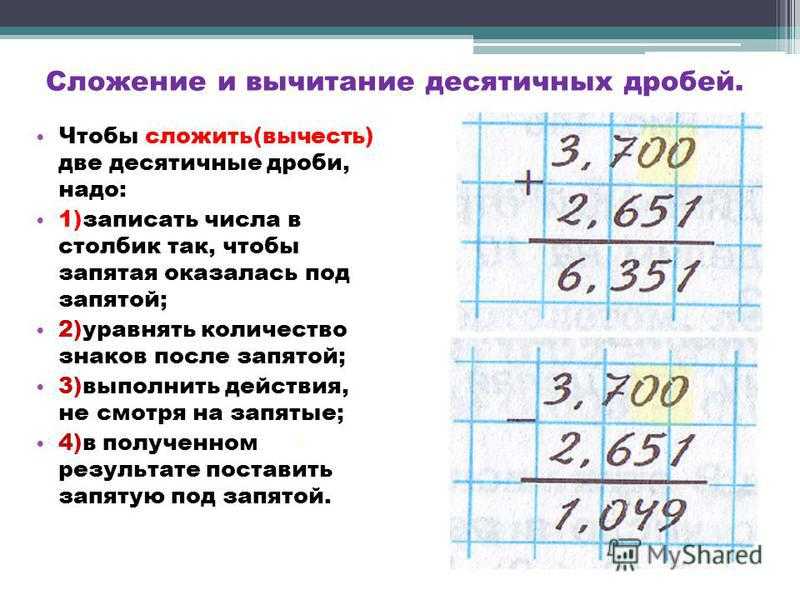
При ее осуществлении значение каждого разряда одного числа нужно записывать под значением аналогичного разряда другого числа.
Вычитание десятичных дробей подчиняется следующим правилам:
• Сначала необходимо произвести уравнивание количество тех знаков, что располагаются после запятой;
• Затем нужно произвести запись десятичных дробей друг под другом таким образом, чтобы содержащиеся в них запятые располагались строго друг под другом;
• Осуществить процедуру вычитания десятичных дробей в полном соответствии с теми правилами, которые действуют для вычитания целых чисел. При этом не нужно обращать никакого внимания на запятые;
• После получения ответа запятую в нем нужно поставить строго под теми, которые имеются в исходных числах.
Операция сложения десятичных дробей осуществляется в соответствии с теми же правилами и алгоритмом, которые описаны выше для процедуры вычитания.
Пример сложения десятичных дробей
Две целых две десятых плюс одна сотая плюс четырнадцать целых девяносто пять сотых равняется семнадцать целых шестнадцать сотых.
0,01 + 14,95 = 17,16
| 2, | 2 |
| + 0, | 01 |
| 14, | 95 |
17, |
16 |
Пример вычитания десятичных дробей
Пятнадцать целых две десятых минус восемь целых три десятых равняется шесть целых девять десятых.
15,2 – 8,3 = 6,9
| 15, | 2 |
| – 8, | 3 |
6, |
9 |
Примеры сложения и вычитания десятичных дробей
Математические операции сложения и вычитания десятичных дробей на практике используются чрезвычайно широко, причем они нередко касаются многих предметов окружающего нас материального мира. Ниже приводится несколько примеров таких вычислений.
Пример 1
Согласно проектно-сметной документации, для строительства небольшого производственного объекта требуется десять целых пять десятых кубометров бетона. Используя современные технологии возведения зданий, подрядчикам без ущерба для качественных характеристик сооружения удалось использовать для проведения всех работ всего девять целых девять десятых кубометров бетона. Размер экономии составляет:
Десять целых пять десятых минус девять целых девять десятых равно ноль целых шесть десятых кубометра бетона.
10,5 – 9,9 = 0,6 м3
Пример 2
Двигатель, устанавливаемый на старую модель автомобиля, потребляет в городском цикле восемь целых две десятых литра топлива на сто километров пробега. Для нового силового агрегата этот показатель составляет семь целых пять десятых литров. Размер экономии составляет:
Восемь целых две десятых литра минус семь целых пять десятых литра равно ноль целых семь десятых литра на сто километров пробега в городском режиме движения.
8,2 – 7,5 = 0,7л
Операции сложения и вычитания десятичных дробей применяются чрезвычайно широко, и их осуществление не составляет никаких проблем. В современной математике эти процедуры отработаны практически идеально, и ими практически все хорошо владеют еще со школьной скамьи.
Сложение и вычитание десятичных знаков | Бухгалтерский учет для менеджеров
Цели обучения
- Использование сложения и вычитания при оценке выражений с десятичными дробями
Понимание того, как работать с десятичными дробями при расчетах с деньгами, очень важно в бизнесе. Мы знаем, что [латекс]$1[/латекс] — это то же самое, что [латекс]$1,00[/латекс]. Но то, как мы пишем [латекс]$1\текст{ или }$1.00[/латекс], зависит от контекста. Точно так же целые числа могут быть записаны в виде десятичных дробей с любым количеством нулей справа от десятичной дроби.
[латекс]\begin{array}{cccc}5=5.0\hfill & & & -2=-2.0\hfill \\ 5=5.
00\hfill & & & -2=-2.00\hfill \\ 5=5.000 \hfill & & & -2=-2.000\hfill \end{array}[/latex]
и так далее [latex]\dots[/latex]
Так что при расчетах с деньгами вам, возможно, придется заполнять нули в качестве заполнителей для правильного выравнивания значений.
Предположим, сегодня утром вы зашли в пекарню Bouchon позавтракать: апельсиновый сок стоил три с половиной доллара, кофе — 1,85 доллара, а булочка — 4 доллара. Все три элемента сначала должны быть представлены в долларах в центах, чтобы мы могли правильно сложить числа.
Мы выстроили доллары под долларами, а центы под центами, разделив их десятичными знаками. Затем мы просто добавляли каждый столбец, как если бы мы складывали целые числа. Выстраивая таким образом десятичные дроби, мы можем складывать или вычитать соответствующие разрядные значения точно так же, как мы это делали с целыми числами.
Сложение или вычитание десятичных знаков
- Пишите числа вертикально, чтобы десятичные точки совпадали.
- При необходимости используйте нули в качестве заполнителей.
- Сложите или вычтите числа, как если бы они были целыми числами. Затем поместите десятичную дробь в ответе под десятичными точками в данных числах.
Мы потренируемся складывать десятичные дроби в приведенном ниже примере. Помните, как и при сложении целых чисел, вам может потребоваться «перенести» десятку на следующее разрядное значение при добавлении каждого столбца.
Пример
Добавить: [латекс]3,7+12,4[/латекс]
Решение
| [латекс]3,7+12,4[/латекс] | |
| Пишите числа вертикально, чтобы десятичные запятые совпадали. | [латекс]\begin{массив}{c}\hfill 3.7\\ \hfill \underset{\text{____}}{+12.4}\end{массив}[/latex] |
| Заполнители не нужны, так как оба числа имеют одинаковое количество знаков после запятой. | |
Сложите числа, как если бы они были целыми числами. Затем поместите десятичную дробь в ответе под десятичными точками в данных числах. | [латекс]\begin{array}{c}\hfill \stackrel{1}{3}.7\\ \hfill \underset{\text{____}}{+12.4}\\ \hfill 16.1\end{array }[/латекс] |
попробовать
пример
Добавить: [латекс]23.5+41.38[/латекс]
Показать ответ
попробуйте
В следующем видео мы покажем еще один пример сложения десятичных знаков.
Вычитание десятичных дробей выполняется так же, как сложение десятичных дробей. Помните — так же, как и при вычитании целых чисел — вам, возможно, придется «одолжить» десять из следующего разряда при вычитании каждого столбца.
пример
Сколько сдачи вы получили бы, если бы передали кассиру купюру [латекс]20$[/латекс] за покупку [латекс]14,65[/латекс]? Мы покажем шаги для расчета этого в следующем примере.
Вычесть: [латекс]20 — 14,65[/латекс]
Показать ответ
попробовать
пример
Вычесть: [латекс]2,51 — 7,4[/латекс]
Показать ответ
попробуй
В этом видео показан еще один пример вычитания одной десятичной дроби из другой.
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Десятичные дроби: сложение и вычитание десятичных дробей
Урок 2: Сложение и вычитание десятичных дробей
/en/decimals/introduction-to-decimals/content/
Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей часто происходит в реальной жизни.
Вы можете обнаружить, что вам нужно сложить стоимость продуктов, чтобы увидеть, достаточно ли у вас денег, чтобы заплатить за них. Или, возможно, вам нужно вычесть стоимость счета с вашего банковского счета.
При сложении или вычитании десятичных чисел важно настроить выражение правильно . Числа должны быть в определенном месте, как и десятичные дроби .
Нажмите на слайд-шоу ниже, чтобы узнать, как настроить эти выражения.
Сначала составим выражение сложения: 21,4 плюс 6,82.
Как и в любом примере сложения, мы собираемся сложить одно число поверх другого.
Но вместо того, чтобы выстраивать наши числа справа…
Но вместо того, чтобы выстраивать наши числа справа… мы выстроим в ряд десятичных знаков .
Независимо от того, сколько чисел находится по обе стороны от десятичной точки, мы всегда будем выстраивать десятичные точки перед сложением.
Как только мы выстроим десятичные точки, наши десятичные дроби готовы к добавлению.
Когда мы вычитаем десятичные дроби, мы устанавливаем десятичные дроби таким же образом. Давайте настроим этот пример.
Вместо того, чтобы выстраивать два числа справа, мы выстроим два десятичных знака.
Теперь наши десятичные дроби готовы к вычитанию.
Добавление десятичных чисел
Теперь, когда мы знаем, как составлять задачи с десятичными дробями, давайте потренируемся, решая несколько. Сначала мы поработаем над , добавив . Если вы чувствуете себя комфортно, добавляя большие числа, вы готовы добавлять десятичные числа.
Щелкните слайд-шоу, чтобы узнать, как добавлять десятичные дроби.
Попробуем решить эту задачу: 1.9 + 2.15.
Во-первых, мы убедимся, что десятичные дроби выровнены.
Начнем с добавления самых дальних цифр к правому .
В этом случае у нас ничего нет сверху и 5 снизу.Ничего плюс 5 равно 5. Мы напишем 5 под чертой.
Теперь мы добавим следующий набор цифр к слева : 9 и 1.
9 + 1 равно 10, но нет места для записи обеих цифр числа 10 под 9 и 1. Нам придется нести .
Мы узнали, как переносить числа на уроке «Сложение двух- и трехзначных чисел».
Запишем правую цифру, 0, под строчкой…
Запишем правильную цифру, 0, под строчкой… потом перенесем левая цифра, 1, до следующего набора цифр в задаче.
Теперь напишем десятичную точку. Мы поместим его непосредственно под двумя другими десятичными точками.
Далее мы переместим влево от , чтобы добавить следующий набор цифр: 1 и 2. Поскольку мы перенесли 1, мы добавим и его.
1 + 1 + 2 равно 4.
Мы напишем 4 под чертой.Готово. 1,9 + 2,15 = 4,05. Мы можем прочитать этот ответ как четыре и пять сотых .
Давайте попробуем решить денежную задачу: $51,99 + $25,32.
Мы убедимся, что наши десятичные точки выстроены правильно.
Как всегда, мы начнем с добавления цифр справа. Здесь 9 и 2.
9 + 2 равно 11, так что, похоже, нам придется нести .
1 на справа остается под 9 и 2.
Мы возьмем 1 на слева и поместите его над следующим набором цифр слева.
Теперь мы переместим влево от , чтобы добавить следующий набор цифр. Поскольку у нас есть 1, мы добавим и его.
1 + 9 + 3 = 13.
Мы поместим 3 под добавленными цифрами.
Мы возьмем 1 и поместим его над в следующем столбце слева.
Теперь пришло время записать десятичную точку. Не забудьте разместить его прямо под двумя другими десятичными точками.
Далее мы переместим влево от и добавим следующий набор цифр. Мы обязательно добавим ту, что у нас была.
1 + 1 + 5 = 7. Под чертой напишем 7.
Чтобы закончить, мы добавим следующий столбец к слева: 5 и 2.
5 + 2 равно 7. Мы напишем 7 под 2. закончить, написав знак доллара ($).
Готово. 51,99 доллара США + 25,32 доллара США = 77,31 доллара США. Мы можем прочитать этот ответ как семьдесят семь долларов и тридцать один цент .
В этом случае у нас ничего нет сверху и 5 снизу.
Мы напишем 4 под чертой.
Попробуйте!
Попробуйте решить эти задачи, чтобы попрактиковаться в сложении десятичных чисел.
12,20 + 12,20 =
5,40 + 45,80 =
3,85 + 9,67 =
Вычитание десятичных чисел
То же самое верно и для вычитание чисел с десятичными знаками.
Если вы можете вычитать большие числа, вы можете вычитать и десятичные числа!
Щелкните слайд-шоу, чтобы узнать, как вычитать десятичные дроби.
Попробуем решить эту задачу: 41.2 — 3.09.
Сначала мы убедимся, что выражение настроено правильно. Здесь 41,2 — большее число, поэтому мы поместим его сверху.
Десятичные точки выстроены.
Как всегда, начнем с самых дальних цифр до справа . Здесь у нас ничего нет сверху и 9 снизу.
Мы не можем отнять 9 из ничего. Нам нужно поместить цифру после 41,2, чтобы мы могли вычесть из нее.
Значение нашего числа не изменится, если мы используем цифру, которая ничего не значит: 0. Мы поместим 0 после 41,2.
Теперь мы можем вычесть цифры справа. 0 меньше 9, поэтому нам нужно позаимствовать , чтобы сделать 0 больше.
Мы научились брать взаймы на уроке «Вычитание двух- и трехзначных чисел».
Заимствуем от цифры до слева от 0. Здесь это 2. От нее возьмем 1 .
2 — 1 = 1. Чтобы помочь нам вспомнить, что мы вычли 1, вычеркнем 2 и напишем 1 над .
Затем мы поместим полученную 1 рядом с 0.
0 станет 10.
10 больше 9, значит, мы можем вычесть. Решаем за 10 — 9.
10 — 9 = 1. Под чертой напишем 1.
Теперь мы переместим влево от , чтобы вычесть следующий набор цифр: 1 — 0.
1 — 0 = 1. Мы напишем 1 под чертой.
Теперь пришло время записать десятичную точку . Мы поместим его непосредственно под двумя другими десятичными точками.
Теперь найдем разность следующего набора цифр слева: 1 — 3.
Поскольку 1 меньше 3, похоже, нам снова придется брать взаймы.
Нам нужно сделать 1 больше.Заимствуем от цифры до слева от 1. Здесь мы заимствуем 1 из 4.
4 — 1 = 3. Запишем 3 над 4.
Затем мы поместим 1, которую мы взяли , рядом с в 1.
1 становится 11.
11 больше 3, что означает, что мы можем вычесть. Найдем 11 — 3.
11 — 3 = 8. Под чертой напишем 8.
Наконец, мы перейдем к слева , чтобы вычесть последний набор цифр. Верхняя цифра 3, но под ней ничего нет.
3 минус ничего равно 3, поэтому мы напишем 3 под чертой.
41,2 — 3,09= 38,11. Мы можем прочитать это как тридцать восемь и одиннадцать сотых .
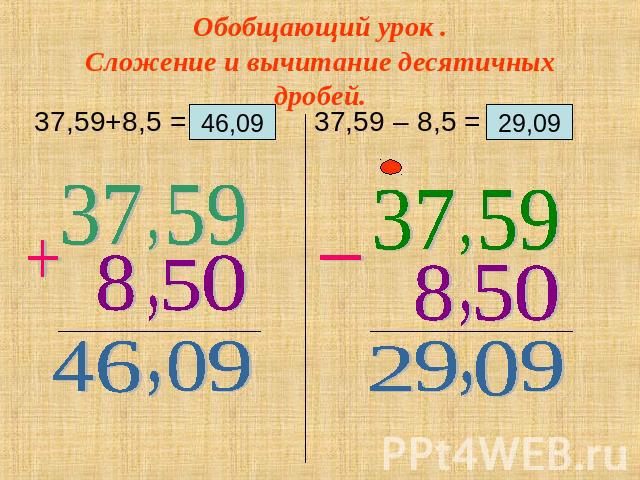
Попробуем вычесть деньги. Давайте посмотрим, сможем ли мы решить $ 14,76 — $ 3,86.
Во-первых, давайте удостоверимся, что выражение настроено правильно. Большее число находится на сверху , а десятичные точки выстроены в ряд .
Как всегда, начнем с нахождения разности цифр справа. Вот, это 6 — 6.
6 — 6 = 0. Под чертой напишем 0.
Мы переместим влево от к следующему набору цифр: 7 и 8. 7 меньше 8, поэтому мы возьмем 7, чтобы сделать 7 больше.
Давайте посмотрим на цифру до осталось из 7. Здесь это 4. Отнимем от нее 1.
4 — 1 = 3. Зачеркнем 4 и напишем 3 над .
Затем мы поместим 1, которую мы взяли , рядом с в 7.
7 становится 17.
Теперь пришло время вычитать. Найдем 17 — 8.
17 — 8 = 9. Под чертой напишем 9.
Мы поместим десятичную точку непосредственно под двумя другими десятичными точками.
Далее мы переместим влево от , чтобы найти разность следующего набора цифр.
Нам нужно сделать 1 больше.
