Умножение. Математика 2 класс Богданович. ГДЗ, решебник.

Категория: —>> Математика 2 класс Богданович  
Задание:  —>>   583 — 600  



наверх

Задание 583.

Сколько всего вишен?

Решение:

2 + 2 + 2 + 2 + 2 = 10

Сложение одинаковых слагаемых называется умножением.
Сумму одинаковых слагаемых 2 + 2 + 2 + 2 + 2 можно записать так:
2 · 5 = 10
Точка (•) — знак умножения. Примеры на умножение читают так: два умножить на пять, равно десяти.

---

Задание 584.

Замени примеры на слоясение примерами на умножение.

2 + 2 + 2 + 2 + 2	4 + 4 + 4	6 + 6
3 + 3 + 3 + 3 + 3	5 + 5 + 5	7 + 7 + 7

Решение:

2 • 5 = 10	4 • 3 = 12	6 • 2 = 12
3 • 5 = 15	5 • 3 = 15	7 • 3 = 21

---

Задание 585.

Замени примеры на умножение примерами на сложение по образцу.
Образец. 9 • 4 = 9 + 9 + 9 + 9.

Решение:

9 • 5 = 9 + 9 + 9 + 9 + 9

3 • 5 = 3 + 3 + 3 + 3 + 3

4 • 4 = 4 + 4 + 4 + 4

6 • 2 = 6 + 6

7 • 3 = 7 + 7 + 7

8 • 4 = 8 + 8 + 8 + 8

---



Задание 586.

Сколько нужно палочек, чтобы составить данные треугольники? Запиши решение сложением, а потом умножением.

Решение:

• 1) 3 + 3 + 3 + 3 + 3 = 15
• 2) 3 • 5 = 15

---

Задание 587.

Решение:

40 + 27 = 67 32 + 27 = 59 57 + 27 = 84

65 — 32 = 33 80 — 32 = 48 72 — 32 = 40 51 — 32 = 19

---

Задание 588.

В киоск привезли 50 батонов. До обеда продали 14 батонов, а после обеда 28. Сколько батонов осталось в киоске?
Реши задачу другим способом.

Решение:

Способ — 1.
• 1) 50 — 14 = 36
• 2) 36 — 28 = 8
• Выражение: 50 — 14 — 28 = 8
• Ответ: 12 батонов.

Способ 2.
• 1) 14 + 28 = 42
• 2) 50 — 42 = 8
• Выражение: 50 — (14 + 28) = 8
• Ответ: 8 батонов.

---

Задание 589.

Сколько всего цветков?
Решение запиши сложением и умножением.

Решение:

• 1) 3 + 3 + 3 + 3 = 12
• 2) 3 • 4 = 12

---

Задание 590.

Компьютерный диск стоит 7 грн. Сколько нужно заплатить за 3 таких диска?
Реши задачу сначала сложением, а потом — умножением.

Решение:

• 1) 7 + 7 + 7 = 21
• 2) 7 • 3 = 21

---

Задание 591.

Прочитай примеры на умножение и проверь ответы сложением по образцу.

Образец: 2 + 2 + 2 + 2 + 2 = 10; 2 • 5

1) 2 • 5 = 10

2) 7 • 3 = 21

3) 8 • 2 = 16

4) 2 • 6 = 12

Решение:

• 1) 2 + 2 + 2 + 2 + 2 = 10
• 2) 7 + 7 + 7 = 21
• 3) 8 + 8 = 16
• 4) 2 + 2 + 2 + 2 + 2 + 2 = 12

---

Задание 592.

Реши примеры. Где можно, замени примеры на сложение примерами на умножение.

4 + 4 + 4	9 + 9 + 6	23 + 32
3 + 3 + 3	14 + 14	15 + 15 + 15 + 15

Решение:

4 • 3 = 12	9 + 9 + 6 = 24	23 + 32 = 55
3 • 3 = 9	14 • 2 = 28	15 • 4 = 60

---

Задание 593.

Какое число взято одинаковым слагаемым в каждом примере? Сколько раз повторяется слагаемое?

1) 6 • 5

2) 2 • 3

3) 2 • 7

4) 10 • 3

5) 12 • 2

Решение:

• 1) 6 повторяется 5 раз
• 2) 2 повторяется 3 раза
• 3) 2 повторяется 7 раз
• 4) 10 повторяется 3 раза
• 5) 12 повторяется 2 раза

---

Задание 594.

Прочитай названия чисел при умножении

Числа, которые умножают, называют множителями. Число, которое получают при умножении, называют произведением.
Выражение 7 • 3 тоже называют произведением чисел 7 и 3.

---

Задание 595.

Как называются числа в примерах?

1) 9 • 5 = 45

2) 2 • 3 = 6

Решение:

• 1) 9 — первый множитель, 5 второй множитель, 45 произведение.
• 2) 2 — первый множитель, 3 второй множитель, 6 произведение.

---

Задание 596.

Назови множители и произведения в примерах.

3 • 9 = 27

2 • 7 = 14

7 • 3 = 21

Решение:

3, 9 — множители, 27 — произведение.

2, 7 — множители, 14 — произведение.

7, 3 — множители, 21 — произведение.

---

Задание 597.

Чашка стоит 3 грн. Сколько нужно заплатить за 4 такие чашки?

Решение:

• 1) 3 + 3 + 3 + 3 = 12
• 2) 3 • 4 = 12
• Ответ: 12 грн.

---

Задание 598.

Брату 12 лет, а сестре 9. Сколько лет будет брату, когда сестре сколько ему сейчас?

Решение:

• 1) 12 — 9 = 3
• 2) 12 + 3 = 15
• Выражение: 12 + (12 — 9) = 15
• Ответ: 15 лет.

---

Задание 599.

Масса одной посылки 3 кг. Какова масса 6 таких посылок?
Запиши решение сложением, а потом — умножением.

Решение:

• 1) 3 + 3 + 3 + 3 + 3 + 3 = 18
• 2) 3 • 6 = 18
• Ответ: 18 кг.

---

Задание 600.

Реши примеры.

Решение:

72 + 18 = 90	64 — 32 = 32	70 + 14 = 84	17 + 17 = 34
20 + 35 = 55	64 — 38 = 26	70 — 34 = 36	17 + 7 = 24

---



Задание:  —>>   164 — 183  

Умножение умноделение | Развивающие игры Мерсибо

«Умножение умноделение» — это набор настольных игр, который поможет объяснить детям принципы арифметических действий, научить применять их на практике и быстрее решать математические примеры. Задания охватывают программу 1-6 классов: сложение и вычитание, умножение, деление и признаки делимости. 

Этапы игр отличаются сложностью, формами подачи и различными методиками. Благодаря этому задания подходят для детей с разным уровнем подготовки, интересами и способностями. Формат игры поможет увлечь детей и заинтересовать их предметом, снять страх плохой отметки за ошибку.

В набор входят: 36 маленьких карточек с примерами из таблицы умножения, 6 больших карточек с ответами на умножение, 8 больших карточек с цифрами от 2 до 9, 48 фигурных двусторонних карточек и инструкция с подробным описанием игр.

Маленькие карточки с примерами умножения 
На карточке нарисовано поле из клеточек 10х10, написан пример умножения и закрашена та область клеточек, которая соответствует множителям. Например, на карточке написан пример 3*4 и закрашен квадрат размером 3 клеточки в высоту и 4 в длину.

На обратной стороне карточки написан пример со сложением или вычитанием, результат которого совпадает с результатом умножения на первой стороне.

Таким образом ребенок может проверить, правильно ли он решил пример с умножением. Например, для карточки 3*4 на обратной стороне будет пример 4+8, который также дает 12. 

Большие карточки с ответами на умножение
На карточке написаны 6 чисел, которые совпадают с ответами на примеры из таблицы умножения. 

Большие карточки с цифрами
На каждой карточке написана одна цифра от 2 до 9 и признак делимости для нее. Например: карточка с цифрой 3 и признак «число делится на 3, если сумма его цифр делится на 3»

Фигурные карточки с примерами деления
На одной стороне написан пример деления, на другой число. Фигурные карточки складываются в восемь квадратов размером с большую карточку с цифрой. Таким образом, ребенок может проверить, правильно ли он решил примеры.

Размер коробки: 25*17,5 см.

Полная инструкция (pdf)

Правила раскрытия скобок: сложение, вычитание, умножение, деление

В данной публикации мы рассмотрим основные правила раскрытия скобок, сопроводив их примерами для лучшего понимания теоретического материала.

Раскрытие скобок – замена выражения, содержащего скобки, на равное ему выражение, но без скобок.

Правила раскрытия скобок

Правило 1

Если перед скобками стоит “плюс”, то знаки всех чисел внутри скобок остаются без изменений.

a + (b – c – d + e) = a + b – c – d + e

Пояснение: Т.е. плюс на плюс дают плюс, а плюс на минус – минус.

Примеры:

• 6 + (21 – 18 – 37) = 6 + 21 – 18 – 37
• 20 + (-8 + 42 – 86 – 97) = 20 – 8 + 42 – 86 – 97

Правило 2

Если перед скобками стоит “минус”, то знаки всех чисел внутри скобок меняются на противоположные.

a – (b – c – d + e) = a – b + c + d – e

Пояснение: Т.е. минус на плюс дают минус, а минус на минус – плюс.

Примеры:

• 65 – (-20 + 16 – 3) = 65 + 20 – 16 + 3
• 116 – (49 + 37 – 18 – 21) = 116 – 49 – 37 + 18 + 21

Правило 3

Если перед или после скобок стоит знак “умножения”, все зависит от того, какие действие выполняются внутри них:

Сложение и/или вычитание

• a ⋅ (b – с + d) = a ⋅ b – a ⋅ c + a ⋅ d
• (b + с – d) ⋅ a = a ⋅ b + a ⋅ c – a ⋅ d

Умножение

• a ⋅ (b ⋅ с ⋅ d) = a ⋅ b ⋅ с ⋅ d
• (b ⋅ с ⋅ d) ⋅ a = b ⋅ с ⋅ d ⋅ a

Деление

• a ⋅ (b : с) = (a ⋅ b) : с = (a : c) ⋅ b
• (a : b) ⋅ c = (a ⋅ c) : b = (c : b) ⋅ a

Примеры:

• 18 ⋅ (11 + 5 – 3) = 18 ⋅ 11 + 18 ⋅ 5 – 18 ⋅ 3
• 4 ⋅ (9 ⋅ 13 ⋅ 27) = 4 ⋅ 9 ⋅ 13 ⋅ 27
• 100 ⋅ (36 : 12) = (100 ⋅ 36) : 12

Правило 4

Если перед или после скобок стоит знак “деления”, то как и в правиле выше, все зависит от того, какие действие выполняются внутри них:

Сложение и/или вычитание

• a : (b – с + d) = a : b – a : c + a : d
• (b + с – d) : a = b : a + c : a – d : a

Умножение

• a : (b ⋅ c) = a : b : c = a : c : b
• (b ⋅ c) : a = (b : a) ⋅ с = (с : a) ⋅ b

Деление

• a : (b : c) = (a : b) ⋅ с = (c : b) ⋅ a
• (b : c) : a = b : c : a = b : (a ⋅ c)

Примеры:

• 72 : (9 – 8) = 72 : 9 – 72 : 8
• 160 : (40 ⋅ 4) = 160 : 40 : 4
• 600 : (300 : 2) = (600 : 300) ⋅ 2

Примеры умножение на 2 и3.

Умножение

И умножение. Как раз об операции умножения и пойдет речь в этой статье.

Умножение чисел

Умножение чисел осваивается детьми во втором классе, и ничего в этом сложного нет. Сейчас мы рассмотрим умножение на примерах.

Пример 2*5 . Это значит либо 2+2+2+2+2, либо 5+5. Берем 5 два раза или 2 пять раз. Ответ, соответственно, 10.

Пример 4*3 . Аналогично, 4+4+4 или 3+3+3+3. Три раза по 4 или четыре раза по 3. Ответ 12.

Пример 5*3 . Делаем так же как и предыдущие примеры. 5+5+5 или 3+3+3+3+3. Ответ 15.

Формулы умножения

Умножение – это сумма одинаковых чисел, например, 2 * 5 = 2 + 2 + 2 + 2 + 2 или 2 * 5 = 5 + 5. Формула умножения:

Где, а – любое число, n – число слагаемых а. Допустим, а=2, тогда 2+2+2=6, тогда n=3 умножая 3 на 2, получаем 6.Рассмотрим в обратном порядке. Например, дано: 3 * 3, то есть. 3 умножить на 3 – это значит, что тройку надо взять 3 раза: 3 + 3 + 3 = 9. 3 * 3=9.

Сокращенное умножение

Сокращенное умножение – сокращение операции умножения в определенных случаях, и специально для этого выведены формулы сокращенного умножения. 2)

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Умножение дробей

Рассматривая сложение и вычитание дробей, прозвучало правило, приведения дробей к общему знаменателю, чтобы выполнить расчет. При умножении этого делать не надо ! При умножении двух дробей, умножается знаменатель на знаменатель, а числитель на числитель.

Например, (2/5) * (3 * 4). Умножим две трети на одну четверть. Умножаем знаменатель на знаменатель, а числитель на числитель: (2 * 3)/(5 * 4), тогда 6/20, совершаем сокращение, получаем 3/10.

Умножение 2 класс

Второй класс – это только начала изучения умножения, поэтому второклассники решают простейшие задачки на замену сложения умножением, умножают числа, учат таблицу умножения. Давайте рассмотрим задачи на умножение уровня второго класса:

Олег живет в пяти этажном доме, на самом верхнем этаже. Высота одного этажа равняется 2 метрам. Какова высота дома?

В коробке находятся 10 упаковок с печеньем. В каждой упаковке их 7 штук. Сколько печенья в коробке?

Миша расставил свои игрушечные машинки в ряд. В каждом ряду их 7, а рядов всего 8. Сколько у Миши машинок?

В столовой стоят 6 столов, а за каждым столом задвинуты 5 стульев. Сколько стульев в столовой?

Мама с магазина принесла 3 пакета с апельсинами. В пакетах находятся по 22 апельсина. Сколько апельсиновпринесла мама?

В саду растет 9 кустов клубники, а на каждом кустике растет 11 ягод. Сколько ягод растет на всех кустиках?

Рома положил друг за другом 8 деталей трубы, одинакового размера по 2 метра. Какова длина полной трубы?

В школу родители на первое сентября привезли детей. Приехало 12 машин, в каждой было по 2 ребенка. Сколькодетей привезли родители на этих машинах?

Умножение 3 класс

В третьем классе даются уже более серьезные задания. Помимо умножения будет так же проходиться Деление .

Среди заданий на умножение будет: умножение двузначных чисел, умножение столбиком, замена сложения умножением и наоборот.

Умножение столбиком:

Умножение столбиком – самый простой способ перемножить большие числа. Рассмотрим данный метод на примередвух чисел 427 * 36.

1 шаг . Запишем числа друг под другом, так чтобы 427 было на верху, а 36 внизу, то есть 6 под 7, 3 под 2.

2 шаг . Умножение начинаем с крайней правой цифры нижнего числа. То есть порядок умножения таков: 6 * 7, 6 * 2, 6 * 4, затем так же с тройкой: 3 * 7, 3 * 2, 3 * 4.

Итак, умножаем сначала 6 на 7, ответ:42. Записываем так: так как получилось 42, то 4 – десятки, а 2 – единицы, запись происходит аналогично сложению, а значит 2 записываем под шестеркой, а 4 прибавляем к двойке числа 427.

3 шаг . Затем аналогично делаем с 6 * 2. Ответ: 12. Первый десяток, который прибавляется к четверке числа 427, а второй – единицы. Складываем полученную двойку с четверкой от предыдущего умножения.

4 шаг . Умножаем 6 на 4. Ответа 24 и прибавляем 1 от предыдущего умножения. Получаем 25.

Итак, умножив 427 на 6, получился ответ 2562

ЗАПОМНИТЕ! Результат второго умножения нужно начать записывать под ВТОРОЙ цифрой первого результата!

5 шаг . Совершаем аналогичные действия с цифрой 3. Получаем ответ умножения 427 * 3=1281

6 шаг . Затем полученные ответы при умножении складываем и получаем итоговый ответ умножения 427 * 36. Ответ: 15372.

Умножение 4 класс

Четвертый класс – это уже умножение только больших чисел. Вычисление выполняются методом умножения в столбик. Метод описан выше доступным языком.

Например, найти произведение следующих пар чисел:

1. 988 * 98 =
2. 99 * 114 =
3. 17 * 174 =
4. 164 * 19 =

Презентация на умножение

Скачайте презентацию на умножение с простейшими заданиями для второклассников. Презентация поможет детям лучше ориентироваться в этой операции, потому что она составлена красочно и в игровом стиле – в лучшем варианте для обучения ребенка!

Таблица умножения

Таблица умножения учится каждым школьником во втором классе. Ее обязан знать каждый!

Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.

Примеры на умножение

Умножение на однозначное

1. 9 * 5 =
2. 9 * 8 =
3. 8 * 4 =
4. 3 * 9 =
5. 7 * 4 =
6. 9 * 5 =
7. 8 * 8 =
8. 6 * 9 =
9. 6 * 7 =
10. 9 * 2 =
11. 8 * 5 =
12. 3 * 6 =

Умножение на двузначное

1. 4 * 16 =
2. 11 * 6 =
3. 24 * 3 =
4. 9 * 19 =
5. 16 * 8 =
6. 27 * 5 =
7. 4 * 31 =
8. 17 * 5 =
9. 28 * 2 =
10. 12 * 9 =

Умножение двузначное на двузначное

1. 24 * 16 =
2. 14 * 17 =
3. 19 * 31 =
4. 18 * 18 =
5. 10 * 15 =
6. 15 * 40 =
7. 31 * 27 =
8. 23 * 25 =
9. 17 * 13 =

Умножение трехзначных чисел

1. 630 * 50 =
2. 123 * 8 =
3. 201 * 18 =
4. 282 * 72 =
5. 96 * 660 =
6. 910 * 7 =
7. 428 * 37 =
8. 920 * 14 =

Игры на развитие устного счета

Специальные развивающие игры разработанные при участии российских ученых из Сколково помогут улучшить навыки устного счета в интересной игровой форме.

Игра «Быстрый счет»

Игра «быстрый счет» поможет вам усовершенствовать свое мышление . Суть игры в том, что на представленной вам картинке, потребуется выбрать ответ «да» или «нет» на вопрос «есть ли 5 одинаковых фруктов?». Идите за своей целью, а поможет вам в этом данная игра.

Игра «Математические матрицы»

«Математические матрицы» великолепное упражнение для мозга детей , которое поможет вам развить его мыслительную работу, устный счет, быстрый поиск нужных компонентов, внимательность. Суть игры заключается в том, что игроку предстоит из предложенных 16 чисел найти такую пару, которая в сумме даст данное число, например на картинке ниже данное число «29», а искомая пара «5» и «24».

Игра «Числовой охват»

Игра «числовой охват» нагрузит вашу память во время занятий с данным упражнением.

Суть игры – запомнить цифру, на запоминание которой отводится около трех секунд. Затем нужно ее воспроизвести. По мере прохождения этапов игры, количество цифр растет, начинаете с двух и далее.

Игра «Угадай операцию»

Игра «Угадай операцию» развивает мышление и память. Главная суть игры надо выбрать математический знак, чтобы равенство было верным. На экране даны примеры, посмотрите внимательно и поставьте нужный знак «+» или «-», так чтобы равенство было верным. Знак «+» и «-» расположены внизу на картинке, выберите нужный знак и нажмите на нужную кнопку. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Упрощение»

Игра «Упрощение» развивает мышление и память. Главная суть игры надо быстро выполнить математическую операцию. На экране нарисован ученик у доски, и дано математическое действие, ученику надо посчитать этот пример и написать ответ. Внизу даны три ответа, посчитайте и нажмите нужное вам число с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Быстрое сложение»

Игра «Быстрое сложение» развивает мышление и память. Главная суть игры выбирать цифры, сумма которых равна заданной цифре. В этой игре дана матрица от одного до шестнадцати. Над матрицей написано заданное число, надо выбрать цифры в матрице так, чтобы сумма этих цифр была равна заданной цифре. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Визуальная геометрия»

Игра «Визуальная геометрия» развивает мышление и память. Главная суть игры быстро считать количество закрашенных объектов и выбрать его из списка ответов. В этой игре на экране на несколько секунд показываются синие квадратики, их надо быстро посчитать, потом они закрываются. Снизу под таблицей написаны четыре числа, надо выбрать одно правильное число и нажать на него с помощью мышки. Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Игра «Математические сравнения»

Игра «Математические сравнения» развивает мышление и память. Главная суть игры сравнить числа и математические операции. В этой игре надо сравнить два числа. На верху, написан вопрос, прочитайте его и ответьте правильно на поставленный вопрос. Ответить можно при помощи кнопок расположенных внизу. Там нарисованы три кнопки «левое», «равно» и «правое». Если вы ответили правильно, вы набираете очки и продолжаете играть дальше.

Развитие феноменального устного счета

Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет.

Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.

Скорочтение за 30 дней

Увеличьте скорость чтения в 2-3 раза за 30 дней. Со 150-200 до 300-600 слов в минуту или с 400 до 800-1200 слов в минуту. В курсе используются традиционные упражнения для развития скорочтения, техники ускоряющие работу мозга, методика прогрессивного увеличения скорости чтения, разбирается психология скорочтения и вопросы участников курса. Подходит детям и взрослым, читающим до 5000 слов в минуту.

Секреты фитнеса мозга, тренируем память, внимание, мышление, счет

Мозгу, как и телу нужен фитнес. Физические упражнения укрепляют тело, умственные развивают мозг. 30 дней полезных упражнений и развивающих игр на развитие памяти, концентрации внимания, сообразительности и скорочтения укрепят мозг, превратив его в крепкий орешек.

Деньги и мышление миллионера

Почему бывают проблемы с деньгами? В этом курсе мы подробно ответим на этот вопрос, заглянем вглубь проблемы, рассмотрим наши взаимоотношения с деньгами с психологической, экономической и эмоциональных точек зрения. Из курса Вы узнаете, что нужно делать, чтобы решить все свои финансовые проблемы, начать накапливать деньги и в дальнейшем инвестировать их.

Знание психологии денег и способов работы с ними делает человека миллионером. 80% людей при увеличении доходов берут больше кредитов, становясь еще беднее. С другой стороны миллионеры, которые всего добились сами, снова заработают миллионы через 3-5 лет, если начнут с нуля. Этот курс учит грамотному распределению доходов и уменьшению расходов, мотивирует учиться и добиваться целей, учит вкладывать деньги и распознавать лохотрон.

С лучшей бесплатной игрой учится очень быстро. Проверьте это сами!

Учить таблицу умножения — игра

Попробуйте нашу обучающую электронную игру. Используя её, вы уже завтра сможете решать математические задачи в классе у доски без ответов, не прибегая к табличке, чтобы умножить числа. Стоит только начать играть, и уже минут через 40 будет отличный результат. А для закрепления результата тренируйтесь несколько раз, не забывая о перерывах. В идеале – каждый день (сохраните страницу, чтобы не потерять). Игровая форма тренажера подходит как для мальчиков, так и для девочек.

Смотрите ниже шпаргалки в полной форме.

Умножение прямо на сайте (онлайн)

*
Таблица умножения (числа от 1 до 20)

×	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
1	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
2	2	4	6	8	10	12	14	16	18	20	22	24	26	28	30	32	34	36	38	40
3	3	6	9	12	15	18	21	24	27	30	33	36	39	42	45	48	51	54	57	60
4	4	8	12	16	20	24	28	32	36	40	44	48	52	56	60	64	68	72	76	80
5	5	10	15	20	25	30	35	40	45	50	55	60	65	70	75	80	85	90	95	100
6	6	12	18	24	30	36	42	48	54	60	66	72	78	84	90	96	102	108	114	120
7	7	14	21	28	35	42	49	56	63	70	77	84	91	98	105	112	119	126	133	140
8	8	16	24	32	40	48	56	64	72	80	88	96	104	112	120	128	136	144	152	160
9	9	18	27	36	45	54	63	72	81	90	99	108	117	126	135	144	153	162	171	180
10	10	20	30	40	50	60	70	80	90	100	110	120	130	140	150	160	170	180	190	200
11	11	22	33	44	55	66	77	88	99	110	121	132	143	154	165	176	187	198	209	220
12	12	24	36	48	60	72	84	96	108	120	132	144	156	168	180	192	204	216	228	240
13	13	26	39	52	65	78	91	104	117	130	143	156	169	182	195	208	221	234	247	260
14	14	28	42	56	70	84	98	112	126	140	154	168	182	196	210	224	238	252	266	280
15	15	30	45	60	75	90	105	120	135	150	165	180	195	210	225	240	255	270	285	300
16	16	32	48	64	80	96	112	128	144	160	176	192	208	224	240	256	272	288	304	320
17	17	34	51	68	85	102	119	136	153	170	187	204	221	238	255	272	289	306	323	340
18	18	36	54	72	90	108	126	144	162	180	198	216	234	252	270	288	306	324	342	360
19	19	38	57	76	95	114	133	152	171	190	209	228	247	266	285	304	323	342	361	380
20	20	40	60	80	100	120	140	160	180	200	220	240	260	280	300	320	340	360	380	400

Как умножать числа столбиком (видео по математике)

Чтобы потренироваться и быстро выучить, можно также попробовать умножать числа столбиком.

Тема: Таблица умножения и деления на 2. (Урок закрепления)

Цель: закрепление вычислительных навыков таблицы умножения и деления.

Задачи урока:

1. Закрепить знания таблицы умножения и деления; отрабатывать умение решать составные задачи; продолжать формировать вычислительные навыки.

2. Развивать логическое и экономическое мышление; умение делать выводы, обобщать.

3. Работая в группах, воспитывать такие качества личности, как сотрудничество, взаимовыручка, толерантность; уважение к труду и людям труда.

Тип урока : урок совершенствования и закрепления навыков.

Ход урока.

1. Оргмомент. Психологический настрой учащихся.

Прозвенел звонок, начинается урок.

— Ребята, представьте себе, что ваши ладошки- это маленькое зеркальце, посмотрите в него, улыбнитесь себе- вы видите, какие вы симпатичные и умные! Посмотрите друг на друга, улыбнитесь, и ваше настроение будет бодрым и приподнятым, вам захочется узнавать новое, ведь это так интересно!

Жил мудрец, который знал всё.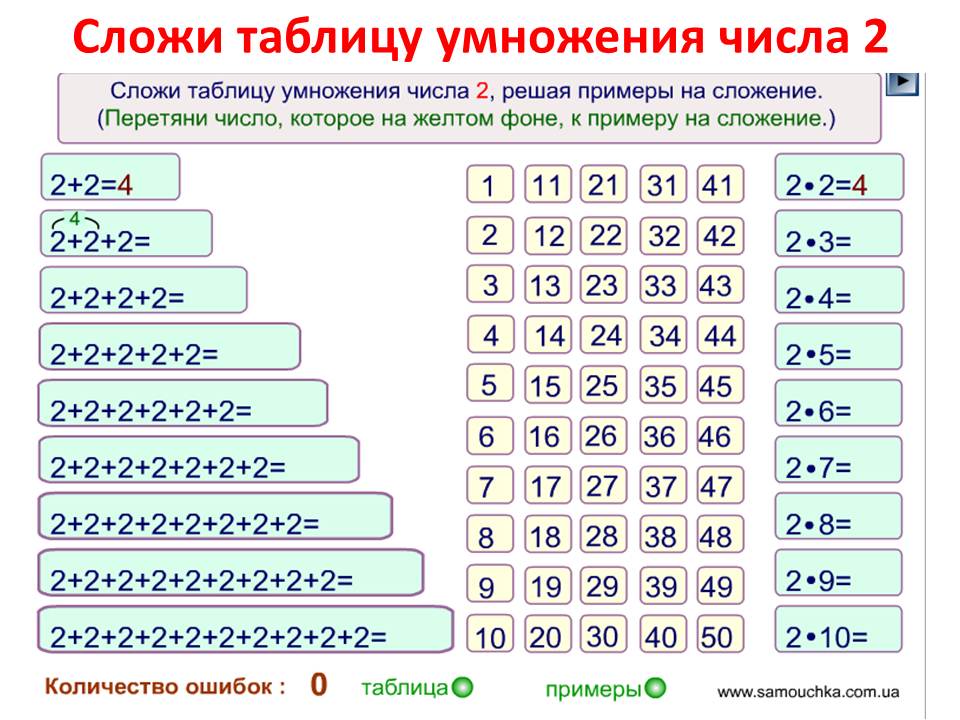 Один человек решил доказать, что мудрец знает не всё. Зажав в ладонях бабочку, он спросил: «Скажите, мудрец, какая бабочка у меня в руках: мёртвая или живая?» А сам думает: «Скажет живая — я ее умертвлю, скажет мёртвая — выпущу». Мудрец, подумав, ответил: «Все в твоих руках».

Ваши знания тоже в ваших руках. Давайте мы это и докажем своей работой на уроке.

(Слайд 1)

II. Актуализация опорных знаний.

Чтобы работать быстро и ловко

Нам нужна для ума тренировка.

а) Какое число лишнее? (Слайд 2)

Какое задание нужно выполнить с числами? (Убрать лишнее число)

7 14 21 27 28 35 42 49

5 10 11 15 20 25 30 35

4 8 12 16 17 20 24 28

Знание чего вам понадобились, чтобы выполнить задание? (Талицы умножения)

Оценивание.

б) Назови слово.

Я предлагаю вам по вопросам узнать тему сегодняшнего урока.

1. Действие, которым можно заменить сумму одинаковых слагаемых (умножение)

2. Число, на которое делят (делитель)

3. Число, которое делят (делимое)

4. Результат действия при умножении (произведение)

5. Результат действия при делении (частное)

6. Компонент действия умножения (множитель)

Слайд 3. Оценивание.

III. Самостоятельное формулирование темы и цели урока. Целевая установка на урок.

Кто догадался, какая тема урока?

Таблица умножения и деления.

Ребята, какую цель поставим перед собой?

Слайд 4

Сегодня закрепим знание таблицы умножения и деления, будем применять таблицу для решения задач, уравнений, нахождения значения выражения.

Проблемный вопрос.

А как вы думаете, можно ли, повторяя и закрепляя, узнать что-то новое? Нам надо разобраться.

4. Устный счет

1. Постановка проблемы. Загадка.

Чтобы узнать, о чем сегодня будет идти речь, вам надо будет отгадать русскую народную загадку “Лежит кучка поросят, кто ни тронет — завизжат”. Сомневаетесь в ответе? А мы сейчас решим эту проблему, выполнив вычисления.

Слайд 5

Что перед нами? (блок-схема)

Как мы будем выполнять вычисления? (по алгоритму)

Что такое алгоритм? (выполнение действий по порядку)

Записанные числа 13, 4, 8, 17, 5 записать в порядке возрастания (4, 5, 8, 13, 17)

Слайд 6

Какое слово получилось? (пчёлы)

О ком ещё будем говорить на уроке?

Оценивание.

Слайд 7

Ребята, пчёлы — неутомимые труженики. А отрасль с/х — пчеловодство. Чем занимается эта отрасль? (разводом пчел)

Человек, какой профессии занимается разводом пчел? (пчеловод).

Ребята, а есть ли у вас в селе пчеловод?

Как вы думаете, всё ли знает он о пчёлах? (да)

Главное в этой профессии, что пчеловод должен знать всё о пчёлах.

А что вы знаете о пчёлах?

К сожалению все о пчелах мы знать не можем, но постараемся узнать как можно больше. Я уверена, что у вас все получится.

Сегодня одна из пчел будет сопровождать нас на уроке. Итак, в путь за пчелой.

Работа в парах. Нахождение значения выражений с переменными.

— Наша дорога начинается от улья. На пасеке обычно находится много ульев. В каждом улье есть свой вход — леток. Для того, чтобы открыть леток, нам нужно выполнить задание. Какую цель мы поставим выполняя это задание? (выполнить выражения переменной) -Что такое выражение с переменной?

Оценивание. Взаимопроверка и самопроверка по эталону.

Слайд 8

Вы замечательно знаете таблицу умножения и деления, леток в ульях открыт и не случайно наши ульи оказались именно таких цветов. (Желтый, синий, белый). Других цветов пчела просто не различает. Но зато она видит ультрафиолетовые лучи, которые нашим глазам неподвластны.

IV. Логическая задача.

А знаете ли вы, сколько глаз у пчелы? (нет)

Давайте устно посчитаем.

У пчелы столько глаз, сколько у тебя, еще раз столько, да еще полстолька. (У пчелы 5 глаз. 2 больших, состоящих в свою очередь из 10 тыс глазков, и расположенных по бокам головы и 3 маленьких на лбу между ними)

V. Работа над закреплением пройденного материала.

1. Математический диктант. Работа в тетрадях.

Пчеловоды ульям на пасеке обычно присваивают свои номера. Такие номера есть и на нашей пасеке. — Но мы их узнаем, когда выполним задание. Записать только ответы.

1) Произведение чисел 2 и 4

2)Увеличь 2 в 9 раза

3) Во сколько раз 14 больше 2

4)1 множитель 2, второй такой же. Произведение?

5)Уменьши 20 в 2 раз

6)Какое число уменьшили в 2 раза, если получили 5

7)На сколько умножили 8, если получили 16

Слайд 9

8 18 7 4 10 10 2

Оценивание. Взаимопроверка со слайда.

2. Выступление о пчёлах. (Рубан Ваня.)

Здравствуйте, ребята! Я рабочая пчела. Мы производим воск, прополис, ценнейшее лекарство — мед и пергу. Перга — это пчелиный хлеб из пыльцы и нектара. Его едим мы, пчелы.

А что вы знаете про пчелиную семью? (Главная в пчелиной семье — матка — она королева. Остальные пчелы рабочие. Они выполняют работу сторожей, чистильщиков ячеек, вентиляторщиков, сборщиков нектара, строителей ячеек. Живут с ними и трутни, которые ничего не делают, но нужны для продолжения рода.)

3. Запись выражений и нахождение их значений. Слайд 10

Пчеле пора на работу. Во сколько начинается рабочий день ученика? (8 час) Как вы определяете время? (по часам)

Пчела хорошо ориентируется во времени. Для этого ей не нужны ни часы, ни солнце. Ей необходимы цветы. Она вылетает тогда, когда начинают работать цветочные часы.

Как вы понимаете мои слова?
Вот и мы поработаем с цветами и найдем значения выражений. Первое число в математическом выражении показывает время, когда цветок “просыпается”, найденный вами ответ — когда “засыпает”.

Что важно знать, чтобы выполнить это задание? (порядок действий)

Шиповник 2*7-10:2=

Мак 5+ 7*2 — 11=

Оценивание. Взаимопроверка.

4. Задание на нахождение периметра прямоугольника. Слайд 11

Что мы видим на слайде? (рамка)

Для чего она нужна пчеловоду?

Какую работу мы можем выполнить? (найти стороны и периметр прямоугольника).

S — 12 дм 2

Длина — 3 дм

Какие формулы помогли?

Формулы нахождения периметра, площади.

Что ёщё помогло?

Таблица умножения и деления.

5. Дифференцированная работа.

Работа по учебнику № 2 (сильные учащиеся) Взаимопроверка.

Работа по карточкам (слабые учащиеся) Самопроверка.

5. Работа над задачей. (Карточки)

Пчёлы-такие труженицы! И мы решим о них задачу.

Прочитайте задачу, к ней есть несколько вариантов решения. Нужно выбрать одно правильное решение, пометить его плюсом. Объяснить свой выбор.

Задача . С одного улья дядя Витя выкачал 7 кг меда, а с другого в 2 раза больше. Сколько всего кг меда дядя Витя выкачал с двух ульев?

Слайд 12

VII. Итог урока.

Наш урок подходит к концу. В начале урока я вас спрашивала, можно ли на уроке повторения и закрепления узнать что-то новое. К какому выводу вы пришли?

Что нового вы узнали на уроке? (отрасль — пчеловодство, профессия — пчеловод. Чем больше пчел вылетит на работу, тем больший урожай мы соберем, тем краше будет наша Земля от благоухающих цветов.)- Чему учились?

Наша пчелка вас благодарит за работу.

Понравилось ли вам сотрудничать, работая в парах, коллективно?

Вы тоже сегодня трудились, как пчелки, и мне очень понравилось работать вместе с вами.

Ни для кого не секрет, как важно знание таблицы умножения и деления, в частности при выполнении арифметических расчётов и решении примеров по математике .

Однако, что если ребёнка пугает этот огромный набор цифр, именующийся «Таблицей умножения и деления », а уж знать его наизусть, представляется совсем непосильной задачей?

Тогда спешим успокоить – Выучить всю таблицу умножения очень просто! Для этого необходимо запомнить всего лишь 36 комбинаций чисел (связки трех чисел) . Здесь мы не учитываем умножение на 1 и 10, так как это является элементарным действием не требующим особых усилий в запоминании.

Описание работы онлайн тренажера

Данный тренажер работает на основе специально разработанного алгоритма повышения сложности примеров: начиная с самых простых цифр «2 x 2», постепенно повышая сложность до «9 x 9». Тем самым плавно завлекая в процесс изучения.

Таким образом, запоминать таблицу умножения придётся небольшими порциями, что существенно снизит нагрузку, так как дети будут направлять своё внимание всего лишь на несколько примеров, забыв про весь «большой» объём.

В Тренажере есть меню настроек для выбора режима изучения таблицы. Имеется возможность выбора дейстия — «Умножение» или «Деление», диапазона примеров «Вся таблица» или «На какое-то число». Все это является рассширенным функционалом сайта и доступно после оплаты .

Каждый новый пример сопровождается справочной подсказкой , так ребёнку будет легче начать своё изучение и запоминать новые неизвестные ему комбинации.

Если же по ходу обучения, какой либо пример вызывает трудность, можно быстро напомнить себе его результат, воспользовавшись дополнительной подсказкой , это поможет эффективнее справляться с запоминанием трудных примеров.

Процентная шкала быстро даст вам понять каким уровнем знания таблицы умножения Вы обладаете.

Пример считается полностью выученным, если правильный ответ был дан 4 раза подряд . Однако при достижении 100% , призываем не бросать изучение, а вернуться на следующий день и освежить свои знания, повторно пройдя все примеры. Ведь именно регулярные занятия развивают память и закрепляют навыки!

Описание интерфейса онлайн тренажера

Во-первых, в тренажере присутствует «панель быстрого доступа», включающая в себя 4 кнопки. Они позволяют: перейти на главную страницу сайта, включить или отключить звуковые сигналы, сбросить результаты обучения (начать изучение сначала), а также попать на страницу отзывов и комментариев.

Во-вторых, это основная структура программы.

Выше всех находится процентная шкала , отобржающая примерный уровень знания таблицы умножения.

Ниже идет поле с примером , на который необходимо дать ответ. Во время ответа оно будет изменять свой цвет: станет красным — если был дан неверный ответ, зеленым — в случае правильного, голубым — после использования подсказки, и желтоватым — во время показа нового примера.

Следом располагается строка сообщений . В ней выводятся текстовая информация об ошибках, правильных ответах, а также справочной и дополнительной подсказками.

В конце находится экранная клавиатура , содержащая только необходимые для работы кнопки: все цифры, «забой» — если нужно исправить ответ, кнопки «Проверить» и «Дополнительная подсказка».

Мы уверены, что данный тренажер «Таблица умножения за 20 минут», поможет .

  Поиск Поиск

• Школьный помощник
  • математика 5 класс
  • математика 6 класс
  • алгебра 7 класс
  • алгебра 8 класс
  • геометрия 7 класс
  • русский язык 5 класс
  • русский язык 6 класс
  • русский язык 7 класс
• математика
• алгебра
• геометрия
• русский язык

«»

следующая предыдущая вернуться на предыдущую страницу

Такой страницы нет !!!

• Популярные запросы
  • Обстоятельство
  • Дополнение
  • Определение
  • Деление дробей
  • Русский язык 7 класс
  • Русский язык 6 класс
  • Математика 6 класс
  • Алгебра 8 класс
  • Русский язык 5 класс
  • Математика 5 класс
  • Наименьшее общее кратное
  • Алгебра 7 класс
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Наибольший общий делитель. Взаимно простые числа
  • Буквы о и а в корнях -кос- / -кас-; -гор- / — гар-; -клан- / -клон-; -зар- / -зор-
  • Деление и дроби
  • Квадратный корень из неотрицательного числа
  • Доли. Обыкновенные дроби
  • Окружность и круг
  • Антонимы. Синонимы
  • Десятичная запись дробных чисел
  • Буквы о – а в корнях -лаг- / -лож-, -рос- / -раст- (-ращ-)

Распределительное свойство сложения и умножения (с примерами)

Обновлено 21 декабря 2020 г.

Мэри Лоуджи

Когда вы изучаете алгебру и смотрите на сложные математические уравнения, вы можете чесать голову. Это очень помогает разбить уравнения на более мелкие части для решения уравнения. Закон о распределительной собственности — инструмент, который вам в этом поможет. Он используется в продвинутом умножении, сложении и алгебре.

Совет: Распределительное свойство сложения и умножения гласит, что:

a × (x + y) = ax + ay

Или, чтобы дать конкретный пример:

3 × (4 + 5) = 3 × 4 + 3 × 5

Что такое распределительная собственность?

Свойство распределения позволяет вам, по сути, перемещать некоторые числа в сложных математических уравнениях всех типов.Если число умножается на два числа в скобках, вы можете решить эту проблему, отдельно умножив первое число на числа в скобках, а затем завершив сложение. Например:

a × (x + y) = ax + ay

3 × (4 + 5) = 3 × 4 + 3 × 5

Разбивка сложного уравнения на более мелкие части упрощает его решение. и упрощает переваривание информации в меньших объемах.

Что такое распределительное свойство сложения и умножения?

К распределительному свойству обычно впервые обращаются студенты, когда они начинают сложные задачи умножения, то есть при сложении или умножении вы должны нести единицу.Это может быть проблематично, если вам придется решать ее в уме, не работая на бумаге. Помимо сложения и умножения, вы берете большее число и округляете его до ближайшего числа, которое делится на 10, а затем умножаете оба числа на меньшее число. Например:

36 × 4 =?

Это можно выразить как:

4 × (30 + 6) =?

Что позволяет использовать распределительное свойство умножения и ответить на вопрос следующим образом:

(4 × 30) + (4 × 6) =? \\ 120 + 24 = 144

Что такое распределительное свойство в простой алгебре?

То же правило перемещения некоторых чисел для решения уравнения используется в простой алгебре.Это делается путем удаления части уравнения в скобках. Например, уравнение a × ( b + c ) =? показывает, что обе буквы в скобках необходимо умножить на букву вне скобок, поэтому вы распределяете умножение a между b и c . Уравнение также можно записать в виде: ( ab ) + ( ac ) =? Например:

3 × (2 + 4) =? \\ (3 × 2) + (3 × 4) =? \\ 6 + 12 = 18

Вы также можете комбинировать некоторые числа, чтобы упростить решение уравнения.Например:

16 × 6 + 16 × 4 =? \\ 16 × (6 + 4) =? \\ 16 × 10 = 160

В качестве другого примера посмотрите видео ниже:

Дополнительные практические проблемы распределительного свойства

a × (b + c) =?

Где a = 3, b = 2 и c = 4

6 × (2 + 4) =? \\ 5 × (6 + 2) =? \\ 4 × (7 + 2 + 3) =? \\ 6 × (5 + 4) =?

Арифметические операции над функциями — объяснения и примеры

Мы привыкли выполнять четыре основных арифметических операции с целыми числами и многочленами, т.е.е., сложение, вычитание, умножение и деление.

Подобно полиномам и целым числам, функции также можно складывать, вычитать, умножать и делить, следуя тем же правилам и шагам. Хотя обозначение функций сначала будет выглядеть иначе, вы все равно получите правильный ответ.

В этой статье мы узнаем , как складывать, вычитать, умножать и делить две или более функций.

Прежде чем мы начнем, давайте познакомимся со следующими концепциями и правилами арифметических операций:

• Ассоциативное свойство: это арифметическая операция, которая дает одинаковые результаты независимо от группировки величин.
• Коммутативное свойство: это двоичная операция, в которой изменение порядка операндов не меняет конечный результат.
• Продукт: произведение двух или более величин является результатом умножения количеств.
• Частное: это результат деления одного количества на другое.
• Сумма: сумма — это сумма или результат сложения двух или более величин.
• Разница: Разница — это результат вычитания одной величины из другой.
• Сложение двух отрицательных чисел дает отрицательное число; положительное и отрицательное число дает число, подобное числу с большей величиной.
• Вычитание положительного числа дает тот же результат, что и добавление отрицательного числа равной величины, а вычитание отрицательного числа дает тот же результат, что и добавление положительного числа.
• Произведение отрицательного и положительного числа является отрицательным, а отрицательное число — положительным.
• Частное положительного и отрицательного чисел отрицательное, а отношение двух отрицательных чисел положительное.

Как добавлять функции?

Чтобы добавить функции, мы собираем похожие термины и складываем их вместе. Переменные складываются путем суммирования их коэффициентов.

Есть два метода добавления функций. Это:

Чтобы добавить функции с помощью этого метода, расположите добавленные функции в горизонтальной линии и соберите все группы похожих терминов, затем добавьте.

Пример 1

Складываем f (x) = x + 2 и g (x) = 5x — 6

Решение

(f + g) (x) = f (x) + g (x)
= (x + 2) + (5x — 6)
= 6x — 4

Пример 2

Добавьте следующие функции: f (x) = 3x ² — 4x + 8 и g (x) = 5x + 6

Решение

⟹ (f + g) (x) = (3x ² — 4x + 8) + (5x + 6)

Соберите похожие термины

= 3x ² + (- 4x + 5x) + (8 + 6)

= 3x ² + x + 14

• Вертикальный или столбчатый метод

В этом методе элементы функций расположены по столбцам, а затем добавлены.

Пример 3

Добавьте следующие функции: f (x) = 5x² + 7x — 6, g (x) = 3x² + 4x и h (x) = 9x²– 9x + 2

Решение

5x² + 7x — 6
+ 3x² + 4x
+ 9x² — 9x + 2
16x ² + 2x — 4

Следовательно, (f + g + h) (x) = 16x ² + 2x — 4

Как вычитать функции?

Чтобы вычесть функции, выполните следующие действия:

• Заключите вычитающую или вторую функцию в круглые скобки и поставьте знак минус перед скобками.
• Теперь удалите круглые скобки, изменив операторы: изменить — на + и наоборот.
• Соберите похожие термины и добавьте.

Пример 4

Вычтите функцию g (x) = 5x — 6 из f (x) = x + 2

Решение

(f — g) (x) = f (x ) — g (x)

Поместите вторую функцию в круглые скобки.
= x + 2 — (5x — 6)

Удалите скобки, изменив знак в скобках.

= x + 2 — 5x + 6

Объединить подобные термины

= x — 5x + 2 + 6

= –4x + 8

Пример 5

Вычесть f (x) = 3x² — 6x — 4 из g (x) = — 2x² + x + 5

Решение

(g -f) (x) = g (x) -f (x) = — 2x² + x + 5 — (3x² — 6x — 4)

Удалите скобки и измените операторы

= — 2x² + x + 5 — 3x² + 6x + 4

Соберите одинаковые термины

= -2x² — 3x² + x + 6x + 5 + 4

= -5x ² + 7x + 9

Как умножать функции?

Чтобы умножить переменные между двумя или более функциями, умножьте их коэффициенты, а затем сложите показатели переменных.

Пример 6

Умножить f (x) = 2x + 1 на g (x) = 3x ² — x + 4

Решение

Применить свойство распределения

⟹ (f * g) (x) = f (x) * g (x) = 2x (3x ² — x + 4) + 1 (3x ² — x + 4)
⟹ (6x ³ — 2x ² + 8x) + (3x ² — x + 4)

Объедините и сложите похожие термины.

⟹ 6x ³ + (−2x ² + 3x ² ) + (8x — x) + 4

= 6x ³ + x ² + 7x + 4

Пример 7

Складываем f (x) = x + 2 и g (x) = 5x — 6

Решение

⟹ (f * g) (x) = f (x) * g (x)
= (x + 2) (5x — 6)
= 5x ² + 4x — 12

Пример 8

Найдите произведение f (x) = x — 3 и g (x) = 2x — 9

Решение

Применить метод FOIL

(f * g) (x) = f (x) * g (x) = (x — 3) (2x — 9)

Произведение первых членов.

= (x) * (2x) = 2x ²

Произведение крайних членов.

= (x) * (- 9) = –9x

Произведение внутренних условий.

= (–3) * (2x) = –6x

Произведение последних членов

= (–3) * (–9) = 27

Сумма частичных произведений

= 2x ² — 9x — 6x + 27

= 2x ² — 15x +27

Как разделить функции?

Так же, как и полиномы, функции можно разделить с помощью синтетических методов или методов деления в столбик.

Пример 9

Разделите функции f (x) = 6x ⁵ + 18x ⁴ — 3x ² на g (x) = 3x ²

Решение

(f ÷ g) (x) = f (x) ÷ g (x) = (6x ⁵ + 18x ⁴ — 3x ² ) ÷ (3x ² )

⟹ 6x ⁵ / 3x ² + 18x ⁴ / 3x ² — 3x ² / 3x ²
= 2x ³ + 6x ² — 1.

Пример 10

Разделите функции f (x) = x ³ + 5x ² -2x — 24 на g (x) = x — 2

Решение

Синтетическое деление:

(f ÷ g) (x) = f (x) ÷ g (x) = (x ³ + 5x ² -2x — 24) ÷ (x — 2)

• Изменить знак константы во второй функции от -2 до 2 и опустите его.

_____________________
x — 2 | x ³ + 5x² — 2x — 24

2 | 1 5 -2 -24

• Также понизьте старший коэффициент.Это означает, что 1 будет первым числом частного.

2 | 1 5 -2 -24
________________________
1

• Умножьте 2 на 1 и прибавьте 5 к произведению, чтобы получить 7. Теперь опустите 7 вниз.

2 | 1 5-2-24
2
________________________
1 7

• Умножьте 2 на 7 и прибавьте — 2 к произведению, чтобы получить 12. Приведите 12 вниз

2 | 1 5-2-24
2 14
__________________________
1 7 12

• Наконец, умножьте 2 на 12 и прибавьте -24 к результату, чтобы получить 0.

2 | 1 5-2-24
2 14 24
__________________________
1 7 12 0

Следовательно, f (x) ÷ g (x) = x² + 7x + 12

Предыдущий урок | Главная страница | Следующий урок

Задачи на умножение слов — урок для третьего класса

Это полноценный урок для третьего класса с обучением и задачами по словам с целью научить детей некоторым основам решения задач умножения слов.Основная идея состоит в том, что у нас есть групп одинакового размера , и детям нужно просто распознавать эти группы, будь то полотенца, кусочки пиццы, шарики или что-то еще. Задачи со словами в уроке также включают сложение и вычитание, поэтому учащимся нужно думать, а не применять данную операцию (умножение), даже не прочитав задачу.

---

Примеры задач

1. Напишите предложение умножения к каждой задаче и решите. Вы можете рисовать картинки, чтобы помочь вам.

а) Четверо детей вместе играют в теннис. Всего они принесли по шесть мячей. Сколько всего у них мячей?	б) Семья Смитов состоит из пяти человек. У каждого члена есть небольшое полотенце и банное полотенце. Сколько полотенец вешают в ванной?
в) Семья Джонсов заказывает четыре пиццы.Каждая пицца нарезана на четыре части. Сколько у них кусочков пиццы?	г) В городе три почтовых отделения. В каждом почтовом отделении по пять рабочие. Сколько всего сотрудников в почтовых отделениях?

Проблемы Word с двумя операциями

Мистер Джонсон обычно ест три раза в день. Как много еды он ест в обычную неделю? Опять же, у нас есть ситуация, когда КАЖДЫЙ ДЕНЬ происходит одно и то же. 7 дней × 3-х разовое питание = _____ нормальное питание неделя.

В эту пятницу он пропустил завтрак. Сколько приемов пищи он ел на этой неделе? Сейчас другой день. Это всего лишь ОДИН день, поэтому мы просто вычтите один прием пищи из общего количества. дня раз обеда забрать пропущенный завтрак 7 × 3 – 1 = ______

На следующей неделе он ел три раза в понедельник, Вторник и пятница, а в остальные дни — четыре раза.Сколько приемов пищи он ел в течение недели? Теперь у нас трижды одна ситуация, а другая ситуации четыре раза. Мы рассчитываем их отдельно, а затем Добавлять. дня раз обеда и остаток дня раз обеда 3 × 3 + 4 × 4 = ______

Примеры задач

1.Впишите числа к числовым предложениям для каждого проблема и решаем. Для последних задач напишите числовое предложение сам. Вы можете написать слова над числами, чтобы описать числа. Вы также можете рисовать картинки, чтобы помочь вам!

а. Мама купила четыре коробки для яиц, в каждой по шесть яиц. Два яйца были плохими. Сколько хороших яиц получила мамочка? яйцо картонные коробки раз яйца в каждом дубль прочь плохие × – =

б. Johnson’s снова заказал 4 пиццы, разрезанные на четыре части каждая. На этот раз собака съела один кусок. Сколько штук сделал люди едят? номер пиццы раз штуки по штуки по взять прочь что съела собака × – =

с. У Джо трое друзей, у всех по пять машинок, и еще два друга, у которых только две машины. Сколько машин у друзей Джо имеют? друзья с 5 легковых автомобилей раз 5 легковых автомобилей и друзья с 2 машины раз 2 легковых автомобиля × + × =

г. На семейном обеденном столе две тарелки на всех и только одна тарелка для маленькой Ханны. На обед пришли 10 человек и Ханна. Сколько тарелок было на столе?

ч. Есть четыре лошади и три человека. Сколько футов там всего?

---

Этот урок взят из книги Марии Миллер «Math Mammoth Multiplication 1», опубликованной на сайте www.HomeschoolMath.net с разрешения автора. Авторские права © Мария Миллер.

---

Базовое сложение, вычитание, умножение и деление

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Решение уравнений с использованием принципов сложения и умножения — видео и стенограмма урока

Принцип умножения

Принцип умножения , аналогично принципу сложения, говорит нам, что если мы умножаем или делим на число с одной стороны уравнения, нам также необходимо умножить или разделить на то же самое число с другой. сторону, чтобы уравнение оставалось прежним.По этому принципу вы можете представить себе две группы кроликов. Сейчас они равны друг другу. Но что, если кролики в одной группе родят по три кролика каждый? Будут ли две группы равны друг другу? Нет, не стали бы. Другая группа также должна будет родить такое же количество детенышей кроликов, чтобы две группы были одинаковыми.

Как мы используем этот принцип умножения? Так же, как и с принципом сложения. Если мы видим, что наша переменная умножается или делится на определенное число, мы выполняем противоположную операцию, чтобы получить нашу переменную отдельно.

Итак, чтобы продолжить решение нашей проблемы с того места, где мы остановились, 3 x = 3, мы разделим обе части нашего уравнения на 3. Если мы сделаем это, мы получим x = 1 для нашего ответа.

Проблема 1

Давайте рассмотрим другую проблему, чтобы увидеть, как все это работает вместе.

5 x — 10 = 0

Сначала мы посмотрим, что происходит с переменной. Мы видим, что переменная слева умножается на 5, а затем вычитается на 10.Что мы можем решить в первую очередь, 10 или 5? Ну а какую обратную операцию выполнить проще? Сложение или разделение? Это сложение, поэтому сначала я добавлю 10 к обеим сторонам.

5 x — 10 + 10 = 0 + 10, что упрощается до 5 x = 10.

Хорошо, теперь моя переменная умножается на 5. Теперь я могу применить принцип умножения и разделить оба значения. сторон на 5.

5 x /5 = 10/5, что упрощается до x = 2.Я закончил, и мой ответ — 2.

Задача 2

Теперь ваша очередь. Попробуй решить эту проблему со мной.

x /2 — 3 = 3

Мы видим деление на 2 и вычитание на 3. 3 — более простая операция. Чтобы удалить 3 из переменной, нам нужно выполнить противоположную операцию — сложение. Итак, мы прибавляем 3 к обеим сторонам по принципу сложения.

x /2 — 3 + 3 = 3 + 3, что упрощается до x /2 = 6.

Теперь у нас есть деление на 2. Чтобы удалить 2, мы выполняем обратную операцию и умножаем. Мы используем принцип умножения, чтобы умножить 2 с обеих сторон.

( x /2) * 2 = 6 * 2, что упрощается до x = 12.

Наша переменная сама по себе, и мы получили ответ 12.

Резюме урока

Что мы узнали ? Мы узнали, что в алгебре, когда мы хотим сохранить уравнение неизменным, манипулируя им, мы используем два принципа.Это принцип сложения и принцип умножения. Принцип сложения говорит нам, что если мы прибавляем или вычитаем число из одной части уравнения, нам также нужно прибавлять или вычитать такое же число из другой стороны, чтобы уравнение оставалось неизменным.

Принцип умножения говорит нам, что если мы умножаем или делим на число с одной стороны уравнения, нам также необходимо умножить или разделить на то же самое число с другой стороны, чтобы уравнение оставалось неизменным.Чтобы решить уравнение, в котором нам нужно выполнить оба типа операций, мы используем оба этих принципа, чтобы помочь нам решить.

Мы всегда в первую очередь занимаемся сложением или вычитанием. Затем последними мы займемся умножением или делением. Чтобы удалить числа из нашей переменной, мы всегда выполняем обратную операцию. Если мы видим сложение, мы вычитаем. Если видим вычитание, складываем. Если мы видим деление, мы умножаемся. Если мы видим умножение, мы делим.

Результаты обучения

Некоторые ожидаемые результаты этого урока включают способность:

• Понимать функции принципов сложения и умножения
• Решение проблем, связанных с практикой

Сложение и вычитание матриц и умножение матрицы на константу

При умножении матрицы на скаляр (константа или число), а также при сложении и вычитании матриц операции выполняются построчно.Давайте рассмотрим каждую операцию отдельно, чтобы увидеть, как это работает.

Содержание

1. Добавление матриц
2. Вычитающие матрицы
3. Умножение матрицы на константу (скалярное умножение)
4. Сочетание сложения, вычитания и скалярного умножения

реклама

Добавление матриц

Чтобы добавить две матрицы, добавьте соответствующие записи, как показано ниже. Обратите внимание, что вам нужно, чтобы матрицы были одинакового размера, чтобы это имело смысл.

Если матрицы разного размера, сложение не определено.

Вычитание матриц

Вычитание матриц работает точно так же. Вы можете вычесть запись за записью.

Как и в случае сложения, это не было бы определено, если бы матрицы были разных размеров. В этой ситуации ваш ответ будет просто «не определен».

Умножение матрицы на константу (скалярное умножение)

Умножение матрицы на константу или число (иногда называемое скаляром) всегда определяется независимо от размера матрицы.Вам просто нужно убедиться, что каждая запись в матрице умножена на число.

Объединение операций

В некоторых вопросах вас могут попросить объединить сложение, вычитание и умножение на константу. Здесь мы рассмотрим несколько примеров, чтобы убедиться, что вы знаете, как это сделать.

Пример

Найдите \ (- 2A + B \) для:

\ (A = \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] \) и \ (B = \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \)

Не забудьте умножать каждую запись на константу и работать с записью при сложении.

\ (\ begin {align} -2A + B & = 2 \ left [\ begin {array} {cc} -4 & 1 \\ 2 & -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} -2 \ times -4 & -2 \ times 1 \\ -2 \ times 2 & -2 \ times -2 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 & -2 \\ -4 & 4 \\ \ end {array} \ right] + \ left [\ begin { массив} {cc} 9 & -4 \\ 0 & 8 \\ \ end {array} \ right] \\ & = \ left [\ begin {array} {cc} 8 + 9 & -2 + (-4) \\ -4 + 0 & 4 + 8 \\ \ end {array} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 17 & -6 \\ -4 & 12 \\ \ end {array} \ right]} \ end {align} \)

Это также работает, когда у вас более двух матриц, как показано в следующем примере.

Пример

Найдите \ (A — 3B + 2C \) для:

\ (A = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] \), \ (B = \ left [\ begin {array} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] \) и \ (C = \ left [\ begin {array} { cc} 5 & 2 \\ 3 & 0 \\ \ end {array} \ right] \)

\ (\ begin {align} A — 3B + 2C & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — 3 \ left [\ begin {массив} {cc} 2 & 1 \\ 1 & 4 \\ \ end {array} \ right] + 2 \ left [\ begin {array} {cc} 5 & 2 \\ 3 & 0 \\ \ end { массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — \ left [\ begin {array} {cc} 3 \ times2 и 3 \ times1 \\ 3 \ times1 & 3 \ times4 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 2 \ times5 & 2 \ times2 \\ 2 \ times3 & 2 \ times0 \\ \ end {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 & 1 \\ 0 & 0 \\ \ end {array} \ right] — \ left [\ begin {array} {cc} 6 & 3 \\ 3 & 12 \\ \ end {array} \ right] + \ left [\ begin {array} {cc} 10 & 4 \\ 6 & 0 \\ \ конец {массив} \ right] \\ & = \ left [\ begin {array} {cc} 1 — 6 + 10 & 1 — 3 + 4 \\ 0 — 3 + 6 & 0 — 12 + 0 \\ \ end {массив} \ right] \\ & = \ boxed {\ left [\ begin {array} {cc} 5 & 2 \\ 3 & — 12 \\ \ end {array} \ right]} \ end {align} \ )

Сводка

Запомните следующее для операций с матрицами:

• Для сложения или вычитания переходите ввод за вводом.
• Сложение и вычитание определяются только в том случае, если матрицы одинакового размера.
• Скалярное умножение всегда определяется — просто умножьте каждый элемент матрицы на скаляр.

реклама

Продолжайте изучение матричных операций

Далее: Умножение матриц

Подпишитесь на нашу рассылку!

Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.

Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!

Связанные

Десятичные и целые числа — свойства целых чисел

те же известные свойства целых чисел применимы и к целым числам. Если ты как и многие студенты, всякий раз, когда вы видите одно из этих «свойств», вы стонете внутри и думаете: «Зачем мне это учить?» Вы не поверите, но свойства чисел не изобрели злые математики. мучить студентов-математиков! Это основные правила нашей математической системы, и вы будете использовать их всю оставшуюся жизнь.Очень важно, чтобы ты понять, как применять каждый из них при решении математических задач. Когда ты переходя к алгебре, вы будете использовать эти свойства снова и снова! Давайте рассмотрим каждый подробно и простым языком.

Коммутативное свойство сложения
Коммутативное свойство Свойство сложения говорит о том, что мы можем складывать числа в любом порядке. Ты можешь вспомнить коммутативное свойство, думая о числах «коммутирующих», или меняются местами.Этот пример показывает нам, что «два отрицательных плюс положительный «четыре» означает «четыре плюс два».

-2 + 4 = 4 + (-2)

Коммутативный свойство умножения
Коммутативность умножения очень похожа. Он говорит, что мы можем умножать числа в любом порядке, не меняя результата. В пример показывает нам, что «отрицательное дважды положительное четыре» — это то же самое, что «положительный четыре раза отрицательный два.«

-2 (4) = 4 (-2)

Ассоциативный свойство сложения
Ассоциативное свойство сложения говорит нам, что мы можем группировать числа в сумма, как мы хотим, и все равно получим тот же ответ. Вы можете вспомнить ассоциативное свойство, думая о двух числах, связанных друг с другом, а затем один уходит, чтобы связать с другим числом.

Пример показывает нам, что мы можем сложить «два отрицательных и четыре положительных». вместе, а затем прибавьте эту сумму к положительным трем, чтобы получить окончательный ответ, или мы можем сначала сложить «положительные четыре и положительные три» а затем прибавьте эту сумму к отрицательным двум, чтобы получить окончательный ответ.Ответ будет таким же независимо от того, как мы это сделаем.

(-2 + 4) + 3 = -2 + (4 + 3)

Ассоциативный свойство умножения
Ассоциативное свойство умножения говорит нам, что мы можем группировать числа в продукте любым желаемым образом и при этом получаем тот же ответ.

Пример показывает нам, что мы можем перемножить «два отрицательных и четыре положительных». вместе, а затем умножьте это произведение на положительное три, чтобы получить окончательный ответ, или мы можем умножить «положительные четыре и положительные три» вместе сначала, а затем умножьте полученный результат на два отрицательных, чтобы получить окончательный ответ.Ответ будет одним и тем же независимо от того, как мы это сделаем.

-2 (4) x 3 = -2 (4 x 3)

Распределительный недвижимость
Распределительное свойство вступает в игру, когда выражение, включающее сложение затем на что-то умножается. Он говорит нам, что мы можем сначала добавить, а затем умножьте или сначала умножьте, а затем сложите. В любом случае умножение «распределено» по всем терминам в круглых скобках.

В этом примере мы можем либо сначала сложить числа в скобках — 4 + 3 — а затем умножьте результат на -2 ; или мы можем умножить -2 и каждый термин отдельно, а затем сложите два продукта вместе. Ответ то же самое в обоих случаях.

-2 (4 + 3) = (-2 х 4) + (-2 х 3)

Часы вне!

Вычитание не является ни коммутативным, ни ассоциативным.

Дивизия ни коммутативные, ни ассоциативные.

Примеры

1. Мы можем добавить номера в любом порядке. (Коммутативное свойство сложения.)

-2 + 4 = 4 + -2

2. Мы умеем умножать номера в любом порядке. (Коммутативное свойство умножения)

-2 х 4 = 4 х-2

3.Мы можем сгруппировать числа в сумме, как мы хотим. (Ассоциативное свойство сложения.)

(-2 + 4) + 3 = -2 + (4 + 3)

4. Мы можем сгруппировать номера в продукте так, как мы хотим. (Ассоциативное свойство умножения)

(-2 х 4) х 3 = -2 х (4 х3)

5. С этим типом выражения, мы можем сначала сложить, а затем умножить,

ИЛИ

сначала умножить, затем добавьте.(Распределительное свойство умножения над сложением.)

-2 х (4 + 3) = (-2 х 4) + (-2 х 3)

назад наверх

.