Карточки по математике. 1 класс. Состав чисел 1-10. | Учебно-методический материал по математике (1 класс) на тему:

Вставь пропущенные числа. …2 …. 4……….7 8 9. Запиши соседей чисел. ….4….        …. 7 ….   … 8…   …. 5 …. Сравни. 4+3….2+4       8-3…3+3       10-2….3+4      7-3….2+5       9-3…3+5        7+2….8-2 Заполни таблицу. Уменьшаемое   7 7 7 7 7 7 7 Вычитаемое 7 2 6 4 1 5 3 Разность Вставь пропущенные знаки.          7      4 = 3        1     6 = 7        7      1 = 6          7      2 = 5        4     3 = 7        2      5 = 7   В книге 8 рассказов. Юра прочитал 3 рассказа. Сколько рассказов осталось прочитать? Прочитал  – Осталось – _________________________ Ответ: ________________________. * Запиши любое число, которое меньше разности 7 и 4. ___________ Запиши любое число, которое больше разности 2 и 6 ___________ Запиши любое число, которое меньше разности 5 и 3. ___________ Запиши любое число, которое больше разности 10 и 8. ___________ Работа № 11 1. Запиши ответы в строчку. А. разность чисел 7 и 3. Б. сумма чисел 3 и 2. В. число, которое меньше 5 на 4. Г. увеличь 4 на 4. Д. уменьши 9 на 7. Е. на сколько 4 меньше 6. Ж. на сколько 6 больше 1.           __________________________________________ Заполни таблицу. Уменьшаемое   9 9 9 9 9 9 9 Вычитаемое 5 3 1 7 Разность 2 4 6 Вставь пропущенные числа, чтобы записи были верными. 5+….=8          4+…=9          2+….=9 …- 6=4           7- …=3          8-….=4 Запиши 3 примера, у которых сумма равна 8. В маршрутном такси ехали 10 человек. На остановке вышли 5 человек, а вошли 3. Сколько человек едет дальше? Ответ: _______________________ Работа № 9а 2+2= 8-2= 9-3= 3+2=             6-2= 10-7= 1+2=               4-2= 10-4= 7+2=               10-2= 10-5= 8+2=               8-6= 10-1= 4+2=               6-4= 9-2= 6+2=               10-8= 9-7= 5+2=               4-2= 8-4= 2+1=               5-2= 10-6= 2+5=               7-5= 10-3= 2+8=               3-2= 10-8= 2+1= 9-2= 10-9= 2+2= 7-2= 10-2= 2+7= 9-2= 10-7= 2+6= 5-2= 10-4= 2+3= 6-2= 10-6= 2+4= 6-4= 10-9= 2+0= 2-2= 10-5= Работа № 11 а. 4+5= 8-5= 6-3= 3+5=             6-5= 10-7= 1+5=               4-4= 10-2= 6+2=               10-5= 10-5= 3+2=               8-5= 10-1= 4+5=               6-5= 9-8= 6+2=               10-8= 9-7= 5+1=               5-2= 8-5= 3+3=               5-3= 9-6= 2+5=               7-5= 10-3= 1+5=               6-5= 10-8= 2+5= 5-4= 10-9= 3+5= 5-2= 10-5= 2+5= 9-5= 10-7= 5+4= 5-4= 10-4= 5+3= 6-5= 10-6= 5+5= 6-4= 10-3= 1+5= 5-5= 10-5=

Запиши ответы в строчку. А. разность чисел 10 и 5. Б. сумма чисел 3 и 6. В. число, которое меньше 8 на 4. Г. увеличь 6 на 4. Д. уменьши 9 на 1. Е. на сколько 5 меньше 8. Ж. на сколько 6 больше 3. __________________________________________ Заполни таблицу. Уменьшаемое   8 8 8 8 8 8 8 Вычитаемое Разность 3 5 2 4 1 6 7 Сравни. 6+3…..8-4       8-6…1+1       10-3…10-7 7-6……9-8       6-4…5-3        8-5…..9-6 Вставь пропущенные знаки. 8….3=5        9…2=7       7…3=10 6….1=5        5…4=1        2…6=8 Бабушка собрала 9 кг клубники. Из 6 кг сварили компот. Сколько килограммов  клубники осталось? Сварила — __________ Осталось — _________ __________________________ Ответ: _________________________________. Работа № 12 Запиши ответы в строчку. А. найди сумму 3 и 6. Б. на сколько 7 меньше 8. В. что прибавили к 2, чтобы получить 10. Г. первое слагаемое – 3, чему равно второе, если        сумма равна 6. Д. найди сумму 2 и 3. Е. найди разность 8и 5.          ______________________________________ Подчеркни примеры с ответом 8. 3+5           10-2           8-4 7-3            3+6            9-6 9-1            1+7            10-6 Вставь подходящее число. 3+4>….         8-4…… 4+6…..           2+3 Заполни таблицу. Уменьшаемое   9 9 9 5 Вычитаемое 5 3 4 1 3 4 Разность 5 2 4 6 У Кати 5 леденцов и 3 батончика. Сколько конфет у Кати? Леденцы -__________ Батончики -_________ ________________________________ Ответ: _________________________ Работа № 10 а. 2+5= 8-5= 6-3= 3+5=             6-5= 10-7= 1+5=               4-4= 10-2= 5+2=               10-5= 10-5= 3+2=               8-5= 10-1= 4+5=               6-5= 9-8= 6+2=               10-8= 9-7= 5+1=               5-2= 8-5= 2+3=               5-3= 9-6= 2+5=               7-5= 10-3= 5+5=               6-5= 10-8= 2+5= 5-4= 10-9= 1+5= 5-2= 10-5= 3+5= 9-5= 10-7= 5+4= 5-4= 10-4= 5+3= 6-5= 10-6= 5+5= 6-4= 10-3= 1+5= 5-5= 10-5= Работа № 12 а. 3+3= 3-1= 10-3= 7+3=             6-4= 8-7= 5+2=               4-4= 8-4= 6+2=               2-1= 9-5= 9-3=               8-8= 9-1= 10-2=               6-5= 6-2= 6+1=               10-6= 8-7= 7-6=               4-2= 5-3= 6-2=               5-2= 10-6= 4+5=               7-6= 10-3= 3+4=               8-4= 10-8= 4+1= 9-5= 9-8= 4+2= 10-3= 8-7= 5+5= 10-8= 8-5= 3+2= 10-9= 6-3= 5-1= 6-3= 2-1= 8-2= 8-4= 10-1= 6-1= 9-4= 10-5=

Пропущенные цифры — Подготовка к школе и развивающие задания для детей Мама7я

Вставь пропущенные цифры

Вставь пропущенные цифры так, чтобы получился верный результат.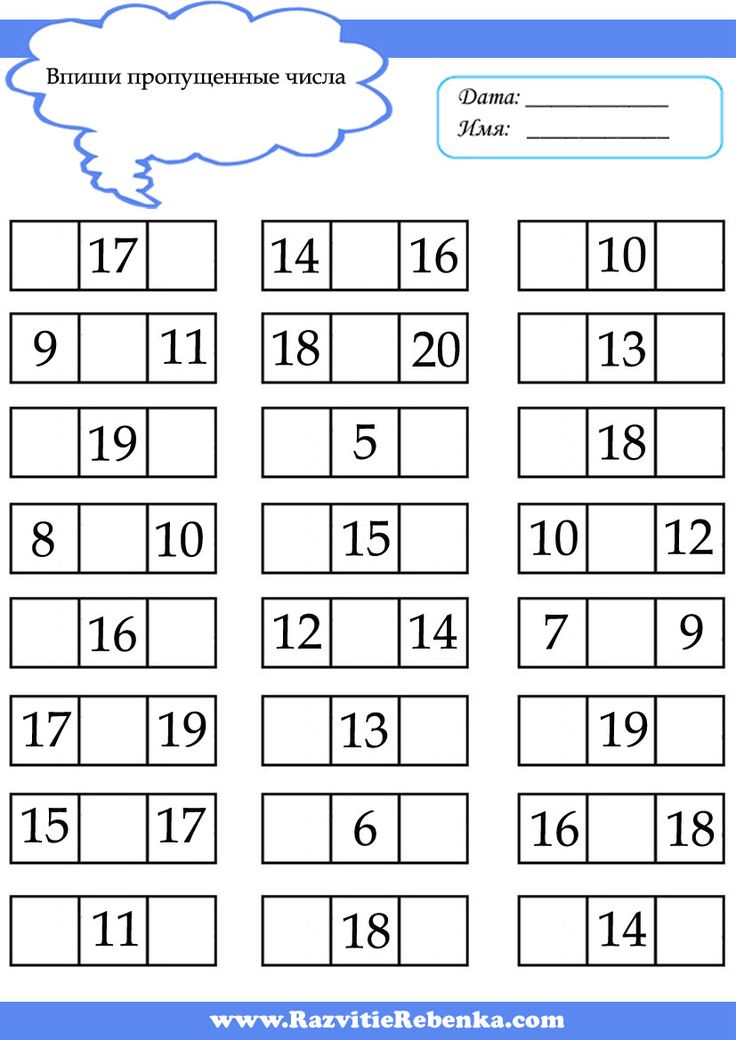 Вставляя пропущенные цифры дети закрепляют изучение цифр. Разнообразные упражнения на вставку пропущенных цифр дают детям разнообразие в математичеких занятиях.

На проведение учебных занятий по вставке пропущенных цифр необходим четкий план, так как ребенок должен знать весь ряд цифр, ведь если он не усвоит все цифры, то ему будет сложно понять какая цифра пропущена в задании.

Запиши пропущенные цифры

Вставляя пропущенные цифры ребёнок запоминает последовательность самих чисел. Вставляя пропущенные цифры ребёнок тренируют внимание, мышление и память. К данному разделу нужно переходить когда ребёнок уже хорошо знает числа. Хорошее знание прямого и обратного счёта помогут ребенку быстро выполнить задание вставить пропущенные цифры.

Восстанови пропущенные цифры

Задание: Восстанови пропущенные цифры, чтобы вычисления стали верными. 

Сложение чисел:

1. 1 + ? = 3
2. 1 + ? = 4
3. 1+ ? = 5
4. 1+ ? = 6
5. 1 + ? = 7
6. 1+ ? = 8
7. 1+ ? = 9
8. 1 + ? = 10
9. 2 + ? = 3
10. 3 + ? = 4

Впиши пропущенные цифры

• 13 , _ , 15 , _ , 17 , _ , 19 , _ , 21
• 21 , _ , 23 , _ , 25 , _ , 27 , _ , 29
• 30 , _ , 32 , _ , 34 , _ , 36 , _ , 38 , _ , 40
• 41 , _ , 43 , _ , 45 , _ , 47 , _ , 49 , _ , 51

Какие цифры пропущены

Перед вами цифры, определите какие цифры пропущены и допиши их:

• 2 4 6 8 9 10
• 3 6 9 12 15
• 4 8 12 16 20

Задания пропущенная цифра

1. Помоги зайчику правильно вставить пропущенные цифры в ленте с шариками.
2. Догадайся какие цифры пропущены и запиши их в нужные места.
3. Запиши недостающие цифры в домики

Поставь пропущенные цифры

Определи какие цифры пропущены и поставь их на свои места:

• 9 — 2 _ + 3 _ — 1 _ + 2 _ — 4 = _
• 6 + 4 _ — 3 _ + 1 — _ 6 + _ = _

Определите какая цифра пропущена

Определив какая цифра пропущена, впиши ее и проверь вычисления еще раз.

• 1 + ? = 2
• 2 + ? = 4
• 3 + ? = 6
• 4 + ? = 8
• 5 + ? = 10
• 6 + ? = 12
• 7 + ? = 14
• 8 + ? = 16
• 9 + ? = 18
• 10 + ? = 20

Найди пропущенные цифры

На рисунке спрятались цифры. Найди все цифры и напиши каких цифр не хватает на картинке.

Запиши в клетки пропущенные цифры

• 1 × □ = 1
• 2 × □ = 4
• 3 × □ = 9
• 4 × □ =16
• 5 × □ = 25
• 6 × □ = 36
• 7 × □ = 49
• 8 × □ = 64
• 9 × □ = 81

Восстанови пропущенные цифры чтобы получились верные решения

Реши примеры восстановив верно пропущенные цифры.

• 5 + 5 — ? = 8
• 8 + 4 — ? = 6
• 7 + 1 + ? = 9
• 2 — 1 + ? = 7

Запишите пропущенный ряд цифр

Необходимо дополнить пропущенный ряд цифр.

• 1, 2, 3, 4, _ , _ , _ , _ , _ , 10
• 1, _ , _ , _ , _ , 5, 6, 7, 8, 9, 10
• 1, 2,  _ , _ , _ , _ , _ , _ , 9, 10

Вместо звездочек поставьте пропущенные цифры

Прорущенные цифры обозначены знаком звездочка. Найди какие цифры нужно вписать, чтобы все решения стали правильными.

Восстанови пропущенные цифры в записи

Восстановив пропущенные цифры — получи верное решение примера.

• 5 + 4 — 6 + _0 = 13
• 6 + _ + 6 = 12
• 1 + 2 — 3 + _5 = 15
• 8 — 4 + 6 — _ = 8

 

Задание вставьте пропущенные цифры

Изучив все цифры настало время перейти на новый уровень и вставлять пропущенные цифры. Каждое задание на вставку пропущенных цифр закрепляет числовой ряд и математическую логику. Выполняя задания на вставку прлпущенных чисел анализируйте с какими цифрами ребенку сложнее справляться, а затем закрепите изучение нужной цифры. Данная методика позволит с легкостью ввполнять задания на вставку пропущенных чисел.

Примеры с пропущенными цифрами

Выпишите пропущенные цифры

Перед вами цепочка чисел. Восстановите пропущенные цифры на свои места.

• 1, 6, 11, _ , 21, 26, _ , 36, _ , 46, 51, _ , 61, _ , 71, _ , _ , 86, 91, _ .
• 2, 10, _ , 26, _ , 42, _ , _ , 63, 71, _ , 87, 95.
• 3, 12, _ , 30, _ , 48, 57, _ , 75, _ , 93.

Расставь пропущенные цифры

Вам потребуется расставить пропущенные цифры в примерах так, чтобы они стали верными. 

• 3 * _ = 6
• 6 * _ = 6
• 5 * _ = 0
• 7 * _ = 14
• 9 * _ = 18
• 5 * _ = 30
• 7 * _ = 49

Вставь пропущенные числа и цифры

Восстанови пропущенные цифры и числа

Восстанови пропущенные числа, чтобы получить верный результат.

• 7 ÷ _ = 1
• 8 ÷ _ = 4
• 25 ÷ _ = 5
• 54 ÷ _ = 6
• 16 ÷ _ = 8
• 21 ÷ _ = 7

Запиши пропущенные цифры и числа

Примеры вставить пропущенные цифры

Подбери пропущенные цифры обозначенные знаком

Вставь пропущенные цифры не выполняя вычислений

Вставь пропущенные цифры не выполняя указанные действия.

Запиши такие пропущенные цифры чтобы равенство стало верным

Напиши пропущенные цифры

Вставьте в рамочки пропущенные цифры

Вставь вместо звездочек пропущенные цифры

Вставь пропущенные цифры чтобы получились верные записи

Вставь пропущенные цифры и сделай проверку

Восстанови пропущенные цифры обозначенные знаком

• 6 * 2 = 4 * _
• 7 * 6 = 6 * _
• 5 * 6 = 10 * _
• 9 * 2 = 3 * _
• 4 * 4 = 8 * _

Вставь пропущенные цифры чтобы получились верные равенства

• 5 + _ = 6 + 4
• 7 + 2 = 6 + _
• 1 + 3 = 2 + _
• _ + 6 = 3 + 3
• 8 + 7 = 10 + _

Игра пропущенные цифры

Вставь в квадраты пропущенные цифры

• 10 + □ = 20
• □ + 5 = 10
• 17 — □ = 14
• □ — 16 = 6
• 22 + □ = 28
• □ — 20 = 4
• 15 + □ = 22

Карточки по математике 1 класс 1-й десяток

КАРТОЧКА 1

 

1.      Выбери числа, которые можно вставить в «окошко», чтобы получились верные неравенства и обведи их в кружок.

 

8, 1, 3, 4, 2, 9, 5 ——-       <   4

 

4, 5, 8, 7, 9, 1, 2 ——-        6      <                 

 

1, 7, 8, 6, 9, 5, 4 ——-        >  5

 

 

2.     Запиши числа в порядке возрастания.

 

7, 3, 4, 2, 1, 5, 6, 9, 8  _______________________________________________

 

4, 7, 8, 5, 1 _________________________________

 

 

 

КАРТОЧКА 2

 

1.     Подбери в «окошки» числа и запиши верные неравенства.

 

              <  2             4  >                                   >   6

 

5  <                               > 9                   1  <              

 

        <  4          2 <                                     <  8

 

 

 

2.      Выбери тот ряд, с помощью которого можно считать предметы и подчеркни его красным карандашом.

 

1, 3, 4, 2, 5, 6, 7, 8, 9

2, 1, 3, 4, 5, 6, 7, 8, 9

1, 2, 3, 4, 5, 6, 7, 8, 9

 

КАРТОЧКА 3

 

 

1.     Выбери верные неравенства и обведи их в кружок.

5 > 2      7 < 8           8 > 9           1 > 2           3 < 4           6 > 2

8 < 7      7 > 5           3 > 1           4 > 5           9 > 6           9 > 0

6 < 5      5 > 6           3 > 2           6 > 7           7 > 8           3 < 2

2 > 3      7 < 9           4 > 3           0 < 1           5 < 4           9 > 8

 

2.                  Запиши числа, которые больше 3, но меньше 8.

_______________________________________________________________________

_______________________________________________________________________

 

КАРТОЧКА 4

 

1.      Запиши верные неравенства.

                                                 

< 5                   < 6                       < 3                      < 8

 

< 7                   < 4              5 <                        3 <            

 

6 <                      8 <                    7 <                        4 <            

 

1 <                            < 2                       < 9              2 <            

 

2.     Запиши числа в порядке убывания.

 

3, 7, 5, 9, 1, 4, 6, 8  __________________________________________

КАРТОЧКА 5

 

1.     Рассмотри рисунок и запиши цифрами, сколько ты видишь на нём:

а) треугольников _____

б) квадратов _____

в) кругов ____

 

 

 

 

 

 

 

 

 

 

КАРТОЧКА 6

 

1.      Рассмотри каждый рисунок и запиши цифрами, сколько ты видишь на нём всего:

а) кругов ______

б) квадратов _____

в) треугольников _____

 

 

2.     Запиши числа в порядке возрастания.

7, 3, 9, 6, 1, 4, 2, 8, 5 ___________________________________________

 

КАРТОЧКА 7

 

1.     Запиши пропущенные числа

 

…., 2, 3, …, …, 6, …, …, 9, 10

 

2.     Запиши все числа, которые меньше 6.

 

_____________________________________________

 

3.     Выбери выражения, в которых одно из слагаемых число 2. Вычисли значения этих выражений.

7 + 1 =____        3 + 2 =__          4 + 1 =___            4 + 2 =___

5 + 4 =____        2 + 7 =__          6 + 2 =___            3 + 4 =___

8 + 1 =____        4 + 3 =__          1 + 2 =___            6 + 3 =___

 

 

 

КАРТОЧКА 8

1.      Вместо точек вставь пропущенные числа:

 

3, …, …, …, …, 8.

 

9, …, …, …, …, …, …, 2.

 

2.     Обведи кружком число, которое следует за числом 9.

 

а) 8, 7, 3, 10.

 

б) 1, 10, 5, 8.

 

3.     Обведи кружком число, которое стоит перед числом 5.

 

а) 2, 3, 4, 6.

 

б) 6, 7, 1, 4.

 

4.     Обведи кружками числа, которые стоят между числами 4 и 7:

 

а) 3, 8, 9, 5, 10, 6.

 

б) 8, 1, 5, 9, 6, 0.

 

5.     Расставь числа по порядку, от большего к меньшему:

 

3, 1, 6, 4, 8.  ______________________________________

 

6.     Рассели числа по этажам.

 

 

КАРТОЧКА 9.

1.– Найдите число, которое больше двух, но меньше четырёх, закрасьте его красным цветом;

— Синим цветом, закрасьте число, которое за ним должно следовать;

— Зеленым цветом закрасьте число, которое на два меньше, чем то, что закрашено синим;

— Самое большое число закрасьте жёлтым цветом;

— Стрелками покажите порядок следования чисел.

 

 

2.Раскрасьте круги в красный и синий цвета так, чтобы кругов красного цвета было больше.

 

 

 

 

 

 

3.Раскрась запись, которая соответствует рисунку:

 

                                                                           

 

 

 

 

 

4.     Впиши недостающие числа. Стрелками покажи порядок следования чисел при счете. (См. Белошистая «Математика в 1 кл.» стр.208 )

 

 

 

 

 

 

 

 

 

1. Вставь пропущенные числа. Раскрась одинаковые полоски одним цветом.

 

2

3

7

 

7

6

2

 

1

5

6

 

8

7

4

 

2. Соедини цифры по порядку.

 

 

3. Обведи в группы по пять штук. Сколько групп получилось?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Раскрась столько предметов, сколько обозначено цифрой.

 

 

         2. Сосчитай предметы в каждой рамке. Соедини друг с другом предметы в тех рамках, где их содержится одинаковое количество.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Сосчитай количество предметов в каждой рамке. Соедини с нужной цифрой.

 

2. В пустые клетки поставь нужное количество точек вместо потерявшихся цифр.

                                               

 

 

 

 

1. Нарисуй столько бусинок, сколько показывает цифра.

 

 

2. Сосчитай, сколько предметов, и обозначь нужной цифрой каждый.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Напиши, сколько углов у каждой фигуры.

 

 

 

 

 

 

 

 

 

 

 

 

2. Нарисуй в пустых клетках нужное количество предметов.

 

 

 

 

1. Впиши соседей чисел в пустые окошки.

 

 

 

 

1		3
5		7
6		8

        

	3
	5
	4
	7

2
6
8
4

 

 

 

 

 

                  

 

 

 

 

 

 

2. Раздели квадрат на два треугольника, а прямоугольник – на два квадрата.

 

 

 

 

 

 

 

 

 

 

1. Проведи стрелки к той картинке, где число предметов увеличивается на один.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1. Какой фигуры не хватает на каждой строчке? Дорисуй.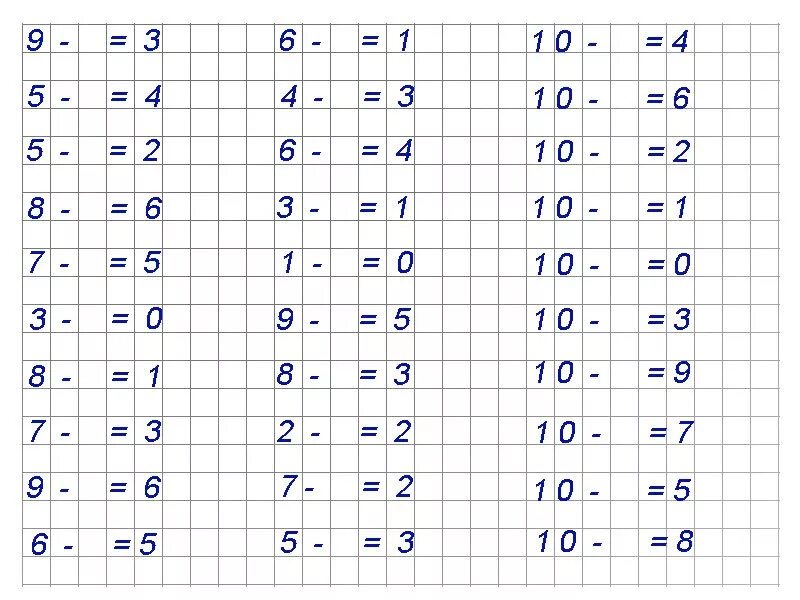

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Дорисуй в каждом ряду нужное количество предметов.

5
8
3
9
7
4
6
10

Графические диктанты.

1.    Самовар

1 – вправо, 1 – вверх, 1 –вправо, 1 – вверх, 1 – вправо, 2 – вверх, 1 – вправо, 1 – вверх, 1 – вправо, 1 – вверх, 1 – вправо, 1 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 2 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 2 – вниз, 1 – влево, 1 – вверх, 1 – влево, 3 – вниз, 1 – влево, 3 – вниз, 1 – влево, 2 – вниз, 2 – вправо, 2 – вниз, 1 – влево, 1 – вверх, 5 – влево, 1 – вниз, 1 – влево, 2 – вверх, 2 – вправо, 2 – вверх, 1- влево, 3 – вверх, 1 – влево, 3 – вверх, 1- влево, 1 – вниз, 1- влево, 2 – вверх.

 

2.   Гусь

1 – вправо, 1 – вверх, 1 – вправо, 1 – вверх, 4 – вправо, 1 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 1 – вниз, 1 – вправо, 8 – вверх, 2 – вправо, 1 – вниз, 3 – влево, 7 – вниз, 1 – влево, 1 – вниз, 10 – влево, 4 – вверх.

 

 

3.   Утка

1 – вправо, 1 – вверх, 2 – вправо, 7 – вниз, 1 – вправо, 1 – вверх, 2 – вправо, 1 – вверх, 2 – вправо, 1 – вверх, 2 – вправо, 1 – вниз, 2 – вправо, 1 – вниз, 1 – вправо, 1 – вверх, 1 – вправо, 2 – вниз, 2 – влево, 1 – вниз, 1 – влево, 1 – вниз, 1 – влево, 1 – вниз, 6 – влево, 1 – вверх, 2 – влево, 1 – вверх, 1 – влево, 2 – вверх, 1 – вправо, 4 – вверх, 2 – влево, 1 – вверх.

 

 

4.   Щенок

2 – вверх, 2 – вправо, 1 – вверх, 1 – вправо, 3 – вниз, 3 – вправо, 1 – вверх, 1 – вправо, 5 – вниз, 2 – влево, 2 – вверх, 1 – влево, 2 – вниз, 2 – влево, 4 – вверх, 2 – влево.

 

5.   Олень

1 – вправо, 1 – вниз, 1 – вправо, 1 – вверх, 1 – вправо, 1 = вниз, 1 – вправо, 1 – вверх, 1 – вправо, 2 – вниз, 1 – вправо, 1 – вниз, 2 – вправо, 2 – вниз, 1 – влево, 3 – вниз, 1 – влево, 5 – вниз, 1 – влево, 2 – вверх, 1 – влево, 2 – вверх, 3 – влево, 2 – вниз, 1 – влево, 2 – вниз, 1 – влево, 6 – вверх, 1 – влево, 2 – вниз, 1 – влево, 3 – вверх, 7 – вправо, 1 – вверх, 1 – влево, 3 – вверх, 3 – влево, 2 – вверх.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                                   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Различаем числа и цифры математика (1 класс)

Тема: Различаем  числа и цифры.

Цель: учить писать цифру 9, ввести понятие «число», и «цифра»; закреплять знание чисел от 1 до 9; продолжить формировать навыка счёта.

Задачи:

Обучающие – формировать представление о числе 9, его составе, познакомить с графическим обозначением числа 9 (печатным и письменным), его изображением на числовом отрезке, сложение и вычитание в пределах 9;

Развивающие – развивать мыслительные операции, речь;

Воспитывающие — способствовать формированию положительной учебной мотивации, развитие чувства взаимопомощи в коллективе.

      Тип урока: знакомство с новым числом, цифрой.

Форма: классно-урочная.

Формы работы: фронтальная, коллективная, в парах, индивидуальная.

Методы: наглядный, диалог, беседа, самостоятельная работа.

Технологии: проблемно-диалогического мышления, развивающая,  личностно-ориентированная, здоровьесберегающая.

      Оборудование.

Для учителя:

1.  Иллюстрация доктора Айболита.

2.  Карточка с темой урока.

3. Карточки с цифрами 1 — 8 на доске, отдельно карточка с цифрой 9.

4. Элементы письменной цифры 9.

Для учащихся:

1. Учебник «Математика»

2. Карточки с цифрами.

3. Карточки с таблицей состава числа 9.

4. Рисунки с термометрами.

5. Линейки.

      Универсальные учебные действия.

Предметные:

соотношение  числа 9 с количеством предметов, письмо цифры 9, соотнесение числа 9 и цифры 9; образование числа 9, определение места числа 9 в последовательности чисел от 1 до 9.

Познавательные:

общеучебные —  уметь ориентироваться в учебнике;

логические – осуществлять синтез как составление целого (число 9) из частей.

Регулятивные: в сотрудничестве с учителем ставить новые учебные задачи; составлять план и последовательность действий; делать выводы о результате совместной деятельности на уроке; оценивать совместно с учителем и одноклассниками результат своих действий, результат деятельности товарища.

Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве; формулировать собственное мнение; договариваться и приходить к общему решению в совместной деятельности; строить монологическое высказывание, владеть диалогической формой речи.

Личностные: иметь желание и умение учиться.

 

 

 

 

 

Ход урока.

 

1. Организационный момент.

                     Вот и прозвенел звонок.

                     Начинается урок.

                     Очень тихо вы садитесь

                     И работать не ленитесь.

 — Кто настроен на хорошую работу на уроке, хлопните в ладоши.

Сегодня к нам на урок пришёл гость и очень надеется на вашу помощь. Кто же это? Отгадайте:

                     Лечит маленьких детей,

                     Лечит птичек и зверей,

                     Сквозь очки свои глядит

                     Добрый доктор… (Айболит).                   

— Кто автор замечательной сказки о докторе Айболите? (К. Чуковский)

      

   2. Актуализация знаний.

                    — А теперь вперёд, за дело.

                    Математика нас ждёт.

                    Начинаем устный счёт.

1. Работа с числовым рядом.

1) – У доктора Айболита случилась беда. Кто-то нарушил порядок у него в шкафу – переставил бутылочки с лекарствами. Надо навести порядок.

 

— Что изображено на баночках? (Числа.)

— Сколько всего баночек?

— Давайте посчитаем. (Счёт.)

— Рассмотрите внимательно ряд чисел. Что вы заметили? (Числа 5 и 7 не на своих местах.)

Поменять местами баночки.

2) – Мы должны убедить Айболита, что хорошо знаем ряд чисел, чтобы он был уверен – мы не перепутаем места бутылочек. Возьмите карточки с цифрами и приготовьтесь показать свои знания.

 

— Какое число идёт при счёте за числом 7?  (8)

— Какое число идёт при счёте перед числом 2?    (1)

— Покажите число, которое стоит между числами 3 и 5.   (4)

— Покажите число, следующее за числом 5.    (6)

— Покажите число, предшествующее при счёте числу 4.    (3)

— Какое число стоит слева от числа 3?   (2)

— Какое число стоит справа от числа 6?  (7)

 

2. Состав числа 8.

Слайд 4.

— Посмотрите внимательно на таблицу. Найдите закономерность и узнаете, сколько животных было на приёме у доктора Айболита вчера.

3	4	6
5	4	2
8	8	?

— Какого числа не хватает?

— Как определили, что 8?

— Как же можно набрать число 8? (отвечают с опорой на таблицу. )

— Какого варианта состава числа 8 нет в таблице? (7 и 1) Дополнить.

 

— С заданиями вы справились, а какие знания и умения вам понадобились, чтобы выполнить их?   (Знание ряда чисел, состава числа 8.)

 

3. Физкультминутка.

 

4. Самоопределение к деятельности.

 

Слайд 5. Числовой отрезок.

                 1             2                            4                            6                            8

 

 

— Что изображено? (Числовой отрезок)

— Покажите пропущенные числа с помощью карточек. Дополнить на слайде.

— Все ли части числового отрезка мы обозначили? Почему?

(Не все. Нужна ещё одна цифра.)

— Какая? (9)

— Сформулируйте тему урока. (Число 9. Цифра 9.)   

Поместить таблицу с темой на доску.

— Чему будем учиться?

(Писать цифру 9, считать в пределах 9, знать состав числа 9.)

 

5. «Открытие» новых знаний.

1) Число 9.

— Каким числом заканчивается наш числовой отрезок? (9)

— Как получить число 9 по числовому отрезку? (8 + 1) Показать стрелкой.

— Расскажите всё, что знаете о числе 9.

(Стоит на числовом луче после числа 8; соседи числа 8 и 10; больше числа 8 на 1, меньше числа 10 на 1.)

— Проверьте, верно ли изобразили число 9?

Слайд 6. Изображение цыплят и прямоугольников.

(Цыплят 9.  Прямоугольников 8, надо добавить ещё один.)

2) Цифра 9.

— Покажите цифру, которой можно дополнить числовой отрезок и подписать наши рисунки.               Выбирают цифру на доске. Дополнить записи на Слайде 6 цифрой 9.

— Используя ваши карточки, можете показать цифру 9?

(Перевернуть цифру 6. )

Учитель показывает карточку с цифрой 6:

 — 9, как и 6, вглядись.

 Только хвост не вверх, а вниз.

Слайд 7

 — Цифра 9 иль девятка,

Числовая акробатка.

Если на голову встанет,

Цифрой 6 девятка станет.

 

— Где в окружающем мире встречается цифра 9?

Слайд 8.  Номер дома,  часы,  линейка.

3). Письмо цифры 9.

— Настала пора научиться писать цифру 9.

1.  Пальчиковая гимнастика.

— Перед тем, как нам писать,

Надо пальчики размять.

2.  Показ образца и объяснение.

Слайд 9

— Посмотрите  на образец написания цифры 9. Из каких элементов состоит цифра 9?

(Из овала и закругления.) Показать элементы цифры 9.

— Пишу сверху овал и веду вниз закругление.

3.  Письмо цифры 9 на с. 19.

— Откройте учебники по закладке. На правой странице внизу найдите цифру 9.

Дополнительно для тех, кто закончит раньше: определить закономерность во второй строчке и продолжите запись.

4.  Состав числа 9. 

— Что ещё должны узнать о числе 9?     (Состав числа)

— Узнаем состав числа 9, а заодно поможем доктору Айболиту раздать градусники. А зачем ему градусники?

(Измерять температуру.)

— Возьмите градусники.  Сколько их?    (9)

Таблица на Слайде 10 и такие же на партах у детей.

— Один из вас будет раздавать градусники, а второй вести учёт, т. е. записывать в таблицу. Отложите в сторону столько градусников, сколько указано в таблице. Посчитайте, сколько осталось градусников. Получившееся число запишите в таблицу:

 

9	1	2	3	4	5	6	7	8

 

— Продолжите самостоятельно.        (Работа в парах)

— Давайте проверим, что у вас получилось. 

Назвать все случаи состава числа 9 и дополнить таблицу на слайде.

— Сколько таких случаев получилось?  (8)

 

6. Физкультминутка.

 

7. Первичное закрепление.

1) Учебник с. 18 № 2.

— Чтобы легче запомнить состав числа 9, выполним одно задание. На левой странице найдите № 2. Рассмотрите внимательно записи.

— Что объединяет первые примеры в каждом столбике?

(Сложение, находим целое, получается 9.)

— Какое равенство в первом столбике? (8 + 1 =)

— Дополним его. ( 9)

— Чем являются числа 8 и 1? (Части.)

— Чем является число 9? (Целое.)

— Как составить следующее равенство? (Переставить части местами.)

— Как нужно рассуждать при составлении следующего равенства?

(Если из целого вычесть одну часть, то останется другая.)

— Каким будет четвёртое равенство?

Составить и записать

— А теперь поработайте самостоятельно. Первый вариант составляет выражения во втором столбике, второй – в третьем. Кто успеет раньше, работает с выражениями четвёртого столбика.

Два ученика работают у доски.

2) Учебник с. 19 № 3.

— Лекарство приготовили, градусники на месте. Можно начинать приём больных. Найдите № 3.

К доктору пришло много животных. Сколько их?

— Прочитайте задание. Кому из зверей нужна помощь?

— А как нам это узнать?

(Решим выражения и получим номера, под которыми изображены звери, нуждающиеся в помощи.)

— Девочки решают выражения первого столбика, мальчики – второго. Кто сосчитает раньше свои примеры, решите примеры другой команды. Кому трудно, можете считать по линейке.

(Девочки: 4, 5, 3 – морской котик, дельфин, ёжик.

Мальчики: 7, 9, 2 – воробей, бабочка, щенок.)

— Какие знания пригодились для выполнения задания?

(Состав чисел, знание взаимосвязи между частями и целым. )

 

8. Итог урока. Рефлексия.

— Что нового узнали на уроке?

— Чему научились?

— Где можно использовать полученные знания?

 

— Проследите глазами за числами в порядке возрастания. Соедините буквы, записанные рядом с ними, и прочитайте слово.

Слайд 11.

 

— Какое слово получилось? (Молодцы!)

— Так вашу работу оценил доктор Айболит. Кто так же оценил свою работу, хлопните в ладоши.

— Кому понравилось работать в паре? Поблагодарите своего соседа.

— Вы славно потрудились! Урок закончен.

 

 

 

Задания по русскому языку 1 класс: для самостоятельной работы

Родители вчерашних первоклассников облегченно выдохнули, так как начались долгожданные для всех летние каникулы. И действительно, какая радость для всех: можно отдыхать, веселиться и резвиться. Но чтобы за лето не забылось все то, что с таким трудом дети учили весь год, нужно понемногу заниматься дома. В материалах этой статьи вы найдете задания для самостоятельной работы для первоклашек по русскому языку.

Содержание

1. Задания по теме «Слово. Предложение»
2. Задания по теме «Звуки речи. Буквы. Алфавит»
3. Задания по теме «Слоги и ударения»
4. Задания по теме «Твердые и мягкие согласные»
5. Задания по теме «Коварные звонкие и глухие звуки»
6. Задания для диктантов

Задания по теме «Слово. Предложение»

Задания и упражнения, размещенные в этом разделе, способствуют развитию речи и формированию графических навыков первоклассников, дают возможность выполнять индивидуальные формы работ, приобщают школьников к творческой и познавательной деятельности.

Задание 1.

Нужно назвать представленные на рисунках предметы. Рассказать, как они связаны между собой. Какие новые слова можно добавить к предложенному слову?

Ответ: На рисунке изображены каштаны: плоды каштана, дерево каштана, листья каштана.

Задание 2.

Из предложенных слов составить правильные предложения и записать их в тетради в нужном порядке.

крыльце, На, уселся, кот.
блестела, пушистая, Его, шубка.
глазки, Зеленые, зажмурились.
добрый, Это, самый, кот.

Задание 3.

Необходимо дополнить предложения таким образом, чтобы получился связный рассказ.

Я живу в________. Мой город расположен _______. Я учусь в школе номер___. Моя школа самая_______. Мои одноклассники_________. Летом я буду отдыхать______.

Задание 4.

Среди предложенных букв нужно найти слова – названия животных, которые обитают в Российской Федерации.

Оажирафзаяцкотлисицаслонгиппопотамволк

Ответ: заяц, кот, лисица, волк.

Задание 5.

В два столбика записаны слова и фразы. Нужно записать их таким образом, чтобы получились правильные выражения.

Что взял взаймы, исполни.
Что обещал, за то благодари.
Что получил даром, отдай.

Ответ:

Что взял взаймы, отдай.
Что обещал, исполни.
Что получил даром, за то благодари.

Задание 6.

Самодиктант. Ребенку необходимо прочитать предложенные слова, запомнить их правописание, а затем постараться записать их без ошибок по памяти.

Благодарю, извините, пожалуйста, до встречи, до свидания, простите, пожалуйста.

Задание 7.

Необходимо прочитать зашифрованную фразы, разбить ее на слова и записать в тетрадь.

Добродобромвернется.
Учисьценитьдоброеслово.
Золотоесердцедоброесердце.
Яблонястоитпосредиогорода.
Медведьоченьлюбитмед.

Задание 8.

Необходимо переписать предложенные слова и разбить их на слоги.

Пчела, нос, вертолет, шарики, ножки, ножницы, корзинка, листочки, хлеб, мед, булочка, дудочка, светлячок, муравей.

Задания по теме «Звуки речи. Буквы.

Алфавит»

В первом классе дети учат алфавит, буквы и звуки. Они уже знают, что такое звуковые схемы слов и умеют их составлять. Особое внимание следует обратить на буквы, которые передают сразу два звука. Ниже приведем несколько задания для самостоятельной работы для первоклассников.

Задание 1.

Необходимо прочитать текст и попытаться составить связный рассказ по прочитанному.

Слово «библиотека» произошло от греческого слова «библион», что означает «книга». Таким образом, можно утверждать, что библиотека – это место, в котором хранятся книги. Кроме книг в библиотеке хранятся газеты и журналы, каждый желающий может прийти в библиотеку и взять что-нибудь почитать.

Задание 2.

Необходимо переписать текст, и объяснить, каким звукам соответствуют буквы, выделенные жирным шрифтом.

С давних пор на Руси дети учились грамоте по букварю. Каждая буква в букваре была обозначена словом. Письмо – одно из самых великих изобретений человечества.

Задание 3.

Ниже приведены звуковые схемы слов. Нужно подобрать слова, которые соответствуют этим схемам.

[– о –]
[= о – о]
[– о – о]
[– о = о]

Где – знак, передающий твердый согласный звук.
= знак, передающий мягкий согласный звук.
о знак, передающий гласный звук.

Примеры слов к первой схеме: кот, пот, рот, раб, сад и т.д.
Примеры слов ко второй схеме: часы, чудо, щука и т.д.
Примеры слов к третьей схеме: нога, нора, руно и т.д.
Примеры слов к четвертой схеме: ноги, буки, лоси и т.д.

Задание 4.

Необходимо дописать слова, по предложенным рисункам. Подчеркнуть те буквы, которые передают гласные звуки.

Огурец, Перец, Морковка, Помидор.

Задание 5.

Составить предложения по предложенным ниже схемам.

I______, ______, _______, _______ — это _______.
I______ _______ _______ _______?
I______ _______ _______ _______!
I______ _______ _______ _______.

Где I_____ — заглавное слово в предложении.
_____ — остальные слова в предложении.

Задание 6.

Необходимо прочитать слова парами так, чтобы при замене одной буквы в предыдущем слове можно было получить новое слово по значению и написанию.

Коса – ко(?)а, удочка – у(?)очка, стог – сто(?), вол – (?)ол.

Записать слова в тетрадь, подчеркнуть заменяемые буквы в каждом слове.

Задание 7.

Необходимо переписать текст, вставив пропущенные буквы.

На дворе ма_т. За окном холо_но. А в клас_е тепло. На ок_е буке_. В бан_ах с водой стоят ве_ки вербы. На вет_ах зеленые ли_точки.

Задание 8.

Необходимо прочитать слова и выписать из них названия городов России.

Самара, Москва, Киев, Харьков, Воронеж,  Львов, Нью-Йорк, Мехико, Симферополь, Севастополь.

Слова, которые обозначают названия городов Украины – разделить на слоги.

Задание 9.

Необходимо переписать текст, вставив пропущенные буквы.

Щегол – ловкая, про_орная птица. У нее я_кий краси_ый окрас. Селится ще_ол в сада_ и парках. П_тается эта пти_а семенами и нас_комыми. Поет гр_мко, весело и к_асиво.

Задание 10.

Ниже приведен отрывок из стихотворения Корнея Чуковского, но в нем пропущены все гласные буквы. Если правильно расставить нужные буквы, то можно прочитать этот отрывок.

Д_ здр_вств_ _ т а а у е
М_л_ д_ш_ст_ _ ы о у и о е
_ п_л_т_нц_ п_ш_ст_ _ и о о е е у и о е
_ з_бн_й п_р_ш_к и у о о о о
_ г_ст_й гр_б_ш_к и у о е е о

Задания по теме «Слоги и ударения»

Перед началом выполнения заданий следует запомнить: слогом называется часть слова. В слове содержится столько слогов, сколько в нем гласных звуков. Например, О-ля, бе-ре-за, пче-ла и т.д.

Задание 1.

Ниже предложены слова. Нужно записать из в три столбика: в первый – слова, имеющие один слог, во второй – слова, имеющие два слога, в третий – слова, имеющие три слога.

Рог, капуста, нога, год, сад, Ира, мальчик, картофель, чайка, майка, помидор, огурец, перец, мед.

Ответ: первый столбик – рог, год, сад, мед. Второй столбик – нога, Ира, мальчик, чайка, майка, перец. Третий столбик – капуста, картофель, помидор, огурец.

Задание 2.

Необходимо переписать текст, изменяя слова в скобках по смыслу. Слова из скобок разбить на слоги карандашом.

Хорошо (лето). Я хожу на (река) купаться и ловить (рыба). А еще я читаю интересные (книга).

Ответ (слова из скобок сразу изменяем по смыслу и делим на слоги): ле-том, ре-ку, ры-бу, кни-ги.

Задание 3.

Ниже представлены слова. Необходимо выписать только те, в которых ударение падает на второй слог.

Синица, ласточка, ворона, сорока, дятел, скворец, гвоздика, дорога, кувшинка, лепесток, цепочка, телефон.

Безударные слоги в этих словах подчеркнуть карандашом.

Ответ: синица, ворона, сорока, скворец, гвоздика, дорога, кувшинка, цепочка.

Задание 4.

Переписать текст в тетрадь, разбить слова на слоги карандашом.

Днем кувшинка нежится на воде. А ночью ныряет под воду. Стиснет лепестки в кулачок и нырнет с головой. Утром вынырнет из воды. Снова развернет лепесточки навстречу солнцу.

Ответ:

Днем кув-шин-ка не-жит-ся на во-де. А ночь-ю ны-ря-ет под во-ду. Стис-нет ле-пест-ки в ку-ла-чок и ныр-нет с го-ло-вой. Ут-ром вы-ны-рнет из во-ды. Сно-ва раз-вер-нет ле-пес-точ-ки на-встре-чу солн-цу.

Задание 5.

Необходимо переписать текст.

На горе стоял старый замок. К замку вела узкая дорога. Справа от дороги – пропасть. Около замка стоит старый фонарь.

Предложите ребенку устно изменить ударение в словах, выделенных жирным шрифтом. Как изменился смысл написанного? Объясните, почему.

Задание 6.

Необходимо ответить на вопросы, используя справочные слова из скобок.

Целью этого задания является развитие речи школьника. Согласно школьной программы изучения русского языка, первоклассники должны уметь правильно составлять ответы на поставленные им вопросы. Чем полнее и развернутее ответы на вопросы, тем лучше.

Куда пошли товарищи? (удить рыбу) – Ответ: Товарищи пошли удить рыбу.

Где находилось озеро (за полем) – Ответ: Озеро находилось за полем.
Что сделали ребята (закинули удочки) – Ответ: Ребята закинули удочки.
Какая рыба поймалась (ерш и лещ) – Ответ: Поймались ерш и лещ.

Задание 7.

Необходимо списать слова, вставляя пропущенные буквы. Карандашом подчеркнуть сочетание «жи» и «ши».

Ш_шки, луж_, ш_ло, груш_, ш_рокий, мащ_на, ш_на, наж_вка, карандаш_, полож_ть, ж_знь, хорош_е, малыш_.

Задание 8.

Необходимо списать слова, вставляя пропущенные буквы. Карандашом подчеркнуть сочетание «ча», «ща», «чу» и «щу».

Рощ_, щ_вель, плач_, ч_до, угощ_, щ_ка, ч_йка, лещ_, ч_жи, ч_й, нач_ло, ч_йник, ч_шка, щ_т, ч_дак, щ_чий, ч_десный, ч_довище, ч_деса, ч_щ_, гущ_, сч_т.

Задания по теме «Твердые и мягкие согласные»

Здесь важно понимать, что твердыми согласными считаются не только те, после которых следуют гласные о, а, у, э, ы, а мягкими – после которых следуют гласные ё, я, ю, е, и. Первоклассники уже должны хорошо понимать, что согласные ц, ж и ш всегда твердые, а согласные ч и щ – всегда мягкие, независимо от того, какая гласная за ними следует.

Задание 1.

Необходимо переписать текст в тетрадь, все цифры записать словами.

Жили-были цифры. Каждая из них знала, кто за кем стоит. Однажды они разбежались. После 3 встала цифра 5, а после 5 – 9. Цифра 1 очутилась перед 6. Соседями 2 стали 8 и 7. Беда!

Подсказка: «после тройки встала цифра пять, а после пятерки – девять. Цифра один очутилась перед шестеркой. Соседями двойки стали восемь и семь».

Подчеркнуть слоги с ж, ц, ч.

Задание 2.

Необходимо переписать текст в тетрадь. Обратить внимание на написание слов «животные», «птицы», «месяцы», «овощи».

Лоси, олени, медведи – это дикие животные.
Куры, утки, индюки – это домашние птицы.
Сентябрь, октябрь, ноябрь – это осенние месяцы.
Морковь, картофель, фасоль – это овощи.

Задание 3.

Необходимо переписать текст в тетрадь, вставляя пропущенные буквы.

Лос_ — лесной жител_. Он есть траву и ветки. Ему нужна сол_. Лесники кладут сол_ на пен_ или камен_. Лоси приходят лизат_ сол_. Тк люди помогают животным.

Подчеркнуть слова с мягким знаком на конце.

Задание 4.

Необходимо прочитать текст и выписать слова, содержащие мягкий знак «ь».

Летом муравьи строят муравейник. Муравьишка нашел шишку. Он позвал братьев. Вся муравьиная семья собирает иголки. Будет у ручья дом.

Сделать звуковой анализ выписанных слов.

Подсказка: мягкий знак звука не передает, но делает мягкий звук буквы, стоящей перед ним.

Задание 5.

По предложенному образцу дописать недостающие слова.

Образец: колос – колосья.

Ручей – _______ (ручьев), дерево – ______ (деревьев), перо – _______ (перьев), кол – ______ (кольев), стул – _______ (стульев).

Подчеркнуть буквосочетания с мягким знаком.

Задания по теме «Коварные звонкие и глухие звуки»

Под «коварными» звуками здесь подразумеваются те, которые передают другой звук. Например, в слове «пруд» на конце пишется звонкая «д», а слышится глухая «т». Задания и упражнения, приведенные ниже, помогут первоклассникам усвоить материал и понять, когда и как следует писать.

Задание 1.

Необходимо записать слова и подчеркнуть карандашом коварные звуки (т.е. безударные глухие и звонкие).

Грядка – грядочка, пруд – пруди, прут – прутик, еж – ежи, уж – ужи, снежки – снежок, лужки – лужок, арбуз – арбузик.

Задание 2.

Прочитать слова и записать их парами в тетрадь. Подчеркнуть в каждом слове звуки, которые выделены жирным шрифтом. Назвать звонкие и глухие звуки.

Тень – день, трава – дрова, коса – коза, пыль – быль, голос – колос, жить – шить.

Задание 3.

Необходимо переписать текст в тетрадь. Подчеркнуть карандашом глухие звуки в коварных словах.

Хорош пруд около нашего села. К пруду ведет узкая дорожка. Вдоль дорожки растут березки и дубки. В тихой воде мелькают рыбки.

Задание 4.

Необходимо переписать пары слов, вставляя пропущенные буквы.

Сле_ — следы, во_ — возы, рука_ — рукава, сне_ — снега, тру_ — труды, моро_ — морозы, ду_ — дубы, са_ — сады.

Подсказка: правильность написания пропущенной буквы нужно проверять ударением.

Задания для диктантов

Школьники, окончившие первый класс, должны уметь писать на слух небольшие диктанты. Чтобы за лето вчерашние первоклассники не утратили этот навык, родителям рекомендуется хотя бы раз в 1-2 недели проводить для детей диктанты. Ниже мы представляем несколько текстов для самоподготовки.

Задание 1.

Все реки текут в моря. Куда девается вода из моря?
Вода из моря поднимается туманов. Из туч вода падает на землю. С земли она стекает в болота, ручьи, реки. Из рек вода снова попадает в моря.

Задание 2.

Вы видели одуванчик?

Цветы одуванчика похожи на солнце. Лепестки одуванчика как золотые лучики. Они цветут все лето. Созревшие их семена собраны в пушистый шарик. Дунешь на шарик – полетят в воздух легкие летучие семена.
Поэтому и называется цветок одуванчиком.

Подсказка: помогайте ребенку правильно проставлять сложные знаки препинания.

Задание 3.

Хамелеон – маленький потомок динозавров. Это животное умеет менять свою окраску. Обычный цвет хамелеона – зеленый. Но он может стать фиолетовым, красным, коричневым и даже черным.

Подсказка: помогайте ребенку правильно проставлять сложные знаки препинания.

Задание 4.

Весна. Журчат вечевые ручьи. Проснулась пчелка от зимнего сна. Прочистила глазки мохнатыми лапками. Разбудила подругу. Полетят мед собирать. Пчелки – труженицы.

Подсказка: помогайте ребенку правильно проставлять сложные знаки препинания.

Задание 5.

Школьники едут отдыхать в летний лагерь. Утром автобус подъехал к школе. Отъезду радовались все. Машины выехали за город. Они объехали поле и въехали в лес. Учитель объявил остановку. Он объяснил школьникам, где они будут жить.

Задание 6.

Первобытные люди охотились и работали вместе. Чтобы охота была успешной, им нужно было общаться. И у людей развилась особая система общения – язык. Он стал позволять выражать мысли с помощью слов и выражений.

Подсказка: помогайте ребенку правильно проставлять сложные знаки препинания.

Задание 7.

Письменная речь – это речь написанная. Люди не сразу придумали буквы. В древние времена они писали рисунками. Сейчас такое письмо можно увидеть на дорожных знаках, вывесках магазинов, кафе.

Задание 8.

Собака яростно лаяла, припадая на передние лапы. Прямо перед ней, прижавшись к забору, сидел маленький котенок. Он широко раскрывал рот и жалобно мяукал. Неподалеку стояли два мальчика. Они прогнали собаку и спасли котенка.

Задание 9.

Дуют холодные ветры. Выпал первый снег. Многие птицы улетели в теплые края. Воробьи, голуби и синицы остались. Мальчик сделал кормушку для птиц и насыпал в нее зерен и крошек хлеба. Птицам будет что поклевать зимой.

Задание 10.

Стала желтой от горячего солнца скошенная трава. Как хорошо в тени строго клена! Его зеленые листья словно шепчут, что до осени еще далеко.

Подсказка: помогайте ребенку правильно проставлять сложные знаки препинания.

Состав числа до 10 карточки: Состав чисел 1-10 (карточки для работы на уроке)

Содержание

Состав числа до 10

Правильный устный и письменный счет (и правильность выполнения заданий по математике в школе) зависит от того, насколько хорошо ребенок понимает состав числа. Усвоить, из чего состоят числа от единицы до десятки, малышу лучше в дошкольном возрасте. И учить его этому лучше в формате математической игры.

Содержание:

• Разбираемся в материале
• Упражнения на сложение
• Упражнения на вычитание

Разбираемся в материале

Состав любого числа – это пара любых слагаемых, которые в сумме дают этот результат. Например, число 10 можно получить как 5 + 5, как 3 + 7, как 1 + 9 и т. д. Для лучшего понимания материала рекомендуется сделать отдельные карточки из пар слагаемых для одной и той же суммы:

• 9 + 0 = 9
• 8 + 1 = 9
• 7 + 2 = 9
• 6 + 3 = 9
• 5 + 4 = 9 и т.д.

Карточки с цифрами можно использовать не просто для рассматривания и запоминания. С ними можно придумать множество игр, составляя примеры из счетных палочек, шашек или других предметов. Например, для карточки 1 + 3 = 4 ребенок должен составить правильную сумму из фруктов, поместив в миску 1 яблоко и 3 банана. Также можно выкладывать в ряд предметы разных цветов: 1 красную палочку и 3 зеленых или наоборот. Еще один вариант – раскрашивать нарисованные на бумаге деревья, домики, другие предметы в нужные цвета: два синих, четыре желтых и т.д.

Упражнения на сложение

Для занятий понадобятся карточки со слагаемыми, без цифр-ответов:

• 1 + 2;
• 1 + 3;
• 1 + 4;
• 1 + 5 и т.д., для всех чисел от 1 до 10.

Когда ребенок изучает состав определенного числа, например, 8, для закрепления материала ему выдаются карточки, где указан состав 8 и несколько других подобных: 1 + 6 = 7, 2 + 3 = 5 и т. д. Малыш должен выбрать из ряда карточек все примеры с составом нужного числа.

Также можно просто показывать ребенку произвольные карточки без ответов, чтобы он посчитал правильную сумму – сначала с помощью пальцев или других предметов, а затем устно. Отвечать можно устно, но также можно писать цифры-ответы на карточке.

Упражнения на вычитание

Сначала ребенку следует объяснить: если в сложении мы соединяем два числа и получаем сумму, то вычитание – это обратный процесс. При вычитании зная сумму и одно из слагаемых, мы находим второе из них. И если кроха назубок знает состав чисел от 1 до 10, неизвестное слагаемое ему долго высчитывать не придется – он его просто «припомнит».

К примеру, из каких слагаемых состоит 7, малыш уже выучил. Сначала нужно вспомнить все его вариации: пусть ребенок их перечислит. Теперь ставите семерку на первое место и вычитаете из нее одно из слагаемых. Второе получится в ответе. Аналогично пробуем другой пример: если 6 + 1 = 7, то сколько будет 7-6? Для занятий лучше приготовить несколько карточек на вычитание без ответов: 7–1, 7–2 и т. д.

Если вычитание у ребенка пока еще вызывает затруднения, приготовьте большие карточки, на которых приведите примеры состава чисел в следующем виде:

• 4 + 1 = 5
• 1 + 4 = 5
• 5 – 1 = ?
• 5 – 4 = ?

Это поможет малышу понять связь вычитания и сложения, что очень важно для решения уравнений в будущем. Если ребенок не усвоит этот материал, решать примеры с неизвестными в школе он будет с трудом.

Рейтинг: 5/5 — 1 голосов

Обучающие карточки «Закрепление состава числа в пределах 10»

Обучающие карточки «Закрепление состава числа в пределах 10″

12+  Свидетельство СМИ ЭЛ № ФС 77 — 70917 Лицензия на образовательную деятельность №0001058

Пользовательское соглашение     Контактная и правовая информация

 

Педагогическое сообщество УРОК. РФ

Бесплатные всероссийские конкурсы

Бесплатные сертификаты за публикации

Нужна помощь? Инструкции для новых участников

Бесплатная   онлайн-школа для 1-4 классов

Всё для аттестацииПубликация в сборникеВебинарыЛэпбукиПрофтестыЗаказ рецензийНовости

Библиотека

▪Учебно-дидактические материалы

▪Обучающие карточки

Материал опубликовала

22

#1 класс #Математика #ФГОС #Учебно-дидактические материалы #Методист #Учитель-предметник #Учитель начальных классов #Воспитатель #Психолог #Дефектолог #Студент-практикант #Высшая категория #Школьное образование #УМК любой #Обучающие карточки

Пояснительная записка

Автор: Антропова М. А., учитель начальных классов МБОУ СОШ № 24» г. Сарапула УР

Предмет: математика

Аудитория: 0 —1 класс

Тема: Состав числа в пределах 10

Цель: совершенствование вычислительных навыков

Описание

Обучающие карточки созданы для закрепления табличных случаев состава числа в пределах 10. Задание учит работать с информацией в нестандартной форме. Развивает пространственное воображение, внимание, вычислительные навыки, формирует устойчивый интерес к изучению математики. 

карточки для печати
PDF / 167.38 Кб

 

Для многоразового использования карточки можно заламинировать.

Ожидаемые результаты:

— знание состава числа в пределах 10;

— развитие познавательного интереса к изучению математики;

— работа с информацией в нестандартной форме

Использованные ресурсы:

https://i. pinimg.com/564x/2b/98/b6/2b98b6162987431a7f4ec4ac2cb395ba. jpg

https://i.pinimg.com/564x/4b/9e/67/4b9e670d11d0c960bed655c26736577f.jpg

https://i.pinimg.com/564x/38/0f/62/380f62ce5b77d6cca0092d392d9c555d.jpg

https://i.pinimg.com/564x/2c/50/11/2c5011dc0bb89ed8b18bd67ee5754a20.jpg

https://i.pinimg.com/564x/f3/22/cd/f322cd494288c791d439625e909aafb7.jpg

Опубликовано 15.08.20 в 20:38 в группе «Дополнительные материалы к уроку»

сменить сортировку

Перминова Елена Федоровна, 15.08.20 в 20:53 3ОтветитьПожаловаться

Спасибо, обязательно воспользуюсь.

Антропова Мария Александровна, 15.08.20 в 21:20 2ОтветитьПожаловаться

Очень рада, что ресурс востребован.

Журавлева Татьяна Анатольевна, 15.08.20 в 21:04 3ОтветитьПожаловаться

Спасибо, для меня актуально!

Антропова Мария Александровна, 15. 08.20 в 21:21 2ОтветитьПожаловаться

Прекрасно, Татьяна Анатольевна!

Янова Татьяна Викторовна, 15.08.20 в 21:07 4ОтветитьПожаловаться

Очень интересные карточки! Спасибо, Мария Александровна, и за ресурс и за идею!!! Для работы с шестилетками пригодится!

Антропова Мария Александровна, 15.08.20 в 21:23 3ОтветитьПожаловаться

Да, я тоже к работе с малышами готовлюсь. Надеюсь, на традиционную форму общения с детьми.
Спасибо Вам, Татьяна Викторовна, за оценку работы!

Кияйкина Наталья Федоровна, 16.08.20 в 01:31 2ОтветитьПожаловаться

Благодарю за актуальный материал!

Антропова Мария Александровна, 16.

08.20 в 08:10 1ОтветитьПожаловаться

Спасибо, Наталья Федоровна!

Елена Владимировна, 16.08.20 в 04:18 4ОтветитьПожаловаться

Спасибо, Мария Александровна! Карточки яркие и полезные, первоклассникам будет очень интересно с ними работать!

Антропова Мария Александровна, 16. 08.20 в 08:10 4ОтветитьПожаловаться

Очень рассчитываю на это! Спасибо за позитивный комментарий к работе, Елена Владимировна!

Чтобы написать комментарий необходимо авторизоваться.

Закрыть

Как обучать составлению и разложению чисел

Содержание

• 1 Что такое составление и разложение чисел
• 2 7 Различные способы обучения разложению чисел
• 3 7 Ресурсы для обучения составлению и разложению чисел
9 Номера

Некоторые ссылки в этом посте являются партнерскими. Это означает, что если вы нажмете на ссылку и купите товар, я получу небольшую комиссию без каких-либо дополнительных затрат для вас. Все мнения остаются моими.

Чтобы выработать четкое представление о числах, дети узнают о составлении и разложении чисел еще в детском саду и будут практиковать эти важные навыки в первом, втором и последующих классах. Я здесь, чтобы объяснить разницу между ними и показать различные способы построения понимания учащимися этих ранних математических концепций.

Что такое составление и разложение чисел

Короче говоря, разложение и составление чисел — это способность разбивать заданное число на части и снова складывать его. Другими словами, это обучение тому, как части составляют целое. Если у вас есть маленькие дети или вы преподаете в начальной школе, вы можете знать это как «часть, часть, целое». Давайте немного подробнее рассмотрим, что это значит и как вы можете научить этому детей.

Составление чисел — это способность соединять две части в одно целое. Например, дети будут собирать наборы объектов меньшего количества, чтобы сделать полный набор.

Разложение чисел — это способность разбивать числа на составные части.

 

7 различных способов обучения разложению чисел

Обучение разложению и составлению чисел выглядит по-разному в каждом классе. Однако здесь, в Little Learning Corner, я делюсь советами и ресурсами для детей младшего возраста, специализируясь на Kinder, первом и втором классе. Поэтому давайте рассмотрим несколько советов по обучению разложению чисел в младших классах. Если вы ищете стратегии обучения детей старшего возраста, ознакомьтесь со статьей «Время изучать математику в средней школе».

1. Модель, модель, модель:   Не могу не подчеркнуть. Когда вы учите числа, говорите о них как можно больше. Вместо того, чтобы говорить, что это число 7, вы можете сказать: «Это число 7. Мы можем составить число 7 разными способами, например, 1 и 6, 2 и 5, 3 и 4, 5 и 2, 6 и 1 или 7 и 0».
2. Разговоры о математике:  Когда вы садитесь и ведете математические или числовые беседы с детьми, происходит что-то особенное. Я создал математические беседы для детского сада, первого и второго класса, чтобы увеличить вовлеченность и способствовать независимому мышлению. Когда вы ведете математический разговор о числах, дети выражают свои мысли в обстановке без суждений. Дети учатся объяснять свои рассуждения, а также учатся на обработке других.
3. Предоставить различные инструменты и материалы:   Чтобы научить детей разлагать числа, подготовьте различные манипуляторы, наглядные материалы и листы для записи, чтобы дети могли работать над процессом. Также важно поощрять маленьких детей использовать картинки, пальцы или предметы для проработки и построения своего понимания.
4. Играйте в игры : изучение математики с помощью игр развивает навыки решения задач, позволяет им практиковать стратегию в неформальной обстановке и позволяет детям обсуждать стратегии со сверстниками. Ниже перечислены забавные игры.
5. Продлить календарное время : Поговорив о погоде и днях недели, вы, вероятно, займетесь подсчетом дней в школе. Используйте это время, чтобы поговорить о числе. Например, если вы только что добавили наклейку на 64-й день, расскажите о том, что означает 64-й день, и о том, какое место занимает каждая цифра. (т.е. осталось 6 групп по 10 и 4 дня)
6. Маленькая группа и целая группа :  При обучении составлению и разложению чисел используйте комбинацию уроков для малых и целых групп. Как правило, работая в детском саду, я знакомил с навыком весь класс, повторно обучал и совершенствовал его в небольшой группе, а затем позволял другим ученикам работать в центрах, давая им время исследовать и практиковаться самостоятельно или со сверстниками.
7. Создайте и отобразите якорную диаграмму:   Когда вы создаете математическую якорную диаграмму ВМЕСТЕ с детьми, она становится значимой. Работайте вместе, чтобы создать якорную диаграмму для разложения чисел, и повесьте ее в таком месте, где они смогут быстро обратиться к ней, когда им понадобится поддержка.

Используйте цветные стикеры для заметок, чтобы сделать опорные диаграммы для чисел до 10. При использовании стикеров вы можете удалить один из цветов и попросить детей составить числовое предложение и найти пропущенное число. Например, на приведенной ниже якорной диаграмме дети сказали бы: «4+_=10, а пропущенное число — 6».

 

7 Учебные материалы по разложению чисел

1. Разложение чисел на карты с 10 точками

Эти красочные карты с 30 точками представляют собой цифры от 1 до 10 с 3 различными расположениями точек. Красные и желтые точки соответствуют стандартным контрманипуляторам, используемым в классе.

2. Числовые связи

В большинстве детских садов, первых и вторых классов вы увидите детей, работающих с числовыми связями.

Числовые связи — это визуальные инструменты, используемые для обучения составлению и разложению чисел. Они также являются отличным способом представить семейства фактов и концепции отсутствующих чисел.

Вот пример того, как показать число 10 с помощью числовой связи. Этот номерной коврик был включен в одну из моих коробок подписки Kindergarten Crate. Если вы хотите попробовать коробку, используйте код CORNER, чтобы получить скидку 10%.

Число десять было выбрано случайным образом из набора тематических карточек с числами.

Вы также можете найти коллекцию материалов для нумерации на Amazon, например:

• магнитные номерные облигации
• Карточки с цифрами для сухого стирания
• карточки с номерами облигаций

3. Игры с разрядностью значений

• Игровая доска Dino-Math Track для разрядов, сложения и вычитания
• Сафари с ценой места
• Магнитная подставка Десять блоков для демонстрации разрядности
• Free Place Value распечатать игру

4.

  I Have, Who Has Ten’s Frames Numbers to 20

I Have… Who Has (Superheroes) – это увлекательная математическая игра с цепной реакцией, позволяющая практиковаться в распознавании чисел и составлении чисел до 20.  Эта математическая игра для детского сада и первого класса можно играть всей группой или небольшими группами на математических станциях.

Учащиеся быстро усваивают схему этой игры и с удовольствием называют свою карточку. «У меня _____, у кого ____?» – считая, сколько в десятках кадров вверху, затем считывая следующее число внизу карточки, рядом с красочным супергероем.

Дети не могут спорить, кто ходит первым, и вам не нужно принимать это решение! Стартовая карта и конечная карта включены. Возьмите «У меня есть, у кого есть?» ЗДЕСЬ.

5. Бесплатные игры «Часть-часть-целое»

• Бесплатная часть, часть, целое (числа до 5)
• Бесплатный мини-блок «Часть-часть-целое»
• Free Math Olympics Shake and Spill для печати. Игры с встряхиванием и разливом лучше всего работают с двухсторонними счетчиками. Дети кладут определенное количество фишек в чашку, встряхивают ее, а затем высыпают. Когда они пролиты, дети могут увидеть, как разложить целое число, используя меньшие числа.

6. Головоломки

Головоломки, даже если они не считаются головоломками, показывают, как работает концепция часть-часть-целое. Когда вы складываете части головоломки вместе, вы получаете целостную картину. Вот несколько головоломок для обучения этому понятию:

• Математическая головоломка The Learning Journey
• Really Good Stuff Kites and Tails Puzzle для разложения чисел до 10
• Шаблоны блоков

 

7. Моя тетрадь с десятками

Потренируйтесь составлять и разлагать десять чисел или чисел от 10 до 20, а затем попросите детей записать свою работу в эту «Книгу с десятками».

Дети будут использовать имеющиеся фишки для вырезания и вставки или использовать другие материалы, такие как точки или наклейки, в сочетании с десятками, чтобы построить показанное число. Затем на каждой странице они должны написать числительное в развернутом виде, показав разрядное значение разряда десятков и разряда единиц.

 

 

Оценка составления и разложения чисел

Теперь, когда вы узнали разницу между составлением и разложением, а также узнали о методах обучения и ресурсах, давайте немного поговорим об оценивании.

При проверке понимания учащимися вы хотите использовать множественные оценки. Например, вы захотите наблюдать и делать заметки, как они манипулируют объектами, играют в игры и участвуют в математических беседах, когда учатся разлагать числа. Вы также можете проверить их прогресс, просматривая готовые образцы работ, такие как книга с десятками кадров, показанная выше.

Если вам нужна официальная оценка, вы можете отслеживать их прогресс в рубрике на основе баллов. Вот примеры математических рубрик для детского сада и первого класса, которые можно использовать для документирования успехов детей в математике.

Рубрики по математике для детского сада

Рубрики по математике для 1-го класса

 

Надеюсь, вы нашли все необходимое, чтобы чувствовать себя уверенно при обучении составлению и разложению чисел в раннем детстве.

 

Перед тем, как вы пойдете, вот несколько популярных постов в блогах, которые вам понравятся:

15 удивительных преимуществ математических бесед с детьми

115 лучших стихов, которые стоит читать с удовольствием

36 занимательных заданий на вычитание

0078 Разложение чисел

Числовые связи – игры, рабочие листы и как их учить

Начальная математика

Помогите своим ученикам узнать числовые связи до 20 и выше с помощью этих идей для уроков, видео и рабочих листов…

по Обучающая проволока

Если вы учитель KS1 или KS2 и хотите преподавать числовые связи или освежить память учеников, у нас есть все рабочие листы, песни и онлайн-игры, которые вам нужны, а также советы ведущих экспертов о том, как преподавать эту тему в творческой форме. и памятные способы.

Перейти к разделу:

• Что такое числовая связь?
• Рабочие листы с номерами облигаций
  • Листы с номерами 10
  • Листы с номерами 20
• Песни с номерами
  • Числовые связи до 5 песен
  • Числовые связи до 10 песен
  • Числовые связи до 20 песен
• Как обучать числовым связям
  • Использование мятных кремов для обучения числовым связям в KS1
  • число облигации в KS1
  • Облигации с числами из 6-10 игр в кости для KS1/2
  • Игра «Очистить колоду»
  • Дополнительные идеи о том, как обучать связям с числами
• Игры с облигациями с числами
  • Облигации с числами к 10 играм
• Количество облигаций – основные сведения
  • Количество облигаций до 5
  • Количество облигаций до 10
  • Количество облигаций до 20
  • Количество облигаций до 100

6 6

Что такое числовая связь?

Связи чисел — это пары чисел, составляющие данное число. Таким образом, они также известны как «пары чисел».

---

Рабочие листы числовых облигаций

Ищете распечатанные рабочие листы по числовым облигациям для использования в классе? Мы вас привели в порядок.

Количество облигаций на 10 листе

Помогите ученикам попрактиковаться с нашим эксклюзивным набором из 10 рабочих листов.

Темы от животных до праздников, от инопланетян до спорта. В бесплатной загрузке вы найдете красочные школьные плакаты, пары карточек и множество иллюстрированных рабочих листов для учеников.

Добавляйте сложение и вычитание в смесь с этим набором из 10 рабочих листов, идеально подходящим для KS1. Это иллюстрированный PDF-файл на четырех страницах, содержащий 12 математических задач, предназначенных для того, чтобы помочь учащимся практиковать числовые связи до 10.

Количество облигаций на 20 листе

Помогите учащимся KS1 попрактиковаться в связях чисел до 20 с помощью этого комплекта рабочих листов.

Он был создан в соответствии с небольшими этапами математических схем работы «Белая роза» и содержит ряд наглядных примеров, которые помогут ученикам и побудят их к более глубокому мышлению.

---

Номер облигации песни

Видеоролики — отличный способ познакомить учащихся с концепцией числовых связей — будьте осторожны, эти запоминающиеся числа будут застрянет у вас в голове на несколько дней.

Номер облигаций на 5 песен

Это число Джека Хартмана, связанное с 5 видео, объясняет концепцию с большим энтузиазмом, чем мы когда-либо могли…

Номер облигации на 10 песен

Вот еще одно видео с нашим милым другом Джеком — на этот раз это песня Джека Хартмана «Количество бондов к 10».

Если вам больше нравится спокойная версия игры «Гребите, гребите, гребите на лодке «, то вот курс миссис Симм для 1-го года обучения, который расскажет вам все, что вам нужно знать о числовых связях до 10: 9.0003

Мы очень усердно работали и практиковали наши числовые связи. Что вы думаете? 👌🏻@crontonceschool @LDSTEducation pic.twitter.com/VJCMnneFvc

— Year 1 (@crontony1) 24 января 2019 г.

Вот текст полностью, так что ваш класс может попробовать:

9 и 1 — числовые связи,
8 и 2 — друзья,
7 и 3, 6 и 4,
5 и 5 — близнецы.

Номер облигации на 20 песен

Если бы Джордж Эзра написал песню об облигациях, она бы звучала примерно так. Мы не совсем уверены, какое отношение к чему имеют бананы и спагетти, но вскоре это станет ушным червем, от которого вы просто не сможете избавиться.

---

Как научить числовым связям

По словам Джеммы Шервуд, заведующей кафедрой математики в средней школе и шестом классе Хейбриджа:

«Лучшее понимание чисел достигается, когда учащиеся знают математические факты, такие как числовые связи […] наизусть, потому что они могут затем работать с этими знаниями — что намного проще, чем работать без него».

Национальная учебная программа гласит, что к концу Y2 учащиеся KS1 должны «знать числовые связи до 20 и быть точными в использовании и понимании разрядного значения. Акцент на практике на этом раннем этапе поможет беглости речи».

Оценка автоматизма с числовыми связями? L демонстрирует с погремушками. Дети YR развили автоматизм не с помощью карточек, а путем изучения композиции, субитизации, паттерна, структуры и отношений в числах. Внедрение глубокого понимания #EYFS #MasteringNumber pic.twitter.com/9Sasxomh4e

— д-р Дебби Морган CBE (@ThinkingMaths) 18 июня 2022 г.

Здесь у нас есть ряд способов помочь ученикам запоминать и рассуждать с числовыми связями до 10 и 20.

---

Использование мятных кремов для обучения числовым связям в KS1

Идея этого урока от Майка Аскью, адъюнкт-профессора педагогики в Университете Монаш, направлена ​​на то, чтобы научить детей KS1 сотрудничать, изучать числовые факты и систематически работать.

Подготовка к уроку

Перед уроком подготовьте листочки, которые дети потом будут использовать для записи своих результатов. На них показаны массивы квадратов, два на пять, которые достаточно велики, чтобы нарисовать простой «мятный крем»9.0003

Вы должны уместить шесть матриц на листе формата А4, но разрежьте их так, чтобы все они были на отдельных листах.

Начать урок

Расскажите о коробках со сладостями, которые вы приготовили для друзей на школьных каникулах. Наличие нескольких мятных кремов для детей на вкус также заставит их сесть и обратить внимание!

«Каждый год я делаю коробки мятных кремов для семьи и друзей на Рождество. Кто делал или пробовал мятные кремы?»

Обсудите эти и другие сладости, которые нравятся детям. Затем поднимите пустой массив, который вы сделали, и скажите:

.

«Я всегда упаковываю свои мятные кремы в вот такую ​​коробку. Повернитесь к человеку рядом с вами. Договоритесь с этим человеком, сколько кремов я могу положить в коробку».

Попросите детей объяснить, откуда они знают, что есть места для 10 кремов, не считая их всех.

Кто видел 5+5? Кто видел 5 лотов по 2?

Далее, произнесите:

Я делаю мятные кремы двух цветов. Некоторые белые, а некоторые зеленые. Я положил немного белого и немного зеленого в каждую коробку. Поговорите со своим партнером, решите, какую коробку кремов сделать и сколько белых и сколько зеленых кремов будет в коробке».

Приняв предложения детей, выберите один пример, скажем, 4 зеленых и 6 белых.

Попросите детей помочь вам решить, куда положить кремы в коробке, записывая это на линейке по ходу дела. Произнесите:

«Обратитесь к своему напарнику. Как вы можете быть уверены, что есть 4 зеленых и 6 белых кремовых?»

Пока дети проверяют, правильно ли вы собрали коробку, запишите другое расположение деления 4/6, например:

или

Покажите детям это второе расположение и попросите партнеров обсудить, другая ли это коробка.

Умышленно оставляю здесь вопрос неконкретным — в каком-то смысле отличается тем, что кремы устроены иначе. В другом смысле не отличается тем, что по-прежнему 6 белых и 4 зеленых мяты.

Продолжение урока

Подведите детей к мысли, что на этом уроке вы будете думать о них как об одной и той же коробке кремов. Коробки будут разными только в том случае, если количество зеленых и белых кремовых разное. Скажи так:

«Мне интересно, если я положу в каждую коробку разное количество зеленых и белых кремов, сколько разных коробок получится? Это проблема, которую я хотел бы, чтобы вы помогли мне решить. Я хотел бы сделать как можно больше коробок с двумя видами мятных кремов».

Предложите парам еще раз объяснить друг другу проблему и проверьте, все ли понятно, а затем скажите:

«Вы будете работать вместе, чтобы записывать разные коробки кремов и брать их по очереди. Вот как — один человек будет записывающим, а другой — выбирающим. Выбирающий скажет, сколько кремов каждого типа положить в коробку, и записывающее устройство быстро нарисует числа каждого типа. Тогда вы поменяетесь местами».

Пригласите ребенка стать вашим партнером и покажите, как вы работаете.

Парное занятие 1

Пока дети садятся за работу в парах, сконцентрируйтесь на том, чтобы они правильно чередовались и слушали инструкции друг друга.

Не позволяйте этой части урока затянуться: как только пары сгенерируют шесть или около того клеток, верните их внимание всем классом к доске.

Назад к проблеме

Собрав всех вместе, обойдите группы и попросите у них одну из их коробок.

Поместите это на доску с помощью Blu-Tack. После того, как каждая пара предложит коробку, спросите класс, думают ли они, что они у вас есть, или есть ли у какой-либо пары еще одна коробка, которой у нас еще нет.

Обычно предлагается больше, и неизбежно вы получите несколько коробок, которые выглядят по-разному, но на самом деле содержат одинаковое количество каждого крема.

Если этого не происходит, «спроектируйте» это, выбрав и отобразив несколько дубликатов.

Теперь, когда выставлено большое количество коробок, попросите детей внимательно посмотреть и проверить, все ли коробки у вас разные.

Как только они начнут замечать дубликаты, попросите их поговорить со своим партнером о том, как вы могли бы организовать ящики, чтобы вы могли видеть, есть ли дубликаты и какие недостающие.

Работая с их предложениями, заказывайте ящики 1,9; 2,8; 3,7 и так далее.

Дубликаты можно размещать друг над другом и оставлять пробелы для любых отсутствующих комбинаций.

Разбейте детей на пары, чтобы они продолжили и попытались собрать полный набор коробок.

Парное занятие 2

Возвращаясь к задаче, дети будут более организованно проверять наличие дубликатов и недостающих комбинаций.

Когда они будут близки к созданию полного набора коробок, предоставьте им сахарную бумагу и клей-карандаши, чтобы они могли «аккуратно» сделать постер из своего набора.

(Большинство найдет 9 решений, хотя всего их 11, если вы разрешите поля, которые будут полностью зелеными или полностью белыми).

Просмотрите и подумайте

Соберите детей вместе, выберите одну или несколько пар, чтобы показать их плакат и рассказать о том, как они организовали свои коробки. Какие закономерности могут увидеть дети?

Наконец, поработайте над записью комбинаций, используя соответствующие цифры и символы.

Покажите плакаты в классе, чтобы показать ориентиры для пар чисел, составляющих 10.

Расширенная деятельность

• Что происходит с тремя видами кремов – белым, розовым и зеленым. Как насчет четырех типов?
• Что, если сделать коробки по 20 штук?
• Предположим, что коробки не обязательно должны быть 2 x 5, и что 12 кремов можно упаковать в коробку 2 x 6. Коробки какой другой формы вмещают 12 кремов? А 24 крема?
• Коробка может иметь более одного слоя. Какие коробки могут вместить 12 кремов?
• Белые сливки стоят 1 пенс, а зеленые кремы — 2 пенса. Сколько стоит каждый из ящиков? Если у вас есть 20 пенсов, какие различные комбинации зеленого и белого крема вы можете купить?

---

Использование куклы-кенгуру для обучения числовым связям в KS1

Используйте этот урок от внештатного консультанта по математике Криса Ингрэма, чтобы помочь своим ученикам KS1 изучить числовые факты и развить навыки решения задач.

Знакомство с проблемой

Подготовьте нить бус и спрячьте ее в сумке куклы кенгуру. Скажи так:

«Сегодня кенгуру спрятала в сумке нитку бус. На нитке 10 бусин. Некоторые красные, а некоторые желтые. Интересно, бусинок больше красных или желтых? Можете ли вы нарисовать картинку или составить числовое выражение, чтобы показать, сколько бусинок может быть красными, а сколько желтыми?»

В этот момент покажите детям большую коробку с бусинами и объясните:

«Можно использовать синие бусы? Почему бы и нет? Можно ли на нитке 14 бусин? Могут ли все 10 быть желтыми?»

Убедитесь, что дети четко понимают, что они собираются составить цепочку из 10 бусин, и что они должны использовать как красные, так и желтые бусины.

Решение проблемы

Дифференциация довольно проста и определяется тем, подходит ли ребенку исследовать и записывать проблему практически, образно или символически.

Кроме того, у вас, вероятно, будут дети, от которых требуется одно решение, тогда как другие дети будут пытаться найти несколько или даже все возможные решения.

Группа 1  

Используя те же ресурсы, что и вы, попросите детей придумать решение, соответствующее критериям – нить из 10 бусин, часть из которых красного цвета, часть желтого.

Это может показаться простым, но наблюдение за детьми в действии показывает, что это больше, чем просто счет.

Большинство маленьких детей не знают пары чисел, составляющих 10, поэтому они случайным образом размещают на нитке красные и желтые бусины.

Некоторые дети считают общее количество, добавляя каждую бусинку, но большинство, кажется, надевают бусинки до тех пор, пока не станет казаться, что они собрали 10 – после чего они пересчитывают их, чтобы узнать.

Если они обнаружат, что бусинок 8 или 11, они, надеюсь, распознают, что их недостаточно/слишком много, и приспособятся соответствующим образом.

Однако будет много детей, чья реакция на эту ситуацию будет заключаться в том, чтобы снять все бусы и начать снова, и снова, и снова.

Это полезный оценочный пункт, и некоторые тщательные вопросы здесь могут привести детей в правильном направлении.

Группа 2

Другие дети также могут решить задачу, используя другие манипуляции. Объясните, что бусинок недостаточно, и предложите ученикам использовать вместо них что-нибудь другое.

Признание того, что бусины можно изображать с помощью другого предмета (кубиков, фишек, цветных мишек и т. д.), и что это не повлияет на их способность понять и решить проблему, является большим шагом вперед.

Группа 3  

Точно так же другие группы могут изобразить решение с помощью краски, цветного карандаша или цветной бумаги.

Это требует более сложного процесса, поскольку дети с меньшей вероятностью будут использовать метод проб и ошибок, как группа 1 (возможно, потому, что будут «доказательства» каждой попытки), и гораздо более вероятно, что они будут использовать «расчет на» как способ отслеживание общей суммы по мере их работы.

Группа 4  

У вас может быть группа детей с более высокими достижениями, которые могут представить свои решения в виде числовых предложений.

Если это так, им может быть предложено найти все возможные решения. Будет интересно посмотреть, работают ли дети систематически при составлении упорядоченного списка – и уверены ли они, что открыли все возможности без повторений!

Назад к проблеме

После того, как дети придумают свое решение (будь то с помощью бисера, красок и т. д.), важно побудить их связать это с исходной задачей. Спросите:

«Как ты думаешь, сколько желтых бусинок у кенгуру, и сколько красных бусинок, и сколько всего бусинок?»

Если это уместно, вы можете спросить:

«Можем ли мы использовать числа, чтобы запомнить вашу идею?»

Дети могут предложить написать цифры желтым и красным карандашом или составить числовое предложение.

Просмотрите и подумайте

Собрать детей вместе после того, как они изучили проблему, — важная часть процесса.

Это возможность для кенгуру напомнить детям об исходной задаче, а ученикам представить различные решения, которые они придумали.

В этот момент ученики могут подумать, что существует столько решений, сколько детей в классе. Ваша роль состоит в том, чтобы помочь учащимся осмыслить эту информацию. Выберите ребенка, который поделится своим решением, и скажите что-нибудь вроде этого:

«Джейк сделал нитку из 3 желтых и 7 красных бусин. У кого-нибудь есть картина или числовое выражение, которое соответствует 3 желтым и 7 красным?»

Соберите вместе все презентации с этой комбинацией, а затем перейдите к другому решению.

На этом этапе вам придется иметь дело с проблемой коммутативности — хотя 3 + 7 явно эквивалентны 7 + 3, вам нужно обращать внимание на контекст и быть осторожным в использовании языка:

---

равно и совпадает с

С какой стороны ни посмотри, есть группа из 10, состоящая из 3 желтых и 7 красных.

---

равно, но не то же, что

Или иметь 3 кошек и 7 собак — это не то же самое, что иметь 3 собак и 7 кошек, хотя в любом случае у вас явно 10 питомцев.

---

Увидеть закономерность

Собирая различные решения, начните перечислять их, чтобы дети поняли, что, организуя решения таким образом, вы сможете увидеть появление закономерности:

Шаблон дает вам уверенность в том, что вы нашли все возможные решения, а также в выявлении отсутствующих решений или повторений.

Некоторые дети с большей вероятностью увидят узор в цветных пятнах, другие найдут узор более четким, если представить его цифрами.

Произнесение рисунка вслух нараспев также поможет детям уловить его.

Реорганизация бусин так, чтобы они представляли две отдельные группы, облегчит субитизацию или подсчет и поможет позже в сеансе с определением закономерностей.

Предоставление практических ресурсов для составления числовых предложений побуждает детей экспериментировать с символической записью как еще одним способом передачи своих идей.

Что в сумке?

В финале этого урока кенгуру показывает бусины, которые у нее есть в сумке, а дети определяют, есть ли у них подходящее решение.

Здесь важно подчеркнуть, что было девять правильных решений проблемы, а не одно.

Завтра, а может быть и до конца недели, кенгуру спрячет в сумке еще 10 бусинок – одни красные, другие желтые – а дети смогут использовать другие свои решения, чтобы угадать, что это могут быть.

Если вы будете показывать решения и регулярно возвращаться к этому занятию в качестве умственного/устного старта, дети вскоре смогут использовать свои знания для решения задач с пропущенными числами:

«У кенгуру в сумке 10 бусинок, одни красные, а остальные желтые. Она даст вам подсказку — она покажет вам все красные бусины, вы можете определить, сколько желтых бусинок? Откуда вы знаете?»

Позже вы можете показать детям, как это связано с такими уравнениями, как 3 + [ ] = 10 или 10 – 3 = [ ].

---

Облигации с номерами из 6-10 игр в кости для KS1/2

Для этого простого задания вам понадобятся игральные кости и несколько цветных карандашей, а также эти бесплатные рабочие листы для игры в кости. Вот как играть:

• Бросьте кубик
• Цвет в количестве кругов на кубике
• Цвет в другой части
• Запишите две части, на которые разбито целое число

---

Очистить колоду

Целью этого задания, проведенного независимым консультантом по вопросам образования Джуди Хорниголд, является помощь учащимся в развитии мгновенного запоминания числовых связей до десяти.

Попробуйте это в качестве разминки в начале урока или в конце для повторения или закрепления.

Как играть

Вам понадобятся четыре набора карт с цифрами от 1 до 9. Перемешайте карты и разложите их лицевой стороной вверх на столе в три ряда по четыре. Игроки по очереди берут пары карт, сумма которых равна 10.

Оставшиеся пробелы заполняются картами из оставшейся колоды. Идея состоит в том, чтобы по очереди находить пары, которые составляют 10, как можно быстрее.

---

Другие идеи о том, как преподавать числовые облигации

Не возражаете рискнуть хорошенько промокнуть Фредди в Y1? Попробуйте это…

Облигации Nerf gun!#StayAtHome #LearnAtHome pic. twitter.com/NNG2CgDri4

— NumBots (Расти) 💎 (@numbots) 27 марта 2020 г.

Эта идея от мисс Уорд требует небольшой предварительной подготовки, но фокусируется на конечное число привязывается к 10 инструменту – наши собственные пальцы…

Часть первая: 😁Привет от меня и моего супер помощника! Сегодня мы рассмотрели числовые связи до 10 и сделали собственный простой ресурс, который вы можете попробовать дома! 😁 pic.twitter.com/K0KJ8IRk3S

— Мисс Уорд (@SomersparkRAW) 26 марта 2020 г.

Вам понадобится только чашка и несколько двусторонних фишек, чтобы воссоздать эту простую игру от миссис Бэйли…

Учим наши числовые связи до 10 с помощью множества различных занятий! Пришлось кинуть двусторонние жетоны и записать расчет 👍 #знания pic. twitter.com/g9ZeBo1l7m

— Миссис Бэйли 🌟 (@MrsBaillie) 8 февраля 2019 г.

---

Игры с числовыми облигациями

Обучение числовым связям до 10 иногда может показаться немного однообразным. Ведь существует лишь небольшое количество комбинаций. Так почему бы не позволить детям заняться чем-нибудь забавным, чтобы либо выучить, либо закрепить свои знания о числовых фактах?

Вот подборка бесплатных, простых в использовании онлайн-игр с числовыми связями, которые может попробовать ваш класс.

Количество облигаций на 10 игр

В этой простой, но удобной игре с десятью рамками есть сетка из 10 ячеек, которые заполняются фишками (или звездами, яблоками или божьими коровками) и спрашивается, сколько их есть или сколько ячеек пусто.

Вы также можете перейти на уровень сборки, где дети должны вставить правильное количество фишек. Затем есть «заполнение», когда их спрашивают, сколько еще фишек нужно, чтобы завершить набор из 10. И «добавить», когда у вас есть два набора из 10, которые нужно заполнить правильным количеством фишек, прежде чем суммировать итоги вместе.

Изучите числовые облигации до 10 в этой игре «Любопытный Джордж: Музей десятков».

Следуйте за ним по музею, где у каждого экспоната должно быть 10 экспонатов, но некоторых не хватает. Задача ваших учеников — помочь Джорджу определить, сколько еще им нужно, чтобы получилось 10.

В этой забавной маленькой игре с числовыми облигациями «Одень своего монстра» дети могут одеть своего монстра в различную одежду и аксессуары.

Но для этого им нужно будет ответить на вопросы числовых связей до 10.

Ряд пронумерованных шаров катится к дыре в этой игре с номером 10, и ваша задача — остановить это. Вы делаете это, запуская свои собственные сферы, чтобы сделать числовые связи 10 и наблюдать, как они исчезают. Это блестяще затягивает.

Игры на время

В этой быстрой игре «Нажми на кнопку» есть ряд вариантов, которые вы можете попробовать, включая удвоение, половинку, таблицу умножения, факты деления и квадратные числа, а также, конечно же, числовые связи.

Даже в числовых облигациях вы можете выбрать числовые облигации до 10, 20 или 100, а затем в них есть разные задачи.

С базовым числом, равным 10, детям дается одно число, и они должны выбрать число, которое составит пару, чтобы получить 10. У них есть минута, чтобы получить как можно больше.

Еще более простая версия — это игра «Минутка безумной математики» (хотя вы можете установить более длительный таймер, если хотите), в которой дети должны за 60 секунд ответить на максимальное количество числовых связей до 10 сумм.

Есть опция справки, которая дает вам цветную рамку из 10 для визуальной помощи, и вы также можете проверить и распечатать свои результаты.

Еще один вариант системы тактового ритма, эта игра «Я могу вспомнить все числовые связи до 10» имеет то преимущество, что в смесь добавляются вопросы на вычитание.

Ответьте правильно на последовательные вопросы, чтобы повысить свой уровень, но будьте осторожны, это увеличивает сложность сумм.

Продвинутая игра

Эта игра с числовыми связями — одна из тех забавных маленьких головоломок, в которые можно играть часами.

Идея состоит в том, чтобы соединить числовые связи с 10, расчистив путь между ними. Ваша линия может согнуться один раз, два или шарики могут быть рядом друг с другом (не по диагонали). Просто не забывайте следить за тем, как долго вы играете!

---

Число облигаций – основы

Хотите освежить в памяти концепцию числовых связей? Вот что вам нужно знать, в двух словах.

Номер облигаций до 5

Числовые связи до 5 — это пары чисел, которые в сумме дают 5. Числовые связи для числа 5:

• 0 + 5
• 1 + 4
• 2 + 3
• 3 + 2
• 4 + 1
• 5 + 0

Количество облигаций от 90 до 2 10

Числовые связи до 10 — это пары чисел, которые в сумме дают 10. Числовые связи для числа 10:

• 0 + 10
• 1 + 9
• 2 + 8
• 3 + 7
• 4 + 6
• 5 + 5
• 6 + 4
• 7 + 3
• 8 + 2
• 9 + 10006 7 + 3
8 + 2

9 + 10006

10 + 0

Номер облигаций до 20

Числовые связи до 20 — это пары чисел, которые в сумме дают 20.

Найти пропущенное число — в сериях, примерах, упражнениях

Поиск пропущенных чисел в последовательности или серии — это увлекательное занятие для учащихся, позволяющее идентифицировать закономерности и запоминать таблицы умножения, числа, основные математические операции или даже счет. . Данная деятельность способствует развитию умственных способностей учащихся. Мы можем найти пропущенные числа, используя графические изображения, в ряду, в формате таблицы или просто используя пробелы. Чтобы найти пропущенные числа, нам нужно наблюдать за данным шаблоном, а затем заполнить пробел.

В этой статье мы обсудим различные действия по поиску пропущенных чисел, а также понаблюдаем за закономерностями и вычислениями. Мы будем выполнять задание с использованием рядов, таблиц и графических изображений для лучшего понимания концепции. Мы найдем недостающие числа в сложении, вычитании, умножении и делении, чтобы лучше понять эти арифметические операции.

1.	Что такое пропущенные номера?
2.	Типы действий с пропущенными номерами
3.	Найти пропавший номер
4.	Найти недостающее число в ряду
5.	Пропущенные числа в сложении и вычитании
6.	Пропущенные числа при умножении и делении
7.	Пропущенные номера — до и после
8.	Часто задаваемые вопросы о недостающих номерах

Что такое пропущенные номера?

Пропущенные числа — это в основном числа, которые были пропущены в последовательности или серии. Мы можем найти эти недостающие числа, определив шаблон. Всякий раз, когда в ряду чисел есть пробелы, несколько чисел были пропущены, и нам нужно соблюдать закономерность и заполнять пробелы подходящими числами. Мы можем использовать метод нахождения пропущенных чисел, чтобы запомнить счет, таблицу умножения и научиться использовать арифметические операции. Упражнения по поиску пропущенных чисел помогают учащимся развивать умственные способности и улучшают их мелкую моторику в процессе обучения.

Типы действий с пропущенными номерами

Мы можем использовать различные формы деятельности, чтобы найти пропущенные числа, такие как:

• Графическое изображение
Серия
• Представление
• Представление стола
• Заполните пробелы между вычислениями

Найти пропавший номер

Мы можем найти недостающее число в действии, наблюдая за шаблоном или используемыми вычислениями. Чтобы сделать занятие по поиску пропущенных чисел интересным для учащихся, мы можем использовать графические изображения и интерактивные изображения. Давайте рассмотрим несколько примеров таких действий, чтобы понять процесс и шаги, которые необходимо выполнить, чтобы найти недостающие числа.

Пример 1: Найдите недостающие числа в данной последовательности: 1, , 5, , 9, 11, 13, , 17, 19.

Решение: , чтобы найти недостающие числа , мы будем следовать шагам, указанным ниже:

• Шаг 1: Соблюдайте закономерность между приведенными последовательными числами. Здесь 9, 11, 13 — последовательные числа, и мы видим, что все они — нечетные числа. 17 и 19 также являются нечетными последовательными числами.
• Шаг 2: Здесь нечетные числа.
• Шаг 3: Подсчитайте и начните вводить числа. 1, 3 , 5, 7 , 9, 11, 13, 15 , 17, 19.
• Шаг 4: Проверьте шаблон после заполнения пропущенных цифр. Паттерн правильный во всей последовательности, то есть числа являются нечетными последовательными числами.

Поскольку последовательность одинакова, ответы верны.

Ответ: Недостающие числа 3, 7 и 15.

Пример 2: Вставьте подходящее число:      + 3 = 8.

Решение: Чтобы найти пропущенное число в данном выражении мы увидим используемую операцию.

• Шаг 1: Вспомните концепцию сложения. Нам нужно найти первое слагаемое.
• Шаг 2: Задумайте число, которое при прибавлении к 3 дает в сумме 8.
• Шаг 3: 5 + 3 = 8. Итак, недостающее число 5.
• Шаг 4. Запишите пропущенное число:  5  + 3 = 8.

Ответ: Недостающее число 5.

Найти недостающее число в ряду

Когда ряд чисел дан с пробелами, то мы находим недостающее число в ряду. Такой ряд следует определенной схеме. Давайте обсудим последовательность счетных чисел от 1 до 10, от 1 до 20 и от 1 до 50. Это поможет нам выучить счетные числа и запомнить их простым способом.

Пропущенные числа 1-10

Запишем последовательность счетных чисел от 1 до 10 с пробелами, а затем заполним пропущенные числа.

1,      , 3, 4, 5, 6,      ,      , 9, 10.

Как мы видим выше, в ряду есть пробелы, и здесь используется схема подсчета чисел. от 1 до 10. Давайте посчитаем и вставим пропущенные числа. Это помогает нам запоминать счетные числа.

1, 2 , 3, 4, 5, 6, 7 , 8 , 9, 10.

Пропущенные числа 1-20

Ниже приведен ряд счетных чисел от 1 до 20 с пробелами. Вспомним счет и заполним пропущенные числа в ряду.

1, , 3, 4, 5, 6, , , 9, 10, 11, , 13, , 15, 16, , , 19, 20.

55

Ответ: 1, 2 , 3, 4, 5, 6, 7 , 8 , 9, 10, 11, 12 , 13, 14 , 15, 16, 17 , 18 , 19, 20.

Пропущенные числа 1-50

Теперь давайте повторим подсчет чисел от 1 до 50, используя задание пропущенных чисел. Ниже приведен ряд чисел от 1 до 50 с пробелами.

1,     , 3, 4, 5, 6,      ,      , 9, 10, 11,      , 13, 13, 16, 190, 0093 , , 19, 20, 21, 22, 23, , , 26, 27, , 29, , 31, , 33, 34, , 36, , 34, 34, , 36, 44444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444н. , , , 40, 41, 42, 43, 44, , 46, , 48, , 50.

Дайте нам теперь заполнить отсутствующие номера.

1, 2 , 3, 4, 5, 6, 7 , 8 , 9, 10, 11, 12 , 13, 14 , 15, 16, 17 , 18 , 19, 20, 21, 23, 23, 24 , 25 , 26, 27, 28 , 29, 29, 25 , 26, 27, 28 , 29, 30 , 31, 32 , 33, 34, 35 , 36, 37 , 38 , 39 , 40, 41, 42, 43, 44, 45 , 4693 4743 4743 4743 47 4743 4743 4743 4743 47 4743 47 47 4743 47 47 47 47 47 4743 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 47 474. , 48,  49  , 50.

Пропущенные числа в сложении и вычитании

Теперь мы пересмотрим концепцию сложения и вычитания, используя упражнение с пропущенными числами. Давайте рассмотрим некоторые из приведенных ниже примеров и поймем, как найти пропущенные числа.

•      + 5 = 9
• 1 — 1 =      
• 10 —       = 4
• 7 + 4 =      
• 18 +       = 20
•       — 3 = 2

Теперь мы решим вышеуказанные проблемы одну за другой.

•       + 5 = 9. Нам нужно найти число, которое при прибавлении к 5 дает сумму, равную 9. При сложении 4 и 5 получается 9. Итак, у нас есть 4 + 5 = 9.
• 1 — 1 =       . Нам нужно найти число, равное 1 минус 1. Когда число вычитается из самого себя, разница равна 0. Итак, мы имеем 1 — 1 =  0  .
• 10 —        = 4. Нам нужно найти число, которое при вычитании из 10 дает разность, равную 4. Итак, 10 —    6    = 4
• 7 + 4 =       . Сумма 7 и 4 равна 13. Таким образом, 7 + 4 =  13 
• 18 +      = 20. Мы знаем, что сумма 18 и 2 равна 20. Итак, имеем 18 +   2    = 20
•      — 3 = 2. Разность 5 и 3 равна 2. Итак, имеем   5   — 3 = 2.

Пропущенные числа при умножении и делении

Так же, как мы выполняли задание по поиску пропущенных чисел при сложении и вычитании в предыдущем разделе, давайте выполним аналогичное задание для умножения и деления, чтобы пересмотреть концепцию и найти пропущенные числа.

• 4 × 2 =     
• 3 ×      = 9
•       × 5 = 25
• 10 ÷ 2 =     
• 12 ÷      = 4
•      ÷ 6 = 3

Теперь мы решим вышеуказанные проблемы одну за другой.

• 4 × 2 =      . Произведение 4 и 2 равно 8. Итак, 4 × 2 = 8
• 3 ×      = 9. Нам нужно найти число, которое при умножении на 3 дает произведение, равное 9. Мы знаем, что произведение 3 на себя равно 9. Итак, 3 ×   3     = 9
•       × 5 = 25. Нам нужно найти число, которое при умножении на 5 дает произведение, равное 25. Мы знаем, что произведение 5 на себя равно 25. Итак,  5  × 5 = 25
• 10 ÷ 2 =      . При делении 10 на 2 в частном получается 5. Итак, 10 ÷ 2 = 9.0093   5   .
• 12 ÷       = 4. Мы знаем, что при делении 12 на 3 частное равно 3. Итак, 12 ÷   3   = 4 
•       ÷ 6 = 3.  Мы знаем, что при делении 18 на 6 частное равно 3. Итак, 18   ÷ 6 = 3.

Итак, мы нашли недостающие числа в данных задачах на умножение и деление.

Отсутствующие номера — до и после

Давайте обсудим деятельность по поиску пропущенных чисел для запоминания чисел до и после определенного числа. Ниже приведен набор примеров для поиска чисел:

•      , 5,      
•      , 10,      
•      , 45,      
•      , 18,      

Теперь найдем недостающие числа.

•      , 5,       . Число до 5 равно 4, а число после 5 равно 6. Итак, у нас есть 4 , 5, 6 .
•      , 10,       . Число до 10 равно 9, а число после 10 равно 11. Итак, у нас есть 9 , 10, 11 .
•      , 45,     .Число до 45 – 44, а после 45 – 46. Итак, имеем   44   , 45,    46   .
•      , 18,     .Число до 18 – 17, а после 18 – 19. Итак, имеем   17   , 18,  19   .

Упражнение по поиску пропущенных чисел помогает запомнить счетные числа.

Важные примечания о пропущенных числах

• Поиск пропущенных чисел в последовательности или ряду — это занятие для детей, позволяющее определить закономерности и запомнить таблицы умножения, числа, основные математические операции или даже счет.
• Мы можем использовать ряды, графические изображения, таблицы и пробелы, чтобы создать задание по поиску пропущенных чисел.
• Нахождение пропущенных чисел для тренировки мелкой моторики.

☛ Похожие темы:

• Целые числа
• Простые числа
• Составные номера

Поиск неизвестных дополнений и пропущенных чисел

1. Учебные ресурсы
3. 1-й класс

Изучение того, как находить неизвестные слагаемые и пропущенные числа, является первым классом, общий базовый математический навык: 1. OA.4. Ниже мы показываем два видеоролика, демонстрирующих этот стандарт. Затем мы даем разбивку по конкретным шагам в видеороликах, которые помогут вам провести урок.

Предварительное обучение

Ваши учащиеся должны быть знакомы с навыком для детского сада: понимать пары чисел, равные 10, и знать все разложения (например, 5=4+1, 5=2+3) чисел меньше 10. Этот навык создает основу для разработки стратегии, понимания значений мест и свойств операций (K.OA.3-4). Ваши ученики также должны понимать, что десять единиц плюс больше единиц считаются «подростками» (K.NBT.1).

Future Learnings

Понимание того, как выполнять сложение и вычитание в пределах 20, позволит вашим учащимся выполнять аналогичные навыки до 100, в конечном итоге расширив эти навыки для работы с большими числами и решения двухэтапных задач со словами (2.OA. 1). Они также смогут применять этот навык с задачами в различных контекстах, включая длину, графические изображения и гистограммы (2. NBT.5).

Общий базовый стандарт: 1.OA.4 — Понимание вычитания как неизвестной задачи на сложение

Учащиеся, понимающие этот принцип, могут:

1. Использовать картинки, предметы, числа и т. д. для объяснения связи между задачами на сложение и вычитание.
2. Представьте, как связаны сложение и вычитание, используя картинки, предметы, числа и т. д.
3. Перепишите уравнения вычитания как уравнения сложения, в которых отсутствует число.

‍ 2 видеоролика, которые помогут вам преподавать стандарт Common Core: список стандартов

Ниже мы приводим и разбираем два видеоролика, которые помогут вам научить своих учеников этому стандарту.

‍ Видео 1: Найдите недостающее число

Видео начинается с двух примеров уравнений и спрашивается, имеют ли они одинаковый ответ:

1. 10 — 2 = ?
2. 10 = 2 + ?

Чтобы помочь решить проблему, видео содержит «счетчики», которые представляют числа. В первом наборе фишек 10, 2 убираются, заканчивая 8 фишками.

Нижний набор счетчиков также имеет 10 и представляет собой сумму во втором уравнении. В среднем наборе 2 фишки, и в видео спрашивается, сколько фишек нужно добавить к 2, чтобы получилось 10. Ответ: 8.

Оба уравнения имеют одинаковый ответ:

1. 10 — 2 = 8
2. 10 = 2 + 8

посчитай и реши уравнение.

‍  Видео 2. Найдите пропущенное число: напитки и уравнения

Видео начинается с обзора того, как работают семейства фактов, и показывает пример уравнения семейства фактов.

«Семейство фактов — это набор из 3 чисел, которые могут составить 2 уравнения сложения и 2 уравнения вычитания».

1. В уравнении 3 — 1 = 2,
2. Можно поменять местами 1 и 2: (3 — 2 = 1) и получить правильный ответ.
3. Уравнение также может образовывать два оператора сложения: (1 + 2 = 3; и 2 + 1 = 3).
4. Числа 1, 2 и 3 — это семейство фактов.

Затем Боддл предлагает вашим ученикам практические задачи, чтобы они могли проверить, что они узнали. В первой практической задаче используются освежающие фруктовые напитки.

1. Всего 10 напитков.
2. 7 из этих напитков со вкусом вишни.
3. Сколько со вкусом апельсина?
4. Вычитая 7 из 10, можно найти ответ.
   а. 10 — 7 = 3
5. Есть 3 напитка со вкусом апельсина.
6. Задачу можно решить, если известно количество апельсиновых напитков вместе с их общим количеством.
   а. 10 — 3 = 7.

Затем видео предлагает дополнительные практические задачи на нахождение неизвестного слагаемого.

1. 2 + __ = 7
   а. Вы можете вычесть 2 из 7, чтобы найти ответ.
   б. 2 + 5 = 7
2. 3 + __ = 4
   а. Вы можете вычесть 3 из 4, чтобы найти ответ.
   б. 3 + 1 = 4
3. 7 + __ = 9
   а. Вы можете вычесть 7 из 9, чтобы найти ответ.
   б. 7 + 2 = 9

Хотите больше практики?  

Предоставьте своим учащимся дополнительную практику в соответствии со стандартами с помощью Boddle Learning. Boddle включает в себя вопросы, связанные со сравнением и измерением длин, а также награждение монетами и играми для ваших учеников, чтобы они были вовлечены. Нажмите здесь, чтобы зарегистрироваться в Boddle Learning и создать свое первое задание сегодня.

*Информация о стандартах взята с веб-сайта New Mexico Instructional Scope for Mathematics Департамента государственного образования штата Нью-Мексико и веб-сайта Common Core.

Урок беглости: приоритезация пропущенных чисел в уравнениях

Если вы хотите повысить беглость чтения фактов вашими учащимися, уделение первоочередного внимания навыку пропущенных чисел в уравнениях является одним из ключей к разблокировке этого навыка у вашего учащегося. Если ваши ученики боролись с этим навыком в прошлом, вы не одиноки! Нахождение пропущенных чисел в уравнениях может быть трудным навыком для изучения, но отдача значительна!

Несколько лет назад я сидел с первоклассным учителем, который работал над пропущенными числами в уравнениях. День закончился, и она сидела за столом с почками, подперев голову руками из-за полного истощения после дня. Она позвала меня на встречу, потому что она выполнила математическую программу на тройку, и все же многие из ее учеников все еще пытались найти пропущенные числа в уравнениях сложения и вычитания.

Я так ясно чувствовал ее разочарование. Я был на ее месте годом ранее, когда пытался поддержать своих студентов-интервентов… каждая моя попытка терпела неудачу. Мои ученики постоянно складывали и вычитали произвольные числа, чтобы найти ответ. Любой ответ . Независимо от того, имел ли ответ смысл.

Мне захотелось сказать оно того стоит? Можем ли мы просто уйти от этого навыка?

Зачем отдавать приоритет пропущенным числам в уравнениях?

Если бы ваши ученики должны были запомнить каждый факт сложения и вычитания, им нужно было бы запомнить более 200 отдельных фактов. Это неразумная задача! Когда ваши учащиеся могут быстро и легко излагать факты, автоматизм и припоминание становятся простым побочным продуктом!

Способность находить пропущенные числа в уравнениях означает, что ваши учащиеся четко понимают взаимосвязь между сложением и вычитанием.

Учащийся, который знает, что 3 + 5 = 8 и понимает связь между сложением и вычитанием, может найти пропущенное число в уравнении 8 – ___ = 5, потому что он понимает, что эти факты связаны.

Кроме того, нахождение отсутствующих чисел в уравнениях обеспечивает нотацию для учащихся, которые хорошо умеют составлять и разлагать числа.

Ваши первоклассники тратят много времени на разложение чисел. Например, учащиеся проводят время, работая с партнерами по десятке, и знают, что 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5 — все это способы сделать десять. Учащиеся не всегда самостоятельно связывают эти разложения и уравнения!

Попросив учащихся решить уравнение, в котором 9 + ____ = 10, вы сможете попрактиковаться в соединении уже известной им математики (9 и 1 составляют 10) с обозначениями и уравнениями.

Как преподавать пропущенные числа в уравнениях

Стратегия № 1: Практика уроков

Когда мы обучаем математическим навыкам и понятиям, мы хотим уделить внимание CRA. Ваши студенты поймут более четко, когда они впервые испытают на конкретном уровне. Если ваша учебная программа или уроки переходят сразу к уравнениям без практической поддержки, вы обречены на провал!

Когда в уравнении отсутствует число, мы либо пропускаем начало изменить или результат .

Предоставление учащимся двух из этих чисел и предоставление им возможности поэкспериментировать с манипуляциями поможет им понять, почему будущие стратегии счета работают.

Работа с пропущенными числами в математическом уравнении. Модуль интервенции

В этом примере учащимся дается контекст «[#]птицы сидят на дереве. Прилетают еще птицы! Всего здесь [#] птиц».

С помощью счетчика учащиеся определяют начальное количество птиц на дереве и результирующее количество птиц на дереве. Затем они используют манипулятивные методы, чтобы определить количество птиц, прилетевших к дереву.

Учащиеся связывают этот практический опыт с уравнением, записывая свою работу.

Как учитель вы также можете моделировать, используя стратегии счета, чтобы найти пропущенное число, используя эти материалы. «Ой! Я вижу, вы начали с 5 птиц на дереве. Затем вы добавили птиц с номерами 6, 7, 8 и 9. Итак, мы начали с 5 и досчитали еще 5, чтобы получить 9. 5 и еще 4 получили 9. Я вижу это в вашем уравнении!»

Стратегия № 2. Остерегайтесь слишком быстрого перехода к репрезентативным моделям!

Это была большая ошибка, которую я совершил . Я был уверен, что если мои ученики понимают семейства фактов и взаимосвязь часть-часть-целое, они легко смогут найти пропущенное число в уравнении. «Просто вставьте числа в связку чисел, и оттуда вы легко найдете недостающее число!»

Я просил их использовать одно абстрактное понятие (часть/часть/целое) для поддержки другого абстрактного понятия (пропущенное число).

Числовые облигации в конечном итоге станут отличной стратегией для ваших учеников, однако они не обязательно являются отправной точкой! Помните, что мы стремимся создать сеть взаимопонимания для наших студентов. После того, как ваши ученики продемонстрируют некоторую уверенность в использовании практических инструментов, попросите их использовать эти инструменты рядом с репрезентативная модель, такая как номерная облигация.

Работа с пропущенными числами в математических уравнениях Модуль вмешательства

Стратегия № 3: Контекст решает!

Учитель, с которым я работала, использовал множество задач по истории, как они были написаны в учебной программе. Проблема заключалась в том, что предоставленные контексты не обязательно были понятны нашим студентам. Хуже того, контекст продолжал меняться!

При первом знакомстве с этим навыком выберите контекст и позвольте учащимся играть с ним снова и снова, чтобы контекст был

.0003 поддерживает их способность придавать смысл, а не добавляет еще одно препятствие для понимания.

Соедините эти простые контексты с практическими инструментами и попросите учащихся записать результаты в виде уравнений. Это потребует времени и практики, но вскоре ваши ученики приобретут необходимые навыки и уверенность.

Упражнение «Отсутствующие числа в математическом уравнении». Модуль интервенции

На фотографии вы можете видеть, как учащиеся играют с контекстом вокруг пиратских сокровищ. В сундуке с сокровищами находится определенное количество сокровищ. Затем ученикам говорят, что пираты либо добавили, либо потеряли часть своих сокровищ. Наконец, ученикам выдается полученное количество сокровищ в сундуке.

Их цель — с помощью практических материалов определить количество потерянных или найденных золотых монет.

Добавление этой концепции вместо того, чтобы просить учащихся работать с голыми числами, придает смысл и, следовательно, большее понимание уравнениям, которые они пишут.

Связанные ресурсы:

Что такое числовые облигации? Использование, преимущества, факты, примеры

Числовая связь: Введение

Числовая связь показывает связь между двумя числами и их суммой.

Наглядно демонстрирует связь между частями (числами) и целым (сумма).

Родственные игры

Что такое числовые облигации?

Числовая связь — это пара чисел, которые в сумме дают определенное число. Используя числовые связи, можно мгновенно сказать ответ без необходимости фактического вычисления.

В приведенном выше примере, когда мы видим связь чисел, мы сразу знаем ответ без необходимости вычислять его. Они помогают нам понять, что целое число состоит из частей и что эти части могут быть в разных пропорциях.

Давайте лучше разберемся в этой концепции с помощью нескольких примеров числовых связей.

Связанные рабочие листы

Облигации чисел 5

В этой связке чисел 5 представляет собой целое число, состоящее из комбинаций различных частей, как показано на рисунке ниже.

Облигации числа 10

В этой облигации числа 10 представляет собой целое число, состоящее из комбинаций различных частей, как показано на рисунке ниже.

Облигации числа 20

В этой облигации числа 20 представляет собой целое число, состоящее из комбинаций различных частей, как показано на рисунке ниже.

Числовые связи: сложение

Числовые связи очень полезны при изучении сложения в основах арифметики.

Например:

В приведенном выше примере мы разбиваем число 7 на две части. Значение первой части равно 2, а значение второй части равно 5.

Хотя мы знакомы с 5 + 5 = 10 долларов, становится легче найти, что 10 + 2 = 12 долларов.

Облигации чисел полезны, когда нам нужно добавить много разных чисел. В таких случаях группировка похожих чисел помогает упростить сложение.

Например: $2 + 7 + 4 + 6 + 8 + 3 =$ ?

В этом случае, если мы знаем количество связей для 10, мы можем легко объединить числа, которые дают нам 10, и сделать наши вычисления проще и быстрее.

Итак, здесь у нас есть 2 доллара + 8 = 10, 7 + 3 = 10 долларов и 4 доллара + 6 = 10 долларов.

Получаем сумму 10$ + 10 + 10 = 30$.

Числовые связи: вычитание

Числовые связи очень полезны при изучении вычитания в основах арифметики.

Например: 10 долл. США −  \underline{} = 8 900 долл.0005

Здесь мы знаем, что 10 — это целое число, а 8 — одно из чисел из пары числовых связей. Другое число, которое в сочетании с 8 дает нам 10, равно 2.

Итак, 10 долларов – 2 = 8 долларов.

Интересный факт!

Если мы знаем 3 числа числовой связи, мы можем составить 2 предложения на сложение и 2 на вычитание с этими 3 числами.

Например:

Числовые связи: Деление

Числовые связи также очень полезны при изучении деления в основах арифметики.

Например, если нам нужно определить $10/5 =$ ?

Здесь 10 — целое число. 5 — это часть пары, составляющей 10. Чтобы найти другую часть пары, нам нужно знать умножение, т. е. 5 при умножении на 2 дает 10.

$5 \times 2 = 10$

Поскольку умножение и деление имеют обратную зависимость, 2 будет другой частью пары.

Итак, 10/5 = 2 доллара.

Преимущества числовых облигаций

Понимание и изучение концепции числовых облигаций имеет следующие преимущества:

• Облегчает использование обратных операций
• Помогает с основами ментальной арифметики
• Простой для запоминания и очень эффективный
• Повышение творческих способностей и навыков решения проблем

Как научить детей числовым связям?

Теперь, когда вы знаете определение числовой связи и ее преимущества, давайте углубимся в то, как вы можете научить детей этому понятию.

Наилучшим подходом к обучению связям чисел в первом классе является подход CPA (конкретно-графический-абстрактный), который состоит из следующих трех этапов:

Бетонный этап

На этом этапе вы можете попросить детей начать считать узнаваемые интерактивные объекты реального мира. Затем попросите их представить реальные объекты с помощью фишек, а затем рассортируйте фишки на две группы.

При этом дети могут открыть для себя различные способы формирования числовых связей после разделения фишек на две группы.

Например, 6 можно составить из суммы пар 4,2; 3,3; 5,1; 0,6, как показано на изображении ниже:

Этап иллюстраций

На этом этапе, после того как дети усвоят концепцию числовых связей через физические объекты, вы можете научить их записывать числовые связи в рабочих тетрадях или на доске.

Вы также можете научить их представлять числовые связи с помощью рисунков и иллюстраций, как показано на рисунке ниже.

Абстрактный шаг

После того, как дети освоят конкретные и изобразительные шаги, вы можете научить их представлять и решать абстрактные задачи с помощью математических обозначений.

Например, графическое представление числа 5, как показано ниже, будет иметь математическое обозначение как $2 + 3 = 5$.

Заключение

Числовая связь в математике относится к комбинации пар, которые при сложении дают в сумме целое число. Это помогает научиться легко выполнять основные арифметические операции, такие как сложение, вычитание, деление и т. Д.

Поскольку числовые связи закладывают основу для понимания сложной математики, крайне важно обучать их только с помощью высокоэффективных подходов, таких как подход CPA. Это помогает детям овладеть концепцией, а также повышает их творческий потенциал и навыки решения проблем.

Решенные примеры

1. Найдите $13 + \underline{} = 21$ .

Решение: Облигации числа на целое число 21 состоят из следующей комбинации пар:

1,20; 2,19; 3,18; 4,17; 5,16; 6,15; 7,14; 8,13; 9,12; 10,11.

Отсюда мы знаем, что 13 и 8 дают 21.

Итак, 13$ + 8 = 21$.

2. Определить 16$ − \underline{} = 9$ .

Решение: Мы знаем, что 16 — целое число. Таким образом, сочетание пар, составляющих 16, таково: 

1,15; 2,14; 3,13; 4,12; 5,11; 6,10; 7,9; 8,8.

Отсюда мы знаем, что 7 и 9 составляют 16.

Итак, 16 долл. США – 7 = 9 долл. США.

3. Вычислить $18\div3$ .

Решение: Здесь 18 — целое число, а 3 — одна часть пары. Чтобы найти другую часть, нам нужно использовать умножение.

Итак, когда 3 и 6 умножаются, произведение равно 18.

Поскольку деление и умножение обратно пропорциональны, окончательный ответ будет 6.

18/3$ = 6$.

4 доллара. 2 + 5 + 10 + 15 + 18 + 10 = $?

Решение: Числа можно сгруппировать в три пары, чтобы получилось 20. Поскольку мы уже знаем числовые связи для 20, мы можем легко найти ответ.

Здесь $2 + 18 = 20 – (i)$

$5 + 15 = 20 – (ii)$

$10 + 10 = 20 – (iii)$

При добавлении (i), (ii), и (iii), мы получим

20$ + 20 + 20 = 60$.

5. Заполните облигацию номера.

Решение: Здесь 15 — целое число, а 5 — часть пары, составляющей 15.  

Чтобы завершить связь, нам нужно найти другую часть пары.

Для этого нам нужно знать комбинацию пар, составляющих 15, а именно:

1,14; 2,13; 3,12; 4,11; 5,10; 6,9; 7,8.

Отсюда видно, что 5 и 10 составляют 15. Таким образом, для завершения числовой связи 10 будет другой частью пары.

Практические задачи

1

Найдите 21 доллар + \underline{} = 30 долларов.

6

8

7

9

Правильный ответ: 9
30 — целое число, которое может быть составлено из нескольких комбинаций пар, включая 21 и 9.
Это означает, что 9 и 21 являются частями пары, которые при сложении дают в сумме 30.

2

Найдите правильный вариант.

28 и 7 — это пара, которая составляет 32.

23 и 5 — это пара, которая составляет 32.

Пара 26 и 6 составляет 32.

Пара 24 и 7 составляет 32.

Правильный ответ: пар составляет 32, включая 26 и 6.

3

Определить $19 – 4 =$ ?

12

15

14

13

Правильный ответ: 15
19 — целое число, которое можно составить из нескольких комбинаций пар, включая 15 и 4.
Это означает, что 15 и 4 являются частями 15 и 4. пара. Когда мы вычтем 4 из 19, мы получим в качестве ответа 15, другую часть пары.

4

Заполните облигацию номера.

40

26

36

21

Правильный ответ: 36
50 — целое число, которое можно составить из многочисленных комбинаций пар, включая 14 и 36.

5 Найдите неверный вариант.

4 и 17 — детали, составляющие 22.

7 и 15 — детали, составляющие 22.

10 и 12 — детали, составляющие 22.

6 и 16 — части, составляющие 22.

Правильный ответ: 4 и 17 — части, которые составляют 22.
Поскольку 22 — целое число, несколько комбинаций пар или частей составляют 22, включая 7,15; 10,12; 6,16; кроме 4,17.

Часто задаваемые вопросы

Как по-другому называются числовые облигации?

Числовые связи также известны как числовые пары.

Используем ли мы числовые связи, чтобы разбить число только на 2 части?

Нет, связку чисел можно использовать для разбиения или разделения чисел на 2, 3 и более частей. Однако удобнее всего разделить его на 2 или 3 части.

Можно ли использовать числовые связи с числами, отличными от целых чисел?

Числовые облигации не ограничены целыми числами. Их также можно использовать с другими числами, например дробями, десятичными знаками, отрицательными числами и т. д.

Зачем нужны числовые связи?

Связи чисел помогают разбивать числа полезными способами. Они помогают учащимся визуализировать и легко решать задачи на сложение и вычитание.

В чем разница между числовыми связями и числовыми фактами?

Числовые связи — это один из многих видов числовых фактов. Числовые связи могут быть дополнительным числовым фактом, поскольку два числа объединяются, чтобы сформировать другое. Числовые факты, с другой стороны, предназначены не только для сложения, но и для вычитания, умножения и деления.

Ссылки по теме:

• Пара номеров  
• Целые числа  
• Подразделение  
• Дополнение  
• Вычесть

Пропущенные цифры | NZ Maths

Цель

Это задание по алгебре 4-го уровня из серии «Разберись».

Цели достижения

NA4-9: Используйте графики, таблицы и правила для описания линейных отношений, обнаруживаемых в числовых и пространственных закономерностях.

Разработка АО и другие учебные ресурсы

Действия учащихся

  

Нажмите на изображение, чтобы увеличить его. Нажмите еще раз, чтобы закрыть. Скачать PDF (213 КБ)

Конкретные результаты обучения

Использование шаблонов умножения для решения задач

Описание математики

Ссылки на числовую структуру
Используйте это упражнение с учащимися на продвинутом этапе умножения, которые хорошо помнят основные факты сложения и умножения и учатся решать числовые задачи с одним или несколькими «неизвестными».

Необходимые материалы

FIO, Уровни 3–4, Чувство чисел и алгебраическое мышление, Книга вторая, Пропущенные цифры, стр. 5

Одноклассник

Упражнение

В этом упражнении учащиеся используют свои знания основных фактов и моделей чисел, чтобы найти пропущенные цифры в числах. Большинство вопросов можно было бы ответить методом проб и улучшений, но учащиеся, скорее всего, сочтут более эффективным (и более удовлетворительным) сначала максимально сузить диапазон вариантов, изучив проблему и посмотрев, какие выводы они могут сделать. Вы можете предположить, что они учатся быть детективами числа.
Вы можете представить упражнение всему классу или группе, используя свои собственные примеры. Таким образом, вы оставляете все задачи в книге для самостоятельного решения учащимися. Ниже приведены возможные примеры группового обучения или обсуждения.

Пример 1: ☐☐3 + 3☐ = 44
• Последняя цифра первого числа — 3; 3 + ☐ дает последнюю цифру суммы, 4.
• Это означает, что пропущенная цифра должна быть 1 (поскольку 3 + 1 = 4). Проверка: 113 + 31 = 144.

Пример 2: 1☐ x 3☐ = ☐2☐
• Когда вы умножаете эту пропущенную цифру саму на себя, ответ (произведение) заканчивается этой же цифрой.
• Есть только три цифры, для которых это верно: 1 (поскольку 1 x 1 = 1), 5 (поскольку 5 x 5 = 25) и 6 (поскольку 6 x 6 = 36).
• Попробуйте 1: 11 x 31 = 341. Значит, это не 1. Попробуйте 5. Если 5 не работает, вы знаете, что должно быть 6. В этом случае работает 5: 15 x 35 = 525.

Пример 3: ☐6 x ☐= 5☐
• Пропущенная цифра четная (поскольку 6 — четное число, и всякий раз, когда вы умножаете целое число на четное число, вы получите четное число).
• Цифра должна быть 2, 4, 6 или 8 (единственные четные цифры, кроме 0, что не сработает, потому что все, что умножается на 0, равно 0).
• 4, 6 или 8 не подходят, потому что первое число должно быть 46, 66 или 86, и если вы умножите эти числа на 4, 6 или 8, вы получите число, которое много больше, чем 50 что-то.
• Остается 2 как единственно возможное четное число. Проверка: 26 x 2 = 52.

Диалог рядом с вопросом 1 моделирует, как ученики должны думать. Во втором вопросе им предлагается записать шаги, которые они использовали для решения каждой проблемы. Например, они могут сделать это с помощью пронумерованных или маркированных пунктов или в виде таблицы.
В вопросе 3 учащиеся должны подумать о шаблонах (или стратегиях), которые они могли использовать, например:
• нечетное + нечетное = четное (например: 9 + 5 = 14)
• нечетное – нечетное = четное (для пример: 9 – 5 = 4)
• четный + четный = четный
• четный + нечетный = нечетный
• четный – нечетный = нечетный
• нечетный – четный = нечетный
• нечетный x нечетный = нечетный
• четный x четный = четный
• нечетное x четное = четное.
Один из подходов к вопросу 4 состоит в том, чтобы учащиеся составили несколько простых числовых предложений в формате «число +/–/x/÷ число = число», а затем искали повторяющуюся цифру, которую они могли бы удалить и заменить квадратом, тем самым создав проблему с пропущенной цифрой, которую должен решить одноклассник.
Например:
• Составьте предложение на вычитание и решите его: 253 – 152 = 101
• Теперь составьте задачу на пропущенную цифру, заменив цифру 2 квадратиком: ☐53 – 15☐ = 101; или цифру 5 на коробка: 2☐3 – 1☐2 = 101; или цифра 1 с квадратиком: 253 – ☐52 = ☐0☐
• Проверьте эти возможности и посмотрите, что нужно для их решения. Некоторые нужно будет отбросить как слишком простые. Не у всех будет уникальное решение (например, 2☐3 – 1☐2 = 101 подходит для любой цифры).
Может потребоваться некоторое испытание и усовершенствование, прежде чем каждый учащийся составит небольшую группу задач, подходящих для передачи однокласснику.

Ответы на задание

1. ☐ = 5
2. Стратегии будут разными, но ответы

3. Ответы будут разными. Возможные варианты:
Дополнительные проблемы, если ☐ стоит на месте единиц, то цифры единиц в ответе и в другом числе подскажут вам, что такое ☐.
Размер ответа в задаче на умножение может сказать вам, насколько большой должна быть цифра в ☐ (когда все ☐ являются одной и той же цифрой). Например, в ☐6 x ☐ = 18☐ ☐ не может быть больше 4, потому что 50 x 5 = 250, что больше 180.
4. Проблемы могут быть разными.

Добавить в план

Четвертый уровень

Найди пропущенные цифры — выучи и реши вопросы

Знаете ли вы, что такое пропущенные цифры? Пропущенные цифры — это цифры, пропущенные в данной серии чисел с одинаковыми вариациями среди них. Вы должны найти номер, который отсутствует. Простой метод нахождения этих пропущенных цифр заключается в выявлении подобных изменений в числах и заполнении цифр в данном ряду.

Теперь вам должно быть любопытно, как найти пропущенные цифры. Но прочитав эту статью и решив несколько практических вопросов, вы сможете понять тему пропущенных цифр в сложении, вычитании и умножении.

Найдите недостающие цифры в сложении

Чтобы найти недостающие цифры в дополнение, выполните действия, описанные в данном примере:

Пример для сложения

• Шаг 1: Сложите ЕДИНИЦЫ: 5 + 9 = 14

7

Шаг 2: Перегруппируйте как 1 Десяток и 4 Единицы

• Шаг 3: Сложите ДЕСЯТКИ: 2 + 1 перенос = 3

• Шаг 4: Впишите 2 в клеточку, чтобы получилось 3 + 2 = 5

• Шаг 5: Сложите СОТНИ: 4 + 1 = 5

• Шаг 6: Сложите ТЫСЯЧИ: 6 + 2 = 8

• Шаг 7: Напишите 2 в рамке. Вот как будет заполнен пропущенный номер.

Найдите пропущенные цифры при вычитании

Чтобы найти пропущенные цифры при вычитании, выполните действия, описанные в данном примере:

Пропущенные цифры при вычитании

Здесь мы видим, что у нас есть одна пропущенная цифра, из которой было вычтено 6, чтобы получить результат как 6. Таким образом, если мы вычтем 6 из 12, мы получим 6. Следовательно, пропущенная цифра на один раз 12. т. е. 12 — 6 = 6.

Для десятков здесь мы видим, что у нас отсутствует одна цифра. У нас есть 8, и если мы вычтем 8 из пропущенной цифры, мы получим результат как 2. Итак, если мы вычтем 6 из 8, мы получим результат как 2. т.е. 8 — 6 = 2

Для сотен, здесь мы видим, что у нас отсутствует одна цифра. У нас есть 17 и 8, и если из 8 вычесть 17, то получится 9. Таким образом, пропущенная цифра станет 9. То есть 17 — 8 = 9

Для тысяч здесь мы видим, что у нас есть одна пропущенная цифра, из которой было вычтено 2, чтобы получить результат как 2. Итак, если мы вычтем 2 из 4, результат, который мы получаем, равен 2. Следовательно, пропущенная цифра для одного раза равна 4. т. е. 4 — 2 = 2.

Найдите пропущенное число в умножении

Чтобы найти пропущенные цифры в умножении, выполните шаги в данный пример:

Пример умножения

• Шаг 1: Прежде всего проверьте, где находится пропущенное место, здесь мы видим, что у нас есть пропущенное место в результате.

• Шаг 2: Умножаем 4$ на 6$ и получаем 24. Итак, 4 будут на месте, и теперь у нас 2 в переноске.

• Шаг 3: Теперь мы умножим $6 на 3$ и получим 18. Поскольку у нас также есть 2 переноса, мы добавим к ним 2. Это станет 20.

• Шаг 4: Следовательно, пропущенная цифра 2.

Обратите внимание на шаблон и найдите пропущенные цифры

Выберите 2 или 3 термина в тексте, к которым будет применено правило для поиска пропущенного числа. Например: если у вас есть пять чисел в серии, выберите первые три числа, чтобы проверить, должно ли применяться какое-либо правило.

При выборе номера для проверки правила выберите номер, с которым легко работать. К ним относятся такие термины, как коэффициенты 2, 3, 5 или 10. Проверьте ряды с помощью некоторых общих правил, таких как сумма членов, квадраты, куб и другие.

Чтобы найти пропущенные цифры в шаблоне, выполните действия, описанные в данном примере:

Найдите пропущенные цифры 1, 2, 6, 24

Данная последовательность состоит из 4 членов. Мы проверим, какое правило применяется, выбрав первые 3 термина. Второе число в последовательности равно 2, а первое число равно 1, что означает, что либо прибавляется 1, либо умножается 2 для получения второго члена.

Третий член равен 6, который мы получаем из 2, умножив его на 3. Итак, теперь у нас есть 1 х 1, 1 х 2, 2 х 3 и 6 х 4. Таким образом, мы определили закономерность и, соответственно, последний член будет 24 х 5 = 120,

Следовательно, отсутствует число 120.

Решенные примеры

Q1. Найдите недостающую цифру, отмеченную желтым прямоугольником.

Пропущенные цифры в сложении

Ответ:

Шаги:

I: Прибавьте один разряд, который равен 9 + 4 + 4 = 17. Поместите 7 в ячейку и отнесите 1 к десяткам.

II: Прибавляем разряд десятков, выходя из рамки, так, чтобы 1 + 3 + 1 = 5. Если 5 + 6 = 11, то получаем 1 в разряде десятков. положите 6 в коробку и несите 1 к сотням.

III: Сложите разряд сотен, включая переносимую 1, так, чтобы 1 + 5 + 2 + 6 = 14. Теперь мы получаем 4 в разряде сотен, а теперь перенесите 1 в разряд тысяч.

IV: Прибавьте тысячи, выходя из клеточки, так, чтобы 1 + 3 + 8 = 12. 12 + 1 = 13. Вставьте 1 в клеточку.

Дополнительные недостающие цифры

Q2. Найдите недостающую цифру, отмеченную желтым прямоугольником.

Дополнительные недостающие цифры

Ответ:

Шаги:

I: Добавьте единицы, не выходя из рамки. 4 + 6 = 10 и 10 + 5 = 15, следовательно, мы получаем 5 вместо единиц. Напишите 5 в рамочке и перенесите 1 на разряд десятков.

II: добавить разряд десятков. 1 + 3 + 4 + 9 = 17. Запишите 7 в разряде десятков и перенесите 1 в разряд сотен.

III: Добавьте разряд сотен, не выходя из поля. 1 + 5 + 3 = 9. 9 + 2 = 11, тогда мы получаем 1 в разряде сотен. Напишите 2 в рамке. Перенесите 1 на разряд тысяч.

IV: добавить разряд тысяч, не вписываясь в поле. 1 + 6 + 1 = 8; 8 + 1 = 9. Впишите 1 в рамку.

Пропущенные цифры в сложении

Практические вопросы

Найдите пропущенные цифры в сложении:

I.