Минус на плюс что дает?

Положительные и отрицательные числа придумали математики. Делать им было нечего, вот они и придумали. Правила умножения и деления положительных и отрицательных чисел придумали всё те же математики. Специально для того, чтобы нам жизнь мёдом не казалась. Как же нам быть? Нужно выучить эти правила, чтобы говорить математикам то, что они хотят от нас слышать.

Запомнить правила умножения или деления положительных и отрицательных чисел очень просто. Если два числа имеют разные знаки, в результате всегда будет знак минус.
Если два числа имеют одинаковые знаки, в результате всегда будет плюс.

Рассмотрим все возможные варианты. Что дает минус на плюс? При умножении и делении минус на плюс дает минус. Что дает плюс на минус? При умножении и делении в результате мы тоже получаем знак минус.

Минус на плюс, плюс на минус.

Как вы видите, все варианты умножения и деления положительных и отрицательных чисел исчерпаны, но знак плюс у нас так и не появился.

Это мы сформулировали правило для себя, чтобы запомнить. Что говорить математикам? При умножении или делении положительных и отрицательных чисел в результате получается отрицательное число. Всегда.

Что дает минус на минус? Всегда будет получаться плюс, если мы выполняем умножение или деление. Что дает плюс на плюс? Здесь совсем просто. Умножение или деление плюса на плюс дает всегда плюс.

 

Минус на минус, плюс на плюс.

Надеюсь, это вы запомнили: минус на минус дает плюс, плюс на плюс дает минус. Что говорить математикам? При умножении и делении положительных или отрицательных чисел в результате получается положительное число.

Если с умножением и делением двух плюсов всё понятно (в результате получается такой же плюс), то с двумя минусами ничего не понятно. По логике, если два плюса дают плюс, то два минуса должны давать минус.

Такой большой, жирный минус. Но не тут-то было. Математики думают иначе. Так почему минус и минус превращаются в плюс?

Могу вас заверить, что интуитивно математики правильно решили задачу на умножение и деление плюсов и минусов. Они записали правила в учебники, не особо вдаваясь в подробности. Для правильного ответа на вопрос, нам нужно разобраться, что же означают знаки плюс и минус в математике.

Давайте попробуем применить правило умножениея и деления положительных и отрицательных чисел на практике. Придумаем какой-нибудь пример из нашей жизни. Думаю, вы слышали про бочку мёда и ложку дёгтя, которая может испортить весь мёд. Пусть мёд — это положительные числа, а дёготь — это числа отрицательные. Пробуем. Смотрим на картинки и описываем правила.

Если в бочку дёгтя добавить ложку мёда, получится бочка дёгтя.
Если в бочку мёда добавить ложку дёгтя, получится бочка дёгтя.
Если в бочку дёгтя добавить ложку дёгтя, получится бочка мёда.
Если в бочку мёда добавить ложку мёда, получится бочка мёда.

Первых два примера с натяжкой можно принять. Последний пример вообще не вызывает вопросов. А вот с предпоследним примером возникают очень большие проблемы — в жизни такого не бывает.

Здесь возможны два варианта:
1. Математики не правильно записали свое правило.
2. Мы не правильно применяем математическое правило.

Лично я за второй вариант. Объясню почему. Математику не только нужно знать, но нею ещё нужно уметь пользоваться.

Приведу пример из собственного опыта. Один учитель математики на уроках нам говорил: «математика – это точная наука, два раза соври – получится правда». Это утверждение однажды мне очень пригодилось. Как-то я решал сложную задачу с длинным решением. Я точно знал, какой результат должен быть. Но результат был другим. Я долго искал ошибку в расчетах, но не смог ее найти. Тогда, за несколько действий до итогового результата, я изменил одно число так, чтобы результат получился правильным. Я в расчетах соврал два раза и получил правильный результат.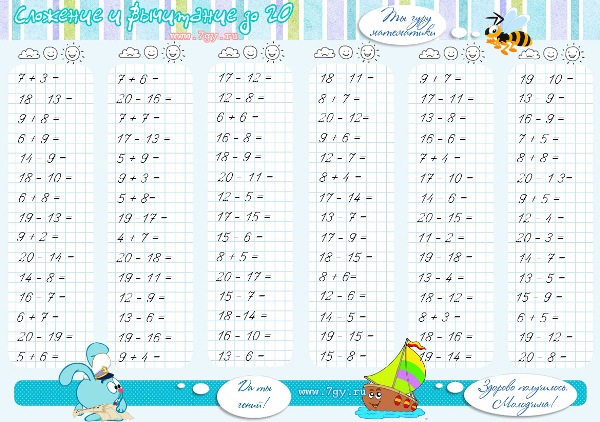

Математические вычисления в тот раз никто не проверял и я получил хорошую оценку. Это очень похоже на правило «минус на минус дает плюс», не так ли?

Но вернемся к нашим бочкам. Кстати, говорят, именно с бочек с вином математики срисовали знак «минус». Виноделы этим знаком обозначали пустые бочки. После наполнения бочек вином они перечеркивали знак «минус» и получался знак «плюс». По сути, знак «минус» заменял виноделам обычный ноль, ведь он обозначал отсутствие вина в бочке. Но математики ловко присобачили знак «минус» к числам и назвали их «отрицательными».

Так что же не так с мёдом и дёгтем в бочках? Мои четыре примера описывают действие сложения — ведь мы прибавляем одно к другому, а математические правила мы рассматриваем для деления и умножения. Это абсолютно разные вещи, сколько бы математики не повторяли, что умножение это и есть сложение. Сложение — это изменение количества. Умножение — это изменение качества. При добавлении ложки дёгтя в бочку мёда, мёд не превращается в дёготь.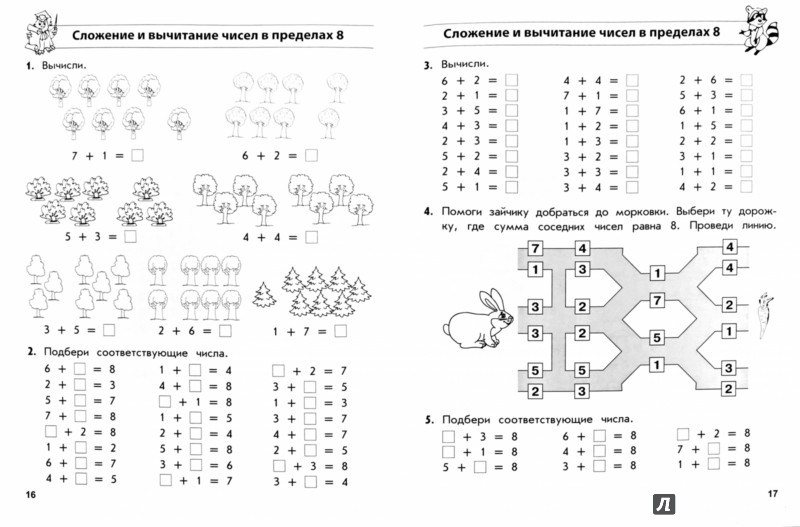 2

В этом примере буква а выполняет роль единицы измерения. Кстати, правило умножения отрицательных чисел наводит на ещё один вопрос математикам: сколько отрицательных чисел нужно сложить, чтобы получилось одно положительное число?

(-2)+(-2)=-4

(-2)*(-2)=+4

Так что же такое знаки «плюс» и «минус» в математике? Существуют ли отрицательные числа? Об этом мы поговорим как-нибудь в другой раз.

Действия с минусом и плюсом. Сложение чисел с разными знаками — Гипермаркет знаний

формирование знаний о правиле сложения чисел с разными знаками, умений применять его в простейших случаях;

развитие умений сравнивать, выявлять закономерности, обобщать;

воспитание ответственного отношения к учебному труду.

Оборудование: мультимедийный проектор, экран.

Тип урока: урок изучения нового материала.

ХОД УРОКА

1.Организационный момент.

Ровно встали,

Тихо сели.

Прозвенел сейчас звонок,

Начинаем наш урок.

Ребята! Сегодня к нам на урок пришли гости. Давай повернемся к ним и улыбнемся друг другу. Итак, мы начинаем наш урок.

Слайд 2 — Эпиграф урока: «Кто ничего не замечает, тот ничего не изучает.

Кто ничего не изучает, тот вечно хнычет и скучает.»

Роман Сеф (детский писатель)

Слад 3 — Предлагаю поиграть в игру «Наоборот». Правила игры : нужно разделить слова на две группы: выигрыш, ложь,тепло, отдал, правда, добро, проигрыш, взял, зло, холодно, положительное, отрицательное.

Противоречий в жизни много. С их помощью мы определяем окружающую действительность. Для нашего занятия мне необходимо последнее: положительное – отрицательное.

О чем мы говорим в математике, когда употребляем эти слова? (О числах.)

Великий Пифагор утверждал: «Числа правят миром». Я предлагаю поговорить о самых загадочных числах в науке – о числах с разными знаками. — Отрицательные числа появились в науке, как противоположность к положительным. Их путь в науку был труден, потому что даже многие ученые не поддерживали идей об их существовании.

Какие понятия и величины люди измеряют положительными и отрицательными числами? (заряды элементарных частиц, температуру, убытки, высоту и глубину и т.д.)

Слайд 4- Слова противоположные по значению – антонимы (таблица).

2.Постановка темы урока.

Слайд 5(работа с таблицей) – Какие числа изучали на предыдущих уроках?
– Какие задания, связанные с положительными и отрицательными числами вы умеете выполнять?
– Внимание на экран. (Слайд 5)
– Какие числа представлены в таблице?
– Назовите модули чисел, записанных по горизонтали.
– Укажите наибольшее число, укажите число с наибольшим модулем.
– Ответьте на те же вопросы для чисел, записанных по вертикали.
– Всегда ли наибольшее число и число с наибольшим модулем совпадают?
– Найдите сумму положительных чисел, сумму отрицательных чисел.
– Сформулируйте правило сложения положительных чисел и правило сложения отрицательных чисел.

– Какие числа осталось сложить?
– Умеете ли вы их складывать?
– Знаете ли вы правило сложения чисел с разными знаками?
– Сформулируйте тему урока.
– Какую цель вы перед собой поставите? .Подумайте, что мы будем делать сегодня? (Ответы детей). Сегодня мы продолжаем знакомиться с положительными и отрицательными числами. Тема нашего урока “Сложение чисел с разными знаками.” А наша цель: научиться без ошибок, складывать числа с разными знаками. Записали в тетрадь число и тему урока .

3.Работа по теме урока .

Слайд 6. – Применяя данные понятия, найдите результаты сложения чисел с разными знаками на экране.
– Какие числа являются результатом сложения положительных чисел, отрицательных чисел?
– Какие числа являются результатом сложения чисел с разными знаками?
– От чего зависит знак суммы чисел с разными знаками? (Слайд 5)
– От слагаемого с наибольшим модулем.
– Это как при перетягивании каната. Побеждает сильнейший.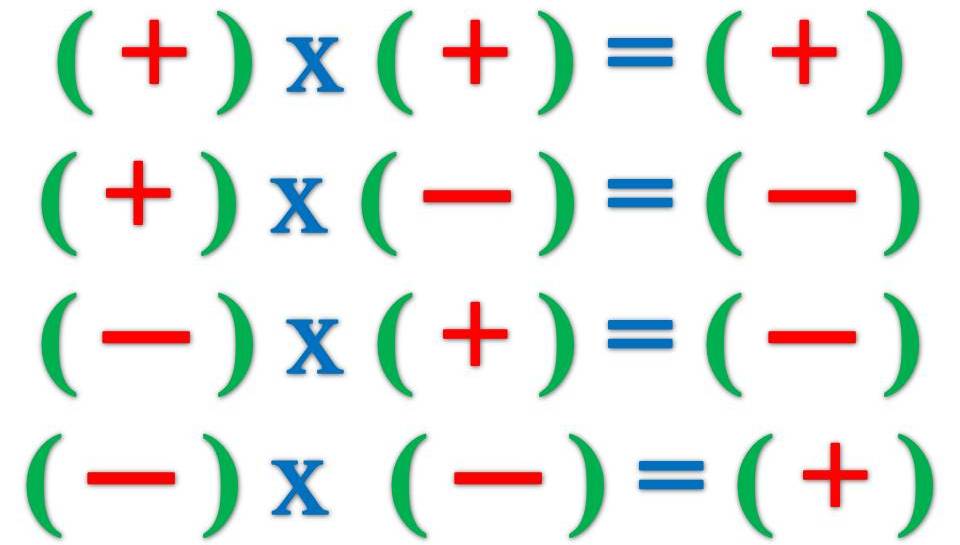

Слайд 7 – Поиграем. Представьте, что вы перетягиваете канат.. Учитель. Соперники обычно встречаются на соревнованиях. И мы сегодня побываем с вами на нескольких турнирах. Первое, что нас ждет – это финал конкурса по перетягиванию каната. Встречаются Иван Минусов под номером -7 и Петр Плюсов под номером +5. Как вы думаете, кто победит? Почему? Итак, победил Иван Минусов, он действительно оказался сильнее соперника, и смог перетащить его на свою отрицательную сторону ровно на два шага.

Слайд 8.- . А теперь побываем на других соревнованиях. Перед вами финал состязания по стрельбе. Лучшими в этом виде оказались Минус Тройкин с тремя воздушными шарами и Плюс Четвериков, имеющий в запасе четыре воздушных шарика. А здесь ребята, как вы думаете, кто станет победителем?

Слайд 9 — Соревнования показали, что в них побеждает сильнейший. Так и при сложении чисел с разными знаками: -7 + 5 = -2 и -3 + 4 = +1. Ребята, как же складываются числа с разными знаками?Учащиеся предлагают свои варианты.

Учитель формулирует правило, приводит примеры.

10 + 12 = +(12 – 10) = +2

4 + 3,6 = -(4 – 3,6) = -0,4

Учащиеся в процессе демонстрации могут комментировать решение, появляющееся на слайде.

Слайд 10 — Учитель- поиграем ещё в одну игру «Морской бой». К нашему побережью приближается вражеский корабль, его необходимо подбить и потопить. Для этого у нас есть пушка. Но чтобы попасть в цель необходимо произвести точные расчеты. Какие вы сейчас увидите. Готовы? Тогда вперед! Прошу не отвлекаться, примеры меняются ровно через 3 сек. Все готовы?

Учащиеся по очереди выходят к доске и вычисляют примеры, появляющиеся на слайде. – Назовите этапы выполнения задания.

Слайд 11- Работа по учебнику: стр.180 п.33 , прочитать правило сложения чисел с разными знаками. Комментирует правило.
– В чём отличие правила, предложенного в учебнике, от составленного вами алгоритма? Рассмотреть примеры в учебнике с комментарием.

Слайд 12- Учитель-А теперь ребята давайте проведем эксперимент. Но не химический, а математический! Возьмем числа 6 и 8, знаки плюс и минус и все хорошенько перемешаем. Получим четыре примера-опыта. Проделайте их у себя в тетради.(двое учащихся решают на крыльях доски, затем ответы проверяются). Какие выводы можно сделать из этого эксперимента? (Роль знаков). Проведем ещё 2 эксперимента , но с вашими числами (выходят по1 человеку к доске). Придумаем друг другу числа и проверим результаты эксперимента (взаимопроверка).

Слайд 13 .- На экран выводится правило в стихотворной форме .

4.Закрепление темы урока.

Слайд 14 – Учитель- «Знаки всякие нужны, знаки всякие важны!» Сейчас, ребята, мы поделимся с вами на две команды. Мальчики будут в команде Деда Мороза, а девочки – Солнышка. Ваша задача, не вычисляя примеры, определить в каких из них получатся отрицательные ответы, а в каких — положительные и выписать в тетрадь буквы этих примеров.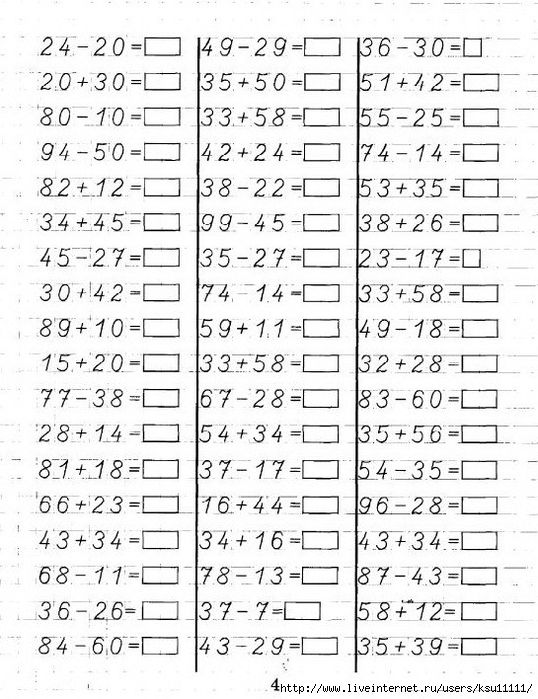 Мальчики соответственно – отрицательные, а девочки – положительные(выдаются карточки с приложения). Проводится самопроверка.

Молодцы! Чутьё на знаки у вас отличное. Это поможет вам выполнить следующее задание

Слайд 15 — Физкульминутка. -10, 0,15,18,-5,14,0,-8,-5 и т. д.(отрицательные числа- приседают, положительные числа- подтягиваются вверх, подпрыгивают)

Слайд 16 -Решить 9 примеров самостоятельно (задание на карточках в приложении). 1человек у доски. Сделать самопроверку. Ответы выводятся на экран, ошибки учащиеся исправляют в тетради. Поднимите руки, у кого верно. (Отметки выставляются только за хороший и отличный результат)

Слайд 17 -Правильно решать примеры нам помогают правила. Давайте их повторим На экране алгоритм сложения чисел с разными знаками.

5.Организация самостоятельной работы.

Слайд 18 -Ф ронтальная работа через игру «Отгадай слово» (задание на карточках в приложении) .

Слайд 19 — Должна получиться оценка за игру — «пятёрочка»

Слайд 20 -А теперь,внимание. Домашнее задание. Домашнее задание не должно вызвать у вас затруднений.

Слайд 21 — Законы сложения в физических явлениях. Придумайте примеры на сложение чисел с разными знаками и задайте их друг другу. Что нового вы узнали? Достигли ли мы поставленной цели?

Слайд 22 — Вот и кончился урок,подведем сейчас итог. Рефлексия. Учитель комментирует и выставляет оценки за урок.

Слайд 23 — Спасибо за внимание!

Желаю вам, чтобы в вашей жизни было больше положительного и меньше отрицательного, Хочу сказать вам, ребята, спасибо за вашу активную работу. Я думаю, что вы легко сможете применить полученные знания на последующих уроках. Урок окончен. Всем большое спасибо. До свидания!

В этой статье мы детально разберемся с тем, как выполняется сложение целых чисел . Сначала сформируем общее представление о сложении целых чисел, и посмотрим, что представляет собой сложение целых чисел на координатной прямой. Эти знания помогут нам сформулировать правила сложения положительных, отрицательных, а также целых чисел с разными знаками. Здесь же мы подробно разберем применение правил сложения при решении примеров и научимся выполнять проверку полученных результатов. В заключение статьи мы поговорим о сложении трех и большего количества целых чисел.

Навигация по странице.

Общее представление о сложении целых чисел

Приведем примеры сложения целых противоположных чисел. Сумма чисел −5 и 5 равна нулю, сумма 901+(−901) равна нулю, результатом сложения целых противоположных чисел 1 567 893 и −1 567 893 также является нуль.

Сложение произвольного целого числа и нуля

Давайте воспользуемся координатной прямой, чтобы понять, что представляет собой результат сложения двух целых чисел, одно из которых равно нулю.

Прибавление к нулю произвольного целого числа a означает перемещение из начала отсчета на расстояние a единичных отрезков. Таким образом, мы оказываемся в точке с координатой a . Следовательно, результатом сложения нуля и произвольного целого числа является прибавляемое целое число.

С другой стороны, прибавление к произвольному целому числу нуля означает переместиться из точки, координату которой задает данное целое число, на расстояние нуль. Иными словами, мы останемся в исходной точке. Следовательно, результатом сложения произвольного целого числа и нуля является данное целое число.

Итак, сумма двух целых чисел, одно из которых есть нуль, равна другому целому числу . В частности, нуль плюс нуль есть нуль.

Приведем несколько примеров. Сумма целых чисел 78 и 0 равна 78 ; результат сложения нуля и −903 равен −903 ; также 0+0=0 .

Проверка результата сложения

После того, как выполнено сложение двух целых чисел, полезно проверить полученный результат. Нам уже известно, что для проверки результата сложения двух натуральных чисел нужно от полученной суммы отнять любое из слагаемых, при этом должно получиться другое слагаемое. Проверка результата сложения целых чисел выполняется аналогично. Но вычитание целых чисел сводится к прибавлению к уменьшаемому числа, противоположного вычитаемому. Таким образом, чтобы проверить результат сложения двух целых чисел, нужно к полученной сумме прибавить число, противоположное любому из слагаемых, при этом должно получиться другое слагаемое.

Разберемся на примерах с проверкой результата сложения двух целых чисел.

Пример.

При сложении двух целых чисел 13 и −9 было получено число 4 , выполните проверку результата.

Решение.

Прибавим к полученной сумме 4 число −13 , противоположное слагаемому 13 , и посмотрим, получится ли другое слагаемое −9 .

Итак, вычислим сумму 4+(−13) . Это сумма целых чисел с противоположными знаками. Модули слагаемых равны 4 и 13 соответственно. Слагаемое, модуль которого больше, имеет знак минус, который мы и запоминаем. Теперь вычитаем из большего модуля вычитаем меньший: 13−4=9 . Осталось перед полученным числом поставить запомненный знак минус, имеем −9 .

При проверке мы получили число, равное другому слагаемому, следовательно, исходная сумма была вычислена правильно. −19 . Так как мы получили число, равное другому слагаемому, то сложение чисел −35 и −19 было выполнено верно.

Сложение трех и большего количества целых чисел

До этого момента мы говорили о сложении двух целых чисел. Иными словами, мы рассматривали суммы, состоящие из двух слагаемых. Однако сочетательное свойство сложения целых чисел позволяет нам однозначно определить сумму трех, четырех и большего количества целых чисел.

На основании свойств сложения целых чисел мы можем утверждать, что сумма трех, четырех и так далее чисел не зависит от способа расстановки скобок, указывающих порядок выполнения действий, а также от порядка следования слагаемых в сумме. Эти утверждения мы обосновывали, когда говорили о сложении трех и большего количества натуральных чисел . Для целых чисел все рассуждения полностью совпадают, и мы не будем повторяться.0+(−101) +(−17)+5 . После этого, расставив скобки любым допустимым способом, мы все равно получим число −113 .

Ответ:

5+(−17)+0+(−101)=−113 .

Список литературы.

• Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.

В этом уроке мы изучим сложение и вычитание целых чисел , а также правила для их сложения и вычитания.

Напомним, что целые числа — это все положительные и отрицательные числа, а также число 0. Например, следующие числа являются целыми:

−3, −2, −1, 0, 1, 2, 3

Положительные числа легко , и . К сожалению, этого нельзя сказать об отрицательных числах, которые смущают многих новичков своими минусами перед каждой цифрой. Как показывает практика, ошибки сделанные из-за отрицательных чисел, расстраивают обучающихся больше всего.

Содержание урока

Примеры сложения и вычитания целых чисел

Первое чему следует научиться, это складывать и вычитать целые числа с помощью координатной прямой. Совсем необязательно рисовать координатную прямую. Достаточно воображать её в своих мыслях и видеть, где располагаются отрицательные числа, и где положительные.

Рассмотрим простейшее выражение: 1 + 3. Значение данного выражения равно 4:

Этот пример можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1, нужно сдвинуться вправо на три шага. В результате мы окажемся в точке, где располагается число 4. На рисунке можно увидеть, как это происходит:

Знак плюса в выражении 1 + 3 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Пример 2. Найдём значение выражения 1 − 3.

Значение данного выражения равно −2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается число 1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −2. На рисунке можно увидеть, как это происходит:

Знак минуса в выражении 1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.

Вообще, надо запомнить, что если осуществляется сложение, то нужно двигаться вправо в сторону увеличения. Если же осуществляется вычитание, то нужно двигаться влево в сторону уменьшения.

Пример 3. Найти значение выражения −2 + 4

Значение данного выражения равно 2

Этот пример опять же можно понять с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на четыре шага. В результате мы окажемся в точке, где располагается положительное число 2.

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на четыре шага, и оказались в точке, где располагается положительное число 2.

Знак плюса в выражении −2 + 4 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Пример 4. Найти значение выражения −1 − 3

Значение данного выражения равно −4

Этот пример опять же можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −1 нужно сдвинуться влево на три шага. В результате мы окажемся в точке, где располагается отрицательное число −4

Видно, что мы сдвинулись из точки где располагается отрицательное число −1 в левую сторону на три шага, и оказались в точке, где располагается отрицательное число −4.

Знак минуса в выражении −1 − 3 указывает нам, что мы должны двигаться влево в сторону уменьшения чисел.

Пример 5. Найти значение выражения −2 + 2

Значение данного выражения равно 0

Этот пример можно решить с помощью координатной прямой. Для этого из точки, где располагается отрицательное число −2 нужно сдвинуться вправо на два шага. В результате мы окажемся в точке, где располагается число 0

Видно, что мы сдвинулись из точки где располагается отрицательное число −2 в правую сторону на два шага и оказались в точке, где располагается число 0.

Знак плюса в выражении −2 + 2 указывает нам, что мы должны двигаться вправо в сторону увеличения чисел.

Правила сложения и вычитания целых чисел

Чтобы сложить или вычесть целые числа, вовсе необязательно каждый раз воображать координатную прямую, и тем более рисовать её. Удобнее воспользоваться готовыми правилами.

Применяя правила, нужно обращать внимания на знак операции и знаки чисел, которые нужно сложить или вычесть. От этого будет зависеть какое правило применять.

Пример 1. Найти значение выражения −2 + 5

Здесь к отрицательному числу прибавляется положительное число. Другими словами, осуществляется сложение чисел с разными знаками. −2 это отрицательное число, а 5 — положительное. Для таких случаев применяется следующее правило:

Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше.

Итак, посмотрим какой модуль больше:

Модуль числа 5 больше, чем модуль числа −2. Правило требует из большего модуля вычесть меньший. Поэтому мы должны из 5 вычесть 2, и перед полученным ответом поставить знак того числа, модуль которого больше.

У числа 5 модуль больше, поэтому знак этого числа и будет в ответе. То есть, ответ будет положительным:

−2 + 5 = 5 − 2 = 3

Обычно записывают покороче: −2 + 5 = 3

Пример 2. Найти значение выражения 3 + (−2)

Здесь как и в предыдущем примере, осуществляется сложение чисел с разными знаками. 3 это положительное число, а −2 — отрицательное. Обратите внимание, что число −2 заключено в скобки, чтобы сделать выражение понятнее. Это выражение намного проще для восприятия, чем выражение 3+−2.

Итак, применим правило сложения чисел с разными знаками. Как и в прошлом примере, из большего модуля вычитаем меньший модуль и перед ответом ставим знак того числа, модуль которого больше:

3 + (−2) = |3| − |−2| = 3 − 2 = 1

Модуль числа 3 больше, чем модуль числа −2, поэтому мы из 3 вычли 2, и перед полученным ответом поставили знак того числа модуль, которого больше. У числа 3 модуль больше, поэтому знак этого числа и поставлен в ответе. То есть, ответ положительный.

Обычно записывают покороче 3 + (−2) = 1

Пример 3. Найти значение выражения 3 − 7

В этом выражении из меньшего числа вычитается большее. Для такого случая применяется следующее правило:

Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее, и перед полученным ответом поставить минус.

3 − 7 = 7 − 3 = −4

В этом выражении есть небольшая загвоздка. Вспомним, что знак равенства (=) ставится между величинами и выражениями тогда, когда они равны между собой.

Значение выражения 3 − 7 как мы узнали равно −4. Это означает, что любые преобразования которые мы будем совершать в данном выражении, должны быть равны −4

Но мы видим, что на втором этапе располагается выражение 7 − 3, которое не равно −4.

Чтобы исправить эту ситуацию, выражение 7 − 3 нужно взять в скобки и перед этой скобкой поставить минус:

3 − 7 = − (7 − 3) = − (4) = −4

В этом случае равенство будет соблюдаться на каждом этапе:

После того, как выражение вычислено, скобки можно убрать, что мы и сделали.

Поэтому, чтобы быть более точным, решение должно выглядеть так:

3 − 7 = − (7 − 3) = − (4) = − 4

Данное правило можно записать с помощью переменных. Выглядеть оно будет следующим образом:

a − b = − (b − a)

Большое количество скобок и знаков операций могут усложнять решение, казалось бы совсем простой задачи, поэтому целесообразнее научиться записывать такие примеры коротко, например 3 − 7 = − 4.

На самом деле сложение и вычитание целых чисел сводится только к сложению. Это означает, что если требуется осуществить вычитание чисел, эту операцию можно заменить сложением.

Итак, знакомимся с новым правилом:

Вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет противоположно вычитаемому.

Например, рассмотрим простейшее выражение 5 − 3. На начальных этапах изучения математики мы ставили знак равенства и записывали ответ:

Но сейчас мы прогрессируем в изучении, поэтому надо приспосабливаться к новым правилам. Новое правило говорит, что вычесть одно число из другого означает прибавить к уменьшаемому такое число, которое будет вычитаемому.

На примере выражения 5 − 3 попробуем понять это правило. Уменьшаемое в данном выражении это 5, а вычитаемое это 3. Правило говорит, что для того, чтобы из 5 вычесть 3 , нужно к 5 прибавить такое число, которое будет противоположно 3. Противоположное для числа 3 это число −3. Записываем новое выражение:

А как находить значения для таких выражений мы уже знаем. Это сложение чисел с разными знаками, которое мы рассмотрели ранее. Чтобы сложить числа с разными знаками, мы из большего модуля вычитаем меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше:

5 + (−3) = |5| − |−3| = 5 − 3 = 2

Модуль числа 5 больше, чем модуль числа −3. Поэтому мы из 5 вычли 3 и получили 2. У числа 5 модуль больше, поэтому знак этого числа и поставили в ответе. То есть ответ положителен.

Поначалу быстро заменять вычитание сложением удаётся не всем. Это связано с тем, что положительные числа записываются без знака плюс.

Например, в выражении 3 − 1 знак минуса, указывающий на вычитание, является знаком операции и не относится к единице. Единица в данном случае является положительным числом, и у неё есть свой знак плюса, но мы его не видим, поскольку плюс перед положительными числами не записывают.

А стало быть, для наглядности данное выражение можно записать следующим образом:

(+3) − (+1)

Для удобства числа со своим знаками заключают в скобки. В таком случае заменить вычитание сложением намного проще.

В выражении (+3) − (+1) в ычитаемое это число (+1), а противоположное ему число это (−1).

Заменим вычитание сложением и вместо вычитаемого (+1) записываем противоположное ему число (−1)

(+3) − (+1) = (+3) + (−1)

Дальнейшее вычисление не составит особого труда.

(+3) − (+1) = (+3) + (−1) = |3| − |−1| = 3 − 1 = 2

На первый взгляд покажется, какой смысл в этих лишних телодвижениях, если можно старым добрым методом поставить знак равенства и сразу записать ответ 2. На самом деле это правило ещё не раз нас выручит.

Решим предыдущий пример 3 − 7, используя правило вычитания. Сначала приведём выражение к понятному виду, расставив каждому числу свои знаки.

У тройки знак плюса, поскольку она является положительным числом. Минус, указывающий на вычитание не относится к семёрке. У семёрки знак плюса, поскольку она является положительным числом:

Заменим вычитание сложением:

(+3) − (+7) = (+3) + (−7)

Дальнейшее вычисление не составляет труда:

(+3) − (−7) = (+3) + (-7) = −(|−7| − |+3|) = −(7 − 3) = −(4) = −4

Пример 7. Найти значение выражения −4 − 5

Перед нами снова операция вычитания. Эту операцию нужно заменить сложением. К уменьшаемому (−4) прибавим число, противоположное вычитаемому (+5). Противоположное число для вычитаемого (+5) это число (−5).

(−4) − (+5) = (−4) + (−5)

Мы пришли к ситуации, где нужно сложить отрицательные числа. Для таких случаев применяется следующее правило:

Чтобы сложить отрицательные числа, нужно сложить их модули, и перед полученным ответом поставить минус.

Итак, сложим модули чисел, как от нас требует правило, и поставим перед полученным ответом минус:

(−4) − (+5) = (−4) + (−5) = |−4| + |−5| = 4 + 5 = −9

Запись с модулями необходимо заключить в скобки и перед этими скобками поставить минус. Так мы обеспечим минус, который должен стоять перед ответом:

(−4) − (+5) = (−4) + (−5) = −(|−4| + |−5|) = −(4 + 5) = −(9) = −9

Решение для данного примера можно записать покороче:

−4 − 5 = −(4 + 5) = −9

или ещё короче:

−4 − 5 = −9

Пример 8. Найти значение выражения −3 − 5 − 7 − 9

Приведём выражение к понятному виду. Здесь все числа, кроме числа −3 являются положительными, поэтому у них будут знаки плюса:

(−3) − (+5) − (+7) − (+9)

Заменим вычитания сложениями. Все минусы, кроме минуса, стоящего перед тройкой, поменяются на плюсы, и все положительные числа поменяются на противоположные:

(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9)

Теперь применим правило сложения отрицательных чисел. Чтобы сложить отрицательные числа, нужно сложить их модули и перед полученным ответом поставить минус:

(−3) − (+5) − (+7) − (+9) = (−3) + (−5) + (−7) + (−9) =

= −(|−3| + |−5| + |−7| + |−9|) = −(3 + 5 + 7 + 9) = −(24) = −24

Решение данного примера можно записать покороче:

−3 − 5 − 7 − 9 = −(3 + 5 + 7 + 9) = −24

или ещё короче:

−3 − 5 − 7 − 9 = −24

Пример 9. Найти значение выражения −10 + 6 − 15 + 11 − 7

Приведём выражение к понятному виду:

(−10) + (+6) − (+15) + (+11) − (+7)

Здесь сразу две операции: сложение и вычитание. Сложение оставляем без изменения, а вычитание заменяем сложением:

(−10) + (+6) − (+15) + (+11) − (+7) = (−10) + (+6) + (−15) + (+11) + (−7)

Соблюдая , выполним поочерёдно каждое действие, опираясь на ранее изученные правила. Записи с модулями можно пропустить:

Первое действие:

(−10) + (+6) = − (10 − 6) = − (4) = − 4

Второе действие:

(−4) + (−15) = − (4 + 15) = − (19) = − 19

Третье действие:

(−19) + (+11) = − (19 − 11) = − (8) = −8

Четвёртое действие:

(−8) + (−7) = − (8 + 7) = − (15) = − 15

Таким образом, значение выражения −10 + 6 − 15 + 11 − 7 равно −15

Примечание . Приводить выражение к понятному виду, заключая числа в скобки, вовсе необязательно. Когда происходит привыкание к отрицательным числам, это действие можно пропустить, поскольку оно отнимает время и может запутать.

Итак, для сложения и вычитания целых чисел необходимо запомнить следующие правила:

Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Сложение отрицательных чисел.

Сумма отрицательных чисел есть число отрицательное. Модуль суммы равен сумме модулей слагаемых .

Давайте разберемся, почему же сумма отрицательных чисел будет тоже отрицательным числом. Поможет нам в этом координатная прямая, на которой мы выполним сложение чисел -3 и -5. Отметим на координатной прямой точку, соответствующее числу -3.

К числу -3 нам нужно прибавить число -5. Куда мы пойдем от точки, соответствующей числу -3? Правильно, влево! На 5 единичных отрезков. Отмечаем точку и пишем число ей соответствующее. Это число -8.

Итак, при выполнении сложения отрицательных чисел с помощью координатной прямой мы все время находимся слева от начала отсчета, поэтому, понятно, что результат сложения отрицательных чисел есть число тоже отрицательное.

Примечание. Мы складывали числа -3 и -5, т.е. находили значение выражения -3+(-5). Обычно при сложении рациональных чисел просто записывают эти числа с их знаками, как бы перечисляют все числа, которые нужно сложить. Такую запись называют алгебраической суммой. Применяют (в нашем примере) запись: -3-5=-8.

Пример. Найти сумму отрицательных чисел: -23-42-54. (Согласитесь, что эта запись короче и удобнее вот такой: -23+(-42)+(-54))?

Решаем по правилу сложения отрицательных чисел: складываем модули слагаемых: 23+42+54=119. Результат будет со знаком «минус».

Записывают обычно так: -23-42-54=-119.

Сложение чисел с разными знаками.

Сумма двух чисел с разными знаками имеет знак слагаемого с большим модулем. Чтобы найти модуль суммы, нужно из большего модуля вычесть меньший .

Выполним сложение чисел с разными знаками с помощью координатной прямой.

1) -4+6. Требуется к числу -4 прибавить число 6. Отметим число -4 точкой на координатной прямой. Число 6 — положительное, значит от точки с координатой -4 нам нужно идти вправо на 6 единичных отрезков. Мы оказались справа от начала отсчета (от нуля) на 2 единичных отрезка.

Результат суммы чисел -4 и 6 — это положительное число 2:

— 4+6=2. Как можно было получить число 2? Из 6 вычесть 4, т.е. из большего модуля вычесть меньший. У результата тот же знак, что и у слагаемого с большим модулем.

2) Вычислим: -7+3 с помощью координатной прямой. Отмечаем точку, соответствующую числу -7. Идем вправо на 3 единичных отрезка и получаем точку с координатой -4. Мы были и остались слева от начала отсчета: ответ — отрицательное число.

— 7+3=-4. Этот результат мы могли получить так: из большего модуля вычли меньший, т.е. 7-3=4. В результате поставили знак слагаемого, имеющего больший модуль: |-7|>|3|.

Примеры. Вычислить: а) -4+5-9+2-6-3; б) -10-20+15-25.

Математический калькулятор. Подробный онлайн калькулятор всех математических операции.

• Главная
• Калькуляторы
• org/ListItem»>Математический калькулятор

Математический-Калькулятор-Онлайн v.1.0

Калькулятор выполняет следующие операции: сложение, вычитание, умножение, деление, работа с десятичными, извлечение корня, возведение в степень, вычисление процентов и др. операции.

Решение:

Как работать с математическим калькулятором

Клавиша	Обозначение	Пояснение
	цифры 0-9	Арабские цифры. Ввод натуральных целых чисел, нуля. Для получения отрицательного целого числа необходимо нажать клавишу +/-
	точка (запятая)	Разделитель для обозначения десятичной дроби. При отсутствии цифры перед точкой (запятой) калькулятор автоматически подставит ноль перед точкой. Например: .5 — будет записано 0.5
	знак плюс	Сложение чисел (целые, десятичные дроби)
	знак минус	Вычитание чисел (целые, десятичные дроби)
	знак деления	Деление чисел (целые, десятичные дроби)
	знак умножения	Умножение чисел (целые, десятичные дроби)
	корень	Извлечение корня из числа. При повторном нажатие на кнопку «корня» производится вычисление корня из результата. Например: корень из 16 = 4; корень из 4 = 2
	возведение в квадрат	Возведение числа в квадрат. При повторном нажатие на кнопку «возведение в квадрат» производится возведение в квадрат результата Например: квадрат 2 = 4; квадрат 4 = 16
	дробь	Вывод в десятичные дроби. В числителе 1, в знаменателе вводимое число
	процент	Получение процента от числа. Для работы необходимо ввести: число из которого будет высчитываться процент, знак (плюс, минус, делить, умножить), сколько процентов в численном виде, кнопка «%»
	открытая скобка	Открытая скобка для задания приоритета вычисления. Обязательно наличие закрытой скобки. Пример: (2+3)*2=10
	закрытая скобка	Закрытая скобка для задания приоритета вычисления. Обязательно наличие открытой скобки
	плюс минус	Меняет знак на противоположный
	равно	Выводит результат решения. Также над калькулятором в поле «Решение» выводится промежуточные вычисления и результат.
	удаление символа	Удаляет последний символ
	сброс	Кнопка сброса. Полностью сбрасывает калькулятор в положение «0»

Алгоритм работы онлайн-калькулятора на примерах

Сложение.

Пример:

Сложение целых натуральных чисел { 5 + 7 = 12 }

Сложение целых натуральных и отрицательных чисел { 5 + (-2) = 3 }

Сложение десятичных дробных чисел { 0,3 + 5,2 = 5,5 }

Вычитание.

Пример:

Вычитание целых натуральных чисел { 7 — 5 = 2 }

Вычитание целых натуральных и отрицательных чисел { 5 — (-2) = 7 }

Вычитание десятичных дробных чисел { 6,5 — 1,2 = 4,3 }

Умножение.

Пример:

Произведение целых натуральных чисел { 3 * 7 = 21 }

Произведение целых натуральных и отрицательных чисел { 5 * (-3) = -15 }

Произведение десятичных дробных чисел { 0,5 * 0,6 = 0,3 }

Деление.

Пример:

Деление целых натуральных чисел { 27 / 3 = 9 }

Деление целых натуральных и отрицательных чисел { 15 / (-3) = -5 }

Деление десятичных дробных чисел { 6,2 / 2 = 3,1 }

Извлечение корня из числа.

Пример:

Извлечение корня из целого числа { корень(9) = 3 }

Извлечение корня из десятичных дробей { корень(2,5) = 1,58 }

Извлечение корня из суммы чисел { корень(56 + 25) = 9 }

Извлечение корня из разницы чисел { корень (32 – 7) = 5 }

Возведение числа в квадрат.

Пример:

Возведение в квадрат целого числа { (3) ² = 9 }

Возведение в квадрат десятичных дробей { (2,2) ² = 4,84 }

Перевод в десятичные дроби.

Пример:

{ 1/3 = 0,33 }

{ ½ = 0,5 }

Вычисление процентов от числа

Пример:

Увеличить на 15% число 230 { 230 + 230 * 0,15 = 264,5 }

Уменьшить на 35% число 510 { 510 – 510 * 0,35 =331,5 }

18% от числа 140 это { 140 * 0,18 = 25,2 }

положительных и отрицательных чисел | SkillsYouNeed

Стандартные числа, большие нуля, описываются как «положительные» числа. Мы не ставим перед ними знак плюс (+), потому что нам это не нужно, так как общее понимание таково, что числа без знака положительны.

Числа меньше нуля называются «отрицательными». Перед ними стоит знак минус (-), указывающий, что они меньше нуля (например, -10 или ‘ минус 10 ‘).

Визуализация отрицательных и положительных чисел

Вероятно, самый простой способ визуализировать отрицательные и положительные числа — использовать числовую прямую, инструмент, с которым вы, возможно, хорошо знакомы, особенно если ваши дети учатся в начальной школе.

Это выглядит примерно так:

Числовая линия может помочь вам визуализировать как положительные, так и отрицательные числа, а также операции (сложение и вычитание), которые вы можете с ними выполнять.

Когда вам нужно вычислить сложение или вычитание, вы начинаете с первого числа и перемещаете второе число разрядов вправо (для сложения) или влево (для вычитания).

Эта числовая линия является упрощенной версией, но вы можете нарисовать их, включив в них все числа, если хотите. Большим преимуществом числовой линии является то, что ее очень легко нарисовать самому себе на обратной стороне конверта или листке бумаги, а также довольно сложно ошибиться при расчете. Пока вы внимательно подсчитываете количество мест, которые вы перемещаете, вы получите правильный ответ.

---

Вычитание отрицательных чисел

Если вы вычитаете отрицательное число, два отрицательных числа объединяются, чтобы получить положительное.

−10−(−10) не равно −20. Вместо этого вы можете думать об этом как о повороте одного из отрицательных знаков вертикально, чтобы пересечь другой и сделать плюс. Тогда сумма будет равна −10+10 = 0.

Краткое примечание о скобках

---

Для ясности: вы никогда не будете писать два отрицательных знака рядом без скобок.

Таким образом, если вас попросят вычесть отрицательное число, оно всегда будет заключено в скобки, чтобы вы могли видеть, что использование двух отрицательных знаков было преднамеренным.

-10—10 неверно (и сбивает с толку)

-10-(-10) правильно (и более ясно)

---

Умножение и деление с положительными и отрицательными числами

При умножении или делении с комбинациями положительных и отрицательные числа, вы можете упростить процесс, сначала игнорируя знаки (+/-) и просто умножая или разделяя числа, как если бы они оба были положительными. Получив числовой ответ, вы можете применить очень простое правило для определения знака ответа:

• Когда знаки двух чисел совпадают с , ответ будет положительным .
• Когда знаки двух чисел отличаются , ответ будет отрицательным .

Итак:

(положительное число) × (положительное число) = положительное число

(отрицательное число) × (отрицательное число) = положительное число

Но:

(положительное число) × (отрицательное число) = отрицательное число

В качестве побочного вопроса это каким-то образом объясняет, почему вы не можете получить квадратный корень из отрицательного числа (подробнее об этом читайте на нашей странице Специальные числа и концепции ). Квадратный корень — это число, которое нужно умножить само на себя, чтобы получить число. Нельзя умножать число само на себя, чтобы получить отрицательное число. Чтобы получить отрицательное число, вам нужно одно отрицательное и одно положительное число.

Правило работает так же, когда у вас есть более двух чисел для умножения или деления. Четное количество отрицательных чисел даст положительный ответ. Нечетное количество отрицательных чисел даст отрицательный ответ.

---

Почему умножение двух отрицательных чисел дает положительный ответ?

---

Тот факт, что отрицательное число, умноженное на другое отрицательное число, дает положительный результат, часто сбивает с толку и кажется нелогичным.

Чтобы объяснить, почему это так, вернитесь к числовым линиям, использованным ранее в этой статье, поскольку они помогают объяснить это визуально.

1. Во-первых, представьте, что вы стоите на числовой прямой в точке ноль и смотрите в положительном направлении, то есть в сторону 1, 2 и так далее. Вы делаете два шага вперед, останавливаетесь, затем делаете еще два шага. Вы прошли 2 × 2 шага = 4 шага.
   Следовательно, положительный × положительный = положительный
2. Теперь вернитесь к нулю и повернитесь лицом в отрицательном направлении, то есть к −1, −2 и т. д. Сделайте два шага вперед, затем еще два. Теперь вы стоите на −4. Вы переместились на 2 × -2 шага = -4 шага.
   Отсюда минус × плюс = минус

В обоих этих примерах вы двигались вперед (т. е. в том направлении, в котором смотрели), положительное движение.

3. Снова вернитесь к нулю, но на этот раз вы пойдете назад (негативное движение). Снова повернитесь лицом в положительном направлении и сделайте два шага назад. Теперь вы стоите на −2. Положительное (направление, в котором вы смотрите) и отрицательное (направление, в котором вы движетесь) приводят к отрицательному движению.
   Следовательно, положительный × отрицательный = отрицательный
4. Наконец, снова вернитесь к нулю, повернитесь лицом в отрицательном направлении. Теперь сделайте два шага назад , а затем еще два назад. Вы стоите на +4. Повернувшись лицом в отрицательном направлении и пройдя назад ( два негатива ), вы достигли положительного результата.
   Отсюда отрицательный × отрицательный = положительный

---

1. Два отрицательных числа компенсируют друг друга. Вы можете увидеть это в речи:
   • «Просто сделай это!» позитивное побуждение к действию.
   • «Не делай этого!» просит кого-то не делать что-то. Это минус.
   • «Не делай этого» означает «пожалуйста, сделай это». Два отрицания компенсируются и дают положительный результат как в математике, так и в речи.
2. Знаки складываются физически. Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный. Если у вас есть положительный и отрицательный, остается одна черточка, и ответ отрицательный. Это простая и наглядная памятка, несмотря на то, что она не обязательно удовлетворит тех, кто хочет понять правило.

---

Заключение

Отрицательные знаки могут показаться немного пугающими, но правила их использования просты и понятны. Помните об этом, и у вас не будет проблем.

Сложение и вычитание отрицательных чисел

IntroMultiplying & DividingExponents

Purplemath

Как вы справляетесь со сложением и вычитанием отрицательных чисел? Процесс работает аналогично сложению и вычитанию положительных чисел. Когда вы добавили положительное число, вы переместились вправо по числовой строке. Когда вы вычитали положительное число, вы двигались влево.

Теперь, если вы добавляете отрицательное значение, вы можете считать, что это почти то же самое, что и при вычитании положительного, если вы рассматриваете «добавление отрицательного значения» как добавление к левому . То есть, прибавляя минус, вы прибавляете в другом направлении. Точно так же, если вы вычитаете минус (то есть минус минус), вы вычитаете в другом направлении; то есть вы будете вычитать, перемещая вправо .

Например:

Содержание продолжается ниже

MathHelp.com

Сложение и вычитание целых чисел

Вернемся к первому примеру с предыдущей страницы: «9 − 5» также можно записать как «9 + (−5)». Графически это будет выглядеть как «стрелка от нуля до девяти, а затем «минусовая» стрелка длиной в пять единиц»:

← проведите пальцем по , чтобы просмотреть полное изображение →

. .. и вы получите «9». + (-5) = 4 дюйма.

Теперь вернитесь к тому вычитанию, которое вы не могли сделать: 5 − 9. Поскольку теперь у вас есть отрицательные числа слева от нуля, у вас также теперь есть «пробел», чтобы завершить это вычитание. Просмотрите вычитание как добавление минус 9; то есть нарисуйте стрелку от нуля до пяти, а затем «отрицательную» стрелку длиной девять единиц:

← смахните , чтобы просмотреть полное изображение →

…или, что то же самое:

← пролистните , чтобы просмотреть полное изображение →

Тогда 5 − 9 = 5 + (−9) = −4.

Конечно, этот метод подсчета вашего ответа на числовой прямой не будет работать так хорошо, если вы имеете дело с большими числами. Например, подумайте о выполнении «465 − 739». Вы, конечно, не хотите использовать числовую линию для этого. Однако с 739 г.больше 465, вы знаете, что ответ на «465 − 739» должен быть отрицательным, потому что «минус 739» приведет вас куда-то левее нуля. Но как определить , какое отрицательное число является ответом?

Посмотрите еще раз на «5 − 9». Теперь вы знаете, что ответ будет отрицательным, потому что вы вычитаете большее число, чем вы начали (девять больше, чем пять). Самый простой способ справиться с этим — сделать вычитание «нормально» (меньшее число вычитается из большего числа), а затем поставить знак «минус» на ответ: 9− 5 = 4, поэтому 5 − 9 = −4. Это работает так же и для больших чисел (и это намного проще, чем пытаться нарисовать картинку): поскольку 739 − 465 = 274, тогда 465 − 739 = −274.

Сложить два отрицательных числа очень просто: вы просто добавляете две «отрицательные» стрелки, так что это похоже на «обычное» сложение, но в противоположном направлении. Например, 4 + 6 = 10 и -4 — 6 = -4 + (-6) = -10. Но что делать, если у вас много как положительных, так и отрицательных чисел?

Вероятно, самое простое, что можно сделать, это преобразовать все в сложение, сгруппировать положительные и отрицательные вместе, объединить и упростить. Выглядит так:

18 — (-16) — 3 — (-5) + 2

= 18 + 16 — 3 + 5 + 2

= 18 + 16 + (-3) + 5 + 2

= 18 + 16 + 5 + 2 + (-3)

= 41 + (-3)

= 41 — 3

= 38

---

Я слышу, как ты говоришь. «Как перейти от «- (-16)» к «+16» на первом этапе? Как «минус минус 16» превратился в «плюс 16»?

На самом деле это довольно важная концепция, и, если вы спрашиваете, я предполагаю, что объяснение вашего учителя не имело для вас особого смысла. Поэтому я не буду давать вам «правильное» математическое объяснение этого правила «минус от минуса — это плюс». Вместо этого вот мысленная картина, на которую я натолкнулся много лет назад в группе новостей по алгебре:

Представьте, что вы готовите какое-то рагу в большой кастрюле, но не на плите. Вместо этого вы контролируете температуру тушеного мяса с помощью магических кубиков. Эти кубики бывают двух типов: горячие кубики и холодные кубики.

Если добавить в кастрюлю горячий кубик (добавьте положительное число), температура рагу повысится. Если вы добавите кубик холода (добавите отрицательное число), температура понизится. Если убрать горячий куб (вычесть положительное число), температура понизится. А если убрать холодный куб (вычесть отрицательное число), температура ПОВЫШАЕТСЯ! То есть вычитание минуса равносильно добавлению плюса.

Теперь предположим, что у вас есть несколько двойных кубиков и несколько тройных кубиков. Если вы добавите три кубика двойного нагрева (добавьте три раза плюс два), температура повысится на шесть. А если убрать два тройных кубика холода (вычесть дважды-отрицательно-три), то получится тот же результат. То есть −2(−3) = + 6.

Вот еще одна аналогия, которую я видел. Позволив «хорошему» быть «позитивным», а «плохому» «негативным», вы могли бы сказать:

хорошие вещи, происходящие с хорошими людьми: хорошие вещи

хорошие вещи, происходящие с плохими людьми: плохие вещи

плохие вещи, происходящие с хорошими людьми: плохие вещи

плохие вещи, происходящие с плохими людьми: хорошие вещи

Приведем конкретный пример:

семья из четырех человек на микроавтобусе добирается до дома в целости и сохранности: хорошо

пьяный водитель на угнанной машине, мчащейся по дороге, не попадается и не останавливается: плохо

семья из четырех человек убита пьяным водителем, в то время как пьяный скрылся с места происшествия без единой царапины: плохо

пьяный водитель пойман и заперт до того, как он причинит кому-либо вред: хорошо

Приведенные выше аналогии не t технических объяснений или доказательств, но я надеюсь, что они сделают правила «минус от минуса плюсом» и «минус, умноженный на минус, будет плюсом» кажутся немного более разумными.

По какой-то причине кажется полезным использовать термины «плюс» и «минус» вместо «сложение», «вычитание», «положительное» и «отрицательное». Так, например, вместо того, чтобы говорить «вычитание отрицательное», вы бы сказали «минусование минуса». Я понятия не имею, почему это так полезно, но я знаю, что эта вербальная техника помогла и отрицаниям «щелкнуть» меня тоже.

Рассмотрим еще несколько примеров:

−43 − (−19) − 21 + 25

= −43 + 19 − 21 + 25 *

= (−43) + (−21) + 19 + 25    *

= (−64) + 44

= 44 + (−64)

Технически я могу перемещать числа так, как я это делал. между двумя звездочками выше только после я преобразовал все в дополнение. Я не могу обратить вычитание, я могу только обратить сложение; только сложение коммутативно. С практической точки зрения это означает, что я могу перемещать числа примерно на 9.0005 только если я также перенесу их знаки с ними . Если я буду перемещать только числа, а не их знаки, я изменю значения и получу неправильный ответ. Продолжаем…

44 + (-64) = 44 — 64

Так как 64 — 44 = 20, то 44 — 64 = -20.

---

84 + (-99) + 44 — (-18) — 43

= 84 + (-99) + 44 + 18 + (-43)

= 84 + 44 + 18 + (-99) + (−43)

= 146 + (−142)

= 146 − 142

= 4

---

URL: https://www.purplemath.com/modules/negative2.htm

Стр. 1 Стр. 3 Стр. 4

Умножение отрицательных чисел — Знаки, примеры, правила, примеры решения и часто задаваемые вопросы

Числа меньше нуля называются отрицательными числами. Числа выше нуля являются положительными числами. Существуют правила сложения, вычитания, умножения или деления положительных и отрицательных чисел.

Учащиеся могут загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта Vedantu. Любой желающий может бесплатно загрузить PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» с веб-сайта. Умножение отрицаний — очень важная тема математики, по которой на экзаменах задают много вопросов. Правильное понимание темы необходимо для студентов, чтобы получить хорошие оценки на экзаменах. Эта тема важна для конкурсных экзаменов, таких как IIT и NEET. Таким образом, студенты должны приложить надлежащие усилия при изучении темы. Преподавательский состав Веданту, имеющий большой опыт обучения студентов, подготовил PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы».

Учащиеся могут использовать PDF-файл «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы» для многих целей. Они могут использовать его для проверки перед экзаменами или для изучения темы.

Таким образом, учащиеся могут получить массу преимуществ, загрузив PDF-файл «Умножение отрицаний — знаки, примеры, правила, примеры решения и часто задаваемые вопросы».

Некоторые из тем, которые были объяснены в PDF-файле «Умножение отрицаний — знаки, примеры, правила, решенные примеры и часто задаваемые вопросы», следующие:

• Знаки

• Правила умножения отрицательных чисел

• Деление отрицательных чисел

• Что происходит, когда мы умножаем отрицательные числа?

Знаки

Мы знаем, что «+» — положительный знак, «-» — отрицательный. Когда знак не обозначается перед числом, это обычно означает, что оно положительное.

Пример: 8 на самом деле +8

Примечание: Чтобы избежать путаницы со знаками, мы можем поставить () вокруг цифр. Например, 5 × −8 можно записать как 5 × (−8)

Правила умножения отрицательных чисел

Мы можем иметь положительные и отрицательные целые значения при работе с целыми числами при умножении. Существуют правила умножения и деления целых чисел, которые очень похожи на правила сложения и вычитания.

• Если знаки разные, то ответ отрицательный.

• Если знаки совпадают, ответ положительный.

См. описание ниже для лучшего понимания.

(Изображение будет загружено в ближайшее время)

Плюс Times Plus is Plus

Пример: 2 × 5 = 10 

(Мы уже обсуждали, что если число не имеет знака, это обычно означает, что оно положительное. )

(Изображение будет загружено в ближайшее время)

Минус умножить минус на плюс

Пример: (-10) × (-5) = 50

Отрицательное, умноженное на Отрицательное, является положительным числом, что означает, что произведение двух отрицательных целых чисел всегда положительный.

(Изображение скоро будет загружено)

Плюс умножить на минус = минус

Пример: 5 x (-5) = — 25

Умножение отрицательных чисел на положительное число всегда дает отрицательное число.

(Изображение будет загружено в ближайшее время)

Минус Умножить Плюс на Минус

Примечание. Эти правила работают так же, как правила деления целых чисел; вам просто нужно заменить «раз» на «делится на».

Деление отрицательных чисел

Деление отрицательных чисел работает так же, как и деление положительных чисел, за исключением того, что результаты иногда бывают отрицательными. От двух чисел, участвующих в этом делении, зависит, будет ли ответ отрицательным. Ответ также будет отрицательным, если только одно из чисел отрицательное. Результат будет положительным, если оба числа отрицательны.

Expression	Quotient	Example
Positive ÷ Positive	Positive	25 ÷ 5 = + 5
Отрицательный ÷ Отрицательный	Положительный	— 25 ÷ — 5 = +5
Отрицательный ÷3 0388	Negative	-25 ÷ 5 = -5
Positive ÷ Negative	Negative	25 ÷ -5 = — 5

What happens when we Умножать негативы с помощью матриц?

Целочисленная матрица — это матрица, все элементы которой являются целыми элементами.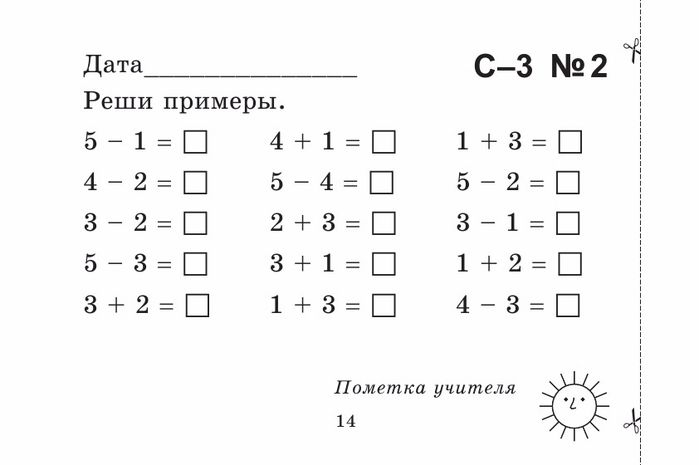 Отрицательное значение матрицы получается путем ее умножения на -1.

Итак, если A — заданная матрица

Тогда − A = − 1 A

Решенные примеры

1. Что такое −6 × 3?

Ответ: 6 х 3 равно 18. Но здесь у нас есть одно отрицательное и одно положительное число. Следовательно, знак ответа будет минус.

Следовательно, ответ равен −18.

2. Что такое −80 ÷ 8?

Ответ: 80 ÷ 8 равно 10. Опять же, у нас есть положительное и отрицательное число. Следовательно, в окончательном ответе знак будет отрицательным.

Следовательно, ответ равен −10.

3. Что такое −50 x −5?

Ответ: 50 x 5 равно 250. На этот раз у нас есть 2 отрицательных числа. Значит, в ответе будет положительный знак. Следовательно, ответ равен 250.

Заключение

Помните только 2 вещи, когда перемножаете отрицательные числа.