Математика Проверка деления с остатком

Материалы к уроку

Конспект урока

33. Проверка деления с остатком
Организационный этап   Прозвенел уже звонок, Он позвал всех на урок. Мы за парту дружно сели И на доску посмотрели. Сегодня мы вспомним правила деления с остатком, будем учиться выполнять проверку деления с остатком. А поможет нам в этом наш знакомый Размышлялкин. Сегодня он не один, а со своей подружкой  — Любознайкой.
Этап подготовки учащихся к активному сознательному усвоению знаний   Устный счёт   Любая в математике работа, Не обходится без устного счёта.   Задание 1 Делить – это здорово, Делить – это классно! Хотя очень часто, С остатком ответ. Все можно вычислить Быстро и четко, Когда в таблице умножения Помнишь каждый ответ! Ребята, запишите  данный ряд чисел в 2 столбика так, чтобы в первом столбике были числа, которые делятся на 5 с остатком, а во втором столбике делятся на 5 без остатка. 21, 22, 23, 24, 25, 26, 27, 28, 30, 33 Проверьте себя. В первый столбик записали числа 21 22 23 24 26 27 28 33 Во второй столбик записали числа   Задание 2 от весёлой Любознайки Если пример делится с остатком, вы поднимаете красную сигнальную карту, если делится без остатка — зеленую. 19 : 8….  делится с остатком (красная) 15 : 4.…. делится с остатком (красная) 18 : 2….. делится без остатка (зелёная) 20 : 5….. делится без остатка (зелёная) 12 : 5….. делится с остатком (красная) 16 : 5….. делится с остатком (красная)   Задание 3 от Размышлялкина Решите задачу. В конструкторе Лего 78 деталей. Чтобы построить паровоз, ему понадобилось 29 деталей. Из остальных деталей Размышлялкин сделал вагоны. Сколько деталей пошло на каждый вагон, если Размышлялкин сделал 7 вагонов? Проверьте себя. 1) 78 — 29 = 49 деталей пошло на 7 вагонов 2) 49 : 7 = 7 деталей пошло на каждый вагон. Вычислите. 75 : 5 90 : 6 28 : 2 49 : 7 Проверьте себя. 75 : 5 = 13 90 : 6 = 15 28 : 2 = 14 49 : 7 =7
Этап усвоения новых знаний   Чтоб ошибки при делении избежать, Надо обязательно всё проверять. Пусть частное будет с остатком — не беда. Проверить вычисление можно всегда.   Как же проверить деление с остатком? 1. Сравниваем делитель и остаток. Остаток должен быть меньше, чем делитель. 2. Делитель умножаем на частное. 3. К полученному результату прибавляем остаток. 4. Делаем вывод: если получили делимое – пример решён правильно. Выполним деление с остатком и проверим его. 47 : 6 Рассуждайте так: 47 не делится на 6 без остатка. Вспомним, ка­кое самое большое число до 47 делится на 6 без остатка. Это 42. Найдём частное: 42 : 6 = 7. Найдём остаток: 47 — 42 = 5 47 : 6 = 7 (ост. 5) Выполним проверку. 1. Сравниваем делитель и остаток. Остаток должен быть меньше, чем делитель. 5 2. Делитель умножаем на частное. 6 ∙ 7 = 42 3. К полученному результату прибавляем остаток. 42 + 5 = 47 Можно записать так: 6 ∙ 7 + 5 = 47 4. Делаем вывод: получили делимое, значит, решили правильно.
Этап закрепления новых знаний   Задание 1 Выполните деление с остатком и сделайте проверку. 13: 9 27:18 66 :20 50:15 Проверьте себя и оцените свои успехи. 13 : 9 = 1 (ост. 4) Проверка. 4 9 ∙ 1 + 4 = 13 27 : 18 = 1 (ост. 9) Проверка. 9 18 ∙ 1 + 9 = 27 66 : 20 = 3 (ост. 6) Проверка. 3 20 ∙ 3 + 6 = 66 80 : 15 = 5 (ост. 5) Проверка. 5 15 ∙ 5 + 5 = 80
Задание 2 Ребята, Любознайка решила примеры. Проверьте и найдите ошибки. 29 : 4 = 7 (ост. 1) 88 : 44 = 2 13 : 4 = 2 (ост. 5) Проверьте себя. В примере 13 : 4 = 2 (ост. 5) есть ошибка: остаток при делении должен быть меньше делителя. Решите правильно и сделайте проверку. 13 : 4 = 3 (ост. 1) Проверка. 1 4 ∙ 3 + 1 = 13 Задание 3 Посчитайте лепестки на цветах. На одном цветке их пять. Сможете вы сосчитать, Сколько будет лепестков, Если семь всего цветков? 5 ∙ 7 = 35 лепестков.
Этап подведения итогов   Давайте повторим основные правила деления с остатком. Вспомним основные правила проверки: 1. Сравниваем   делитель и остаток. Остаток  должен быть меньше, чем делитель. 2. Делитель умножаем на частное. 3. К полученному результату прибавляем остаток. 4. Делаем вывод: если получили делимое – пример решён правильно.
Рефлексия   Если на уроке  вам было всё понятно, нарисуйте  лепестки красного цвета, если понятно, но не совсем, то лепестки желтого цвета, а если не понятно ничего –  зелёные лепестки. Спасибо  за работу!

Остались вопросы по теме? Наши репетиторы готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать репетитораОставить заявку на подбор

как найти остаток от деления, примеры в 2023 году

Что такое деление с остатком?

Поскольку не всегда одно натуральное число можно разделить на другое нацело, возникает необходимость деления чисел с остатком. Рассмотрим пример, когда нужно выполнить деление с остатком.

Задача. Папа купил двум сыновьям 9 апельсин. Как можно разделить фрукты поровну?

Выполним деление: 9 : 2 = 4 (1 ост.) – говорят, что деление выполнено с остатком. Каждый получит по 4 апельсина, 1 апельсин останется в остатке. Читают данное действие следующим образом: 9 разделить на 2 получится 4 и остаток 1.

Компоненты при делении чисел с остатком: делимое, делитель, неполная доля, остаток.

В нашей задаче 9 – делимое, 2 – делитель, 4 – неполное частное, 1 – остаток

Таким образом, деление с остатком – это деление одного натурального числа на другое, при котором остаток не равен нулю. Результат деления называется неполным частным. Разность между делимым и произведением делителя на неполную долю называется

остатком. Остаток всегда меньше делителя. Если остаток равен нулю, то деление натуральных чисел произошло нацело.

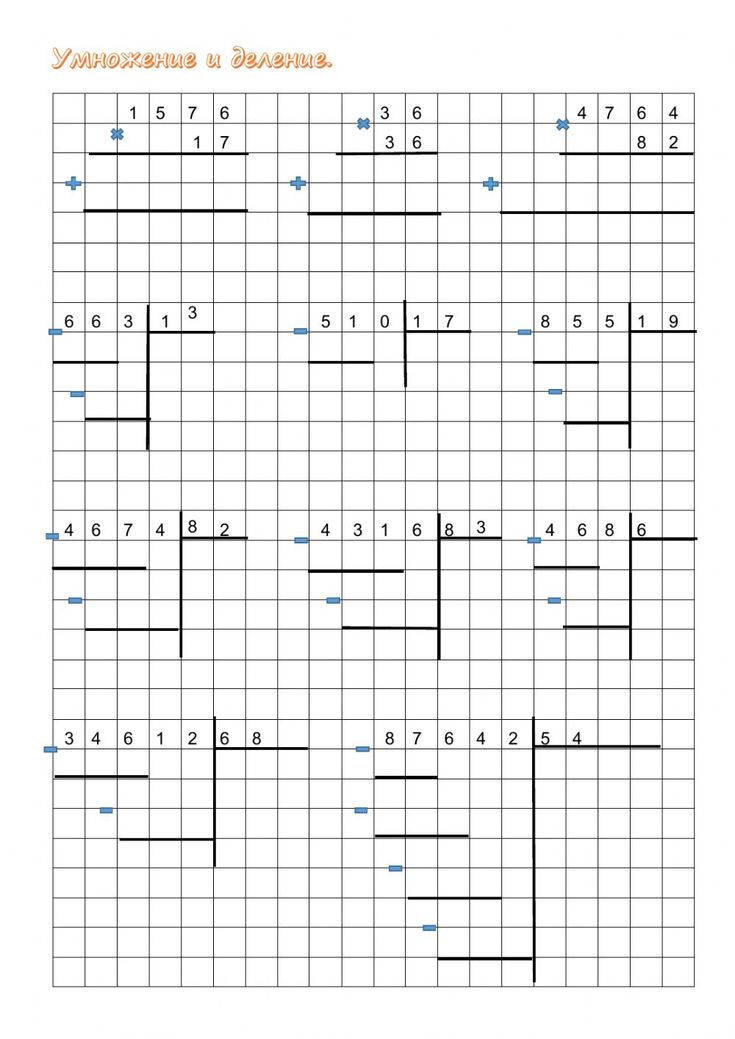
Алгоритм деления с остатком

Поделим 22 на 3 с остатком

1. Находим наибольшее целое число к делимому, которое делится на делитель без остатка. В нашем примере нужно найти наибольшее число до 22, которое делится на 3 без остатка. Очевидно, это число – 21. 21 : 3 = 7
2. Вычитаем из делимого наибольшее целое число (из пункта 1). То есть 22 – 21 = 1
3. Сравним остаток с делителем: 1 < 3. Поскольку остаток меньше делителя, действие выполнено правильно.
4. Ответ: 22 : 3 = 7 остаток (1)

Обратите внимание, если при проверке остаток больше делителя, это означает, что неправильно найдено наибольшее целое число. Соответственно, нужно вернуться к решению первого пункта и нахождению наибольшего целого числа.

Поделим 190 : 24 с остатком

Путем подбора поищем число, при умножении которого на 24 получим произведение, максимально приближенное к 190.

Попробуем подставить число 6. 24 умножить на 6 равно 144. Считаем остаток: 190 – 144 = 46. Поскольку 46 > 24, то есть остаток больше делителя, значит множитель 6 не подходит и попытаемся увеличить его.

Умножим 7 на 24. 7 ⋅ 24 = 168. Найдем остаток 190 – 168 = 22. Остаток 22 < 24 (делитель), поэтому деление выполнено правильно. Итак, 190 : 24 = 7 остаток (22)

Деление с остатком, если делимое меньше делителя

Попробуем поделить натуральные числа, когда делитель больше делимого. Например, 5:10

В этом случае действует правило: 

Если делимое меньше делителя, то при делении с остатком их неполное частное равно нулю, а остаток равен делимому.

5 : 10 = 0 остаток (5)

36 : 253 = 0 остаток (36)

Как найти делимое, делитель при делении с остатком? Буквенная запись и задачи

Как найти делимое? Чтобы найти делимое при делении с остатком, необходимо делитель умножить на частное и добавить остаток.

Решим задачу на деление с остатком, где нужно 25 конфет поделить поровну между тремя детьми.

Поскольку 25 не делится на 3, можем записать:

25 = 3 ⋅ 8 + 1

25 — делимое, 3 – делитель, 8 – неполное частное и 1 – остаток

Пример

Если 51 : 7 = 7 (ост. 2), тогда  51 = 7 ⋅ 7 +2

Как найти делитель при делении с остатком?

Изменение остатка

124100: 400, при делении данных чисел можем «сократить» нули, доля не изменится и будет соответствовать делению 1241 на 4, однако остаток увеличится тоже в 100 раз.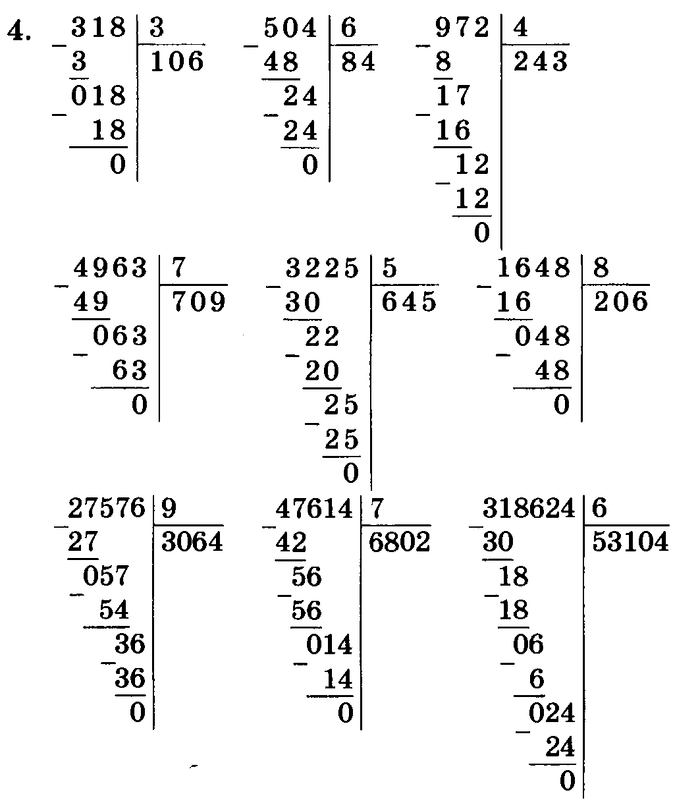 В данном примере остаток – 1 сотня, то есть 100.

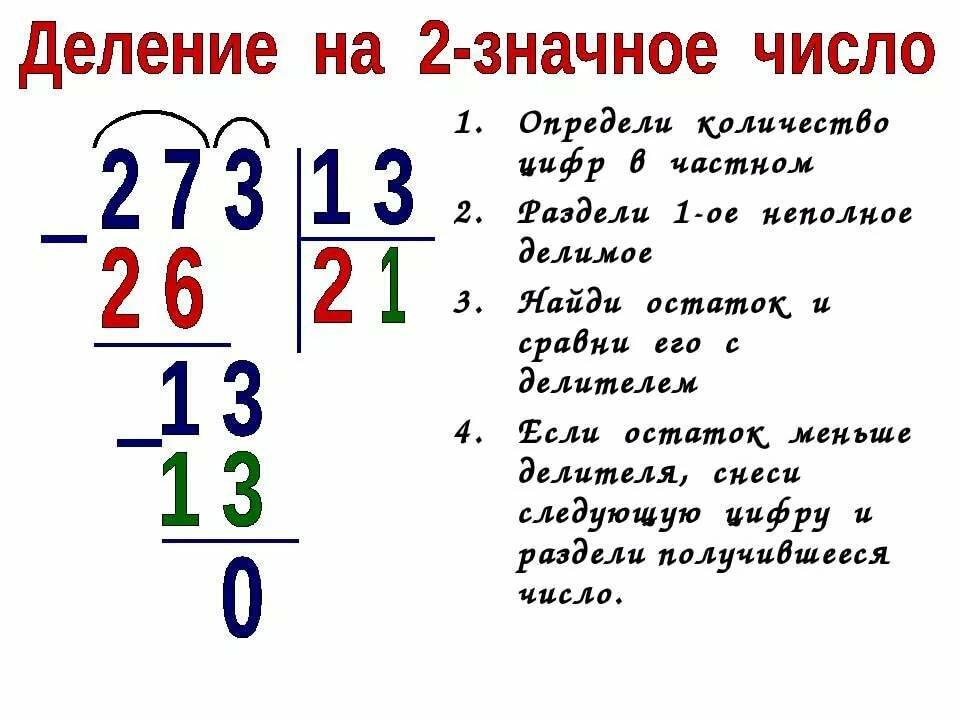
Деление многоцифровых натуральных чисел с остатком

12565 : 251

Выполним деление с остатком в столбик

Деление начинаем с высших разрядов, поскольку 125<251, начинаем делить с 1256 : 251, в частное записываем 5. Из 1256 вычитаем произведение 5 на 251, получим 15. Поскольку 15 не делится на 251, в долю записываем 0. Число 15 < 251 и это есть остаток. Частное – число 50.

Проверим, правильно ли мы поделили. 50 ⋅ 251 + 15 = 12565.

425638 : 586

Начинаем деление с 4256: 586 (поскольку 425 < 586). В частное записываем 7, от 4256 вычитаем произведение 7 на 586, получим 154. К числу 154 сносим 3 из делимого, 1543 : 586, в частное записываем 2. Из 1543 вычтем произведение 586 на 2 и получим 371. Сносим 8 и делим 3718 на 586, в частное записываем 6. Найдем разность чисел 3718 и 3516 (произведение чисел 6 и 586), получим 202 – остаток. Частное — 726

Проверим, меньший ли остаток от делителя: 202 < 586

Кроме того, проверим деление с остатком, умножив частное и делитель и добавив остаток.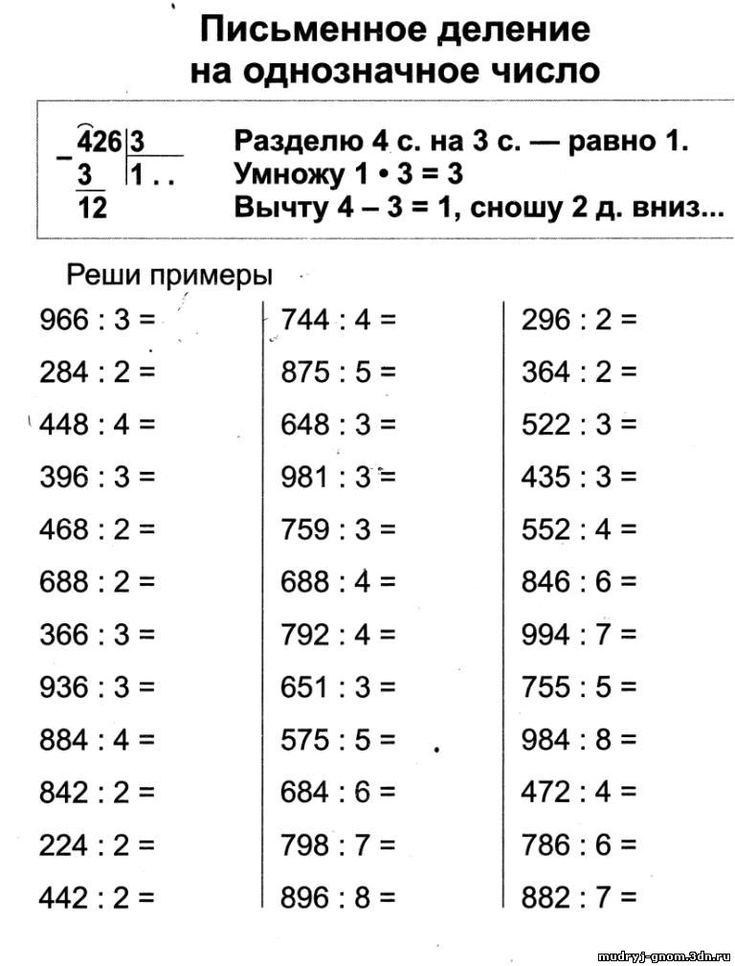 Если в результате получим делимое, то пример решен правильно.

726 ⋅ 586 + 202 = 425436 + 202 = 425638

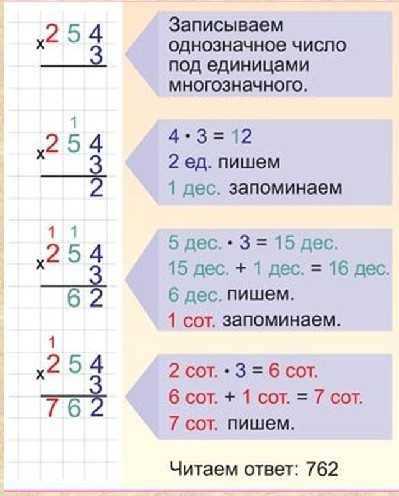
Умножаем 726 на 586 в столбик:

Поскольку результат соответствует делимому, это означает, что деление с остатком выполнено правильно.

Какой наибольший остаток от деления на число 8?

7 – наибольший остаток от деления на 8

Какой наибольший остаток от деления на число 9?

Наибольший остаток от деления на число 9 – это число 8.

Как сделать длинное деление? Определение, шаги, метод, примеры

Определение длинного деления

В математике длинное деление — это математический метод деления больших чисел на более мелкие группы или части. Это помогает разбить проблему на простые и легкие шаги. Длинные деления имеют делимые, делители, частные и остатки. В задаче на длинное деление делимое — это большое число, которое делится на другое число, называемое делителем . частное есть результат деления, а избыточное количество, которое нельзя разделить, называется остатком .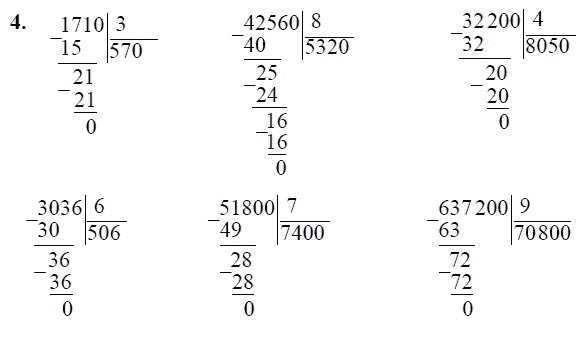

Связанные игры

Пример длинного деления

Вот пример, который поможет нам понять эту концепцию:

Поскольку 75 не кратно 4, оно не делится на 4 и оставит остаток в конце.

Связанные рабочие листы

Символ деления

Чтобы показать, что два числа делятся, мы можем добавить между ними знак деления «÷». Так, например, если нам нужно показать 36, разделенное на 6, мы можем записать это как 36 ÷ 6. 

Мы также можем представить это в форме дроби как 366. 

Шаги для выполнения длинного деления

Есть пять шагов, чтобы легко решить любую задачу на длинное деление.

Давайте посмотрим на приведенные ниже примеры, чтобы лучше понять концепцию.

Деление десятичных чисел с помощью длинного деления

Длинное деление также можно использовать для деления десятичных чисел на равные группы. Он следует тем же шагам, что и при делении в длину, а именно — разделить, умножить, вычесть, свести и повторить или найти остаток.

Вот пример длинного деления с десятичными дробями.

Интересные факты о длинном делении

• Если делимое равно 0, частное всегда будет равно нулю.
• Остаток всегда меньше делимого.
• Умножение частного на делитель и добавление остатка даст делимое.

(делитель x частное) + остаток = делимое 

• Когда остаток равен 0, делимое является произведением делителя и частного.

Делитель x Частное = Делимое, когда остаток = 0

Заключение

Длинное деление — это инструмент, позволяющий разделить большие числа на несколько меньших групп или частей. Когда мы делим делимое на делитель, полученное частное представляет собой количество групп, которые можно составить, а остаток определяет, сколько элементов или чисел останется несгруппированным. Чтобы еще лучше понять эту концепцию, ознакомьтесь с широким спектром интересных упражнений, доступных на SplashLearn, и станьте мастером деления на деления!

Решенные примеры

Вопрос 1: Разделите 726 на 4  

Ответ:

Следовательно, частное задачи равно 181, а остаток равен 9, когда

Вопрос3. делим 248 на 8?

Ответ:

Следовательно, частное задачи равно 31, а остаток равен 0.

Вопрос 3: Мама Лейлы собрала все семейные фотографии и хотела поместить их все в альбом. Если каждая страница альбома может содержать 9фотографий, сколько страниц альбома ей понадобится, если фотографий 285?

Ответ:

Частное задачи равно 31, а остаток равен 6. Значит, ей нужно 31 + 1 (для оставшихся шести картинок) или 32 страницы.

Практические задачи

1

На разделении 426 на 4, мы получаем остаток как

2

4

6

Правильный ответ: 2
на разделение 426 на 4, мы получим котировку. и остаток как 2.

2

Найдите дивиденд, если делитель равен 8, коэффициент 71, а остаток — 4.

562

560

576

572

Правильный ответ — 572
Dividend = (DivisiSISISTIST). Остаток = (8 x 71) + 4 = 572

3

Найдите цифру, которая может заменить A в следующей задаче на деление.

3

4

5

6

Правильный ответ: 6
A × 5 = 30. Таким образом, A должно быть 30 ÷ 5 или 6,

Часто задаваемые вопросы

Может ли делитель быть 0?

Нет, деление на 0 в математике вообще не определено.

Что такое метод длинного деления?

В математике длинное деление — это математический метод деления больших чисел на несколько меньших групп или частей. Число, которое мы делим на маленькие группы, называется делимым, число, на которое мы делим, называется делителем. Это помогает разбить проблему на простые и легкие шаги.

Как мы можем проверить частное и остаток от задачи деления?

Мы можем проверить частное и остаток от деления, используя формулу деления: (Делитель x Частное) + Остаток = Делимое 

В чем разница между прямым делением и коротким делением?

Короткое деление удобно для деления больших чисел на однозначные числа, тогда как длинное деление удобно для деления больших чисел на числа с двумя и более цифрами.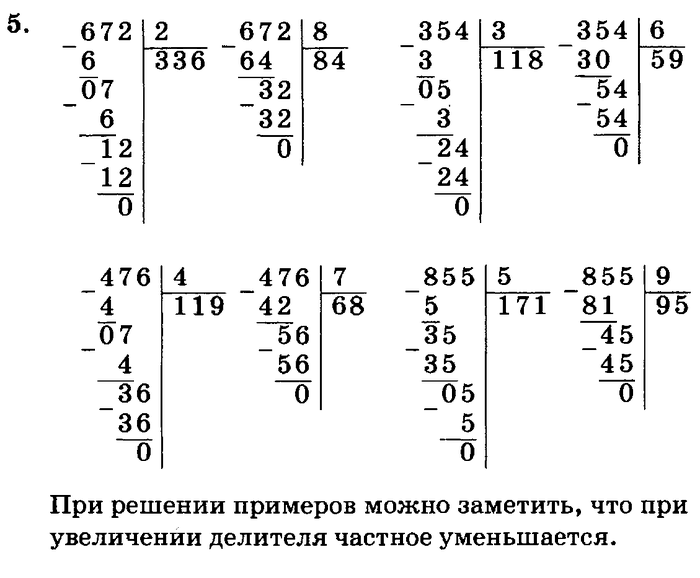

Длинная часть

Длинная часть

Показать рекламу

Скрыть рекламу
О рекламе

Ниже Процесс выписан полностью.
Вы часто будете видеть другие версии, которые, как правило, являются просто укороченной версией процесса ниже .
Вы также можете увидеть это в Long Division Animation.

Давайте посмотрим, как это делается с помощью:

• число, на которое нужно разделить, называется делимое
• Число, на которое делится другое число, называется делителем

И вот:

	4 ÷ 25 = 0 остаток 4	Первая цифра делимого (4) делится на делитель.
		Целое число помещается вверху. Любые остатки в этот момент игнорируются.
	25 × 0 = 0	Ответ из первой операции: умножить на делитель. Результат помещается под числом, разделенным на.
	4 − 0 = 4	Теперь мы вычитаем нижнее число из верхнего числа.
		Сократите следующую цифру делимого.
	42 ÷ 25 = 1 остаток 17	Разделите это число на делитель.
		Целое число помещается вверху. Любые остатки в этот момент игнорируются.
	25 × 1 = 25	Ответ от вышеприведенной операции равен , умноженному на 9019.1 на делитель. Результат помещается под последним числом, на которое делится.
	42 − 25 = 17	Теперь мы вычитаем нижнее число из верхнего числа.
		Сократите следующую цифру делимого. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт