Сложение и вычитание в пределах 20
Описание
Сложение и вычитание в пределах 20 – это первые примеры, с которых начинается формирование логического мышления ребенка. Простое заучивание наизусть не всегда дает быстрый и прочный результат. Именно поэтому нужна практика, которая поможет развить внимательность и закрепить навыки устного счета у детей. Для этого достаточно заниматься 10-15 минут в день. Программа будет полезна как дошкольникам, так и ученикам 1 класса.
Программа представляет собой тренажер для счета в пределах 20. Она написана в Excel с помощью макросов. С помощью генератора примеров можно создать и распечатать готовые примеры в пределах 20 на сложение и вычитание.
Формируются примеры: 4 столбика по 23 примера на листе формата А4. Примеры генерируются случайным образом, количество генераций не ограничено. Для ответов есть клеточки, которые позволяют ребенку тренировать не только устный счет, но и правильное написание цифр.
Генератор примеров по математике будет очень удобен как для родителей, так и для учителей, так как не нужно заранее покупать задачники и пособия по математике с примерами. Можно скачать файл и сгенерировать карточки в любое время независимо от подключения к интернету и распечатать.
Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы.
Для получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.
Также есть программы, в которых можно выбрать уровень сложности. В них можно начать с решения легких примеров, а затем перейти к более сложным.
На сайте представлен каталог программ, в котором все программы распределены по группам с указанием различий в программах внутри каждой группы. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.
Как научить ребенка считать примеры в пределах 20
Итак, первые шаги в математической науке уже пройдены, и теперь родителям предстоит объяснить ребенку, как же складывать или вычитать числа в пределах 20-ти. Безусловно, самое главное в математике – понять все премудрости этой науки. Не подсмотреть у соседа по парте, не посчитать на палочках или пальцах (рук и ног), а именно понять, почему нужно поступать так, а не иначе.
Эта сложная наука – математика
Некоторым деткам научиться математическому счету бывает намного труднее, чем, например, научиться читать. Поэтому, чтобы у ребенка появилась так называемая «симпатия» к предмету, родителям придется постараться привить любовь ребенка к математике.
Некоторые родители не желают обременять себя подобными делами и перекладывают обучение вычислениям на плечи педагогов начальной школы. Безусловно, именно учителя и выполняют обучение счету детей, но родители не должны самоустраняться, а обязаны помогать ребенку, помогать находить ошибки, анализировать их.
Даже если вы решили воспользоваться услугами репетитора, заниматься с ребенком дома все равно придется, ведь учитель задает домашние задания, которые следует добросовестно выполнять. В противном случае знания, не подкрепленные практикой, очень быстро забудутся.
Как научить считать в пределах 20-ти
Педагоги с опытом рекомендуют использовать для объяснения азов вычитания и сложения в пределах второго десятка по уже разработанным алгоритмам. Это поможет детям понять и осмыслить, что представляет собой один и два десятка, как складывать числа или вычитать их, если они переваливает через десяток. Занимаясь с ребенком, каждый раз следует проверять, насколько хорошо он понял пройденный материал, закрепить его, и не перескакивать на следующие темы, если в предыдущей остались пробелы.
С чего начать?
Прежде всего ребенок должен знать, как называются числа второго десятка и в каком порядке они идут друг за другом. После этого понадобится двадцать одинаковых деталей чего-либо: кубиков, счетных палочек, карточек от игр и прочее.
После этого понадобится двадцать одинаковых деталей чего-либо: кубиков, счетных палочек, карточек от игр и прочее.
Разложите с ребенком кубики (карточки, палочки и прочее) в два ряда по 10 штук в каждом ряду. Первый ряд – это первый десяток, можете даже пронумеровать все кубики первого десятка. Второй ряд – это числа второго десятка. Выложите их один под другим, т.е. кубики с порядковыми номера «один» и «одиннадцать» должны располагаться один над другим, «два» над «двенадцать», «пять» над «пятнадцать» и так далее.
Запоминать названия чисел второго десятка так будет намного проще: 11 – к слову «один» прибавляет окончание «-дцать», лежит на нем «один», так и получает «один-на-дцать». Таким же образом получаем и другие числа «две-на-дцать», «три-на-дцать» и так далее. Повторяйте с ребенком такое упражнение до тех пор, пока он не запомнит числа.
Вычисления без перехода через десяток
Перед тем, как начать обучение счету в пределах двух десятков, ребенок должен четко понимать, где у числа десятки, а где – единицы. Если вы будете объяснять ребенку правила вычисления «на пальцах», то скорее всего, он ничего не поймет. Для обучения вам потребуются наглядные пособия, например, кубики.
Чтобы объяснить ребенку, как делать вычисления без перехода через десяток, попросите его выложить в линию 10 кубиков. Это десяток. Теперь попросите его прибавить к ним еще 3 кубика, поставив их сверху на первые десяток (одиннадцатый кубик на первых, двенадцатый на второй, тринадцатый на третий). Проговаривайте свои действия – «десять плюс три равно тринадцать». Подобный образом составьте и другие числа, без перехода через десяток.
Примерами на сложение и вычитание без перехода через десяток считаются такие, в которых все математические действия совершаются с целым или целыми десятками и еще несколькими единицами.
Например:
10+5=15 16-6=10
10+8=18 17-10=7
После того, как ребенок поймет, как совершается сложение, можно переходить к примерам на вычитание.
Вычисления с переходом через десяток
Математические примеры на сложение и вычитание с переходом через десяток несколько сложнее, и поэтому ребенок долен быть готов к этому этапу обучения. Для этого ему необходимо выучить состав чисел первого десятка.
Например, состав числа 2 – то 1 и 1, а состав числа 3 – это две пары чисел: 2 и 1 или 1 и 2, а состав числа 5 – это следующие пары: 1 и 4, 2 и 3, 3 и 2, 4 и 1. И так для каждого числа первого десятка.
Для чего это необходимо? Выполняя арифметические действия ребенку придется сначала письменно, а затем и устно раскладывать прибавляемое или вычитаемое число так, чтобы оно дало десяток при сложении или вычитании с первым.
Вторым важным условием для перехода к этому этапу является быстрый устный счет в пределах первого десятка. Без этого, ребенку будет сложно удержать в голове видимые числа и те, на которые он раскладывает одно из видимых.
Рассмотрим на примере алгоритм решения примеров на сложение с переходом через десяток.
Нужно прибавить к 8 число 6.
8+6=
Запишем этот пример так:
8+(2+4) =
Т.е. мы раскладываем второе слагаемое 6 на два числа, чтобы в сумме с первым слагаемым 8 получить десятку. После того, как мы складываем 8 и 2 и получаем десятку, нам видно, что при добавлении к нему числа 4 мы получим число 14
Значит 8+(2+4) = 14 или 8+6 = 14
Для закрепления рассмотрим еще несколько примеров на сложение.
6+9 =
Этот пример можно записать следующим образом:
6+(4+5) = 15
И еще один
7+8 =
Записываем его в таком виде:
7+(3+5) = 15
Рассмотрим на примере алгоритм решения примеров на вычитание с переходом через десяток.
Чтобы вычесть из одного числа другое с переходом через десятку, нужно разложить вычитаемое таким образом, чтобы у нас получилась десятка при первом отнимании.
15-7 =
В данном случае число 7 состоит из 5 и 2. Запишем этот пример так, чтобы в первом действии у нас получилась десятка
(15-5)-2 = 8
Ребенку легче будет решать такие примеры, если он запомнит, что при вычитании нужно раскладывать вычитаемое так, чтобы сразу же отнять у первого числа единицы.
Например:
14-6=
Раскладываем вычитаемое (6 состоит из 4 и 2)
(14-4)-2 = 8
16-9=
Раскладываем вычитаемое (9 состоит из 6 и 3)
(16-6)-3=7
Т.е. при вычитании какое бы число не нужно было разложить, сначала вычитаем единицы из первого числа, чтоб осталась десятка, а затем уже вычитаем оставшееся число.
Рекомендации родителям
Не стоит рассчитывать, что эти простые истины математики дадутся ребенку с легкостью. Даже если соседская девочка или сын сотрудницы освоил сложение и вычитание за один день, это не повод впадать в отчаяние. Во-первых, все дети разные и у всех индивидуальные особенности усвоения информации, а во-вторых, если кто-то что-то освоил быстрее, еще не значит, что учиться ему будет легче.
Кроме того, при обучении малыша родителям нужно следить за реакцией ребенка на это обучение. Если вы видите, что ему не интересно, попробуйте сменить тактику. Считайте конфеты, яблоки, книжки, можно вырезать одинаковые фигурки для обучения, а затем сделать из них праздничную гирлянду.
Если в определенный период времени ребенок отказывается учиться, у него плохое настроение или самочувствие, не настаивайте. Перенесите время урока на более благоприятный период. Зато у малыша не пропадет желание к учебе, как к чему-то неприятному и неизбежному. Ну и самое главное, проявляйте терпение к его стараниям и почаще хвалите. Для него это очень важно.
урок математики в 1 классе «Решение примеров и задач в пределах 20» | Уроки по Математике
урок математики в 1 классе «Решение примеров и задач в пределах 20»
09. 02.2018 786 216 Говоркова Евгения Васильевна
02.2018 786 216 Говоркова Евгения ВасильевнаМатематика, 1 класс
Тема урока: Решение примеров и задач в пределах 20
Тип урока: Урок закрепления ранее усвоенных навыков
Цель урока: Закрепление навыка вычислительных действий в пределах 20
Задачи урока:
1. Применять на практике навыки выполнения действий сложения и вычитания в пределах 20.
2. Развивать мыслительную деятельность учащихся при решении нестандартных задач.
3. Воспитывать интерес к учебной деятельности и устранять напряженность при ответах на вопросы заданий.
Ход урока
1. Организационный момент. Психологический настрой
2. Изучение нового материала
— Сегодня на уроке мы потренируемся в выполнении действий в пределах 10, чтобы к концу урока все считали быстро и без ошибок; продолжим учиться считать в пределах 20; будем учиться рассуждать, делать выводы, решать головоломки.
— А проведем мы наш урок в необычной форме. Кто из вас любит смотреть кукольные спектакли? Тогда мы вместе отправляемся Театр кукол. Афиша нам говорит о том, что в театре сегодня «Математическая радуга».
— Кто может сказать, из скольки цветов состоит радуга? Правильно, из семи, поэтому и заданий будет тоже семь, их и предстоит преодолеть.
— Готовы?
— Чтобы получить входной билет, надо произвести небольшую разминку
Устный счет:
Увеличить 8 на 2, объяснить.
Как называются числа при сложении?
Найти сумму чисел 10 и 7.
Как называются числа при вычитании?
Найти разность чисел 9 и 6.
— Разминка окончена, и можно идти приобретать билеты в театр. Но билет эти не простые: в них примеры на сложение и вычитание. В театр попадет только тот , кто правильно решит пример. Но тот, кто захочет выручить друга, может ему помочь и взять с собой в театр.
 Решать нужно очень быстро, а то можно не успеть к началу спектакля.
Решать нужно очень быстро, а то можно не успеть к началу спектакля. 14 билетов. 14 детей выходят к доске, каждый берет билет и решает пример.
— Билеты мы приобрели, каждый на два лица, теперь можем идти в театр.
Дети занимают места. Гаснет свет. Звенит звонок. Над ширмой появляется Петрушка.
Петрушка: Здравствуйте, ребята! Добро пожаловать к нам в театр! Вы любите театр? А что вы любите смотреть? Сказки? Я тоже люблю сказки, и сегодня к нам придут сказочные герои. Но вы, ребята, тоже можете принять участие в спектакле – будете помогать сказочным героям решать задачи, рассуждать. Но сначала я вас поспрашиваю. Сумеете ли вы ответить на мои вопросы?
2. Что надо, сделать со слагаемым, чтобы сумма увеличилась на 3, объясните свое решение.
3. Как можно разложить 10 карандашей в две коробки? А 20 карандашей?
4. Чем отличаются числа 1, 3, 5, от 2, 4, 6?
А теперь напишите в тетради четыре четных числа, только после этого к вам придет сказочный герой.
( Дети пишут ряд четных чисел в тетради. Над ширмой появляется Зайчик.)
Зайчик: Здравствуйте, ребята! Вы хорошо отвечали Петрушке! Ну, а мои задачи вы сумеете решить? Ну-ка, попробуйте!
Зайчик: Я утром был в огороде и нашел там 7 морковок. 2 съел сразу. Мне показалось, что у меня осталось 6 морковок. Правильно? Вот молодцы, что помогли мне! Запишите в тетрадь пример решения этой задачи!
( Дети работают в тетрадях)
Зайчик: А вчера я бегал в лесу. Как там красиво! Под одной сосенкой я видел 5 рыжиков, а под другой на один гриб больше. Сколько всего я видел грибов? Белочка записала такое решение: 5+1, а я решил так: 5+5+1.
Кто записал верное решение? Кто не согласен? Сколько же всего грибов я видел?
(Дети отвечают.)
Зайчик: Но самое трудное задание я подсмотрел у ребят в классе. Им учительница предложила выбрать пары чисел, разность которых равна 2. Вот эти числа: 8, 17, 20, 10, 6, 18, 15, 4.
 Посовещайтесь в паре.
Посовещайтесь в паре. (Дети находят пары чисел, а два примера записывают в тетрадь.)
Зайчик: Спасибо, ребята, вы помогли мне решить многие проблемы. Желаю вам успехов в учебе, а я тоже пойду в школу учиться. Ой, кто-то сюда идет! Я убегаю!
Лиса: Здравствуйте, ребята! Заяц убежал, думая, что я его обижу; а я сегодня добрая, я тоже пришла к вам с заданиями. Сумеете ли вы решить мои задачи? Для этого понадобится смекалка и навык счета. Я, лиса, быстро бегаю по кругу и хорошо запутываю следы, так что никто их не распутает! А вы попробуйте!
(Круговые примеры.)
3+6=9-4=5+5=10-6=4+3=7-5=2+8=10-7=3. Разве можно ставить знак равенства?
Лиса: Молодцы, ребята! А как вы догадались, что это замкнутый круг? Помните сказку « Лиса и Волк»? Как я обхитрила волка и наловила полный воз рыбы?
(Дети возражают, что это, не она наловила, а старик)
Лиса: Ну, я немного подзабыла. А вы любите ловить рыбку?
Игра-соревнование «Кто больше поймает рыбки».
( Три ученика по очереди берут рыбок и решают примеры, которые на них написаны. Дети оценивают правильность решения и определяют победителя.)
Лиса: Молодцы, рыбаки! А не хочет ли победитель поделиться рыбкой с ребятами?
(Дети решают примеры, написанные на рыбках, которые дарит им победитель. Над ширмой появляется Собачка.)
Собачка: Здравствуйте, ребята! Вас лиса сегодня угостила рыбкой? Прочитайте мне, какие вы примеры решили.
(Дети читают.)
Собачка: Я вам предлагаю кроссворд, отгадав который, мы узнаем, куда пошли наши звери.
Кроссворд «Школа».
(Дети решают примеры и записывают названия животных, из которых складывается слово «школа».)
Собачка: Вот и я приеду туда учиться!
Учитель: Чтобы много знать, надо многому учиться. А кто нас может всему научить? ( Школа, семья, родители, товарищи.)
Все звери сели в поезд, но и нам оставили 3 вагона! Кто поедет?
(Дети берут конверт с номерами вагона, а внутри – 4 примера на сложение и вычитание.)
Поехали в школу?
— Волшебный поезд привез нас в тридевятое царство-тридесятое государство к Василисе Премудрой.

Василиса: Добро пожаловать в мою школу мудрости! В этой школе вы будете не просто считать примеры, но и решать самые сложные проблемы. Для этого нам надо сосредоточить все внимание, научиться сравнивать, принимать нужное решение. Готовы?
Задание 1: таблица, на которой изображены утенок и несколько мячей разного цвета: синего, красного, желтого.
Какой мяч выбрал утенок, если он не синий, а справа от него лежит красный мяч? (Желтый. Дети должны показать и объяснить, почему именно этот мяч выбрали. )
Задание 2: Четыре тарелки с нарисованной клубничкой: на одной- 4 штуки, на другой-3, на третьей- 2, а на четвертой- 1. Как разделить клубничку поровну на две группы, не перекладывая ягоды из тарелки в тарелку? (Объединить в группы: 4и 1, 2 и 3.)
А теперь я вам даю карточки с примерами, а вы выпишите те из них, ответы которых равны четным числам.
Петрушка: Я думаю, что все звери и Василиса остались вами довольны. А вы сегодня продемонстрировали свои умения, навыки, математическое мышление.
Учитель: Тут и сказочке конец! А кто работал- молодец! Все получите сувенир – медаль из шоколада! Молодцы! До свидания, ребята!
Полный текст материала смотрите в скачиваемом файле.
На странице приведен только фрагмент материала.
Примеры в пределах 20 онлайн. Вычитание и сложение чисел с переходом через десяток
Тренажер устного счета — легко и существенно повышает интеллектуальный потенциал человека.
Результатом приобретения навыков и здачи нормативной квалификации будет присвоение спортивного разряда (I разряд, II разряд, III разряд, кандидат в мастера спорта, мастер спорта и гроссмейстер).
- Людей из группы выделяют как по умению красиво и правильно говорить, так и по умению быстро считать в уме, и относят их, как правило, к категории умных. Школьнику умение быстро считать в уме позволяет более успешно учиться, а инженеру и ученому сократить время получения результата их деятельности.

- УС нужен не только школьникам, но и инженерам, учителям, медицинским работникам, ученым и руководителям разного уровня. Кто быстро считает, тому легче учиться и работать. УС – это не игрушка, хотя и развлекает. Он позволяет вернуться ученику на те “рельсы”, с которых он упал когда-то; повышает скорость и качество восприятия информации; дисциплинирует и производит точность во всем; приучает замечать детали и мелочи; приучает к экономии; создает образы предметов и явлений; позволяет предвидеть будущее и развивает интеллект человека.
- «Евроремонт» в голове нужно начинать с простых арифметических действий, которые позволяют структурировать мозг.
- Умение быстро считать в уме дает ученику уверенность в себе. Как правило, быстрее всех считают в уме те, кто хорошо учится в школе или в ВУЗе. Если отстающего ученика научить быстро считать в уме, то это обязательно благотворно повлияет на его успеваемость, и не только в естественных, но и во всех других предметах. Это доказано практикой.
- Произвольное внимание и интерес во время устного счета меняет блуждающий взгляд отстающего ученика на фиксированный, а концентрация внимания достигает нескольких этажей глубины предмета или процесса, который изучается.
- “Изучение математики дисциплинирует мышление, приучает к правильному словесному выражению мыслей, к точности, сжатости и ясности речи, воспитывает настойчивость, умение достигать намеченной цели, развивает работоспособность, способствует правильной самооценке владения предметом, который изучается”. (Кудрявцев Л.Д. – член-кор. РАН. 2006.).
- Ученик, который научился быстро считать в уме, как правило, начинает и быстрее мыслить.
- Тот, кто по своей природе хорошо считает, естественно обнаружит ум и в любой другой науке, а тот, кто считает медленно, учась этому искусству и овладевая им, сможет улучшить свой ум, сделать его острее (Платон).
- Приобретенных навыков устного счета одним хватит на 5 — 10 лет, а другим на всю жизнь.

- Нашим потомкам будет легче учиться и получать знания. Однако, культура устного счета всегда будет являться неотъемлемой частью общечеловеческой культуры.
- Кто быстро считает в уме, тот, как правило, ясно мыслит, быстро воспринимает и глубже видит.
- Освоение УС развивает образное, диаграммное и системное мышление, расширяет оперативную память, диапазон восприятия, приучает к мышлению на несколько ходов вперед, повышает качество мышления, оперируя количественными характеристиками объектов.
- УС повышает ясность мышления, уверенность в себе, а также волевые качества (терпение, усидчивость, выносливость, трудолюбие). Приучает к глубокой и устойчивой концентрации внимания, домысливанию и договариванию начатых фраз (особенно у дошкольников и учеников начальных классов).
Самые первые примеры, с которыми знакомится ребенок еще до школы — это сложение и вычитание. Не так уж сложно посчитать животных на картинке и, зачеркнув лишних, посчитать оставшихся. Или перекладывать счетные палочки, а потом считать их. Но для ребенка несколько труднее оперировать с голыми цифрами. Именно поэтому нужна практика и еще раз практика. Не бросайте заниматься с ребенком и летом, поскольку за лето школьная программа из маленькой головки просто выветривается и долго приходится наверстывать потерянные знания.
Если ваш ребенок первоклашка или только идет в первый класс — начните с повторения состава числа по домикам. А теперь можно браться и за примеры. Фактически сложение и вычитание в пределах десяти — это и есть первое практическое применение ребенком знания состава числа.
Кликайте по картинкам и открывайте тренажер в максимальном увеличении, далее можно скачать изображение себе на компьютер и распечатать в хорошем качестве.
Есть возможность разрезать А4 пополам и получить 2 листа с заданиями, если хотите уменьшить нагрузку на ребенка, или давать решать по столбику в день, если решили позаниматься летом.
Решаем столбик, отмечаем успехи: тучка — не очень хорошо решили, смайлик — хорошо, солнышко — замечательно!
Сложение и вычитание в пределах 10
А теперь вразброс!
И с пропусками (окошками):
Примеры на сложение и вычитание в пределах 20
К моменту, когда ребенок приступит к изучению этой темы математики, он должен очень хорошо, на зубок знать состав чисел первого десятка. Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .
Если ребенок состав чисел не освоил, ему сложно придется в дальнейших вычислениях. Поэтому постоянно возвращайтесь к теме состава чисел в пределах 10, пока первоклассник не освоит его до автоматизма. Также первоклассник должен знать, что значит десятичный (разрядный) состав чисел. На уроках математики учитель рассказывает, что 10 — это, по-другому, 1 десяток, поэтому число 12 состоит из 1 десятка и 2 единиц. При сложении единицы складываются с единицами. Именно на знании десятичного состава чисел основываются приемы сложения и вычитания в пределах 20 без перехода через десяток .
Примеры для печати без перехода через десяток вперемешку:
Сложение и вычитание в пределах 20 с переходом через десяток основаны на приемах добавления до 10 или убавления до 10 соответственно, то есть на теме «состав числа 10», поэтому ответственно подойдите к изучению с ребенком этой темы.
Примеры с переходом через десяток (половина листа сложение, половина вычитание, лист также можно распечатать в формате А4 и разрезать пополам на 2 задания):
На данном уроке вы вспомните, как складывать и вычитать числа с переходом через десяток. Решая интересные задания, вы повторите алгоритм сложения и вычитания чисел с переходом через десяток. У вас будет возможность попрактиковать изученный ранее материал вместе с веселыми пчелками.
Тема: Повторение
Урок: Вычитание и сложение чисел с переходом через десяток
Посмотрите на числовой ряд. (рис. 1)
Рис. 1
Как связаны пары чисел между собой? В сумме они дают 10.
Запомните эти пары. (рис. 2)
Рис. 2
Это свойство чисел нам пригодится при решении задач.
Выполним сложение по частям, для этого разбиваем второе слагаемое 6 на две части так, чтобы первая часть дополняла число 9 до десяти. (рис. 3)
Рис. 3
Первая часть — число 1, вторая часть — все что осталось — 5. (рис. 4)
(рис. 4)
Рис. 4
Значит, 9 + 6 = 15.
1. Читаю пример
Первое слагаемое …
Второе слагаемое …
2. Нахожу число, которое дополнит первое слагаемое до 10. Это число …
3. Разбиваю второе слагаемое на 2 части … и …
4. Дополняю первое слагаемое до 10 и прибавляю оставшиеся единицы. 10 + …
5. Читаю ответ …
Потренируемся в счёте.
Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар. (рис. 5)
Рис. 5
Решение представлено на рисунке. (рис. 6)
Рис. 6
Если у вас возникли затруднения, повторите состав чисел, это вам обязательно поможет.
А теперь рассмотрим пример на вычитание.
Находим количество единиц в уменьшаемом — число 11 состоит из 1 десятка и 1 единицы. Разбиваем вычитаемое 6 на две части: первая равна количеству единиц уменьшаемого — 1, вторая — оставшихся единиц — 5. (рис. 7)
Рис. 8
Значит, 11 — 6 = 5
1. Читаю пример
Уменьшаемое …
Вычитаемое …
2. В разряде единиц уменьшаемого число …
3. Разбиваю вычитаемое на две части … и …
4. Вычитаю первую часть …, получаю 10, вычитаю из 10 вторую часть …
5. Читаю ответ.
Закрепим новое знание.
У нас три кошки: рыжая, белая и чёрная. (рис. 9)
Рис. 9
У них родились котята. Хотите узнать сколько? Тогда правильно решите примеры и назовите цвет кошки, у которой больше всего котят. (рис. 10)
Рис. 10
Следовательно, больше всех котят у рыжей кошки.
На данном уроке вы вспомнили алгоритм сложения и вычитания чисел с переходом через десяток. Вы закрепили изученный ранее материал, решая веселые задачи, что поможет вам в дальнейшем изучении математики.
Список литературы
- Александрова Л.А., Мордкович А.Г. Математика 1 класс. — М: Мнемозина, 2012.
- Башмаков М.И., Нефедова М.Г. Математика.
 1 класс. — М: Астрель, 2012.
1 класс. — М: Астрель, 2012. - Беденко М.В. Математика. 1 класс. — М7: Русское слово, 2012.
- Пособия для начальной школы ().
- Социальная сеть работников образования ().
- 5klass.net ().
Домашнее задание
1. Вспомните алгоритм сложения и вычитания чисел с переходом через десяток.
2. Решите примеры и узнайте, с какого цветка пчёлки соберут сладкий нектар.
3. Решите примеры:
Подготовка к игре — настройки
- Любые параметры и настройки могут быть изменены когда угодно, даже во время игры.
- Изначально игра настроена так:
- Тип вычисленией — Сложение до 10
- Премия 1 — шоколадка, премия 2 — печенье
- В игровой сессии 10 вычислений (арифметических примеров)
- Процент примеров, которые надо решить правильно для получения Премии 1 — 90%
- Процент примеров, которые надо решить правильно для получения Премии 2 — 70%
- Вы можете выбрать любой другой тип вычислений — в зависимости от того, что ребенок знает и что проходит в школе в данный момент. Типы вычислений в игре:
- Сложение, вычитание, сложение и вычитание (вперемешку):
- До 10
- До 20 (с переходом через десятку)
- До 20 (с переходом через десятку и без)
- До 30
- До 100
- Умножение, деление или любые комбинации -на 1, -на 2, -на 3…….и т. д. до 10
- Сравнение чисел
- Сложение, вычитание, сложение и вычитание (вперемешку):
- Установите, сколько примеров будет в игровой сессии. Лучше начать с небольшого количества попыток — 5 или 10, чтобы не отбить у ребенка желание продолжать игру. Когда ребенок повысит надои:) улучшит показатели, можно переходить к серьезной игре с 100-200 примерами.
- Внесите процент правильно решенных примеров, за который выдаются 1 и 2 премии. Для начала лучше понизить процент. Например выбрать 70 и 50 процентов для 1 и 2 премий, соответственно.
 Позже ставки можно увеличить до 90 — 70. Или даже до 98% — 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %!
Позже ставки можно увеличить до 90 — 70. Или даже до 98% — 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %! - Запишите премии, которые ребенок получит за 1 и 2 место.
- Настройки будут сохранены с помощью cookie (небольшого скрипта) и восстановлены, когда вы следующий раз откроете в браузере страницу с игрой.
Теперь можно начинать игру!
- Чтобы начать игру, нажмите кнопку СТАРТ
- Когда на экране появится пример, ребенок должен внести ответ после знака «=»
- Если играем в «сравнения», нужно внести соответствующий знак: . Для этого удобнее всего пользоваться кнопками, которые появятся рядом с кнопкой ДАЛЬШЕ
- После того, как внесен результат, нужно нажать на кнопку ОК (или ENTER на клавиатуре), чтобы проверить правильно ли был решен пример.
- Если пример был решен правильно, на экране появится «Правильно». Если нет, «Неправильно» и верный ответ. В то же время, игра посчитает процент правильно решенных примеров
- Чтобы перейти к следующему примеру, нужно нажать кнопку ДАЛЬШЕ
- Когда сессия закончится, на экране появится премия, которую выиграл ребенок (или «ничего не выиграл») и процент правильно решенных за сессию примеров
- Чтобы начать новую сессию, нажмите кнопку НАЧАТЬ СНАЧАЛА.
Большие надежды:)
Чего можно ожидать от этой игры? Большой помощи в прохождении школьной программы! Как правило за 5-7 дней, в которые ребенок играет по 30-40 минут, он твердо усваивает очередной тип вычислений (например, сложение до 20 с переходом через десятку). И практически перестает делать ошибки в классе.
Математические прописи и примеры на четыре арифметических действия
Главная > Образование > Математика >
Разумеется, нет ничего сложного в том, чтобы взять тетрадку в крупную клетку и выписать там от руки для ребенка образцы цифр или несколько простеньких упражнений по арифметике. И всё же лучше, если эту нудную, тупую работу будет делать за нас компьютер.
И всё же лучше, если эту нудную, тупую работу будет делать за нас компьютер.
На этой странице представлены прописи с цифрами и сборники арифметических примеров, изготовленные с помощью онлайнового генератора Primo-Arithmetic.
«СТАТИЧЕСКИЕ» ПРОПИСИ: отдельные цифры
Прописи с цифрами построены по такому же принципу, что и прописи с буквами. Черные цифры служат образцом для подражания, серые цифры предназначены для обводки, а пустые клетки заполняются ребенком самостоятельно. В прописях используется шрифт Primo.
Файл для скачивания:
digits.pdf
Этот же файл с возможностью редактировать в генераторе:
primo-arithmetic.html
«ДИНАМИЧЕСКИЕ» ПРИМЕРЫ-ПРОПИСИ: это одновременно и прописи, и примеры по арифметике, причем сгенерированные автоматически
Тут приведено множество готовых файлов в формате PDF с заранее сгенерированными примерами-прописями. Такие файлы названы «образцами». Рядом с каждым образцом дана ссылка на «генератор», который настроен на создание файлов, подобных приведенному образцу. Генератор умеет, используя случайные числа, «придумывать» арифметические примеры и записывать их аккуратным почерком (точнее говоря, шрифтом Primo) на листке в клеточку. Цвет записи может быть черным или серым — в последнем случае у ребенка есть возможность дополнительно попрактиковаться в обводке цифр.
Сборники примеров (образцы и генераторы)
[В квадратных скобках указаны соответствующие главы учебника «Математика «с нуля»»]
Сложение и вычитание в пределах 20-ти («серый» шрифт для обводки): образец (pdf), генератор [1.2]
То же с «уравнениями» (т.е. пробелами для вставки чисел): образец (pdf), генератор [1.2]
Сложение и вычитание в пределах 20-ти (разность может быть отрицательной): образец (pdf), генератор [1.2]
То же с «уравнениями»: образец (pdf), генератор [1. 2]
2]
Сложение и вычитание в пределах 100: образец (pdf), генератор [1.3]
То же с «уравнениями»: образец (pdf), генератор [1.3]
Сложение и вычитание в пределах 100 (разность может быть отрицательной): образец (pdf), генератор [1.3]
То же с «уравнениями»: образец (pdf), генератор [1.3]
Сложение и вычитание в пределах 1000 : образец (pdf), генератор [1.4]
То же с «уравнениями»: образец (pdf), генератор [1.4]
Сложение и вычитание в пределах 1000 с возможным «приписыванием нулей»: образец (pdf), генератор [1.4]
То же с «уравнениями»: образец (pdf), генератор [1.4]
Сложение и вычитание в пределах 1000 (с возможным «приписыванием нулей», разность может быть отрицательной): образец (pdf), генератор [1.4]
То же с «уравнениями»: образец (pdf), генератор [1.4]
Таблица умножения: образец (pdf), генератор [1.5]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Умножение в пределах таблицы 24×24: образец (pdf), генератор [1.5]
Умножение и деление нацело в пределах таблицы умножения: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Все четыре арифметические действия в пределах 100: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Деление с остатком в пределах 100: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Умножение и деление с остатком в пределах 100: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Все четыре арифметические действия в пределах 100 (разность может быть отрицательной, деление с остатком): образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Деление нацело в пределах таблицы 24×24: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Умножение и деление в пределах таблицы 24×24: образец (pdf), генератор [1. 6]
6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Сложение и вычитание до 1000 (с возможным «приписыванием нулей»), умножение и деление в пределах 24×24: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Сложение и вычитание до 1000 (с возможным «приписыванием нулей», разность может быть отрицательной), умножение и деление в пределах 24×24: образец (pdf), генератор [1.6]
То же с «уравнениями»: образец (pdf), генератор [1.6]
Приложение:
Описание генератора примеров-прописей «Primo-Arithmetic»
Примечание. Первоначальный вариант этой страницы — с примерами-прописями, изготовленными с помощью старой версии генератора прописей (макросом Microsoft Word) — доступна здесь.
№ п/п | Этапы урока | Организация этапа, оборудование | Основное содержание этапа | ||||||||||||||||||||||||||||||||||||||
Деятельность учителя | Деятельность ученика | ||||||||||||||||||||||||||||||||||||||||
1 | 2 | 3 | 4 | 5 | |||||||||||||||||||||||||||||||||||||
I | Мотивация к учебной деятельности. | 1.Организационный момент. Слайд № 1. 2.Устный счёт. (Устная фронтальная работа) Слайд № 2. Слайд № 3. | — Сегодня, мы будем работать в группах. Поэтому, прошу сесть на 1 стол – первых четырех учащихся по списку журнала, а остальных четырех учащихся – на 2 стол. — Сегодня у нас гости. Давайте улыбнемся гостям и подарим им наше хорошее настроение, а они порадуются за наши успехи. Желаю вам, сохранить такое же настроение до конца урока. Успехов вам. — Все вы готовы уроку. Начнем урок. — Сегодня у нас необычный урок. — Давайте решим эти примеры и вы узнаете с каким героем будем путешествовать. Прочитайте примеры и сразу назовите ответ. — Вставляем под числами соответствующие буквы. — Итак, прочитайте, какое слово получилось? — Кто догадался, с каким же героем мы будем путешествовать? Кого мы можем назвать болтливой? Какую сказку мы читали? Кто написал сказку? — Правильно. Путешествовать будем с героиней сказки Абдуллы Алиша «Болтливая утка», которая отправилась в поиск своего хозяина, и с другими жителями сказочного леса. — Ваша задача сегодня состоит в том, чтобы на уроке — помочь героине отыскать хозяина. А помогут вам в этом ваши знания. — Отправляемся в путь. | Садятся по группам. С места читают примеры и называют ответы. — болтливая… — Утку — Сертотмас үрдәк | |||||||||||||||||||||||||||||||||||||
II | Формулирование темы и цели урока. | Постановка учебной задачи. Слайд № 4. | — Но перед этим еще раз посмотрите на задание. Вы решили примеры, скажите: на какие две группы можно разделить эти примеры? — Прочитайте примеры 1 – ой группы (на сложение). — При сложение как мы называем компоненты чисел? — Еще как можно прочитать примеры? — А теперь прочитайте примеры 2 – ой группы (на вычитание). — … — Попробуйте назвать тему сегодняшнего урока? — Самое большое число среди чисел – какое? — Итак тема нашего урока: Сложение и вычитание чисел в пределах 20. — А какие задачи вы поставите перед собой на уроке? — Решать примеры. — Решать задачи. — Узнать новое. — Таковы задачи нашего урока и мы должны их выполнить. (Задачи урока прикрепляются на доске. | — Примеры на сложение и вычитание. — 4+6 … — Слагаемое, сумма — 9-4 … — Из 20 вычитаем 1… — ? — 20 — Решать примеры, задачи с помощью действий сложения и вычитания. Узнать новое. | |||||||||||||||||||||||||||||||||||||
III | Актуализация знаний. | Самостоятельная работа. Слайд № 5. Слайд № 6. Слайд № 7. Самоконтроль, самооценка. | — Идем по лесной дорожке и первым нас встречает – Ёжик. Он предлагает, такое задание: «Найди ответ в конце цепочки!». Если мы правильно выполним его задание, то, он укажет нам дорогу и даст Утке умный совет. — Задание Ежика можете найти у вас на партах. -Проверяем. Какой ответ вы получили? Правильно. Прочитайте, какой же совет дал Ежик Утке. А вы согласны с этим? — Теперь оцените вашу работу. У вас у каждого на партах лежат карточки. Отметьте каждое правильно выполненное задание «+». Заполните таблицу.
| Самостоятельно работают на карточках. 1 ученик работает у доски. Проверяют и оценивают свои работы. | |||||||||||||||||||||||||||||||||||||
IV | Физкультминутка | — Мы с вами устали, и я предлагаю выполнить физкультминутку: — Столько раз ногами топнем 6+4 — Столько раз в ладоши хлопнем 5+3 — Мы присядем столько раз 12-6 — Громко крикнем столько раз 9-9 — Мы наклонимся сейчас столько раз 7-2 — Ай да счет! Игра и только! —Тихо сели. Работаем дальше. | Выполняют движения, которые слышат при чтении стихотворения. | ||||||||||||||||||||||||||||||||||||||
V | Систематизация и повторение. | Слайд № 8. Слайд № 9. Самоконтроль, самооценка. Самостоятельная групповая работа с самопроверкой по эталону. Слайд № 10. Слайд № 11. | — Открываем тетради. Запишите число. Классная работа. – Продолжаем наше путешествие и встречаем следующего героя – Зайца. Он предлагает вам решить задачу. — Откройте учебник на стр.83, найдите задание № 9. — Работаем парами, прочитайте задание. — Поняли задачу? А теперь обсуждаем между собой. Решение запишите в тетрадях. Работаем. Вам на выполнение этого задания 2 минуты.
— Один из вас (по желанию) будет решать задачу у доски, а остальные самостоятельно в тетрадях. — Время вышло. Проверяем. Сверьте свое решение с решением вашего одноклассника на доске. Вам удалось правильно решить задачу. — А теперь оцените вашу работу и заполните таблицу.
— Выполняя задание Зайца, чему вы научились? — Мы выполнили ещё одну из поставленных задач к уроку. — Продолжаем наше путешествие и встречаем следующего героя – Волка. Он предлагает задание на выбор. Выберите, то задание, с которым вы сможете успешно справиться. Работаем в тетрадях. — Проверяем по эталону. — Мы правильно решили и помогли Утке уйти от волка. Оцените ваши работы.
— Чему мы научились? — Мы выполнили ещё одну задачу, которую поставили перед собой в начале урока. Молодцы! | Обсуждают в парах и пишут решение в тетрадях. Проверяют и оценивают свои работы. — Решать задачу. Выбирают (договариваются) себе задание из трех по степени трудности. Проверяют и оценивают свои работы. — решать примеры | |||||||||||||||||||||||||||||||||||||
VI | Закрепление. | Слайд № 12. Слайд № 13. Слайд № 14. | — Продолжаем наше путешествие и встречаем по пути следующего героя – Медведя. Он предлагает вам домашнее задание, и выполнить тест. — Домашнее задание тоже волшебное, конверты откроете только дома. Там вы увидите интересные задания. У каждого свое. Можете выполнить 1 задание или все задания. — Если вы правильно выполните тест, то получите кодовое слово («отлично») -Молодцы! Вы получили разрешение, и в добрый путь.
| Получают конверты с домашним заданием. Работают в парах. Проверяют и оценивают свои работы. | |||||||||||||||||||||||||||||||||||||
VII | Геометрический материал. | Слайд № 15. Слайд № 16. | — Продолжаем наше путешествие и встречаем следующего героя – Лису. Но сначала, ребята, давайте вспомним, чем же закончилась эта сказка? — А вам нравится такой конец сказки? — Давайте, изменим сказку и поможем уточке спастись от лисы и найти хозяина. Для этого вам нужно выполнить задание: составить силуэт человечка из геометрических фигур. — У каждого из вас на парте лежат конверты. Достаньте, пожалуйста, фигуры. — Все препятствия преодолели. Наша утка нашла своего хозяина, а помогли в этом вы. Назовите, из каких геометрических фигур состоит человечек? — Вам понравилось составлять человечка? — Это называется танграм. Танграм – это самая древняя геометрическая головоломка, состоящая из семи плоских фигур, которые складывают определённым образом для получения другой, разных фигур. Необходимо использовать все семь фигур танграма, и второе — фигуры не должны накладываться друг на друга. Она придумана много – много лет тому назад. Более тысячу лет назад.
— Оцените себя. | — Лиса съела утку. — Нет, она должна спастись и найти своего хозяина. Собирают человечка, используя геометрические фигуры. — Узнали новое. Оценивают свои работы. | |||||||||||||||||||||||||||||||||||||
VIII | Рефлексия. | Итоговая рефлексия. Самооценка. Слайд № 17. | — А теперь нам пора возвращаться домой. Наше путешествие по сказке подошло к концу. — Чем занимались? Чему научились? — Где в жизни вам понадобится эти знания? — Используя шкалу оценивания, выставьте себе оценки.
— Ребята, давайте вспомним Ежика. — Спасибо за урок! | Решали задачи, решали примеры. Выставляют себе оценки по своим оценочным листам. Прикрепляют яблоки к доске. | |||||||||||||||||||||||||||||||||||||
примеры по математике 1 класс до 20
Image Wallpaper and More collection of примеры по математике 1 класс до 20 contain 30+ more images free download Узорова, Нефедова: Математика. 1 класс. Цепочки примеров. Счет в …
Тренажёр по математике (1, 2 класс) на тему: Тренажер по …
Математика сложение и вычитание – Математика. Сложение и вычитание …
Иллюстрация 15 из 20 для Математика. 1 класс. 3000 примеров. Счет …
Книга: «Математика. 1 класс. Тренировочные примеры. Счет от 1 до 5 …
Математика: Решаем примеры в пределах 20 с переходом через десяток
Примеры Для 1 Класса По Математике До 20
Состав числа от 11 до 20
Сложение двух чисел. Задания по математике для 1 класса. Сумма до …
Счет с переходом через десяток, счет во втором десятке (счет от 10 …
Купить книгу Математика. Все цепочки примеров для устных и …
Учим детей математике сами. Часть 1 «Знакомство».: uspevai_s_detmi …
Купить 3000 примеров по математике. 1 класс. Цепочки примеров …
Математика сложение и вычитание – Математика. Сложение и вычитание …
Узорова нефедова счет в пределах 20 скачать бесплатно — zeilingheadnea
Сравнение чисел до 20 (1 класс)
Математика: Решаем примеры в пределах 20 с переходом через десяток
Урок математики «Сложение и вычитание в пределах 20.
 Закрепление …
Закрепление …Иллюстрация 9 из 13 для Математика. 1 класс. 3000 примеров по …
Книга 3000 примеров по математике. Цепочки примеров. Счет в …
Примеры до 10 первый класс распечатать без ответов :: eronearri
Книга «Математика. 1 класс. 3000 примеров. Счет в пределах 10 …
Купить 30000 примеров по математике. 1 класс: Счет до 20 , цепочки …
Тренажёр по математике (1, 2 класс) на тему: Тренажер по …
Моя математика. 1 класс. Рабочая тетрадь. В 2-х частях. Часть 2 …
Примеры До 20 Для 2 Класса
30000 примеров по математике. 1 класс: Счет до 20 , цепочки …
Задания по математике для 1 класса и подготовки к школе. Сложение …
Состав числа до 20 — Распечатать числовую таблицу
примеры до 20 для 1 класса бесплатно распечатать (с изображениями …
Таблица сложения до 20: скачать и распечатать — 3mu.ru
Книга «Математика. 1 класс. 3000 примеров. Цепочки примеров. Счет …
Примеры на сложение и вычитание в пределах 10
Таблица сложения до 20: скачать и распечатать — 3mu.ru
Сравнение чисел: больше, меньше, равно, маленький, равно, задачи …
Купить книгу 3000 примеров по математике. 1 класс. Цепочки …
Узорова нефедова 3000 примеров по математике 1 класс скачать …
Примеры По Математике 1 Класс До 20 Распечатать
p3nEIrRYJgDwAM
Книга «Математика. 1 класс. 3000 примеров. Счет в пределах 10 …
Математика. 3 класс. 3000 примеров. Счет в пределах 100 …
примеры по математике 1 класс до 20 Images Collection Таблица сложения до 20: скачать и распечатать — 3mu.ru Купить книгу Математика. Все цепочки примеров для устных и … Сравнение чисел до 20 (1 класс)
120 Замечательные математические задания со словами, чтобы заинтересовать и заинтересовать учащихся
120 Замечательные математические задания со словами, чтобы заинтересовать и заинтересовать учеников | Prodigy Education Вы сидите за своим столом, готовые провести математическую викторину, тест или задание. Вопросы перетекают в документ, пока вы не дойдете до раздела, посвященного проблемам с текстом. Помог бы толчок творчества. Но этого не произошло. Этот ресурс даст вам толчок к творчеству. Он предоставляет примеры и шаблоны математических задач на слова для 1-8 классов.Всего 120 примеров. Помогая вам разобраться в них, чтобы найти вопросы для ваших учеников, ресурс разделен на категории по следующим навыкам с некоторым перекрытием между темами: Список примеров дополнен советами по созданию увлекательных и сложных математических словесных задач.
Вопросы перетекают в документ, пока вы не дойдете до раздела, посвященного проблемам с текстом. Помог бы толчок творчества. Но этого не произошло. Этот ресурс даст вам толчок к творчеству. Он предоставляет примеры и шаблоны математических задач на слова для 1-8 классов.Всего 120 примеров. Помогая вам разобраться в них, чтобы найти вопросы для ваших учеников, ресурс разделен на категории по следующим навыкам с некоторым перекрытием между темами: Список примеров дополнен советами по созданию увлекательных и сложных математических словесных задач.120 математических словесных задач, классифицированных по навыкам
Дополнение 1. Дополнение к 10: Ариэль играла в баскетбол. 1 из ее выстрелов попал в обруч. 2 ее выстрела не попали в обруч.Сколько всего было выстрелов? 2. Добавление к 20: У Адрианны есть 10 кусочков жевательной резинки, которыми она может поделиться с друзьями. На всех ее подруг не хватило жевательной резинки, поэтому она пошла в магазин за еще тремя кусочками жевательной резинки. Сколько кусочков жевательной резинки сейчас у Адрианны? 3. Добавление к 100: У Адрианны есть 10 кусочков жевательной резинки, которыми она может поделиться с друзьями. На всех ее подруг не хватило жевательной резинки, поэтому она пошла в магазин и купила 70 кусочков клубничной жевательной резинки и 10 кусочков жевательной резинки.Сколько кусочков жевательной резинки сейчас у Адрианны? 4. Добавление чуть больше 100: В ресторане 175 обычных стульев и 20 стульев для младенцев. Сколько всего стульев в ресторане? 5. Добавляем к 1000: Сколько печенья вы продали, если продали 320 шоколадных печений и 270 ванильных печений? 6. Добавление до 10 000 и более: Обычно магазин товаров для хобби продает 10 576 торговых карточек в месяц. В июне в магазине товаров для хобби было продано на 15 498 карточек больше, чем обычно.В целом, сколько коллекционных карточек было продано в магазине для хобби в июне? 7. Сложение 3 чисел: У Билли дома было 2 книги. Он пошел в библиотеку, чтобы достать еще 2 книги. Затем он купил 1 книгу. Сколько книг у Билли сейчас? 8. Добавление трех чисел к 100 и более: Эшли купила большой мешок конфет. В сумке было 102 синих конфеты, 100 красных и 94 зеленых. Сколько всего было конфет?
Сложение 3 чисел: У Билли дома было 2 книги. Он пошел в библиотеку, чтобы достать еще 2 книги. Затем он купил 1 книгу. Сколько книг у Билли сейчас? 8. Добавление трех чисел к 100 и более: Эшли купила большой мешок конфет. В сумке было 102 синих конфеты, 100 красных и 94 зеленых. Сколько всего было конфет?Вычитание
9. Вычитание до 10: Всего в пиццерии было 3 пиццы.Покупатель купил 1 пиццу. Сколько пиццы осталось? 10. Вычитая до 20: Ваша подруга сказала, что у нее 11 наклеек. Когда вы помогли ей убрать стол, у нее было всего 10 наклеек. Сколько наклеек не хватает? 11. Вычитая до 100: У Адрианны есть 100 кусочков жевательной резинки, которыми она может поделиться с друзьями. Когда она пошла в парк, она разделила 10 кусочков клубничной жевательной резинки. Когда она вышла из парка, Адрианна поделилась еще 10 кусочками жевательной резинки. Сколько кусочков жевательной резинки сейчас у Адрианны? Занимаясь математикой, школы, использующие Prodigy, постоянно превосходят те, которые не используют стандартизированные тесты [/ caption] 12.Вычитание Чуть больше 100: Всего ваша команда набрала 123 очка. В первом тайме было набрано 67 очков. Сколько было забито во втором тайме? 13. Вычитаем до 1000: У Натана большая муравьиная ферма. Он решил продать несколько своих муравьев. Он начал с 965 муравьев. Продал 213. Сколько муравьев у него сейчас? 14. Вычитая и больше 10 000: Обычно магазин товаров для хобби продает 10 576 торговых карточек в месяц. В июле в магазине товаров для хобби было продано 20 777 коллекционных карточек.Сколько коллекционных карточек было продано в магазине в июле по сравнению с обычным месяцем? 15. Вычитание трех чисел: У Шарлин была упаковка из 35 карандашей. 6 она отдала своей подруге Терезе. Она дала 3 своей подруге Мэнди. Сколько мелков осталось у Шарлин? 16. Вычитание трех чисел из 100: Эшли купила большой мешок конфет, чтобы поделиться с друзьями. Всего конфет было 296 штук. Она подарила Мариссе 105 конфет. Еще она подарила Кайле 86 конфет.Сколько конфет осталось?
Всего конфет было 296 штук. Она подарила Мариссе 105 конфет. Еще она подарила Кайле 86 конфет.Сколько конфет осталось?Умножение
17. Умножение однозначных целых чисел: Адрианне нужно разрезать сковороду с пирожными на кусочки. Она нарезает на сковороду 6 ровных столбиков и 3 ровных ряда. Сколько у нее пирожных? 18. Умножение двухзначных целых чисел: В кинотеатре 25 рядов сидений по 20 мест в каждом ряду. Сколько всего мест? 19. Умножение целых чисел, заканчивающееся на 0: Компания по производству одежды предлагает 4 различных вида толстовок.Ежегодно компания производит 60 000 толстовок каждого вида. Сколько свитшотов компания производит каждый год? 20. Умножение 3 целых чисел: Каменщик укладывает кирпичи в 2 ряда по 10 кирпичей в каждом ряду. Сверху каждого ряда находится стопка из 6 кирпичей. Сколько всего кирпичей? 21. Умножение 4 целых чисел: Кэли зарабатывает 5 долларов в час, разнося газеты. Она доставляет газеты 3 дня в неделю по 4 часа за раз. Сколько денег заработает Кэли после доставки газет в течение 8 недель?Отдел
22.Деление однозначных целых чисел: если у вас есть 4 конфеты, поровну разделенных на 2 пакета, сколько конфет находится в каждом пакете? 23. Разделение 2-значных целых чисел: Если у вас есть 80 билетов на ярмарку и каждая поездка стоит 5 билетов, сколько поездок вы сможете совершить? 24. Разделительные числа, заканчивающиеся на 0: У школы есть 20 000 долларов на покупку нового компьютерного оборудования. Если каждая единица оборудования стоит 50 долларов, сколько всего ее может купить школа? 25.Деление 3 целых чисел: Мелисса покупает 2 пачки теннисных мячей на общую сумму 12 долларов. Всего 6 теннисных мячей. Сколько стоит 1 упаковка теннисных мячей? Сколько стоит 1 теннисный мяч? 26. Переводчик: Итальянский ресторан получил партию из 86 котлет из телятины. Если на блюдо нужно 3 котлеты, сколько котлет останется в ресторане после приготовления как можно большего количества блюд?
Если на блюдо нужно 3 котлеты, сколько котлет останется в ресторане после приготовления как можно большего количества блюд?Смешанные операции
27. Смешивание сложения и вычитания: В библиотеке 235 книг.В понедельник вывозят 123 книги. Во вторник возвращено 56 книг. Сколько сейчас книг? 28. Смешивание, умножение и деление: Есть группа из 10 человек, которые заказывают пиццу. Если каждый человек получает 2 куска, а у каждой пиццы 4 куска, сколько пиццы им следует заказать? 29. Смешивание, умножение, сложение и вычитание: У Ланы есть 2 пакета по 2 шарика в каждом. У Маркуса 2 сумки по 3 шарика в каждой. Сколько еще шариков у Маркуса? 30.Подразделение смешивания, сложения и вычитания: У Ланы 3 мешка с одинаковым количеством шариков, всего 12 шариков. У Маркуса 3 сумки с таким же количеством шариков, всего 18 шариков. Сколько еще шариков у Маркуса в каждой сумке?Порядок и определение числа
31. Подсчет для предварительного умножения: в вашем классе есть 2 классные доски. Если на каждую классную доску нужно 2 куска мела, сколько всего кусков вам нужно? 32. Подсчет перед предварительным просмотром: В вашем классе 3 классные доски.На каждой доске по 2 мелка. Это означает, что всего есть 6 мелков. Если вы уберете по 1 мелу с каждой доски, сколько всего их будет? 33. Составление чисел: Какое число 6 десятков и 10 единиц? 34. Числа для угадывания: У меня 7 в разряде десятков. У меня четное число вместо единиц. Мне меньше 74. Какой я номер? 35. В поисках заказа: В хоккейном матче Митчелл набрал больше очков, чем Уильям, но меньше очков, чем Остон.Кто набрал больше всего очков? Кто набрал меньше всего очков?Fractions
36. Поиск фракций группы: Джулия пошла в 10 домов на своей улице на Хэллоуин. В 5 домах ей подарили плитку шоколада. В какой части домов на улице Джулии ей дали плитку шоколада? 37. Поиск фракций единиц: Хизер рисует портрет своей лучшей подруги Лизы. Чтобы было легче, она делит портрет на 6 равных частей. Какая дробь представляет каждую часть портрета? 38.Сложение дробей с одинаковыми знаменателями: Ной проходит ⅓ километра до школы каждый день. Он также проходит ⅓ километра, чтобы вернуться домой после школы. Сколько всего километров он проходит? 39. Вычитание дробей с одинаковыми знаменателями: На прошлой неделе Уитни подсчитала количество коробок сока, которые у нее были на школьные обеды. У нее было случая. На этой неделе осталось ⅕ случая. Сколько вина выпила Уитни? 40. Сложение целых чисел и дробей с одинаковыми знаменателями: В обеденное время в кафе-мороженом подавалось 6 ложек шоколадного мороженого, 5 ложек ванили и 2 ложки клубники.Сколько всего шариков мороженого обслужили в салоне? 41. Вычитание целых чисел и дробей с одинаковыми знаменателями: На вечеринке у Хайме было 5 ⅓ бутылок колы для своих друзей. Она сама выпила бутылки. Ее друзья выпили 3 ⅓. Сколько бутылок колы осталось у Хайме? 42. Сложение дробей с непохожими знаменателями: Кевин выполнил ½ задания в школе. Вернувшись в тот вечер домой, он выполнил ⅚ другого задания.Сколько заданий выполнил Кевин? 43. Вычитание дробей с непохожими знаменателями: Собирая школьные обеды для своих детей, Пэтти использовала упаковки ветчины. Еще она использовала ½ упаковки индейки. Насколько больше ветчины, чем индейки, использовала Пэтти? 44. Умножение дробей: Во время урока физкультуры в среду ученики пробежали километра. В четверг они пробежали ½ километра, как в среду. Сколько километров пробежали студенты в четверг? Запишите свой ответ дробью. 45. Разделение на фракции: Производитель одежды использует ⅕ флакона цветного красителя для изготовления одной пары брюк. Производитель вчера использовал бутылки. Сколько пар брюк изготовил производитель? 46.
Поиск фракций единиц: Хизер рисует портрет своей лучшей подруги Лизы. Чтобы было легче, она делит портрет на 6 равных частей. Какая дробь представляет каждую часть портрета? 38.Сложение дробей с одинаковыми знаменателями: Ной проходит ⅓ километра до школы каждый день. Он также проходит ⅓ километра, чтобы вернуться домой после школы. Сколько всего километров он проходит? 39. Вычитание дробей с одинаковыми знаменателями: На прошлой неделе Уитни подсчитала количество коробок сока, которые у нее были на школьные обеды. У нее было случая. На этой неделе осталось ⅕ случая. Сколько вина выпила Уитни? 40. Сложение целых чисел и дробей с одинаковыми знаменателями: В обеденное время в кафе-мороженом подавалось 6 ложек шоколадного мороженого, 5 ложек ванили и 2 ложки клубники.Сколько всего шариков мороженого обслужили в салоне? 41. Вычитание целых чисел и дробей с одинаковыми знаменателями: На вечеринке у Хайме было 5 ⅓ бутылок колы для своих друзей. Она сама выпила бутылки. Ее друзья выпили 3 ⅓. Сколько бутылок колы осталось у Хайме? 42. Сложение дробей с непохожими знаменателями: Кевин выполнил ½ задания в школе. Вернувшись в тот вечер домой, он выполнил ⅚ другого задания.Сколько заданий выполнил Кевин? 43. Вычитание дробей с непохожими знаменателями: Собирая школьные обеды для своих детей, Пэтти использовала упаковки ветчины. Еще она использовала ½ упаковки индейки. Насколько больше ветчины, чем индейки, использовала Пэтти? 44. Умножение дробей: Во время урока физкультуры в среду ученики пробежали километра. В четверг они пробежали ½ километра, как в среду. Сколько километров пробежали студенты в четверг? Запишите свой ответ дробью. 45. Разделение на фракции: Производитель одежды использует ⅕ флакона цветного красителя для изготовления одной пары брюк. Производитель вчера использовал бутылки. Сколько пар брюк изготовил производитель? 46. Умножение дробей на целые числа: Марк на этой неделе выпил пакета молока. Фрэнк выпил в 7 раз больше молока, чем Марк. Сколько пакетов молока выпил Фрэнк? Запишите свой ответ дробью, целым или смешанным числом.
Умножение дробей на целые числа: Марк на этой неделе выпил пакета молока. Фрэнк выпил в 7 раз больше молока, чем Марк. Сколько пакетов молока выпил Фрэнк? Запишите свой ответ дробью, целым или смешанным числом.Десятичные
47.Добавление десятичных знаков: у вас в миске 2,6 грамма йогурта, и вы добавляете еще одну ложку 1,3 грамма. Сколько всего йогурта у вас есть? 48. Вычитание десятичных знаков: У Джеммы было 25,75 грамма глазури для изготовления торта. Она решила использовать только 15,5 грамма глазури. Сколько глазури осталось у Джеммы? 49. Умножение десятичных дробей на целые числа: Маршалл проходит в общей сложности 0,9 км до школы и обратно каждый день. Сколько километров он пройдет через 4 дня? 50.Разделение десятичных дробей на целые числа: Чтобы сделать Пизанскую башню из спагетти, миссис Робинсон купила 2,5 килограмма спагетти. Всего ее ученики смогли построить 10 наклонных башен. Сколько килограммов спагетти нужно для изготовления 1 падающей башни? 51. Смешивание сложения и вычитания десятичных знаков: У Рокко в холодильнике 1,5 литра апельсиновой соды и 2,25 литра виноградной соды. У Антонио есть 1,15 литра апельсиновой газировки и 0,62 литра виноградной газировки. Насколько больше газировки у Рокко, чем у Анджело? 52.Смешивание умножения и деления десятичных знаков: 4 дня в неделю Лаура занимается боевыми искусствами в течение 1,5 часов. Учитывая, что в неделе 7 дней, каково ее среднее время занятий в день каждую неделю? Сравнение и упорядочение 53. Сравнение однозначных целых чисел: у вас 3 яблока, а у вашего друга 5 яблок. У кого больше? 54. Сравнение 2-значных целых чисел: У вас 50 конфет, а у вашего друга 75 конфет. У кого больше? 55.Сравнение различных переменных: На детской площадке 5 баскетбольных мячей. На детской площадке установлено 7 футбольных мячей. Есть еще баскетбольные мячи или футбольные мячи? 56. Последовательность однозначных целых чисел: У Эрика 0 наклеек. Каждый день он получает еще 1 наклейку. Сколько дней до того, как он получит 3 наклейки? 57. Пропуск по нечетным числам: Натали начала счет с 5. Она пропускала счет по пятеркам. Могла ли она сказать число 20? 58. Пропуск по четным числам: Наташа начала с 0.Она досчитала до восьмерок. Могла ли она сказать число 36? 59. Последовательность 2-значных чисел: Каждый месяц Джереми добавляет такое же количество карточек в свою коллекцию бейсбольных карточек. В январе у него было 36. В феврале 48. 60 марта. Сколько бейсбольных карточек будет у Джереми в апреле?
Последовательность однозначных целых чисел: У Эрика 0 наклеек. Каждый день он получает еще 1 наклейку. Сколько дней до того, как он получит 3 наклейки? 57. Пропуск по нечетным числам: Натали начала счет с 5. Она пропускала счет по пятеркам. Могла ли она сказать число 20? 58. Пропуск по четным числам: Наташа начала с 0.Она досчитала до восьмерок. Могла ли она сказать число 36? 59. Последовательность 2-значных чисел: Каждый месяц Джереми добавляет такое же количество карточек в свою коллекцию бейсбольных карточек. В январе у него было 36. В феврале 48. 60 марта. Сколько бейсбольных карточек будет у Джереми в апреле?Время и деньги
60. Добавление денег: Томас и Мэтью копят деньги, чтобы вместе купить видеоигру. Томас сэкономил 30 долларов. Мэтью сэкономил 35 долларов. Сколько денег они накопили в общей сложности? 61.Вычитание денег: Томас накопил 80 долларов. На свои деньги он покупает видеоигру. Видеоигра стоит 67 долларов. Сколько денег у него осталось? 62. Умножение денег: Тим получает 5 долларов за доставку бумаги. Сколько у него будет денег после 3-х раздачи бумаги? 63. Разделение денег: Роберт потратил 184,59 доллара на покупку 3 хоккейных клюшек. Если бы каждая хоккейная клюшка имела одинаковую цену, сколько стоила бы 1 клюшка? 64. Сложение денег с десятичными знаками: Вы пошли в магазин и купили жевательную резинку за 1 доллар.25 и присоска за 0,50 доллара. Сколько было у вас всего? 65. Вычитание денег с десятичными знаками: Вы пошли в магазин с 5,50 долларами. Вы купили жевательную резинку за 1,25 доллара, плитку шоколада за 1,15 доллара и присоску за 0,50 доллара. Сколько у тебя осталось денег? 66. Преобразование часов в минуты: Джереми помогал своей маме 1 час. Сколько минут он ей помогал? 67. Применение пропорциональных отношений к деньгам: Якоб хочет пригласить 20 друзей на свой день рождения, что обойдется его родителям в 250 долларов. Если он вместо этого решит пригласить 15 друзей, сколько денег это будет стоить его родителям? Предположим, что отношение прямо пропорционально. 68. Применение процентов к деньгам: Ретта положил 100 долларов США на банковский счет, который приносит 20% годовых. Сколько процентов будет накоплено за 1 год? И если она не снимает деньги, сколько денег будет на счету через 1 год? 69. Добавление времени: Если вы просыпаетесь в 7:00 утра и вам требуется 1 час 30 минут, чтобы собраться и пойти в школу, в какое время вы придете в школу? 70.Время вычитания: Если поезд отправляется в 14:00. и прибывает в 16:00, сколько времени пассажиры находились в поезде? 71. Определение времени начала и окончания: Ребекка вышла из магазина своего отца, чтобы пойти домой в двадцать семь вечера. Через сорок минут она была дома. Во сколько она приехала домой?
Если он вместо этого решит пригласить 15 друзей, сколько денег это будет стоить его родителям? Предположим, что отношение прямо пропорционально. 68. Применение процентов к деньгам: Ретта положил 100 долларов США на банковский счет, который приносит 20% годовых. Сколько процентов будет накоплено за 1 год? И если она не снимает деньги, сколько денег будет на счету через 1 год? 69. Добавление времени: Если вы просыпаетесь в 7:00 утра и вам требуется 1 час 30 минут, чтобы собраться и пойти в школу, в какое время вы придете в школу? 70.Время вычитания: Если поезд отправляется в 14:00. и прибывает в 16:00, сколько времени пассажиры находились в поезде? 71. Определение времени начала и окончания: Ребекка вышла из магазина своего отца, чтобы пойти домой в двадцать семь вечера. Через сорок минут она была дома. Во сколько она приехала домой?Физические измерения
72. Сравнение измерений: линейка Кассандры имеет длину 22 сантиметра. Линейка апреля имеет длину 30 сантиметров. На сколько сантиметров длиннее линейка апреля? 73.Измерения в контексте: Представьте школьный автобус. Какая единица измерения лучше всего описывает длину автобуса? Сантиметры, метры или километры? 74. Добавление измерений: Папа Миши хочет сэкономить на бензине, поэтому он отслеживает, сколько он потребляет. В прошлом году папа Миши использовал 100 литров бензина. В этом году ее отец использовал 90 литров бензина. Сколько всего газа он использовал за два года? 75. Вычитающие измерения: Папа Миши хочет сэкономить на бензине, поэтому он отслеживал, сколько он потребляет.За последние два года папа Миши использовал 200 литров бензина. В этом году он использовал 100 литров газа. Сколько газа он использовал в прошлом году? 76. Умножение объема и массы: Кира хочет убедиться, что у нее крепкие кости, поэтому она выпивает 2 литра молока каждую неделю. Сколько литров молока выпьет Кира через 3 недели? 77. Разделение объема и массы: Лилиан занимается садоводством, поэтому она купила 1 килограмм земли. Она хочет равномерно распределить почву между двумя растениями.Сколько получит каждое растение? 78. Преобразование массы: Ингер идет в продуктовый магазин и покупает 3 тыквы, каждая из которых весит 500 грамм. Сколько килограммов кабачков купила Ингер? 79. Преобразование объема: У Шэда есть киоск с лимонадом, и он продал 20 чашек лимонада. Каждая чашка была 500 миллилитров. Сколько литров всего продала Шэд? 80. Длина преобразования: Стейси и Мильда сравнивают свой рост. Рост Стейси 1,5 метра. Милда на 10 сантиметров выше Стейси.Какой рост у Милды в сантиметрах? 81. Расстояние и направление: Автобус отправляется из школы, чтобы отвезти учащихся на экскурсию. Автобус едет на 10 километров на юг, 10 километров на запад, еще 5 километров на юг и 15 километров на север. В каком направлении должен ехать автобус, чтобы вернуться в школу? Сколько километров он должен пройти в этом направлении? Соотношения и проценты 82. Нахождение недостающего числа: Соотношение трофеев Дженни и трофеев Мередит составляет 7: 4.У Дженни 28 трофеев. Сколько у Мередит? 83. Поиск недостающих номеров: Соотношение трофеев Дженни и трофеев Мередит составляет 7: 4. Разница между числами — 12. Какие числа? 84. Сравнительные показатели: В младшем школьном оркестре работают 10 саксофонистов и 20 трубачей. В старшем оркестре школы 18 саксофонистов и 29 трубачей. У какого оркестра более высокое соотношение трубачей и саксофонистов? 85.Определение процентного соотношения: Мэри опросила учеников своей школы, чтобы определить их любимые виды спорта. 455 из 1200 студентов назвали хоккей своим любимым видом спорта. Какой процент студентов назвал хоккей своим любимым видом спорта? 86. Определение процента изменения: Десять лет назад население Оквилла составляло 67 624 человека.
Разделение объема и массы: Лилиан занимается садоводством, поэтому она купила 1 килограмм земли. Она хочет равномерно распределить почву между двумя растениями.Сколько получит каждое растение? 78. Преобразование массы: Ингер идет в продуктовый магазин и покупает 3 тыквы, каждая из которых весит 500 грамм. Сколько килограммов кабачков купила Ингер? 79. Преобразование объема: У Шэда есть киоск с лимонадом, и он продал 20 чашек лимонада. Каждая чашка была 500 миллилитров. Сколько литров всего продала Шэд? 80. Длина преобразования: Стейси и Мильда сравнивают свой рост. Рост Стейси 1,5 метра. Милда на 10 сантиметров выше Стейси.Какой рост у Милды в сантиметрах? 81. Расстояние и направление: Автобус отправляется из школы, чтобы отвезти учащихся на экскурсию. Автобус едет на 10 километров на юг, 10 километров на запад, еще 5 километров на юг и 15 километров на север. В каком направлении должен ехать автобус, чтобы вернуться в школу? Сколько километров он должен пройти в этом направлении? Соотношения и проценты 82. Нахождение недостающего числа: Соотношение трофеев Дженни и трофеев Мередит составляет 7: 4.У Дженни 28 трофеев. Сколько у Мередит? 83. Поиск недостающих номеров: Соотношение трофеев Дженни и трофеев Мередит составляет 7: 4. Разница между числами — 12. Какие числа? 84. Сравнительные показатели: В младшем школьном оркестре работают 10 саксофонистов и 20 трубачей. В старшем оркестре школы 18 саксофонистов и 29 трубачей. У какого оркестра более высокое соотношение трубачей и саксофонистов? 85.Определение процентного соотношения: Мэри опросила учеников своей школы, чтобы определить их любимые виды спорта. 455 из 1200 студентов назвали хоккей своим любимым видом спорта. Какой процент студентов назвал хоккей своим любимым видом спорта? 86. Определение процента изменения: Десять лет назад население Оквилла составляло 67 624 человека. Теперь он на 190% больше. Каково население Оквилля в настоящее время? 87. Определение процентов чисел: В пункте проката коньков 60% из 120 коньков предназначены для мальчиков.Если остальные коньки для девочек, сколько их? 88. Расчет средних значений: В течение 4 недель Уильям вызвался помощником на занятиях по плаванию. Первую неделю он работал волонтером по 8 часов. Он работал волонтером 12 часов на второй неделе и еще 12 часов на третьей неделе. На четвертой неделе он работал волонтером по 9 часов. Сколько часов в среднем он работал волонтером в неделю? Вероятность и взаимосвязь данных 89.Понимание предпосылки вероятности: Джон хочет узнать любимое телешоу своего класса, поэтому он опрашивает всех мальчиков. Будет ли выборка репрезентативной или необъективной? 90. Понимание материальной вероятности: Грани на большом количестве кубиков помечены цифрами 1, 2, 3, 4, 5 и 6. Вы бросаете кубик 12 раз. Сколько раз вы должны ожидать, что вам выпадет 1? 91. Изучение дополнительных событий: Цифры от 1 до 50 в шляпе. Если вероятность выпадения четного числа составляет 25/50, какова вероятность НЕ выпадать четное число? Выразите эту вероятность дробью. 92. Исследование экспериментальной вероятности: В пиццерии недавно было продано 15 пицц. 5 из этих пицц были пепперони. Отвечая дробью, какова экспериментальная вероятность того, что следующая пицца будет пепперони? 93. Знакомство с взаимосвязями данных: Маурита и Феличе проходят по 4 теста. Вот результаты 4 тестов Мауриты: 4, 4, 4, 4. Вот результаты 3 из 4 тестов Феличе: 3, 3, 3. Если среднее значение Мауриты по 4 тестам на 1 балл выше, чем у Феличе, каков результат? оценка 4-го теста Феличе? 94.Представляем пропорциональные отношения: Магазин А продает 7 фунтов бананов за 7 долларов. Магазин B продает 3 фунта бананов по цене 6 долларов. В каком магазине выгоднее? 95.
Теперь он на 190% больше. Каково население Оквилля в настоящее время? 87. Определение процентов чисел: В пункте проката коньков 60% из 120 коньков предназначены для мальчиков.Если остальные коньки для девочек, сколько их? 88. Расчет средних значений: В течение 4 недель Уильям вызвался помощником на занятиях по плаванию. Первую неделю он работал волонтером по 8 часов. Он работал волонтером 12 часов на второй неделе и еще 12 часов на третьей неделе. На четвертой неделе он работал волонтером по 9 часов. Сколько часов в среднем он работал волонтером в неделю? Вероятность и взаимосвязь данных 89.Понимание предпосылки вероятности: Джон хочет узнать любимое телешоу своего класса, поэтому он опрашивает всех мальчиков. Будет ли выборка репрезентативной или необъективной? 90. Понимание материальной вероятности: Грани на большом количестве кубиков помечены цифрами 1, 2, 3, 4, 5 и 6. Вы бросаете кубик 12 раз. Сколько раз вы должны ожидать, что вам выпадет 1? 91. Изучение дополнительных событий: Цифры от 1 до 50 в шляпе. Если вероятность выпадения четного числа составляет 25/50, какова вероятность НЕ выпадать четное число? Выразите эту вероятность дробью. 92. Исследование экспериментальной вероятности: В пиццерии недавно было продано 15 пицц. 5 из этих пицц были пепперони. Отвечая дробью, какова экспериментальная вероятность того, что следующая пицца будет пепперони? 93. Знакомство с взаимосвязями данных: Маурита и Феличе проходят по 4 теста. Вот результаты 4 тестов Мауриты: 4, 4, 4, 4. Вот результаты 3 из 4 тестов Феличе: 3, 3, 3. Если среднее значение Мауриты по 4 тестам на 1 балл выше, чем у Феличе, каков результат? оценка 4-го теста Феличе? 94.Представляем пропорциональные отношения: Магазин А продает 7 фунтов бананов за 7 долларов. Магазин B продает 3 фунта бананов по цене 6 долларов. В каком магазине выгоднее? 95. Написание уравнений для пропорциональных отношений: Лайонел любит футбол, но у него проблемы с мотивацией тренироваться. Итак, он стимулирует себя с помощью видеоигр. Существует пропорциональная зависимость между количеством упражнений, которые Лайонел выполняет, в x , и тем, сколько часов он играет в видеоигры, в y .Когда Лайонел выполняет 10 упражнений, он 30 минут играет в видеоигры. Напишите уравнение отношения между x и y .
Написание уравнений для пропорциональных отношений: Лайонел любит футбол, но у него проблемы с мотивацией тренироваться. Итак, он стимулирует себя с помощью видеоигр. Существует пропорциональная зависимость между количеством упражнений, которые Лайонел выполняет, в x , и тем, сколько часов он играет в видеоигры, в y .Когда Лайонел выполняет 10 упражнений, он 30 минут играет в видеоигры. Напишите уравнение отношения между x и y . Геометрия
96. Представляем периметр: В театре 4 стула в ряд. Всего 5 рядов. Если использовать строки в качестве единицы измерения, каков периметр? 97. Зона представления: В театре 4 стула в ряд. Всего 5 рядов. Сколько всего стульев? 98. Введение Том: Аарон хочет знать, сколько конфет может вместить его контейнер.Контейнер имеет высоту 20 сантиметров, длину 10 сантиметров и ширину 10 сантиметров. Каков объем контейнера? 99. Понимание 2D-форм: Кевин рисует фигуру с 4 равными сторонами. Какую форму он нарисовал? 100. Поиск периметра 2D-форм: Митчелл написал свои домашние вопросы на листе квадратной бумаги. Каждая сторона бумаги по 8 сантиметров. Какой периметр? 101. Определение площади 2D-форм: Одна торговая карточка имеет длину 9 см и ширину 6 см.Какая у него площадь? 102. Что такое 3D-фигуры: Марта рисует фигуру с 6 квадратными гранями. Какую форму она нарисовала? 103. Определение площади поверхности трехмерных фигур: Какова площадь поверхности куба шириной 2 см, высотой 2 см и длиной 2 см? 104. Определение объема трехмерных фигур: Контейнер для конфет Аарона имеет высоту 20 см, длину 10 см и ширину 10 см. Контейнер Брюса имеет высоту 25 сантиметров, длину 9 сантиметров и ширину 9 сантиметров.Найдите объем каждого контейнера. В зависимости от объема, чей контейнер может вместить больше конфет? 105. Определение прямоугольных треугольников: Треугольник имеет следующие длины сторон: 3 см, 4 см и 5 см.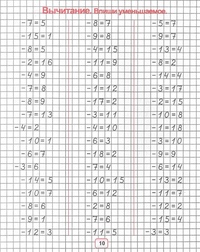 Этот треугольник прямоугольный? 106. Определение равносторонних треугольников: Треугольник имеет следующие длины сторон: 4 см, 4 см и 4 см. Что это за треугольник? 107. Определение равнобедренных треугольников: Треугольник имеет следующие длины сторон: 4 см, 5 см и 5 см.Что это за треугольник? 108. Определение треугольников из чешуи: Треугольник имеет следующие длины сторон: 4 см, 5 см и 6 см. Что это за треугольник? 109. Определение периметра треугольников: Луиджи построил палатку в форме равностороннего треугольника. Периметр 21 метр. Какова длина каждой стороны палатки? 110. Определение площади треугольников: Какова площадь треугольника с основанием в 2 единицы и высотой 3 единицы? 111.Применение теоремы Пифагора: Прямоугольный треугольник имеет одну сторону без гипотенузы 3 дюйма, а длину гипотенузы 5 дюймов. Какова длина другой стороны без гипотенузы? 112. Определение диаметра круга: Жасмин купила новый круглый рюкзак. Его площадь составляет 370 квадратных сантиметров. Какой диаметр у круглого рюкзака? 113. Поиск области круга: Круглый щит Капитана Америки имеет диаметр 76,2 сантиметра. Какова площадь его щита? 114.Определение радиуса круга: Скайлар живет на ферме, где его отец держит круглый кукурузный лабиринт. Кукурузный лабиринт имеет диаметр 2 километра. Каков радиус лабиринта?
Этот треугольник прямоугольный? 106. Определение равносторонних треугольников: Треугольник имеет следующие длины сторон: 4 см, 4 см и 4 см. Что это за треугольник? 107. Определение равнобедренных треугольников: Треугольник имеет следующие длины сторон: 4 см, 5 см и 5 см.Что это за треугольник? 108. Определение треугольников из чешуи: Треугольник имеет следующие длины сторон: 4 см, 5 см и 6 см. Что это за треугольник? 109. Определение периметра треугольников: Луиджи построил палатку в форме равностороннего треугольника. Периметр 21 метр. Какова длина каждой стороны палатки? 110. Определение площади треугольников: Какова площадь треугольника с основанием в 2 единицы и высотой 3 единицы? 111.Применение теоремы Пифагора: Прямоугольный треугольник имеет одну сторону без гипотенузы 3 дюйма, а длину гипотенузы 5 дюймов. Какова длина другой стороны без гипотенузы? 112. Определение диаметра круга: Жасмин купила новый круглый рюкзак. Его площадь составляет 370 квадратных сантиметров. Какой диаметр у круглого рюкзака? 113. Поиск области круга: Круглый щит Капитана Америки имеет диаметр 76,2 сантиметра. Какова площадь его щита? 114.Определение радиуса круга: Скайлар живет на ферме, где его отец держит круглый кукурузный лабиринт. Кукурузный лабиринт имеет диаметр 2 километра. Каков радиус лабиринта?Переменные
115. Определение независимых и зависимых переменных: Виктория печет кексы для своего класса. Количество кексов, которые она готовит, зависит от того, сколько у нее одноклассников. Для этого уравнения м — это количество кексов, а c — количество одноклассников. Какая переменная является независимой, а какая зависимой? 116.Написание переменных выражений для сложения: В прошлом футбольном сезоне Триш забила г голов. Алекса забила на 4 гола больше, чем Триш. Напишите выражение, показывающее, сколько голов забила Алекса. 117. Написание выражений переменных для вычитания: Элизабет ест здоровый, сбалансированный завтрак b раза в неделю. Мэдисон иногда пропускает завтрак. В общей сложности Мэдисон съедает на 3 завтрака меньше в неделю, чем Элизабет. Напишите выражение, показывающее, сколько раз в неделю Мэдисон завтракает. 118. Написание выражений переменных для умножения: В прошлом хоккейном сезоне Джек забил г голов. Патрик забил вдвое больше голов, чем Джек. Напишите выражения, показывающие, сколько голов забил Патрик. 119. Написание выражений переменных для деления: У Аманды c плиток шоколада. Она хочет равномерно распределить плитки шоколада между 3 друзьями. Напишите выражение, показывающее, сколько плиток шоколада получит один из ее друзей. 120. Решение уравнений с двумя переменными: Это уравнение показывает, как сумма, которую Лукас зарабатывает на внешкольной работе, зависит от того, сколько часов он работает: e = 12h . Переменная ч показывает, сколько часов он работает. Переменная e показывает, сколько денег он зарабатывает. Сколько денег заработает Лукас, проработав 6 часов? Как легко создавать свои собственные математические задачи со словами Вооружившись 120 примерами, которые вдохновят идеи, создание собственных математических задач со словами может заинтересовать ваших учеников и обеспечить согласованность с уроками. Do:
Напишите выражение, показывающее, сколько голов забила Алекса. 117. Написание выражений переменных для вычитания: Элизабет ест здоровый, сбалансированный завтрак b раза в неделю. Мэдисон иногда пропускает завтрак. В общей сложности Мэдисон съедает на 3 завтрака меньше в неделю, чем Элизабет. Напишите выражение, показывающее, сколько раз в неделю Мэдисон завтракает. 118. Написание выражений переменных для умножения: В прошлом хоккейном сезоне Джек забил г голов. Патрик забил вдвое больше голов, чем Джек. Напишите выражения, показывающие, сколько голов забил Патрик. 119. Написание выражений переменных для деления: У Аманды c плиток шоколада. Она хочет равномерно распределить плитки шоколада между 3 друзьями. Напишите выражение, показывающее, сколько плиток шоколада получит один из ее друзей. 120. Решение уравнений с двумя переменными: Это уравнение показывает, как сумма, которую Лукас зарабатывает на внешкольной работе, зависит от того, сколько часов он работает: e = 12h . Переменная ч показывает, сколько часов он работает. Переменная e показывает, сколько денег он зарабатывает. Сколько денег заработает Лукас, проработав 6 часов? Как легко создавать свои собственные математические задачи со словами Вооружившись 120 примерами, которые вдохновят идеи, создание собственных математических задач со словами может заинтересовать ваших учеников и обеспечить согласованность с уроками. Do: - Ссылка на интересы студентов: Обрамляя свои текстовые задачи интересами студентов, вы, вероятно, привлечете внимание. Например, если большинство из ваших учеников любит американский футбол, задача измерения может включать расстояние броска известного квотербека.
- Задайте актуальные вопросы: Написание словесной задачи, отражающей текущие события или проблемы, может заинтересовать учащихся, давая им четкий, осязаемый способ применения своих знаний.

- Включите имена учащихся: Назовите символы вопроса в честь учащихся — это простой способ сделать предмет понятным, помогая им справиться с проблемой.
- Будьте явными: Повторение ключевых слов определяет вопрос, помогая учащимся сосредоточиться на основной проблеме.
- Тест на понимание прочитанного: Цветочный выбор слов и длинные предложения могут скрыть ключевые элементы вопроса.Вместо этого используйте краткие фразы и лексику на уровне своего класса.
- Сосредоточьтесь на схожих интересах: Слишком много вопросов, связанных с интересами, такими как футбол и баскетбол, может оттолкнуть некоторых учащихся или оттолкнуть их.
- Особые опасения: Включение ненужной информации вводит еще один элемент решения проблем, подавляющий многих учеников начальной школы.
Базовая математика в JavaScript — числа и операторы — Изучение веб-разработки
На этом этапе курса мы обсуждаем математику в JavaScript — как мы можем использовать операторы и другие функции для успешного манипулирования числами для выполнения наших ставок.
| Предварительные требования: | Базовая компьютерная грамотность, базовое понимание HTML и CSS, понимание того, что такое JavaScript. |
|---|---|
| Цель: | Чтобы познакомиться с основами математики в JavaScript. |
Ладно, может и нет. Некоторые из нас любят математику, некоторые из нас ненавидят математику с тех пор, как нам пришлось изучать таблицы умножения и деление в столбик в школе, а некоторые из нас сидят где-то посередине. Но никто из нас не может отрицать, что математика — это фундаментальная часть жизни, без которой мы далеко не продвинемся. Это особенно верно, когда мы учимся программировать JavaScript (или любой другой язык в этом отношении) — так много из того, что мы делаем, полагается на обработку числовых данных, вычисление новых значений и т. Д., Что вы не удивитесь, узнав этот JavaScript имеет полнофункциональный набор доступных математических функций.
В этой статье обсуждаются только основные части, которые вам нужно знать сейчас.
Типы чисел
В программировании даже простая десятичная система счисления, которую мы все так хорошо знаем, сложнее, чем вы думаете. Мы используем разные термины для описания различных типов десятичных чисел, например:
- Целые числа — целые числа, например 10, 400 или -5.
- Числа с плавающей запятой (с плавающей запятой) имеют десятичные и десятичные знаки, например 12.5 и 56.7786543.
- Двойные числа — это особый тип чисел с плавающей запятой, которые имеют большую точность, чем стандартные числа с плавающей запятой (что означает, что они точны до большего числа десятичных знаков).
У нас даже есть разные типы систем счисления! Десятичное число — это основание 10 (это означает, что в каждом столбце используется 0–9), но у нас также есть такие вещи, как:
- Двоичный — язык самого низкого уровня компьютеров; 0 и 1.

- Octal — База 8, использует 0–7 в каждом столбце.
- Шестнадцатеричный — База 16, использует 0–9, а затем a – f в каждом столбце. Возможно, вы уже встречались с этими числами при настройке цветов в CSS.
Прежде чем вы начнете беспокоиться о таянии вашего мозга, остановитесь прямо здесь! Для начала мы будем придерживаться десятичных чисел в этом курсе; вы редко будете сталкиваться с необходимостью начать думать о других типах, если вообще когда-нибудь.
Вторая хорошая новость заключается в том, что в отличие от некоторых других языков программирования, JavaScript имеет только один тип данных для чисел, как целых, так и десятичных дробей — как вы уже догадались, Number .Это означает, что с какими бы типами чисел вы ни работали в JavaScript, вы обрабатываете их точно так же.
Примечание : На самом деле в JavaScript есть второй числовой тип BigInt, используемый для очень и очень больших целых чисел. Но для целей этого курса мы просто будем беспокоиться о значениях Number .
Для меня все числа
Давайте быстро поиграем с числами, чтобы заново познакомиться с основным синтаксисом, который нам нужен. Введите перечисленные ниже команды в консоль JavaScript инструментов разработчика.
- Прежде всего, давайте объявим пару переменных и инициализируем их целым числом и числом с плавающей запятой, соответственно, затем снова введем имена переменных, чтобы убедиться, что все в порядке:
пусть myInt = 5; пусть myFloat = 6,667; myInt; myFloat; - Числовые значения вводятся без кавычек — попробуйте объявить и инициализировать еще пару переменных, содержащих числа, прежде чем двигаться дальше.
- Теперь давайте проверим, что обе наши исходные переменные имеют один и тот же тип данных.В JavaScript есть оператор
type of, который делает это. Введите следующие две строки, как показано:
Введите следующие две строки, как показано:
Вы должны получитьtypeof myInt; typeof myFloat;«число», возвращенное в обоих случаях — это значительно упрощает нам задачу, чем если бы разные числа имели разные типы данных, и нам приходилось обращаться с ними по-разному. Уф!
Полезные числовые методы
Объект Number , экземпляр которого представляет все стандартные числа, которые вы будете использовать в своем JavaScript, имеет ряд полезных методов, доступных для вас, чтобы управлять числами.Мы не рассматриваем их подробно в этой статье, потому что мы хотели сохранить ее как простое введение, а пока охватить только самые основные основы; однако, прочитав этот модуль несколько раз, стоит перейти на страницы со ссылками на объекты и узнать больше о том, что доступно.
Например, чтобы округлить ваше число до фиксированного числа десятичных знаков, используйте метод toFixed () . Введите в консоль браузера следующие строки:
пусть лотыOfDecimal = 1.766584958675746364;
lotOfDecimal;
let twoDecimalPlaces = lotOfDecimal.toFixed (2);
twoDecimalPlaces; Преобразование в числовые типы данных
Иногда может получиться число, которое хранится как строковый тип, что затрудняет выполнение вычислений с ним. Чаще всего это происходит, когда данные вводятся в форму ввода, а тип ввода — текст. Есть способ решить эту проблему — передать строковое значение в конструктор Number () , чтобы вернуть числовую версию того же значения.
Например, попробуйте ввести в консоль следующие строки:
пусть myNumber = '74';
myNumber + 3; Вы получите результат 743, а не 77, потому что myNumber фактически определен как строка. Вы можете проверить это, набрав следующее:
typeof myNumber; Для исправления расчета можно сделать так:
Число (myNumber) + 3; Арифметические операторы — это основные операторы, которые мы используем для суммирования в JavaScript:
| Оператор | Имя | Назначение | Пример |
|---|---|---|---|
+ | Дополнение | Складывает два числа. | 6 + 9 |
- | Вычитание | Вычитает правое число из левого. | 20-15 |
* | Умножение | Умножает два числа. | 3 * 7 |
/ | Дивизия | Делит левое число на правое. | 10/5 |
% | Остаток (иногда называется по модулю) | Возвращает остаток, оставшийся после того, как вы разделили левое число на количество целых частей, равное правому числу. | |
** | Показатель | Возводит число с основанием в степень степени , то есть число | 5 ** 2 (возвращает 25 , что совпадает с 5 * 5 ). |
Примечание : Иногда в арифметических операциях можно встретить числа, называемые операндами.
Примечание : иногда можно увидеть экспоненты, выраженные с помощью более старого метода Math.pow () , который работает очень похожим образом. Например, в Math.pow (7, 3) , 7 - это основание, а 3 - показатель степени, поэтому результатом выражения будет 343 . Math.pow (7, 3) эквивалентно 7 ** 3 .
Нам, вероятно, не нужно учить вас выполнять основы математики, но мы хотели бы проверить ваше понимание синтаксиса. Попробуйте ввести приведенные ниже примеры в консоль JavaScript инструментов разработчика, чтобы ознакомиться с синтаксисом.
- Сначала попробуйте ввести несколько собственных простых примеров, например
10 + 7 9 * 8 60% 3 - Вы также можете попробовать объявить и инициализировать некоторые числа внутри переменных и попробовать использовать их в суммах - переменные будут вести себя точно так же, как значения, которые они содержат для целей суммы.Например:
пусть num1 = 10; пусть num2 = 50; 9 * число1; num1 ** 3; num2 / num1; - Наконец, в этом разделе попробуйте ввести несколько более сложных выражений, например:
5 + 10 * 3; число2% 9 * число1; число2 + число1 / 8 + 2;
Некоторые из этих последних вычислений могут дать не совсем тот результат, которого вы ожидали; раздел ниже может дать ответ, почему.
Приоритет оператора
Давайте посмотрим на последний пример сверху, предполагая, что num2 содержит значение 50, а num1 содержит значение 10 (как первоначально указано выше):
число2 + число1 / 8 + 2; Как человек, вы можете прочитать это как "50 плюс 10 равно 60" , затем "8 плюс 2 равно 10" и, наконец, "60, разделенное на 10, равно 6" .
Но браузер делает "10, деленное на 8, равно 1,25" , затем "50 плюс 1,25 плюс 2 равняется 53,25" .
Это связано с приоритетом оператора . - некоторые операторы применяются раньше других при вычислении результата вычисления (в программировании оно называется выражением , ). Приоритет операторов в JavaScript такой же, как и на уроках математики в школе - сначала всегда выполняются умножение и деление, затем сложение и вычитание (вычисление всегда выполняется слева направо).
Если вы хотите переопределить приоритет операторов, вы можете заключить в круглые скобки те части, которые должны быть обработаны в первую очередь. Итак, чтобы получить результат 6, мы могли бы сделать это:
(число2 + число1) / (8 + 2); Попробуйте и убедитесь.
Иногда вам нужно многократно прибавлять или вычитать единицу к значению числовой переменной или из него. Это удобно сделать с помощью операторов инкремента ( ++ ) и декремента (–). Мы использовали ++ в нашей игре «Угадай число» еще в нашей первой заставке по JavaScript, когда мы добавили 1 к нашей переменной guessCount , чтобы отслеживать, сколько предположений пользователь оставил после каждого поворота.
guessCount ++; Примечание : Эти операторы чаще всего используются в циклах, о которых вы узнаете позже в этом курсе. Например, вы хотите просмотреть список цен и добавить к каждой из них налог с продаж. Вы могли бы использовать цикл, чтобы просмотреть каждое значение по очереди и выполнить необходимые вычисления для добавления налога с продаж в каждом случае. Инкрементор используется для перехода к следующему значению, когда это необходимо. На самом деле мы предоставили простой пример, показывающий, как это делается - проверьте его вживую и посмотрите исходный код, чтобы увидеть, сможете ли вы определить инкременторы! Мы подробно рассмотрим петли позже в этом курсе.
Давайте попробуем поиграть с ними на вашей консоли. Для начала обратите внимание, что вы не можете применить их непосредственно к числу, что может показаться странным, но мы присваиваем переменной новое обновленное значение, а не работаем с самим значением. Следующее вернет ошибку:
3 ++; Итак, вы можете увеличивать только существующую переменную. Попробуйте это:
пусть num1 = 4;
num1 ++; Ладно, странность номер 2! Когда вы это сделаете, вы увидите, что возвращается значение 4 - это потому, что браузер возвращает текущее значение, , затем увеличивает переменную.Вы можете увидеть, что оно увеличилось, если вы снова вернете значение переменной:
num1; То же самое и с - : попробуйте следующий
пусть num2 = 6;
num2--;
num2; Примечание : вы можете заставить браузер делать это наоборот - увеличивать / уменьшать переменную , затем возвращать значение - поместив оператор в начало переменной, а не в конец. Попробуйте еще раз приведенные выше примеры, но на этот раз используйте
Попробуйте еще раз приведенные выше примеры, но на этот раз используйте ++ num1 и --num2 .
Операторы присваивания - это операторы, которые присваивают значение переменной. Мы уже использовали самый простой, = , множество раз - он присваивает переменной слева значение, указанное справа:
пусть x = 3;
пусть y = 4;
х = у; Но есть и более сложные типы, которые предоставляют полезные ярлыки, чтобы сделать ваш код более аккуратным и эффективным. Наиболее распространенные перечислены ниже:
| Оператор | Имя | Назначение | Пример | Ярлык для |
|---|---|---|---|---|
+ = | Дополнительное задание | Добавляет значение справа к значению переменной слева, затем возвращает новое значение переменной | х + = 4; | х = х + 4; |
- = | Присваивание вычитания | Вычитает значение справа из значения переменной слева и возвращает новое значение переменной | х - = 3; | х = х - 3; |
* = | Назначение умножения | Умножает значение переменной слева на значение справа и возвращает новое значение переменной | х * = 3; | х = х * 3; |
/ = | Назначение дивизии | Делит значение переменной слева на значение справа и возвращает новое значение переменной | х / = 5; | х = х / 5; |
Попробуйте ввести некоторые из приведенных выше примеров в свою консоль, чтобы понять, как они работают.В каждом случае проверьте, сможете ли вы угадать значение, прежде чем вводить вторую строку.
Обратите внимание, что вы вполне можете использовать другие переменные в правой части каждого выражения, например:
пусть x = 3;
пусть y = 4;
х * = у; В этом упражнении вы будете управлять некоторыми числами и операторами, чтобы изменить размер поля. Коробка рисуется с помощью API браузера, называемого Canvas API. Не нужно беспокоиться о том, как это работает - просто сконцентрируйтесь на математике.Ширина и высота поля (в пикселях) определяются переменными x и y , которым изначально присвоено значение 50.
Открыть в новом окне
В редактируемом поле кода выше есть две строки, отмеченные комментарием, который мы хотели бы, чтобы вы обновили, чтобы поле увеличивалось / уменьшалось до определенных размеров, используя определенные операторы и / или значения в каждом случае. Попробуем следующее:
- Измените строку, которая вычисляет x, чтобы поле оставалось шириной 50 пикселей, но 50 вычислялось с использованием чисел 43 и 7 и арифметического оператора.
- Измените строку, которая вычисляет y, так, чтобы прямоугольник был высотой 75 пикселей, но 75 вычисляется с использованием чисел 25 и 3 и арифметического оператора.
- Измените строку, в которой вычисляется x, чтобы поле было шириной 250 пикселей, но 250 вычисляется с использованием двух чисел и оператора остатка (по модулю).
- Измените строку, которая вычисляет y, так, чтобы прямоугольник был высотой 150 пикселей, но 150 вычисляется с использованием трех чисел и операторов вычитания и деления.
- Измените строку, вычисляющую x, так, чтобы поле было шириной 200 пикселей, но 200 вычисляется с использованием числа 4 и оператора присваивания.
- Измените строку, в которой вычисляется y, так, чтобы поле было высотой 200 пикселей, но 200 вычисляется с использованием чисел 50 и 3, оператора умножения и оператора присваивания сложения.
Не волнуйтесь, если вы полностью испортили код. Вы всегда можете нажать кнопку «Сброс», чтобы все снова заработало. После того, как вы правильно ответили на все вышеперечисленные вопросы, не стесняйтесь еще немного поиграть с кодом или создать свои собственные задачи.
Иногда нам нужно запустить тесты «правда / ложь», а затем действовать соответственно в зависимости от результата этого теста - для этого мы используем операторы сравнения .
| Оператор | Имя | Назначение | Пример |
|---|---|---|---|
=== | Строгое равенство | Проверяет, идентичны ли значения left и right друг другу | 5 === 2 + 4 |
! == | Строгое неравенство | Проверяет, идентичны ли левое и правое значения друг другу | 5! == 2 + 3 |
< | Менее | Проверяет, меньше ли левое значение правого. | 10 <6 |
> | Больше | Проверяет, больше ли левое значение правого. | 10> 20 |
<= | Меньше или равно | Проверяет, действительно ли левое значение меньше или равно правому. | 3 <= 2 |
> = | Больше или равно | Проверяет, больше ли левое значение правому или равно ему. | 5> = 4 |
Примечание : вы можете увидеть, как некоторые люди используют == и ! = в своих тестах на равенство и неравенство. Это допустимые операторы в JavaScript, но они отличаются от === /! == . В предыдущих версиях проверяется, совпадают ли значения, но не совпадают ли типы данных значений. Последние, строгие версии проверяют равенство как значений, так и их типов данных.Строгие версии, как правило, приводят к меньшему количеству ошибок, поэтому мы рекомендуем вам их использовать.
Если вы попытаетесь ввести некоторые из этих значений в консоль, вы увидите, что все они возвращают истинных / ложных значений - те логические значения, которые мы упоминали в прошлой статье. Они очень полезны, поскольку позволяют нам принимать решения в нашем коде, и используются каждый раз, когда мы хотим сделать какой-то выбор. Например, логические значения могут использоваться для:
- Отображение правильной текстовой метки на кнопке в зависимости от того, включена функция или выключена
- Отображение сообщения о завершении игры, если игра окончена, или сообщения о победе, если игра была выиграна.
- Отображать правильное сезонное приветствие в зависимости от сезона праздников
- Увеличение или уменьшение масштаба карты в зависимости от выбранного уровня масштабирования
Мы рассмотрим, как кодировать такую логику, когда рассмотрим условные операторы в будущей статье.А пока давайте посмотрим на быстрый пример:
Машина остановлена.
const btn = document.querySelector ('кнопка');
const txt = document.querySelector ('p');
btn.addEventListener ('щелчок', updateBtn);
function updateBtn () {
if (btn.textContent === 'Запустить машину') {
btn.textContent = 'Остановить машину';
txt.textContent = 'Машина запустилась!';
} еще {
btn.textContent = 'Запустить машину';
текст.textContent = 'Машина остановлена.';
}
} Открыть в новом окне
Вы можете увидеть, что оператор равенства используется внутри функции updateBtn () . В этом случае мы не проверяем, имеют ли два математических выражения одно и то же значение - мы проверяем, содержит ли текстовое содержимое кнопки определенную строку, - но действует тот же принцип. Если при нажатии на кнопку в данный момент отображается «Запустить машину», мы меняем ее метку на «Остановить машину» и обновляем метку соответствующим образом.Если при нажатии кнопки в данный момент отображается сообщение «Остановить машину», мы снова меняем местами дисплей.
Примечание : такой элемент управления, который переключается между двумя состояниями, обычно называется переключателем . Он переключается между одним состоянием и другим - свет включен, свет выключен и т. Д.
Вы дошли до конца этой статьи, но можете ли вы вспомнить самую важную информацию? Вы можете найти дополнительные тесты, чтобы убедиться, что вы сохранили эту информацию, прежде чем двигаться дальше - см. Проверка своих навыков: математика.
В этой статье мы рассмотрели основную информацию, которую вам нужно знать о числах в JavaScript на данный момент. Вы будете видеть числа, используемые снова и снова, на протяжении всего изучения JavaScript, так что сейчас неплохо избавиться от этого. Если вы один из тех людей, которым не нравится математика, вас может утешить тот факт, что эта глава была довольно короткой.
В следующей статье мы исследуем текст и то, как JavaScript позволяет нам манипулировать им.
Примечание : Если вам нравится математика и вы хотите узнать больше о том, как она реализована в JavaScript, вы можете найти более подробную информацию в основном разделе JavaScript MDN.Отличное место для начала - это статьи о числах и датах, а также о выражениях и операторах.
Общие математические символы и терминология
Математические символы и терминология могут сбивать с толку и мешать изучению и пониманию основ математики.
Эта страница дополняет наши страницы навыков счета и содержит краткий глоссарий общих математических символов и терминологии с краткими определениями.
Мы что-то упускаем? Дайте нам знать.
Общие математические символы
+ сложение, плюс, положительное
Символ сложения + обычно используется для обозначения того, что два или более числа должны быть сложены вместе, например, 2 + 2.
Символ + также может использоваться для обозначения положительного числа, хотя он встречается реже, например, +2. На нашей странице о положительных и отрицательных числах объясняется, что число без знака считается положительным, поэтому плюс обычно не требуется.
Подробнее см. На нашей странице Дополнение .
- вычитание, минус, отрицательный
Этот символ имеет два основных применения в математике:
- - используется, когда нужно вычесть одно или несколько чисел, например, 2 - 2.
- Символ - также обычно используется для обозначения отрицательного или отрицательного числа, например −2.
См. Дополнительную информацию на нашей странице о вычитании .
× или * или. Умножение
Эти символы имеют то же значение; обычно × используется для обозначения умножения, когда написано от руки или используется на калькуляторе, например, 2 × 2.
Символ * используется в электронных таблицах и других компьютерных приложениях для обозначения умножения, хотя * имеет другие, более сложные значения в математике.
Реже умножение также может быть обозначено точкой.или вообще без символа. Например, если вы видите число, написанное вне скобок без оператора (символа или знака), то его следует умножить на содержимое скобок: 2 (3 + 2) совпадает с 2 × (3 + 2).
См. Дополнительную информацию на нашей странице Умножение .
÷ или / Подразделение
Оба эти символа используются для обозначения деления в математике. ÷ обычно используется в рукописных вычислениях и на калькуляторах, например, 2 ÷ 2.
/ используется в электронных таблицах и других компьютерных приложениях.
Подробнее см. На нашей странице в Division .
= равно
Символ = равно используется, чтобы показать, что значения по обе стороны от него одинаковы. Чаще всего используется для отображения результата вычислений, например 2 + 2 = 4, или в уравнениях, например 2 + 3 = 10-5.
Вы также можете встретить другие похожие символы, но они встречаются реже:
- ≠ означает не равно.Например, 2 + 2 ≠ 5 - 2. В компьютерных приложениях (например, Excel) символы <> означают не равно.
- ≡ означает идентично. Это похоже на, но не совсем то же самое, что на равно. Поэтому, если сомневаетесь, придерживайтесь =.
- ≈ означает примерно равно или почти равно. Две стороны отношения, обозначенные этим символом, будут , а не достаточно точными для математических манипуляций.
<Меньше и> Больше
Этот символ < означает меньше, например 2 <4 означает, что 2 меньше 4.
Этот символ > означает больше, например, 4> 2.
≤ ≥ Эти символы означают «меньше или равно» и «больше или равно» и обычно используются в алгебре. В компьютерных приложениях используются <= и> =.
≪ ≫ Эти символы встречаются реже и означают намного меньше или намного больше чем.
± плюс или минус
Этот символ ± означает «плюс или минус». Он используется, например, для обозначения доверительных интервалов вокруг числа.
Ответом считается «плюс-минус» другое число, или, другими словами, в пределах диапазона данного ответа.
Например, 5 ± 2 на практике может быть любым числом от 3 до 7.
∑ Сумма
Символ ∑ означает сумму.
∑ - это символ сигмы с заглавной буквы. Он обычно используется в алгебраических функциях, и вы также можете заметить его в Excel - кнопка Автосумма имеет сигму в качестве значка.
° градус
Градусы ° используются по-разному.
- Как мера поворота - угол между сторонами фигуры или поворот круга. Круг равен 360 °, а прямой угол - 90 °. Смотрите наш раздел о Geometry для получения дополнительной информации.
- Мера температуры. градуса Цельсия или Цельсия используются в большинстве стран мира (за исключением США).Вода замерзает при 0 ° C и закипает при 100 ° C. В США используется градус Фаренгейта. По шкале Фаренгейта вода замерзает при 32 ° F и закипает при 212 ° F. Смотрите нашу страницу: Системы измерения для получения дополнительной информации.
∠ Угол
Символ угла ∠ используется как сокращение в геометрии (изучении форм) для описания угла.
Выражение ∠ABC используется для описания угла в точке B (между точками A и C). Точно так же ∠BAC можно использовать для описания угла точки A (между точками B и C).Подробнее об углах и других геометрических терминах см. На наших страницах Geometry .
√ Квадратный корень
√ - символ квадратного корня. Квадратный корень - это число, которое при умножении на себя дает исходное число.
Например, квадратный корень из 4 равен 2, потому что 2 x 2 = 4. Квадратный корень из 9 равен 3, потому что 3 x 3 = 9.
См. Нашу страницу: Специальные числа и понятия для получения дополнительной информации о квадратных корнях.
n Мощность
Целое число с верхним индексом (любое целое число n ) - это символ, используемый для обозначения степени числа.
Например, 3 2 означает 3 в степени 2, что совпадает с 3 в квадрате (3 x 3).
4 3 означает 4 в степени 3 или 4 в кубе, то есть 4 × 4 × 4.
См. Наши страницы Расчетная площадь и Расчет объема , где приведены примеры использования чисел в квадрате и кубе .
Степень также используется как сокращенный способ записи больших и малых чисел.
Большие числа
10 6 - 1 000 000 (один миллион).
10 9 - 1 000 000 000 (один миллиард).
10 12 - 1 000 000 000 000 (один триллион).
10 100 , написанное длинной рукой, будет равно 1 со 100 нулями (один гугол).
Маленькие числа
10 -3 - 0,001 (одна тысячная)
10 -6 равно 0.6 = 10 6 = 1000000 (один миллион).
. Десятичная точка
. - символ десятичной точки, часто называемый просто «точкой». См. Нашу страницу Decimals для примеров его использования.
, Разделитель тысяч
Запятую можно использовать для разделения больших чисел и облегчения их чтения.
Тысячу можно записать как 1000, а также как 1000 и миллион как 1000000 или 1000000.Запятая разделяет большие числа на блоки по три цифры.
В большинстве англоязычных стран, не имеет математической функции, он просто используется для облегчения чтения чисел.
В некоторых других странах, особенно в Европе, запятая может использоваться вместо десятичной точки, и действительно, десятичная точка может использоваться вместо запятой в качестве визуального разделителя. Это объясняется более подробно на нашей странице Introduction to Numbers .
[], () Скобки, круглые скобки
Скобки () используются для определения порядка вычислений в соответствии с правилом BODMAS.
Сначала вычисляются части расчета, заключенные в скобки, например
- 5 + 3 × 2 = 11
- (5 + 3) × 2 = 16
% В процентах
Символ% означает процент или число из 100.
Узнайте все о процентах на нашей странице: Введение в проценты
π Pi
π или пи - греческий символ звука «п».Это часто встречается в математике и является математической константой. Пи - это длина окружности круга, деленная на ее диаметр, и имеет значение 3,1415. Это иррациональное число, что означает, что его десятичные разряды продолжаются до бесконечности.
∞ Бесконечность
Символ ∞ означает бесконечность - понятие, согласно которому числа существуют вечно.
Каким бы большим у вас ни было число, у вас всегда может быть номер побольше, потому что вы всегда можете добавить к нему единицу.
Бесконечность - это не число, а идея , чисел, существующая вечно. Вы не можете прибавить единицу к бесконечности, как нельзя прибавить единицу к человеку, полюбить или ненавидеть.
\ (\ bar x \) (x-bar) Среднее значение
\ (\ bar x \) - среднее из всех возможных значений x.
Чаще всего этот символ встречается в статистике.
Дополнительную информацию см. На нашей странице Средние значения .
! Факториал
! это символ факториала.
н! - произведение (умножение) всех чисел от n до 1 включительно, то есть n × (n − 1) × (n − 2) ×… × 2 × 1.
Например:
5! = 5 × 4 × 3 × 2 × 1 = 120
10! = 10 × 9 × 8 × 7 × 6 × 5 × 4 × 3 × 2 × 1 = 3,628,800
| Труба
Труба '|' также называется вертикальной чертой, vbar, pike и имеет множество применений в математике, физике и вычислениях.
Чаще всего в базовой математике он используется для обозначения абсолютного значения или модуля действительного числа, где \ (\ vert x \ vert \) - это абсолютное значение или модуль \ (x \) .
Математически это определяется как
$$ \ vert x \ vert = \ biggl \ {\ begin {eqnarray} -x, x \ lt 0 \\ x, x \ ge 0 \ end {eqnarray} $$
Проще говоря, \ (\ vert x \ vert \) - неотрицательное значение \ (x \). Например, модуль 6 равен 6, а модуль −6 также равен 6.
Он также используется в вероятности, где P (Z | Y) обозначает вероятность X при условии Y.
∝ Пропорционально
∝ означает «пропорционально » и используется, чтобы показать что-то, что меняется по отношению к чему-то другому.
Например, если x = 2y, то x ∝ y.
∴ Следовательно
∴ - это удобная сокращенная форма слова «поэтому», используемая в математике и естественных науках.
∵ Потому что
∵ - удобная сокращенная форма слова «потому что», не путать с «поэтому».
Математическая терминология (A-Z)
Амплитуда
Когда объект или точка движется циклически, или подвергается вибрации или колебаниям (например,грамм. маятник), амплитуда - это максимальное расстояние, на которое он перемещается от своей центральной точки. См. Введение в геометрию для получения дополнительной информации.
Apothem
Линия, соединяющая центр правильного многоугольника с одной из его сторон. Линия перпендикулярна (под прямым углом) в сторону.
Площадь
Геометрическая площадь определяется как пространство, занимаемое плоской формой или поверхностью объекта. Площадь измеряется в квадратных единицах, например в квадратных метрах ( м 2 ).Для получения дополнительной информации см. Нашу страницу о площади , площади поверхности и объеме .
Асимптота
Асимптота - это прямая линия или ось, которая конкретно связана с изогнутой линией. По мере того, как кривая линия расширяется (стремится) к бесконечности, она приближается к своей асимптоте (то есть расстояние между кривой и асимптотой стремится к нулю, но никогда не касается ее). Это происходит в геометрии и тригонометрии .
Ось
Опорная линия, вокруг которой нарисован, повернут или измерен объект, точка или линия.В симметричной форме ось обычно представляет собой линию симметрии.
Коэффициент
Коэффициент - это число или величина, умножающая другую величину. Обычно он помещается перед переменной . В выражении 6 x , 6 - коэффициент, а x - переменная.
Окружность
Окружность - это длина расстояния по краю круга. Это тип с периметром , который уникален для круглых форм.Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Данные
Данные представляют собой набор значений, информации или характеристик, которые часто имеют числовой характер. Они могут быть собраны с помощью научного эксперимента или других средств наблюдения. Это могут быть количественных или качественных переменных. Датум - это отдельное значение одной переменной. См. Нашу страницу Типы данных для получения дополнительной информации.
Диаметр
Диаметр - это термин, используемый в геометрии для определения прямой линии, которая проходит через центр круга или сферы, касаясь окружности или поверхности с обоих концов.Диаметр в два раза больше радиуса .
Экстраполировать
Экстраполяция - это термин, используемый при анализе данных. Это относится к расширению графика, кривой или диапазона значений в диапазон, для которого нет данных, с выводом значений неизвестных данных из тенденций в известных данных.
Фактор
Коэффициент - это число, которое мы умножаем на другое число. Фактор делится на другое число целое число раз. У большинства чисел есть четное число факторов.Квадратное число имеет нечетное количество множителей. Простое число имеет два множителя - само себя и 1. Простой множитель - множитель, который является простым числом. Например, простые множители 21 равны 3 и 7 (потому что 3 × 7 = 21, а 3 и 7 - простые числа).
Среднее значение, Медиана и мода
Среднее значение (среднее значение) набора данных вычисляется путем сложения всех чисел в наборе данных и последующего деления на количество значений в наборе.Когда набор данных упорядочен от наименьшего к наибольшему, среднее значение составляет . Режим - это число, которое встречается чаще всего.
Операция
Математическая операция - это шаг или этап в вычислении, или математическое «действие». Основные арифметические операции - сложение, вычитание, умножение и деление. Порядок, в котором выполняются операции при вычислении, важен. Порядок операций известен как BODMAS .
Математические операции часто называют «суммами». Строго говоря, «сумма» - это операция сложения. В SYN мы имеем в виду операции и вычисления, но в повседневной речи вы часто можете услышать общий термин «суммы», который неверен.
Периметр
Периметр двухмерной фигуры - это непрерывная линия (или длина линии), определяющая контур фигуры. Периметр круглой формы называется ее окружностью .Наша страница на Perimeter объясняет это более подробно.
Пропорции
Пропорция - это относительное отношение. Соотношения сравнивают одну часть с другой, а пропорции сравнивают одну часть с целым. Например, «3 из 10 взрослых в Англии имеют избыточный вес». Пропорция относится к фракциям .
Пифагор
Пифагор был греческим философом, которому приписывают ряд важных математических и научных открытий, возможно, наиболее значительное из которых стало известно как Теорема Пифагора .
Это важное правило применяется только к прямоугольным треугольникам. В нем говорится, что «квадрат гипотенузы равен сумме квадратов на двух других сторонах».
Количественный и качественный
Количественные данные - это числовые переменные или значения, которые могут быть выражены численно, то есть сколько, сколько, как часто, и получаются путем подсчета или измерения.
Качественные данные - это переменные типа, которые не имеют числового значения и могут быть выражены описательно, т.е.е. с использованием имени или символа и получаются путем наблюдения.
Подробнее см. Нашу страницу о типах данных .
Радиан
Радиан - это единица измерения угла в системе СИ. Один радиан эквивалентен углу, образуемому в центре круга дугой, равной по длине радиусу. Один радиан чуть меньше 57,3 градуса. Полный оборот (360 градусов) составляет 2π радиан.
Радиус
Термин «радиус» используется в контексте окружностей и других изогнутых форм.Это расстояние от центральной точки круга, сферы или дуги до ее внешнего края, поверхности или окружности . Диаметр в два раза больше радиуса. Для получения дополнительной информации см. Нашу страницу о изогнутых форм .
Диапазон
В статистике диапазон данного набора данных - это разница между наибольшим и наименьшим значениями.
Передаточное отношение
Отношение- это математический термин, используемый для сравнения размеров одной детали с другой.Соотношения обычно отображаются в виде двух или более чисел, разделенных двоеточием, например, 7: 5, 1: 8 или 5: 2: 1.
Стандартное отклонение
Стандартное отклонение набора данных измеряет, насколько данные отличаются от среднего значения, то есть это мера вариации или разброса набора значений. Если разброс данных невелик и все значения близки к среднему, стандартное отклонение будет низким. Высокое стандартное отклонение указывает на то, что данные разбросаны по более широкому диапазону
Срок
Термин - это отдельное математическое выражение.Это может быть одно число, одна переменная (например, x ) или несколько констант и переменных, умноженных вместе (например, 3 x 2). Термины обычно разделяются операциями сложения или вычитания. Термин может включать операции сложения или вычитания, но только в скобках, например 3 (2 -x3).
переменная
Переменная - это коэффициент в математическом выражении, арифметическом соотношении или научном эксперименте, который может изменяться.В эксперименте обычно используются три типа переменных: независимые, зависимые и контролируемые. В выражении 6 x , 6 - это коэффициент , а x - это переменная.
Вариант
Дисперсия - это статистическое измерение, которое указывает разброс между элементами в наборе данных. Он измеряет, насколько далеко каждый член в наборе от среднего и, следовательно, от всех остальных членов в наборе.
Вектор
Векторы описывают математические величины, которые имеют как величину, так и направление.Векторы встречаются во многих математических и физических приложениях, например. изучение движения, где скорость, ускорение, сила, смещение и импульс являются векторными величинами.
Том
Объем - это трехмерное пространство, занимаемое твердой или полой формой. Он измеряется кубическими размерами пространства, ограниченного его поверхностями. Объем измеряется в кубических единицах, например м 3 .
Дополнительные материалы по навыкам, которые вам нужны
Руководство по навыкам, которые вам нужны
Это руководство из четырех частей познакомит вас с основами математики от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрии и статистике.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
Математический глоссарий: математические термины и определения
Это глоссарий общих математических терминов, используемых в арифметике, геометрии, алгебре и статистике.
Abacus : ранний счетный инструмент, используемый для базовой арифметики.
Абсолютное значение : Всегда положительное число, абсолютное значение относится к расстоянию числа от 0.
Острый угол : угол, размер которого составляет от 0 ° до 90 ° или меньше 90 ° радиан.
Приложение : Число, связанное с проблемой сложения; добавляемые числа называются слагаемыми.
Алгебра : Раздел математики, в котором числа заменяются буквами для поиска неизвестных значений.
Алгоритм : процедура или набор шагов, используемых для решения математического вычисления.
Угол : два луча имеют одну и ту же конечную точку (называемую вершиной угла).
Биссектриса угла : линия, разделяющая угол на два равных угла.
Площадь : двумерное пространство, занимаемое объектом или формой, выраженное в квадратных единицах.
Массив : набор чисел или объектов, соответствующих определенному шаблону.
Атрибут : характеристика или особенность объекта, такая как размер, форма, цвет и т. Д., Которая позволяет его группировать.
Среднее значение : Среднее значение совпадает со средним.Сложите ряд чисел и разделите сумму на общее количество значений, чтобы найти среднее.
База : нижняя часть фигуры или трехмерного объекта, на которую опирается объект.
Base 10 : Система счисления, которая присваивает значения разрядам числам.
Гистограмма : диаграмма, которая визуально представляет данные с использованием столбцов разной высоты или длины.
BEDMAS или PEMDAS Определение: Акроним, используемый для помощи людям в запоминании правильного порядка операций при решении алгебраических уравнений.BEDMAS означает «скобки, экспоненты, деление, умножение, сложение и вычитание», а PEMDAS означает «круглые скобки, экспоненты, умножение, деление, сложение и вычитание».
Колоколообразная кривая : форма колокола, созданная при построении линии с использованием точек данных для элемента, который соответствует критериям нормального распределения. Центр колоколообразной кривой содержит точки наивысшего значения.
Биномиальное : полиномиальное уравнение с двумя членами, обычно соединенными знаком плюс или минус.
Ящик и усовидная диаграмма / диаграмма : графическое представление данных, которое показывает различия в распределениях и отображает диапазоны наборов данных.
Исчисление : Раздел математики, включающий производные и интегралы, Исчисление - это исследование движения, в котором изучаются изменяющиеся значения.
Вместимость : Объем вещества, который может вместить контейнер.
Сантиметр : метрическая единица измерения длины, сокращенно см.2,5 см примерно равны дюйму.
Окружность : полное расстояние по кругу или квадрату.
Хорда : отрезок, соединяющий две точки на окружности.
Коэффициент : буква или число, представляющие числовую величину, прикрепленную к термину (обычно в начале). Например, x - это коэффициент в выражении x (a + b), а 3 - это коэффициент в члене 3 y.
Общие множители : коэффициент, общий для двух или более чисел, общие множители - это числа, которые делятся точно на два разных числа.
Дополнительные углы: Два угла, которые вместе составляют 90 °.
Составное число : положительное целое число, у которого есть хотя бы один множитель помимо собственного. Составные числа не могут быть простыми, потому что их можно точно разделить.
Конус : трехмерная форма только с одной вершиной и круглым основанием.
Коническое сечение : Сечение, образованное пересечением плоскости и конуса.
Константа : значение, которое не изменяется.
Координата : упорядоченная пара, которая дает точное местоположение или положение на координатной плоскости.
Congruent : объекты и фигуры одинакового размера и формы. Конгруэнтные формы можно превращать друг в друга с помощью переворота, поворота или поворота.
Косинус : В прямоугольном треугольнике косинус - это отношение, которое представляет длину стороны, прилегающей к острому углу, к длине гипотенузы.
Цилиндр : трехмерная форма с двумя круглыми основаниями, соединенными изогнутой трубкой.
Десятиугольник : многоугольник / фигура с десятью углами и десятью прямыми линиями.
Десятичное число : Действительное число в стандартной десятичной системе счисления.
Знаменатель : нижнее число дроби. Знаменатель - это общее количество равных частей, на которые делится числитель.
Градус : Единица измерения угла, представленная символом °.
Диагональ : отрезок линии, соединяющий две вершины многоугольника.
Диаметр : линия, которая проходит через центр круга и делит его пополам.
Разница : Разница - это ответ на задачу вычитания, в которой одно число отнимается от другого.
Цифра : Цифры - это цифры от 0 до 9 во всех числах. 176 - это трехзначное число, состоящее из цифр 1, 7 и 6.
Дивиденды : Число, разделенное на равные части (в скобках в длинном делении).
Делитель : число, которое делит другое число на равные части (вне скобки в длинном делении).
Край : линия - это место, где встречаются две грани в трехмерной структуре.
Эллипс : эллипс выглядит как слегка сплющенный круг и также известен как плоская кривая. Планетарные орбиты имеют форму эллипсов.
Конечная точка : «точка», в которой заканчивается линия или кривая.
Равносторонний : термин, используемый для описания формы, все стороны которой имеют одинаковую длину.
Уравнение : утверждение, которое показывает равенство двух выражений путем их соединения знаком равенства.
Четное число : число, которое делится или делится на 2.
Событие : этот термин часто относится к результату вероятности; он может ответить на вопрос о вероятности того, что один сценарий повторится над другим.
Оценить : это слово означает «вычислить числовое значение».
Показатель : число, обозначающее многократное умножение термина, показанное в виде надстрочного индекса над этим термином.Показатель 3 4 равен 4.
Выражения : символы, представляющие числа или операции между числами.
Face : плоские поверхности трехмерного объекта.
Фактор : число, которое точно делится на другое число. Множители 10 равны 1, 2, 5 и 10 (1 x 10, 2 x 5, 5 x 2, 10 x 1).
Факторинг : процесс разбивки чисел на все факторы.
Факториальная нотация : Факториальная нотация, часто используемая в комбинаторике, требует, чтобы вы умножали число на каждое меньшее число.В факториальной записи используется символ! Когда вы видите x !, требуется факториал x .
Дерево факторов : графическое представление, показывающее факторы определенного числа.
Последовательность Фибоначчи : Последовательность, начинающаяся с 0 и 1, при этом каждое число является суммой двух предшествующих ему чисел. «0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ...» - последовательность Фибоначчи.
Рисунок : Двумерные формы.
Finite : не бесконечно; есть конец.
Flip : отражение или зеркальное отображение двумерной формы.
Формула : Правило, которое численно описывает взаимосвязь между двумя или более переменными.
Дробь : величина, не являющаяся целым, содержащая числитель и знаменатель. Дробь, представляющая половину от 1, записывается как 1/2.
Частота : количество раз, когда событие может произойти за заданный период времени; часто используется в расчетах вероятностей.
Ферлонг : Единица измерения, представляющая длину стороны одного квадратного акра. Один стадион составляет примерно 1/8 мили, 201,17 метра или 220 ярдов.
Геометрия : Изучение линий, углов, форм и их свойств. Геометрия изучает физические формы и размеры объектов.
Графический калькулятор : Калькулятор с расширенным экраном, способный отображать и рисовать графики и другие функции.
Теория графов : Раздел математики, посвященный свойствам графов.
Наибольший общий множитель : наибольшее число, общее для каждого набора множителей, которое точно делит оба числа. Наибольший общий делитель 10 и 20 равен 10.
Шестиугольник : шестиугольник с шестью углами.
Гистограмма : график, на котором используются столбцы с равными диапазонами значений.
Гипербола : Тип конического сечения или симметричной открытой кривой. Гипербола - это совокупность всех точек на плоскости, разность расстояний которых от двух фиксированных точек на плоскости является положительной константой.
Гипотенуза : самая длинная сторона прямоугольного треугольника, всегда противоположная самому прямому углу.
Идентификатор : уравнение, которое справедливо для переменных любого значения.
Неправильная дробь : дробь, знаменатель которой больше или равен числителю, например 6/4.
Неравенство : Математическое уравнение, выражающее неравенство и содержащее знак больше (>), меньше (<) или не равно (≠).
Целые числа : все целые числа, положительные или отрицательные, включая ноль.
Иррациональное : число, которое не может быть представлено в виде десятичной дроби или дроби. Число, подобное пи, иррационально, потому что оно содержит бесконечное количество повторяющихся цифр. Многие квадратные корни также являются иррациональными числами.
Равнобедренный : многоугольник с двумя сторонами равной длины.
Километр : Единица измерения, равная 1000 метрам.
Узел : замкнутый трехмерный круг, который не может быть распутан.
Как термины : термины с одинаковой переменной и одинаковыми показателями / степенями.
Как дроби : дроби с одинаковым знаменателем.
Линия : прямой бесконечный путь, соединяющий бесконечное количество точек в обоих направлениях.
Отрезок линии : прямой путь с двумя конечными точками, началом и концом.
Линейное уравнение : уравнение, которое содержит две переменные и может быть отображено на графике в виде прямой линии.
Линия симметрии : линия, разделяющая фигуру на две равные формы.
Логика : здравое рассуждение и формальные законы рассуждения.
Логарифм : Степень, до которой необходимо возвести основание, чтобы получить заданное число. Если nx = a , логарифм a с n в качестве основания будет x .Логарифм противоположен возведению в степень.
Среднее значение : Среднее значение равно среднему. Сложите ряд чисел и разделите сумму на общее количество значений, чтобы найти среднее значение.
Медиана : Медиана - это «среднее значение» в ряду чисел, упорядоченных от наименьшего к наибольшему. Когда общее количество значений в списке нечетное, медиана является средней записью. Когда общее количество значений в списке четное, медиана равна сумме двух средних чисел, деленной на два.
Середина : точка, которая находится точно на полпути между двумя местоположениями.
Смешанные числа : Смешанные числа относятся к целым числам, объединенным с дробями или десятичными знаками. Пример 3 1 / 2 или 3.5.
Режим : Режим в списке чисел - это значения, которые встречаются наиболее часто.
Модульная арифметика : Система арифметики для целых чисел, в которой числа "оборачиваются" при достижении определенного значения модуля.
Моном : алгебраическое выражение, состоящее из одного члена.
Кратное : Кратное число является произведением этого числа и любого другого целого числа. 2, 4, 6 и 8 кратны 2.
Умножение : Умножение - это повторное сложение одного и того же числа, обозначенного символом x. 4 х 3 равно 3 + 3 + 3 + 3.
Множаемое : количество, умноженное на другое. Произведение получается путем умножения двух или более множимых.
Натуральные числа : регулярные счетные числа.
Отрицательное число : число меньше нуля, обозначенное символом -. Отрицательный 3 = -3.
Net : Двумерная форма, которую можно превратить в двухмерный объект путем склеивания / скотча и складывания.
N-й корень : -й корень -го числа - это число, которое нужно умножить на само число, чтобы получить указанное значение.Пример: корень 4-й степени из 3 равен 81, потому что 3 x 3 x 3 x 3 = 81.
Норма : среднее или среднее значение; установленный образец или форма.
Нормальное распределение : также известное как распределение Гаусса, нормальное распределение относится к распределению вероятности, которое отражается через среднее значение или центр колоколообразной кривой.
Числитель : верхнее число дроби. Числитель делится знаменателем на равные части.
Number Line : линия, точки которой соответствуют числам.
Цифра : письменный символ, обозначающий числовое значение.
Тупой угол : угол от 90 ° до 180 °.
Тупой треугольник : Треугольник, по крайней мере, с одним тупым углом.
Восьмиугольник : многоугольник с восемью сторонами.
Шансы : отношение вероятности наступления события к вероятности. Шансы подбросить монету и выпасть орлом - один к двум.
Нечетное число : целое число, не делимое на 2.
Операция : относится к сложению, вычитанию, умножению или делению.
Порядковый номер : Порядковые числа указывают относительное положение в наборе: первое, второе, третье и т. Д.
Порядок операций : Набор правил, используемых для решения математических задач в правильном порядке. Об этом часто вспоминают с помощью аббревиатур BEDMAS и PEMDAS.
Результат : Используется с вероятностью для обозначения результата события.
Параллелограмм : четырехугольник с двумя наборами противоположных сторон, параллельных друг другу.
Парабола : открытая кривая, точки которой равноудалены от фиксированной точки, называемой фокусом, и фиксированной прямой линии, называемой направляющей.
Пентагон : пятисторонний многоугольник. У правильных пятиугольников пять равных сторон и пять равных углов.
Процент : отношение или дробь со знаминателем 100.
Периметр : общее расстояние вокруг внешней части многоугольника. Это расстояние получается путем сложения единиц измерения с каждой стороны.
Перпендикуляр : две прямые или отрезки, пересекающиеся под прямым углом.
Pi : Pi используется для обозначения отношения длины окружности к ее диаметру, обозначается греческим символом π.
Плоскость : когда набор точек соединяется вместе, образуя плоскую поверхность, простирающуюся во всех направлениях, это называется плоскостью.
Многочлен : сумма двух или более одночленов.
Многоугольник : отрезки линии, соединенные вместе, чтобы образовать замкнутую фигуру.Прямоугольники, квадраты и пятиугольники - это всего лишь несколько примеров многоугольников.
Простые числа : простые числа - это целые числа больше 1, которые делятся только на себя и 1.
Вероятность : вероятность того, что событие произойдет.
Произведение : сумма, полученная путем умножения двух или более чисел.
Правильная дробь : дробь, знаменатель которой больше числителя.
Транспортир : полукруглое устройство, используемое для измерения углов.Кромка транспортира делится на градусы.
Квадрант : одна четверть ( как) плоскости в декартовой системе координат. Самолет разделен на 4 секции, каждая из которых называется квадрантом.
Квадратное уравнение : уравнение, которое может быть записано с одной стороной, равной 0. Квадратные уравнения просят вас найти квадратный многочлен, равный нулю.
Четырехугольник : четырехсторонний многоугольник.
Четверной : для умножения или умножения на 4.
Качественный : Свойства, которые следует описывать с использованием качеств, а не чисел.
Quartic : многочлен, имеющий степень 4.
Quintic : многочлен со степенью 5.
Частное : Решение проблемы разделения.
Радиус : расстояние, определяемое путем измерения отрезка прямой, идущего от центра круга до любой точки на окружности; линия, идущая от центра сферы до любой точки на внешнем крае сферы.
Соотношение : отношение между двумя величинами. Отношения могут быть выражены словами, дробями, десятичными знаками или процентами. Пример: при победе команды в 4 из 6 игр соотношение составляет 4/6, 4: 6, четыре из шести или ~ 67%.
Ray : прямая линия только с одной конечной точкой, которая продолжается бесконечно.
Диапазон : разница между максимумом и минимумом в наборе данных.
Прямоугольник : параллелограмм с четырьмя прямыми углами.
Повторяющееся десятичное число : десятичное число с бесконечно повторяющимися цифрами. Пример: 88 разделить на 33 равно 2,6666666666666 ... («2,6 повторения»).
Отражение : Зеркальное отображение формы или объекта, полученное путем отражения формы на оси.
Остаток : число, оставшееся, когда количество не может быть разделено поровну. Остаток может быть выражен как целое, дробное или десятичное число.
Прямой угол : угол, равный 90 °.
Прямой треугольник : треугольник с одним прямым углом.
Ромб : параллелограмм с четырьмя сторонами равной длины без прямых углов.
Треугольник Масштаба : Треугольник с тремя неравными сторонами.
Сектор : область между дугой и двумя радиусами окружности, иногда называемая клином.
Наклон : Наклон показывает крутизну или уклон линии и определяется путем сравнения положения двух точек на линии (обычно на графике).
Квадратный корень : Квадратное число умножается само на себя; квадратный корень из числа - это любое целое число, которое дает исходное число при умножении на само себя. Например, 12 x 12 или 12 в квадрате равно 144, поэтому квадратный корень из 144 равен 12.
Стебель и лист : графический органайзер, используемый для организации и сравнения данных. Подобно гистограмме, стержневые и листовые графы организуют интервалы или группы данных.
Вычитание : Операция нахождения разницы между двумя числами или величинами путем «удаления» одного из другого.
Дополнительные углы : два угла являются дополнительными, если их сумма равна 180 °.
Симметрия : Две половинки, идеально совпадающие и идентичные по оси.
Касательная : прямая линия, касающаяся кривой только из одной точки.
Член : Часть алгебраического уравнения; число в последовательности или серии; произведение действительных чисел и / или переменных.
Тесселяция : конгруэнтные плоские фигуры / формы, которые полностью покрывают плоскость без перекрытия.
Перевод : Перевод, также называемый скольжением, представляет собой геометрическое движение, при котором фигура или фигура перемещается из каждой своей точки на одинаковое расстояние и в одном направлении.
Transversal : линия, которая пересекает / пересекает две или более линий.
Трапеция : четырехугольник с двумя параллельными сторонами.
Древовидная диаграмма : Используется с вероятностью для отображения всех возможных результатов или комбинаций события.
Треугольник : трехсторонний многоугольник.
Трехчлен : многочлен с тремя членами.
Единица : стандартная величина, используемая при измерении. Дюймы и сантиметры - единицы длины, фунты и килограммы - единицы веса, а квадратные метры и акры - единицы площади.
Униформа : термин, означающий «все одинаково». Униформа может использоваться для описания размера, текстуры, цвета, дизайна и т. Д.
Переменная : буква, используемая для представления числового значения в уравнениях и выражениях.Пример: в выражении 3 x + y обе переменные - y и x .
Диаграмма Венна : Диаграмма Венна обычно отображается как два перекрывающихся круга и используется для сравнения двух наборов. Перекрывающийся раздел содержит информацию, которая истинна для обеих сторон или наборов, а каждая неперекрывающаяся часть представляет набор и содержит информацию, которая истинна только для их набора.
Объем : Единица измерения, описывающая, сколько места занимает вещество или вместимость контейнера, выраженная в кубических единицах.
Вершина : точка пересечения двух или более лучей, часто называемая углом. Вершина - это место, где встречаются двумерные стороны или трехмерные ребра.
Вес : Мера того, насколько что-то тяжело.
Целое число : целое число является положительным целым числом.
Ось X : горизонтальная ось в координатной плоскости.
X-Intercept : значение x в месте пересечения прямой или кривой с осью x.
X : римская цифра 10.
x : символ, используемый для представления неизвестной величины в уравнении или выражении.
Ось Y : вертикальная ось в координатной плоскости.
Y-Intercept : значение y в месте пересечения прямой или кривой с осью y.
Ярд : единица измерения, равная приблизительно 91,5 сантиметру или 3 футам.
7 Эффективное преподавание: примеры из истории, математики и естествознания | Как люди учатся: мозг, разум, опыт и школа: расширенное издание
Это означает, что новые учителя должны развивать способность «понимать педагогически рефлексивным способом; они должны не только знать свой собственный подход к дисциплине, но и знать «концептуальные барьеры», которые могут мешать другим »(McDonald and Naso, 1986: 8).Эти концептуальные барьеры различаются от дисциплины к дисциплине.
Акцент на взаимодействии между дисциплинарными знаниями и педагогическими знаниями прямо противоречит распространенным заблуждениям о том, что учителя должны знать, чтобы создавать эффективную среду обучения для своих учеников. Заблуждения состоят в том, что обучение состоит только из набора общих методов, что хороший учитель может преподавать любой предмет или что достаточно только предметных знаний.
Некоторые учителя - могут преподавать в различных дисциплинах.Однако их способность делать это требует большего, чем набор общих педагогических навыков. Рассмотрим случай Барб Джонсон, которая 12 лет проработала учителем шестого класса в средней школе Монро. По общепринятым меркам Монро - хорошая школа. Результаты стандартизированных тестов примерно средние, размер класса небольшой, здания содержатся в хорошем состоянии, администратор является сильным руководителем преподавательского состава, а текучесть преподавателей и персонала незначительна. Однако каждый год родители отправляют своих пятиклассников из местных начальных школ к жокею Монро, чтобы их дети отправляли в классы Барб Джонсон.Что происходит в ее классе, что дает ему репутацию лучшего из лучших?
В течение первой недели в школе Барб Джонсон задает своим шестиклассникам два вопроса: «Какие вопросы у вас есть о себе?» и "Какие у вас вопросы о мире?" Учащиеся начинают перечислять свои вопросы: «Могут ли они рассказывать о глупых мелочах?» - спрашивает один студент. «Если это ваши вопросы, на которые вы действительно хотите получить ответы, они ни глупые, ни маленькие», - отвечает учитель.После того, как ученики составят список своих индивидуальных вопросов, Барб объединяет учеников в небольшие группы, где они делятся списками и ищут общие вопросы. После долгого обсуждения каждая группа придумывает приоритетный список вопросов, упорядочивая вопросы о себе и о мире.
Снова вместе на групповом занятии Барб Джонсон выясняет приоритеты групп и работает над достижением консенсуса по объединенным спискам вопросов класса. Эти вопросы становятся основой учебной программы в классе Барб.Один вопрос: «Доживу ли я до 100 лет?» породил образовательные исследования по генетике, семейному и устному анамнезу, актуарной науке, статистике и вероятности, сердечным заболеваниям, раку и гипертонии. У студентов была возможность получить информацию от членов семьи, друзей, экспертов в различных областях, онлайн-компьютерных услуг и книг, а также от учителя. Она описывает то, что им пришлось сделать, как стать частью «обучающегося сообщества». По словам Барб Джонсон: «Мы решаем, какие интеллектуальные проблемы являются наиболее важными, и разрабатываем способы их исследования».
Помогите вашему ребенку развить ранние математические навыки • НОЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях.Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, стр. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь с ребенком - например, подсчета шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, на которых строится учебная программа по математике в первом классе, включают: (Bowman et al., 2001, p. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознающие цифры
Определение большего и меньшего количества
Понимание однозначной корреспонденции (т.е., совпадающие наборы или зная, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» - точно так же, как дом построен на прочном фундаменте. В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Смысл числа
Это умение точно считать - первый нападающий.Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, - это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Воплощение математических идей в реальность с помощью слов, изображений, символов и предметов (например, блоков). Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. "Что тут смешного?" - недоумевала его тетя. «Я подошел, - сказал Азиз, - а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты.Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром. «Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно.Вы можете помочь им, показав им значения таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой - мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Узоры
Узоры - это вещи, числа, формы, изображения, которые логически повторяются.Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Умение обдумать проблему, признать, что к ответу существует более одного пути.Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы - пластиковый барабан с тремя отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки - это лишь одна часть более широкой сети навыков, которые дети развивают в ранние годы, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она посмотрела на своего отца и показала ему блок, который ей не удалось достичь, чтобы оставаться на вершине, по сути говоря ему своим жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него возьмет квадратный, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет папе реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание. Большинство этих советов предназначены для детей старшего возраста - в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Поднимитесь.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме - посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или назначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И распределить по категориям (посмотреть, есть ли можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (находится ли парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Поднимитесь.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Спойте рифмующиеся, повторяющиеся или содержащие числа песни.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить социальные навыки, такие как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными кубиками, пластиковыми блокировками, пустыми коробками, пакетами из-под молока и т. Д.Сложение этих игрушек друг на друга и управление ими помогает детям узнать о формах и отношениях между ними (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Туннельное время.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры - круг, квадрат, треугольник - из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, различные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно следите за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-то желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры на его одежде - например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или, ваша рубашка покрыта пони - большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой ребенок сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько именно.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучаем дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C. & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр. 47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999, июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.Проверенные основные элементы по математике
ПРИМЕЧАНИЕ. В приведенных ниже документах подробно описаны проверяемые основные элементы. Полный список всех основных элементов, которые в настоящее время являются частью модели обучающей карты Dynamic Learning Maps ® , см. В разделе «Основные элементы для математики».
ПРИМЕЧАНИЕ: Существенные элементы, отмеченные серым флажком (), не оцениваются в состояниях на конец года.
Оценка 3: оценка основных элементов
3.NBT.2 Продемонстрировать понимание разряда десятков.
3.NBT.3 Считайте по десяткам, используя такие модели, как объекты, блоки базовой десятки или деньги.
3.НФ.1-3 Отличить дробную часть от целого.
3.OA.4 Решает проблемы сложения и вычитания, когда результат неизвестен, ограничивается операндами и результатами в пределах 20.
3.G.2 Признайте, что фигуры можно разделить на равные области.
3.MD.1 Назовите время с точностью до часа на цифровых часах.
3.MD.4 Измерьте длину объектов с помощью стандартных инструментов, таких как линейки, мерки и измерители.
3.MD.3 Используйте данные изображения или гистограммы, чтобы ответить на вопросы о данных.
3.OA.1-2 Используйте повторное сложение, чтобы найти общее количество объектов и определить сумму.
3.OA.8 Решайте одношаговые задачи реального мира, используя сложение или вычитание с точностью до 20.
3.OA.9 Определение арифметических шаблонов.
Все учебные пособия по математике для 3-го класса в одном pdf
4 класс: оценка основных элементов
4.NF.1-2 Определите модели половины (1/2) и одной четверти (1/4).
4.NF.3 Различия между целым и половиной.
4.NBT.2 Сравните целые числа с 10, используя символы (<,>, =).
4.NBT.3 Округлите любое целое число от 0 до 30 до ближайшей десятки.
4.NBT.4 Сложить и вычесть двузначные целые числа.
4.G.1 Распознавать параллельные и пересекающиеся прямые.
4.MD.5 Распознавать углы в геометрических формах.
4.MD.6 Определяет углы как большие, так и меньшие.
4.MD.3 Определите площадь квадрата или прямоугольника путем подсчета единиц измерения (единичных квадратов).
4.MD.2.a Считайте время с помощью цифровых часов. Назовите время с точностью до ближайшего часа с помощью аналоговых часов.
4.MD.2.b Измерьте массу или объем с помощью стандартных инструментов.
4.MD.2.d Определите монеты (пенни, никель, десять центов, четверть) и их стоимость.
4.MD.4.b Интерпретация данных с изображения или гистограммы.
4.OA.1-2 Продемонстрируйте связь между повторным сложением и умножением.
4.OA.3 Решайте одношаговые задачи реального мира, используя сложение или вычитание в пределах 100.
4.OA.5 Используйте повторяющиеся шаблоны для прогнозов.
Все учебные задания по математике для 4-го класса в одном pdf
Оценка 5: оценка основных элементов
5.NF.1 Определите модели половинок (1/2, 2/2) и четвертей (1/4, 2/4, 3/4, 4/4).
5.NF.2 Определить модели третей (1/3, 2/3, 3/3) и десятых (1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 10/10).
5.NBT.1 Сравните числа до 99, используя модели базовой десятки.
5.NBT.3 Сравните целые числа до 100, используя символы (<,>, =).
5.NBT.4 Округлить двузначные целые числа до ближайшего 10 от 0 до 90.
5.NBT.5 Умножение целых чисел до 5x5.
5.NBT.6-7 Проиллюстрируйте концепцию разделения с использованием справедливых и равных долей.
5.G.1-4 Отсортируйте двумерные фигуры и определите общие атрибуты (углы, количество сторон, углы, цвет).
5.MD.3 Определение общих трехмерных форм.
5.MD.4-5 Определите объем прямоугольной призмы путем подсчета единиц измерения (единичных кубов).
5.MD.1.a Считайте время с помощью аналоговых или цифровых часов с точностью до половины или четверти часа.
5.MD.1.b Используйте стандартные единицы измерения веса и длины предметов.
5.MD.1.c Указывает относительную стоимость коллекций монет.
5.MD.2 Представление и интерпретация данных на картинке, линейном графике или гистограмме.
5.OA.3 Определение и расширение числовых шаблонов.
Все учебные задания по математике для 5-го класса в одном PDF-файле
6 класс: оценка основных элементов
6.RP.1 Продемонстрируйте простое соотношение отношения.
6.NS.1 Сравните отношения между двумя дробями.
6.NS.5-8 Поймите, что положительные и отрицательные числа используются вместе для описания величин, имеющих противоположные направления или значения (например, температура выше / ниже нуля).
6.NS.2 При разделении применяется концепция справедливой доли и равных долей.
6.NS.3 Решите задачи двухфакторного умножения с произведениями до 50, используя конкретные объекты и / или калькулятор.
6.G.1 Решайте реальные и математические задачи о площади, используя единичные квадраты.
6.G.2. Решать реальные и математические задачи об объеме с помощью единичных кубов.
6.SP.5 Обобщите распределения данных, представленные в виде графиков или таблиц.
6.EE.1-2 Определите предложения с эквивалентными числами.
6.EE.3 Примените свойства сложения для идентификации эквивалентных числовых выражений.
6.EE.5-7 Сопоставьте уравнение с реальной проблемой, в которой переменные используются для представления чисел.
Все учебные задания по математике для 6-го класса в одном pdf
7 класс: оценка основных элементов
7.NS.2.c-d Выразите дробь со знаминателем 10 как десятичную дробь.
7.RP.1-3 Используйте соотношение для моделирования или описания отношений.
7.NS.3 Сравните количества, представленные десятичными дробями в реальных примерах, с десятыми долями.
7.NS.1 Сложите дроби с одинаковыми знаменателями (половины, трети, четвертые и десятые) с суммами меньше или равными единице.
7.NS.2.a Решите задачи умножения с произведениями на 100.
7.NS.2.b Решите задачи деления с делителем до пяти, а также с делителем 10 без остатка.
7.G.1 Совместите две одинаковые геометрические фигуры пропорционального размера и в одной ориентации.
7.G.2 Распознавать геометрические фигуры в заданных условиях.
7.G.5 Распознавать острые, тупые и прямые углы.
7.G.4 Определите периметр прямоугольника, сложив размеры сторон.
7.SP.3 Сравните два набора данных на одном экране данных, например графическое изображение, линейный график или гистограмму.
7.SP.5-7 Опишите вероятность того, что события произойдут, как возможные или невозможные.
7.EE.1 Используйте свойства операций как стратегии, чтобы продемонстрировать эквивалентность выражений.
7.EE.2 Идентифицировать арифметическую последовательность целых чисел с общей разницей целых чисел.
Все учебные задания по математике для 7-го класса в одном PDF-файле
8-й класс: оценка основных элементов
8.NS.2.a Выразите дробь со знаминателем 100 как десятичную дробь.
8.NS.2.b Сравните количества, представленные в виде десятичных знаков в реальных примерах, с сотыми.
8.EE.1 Определите значение показателя степени (ограничивается показателем степени 2 и 3).
8.NS.1 Вычтите дроби с одинаковыми знаменателями (половины, трети, четвертые и десятые) с минусом меньше или равным единице.
8.G.1 Распознавать перемещения, вращения и отражения форм.
8.G.2 Определите конгруэнтные формы.
8.G.4 Определить похожие формы с вращением и без него.
8.G.5 Сравните любой угол с прямым углом и опишите угол как больший, меньший или равный прямому углу.
8.G.9 Используйте формулы для периметра, площади и объема для решения реальных и математических задач (ограниченных периметром и площадью прямоугольников и объемом прямоугольных призм).
8.SP.4 Постройте график или таблицу из заданных категориальных данных и сравните данные, отнесенные к категориям на графике или таблице.
8.EE.7 Решите простые алгебраические уравнения с одной переменной, используя сложение и вычитание.
8.EE.2 Определите геометрическую последовательность целых чисел с общим отношением целых чисел.
8.F.1-3 Для таблицы функций, содержащей не менее 2 полных упорядоченных пар, определите недостающее число, которое завершает другую упорядоченную пару (ограничено линейными функциями).
8.F.4 Определите значения или правило функции, используя график или таблицу.
Все EE по математике для 8-го класса в одном pdf
Средняя школа: оценка основных элементов
N-CN.2.a Используйте свойства коммутативности, ассоциативности и распределения для сложения, вычитания и умножения целых чисел.
N-CN.2.b Решайте реальные проблемы, связанные с сложением и вычитанием десятичных знаков, используя при необходимости модели.
N-CN.2.c Решайте реальные проблемы, связанные с умножением десятичных и целых чисел, используя при необходимости модели.
N-RN.1 Определяет значение величины, возведенной в квадрат или куб.
S-CP.1-5 Определяет, когда события являются независимыми или зависимыми.
S-IC.1-2 Определите вероятность наступления события, когда вероятность наступления его исходов одинакова.
G-CO.1 Знать атрибуты перпендикулярных прямых, параллельных прямых и отрезков; углы и круги.
G-CO.4-5 Учитывая геометрическую фигуру и вращение, отражение или перемещение этой фигуры, определите компоненты двух совпадающих фигур.
G-CO.6-8 Обозначить соответствующие совпадающие и похожие части форм.
G-MG.1-3 Используйте свойства геометрических фигур для описания реальных объектов.
G-GPE.7 Найдите периметр и площадь квадратов и прямоугольников для решения реальных проблем.
N-Q.1-3 Выразите величины с соответствующей точностью измерения.
S-ID.1-2 По заданным данным постройте простой график (таблица, линия, круговая диаграмма, столбец или изображение) и интерпретируйте данные.
S-ID.3 Интерпретируйте общие тенденции на графике или диаграмме.
S-ID.4 Вычислить среднее значение заданного набора данных (ограничить количество точек данных менее чем пятью).
A-CED.1 Создайте уравнение, включающее одну операцию с одной переменной, и используйте его для решения реальной проблемы.
A-CED.2-4 Решите одношаговые неравенства.
A-SSE.1 Определите алгебраическое выражение, включающее одну арифметическую операцию, для представления реальной проблемы.
A-SSE.3 Решите простые алгебраические уравнения с одной переменной, используя умножение и деление.
A-REI.10-12 Интерпретировать значение точки на графике линии. Например, на графике покупок пиццы проследите график до точки и укажите количество купленных пицц и общую стоимость пиццы.
A-SSE.4 Определите следующий член в геометрической последовательности с учетом общего отношения.
F-BF.1 Выберите соответствующее графическое представление (первый квадрант) для ситуации, требующей постоянной скорости изменения.


 1 класс. — М: Астрель, 2012.
1 класс. — М: Астрель, 2012. Позже ставки можно увеличить до 90 — 70. Или даже до 98% — 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %!
Позже ставки можно увеличить до 90 — 70. Или даже до 98% — 95% для совсем уж жутко умных детей:). Вносите только цифры, без знака %! 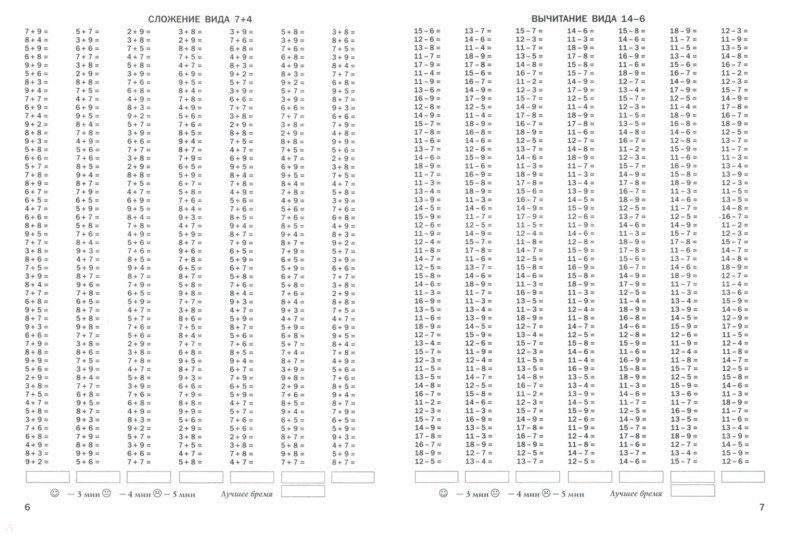
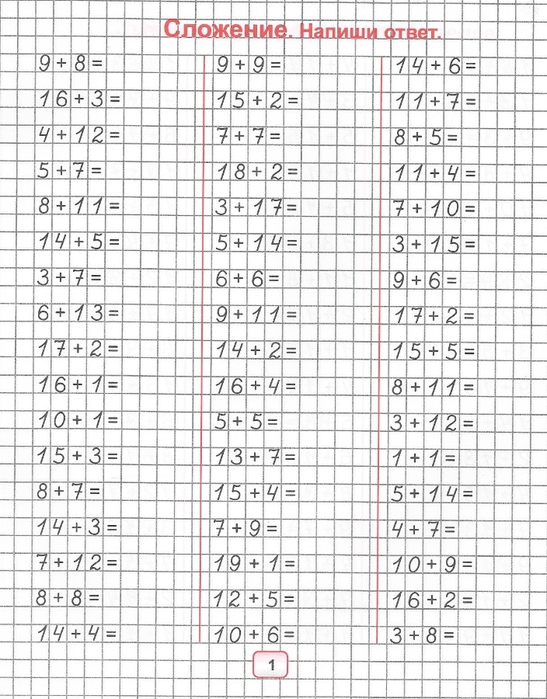 А урок – путешествие. И отправимся мы туда с одним из героев сказок.
А урок – путешествие. И отправимся мы туда с одним из героев сказок. Учитель напоминает учащимся, что в течение урока к этим задачам еще вернутся).
Учитель напоминает учащимся, что в течение урока к этим задачам еще вернутся).
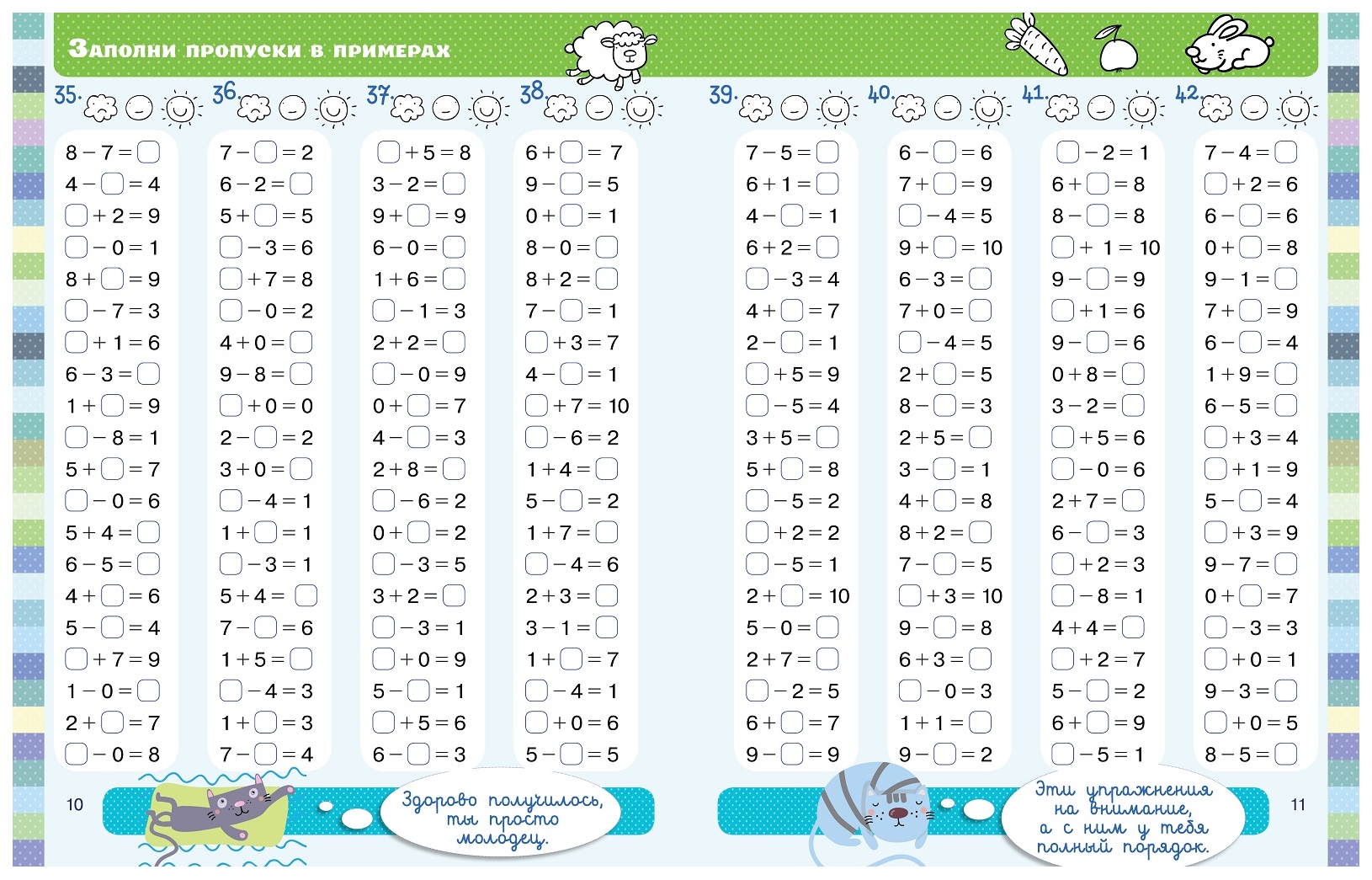
 Оцените себя.
Оцените себя. Изобрели игру — в Китае. Если хотите узнать побольше о танграме, можете принести материалы на следующий урок. Какую еще задачу выполнили? Значит, все задачи выполнены. Молодцы!
Изобрели игру — в Китае. Если хотите узнать побольше о танграме, можете принести материалы на следующий урок. Какую еще задачу выполнили? Значит, все задачи выполнены. Молодцы!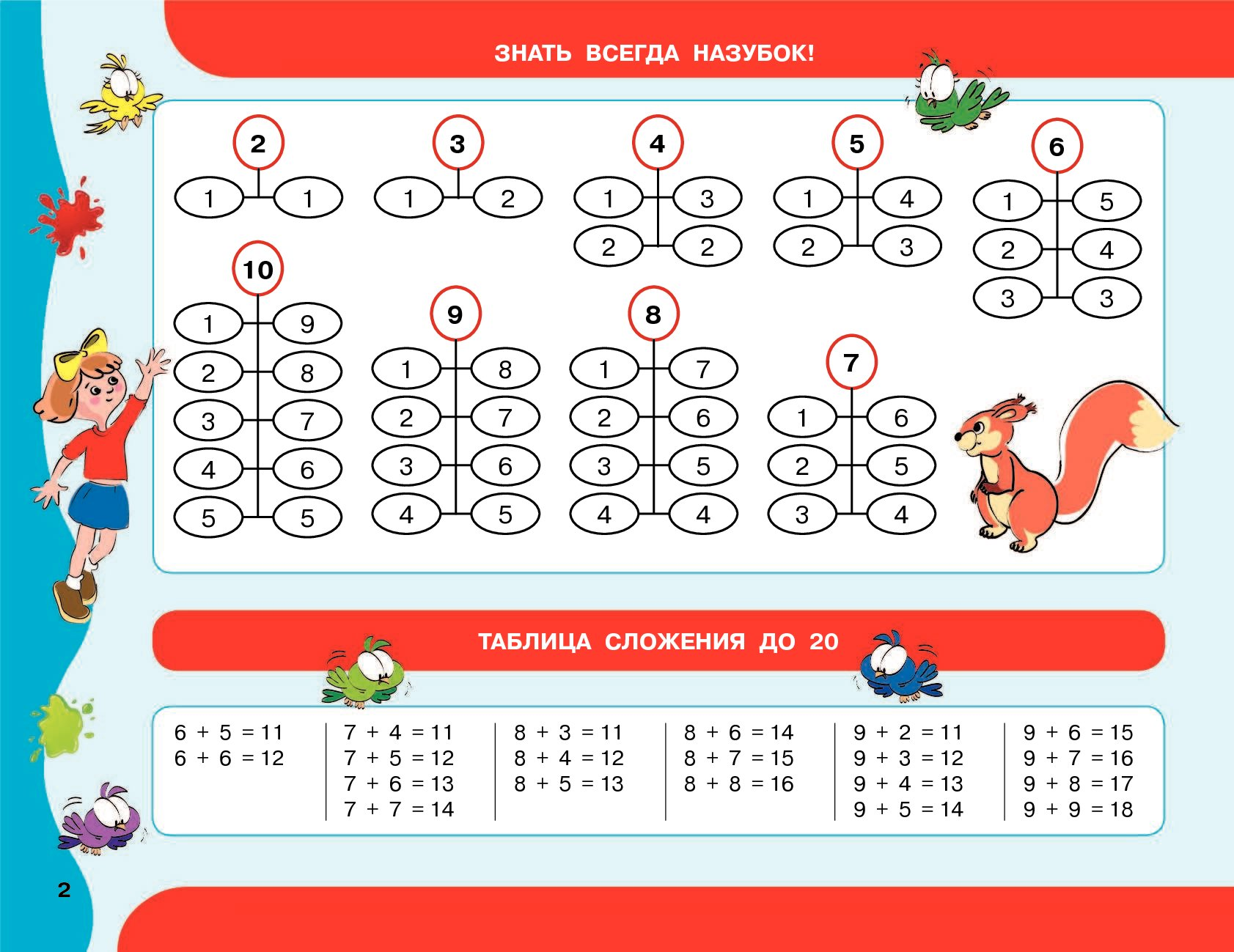 Он дал хороший совет и давайте поблагодарим его за совет угостим яблоками. Кому понравился урок, берите красные яблоки, если нет – то зеленые.
Он дал хороший совет и давайте поблагодарим его за совет угостим яблоками. Кому понравился урок, берите красные яблоки, если нет – то зеленые.

 Введите следующие две строки, как показано:
Введите следующие две строки, как показано: