Примеры по математике для 4 класса на деление: 4 класс, деление, задачи на деление многозначных чисел столбиком, свойство

admin

Образец ВПР по математике в 4 классе

Образец проверочной работы для четвероклассников на 2021 год.

ВПР по математике пройдёт с 15 марта по 21 мая. Точную дату устанавливает образовательная организация самостоятельно.

Время на выполнение — 45 минут.
В работе 12 заданий.
Ответы идут после заданий.

Скачать демоверсию (образец): math5-vpr2021.pdf
Описание работы: math5-vpr2021-o.pdf












Типы заданий, сценарии выполнения заданий

В заданиях 1, 2, 7 проверяется умение выполнять арифметические действия с числами и числовыми выражениями. В частности, задание 1 проверяет умение выполнять сложение, вычитание, умножение и деление однозначных, двузначных и трехзначных чисел в случаях, сводимых к действиям в пределах 100 (в том числе с нулем и числом 1). Задание 2 проверяет умение вычислять значение числового выражения, соблюдая при этом порядок действий.

Заданием 7 контролируется умение выполнять письменно действия с многозначными числами (сложение, вычитание, умножение и деление на однозначное, двузначное числа в пределах 10 000).

Выполнение заданий 3 и 8 предполагает использование начальных математических знаний для описания и объяснения окружающих предметов, процессов, явлений, для оценки количественных и пространственных отношений предметов, процессов, явлений. Так, задания 3 и 8 поверяют умение решать арифметическим способом (в одно-два действия) учебные задачи и задачи, связанные с повседневной жизнью.

Задание 4 выявляет умение читать, записывать и сравнивать величины (время), используя основные единицы измерения величин и соотношения между ними.

Умение решать текстовые задачи в три-четыре действия проверяется заданием 8. При этом в задании 8 необходимо выполнить действия, связанные с использованием основных единиц измерения величин (длина, вес).

Умение исследовать, распознавать и изображать геометрические фигуры проверяется заданием 5. Пункт 1 задания предполагает вычисление периметра прямоугольника и квадрата, площади прямоугольника и квадрата. Пункт 2 задания связан с построением геометрических фигур с заданными измерениями (отрезок, квадрат, прямоугольник) с помощью линейки, угольника.

В задании 6 проверяется умение работать с таблицами, схемами, графиками, диаграммами, анализировать и интерпретировать данные. Задание предполагает чтение и анализ несложных готовых таблиц.

Овладение основами логического и алгоритмического мышления контролируется заданиями 9 и 12. Задание 9 связано с интерпретацией информации (объяснять, сравнивать и обобщать данные, делать выводы и прогнозы). Задание 12 требует умения решать текстовые задачи в три-четыре действия.

Задание 10 проверяет умение извлекать и интерпретировать информацию, представленную в виде текста, строить связи между объектами.

Овладение основами пространственного воображения выявляется заданием 11. Оно предполагает описание взаимного расположения предметов в пространстве и на плоскости.

Успешное выполнение обучающимися заданий 10–12 в совокупности с высокими результатами по остальным заданиям говорит о целесообразности построения для них индивидуальных образовательных траекторий в целях развития их математических способностей.

Система оценивания выполнения отдельных заданий и проверочной работы в целом

Каждое верно выполненное задание 1, 2, 4, 5 (пункт 1), 5 (пункт 2), 6 (пункт 1), 6 (пункт 2), 7, 9 (пункт 1), 9 (пункт 2) оценивается 1 баллом. Задание считается выполненным верно, если ученик дал верный ответ: записал правильное число, правильную величину, изобразил правильный рисунок.

Выполнение заданий 3, 8, 10–12 оценивается от 0 до 2 баллов.

Перевод баллов в оценку

«2»: 0-5
«3»: 6-9
«4»: 10-14
«5»: 15-20

ГДЗ по математике 4 класс учебник Моро, Бантова 2 часть

  • Тип: ГДЗ, Решебник.
  • Автор: Моро М. И., Волкова С. И., Бантова М. А.
  • Год: 2020.
  • Серия: Школа России (ФГОС).
  • Издательство: Просвещение.

❤️️Ответ к странице 30. Математика 4 класс учебник 2 часть. Авторы: М.И. Моро, М.А. Бантова.

Решебник — страница 30Готовое домашнее задание

Номер 109.

Объясни по записи, как выполнили деление 3570 : 90. Назови частное и остаток.

Ответ:

3570 : 90 = 39 (ост. 60)

Объяснение: Первое неполное делимое – 357 десятков. В записи частного будет 2 цифры. Разделю 357 на 90. Для этого разделю 35 на 9, получу 3 – столько десятков будет в частном. Умножу 90 на 3, получу 270 – столько десятков разделили. Вычту 270 из 357, получу 87 – столько десятков осталось разделить. Сравню остаток с делителем: десятков осталось меньше, чем 90.
Второе неполное делимое – 870 единиц. Разделю 870 на 90. Для этого разделю 87 на 9, получу 9 – столько единиц будет в частном. Умножу 90 на 9, получу 810. Вычту 810 из 870, получу 60 – столько единиц осталось разделить. Сравню остаток с делителем: единиц осталось меньше, чем 90. Читаю ответ: частное равно 39, остаток 60.
Краткий ответ: Деление выполнено так: попробуем по 3. 3 умножить на 90 будет 270. 357 минус 270 будет 87 сносим нуль. Попробуем по 9. 9 умножить на 90 будет 810. 870 минус 810 будет 60, и это остаток, а 39 – неполное частное.

Номер 110.

Ответ:


Номер 111.

Выполни деление с остатком.

Ответ:

Номер 112.

На завод отправлено 3600 т угля в вагонах, по 60 т в каждом, и столько же угля в вагонах, по 90 т в каждом. Каких вагонов потребовалось больше и на сколько больше?

Ответ:

1) 3600 : 60 = 60 (в. ) – угля, было по 60 т. 2) 3600 : 90 = 40 (в.) – угля, было по 90 т. 3) 60 − 40 = 20 (в.) Ответ: на 20 штук потребовалось больше вагонов вместимостью 60 тонн.

Номер 113.

За 8 мин самолёт, двигаясь с одинаковой скоростью, пролетел 96 км. Какое расстояние он пролетит за 40 мин, если его скорость увеличится на 2 км/мин?

Ответ:

1) 96 : 8 = 12 (км/мин) – была скорость самолета. 2) 12 + 2 = 14 (км/мин) – увеличенная скорость самолета. 3) 14 ∙ 40 = 560 (км) Ответ: 560 км пролетит самолёт за 40 мин.

Задание внизу страницы

Выполни деление с остатком и сделай проверку.

Ответ:

Задание на полях страницы

Начерти узор

Ответ:

Рейтинг

Выберите другую страницу

1 часть

Учебник Моро3456789
10		11121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192
93		949596979899100101102103104105106107108109110111

2 часть

45678910111213141516171819202122
23		24252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127

Руководство для учителей начальной школы

Деление в начальной школе составляет последнюю часть «Четырех операций» — четырех основных математических понятий, которые должны знать все учащиеся. Этот блог поможет вам убедиться, что все ваши ученики могут подойти к разделению с уверенностью, необходимой им для достижения успеха.

Рабочие листы с длинными делениями — 3–5 классы

Загрузите этот бесплатный комплект рабочих листов с делениями, которые идеально подходят для обучения математике в классах 3, 4 и 5.

Разделение — это навык, который развивается каждый год в начальной школе. К концу 3-го класса учащиеся, работающие на уровне класса, смогут «знать по памяти все произведения двух однозначных чисел».

Учителям 4-го класса всегда полезно убедиться, что ученики очень хорошо это знают. Под этим я подразумеваю не просто то, что они могут, как попугаи, воспроизводить перед вами факты умножения и их обратные, но то, что они действительно понимают, как представлять эти факты как с помощью конкретных представлений, словесных объяснений, так и с помощью других изобразительных методов.

Учащиеся, которые не могут этого сделать, но которые могут устно рассказать вам о делении, имеют очень поверхностное понимание деления, и для того, чтобы они могли перейти к более сложным действиям по решению проблем, углубить свое концептуальное понимание деления обязательно в 4 классе.

Единые базовые государственные стандарты помещают раздел в «Числа и операции» по основанию 10 для классов 3–5 и помещают его в раздел «Система счисления» для 6-го класса. Части, взятые из CCSS, относятся только к тем, в которых конкретно упоминается разделение. Другие элементы этих разделов можно найти в блоге об умножении или сложении и вычитании, где это уместно.

Ознакомьтесь с нашим руководством по методам деления и нашей коллекцией рабочих листов для начальной школы.

Что такое деление?

Деление — это одна из четырех операций — четырех основных математических понятий, которые должны знать учащиеся — наряду с сложением, вычитанием и умножением.

Там, где умножение объединяет одно число несколько раз, деление работает наоборот: выясняется, сколько раз одно число содержится в другом. Например, деление 10 на 2 — это вопрос, сколько раз 2 содержится в числе 10.

При делении первое число (сумма, которую делят) называется дивидендом ; второе число (на что делится делимое) называется делителем ; ответ называется частное . В приведенном выше примере делимое равно 10, делитель равен 2, а частное равно 5.

Деление и умножение обратны друг другу, как показано на этом слайде
из онлайн-вмешательства Third Space Learning по математике.


Учебный отдел – совместное использование, группировка и масштабирование

Деление обратное умножению. Как и в блоге умножения, обучение делению содержит три основные структуры, которые в сочетании с фактами деления и концептуальным пониманием дадут учащимся наилучшие возможности для успешного решения задач, связанных с делением.

Три структуры: совместное использование, группировка и масштабирование. Хотя у нас недостаточно времени, чтобы изучить их подробно, далее будет лишь краткое введение в них.

Совместное использование и группировка

Совместное использование и группировка обратны умножению как многократному сложению. Совместное использование — это структурное понятие, которое вводится в младших классах начальной школы, где, как следует из названия, сумма распределяется между равными группами.

Например, 12 яблок поделили между собой 3 ученика. Сколько яблок получил каждый ученик?

Здесь мы знаем всю сумму или дивиденд (12 яблок) и, что особенно важно, мы знаем, на какую сумму мы собираемся разделить (3 – делитель).

В зависимости от того, на каком этапе своего математического путешествия ученики находятся, они могут несколько раз вычитать некоторое число (1, 2, 3 или 4) из суммы в три стопки, которые представляют трех учеников.

Как видно из вышеизложенного, вся сумма была поделена на три равные группы.

Группировка похожа на совместное использование, но то, что мы знаем, немного отличается от совместного использования. В структуре обмена мы знаем количество групп, в которых будет происходить обмен. В структуре группировки мы знаем количество в каждой группе, но не количество фактических групп, которые существуют.

Например, 12 яблок разделены на группы по 4 человека. Сколько будет групп? Хотя этот вопрос очень похож на вопрос выше, теперь он принимает структуру группировки, поскольку мы знаем, сколько войдет в каждую группу, но больше не знаем, сколько групп теперь будет.

Поскольку мы знаем, что в каждой группе по 4 яблока, мы можем сгруппировать 4 яблока, пока не охватим все 12, чтобы увидеть, что есть 3 группы.

Масштабирование

Окончательная структура деления масштабируется. В то время как при умножении мы увеличивали значение, структура деления уменьшалась. Например, у Шеннен 6 ручек, а у Джен в 3 раза меньше. Сколько ручек у Джен?

Здесь мы видим, что для определения общего количества ручек, которые есть у Джен, нам нужно было взять количество ручек, которое было у Шеннен, и уменьшить его в 3 раза, чтобы у Джен оказалось 2 ручки.

Исходя из опыта, это самая трудная для понимания и понимания учащимися структура деления, и ее необходимо пересмотреть в сочетании с масштабированием как умножением, поскольку это важный навык при преобразовании единиц измерения и валюты из большей суммы в меньшую. , например километры в мили.


Раздел 3-й класс

В Общегосударственных стандартах по математике раздел преподается в области «Операции и алгебраическое мышление». Стандарты, описанные в разделе «Операции и алгебраическое мышление», следующие:

  • интерпретируют целочисленные частные целых чисел, например, интерпретируют 56 ÷ 8 как количество объектов в каждой доле, когда 56 объектов поровну разделены на 8 долей, или как количество долей при разделении 56 объектов на равные доли по 8 объектов в каждой.
  • Используйте умножение и деление в пределах 100 для решения текстовых задач в ситуациях, связанных с равными группами, массивами и измеряемыми величинами, например, используя рисунки и уравнения с символом неизвестного числа для представления задачи.
  • Определите неизвестное целое число в умножении или делении уравнения, связывающего три целых числа.
  • Применение свойств операций как стратегий умножения и деления.
  • Понимайте деление как задачу с неизвестным фактором.
  • Свободно умножайте и делите в пределах 100, используя такие стратегии, как взаимосвязь между умножением и делением или свойства операций.
  • Знать наизусть все произведения двух однозначных чисел.
  • Решите двухэтапные текстовые задачи, используя четыре операции.
Разделение: идеи для урока 3-й класс

Это не описание урока, а руководство о том, как можно преподавать деление с некоторым концептуальным пониманием на данном этапе. Предпосылкой для этого было бы изучение связанных фактов умножения и таблиц умножения, прежде чем преподавать какое-либо связанное деление.

Размышляя о структуре, лучше всего на этом этапе обучения учащихся придерживаться группировки и совместного использования. В следующих примерах мы рассмотрим развитие у учащихся понимания деления на 4. Он будет следовать подходу «Конкретно-Репрезентативный-Абстрактный».

Часто понимание числа учащимися может ограничить их прогресс в делении. Особенно, когда дело доходит до группирования и обмена, когда они постоянно отнимают только одно от целого.

С самого начала обучения преподаватели должны опираться на то, что учащиеся уже знают о четных числах и других фактах о числах, чтобы научить учащихся считать любыми числами, которые могут быть уместны.

Счетчики можно использовать для демонстрации связанных фактов деления, так как учащиеся использовали их при построении своего концептуального понимания умножения. Следует задавать такие вопросы, как «Сколько групп по 4 человека?» и «Сколько человек в каждой группе?», и ответы должны относиться к тому, как это показывает разделение.

Учитель: Сколько жетонов?

Ребенок: Четыре.

Учитель: Хорошо. Это группа из четырех человек. Сколько групп по четыре человека есть?

Ребенок: Один.

Учитель: Отлично. У нас есть четыре счетчика в одной группе. Мы сгруппировали четыре счетчика в одну группу. Что мы наделали?

Ребенок: Сгруппированы четыре счетчика в одну группу.

Учитель: Великолепно. Когда мы объединяем четыре счетчика в одну группу, мы делаем математический расчет деления четырех на один. Какой расчет мы сделали?

Ребенок: Четыре разделить на один.

Учитель: И когда мы решим четыре, разделив их на один, ответ будет четыре, потому что мы создали одну группу, в которой четыре элемента. Четыре разделить на один будет четыре. Сколько будет четыре разделить на один?

Ребенок: Четыре разделить на один равно четырем.

Учитель: Отлично.

Вы можете видеть, как это будет повторяться для следующего:

Учитель: Сколько жетонов есть?

Ребенок: восемь.

Учитель: Хорошо, это группа из четырех человек. Сколько групп по четыре человека есть?

Ребенок: Два.

Учитель: Отлично. У нас есть четыре счетчика в одной группе. Мы сгруппировали четыре счетчика в две группы. Что мы наделали?

Ребенок: Сгруппированы четыре счетчика в две группы.

Учитель: Отлично. Когда мы объединяем четыре счетчика в две группы, мы делаем математический расчет деления восьми на два. Какой расчет мы сделали?

Ребенок: восемь разделить на два.

Учитель: И когда мы решим число восемь разделить на два, ответ будет четыре, потому что мы создали две группы, в которых по четыре элемента. Восемь разделить на два равно четырем. Сколько восемь разделить на два?

Ребенок: Восемь разделить на два равно четырем.

Учитель: Отлично.

Когда ученики освоятся с этим, мы можем перейти к другим моделям, таким как удилища Кюизенера.

Здесь вся сумма представлена ​​верхним поездом и фиолетовым стержнем (который в данном случае представляет 4, и если вы читали другие блоги из этой серии, надеюсь, вы знаете, насколько я защитник их использовать в классе, чтобы к тому времени учащиеся знали о его ценности) используется, чтобы показать, сколько раз группы из 4 человек могут войти в общую сумму.

Затем учащиеся могут перейти к составлению сценариев на основе расчетов деления, прочитанных учителем. Например, есть 24 кнопки и их нужно сгруппировать в 4. Сколько групп? Учащиеся могут нарисовать эти кнопки и сгруппировать их по 4 и т. д.

Как только учащиеся привыкнут визуализировать эти групповые или общие сценарии разделения в различных контекстах, они могут перейти к более абстрактным представлениям с использованием математических символов.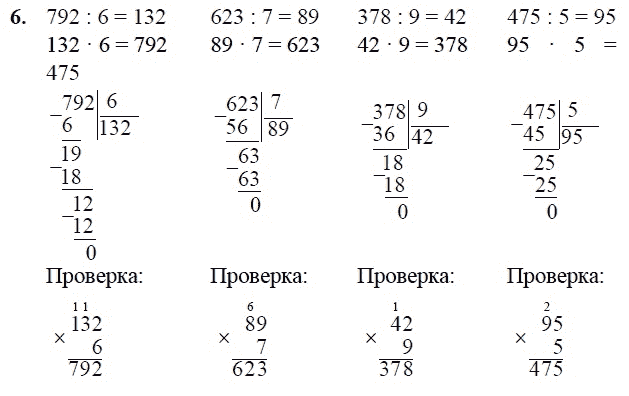

Раздел: задачи со словами 3-й класс

задачи со словами в 3-м классе обычно используют структуру группировки или совместного использования.

Есть 40 пирожных и 10 учеников. Сколько тортов получит каждый ученик?

Поскольку мы знаем, сколько существует групп (10), нам нужно рассчитать количество на группу, так что это структура совместного использования. Без прочного знания таблицы умножения на 4 учащиеся будут бороться с процессом деления, поскольку им нужно будет использовать эти знания, чтобы получить ответ 4.

Раздел: Рассуждения и решение проблем 3-й класс

Для рассуждений и решения проблем я считаю хорошим занятием сопоставить словесную задачу с расчетом. Например:

Сопоставьте словесные задачи, которые решаются путем деления 20 на 4.

  • Есть 20 карандашей, и их нужно разложить по 5 штук в пачках. Сколько в каждой пачке?
  • Было 20 карандашей, затем ученик принес еще 4. Сколько сейчас карандашей?
  • Есть 20 карандашей, и их нужно разложить по 4 штуки. Сколько в каждой упаковке?
  • Было 20 карандашей, а потом 4 пропали. Сколько сейчас карандашей?

Попросить учащихся записать свои объяснения по каждому вопросу полезно, так как это позволяет им увидеть, как они думают. Вопросы были тщательно отобраны, чтобы числа в каждом вопросе соответствовали числам в вопросе, чтобы учащиеся полагались на свои математические навыки, чтобы вывести правильный ответ.


Дивизион 4-й класс

В Общегосударственных стандартах по математике деление преподается в областях «Операции и алгебраическое мышление» и «Числа и операции с основанием 10». Стандарты, описанные в разделе «Операции и алгебраическое мышление», следующие:

  • Умножение или деление для решения текстовых задач, включающих мультипликативное сравнение, например, с использованием рисунков и уравнений с символом неизвестного числа для представления задачи, отличающей мультипликативное сравнение от аддитивного. сравнение.
  • Решите многошаговые текстовые задачи, поставленные с целыми числами и имеющие целочисленные ответы, используя четыре операции, включая задачи, в которых необходимо интерпретировать остатки. Представьте эти проблемы, используя уравнения с буквой, обозначающей неизвестную величину. Оцените обоснованность ответов, используя вычисления в уме и стратегии оценки, включая округление.

Числа и операции с основанием 10:

  • Найдите целые числа и остатки с делимыми до четырех цифр и однозначными делителями, используя стратегии, основанные на разрядном значении, свойствах операций и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
Деление: идеи для урока 4-й класс

В этом уроке я рассмотрю, как можно начать преподавать деление, используя модель площади с манипуляциями рядом с ней, чтобы делить все более крупные числа.

Скажем, мы собираемся учить студентов делению на вопрос 168, разделенному на 8.

Обычно мы пишем это в так называемой «собачьей будке». Но что интересно, в разных местах мира это пишут по-разному.

Причина этого довольно проста. То, что на самом деле представляет собой «собачья будка», — это сокращенный способ представления прямоугольника.

Когда мы учим формальному делению, мы фактически говорим, что вам нужно представить прямоугольник, ширина которого равна 8. Общая площадь прямоугольника равна 168, и мы пытаемся найти недостающую длину в верхней части. Так как же нам показать это с помощью манипулятивных средств? Блоки с основанием 10 являются полезным инструментом для этого.

Мы знаем, что общее количество равно 168. Поэтому нам нужно собрать 168 блоков с основанием 10, используя наименьшее возможное количество блоков. Это показано ниже.

Возвращаясь к вопросу, мы знаем, что ширина равна 8. Это означает, что теперь нам нужно манипулировать блоками, чтобы получить ширину, равную 8. Обратите внимание, что прямоугольник должен быть сплошным и не должен иметь недостающих частей. Например, ниже не будет разрешено, несмотря на то, что по ширине идет 8 единиц.

Вместо этого учащиеся могут разбить блок из 100 на блоки из 10–10. Обратите внимание, что теперь вы можете разместить 8 в каждом столбце, и это сплошной объект.

Последняя часть, которую должны сделать учащиеся, — это использовать оставшиеся блоки для создания сплошного прямоугольника, сохраняя при этом ширину 8. Это может занять некоторое время, но с практикой учащиеся делают это быстрее. Через некоторое время учащиеся произведут это:

Мы видим, что все 168 блоков уже израсходованы, а ширина по-прежнему равна 8. Чтобы найти ответ, учащиеся должны посчитать длину, которая в данном случае равна 21. Ниже я наложил оба метода, чтобы вы можно увидеть, как они дополняют друг друга.

Это полезная стратегия для обучения учащихся 4-го класса, так как она оказывает огромное влияние на другие области учебной программы, которые уже освещены учащимся.

Хотя они могут еще этого не распознать, обучая делению таким образом, они уже знакомятся с периметром и площадью — подумайте, сколько времени на обучение можно сэкономить, установив эту связь. Мало того, в средней школе этот подход переносится на алгебраическое мышление.

Раздел: задачи со словами 4-й класс

Ожидается, что учащиеся будут использовать свои знания о разрядных значениях для решения задач на деление, поэтому подходящей задачей со словами будет:

В саду растет 4800 яблок за сезон. Перед поступлением на рынок их расфасовывают по 4 штуки. Сколько упаковок?

Здесь учащиеся должны использовать тот факт, что 4 x 12 = 48, а поскольку 4800 в сто раз больше, чем 48, 12 также необходимо умножить на 100, чтобы получить 1200

Раздел: Рассуждение и решение задач 4 класс

Всегда ли, иногда или никогда верно, что сумма трех четных чисел делится на 4?

Этот вопрос дает учащимся широкие возможности поэкспериментировать с заданными параметрами. Учащиеся, которым требуется дополнительная поддержка, могут смотреть на однозначные четные числа, а учащиеся могут выбирать любые удобные для себя варианты.

Для таких открытых вопросов, как этот, полезно указать минимальное количество попыток, которые должны сделать учащиеся, иначе они часто будут выбирать самый минимум.

Быстрый «трюк», чтобы узнать, делится ли число на 4, состоит в том, чтобы посмотреть на две последние цифры числа и посмотреть, делятся ли они на 4.

Например, если ребенок нашел сумму 34, 36 и 38 и получил 108, как учитель я знаю, что это число делится на 4, так как последние две цифры (08) составляют 8 и делятся на 4. Если ребенок выбрал 34, 36 и 48, чтобы получить 118, я знаю что это число не делится на 4, поскольку 18 — последние две цифры числа 118 — не делятся на 4.


Раздел 5-й класс

В Общегосударственных стандартах по математике деление преподается в предметах «Числа и операции с основанием 10» и «Числа и операции — дроби». Стандарты, описываемые в разделе «Числа и операции с основанием 10», следующие:

  • Найдите целые числа в частном с до четырехзначных делимых и двузначных делителей, используя стратегии, основанные на разрядном значении, свойствах операций, и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
  •  Складывать, вычитать, умножать и делить десятичные дроби до сотых, используя конкретные модели или чертежи и стратегии, основанные на разрядном значении, свойствах операций и/или отношениях между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию.

Числа и операции – дроби: 

  • Интерпретировать дробь как деление числителя на знаменатель (a/b = a ÷ b). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.
  • Примените и расширите предыдущее понимание деления, чтобы разделить дробные единицы на целые числа и целые числа на дробные единицы.
    • а. Интерпретируйте деление единичной дроби на ненулевое целое число и вычислите такие частные. Например, создайте контекст истории для (1/3) ÷ 4 и используйте визуальную дробную модель, чтобы показать частное. Используйте связь между умножением и делением, чтобы объяснить, что (1/3) ÷ 4 = 1/12, потому что (1/12) × 4 = 1/3.
    • б. Интерпретируйте деление целого числа на единичную дробь и вычислите такие частные. Например, создайте контекст истории для 4 ÷ (1/5) и используйте визуальную дробную модель, чтобы показать частное. Используйте связь между умножением и делением, чтобы объяснить, что 4 ÷ (1/5) = 20, потому что 20 × (1/5) = 4.
    • с. Решайте реальные задачи, связанные с делением единичных дробей на ненулевые целые числа и делением целых чисел на единичные дроби, например, с помощью визуальных моделей дробей и уравнений для представления задачи. Например, сколько шоколада получит каждый, если 3 человека разделят 1/2 фунта шоколада поровну? Сколько порций по 1/3 стакана содержится в 2 стаканах изюма?
Дивизион: идеи для урока 5-й класс

Дивизион в 5-м классе развивается за счет использования остатков в ответах. В этом упражнении я рассмотрю другое использование манипуляций, которые учителя могут использовать для обучения делению на 4 цифры на 1 цифру.

Если бы вопрос заключался в том, чтобы разделить 5642 на 4, мы могли бы представить это с помощью таблицы стоимостей мест и счетчиков стоимостей мест, как показано ниже.

Следующим шагом будет группировка счетчиков по 4, так как это наш делитель. Однако, как видно, мы быстро приходим к проблеме в столбце 1000, поскольку мы можем сгруппировать 4 счетчика, но тогда мы не можем сгруппировать оставшийся счетчик в группу из 4.

Чтобы решить эту проблему, 1000 счетчик, который не был сгруппирован, можно обменять на десять счетчиков по 100. Затем их можно сгруппировать в группы по 4, и это может произойти без каких-либо оставшихся счетчиков сотен. Оттуда это простой случай перехода к 10-м и, наконец, к 1-м.

Поскольку имеется девять жетонов с единицами, мы можем сгруппировать 8 из них в 2 группы по 4 и утверждать, что остался один лишний*. Чтобы найти ответ, все, что требуется, — это подсчитать количество групп, образованных в каждом разряде, и использовать их для записи цифр, чтобы получить окончательный ответ. В этом случае ответом будет 1412, остаток 1. 

* Когда вы смотрите на десятичные дроби, вы можете обменять оставшийся счетчик 1 на десять счетчиков 0,1 и продолжить деление, как описано выше.

Учащимся полезно ознакомиться с этой моделью, поскольку она может помочь демистифицировать десятичные дроби, с которыми учащиеся могут столкнуться с трудностями.

Это помогает им понять, что это продолжение процесса, с которым они уже знакомы, а не что-то новое.

Раздел: задачи со словами 5-й класс

При разделении в 5-м классе учащиеся столкнутся со сценариями, в которых им нужно будет округлить свой ответ, чтобы ответ имел смысл в контексте. Уместным вопросом, демонстрирующим это, может быть что-то вроде следующего:

В школе планируется дискотека, на которой каждому ученику будет предложено по 250 мл сока. Они могут купить 2-литровые бутылки сока. Ожидается прибытие 33 студентов, поэтому они знают, что им выдадут 8,25 литров сока. Сколько бутылок сока им нужно будет купить?

Обычный ответ: учащиеся скажут 4 с четвертью. Однако, поскольку вы не можете купить четверть бутылки, в этом случае правильным ответом будет 5 бутылок сока, необходимых для того, чтобы все учащиеся могли пить.

Раздел: Рассуждение и решение задач 5-й класс

Заставить учащихся создавать свои собственные задачи, используя диапазон предоставленного контекста, может быть действительно сложной задачей, которая заставляет учащихся математически думать о контексте и делении.

Затем учащиеся могут поменяться этими вопросами, которые они создали, с партнером, а затем приступить к их решению и свериться с создателем исходного вопроса, если у них есть правильный ответ.


отделение 6 класс

В Общегосударственных стандартах по математике деление преподается в предметной области «Система счисления». Стандарты, описанные в The Number System, следующие:

  •  Свободно делите многозначные числа, используя стандартный алгоритм.
  • Свободно складывать, вычитать, умножать и делить многозначные десятичные числа, используя стандартный алгоритм для каждой операции.
  • Интерпретация и вычисление частных дробей, а также решение текстовых задач, связанных с делением дробей на дроби, например, с использованием визуальных моделей дробей и уравнений для представления задачи
Раздел: Идеи для уроков 6-й класс

Софи Бартлетт (@_MissieBee) создала отличный блог по обучению делению на столбики, подробно описывая, как она будет преподавать деление на столбики в 6-м классе. Поскольку деление в столбик — единственное новое учение о делении для 6-го класса, это идеальный способ ввести процедуру деления в столбик.

Подробнее: Примеры деления на длинное деление
Разделение: словесные задачи 6-й класс

Типичная словесная задача на деление, с которой может столкнуться ученик 6-го класса:

Школа собрала 3146 долларов на распродаже выпечки. В мероприятии приняли участие 104 родителя. Если все родители потратили одинаковую сумму денег, сколько потратил каждый родитель?

Здесь учащиеся должны использовать метод деления в длину, чтобы решить этот вопрос и получить ответ $30,25.

Раздел: Рассуждения и решение проблем 6-й класс

Что-то такое процедурное, как деление в длинную, хорошая логическая деятельность состоит в том, чтобы побудить учащихся находить ошибки.

Как видно из приведенного ниже вопроса, учащийся проделал всю тяжелую работу, но допустил небрежную ошибку при подсчете групп из 59означает, что ребенок считал, что 59 х 7 равно 472, а не 59 х 8.

Правильный ответ был бы 38.

Деление является ключевой темой математики не только в начальной школе, но и в математике в целом. Надеюсь, этот пост дал вам несколько хороших идей, которые помогут вашим ученикам подойти к этому с уверенностью.

См. также:

  • Раздел Вопросы, которые проверят ваших учеников начальной школы
  • длинных вопроса, которые проверят всех учащихся от шестого до старшего класса
  • Объяснение разметки для учителей, родителей и детей
  • Раздел «Как преподавать: учебный лагерь по математике»

Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.

Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.

Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.

Содержание этой статьи было изначально написано ведущим учителем начальных классов Нилом Алмондом, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Кристи Кулешей.

Рабочие листы отдела

Реклама

Ищете лучшие рабочие листы деления в Интернете? Не смотрите дальше! Мы предоставим вам наши бесплатные распечатанные рабочие листы по разделам. Наши рабочие листы на деление варьируются от основ зрительных задач до более сложных задач на длинное деление и задач, связанных с умножением. Благодаря нашим полезным ресурсам ваши ученики поймут ключевые понятия, такие как умножение и остаток, и получат удовольствие от изучения математики. Взгляните на нашу подборку бесплатных рабочих листов для разделения сегодня — это обязательно поможет вашим ученикам практиковаться и учиться с уверенностью.

Просмотр листов по типу проблемы

делениечисловойгоризонтальныйсверлавизуальныйслововертикальныйумножениечисловые линиикороткое предложениевычитаниемножественный выбор

Представление сетки (новое)

×

Подготовка к разделу Ссылка

Деление относительно умножения

3oa6

Каждый рабочий лист содержит 20 задач на деление и умножение.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Таблицы деления/умножения

3oa6

Каждый рабочий лист содержит 24 задачи на заполнение таблицы, чтобы уравнение было правильным.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Разделение с числовыми линиями

3oa1

Каждый рабочий лист содержит 11 задач, использующих числовую прямую для решения уравнения.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Подготовка к длинному дивизиону

4nbt6

Каждый рабочий лист содержит 20 задач, чтобы помочь учащимся разобраться с основной концепцией деления (сколько раз X переходит в Y).

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Проверка ответов отдела

4nbt6

Каждый рабочий лист содержит 12 задач на умножение для проверки ответа на деление.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все

Понимание ответов отдела

4oa3

Каждый рабочий лист содержит 12 задач, в которых учащиеся должны интерпретировать значение ответа по отношению к словесной задаче.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 100005

Grab ‘Em Em

Версия

Версия 100005

Grab’ EM EM

Версия

Версия 1000050005

Создать новый лист

Поиск остатков дивизии

Каждый рабочий лист содержит 20 задач на нахождение остатков от деления на 2, 5 и 10.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘Em All

Создайте новый лист.

Деление как многократное вычитание (числовая строка)

Каждый рабочий лист содержит 10 задач с использованием числовой прямой для решения задач на деление с использованием многократного вычитания.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Деление как повторное вычитание с остатком (числовая строка)

Каждый рабочий лист содержит 10 задач на числовую прямую для решения задач на деление с остатком на многократное вычитание.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Реклама

Визуальный отдел Ссылка

Нет остатка

3oa2

Каждый рабочий лист содержит 11 задач на определение количества групп, которые вы можете создать.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘Em All

Создайте новый лист

.

С остатком

4nbt6

Каждый рабочий лист содержит 20 задач на определение количества групп, которые вы можете составить, а также оставшейся суммы.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Реклама

Традиционный дивизион Ссылка

Дивизионные тренировки

3oa7

Каждый рабочий лист содержит 100 задач на деление от 10 ÷ 10 до 1 ÷ 1.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Горизонтальное деление

4nbt6

Каждый рабочий лист содержит 12 задач на решение традиционной задачи на деление.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Grab ‘Em All

Создайте новый лист

3 ÷ 1 (с остатком)

4nbt6

Каждый рабочий лист содержит 12 задач на деление трехзначного делимого и однозначного делителя.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Деление с частичными коэффициентами

4nbt6

Каждый рабочий лист содержит 12 задач на деление трехзначного делимого и однозначного делителя с использованием неполных частных для решения.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Деление целых чисел на ноль

4nbt6

Каждый рабочий лист содержит 12 задач на деление с нулем в частном.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘Em All

Создайте новый лист.

Вертикальное деление с вспомогательной сеткой

4nbt6

Каждый рабочий лист содержит 9 задач на деление с помощью вспомогательной сетки.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все

Создать новый лист

4 ? 2 (с остатком)

5nbt6

Каждый рабочий лист содержит 12 задач на деление четырехзначного делимого и двузначного делителя.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Деление кратных десяти

5nbt2

Каждый рабочий лист содержит 20 задач на деление кратных десяти.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM All

Создайте новый лист

.

Смешанный дивизион

6ns2

Каждый рабочий лист содержит 12 задач на деление.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 100005

Grab ‘Em Em

Версия

Версия 100005

Grab’ EM EM

Версия

Версия 1000050005

Создать новый лист

Деление (международное) с вспомогательной сеткой

Каждый рабочий лист содержит 9 задач на решение задачи на деление.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Деление (международное) с вспомогательной сеткой

На каждом листе 9задачи на решение задачи на деление.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все

Создать новый лист

Деление кратных десяти

5нбт2

Каждый рабочий лист содержит 20 задач на деление кратных десяти.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Настроить

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Реклама

Текстовые задачи Ссылка

1-значный коэффициент (без остатка)

3oa8

Каждый рабочий лист содержит 15 задач на деление фактов на однозначное частное от 1×1 до 9×9.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

1-значный коэффициент (с остатком)

3oa8

Каждый рабочий лист содержит 15 задач на деление фактов на однозначное частное от 1×1 до 9×9.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все

3 ÷ 1 (без остатка)

4nbt6

Каждый рабочий лист содержит 12 задач с 3-значным делимым, 1-значным делителем и без остатка.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

3 ÷ 1 (с остатком)

4nbt6

Каждый рабочий лист содержит 12 задач с 3-значным делимым, 1-значным делителем и остатком.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘Em All

Создайте новый лист.

3 ÷ 2 (с остатком)

5nbt6

Каждый рабочий лист содержит 12 задач с 3-значным делимым, 2-значным делителем и остатком.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

Реклама

Раздел — Оценка Ссылка

3 цифры ÷ 2 цифры

4nbt6

Каждый рабочий лист содержит 18 задач с округлением для поиска ближайшего ответа.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

Слово 3 ÷ 2

4nbt6

Каждый рабочий лист содержит 10 задач на округление для определения частного.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Создать

Создать 25 Листов Все 900 Реклама

Дивизионные тренировки Ссылка

2 с

Каждый рабочий лист содержит 100 задач на деление на 2.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 100005

Grab ‘Em Em

Версия

Версия 100005

Grab’ EM EM

Версия

Версия 1000050005

Создать новый лист

3 с

Каждый рабочий лист содержит 100 задач на деление на 3.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Grab ‘Em All

Создайте новый лист

4 с

Каждый рабочий лист содержит 100 задач на деление на 4.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

5 с

Каждый рабочий лист содержит 100 задач на деление на 5.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все

Создать новый лист

6 с

Каждый рабочий лист содержит 100 задач на деление на 6.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

7 с

Каждый рабочий лист содержит 100 задач на деление на 7.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

5 9 9

Версия 10

Захватить все

Создать новый лист

8 с

Каждый рабочий лист содержит 100 задач на деление на 8.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘Em All

Создайте новый лист.

9 с

Каждый рабочий лист содержит 100 задач на деление на 9.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист>

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия

Версия 10

Grab ‘EM EM

Версия

Версия 100005

Создать новый лист

10 с

Каждый рабочий лист содержит 100 задач на деление на 10.

Один атта раз

Флэш-карты

Дистанционное обучение

Создать новый лист

Выберите рабочий лист >

Версия 1

Версия 2

Версия 3

Версия 4

Версия 5

Версия 6

Версия 7

Версия 8

Версия 9

Версия 10

Захватить все 00 Новый лист

5

Смешанный

Каждый рабочий лист содержит 100 задач в диапазоне от 1÷1 до 10÷10.

admin

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *